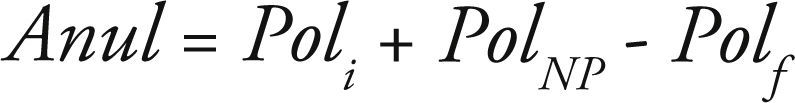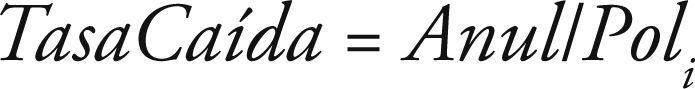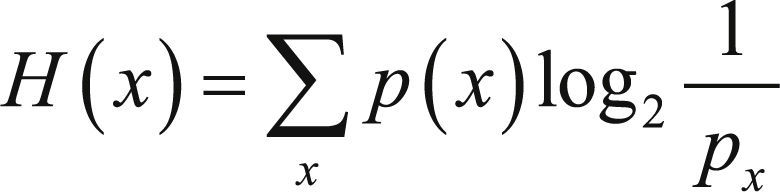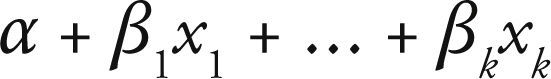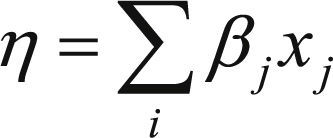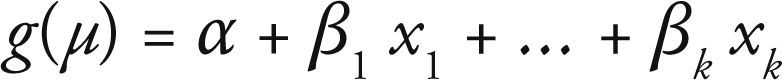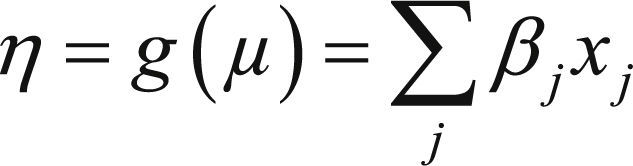Análisis del Riesgo de Caída de Cartera en Seguros: Metodologías de “Inteligencia Artificial” vs “Modelos Lineales Generalizados”

Resumen

En este artículo se muestra la posibilidad de utilizar dos enfoques metodológicos distintos para la evaluación de riesgos: uno no paramétrico para lo cual se recurrirá a las técnicas de Inteligencia Artificial y, en contraste, la aplicación de los Modelos Lineales Generalizados provenientes de la estadística paramétrica. La aplicación práctica de ambas metodologías, se llevará a cabo con la finalidad de analizar el Riesgo de Caída de Cartera; haciendo referencia a uno de los tantos riesgos medibles que el sector asegurador ha de tener en cuenta de acuerdo a Solvencia II. Los resultados obtenidos y sus conclusiones muestran el nuevo enfoque y cómo dichas técnicas pueden ser utilizadas por las aseguradoras como una mejora en la Gestión de Riesgos; animando al sector a indagar en nuevas metodologías y técnicas, para cubrir con las necesidades y requerimientos exigidos por Solvencia II.

Abstract

This paper describes the use of two different methodological approaches for risk assessment: nonparametric coming from Artificial Intelligence techniques and, in contrast, Generalized Linear Models from statistical parametric. Both practical applications will analyze Lapse Risk, one of the measurable risks that insurance sector must take into account according to Solvency II. Results and conclusions show a new approach and how these techniques can be used by insurance companies as an improvement in Risk Management; encouraging the insurance sector to investigate new methodologies and techniques to deal requirements demanded by Solvency II regulation.

1

Introducción

Después de varios años y a pesar de sus prórrogas, Solvencia II (Comisión de las Comunidades Europeas, Directiva 2009/138/CE) es una realidad que ha puesto de manifiesto la adopción de medidas concretas para adaptarse al nuevo sistema; ya no es una práctica recomendable sino una materia exigible a las entidades. De esta forma, Solvencia II, sin lugar a dudas, es un desafío para la industria aseguradora.

Este proyecto es una verdadera transformación del modelo de gestión de riesgos y de la toma de decisiones en las entidades aseguradoras; por lo que el proceso de adaptación a esta nueva norma y filosofía exigirá un gran esfuerzo por parte de las entidades.

El objetivo de Solvencia II (González de Frutos, 2013) es el desarrollo y establecimiento de un nuevo sistema que permita determinar los recursos propios mínimos a requerir a cada aseguradora, en función de los riesgos asumidos y la gestión que se realice de ellos. Así mismo, engloba un conjunto de iniciativas para la revisión de la normativa existente, la valoración y supervisión de la situación financiera global de las entidades aseguradoras y modos de actuación interna de las mismas.

Existen varios motivos y necesidades que promueven el inicio de este proyecto, como son: el mantenimiento de la confianza en el sistema financiero-asegurador, el fortalecimiento de la gestión de riesgos, la armonización de las prácticas de valoración contables y regulatorias y el común acuerdo sobre las medidas de intervención. Todos estos conceptos e inquietudes han provocado que paulatinamente, el sector asegurador se cuestione sobre la innovación de los modelos y planteamientos en vigor; en otras palabras, se busca introducir al sector asegurador dentro de una nueva cultura del riesgo y su gestión. Ante la necesidad de evolución del sector asegurador, surge el interés en temas como la gestión de riesgos y solvencia con la que es capaz de enfrentarse una entidad aseguradora (Romera, 2011).

Uno de los temas más controvertidos bajo esta regulación es cómo conseguir una adecuada evaluación de los riesgos asumidos por las entidades. Esto se traduce en lograr identificar las causas que puedan suponer una pérdida en sus recursos; así como en innovar en el campo técnico para lograr una correcta cuantificación de los riesgos posibles en los que podrían estar expuestas las entidades. Es así como las compañías aseguradoras están siendo sometidas a desarrollar nuevas técnicas para la cuantificación y control de los riesgos a los que se encuentran expuestas. Todo ello con el fin de lograr implementar una gestión integral del riesgo que contemple un adecuado nivel de solvencia (eiopa, 2015).

Bajo otra perspectiva, en un competitivo mercado asegurador donde cada día toman relevancia temas como la guerra de precios, accesibilidad a múltiples cotizaciones, así como la constante innovación en el desarrollo de productos, surge la necesidad de retener y fidelizar a los clientes. De esta forma, ya no sólo se presta atención a niveles de primas altos sino a la capacidad de garantizar la rentabilidad de la entidad, lo cual no es una tarea fácil ante una situación de crisis financiera como la que se ha vivido recientemente. De aquí la importancia del riesgo de caída de cartera que exige la nueva regulación de Solvencia II, entendido como el riesgo que supone la pérdida de clientes ante la cancelación de cierto volumen de pólizas a su vencimiento por parte de los asegurados dentro de una entidad.

El objetivo de este trabajo es mostrar la posibilidad de utilizar dos enfoques metodológicos distintos para la evaluación de riesgos: uno no paramétrico para lo cual se recurrirá a las técnicas de Inteligencia Artificial (un árbol de decisión, el algoritmos C4.5, y, un algoritmo de inducción de reglas, la metodología Rough Set) y, en contraste, la aplicación de los Modelos Lineales Generalizados provenientes de la estadística paramétrica.

La aplicación práctica de ambas metodologías, se llevará a cabo con la finalidad de analizar el Riesgo de Caída de Cartera, el cual hace referencia a uno de los riesgos medibles que el sector habrá de tener en cuenta de acuerdo a Solvencia II. La relevancia de ambas aplicaciones empíricas, será poder tener una aproximación a la probabilidad de cancelación del cliente mediante dichos patrones que se traduciría en una mejora en la gestión del Riesgo de Caída de Cartera; contribuyendo al equilibrio y estabilidad de los niveles de solvencia de las entidades.

Para la realización de la aplicación empírica se utilizará una cartera española de pólizas del ramo de vida representativa de todas las regiones españolas. Los mercados avanzados, al que pertenece la muestra española de datos que utilizaremos en nuestro estudio, se han mantenido en un estancamiento desde la crisis económica del 2008, a pesar del crecimiento que experimentaron las primas en el año 2014 que se situó en el 2,9%, sin embargo, este porcentaje está todavía por debajo al 3,4% de la tasa de crecimiento a largo plazo de la situación anterior a la crisis (Swiss Reinsurance Company, Informe Sigma 4/2015, pp.7). Por tanto, en el contexto actual del mercado asegurador donde existe una disminución del volumen de negocio y tendencia creciente a la pérdida de la cartera de clientes; cobra importancia el tema de retención de clientes y con ello cobra importancia poder identificar el tipo de clientes propensos a causar baja (Guillen et al., 2008). De esta forma, se podrán anticipar pérdidas mediante la implementación de estrategias para la retención y atracción de nuevos clientes, es decir, lograr orientar la toma de decisiones por medio de la localización de algún patrón de comportamiento del tipo de cliente “cancelador” que permita establecer políticas comerciales atractivas para la captación y fidelización de su cartera. De aquí la relevancia de la presente aplicación empírica, para poder tener una aproximación a la probabilidad de cancelación del cliente mediante dichos patrones que se traduciría en una mejora en la gestión del riesgo de caída de cartera que a su vez, contribuiría al equilibrio y estabilidad de los niveles de solvencia que las compañías aseguradoras requieren.

El artículo se estructura como sigue: en la sección 2 se presenta Solvencia II; la sección 3 explica el problema objeto de nuestro estudio, es decir la caída de cartera; en la cuarta sección se explican las tres metodologías utilizadas, es decir, árbol de decisión, rough set y mínimos cuadrados generalizados; la quinta sección contiene el análisis empírico y finalmente la última sección incluye las conclusiones.

En el contexto actual del mercado asegurador donde existe una disminución del volumen de negocio y tendencia creciente a la pérdida de la cartera de clientes; cobra importancia el tema de retención de clientes y con ello cobra importancia poder identificar el tipo de clientes propensos a causar baja.

2

El proyecto solvencia ii: nuestro antecedente

Desde hace tiempo en algunos países surgió la inquietud de referenciar a la solidez financiera con los riesgos asumidos de manera implícita a la propia actividad de la entidad aseguradora.

En la década de los 50, los pioneros en la aplicación de esquemas basados en el riesgo fueron los finlandeses, quienes empezaron a utilizar un modelo de capital considerando el carácter estocástico de la actividad aseguradora mediante las “Reservas Especiales de Nivelación” (Pentikäinen y Rantala, 1982). Posteriormente, le secundó Canadá que a mediados de los 80 comienza a aplicar modelos que intentan englobar la totalidad de los riesgos mediante la generación de escenarios para el diseño de sus planes de negocio a través de las llamadas “Exigencias de Capital Mínimo para la Continuación” (Hardy y Panjer, 1998).

Bajo una línea similar, en los años 90, ee uu mediante la NAIC desarrolla el modelo RBC (Risk-based Capital) basado en un conjunto de normas haciendo una primera definición y basando los requerimientos de capital en una serie de riesgos independientes entre sí (Jacques y Nigro, 1997).

Se llega al año 2004 con el modelo suizo conocido como “Test Suizo de Solvencia” buscando un enfoque basado en el análisis de los riesgos reales que soporta una entidad aseguradora de una forma integrada (Keller et al., 2005). Sin dejar de mencionar al modelo británico el cual funciona desde el año 2005 que también ha buscado relacionar los requerimientos de capital con los riesgos a los que están expuestos las entidades (Eling et al., 2007).

Los antecedentes más directos de Solvencia II se sitúan en su predecesor, Solvencia I. Estaba basado en un conjunto de ratios que relacionan el capital exigido con el volumen del negocio obtenido a partir del cálculo del Margen de Solvencia Obligatorio y el Fondo Mínimo de Garantía. Sólo se dirigía a los riesgos técnicos que surgen del pasivo de las entidades, sin tener en cuenta los riesgos asociados al activo como son las inversiones o la calidad crediticia de las operaciones. Sin dejar de mencionar que esta valoración y exigencias de capital no se hacen de acuerdo al mercado y sin considerar diversificación o transferencia de riesgos que implicase reducción de dichos requerimientos. Todas estas limitaciones dieron lugar a la necesidad de la creación de un nuevo modelo, materializado en la implementación de Solvencia II¹ (Ariza, 2013).

Se observa, por tanto, que el tema de la solvencia dentro del sector asegurador no es un tópico nuevo, así como su regulación, ya que existen varias directivas y normas que se perfeccionan y complementan entre sí. De ahí la necesidad de lograr establecer un conjunto de normas comunes que engloben la actual coyuntura, con el objetivo de adecuar la regulación a la situación actual, sin buscar cubrir una carencia sino completar las directrices ya existentes. Es así como el sector asegurador se encamina hacia a la propuesta por parte de la Comisión Europea de una nueva Directiva en materia de seguros y reaseguros, tanto del ramo de vida como de ramos distintos del de vida, bajo la denominación de “Solvencia II” (Solá, 2013).

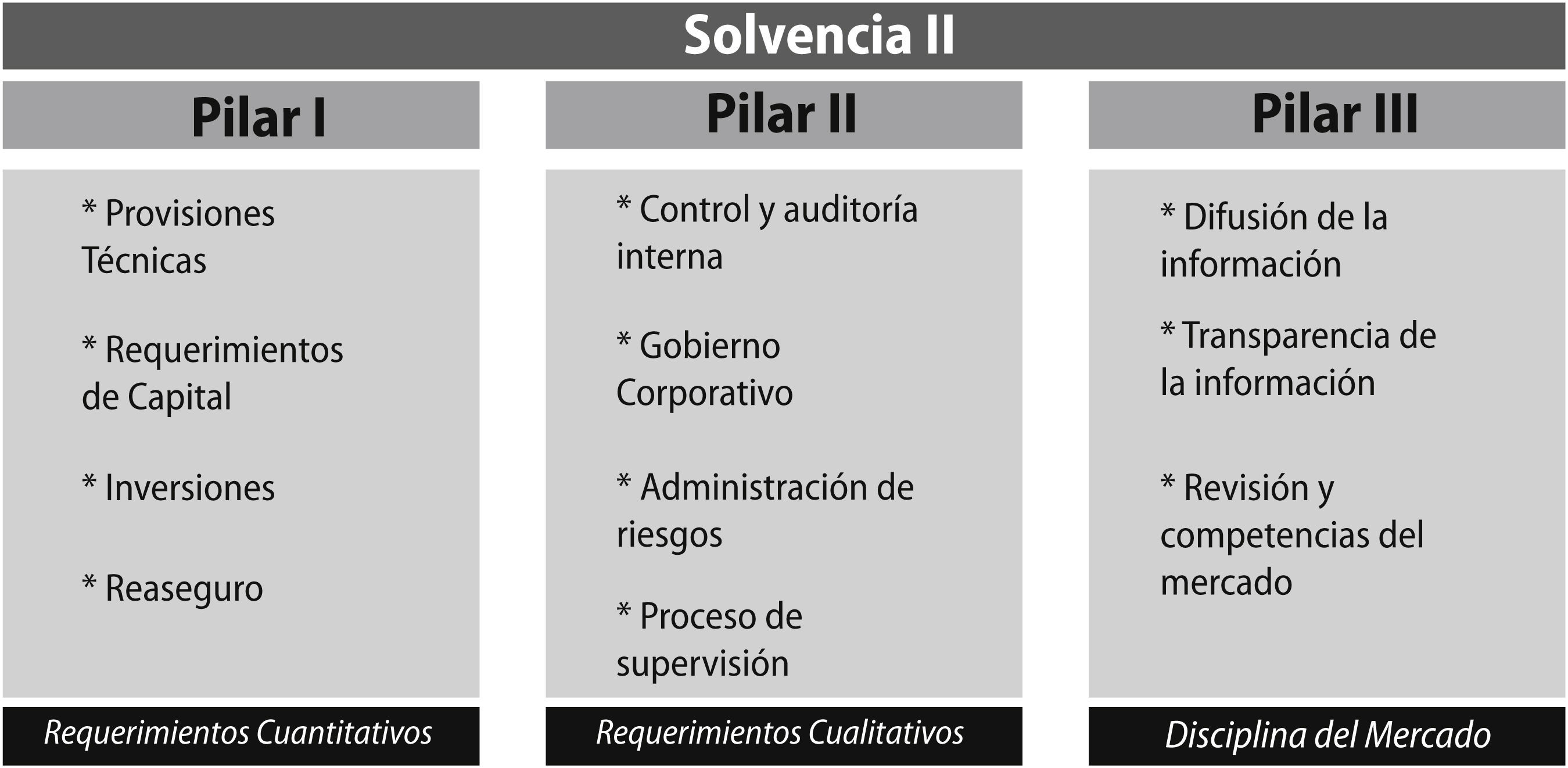
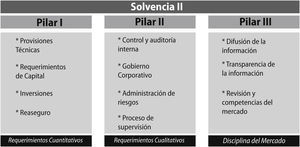
El entorno normativo de Solvencia II, se compone de un conjunto de elementos que se ordena bajo una estructura basada en tres pilares (Figura 1), que se resumen de la siguiente forma (UNESPA, 2015):

• •

  Pilar I – Cuantitativo: Se destina a los requerimientos cuantitativos. Este primer Pilar I se le ubica como el pilar técnico de Solvencia II;² ya que se busca la construcción de un primer Pilar matemáticamente sólido y, capaz de abarcar la totalidad de riesgos que se deben calcular en una adecuada valoración del perfil de riesgo de un negocio. Para cumplir con estos requisitos es necesario que primeramente las entidades aseguradoras establezcan y definan las reglas de valoración que seguirán para cuantificar todas las partidas relevantes del balance económico tanto del activo como del pasivo en conjunto, de tal forma que, se pueda obtener los niveles de capital adecuados al perfil de riesgos asumidos por la entidad.

• •

  Pilar II – Cualitativo: Se destina a los requerimientos cualitativos y las normas de supervisión. Busca una supervisión de alta calidad por parte de los organismos reguladores, con rigurosas exigencias en materia del gobierno en las entidades aseguradoras, que afectan a los órganos de gestión y dirección de la misma quienes son los principales responsables de los procesos de identificación, medición y gestión activa del riesgo. De esta forma, se ven obligadas a buscar mejoras en la gestión interna y así conseguir reforzar la estabilidad y solvencia del sector asegurador. Por otro lado, el Pilar II hace especial hincapié en la necesidad de preservar la coherencia entre las exigencias impuestas entre los distintos elementos que conforman el sector financiero. Se hace mención a fomentar una supervisión prudencial destinada a detectar aquellas entidades que presentan un riesgo elevado, por sus características financieras, organizativas o de cualquier otra índole; ya que ello podría tener graves consecuencias sobre la solidez financiera de las entidades.

• •

  Pilar III – Disciplina del mercado: Se busca desarrollar la comunicación de la información entre el supervisor y la entidad aseguradora con el fin de favorecer la disciplina y transparencia. Así se podrá lograr conseguir una mayor estabilidad financiera mediante una tendencia hacia la obtención de una contabilidad internacional homogénea. Mediante la implementación de este tercer Pilar, se verá reforzada la convergencia y transparencia de la actividad aseguradora, que se traducirá en el fortalecimiento de la supervisión del seguro.

Figura 1.

Esquema conceptual del Proyecto Solvencia II

Fuente: Propia de los autores.

3

El riesgo de caída de cartera: nuestro problema de estudio

Para cubrir con los requisitos exigidos por Solvencia II, las aseguradoras deberán cuantificar los niveles de capital adecuados al perfil de riesgos asumidos por la entidad, estableciendo y definiendo las reglas de valoración que seguirán para ello.

Es así como surge el término de Capital de Solvencia Obligatorio (SCR – Solvency Capital Requirement) que se define como el capital necesario para hacer frente a las posibles pérdidas económicas teniendo en cuanta todos los riegos cuantificables a los que está expuesta, en un horizonte temporal de un año y con un nivel de confianza del 99.5% (VaR al 99.5%). Para la cuantificación de dicho Capital Requerido, Solvencia II facilita su propia metodología a través del denominado “modelo estándar”, o bien permite a cada entidad implementar un “modelo interno” basado en la experiencia propia de la compañía (Pozuelo de Gracia, 2008).

En términos generales, los “modelos internos” deberán construir sus propias hipótesis basadas en la experiencia de la compañía, justificando y documentando cada una de éstas, así como la estructura y calibración de cada riesgo considerado. Así mismo, si la entidad opta por utilizar su propio modelo, éste deberá ser presentado y aprobado por los órganos supervisores.

Por el contrario, el “modelo estándar” establece una fórmula general para el cálculo del SCR, la cual fue definida por el Comité Europeo de Supervisores de Seguros y de Pensiones de Jubilación (CEIOPS). Se resumen con un conjunto de normas que asume un enfoque general de identificación y valoración de los riesgos que afectan a las entidades aseguradoras. Con base en dicha evaluación, se cuantifican cada uno de los riesgos y se calcula el capital necesario para cubrirlos. Dentro del planteamiento que sugiere la fórmula estándar, se identifican los riesgos más relevantes de la entidad aseguradora, tanto en la estimación de las provisiones técnicas como en la valoración de los activos bajo la generación de diferentes escenarios.

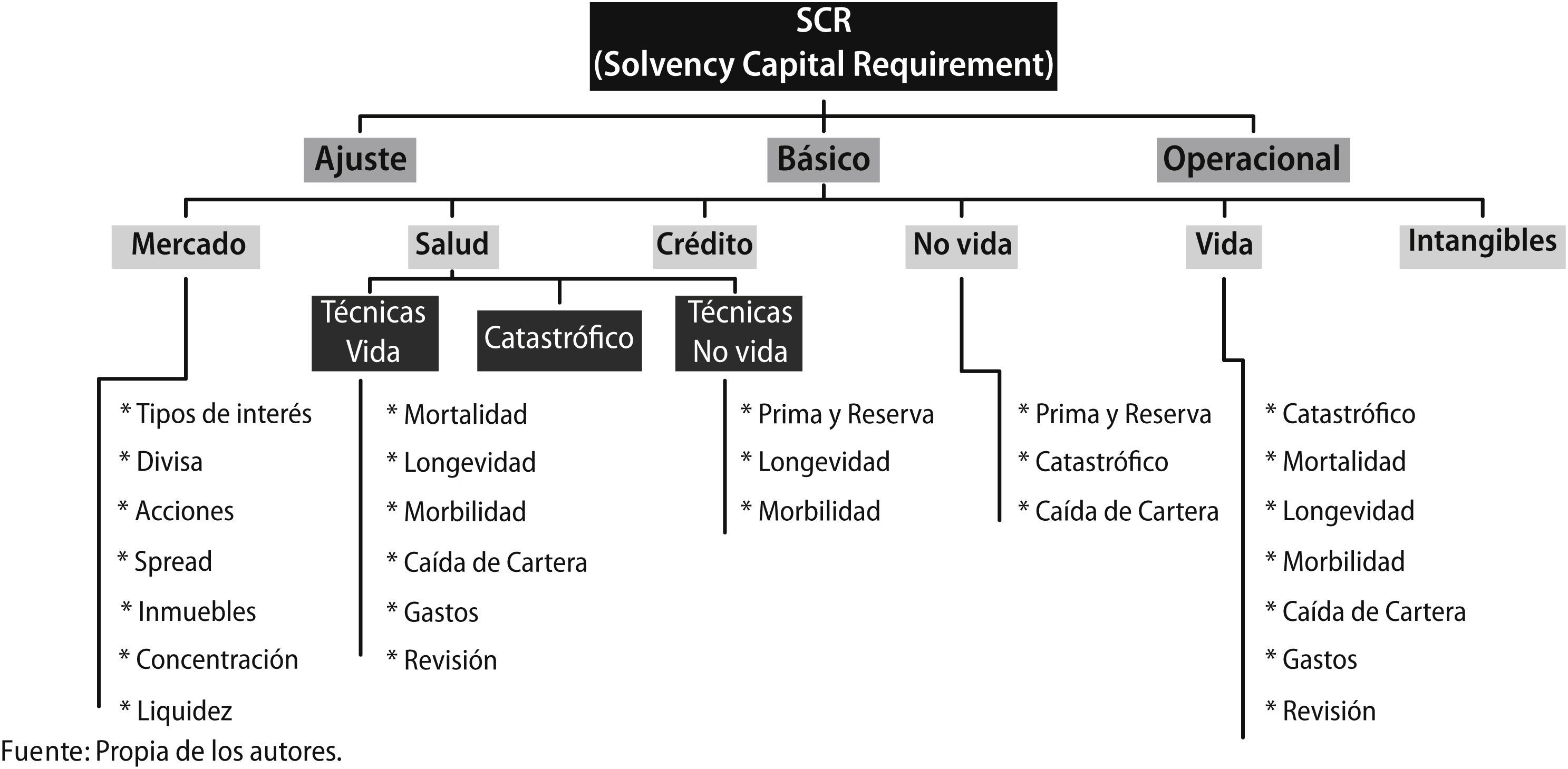
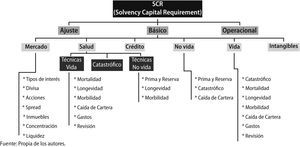
De esta forma, la valoración del requerimiento de capital se obtiene mediante el desglose de seis sub-módulos de cálculo correspondiente a la valoración de los riesgos asumidos por la entidad. Posteriormente mediante una matriz de varianza y covarianzas, se realiza la agregación de riesgos y se obtiene el SCR global, es decir, el Requerimiento de Capital de Solvencia bajo el enfoque de la Fórmula Estándar (Figura 2).

Figura 2.

Cálculo del SCR (Requerimiento de Capital de Solvencia) bajo la Fórmula Estándar

Fuente: Propia de los autores.

Uno de dichos riesgos contemplados es la caída de cartera que registra una entidad, entendiéndose como tal a la rotación o salida de asegurados, lo cual se ve directamente reflejado en el decrecimiento en el volumen de primas de la entidad.

De aquí la importancia del estudio del problema en cuestión, la cuantificación del riesgo de caída de cartera, que es exigido por Solvencia II, así como los principales agentes causantes del mismo y sus implicaciones, ya que se reflejan directamente sobre los márgenes de solvencia de la entidad (Ayuso et al., 2011; 2012).

Siendo así que surge el concepto de “Caída de Cartera”, del cual no existe una definición precisa; por lo que puede precisar como el conjunto de pólizas que no optan por la renovación a su vencimiento por parte de los asegurados (Millán y Colomina, 2001).

En términos matemáticos, el número de pólizas que se anulan o cancelan durante un período determinado, se puede expresar de la siguiente manera:

• siendo: Pol_i = núm. Pólizas en Vigor al inicio del período

• Pol_NP = núm. Pólizas de Nueva

• Producción registradas durante el

• período

• Pol_f = núm. Pólizas en Vigor al

• final del período

De esta forma, se puede expresar el concepto de Caída de Cartera en términos de porcentajes de la siguiente manera:

En la actualidad, cada entidad aseguradora ha ido desarrollando metodologías novedosas con el objetivo de estimar la caída de cartera que se registrará en un futuro (Brockett et al., 2008). En la mayoría de los casos, basándose en su información histórica, utilizan modelos estadísticos medianamente complejos, y determinan los porcentajes de caída que definan mejor el riesgo al que está expuesto.

4

Metodologías propuestas: marco teórico

En primer lugar, se debe situar a la “Inteligencia Artificial” dentro de las metodologías que se manejan en la rama de la disciplina de Aprendizaje Automático (Machine Learning, por sus siglas en inglés). Este enfoque utiliza algoritmos para analizar registros en bases de datos internas de los clientes de una empresa, para descubrir ciertos patrones, interacciones o reglas que pueden describir o predecir las futuras tendencias que puedan indicar cualquier tipo de oportunidades competitivas (Mena, 1996) y, ayude a tomar decisiones o mejorar la comprensión o conocimiento que se pueda extraer a través de dichas bases de datos.

Ahora bien, dentro de esta disciplina se engloban las técnicas de Inteligencia Artificial, las cuales se basan en el aprendizaje a partir de los datos y de su semejanza con un pensamiento estructurado similar al comportamiento humano. Existen varias técnicas sugeridas dentro de esta rama de la Inteligencia Artificial como son las Redes Neuronales, los Vectores Soporte, los Algoritmos Genéticos, los Sistemas de Inducción de Reglas, los árboles de Decisión o la Teoría de Rough Set.

Por otro lado, los Modelos Lineales Generalizados (GLM –Generalized Linear Models–) introducidos a comienzos de los años 70 (Nelder y Wedderbum, 1972), se han convertido en una de las principales herramientas de análisis estadístico en toda clase de áreas. De acuerdo con esta metodología, tras un análisis de regresión se obtiene la variable respuesta o dependiente (número de siniestros o importe reclamado), basándose en un conjunto de variables explicativas, es decir, una serie de factores relacionados con el evento que simula dicha variable respuesta (generalmente características propias del asegurado de la póliza) (Díaz et al., 2010).

4.1

Metodologia no parametrica. arbol de decisión c4.5

A partir de un conjunto de datos se construyen diagramas de construcciones lógicas que hacen referencia a una clasificación óptima de los datos de acuerdo a sus características o atributos. De esta forma, se crean particiones recursivas que sirven para categorizar y representar una serie de condiciones que ocurren de forma sucesivas, comúnmente llamadas reglas sobre la decisión que se debe tomar, para solucionar el problema planteado asignando un valor de salida a un determinado registro de entrada.

Dichas reglas, gráficamente, se representan en forma de árbol a través de hojas o ramas, de ahí el nombre de Árbol de Decisión. De esta forma, permite obtener de forma visual las reglas de decisión y, de aquí su principal ventaja que es la fácil interpretación de los resultados (Araya, 1994).

Existen varios algoritmos para la construcción de árboles de decisión: CLS (Concept Learning Systems), Método CHAID (Kass, 1980), Método CART (Breiman et al., 1996), Algoritmo C4.5 (Quinlan,1993). La diferencia entre estos algoritmos de aprendizaje radica en el criterio utilizado para realizar las particiones o Reglas.

El Algoritmo C4.5 (cuyo precedente está en ID3 (Quinlan, 1986) y cuyas mejoras se incorporan en la versión comercial C5.0) es uno de los algoritmos más utilizados en el ámbito de los árboles de decisión, habiendo sido aplicado a problemas de clasificación en general, y a problemas financieros, en particular (Díaz et al., 2005 y 2009; Miranda et al., 2013). Esta es la razón por la cual fue elegido este tipo de algoritmo para su uso en la aplicación empírica realizada.

El algoritmo C4.5 se basa en conceptos procedentes de la Teoría de la Información para hacer las particiones y fue desarrollado por Quinlan (Quinlan, 1993). Parte de la premisa de tomar en cada rama del árbol, para hacer la correspondiente partición, aquella variable que proporciona más información de cara a clasificar los elementos que constituyen el conjunto de entrenamiento o conjunto de datos usados para construir el árbol (Díaz et al., 2004).

La información que proporciona un mensaje o la realización de una variable aleatoria x es inversamente proporcional a su probabilidad P_X (Reza, 1961) Con frecuencia en Ingeniería de Comunicaciones o en Estadística se mide esta cantidad en bits, que se obtienen como log₂ 1/P_X. El promedio de esta magnitud para todas las posibles ocurrencias de la variable aleatoria x recibe el nombre de entropía de x, es decir, el promedio se obtendría multiplicando los posibles estados que puede tomar la variable x, log₂ 1/P_X, por su probabilidad de ocurrencia, p(x). Luego la entropía de x será, H(x):

En consecuencia, la entropía es una medida de la aleatoriedad o incertidumbre de o de la cantidad de información que, en promedio, nos proporciona conocimiento de.

Originariamente (Quinlan, 1986 y 1993) seleccionaba para hacer cada partición aquella variable que proporcionaba la máxima información sobre x, es decir, maximizaba I(x; y_i) (magnitud denominada Gain). En las versiones posteriores del algoritmo, para establecer la variable que proporciona la mayor información, se selecciona aquella y_i que maximiza la magnitud I(x;y_i)/H(y_i). En el caso del C4.5 se emplea este ratio de ganancia (denominado Gain Ratio). Si el procedimiento descrito, se aplica de manera reiterada se va construyendo el árbol de decisión, hasta que se alcanza la pureza del nodo y con ello finaliza el proceso.

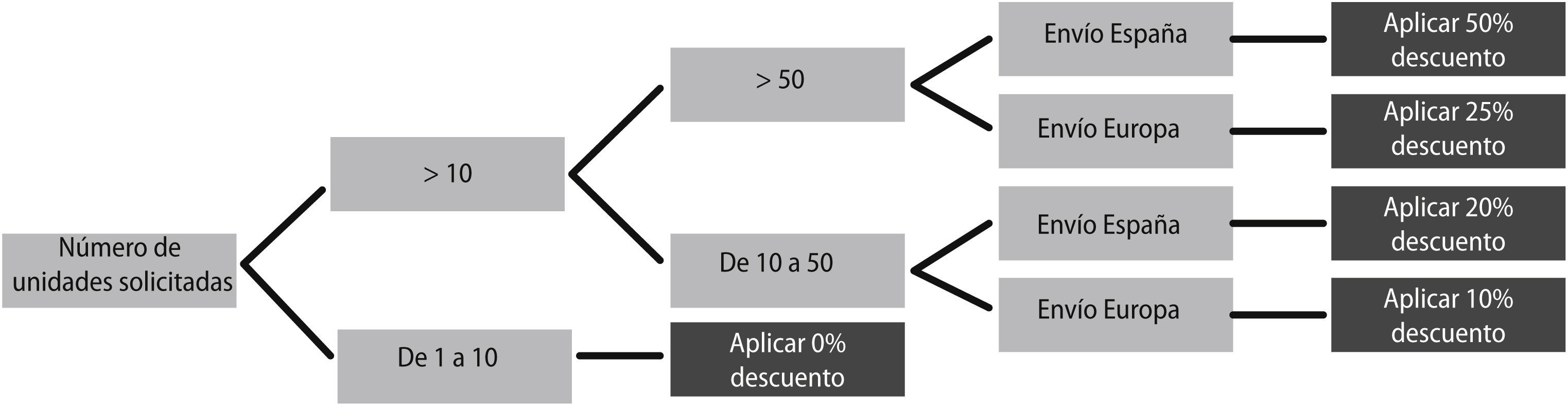
Se puede observar, mediante el ejemplo (Figura 3), que la interpretación de los resultados es sencilla y es fácil ver la lógica que se debe seguir para su aplicación a través del recorrido de sus reglas o ramas del árbol dibujado. De ahí su atractivo ya que puede ser analizado incluso por personas con poca experiencia en el tema.

Figura 3.

Ejemplo de Árbol de Decisión

Fuente: Propia de los autores.

4.2

Metodología no paramétrica. Metodología Rough Set

La Inteligencia Artificial cuenta con numerosas técnicas dentro de las cuales se tienen los algoritmos de Inducción de Reglas. Es aquí donde se engloba la Teoría de Rough Sets (Método de Conjuntos Aproximados).

Esta metodología se ha aplicado con éxito en diversos problemas financieros (Witlox y Tindemans, 2004; Huang y Jane, 2009; Yao y Herbert, 2009; Shyng et al., 2010 y Boudreau-Trudel y Kazimierz 2012). También hay estudios que lo han aplicado al sector asegurador (Sanchis, et al., 2007; Shyng et al., 2007 y Segovia-Vargas et al., 2015), motivo que justifica su aplicación al problema que nos ocupa relativo a la caída de cartera al sector asegurador.

Esta teoría fue introducida en el año 1982 por Pawlak como una nueva técnica de gran utilidad para el análisis y contenido de tablas de información que describen a un conjunto de objetivos por medio de una serie de atributos (Pawlak, 1991).

Esta teoría utiliza la experiencia en eventos pasados acumulados sobre una serie de patrones de datos, para finalmente poder obtener una serie de reglas en forma de sentencias lógicas que nos ayuden en la toma de decisiones futuras. Es así como hace necesario referenciar que un problema de decisión implica un conjunto de objetos descritos por un conjunto de atributos y, el cual se puede representar mediante una tabla de decisión (Skowron y Grzyma la Busse, 1991).

De esta forma, se puede enumerar las siguientes ventajas que caracterizan a la Teoría Rough Set destacando:

• •

  Utilización de variables tanto de tipo cuantitativo como cualitativo

• •

  No necesita de ningún tipo de información preliminar o adicional de los datos como distribuciones de probabilidades estadísticas.

• •

  Eliminación de variables redundantes y de esto modo enfocarnos en conjuntos mínimos de variables logrando una reducción del costo y tiempo del proceso asumido por el centro decisor

• •

  Obtención de una serie de reglas de decisión de fácil comprensión. Así mismo dichas reglas están bien respaldadas por experiencia pasada lo cual argumenta las decisiones que se toman.

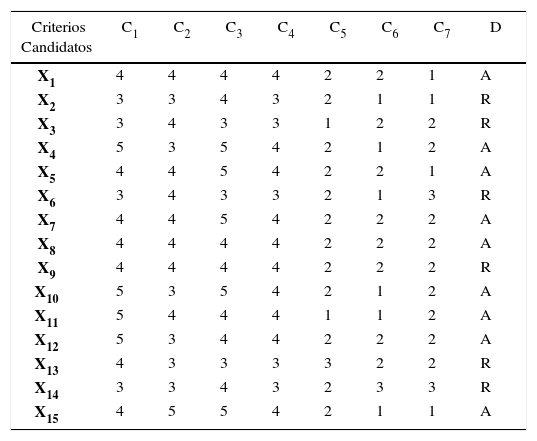
La Teoría Rough Set representa dicho conocimiento de los objetos en forma de una tabla de información: En la filas x se indican los objetos (acciones, empresas, etc.) y en las columnas q se representan los atributos. Los valores del atributo son las entradas de la tabla tomando el valor f(x,q). De esta forma, cada fila en la tabla representa la información sobre un objeto S; siendo éste el sistema de información denominado como sistema de representación del conocimiento.

El conjunto de atributos se divide en un subconjunto de atributos de condición y otro subconjunto de atributos de decisión; en este caso, si se distingue entre ambos conjuntos, se obtiene la tabla de decisión.

Tabla 1.

Ejemplo Tabla de Decisión

Criterios Candidatos	C1	C2	C3	C4	C5	C6	C7	D
X1	4	4	4	4	2	2	1	A
X2	3	3	4	3	2	1	1	R
X3	3	4	3	3	1	2	2	R
X4	5	3	5	4	2	1	2	A
X5	4	4	5	4	2	2	1	A
X6	3	4	3	3	2	1	3	R
X7	4	4	5	4	2	2	2	A
X8	4	4	4	4	2	2	2	A
X9	4	4	4	4	2	2	2	R
X10	5	3	5	4	2	1	2	A
X11	5	4	4	4	1	1	2	A
X12	5	3	4	4	2	2	2	A
X13	4	3	3	3	3	2	2	R
X14	3	3	4	3	2	3	3	R
X15	4	5	5	4	2	1	1	A

Fuente: Moscarola, 1978 y Slowiski, 1993

Ahora bien, otro de los conceptos tratados en este tipo de metodología son las reglas de decisión, siendo éstas el conjunto de datos que representan la experiencia. Se entiende que el conjunto de datos contiene información de un conjunto de objetos descritos por un conjunto de atributos. Por lo tanto, el tema consiste en encontrar reglas que determinen si un objeto pertenece a un subconjunto particular denominado clase de decisión o a un concepto. Como ya se ha mencionado, este tipo de reglas se presentan en forma de sentencias lógicas: SI ENTONCES (Sanchis et al., 2007; Segovia-Vargas, 2003; Segovia-Vargas et al., 2003).

Así, cada regla de decisión se caracteriza por el número de objetos que satisfacen la parte de la condición de la regla y pertenecen a la clase de la decisión sugerida, esto es, la denominada fuerza de la regla. Así se tiene que no todas las reglas son igual de importantes o fiables para el agente decisor, cuanto más débil la regla es, menos fiable es en la toma de decisión.

La técnica de Rough Set busca la mínima descripción posible en términos de atributos. Una descripción mínima permite un minucioso análisis de los conflictos. Además si los atributos son consecuencias de algunas decisiones, lo que en ciertas aplicaciones se puede interpretar como relaciones “causa-efecto”, la metodología Rough Set permite descubrir las mínimas dependencias elementales entre las consecuencias. Todo esto, en el contexto del presente trabajo sería de gran utilidad, ya que mediante mínimas interdependencias de las variables cualitativas que caracterizan a cada uno de los clientes dentro de una entidad aseguradora, se pueda definir el perfil de dichos clientes con mayor propensión a la anulación de su contrato de seguros (Shyng et al., 2007).

4.3

Metodología parametrica. modelos lineales generalizados (glms)

Existen pocos estudios que utilizan la metodología ofrecida por los glm para el análisis del riesgo de caída de cartera al que está expuesta una entidad aseguradora (Cerchiara et al., 2008). Sin embargo, mediante la utilización de dicha metodología, se puede lograr identificar la información o características del asegurado que describan el tipo de clientes propensos a la anulación de su contrato de seguros. De esta forma, la metodología de los glm podría ofrecer una herramienta que reconozca ciertas relaciones no lineales que podrían ayudar al análisis de los parámetros que afectan a este riesgo, y así permitir tener conocimiento sobre las correlaciones y dependencias de los factores que lo propician con el fin de lograr un control y gestión del riesgo en su globalidad.

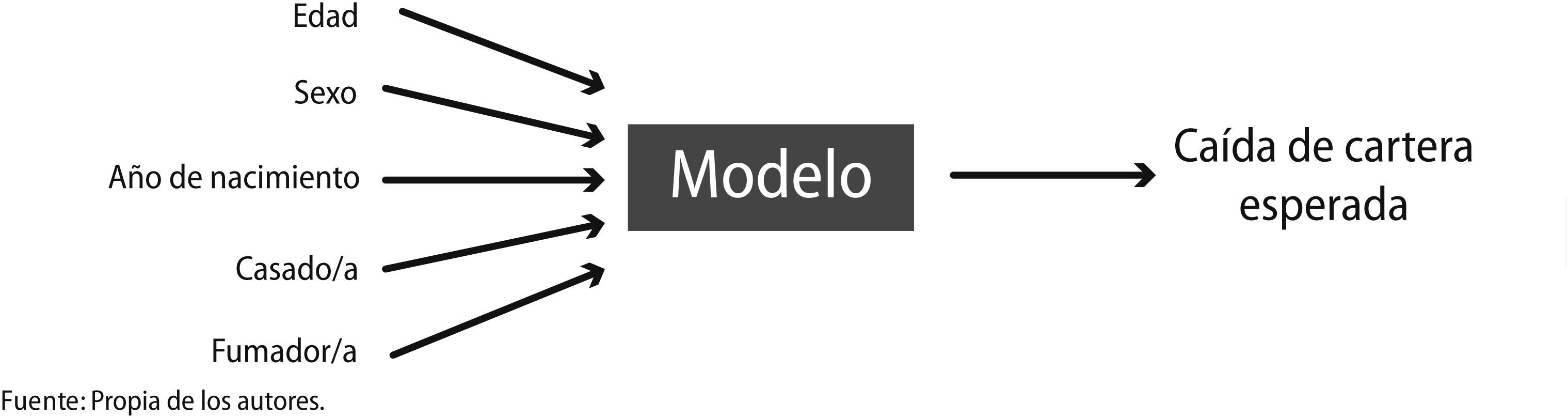
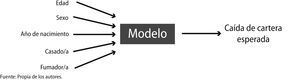
Es así como se encuentran los modelos predictivos que trabajan relacionando un evento determinado (en este caso, la anulación o caída de cartera que puede presentar una entidad aseguradora), con un cierto número de factores (Figura 4):

Figura 4.

Traducción del Modelo Predictivo en Seguros de Vida

Fuente: Propia de los autores.

Dentro de dichos modelos predictivos, se encuentran los Modelos Lineales Generalizados (glm, por sus siglas en inglés), que constituyen una generalización de los tradicionales Modelos Lineales (LM – Linear Models –), donde se asume que el valor esperado de la variable dependiente se encuentra condicionado a las variables independientes expresándose como una combinación lineal de los valores que dichas variables.

Los Modelos Lineales Generalizados, introducidos a comienzos de los años 70 (Nelder y Wedderburn, 1972), resumen un grupo homogéneo de métodos de regresión (logística, Poisson, gamma, etc.), previamente consideradas de forma independiente.

Los glm cuentan con su propia estructura, elementos y método de análisis e interpretación de los resultados, que los hace más atractivos y ofrece mayor facilidad en su aplicación.

4.3.1

Estructura

La estructura de un glm presenta una relación lineal entre las variables explicativas y una transformación de la media de la variable respuesta. Esto es, que no existe una relación líneal entre ambas, sino entre una función de enlace (función “link”) y las variables explicativas:

4.3.2

Componentes

Los Modelos Lineales Generalizados tienen tres componentes básicos, que se detallan a continuación:

• Componente Aleatorio:

Identifica la variable respuesta y su distribución de probabilidad. Este componente consiste en una variable aleatoria Y con observaciones independientes (y₁, …, y_N).

En muchas aplicaciones las observaciones de Y son binarias y se identifican como éxito y fracaso. Aunque de modo más general, cada Y_i indicaría el número de éxitos de entre un número fijo de ensayos; y se modelarizaría como una distribución binomial. En otras ocasiones cada observación es un recuento, con lo que se puede asignar a Y una distribución de Poisson o una distribución binomial negativa.

En otras ocasiones, las observaciones son continuas y se puede asumir para Y una distribución normal. Todos estos modelos se pueden incluir dentro de la llamada familia exponencial de distribuciones.

• Componente Sistemático:

Específica las variables explicativas, que entran en forma de efectos fijos en un modelo lineal, es decir las variables x_j que se relacionan como:

Esta combinación lineal de variables explicativas se denomina predictor lineal, el cual se puede expresar como:

• Función Link:

Como ya se ha comentado, existe una relación entre la variable respuesta y las explicativas, la cual no siempre corresponde a una relación lineal entre ambas. Pues bien, de aquí surge el concepto de “función vínculo” o “función enlace” que se ocupa de linealizar la relación entre la variable dependiente y las variables explicativas mediante la transformación de la variable respuesta.

Se denota el valor esperado de Y como μ = E[Y], entonces la función link especifica una función que relaciona a μ con el predictor lineal como:

En otras palabras, la función link g(μ) o función enlace que relaciona el componente aleatorio y el componente sistemático; de tal forma que:

En la siguiente tabla, se resumen algunas de las funciones vínculos comúnmente más utilizados (Tabla 2):

Tabla 2.

Funciones Vínculo

Función vínculo	g(x)	g^-1(x)
Identidad	x	x
Log	ln (x)	e^x
Logit	ln (x/(1-x))	e^x /(1+e^x)
Reciproca	1/x	1/x

Fuente: Propia de los autores a partir de Anderson et al., 2007.

4.3.3

Estructura de modelos comunes

Dependiendo de la naturaleza de los valores que toma la variable Y = (y₁, …, y_N); se deberá tomar la combinación idónea de la distribución de probabilidad y la función de enlace que mejor se adapte al objetivo que se plantea. De esta forma, algunos de los modelos más comunes con sus respectivas estructuras, se resumen a continuación (Tabla 3):

Tabla 3.

Estructura de los modelos más comunes

Y	Frecuencias de Siniestros	Número de Siniestros	Coste medio de Siniestros	Probabilidad (renovación/cancelación)
Función enlace g(x)	ln (x)	ln (x)	ln (x)
Error	Poisson	Poisson	Gamma	Binomial
Parámetro Escalar	1	1	Estimado	1
Función Varianza V(x)	x	x	x^2	x(1-x)
Pesos ω	Exposición	1	# siniestros	1
Offset ζ	0	ln (exposición)	0	0

Fuente: Propia de los autores a partir de Anderson et al., 2007.

4.3.4

GLM en la Práctica

Es importante tener en cuenta que no existe un único modelo válido que se pueda ajustar a la muestra de datos analizados. Es decir, la mayoría de las veces existe más de un modelo posible y es por ello, que el tema más complicado es saber y comprobar cuál ajusta mejor y por lo tanto, es el más adecuado de todos ellos.

Para ello, se pueden identificar cuatro fases que permiten estructurar la construcción de un glm (Anderson et al., 2007; McCullagh y Nelder, 1989), que serían:

Análisis Preliminar: El cual considera la etapa de preparación de los datos, así como un análisis exploratorio de las variables que serán consideradas dentro del modelo

• •

  Distribución de los datos (frecuencias, n° de pólizas, importe de siniestros)

• •

  Análisis Univariantes y Bivariantes

• •

  Análisis de Correlaciones

• •

  Categorización o Interacciones de Factores

Iteración del Modelo: En esta fase, se recurre a la selección adecuada de factores que mejor se ajustan a los datos, y por tanto, hacer uso recurrente del diagnóstico de las hipótesis y parámetros del modelo

• •

  Selección de Factores

• •

  Errores Estándar

• •

  Pruebas de Devianza

• •

  Consistencia en el tiempo

• •

  Sentido Común

Depuración del Modelo: Implica refinar el modelo buscando la máxima simplificación posible, encontrando la interacción entre las variables y haciendo uso de la suavización de los resultados

• •

  Residuos: Se pueden obtener varios tipos de residuos para analizar cómo los valores esperados varían de los observados; conviene analizarlos a través de los siguientes gráficos: histograma de los residuos,gráfico de residuos vs valores estimados, etc.

• •

  Leverage: Esta prueba ayuda a identificar las observaciones que tienen influencia excesiva en el modelo; es decir, es útil en la identificación de observaciones puntuales con bastante influencia sobre los resultados del ajuste del modelo, esto es, valores atípicos.

• •

  Suavizado: Se procede a la suavización de los parámetros en busca de una mejora en el poder predictivo del modelo; incorporando ciertos conocimientos o juicio del experto buscando un comportamiento natural del evento estimado o modelado.

Interpretación de Resultados: Finalmente, lograr traducir los resultados obtenidos para conseguir la mejor explicación del modelo e información obtenida del glm planteado y, que de esta forma, se puedan entregar los resultados para una correcta toma de decisiones de una forma atractiva y que aporte valor.

5

Aplicación empírica: métodos paramétricos y no paramétricos en el análisis de la caída de cartera

5.1

Tratamiento de la información: inicio de la aplicación empírica

En esta sección se presentan los resultados obtenidos tras la aplicación de las metodologías propuestas a una cartera real de pólizas de Seguros de Vida Individual de una entidad que actualmente opera dentro del mercado asegurador español. Los datos no están disponibles a nivel general debido a la política de privacidad existente en España relativa a la protección de datos y a cuestiones de confidencialidad industrial. La muestra analizada consta de 19.784 pólizas para el estudio en cuestión. Dado que la compañía opera a nivel nacional y el territorio español está dividido en 17 comunidades autónomas y dos ciudades autónomas, la muestra incluye todas las regiones autónomas y es por tanto representativa a nivel nacional.

La selección de variables en modelos de estimación de tasas de anulación de pólizas dentro de una entidad aseguradora es un tema complicado, ya que pueden existir diversos factores influyentes en la caída de cartera. Por un lado, hay factores ligados al propio cliente como la edad o el sexo. Por otro, hay factores directamente ligados a las características de la póliza como son la antigüedad, el tipo de seguro. Finalmente hay factores ligados o bien al canal de venta o a niveles de competencia en que ha sido adquirido el contrato de seguros. Además, dicha selección se podrá ver limitada por la propia información disponible que se pueda considerar.

Con base en esta situación, y teniendo en cuenta la accesibilidad que se ha tenido a los datos utilizados, se ha seleccionado las siguientes variables que son susceptibles a explicar el comportamiento de la tasa de caída que presenta una entidad aseguradora, y las cuales han sido consideradas en las aplicaciones empíricas que se abordan (Tabla 4):

Tabla 4.

Variables seleccionadas para la aplicación empírica

Nombre	Descripción
SEXO	Sexo del asegurado
EDAD_ACTUARIAL	Edad del asegurado al cierre del ejercicio
ANTIGUEDAD	Años de antigüedad de la póliza desde su Fecha de Emisión hasta la Fecha de Cálculo
TIPO_PRODUCTO	Tipo de Producto contratado: Individual o Colectivo; Ahorro o Riesgo
TIPO_PRIMA	Tipo de Prima: Única o Periódica
RED	Tipo de Red: Propietaria o No Propietaria
FORMA_PAGO	Periodicidad del pago de la prima
ANO_EFECTO	Año de Emisión o Efecto de la póliza
EDO_CIVIL	Estado Civil del asegurado, si lo ha comunicado
HIJOS	Tiene (o no) hijos el asegurado, si lo ha comunicado
VALOR_CLIENTE	Valor “comercial” definido por la Aseguradora de acuerdo a metodologías internas
ICE	Índice de Capacidad Económica
NIV_INGRESOS	Nivel de Ingresos
NIV_ESTUDIOS	Nivel de Estudios
TIPO_PRESTACION	Indica si la póliza esta en Vigor o Anulada

Fuente: Propia de los autores

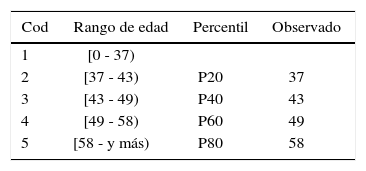
La única variable continua que se tiene en la muestra es la correspondiente a la EDAD. El empleo de este tipo de información implica una división del dominio original en algunos subintervalos; así como su correspondiente asignación de códigos cualitativos a dichos subintevalos (Segovia-Vargas, 2003). Esta manipulación o discretización hace que la interpretación de los resultados finales sea más sencilla. No existe una única forma para establecer los subintervalos; por lo que se toma la recomendación que se utiliza frecuentemente en los trabajos de investigación (Laitinen (1992), McKee, (2000) o Segovia-Vargas et al., (2003)), que es el uso de percentiles que siguen las distribuciones en las variables continuas.

Por lo que la discretización y asignación de códigos para esta variable quedaría de la siguiente forma (Tabla 5):

Tabla 5.

Códigos asignados a la variable Edad

Cod	Rango de edad	Percentil	Observado
1	[0 - 37)
2	[37 - 43)	P20	37
3	[43 - 49)	P40	43
4	[49 - 58)	P60	49
5	[58 - y más)	P80	58

Fuente: Propia de los autores

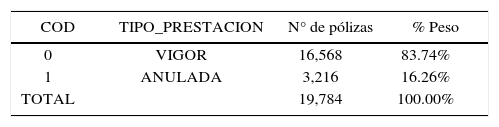
5.2

Resultados obtenidos y estudio comparativo

En esta sección, se analizan los resultados obtenidos tras la aplicación empírica de las metodologías propuestas sobre la cartera muestra. En dicha muestra se tiene la distinción de dos categorías que vienen dadas según el criterio que toma la variable de decisión TIPO DE PRESTACION. Esta variable toma el valor de 0 indicando que la póliza se encuentra en Vigor o por el contrario, toma el valor 1 si la póliza se encuentra Anulada (Tabla 6):

Tabla 6.

Códigos Variable Tipo de Prestación

COD	TIPO_PRESTACION	N° de pólizas	% Peso
0	VIGOR	16,568	83.74%
1	ANULADA	3,216	16.26%
TOTAL		19,784	100.00%

Fuente: Propia de los autores

Ambas categorías han sido evaluadas de acuerdo a los valores que tomas las 14 variables cualitativas y cuantitativas seleccionadas (Tabla 6) considerando una misma base de datos.

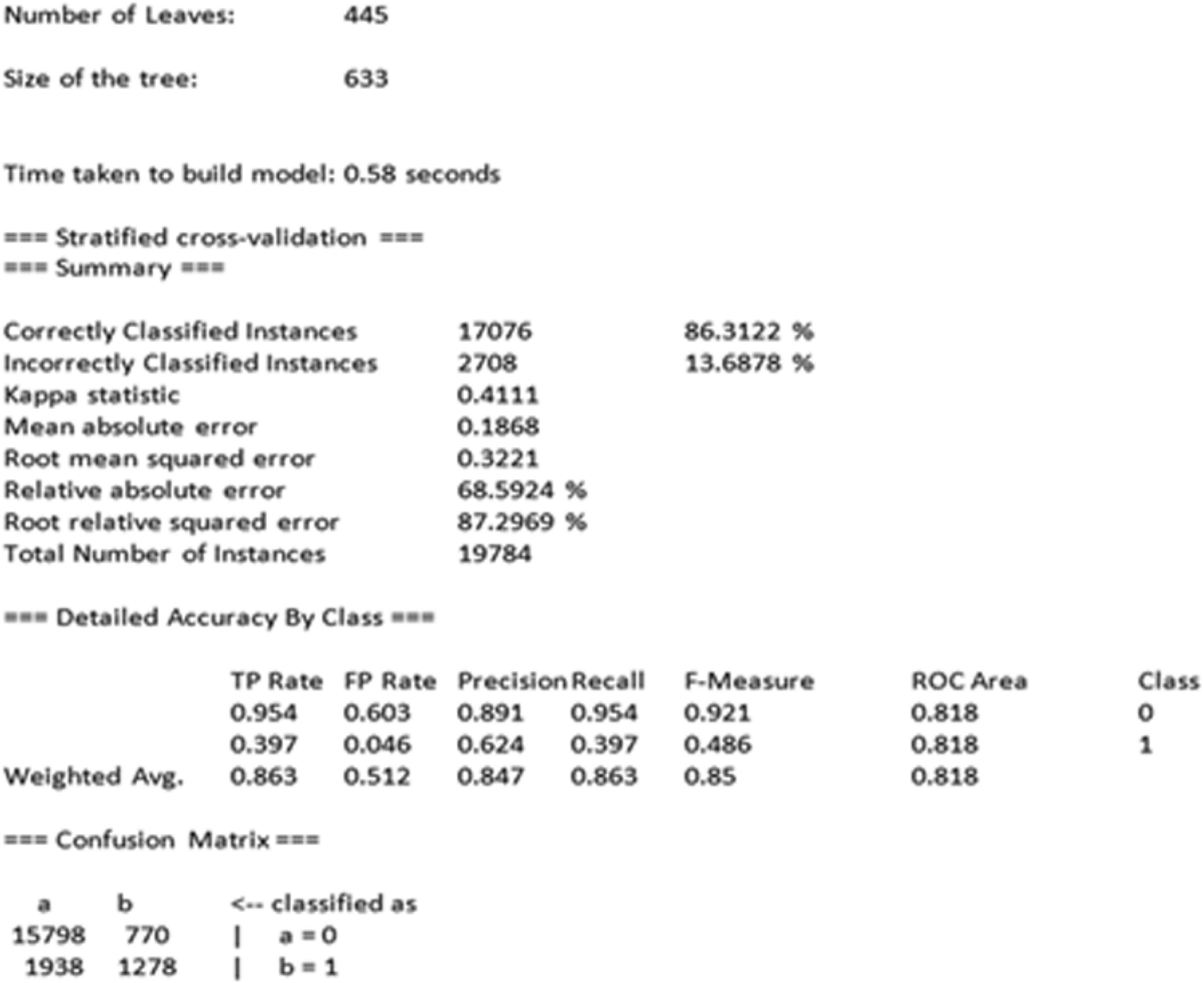
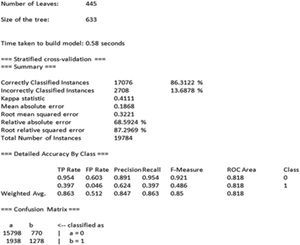
5.2.1

Árboles de Decisión

En primer lugar, la base de datos se ha introducido y programado en WEKA (Witten y Frank, 2005),³ programa informático que ha desarrollado el análisis del algoritmo C4.5. Se puede observar que los resultados cuenta con un porcentaje de aciertos del 86.31% (Correctly Classified Instances) de acuerdo al Resumen de Validación de Resultados que arroja el programa; lo cual justifica su interpretación (Figura 5).

Figura 5.

Salida de Resultados- WEKA (Algoritmo C4.5)

Fuente: Propia de los autores.

Además, si se observa la diagonal de la matriz de confusión, se tienen unos valores superiores a los elementos a₂₁ y a₁₂. Esto es, a₁₁=15.798 es mayor que a₂₁=1938; y por otro lado, a₂₂=1.278 es mayor que a₁₂=770. En concreto, se observa que un 39,7% de las pólizas anuladas son clasificadas correctamente y un 95,4% de las pólizas en vigor. Para analizar el modelo obtenido por la metodología C4.5 e interpretar dicho árbol, habría que ir descendiendo, hasta completar la totalidad de sus hojas (regla de decisión).

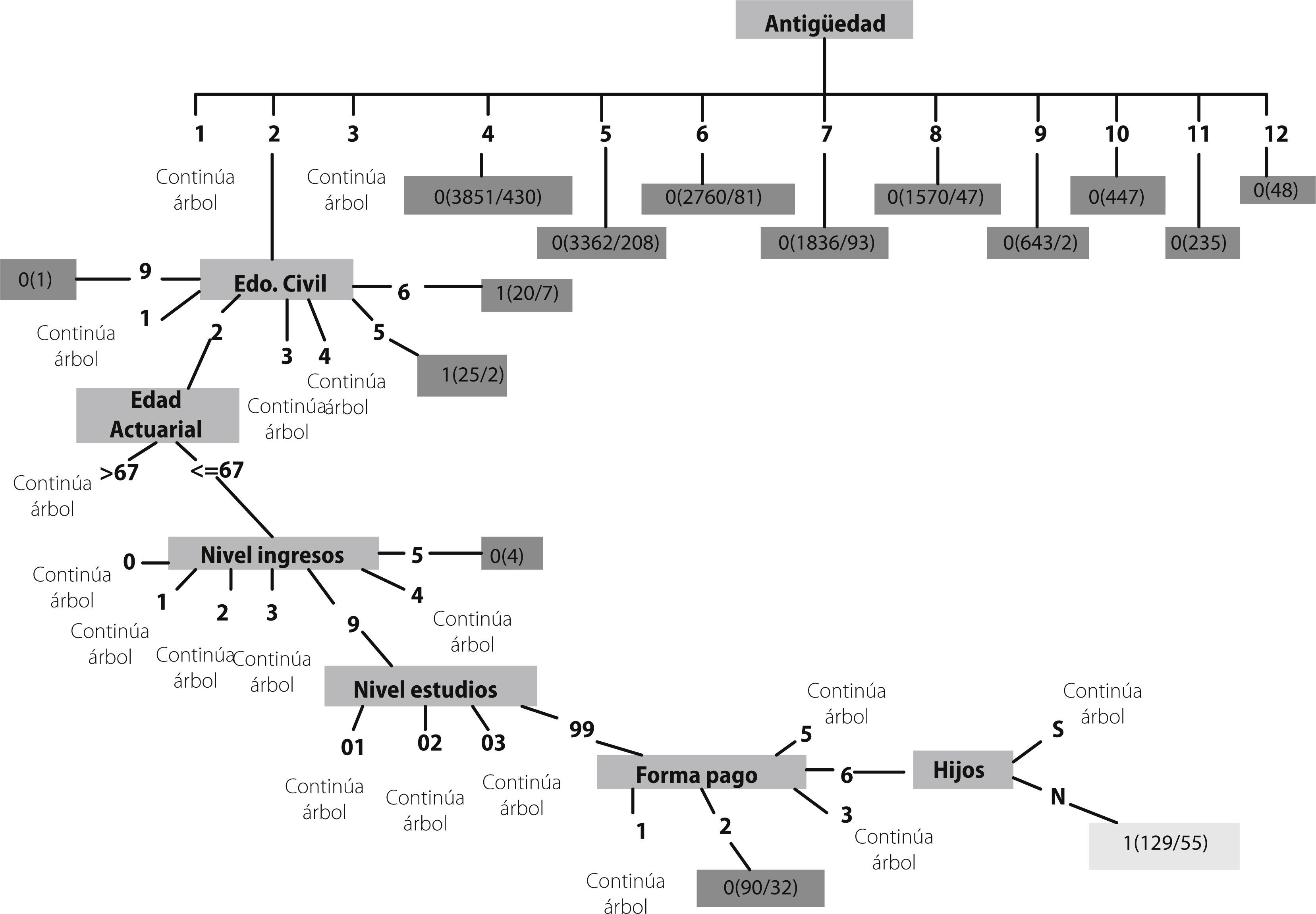
La variable ANTIGÜEDAD es una pieza clave en el modelo y suena lógico desde el punto de vista de la existencia de cierto nivel de fidelización por parte de los clientes. Por tanto, a mayor antigüedad dentro de la compañía de seguros, menor es la propensión o susceptibilidad que se tiene de cancelar su contrato de seguros. Sin embargo, existe cierto punto de inflexión a partir del cuarto -quinto año con la compañía, ya que a partir de que la variable ANTIGÜEDAD toma el valor de 4 y, el algoritmo de árboles no recoge alguna otra variable que nos indique cierto patrón de comportamiento de los clientes.

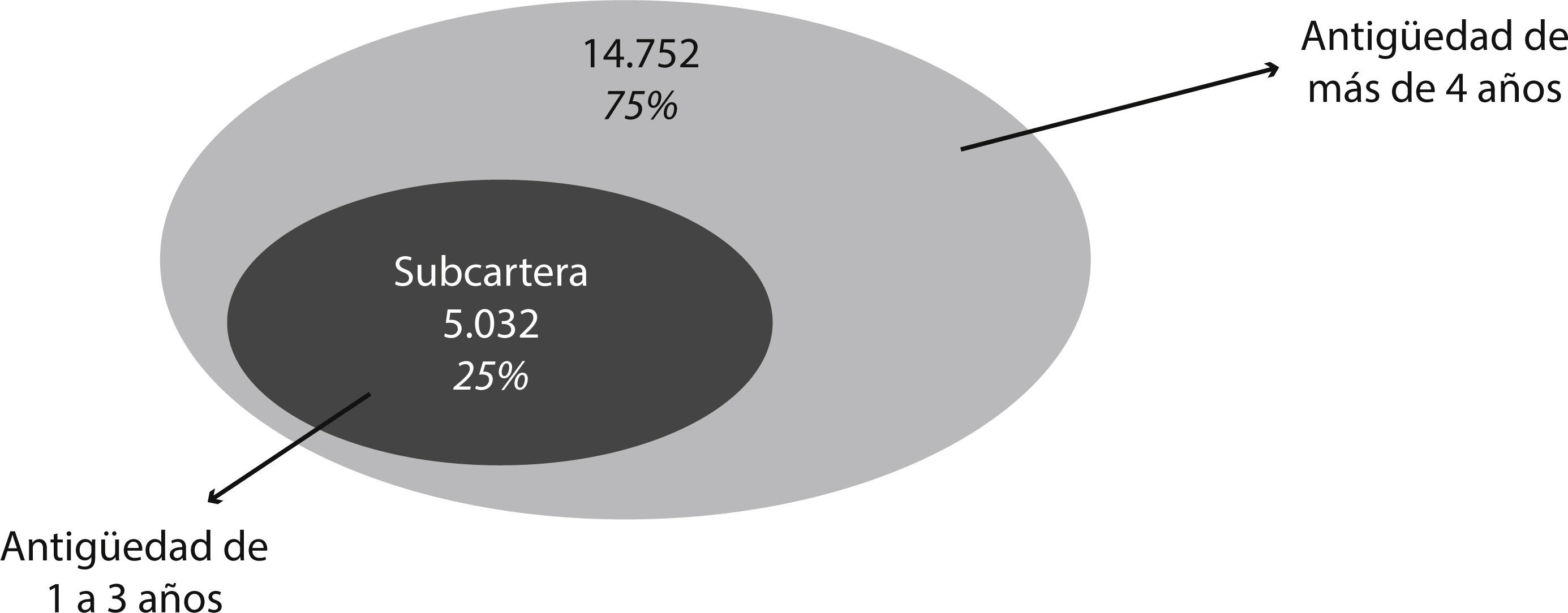
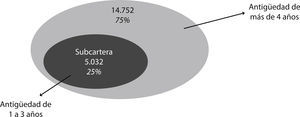
El problema para la compañía es que su cartera sobrepase los 4 años de antigüedad, es decir, el análisis de caída de cartera tendría que centrarse en los primeros años de vida de las pólizas, que es donde realmente se presenta el riesgo de caída de cartera. Siendo así, ha sido necesario realizar el análisis del árbol, subdividiendo la muestra de acuerdo con la variable ANTIGÜEDAD, ya que dicha variable es un factor clave en el comportamiento de los clientes (es decir, de la cartera total de 19.784 pólizas, 14.752 pólizas son clasificadas por el árbol únicamente como pólizas en VIGOR mediante la variable ANTIGÜEDAD). Siendo así, se tiene que el 75% de la muestra, cuenta con más de 4 años de antigüedad dentro de la compañía, sin poder distinguir otro tipo de variable o característica del asegurado que determine específicamente el tipo de clientes que se retienen en cartera. Y es así como se debe substraer un tipo “subcartera” correspondiente a la cartera de clientes más recientes.

De esta forma se puede tener una fuerza global muy alta para la cartera total explicada principalmente por la variable ANTIGÜEDAD y, complementarla con una fuerza relativa determinada con respecto a la subcartera. Así, se centrará el análisis en los patrones de las antigüedades 1, 2 y 3 que corresponde al 25% de la muestra (5.032 pólizas), cuyo comportamiento de los asegurados dentro de esta subcartera se podría considerar independiente al resto de la muestra (Figura 6).

Figura 6.

Composición de la cartera para la subdivisión de acuerdo a la variable ANTIGÜEDAD

Fuente: Propia de los autores.

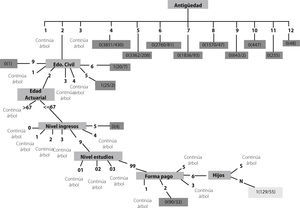
Por tanto, se centra el análisis de los patrones sobre la subcartera de pólizas más recientes de la compañía cuya ANTIGÜEDAD se encuentra entre 1 y 3 años de duración. A partir de esta subcartera, se obtienen las principales reglas de decisión sobre los 2 posibles comportamientos del asegurado:

• •

  TIPO PRESTACIÓN = 1 correspondiente a los factores determinantes de los clientes susceptibles a la cancelación de su póliza; y

• •

  TIPO PRESTACIÓN = 0 correspondiente a los patrones presentados en los clientes propensos a mantener su contrato de seguros en vigor

A continuación se presentan, a manera de ejemplo, una de estas ramas del árbol que dan lugar a las principales reglas detectadas para la CLASE 1; esto es, las reglas de decisión que determinarían el tipo de clientes propensos a la cancelación de su póliza de seguros.

De tal forma, que descendiendo por cada uno de las ramas, se obtiene el perfil del cliente susceptible a anular su póliza de seguros o, para la categoría contraria, el perfil del cliente con mayor propensión a continuar con su contrato de seguros. Así finalmente se obtiene en términos matemáticos el cumplimiento del patrón: total de casos y el porcentaje de fuerza que tiene cada rama analizada.

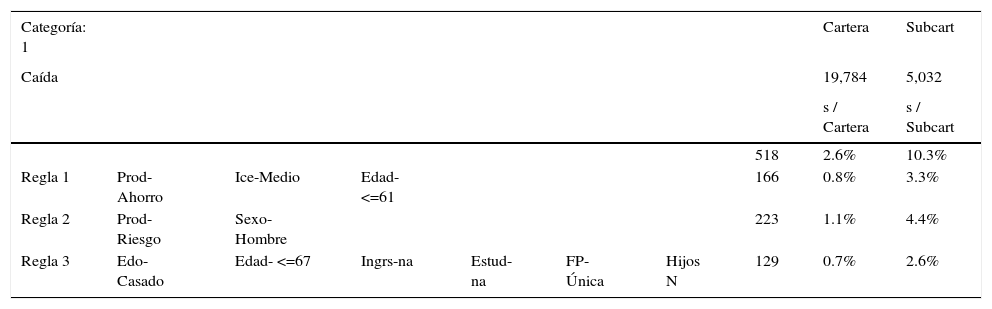
El resumen de reglas para la Clase 1=Cancelación, sumando estas 3 reglas acumulan una fuerza del 2.6% sobre la cartera total de pólizas; y a su vez, representa un 10.3% como fuerza relativa sobre la subcartera (Tabla 7).

Tabla 7.

Resumen de Resultados Arboles de Decisión- Clase 1_CAIDA

Categoría: 1								Cartera	Subcart
Caída								19,784	5,032
								s / Cartera	s / Subcart
							518	2.6%	10.3%
Regla 1	Prod-Ahorro	Ice-Medio	Edad-<=61				166	0.8%	3.3%
Regla 2	Prod-Riesgo	Sexo-Hombre					223	1.1%	4.4%
Regla 3	Edo-Casado	Edad- <=67	Ingrs-na	Estud-na	FP-Única	Hijos N	129	0.7%	2.6%

Fuente: Propia de los autores

Por otro lado, el resumen general de reglas para la Clase 0=Retención engloba 4 reglas que acumulan una fuerza del 4.4% sobre la cartera total de pólizas, y a su vez, representa un 17.5% como fuerza relativa sobre la subcartera (Tabla 8).

Tabla 8.

Resumen de Resultados Arboles de Decisión- Clase 0_RETENCIÓN

Categoría: 0							Cartera	Subcart
Retención							19,784	5,032
							s / Cartera	s / Subcart
						880	4.4%	17.5%
Regla 1	Prod-Riesgo	Sexo - Mujer				147	0.7%	2.9%
Regla 2	Edo-Casado	Edad - <=67	Ingrs - na	Estud - na	FP - Sem	90	0.5%	1.8%
Regla 3	Red-Prop	Edo - Soltero				211	1.1%	4.2%
Regla 4	Red-Prop	Edo - Casado	Prod - Riesgo	Edad - <=61		432	2.2%	8.6%

Fuente: Propia de los autores

A raíz de la aplicación de la técnica que ofrecen los Árboles de Decisión, se pueden resumir los principales resultados obtenidos con algunas de las variables que definen al perfil del cliente “cancelador” como son: primeramente, la ANTIGÜEDAD de la póliza; otra de las variables que se encuentra relacionada con la duración del contrato es el TIPO PRODUCTO, el cual resulta ser un segundo patrón de comportamiento identificado; otras tres variables detectadas para ambas categorías analizadas, tanto Retención como Cancelación, son la EDAD y ESTADO CIVIL, con lo cual esto puede de ser de vital importancia en la toma de decisión para la contención del riesgo de caída de cartera; la FORMA PAGO sugiere ser otra característica interesante que resulta del modelo y, finalmente, otra de las variables con menor fuerza, pero no por ello poco significativa, es la variable HIJOS, es decir, si se ha declarado tener o no Hijos.

5.2.2

Rough set

Uno de los primeros pasos que se debe realizar en la aplicación de este tipo de modelo, es la validación del mismo. Para ello, se efectuado un procedimiento de validación cruzada, la cual consiste en hacer ciertas particiones de igual tamaño en los datos dejando una muestra para estimar el modelo y otro conjunto de datos para su validación. Este proceso se repite tantas veces como particiones se hacen. El resultado final es la media de los resultados obtenidos, con frecuencia se suele utilizar 10 particiones. Así se tiene que cuanto más más alta es la tasa de validación cruzada, mayor fiabilidad del modelo obtenido.

Figura 7.

Árbol de Decisión (Rama de Antigüedad=2_Regla 3 de la Clase 1)

Fuente: Propia de los autores.

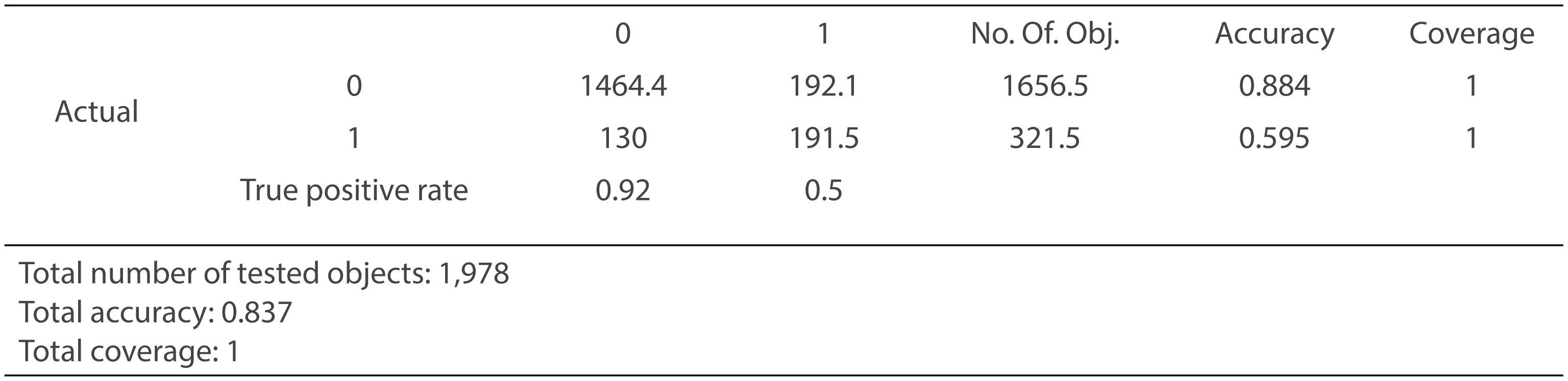
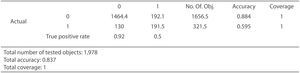
Pues bien, siendo así la aplicación de la metodología Rough Set ha presentado una precisión satisfactoria utilizando dicha validación cruzada en 10 pliegues. Dando como resultado un 83.7%, indicando un porcentaje de pólizas correctamente clasificadas considerablemente bueno elevando el poder de predicción del modelo (Figura 8).

Figura 8.

Salida de validación cruzada (Rough Set)

Fuente: Propia de los autores.

Al igual que se hiciese en la aplicación de Arboles de Decisión, se observa la diagonal de la matriz de confusión. Se tiene que el valor de =1.464,4 es mayor que =191,5; y por otro lado, =192,1 es mayor que =130. Por lo que se tiene que un 59,5% de las pólizas anuladas son clasificadas correctamente y un 88,4% de las pólizas en vigor; dejando evidencia la fiabilidad del poder predictivo de las reglas de decisión obtenidas del modelo.

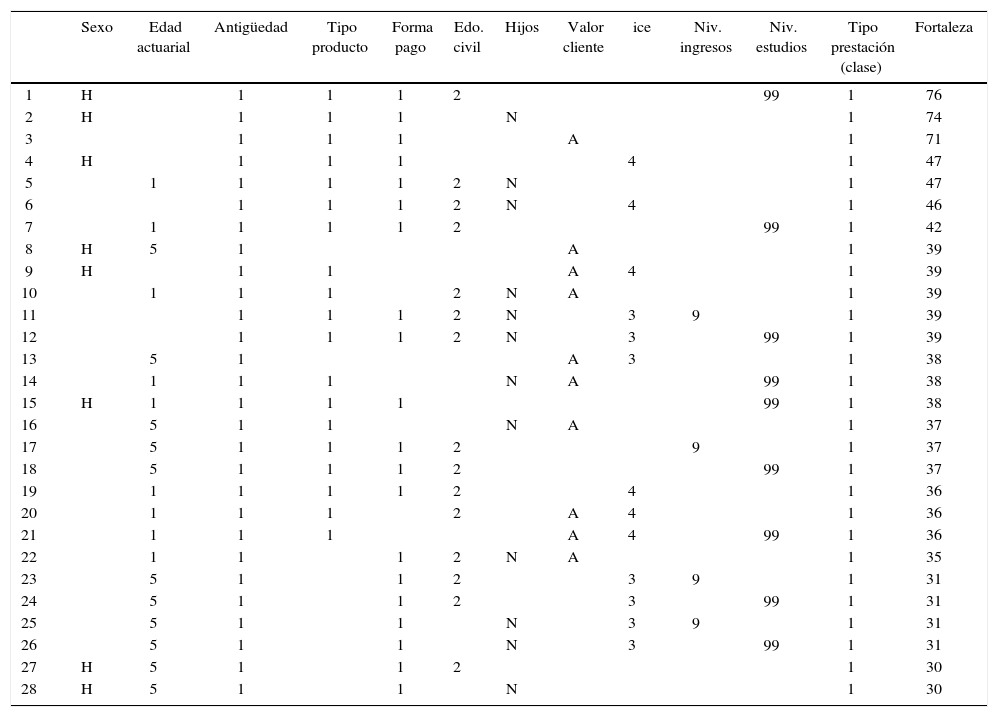
A continuación, a manera de ejemplo, se presenta los principales resultados que arroja el modelo. Esto es, una selección de las sentencias o reglas con mayor fuerza que clasifican a la muestra de pólizas del estudio ena la Categoría1=Cancelación de la Póliza (Tabla 9).

Tabla 9.

Reglas con Mayor Fuerza- Rough Set (CATEGORIA 1= Cancelación)

	Sexo	Edad actuarial	Antigüedad	Tipo producto	Forma pago	Edo. civil	Hijos	Valor cliente	ice	Niv. ingresos	Niv. estudios	Tipo prestación (clase)	Fortaleza
1	H		1	1	1	2					99	1	76
2	H		1	1	1		N					1	74
3			1	1	1			A				1	71
4	H		1	1	1				4			1	47
5		1	1	1	1	2	N					1	47
6			1	1	1	2	N		4			1	46
7		1	1	1	1	2					99	1	42
8	H	5	1					A				1	39
9	H		1	1				A	4			1	39
10		1	1	1		2	N	A				1	39
11			1	1	1	2	N		3	9		1	39
12			1	1	1	2	N		3		99	1	39
13		5	1					A	3			1	38
14		1	1	1			N	A			99	1	38
15	H	1	1	1	1						99	1	38
16		5	1	1			N	A				1	37
17		5	1	1	1	2				9		1	37
18		5	1	1	1	2					99	1	37
19		1	1	1	1	2			4			1	36
20		1	1	1		2		A	4			1	36
21		1	1	1				A	4		99	1	36
22		1	1		1	2	N	A				1	35
23		5	1		1	2			3	9		1	31
24		5	1		1	2			3		99	1	31
25		5	1		1		N		3	9		1	31
26		5	1		1		N		3		99	1	31
27	H	5	1		1	2						1	30
28	H	5	1		1		N					1	30

Fuente: Propia de los autores

Cabe observar que no existe regla alguna donde aparezcan todos los atributos, lo que significa que no existe una combinación global de todos las características de un cliente que distingan exactamente el perfil del cliente “cancelador”. En otras palabras no existe alguna variable en especial que sobresalga sobre otras, sino por el contrario la interrelación entre los factores es lo que conforma cada una de las opciones que llevarían a definir y categorizar a los clientes. Sin embargo, sí existe la posibilidad ciertas condiciones o tipos de clientes determinen el nivel de riesgo de anulación o caída de cartera.

Por otro lado, se tiene el conjunto de reglas que clasifican a la Categoría 0=Retención de la Póliza (clientes susceptibles a conservar sus pólizas con la entidad aseguradora), se clasifican mejor, no sólo por la mayor fuerza que presentan sus reglas, sino por la cantidad de reglas de decisión que resultan.

A manera de resumen general de las variables más significativas para cada una de las categorías, se tiene (Tabla 10).

Tabla 10.

Resumen de Resultados Rough Set por categoría (Caída_1 y Retención_0)

Categoría: 1 Caída		Categoría: 0 Retención
	Variables significativas		Variables significativas
*	Antigüedad	*	Antigüedad
*	Forma Pago	*	Tipo Producto
*	Tipo Producto	*	Forma Pago
*	Edo Civil
*	Hijos

Fuente: Propia de los autores

Así finalmente, se puede concluir que las variables que en ambas categorías están contenidas con mayor frecuencia y por tanto, pueden ser consideradas como los atributos que clasificarían el éxito o fracaso de la conservación o anulación de la cartera de pólizas de una compañía aseguradora son: ANTIGÜEDAD, TIPO PRODUCTO y FORMA PAGO.

5.2.3

Mínimos cuadrados generalizados (glms)

Se abordará la aplicación empírica de un modelo predictivo como lo son los glm, para la identificación de variables o factores que indiquen el posible abandono de una póliza de vida en una entidad aseguradora.

Así mismo, dicha aplicación, más que buscar la exactitud de los resultados numéricos, busca ser una metodología contraste para las técnicas de Inteligencia Artificial. Es decir, mediante un modelo paramétrico como lo son los glm se pretende complementar y fortalecer las conclusiones obtenidas del modelo no paramétrico que proporciona la Inteligencia Artificial.

Para la validación del modelo, así como de las variables, se trata de ir quitando los factores menos significativos, hasta conseguir que todos o la mayoría de sus p-valor se encuentren por debajo de cierto intervalo de confianza. Inicialmente se puede considerar el 95% de confianza, aunque poco a poco seguramente se tenga que ser más conservador y bajar este intervalo de confianza.

Por otro lado, también se debe ir monitoreando como se mueve la medida de bondad de ajuste del Criterio de Información de Akaike (AIC), ya que nos proporcionará un dato de referencia para la selección del modelo óptimo. Así se busca tener que dicho indicador deje de descender, con lo cual se podría decir que se ha encontrado el modelo adecuado.

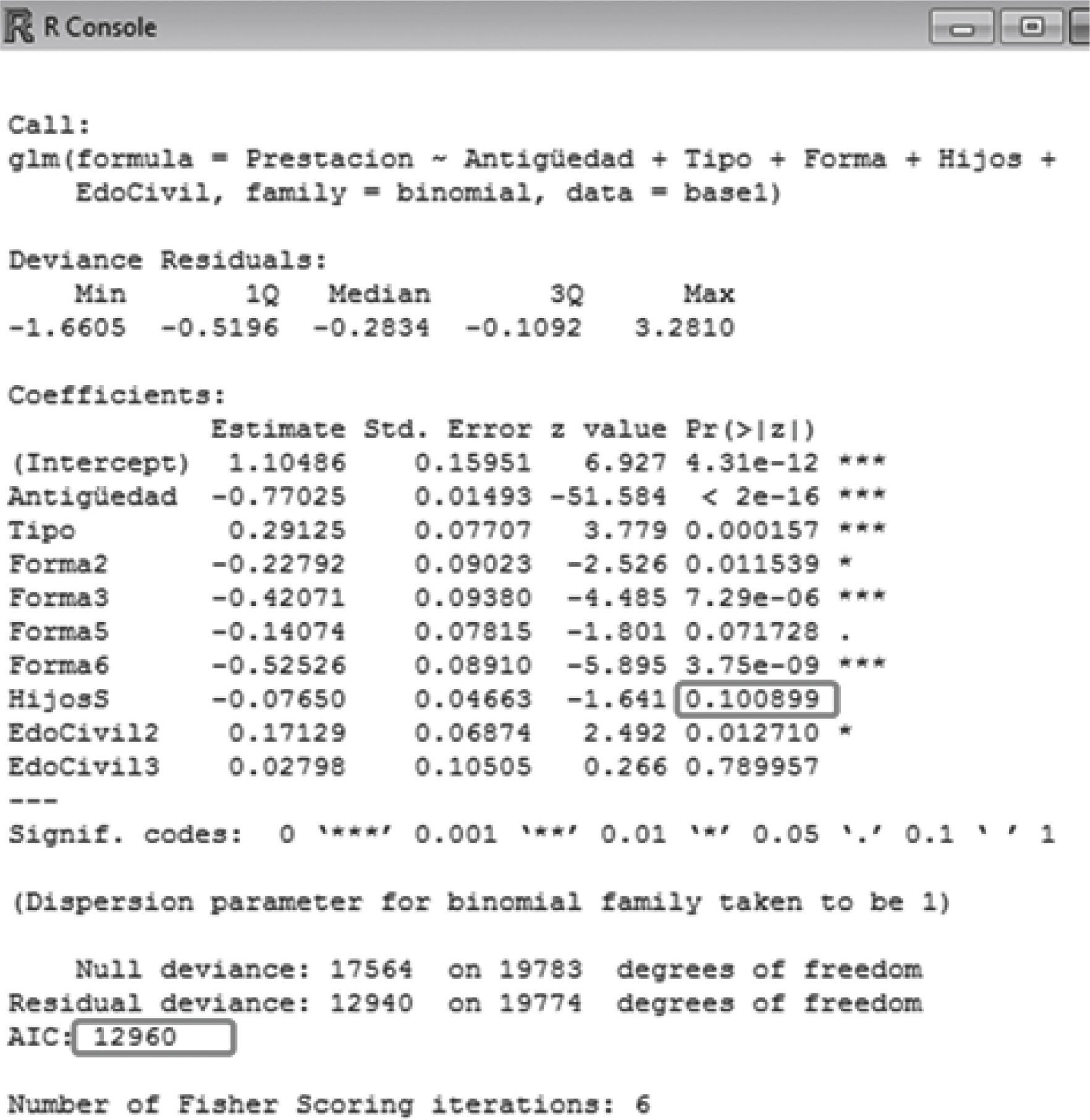
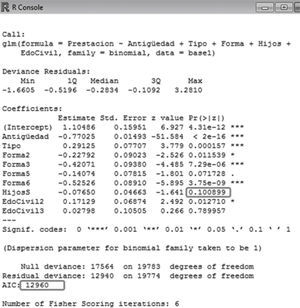
Siguiendo la técnica que se tomó de “prueba-error”, se han ido obteniendo resultados, logrando obtener el nivel de AIC más bajo. En consecuencia, se obtiene el siguiente cuadro resumen de resultados (Figura 9).

Figura 9.

Salida de Resultados Modelo V- R (GLM, Binomial, Logit)

Fuente: Propia de los autores.

Para el diagnóstico del modelo se observa que todos los p-valores se encuentran por debajo del nivel objetivo, es decir, menor que el 0.05, lo que indicaría que se trata del mejor modelo. Este modelo no era el que obtiene el AIC más bajo (de hecho se obtiene un AIC un punto por arriba con respecto al menor AIC), sin embargo, se gana en ajuste, logrando algo por arriba del 95% inclusive.

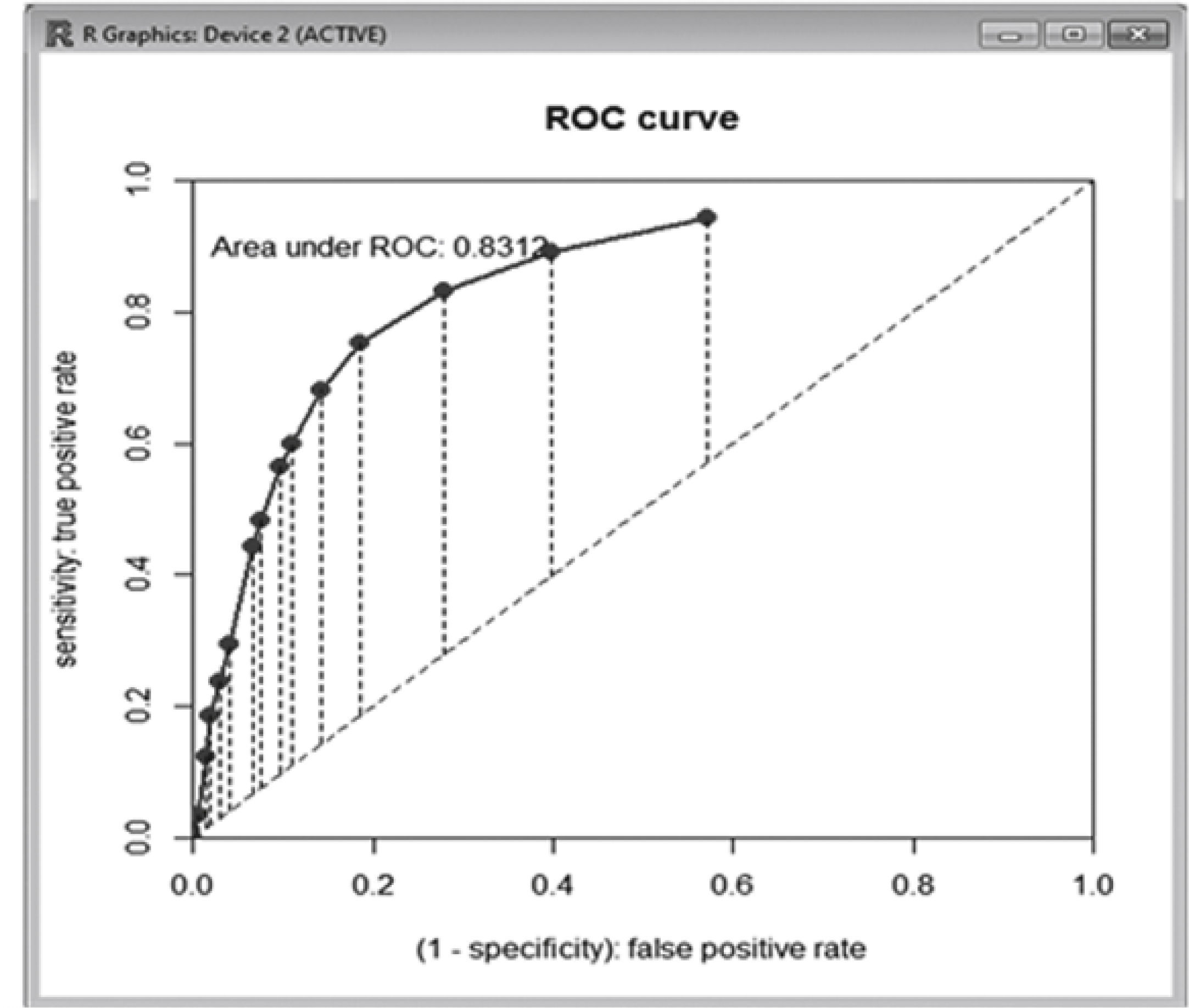
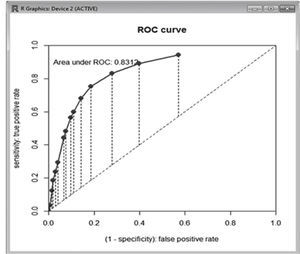
Para hacer el diagnóstico del modelo, se suele hacer un análisis visual de los resultados, recurriendo a la Curva ROC (siglas en inglés Receiver Operating Characteristic). Se trata de una Teoría de detección de señales donde mediante la representación gráfica del ratio de “Verdaderos Positivos” frente al ratio de “Falsos Positivos”. El análisis de la curva ROC proporciona una herramienta para seleccionar los modelos posiblemente óptimos. Se suele utilizar como una medida para la elección entre pruebas diagnósticas distintas. A continuación la curva ROC resultante del modelo seleccionado sería (Figura 10).

Figura 10.

Curva de ROC del Modelo VI- R (GLM, Binomial, Logit)

Fuente: Propia de los autores.

Es decir, el resultado arroja un 83,12% lo cual significa que se trata de un test bueno, ya que supone que la probabilidad de “diagnosticar” a una póliza como candidata a ser anulada sea correctamente clasificada es del 83,12%. Únicamente, a manera de contraste, se ha generado la curva ROC para los otros modelos anteriores al seleccionado, y en todos los casos, éste último es el que resulta con el mejor porcentaje, lo cual confirma que la elección del modelo ha sido acertada. Con lo cual, el modelo óptimo es elque arroja las variables ANTIGÜEDAD, TIPO PRODUCTO, FORMA PAGO y EDO CIVIL.

5.2.4

Resumen de los resultados de las distintas metodologías

El objetivo básico de este trabajo es mostrar la complementariedad de las metodologías paramétricas (glm) y no paramétricas (Árbol de decisión y Rough Set). En este sentido, a manera de resumen general, en la Tabla 11 se comparan los resultados obtenidos entre los distintos modelos en cuanto al porcentaje de clasificaciones correctas de las pólizas.

Tabla 11.

Comparativa de Resultados: Precisión de la clasificación

	Metodologías
	Árbol de Decisión	Rough Set	GLM
Precisión de la clasificación: porcentaje de clasificaciones correctas	86,31%	83,7%	83,12%

Fuente: Propia de los autores

Como puede observarse el porcentaje de aciertos en las clasificaciones es muy superior al 80% en las tres metodologías, lo cual valida los modelos obtenidos en nuestra aplicación práctica y justificaría su aplicación.

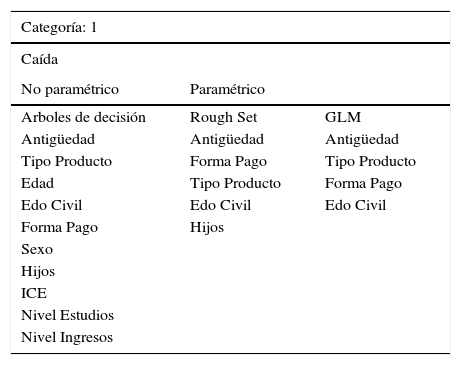
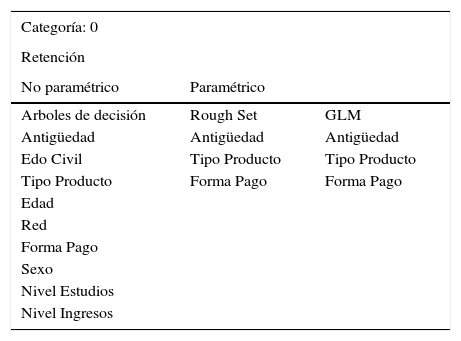
Por otro lado, las Tablas 12 y 13 muestran una comparativa del modelo paramétrico con respecto a las variables significativas que se han obtenido de las técnicas no paramétricas de la Inteligencia Artificial para cada una de las categorías o clases analizadas: Categoría 1- CAÍDA (Tabla 12) y Categoría 0 – RETENCIÓN (Tabla 13):

Tabla 12.

Comparativa de Resultados de Metodologías – CLASE 1_Caída

Categoría: 1
Caída
No paramétrico	Paramétrico
Arboles de decisión	Rough Set	GLM
Antigüedad	Antigüedad	Antigüedad
Tipo Producto	Forma Pago	Tipo Producto
Edad	Tipo Producto	Forma Pago
Edo Civil	Edo Civil	Edo Civil
Forma Pago	Hijos
Sexo
Hijos
ICE
Nivel Estudios
Nivel Ingresos

Fuente: Propia de los autores

Tabla 13.

Comparativa de Resultados de Metodologías – CLASE 0_Retención

Categoría: 0
Retención
No paramétrico	Paramétrico
Arboles de decisión	Rough Set	GLM
Antigüedad	Antigüedad	Antigüedad
Edo Civil	Tipo Producto	Tipo Producto
Tipo Producto	Forma Pago	Forma Pago
Edad
Red
Forma Pago
Sexo
Nivel Estudios
Nivel Ingresos

Fuente: Propia de los autores

Como puede observarse en la Tabla 12, para la CLASE 1 correspondiente a las variables o patrones de comportamiento que definen a los clientes susceptibles a la anulación de su contrato de seguros, se obtienen las mismas variables significativas que arroja el modelo glm como factores con mayor significancia. Ahora bien, la Tabla 13 muestra que para la CLASE 0, correspondiente a los clientes propensos a quedarse en la compañía conservando su póliza contratada, sucede algo similar aunque en diferente orden de aparición, pero manteniéndose las variables más significativas para clasificar a los clientes.

6

Conclusiones

Como se ha comentado, existen varias causas y finalidades que han provocado el surgimiento, desarrollo y lanzamiento del marco normativo sobre el que descansará el sector asegurador, mejor conocido como Solvencia II. Solvencia II es un proyecto sumamente ambicioso ya que busca rediseñar la actual metodología de cuantificación de la solvencia de las entidades aseguradoras y establecer los niveles de requisitos de capital que necesitan para hacer frente a los riesgos adquiridos frente a sus asegurados.

Además, a partir de su estructura de tres pilares, aporta una nueva cultura enfocada a optimizar la gestión de riesgos dentro del sector asegurador. Es más, dentro del Pilar I se busca analizar y determinar el perfil de riesgos que pretende administrar y soportar cada entidad. Esto se obtendrá en la medida en que se logre una mayor calidad en la gestión de riesgos a través de mejores técnicas de estrategia, planeación y administración de tal forma que, las compañías aseguradoras puedan ser capaces de mantener su posicionamiento frente a los diferentes riesgos que soportan mediante su identificación y control ante constante evolución.

Por lo tanto, es evidente que Solvencia II necesita entidades aseguradoras solventes cuyas decisiones estratégicas se tomen en función de esta nueva “cultura” sobre la gestión del riesgo, sin verse por ello amenazadas ante posibles debilidades de su patrimonio y prestigio. Todo esto se traducirá en un inminente fortalecimiento del sector asegurador.

Dentro de esta cultura de gestión de riesgos que propicia Solvencia II, nuestro estudio se ha centrado en el riesgo de caída de cartera. A través de la aplicación práctica realizada se han identificado una serie de variables o patrones de conducta que caracterizan a los tipos de clientes susceptibles a la cancelación de su contrato de seguros. Esto permitiría establecer estrategias comerciales de retención de clientes en aquellas pólizas con poca propensión a la anulación de su póliza o bien lograr una gestión eficiente de la caída de cartera y el riesgo que conlleva.

Recapitulando los resultados de la aplicación práctica a la muestra de datos, las metodologías sugieren que las variables que se deben tener en cuenta como posibles patrones de comportamiento son:

• •

  Antigüedad de la Póliza

• •

  Tipo de Producto a la que pertenece la Póliza

• •

  Forma de Pago de la Póliza

• •

  Estado Civil del Asegurado

Así mismo, mencionar que al tener una variable respuesta dicotómica (cancela o renueva), es posible estudiar el efecto contrario a la anulación del contrato de seguros. Es decir, se podría plantear el objetivo de manera inversa y analizar el patrón de comportamiento del perfil del asegurado fiel a la entidad. De aquí la propuesta de utilizar dichas metodologías para temas de retención o conservación de clientes.

Para lograr buscar estos patrones, en este contexto de exigencia que propone el entorno regulatorio, surge la necesidad de buscar metodologías de análisis novedosas. De esta forma se logrará incluir o detectar las características de los clientes con perfil de “anulador” que ayuden a complementar los métodos que hasta el día de hoy se han venido utilizando dentro del sector asegurador. Con base a ello, se ha procedido a aplicar una técnica estadística (paramétrica) y dos técnicas no paramétricas.

Con respecto a las técnicas no paramétricas que provienen de la Inteligencia Artificial (Teoría Rough Set y árbol de decisión C4.5) queremos resaltar las siguientes ventajas:

• •

  En primer lugar su carácter descriptivo, que permite entender e interpretar fácilmente las decisiones tomadas por el modelo, ya que tenemos acceso a las reglas que se utilizan en la tarea predictiva. El modelo de la metodología rough set es está formado por reglas con la forma de sentencias lógicas pero, es también posible derivar fácilmente reglas de decisión (para cada rama terminal) siguiendo las rutas marcadas en la estructura del árbol también en forma de sentencias lógicas. En consecuencia, tanto con la metodología Rough Set como con el C4.5 se pueden obtener sentencias lógicas fácilmente entendibles por el usuario final, sea o no experto.

• •

  Además, las reglas de decisión proporcionadas por los modelos pueden usarse con fines predictivos y no sólo descriptivos. Esto es así porque se puede evaluar su precisión a partir de unos datos independientes (datos test o muestra de test que se puede utilizar para validar el modelo) a los utilizados en la construcción del modelo (datos o muestra de entrenamiento utilizada para estimar el modelo).

• •

  Otra ventaja es que permiten trabajar con un número elevado de variables de entrada y no necesitan para trabajar un número elevado de datos.

• •

  Su carácter estrictamente no paramétrico presenta una indudable ventaja para su aplicación al ámbito financiero ya que muchas de las variables económico-financieras, utilizadas habitualmente en los análisis, no suelen cumplir las hipótesis requeridas por las técnicas estadísticas.

Por otro lado, también se ha propuesto la aplicación de una técnica paramétrica con el fin de contrastar los resultados obtenidos por las técnicas no paramétricas que ofrece la Inteligencia Artificial. La técnica paramétrica utilizada son los Modelos Lineales Generalizados (glms), técnica muy utilizada en la actualidad en el sector asegurador aunque no tanto para el problema que nos ocupa. La ventaja de los glms es lograr un mayor ajuste al riesgo y poder al mismo tiempo ser más ecuánimes con los asegurados. Además, este tipo de modelos permite a las aseguradoras ser más dinámicas, ya que la tarifa está en continuo movimiento, y va cambiando los coeficientes, en un breve periodo de tiempo.

En definitiva, la mayor aportación de este trabajo es la de incentivar al sector a buscar otro tipo de técnicas para la gestión de sus riesgos (Rodríguez-Pardo, 2012). Entre líneas, se debe leer que Solvencia II es una “cultura de cambio” y como parte de esa renovación, surge el planteamiento de este nuevo tipo de técnicas. Si bien, no buscando que éstas suplanten a las ya tradicionales técnicas estadísticas, sí podrían complementar la experiencia de los expertos dedicados a modelos de gestión de riesgos dentro de las entidades. De alguna manera darían un enfoque distinto y complementario a los tradicionales modelos de gestión de riesgos usados por el sector.

No es por demás comentar que, este estudio no está exento de limitaciones. Por un lado, el tema de la muestra se ha limitado a los productos con mayor volumen de producción de la entidad aseguradora y sólo se ha considerado un año de ejercicio contable de la entidad; con lo cual se trata de una muestra limitada en cuanto al número de casos analizados. Por otro lado, el número de variables cualitativas analizadas también se encuentra limitado, ya que las entidades aseguradoras han tenido poco interés en capturar en sus bases de datos demasiada información cualitativa del asegurado. No es hata hace algunos años, cuando se empezó a hablar de la “Calidad de los Datos” a raíz de las exigencias marcadas por Solvencia II en el tema.

Finalmente, es necesario recalcar que aunque los resultados en términos de clasificación obtenidos por los modelos son bastante satisfactorios, lo que se perseguía con este estudio no era tanto la bonanza, fiabilidad y precisión de los resultados, sino presentar, aplicar y discutir la factibilidad y capacidad de aplicar las metodologías ofrecidas por la teoría de Inteligencia Artificial en el campo de los Seguros de Vida. Lo mismo sucede con los resultados obtenidos del modelo glm, ya que de hecho no se buscaba obtener la ecuación multivariada final con la que se podría predecir una tasa de caída o anulación.

En consecuencia, se puede afirmar que se ha cumplido con el objetivo marcado inicialmente: por un lado, logrando aplicar unas nuevas metodologías que han identificado perfiles o patrones de comportamiento de los clientes susceptibles a anular su póliza de seguros; y por el otro, se ha puesto de manifiesto la conveniencia del uso de los glm en el campo de la estadística actuarial. Se ha pretendido, en definitiva, fomentar su uso como una alternativa novedosa o bien como un complemento a los actuales métodos utilizados en el sector, para que de manera conjunta, ofrezcan una gestión oportuna de los riesgos ante la propuesta de la nueva regulación de Solvencia II.