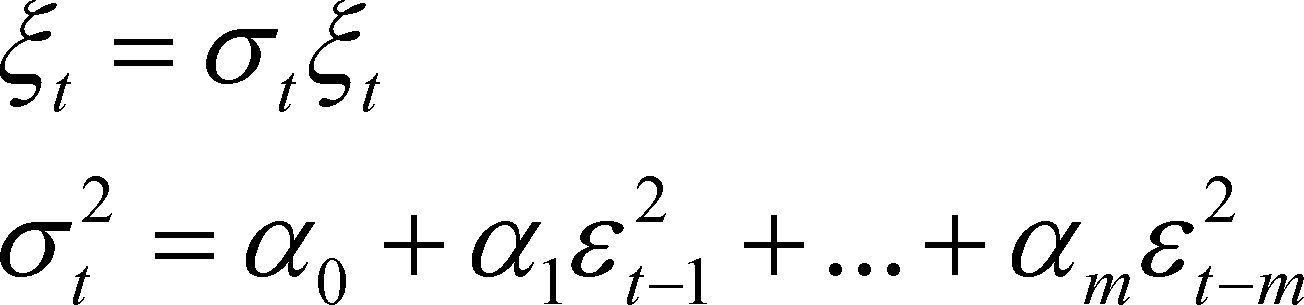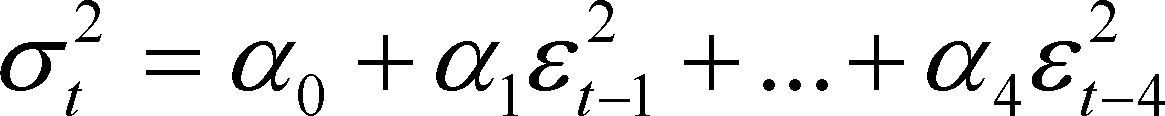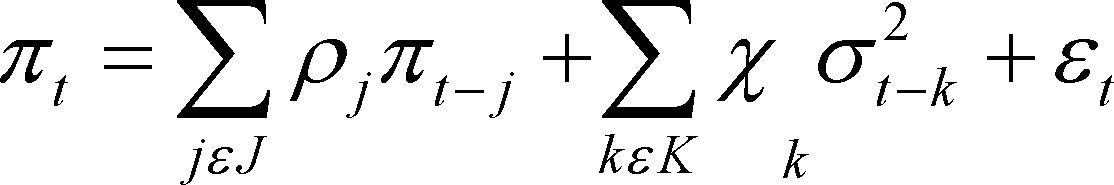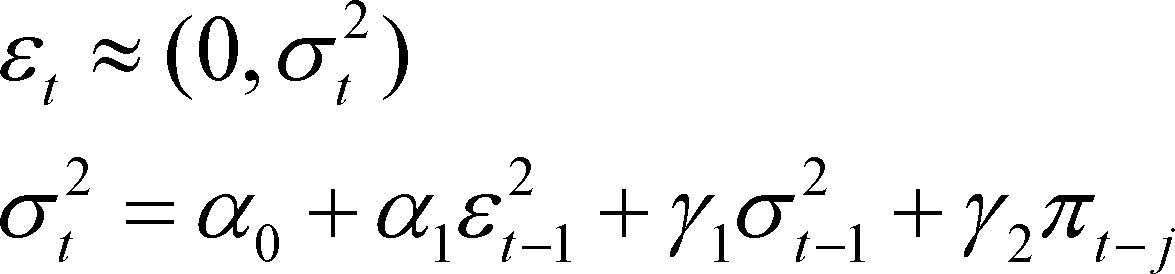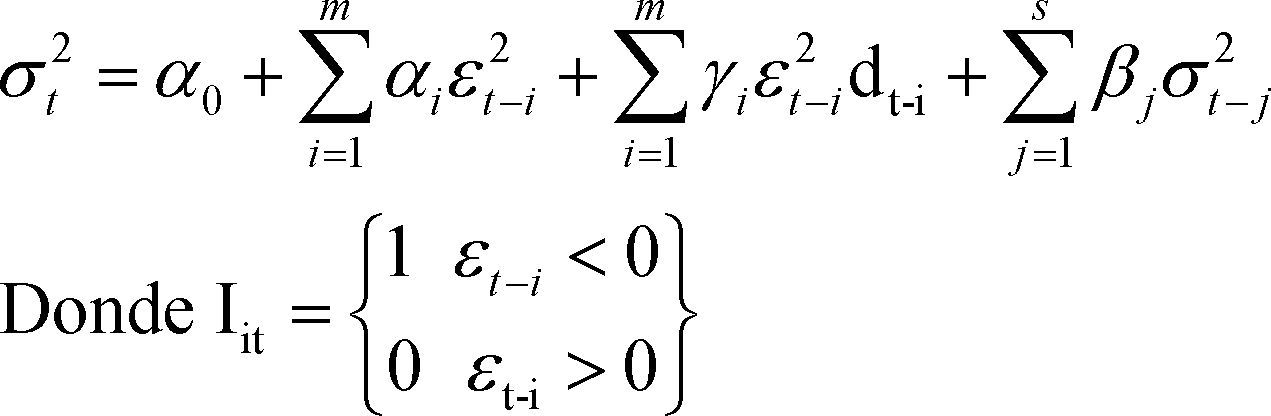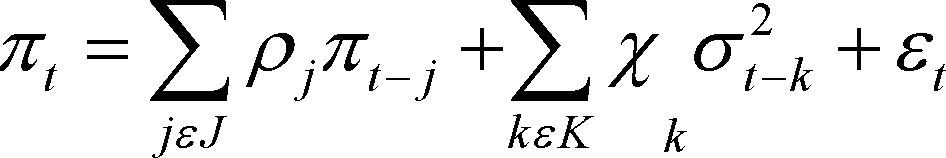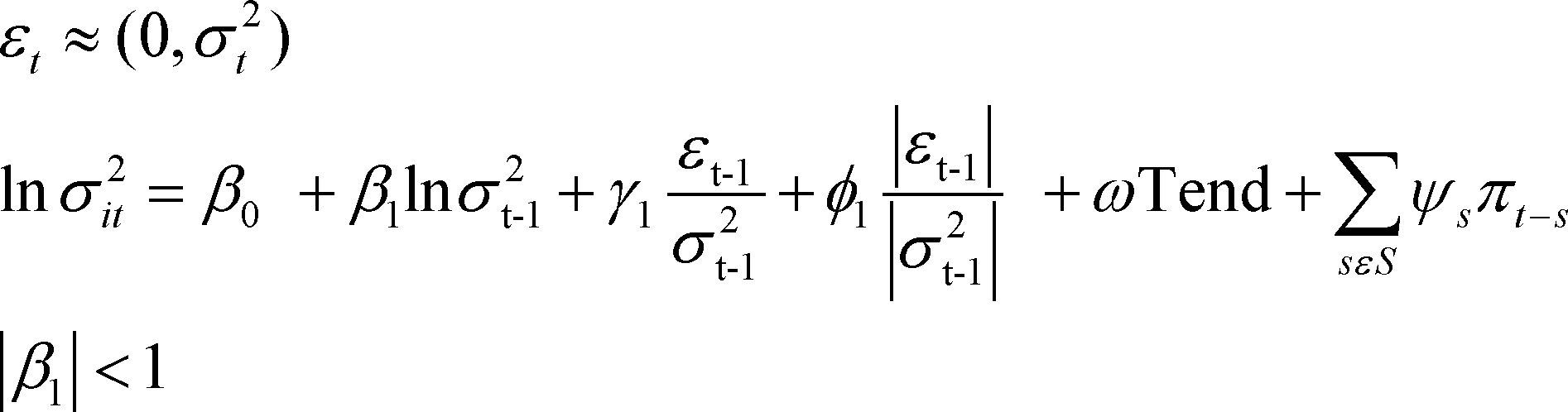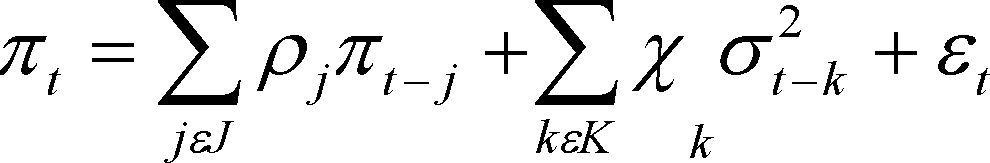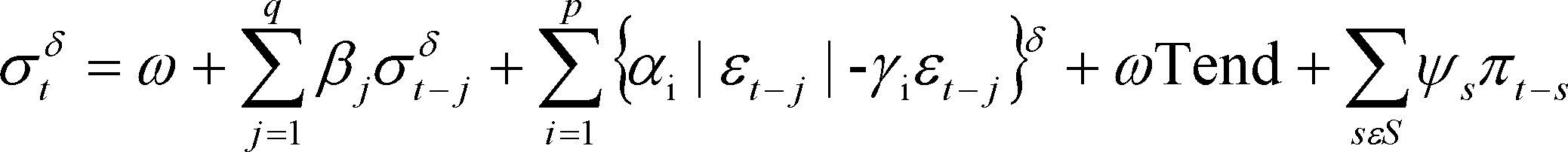Este documento de investigación analiza la evolución de la inflación mensual de Bolivia en el periodo 1990:01 a 2013:03 y presenta evidencia a favor de la hipótesis de Friedman y Ball, la cual establece que altos niveles de inflación incrementan la incertidumbre inflacionaria, y en menor magnitud y significancia también se acepta la hipótesis de Cukierman y Metzler, la cual postula que altos niveles de incertidumbre inflacionaria incrementan la tasa de inflación promedio, al mismo tiempo podemos también afirmar que para el caso de Bolivia no se cumple la hipótesis de Holland, Grier y Perry, la cual afirma que existe una relación inversa entre la incertidumbre inflacionaria y la tasa de inflación y en la misma presupone que la dirección de causalidad va de la incertidumbre hacia el nivel de inflación. Además, se encuentra evidencia de que shocks de inflación positivos tienen un impacto mayor sobre la incertidumbre inflacionaria que shock negativos, y que la incertidumbre inflacionaria tiene una tendencia decreciente a través del tiempo, esta última afirmación producto de la buena labor y desempeño de las autoridades monetarias, para promover la estabilidad de precios y mantener así una macroeconomía con inflación baja.
This research paper examines the evolution of the monthly inflation of Bolivia in the period 1990:01- 2013:03 and presents evidence for the hypothesis of Friedman and Ball,which states that high inflation increases inflation uncertainty, and to a lesser extent and significance the hypothesis Cukierman and Metzler is also accepted, which postulates that high levels of inflation uncertainty increase the average rate of inflation. At the same time we can also say that in the case of Bolivia not the hypothesis Holland, Grier and Perry, which states that there is an inverse relationship between inflation uncertainty and inflation is fulfilled. In addition, there is evidence that positive inflation shocks have a greater impact on the negative shock to inflation uncertainty, and inflation uncertainty has a decreasing trend over time, this last statement product of good work and performance of authorities monetary, to promote price stability and thus maintain low inflation macroeconomics.
En la actualidad existen distintos enfoques que explican los determinantes de la inflación y al mismo tiempo existe un consenso de que una inflación alta tiene múltiples efectos nocivos sobre una economía. Por lo mismo uno de los costos que genera la inflación es la incertidumbre inflacionaria. Un ambiente de incertidumbre de manera general tiende ir en desmedro de los agentes económicos, entorpeciendo sus decisiones y planeaciones futuras.
En esa línea, hoy en día existe un consenso que una inflación elevada es “mala”, y que la misma introduce perturbaciones importantes en una economía. Por lo mismo Barro (1997) realiza un estudio y utiliza datos de 100 países durante las últimas tres décadas, estima que un incremento de 10 puntos porcentuales en la tasa de inflación conlleva a una caída de 0.3 o 0.4 puntos porcentuales en la tasa anual de crecimiento del pib per cápita.
Por lo tanto este documento realiza una aproximación, con base en la experiencia boliviana, a las relaciones entre la tasa de inflación y su nivel de incertidumbre. Para tal efecto se estudia para el caso de Bolivia si se cumple de manera conjunta tres hipótesis que se encuentran relacionadas, como son: la hipótesis de Friedman (1977) y Ball (1992), la hipótesis propuesta por Cukierman y Metzler (1986) y la hipótesis de Holland (1995), Grier y Perry (1998). Como el comportamiento de la inflación en Bolivia ha sido variado, combinando periodos de alta y baja inflación, es de suma importancia tener un conocimiento cabal sobre la evolución de la inflación. Por lo mismo el objetivo de este trabajo es examinar las hipótesis antes expuestas, usando modelos autorregresivos con heterocedasticidad condicional (Arch, Garch-M, TGarch, Egarch-M y Parch-M) para modelar la relación entre inflación e incertidumbre inflacionaria.
El artículo esta estructurado en cuatro secciones. En la segunda sección se describe la relación económica entre inflación y la incertidumbre inflacionaria. En la tercera sección se describe de manera breve la metodología econometrica y se presentan nuestros resultados econométricos y finalmente, en la última sección se muestran las conclusiones finales sobre los resultados.
2Incertidumbre inflacionaria e inflaciónMilton Friedman (1977) en su discurso de premio Nobel, afirma que mayores niveles de inflación causan mayores niveles de incertidumbre sobre tasas de inflación futuros, entre otras palabras nos quiere decir que si en el momento “t” tenemos una inflación elevada, mayor será la incertidumbre en las tasas de inflación en el periodo “t+1”. A su vez, Ball (1992), le da sustento teórico a esta hipótesis y presenta un modelo en el que introduce información asimétrica, mediante un modelo de juego repetido a la Barro-Gordon. Sin embargo en los dos casos mencionados anteriormente, supone que mayores niveles de inflación crean mayor incertidumbre inflacionaria en el futuro, dándose una relación positiva entre ambas variables y que la dirección de causalidad va de la inflación a la incertidumbre, Rocabado (2009). Sin embargo, la hipótesis de Friedman (1977) va más allá de afirmar la existencia de una relación positiva entre inflación e incertidumbre inflacionaria. Como paso adicional en ese trabajo Friedman postula también la existencia de una relación negativa entre incertidumbre inflacionaria y crecimiento económico. La incertidumbre actuaría distorsionando la eficacia de los precios como mecanismo de asignación eficiente de recursos en una economía, generando a un efecto adverso sobre el crecimiento del output. La evidencia empírica que investiga la interacción entre incertidumbre inflacionaria y crecimiento económico, se da en Fountas et al. (2006), Fountas y Karanasos (2007) y Fountas (2010). Por último, aunque tradicionalmente se atribuye a Friedman (1977) el haber planteado por primera vez esta relación, fue Artur Okun (1971) el primero en argumentar que la política monetaria es más impredecible en momentos de elevada inflación, lo que justificaría esa relación positiva desde inflación hacia incertidumbre inflacionaria. En sentido opuesto a la hipótesis de Friedman. Pourgerami y Maskus (1978) y Ungar y Zilberfarb (1993) plantean que en un ambiente de inflación creciente los agentes pueden invertir más recursos en predecir la inflación de forma que entre ésta y la incertidumbre inflacionaria se establecería una relación negativa, aunque la literatura sobre la misma es escasa.
Por su parte Cukierman y Meltzer (1986) y Cukierman (1992) postulan un modelo en el cual al banco central le desagrada la inflación pero, al mismo tiempo, este se predispone a actuar de manera oportunista y así aprovechar el periodo de incertidumbre para crear sorpresas inflacionarias mediante el uso de políticas de corte monetario expansivo. Asimismo los autores trabajan bajo el supuesto de que existen componentes aleatorios en el proceso de oferta del dinero y la función objetiva de los políticos. Por lo mismo, cuando existe una inflación elevada en una economía, los agentes económicos no tienen certeza de que factores han causado esta alza de precios y suponen que la misma se debe a un cambio en la oferta monetaria o a las preferencias del banco central. Esta incertidumbre fomenta al banco central para crear inflación inesperada. En resumen, Cukierman (1992) supone de que existe una relación positiva entre los niveles de incertidumbre inflacionaria e inflación y que la dirección de causalidad va de la incertidumbre a la inflación. Devereux (1989) extiende el trabajo de Cukierman y Meltzer (1986) indicando que en economías con bajos niveles de indiciación salarial, los policymakers tienen un incentivo adicional para crear sorpresas en la inflación, dando lugar a mayores tasas medias de inflación. De esta forma la hipótesis Cukierman-Meltzer-Devereux de comportamiento oportunista de la autoridad monetaria anticipa una relación positiva desde incertidumbre (inflacionaria) hacia inflación.
Al contrario, Holland (1995); Grier y Perry (1998) mencionan como la incertidumbre inflacionaria es costosa para cualquier economía, el banco central puede actuar de manera estabilizadora. En otras palabras, el temor a la incertidumbre sobre niveles de inflación futuros puede fomentar al banco central a disminuir los niveles de inflación para así minimizar los costos de la incertidumbre. Por lo tanto, Grier y Perry (1996) usan el término de que la incertidumbre inflacionaria tiene efectos perversos en la economía debido al estudio que realizaron para la economía americana, en cuyos resultados muestran que mayores niveles de incertidumbre inflacionaria están asociados a una caída en la tasa de crecimiento económico en Estados Unidos. Asimismo, Grier y Perry (1998) muestran que en el grupo G-7, solamente los Bancos Centrales más independientes (Estados Unidos y Alemania) han actuado de esta manera (es decir se cumpliría la hipótesis de Holland, Grier y Perr). En ese sentido, Cukierman ordena los bancos centrales de 68 países desde 1, lo más independientes, a 68, lo menos independientes. En donde Alemania y Estados Unidos reciben las calificaciones de 2 y 5, en cuyos países se habría cumplido esta última hipótesis. En síntesis, Holland (1995); Grier y Perry (1998) suponen de que existe una relación negativa entre los niveles de incertidumbre inflacionaria y la inflación, y que cambios en el nivel de incertidumbre preceden temporalmente a cambios en el nivel de inflación. En este documento de investigación, se probarán las tres hipótesis mencionadas para el caso de Bolivia.
3Metodología para estimar incertidumbre inflacionariaA la hora de estimar la incertidumbre inflacionaria existen generalmente dos estrategias; primero la estrategia de encuestas y segundo la estrategia de modelos de predicción, la primera utiliza encuestas realizadas a consumidores y economistas. Una aproximación para medir la incertidumbre inflacionaria a partir de las encuestas es pedir al encuestado un rango sobre sus expectativas de inflación y ver qué tan amplios son estos rangos a través de la muestra. Una segunda aproximación se basa simplemente en la dispersión que muestran las expectativas puntuales de los individuos encuestados. Sin embargo Zamowitz y Lambros (1987) debaten el uso de las encuestas como una aproximación de la incertidumbre inflacionaria y mencionan que esta metodología tiene la desventaja de que la encuesta sólo muestra la gama de desacuerdo entre los pronosticadores y no representa bien el grado de incertidumbre en la economía. Es muy probable que cada encuestado tenga mucha incertidumbre sobre su pronóstico, pero los resultados muestran estimaciones semejantes.1
El segundo método para estimar la incertidumbre inflacionaria utiliza modelos econométricos de pronóstico para proyectar la inflación futura. Así grandes errores de proyección del modelo, implican mayor incertidumbre, y viceversa. Así, la incertidumbre está asociada a la dificultad de predecir la inflación.
En ese sentido Holland (1993) y Golob (1993) señalan que la incertidumbre del modelo de Cukierman (1992) puede ser capturado correctamente como una medida de la varianza del componente estático de la variable. Es decir, solo con un Modelo Garch y/o una de sus familias, que mide las innovaciones no esperadas y no la varianza, se lograría representar la incertidumbre de Cukierman y Meltzer. Por lo mismo antes de la aparición de los modelos de las familias Arch de Engle (1982) y el modelo más generalizado de Bollerslev (1986) Garch, las medidas comúnmente utilizadas, fueron la dispersión transversal de las proyecciones realizadas por un panel de analistas y la desviación estándar móvil de la variable en estudio. El principal inconveniente que presentaban estas medidas era su incapacidad para diferenciar variabilidad de incertidumbre. Por lo mismo la metodología Garch y sus familias, permiten estimar un modelo para la varianza condicional de la parte no predecible de la variable, lo que por otra parte se ajusta mejor al concepto de incertidumbre que postulan Friedman, Ball, Cukierman y Meltzer, entre otros.
Al mismo tiempo el uso de los modelos de las familias Arch, permitiría estimar tanto las ecuaciones en promedio y la ecuación de la varianza condicional para las variables en estudio y así poder probar de manera conjunta las tres hipótesis de estudio para el caso de Bolivia. Además, la evidencia empírica muestra que la inflación tiende generalmente a mostrar signos de heteroscedasticidad condicional significativa, por dos razones fundamentales: la primera debido a las grandes fluctuaciones en los índices de precios al consumidor de los distintos países y segundo por los problemas hiperinflacionarios que tuvo en anteriores décadas varios países de Sudamérica, de tal forma que la utilización de mínimos cuadrados ordinarios (en lugar de Arch) daría como resultado estimaciones ineficientes. A su vez Robert Engle (1983) recalca que es mucho mejor, con respecto a la eficiencia de los estimadores, usar un modelo de las familias Arch cuando existen indicios de heteroscedasticidad, Loria (2007); Loria et al. (2009) y Sánchez et al. (2009). Por todo lo señalado anteriormente es que para el caso de Bolivia se utiliza los modelos de las familias Arch para probar las hipótesis de estudio.
En el trabajo de investigación se combinarán las metodologías Sarima (Autoregressive Integrated Moving Average)2 y Garch (General Autoregressive Conditional Heteroskedasticity) tomando como proxy de inflación la variación mensual del Índice de Precios al Consumidor de Bolivia (ipc) para el periodo 1990:01-2013:03. De este modo se puede estimar tanto la media condicional, como la varianza condicional, a través de métodos de máxima verosimilitud. La modelación de la serie de inflación inicialmente se modela a través de un proceso Sarima, basándose en la información contenida en la serie en los periodos anteriores, es decir, en los rezagos de la serie y capturando la estacionalidad de la misma. Así, se obtienen los errores de predicción para cada periodo. La utilización de un modelo Garch, por su parte, permite obtener una serie temporal de la varianza de los errores que sirve como aproximación de la incertidumbre bajo la línea de Holland (1993) y Golob (1993).
Utilizando el paquete estadístico3 sugiere un modelo Arima(1,1,2) (0,1,1), con lo cual el paquete sugiere una diferenciación, dos parámetros de medias móviles en la parte regular y un parámetro autorregresivo en la misma parte regular, así como una diferenciación y un parámetro de medias móviles en la parte estacional. También el modelo identifica una de serie (outliers).
Tomando como base el modelo sugerido anteriormente, se realizó varias pruebas sobre la misma, específicamente salvaguardando que nuestro modelo final cumpla fundamentalmente los supuestos de no autocorrelación de los errores, estabilidad del modelo Sarima final4 y que tenga los valores más grandes en valor absoluto de los criterios estadísticos no paramétricos (akaike, schwarz) que es lo deseable en modelos de series de tiempo.5 En esa línea los mejores resultados se obtuvieron para un modelo con una diferenciación tanto en la parte regular como estacional, un componente ar(1), ar(6) y ma(3) en la parte regular y un componente sma(1) en la parte estacional, incluyendo también una dummy de intervención para octubre 2003.6 La estimación del modelo se presenta en el cuadro 1, entre otras cosas se sugiere una alta significancia de las variables con estadísticos “t” mayor a dos en valor absoluto y la ausencia de correlación entre los errores a través de la prueba de Breusch-Godfrey.7 Sin embargo, se requiere verificar si la varianza residual de la inflación es constante en el tiempo, para lo cual se incluye en el cuadro 1 el estadístico para el test Arch,8 que evalúa si la varianza de los residuos, ¿t, es constante. El test indica que se rechace la hipótesis nula de existencia de un proceso con varianza constante, que la misma se puede advertir en el anexo nro. 2 (cuadro A3 y gráfico A6), en vista de lo cual se puede modelar el proceso de varianza condicional para los residuos por medio de los modelos autoregresivos de heterocedasticidad condicional Arch.
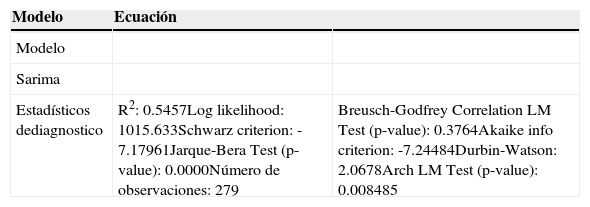
Modelo Sarima para la inflación en Bolivia
| Modelo | Ecuación | |
|---|---|---|
| Modelo | ||
| Sarima | ||
| Estadísticos dediagnostico | R2: 0.5457Log likelihood: 1015.633Schwarz criterion: -7.17961Jarque-Bera Test (p-value): 0.0000Número de observaciones: 279 | Breusch-Godfrey Correlation LM Test (p-value): 0.3764Akaike info criterion: -7.24484Durbin-Watson: 2.0678Arch LM Test (p-value): 0.008485 |
Elaboración propia de los autores
Cabe recalcar que las pruebas de diagnóstico del modelo Sarima se encuentran en el anexo nro. 2, la misma nos confirma que el modelo del cuadro 1 no tiene problemas de autocorrelación a través de la prueba de Breusch-Godfrey, por su parte el estadístico Jarque-Bera nos confirma que existe problemas de normalidad de los residuos, que podría deberse a las fluctuaciones que existe en la variable índice de precios al consumidor en los periodos de volatilidad, la misma que provoca que su distribución sea leptocurtica y sesgada a la derecha, dando lugar a outliers (+) relacionados con choques inflacionarios y outliers (-) con choques deflacionarios, como es el caso del año 2001, 2002, Rocabado (2009). Asimismo en el anexo nro. 2, se muestra que el modelo del cuadro 1 tiene problemas de efectos Arch, en vista de lo cual se puede modelar el proceso de varianza condicional para los residuos por medio de los modelos autoregresivos de heterocedasticidad condicional Arch, y finalmente también se verifica la estabilidad del modelo, por lo que las raíces características son menores a la unidad o dicho en otras palabras se encuentran dentro del circulo unitario,9Loria (2007).
Mientras, que las pruebas de raíz unitaria aplicadas a la serie índice nacional de precios al consumidor de frecuencia mensual, se encuentran en el anexo nro. 1 (Cuadro A1), dichas pruebas raíz unitaria son con y sin quiebre estructural, las pruebas confirman que la variable índice de precios al consumidor de Bolivia, sigue un proceso integrado de orden I(1).
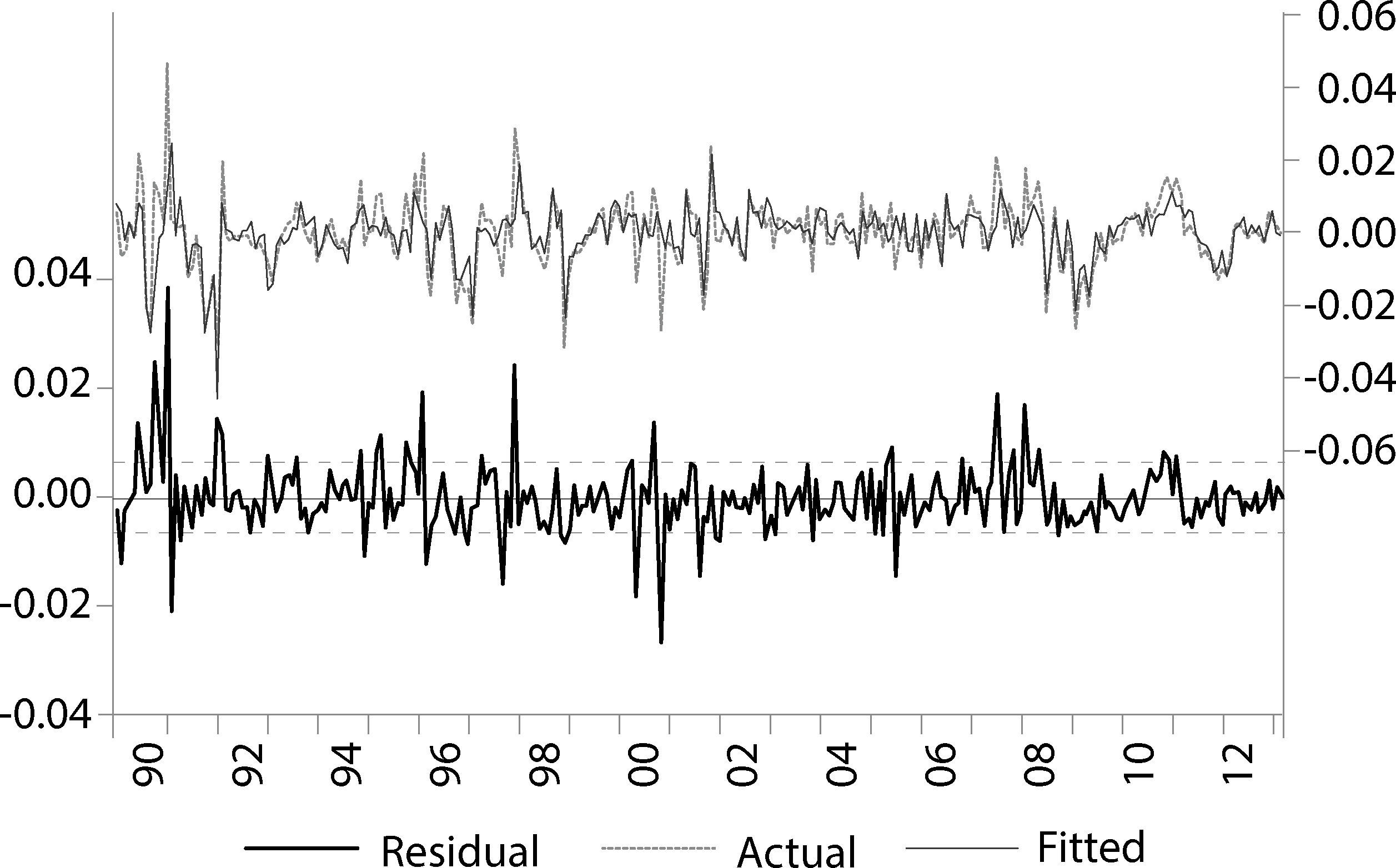
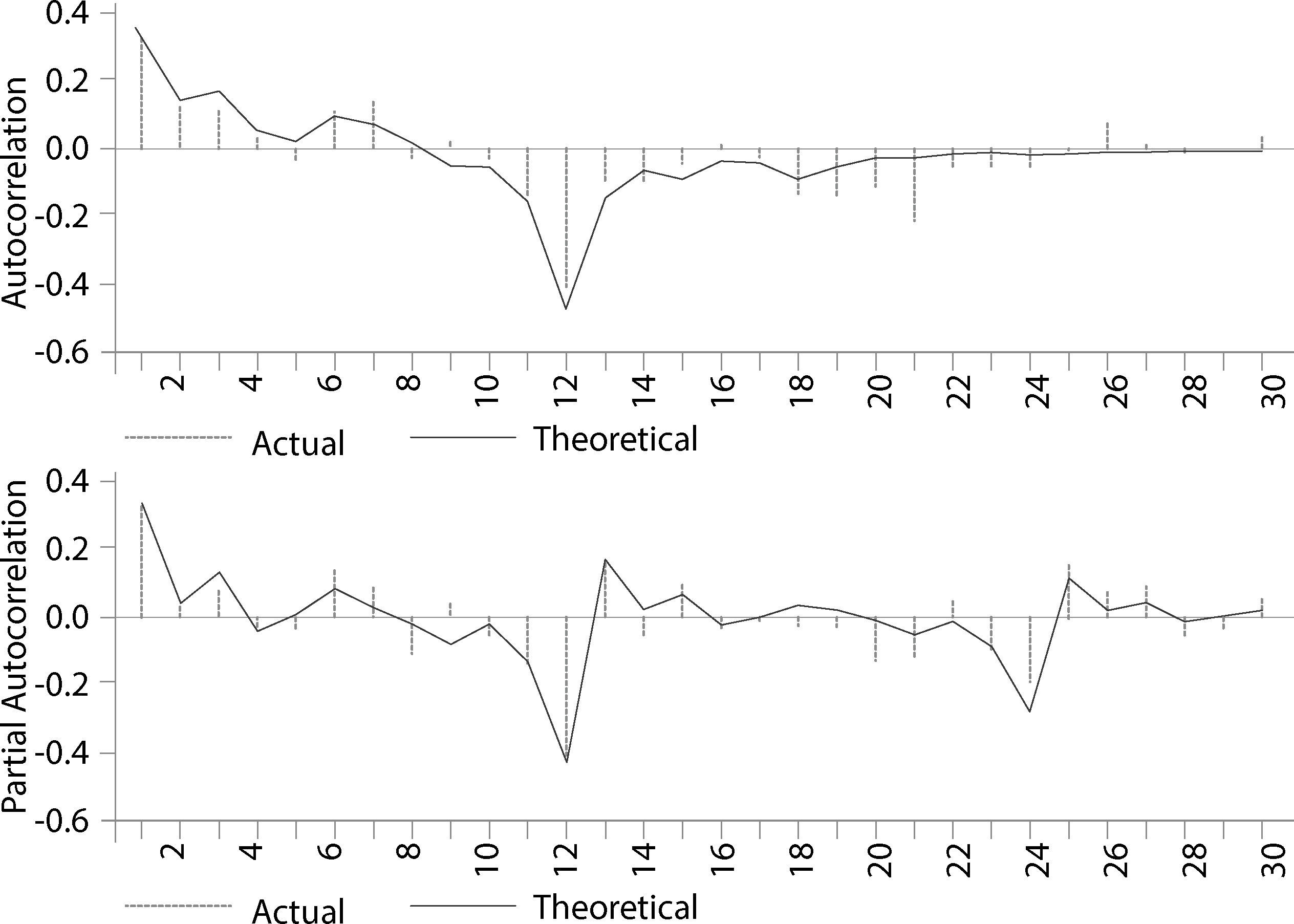
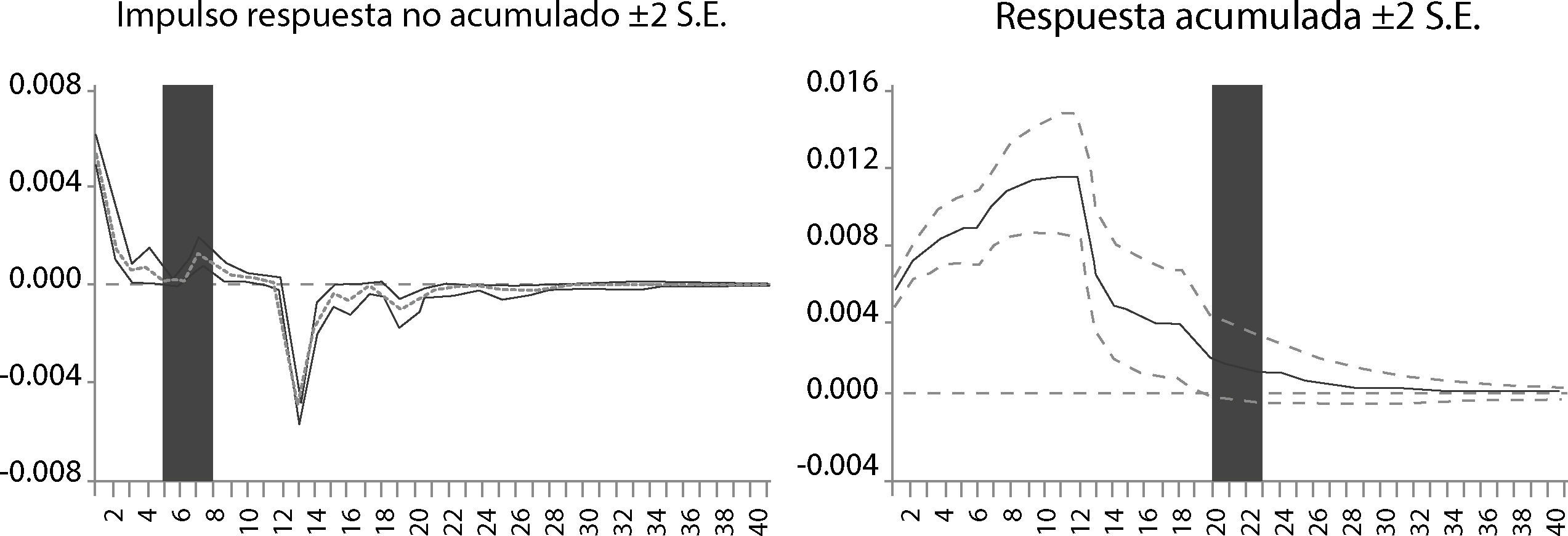
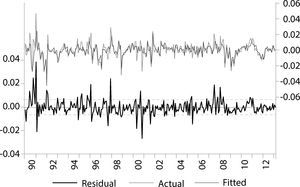
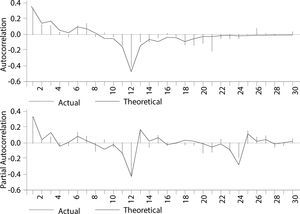
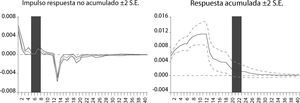
La gráfica 1 nos muestra el valor actual y pronosticado del modelo sarima estimado del cuadro 1. Se puede advertir que existe un buen ajuste entre el valor actual (linea color rosa) y el valor pronosticado por nuestro modelo (gráfica 1). Asimismo, tambien se muestra en la gráfica 2 los correlogramas del modelo del cuadro 1. Por otro lado, en la gráfica 3 se muestran las funciones impulso respuesta que en un modelo ARMA, correctamente especificado, teóricamente se esperaría que la respuesta ante una innovación desaparezca en forma asintótica, Loria (2007); Loria et al. (2009) y Sánchez et al. (2009), es decir que tienda a cero en un horizonte de corto plazo.10 Esto es un indicador de que el modelo es estacionario. En tanto el impulso respuesta acumulado deberá tender al valor de largo plazo de la variable que se está modelando, también en un horizonte de corto plazo.
En este caso se advierte que la respuesta acumulada y sin acumular de la tasa de inflación (dlog (ipc,1,12)), debido al impulso de un shock equivalente al valor de una unidad de desviación estándar de la innovación, es positivo, estadísticamente significativo y además desaparece en forma asintótica en un lapso no más de 10 meses en promedio.
Por último, hay que recordar que el estadístico para el test Arch, que evalúa si la varianza de los residuos, ¿t del modelo Sarima del cuadro 1, es constante. La prueba11 indica que se rechace la hipótesis nula de existencia de un proceso con varianza constante, en vista de lo cual se puede modelar el proceso de varianza condicional para los residuos por medio de modelos de las familias Arch, Loria (2007), y así tener una aproximación correcta de la incertidumbre bajo la línea de Holland (1993) y Golob (1993).
3.1Modelos ArchEl modelo Arch de Engle (1982), en el caso general Arch (m) es:
Donde, α0 ≥ 0, αi ≥ 0, i=1,2,…, m, y {¿t} es una secuencia de variables aleatorias que se distribuyen idéntica e independientemente (i.i.d.) con media 0 y varianza unitaria. Por lo tanto, según nuestras estimaciones econométricas, el mejor modelo de las familias Arch, que tiene los mejores criterios estadísticos no paramétricos (akaike, schwarz)12, resulto ser, un Arch (4).
3.1.1Estimación con una especificación estocástica Arch (4)Se postula entonces el modelo siguiente para la varianza condicional σt2.
La estimación de la ecuación (2) por medio del método máximo de verosimilitud proporciona los resultados presentados en el cuadro 2. Se puede ver que los parámetros estimados βQMVson significativos debido a que tienen una Z-estadístico mayor a dos en valor absoluto.
Modelo Arch (4)
| Modelo | Ecuación | |
|---|---|---|
| Media | ||
| Arch (4) | ||
| Varianza | ||
| Arch (4) | ||
| Estadísticos dediagnostico | R2: 0.5442Log likelihood: 1042.525Schwarz criterion: -7.27146Número de observaciones: 279 | Akaike info criterion: -7.401611Durbin-Watson: 2.13727Arch LM Test (p-value): 0.8796 |
| Condición de estacionariedad del proceso Arch (4): | ∑εi^2=0.674<1 |
Elaboración propia de los autores
El supuesto más importante de ésta estimación, reside en que la condición ∑εi^2<1 de estacionaridad del proceso Arch tiene que verificarse, en este caso se puede afirmar que se verifica tal supuesto de estacionariedad.
Al mismo tiempo, los resultados señalan que el mejor modelo que se ajustó a la información mensual fue un modelo Arch (4) ya que éste presentó en valor absoluto los valores más grandes de criterios estadísticos13 no paramétricos. Al mismo tiempo, al realizar el cálculo del test Arch para esta variante del modelo, no se puede rechazar la hipótesis nula de un proceso no Arch de los residuos. Es decir, se ha identificado un modelo adecuado para remover el problema de heteroscedasticidad autoregresiva.
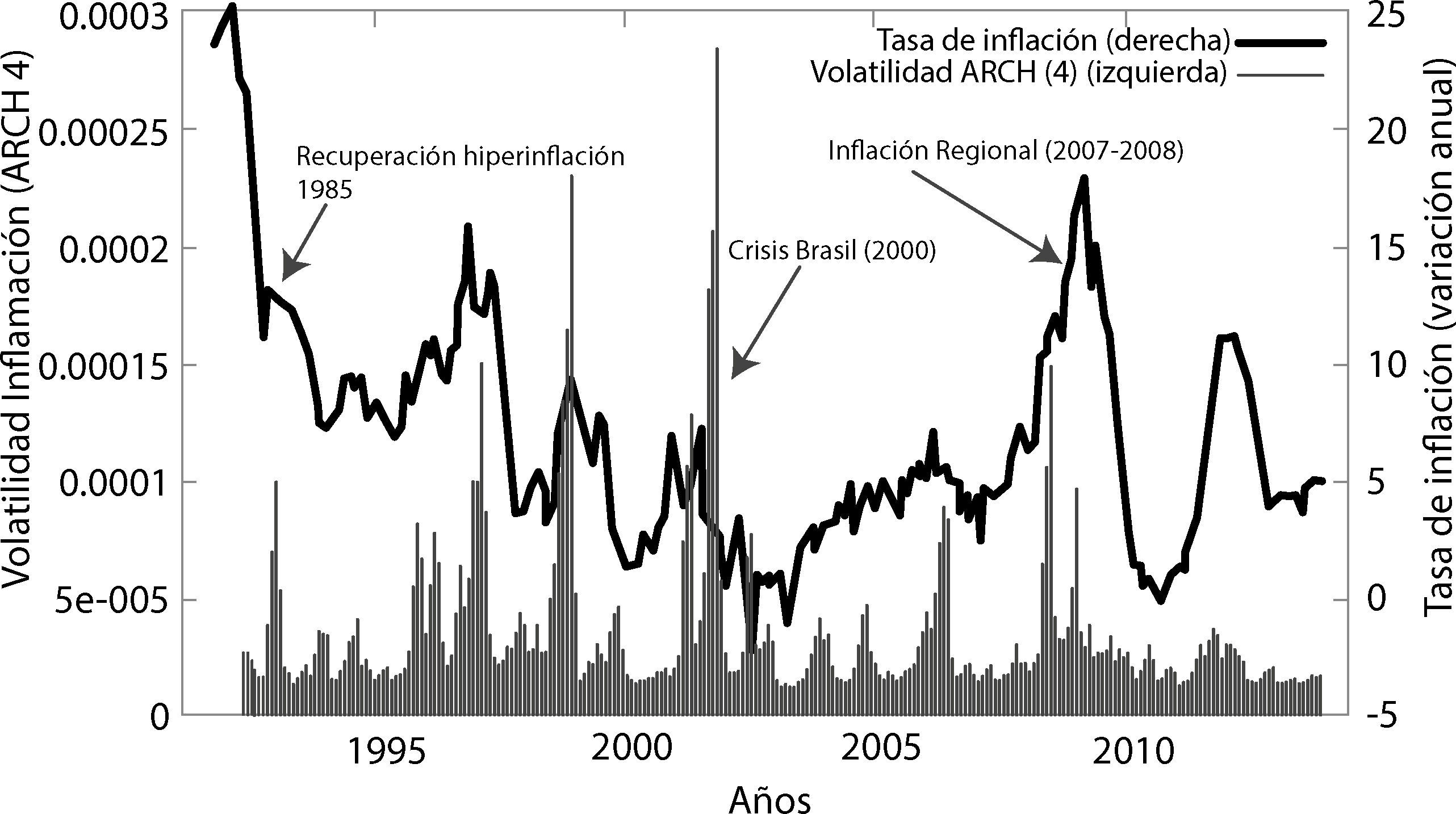
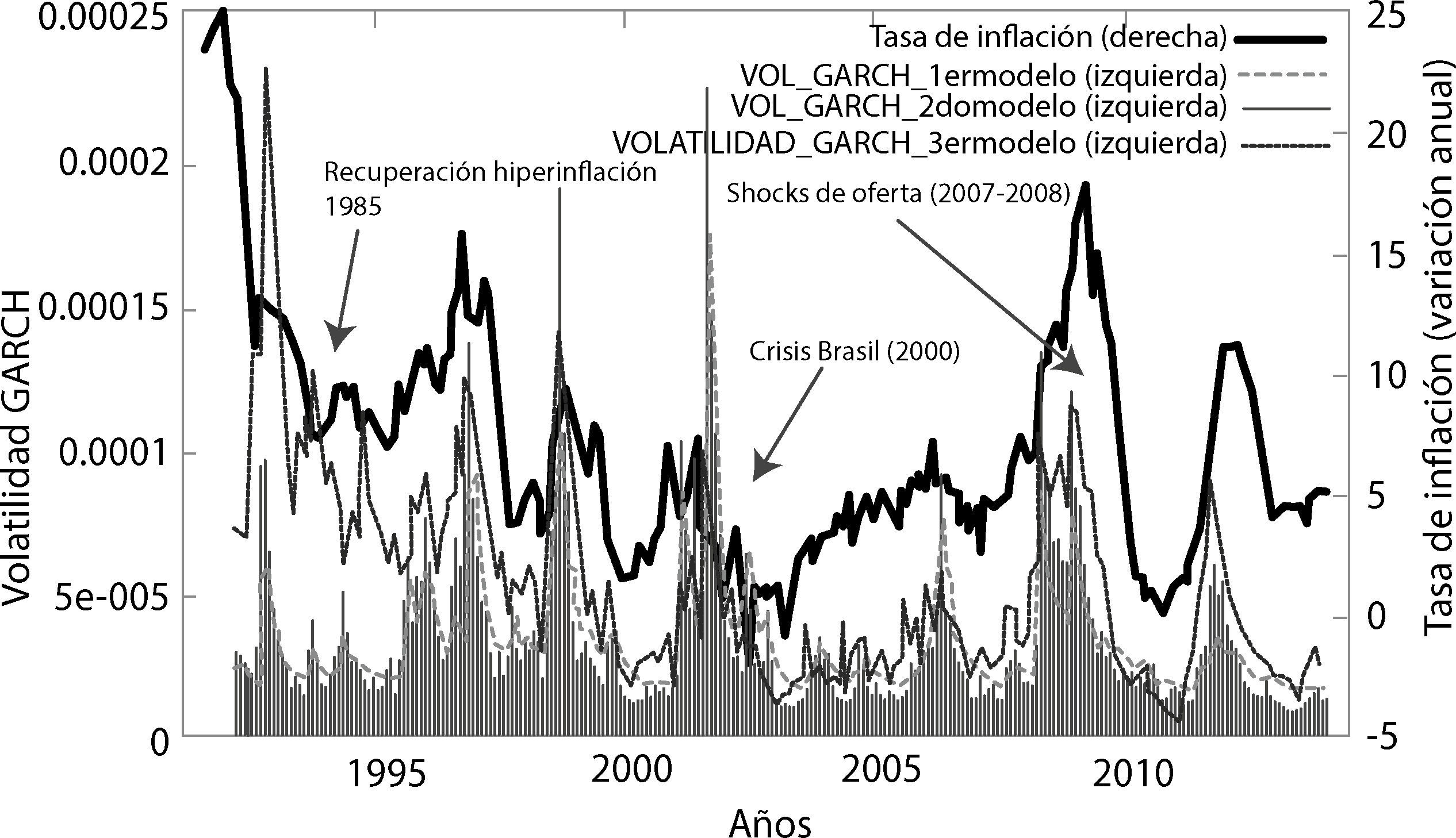
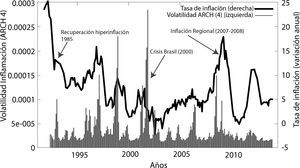
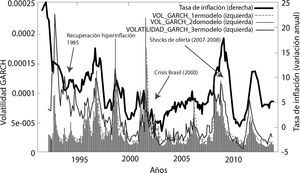
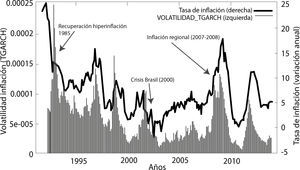
En la gráfica 4 se puede advertir que a principios de los 90 existen picos pronunciados de volatilidad debido al proceso de recuperación de la economía boliviana de la hiperinflación que se dio a mitad de los años 80. Por otro lado a principios del nuevo siglo, se dio la devaluación del real brasileño (efecto samba) que provoco que la economía boliviana pueda caer incluso en fase de deflación. Asimismo los años 2007 y 2008 se da dos crisis: primero, la crisis subprime y segundo una inflación regional que se debió en gran parte a un incremento inusitado del precio de las materias primas y energía, lo que en el contexto de la economía de Bolivia se conoció como el efecto de la inflación importada, Mendieta y Rodríguez (2008).
3.2Modelos GarchSi se introduce el mecanismo de aprendizaje para la varianza condicional σt2 en un proceso Garch (1,1)-M14.
Donde ϖt representa la tasa de inflación mensual; ¿t es un error estocástico que mide las innovaciones impredecibles en la inflación; σt es la desviación estándar condicional de ¿t, la cual representa la incertidumbre inflacionaria. La ecuación (3.1) representa la ecuación para la tasa de inflación media, y es la que utilizan los agentes para proyectar la inflación. Como se puede ver, esta depende en nuestro caso de los componentes (ar y ma y sar y sma) que fueron detectados en la estimación del modelo sarima del cuadro nro. 1 y de rezagos de la incertidumbre inflacionaria σt-k.
Al mismo tiempo éste sistema permite probar todas las hipótesis a la vez. Para determinar si un aumento en la tasa de la inflación causa más incertidumbre, es necesario investigar el signo y el significado del parámetro γ2 de la ecuación 3.2. Los modelos de Friedman y Ball pronosticarían que γ2 fuera positivo y significativo. Por otro lado, para distinguir entre las dos hipótesis sobre el comportamiento del banco central cuando enfrente un aumento en la incertidumbre de la inflación, el parámetro clave es χk de la ecuación 3.1. Un valor de χk> O de la ecuación 3.1 sería consecuente con los pronósticos del modelo de Cukierman y Meltzer, donde el banco central actúa de una manera oportunista. Asimismo, un valor de χk< O sería consecuente con la idea de Holland (1995) y Grier & Perry (1998), que el banco central puede actuar de una manera estabilizadora. Cabe recalcar que estas tres hipótesis se evalúan tanto en el modelo Garch-M, asimismo como en el EGarch-M.
Los resultados de la estimación son presentados en el cuadro 3. Los Z-estadísticos los parámetros estimados βQMV son parecidos a los de la especificación Arch (4) y en su mayoría son significativos al 0.05 de significancia, nuevamente, la condición de estacionaridad α1+γ1<1 se verifica en los modelos 1, 2 y 3 del cuadro 3.
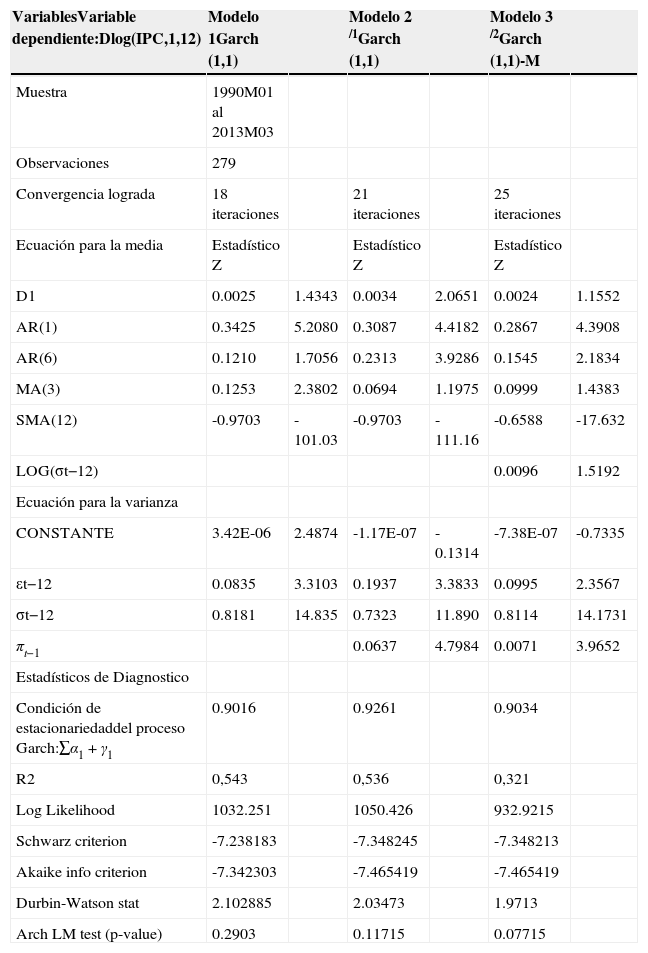
Modelo Garch (1,1)
| VariablesVariable dependiente:Dlog(IPC,1,12) | Modelo 1Garch (1,1) | Modelo 2 /1Garch (1,1) | Modelo 3 /2Garch (1,1)-M | |||
|---|---|---|---|---|---|---|
| Muestra | 1990M01 al 2013M03 | |||||
| Observaciones | 279 | |||||
| Convergencia lograda | 18 iteraciones | 21 iteraciones | 25 iteraciones | |||
| Ecuación para la media | Estadístico Z | Estadístico Z | Estadístico Z | |||
| D1 | 0.0025 | 1.4343 | 0.0034 | 2.0651 | 0.0024 | 1.1552 |
| AR(1) | 0.3425 | 5.2080 | 0.3087 | 4.4182 | 0.2867 | 4.3908 |
| AR(6) | 0.1210 | 1.7056 | 0.2313 | 3.9286 | 0.1545 | 2.1834 |
| MA(3) | 0.1253 | 2.3802 | 0.0694 | 1.1975 | 0.0999 | 1.4383 |
| SMA(12) | -0.9703 | -101.03 | -0.9703 | -111.16 | -0.6588 | -17.632 |
| LOG(σt−12) | 0.0096 | 1.5192 | ||||
| Ecuación para la varianza | ||||||
| CONSTANTE | 3.42E-06 | 2.4874 | -1.17E-07 | -0.1314 | -7.38E-07 | -0.7335 |
| εt−12 | 0.0835 | 3.3103 | 0.1937 | 3.3833 | 0.0995 | 2.3567 |
| σt−12 | 0.8181 | 14.835 | 0.7323 | 11.890 | 0.8114 | 14.1731 |
| πt−1 | 0.0637 | 4.7984 | 0.0071 | 3.9652 | ||
| Estadísticos de Diagnostico | ||||||
| Condición de estacionariedaddel proceso Garch:∑α1+γ1 | 0.9016 | 0.9261 | 0.9034 | |||
| R2 | 0,543 | 0,536 | 0,321 | |||
| Log Likelihood | 1032.251 | 1050.426 | 932.9215 | |||
| Schwarz criterion | -7.238183 | -7.348245 | -7.348213 | |||
| Akaike info criterion | -7.342303 | -7.465419 | -7.465419 | |||
| Durbin-Watson stat | 2.102885 | 2.03473 | 1.9713 | |||
| Arch LM test (p-value) | 0.2903 | 0.11715 | 0.07715 |
Elaboración propia de los autores.
/1 Se prueba la hipótesis de Friedman y Ball, donde se incluye la inflación como regresor en la ecuación de la varianza para el modelo 2 del cuadro 3.
/2 Se prueba la hipótesis de Friedman y Ball, donde se incluye la inflación como regresor en la ecuación de la varianza para el modelo 3 del cuadro 3. Asimismo se prueba la hipótesis de Cukierman y Metlze, para el mismo efecto se incluye el logaritmo de la varianza condicional de la inflación en la ecuación de la media del modelo 3 del cuadro 3.
En referencia al modelo Garch se estima el proceso Garch (1,1) y Garch (1,1)-M ya que solamente este tipo de modelo, permite cuantificar si la volatilidad condicional crecerá en el futuro o no, con la simple suma de los coeficientes de los términos Arch y Garch. Los resultados se presentan a continuación.
Los resultados enmarcados en el cuadro 3 (modelos 1, 2 y 3) muestran que los procesos Garch (1,1) con y sin inclusión de la inflación como regresor en la varianza condicional, fueron significativos para el periodo de análisis, utilizando un nivel de significancia del 5% tanto para la media, así como la ecuación de la varianza. De igual manera podemos apreciar que la suma de los coeficientes en ambos procesos Garch (α1+γ1<1), la misma que sugiere que la volatilidad de la inflación, tiende a disminuir en el futuro.
Para probar la hipótesis respecto a la relación entre la inflación promedio y la incertidumbre de la inflación se puede utilizar un modelo estadístico Garch(1,1) con la inflación desfasada en un periodo en la ecuación de la varianza condicional del modelo 2 (cuadro 3). Esto permite probar directamente si el nivel de la inflación en este periodo afecta significativa y positivamente la varianza de la inflación en el siguiente período. Los resultados se presentan en el modelo 2 (cuadro 3). El mismo indica que el nivel de inflación aumenta significativamente la varianza condicional de la inflación a un nivel de 0.063 significativo al 0.01 de nivel de significancia. Esto representa una primera evidencia en favor de la Hipótesis de Friedman y Ball de que un aumento en la tasa de la inflación causa una mayor incertidumbre inflacionaria.
Mientras el modelo 3 (cuadro 3) una estimación de Garch (1,1)-Media con la inflación en la ecuación de la varianza condicional y la varianza estimada de los errores en la ecuación de la media de inflación, estaría, al igual que el modelo 2 (cuadro 3), confirmando la Hipótesis de Friedman y Ball y al mismo tiempo, también se confirmaría la Hipótesis de Cukierman y Metzler, por lo que niveles de incertidumbre inflacionaria más bajos llevan a niveles promedio de inflación más bajos.
Por lo tanto, la ecuación de la varianza para los dos modelos Garch aproxima la varianza condicional de la inflación no esperada y viene a constituirse en una medida de la incertidumbre inflacionaria. Todos los coeficientes de esta ecuación son significativos al nivel del 1%. La inclusión de los parámetros Garch elimina el proceso heteroscedástico de los residuos como lo indica el test Arch.15
Por lo tanto, hasta el momento se constató que las especificaciones Arch (4) y Garch (1,1) cumplen con una condición teórica importante: la estacionaridad débil del proceso.
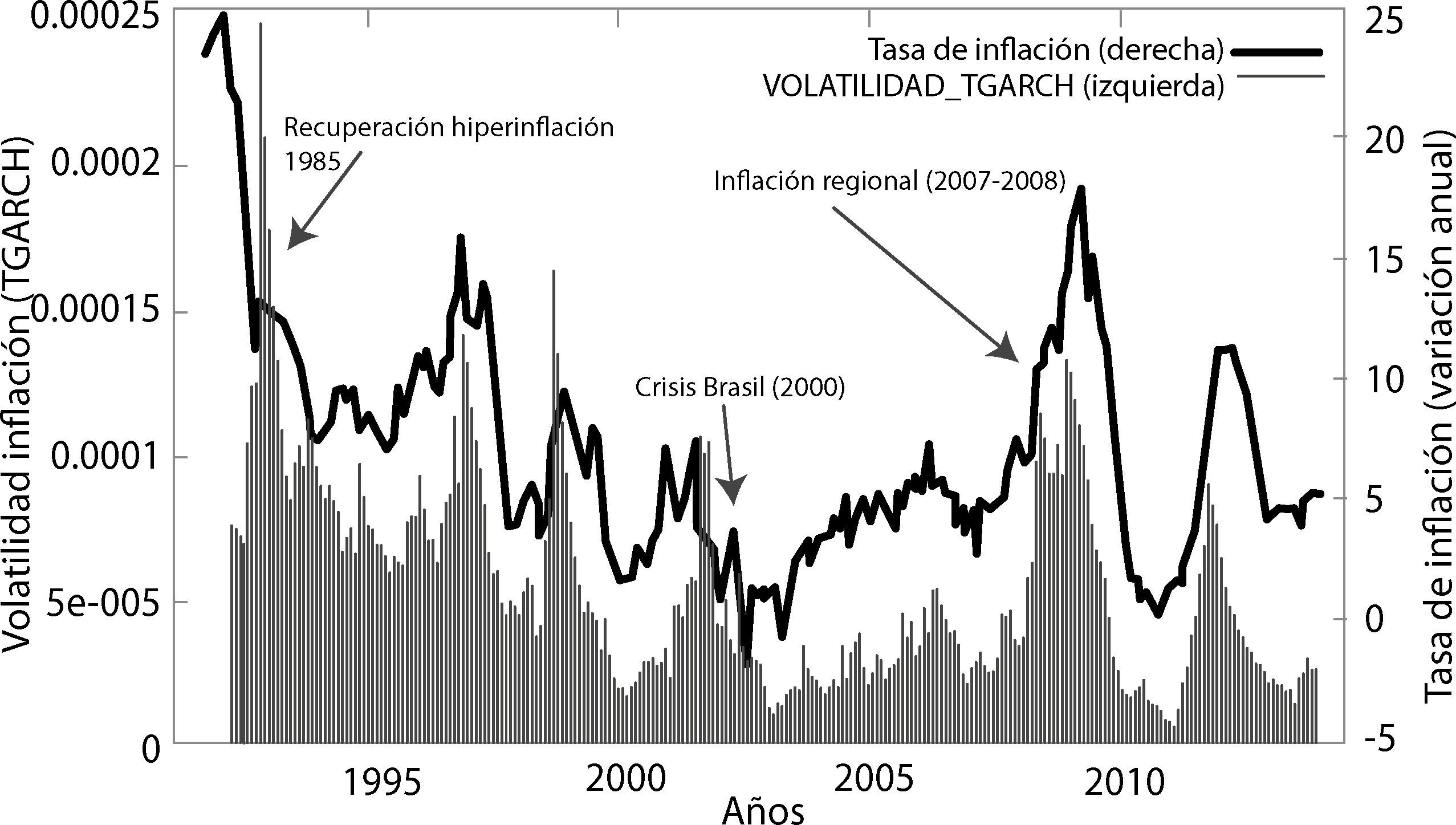
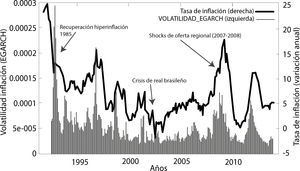
En las gráficas 5 de volatilidad, las áreas sombreadas de colores, representan los periodos de volatilidad, por ejemplo en los años 90 existe picos pronunciados debido al proceso de desinflación que se daba en la economía boliviana, producto de la inflación elevada de los 85, los periodos de 1995, 1996, 2007, 2008 y 201016 tienen un común denominador, ya que la volatilidad se debe a shocks de oferta, es decir un incremento inusitado en los precios de los commodities internacionales, materias primas y precio de la energía, demanda nacional insatisfecha, producto en muchos casos por el desabastecimiento de bienes de primera necesidad, por fenómenos climatológicos (fenómeno del niño y niña), conflictos sociales y a ello se suma, para los años 2007 y 2008 una fuerte apreciación de las monedas de los principales socios comerciales de Bolivia. Para el año 2000 y 2001 la volatilidad se debe al efecto que tuvo la devaluación brasileña (efecto samba) en las monedas de los países latinoamericanos, Humerez (2004), la misma que provoco que la economía Bolivia en los años 2000 incluso haya tenido el riesgo de caer en deflación (tasas de inflación menores a cero). Por último, para los años 2009 y 2010 se tiene un contraste de resultados, por un lado el año 2009 cierra con una tasa de inflación acumulada a diciembre del 2009 de 0.29%, que fue la segunda tasa de inflación más baja de Latinoamérica, solo por detrás de Perú, pero el 2010 la inflación nuevamente aumente de manera suave, explicado en parte por fenómenos climatológicos naturales.
3.3Modelos TGarch17Una desventaja que presenta la especificación Garch es que impone simetría en los shocks de inflación. El coeficiente del termino Arch (α1) del Modelo Garch (1,1) de la ecuación 3.2, recoge los efectos de los shocks sin distinguir entre el signo de los mismos. Si la varianza condicional de los errores responde de manera distinta a shocks negativos y positivos, se estaría incurriendo en un error de especificación en la especificación Garch (1,1)-M.
Por su parte, como se mencionó, los modelos asimétricos permiten acomodar la asimetría producida por el “efecto apalancamiento” al capturar el efecto más fuerte que tienen los rendimientos negativos en la volatilidad. Por ejemplo, el modelo TGarch de Glosten, Jagannathan y Runkle (gjr) se puede expresar como:
En la ecuación 4, donde dt-i es una variable dummy que toma el valor de 1 si ξt-i < 0, y de 0 si ξt-i ≥ 0. El parámetro γi recoge la asimetría producida por valores negativos de ξt-i (efecto apalancamiento). Cuando se modela la volatilidad condicional en lugar de la varianza condicional se obtiene la versión de Zakoian (1994).
Una variante del modelo anterior permite que el parámetro Arch del primer rezago del error cambie, dependiendo de si el error rezagado excede cierto umbral (normalmente cero). Esta variante se conoce como TGarch (Threshold Garch) y permite evaluar si inflaciones por sobre lo esperado tienen un efecto sobre la incertidumbre distinto del que tendría una inflación menor a la esperada. Para capturar esta asimetría se hace depender a la varianza condicional de la magnitud y signo de los errores anteriores.
Por lo tanto la estimación del TGarch se encuentra en el cuadro 4.
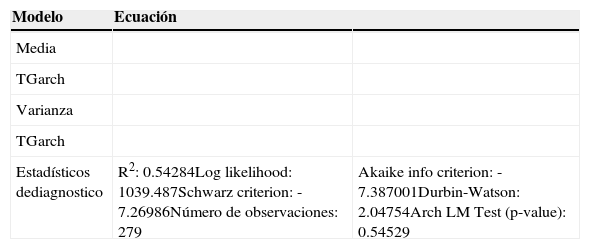
Modelo TGarch
| Modelo | Ecuación | |
|---|---|---|
| Media | ||
| TGarch | ||
| Varianza | ||
| TGarch | ||
| Estadísticos dediagnostico | R2: 0.54284Log likelihood: 1039.487Schwarz criterion: -7.26986Número de observaciones: 279 | Akaike info criterion: -7.387001Durbin-Watson: 2.04754Arch LM Test (p-value): 0.54529 |
Elaboración propia de los autores
El cuadro 4 presenta la estimación conjunta del modelo Arima-TGarch, el parámetro correspondiente al componente Threshold (εt−12 x d1) resulta significativo al 5% y con signo negativo. El resultado anterior sugiere la existencia de efectos asimétricos de la inflación sobre la incertidumbre. Por otra parte, el signo negativo del parámetro puede interpretarse en el sentido de que inflaciones por debajo de lo proyectado tienden a reducir la incertidumbre inflacionaria, pero esta reducción (en valor absoluto) es menor que el incremento que se presenta cuando la inflación supera las proyecciones. Es decir, una caída inesperada de la inflación no tiene el mismo impacto sobre la incertidumbre que en el caso contrario, un incremento inesperado de la inflación, siendo el impacto de este último mayor. Además, se puede argumentar que si el componente Threshold (εt−12 x d1) > 0 existe efecto leverage y si este Threshold (εt−12 x d1) es distinto de cero sugeriría la existencia de efectos asimétricos de la inflación sobre la incertidumbre, es decir que la incertidumbre en Bolivia ha tendido a incrementarse más cuando la inflación supera las expectativas que cuando esta es menor a la esperada. Ahora con relación al componente εt−12 nos confirmaría que los shocks positivos tienen un efecto positivo sobre la varianza de la inflación y si sumamos los componentes (εt−12;εt−12 x d1) tendremos el efecto de los shocks negativos.
Al realizar el cálculo del test Arch18 para esta variante del modelo, no se puede rechazar la hipótesis nula de un proceso no Arch de los residuos. Es decir, se ha identificado un modelo adecuado para remover el problema de heteroscedasticidad autorregresiva.
3.4Modelos EGarchOtro modelo capaz de recoger asimetrías es el modelo EGarch ó modelo Garch exponencial, propuesto por Nelson (1991)Nelson, 1991b. La especificación de la varianza condicional viene dada por la ecuación 5.2. Se puede observar que la varianza condicional viene transformada en logaritmos, y esta representación garantiza la no negatividad de la misma e implica que el efecto apalancamiento es exponencial, en lugar de cuadrático. La presencia de efectos asimétricos ocurre cuando γi ≠ 0 y se puede hablar de efecto apalancamiento cuando γi < 0. El modelo de Nelson (1991)Nelson, 1991b es utilizado en esta sección, y además utilizaremos la metodología de Berument et al. (2001) y Bello y Gámez (2006), con la finalidad de averiguar si se cumple las tres hipótesis que se plantearon en el documento.
Al mismo tiempo este sistema permite probar todas nuestras hipótesis a la vez. Para determinar si un aumento en la tasa de la inflación causa más incertidumbre, necesitamos investigar el signo y el significado del parámetro ψs de la ecuación 5.2. Los modelos de Friedman y Ball pronosticarían que ψs fuera positivo y significativo. Por otro lado, para distinguir entre las dos hipótesis sobre el comportamiento del banco central cuando enfrente un aumento en la incertidumbre de la inflación, el parámetro clave es χk de la ecuación 5.1. Un valor de χk> O sería consecuente con los pronósticos del modelo de Cukierman y Meltzer, donde el banco central actúa de una manera oportunista. Asimismo, un valor de χk< O sería consecuente con la idea de Holland (1995) y Grier & Perry (1998), que el banco central puede actuar de una manera estabilizadora.
Asimismo en la ecuación 5.1, donde ϖt representa la tasa de inflación mensual; ¿t es un error estocástico que mide las innovaciones impredecibles en la inflación; σt es la desviación estándar condicional de ¿t, la cual representa la incertidumbre inflacionaria; y Tend en la ecuación 5.2, es una variable de tendencia. Por último, la ecuación (5.2) nos da la varianza condicional del error de estimación en logaritmo (log σt2) que está en función de ¿t−1/σt−1 el error rezagado estandarizado, el error rezagado estandarizado en valor absoluto |¿t−1/σt−1|, de un rezago de ella misma, de un término de tendencia (tend) y de rezagos de la tasa de inflación.
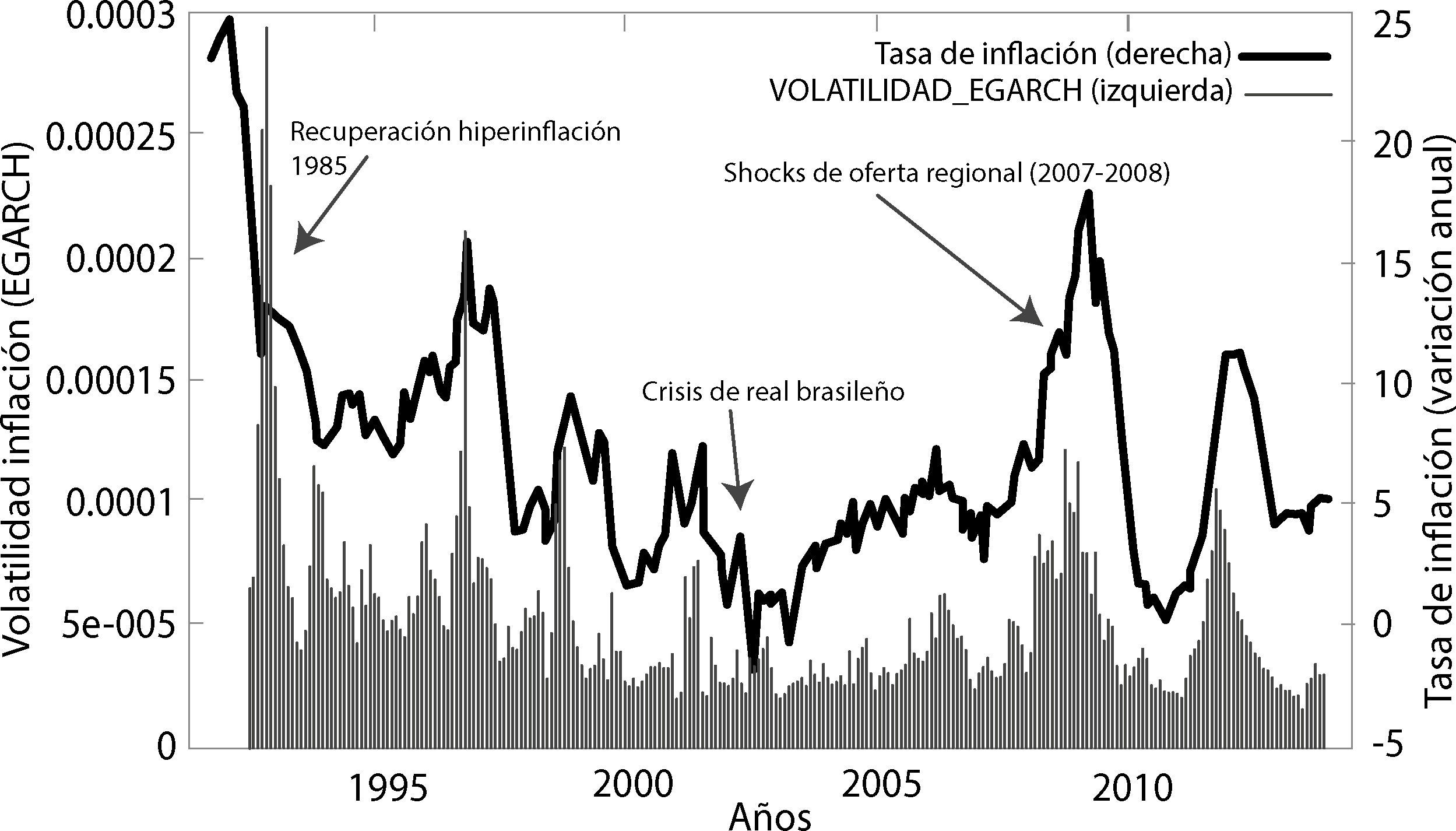
Con relación al componente εit−1σit−12 como es distinto de cero, afirma que primero, los shocks son asimétricos, luego como es significativo al 1% y con signo positivo, implica que shocks positivos de inflación tienen un impacto mayor sobre la incertidumbre inflacionaria que shocks negativos de la misma magnitud. De hecho, el efecto estimado de los shocks positivos en el presente modelo EGarch-M tiene el mismo signo y son significativos al 1% al estimado en el modelo TGarch, 0.2447 vs. 0.1611, respectivamente.
El coeficiente asociado a la tendencia (Tend) es negativo y estadísticamente significativo al 10%, lo cual indica que la incertidumbre inflacionaria ha tenido una tendencia decreciente en el tiempo. Esto puede ser el resultado de una mayor comprensión de los agentes del modelo que rige a la economía, así como del buen desenvolvimiento del Banco Central de Bolivia para mantener tasas de inflación bajas.
La hipótesis de Ball y Friedman (πt−s>0) no es rechazada a un nivel de significancia de 1%, de hecho es de magnitud elevada, por lo que se valida la hipótesis de que en Bolivia, mayores niveles de inflación están asociados con mayor incertidumbre inflacionaria, cuyo resultado es similar a la estimación de Garch (1,1)-M (Cuadro 3, modelo 3). Este resultado es de suma importancia, ya que sería uno de los principales argumentos de la autoridad monetaria para perseguir políticas que conduzcan a niveles bajos de inflación.
La hipótesis de Cukierman y Metzler(σt−k2>0) no es rechazada al 10% de significancia, aunque hay que reconocer que su magnitud es muy baja, pero ello indicaría que niveles de incertidumbre inflacionaria más bajos llevan a niveles promedio de inflación más bajos. Por lo tanto, rechazamos la hipótesis de Holland, Grier & Perry al nivel 0.10 mientras que no podemos rechazar la hipótesis de Cukierman & Metzler al mismo nivel.
El primer resultado sobre La hipótesis de Ball y Friedman muestra un costo potencial real de la inflación en Bolivia. Es decir, si la incertidumbre de la inflación es costosa para la economía, un alto nivel de inflación es costosa también porque una tasa elevada de esta causa incertidumbre. El segundo resultado muestra evidencia a favor de la hipótesis de Cukierman y Metzler, aunque este último sus coeficientes no son de magnitud significativa.
Por ultimo se puede afirmar que ni la Hipótesis de Holland, Grier y Perry ni la Hipótesis de Cukierman y Metzler se cumplen para el caso de Bolivia, pese que para esta última hipótesis, existe una evidencia a favor parcial, pero de magnitud leve y a un nivel de significancia del 0.10.
3.5Modelos ParchModeliza las potencias de la desviación típica. Originalmente fue propuesto por Taylor (1986) y Schwert (1989) para modelizar las desviaciones típicas y posteriormente fue generalizado por Ding et al. (1993).
Donde δ>0, |γi|≤, 1 i=1, ..., r, γi=0i>ryr≤p Obsérvese que si δ=2 y todos los coeficientes γi son nulos, se tiene la especificación del modelo Garch simétrico. La ecuación 6.1, donde ϖt representa la tasa de inflación mensual; ¿t es un error estocástico que mide las innovaciones impredecibles en la inflación; σt es la desviación estándar condicional de ¿t, la cual representa la incertidumbre inflacionaria; y Tend en la ecuación 6.2, es una variable de tendencia.
La ecuación (6.1) representa la ecuación para la tasa de inflación media, y es la que utilizan los agentes para proyectar la inflación. Asimismo, la ecuación (6.2) da a conocer la ecuación en varianza para la tasa de inflación y es la que nos interesa para probar las tres hipótesis que nos hemos planteado en un principio.
Si se cumple la hipótesis de Ball y Friedman, el parámetro ψs de la ecuación 6.2 debería ser estadísticamente significativo con signo positivo. Por otro lado, si se cumple la hipótesis de Cukierman y Meltzer, el parámetro χk de la ecuación de la media 6.1 debería ser positivo y estadísticamente significativo.
El coeficiente asociado a la tendencia (Tend) en la ecuación de la varianza es negativo y estadísticamente significativo al 1% de significancia, lo cual indica que la incertidumbre inflacionaria ha tenido una tendencia decreciente en el tiempo. Esto puede ser el resultado como lo señalamos anteriormente de un buen desenvolvimiento del Banco Central de Bolivia para mantener una macroeconomía con una inflación controlada.
Asimismo La hipótesis de Ball y Friedman (πt−s>0) en la ecuación de la varianza no es rechazada a un nivel de significancia de 1%, por lo que validaríamos la hipótesis de que en Bolivia, mayores niveles de inflación están asociados con mayor incertidumbre inflacionaria, cuyo resultado es similar a la estimación de Garch (1,1)-M (Cuadro 3, modelo 3) y al modelo E-Garch del cuadro 5.
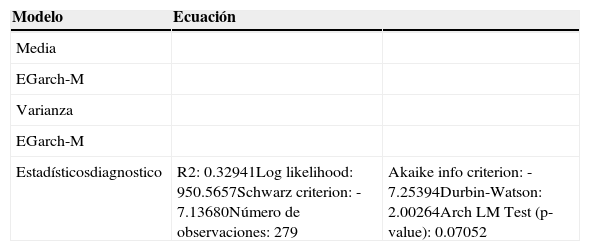
Modelo EGarch-M
| Modelo | Ecuación | |
|---|---|---|
| Media | ||
| EGarch-M | ||
| Varianza | ||
| EGarch-M | ||
| Estadísticosdiagnostico | R2: 0.32941Log likelihood: 950.5657Schwarz criterion: -7.13680Número de observaciones: 279 | Akaike info criterion: -7.25394Durbin-Watson: 2.00264Arch LM Test (p-value): 0.07052 |
Elaboración propia de los autores
La hipótesis de Cukierman y Metzler(σt−k2>0) en la ecuación de la media no es rechazada, aunque hay que reconocer que su magnitud es muy baja y no significativa, pero el signo del coeficiente asociado a esta variable, indicaría que niveles de incertidumbre inflacionaria más bajos llevan a niveles promedio de inflación más bajos.Tabla 6
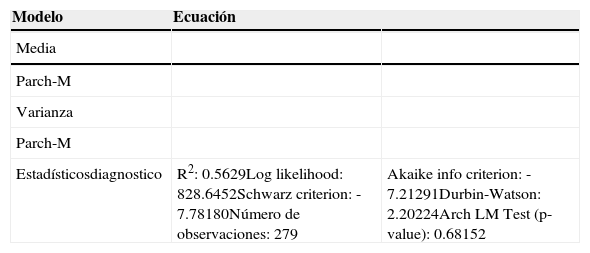
Modelo Parch-M
| Modelo | Ecuación | |
|---|---|---|
| Media | ||
| Parch-M | ||
| Varianza | ||
| Parch-M | ||
| Estadísticosdiagnostico | R2: 0.5629Log likelihood: 828.6452Schwarz criterion: -7.78180Número de observaciones: 279 | Akaike info criterion: -7.21291Durbin-Watson: 2.20224Arch LM Test (p-value): 0.68152 |
Elaboración propia de los autores
Con relación a la negación de la hipótesis de Holland, Grier y Perry, en los modelos Garch-M, EGarch-M y Parch-M podemos afirmar que este resultado es muy interesante, ya que los autores muestran que en el grupo G7, solo los Bancos Centrales que gozan de más independencia (E.U.A. y Alemania) se han comportado de esta forma (se cumple la hipótesis de Holland, Grier y Perr). En ese sentido, Cukierman realiza una ordenación de los bancos centrales de 68 países en estudio, y califica desde 1, lo más independientes, a 68, lo menos independientes. Los resultados del autor muestran que E.U.A. y Alemania reciben calificaciones de 2 y 5, de tal forma que para ambos países se cumpliría la hipótesis de Holland, Grier y Perry. Sin embargo respecto a este tema, existe una discusión debido a que es posible que las calificaciones de la independencia de los Bancos Centrales sólo tengan sentido para los países desarrollados. Por lo mismo, Alberto Alesina (1988) y Grilli, Masciandaro y Tabellini (1991) encuentran una relación entre la independencia de un Banco Central y el nivel de inflación promedio, pero ellos restringen su muestra a los países muy desarrollados. Ello implica que de alguna forma los resultados de investigación de los últimos autores podrían estar sesgados a favor de países industrializados. Por último, Cukierman (1992) habla un poco del problema de separar la realidad y la ficción en los países no desarrollados. Hay países que tienen reglas y cartas especificando que el Banco Central es independiente. Por ultimo podemos afirmar que ni la Hipótesis de Holland, Gier y Perry ni la Hipótesis de Cukierman y Metzler se cumplen para el caso de Bolivia, pese que para esta última hipótesis, existe una evidencia a favor parcial, pero de magnitud leve y a un nivel de significancia del 0.10.
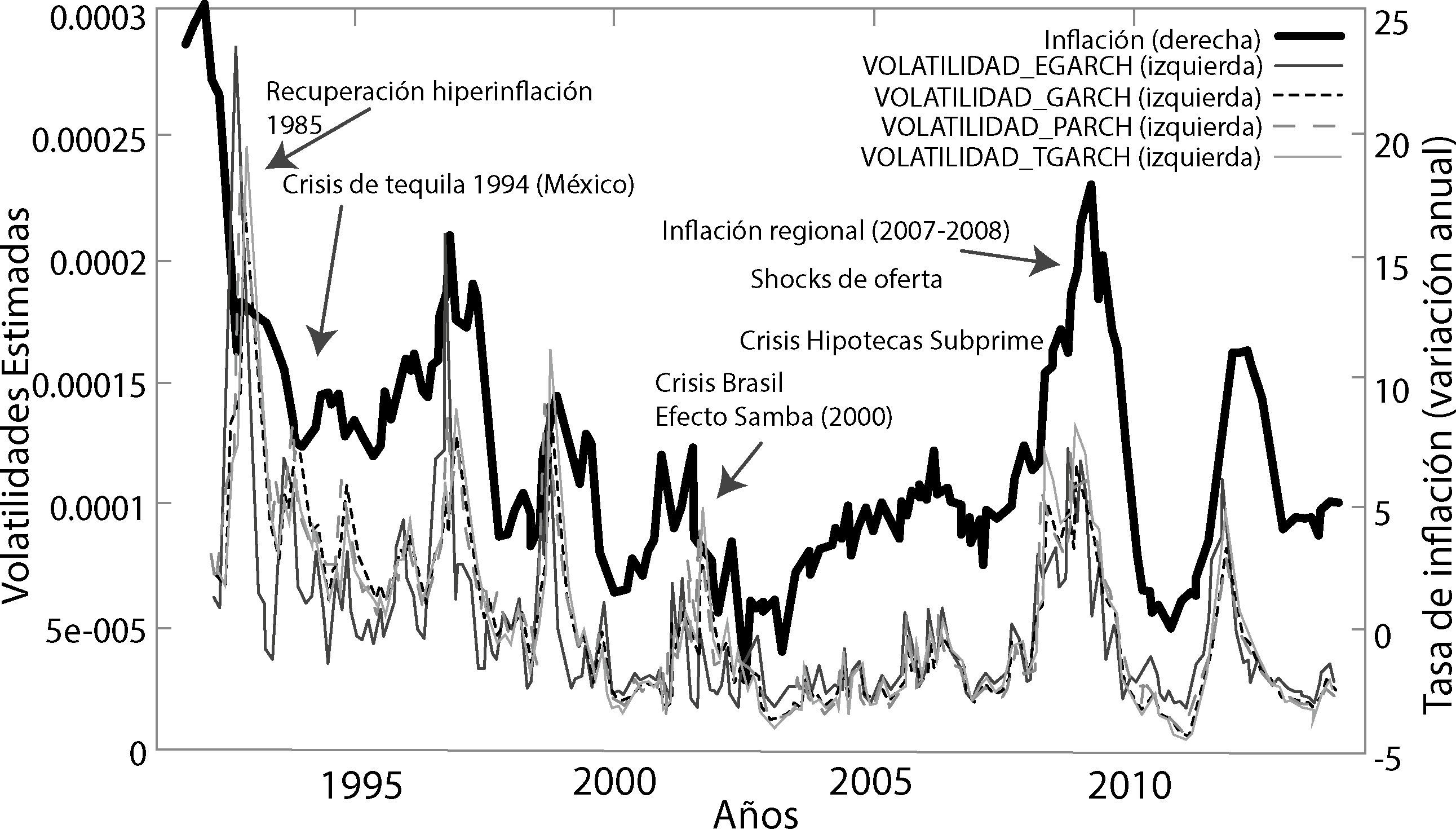
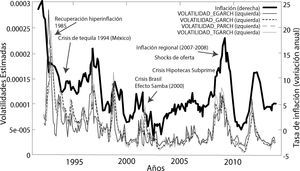
En el gráfico 8 se puede advertir de manera clara, la relación directa que existe entre la tasa de inflación de Bolivia y las volatilidades estimadas a través de los modelos Parch-M, EGarch-M, Garch-M y TGarch
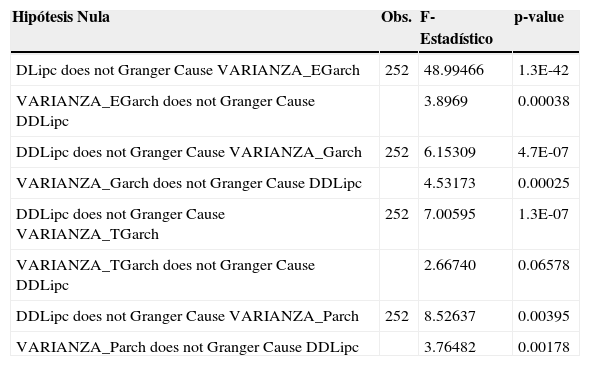
3.6Causalidad de GrangerEstimado la incertidumbre inflacionaria, por medio de la técnica Parch-M, EGarch-M, TGarch y Garch-M, es necesario vincularlo con la tasa de inflación. El mismo puedo realizarse por medio de una evaluación de la causalidad en el sentido de Granger, buscando evidencia estadística para determinar si el nivel de la inflación causa en el sentido de Granger al nivel de la incertidumbre.19 Los resultados de las pruebas de causalidad en el sentido de Granger se presentan en el cuadro 7, tanto para la medida Parch-M, EGarch-M, TGarch y Garch de incertidumbre inflacionaria. Para las cuatro medidas, tomando en cuenta un rezago óptimo de 12 periodos, se rechaza a un 1% de significancia la hipótesis nula de que la inflación no causa, en el sentido de Granger, una mayor incertidumbre inflacionaria. Por el contrario la hipótesis nula de que la incertidumbre no causa, en el sentido de Granger, una mayor inflación no se puede rechazar solo en el modelo TGarch. Los resultados anteriores, sugieren que existe evidencia de que una mayor inflación precede temporalmente una mayor incertidumbre inflacionaria, con lo cual se confirma, para el caso de Bolivia, la hipótesis enunciada por Friedman y Ball y con menor magnitud la hipótesis de Cukierman y Metzler.
Tests de causalidad o precedencia de Granger /1 Sample: 1990M01 2013M03
| Hipótesis Nula | Obs. | F-Estadístico | p-value |
|---|---|---|---|
| DLipc does not Granger Cause VARIANZA_EGarch | 252 | 48.99466 | 1.3E-42 |
| VARIANZA_EGarch does not Granger Cause DDLipc | 3.8969 | 0.00038 | |
| DDLipc does not Granger Cause VARIANZA_Garch | 252 | 6.15309 | 4.7E-07 |
| VARIANZA_Garch does not Granger Cause DDLipc | 4.53173 | 0.00025 | |
| DDLipc does not Granger Cause VARIANZA_TGarch | 252 | 7.00595 | 1.3E-07 |
| VARIANZA_TGarch does not Granger Cause DDLipc | 2.66740 | 0.06578 | |
| DDLipc does not Granger Cause VARIANZA_Parch | 252 | 8.52637 | 0.00395 |
| VARIANZA_Parch does not Granger Cause DDLipc | 3.76482 | 0.00178 |
Elaboración propia de los autores.
/1 La prueba de Precedencia de Granger se realiza con 12 rezagos, debido a que se trabaja con información mensual.
Los resultados finalmente conseguidos constatan la existencia de una relación causal positiva desde inflación e incertidumbre, algo habitual en la literatura, lo que supone respaldar la conocida como Hipótesis Friedman-Ball. Este primer resultado muestra un costo potencial de la inflación en Bolivia. Ello implica, que si la incertidumbre inflacionaria es costosa para la economía, niveles de inflación elevados es costoso también, porque una tasa elevada de esta causa incertidumbre y más aun teniendo el recuerdo del suceso económico de 1985, en esa línea es muy importante que el Banco Central de Bolivia siga aunando esfuerzos, para mantener una macroeconomía con inflación baja.
Con relación a la hipótesis de Cukierman y Metzler, el cual enfatiza la posibilidad de que existan comportamientos oportunistas por parte de la autoridad monetaria. Es decir, en momentos de elevada incertidumbre inflacionaria el banquero central podría encontrar un incentivo para generar “sorpresas” en el crecimiento monetario con el fin de estimular la economía se cumple para la economía de Bolivia, pero hay que reconocer que su magnitud es muy leve y aún nivel de significancia del 0.10. Así lo confirman tres de cuatro de las especificaciones estimadas como ser los Garch-M; EGarch-M y Parch-M. Con relación a la hipótesis de Holland, Grier y Perry, no se cumple para el caso de Bolivia. En esa línea Grier y Perry (1998) muestran que en el grupo G-7, solamente los Bancos Centrales de E.U.A. y Alemania, han actuado de esta manera.
Otro resultado muy importante es el efecto asimétrico de los shocks positivos. A partir de la especificación TGarch como de la EGarch-M se puede inferir que son los shocks positivos los que inciden en la varianza condicional de la inflación con un efecto pequeño de los shocks negativos. Estos resultados son relevantes para la política monetaria. Primero, ya que pudiera indicar que se necesite de un período relativamente largo de estabilidad de precios para revertir este resultado. Asimismo, y estando de acuerdo de que el principal objetivo del Banco Central es la estabilidad de precios y sabiendo que la varianza condicional de la inflación está más afectada por shocks positivos (ejemplo, un aumento no esperado en los precios de las materias primas, energía y/o combustibles), las autoridades monetarias a través de la consecución de niveles bajos de inflación podrían eximir a la economía boliviana de los efectos negativos que provoca la incertidumbre inflacionaria y que conllevan en última instancia una disminución de la actividad económica.
Se encuentra también evidencia de que la incertidumbre tiene una tendencia decreciente a través del tiempo, por medio del signo y significancia de la dummy de tendencia (tend) en los modelos EGarch-M y Parch-M, así como en la condición de estacionariedad débil del modelo Garch, que en los tres casos se debería fundamentalmente a la buena labor y desempeño de las autoridades monetarias, para promover la estabilidad de precios y así mantener una macroeconomía con inflación controlada.
Los documentos de investigación de Golob (1993) y de Holland (1993) dan a conocer un mix de resúmenes de artículos que usan estos dos métodos, incluyendo la medida usada para medir la incertidumbre.
Los modelos Arima son parte de la metodología habitual de series de tiempo y permiten estudiar el comportamiento de una variable aleatoria a través del tiempo, utilizando sólo la información contenida en la serie histórica de la propia variable. La forma genérica de un modelo Arima para una variable X se escribe en la terminología habitual de Box y Jenkins y su desarrollo se puede encontrar en Hamilton (1994).
Estimado por el paquete Tramo Seats.
La elección del modelo Sarima final del cuadro 1, se basó también en la elección de aquel modelo que tenga los mejores estadísticos no paramétricos (Criterios de Akaike y Schwarz), es decir eligiendo aquel que tenga los valores de Akaike y Schwarz más grandes en valor absoluto.
En modelos de series de tiempo es deseable que se cumpla los supuestos de no autocorrelación de los errores y estabilidad del modelo, con la finalidad de obtener estimadores eficientes. Véase William Greene, Análisis Econométrico, séptima edición (capítulos 20 y 21).
La dummy de pulso para octubre del 2003 se refiere a octubre negro de ese mismo año, que se debe a la defensa de gas natural de Bolivia, protagonizado por ciudadanos de a pie.
Es importante recordar que en los modelos autorregresivos los valores del R2 y R2 ajustado no se deben interpretar en su sentido tradicional y pierden relevancia, dado que en estos modelos lo que se tiene es un aprovechamiento de las correlaciones de las observaciones históricas de la misma variable para explicar su valor en el momento t (Veáse David A. Pierce, “R2 Measures for Time Series”, Journal fo the American Statistical Association, December 1979, Volumen 74, Number 368). Al mismo tiempo, los R2 tampoco deben ser interpretados a la ligera en los modelos de las familias Arch, debido a que se trata de modelos no lineales, en su lugar más bien se compara los criterios estadísticos no parametricos (Akaike, Hann-Quin, Schwarz) y el loglikelihood.
Arch LM Test (p-value):0.008485, afirmando que existe efectos Arch en el modelo Sarima del cuadro 1.
Más detalles en al anexo nro. 2 (Cuadro A4).
Se recomienda evaluar 24 meses, que precisamente es el valor que los software evalúan “por default”.
Véase anexo nro 2 (gráfico 2A.7 y gráfico 2A.7.1)
En la investigación se estima modelos Arch (1), Arch (2), Arch (3), Arch (4) y Arch (5), y se eligió como modelo final, el modelo Arch (4), ya que el mismo presentaba los criterios estadísticos no paramétricos más negativos o mayores en valor absoluto.
Con criterios estadísticos no paramétricos nos referimos a: Schwarz criterion, Akaike info criterion, etc. que son criterios que permiten seleccionar entre dos o mas modelos que compiten.
Garch significa “Generalized Autoregressive Conditional Heteroskedacity” y Garch-M es un modelo Garch con la varianza condicional incluido en la ecuación del promedio de variable dependiente. Véase Bollerslev (1986) y Engle, Liiien, & Robins (1987).
Véase el cuadro 3: Estadísticos de diagnosticó: Arch LM test (p-value)
A nivel mundial en los años 2007 y 2008 existió problemas inflacionarios, que se debieron a shocks de oferta (variación de los tipos de cambio, materias primas y energía), al mismo tiempo los shocks de oferta de los años 2007 y 2008, fueron acompañados por un aumento exacerbado de la demanda de materias primas y energía por parte de economías emergentes pujantes, tal es el caso de China e India, el resultado fue, un aumento de los precios de los productos básicos y bienes de primera necesidad, que en el caso de los productos agrícolas, algunos investigadores acuñaron el término de “Agflación” para referirse justamente al incremento de precios de productos agrícolas. En el caso de Bolivia, se establecieron distintas medidas monetarias y gubernamentales para contrarrestar la inflación en esos años, por ejemplo: la apreciación del tipo de cambio, operaciones de mercado abierto, el gobierno por su parte aplico dos medidas: como la subvención a la importación de productos de primera necesidad: harina, arroz y aceites y al mismo tiempo implemento un sistema impositivo para la exportación de productos de primera necesidad, ejemplo el aceite, todo ello con la finalidad de satisfacer la demanda nacional boliviana de los años 2007 y 2008.
Threshold Garch.
Véase el cuadro 4: Estadísticos de diagnosticó: Arch LM test (p-value)
La idea detrás de la prueba de causalidad de Granger es que si X causa Y, entonces cambios en X deberían preceder cambios en Y. Esta hipótesis es corroborada mediante regresiones donde se incorporan, como variables explicativas de la variable Y, no sólo los valores pasados de Y sino igualmente los de X y se estudia el grado de significancia de los coeficientes en estas últimas variables.