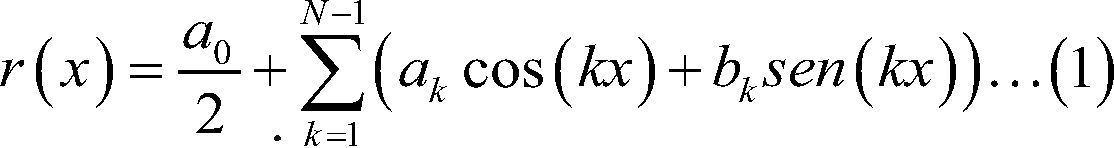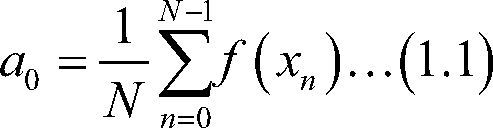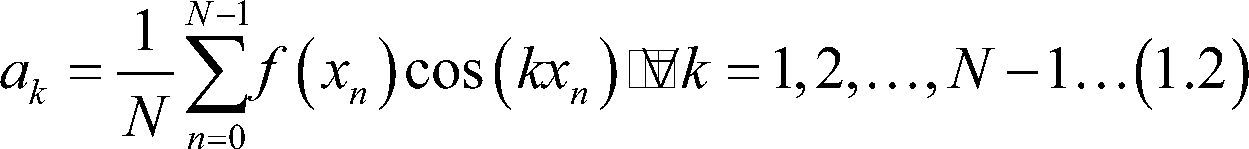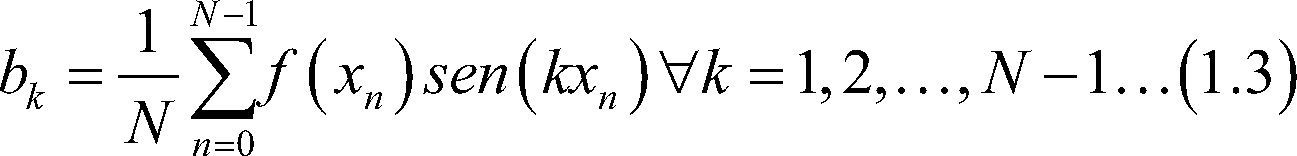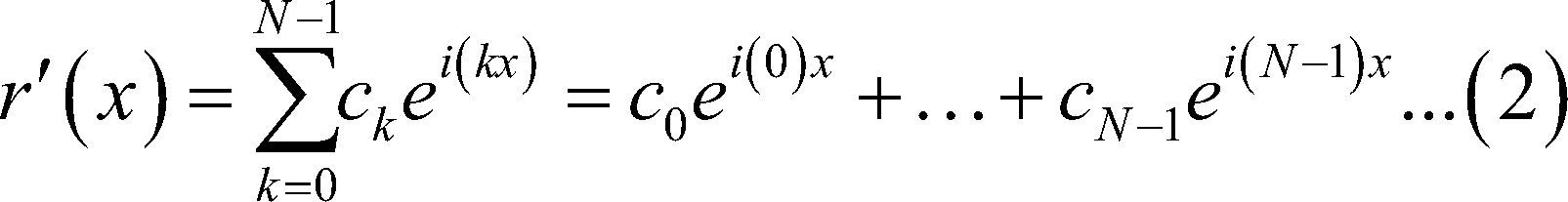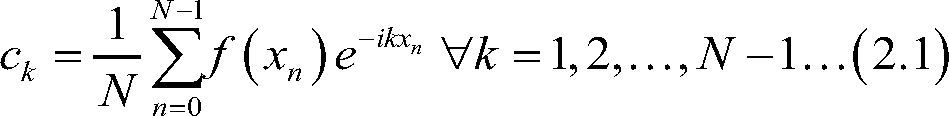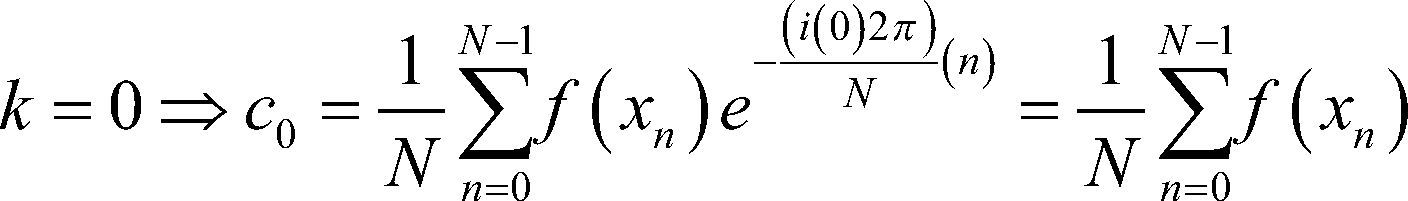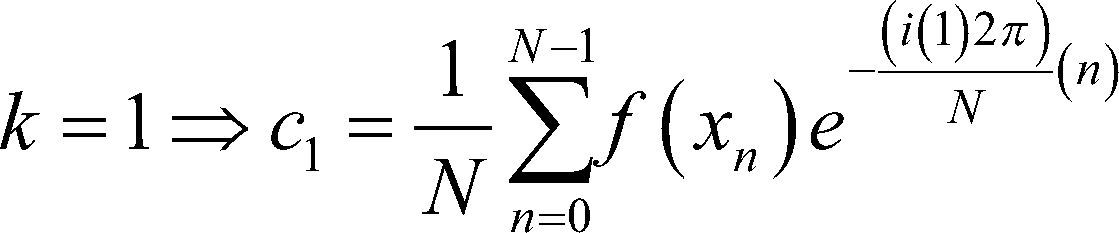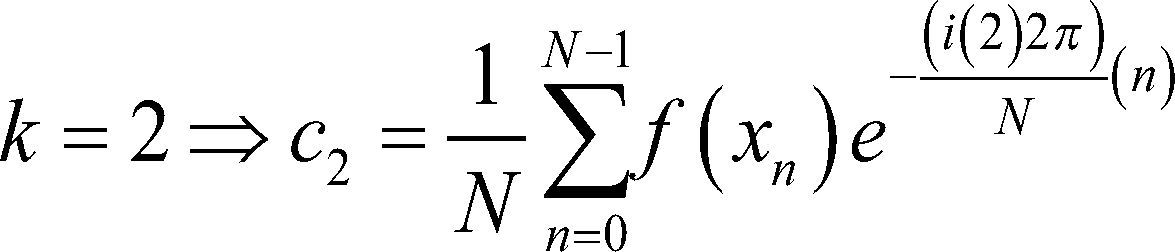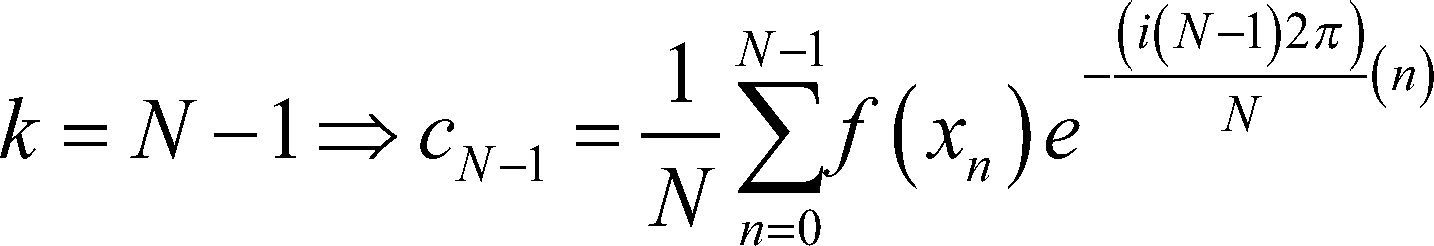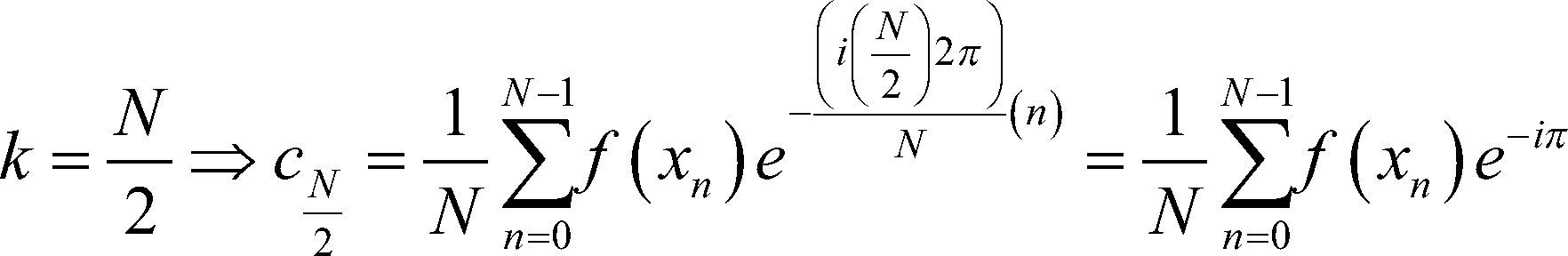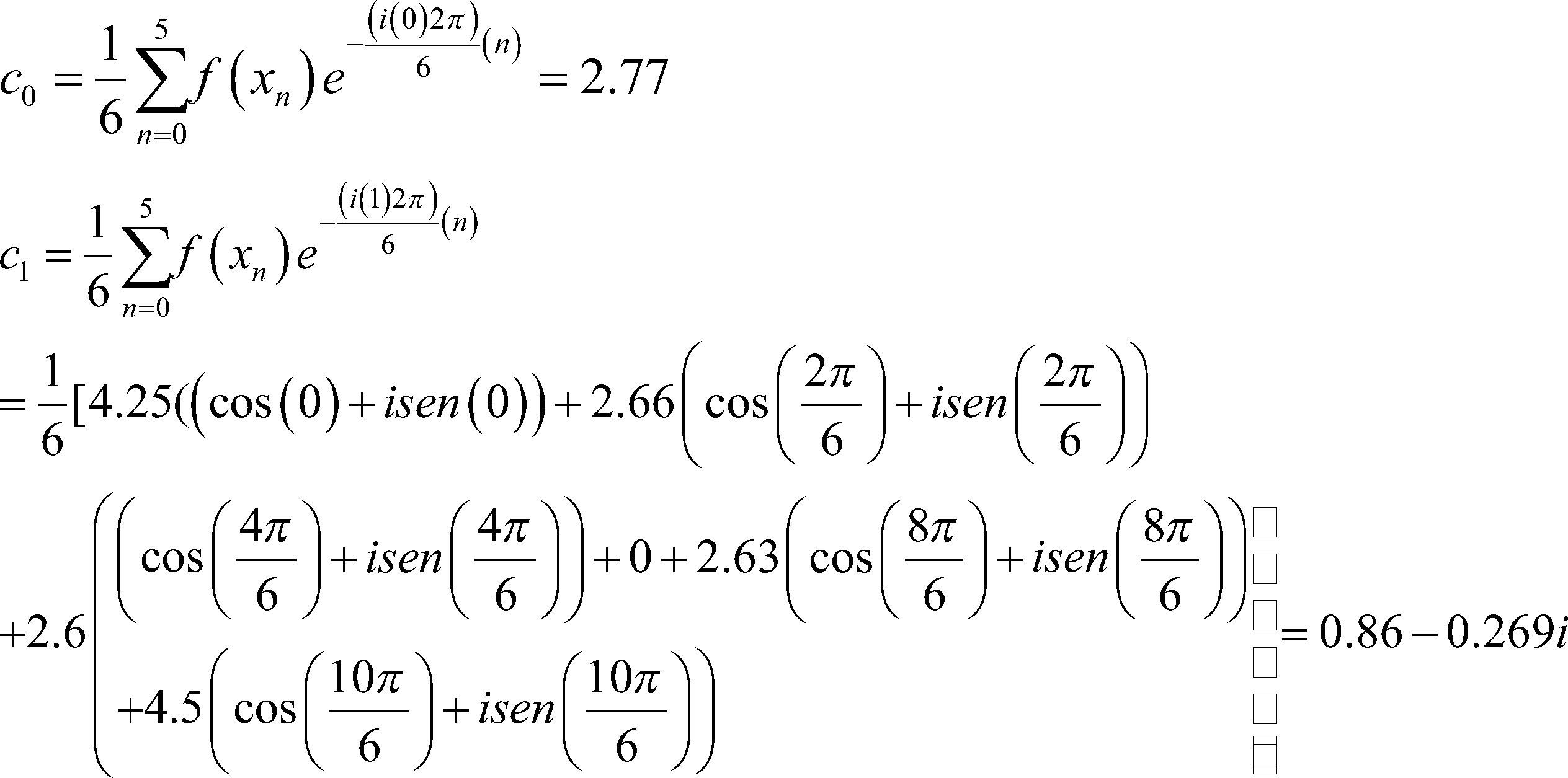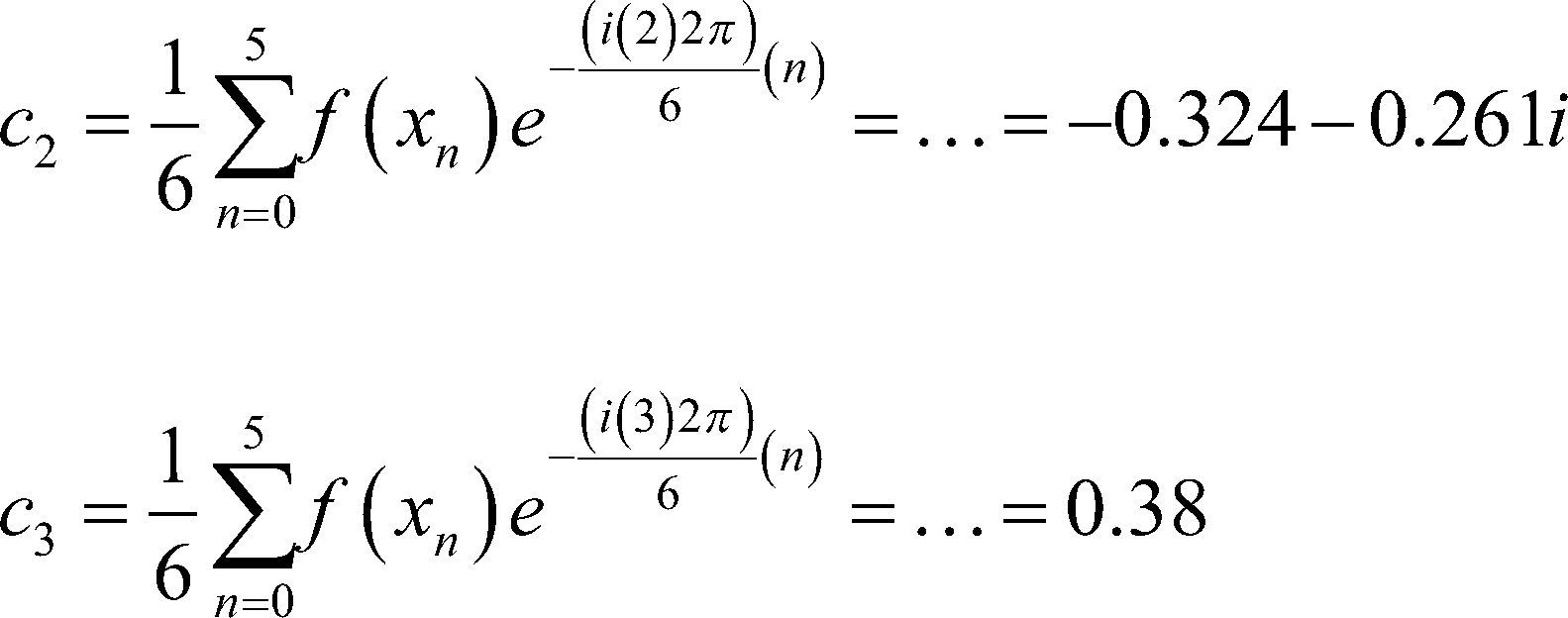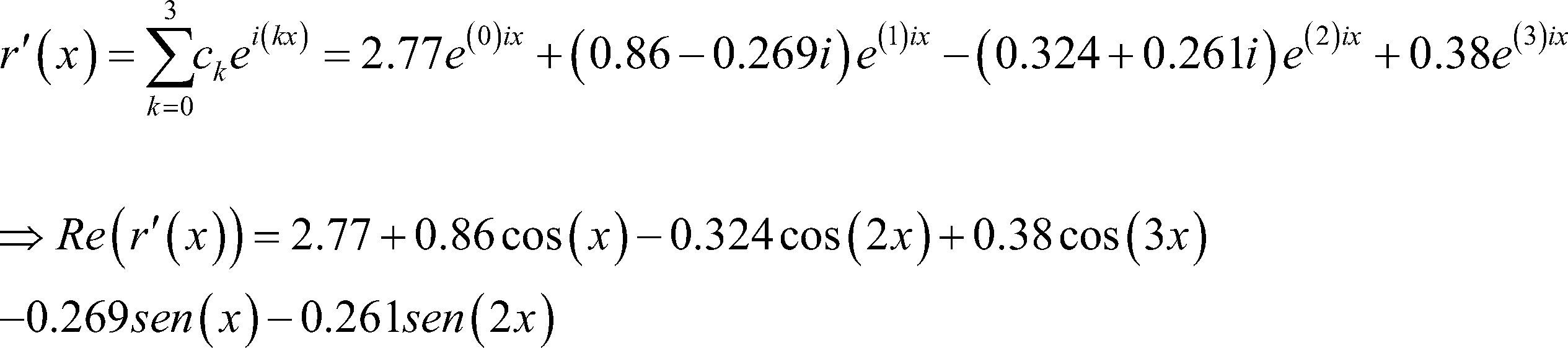En el presente trabajo se pretende mostrar la Serie de Fourier (sf) como una alternativa para estimar observaciones que no se encuentran disponibles en nuestro conjunto de datos. Así, para empezar a indagar en el tema, es necesario conocer ciertos conceptos básicos sobre la Serie de Fourier. La familiarización de entrada con dicho tema, nos ayuda a comprender, de una forma simple, las explicaciones de los componentes de la sf sabiendo la función de cada uno.
En el primer inciso empezaremos por explicar conceptos básicos sobre la Serie de Fourier. En el segundo punto explicaremos sus componentes y que nos indica cada uno con el fin de realizar una pequeña aplicación en la economía, en el tercer punto. Y por último daremos algunas conclusiones sobre el tema.
¿Qué es la Serie de Fourier?La Serie de Fourier es una herramienta matemática que nos permite obtener información de una función determinada mediante una transformación (donde entenderemos por “transformación” al proceso que reduce la complejidad de una ecuación). Por lo tanto, cuando se hace referencia a la Serie de Fourier (sf), realmente hablamos de la transformación que nos permite extraer información sobre la frecuencia de un ciclo –puede ser cualquier función– cuando conocemos sólo una parte de su comportamiento.
La idea intrínseca de la sf nos indica que cualquier función, generalmente periódica, se puede aproximar por medio de funciones simples sinusoidales1. De forma que cuanto más coincide una onda simple con el dato observado, más peso tiene en la determinación de la función original. (Con este procedimiento es posible representar funciones deterministas o de índole aleatoria.)
Con la sf se adquiere un cambio en el dominio de la función; al pasar de la información contenida en una señal, al dominio en el tiempo, para transitar al de la frecuencia y viceversa, de suerte tal que se mejora el análisis de la señal (Carrillo, 2003). Así que las sf son útiles en el estudio de funciones periódicas, aunque, desafortunadamente, no aparecen con la misma frecuencia en la vida real como las no periódicas.
No obstante, antes de continuar con el tema debemos mencionar, al menos, la versión más intuitiva de una función periódica2. Formalmente, una función periódica cumple f(t) = f(t+T) para toda t, donde T es la constante mínima que satisface la igualdad y se denomina periodo. Asimismo, definimos a la frecuencia fr=T-1(inversa de T) y llamamos “ciclo” a la parte de la función que abarca un tiempo equivalente a un periodo T (usualmente 2π).
Dicho lo anterior, buscamos aproximar una función f de periodo 2π y N observaciones (xn ,f(xn)) con xn=2πNn,∀n=1,...,N−1 sub intervalos equi-distribuidos en [0,2π] por medio de un polinomio r(x) compuesto de funciones trigonométricas, de tal manera que el punto observado f(xn) sea el mismo en el polinomio, i.e., f(xn)=r(xn). Iniciaremos por definir qué es un polinomio trigonométrico:
Definición: Un polinomio trigonométrico de grado, a lo más, n es cualquier función de la forma
Donde r(x) es una función periódica de periodo 2π, ie,r(x)=r(x+2π) para toda x∈R con coeficientes
De (1) haremos las siguientes observaciones:eix=cos(x)+isen(x) y por Moivre se tiene ei(kx)=cos(kx)+isen(kx), donde recordemos que para todo c∈C c=a+ibt para todo a,b∈R y si adicionalmente en (1) iniciamos la suma desde,entonces podemos reescribir a (1) como:
Con coeficientes
No debemos olvidar que r’(x) está compuesto por coeficientes complejos, por lo que r’(x)=Re(r’(x))+Im(r’(x)) , además r(x)=Re(r’(x)) y por construcción tenemos la peculiaridad de f(xn)=r(xn)=r’(xn)∀.n=1,...,N-1
II. ¿Cómo se utiliza la Serie de Fourier?Antes de intentar utilizar la tf, debemos conocer cada uno de los términos que la comprenden. Por consiguiente, empezaremos por decir que N es el número de muestras observadas, n indica la frecuencia que se quiere analizar y f(xn) se refiere a la muestra tomada en el instante xn. Así, si desarrollamos la sf será más visible:
El desarrollo anterior nos muestra cómo f(x0),f(x1),...,f(xn) son las observaciones que deseamos analizar dentro de la suma, para una K y N fijas. Donde queda de manifiesto que n indica la frecuencia de estudio.
Para se k=0 vuelve evidente que el término c0=a0, es decir que la constante del polinomio exponencial es igual a la constante del polinomio trigonométrico, además c0 se obtiene al hacer la media aritmética de los valores observados indicando así que es el término constante.
No es necesario trabajar con toda la muestra de datos observados; basta con tomar 0≤k≤N2 o bien N2≤k≤N−1 pues el valor de k=0 coincide con:
Por último, nos falta conocer el papel que tiene la expresión re−i2πnN donde r es el modulo del numero complejo y −i2πnN es su argumento. Además re−i2πnN=rcosi2πnN−iseni2πnN y el término n nos indica que el número complejo va a estar girando en el círculo unitario (recorrido de cada muestra) con velocidad angular 2π y saltos con razón nN medido en radianes.
Por ende, el resultado de ésta expresión, representa la similitud de la observación analizada con el seno y coseno de la frecuencia dependiente de n, en donde la parte real representa la semejanza entre las señales.
III. Una sencilla aplicación en economíaLa economía es una ciencia que utiliza una gran variedad y cantidad de datos, especialmente en la rama de la econometría para aceptar o refutar hipótesis sobre parámetros que nos permiten entender y/o modelar los fenómenos económicos, entre otras razones. No obstante, en muchas ocasiones, las estadísticas con las que se cuenta están incompletas al faltar observaciones; esto principalmente cuando nos vemos en la necesidad de construir nuestra propia base de datos. Ergo, es necesario hacer una aproximación de los datos.
En ese sentido, la Serie de Fourier representa una herramienta útil, pues recupera la información de las observaciones construyendo una función que pasa por datos observados y se aproxima a los datos omitidos. Si bien es cierto que la sf, en principio, fue pensada para funciones periódicas, se puede extender este concepto a toda función; si pensamos en las funciones no-periódicas como funciones periódicas de periodo infinito.
Supongamos que tenemos las siguientes observaciones que representan los datos observados de la tasa de interés mensual del Banco del Centro y queremos conocer su comportamiento no sólo de forma mensual (x0,4.25),(x1,2.66),(x2,2.6),(x3,0), (x4,2.63),(x5,4.5)
Entonces, calculamos la sf
Por tanto, sustituyendo los coeficientes en (2) tenemos
Recordemos que el polinomio exponencial tiene la siguiente representación r’(x)=Re(r’(x))+Im(r’(x)) de donde se puede comprobar de manera fácil (en el ejemplo) que el desarrollo del polinomio trigonométrico tiene r(x)=Re(r’(x)) que corresponde a la serie de Fourier que más se aproxima a los datos observados. También queda de manifiesto que c0=a02=2.77 es la media aritmética de los datos
El análisis pertinente, en sentido económico, se da en el sentido de que al contar con un numero de observaciones finito (en el ejemplo tuvimos 6 observaciones mensuales) se puede recrear el comportamiento de los datos a lo largo del tiempo y de esta manera obtener observaciones quincenales, semanales o diarias (de acuerdo a nuestras necesidades)
ConclusionesPor una parte, la sf es un método más completo y más real que otras aproximaciones obtenidas por métodos como mínimos cuadrados ordinarios (mco), promedios, entre otros; pues como comentamos a lo largo del trabajo, ésta incorpora el comportamiento de las observaciones, permitiéndonos observar tendencias y ciclos de los datos. Empero, ese tema sobrepasa por mucho los alcances de este artículo, por lo que se dejará para otro tema de investigación.
Por otra parte, la sf nos ayuda a conocer el comportamiento de nuestros datos, por medio de una aproximación trigonométrica, pero hay que mencionar que a una mayor cantidad de datos observados mejor es la estimación realizada. En otras palabras, si el número de datos tiende a infinito, entonces nuestro error tiende a cero, lo cual podría ser un inconveniente a pesar de que el polinomio obtenido pasa por los datos observados.
En adición, la aproximación realizada por medio de Fourier es un método completamente determinístico, ausente de perturbaciones aleatorias. Puesto que con el conjunto de datos establecido, siempre obtendremos la misma reproducción a menos que implementemos una variación al agregar o quitar datos de la muestra. Existen modelos (AR(p),MA(q),ARMA(p,q),SARIMA(,p,q),ARCH(p),GARCH(p,q)) mucho más completos que toman en cuenta estas perturbaciones; además de incorporar tendencias, ciclos, estacionalidad etc.; y que utiliza la sf para estimar sus densidades espectrales para obtener funciones de covarianza, así como la autocorrelación de los mismos.
Otro inconveniente a tomar en cuenta, es el costo en tiempo de la sf, pues consta de la realización de vario cálculos y pasos (primeramente para obtener los coeficientes de la sf y posteriormente a la hora de obtener el polinomio). Afortunadamente, existe una versión más eficiente en tiempo (Transformada Rápida de Fourier) con costo comparativo en tiempo más bajo a la hora de realizar los cálculos. Pero será analizado posteriormente.
Es importante mencionar el hecho de que toda función f puede ser vista como una función periódica implementando el concepto de “periodo de tiempo infinito”, el cual tiene mucho sentido al recordar que un intervalo de longitud positiva es cardinalmente comparable con R. De esta manera, no importa la cantidad de observaciones con las que contamos (inclusive si son infinitas), pues a todas se les puede incorporar en distancias de la misma longitud dentro de nuestro intervalo de análisis