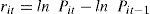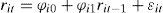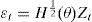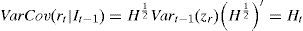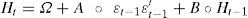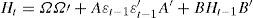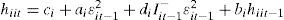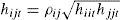La hipótesis de eficiencia y la modelación de series bursátiles mexicanas: un análisis multivariado

Resumen

Estudiamos la Hipótesis de Eficiencia de los Mercados (emh) y modelamos las series de rendimientos bursátiles mexicanos. El estudio utiliza pruebas de raíces unitarias y doce modelos garch multivariados. Los principales resultados sugieren que: 1) El mercado bursátil mexicano es ineficiente en forma débil; 2) la eficiencia ha disminuido desde el año 2007; 3) los modelos de Correlación Condicionada Constante (ccc) son los que mejor describen los rendimientos; 4) las buenas y malas noticias tienen impactos asimétricos sobre la volatilidad; y 5) las perturbaciones parecen seguir una distribución t de Student multivariada. El estudio usa series diarias de los precios de 20 acciones y del Índice de Precios y Cotizaciones (ipc) para el periodo 02/10/2000-10/10/2012.

Abstract

We study the Efficient-Market Hypothesis (emh) and we model the series of Mexican stock returns. The study uses unit-root tests and twelve multivariate garch models. The main results suggest that: 1) The Mexican stock market is weakly inefficient; 2) efficiency has declined since 2007; 3) Constant Conditional Correlation (ccc) models are best ones that describe the returns; 4) good and bad news have asymmetric impacts on volatility; and 5) perturbations seem to follow a multivariate Student's t distribu-tion. The study uses 20 daily series of stock prices and of the Mexican Stock-Market Index (ipc) for the period 02/10/2000-10/10/2012.

1

Introducción

Tradicionalmente se considera que los mercados bursátiles son importantes medios de desarrollo económico y financiero. En la literatura se sustenta dicha importancia con base en la consideración de que los mercados bursátiles cumplen funciones necesarias para el buen desempeño de las economías.¹ Entre otras, estas funciones incluyen: 1) la provisión liquidez para financiar proyectos; 2) la diversificación de riesgos; 3) la provisión de información de las empresas; 4) el control de malas prácticas de gobierno corporativo; y 5) la movilización de ahorros. Usualmente se considera que el cumplimiento de estas funciones depende en gran medida de la eficiencia de los mercados bursátiles.

Paradójicamente, el término de “eficiencia del mercado bursátil” es relativamente reciente y sujeto a controversias en la economía financiera. Euge-ne Fama introduce el término para hacer referencia a aquellos mercados en donde los precios de los activos reflejan plenamente la información disponible (Fama, 1965). Más aun, Fama define una teoría alrededor de dicho término. La Hipótesis de Eficiencia de los Mercados (Efficient-Market Hypothesis, emh), señala que no es posible obtener consistentemente rendimientos financieros superiores a aquellos del promedio del mercado. Asimismo, postula la imposibilidad de describir los precios de los activos usando modelos estadísticos.

En las literaturas teórica y empírica existen agudas controversias sobre la validez de la hipótesis de eficiencia de los mercados bursátiles. Las revisiones de estudios no ofrecen evidencia concluyente en ningún sentido. Los hallazgos empíricos relativos a la emh dependen en buena medida del nivel de desarrollo, de los periodos considerados y de las economías analizadas. Las posiciones entre quienes argumentan en favor y en contra de la validez de la emh se han polarizado tras la crisis financiera global. Por una parte, están quienes atribuyen esta crisis a la suposición de validez de la emh. Por otra, están quienes sustentan que la emh ha sido entendida de una manera muy restrictiva.²

En esta investigación se estudia la validez de la hipótesis de eficiencia en el mercado bursátil mexicano y se modelan sus series de rendimientos bursátiles. La evaluación de la emh, en su forma débil, se realiza mediante estadísticas descriptivas, pruebas de raíces unitarias y de correlación. Los ejercicios de modelación y análisis econométricos utilizan doce modelos garch multiva-riados con fines de comparativos y de caracterización de las series durante periodos de calma e inestabilidad financiera. El estudio se sustenta en una muestra de series de precios diarios de veinte acciones y del Índice de Precios y Cotizaciones (ipc) que abarca datos del 2 de octubre de 2000 al 10 de octubre de 2012.

Académicamente, la investigación complemente la literatura referida a la evaluación de la eficiencia del mercado bursátil mexicano; y la literatura referida a la modelación de series con modelos garch multivariados. Particularmente, a diferencia de otros estudios, aquí se utilizan pruebas de estaciona-riedad y de correlación para evaluar la emh. Asimismo, se modelan y analizan las series de rendimientos bursátiles, de manera conjunta, mediante diversos modelos garch multivariados. En este contexto, vale la pena señalar que se analizan, modelan y comparan las series bursátiles considerando periodos de relativa “calma” e “inestabilidad” en los mercados internacionales.

El estudio está organizado en siete secciones. La Sección 2 incluye la revisión de la literatura. En la Sección 3 se describe la metodología de análisis. La Sección 4 describe la base de datos y muestra la estadística descriptiva de las series de rendimientos. La Sección 5 muestra los resultados del análisis de estacionariedad. La Sección 6 muestra los ejercicios de modelación y análisis econométricos. Asimismo, desarrolla el análisis comparativo. La Sección 7 sintetiza los resultados y menciona algunas líneas de investigación futura.

2

Revisión de la literatura

En esta sección se revisan los estudios referentes a la hipótesis de la eficiencia de los mercados, los modelos garch multivariados y el concepto de estacionariedad. Por esta razón, la sección se divide en dos apartados. En el primer apartado se explica la Hipótesis de Eficiencia de los Mercados (emh), sus implicaciones y las controversias que la misma ha planteado. En el segundo se describen las estructuras de los modelos garch multivariados y se analiza la vinculación entre la emh y la estacionariedad de las series de tiempo. En ambos apartados se hace énfasis en los estudios empíricos realizados en el contexto mexicano. Esto con fines de contextualizar y justificar el estudio desarrollado.

2.1

La Hipótesis de Eficiencia de los Mercados

En la economía y las finanzas existen varias teorías que explican el comportamiento de los mercados y las series bursátiles. Probablemente la más conocida es la Hipótesis de Eficiencia de los Mercados (emh) propuesta por Fama (1965).³ Esta teoría postula que, en un mercado “eficiente”, los precios de los activos reflejan plenamente la información disponible en dicho mercado.⁴ Más aun, postula la imposibilidad de describir y predecir los precios de los activos de manera sistemática usando modelos estadísticos. Por tanto, si un mercado es eficiente, el mejor pronóstico para el precio de mañana de un activo cualquiera será su precio del día de hoy.

Empíricamente, la hipótesis de eficiencia tiene importantes implicaciones econométricas.⁵ Particularmente, si se considera que su cumplimiento conlleva a la imposibilidad de que los agentes puedan obtener ganancias sistemáticas por hacer transacciones bursátiles; la emh implica que el valor esperado de los rendimientos debiera ser cero. La emh también implica que los rendimientos no pueden estar correlacionados en el tiempo y que los modelos estadísticos carecen de utilidad práctica. Esto ocurre debido a que la emh explica los movimientos de los precios como procesos de caminata aleatoria (Fama, 1965); o, más generalmente, como martingalas (Samuelson, 1965; Mandelbrot, 1966).

En la literatura empírica existen varias revisiones de estudios que han evaluado la validez de la emh en los mercados bursátiles. Sin embargo, las revisiones no ofrecen evidencia concluyente en ningún sentido. Aparentemente, los resultados reportados dependen del nivel de desarrollo, de los periodos considerados y de las economías analizadas. Entre las revisiones que reportan evidencia en favor de la emh están las de Fama (1970) y Malkiel (2003) y (2005). Entre las revisiones que hallan evidencia en contra están las de Shleifer (2001) y Timmermann y Granger (2004). Entre las revisiones que ofrecen evidencia mixta se encuentran las de Hyme (2003), Yen y Lee (2008) y Duarte y Mascareñas (2013).

Empíricamente, la falta de evidencia concluyente puede atribuirse, entre otros factores, a que no existe una definición única de la emh. La literatura especializada distingue entre las formas de eficiencia débil, semi-fuerte y fuerte. Particularmente, la forma débil establece que los precios presentes incorporan toda la información de los precios pasados (Aragonés y Mascareñas, 1994). La forma semi-fuerte establece que los precios incorporan toda la información hecha pública que afecte el valor de los activos. La forma fuerte establece que los precios incorporan toda la información pública y privada que se puede conocer (Mehrara y Oryoie, 2012).

En México, existen algunos estudios que han analizado la hipótesis de eficiencia en el mercado bursátil en su forma débil. Particularmente, López-Herrera (1998) argumenta en contra de la misma mediante un análisis los precios del Índice de Precios y Cotizaciones (ipc) entre 1987 y 1997. El estudio se sustenta en regresiones de mínimos cuadrados ordinarios (mco-ols) y en tests de autocorrelación. Santillán-Salgado (2011) argumenta en favor de la emhmediante un análisis de los rendimientos, a nivel agregado y desagregado, entre 2000 y 2010. El estudio también se sustenta en regresiones mco-ols. Por tanto, los estudios referidos al mercado mexicano también proveen resultados mixtos.⁶

Metodológicamente, los estudios realizados muestran que existen áreas de oportunidad para el desarrollo de investigación en el contexto del mercado bursátil mexicano. Los estudios existentes, en su mayoría, asumen que se cumplen los supuestos del modelo de regresión lineal clásico de mínimos cuadrados (mco-ols). Sin embargo, es posible argumentar que las series bursátiles suelen mostrar comportamientos no lineales, autorregresivos y heteros-cedásticos que no son compatibles con los supuestos de mco-ols. Además, la teoría sugiere que las evaluaciones de la emh deben centrarse en los precios de los activos bursátiles y en sus rendimientos, tanto a nivel agregado como desagregado.

Los comentarios señalados muestran que es necesario hacer investigación relativa a la validez de la emh en el mercado bursátil mexicano y a la modelación de series de rendimientos. El mercado bursátil mexicano refleja la confianza y las expectativas de los agentes en la economía. Muchas decisiones de financiamiento empresarial, de ahorro e inversión y de administración de riesgos dependen del comportamiento y de la volatilidad de este mercado. Por esta razón, los ejercicios de modelación y análisis econométricos resultan pertinentes y complementarios a la evaluación de la emh. De hecho, la investigación aquí planteada se sustenta en estas consideraciones.

2.2

Modelación econométrica de series bursátiles y la estacionariedad de las series

La modelación econométrica de series bursátiles ha tenido gran desarrollo en las últimas décadas. Particularmente, los modelos de la familia arch ha sido los más usados para describir y analizar dichas series. Estos modelos asumen la existencia de procesos autorregresivos con heteroscedasticidad condicionada (AutoRegressive Conditional Heteroskedasticity, arch). Los modelos arch permiten describir series con comportamientos caracterizados por no linealidades, volatilidades excesivas clusters de volatilidad, volatilidades no constantes y distribuciones no normales.⁷ Los primeros modelos de esta familia fueron desarrollados por Engle (1982) y Bollerslev (1986).

Los modelos de la familia arch se dividen en univariados y multivariados. Los modelos univariados modelan la media y la varianza de series individuales. Los modelos multivariados lo hacen para conjuntos de series. En la literatura empírica se usan modelos univariados con fines de descripción y análisis de series financieras y bursátiles.⁸ Paradójicamente, es reconocido que los mercados y activos financieros suelen moverse de manera conjunta a lo largo del tiempo. Sin embargo, los trabajos que usan modelos multivariados son relativamente escasos.⁹ Esta situación se justifica, entre otras razones, porque estos modelos requieren la estimación de un gran número de parámetros.

Los modelos garch multivariados asumen diversos supuestos sobre la dinámica conjunta de las series económicas y financieras. Estas dinámicas se postulan mediante supuestos relativos al vector de la media condicional, de la matriz de varianza-covarianza condicional y de la distribución de densidad multivariada de las perturbaciones. Particularmente, las matrices de varianzacovarianza son importantes porque las mismas definen la estructura dinámica de los modelos multivariados. En la literatura especializada, las matrices de varianza-covarianza más usadas son de los tipos dvech (Diagonal vech), dbekk (Diagonal bekk) y ccc (Constant Conditional Correlation).

Los modelos garch multivariados (mgarch, Multivariate garch) muy pocas veces se han usado para analizar y modelar series económicas y financieras mexicanas. La mayoría de los estudios publicados modelan y analizan los rendimientos bursátiles a nivel agregado y su relación con las dinámicas de otras series internacionales.¹⁰ Metodológicamente, estos estudios suelen asumir especificaciones de tipo garch sin efectos apalancamiento. Entre los estudios que han usado modelos mgarch destacan los de Ludlow y Mota (2006), Domínguez (2006), López-Herrera, Ortiz y Cabello (2009) y Lorenzo-Valdés, Durán-Vázquez y Armenta-Fraire (2012).

Los estudios arriba señalados han analizado diversas temáticas bursátiles, aunque ninguno analiza la validez de la hipótesis de eficiencia a nivel agregado y desagregado. Particularmente, Ludlow y Mota (2006) estudian la dinámica conjunta de los rendimientos de los índices del ipc, Nasdaq y S&P500. Domínguez (2007) analiza la dinámica del ipc con otros índices latinoamericanos. López-Herrera, Ortiz y Cabello (2009) estudian las relaciones entre los mercados de valores del tlcan. Lorenzo-Valdés, Durán-Vázquez y Armenta-Fraire (2012) analizan los rendimientos del ipc y los cambios en los precios del petróleo usados como referencia en el mercado internacional.

Estadísticamente, los modelos de la familia arch requieren que las series de tiempo satisfagan ciertos requisitos para que puedan usarse con fines de modelación y pronóstico. ¹¹ Estos requisitos han limitado el uso de los modelos de la familia arch y, en particular, de los modelos garch multivariados. El más importante requisito estadístico es que las series de tiempo deben ser estacionarias a fin de evitar la posibilidad de correlaciones espurias. Esto significa que la media y varianza de las series no deben variar sistemáticamente en el tiempo. Naturalmente, esto conlleva a que las series modeladas no deban comportarse como procesos de caminata aleatoria.

La validación de la hipótesis de eficiencia de los mercados (emh) está fuertemente vinculada al concepto de estacionariedad. La emh, en su forma débil, requiere que las series de precios bursátiles sean expresadas como procesos de caminata aleatoria. Esta consideración sugiere que la eficiencia de las series de precios bursátiles podría analizarse con base en pruebas de estacionariedad de las series. Particularmente, una condición necesaria para validar la emh seria que las series de precios fueran no estacionarias.¹² Si ese fuera el caso, la validación de la emh podría justificarse a condición de que no hubiera una correlación significativa entre los rendimientos presentes y rezagados.

Metodológicamente, hay que enfatizar que esta revisión justifica y sugiere algunos criterios para estudiar las series bursátiles mexicanas a nivel agregado y desagregado. Particularmente, el estudio se justifica debido a las transformaciones que han experimentado los mercados financieros tras la crisis global. En este contexto, la revisión sugiere que la evaluación de la hipótesis de eficiencia en su forma débil podría realizarse mediante pruebas de estacionariedad y de correlación. Asimismo, sugiere que la modelación y el análisis de las series estacionarias podrían hacerse mediante modelos mgarch y especificaciones del tipo garch y tgarch.

3

Metodología de análisis

En esta sección se describe la metodología usada para analizar la hipótesis de eficiencia y la modelación de series bursátiles mexicanas. En este contexto debe señalarse que los activos analizados aquí son aquellos que cotizaron continuamente en la Bolsa Mexicana de Valores (bmv) entre los años 2000 y 2012. Estos activos son los que definen las series de precios y rendimientos utilizadas aquí. Particularmente, las series de rendimientos de estos activos se estiman con los precios de cierre de cada activo i en el periodo t, P_it. Así se define el rendimiento de un activo i en el periodo t, r_it, como:

Metodológicamente, el estudio se sustenta en un enfoque multivariado para evaluar la hipótesis de eficiencia y la modelación de series bursátiles. Particularmente, se sustenta en análisis de estadística descriptiva, pruebas estadísticas de raíces unitarias y en el uso de modelos mgarch. El análisis de estadística descriptiva se usa para caracterizar el comportamiento de las series de rendimientos. Las pruebas de raíz unitaria se usan para evaluar el orden de integración de las series de precios y rendimientos. Los modelos mgarch se usan con fines de descripción y análisis de las series. Además, los modelos mgarch y las pruebas de raíz unitaria se usan conjuntamente para evaluar la emh.

Estadísticamente, el análisis de estacionariedad se usa para analizar la pertinencia de modelar las series bursátiles y la validez de la hipótesis de eficiencia. La modelación econométrica de series requiere que las mismas sean integradas de orden cero I(0) (i.e., estacionarias). Asimismo, y tal como ya se ha mencionado, la hipótesis de eficiencia requiere que las series de precios no sean estacionarias, lo cual implica que las mismas deben ser al menos de orden uno I(1). En este contexto, aquí se usa el test Aumentado de Dickey-Fuller (adf) para analizar el orden de integración de las series bursátiles. La hipótesis nula en dicho test es que existen raíces unitarias (i.e., la serie es no-estacionaria).

Estadísticamente, las series bursátiles no solo deben ser estacionarias para ser modeladas econométricamente. También deben manifestar efectos arch (i.e., los rendimientos cuadráticos deben estar autocorrelacionados).

Los modelos mgarch se usan con fines de modelación econométrica y de análisis de las series bursátiles. Los modelos usados aquí son de los tipos dvech (Diagonal vech), dbekk (Diagonal bekk) y ccc (Constant Conditional Correlation). Estos modelos son variaciones de los propuestos, respectivamente, por Bollerslev, Engle y Wooldridge (1988), Engle y Kroner (1995) y Bollerslev (1990). Particularmente, los modelos empleados consideran especificaciones de tipo garch y tgarch para analizar los posibles efectos de los shocks informacionales sobre la volatilidad de las series. Asimismo, los modelos consideran distintas distribuciones de densidad multivariada (Normal y t de Student).

Los modelos mgarch estimados permiten estudiar diversos patrones de comportamiento dinámico de las series bursátiles considerando los periodos previo y posterior a 2007. Cada modelo se construye mediante una matriz de varianza-covarianza condicionada, una especificación y una distribución de densidad multivariadas. Las matrices de varianza-covarianza condicionada, H_t, son aquellas de los modelos dvech, dbekk y ccc.¹³ Las especificaciones son la garch y la tgarch. Las distribuciones son la normal y t de Student multivariadas. Así, en esta investigación se usan doce modelos multivariados distintos para efectos comparativos y de estimación econométrica.

Tradicionalmente las estructuras dinámicas de los modelos mgarch se plantean como sistemas de ecuaciones. Las tres expresiones matriciales que definen a los modelos usados en esta investigación son las siguientes:

, donde r_t es un vector que incluye una serie de tiempo multivariada de N procesos estocásticos; θ es un vector de parámetros; H12(θ) es una matriz definida positiva N × N; y z_t es un vector aleatorioN × 1, tal que E(zt)=0 y Var(z_t) = I_N.

Metodológicamente, los ejercicios de modelación y análisis utilizan grupos de estimaciones que describen la dinámica conjunta de las series durante tres periodos específicos. Los periodos analizados corresponden a los años 2000–2012, 2000–2007 y 2007–2012. Así se facilita el análisis comparativo de los periodos previo y posterior a la manifestación de la crisis global. Cada grupo de estimaciones modela la dinámica conjunta de las series usando cada uno de los modelos mgarch. Por tanto, cada grupo de estimaciones se integra por doce estimaciones distintas por periodo. Estadísticamente, todas las estimaciones se realizan usando el método de Máxima Verosimilitud (Maximum Likelihood, ML).

Estadísticamente, y por consistencia con otros estudios, en todos los modelos estimados se asume que las perturbaciones siguen un proceso AR(1). Este supuesto se explícita en términos de la definición de la perturbación, ε_it, como:ε_it = c + ρ_iε_it + v_it, donde c es una constante y v_it es ruido blanco. En este contexto, la evaluación de la significancia de ρ_i resulta un test adicional sobre la validez de la EMH. Esto en virtud de que la significancia de ρ_i implicaría la existencia de autocorrelación, eventualmente de orden infinito, en las series de rendimientos. Por esta razón, aquí se hacen explicitas las estimaciones y los p-values asociados a las estimaciones de ρ_i.

Finalmente, el análisis comparativo y de evaluación de los modelos mgarch se sustenta en estimadores de bondad de ajuste. Particularmente, los estimadores usados aquí son aquellos del logaritmo de verosimilitud (Log-Likelihood) y del criterio de información de Akaike (aic). La relevancia de usar estos estimadores es que proporcionan criterios alternativos para elegir al mejor modelo descriptivo de las series cuando las matrices de varianza-covarianza son semidefinidas positivas. Más aun, proveen elementos para sugerir la existencia de algunos patrones de comportamiento dinámico conjunto de las series bursátiles mexicanas durante los periodos considerados.

4

Base de datos y estadística descriptiva

Este estudio usa una muestra de datos bursátiles desagregados y agregados obtenida de Infosel. La muestra incluye los precios de cierre diarios de veinte acciones individuales que cotizaron entre el 2 de octubre de 2000 y el 10 de octubre de 2012. Asimismo incluye datos diarios del Índice de Precios y Cotizaciones (ipc). Todos los datos considerados son nominales. Los activos incluidos en la muestra son aquellos para los que existen datos completos para el periodo. Por conveniencia estadística, las series de precios son expresadas de forma logarítmica. Así, la muestra se integra por un total de 21 series de logaritmos de precios. Cada serie incluye 3022 observaciones diarias.

La muestra analizada se caracteriza por experimentar periodos de relativa calma e inestabilidad en los mercados bursátiles internacionales. Por esta razón, las series de precios se agrupan considerando tres periodos. El primero incluye las series completas. El segundo incluye datos de las series para el periodo entre el 02 de octubre de 2000 al 9 de agosto de 2007. El tercero incluye datos para el periodo del 10 de agosto de 2007 al 10 de octubre de 2012. Los periodos utilizados se usan con fines de comparación y análisis. Así, el primer periodo se usa como referencia. El segundo refiere a una etapa de “calma” en los mercados. El tercero, por contraste, refiere a una etapa de “inestabilidad” financiera.¹⁴

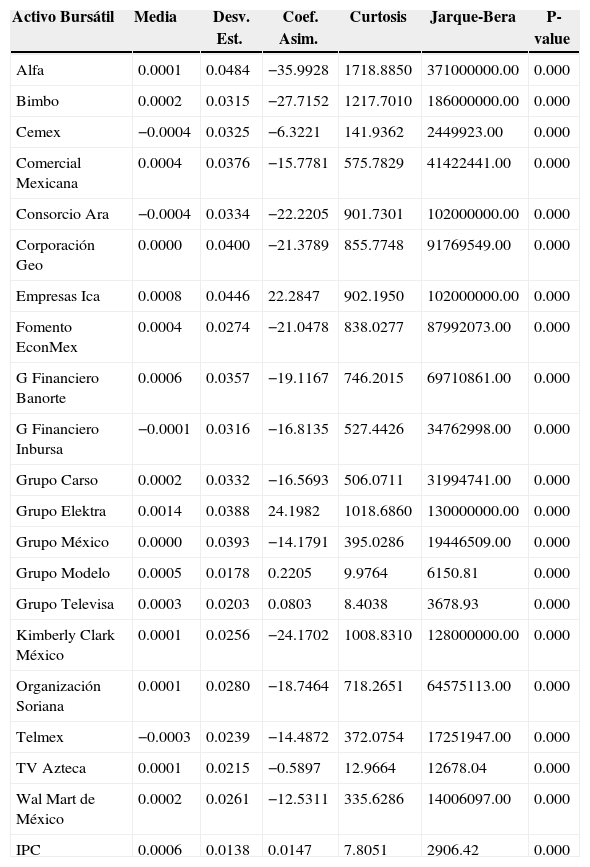
El cuadro 1 muestra la estadística descriptiva de las series de rendimientos bursátiles considerando la totalidad de los datos. Esta cuadro es importante porque provee valores de referencia para evaluar la hipótesis de eficiencia. El cuadro muestra que la media estimada de rendimientos del Índice de Precios y Cotizaciones (ipc) es positiva. A nivel desagregado, el cuadro muestra que la mayoría de las medias de los activos individuales tienden a cero. El cuadro también muestra que 16 series exhiben un sesgo negativo y las restantes un sesgo positivo. Por tanto, la evidencia sugiere que las series son asimétricas. Además, el cuadro muestra todas las series son leptocúrticas y que ninguna se distribuye normalmente.

Cuadro 1.

Estadística descriptiva de los rendimientos de los activos para el periodo del 2 de octubre de 2000 al 10 de octubre de 2012 y prueba de normalidad de Jarque-Bera.

Activo Bursátil	Media	Desv. Est.	Coef. Asim.	Curtosis	Jarque-Bera	P-value
Alfa	0.0001	0.0484	−35.9928	1718.8850	371000000.00	0.000
Bimbo	0.0002	0.0315	−27.7152	1217.7010	186000000.00	0.000
Cemex	−0.0004	0.0325	−6.3221	141.9362	2449923.00	0.000
Comercial Mexicana	0.0004	0.0376	−15.7781	575.7829	41422441.00	0.000
Consorcio Ara	−0.0004	0.0334	−22.2205	901.7301	102000000.00	0.000
Corporación Geo	0.0000	0.0400	−21.3789	855.7748	91769549.00	0.000
Empresas Ica	0.0008	0.0446	22.2847	902.1950	102000000.00	0.000
Fomento EconMex	0.0004	0.0274	−21.0478	838.0277	87992073.00	0.000
G Financiero Banorte	0.0006	0.0357	−19.1167	746.2015	69710861.00	0.000
G Financiero Inbursa	−0.0001	0.0316	−16.8135	527.4426	34762998.00	0.000
Grupo Carso	0.0002	0.0332	−16.5693	506.0711	31994741.00	0.000
Grupo Elektra	0.0014	0.0388	24.1982	1018.6860	130000000.00	0.000
Grupo México	0.0000	0.0393	−14.1791	395.0286	19446509.00	0.000
Grupo Modelo	0.0005	0.0178	0.2205	9.9764	6150.81	0.000
Grupo Televisa	0.0003	0.0203	0.0803	8.4038	3678.93	0.000
Kimberly Clark México	0.0001	0.0256	−24.1702	1008.8310	128000000.00	0.000
Organización Soriana	0.0001	0.0280	−18.7464	718.2651	64575113.00	0.000
Telmex	−0.0003	0.0239	−14.4872	372.0754	17251947.00	0.000
TV Azteca	0.0001	0.0215	−0.5897	12.9664	12678.04	0.000
Wal Mart de México	0.0002	0.0261	−12.5311	335.6286	14006097.00	0.000
IPC	0.0006	0.0138	0.0147	7.8051	2906.42	0.000

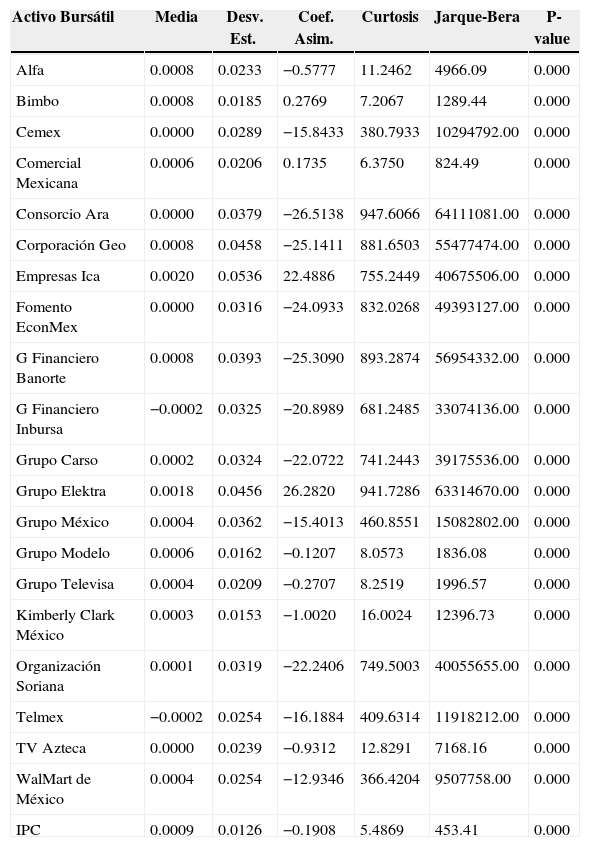
El cuadro 2 muestra la estadística descriptiva de las series considerando el periodo del 3 de octubre de 2000 al 09 de agosto de 2007. Esta cuadro es importante porque provee escasa evidencia en favor de la emh. Esto ocurre porque las medias de los rendimientos a nivel agregado y desagregado, aunque tendientes a cero, son mayores que las registradas en el cuadro 1. Además, las desviaciones estándar tienden a ser consistentemente menores (lo cual sugiere la existencia de clusters de volatilidad). El cuadro también muestra que 17 series exhiben un sesgo negativo y, las restantes, un sesgo positivo. Asimismo, el cuadro confirma que las series son leptocúrticas y que ninguna se distribuye normalmente.

Cuadro 2.

Estadística descriptiva de los rendimientos de los activos para el periodo del 2 de octubre de 2000 al 9 de agosto de 2007 y prueba de normalidad de Jarque-Bera.

Activo Bursátil	Media	Desv. Est.	Coef. Asim.	Curtosis	Jarque-Bera	P-value
Alfa	0.0008	0.0233	−0.5777	11.2462	4966.09	0.000
Bimbo	0.0008	0.0185	0.2769	7.2067	1289.44	0.000
Cemex	0.0000	0.0289	−15.8433	380.7933	10294792.00	0.000
Comercial Mexicana	0.0006	0.0206	0.1735	6.3750	824.49	0.000
Consorcio Ara	0.0000	0.0379	−26.5138	947.6066	64111081.00	0.000
Corporación Geo	0.0008	0.0458	−25.1411	881.6503	55477474.00	0.000
Empresas Ica	0.0020	0.0536	22.4886	755.2449	40675506.00	0.000
Fomento EconMex	0.0000	0.0316	−24.0933	832.0268	49393127.00	0.000
G Financiero Banorte	0.0008	0.0393	−25.3090	893.2874	56954332.00	0.000
G Financiero Inbursa	−0.0002	0.0325	−20.8989	681.2485	33074136.00	0.000
Grupo Carso	0.0002	0.0324	−22.0722	741.2443	39175536.00	0.000
Grupo Elektra	0.0018	0.0456	26.2820	941.7286	63314670.00	0.000
Grupo México	0.0004	0.0362	−15.4013	460.8551	15082802.00	0.000
Grupo Modelo	0.0006	0.0162	−0.1207	8.0573	1836.08	0.000
Grupo Televisa	0.0004	0.0209	−0.2707	8.2519	1996.57	0.000
Kimberly Clark México	0.0003	0.0153	−1.0020	16.0024	12396.73	0.000
Organización Soriana	0.0001	0.0319	−22.2406	749.5003	40055655.00	0.000
Telmex	−0.0002	0.0254	−16.1884	409.6314	11918212.00	0.000
TV Azteca	0.0000	0.0239	−0.9312	12.8291	7168.16	0.000
WalMart de México	0.0004	0.0254	−12.9346	366.4204	9507758.00	0.000
IPC	0.0009	0.0126	−0.1908	5.4869	453.41	0.000

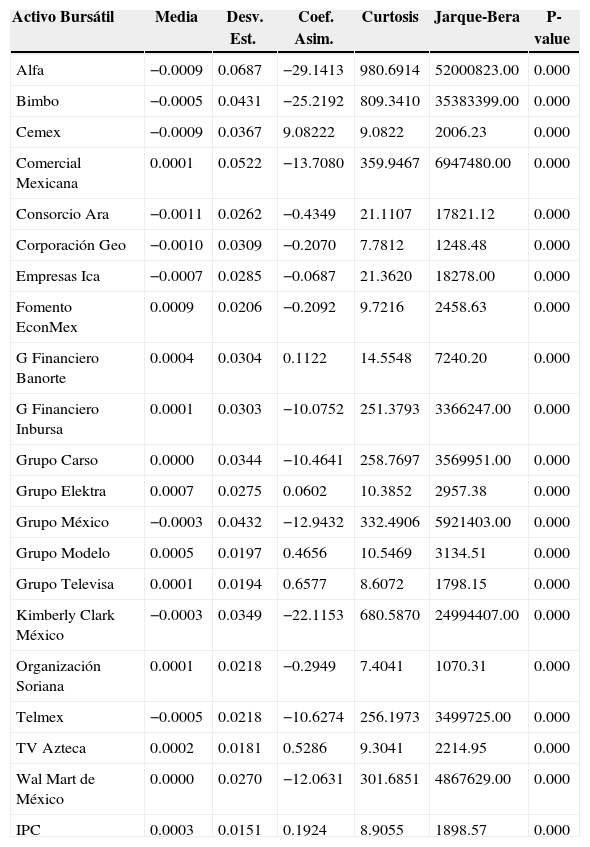
El cuadro 3 muestra la estadística descriptiva de las series de rendimientos bursátiles considerando el periodo del 10 de agosto de 2007 al 10 de octubre de 2012. En este cuadro, las medias de los rendimientos tienden a ser menores que las registradas en el cuadro 1. Las desviaciones estándar, por su parte, tienden a ser mayores. Por tanto, las estimaciones de los tres cuadros sugieren la existencia de movimientos conjuntos de las medias y las varianzas. El cuadro también muestra que catorce series exhiben un sesgo negativo y las restantes un sesgo positivo. Nuevamente, el cuadro confirma que todas las series son leptocúrticas y que ninguna se distribuye normalmente.

Cuadro 3.

Estadística descriptiva de los rendimientos de los activos para el periodo del 10 de agosto de 2007 al 10 de octubre de 2012 y prueba de normalidad de Jarque-Bera.

Activo Bursátil	Media	Desv. Est.	Coef. Asim.	Curtosis	Jarque-Bera	P-value
Alfa	−0.0009	0.0687	−29.1413	980.6914	52000823.00	0.000
Bimbo	−0.0005	0.0431	−25.2192	809.3410	35383399.00	0.000
Cemex	−0.0009	0.0367	9.08222	9.0822	2006.23	0.000
Comercial Mexicana	0.0001	0.0522	−13.7080	359.9467	6947480.00	0.000
Consorcio Ara	−0.0011	0.0262	−0.4349	21.1107	17821.12	0.000
Corporación Geo	−0.0010	0.0309	−0.2070	7.7812	1248.48	0.000
Empresas Ica	−0.0007	0.0285	−0.0687	21.3620	18278.00	0.000
Fomento EconMex	0.0009	0.0206	−0.2092	9.7216	2458.63	0.000
G Financiero Banorte	0.0004	0.0304	0.1122	14.5548	7240.20	0.000
G Financiero Inbursa	0.0001	0.0303	−10.0752	251.3793	3366247.00	0.000
Grupo Carso	0.0000	0.0344	−10.4641	258.7697	3569951.00	0.000
Grupo Elektra	0.0007	0.0275	0.0602	10.3852	2957.38	0.000
Grupo México	−0.0003	0.0432	−12.9432	332.4906	5921403.00	0.000
Grupo Modelo	0.0005	0.0197	0.4656	10.5469	3134.51	0.000
Grupo Televisa	0.0001	0.0194	0.6577	8.6072	1798.15	0.000
Kimberly Clark México	−0.0003	0.0349	−22.1153	680.5870	24994407.00	0.000
Organización Soriana	0.0001	0.0218	−0.2949	7.4041	1070.31	0.000
Telmex	−0.0005	0.0218	−10.6274	256.1973	3499725.00	0.000
TV Azteca	0.0002	0.0181	0.5286	9.3041	2214.95	0.000
Wal Mart de México	0.0000	0.0270	−12.0631	301.6851	4867629.00	0.000
IPC	0.0003	0.0151	0.1924	8.9055	1898.57	0.000

Finalmente debe señalarse que el análisis de estadística descriptiva sugiere que hay escasa evidencia para sustentar la hipótesis de eficiencia en el mercado bursátil mexicano. Las medias de los rendimientos, si bien tienden a cero, son positivas durante los periodos considerados. Asimismo, la evidencia muestra que las series tienden a manifestar curtosis excesivas, clusters de volatilidad, asimetrías, distribuciones no normales, volatilidades no constantes y movimientos conjuntos de medias y varianzas. Estas características implican que las series de rendimientos pudieran ser analizables mediante modelos de la familia arch (y, por tanto, potencialmente inconsistentes con la emh).

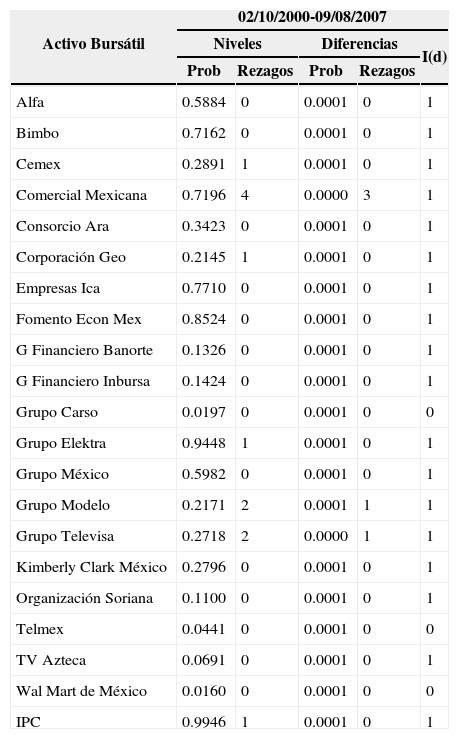
5

Análisis de estacionariedad

Metodológicamente, el análisis de estacionariedad se usa para analizar la pertinencia de modelar las series bursátiles y la validez de la hipótesis de eficiencia (emh). Como es conocido, la modelación econométrica de series requiere que las mismas sean integradas de orden cero I(0). Asimismo, la emh requiere que las series de precios bursátiles no sean estacionarias. En este contexto, aquí se usa el test Aumentado de Dickey-Fuller (adf) para analizar el orden de integración de las series de logaritmos de precios. Las estimaciones del test adf, considerando las series completas, se muestran en el cuadro 4. Las estimaciones obtenidas considerando las series en los otros periodos se muestran en el cuadro 5.

Cuadro 4.

Prueba adf para las series de los logaritmos de precios (niveles) y de los rendimientos (diferencias) para el periodo del 2 de octubre de 2000 al 10 de octubre de 2012.

Activo Bursátil	02/10/2000-09/08/2007
	Niveles		Diferencias		I(d)
	Prob	Rezagos	Prob	Rezagos
Alfa	0.5884	0	0.0001	0	1
Bimbo	0.7162	0	0.0001	0	1
Cemex	0.2891	1	0.0001	0	1
Comercial Mexicana	0.7196	4	0.0000	3	1
Consorcio Ara	0.3423	0	0.0001	0	1
Corporación Geo	0.2145	1	0.0001	0	1
Empresas Ica	0.7710	0	0.0001	0	1
Fomento Econ Mex	0.8524	0	0.0001	0	1
G Financiero Banorte	0.1326	0	0.0001	0	1
G Financiero Inbursa	0.1424	0	0.0001	0	1
Grupo Carso	0.0197	0	0.0001	0	0
Grupo Elektra	0.9448	1	0.0001	0	1
Grupo México	0.5982	0	0.0001	0	1
Grupo Modelo	0.2171	2	0.0001	1	1
Grupo Televisa	0.2718	2	0.0000	1	1
Kimberly Clark México	0.2796	0	0.0001	0	1
Organización Soriana	0.1100	0	0.0001	0	1
Telmex	0.0441	0	0.0001	0	0
TV Azteca	0.0691	0	0.0001	0	1
Wal Mart de México	0.0160	0	0.0001	0	0
IPC	0.9946	1	0.0001	0	1

Nota: La hipótesis nula asociada a la prueba adf se rechaza cuando Prob < 0.05.

Cuadro 5.

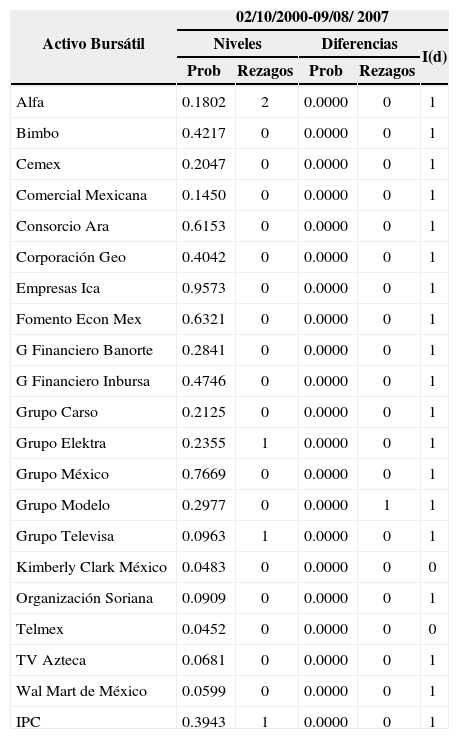
Prueba adf para las series de los logaritmos de precios (niveles) y de los rendimientos (diferencias) para los periodos del 2 de octubre de 2000 al 9 de agosto de 2007, y del 10 de agosto de 2007 al 10 de octubre de 2012.

Activo Bursátil	02/10/2000-09/08/ 2007
	Niveles		Diferencias		I(d)
	Prob	Rezagos	Prob	Rezagos
Alfa	0.1802	2	0.0000	0	1
Bimbo	0.4217	0	0.0000	0	1
Cemex	0.2047	0	0.0000	0	1
Comercial Mexicana	0.1450	0	0.0000	0	1
Consorcio Ara	0.6153	0	0.0000	0	1
Corporación Geo	0.4042	0	0.0000	0	1
Empresas Ica	0.9573	0	0.0000	0	1
Fomento Econ Mex	0.6321	0	0.0000	0	1
G Financiero Banorte	0.2841	0	0.0000	0	1
G Financiero Inbursa	0.4746	0	0.0000	0	1
Grupo Carso	0.2125	0	0.0000	0	1
Grupo Elektra	0.2355	1	0.0000	0	1
Grupo México	0.7669	0	0.0000	0	1
Grupo Modelo	0.2977	0	0.0000	1	1
Grupo Televisa	0.0963	1	0.0000	0	1
Kimberly Clark México	0.0483	0	0.0000	0	0
Organización Soriana	0.0909	0	0.0000	0	1
Telmex	0.0452	0	0.0000	0	0
TV Azteca	0.0681	0	0.0000	0	1
Wal Mart de México	0.0599	0	0.0000	0	1
IPC	0.3943	1	0.0000	0	1

Activo Bursátil	10/08/2007-10/10/2012
	Niveles		Diferencias		I(d)
	Prob	Rezagos	Prob	Rezagos
Alfa	0.4209	0	0.0000	0	1
Bimbo	0.4691	0	0.0000	0	1
Cemex	0.1877	1	0.0000	0	1
Comercial Mexicana	0.5978	4	0.0000	3	1
Consorcio Ara	0.0587	0	0.0000	0	1
Corporación Geo	0.2065	0	0.0000	0	1
Empresas Ica	0.2570	1	0.0000	0	1
Fomento Econ Mex	0.1020	0	0.0000	0	1
G Financiero Banorte	0.7790	0	0.0000	0	1
G Financiero Inbursa	0.2031	0	0.0000	0	1
Grupo Carso	0.0237	0	0.0000	0	0
Grupo Elektra	0.1942	1	0.0000	0	1
Grupo México	0.4806	0	0.0000	0	1
Grupo Modelo	0.2699	2	0.0000	1	1
Grupo Televisa	0.0353	0	0.0000	0	0
Kimberly Clark México	0.5341	0	0.0000	0	1
Organización Soriana	0.0490	1	0.0000	0	0
Telmex	0.2330	0	0.0000	0	1
TV Azteca	0.1674	0	0.0000	0	1
Wal Mart de México	0.0836	0	0.0000	0	1
IPC	0.5364	0	0.0000	0	1

Nota: La hipótesis nula asociada a la prueba adf se rechaza cuando Prob < 0.05.

Los cuadros 4 y 5 muestran que la gran mayoría de las series de logaritmos de precios son I(1). Esto conlleva a que la mayoría de los activos aparentemente puedan validar el cumplimiento de la emh. Particularmente, el cuadro 4 muestra que, si se considera las series completas, hay 18 series de precios I(1). El cuadro 5 muestra que durante el periodo de “calma”, entre el 2 de octubre de 2000 y el 9 de agosto de 2007, hay 19 series I(1). Asimismo muestra que, si se considera el periodo de “inestabilidad”, entre el 10 de agosto de 2007 y el 10 de octubre de 2012 hay 18 series I(1). Por tanto, la comparación muestra que el número de series que validan la emh ha tendido a disminuir a lo largo del tiempo.

Las series de logaritmos de precios que son I(0) son susceptibles de ser descritas y analizadas de manera directa mediante modelos econométricos. Por tanto refieren a activos individuales que no cumplen con la hipótesis de eficiencia. Si se considera la totalidad del periodo analizado, estas series corresponden a Grupo Carso, Telmex y Walmart de México. Si se considera el periodo de “calma”, las series corresponden a Kimberly Clark México y Telmex. Si se considera el periodo de “inestabilidad”, las series corresponden a Grupo Carso, Organización Soriana y Grupo Televisa. Por tanto, el número de series a nivel desagregado que no validan la emh es pequeño, pero creciente, en el tiempo.

Analíticamente, los resultados estimados tienen implicaciones sobre el mercado bursátil mexicano. Particularmente la validación de que la mayoría de las series de logaritmos de precios son I(1) sugiere que la hipótesis de eficiencia prevalece en el mercado a nivel agregado y desagregado. Sin embargo, los resultados también sugieren que la eficiencia del mismo ha tendido a disminuir a nivel desagregado desde agosto de 2007. Econométricamente, la validación de que las series de precios sean I(1) conlleva a que las diferencias de las mismas sean modelables. Esto significa que la mayoría de las series de rendimientos bursátiles son susceptibles de ser descritas y analizadas estadísticamente.

6

Ejercicios de modelación y análisis econométricos

Los modelos garch multivariados (mgarch) usados en esta investigación comparten una estructura similar para efectos de estimación econométrica. En todos los modelos, los vectores de la media condicional requieren estimar los coeficientes φ_i1 y ρ_i. Asimismo, requieren hacer estimaciones de las matrices de varianza-covarianza. Por comparabilidad y simplicidad, la dinámica conjunta de las series de rendimientos se describe usando los doce modelos multivariados señalados anteriormente. Al igual que en los análisis anteriores, las estimaciones se agrupan por periodos. Estas estimaciones están sintetizadas en los cuadros 67 y 8. La comparación econométrica de las estimaciones se realiza con base en el cuadro 9.

Cuadro 6.

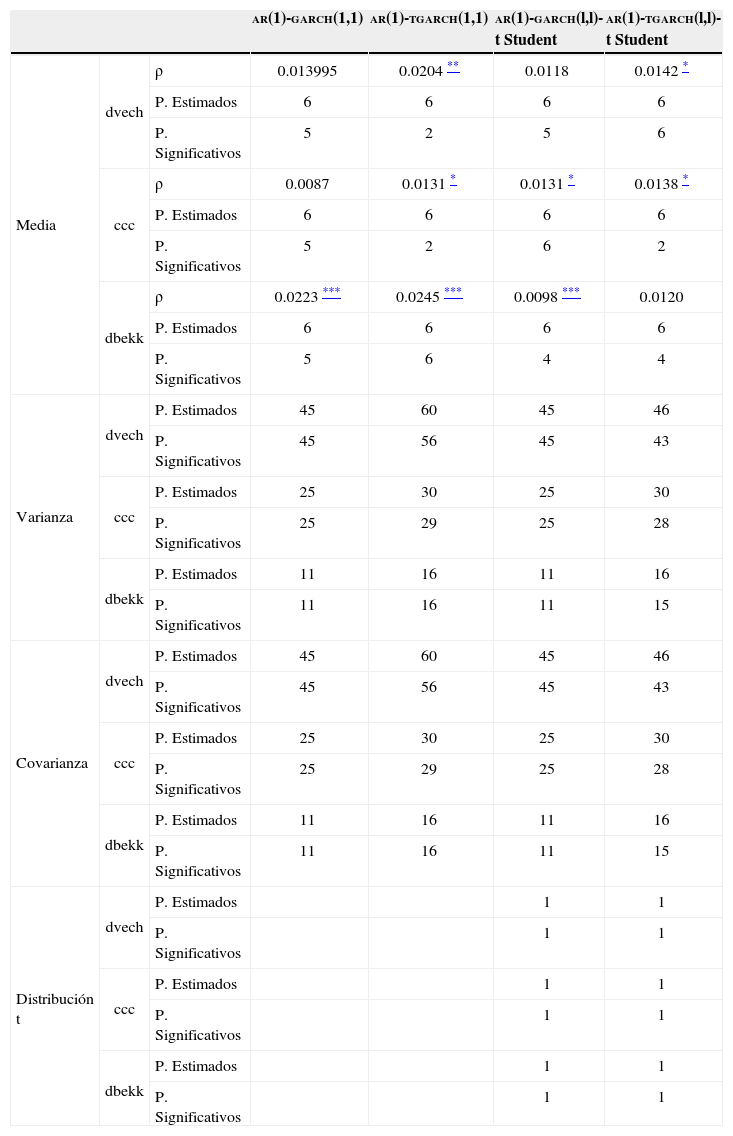
Estimaciones obtenidas mediante los modelos garch multivariados para las series de rendimientos durante el periodo del 2 de octubre de 2000 al 10 de octubre de 2012.

			ar(1)-garch(1,1)	ar(1)-tgarch(1,1)	ar(1)-garch(l,l)-t Student	ar(1)-tgarch(l,l)-t Student
Media	dvech	ρ	0.013995	0.0204 ^**	0.0118	0.0142 ^*
		P. Estimados	6	6	6	6
		P. Significativos	5	2	5	6
	ccc	ρ	0.0087	0.0131 ^*	0.0131 ^*	0.0138 ^*
		P. Estimados	6	6	6	6
		P. Significativos	5	2	6	2
	dbekk	ρ	0.0223 ^***	0.0245 ^***	0.0098 ^***	0.0120
		P. Estimados	6	6	6	6
		P. Significativos	5	6	4	4
Varianza	dvech	P. Estimados	45	60	45	46
		P. Significativos	45	56	45	43
	ccc	P. Estimados	25	30	25	30
		P. Significativos	25	29	25	28
	dbekk	P. Estimados	11	16	11	16
		P. Significativos	11	16	11	15
Covarianza	dvech	P. Estimados	45	60	45	46
		P. Significativos	45	56	45	43
	ccc	P. Estimados	25	30	25	30
		P. Significativos	25	29	25	28
	dbekk	P. Estimados	11	16	11	16
		P. Significativos	11	16	11	15
Distribución t	dvech	P. Estimados			1	1
		P. Significativos			1	1
	ccc	P. Estimados			1	1
		P. Significativos			1	1
	dbekk	P. Estimados			1	1
		P. Significativos			1	1

*,** y ***

Notas: denotan niveles de significancia del 10, 5 y 1 por ciento respectivamente. Las estimaciones se refieren a los 5 activos cuyas series de rendimientos manifestaron efectos arch.

Cuadro 7.

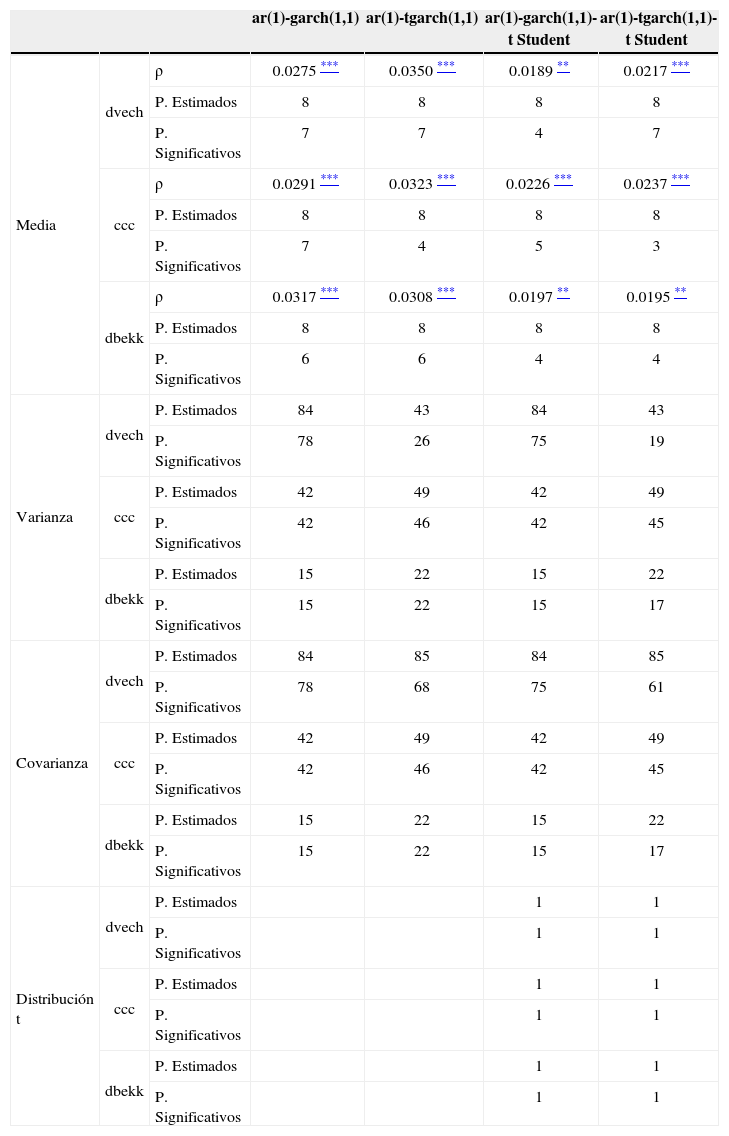
Estimaciones obtenidas mediante los modelos garch multivariados para las series de rendimientos durante el periodo del 2 de octubre de 2000 al 9 de agosto de 2007.

			ar(1)-garch(1,1)	ar(1)-tgarch(1,1)	ar(1)-garch(1,1)-t Student	ar(1)-tgarch(1,1)-t Student
Media	dvech	ρ	0.0275 ^***	0.0350 ^***	0.0189 ^**	0.0217 ^***
		P. Estimados	8	8	8	8
		P. Significativos	7	7	4	7
	ccc	ρ	0.0291 ^***	0.0323 ^***	0.0226 ^***	0.0237 ^***
		P. Estimados	8	8	8	8
		P. Significativos	7	4	5	3
	dbekk	ρ	0.0317 ^***	0.0308 ^***	0.0197 ^**	0.0195 ^**
		P. Estimados	8	8	8	8
		P. Significativos	6	6	4	4
Varianza	dvech	P. Estimados	84	43	84	43
		P. Significativos	78	26	75	19
	ccc	P. Estimados	42	49	42	49
		P. Significativos	42	46	42	45
	dbekk	P. Estimados	15	22	15	22
		P. Significativos	15	22	15	17
Covarianza	dvech	P. Estimados	84	85	84	85
		P. Significativos	78	68	75	61
	ccc	P. Estimados	42	49	42	49
		P. Significativos	42	46	42	45
	dbekk	P. Estimados	15	22	15	22
		P. Significativos	15	22	15	17
Distribución t	dvech	P. Estimados			1	1
		P. Significativos			1	1
	ccc	P. Estimados			1	1
		P. Significativos			1	1
	dbekk	P. Estimados			1	1
		P. Significativos			1	1

*, ** y ***

Notas: denotan niveles de significancia del 10, 5 y 1 por ciento respectivamente. Las estimaciones se refieren a los 7 activos cuyas series de rendimientos manifestaron efectos arch.

Cuadro 8.

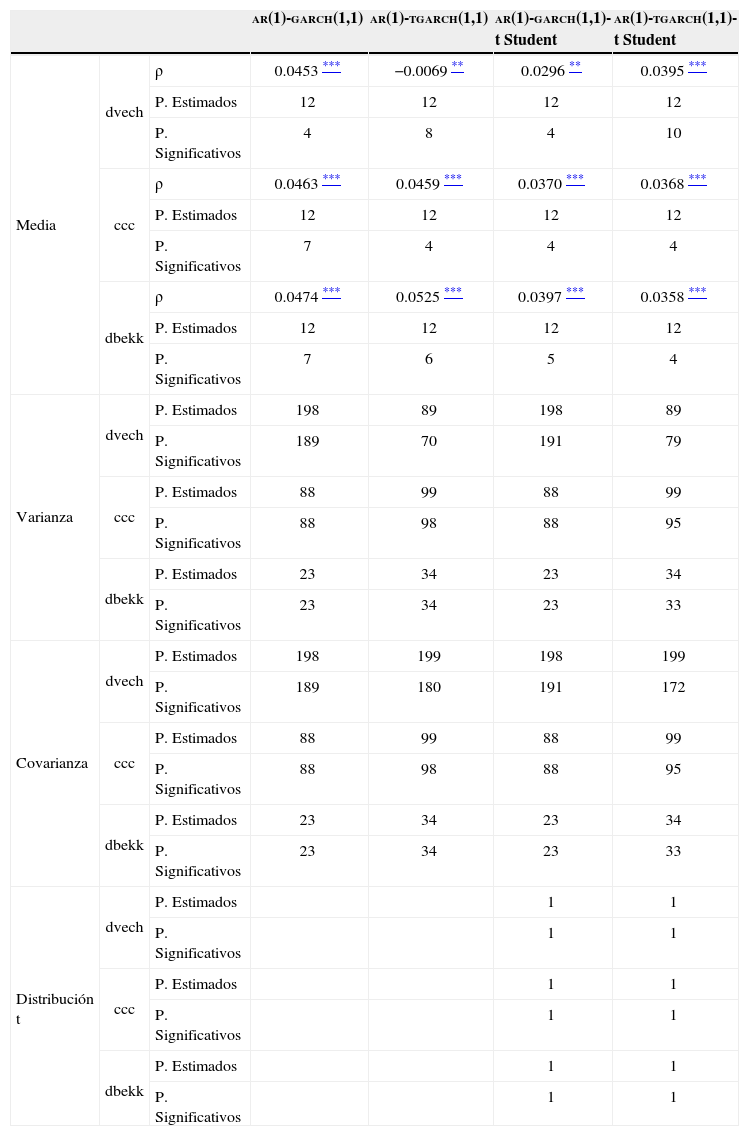
Estimaciones obtenidas mediante los modelos garch multivariados para las series de rendimientos durante el periodo del 10 de agosto de 2007 al 10 de octubre de 2012.

			ar(1)-garch(1,1)	ar(1)-tgarch(1,1)	ar(1)-garch(1,1)-t Student	ar(1)-tgarch(1,1)-t Student
Media	dvech	ρ	0.0453 ^***	−0.0069 ^**	0.0296 ^**	0.0395 ^***
		P. Estimados	12	12	12	12
		P. Significativos	4	8	4	10
	ccc	ρ	0.0463 ^***	0.0459 ^***	0.0370 ^***	0.0368 ^***
		P. Estimados	12	12	12	12
		P. Significativos	7	4	4	4
	dbekk	ρ	0.0474 ^***	0.0525 ^***	0.0397 ^***	0.0358 ^***
		P. Estimados	12	12	12	12
		P. Significativos	7	6	5	4
Varianza	dvech	P. Estimados	198	89	198	89
		P. Significativos	189	70	191	79
	ccc	P. Estimados	88	99	88	99
		P. Significativos	88	98	88	95
	dbekk	P. Estimados	23	34	23	34
		P. Significativos	23	34	23	33
Covarianza	dvech	P. Estimados	198	199	198	199
		P. Significativos	189	180	191	172
	ccc	P. Estimados	88	99	88	99
		P. Significativos	88	98	88	95
	dbekk	P. Estimados	23	34	23	34
		P. Significativos	23	34	23	33
Distribución t	dvech	P. Estimados			1	1
		P. Significativos			1	1
	ccc	P. Estimados			1	1
		P. Significativos			1	1
	dbekk	P. Estimados			1	1
		P. Significativos			1	1

*, ** y ***

Notas: denotan niveles de significancia del 10, 5 y 1 por ciento respectivamente. Las estimaciones se refieren a los 11 activos cuyas series de rendimientos manifestaron efectos arch.

Los cuadros 6, 7 y 8 muestran las estimaciones obtenidas mediante los modelos multivariados para las series de rendimientos a nivel agregado y desagregado. El cuadro 6 incluye las estimaciones considerando la totalidad del periodo analizado. El cuadro 7 incluye las estimaciones considerando el periodo de “calma” financiera. El cuadro 8 incluye las estimaciones considerando el periodo de “inestabilidad”. Los activos incluidos en las estimaciones fueron aquellos cuyas series de precios fueran I(1) y cuyas series de rendimientos hubieran manifestado efectos arch.¹⁵Así, el número de activos incluidos en las estimaciones de los cuadros 6, 7 y 8 son, respectivamente, 5, 7 y 11.¹⁶

El cuadro 6 muestra las estimaciones que describen la dinámica del conjunto de series de rendimientos bursátiles considerando el periodo completo. Este cuadro provee valores de referencia para evaluar la hipótesis de eficiencia y la distribución de las perturbaciones. El cuadro muestra que los rendimientos tienden a estar correlacionados entre sí: Todas las estimaciones de ρ_i y la mayoría de φ_i1 son significativas. Por tanto, la evidencia provee escasa evidencia para validar la hipótesis de eficiencia. Además, el cuadro provee evidencia de que las perturbaciones se distribuyen siguiendo una distribución t de Student multivariada: Todas las estimaciones referidas a los grados de libertad son significativas.

El cuadro 7 muestra las estimaciones que describen la dinámica del conjunto de series de rendimientos bursátiles considerando el periodo del 3 de octubre de 2000 al 9 de agosto de 2007. Este cuadro confirma los resultados obtenidos anteriormente. Los rendimientos tienden a estar correlacionados en el tiempo ya que todas las estimaciones de ρ_i y la mayoría de φ_i1 son significativas. Por tanto, la evidencia confirma que existe escasa evidencia para validar la hipótesis de eficiencia. Además, el cuadro confirma que las perturbaciones se distribuyen siguiendo una distribución t de Student multivariada. Al igual que antes, todas las estimaciones referidas a los grados de libertad son significativas.

El cuadro 8 muestra las estimaciones que describen la dinámica del conjunto de series de rendimientos bursátiles considerando el periodo del 10 de agosto de 2007 al 10 de octubre de 2012. Este cuadro también confirma los resultados obtenidos anteriormente. Al igual que antes, los rendimientos tienden a estar significativamente correlacionados entre sí. Sin embargo, debe mencionarse que las magnitudes absolutas de p_i obtenidas tienden a ser mayores que las obtenidas en los periodos previos. Además, el cuadro también confirma que las perturbaciones se distribuyen siguiendo una distribución t de Student multivariada. Asimismo, todas las estimaciones referidas a los grados de libertad son significativas.

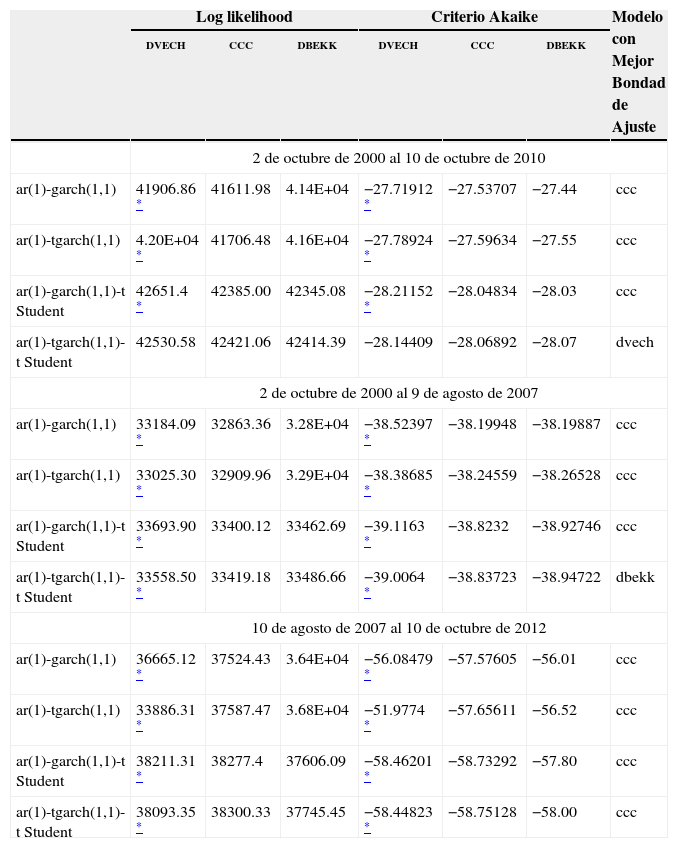
El cuadro 9 muestra y compara los estimadores de bondad de ajuste para cada una de las estimaciones realizadas. Esta evaluación se hace comparando los valores absolutos de los estimadores. La mayoría de las comparaciones muestran que los modelos de tipo ccc (Constant Conditional Correlation) son los que tienden a describir mejor la dinámica conjunta de las series. Particularmente, las comparaciones entre modelos similares muestran que la especificación tgarch parece caracterizar de mejor manera a la volatilidad de las series. Más aún, las comparaciones confirman que la distribución de densidad t de Student multivariada describe de mejor manera a las perturbaciones.

La consistencia de los resultados econométricos sugiere que hay patrones definidos de comportamiento de las series de rendimientos. Particularmente, el número creciente de series modelables confirma que la ineficiencia ha tendido a aumentar desde 2007. La predominancia de los modelos de tipo ccc sugiere que las correlaciones condicionales explican la dinámica conjunta de comportamiento de dichas series. La predominancia de la especificación tgarch sugiere que las buenas y malas noticias tienen impactos asimétricos sobre la volatilidad de los rendimientos. La predominancia de la distribución t de Student multivariada sugiere que las perturbaciones no se distribuyen normalmente.

	Log likelihood			Criterio Akaike			Modelo con Mejor Bondad de Ajuste
	dvech	ccc	dbekk	dvech	ccc	dbekk
	2 de octubre de 2000 al 10 de octubre de 2010
ar(1)-garch(1,1)	41906.86 ^*	41611.98	4.14E+04	−27.71912 ^*	−27.53707	−27.44	ccc
ar(1)-tgarch(1,1)	4.20E+04 ^*	41706.48	4.16E+04	−27.78924 ^*	−27.59634	−27.55	ccc
ar(1)-garch(1,1)-t Student	42651.4 ^*	42385.00	42345.08	−28.21152 ^*	−28.04834	−28.03	ccc
ar(1)-tgarch(1,1)-t Student	42530.58	42421.06	42414.39	−28.14409	−28.06892	−28.07	dvech
	2 de octubre de 2000 al 9 de agosto de 2007
ar(1)-garch(1,1)	33184.09 ^*	32863.36	3.28E+04	−38.52397 ^*	−38.19948	−38.19887	ccc
ar(1)-tgarch(1,1)	33025.30 ^*	32909.96	3.29E+04	−38.38685 ^*	−38.24559	−38.26528	ccc
ar(1)-garch(1,1)-t Student	33693.90 ^*	33400.12	33462.69	−39.1163 ^*	−38.8232	−38.92746	ccc
ar(1)-tgarch(1,1)-t Student	33558.50 ^*	33419.18	33486.66	−39.0064 ^*	−38.83723	−38.94722	dbekk
	10 de agosto de 2007 al 10 de octubre de 2012
ar(1)-garch(1,1)	36665.12 ^*	37524.43	3.64E+04	−56.08479 ^*	−57.57605	−56.01	ccc
ar(1)-tgarch(1,1)	33886.31 ^*	37587.47	3.68E+04	−51.9774 ^*	−57.65611	−56.52	ccc
ar(1)-garch(1,1)-t Student	38211.31 ^*	38277.4	37606.09	−58.46201 ^*	−58.73292	−57.80	ccc
ar(1)-tgarch(1,1)-t Student	38093.35 ^*	38300.33	37745.45	−58.44823 ^*	−58.75128	−58.00	ccc

^* Notas: El asterico denota que los modelos no cumplen con la condición de que la matriz de covarianza es semidefinida positiva. El modelo con mejor bondad de ajuste se determina con base en los estimadores considerados.

7

Conclusiones y discusión

En esta investigación se ha estudiado la validez de la hipótesis de eficiencia (emh) en el mercado bursátil mexicano y se han modelado las series de rendimientos bursátiles. La evaluación de la emh, en su forma débil, se ha realizado mediante estadísticas descriptivas, pruebas de raíces unitarias y de correlación. Los ejercicios de modelación y análisis econométricos han utilizado doce modelos garch multivariados con fines de comparativos y de caracterización de las series durante periodos de calma e inestabilidad financiera. El estudio se ha sustentado en una muestra de series de precios diarios de veinte acciones y del ipc que abarca datos del 2 de octubre de 2000 al 10 de octubre de 2012.

Los resultados de la investigación sugieren que hay escasa evidencia para sustentar la emh en el mercado bursátil mexicano. El análisis de estacionariedad sugiere que la hipótesis de eficiencia predomina, hasta cierto punto, en el mercado cuando se consideran únicamente las series de precios de los activos. Sin embargo, la evidencia también sugiere que la eficiencia del mercado ha tendido a disminuir desde el año 2007. Por otra parte, la evidencia sugiere que las series de rendimientos bursátiles tienden a manifestar curtosis excesivas, clusters de volatilidad, asimetrías, distribuciones no normales, volatilidades no constantes y movimientos conjuntos de medias y varianzas.

Los ejercicios de modelación y análisis econométricos de las series de rendimientos validan las conclusiones anteriores. Los mismos muestran que: 1) Las series no validan la hipótesis de eficiencia porque los rendimientos tienden a estar significativamente correlacionados; 2) los modelos de tipo ccc son los que, en principio, mejor describen la dinámica de los series; 3) las buenas y malas noticias tienen impactos asimétricos sobre la volatilidad de los rendimientos; 4) por tanto, la especificación tgarch caracteriza de mejor manera a la volatilidad de las series; y 5) la distribución t de Student multivariada describe de mejor manera a las perturbaciones de los modelos.

La consistencia de los resultados obtenidos bien puede servir para justificar el estudio de las causas de la persistente ineficiencia del mercado bursátil mexicano. Particularmente, es nuestra creencia que esta se explica, parcialmente, por el escaso desarrollo del mercado. Este subdesarrollo se manifiesta en varios hechos estilizados. Entre estos se incluyen: 1) el pequeño y volátil número de empresas que hacen transacciones;¹⁷2) la gran concentración de la bursatilización en un pequeño conjunto de acciones de empresas de gran tamaño;¹⁸ y 3) la existencia de problemas de asimetría de información.¹⁹ El estudio de estos hechos bien podría complementar el análisis aquí desarrollado.

Finalmente, debe enfatizarse que la investigación referida a los mercados bursátiles tiene amplias posibilidades de desarrollo. En las economías emergentes, la importancia de este tipo de investigación se vincula directamente con el desarrollo económico y financiero. Esto ocurre porque los mercados bursátiles permiten financiar empresas, administrar riesgos, canalizar ahorros y asignar recursos para la inversión pública y privada. En este contexto, el desarrollo de investigación bursátil podría contribuir a que estas tareas pudieran realizarse de mejor manera. Por tanto, la importancia de realizar nuevas investigaciones puede justificarse plenamente desde las perspectivas teórica y empírica.