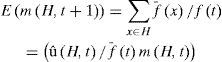En el modelo clásico de Cournot se emplea un mecanismo de variación conjetural en la producción, donde el equilibrio se encuentra entre el monopolio y el equilibrio competitivo, por lo que las empresas y consumidores no son indiferentes ante las cantidades y precios alcanzados. Es decir, las cantidades a producir son mayores que en el monopolio pero con un beneficio menor. En el artículo se muestran los resultados alcanzados en el modelo ante el aprendizaje individual y social a través de esta metodología. Se exponen las implicaciones, adaptaciones y alcances de los Algoritmos Genéticos para resolver el problema de aprendizaje de las empresas en el modelo de Cournot mediante una visión de racionalidad limitada, en la computación evolutiva y en la teoría de juegos evolutivos.
In the classical model is employed Cournot conjectural variation mechanism in production, where the balance lies between monopoly and competitive balance, so that businesses and consumers are not indifferent to the quantities and prices achieved. That is, the production quantities are higher than in the monopoly but with a smaller profit. The article shows the results achieved in the model to the individual and social learning through this methodology. We describe the implications, adaptations and scope of genetic algorithms to solve the learning problem of firms in Cournot model by a vision of bounded rationality in evolutionary computation and evolutionary game theory.
Con la publicación del libro de Von Neumann y Morgenstern Theory of Games and Economic Behavior en 1944 se inicia formalmente la teoría de juegos, la cual tenía como idea central confrontar las limitaciones de la teoría neoclásica (que sólo estudiaba situaciones donde el agente no era expuesto a ningún conflicto-monopolio y competencia perfecta) y aportar una visión de interacción entre los agentes. Por ejemplo, cuando nos encontramos con estructuras de mercado donde solo algunas empresas compiten (oligopolio).
Uno de los antecedentes de la teoría de juegos es el modelo de Cournot (desarrollado en 1838) el cual emplea un mecanismo de variación conjetural en la producción, donde el equilibrio se encuentra entre el monopolio y el equilibrio competitivo, por lo que las empresas y consumidores no son indiferentes ante las cantidades y precios alcanzados (Mas-Colell et al., 1995). Es decir, las cantidades a producir son mayores que en el monopolio pero con un beneficio menor. El análisis tradicional en este modelo de duopolio se basa principalmente en la función de reacción, pero al incluir más empresas a competir, los resultados se vuelven inestables al tratar de seguir los supuestos establecidos en el modelo.
El desarrollo reciente de la teoría de juegos evolutivos impulsado por Maynard-Smith (1982) ha contribuido a brindar otro tipo de adaptación dinámica, en lugar de la función de reacción (Vallée y Yildizoglu, 2009) lo que ha permitido introducir un análisis más sofisticado donde se desee incluir el aprendizaje de las empresas, por lo que los métodos de búsqueda utilizados son adaptativos y sobre todo estables, dando lugar a los Algoritmos Genéticos (ag), los cuales están inspirados en la evolución biológica.
Existe literatura especializada que ha logrado generar cierto consenso en los resultados cuando se analiza el modelo de Cournot con metodologías evolutivas. Por ejemplo, en Vallée y Yildizoglu (2009) se muestran estos consensos y discusiones sobre la convergencia que alcanza el modelo ante el aprendizaje individual y social. Sin embargo, ante la robustez de este tipo de investigaciones se deja casi de lado las implicaciones teóricas y prácticas de utilizar herramientas que emanan de la Inteligencia Artificial (ia) o las adaptaciones fueron requeridas para que los ag resuelvan problemas económicos.
Lo anterior se debe a que este tipo de investigaciones se dedican a ofrecer resultados sobre sus experimentos computacionales y discutir sus diferencias con respecto a otros experimentos de la misma naturaleza. Así, la motivación de esta investigación es realizar un punto de encuentro entre diversas disciplinas (economía, biología, psicología y otras) y exponer sus relaciones de una forma sencilla para un caso específico.
El objetivo de la investigación es exponer las implicaciones teóricas y prácticas, adaptaciones y alcances de los ag para resolver el problema de aprendizaje de las empresas en el modelo de Cournot. Para lograr nuestro objetivo nos apoyamos en la visión de racionalidad limitada (representada por los ag), en la computación evolutiva (que especifica la construcción y funcionamiento de los ag) y en la teoría de juegos evolutivos (que relaciona métodos evolutivos y las interacciones de los agentes).
La investigación está estructurada de la siguiente forma. En el segundo apartado, se expone la visión ideológica, elementos y funcionamiento de los ag. En esencia, nos apoyamos en la visión de racionalidad limitada (que se caracteriza por considerar los avances en psicología, biología, ingeniería, entre otras) que da sustento a la ia y en la metodología que sigue la computación evolutiva para la construcción de un ag. En el tercer apartado, se estudia desde el modelo clásico de Cournot, donde el análisis se hace a través de la función de reacción (estático) y se logra un equilibrio estable (Nash-Cournot), hasta la versión evolutiva donde los ag toman lugar. En el cuarto, se exponen los hallazgos más sobresalientes encontrados en la investigación. Y finalmente, las conclusiones.
2Algoritmos genéticosEn 1975 con la publicación del libro Adaptation in Natural and Artificial Systems, Holland presenta a los ag como una abstracción de la evolución biológica. Holland1 lo define como un método de cambio de una población de cromosomas a una nueva población, usando un tipo de “selección natural” junto con los operadores genéticos (recombinación, mutación e inversión). Teniendo como principal atractivo utilizarlos como métodos de búsqueda ante problemas altamente complejos o incluso como diseñadores de soluciones innovadoras, entre otros (Mitchell, 1999).
2.1Marco teóricoUno de los supuestos de la visión neoclásica es la racionalidad de los agentes, que busca maximizar el beneficio o utilidad. Lo anterior implica, entre otros aspectos, que el agente tiene una alta capacidad de procesamiento sobre todas sus alternativas y consecuencias y, por ende, puede optimizar. Así, la función de utilidad refleja una confianza absoluta en las preferencias, donde éstas se conciben racionales, consistentes y transitivas, es decir, existe una idealización del agente. Sin embargo, existe evidencia de que las elecciones humanas son susceptibles a cambios e incluso a ser erróneas (Kahneman, 2011).
Lo anterior, ha impulsado el surgimiento de diversas visiones para dar respuesta a fenómenos que desde la visión ortodoxa no parecen tener lugar. Por ejemplo, para dar respuesta a los acontecimientos surgidos en la Gran Depresión de 1929, Keynes incluyó diversos elementos en su teoría, como el actuar de los empresarios, el cual se basaban en conceptos psicológicos y rechazaba los supuestos de la economía clásica sobre la información y la previsión del futuro (axioma de ergodicidad), donde este último presupone que cualquier dato futuro puede ser confiablemente pronosticado a través del análisis estadístico. Así, en el largo plazo el equilibrio está predeterminado y, por lo tanto, no puede ser modificado por ninguna acción humana o gubernamental (regulación) (Davidson, 2008).
Otro ejemplo, es la teoría de juegos que se basa en estrategias que involucran no sólo el actuar del agente, sino también de los demás, aunque sigue manteniendo el supuesto de racionalidad. Sin embargo, ésta busca tener un mayor acercamiento con la realidad (modelando los conflictos entre los agentes) y evidenciar el aislamiento de la economía con otras disciplinas (Von Neuman y Morgenstern, 1953).
Al mismo tiempo pero bajo otro enfoque, el modelo de decisión racional es seriamente discutido bajo el contexto del comportamiento administrativo y de gestión. Como resultado, a mediados de la década de los cincuenta, se inicia la teoría de racionalidad limitada en la Universidad de Carnegie Mellon con H. Simon y otros. La investigación proponía el estudio de métodos de control y de procesos de decisión en las empresas, de este modo surgen las nociones de la racionalidad limitada o acotada como un método de observación empírica y directa de los fenómenos psicológicos a nivel individual (Egidi, 2008).
Así, H. Simon da origen a una corriente de investigación sobre los fundamentos cognitivos en la economía. Como parte de esta corriente Kahneman y Tverky se enfocaban en la complejidad del razonamiento humano a través de los juicios, la memoria, la relevancia dada a ciertos eventos o experiencias, las cuales rompen con reglas establecidas en la probabilidad. Lo que implica, que la racionalidad tal y como se concibe no es adecuada (Kahneman, 2011).
En el libro Las Ciencias de lo Artificial de H. Simon2 se expone la relación entre el enfoque de racionalidad limitada y la ia. Esta relación se divide para nuestros fines en tres temáticas. En la primera, se establecen cuáles son las características de los objetos artificiales y cómo es posible imitar el comportamiento humano. Para dar respuesta Simon considera a los objetos artificiales como sintetizados, que pueden tener o no aspectos de los objetos naturales, que pueden caracterizarse en términos de funciones, objetivos y adaptación, y que son susceptibles a rediseñarse. En cuanto al hecho de la imitación, se menciona que un artefacto puede ser concebido como un punto de encuentro entre un entorno interno y externo. La ciencia de lo artificial depende de la simplicidad relativa entre ambiente interno y externo como fuente de abstracción y generalidad. En esencia, el objeto artificial imita al real para interactuar con el sistema externo, adaptándose en relación con los mismos objetivos a rangos comparables de tareas externas. La imitación es posible porque sistemas físicos distintos pueden organizarse para mostrar un comportamiento casi idéntico.
En la segunda, se profundiza sobre los alcances de la simulación (o imitación). Donde se trata de entender al sistema imitado poniendo a prueba la simulación en computadora con diferentes entornos imitados. Sin olvidar que una simulación se basa en supuestos y solo puede hacer aquello para lo que está programado. Sin embargo, la simulación puede enseñarnos cosas que desconocemos, es decir, pudiera ofrecer conocimiento nuevo de los mecanismos que gobiernan nuestro comportamiento y puede ser de gran ayuda cuando no se sabe mucho acerca de las leyes naturales que gobiernan el comportamiento del sistema interno.
Y en la tercera, la relación con los avances en la psicología experimental. Dado que en el mundo real la optimización, con o sin computadoras es imposible, el actor económico real acepta alternativas “bastante buenas” no porque se conforme con menos sino porque no tiene otra alternativa. Los avances en psicología de la elección indican que algunas de las propiedades que debiera tener un termómetro de la satisfacción son: 1) Que a diferencia de la función de utilidad, no debiera limitarse a seguir valores positivos y 2) Las lecturas periódicas de individuos en circunstancias estables no suelen estar muy alejados de cero (aceptación mínima) en una u otra dirección y los registros divergentes tenderían a volver con el tiempo al punto cero, por lo que los registros de la mayoría de la gente se hallarían ligeramente bajo cero (descontento leve) o un poco por encima (satisfacción moderada).
En resumen, la ia proporciona a menudo una forma de búsqueda heurística donde se encuentran decisiones satisfacientes (bastante buenas) en lugar de soluciones óptimas. Las metodologías que comparten estas características son los ag, los autómatas celulares, las redes neuronales, entre otras.
Como consecuencia, la visión de Simon resalta que:
El ser humano como sistema de comportamiento, es bastante simple. La complejidad aparente de nuestro comportamiento es fundamentalmente un reflejo de la complejidad del entorno en que nos encontramos.
Para entender mejor esta idea, es necesario saber que se considera como entorno a la memoria profunda (tamaño ilimitado) y a la información almacenada en libros, por lo que se pone especial énfasis en la memoria a corto plazo (tamaño limitado) a través de estudios de la psicología experimental. Además, queda implícito que más memoria no implica necesariamente más complejidad; ya que existe evidencia sobre el desempeño humano y su simulación computacional, que por lo general apoyan la hipótesis de simplicidad (Simon, 2006).
Antes de Simon la idea del modelado del cerebro y de la evolución biológica para solucionar problemas complejos era discutida desde los inicios de la era computacional. Los principales pioneros fueron Alan Turing, John von Neumann, Norbert Wiener, entre otros. Es decir, los científicos computacionales no sólo creían que sus herramientas podrían ser destinadas para fines militares sino incluso crear ia, por lo que se concentraban en estudios sobre biología y psicología principalmente (Mitchell, 1999).
2.2ElementosEn este subapartado relacionamos cada uno de los elementos de los ag bajo dos posturas. Por un lado, desde la visión biológica y por otro, de la computación evolutiva (Griffiths et al., 2002; Mitchell, 1999).
- a)
Una población de cromosomas: el organismo humano está formado de células y cada núcleo contiene dos dotaciones de 23 cromosomas, al desenrollar un cromosoma encontramos al gen (figura 1). En el contexto de los ag el término “cromosoma” típicamente se refiere a una solución candidata a un problema usualmente codificado como una cadena bit. El “gen” es un bit que codifica a un elemento en particular de la solución candidata y cada locus (o posición) en el cromosoma tiene dos posibles alelos: 0 o 1. Aquí, cada cromosoma puede ser tomado como un punto en el espacio de búsqueda de soluciones candidatas.
- b)
Selección de acuerdo a la aptitud: la aptitud de un organismo es generalmente definida como la probabilidad de un organismo de vivir y reproducirse. Para los ag la aptitud de un “cromosoma” depende de que tan bien resuelva este el problema. Y el operador de selección determina que “cromosoma” de la población será el más apto.
- c)
Recombinación: los cromosomas homólogos pueden intercambiar parte de su material en un proceso denominado entrecruzamiento, durante la meiosis (reproducción celular). Para los ag este operador aleatoriamente selecciona un locus e intercambia las secuencias antes o después entre dos cromosomas para crear dos descendientes. Por ejemplo, las cadenas 10000100 y 11111111 podría haber una recombinación después del tercer locus 10011111 y 11100100.
- d)
Mutación: surge cuando un gen ha pasado de una forma alélica a otra, es decir, la mutación no sólo es causa de una variación dentro de una especie, sino a largo plazo de la materia prima de la evolución. Estas pueden provocar la pérdida de una función de un gen o la aparición de una nueva. Estas ocurren al azar, en cualquier momento y en cualquier célula de un organismo. Para los ag este operador cambia aleatoriamente algunos bits en un cromosoma. Por ejemplo, la cadena 00000100 podría mutar en la segunda posición 01000100. Esta mutación puede ocurrir en cada bit de la cadena con la misma probabilidad.
El objetivo de un algoritmo es solucionar un problema, para ello se especifica un conjunto ordenado y finito de operaciones. Y aunque existen diversos tipos podemos hablar de aquellos que encuentran soluciones óptimas y de aquellos evolutivos. De este último tipo se expone el caso de los ag, en su versión original.
La visión de Holland establece que un esquema es un conjunto de cadenas bits que pueden ser descritas como una plantilla formada de unos, ceros y asteriscos (comodines). Por ejemplo, el esquema H=1****1 es el conjunto de cadenas con 6 bits, que inician y finalizan con 1 o que cuenta con 2 bit definidos (orden 2), es decir, que no sean asteriscos y con una distancia definida por la distancia entre sus bits definidos. Las cadenas que se ajustan a esta plantilla3 se dicen que son casos de H.
Entonces, si H es un esquema con al menos un caso presente en la población al tiempo t.Tenemos que m(H,t) es el número de casos de H al tiempo t y Û(H,t)es la aptitud promedio observada de H en el tiempo t. Si deseamos calcular E(m(H,t+1)) es decir, el número de casos esperados para H en el tiempo
También definimos f(t) como la aptitud promedio de la población al tiempo t. Entonces, asumimos que x es en la población al tiempo t un caso de H definido como xÎH. Por ahora, tenemos que:
Si tenemos que ÛH(H,t)=(ξ xÎH f(x) / im(H,x) para x en la población al tiempo t. Por tanto, a través de los ag no se calcula explícitamente Û(H,t). La recombinación y la mutación pueden destruir o crear casos para H. Incluyendo sólo sus efectos destructivos, se puede modificar el lado derecho de la ecuación anterior. Si tenemos que Pc es la probabilidad de que en un solo punto la recombinación tenga lugar en la cadena. El esquema H se dice que sobrevive en un solo punto de recombinación si uno de los descendientes es también un caso del esquema H. En el caso de la mutación la probabilidad de que cualquier bit sea mutado es Pm.
Estos efectos modifican la ecuación (I), teniendo:
Donde d(H) es la distancia definida de H y 0(H) es el orden de H.
Lo anterior es conocido como el Teorema de Esquema, aunque en este caso sólo conlleva los efectos destructivos de la recombinación y la mutación. Pero en la evaluación de una población de n cadenas, el ag implícitamente estima el promedio de la aptitud de todos los esquemas de la población. Existen actualmente, nuevas adaptaciones a la formulación inicial de Holland, en especial con lo que tiene que ver con el operador de recombinación (véase, Mitchell, 1999).
3El modelo de CournotEn este apartado, se muestra el desarrollo y avances en el modelo de Cournot. Se expone desde la visión clásica hasta la versión evolutiva donde se modela el aprendizaje social (con mutaciones homogéneas o variaciones en cantidades en una sola dirección) y el aprendizaje individual (con mutaciones heterogéneas o variaciones en cantidades en ambas direcciones) a través de los ag.
3.1La versión clásicaEn el modelo de Cournot la competencia entre las firmas es a través de cantidades, así cuando ambas firmas deciden simultáneamente la cantidad a producir, q1 y q1, con una función de demanda inversa, p(.) = x-1 (.) y se asume que p(.) es diferenciable con p(q)<0 para todo <0 (q)≥ 0 <0. Las empresas producen a un costo c>0 por unidad. Pero también se tiene que p(0)>c y que existe un único nivel de producción, donde º ∈(0,∞), donde º es el nivel competitivo. Entonces para encontrar un equilibrio de Nash se considera un problema de maximización para la empresa j dado un nivel de producción qk, k≠j:
Donde para cada qk, se denota bj(qk) como el conjunto de cantidades óptimas para la empresa j;b(.) es la mejor respuesta de la empresa j. Entonces el par (q1∗,q2∗) es un equilibrio de Nash si qj∗∈bjqk∗ para k≠j. Debe satisfacer:
Entonces manteniendo que q1∗,q2∗>0 y agregando (4) y (5) tenemos:
En esencia, tenemos que el precio de mercado en el duopolio de Cournot es mayor que el costo marginal, es decir, es mayor que el precio competitivo (CMg=Demanda) pero menor que el precio de monopolio donde el ingreso marginal se iguala con el costo marginal (IMg=CMg). Mientras que las cantidades a producir son mayores que en el monopolio q1∗+q2∗>qm pero menores que en el mercado competitivo qº ∈ (0,∞) (Mas-Colell et al., 1995), por lo que las empresas y consumidores no son indiferentes ante las cantidades y precios alcanzados. En otras palabras, las empresas preferirán producir menos a un precio mayor; mientras que los consumidores preferirán que su demanda sea satisfecha.
Para visualizar lo anterior, en Mas-Colell et al. (1995) se considera una función de demanda inversa p(q)=a-bp, a>c≥0 b>0 y con rendimientos constantes a escala, donde el costo por unidad es c.
Además, se considera las cantidades y precios para los casos extremos en un mercado:
Para el caso de monopolio es: qm=a−c/2b y pm=pm=a+c/2b
Para el caso de competencia competitiva es: qº=a−c/b y pqº=c
Entonces, para la empresa j se tiene la ecuación (3) y por tanto, la siguiente función de reacción, donde la cantidad de la empresa k es fija:
Así, la mejor respuesta de la empresa j, es ser un monopolio (qm=a-c /2b) y que la empresa k, no produzca (toca el eje de las abscisas). Pero también podría ser el caso, en que la empresa k, mantuviera un nivel competitivo (q°=a-c/b) y por ende no participaría k, ya que incurre en pérdidas (toca el eje de las ordenadas). Para el caso de la empresa k, se sigue con el mismo procedimiento pero ahora se mantiene fija j. Las funciones de reacción de las dos empresas se muestran en la figura (2) junto con las cantidades a producir.
Por ejemplo, si las empresas producen como monopolio cada una tendrían la mitad de la cantidad requerida (q=a-c /4b). Esto no sería factible ya que las empresas tendrían que coludir. Pero ante una interacción estrategia, la mejor respuesta a que llegarían ambas empresas (equilibrio de Nash) sería donde la producción fuera mayor para cada una (q=a-c /3b) pero menor que en un nivel competitivo (q=a-c/2b). Es decir, en el equilibrio alcanzado si se generan ganancias pero no tan altas como en el monopolio, por lo que las empresas preferirán este equilibrio a los niveles competitivos. Mientras que los consumidores preferirán un nivel competitivo.
Para el caso de más competidores Theocharis demostró en 1959, que bajo los supuestos del modelo clásico de Cournot4 a partir de cuatro empresas el equilibrio se vuelve inestable. En su modelo especifica que cada firma asume que todos los competidores conservan su oferta del periodo anterior y que a través de un análisis del determinante jacobiano se tiene que para n-1 valores propios λ,…,n−1=12 y con el último λn=n−12. Theocharis concluye que para el caso de dos empresas el equilibrio de Cournot es estable (los valores absolutos son menores a la unidad), en el caso de tres empresas el equilibrio es neutralmente estable (donde cualquier perturbación lleva al sistema a una oscilación interminable) y para cuatro empresas en adelante el equilibrio es inestable (Cánovas et al, 2008).
3.2Algunos experimentosLos estudios sobre el modelo de Cournot han sido vastos y recientemente puestos a discusión dentro del campo evolutivo. Sin embargo, esta transición fue el resultado de diversos experimentos incluso de aquellos de quienes no tenían en mente a la evolución humana como inspiración, sino que simplemente evidenciaban distintos comportamientos que de alguna debían incluirse. Por ejemplo, en Bosch-Domenech y Vriend (2008) se exponen algunos experimentos clásicos al modelo de Cournot.
En ellos se muestran la necesidad de incluir el aprendizaje de las firmas (como un factor cualitativo de decisión), el grado de información disponible y la comunicación.
3.3La versión evolutivaEl distintivo de los modelos evolutivos es que combinan dos procesos: el proceso de selección que favorece a unas especies sobre otras, y el proceso de mutación que crea esta variedad (Weibull, 1998). En una población de la misma especie que interactúa generación tras generación, la mutación y la selección remplazan estrategias por otras con mayor éxito reproductivo. Así, los pagos están en términos de aptitud como medida de éxito reproductivo. La teoría de juegos evolutivos al basarse en el proceso de “selección natural”, lleva a los organismos hacia el éxito reproductivo. Y al considerar una población donde todos sus miembros juegan la misma estrategia, se asume que un mutante surge cuando juega una estrategia diferente, por lo que la estrategia jugada por la mayoría de la población es estable y se contrapone con la mutante. En esencia, una Estrategia se dice que es Evolutivamente Estable (eee) si elimina de su población cualquier estrategia diferente (Hammerstein y Selten, 1994).
En un juego de población finita con un perfil de estrategias q* se dice que es eee si en la presencia de una firma mutante j juega qjm≠qj∗:
En nuestro juego de oligopolio, esta definición significa que el beneficio de la firma i debe ser mayor si enfrenta a un mutante que juega qm en el caso de serlo.
Aquí en cada periodo t, cada estrategia es evaluada usando el mismo precio dado pt-1.Y considerando el mecanismo de estrategia de selección “roulette wheel” donde la probabilidad de selección de una estrategia es proporcional a su aptitud relativa fij=Fij/∑Fij de una estrategia dada j del jugador i.
En Vallée y Yildizoglu (2009) se especifica que bajo el contexto de oligopolio los ag se utilizan para representar la capacidad de aprendizaje de las firmas. Estos hacen evolucionar a la población de cromosomas y el algoritmo (aleatoriamente) genera una población inicial de cromosomas candidatos que son evaluados en cada periodo usando una función de aptitud (beneficio). Estos cromosomas se utilizan para la composición de la nueva población en el próximo periodo. Donde cada cromosoma tiene una probabilidad mayor de ser seleccionado al incrementar su beneficio relativo.
En cuanto al modelo de Cournot existe un consenso acerca de la convergencia al equilibrio competitivo con aprendizaje social (mutaciones homogéneas), sin embargo, se ha cuestionado cuando el aprendizaje es individual (mutaciones heterogéneas) y su convergencia al equilibrio de Cournot.
Para efectos de nuestra investigación nos enfocaremos en el caso más sencillo que es cuando al modelo de Cournot se incluye el aprendizaje social. Aquí, la única estrategia que se imitará será dejar el equilibrio de Cournot incrementando las cantidades a producir, y aunque el beneficio se reduce no será tanto como aquellas que no imitan la estrategia. Para dar una idea sobre el funcionamiento de estos procedimientos se presenta la tabla (1). Aquí se realiza un comparativo entre un caso simple y el caso del modelo de Cournot incluyendo el aprendizaje social.
En cuanto al aprendizaje individual la formulación se complica debido a que existen tantos ag como firmas y las mutaciones son simultáneas y heterogéneas. Las diferencias que surgen en cuanto a los experimentos computacionales en el aprendizaje individual obedecen principalmente a los mecanismos utilizados en el funcionamiento del ag, es decir, a la naturaleza de las mutaciones y al proceso de selección. En esencia, es sobre los supuestos acerca del proceso de aprendizaje de las firmas con racionalidad limitada a partir del grado de información.
Algunas reflexionesEn este apartado se exponen las implicaciones, adaptaciones y alcances de los ag y su relación con el modelo de Cournot. Para ello se han clasificado de acuerdo a su naturaleza:
ImplicacionesTeóricas- a)
La visión de racionalidad limitada puede verse como una corriente de pensamiento basada en la observación del agente como un ser real, donde es posible no contar con toda la información (principalmente), por lo que encontrar soluciones óptimas se ve como un hecho ficticio.
- b)
Las metodologías que emanan de la ia se basan en procesos adaptativos, donde la historia cobra gran relevancia y así pueden llegar a ofrecer soluciones “muy buenas” para problemas altamente complejos. Sin embargo, la mayoría de estas metodologías se basan en métodos heurísticos.
- c)
Los ag se han posicionado como una herramienta altamente sofisticada en diversos campos de la economía y las finanzas. Esto se debe a que logran encontrar soluciones de una manera rápida y eficiente dentro de un espacio complejo y muy grande que bajo otros instrumentos sería exhaustivo o imposible de resolver. Pero también, presuponen una población inicial con alta calidad, una función de aptitud promedio estática y la exclusión de factores externos que pudieran influir en el proceso evolutivo.
- d)
En un contexto económico es necesario hacer adaptaciones e incluso consideraciones específicas sobre la evolución de la racionalidad, el equilibrio y las normas.
- e)
Para el caso del oligopolio los ag consideran una población donde todos sus miembros juegan la misma estrategia y se asume que un mutante surge cuando juega una estrategia diferente y que solo representa una pequeña fracción de la población al inicio del juego, por lo que la estrategia mutante tiene una menor tasa de reproducción y tenderá a desaparecer. Es decir, se necesita de una definición adaptada de eee, donde todos compitan simultáneamente.
- f)
La aplicación de los ag se justifica porque se requiere de un proceso de adaptación dinámica que pueda incluir de alguna forma la historia reflejada en el aprendizaje de las empresas, desde una perspectiva muy sofisticada (ya que no sólo incluye el actuar de los otros agentes sino también la capacidad de imitar, experimentar, crear expectativas.).
- g)
Los problemas que surgen en la versión evolutiva del modelo de Cournot, se deben principalmente al tipo de información y a los beneficios que representan en la función de aptitud.
El modelo clásico de Cournot ofrece resultados basados en la variación conjetural de la producción bajo una modalidad estática. Así, la teoría de juegos evolutivos incluye nuevas formas de análisis cuando se considera el aprendizaje de las empresas. La relevancia de esta nueva versión es que permite modelar un comportamiento dinámico a partir de situaciones complejas. Para el caso del oligopolio de Cournot toma lugar cuando las empresas compiten simultáneamente, y la mutación cuando las empresas deciden incrementar o disminuir las cantidades ofrecidas, por lo que la aplicación de los ag permite explorar esta problemática.
Lo anterior muestra la utilidad de los ag para explorar más allá de lo que podríamos hacer con herramientas tradicionales, es decir, efectivamente la simulación de escenarios nos permite corroborar hechos u obtener nueva información.
Sin embargo, aunque se evidencian las limitaciones que pueden surgir con la aplicación de metodologías inteligentes, es claro el potencial de éstas y en específico para el caso del modelo de Cournot.