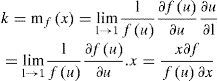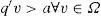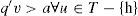Tecnología, reflexiones matemáticas

Resumen

El trabajo presenta elementos de economía matemática necesarios para entender el papel de la tecnología en la generación de funciones de producción, isocuantas y para determinar la eficiencia en la producción.

Abstract

The paper shows concepts on mathematic economics needed to get a better understanding of technology and its relationship with the concepts of production function, isoquant, and economic efficiency.

1

Introducción

El presente ensayo revisa, teóricamente, las posibilidades de una tecnología, entendiéndola como una transformación matemática de un conjunto de insumos a un conjunto de productos, para producir un excedente de bienes, ya sea para consumirse o invertirse, permitiendo la satisfacción de necesidades sociales y el crecimiento del sistema productivo. El trabajo se centra en caracterizar el concepto tecnología. La segunda sección trata de la definición del concepto tecnología, la tercera caracteriza los rendimientos a escala para la producción de un bien a partir de n insumos y la última, presenta una generalización de la producción simultánea de varios bienes.

Propongo partir de la siguiente idea: el proceso de producción de m bienes a partir de n insumos se define por una transformación del cono positivo de ℝⁿ, un espacio de insumos, al cono positivo de ℝ^m, espacio de productos. Para m = 1, la producción eficiente de un bien será caracterizada por una función, llamada función de producción, de insumos a productos, esto es del cono positivo a la recta real positiva. Utilizando los supuestos teóricos clásicos, la función de producción es al menos cuasi-cóncava y la noción de rendimientos constantes a escala se identifica con funciones de producción homogéneas de primer grado. En este sentido, la gráfica de la tecnología es un cono convexo.¹

En aras de generalizar el concepto y capacidades descriptivas de las funciones de producción es necesario desarrollar dos ideas: primero, la definición general de eficiencia; y segundo, una definición general de rendimientos a escala. La sección cuarta desarrolla tales objetivos. En dicha sección se amplia el concepto de eficiencia, primero en el caso general en el que la correspondencia de insumos tenga imágenes convexas y, posteriormente, el de tecnologías de rendimientos no crecientes a escala, es decir, de gráfica convexa.

Por su importancia en la construcción de producción y la centralidad en modelos económicos es necesario revisar los conceptos que permiten generar las funciones de producción: para tal objetivo es necesario entender el constructo matemático llamado tecnología.

2

La correspondencia de producción

Se asume que cualquier economista está familiarizado con la función de producción, ℝ+n→fℝ+, monótona no decreciente y que presenta rendimientos marginales decrecientes. La función de producción representa únicamente la producción eficiente, en el sentido de que, con insumos x, no es posible producir más de f(x). Vamos a considerar una representación de la tecnología en términos que se permita analizar:

• a)

  La producción simultánea de varios bienes.

• b)

  Todas las posibilidades de producción.²

Lo último es necesario para definir qué es producción eficiente de varios bienes, que implica combinaciones de productos y no simplemente la cantidad de uno sólo de ellos, como en el caso de la función de producción.³ Entonces, nos referimos a la producción de m bienes a partir de n insumos, con una tecnología que es una transformación de insumos en productos. Por lo tanto, la tecnología se entenderá como una transformación matemática P, de un espacio de insumos X a un espacio de productos Y. Un elemento x del espacio de insumos es una lista de cantidades de distintos bienes, que la tecnología usa para producir otra lista de bienes y, que es un elemento del espacio de productos. La imagen P(x) de un elemento del espacio de insumos es el conjunto de todas las listas de productos que la tecnología P puede producir a partir de x.⁴

La forma en que se describe, hace que su representación matemática sea como una función del espacio de insumos a la clase de los subconjuntos del espacio de productos: ∀x∈ℝ+n, Px⊂ℝ+n.p se verá entonces como una correspondencia.

ℝ+n→ℝ+m:P:ℝ+n..ℝ+m

La correspondencia P se llama correspondencia de producción. La correspondencia P^–1, inversa de P, del espacio de productos al de insumos, de imágenes P−1y=x∈ℝ+n y∈Px, es la correspondencia de insumos; la imagen de un vector de productos y bajo la correspondencia de insumos contiene a las listas de bienes con las que se puede producir el vector y: x ∈ P^–1(y) sí y sólo si x sirve para producir y. la gráfica de P es el conjunto grP=x,y∈ℝ+n×∈ℝ+n y∈Px. Un punto (x, y) ∈ grP es un programa de producción.

Ahora ya estamos en condiciones de proporcionar una definición formal. Para ello seguiremos la propuesta de Shepard. Por lo que se define lo siguiente:

Sean X, Y dos espacios vectoriales normados y ordenados por el orden parcial. La correspondencia P : X^.. Y, con espacio de insumos Xy espacios de productos Y, es una tecnología si satisface:

• Pl)

  P(0) = {0}

• P2)

  || x || finito que P(x) es un conjunto acotado

• P3)

  Si x ≥ 0 y, para algún escalar I¯>0, PI¯x≠0, entonces ∀y∈PI¯y y todo escalar m> 0, εI_p, tal que my ∈ P(I _mx)

• P4)

  x'≥_;x⇒Px⊂Px'

• P5)

  y'≥_;y∧y∈Px⊂Px'⇒y'∈Px

• P6)

  P^–1(y) es convexo para todo y en el rango de P.

• P7)

  La gráfica de P es un subconjunto cerrado de X × Y.

Los anteriores postulados serán de utilidad más adelante.

3

Funciones de producción y rendimientos a escala

La presente sección trata el caso particular de m = 1, para caracterizar, en términos de la correspondencia de producción, a la función de producción.⁵ Cuando m > 1 este concepto no es utilizable, por lo que más adelante se presenta la generalización. Sea P:ℝ+n ..ℝ+ una tecnología que produce un solo bien a partir de n insumos. Partiendo de que P2 se sostiene, se tiene que f:ℝ+nf→ℝ+, definida porfx=supyy∈Px=supPx

Es una función y está definida para todo x ∈ domP. Entonces, f se llama la función de producción asociada a P.⁶ De aquí en adelante, llamaremos función de producción a cualquier función f:ℝ+n→ℝ+ que satisfaga FI-F3 y F5.⁷

Ahora es necesaria otra definición.⁸

La función rendimientos a escala asociada a la función de producción f de clase C¹ se define como:mfx=liml→1lflx∂lx∂l

Si tal límite existe.⁹

Con la definición anterior podemos construir el siguiente teorema

Teorema 1. Sí y solamente si f es homogénea de grado k < 0, m_f = k ∀x ∈ Dom_f.

Demostración. Primera parte. Suponga que existe m_f (x) = k para todo x. Si hacemos u = lx. Entonces:

De donde por el teorema de Euler, f es homogénea de grado k.¹⁰

Segunda parte. Sea f (l x) = l ^kf (x). Entonces:=liml→1lflx∂lx∂l=liml→1llkfx∂lfx∂l=liml→1lflxklk−1=k

Q.E.D.

Teniendo el anterior teorema ahora se requiere la siguiente definición:

Se dice que f tiene rendimientos crecientes (constantes, decrecientes a escala si m_f (x) = k, con k > 1(= 1, < 1, respectivamente), para todo x ∈ Dom_f. Esto nos conduce al siguiente teorema:

Teorema 2. Sea f:ℝ+n→ℝ+. Los siguientes asertos son equivalentes:

• a)

  f es cuasicóncava y homogénea de primer grado.

• b)

  La hipográfica de f es un cono convexo cerrado en punta.

Demostración. Al ser f cuasicóncava y homogénea implica que f es cóncava, de donde hipo f es un subconjunto convexo de ℝ+n+1. Dado que es f cóncava es continua, de donde hipo f es un conjunto cerrado. También por homogeneidad, (x,y)∈ hipo f, implica l y < l f (x) = f (l x), de donde (l x, l y) ∈ hipo f, que es un cono.Como hipo f es un subconjunto de ℝ+n+1, (x,y) ∈ hipo f y (–x, –y) ∈ hipo f implican x = 0, y = 0, donde hipo f es un cono en punta.

Recíprocamente, la convexidad de hipo f implica la concavidad y por tanto la cuasiconcavidad de f. Para demostrar la homogeneidad recuérdese que por ser cerrada la hipográfica def para cada x, (x, fx)) es un punto de hipo f, que es un cono, por lo que (l x, l f (x)) ∈ hipo f, o sea que l f (x) ≤ f (l x). Si dicha igualdad no se sostiene, es decir, l f (x) < f (l x), existirá algún ε < 0 tal que (1 + e)l f (x) ≤ f (l x). De nuevo por ser hipo f un cono, esto implica que (l+e)(x) f(x) ∈ hipo f, o sea que (1 + e) f (x) ≤ f (x), que es un absurdo. Q.E.D.

Esta equivalencia será generalizada más adelante con el concepto de rendimientos constantes a escala para la producción de más de un bien.

4

Producción eficiente

En esta sección el objetivo es caracterizar el subconjunto de puntos eficientes de una tecnología que produce m bienes a partir de n insumos. Para ellos se plantea la siguiente definición:

Sea P:ℝ+n ..ℝ+ una correspondencia de producción x ∈ P^–1(y) es un método eficiente para producir y si x’ ≤ x implica x’ ∈ P^–1(y).

En otras palabras, x es un método eficiente para producir y si y es producible con x pero no lo es con ningún vector x’ en el que la cantidad de algún insumo sea menor que la que contiene x.

El conjunto de los métodos eficientes para producir y se denotará por E(y), que se define como: x∈P−1y v≥0⇒x−v∉P−1y.ℝ+m ..ℝ+n es la correspondencia de métodos eficientes de producción. Podemos definir a E mediante postulados.

• a)

  Para todo y∈ℝ+m, Ey⊂P−1y.

• b)

  Para todo y∈ℝ+m, Ey−ℝ+n⊂P−1cy.

En este punto conviene presentar una definición adicional.

Sea P:ℝ+n ..ℝ+m una correspondencia de producción, x ∈ P(x) es un producto eficiente del vector de insumos x∈ℝ+n si, para todo u ≥ 0, y + u ∉ P(x).

Por lo anterior se entiende que y es un producto eficiente de x si x puede producir y. Sin embargo, no puede producir ningún vector en el que la cantidad de algún producto exceda a la que contiene y. Entonces, el conjunto de productos eficientes a partir de x se denota por E(x), cuyo conjunto y∈Pxu≥0⇒y+u∉Px, E:ℝ+m ..ℝ+n es la correspondencia de productos eficientes.¹¹

Ahora es necesario generalizar a la producción de m productos el concepto de isocuanta. Para ello ocuparemos las siguientes definiciones:

• •

  El conjunto Iy=x∈P−1ylx∉P−1y⇒x∉P−1y es el conjunto isocuanta de insumos para y.

• •

  El conjunto Ix=u∈PxI>I u∉Px es el conjunto isocuanta de productos para x.

Aquí se tiene que Ey⊂Iy⊂∂P−1y y Ex⊂Ix. Por lo que no todo punto de I(y) es un método eficiente para producir y es evidente, incluso para algún y escalar.¹²

Se destaca que las isocuantas de una función de producción se mapean como la gráfica de una función convexa. Para cada y > 0 escalar, se considera el conjunto de nivel P^–l(y) = L_f (y). Definiendo x_n = j (x₁,...,x_n–1) = j (x_–n) = y sí y sólo sí f (x₁,...,x_n) = y. Ahora, se sabe que f (x₁,...,x_n) ≥ y implica quex_n ≥j _y(x_–n). En otras palabras, x=x−nxn∈Lfy que implica x=x−nxn∈epijy y por ende L_f (y) ⊂ epij _y. De igual manera se tiene que x_n ≥ j _y(x_–n) implica que f (x₁,...,x_n) ≥ y, lo que epij _y ⊂ L_f (y). Ahora, epij _y es convexo y j_y expresa la enésima coordenada de x, uso eficiente del insumo n, como función de las otras n – 1, a lo largo de la isocuanta f(x) = y es convexa. Para el caso general, dónde la correspondencia de producción presente gráfica convexa, y no necesariamente un cono, se puede emplear un teorema de dualidad, que relacione la producción eficiente con un sistema de precios soporte.¹³

Estamos en condiciones de definir lo siguiente. El conjunto T=−z,yz.y∈grP es el conjunto de tecnología asociado a la correspondencia de producción P. Sabemos que la gráfica de P toma el nombre de conjunto de posibilidades de producción. El conjunto de tecnología es la reflexión, sobre los ejes de producto, del conjunto de posibilidades de producción. Las propiedades topológicas de de convexidad de los dos conjuntos son las mismas. Al especificar T, los insumos aparecen con signo negativo y los productos con signo positivo.

Ahora, definamos. Sea h = (–x,y) ∈ T es un programa de producción eficiente si para ningún z ∈ T vale z ≥ h.

Empleando un teorema de Takayama¹⁴ tenemos.

Teorema 3. Si T es convexo, h ∈ T es eficiente sí y sólo sí maximiza alguna funcional lineal no negativa.

Demostración. Se demostrará de la manera siguiente. Primero, la suficiencia es inmediata. La necesidad requiere que para todo z ∈ T, z – h > 0 es imposible si h es eficiente, de dondeT – {h} está estrictamente separado del interior de ℝ+n+m, el cual denotaremos por Ω. Entonces, sea H_q,a un hiperplano separador, de tal forma que:

• •

  Si α< 0, como 0 ∈ T – {h}, se tendría que q’0 < 0. Se concluye que α < 0.

• •

  Ahora, suponga que algún q_i es <0. Entonces, como v ∈ Ω implica que vi puede hacerse arbitrariamente grande, se tendría que, apara algún v ∈ Ω, q’v < 0 ≤ a, contradiciendo la definición de a y la de q, de donde q ≥ 0.

• •

  Como ||v|| puede hacerse arbitrariamente pequeño para v ∈ Ω. no importa qué tan pequeño sea α > 0 se tendría q’v < a para algún v ∈ Ω, contradiciendo la definición de α como la altura del hiperplano H_q,a de modo que α ≤ 0 y, por el punto anterior, α = 0

• •

  Se tiene que q’u = q’(z – h) ≤ 0 para todo z ∈ T.

Q.E.D.

Se aprecia que el hiperplano de normal q soporta a T en h. La propiedad de ser un punto de soporte de un hiperplano de normal no negativo equivale a la propiedad de ser un programa eficiente de producción.

Con lo anterior se puede inferir la siguiente definición:

Sea h un punto eficiente de T. Si h maximiza a q en T, se dice que q es un sistema de precios de eficiencia o precios de soporte asociado a h.