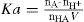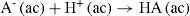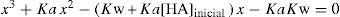This article presents a simple and conceptual application of the spreadsheet and the scroll bar to find the composition of a system in chemical equilibrium, for various situations related to monoprotic acid equilibrium. This method allows to simulate different situations such as a) weak acid dilution, b) common ion effect, c) buffer solutions, and d) the composition of a very dilute acid or an acid of very low acid-dissociation constant.
En este trabajo se desarrolla un método sencillo y conceptual de aplicación de la hoja de cálculo y de la barra de desplazamiento para hallar la composición de un sistema ácido-base en equilibrio químico, en particular para diversas situaciones de un ácido monoprótico en equilibrio. Este método permite simular diversas situaciones como la dilución de un ácido débil, el efecto del ion común, las disoluciones amortiguadoras y la composición de un ácido muy diluido o de constante de disociación muy baja.
Un artículo anterior (Raviolo, 2011) se dedicó a describir la potencialidad y versatilidad de las hojas de cálculo para la enseñanza de la química y brindar algunos ejemplos de actividades sencillas para realizar con los alumnos. En otro artículo (Raviolo, 2012) se mostró cómo la hoja de cálculo puede emplearse para la verificación y re-creación de simulaciones. Además se encuentran otros dos trabajos aparecidos en Educación Química con aplicaciones específicas de la hoja de cálculo: Rojas y otros (2010) sobre química analítica y Quílez y Castelló (1996) sobre el equilibrio químico. En este último se presenta el programa equil conformado por planillas de cálculo ya terminadas que contienen macros, que permiten arribar a la solución de situaciones donde el principio de Le Chatelier está limitado o incorrectamente aplicado. En la bibliografía se aprecia que, en general, las aplicaciones de la hoja de cálculo para la enseñanza del equilibrio químico son más complejas y se basan en el uso de macros, como la recientemente publicada por Vander Griend (2011); en cambio, la propuesta de este artículo es original por su sencillez y está orientada a que los propios estudiantes la desarrollen en su totalidad.
Entre las ventajas de las hojas de cálculo para la enseñanza de la química, que se tienen en cuenta en esta propuesta, se destacan: (a) su rápido aprendizaje y uso inmediato, (b) que en muchos casos pueden reemplazar a un lenguaje de programación de difícil aprendizaje y (c) su capacidad para simular, y responder preguntas del tipo “¿qué pasa si?”.
Una síntesis bastante exhaustiva sobre las investigaciones realizadas sobre las concepciones alternativas y dificultades de los estudiantes en relación con el tema equilibrio químico se encuentra en Raviolo y Martínez Aznar (2003). Allí se verifica que el aspecto más estudiado (aproximadamente el 60% de las investigaciones) y sobre el cual se ha debatido mucho, es el referido a la utilización del principio de Le Chatelier para predecir la evolución de un sistema en equilibrio al ser perturbado. También se sostiene que el hecho de indagar exclusivamente las ideas de los estudiantes sobre este aspecto del fenómeno, puede pasar por alto la influencia que sobre él ejercen concepciones más básicas como: (a) la imagen del sistema en equilibrio (recipiente cerrado, dinamismo, constancia de concentraciones a temperatura constante, composición de la mezcla en equilibrio) y (b) los aspectos cinéticos (modelo de colisiones, constancia y cambio de velocidades de reacción en distintos momentos).
Investigaciones sobre las concepciones alternativas y dificultades de los estudiantes sobre la composición de un sistema en equilibrio químico, han mostrado que algunos alumnos (de nivel medio y primer año de universidad):
- –
No distinguen entre las composiciones iniciales y las de equilibrio, o no admiten la coexistencia de todas las especies en el equilibrio (por ej. Van Driel y otros, 1998).
- –
Conciben que las cantidades presentes de reactivos y productos en el equilibrio son iguales entre sí, o son iguales a los coeficientes estequiométricos (por ej. Hackling y Garnet, 1985; Huddle y Pillay, 1996; Raviolo, 2006).
- –
Presentan confusiones al relacionar los conceptos de reactivo limitante y composición del equilibrio químico (por ej. Bergquist y Heikkinen, 1990).
La propuesta que se desarrolla a continuación, de utilidad para cursos universitarios de química general (y también por su sencillez para cursos de nivel medio), permite arribar a la composición de un sistema químico en el equilibrio, mediante la aplicación de los principios estequiométricos, que permiten distinguir cantidades de concentraciones. Ello contribuye a la superación de las concepciones alternativas anteriormente enumeradas.
La composición de una disolución acuosa de ácido débil monopróticoLa ionización de un ácido monoprótico débil como el ácido acético puede expresarse como:
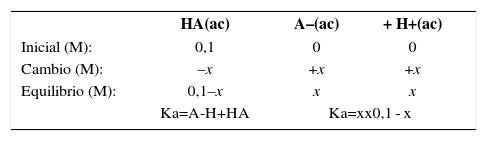
o expresarse en forma más simple:La constante de equilibrio para esta reacción, o constante de ionización del ácido, Ka es 1,8×10–5 a 25°C (Chang, 2008). Con el valor de Ka y de la concentración inicial del ácido se puede calcular la concentración en el equilibrio del ion hidrógeno y con ello el pH de la disolución. Para ello suele realizarse el siguiente planteamiento, por ejemplo para una concentración inicial de ácido de 0,1 M.
El procedimiento de obtención de las concentraciones al equilibrio implica la resolución de una ecuación cuadrática:
Suele realizarse una simplificación, válida sólo en condiciones determinadas, consistente en despreciar la x que resta en el denominador, cuando ésta es menor que el 5% de la concentración inicial a la cual se resta. También la ecuación anterior de la constante de equilibrio puede expresarse en función de los números de moles y el volumen.
En los equilibrios ácido-base también interesa calcular el pH (– log[H+]) y el porcentaje de ionización o desprotonación porcentual ([H+]/[HA]inicial ×100).
El método de simulación que se propone consiste en asignar un rango de posibles valores de x empleando la barra de desplazamiento en una hoja de cálculo y, sobre la base de las relaciones estequiométricas planteadas, determinar las cantidades o las concentraciones de los reactivos y productos en el equilibrio. Con estas concentraciones se calculan los valores resultantes de Ka. La solución final es la composición del sistema cuando el valor de Ka coincide, o es la más cercana, con su valor disponible a la temperatura dada. Esta propuesta se inspira en el método interactivo sugerido por Finnemore (1990) para el proceso Haber, aunque este método resulta más engorroso dado que no emplea la barra de desplazamiento.
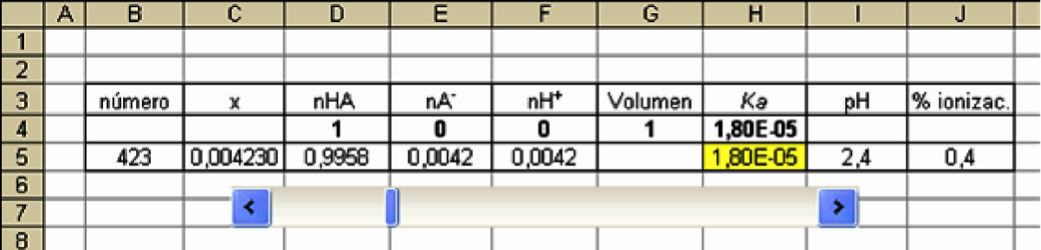
Se realiza una tabla como se muestra en la figura 1. En la celda B5 aparecerá un número del 1 al 2000 que se asigna con la barra de desplazamiento.
La barra de desplazamiento es una herramienta que permite incorporar o cambiar rápidamente valores que se hallan dentro de un intervalo. Para insertar la barra de desplazamiento en el programa Excel se procede de la siguiente manera. En la versión 2003, las barras de desplazamiento se insertan desde: Ver, Barra de herramientas, Formularios, se hace clic en el icono de Barra de desplazamiento y se dibujan en la hoja. En la versión 2007, con Botón de Office, Opciones de Excel, Comandos disponibles en, Ficha (o Cinta) del programador, Insertar controles, Agregar, Aceptar, aparece en la parte superior de la pantalla (barra de herramientas de acceso rápido) un icono de Insertar controles. Las barras de desplazamiento se insertan desde esa barra: Insertar controles, Controles de formulario, Barra de desplazamiento.
Una vez insertada la barra de desplazamiento, sobre ella y con el botón derecho del ratón se abre Formato de control y se completa Valor mínimo, Valor máximo, Incremento y Vincular con la celda, como se muestra en la figura 2.
El valor asignado por la barra de desplazamiento (del 1 al 2000) aparece en la celda B5, y dado que como valor mínimo no se puede insertar números decimales, en la celda C5 el valor asignado se lo divide por 100000 (1×10–5); el resultado constituye x, cuya unidad en esta simulación es mol. De esta forma x puede variar por incrementos de 1×10–5, desde 0 hasta 2×10–2. Para otra situación puede resultar necesario modificar el número 100000 por otro distinto para obtener, en la simulación correspondiente, un valor próximo a Ka.
Efecto de la dilución de un ácido débilAl agregarle agua a un ácido débil la disolución se vuelve menos ácida, es decir disminuye la concentración de iones H+, el pH aumenta. Pero, de acuerdo con el principio de Le Chatelier, para contrarrestar la “perturbación” (la dilución) el equilibrio se desplaza en el sentido de una mayor disociación. Esta aparente contradicción se resuelve comparando el pH con el porcentaje de ionización. Cuanto más diluida sea la disolución del ácido, tanto mayor será el porcentaje de ionización, aunque la concentración de iones H+ disminuye.
Al hacer variar el valor del volumen para una misma cantidad de moles iniciales de ácido, por ejemplo 1 mol, se encuentra rápidamente la nueva composición del sistema desplazando el cursor de la barra hasta alcanzar nuevamente el valor de la constante de equilibrio Ka a 25°C (figura 3).
Los valores encontrados para cuatro volúmenes diferentes se presentan en la tabla 1.
Resultados obtenidos para la dilución de un ácido débil.
| V (L) | nHA inicial | nHA eq | nA– eq | nH+ eq | [H+] eq | Ka | pH | % de ionización |
|---|---|---|---|---|---|---|---|---|
| 0,5 | 1 | 0,997 | 0,003 | 0,003 | 0,0060 | 1,79E-05 | 2,2 | 0,3 |
| 1 | 1 | 0,996 | 0,004 | 0,004 | 0,0042 | 1,80E-05 | 2,4 | 0,4 |
| 2 | 1 | 0,994 | 0,006 | 0,006 | 0,0030 | 1,80E-05 | 2,5 | 0,6 |
| 10 | 1 | 0,987 | 0,013 | 0,013 | 0,0013 | 1,80E-05 | 2,9 | 1,3 |
Los mismos valores de pH y % de ionización se obtendrían si se dejara fijo el volumen en 1 L y se cambiara el número de moles iniciales del ácido a 2, 1, 0,5 y 0,1 respectivamente.
En definitiva, con la simulación se verifican los resultados cualitativos predichos por el principio de Le Chatelier y, explícitamente, se hace la diferencia entre cantidad de materia y concentración, aspecto sobre el cual los estudiantes tienen dificultades (Johnstone, MacDonald y Webb, 1977; Furió y Calatayud, 2000).
Efecto del ion comúnLa simulación con la barra de desplazamiento permite estudiar la ionización de un ácido débil en una disolución que contiene ya disuelto uno de los iones (anión o catión) que se denomina ion común. Por ejemplo, cuando se disuelve ácido acético en una disolución de acetato de sodio.
El acetato de sodio es un electrolito fuerte y se disocia totalmente aportando iones acetatos a la solución. De acuerdo con el principio de Le Chatelier, el aumento en la concentración de producto desplaza el equilibrio hacia los reactivos, con lo que disminuye la concentración de iones H+ en el equilibrio.
En la figura 4 se presenta la simulación correspondiente, donde se ha modificado la cantidad inicial del anión A–, por ejemplo una cantidad inicial de 0,2 moles, para un volumen de 1 L y una cantidad inicial de ácido de 1 mol. Nuevamente se desplaza el cursor de la barra hasta que Ka = 1,8×10–5.
Como se aprecia en los resultados presentados en la tabla 2, se verifica que cuanto mayor concentración inicial del anión tanto menor es la acidez de la disolución. El efecto del ion común puede interpretarse como un caso especial de aplicación del principio de Le Chatelier.
Resultados obtenidos para distintas cantidades del ion común acetato.
| V (L) | nHA inicial | nA inicial | nHA eq | nA– eq | nH+ eq | Ka | pH | % de ionización |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 0,99577 | 0,0042 | 0,00423 | 1,80E-05 | 2,4 | 0,423 |
| 1 | 1 | 0,1 | 0,99982 | 0,1002 | 0,00018 | 1,80E-05 | 3,7 | 0,018 |
| 1 | 1 | 0,2 | 0,99991 | 0,2001 | 0,00009 | 1,80E-05 | 4,0 | 0,009 |
| 1 | 1 | 0,3 | 0,99994 | 0,3001 | 0,00006 | 1,80E-05 | 4,2 | 0,006 |
Las disoluciones amortiguadoras o buffer tienen la capacidad de resistir los cambios de pH cuando se agregan pequeñas cantidades de ácido o base fuerte. Se forman, por ejemplo, con una mezcla de una disolución de ácido débil (ácido acético, por ejemplo) con una disolución de su sal, de su base conjugada (acetato de sodio). La disolución amortiguadora debe contener una concentración relativamente alta de ácido para que reaccione con los iones OH– que se agreguen y también una cantidad semejante de su base conjugada para reaccionar con los iones H+ que se añaden:
Esta última ecuación puede expresarse en forma más simple como:
Se asume que los iones H+ cedidos por el ácido fuerte agregado (HCl por ejemplo) reaccionan totalmente con la base A– para formar HA, y también se asume que en esa mezcla el volumen de la disolución permanece constante. Por ejemplo, el agregado de 0,1 mol de HCl a una disolución buffer que contiene 1,0 mol de acetato y 1,0 mol de ácido acético, en un litro de disolución, genera una cantidad inicial de ácido de 1,1 mol y de 0,9 mol de acetato. Por ello, a la simulación anterior del efecto del ion común se le incorporan unas nuevas celdas (figura 5) donde aparecen la cantidad de iones H+ añadidos (celda F5) y las nuevas cantidades iniciales de HA (celda D6) y A– (celda E6).
Simulación para una disolución amortiguadora formada por 1 mol de HA y 1 mol de A–, y agregado de 0,1 mol de H+ proveniente del HCl, en un volumen de 1 L a 25° C.
Operaciones:
Celda C7: =B7/1000000
Celda D7: =D6–C7
Celda E7: =E6+C7
Celda H7: =E7*F7/(D7*G4)
Celda D6: =D4+F5
Celda E6: =E4–F5
Celda F7: =F4+C7
Se obtienen valores de Ka más cercanos a 1,8×10–5 si dividimos el número dado por la barra de desplazamiento por 1×106 (celda C7). El pH de la disolución buffer formada por 1,0 M de ácido acético y 1,0 M de acetato de sodio es 4,74. En la tabla 3 se aprecia que ese valor de pH se modifica poco con el agregado de pequeñas cantidades de ácido fuerte.
Resultados obtenidos en la disolución amortiguadora para distintas cantidades de H+ agregado.
| V | nHA | nA– inicial | nH+ agreg | nHA equil | nA– equil | nH+ equil | Ka | pH | % de ionización |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1,0 | 1,0 | 0 | 0,99998 | 1,00002 | 0,000018 | 1,8E-05 | 4,74 | 0,0018 |
| 1 | 0,5 | 0,5 | 0,10 | 0,59997 | 0,40003 | 0,000027 | 1,8E-05 | 4,57 | 0,0054 |
| 1 | 1,0 | 1,0 | 0,10 | 1,09998 | 0,90002 | 0,000022 | 1,8E-05 | 4,66 | 0,0022 |
| 1 | 1,5 | 1,5 | 0,10 | 1,59998 | 1,40002 | 0,000021 | 1,8E-05 | 4,68 | 0,0014 |
| 1 | 2,0 | 2,0 | 0,10 | 2,09998 | 1,90002 | 0,000020 | 1,8E-05 | 4,70 | 0,0010 |
La simulación anterior permite estudiar el efecto de la cercanía (semejanza) entre las concentraciones iniciales de HA y de A– en la efectividad de la disolución buffer o capacidad amortiguadora (figura 6).
En la tabla 4 se aprecia que cuando las cantidades iniciales de HA y A– son iguales se obtiene el valor más cercano al pH 4,74 de la disolución buffer, para el mismo agregado de ácido fuerte.
Resultados obtenidos en la capacidad amortiguadora producto de la semejanza entre las concentraciones de HA y A–.
| V (L) | nHA inicial | nA– inicial | nH+ agreg | nHA eq | nA– eq | nH+ eq | Ka | pH | % de ionización |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1,0 | 1,0 | 0 | 0,999982 | 1,000018 | 0,000018 | 1,8E-05 | 4,74 | 0,0018 |
| 1 | 1,0 | 0,5 | 0,1 | 1,099950 | 0,400050 | 0,000050 | 1,8E-05 | 4,30 | 0,0050 |
| 1 | 1,0 | 1,0 | 0,1 | 1,099978 | 0,900022 | 0,000022 | 1,8E-05 | 4,66 | 0,0022 |
| 1 | 1,0 | 1,5 | 0,1 | 1,099986 | 1,400014 | 0,000014 | 1,8E-05 | 4,85 | 0,0014 |
| 1 | 1,0 | 2,0 | 0,1 | 1,099990 | 1,900011 | 0,000011 | 1,8E-05 | 4,98 | 0,0011 |
La efectividad de la disolución amortiguadora, o capacidad amortiguadora, será tanto mayor cuanto mayor sean las concentraciones iniciales de ácido y de su base conjugada. Este hecho se puede también verificar fácilmente con la simulación (figura 7).
En la tabla 5 se aprecia que cuanto mayores son las cantidades iniciales del ácido débil y de su base conjugada, tanto mayor es la capacidad amortiguadora, dado que se obtienen valores de pH más cercanos a 4,74.
Resultados obtenidos en la capacidad amortiguadora producto de distintas concentraciones iniciales de HA y A–.
| V (L) | nHA inicial | nA– inicial | nH+ agreg | nHA eq | nA– eq | nH+ eq | Ka | pH | % de ionización |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0,99998 | 1,00002 | 0,000018 | 1,8E–05 | 4,74 | 0,0018 |
| 1 | 1 | 1 | 0,10 | 1,09998 | 0,90002 | 0,000022 | 1,8E–05 | 4,66 | 0,0022 |
| 1 | 1 | 1 | 0,15 | 1,14998 | 0,85002 | 0,000024 | 1,8E–05 | 4,62 | 0,0024 |
| 1 | 1 | 1 | 0,20 | 1,19997 | 0,80003 | 0,000027 | 1,8E–05 | 4,57 | 0,0027 |
Cuando un ácido es muy débil o está muy diluido, tal que la concentración de iones H+ sea menor que 10–6 mol/L, la autoprotólisis del agua contribuye al pH en forma significativa. Para saber la composición de este sistema, donde existen cuatro especies en la disolución acuosa: HA, A–, H+ y OH–, es decir cuatro incógnitas, se requiere de cuatro ecuaciones. Estás cuatro ecuaciones se combinan y dan por resultado una expresión de Ka más compleja (Atkins y Jones, 2006):
Para hallar el valor de [H+], y con ello el pH, se debe resolver una ecuación cúbica:
La resolución algebraica de esta ecuación puede evitarse empleando la simulación propuesta donde se reemplaza la ecuación de Ka anterior por esta nueva más compleja, que incorpora el valor de Kw = 1,0×10–14. La figura 8 presenta la simulación que resuelve el ejercicio planteado en Atkins y Jones (pág. 401), que solicita calcular el pH de una solución acuosa de fenol (ácido muy débil: Ka = 1,3×10 –10) de concentración inicial 1,0×10 – 4 M.
Para entrar en la escala de Ka, el número obtenido desde la barra de desplazamiento se divide por 1×10 8.
Dado que la disolución es eléctricamente neutra, el balance de carga se expresa como: [H+] = [OH–] + [A–], con lo que la concentración en el equilibrio del anión A– es:
A su vez, del balance de masa: [HA]inicial = [HA] + [A–], se puede obtener la expresión de la concentración de ácido HA en el equilibrio: [HA] = [HA]inicial – [A–].
Para otro ácido muy débil, u otra concentración inicial de ácido, basta simplemente con cambiar en la simulación el valor deKa y de [HA] inicial, y con la barra de desplazamiento obtenemos la nueva composición del sistema y su pH.
ConclusionesSe ha desarrollado una forma diferente de abordar y resolver problemas químicos relacionados con la composición de un sistema ácido-base en equilibrio químico, que hace hincapié en aspectos conceptuales (de estequiometría, de disoluciones, de equilibrio químico) por sobre la resolución de ecuaciones algebraicas. Los estudiantes, haciendo uso de las relaciones estequiométricas que se establecen entre todas las sustancias (reactivos y productos), desarrollan un método que les permite hallar la composición del sistema a medida que avanza la reacción, partiendo de las condiciones iniciales. En este proceso es importante que los profesores fomenten la discusión sobre la composición del sistema en el equilibrio y cuando éste es perturbado.
Las hojas de cálculo disponen de diversas herramientas que pueden ayudar en la didáctica de los equilibrios químicos con el diseño de planillas interactivas de complejidad gradual que permiten adaptarse a diversos niveles de preparación de los estudiantes. En este trabajo se comienza con el diseño de una planilla muy simple cuya función es que el usuario visualice el efecto de la variable grado de avance de la disociación hasta alcanzar el equilibrio y luego la planilla se modifica para explicar otros fenómenos conexos como el efecto amortiguador y la disociación en disoluciones menos habituales en los libros de texto como son las de ácidos muy débiles y/o muy diluidos.
La superación de las concepciones alternativas y dificultades en la temática del equilibrio químico, como las mencionadas en la introducción de este trabajo, puede verse incrementada si el profesor llama la atención a sus alumnos sobre la contribución explícita de estas simulaciones a ese objetivo.
A modo de síntesis, esta simulación presenta las siguientes ventajas:
- •
Es un procedimiento sencillo que se aplica a todo tipo de equilibrio químico, y abarca el tema del equilibrio ácido-base exhaustivamente incorporando el efecto ion común, disoluciones amortiguadoras y disoluciones muy diluidas.
- •
Permite abordar conceptos complejos y centrales de la temática.
- •
Evita la complejidad matemática, la resolución de ecuaciones cuadráticas, al cubo o a la cuarta y pone la atención en los aspectos químicos.
- •
Evita emplear la regla del 5% para despreciar o no el x restando en el denominador de la expresión de Ka.
- •
Aplica los principios de la relación estequiométrica, aportando a la diferenciación entre la interacción química y la composición presente en el sistema.
- •
Permite distinguir explícitamente cantidad de materia y concentración.
- •
Diferencia explícitamente la situación inicial de la situación en equilibrio.
- •
Verifica cuantitativamente el principio de Le Chatelier, con lo que se supera el inconveniente de su uso exclusivo como regla memorística.
- •
Da respuestas a preguntas del tipo ¿qué pasa si…?; por ejemplo: ¿qué ocurre si aumenta el volumen del sistema? Es decir, permite pronosticar el comportamiento del sistema cuando cambian sus variables de influencia.
Las hojas de cálculo presentadas en este artículo pueden ser solicitadas al autor.