Enseñanza de la estequiometría: uso de analogías y comprensión conceptual

Resumen

Este trabajo relaciona la enseñanza de la estequiometría con analogías y la resolución conceptual de problemas de química. Se elabora una secuencia didáctica sobre el tema, de dificultad progresiva. Esta secuencia, basada en analogías, se aplica con alumnos de primer año de universidad. La experiencia se evalúa con un cuestionario escrito, en el que figuran, entre otros, los 2 ítems de estequiometría conceptual de Nurrenbern y Pickering (1987). Los resultados muestran una comprensión parcial de la temática dado que no se logran superar algunas dificultades expresadas por la bibliografía. Se discute en qué medida y en qué condiciones son útiles las analogías para aprender este tema.

Abstract

This work makes a connection between the teaching of stoichiometry, analogies and the conceptual resolution of chemistry problems. A didactic sequence on the topic is drawn up, progressive in difficulty. This sequence, based on analogies, is applied by first year university students. The experience is evaluated by means of a written questionnaire, where, amongst others, Nurrenbern and Pickering's (1987) 2 conceptual stoichiometry items figure (Nurrenbern y Pickering, 1987). The results show only partial understanding of the subject since some difficulties expressed in the bibliography were not overcome. To what extent and under which conditions analogies are helpful in the learning of this subject are discussed.

Introducción

Uno de los núcleos conceptuales de la química, la estequiometría, se ocupa de los aspectos cuantitativos de la reacción química, entendida como un proceso en el cual una sustancia o varias sustancias se forman a partir de otra u otras. La química se interesa por la composición y la cantidad de las sustancias que reaccionan o se producen en un proceso químico. Estos conceptos pueden enseñarse en distintos niveles educativos con diferentes grados de complejidad.

La estequiometría aborda las relaciones cuantitativas de la química sobre una base cualitativa, conceptual. Resolver situaciones sobre estequiometría implicaría la comprensión de los conceptos de fórmula química, reacción química, ecuación química, reactivos y productos, subíndices y coeficientes estequiométricos. Por su complejidad los estudiantes presentan dificultades que van más allá de cuestiones matemáticas (como el dominio de la proporcionalidad) y mantienen concepciones alternativas luego de la enseñanza.

En este caso, como en la enseñanza de muchos otros conceptos de la química, se aprecia cierta monotonía metodológica centrada en la resolución de ejercicios con, generalmente, poco trabajo experimental y escaso uso de variados recursos didácticos. Una alternativa de uso frecuente es emplear estrategias de enseñanza que incluyan analogías.

Para Johnstone (1982) la química presenta un cuerpo de conceptos abstractos y complejos y su aprendizaje profundo requiere poder describir y explicar el fenómeno abordado en 3 niveles de representación: (1) sensorial (macroscópico), (2) simbólico (ecuaciones, fórmulas) y (3) de partículas (submicroscópico: átomos, moléculas, iones). Al respecto Gabel (1993) destaca que muchas de las dificultades de los estudiantes se deben a: (i) el énfasis puesto sobre el nivel simbólico y la resolución de problemas algorítmicos a expensas de los niveles macro y de partículas, (ii) las insuficientes conexiones entre los 3 niveles, si es que son presentados en la enseñanza, y (iii) la falta de relación de los fenómenos con la vida cotidiana del alumno.

Dado que las analogías tienden un puente entre situaciones de la vida cotidiana del estudiante y el conocimiento escolar que se desea construir, en este trabajo nos planteamos estudiar su efecto en el aprendizaje de la estequiometría. Nos preguntamos: en qué condiciones, cuándo y cómo la enseñanza con analogías favorece el aprendizaje conceptual de la estequiometría.

Dificultades en el aprendizaje de la estequiometría

Los estudiantes presentan muchas dificultades en el aprendizaje de la estequiometría, entre ellas:

• -

  confunden distintas cantidades químicas (moles, concentraciones, masas, volúmenes) que se ponen en juego en la resolución de problemas (Frazer y Servant, 1987)

• -

  no comprenden las fórmulas químicas en términos de partículas y el significado de los subíndices o de los coeficientes estequiométricos, aun cuando ajusta correctamente las ecuaciones químicas (Yarroch, 1985)

• -

  no conservan la masa y los átomos en una reacción química, o presentan problemas con la conservación de los átomos y la no conservación de las moléculas en el cambio químico (Mitchell y Gustone, 1984)

• -

  sostienen que el reactivo limitante es la sustancia que tiene el menor coeficiente estequiométrico en la ecuación química balanceada (Huddle y Pillay, 1996)

• -

  comprenden en forma incompleta la ecuación química y su relación con la situación empírica. Algunos estudiantes partiendo de la composición inicial del sistema no logran determinar el estado final empleando la ecuación química (Arasasingham, Taagepera, Potter y Lonjers, 2004)

• -

  afirman que para que se produzca el cambio químico es necesario que los reactivos estén en la situación inicial en una proporción particular (por ejemplo la proporción dada por los coeficientes estequiométricos), dado que se confunde el lado izquierdo de la ecuación química con el estado inicial del sistema (Gauchon y Méheut, 2007; Raviolo, 2006).

Resolución de problemas de química y comprensión conceptual

Una línea de investigación de la Didáctica de la Química aborda la problemática de la resolución de ejercicios/problemas y si su resolución implica la comprensión de los conceptos implicados y, en particular, la comprensión a una escala submicro o de partículas (átomos, moléculas, iones). Muchos estudios han comprobado que alumnos que resuelven bien problemas empleando algoritmos o ecuaciones, no siempre visualizan ni comprenden los conceptos químicos que están detrás. Uno de los trabajos más conocidos de esta línea es el de Nurrenbern y Pickering (1987). Estos autores administraron a estudiantes universitarios de un curso de Química general, para los temas gases y estequiometría, 2 tipos de problemas: (a) problemas tradicionales, del tipo matemático-algorítmico y (b) problemas conceptuales, con la utilización de representaciones de partículas. Los resultados de este estudio mostraron que los estudiantes tenían notablemente más éxito en el primer tipo de problemas que en el segundo; es decir, resolvían problemas algorítmicos sin una verdadera comprensión conceptual del mismo, en este caso sin un conocimiento profundo de la naturaleza de un gas o de la naturaleza del cambio químico. Pickering (1990) encontró que el 95% de los estudiantes indagados resolvieron correctamente problemas numéricos tradicionales pero solo el 38% pudo resolver con éxito los problemas conceptuales. Sawrey (1990) replicó esta indagación con muestras numerosas de alumnos y verificó que las dificultades permanecían aun en los mejores alumnos.

Las cuestiones conceptuales requieren habilidades de alto orden (higher-order) dado que el estudiante tiene que sintetizar respuestas o evaluar un problema para seleccionar las herramientas matemáticas necesarias para arribar a una solución. Son cuestiones mayoritariamente cualitativas y pueden tener más de una respuesta aceptable. Estos autores distinguen 6 tipos de cuestiones conceptuales:

• (1)

  Preguntas de elección múltiple, que solicitan primero la selección de una respuesta sobre lo que ocurre y luego la selección de una razón o explicación de la respuesta anterior.

• (2)

  Cuestiones con partículas que representan una situación química, donde se utilizan círculos o esferas de diferentes colores y tamaños para representar átomos o moléculas.

• (3)

  Resolución de cuestiones de laboratorio, donde los estudiantes usan tablas, gráficos y otros datos para predecir o explicar lo que ocurre en una situación experimental.

• (4)

  Cuestiones sobre demostraciones, que solicitan a los alumnos respuestas a preguntas formuladas a partir de la observación de una demostración, vídeo o simulación.

• (5)

  Cuestiones analógicas, basadas en el razonamiento A es a B (relación dada) como C es a D (relación a elegir por el estudiante).

• (6)

  Selección de un ítem que mejor completa una serie, por ejemplo una serie de especies ordenadas por su fuerza ácido base.

Por ejemplo, las cuestiones conceptuales propuestas para estequiometría por Nurrenbern y Pickering (1987) corresponden al segundo tipo de la enumeración anterior. En ellas los estudiantes deben establecer relaciones entre situaciones iniciales y o finales de un cambio químico, expresadas con partículas, y la ecuación química.

La comprensión conceptual implica habilidades y conocimientos como: poder justificar una elección, predecir lo que va a ocurrir, explicar cómo y por qué algo ocurre, extraer datos útiles de un exceso de información, etc. Esto conlleva un cambio desde la pregunta «¿qué es lo que los alumnos recuerdan?» a «¿qué es lo que los estudiantes comprenden?» (Halakova y Proksa, 2007). Estos autores llevaron adelante un diseño de investigación para comprobar si el formato en que se presentan las cuestiones conceptuales influía en los resultados de elección de respuestas correctas. Para ello adaptaron el test original de Robinson y Nurrenbern convirtiéndolo en un test de 14 ítems de elección múltiple, cada uno de ellos con un formato pictórico (dibujos esquemáticos, «diagrams») y con un formato verbal. Verificaron que no se presentaron diferencias, que la elección de las respuestas correctas no dependió del formato de la pregunta. Obtuvieron resultados bajos en promedio y cercanos al 37%, que atribuyeron al contenido y a la falta de comprensión conceptual. Declaran que entre los factores que pueden dificultar la elección de la respuesta correcta en el formato verbal está la extensión del mismo y la elección de palabras que resulten complicadas; por otro lado, el formato pictórico no siempre es claro o puede no llamar la atención de los estudiantes que consideran los dibujos como solo algo decorativo adicionado al texto. Presumen que la combinación de ambos formatos podría mejorar la comprensión conceptual.

Enseñanza con analogías

El empleo de analogías como estrategia didáctica permite involucrar a los estudiantes desde su conocimiento previo. Una analogía es una comparación de estructuras y/o funciones entre 2 dominios (Duit, 1991): un dominio conocido (análogo) y un dominio nuevo o parcialmente nuevo de conocimiento (objetivo). Entre ellos se establece un conjunto de relaciones y, además, existen atributos no compartidos que constituyen las limitaciones de la analogía (Oliva, Aragón, Mateo y Bonat, 2001).

El término razonamiento analógico se refiere a un proceso del pensamiento que se realiza sobre la base de analogías, permitiendo la comprensión, representación y explicación de algún fenómeno. Este tipo de razonamiento está íntimamente relacionado con el aprendizaje, la formación de conceptos y la resolución de situaciones problemáticas. De ahí su importancia y su uso tan amplio entre los científicos y educadores.

El razonamiento analógico es no lineal (VerLee, 1986) como lo muestran algunos ejemplos del pensamiento científico en los que las soluciones a muchos problemas de la ciencia no responden a ninguna lógica sino a percepciones, como es el caso de la estructura del benceno de Kekulé.

En contextos de aprendizaje, Holyoak y Nisbett (1988) consideran que el razonamiento analógico se produce en situaciones que van desde la intervención directa del docente (nivel menos autónomo) hasta la total autonomía del sujeto que aprende, es decir, desde el aprendizaje guiado hasta el aprendizaje autónomo. En dicho sentido, este tipo de razonamiento promueve la autonomía en el aprendizaje al estar ligado a las inferencias propias de cada sujeto.

Al explicar alguna idea que no es familiar, tanto en la vida cotidiana como en un entorno escolar, se emplean espontáneamente analogías. Es común escuchar expresiones como «pensemos en algo similar...», «es lo mismo que hicimos cuando...», entre otras. Este uso espontáneo en el aula, si bien llama la atención de los estudiantes, puede ser la causa o refuerzo de confusiones o de concepciones alternativas. Esto último se debe, en gran parte, a su presentación asistemática, sin un encuadre metodológico adecuado, tanto de profesores como de autores de libros.

Como producto de la experiencia y de la investigación se han sugerido secuencias para enseñar con analogías. Por ejemplo, la secuencia TWA (Glynn, 1991), que consta de 6 pasos: (1) introducir el concepto objetivo; (2) recordar el concepto análogo (activarlo); (3) identificar características relevantes del objetivo y del análogo; (4) establecer las correspondencias de similitudes (transferir y aplicar); (5) indicar las limitaciones de la analogía, y (6) sacar conclusiones. El orden de estos pasos puede variar pero lo importante es que se den todos los pasos. Harrison y Coll (2008) presentan otra secuencia metodológica basada en la guía FAR (Foco, Acción y Reflexión) y muestran, entre muchos ejemplos de aplicación de la secuencia, uno sobre estequiometría. Por su parte, Raviolo y Garritz (2007) proponen un decálogo a tener en cuenta cuando se emplean analogías para enseñar.

La efectividad de una analogía estará dada por el conocimiento de los atributos del análogo, el aprovechamiento que pueda hacerse de los atributos compartidos para comprender el objetivo, la profundidad de las conclusiones que se obtengan y las reflexiones metacognitivas realizadas.

El empleo de analogías es un recurso didáctico muy frecuente en la enseñanza de la química, y en particular en la enseñanza de la estequiometría y del concepto de reactivo limitante. Recientemente es destacado como una forma efectiva de establecer conexiones entre el pensamiento macroscópico y el molecular (Avargil, Bruce, Amar y Bruce, 2015).

Enseñanza de la estequiometría con analogías

Entre las primeras propuestas de analogías para la enseñanza de la estequiometría se halla la de Last (1983) que utiliza a la pareja de baile, formada por un chico y una chica como análogo de la reacción NH₃(g) + HCl(g) → NH₄Cl(s). Con esta analogía aborda los conceptos de reactivo limitante, en exceso y de rendimiento porcentual. Incluso amplía la analogía para el caso de una danza en la que cada equipo está formado por un chico y 2 chicas, para ilustrar la reacción C(s) + 2S(g) → CS₂(g). La analogía de las parejas de baile es una de las más antiguas, y fue muy utilizada en equilibrio químico (Caldwell, 1932; Hildebrand, 1946; DeLorenzo, 1977; Baisley, 1978).

Bleam (1981) sugiere la analogía de la fruta-frutera para introducir el tema de estequiometría en el nivel medio. La frutera, compuesta por 2 manzanas y 3 bananas, para abordar las relaciones estequiométricas, reactivo limitante y rendimiento teórico. Felty (1985) emplea una receta simple de ensalada de frutas, formada por igual número de uvas y de cerezas. Supone que las cerezas pesan el doble que las uvas, y con ello aborda los temas de masas relativas y masas molares.

Varios autores emplean la composición dada por una receta como analogía. Umland (1984) utiliza la analogía de la receta de cupcakes (en la que se utilizan 2 tazas y un cuarto de harina y 2 huevos, más otros ingredientes, para formar 30 cupcakes) como una forma de introducir el concepto de reactivo limitante y rendimiento teórico. Haim (2005) profundiza la analogía de la receta de cocina a otros conceptos y habilidades químicas, justificando las actividades propuestas desde la teoría de Ausubel como una forma de construir anclajes donde se subsuma el nuevo conocimiento.

McMinn (1984) recomienda la analogía de la compra de un vaso de café con monedas de 25, 10 y 5 centavos. Plantea 2 situaciones: (a) ¿cuántos vasos de café se pueden comprar con 100 g de cada una de las monedas? (se da el peso promedio de cada moneda y el costo de un vaso de café) y (b) ¿cuántos vasos se pueden comprar en una máquina que acepta por vaso una de 25, 2 de 10 y una de 5 centavos?

Silversmith (1985) se propone hacer frente a la concepción alternativa, que sostienen algunos estudiantes, de que el reactivo presente en menor número de moles es el reactivo limitante (Huddle y Pillay, 1996), a través de la presentación de la analogía del ensamble de una bicicleta, formada por un cuadro y 2 ruedas, incluye la ecuación con palabras (cuadro + 2 ruedas → bicicleta) y el siguiente tipo de ecuación con símbolos (A + 2B → P). Fortman (1994) presenta la analogía del ensamble de un carrito formado por un cuerpo y 4 ruedas y plantea situaciones con componentes en exceso.

Last (1998) sugiere para abordar el concepto de concentración de iones en una disolución la analogía de la bicicleta formada por un cuadro y 2 ruedas como un análogo del soluto MgCl₂.

Witzel (2002) emplea un juego de construcción a partir de piezas, como es el Lego, para determinar las relaciones entre el número y masa de los componentes requeridos (reactivos) y la masa del producto final. En lugar de la ecuación química se usa el folleto de indicaciones de cada producto (autos en este caso). El autor afirma que la analogía es buena para introducir o revisar el tema de la estequiometría y reforzar los conceptos de reactivo limitante, en exceso y conservación de la masa. La mayoría de estas analogías hacen frente a la dificultad de algunos estudiantes que no conservan la masa y los átomos en una reacción química (Mitchell y Gustone, 1984), dado que permiten visualizar la conservación de los átomos y la no conservación de las moléculas en el cambio químico.

Haim, Cortón, Kocmur y Galagovsky (2003) proponen la analogía del sándwich de hamburguesa triple (P₃H₂Q), siendo P (rodaja de pan), H (hamburguesa de carne) y Q (rebanada de queso), formado a partir de otros sándwiches P₂H₂ y P₂Q₂, a través de 4 actividades: (1) comprender las fórmulas y usar ecuaciones, (2) comprender la conservación de la masa, (3) comprender el concepto de reactivo limitante y (4) comprender el concepto de rendimiento.

La bondad del uso didáctico de estas analogías debería asentarse en hacer frente, de una forma planificada, a las concepciones alternativas mencionadas en el apartado anterior.

Metodología

La pregunta que se formula esta investigación es: Si la resolución algorítmica/matemática de problemas químicos no garantiza la comprensión conceptual de la temática, ¿lo hará un abordaje con analogías? Se plantea si con un trabajo complementario (a la enseñanza tradicional de la temática) con analogías se mejoran los resultados en las cuestiones conceptuales ya empleadas en investigaciones previas.

Los objetivos que se persiguen son:

• -

  Llevar adelante una experiencia de enseñanza de la estequiometría con analogías.

• -

  Evaluar dicha experiencia a través de un cuestionario.

• -

  Confrontar los resultados de la experiencia con los obtenidos en la línea de investigación de la comprensión conceptual de problemas de química.

El diseño de este estudio, llevado a cabo al mes de comenzar el curso, consistió en una instancia de 3 h donde los estudiantes trabajaron sobre una secuencia de enseñanza de la estequiometría con analogías. A la semana siguiente se les suministró un cuestionario sobre la tarea realizada.

La muestra de estudiantes estuvo conformada por 42 alumnos de primer año, de las carreras de Licenciatura en Biología, Profesorado en Física y en Química, que cuentan con el mismo profesor. Estos alumnos tuvieron química en todos los años de nivel medio con una carga horaria reducida y con poca asistencia al laboratorio. En la mayoría de los casos aprobaron un curso de nivelación no restrictivo de ingreso a la universidad que hizo hincapié en la resolución de ejercicios, incluyendo el tema estequiometría, basado en un conocimiento operativo.

La propuesta de enseñanza, que se desarrolla en el próximo apartado, fue dada a 3 especialistas para que la evaluaran, con el fin de garantizar su validez de contenido y validez didáctica. Una versión ampliada de la propuesta de enseñanza se encuentra en Raviolo, Lerzo y Piovano (2014).

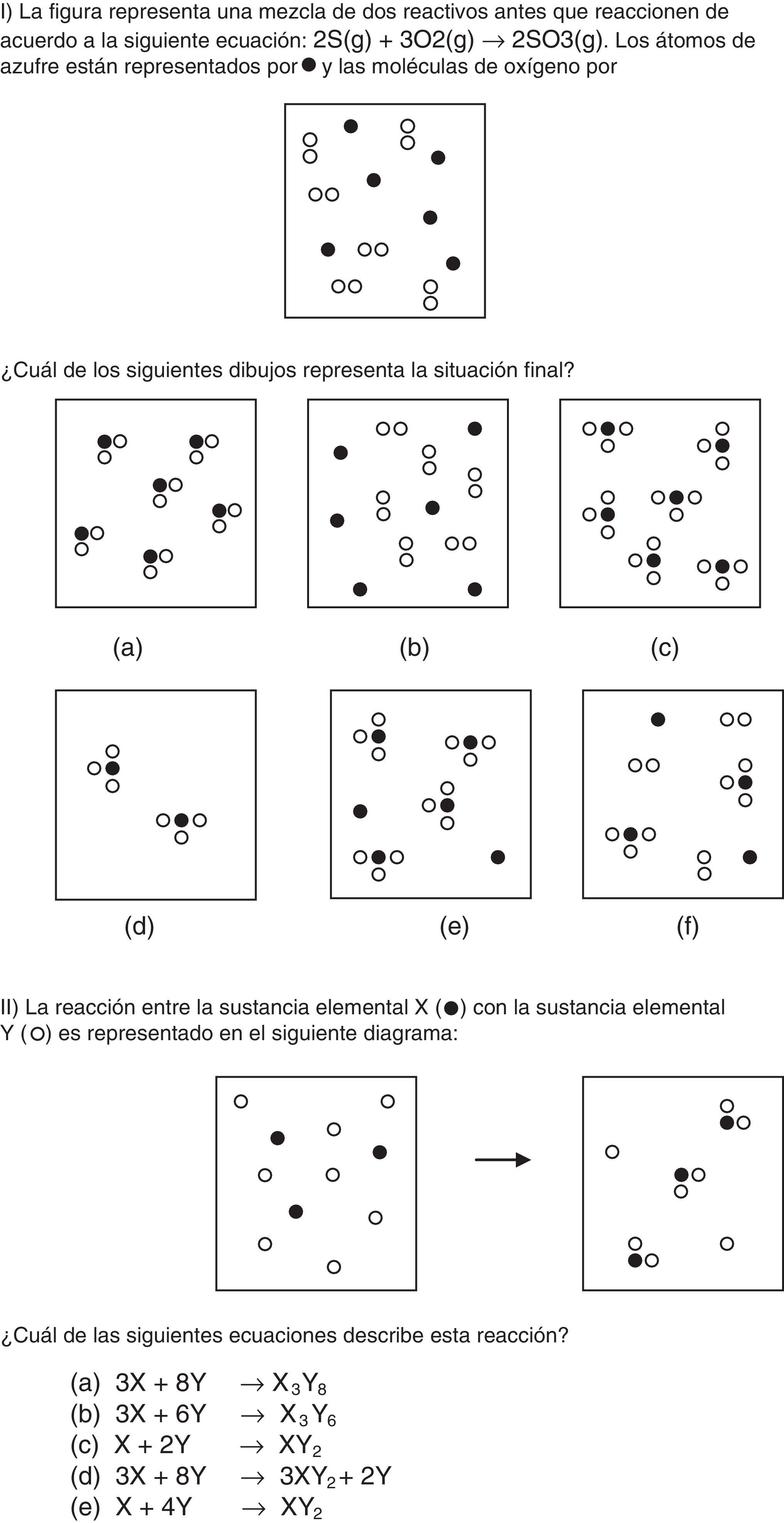
El cuestionario final consistió en: (1) un problema tradicional en moles; (2) el problema i de Nurrenbern y Pickering (1987) donde deben reconocer la situación final de un cambio químico, expresada a nivel submicroscópico, a partir de la situación inicial y de la ecuación química (ítem i del anexo); (3) el problema ii de Nurrenbern y Pickering (1987) donde deben identificar la ecuación química correspondiente a una reacción representada por las situaciones inicial y final a nivel submicroscópico (ítem ii del anexo); y (4) una pregunta de opinión sobre la propuesta vivenciada.

La propuesta de enseñanza

El material de estudio consistió en una secuencia con orden progresivo de complejidad, en la que en todo momento se sigue un paralelismo entre una situación análoga (preparación de sándwich de jamón) y otra química. El orden de reacciones seguido se aprecia en la tabla 1. Siendo P: rodaja de pan, J: rodaja de jamón, JP₂: sándwich simple de jamón, P₂: paquete de 2 rodajas de pan, P₄: paquete de 4 rodajas de pan, J₂: paquete de 2 rodajas de jamón, P₂J₂: sándwich doble de jamón y P₂J₄: sándwich cuádruple de jamón.

Tabla 1.

Secuencia de reacciones y paralelismo entre análogo y objetivo

Orden	Análogo	Objetivo
1	2P + J → JP2	2S + C → CS2
2	P2 + J → JP2	O2 + C → CO2
3	2P2 + J2 → 2P2J	2H2 + O2 → 2H2O
4	P4 + 4J2 → 2P2J4	P4 + 4I2 → 2P2I4
5	2P2J + J2 → 2P2 J2	2H2O + O2 → 2H2O2

La elección de la primera reacción objetivo de esta analogía se basó en la propuesta de Last (1983) sobre la síntesis del disulfuro de carbono a alta temperatura, C(s) + 2S(g) → CS₂(g), que considera al azufre como atómico.

El tratamiento didáctico de las analogías siguió la secuencia TWA de Glynn (1991), en la que se identifican las correspondencias y limitaciones de las analogías. En el establecimiento de correspondencias se discutió un cuadro comparativo como el mostrado en la tabla 2.

Tabla 2.

Correspondencias entre análogo y objetivo

Análogo	Objetivo
2P + J → JP2	2S + C → CS2
Relación: 2 P a 1 J	Relación: 2 átomos de S a 1 átomo de C
P = rodaja de pan	S = 1 átomo de azufre
2P = 2 rodajas de pan	2S = 2 átomos de azufre
J = rebanada de jamón	C = 1 átomo de carbono
2J = 2 rebanadas de jamón	2C = 2 átomos de carbono
P2J = es un sándwich	CS2 = 1 molécula de disulfuro de carbono
2P2J = 2 sándwiches	2CS2 = 2 moléculas de disulfuro de carbono

La discusión de las fórmulas químicas fue esencial. Cada especie tiene su composición definida, que constituye una identidad propia, que es distinta a la mezcla de sus partes. Por ejemplo en el análogo de la pareja de baile, una pareja es algo distinto a una chica y un chico juntos. Por ello, es importante que la expresión del producto permita apreciar la composición y nombrar adecuadamente el compuesto, por ejemplo JP₂, que es un «sándwich de jamón» y no «pan y jamón».

Porque comprender correctamente las relaciones estequiométricas, o relaciones cuantitativas en una reacción química, implica entender aspectos del lenguaje químico, las actividades hicieron hincapié en diferenciar explícitamente coeficiente estequiométrico y subíndice. Por ejemplo: 2P es distinto P₂, 2 rodajas de pan es distinto a una bolsa (o paquete) de 2 rodajas de pan.

A continuación el material presentaba una secuencia gradual de preguntas, que mantenían un paralelismo entre análogo y objetivo:

• -

  ¿Cuántas rodajas de pan se necesitan para 8 rebanadas de jamón?

• -

  ¿Cuántos sándwiches se pueden hacer con 10 rodajas de pan y 5 rodajas de jamón?

• -

  ¿Cuántos sándwiches puedo hacer con 18 rodajas de pan y 12 rodajas de jamón?

• -

  ¿Cuántos átomos de S se necesitan para combinarse con 10 átomos de carbono?

• -

  ¿Cuántas moléculas de disulfuro de carbono se pueden formar con 20 átomos de azufre y 10 átomos de carbono?

• -

  ¿Cuántas moléculas de disulfuro de carbono se pueden formar con 24 átomos de azufre y 17 átomos de carbono?

• -

  ¿Con 8 paquetes de pan (de 2 panes cada uno) cuántos sándwiches se puede hacer?

• -

  ¿Cuántas moléculas de dióxido de carbono se forman a partir de 25 moléculas de oxígeno y suficiente carbono?

Se fomentó que las distintas situaciones, con diferentes cantidades iniciales de reactivos, se analizaran desde la ecuación química única, en la que no figuran las cantidades experimentales ni la sustancia que está en exceso como producto.

Posteriormente al establecimiento de las relaciones entre el análogo y el objetivo a nivel partículas (átomos y moléculas) se pasó a situaciones en las que se establecían relaciones entre el análogo y el objetivo a nivel macro (moles y gramos).

• -

  Si una rodaja de pan pesa 40 g y un rebanada de jamón pesa 25 g, ¿cuántos sándwiches se pueden hacer con 1,200 g de pan y 500 g de jamón?, ¿qué faltó?, ¿qué sobró?

• -

  ¿Cuántos gramos de disulfuro de carbono se formarán si se hacen reaccionar 450 gramos de azufre con 60 gramos de carbono? ¿Cuál es el reactivo limitante y cuál es el reactivo en exceso? ¿Qué cantidad de reactivo hay en exceso?

  Siendo coherentes con la secuencia de presentación de analogías, se discutieron con los estudiantes las siguientes limitaciones de la misma:

  • -

    El pan y el jamón no reaccionan. No hay fuerzas o «uniones químicas» que mantengan unidas a las rodajas de pan entre sí, ni al pan con el jamón.

  • -

    En el análogo, con 2 rodajas de pan y una rebanada de jamón preparo un sándwich de jamón y con una bolsa de 2 rodajas de pan y una rebanada de jamón también lo preparo, el ingrediente pan es la misma especie (solo cambia el envase) y se obtiene el mismo producto. En cambio en el objetivo, el cambio de la atomicidad significaría un cambio de especie, un cambio de sustancia. Por ejemplo, la sustancia oxígeno (O₂) no es la misma sustancia que el ozono (O₃).

  • -

    La principal limitación que tiene esta analogía es que la ecuación química puede leerse en términos microscópicos (submicro) o macroscópico (macro); es decir en términos de átomos y moléculas (supongamos sustancias moleculares) y en términos de sustancias y moles (o su equivalente en gramos). Para pasar de un nivel a otro, del nivel submicro al macro, se considera un número muy grande de partículas, el número de Avogadro (6,022 × 10²³ partículas/mol). En cambio, con el análogo no se cumple esta doble lectura de la ecuación química. La imagen de un sándwich es el análogo a la molécula, sin embargo pesa (en esta analogía) como la masa molar.

Las primeras reacciones de la secuencia de elaboración de sándwiches son reacciones que corresponden a reacciones de síntesis de un compuesto a partir de las sustancias elementales. El material de enseñanza finaliza presentando situaciones en las que se parte de uno o 2 compuestos para formar otro compuesto. Por ejemplo, la elaboración de un sándwich doble: 2JP₂ + J₂ → 2J₂P₂.

• -

  Vamos a hacer sándwiches dobles (J₂P₂) desarmando sándwiches simples (JP₂) y combinándolo con paquetes de 2 rodajas de jamón (J₂). ¿Cuál sería la «ecuación química» de este proceso? ¿Cuántos sándwiches dobles se pueden hacer a partir de 12 sándwiches simples y 5 paquetes de jamón?

• -

  El agua y el oxígeno reaccionan para producir peróxido de hidrógeno («agua oxigenada») ¿Cuál es la ecuación química ajustada? ¿Cuántos gramos de peróxido de hidrógeno se formarán al reaccionar 100 g de agua con 60 g de oxígeno?

Tres profesores de química, con experiencia en nivel medio y en universidad, evaluaron el contenido del material de enseñanza y su adecuación didáctica. Más allá de algunas dudas relacionadas con las limitaciones del análogo, los 3 coincidieron sobre la adecuación del contenido y la correcta graduación de la secuencia.

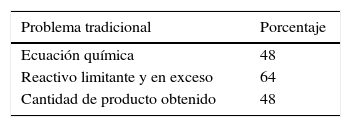
Resultados

En la tabla 3 se aprecian los porcentajes de respuestas correctas a la primera cuestión del cuestionario final. Esta consistió en un problema tradicional: ¿Cuántos moles de dióxido de nitrógeno (NO₂) se pueden formar con 6 moles de nitrógeno gaseoso (N₂) y 10 moles de ozono gaseoso (O₃)? ¿Cuál es el reactivo limitante?

Tabla 3.

Porcentajes de respuestas correctas para el problema tradicional

Problema tradicional	Porcentaje
Ecuación química	48
Reactivo limitante y en exceso	64
Cantidad de producto obtenido	48

Un 7% de los 42 estudiantes ajustó incorrectamente la ecuación química. Por ejemplo:

3 N₂ + 2O₃ → 3 NO₂

Y un 17% incluyó ecuaciones químicas con cantidades experimentales, por ejemplo:

6 N₂ + 10 O₃ → 12 NO₂

6 N₂ + 10 O₃ → 12 NO₂ + 2O₃

6 N₂ + 10 O₃ → 6 NO₂

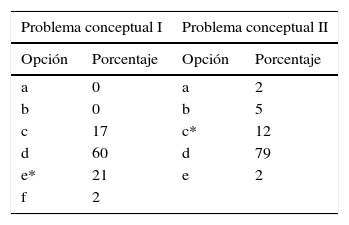
Los resultados en los problemas conceptuales i y ii se muestran en la tabla 4.

Tabla 4.

Resultados obtenidos en los 2 problemas de estequiometría conceptual. Respuestas correctas con asterisco

Problema conceptual I		Problema conceptual II
Opción	Porcentaje	Opción	Porcentaje
a	0	a	2
b	0	b	5
c	17	c*	12
d	60	d	79
e*	21	e	2
f	2

Por último, ante la pregunta final de evaluación de la experiencia: ¿Cuál es tu opinión sobre emplear la analogía del sándwich para comprender los conceptos de química tratados? El 71% opinó positivamente, el 19% también lo hizo pero señalando alguna limitación y un 10% no contestó.

«Creo que la analogía es muy útil porque permite ver de manera directa (al hacer sándwiches) las relaciones proporcionales entre átomos y moléculas»

«Es más entendible la química con esta analogía»

«Me parece interesante porque ayuda a comprender que las relaciones estequiométricas no siempre son como las ecuaciones matemáticas»

«…para entender un concepto más complejo»

Entre las opiniones de los estudiantes que plantearon algunas limitaciones se destacan:

«Si se tienen en cuenta las limitaciones con respeto a las combinaciones químicas creo que es un buen método»

«Es excelente en la primera instancia donde se desconocen los conceptos básicos de proporción estequiométrica y reactivos limitantes y en exceso. Pero se debe tener cuidado y conocer bien las limitaciones de la misma»

«Me parece muy sencillo comprender la analogía y los conceptos inherentes a la misma, pero de igual manera pienso que me resultaría más edificante profundizar en el tema utilizando verdaderas relaciones entre sustancias»

Discusión

Consideramos la analogía del sándwich como una de las más apropiadas por su familiaridad y su versatilidad, dado que permite aumentar gradualmente su complejidad y un buen abordaje de la ecuación química. También admite obtener distintos productos finales, que otras analogías no permiten.

En la preparación del sándwich simple, cuya ecuación «química» es 2P + J → P₂J, lo importante es discutir la diferencia entre reactivos y productos, entre coeficientes y subíndices, entre átomo y molécula, además de la proporción: 2 rodajas de pan es a una de jamón. Este análogo también permite el planteo de situaciones donde los panes vienen en bolsitas de a 2 (P₂ + J → P₂J), obteniéndose en todos los casos el mismo producto sándwich. Con ello se abordan situaciones donde la relación estequiométrica entre los reactivos no es la misma. Este análogo evita el inconveniente que presenta la analogía del sándwich de hamburguesa, ya que el pan de hamburguesa puede confundir dado que es una unidad formada por 2 tapas.

En el estudio llevado a cabo se observó que 2 tercios de la muestra resuelven bien el problema tradicional. Aunque la propuesta hacía hincapié en la solución de situaciones a partir de la ecuación química, varios estudiantes llegaron a determinar el reactivo limitante y en exceso, incluso a hallar la cantidad en exceso, sin partir de la ecuación química. Lo hicieron siguiendo otros razonamientos, por ejemplo analizando la fórmula del producto NO₂ (1 N por 2 O).

Los porcentajes de respuestas correctas obtenidos en los 2 problemas estandarizados de estequiometría conceptual son bajos, el 21% y el 12%. Nurrenbern y Pickering obtienen porcentajes algo mayores, el 29% y el 17% respectivamente. Estos mejores resultados pueden deberse a que ellos administraron el test como parte de un examen parcial. En nuestro caso los alumnos contestaron el test a la semana siguiente de realizar la actividad con la analogía, al mes de comenzar el curso. Sin embargo, Sawrey (1990) con una muestra numerosa de estudiantes obtuvo para el problema ii (el problema i no se indagó), un porcentaje de respuestas correctas similar a nuestro estudio (11.5%).

Los alumnos (60%) que seleccionan la respuesta d del problema i (que muestra 2 moléculas de SO₃) pueden estar confundiendo la ecuación química (2S + 3O₂ → 2SO₃) con la situación real; para ellos los coeficientes estequiométricos son las cantidades presentes en una situación experimental.

En forma similar, en el problema ii, cuya respuesta correcta era X + 2Y→ XY₂, los alumnos (79%) que seleccionan la respuesta d (3X + 8Y → 3XY₂ + 2Y), coincidente con el número de partículas mostrado en los dibujos, parecen tener esta misma dificultad y desconocen que el reactivo en exceso no se incluye en las ecuaciones químicas. Estas dificultades no se detectaron en esta magnitud en el problema tradicional dado que solo el 17% escribió ecuaciones químicas con las cantidades experimentales, confirmando que su resolución no implica la comprensión acabada de los conceptos involucrados.

Un estudio reciente (Tang, Kirk y Pienta, 2014), realizado con instrumentos de seguimiento visual (eye tracking), confirma la persistencia de las dificultades de los estudiantes en interpretar la ecuación química. Esta investigación indagó sobre la complejidad de los factores que influyen en la resolución de problemas de estequiometría y halló que los alumnos presentan inconvenientes en 3 factores: las unidades de las magnitudes, el formato de los números y la ecuación química; es decir, al enfrentar problemas de estequiometría dedicaban gran parte de su actividad cognitiva en interpretar la ecuación química.

En definitiva, a partir de problemas que incluyen situaciones representadas con partículas (moléculas) los estudiantes presentaron confusiones al relacionar estas con los niveles macro y simbólico. Sin embargo, y comparando con los resultados presentados en la bibliografía, el trabajo con analogías mejoró la comprensión del concepto de fórmula química (SO₃ y XY₂ respectivamente) dado que los estudiantes no eligieron la opción «a» (SO₂) en el problema i y muy pocos eligieron las opciones «a» y «b» (X₃Y₈ o X₃Y₆) del problema ii. En la opción «a» del problema i, los subíndices del producto coinciden con los de los reactivos (S + O₂ → SO₂). En el estudio realizado con alumnos de nivel medio de la misma ciudad (Casado y Raviolo, 2005) el 40% de los estudiantes eligió la opción a en el problema ii (3X + 8Y→ X₃Y₈), donde los coeficientes de la ecuación química de los reactivos se corresponden con las cantidades de partículas presentes en la situación inicial, sin prestar atención a la distribución de los átomos en el producto (XY₂).

Un logro de la secuencia de enseñanza llevada adelante es que no fomentó la confusión entre coeficientes y subíndices. Esta dificultad parece ser difícil de superar aun con propuestas basadas en la utilización de TIC (Cotes y Cotuá, 2014). En la revisión y análisis de analogías sobre estequiometría que aparecen en un búsqueda de páginas Web (Raviolo y Lerzo, 2014) se comprobó que muchas propuestas generalizan la idea errónea de que los coeficientes estequiométricos son los subíndices del producto; en otras palabras, que los coeficientes estequiométricos de los reactivos determinan la fórmula del producto, por ejemplo, para las analogías: (1) del ensamble tornillo, tuerca y rondana, (2) elaboración del sándwich de queso y jamón y (3) el ensamble de una bicicleta formada por 2 ruedas un cuadro y un manubrio. Estas propuestas incluían las siguientes ecuaciones:

1To + 3Tu + 6Ro → ToTu₃Ro₆

3P + 2Q + J → P₃Q₂J

2R + C + M → R₂CM

Finalmente, las confusiones de mayor gravedad que pueden fomentar las analogías sobre la estequiometría se presentan al incluir relaciones con gramos. En la analogía del sándwich, o de los ensambles tuercas tornillos, se usa el peso real de los objetos (la rodaja de pan, la rebanada de jamón, el tornillo, la tuerca, que hasta ese momento representaban a átomos) como masa molar. Se arman «moléculas» que pesan como «moles», fomentando confusiones entre los niveles de representación macro y submicro. Se usan objetos macro, que tienen una masa perceptible, para representar entidades del mundo submicro. Esto puede inducir a pensar la idea errónea de que una partícula (átomo, molécula, ion) pesa la masa molar («un átomo de carbono tiene una masa de 12 g», «una molécula de hidrógeno tiene una masa de 2 g»). Una forma de abordar este inconveniente se desarrolla en la propuesta de Raviolo et al. (2014), donde se sugiere realizar un planteo analógico a partir de la metáfora «el mol es la docena del químico», un camino análogo al número de Avogadro como puente entre lo macro y lo submicro. De este modo, se plantea la situación en que los insumos para preparar sándwiches se compran en un almacén mayorista «todo por docena», en donde se pueden adquirir por docenas rodajas individuales o de paquetes de 2, 3 o 4 unidades. Los planteos deben abordar las situaciones desde la ecuación química o desde la ecuación análoga, respectivamente, pero haciendo hincapié en la lectura de los coeficientes de la ecuación análoga como números de docenas.

En ocasiones se emplean términos propios de un dominio en otro y esto puede resultar muy contraproducente, como en el caso de que se habla de «moles de pan»: «¿cuántos moles de P₂QJ se obtienen a partir de 150 moles de pan?»

Conclusiones

Nakhleh (1993) llama la atención sobre el hecho de que el énfasis en la resolución de problemas algorítmicos contribuye a la pérdida de interés que muestran los estudiantes por los cursos de química, donde a menudo para aprobar las evaluaciones es suficiente con la manipulación mecánica de números y símbolos.

La experiencia con analogías es valiosa como una forma de diversificar la metodología de presentación del tema estequiometría, dado que produce un efecto motivador, además de relacionar con la vida cotidiana y es evaluada muy positivamente por los estudiantes.

La presentación rápida de una analogía es frecuentemente para abordar la relación estequiométrica entre 2 reactivos o la idea de reactivo limitante. Esta surge de modo espontáneo en los docentes. Por ejemplo formulaciones del tipo: «Esto es como si en una fiesta hay más hombres que mujeres, habrá hombres sin pareja de baile, las mujeres limitan el número de parejas que se pueden formar…». Posiblemente este tipo de presentación desvalorice el potencial de la analogía y desperdicie una oportunidad de aprendizaje. Por el contrario, llevar estas analogías demasiado lejos podría ser contraproducente por sus limitaciones y podrían fomentar confusiones; por ejemplo, al incluir cálculos con masas. Se debería buscar un equilibrio entre estos 2 extremos.

El hecho de que la representación simbólica del fenómeno, la ecuación química, pueda interpretarse desde los otros 2 niveles, el submicro y el macro (tal como lo hacen todos los textos universitarios consultados), le suma complejidad a la temática. Por ello se recomienda, o bien no incluir cálculos en moles y/o gramos, o bien seguir la propuesta de Raviolo et al. (2014) y discutir con mucha profundidad las limitaciones que tiene el análogo en este aspecto y las confusiones que podría inducir.

La analogía, tal como fue abordada (sin emplear representaciones micro), apoyó la construcción del concepto de ecuación química desde el nivel simbólico y resultó de utilidad en el aprendizaje de los conceptos de fórmula química, coeficiente estequiométrico y subíndice. Sin embargo, el uso de las analogías no garantizó mejores resultados en los problemas conceptuales estandarizados que requieren la interpretación de situaciones con partículas y su relación con los otros 2 niveles de representación (macro y simbólico). Persistieron confusiones entre las cantidades experimentales y los coeficientes estequiométricos de la ecuación química.

En estos cursos de primer año de universidad se observaron inconvenientes al escribir la ecuación química a partir de un diagrama con partículas dado. Al respecto Gabel, Samuel y Hunn (1987) sostienen que la habilidad de representar la materia a nivel de partículas no mejora por el simple hecho de aumentar el número de cursos de química, si no existe un tratamiento específico. Es necesario que el abordaje incluya en forma sistemática un trabajo con representaciones con partículas.

Para superar estas dificultades se requiere de un abordaje conceptual en el que prime el diálogo con los estudiantes que permita ir evaluando sus comprensiones parciales y apoyando la construcción de imágenes mentales sobre el sistema químico abordado. Especial atención debe prestarse a las relaciones entre las cantidades experimentales, las representaciones a nivel submicroscópico y el simbolismo de la ecuación química y lo que ella representa. Al respecto, Casado (2003) mostró, en cursos de nivel medio, que una unidad didáctica sobre la reacción química basada en la vinculación sistemática de los niveles macro, submicro, simbólico y gráfico, donde las representaciones con partículas tenían un rol relevante, tuvo un impacto positivo en el aprendizaje conceptual. Estos estudiantes, luego del desarrollo de esta unidad de una duración de 12 h, obtuvieron porcentajes de respuestas correctas en los 2 problemas conceptuales de estequiometría del 55% y del 46% respectivamente.

Se han dado respuesta a las preguntas iniciales de este trabajo: en qué condiciones, cuándo y cómo la enseñanza con analogías favorece el aprendizaje conceptual de la estequiometría, en un abordaje sistemático que siga una metodología probada y sugerida por la investigación didáctica.

Como proyección de este estudio preliminar sería conveniente ampliar la muestra de alumnos, con la finalidad de validar la generalización de los resultados obtenidos y permitir un tratamiento estadístico más completo, que favorezca confirmar la validez de las discusiones sostenidas.

La resolución de ejercicios no garantiza la comprensión conceptual de los conceptos involucrados en la estequiometría, tampoco se logra con un empleo de analogías complementario al anterior. Por lo desarrollado en este trabajo, se requerirá de un abordaje integrado (que combine otros recursos como experimentos, animaciones y simulaciones) y sistematizado basado en resultados de investigación, que incluya permanentemente reflexiones metacognitivas, que lleven a pensar sobre el nivel de representación que se está empleando, sus relaciones y correspondencias con otros, la naturaleza del pensamiento analógico, la existencia de correspondencias y limitaciones y la exteriorización permanente de conclusiones.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.