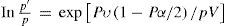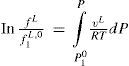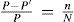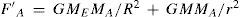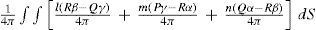John Henry Poynting (1852-1914) is known for his work related to the determination of the effect of pressure on the changes of phase and osmotic pressure (the Poynting effect), the determination of the constant of gravity and the mean density of the Earth¡ the pressure exerted by radiation, the transfer of energy in an electromagnetic field¡ and the connection between electric current and the electric and magnetic inductions in the surrounding field (the Poynting vector).
John Henry Poynting (1852-1914) es conocido por sus trabajos relacionados con la determinación del efecto de la presión sobre los cambios de fase y la presión osmótica (efecto Poynting) ; la determinación de la constante de la gravedad y la densidad media de la Tierra; la presión ejercida por la radiación; la transferencia de energía en un campo electromagnético¡ y la conexión entre la corriente eléctrica y la inducción eléctrica y magnética en el campo de alrededor (el vector de Poynting).
John Henry Poynting was born on September 9, 1852, at Monton, near Manchester, the youngest son of the Reverend Thomas Elford Poynting (1830-1878), Unitarian Minister of Monton. He received his first education at the school run by his father, and then, from 1867-1872, he attended Owens College, Manchester, after gaming a Dalton Entrance Exhibition in Mathematics. In due time Charles would follow the steps of his father and become Unitarian Minister at Fallow- field, near Manchester. His second brother, Frank Poynting (1848-1897), became a well-known ornithologist who studied the eggs of British birds.
At that time Owens had not the authority of granting degrees and most of the students prepared for the external examinations of the University of London. Poynting took second place at the London Matriculation exam in 1869, obtained Second Class Honors in both Physics and Mathematics in the First B.Sc. examination in 1871, and took the B.Sc. degree in 1872. In the same he was awarded an entrance scholarship to Trinity College, Cambridge. At Trinity he studied mathematics with Edward John Routh (1831-1907) and obtained his Major Scholarship in due course. He joined the Second Trinity Boat Club and rowed in the first boat in 1875. He took his degree in the Mathematical Tripos of 1876 as Third Wrangler (i.e., third in his year), tied with another student by the name of Trimmer, of Trinity College (Thomson, 1914).
After graduation Poynting returned for a short time to Owens College as a demonstrator in the Physical Laboratory under Balfour Stewart (1828-1887), who had succeeded Jack as Professor of Natural Philosophy shortly before Poynting s departure for Cambridge. While at Owens he began a lifelong friendship with his fellow student Joseph John Thomson (1856-1940, 1906 Nobel Prize for Physics for his discovery of the electron). In 1887 Cambridge awarded him his doctoral degree.
In 1878 Poynting received a Fellowship to continue his studies at Trinity College; there, in the Cavendish Laboratory under Clerk Maxwell, he begun his experiments on the mean density of the Earth, which were to occupy much of his time for the next 10 years and be the subject of his doctoral dissertation. He stayed at Cambridge until 1880 when he was appointed to the Chair of Physics in Mason College, Birmingham, which had just been founded; he held this post until his death (Thomson, 1914). In the same year he married Maria A. Cropper, daughter of John Cropper, Unitarian Minister of Stand, near Manchester, with whom he had three children.
Poynting was one of the prime movers in the development of Mason College into the University of Birmingham in 1900 and was largely responsible for the planning and organization of the new technological departments and their buildings (Thomson, 1914). In 1900 Poynting was elected Dean of the Faculty of Science (Lodge, 1914).
Poynting carried out all this despite continual poor health, showing the first signs of diabetes. In the 1880s he and his family moved to Alvechurch, near Birmingham, where Poynting took up farming in his spare time, an activity that did not prove to be profitable. In the spring of 1912 a severe attack of influenza was followed by a recrudescence of diabetes and he was ordered to take a long rest, which kept him away from Birmingham for two terms. Another attack of influenza in the spring of 1914 brought on a very severe attack of diabetes and led to his death on March 30,1914 (Lodge, 1914; Thomson, 1914).
While at Owens Poynting published his first memoir (Poynting, 1877), which was not exactly of an academic nature; it dealt with an analysis of the statistics for drunkenness in England and Wales, which Chamberlain had published in February of 1877. According to the latter, the data was contrary to the proposition that the multiplication of public houses (pubs) had a tendency to diminish intemperance. Poynting grouped the data as a histogram and obtained the opposite result: the number of apprehensions for drunkenness increased considerably as the number of public housed decreased in proportion to the population. His method of analysis seemed more justified because instead of considering the information on a town-by-town basis, he grouped the towns having more or less the same number of pubs and plotted the average of apprehensions of each group against their number of public houses. In this way he neutralized the effect of more or less stringent police regulations and other circumstances peculiar to individual towns. This work, done in collaboration with John Dendy (1827-1894) and forming part of a report to the Select Committee of the House of Lords on Intemperance, concluded among other things, that there was a marked geographical distribution of drunkenness, northern England being decidedly more drunken than southern England, and that there appeared to be a direct relation between the rate of increase of population and the rate of drunkenness (Poynting and Dendy, 1878).
Another publication in the area of statistics was related to the fluctuations in the price of wheat and in the cotton and silk imports into Great Britain and the possible relations between this phenomenon and common meteorological causes (Poynting, 1884a).
Poynting's well-known works on the use of a common balance for determining the mean density of the Earth and the gravity constant were also started during 1877 in Owens. The gravitational experiments were moved first to Cambridge, and then to Mason College. The results of this work gained him Cambridge University's Adams Prize.
Poynting's memoir on the transfer of energy (Poynting, 1884b) aroused universal attention. The paths by which energy travels from an electromotive source to various parts of a circuit were displayed, and their intricacies unraveled. These papers are the basis of the fundamental generalization connecting mechanical motion with electric and magnetic forces, which is known as Poynting's Theorem (Lodge, 1914).
Poynting's work on radiation and radiation pressure (Poynting, 1903a, 1904ab, 1905, 1910a) analyzing and proving the tangential pressure of radiation; shows, both theoretically and experimentally, that a beam of light behaves essentially as a stream of momentum, and produces all the mechanical results which may thus be expected, in spite of being extremely small. His results allow a way to determine the absolute temperatures of the Sun and the planets, and of other masses in space (Lodge, 1914).
Poynting also took great interest in the philosophical aspects of physical science, and Ward acknowledges his help in connection with the publication of the Gifford Lectures delivered before the University of Aberdeen in the years 18961898, entitled Naturalism and Agnosticism (Ward, 1899). Poynting was strongly inclined to limit the realm of science to description and to regard a law of nature as nothing but a formulation of observed correspondences. He wished to abolish the idea of cause in physics.
Some of Poynting's philosophic views were exposed in his Presidential Address to Section A of the British Association for 1899 (Poynting, 1899): “Concurrently with the change in our conception of physical law has come a change in our conception of physical explanation [...] we have explained anything when we know the cause of it, or when we have found out the reason why [...] We explain an event not when we know why it happened, but when we show how it is like something else happening elsewhere or other when, w2hen in fact, we can include it's a case described by some law already set forth. In explanation we do not account for the event, but we improve our account of it by likening to what we already know [...] the physicist is examining the garment of Nature, learning of how many, or rather of how few different kinds of thread it is woven, finding how each separate thread enters into the pattern, and seeking from the pattern woven in the past to know the pattern yet to come We stand in front of Nature's loom as we watch the weaving of the garment; while we follow a particular thread in the pattern it suddenly disappears, and a thread of different color takes its place. Is this a new thread or is merely the old thread turned around and presenting a new face to us? So as we watch the weaving of the garment in Nature, we resolve it in imagination into threads of ether spangled over with beads of matter. We look still closer, and the beads of matter vanish; they are mere knots, and loops in the threads of ether [...] Do we, or do we not, as a matter of fact, make any attempt to apply the physical method to describe and explain those motions of matter which on the psychical view we term voluntary?
Honors and awardsPoynting was awarded much recognition as a result of his brilliant research in many areas, and his public activities. He was elected a Fellow of the Royal Society (1888); he received the 1893 Adams Prize from the University of Cambridge, the 1903 Hopkins Prize of the Cambridge Philosophical Society, and in 1905 a medal from the Royal Society “for his researches in physical science, especially in connection with the constant of gravitation and theories of electro-dynamics and radiation.” Poynting served on the Council of the Royal Society from 1909 to 1911 and as its Vice-President in the period 1910-11. He was President of Section A at the 1899 meeting in Dover of the British Association for the Advancement of Science; he also served as President of the Physical Society in 1909-1911. In addition to the effort involved in twice planning and equipping a new physics laboratory, preparing lectures and doing research, he found time to serve as a Justice of the Peace, Chairman of the Birmingham Horticultural Society, and as member of the licensing committee, the Gassiot Committee of the Royal Society, and on the Sights Test Committee of the Board of Trade (Thomson, 1914).
Scientific contributionPoynting is remembered particularly for the equation he developed to describe the variation of the vapor pressure with the external pressure (the Poynting effect) and the Poynting vector, which he formulated in 1884 to describe the flow of energy in an electromagnetic field.
In addition to over 100 papers published in several scientific journals Poynting wrote The Mean Density of the Earth (Poynting, 1894; the Adams Prize Essay for 1893), The Pressure of Light (Poynting, 191 Ob; “Romance of Science” Series) and The Earth (Poynting, 1913). To the Text Book of Physics written in conjunction with Thomson (Poynting and Thomson, 1914) he contributed the whole of the volumes on Sound and Heat and of the first volume of Electricity and Magnetism and the chapters on Gravitation in the Properties of Matter.
Poynting's papers may be divided into four groups: (a) on the change of state, (b) studies on gravitational attraction, (c) on the transfer of energy in the electromagnetic field, and (d) on the pressure of light. The content of these papers is briefly discussed below.
Change of stateIn the introduction to his first paper on the subject (Poynting, 1881a) Poynting summarized the findings of Thomson on the effect of the curvature of a liquid surface on its vapor pressure (Thomson, 1872). According to Thomson, when a liquid rises in a capillary tube so that its surface is concave upwards, then its vapor pressure is less than at the plane surface. If the liquid falls in the tube so that its surface is now convex, then its vapor pressure is larger than at the plane surface. Thomson derived the following equation to express these results:
where p and p’ are the vapor pressures over the plane surface and over the curved surface of the meniscus, (ρL and ρV the densities of the liquid and vapor respectively, σ the surface tension of the liquid, and r the radius of curvature of the curved surface. In equation (1) the term 2σ/ρ represents the difference in pressure between the upper and the lower part of the meniscus. Since ρL>>ρv the sign of (p - p’) will depend on the sign of r. For non-wetting liquids such as mercury r > 0 and consequently, the vapor pressure of a drop will increase above that over a plane surface, inversely proportional to the decrease in the radius of the drop. For example, for mercury drops with r = 10-7 cm, the increase in vapor pressure is 100 percent.Poynting proceed to show that the same equation was applicable to both the solid and the liquid state, making Thomson's result more general. His starting point was the accepted assumption that the maximum vapor pressure of a substance at a given temperature is an indication of the number of molecules escaping from its free surface. Two different phases will then be in the equilibrium when the escaping tendency of the molecules is the same for the two phases. To explain the fact that the melting point of a substance is affected by pressure it becomes necessary to assume that the pressure alters the vapor pressure, and therefore the rate of escape of the molecules, and that this alteration is different for the two states. Equality of the vapor pressures will now occur at the new melting point. Pressure increases the number of molecules escaping from the surface of the two phases in contact, but the increase is greater in the less dense state. For the particular case of ice + water, ice is the dense state and below 0°C it has the less vapor pressure. Hence a sufficiently great increase of pressure, while increasing both vapor pressures, can make that of ice overtake that of water and lower the melting point.
Suppose now that only one of the states (ice) is subjected to an increase in pressure. In this situation the new pressure will increase the rate at which molecules escape from the ice into the water but will not affect the rate of escape of water molecules into the ice. Assuming the applied pressure δP to he represented by 2σ/r and substituting in equation (1) we get
In a second paper on the subject (Poynting, 1881b) Poynting extended his analysis to the evaporation of a liquid. In this situation the effect of surface tension on vapor pressure originates from the hydrostatic pressure 2σ/r produced on the surface, hence the vapor pressure over a flat surface should increase when the pressure on the liquid in increased, for example, by addition of an inert gas into a vessel containing liquid in equilibrium with its vapor. Poynting derived an expression for the variation of the vapor pressure of the liquid with the external pressure by analyzing the following isothermal cycle: (a) evaporation of one gram of liquid under the total pressure p + P, (b) expansion of the vapor produced to the pressure p assuming ideal behavior, (c) condensation of the vapor at pressure p, and (d) closing the cycle by compressing the liquid formed back to the original pressure p + P. Let v, v’, and V’ be the corresponding volumes of the liquid and vapor respectively, and a the isothermal compressibility7 of the liquid. According to the First law of thermodynamics the total work done by the cycle is zero, that is
Equation (3) can be simplified significantly using the facts that PV-p’V’ and that terms containing αp are negligible, to yield
Hence if P is not very great
the same result as equation (2), obtained by a different process.All the assumptions regarding the ideality of the gas phase may be removed by considering the modem term of fugacity, f instead of the pressure. We know that (Smith, 2006):
Separating variables and integrating at constant temperature between vapor pressure P10 and any external pressure P, we get
Assuming the liquid to be incompressible, the expression for the Poynting effect becomes
where P10 is now the vapor pressure of the component at temperature T. Nowadays, equations (8) and (9) expressing the effect of the external pressure on the vapor pressure of a liquid are called the Poynting effect. These equations convert the fugacity of a pure saturated liquid from the vapor pressure to the system pressure at the same temperature. Calculation of the Poynting effect plays an important role in the analysis of vapor-liquid equilibrium.
Osmotic pressureAccording to Poynting (Poynting, 1896ab), the phenomena of liquid viscosity, diffusion, and surface evaporation may be analyzed by imagining the liquid to be a solid structure, inasmuch as the molecules cohere and resist strain of any kind’ Anyhow, it is clear that the amount of kinetic and potential energy of the molecules puts this structure not far from instability. In a mass of connected molecules irregularly distributed and irregularly vibrating, concentrations of energy must occur and at the points of concentration individual molecules may receive enough energy to free themselves from their immediate surroundings. The near unstable solid structure is thus continually breaking down and renewing itself. If the breaking down of the structure takes place near the surface of the liquid some of the moving molecules have a velocity vector that allows them to escape the liquid and become part of the gas space. Based on these ideas, Poynting coined the term mobility to quantify the number of free or mobilized molecules crossing a square centimeter per second of liquid, where by free or mobilized molecules he meant those that were changing their surroundings and forming new connections. When the square centimeter is located on the surface of the liquid, the upward mobility corresponds to the rate of vaporization and the downward mobility of the vapor is the rate of condensation; when both mobilities are equal the pressure on the system becomes the vapor pressure.
Assume now a closed chamber maintained at constant temperature and holding two partly filled deep vessels, one containing pure solvent and the other a dilute solution of a non-volatile salt. As a result of the difference in vapor pressures, the pure solvent will distill over into the solution and will continue to do so until the difference in level in the two vessels is such that each surface is in equilibrium with the vapor at its level. The hydrostatic pressure in the solution at the level of the surface of the pure solvent will then be the osmotic pressure.
These remarks may he used to explain in general terms the rise that takes place when a semi-permeable vessel containing a solution is placed inside another vessel containing pure solvent. The molecules of the solvent began entering the membrane from both sides but since the vapor pressure over the pure solvent is larger than that over the solution, the mobility or number of molecules set free from the pure solvent is greater than the number set free from the solution. According to Poynting, the membrane continues to absorb the solvent from both sources until it becomes saturated, that is, it returns as many molecules as it receives. The membrane is receiving more molecules from the pure solvent side, and therefore when saturated for that side it is supersaturated for the other. Consequently more molecules are sent into the solution than are received from it, and the volume of the solution grows until the growing hydraulic pressure so much increases the mobility that it becomes identical on both sides of the membrane (Poynting, 1896a).
Poynting now applies the same idea to the change of melting point in a solution. In the solid the mobility is unchanged but that of the solution is lowered by the fraction PρV/PoρL, where P is the osmotic pressure and P° the vapor pressure of the pure solvent. To find the new melting point it is necessary to find the temperature dθ below the normal melting point at which this is equal to the difference between tire liquid and solid mobilities. Taking the pressure to represent mobilities Poynting derives the relation
where L is the heat of change of phase.Poynting now assumes an unusual mechanism to explain the decrease in vapor pressure caused by the solute: he imagines that the latter probably combines with the solvent to form unstable molecular aggregates, which continuously interchange constituents so that when located near the surface they compete with the non associated molecules to capture the vapor molecules hitting the surface. This capture is done by pure solvent molecules or by the complex molecules exchanging their attached solvent molecules for the ones arriving from the vapor phase. Poynting's view differs from the one accepted today where it is said that in a solution the fraction of the free surface of the liquid available for the solvent molecules to escape is proportional to the mole fraction of the solvent, but the return surface for the vapor molecules is the total surface.
The trapping-exchange phenomenon may be quantified as follows: Assume that each molecule of salt associates with a molecules of the solvent in such a way that it prevents them from evaporating. The solution may be considered as solvent having a number of the molecules forming aggregates that are inactive as regards evaporation but active in effective condensation. If N is the number of solvent molecules per liter and n the number of solute molecules added, then the number of molecules of free solvent left is (N - an). In other words, the solution contains (N - an) molecules active for evaporation, while there is still N for condensation. As a result, the vapor pressure has decreased in the ratio (N - an)/N and
Assuming that a = 1, we have
which is the result obtained by van’t Hoff for the value of the osmotic pressure (van’t Hoff, 1887).Poynting closed his paper with the remark that although his was a crude model, it showed that it was not necessary to ascribe osmotic pressure to dissociation but rather to association or some of the processes operative in solutions (Poynting, 1896a),
Gravitational attraction and the density of the EarthThe works for which Poynting is best known in the area of physics are his determination of the Newtonian constant of gravitation and the average density of the Earth by a very accurate use of an ordinary balance with an adjustable mass under one or other of the arms, a determination which is popularly known as weighing the Earth. These experiments were begun Cambridge in 1878 and only after twelve years they gave results which satisfied him. In his final memoir about the experiments to the Royal Society in 1891 (Poynting, 1892) Poynting gave the measurement of G, the gravitational constant, as the first aim of the experiment, and then went on to discuss the use of the results to measure the mass of the Earth (Falconer, 1999),
Newton's theory of gravitation explained the motion of terrestrial objects and celestial bodies by postulating that pairs of massive objects attracted each other with a force proportional to the product of the two masses and inversely proportional to the square of the distance between them. In his book Principia (Newton, 1687) Newton reported the relative densities of the Sun, Jupiter, Saturn, and the Earth as 100, 94.5, 67, and 400, respectively, so that if the density of the Earth were known the densities of the Sun and the two planets could be calculated. On the basis of the known density of rocks at the surface of the Earth and rocks from mines, Newton guessed that the average density of the Earth is 5 to 6 times the density of water (Newton, 1687). After Newton, and at different times, British and French scientists attempted to weight the Earth by observing the gravitational force on a test mass from a nearly large mountain. The experimental procedure involved measuring the line of a pendulum hung near a mountain and comparing it to the line expected if the mountain was not there. These effects were hampered, however, by a very imperfect knowledge of the composition and average density of the rock composing the mountain (Wisniak, 2004).
The determination of the structure and composition of the interior of the Earth was one of the many subjects that interested Henry Cavendish (1731-1810). In an exchange of letters with his friend John Mitchell (1724-1793) they discussed the possibility of devising an experiment to weigh the Earth. Mitchell suggested an arrangement similar to the one used by Charles Coulomb (1736-1806) for measuring the electrical force between small charged metal spheres; that is, using a torsion balance to detect the very small gravitational attraction between metal spheres. Mitchell built a first prototype of the equipment but died (1793) before he was able to conduct the experiments. Cavendish rebuilt the apparatus into a balance constructed from a 6-foot wooden rod suspended at his middle point by a long metal fibre and carrying two 2-inch diameter lead spheres at each extremity. Two 350-pound lead spheres, brought close to the enclosure housing the rod, provided the attraction effect. This arrangement set up vibrations between the attractive force and the torsion of the wire and equilibrium was determined between the turning moment and the moment of torsion (Wisniak, 2004). Cavendish made seventeen experiments and concluded that the density of the Earth should be 5.48 greater than that of water (Cavendish, 1798). In 1841 Francis Baily (1774-1844) reviewed Cavendish's calculations and found a small mistake of simple arithmetic that decreased the expected density of the Earth from 5.48 to 5.45 (Berry, 1960). Between 1894 and 1896, Charles Vernon Boys (1855-1944), while repeating Cavendish's experiments, made the discovery that the sensitiveness of the apparatus could be greatly increased by reducing its dimensions (Boys, 1896). He reported the density of the Earth as 5.527 times the density of water.
Poynting's approach to the problem was similar to that of Cavendish, except that he substituted the torsion, balance by a common one (Poynting, 1879). In his words: “In using the common balance to find the attraction between two masses, perhaps the most direct mode of proceeding would consist in suspending a mass from one arm of a balance by a long wire and counterpoising it in the other pan. Then bringing under it a known mass, its weight would be slightly increased by the attraction of this mass [...]” (Poynting, 1892). The balance used in the later experiments was built specially by Ludwig Oertling (1818-1893) and had abeam 123 cm long (note the extremely large size of the balances used by Cavendish and Poynting). With a balance of this size overcoming the difficulties arising from air currents proved to he quite an experimental challenge.
The mechanic principles of Poynting's method are straightforward. Consider a balance with two equal masses MA and MB; both are equally attracted to the Earth with a force
where FA,FB are the forces on MA and MB respectively. ME and R are the mass and the radius of the Earth, respectively, and G is the universal gravitational constant (Falconer, 1999). As Poynting writes: “To determine G we must measure GMAMB/R2 in some situation in which both MA and MB are known, whether they be a mountain and a plumb-bob, or two spheres of known mass and dimensions [...]” (Poynting, 1892).Now, if a large extra mass M is put under MA at a distance r, then the additional force attracts MA down by the amount
while the force on MB remains constant. Hence the balance tilts, giving a measure ofSince M, MA, r, and 0, are known, G can be evaluated and from it, the mean density of the Earth can he calculated from the expression:
where Δ is the density and V the volume of the Earth considered as a sphere of radius R. Hence Δ = gR2/GV (Falconer, 1999).The experiments were much more complex than the theoretical equations suggest. Allowance had to be made for the attraction between M and MA before M was moved into position, for the attraction of the beam and of MB to M, and methods devised for measuring or canceling these. The apparatus was operated from a distance sufficient to prevent disturbances caused by the attraction and temperature effects of the body of the operator. A hole in the wall of the balance room permitted the experimenter to observe the setup with the help of a telescope (Falconer, 1999).
Traditionally, the common balance was considered unsuitable for measuring such small forces, first because of the greater disturbance produced by changes of temperature, such as convection currents and unequal expansion of the arms of the balance, and second because of the errors arising from raising the beam between each weighing, resulting in varying flexure of the beam and in constancy of the points of contact of the knife edges and planes (Poynting, 1879). Poynting later picturesquely summed up the sensitivity and accuracy of his experiment (Poynting, 1894ab): “Imagine a balance large enough to contain on one pan the whole population of the British Islands and that all the population were placed there but one medium-sized boy. Then the increase in weight, which had to be measured, was equivalent to measuring the increase due to putting that boy on with the rest. The accuracy of measurement was equivalent to observing from the increase in weight whether or no he had taken off one of his boots before stepping on to the pan” (Falconer, 1999).
Poynting reasoned that if the attraction between two spheres was different according to whether their axes were parallel or crossed, then there would be a directive action on one sphere in the field of the other. He and P. L. Gray attempted to detect such directive action by rotating one sphere and attempting to force rotational oscillations of the other (Poynting and Gray, 1899). They found no significant oscillations within the limits of accuracy of the experiment. Poynting and Percy Phillips also did careful experiments (Poynting and Phillips, 1905) to determine if a change of temperature had any effect on weight. The results were negative, between 150° and 100°C, the change was smaller than one part in 109 and between 16.6° and -186°C it was smaller than one part in 1010 per 10°C.
Poynting's final results for the mean density of the Earth and the gravitational constant were 5.4934 times the density of water and 6.6984 x 10-8 dynes cm2 g-2, respectively (Poynting, 1892). The present accepted value of the average mean density of the Earth is 5.52 times the density of water (Wisniak, 2004).
Poynting reported the results of his experiments to Trinity College, Cambridge, as a fellowship dissertation and Clerk Maxwell acted as referee (Falconer, 1999).
In his 1900 address to the Royal Institution on recent studies in gravitation (Poynting, 1900) Poynting closed his lecture with the following remarks: “So while the experiments to determine g are converging on the same value, the attempts to show that under certain conditions it may not be constant, have resulted so far in failure all along the line. No attack on gravitation has succeeded in showing that it is related to anything but the masses of the attracting and the attracted bodies. It appears to have no relation to physical or chemical composition of the acting masses or to the intervening medium [...] But gravitation still stands alone. The isolation, which Faraday sought to break down, is still incomplete. We at least know something in knowing what qualities gravitation does not possess, and when the time shall come for explanation, all these laborious, and at first sight, useless experiments will take their place in the foundation on which that explanation will be built” (Poynting, 1900),
Transfer of energy in the electromagnetic fieldThe researches by which Poynting is most widely known are those published in his papers for the period 1885-1887 (Poynting, 1884b, 1885, 1887). The subject is described in the introduction to his first paper: “A space containing electric currents may be regarded as a field where energy is transformed at certain points into the electric and magnetic kinds by means of batteries, dynamos, thermoelectric actions, and so on, while in other parts of the field this energy is again transformed into heat, work done by electromagnetic forces, or any form of energy yielded by currents [...] the existence of induced currents and of electromagnetic actions at a distance has led [...] to look upon the medium surrounding the conductor as playing a very important part in the development of the phenomena. If we believe in the continuity of the motion of energy [..,] we are forced to conclude that the surrounding medium contains at least part of the energy, and that it is capable of transferring it from point to point [...] How does the energy about an electric current pass from point to point [...] according to what law does it travel from [...] where it is recognizable as electric and magnetic to the parts where it is changed into heat or other forms? The aim of this paper is to prove that there is a general law for the transfer of energy, according to which it moves at any point perpendicularly to the plane containing the lines of electric and magnetic force, and that the amount crossing unit of area per second of this plane is equal to the product of the two forces multiplied by the sine of the angle between them divided by 4π, while the direction of the flow of energy is that in which a right-handed screw would move if turned round from the positive direction of the electromotive to the positive direction of the magnetic intensity” (Poynting, 1884b).
Poynting goes on to the full mathematical proof of his law and uses the equation of the electromagnetic field to show that the rate of increase in the energy inside a closed surface is equal to:
where dS is an element of the closed surface, l, m, n the direction cosines of the normal to the surface; P, Q, R the components of the electromotive intensity, and α, β, γ, those of the magnetic force. The first two terms of Poynting's final equation express the gain per unit time in electric and magnetic energies, the third term, the work done per unit time of the electromagnetic forces, and the fourth one, the energy transformed by the conductor into heat, chemical energy, and so on. F^uation (18) maybe regarded as showing that the energy comes through the bounding force, the components of flux being Rβ−Qγ/4π, Pγ−Rα/4π, and Qα−Pβ/4π, and that each element is contributing the indicated amount (Poynting, 1884b).
The vector having these components is now universally known as Poynting's vector, it is at right angles to both the electric and magnetic forces and is proportional to the product of these forces and the sine of the angle between them. Thus when we can draw equipotential surfaces for both the electric and magnetic forces the energy flows along the lines of intersection of the two sets of surfaces.
In modern vector terms:
where the vector S→ is the rate of energy transport per unit area in the direction of the propagation of the wave, vectors H→ and B→ the magnetic field and the magnetic field flux density, respectively, vector E→ the electric field normal to B→, and 1 /μ0 the permeability of the free space.Poynting illustrated his theorem by applying it to a constant current flowing along a straight wire, a condenser discharged by short-circuiting the plates by a wire of great resistance, a voltaic battery, and a thermo-electric circuit. His results indicated that in the case of a wire, none of the energy travels along the wire but comes in from the non-conducting medium surrounding the wire, and that as soon as it enters it begins to be transformed into heat. The amount of energy crossing successive layers of the wire decreases systematically until the time when it reaches the center of the wire. At the axis there is no magnetic force and no energy passing, it has all been transformed into heat (Poynting, 1884b).
Before the publication of this paper the general opinion was that the energy was transferred along the wire much in the same way as hydraulic power is carried through a pipe. On Poynting's view the energy flows out from the space between the plates and then converges sideways into the wire, where it is converted into heat. In Poynting's words: “A current in a conductor is rather to be regarded as consisting essentially of a convergence of electric and magnetic energy from the medium upon the conductor and its transformation there into other forms. The current [...] consists essentially of a divergence of energy from the conductor into the medium [...] This mode of regarding the relations of the various parts of the circuit is [...] very different from that usually given, but it seems to me to give us a better account of the known facts” (Poynting, 1884b). In the second paper Poynting takes the view that the electromagnetic field consists of distributions of lines of electric and magnetic force and discusses the question of the transfer of energy from the point of view of the movement of these lines.
Poynting's vector occurs as a quantity of fundamental importance in many theories of electromagnetic action in which the subject is approached from a point of view somewhat different from the one described above. It appears, for example, as a measure of the momentum per unit volume when the electromagnetic field is regarded as a mechanical system and the properties of the field as the result of the laws of motion of such a system. It appears, too, when we regard magnetic force as the result of the motion of tubes of electric force, the direction of motion of these tubes being parallel to Poynting's vector (Thomson, 1914),
Pressure of LightPoynting published a well-known paper on the theory of the subject (Poynting, 1903ab). In the first part of it he discussed the application of the fourth-power law of radiation [Stefan's law] to determine the temperature of planets such as Mercury, Venus, Mars, and Neptune. Among some of the interesting results he arrived at was that since the temperature of the Sun lies between 6000 Å and 7000 Å, then the effective temperature of space must be 10 Å; and that the average temperature of Mars is about 235 K, not different from the freezing point of mercury, that is, so low that life, as we know it, would be impossible on its surface.
The second part of the paper (Poynting, 1903b) discusses and calculates the pressure exerted by radiation against a surface on which it falls. His results indicate, for example, that a full absorber exposed normally to the solar radiation at the distance of the Earth, is subject to a pressure of 5.8 x 10-5 dyne·cm2. He then calculated the repulsive force between two hot spheres, arising from the radiation from the one tending to repel the other and showed that if the bodies were in radiation equilibrium with the Sun at the distance of the Earth from it, the repulsive effect would be greater than the gravitational attraction between them if their radii are less than 19.6 cm, if their density were that of water; if they were made of lead the corresponding radius would be 1.78 cm.
There is a remarkable effect of size on the relation between the radiation pressure and the gravitational pull, the first one acts on the surface and is thus proportional to it, the second penetrates the surface and pulls every1 particle of matter throughout the entire volume. Poynting's calculations indicate that the radiation pressure on a minuscule speck of dust of 1 /40,000 cm radius and density equal to that of the Earth, balances exactly the pull of gravity and it would be neither attracted nor repelled by the Sun. This effect should be taken into account in the motion of Saturn's rings if these consisted of very small particles: it is perfectly possible that the effect of radiation might make them repel instead of attract each other. Each particles in the ring, having about 2.5 cm diameter, would neither attract nor repel each other, and each would move in circles around the planet as if the rest were absent (Poynting, 1905, 1906, 1909, 1910ab). At the end of the paper Poynting analyzes the effect produced by radiation on the orbits of small bodies around the Sun and shows that this would ultimately cause them to fall into that body. To quote his own words: “Thus the Sun is ever at work keeping the space round him free from dust, if the particles are very minute he drives them forth into outer space, if they are larger, he draws them in. It is just possible that we have evidence of this drawing in, in the zodiacal light, that vast dust-like ring which stretches from the Sun outwards far beyond the orbit of the Earth, and is at once the largest and the most mysterious member of the solar system (Poynting, 1906).
This idea was later developed by the American physicist Howard Percy Robertson [1903-1961] and is now known as the Poynting-Robertson effect.