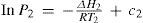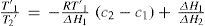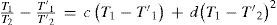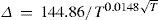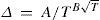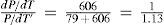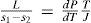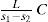Sidney Young (1857-1937) was a pioneer in the separation and specification of pure organic compounds, and developed crucial thermodynamic relationships for solids and liquids. He examined in great detail the P–T–V phase space of pure substances and proved that below their triple point ice and other substances sublime but will not melt even under heating. In addition, he demonstrated that the mean linear rectilinear law of Cailletet and Mathias was valid only for temperatures above the boiling point of the substance. Young studied the distillation of petroleum and its fractions and separated for the first time n-pentane, n-hexane, and isopentane. Of particular significance is his discovery of the ternary minimum boiling temperature azeotrope of benzene + water + ethanol, which led to the industrial manufacture of absolute alcohol.
Sidney Young (1857-1937) fue un pionero de la separación y especificación de compuestos orgánicos puros y desarrolló relaciones termodinámicas clave entre sólidos y líquidos. En particular, estudió el dominio P–T–V de sustancias puras y demostró que bajo su punto triple el hielo y otras sustancias subliman pero no funden, aun bajo la acción del calor. Además, demostró que la regla de los diámetros lineales de Cailletet y Mathias es válida sólo para temperaturas superiores a la de ebullición. Young estudió la destilación del petróleo y sus fracciones y consiguió separar por primera vez n-pentano, n-hexano e isopentano. De especial importancia es su descubrimiento del azeótropo ternario con temperatura de ebullición mínima en el sistema benceno + agua + etanol, que llevó a la fabricación industrial del alcohol absoluto.
Sidney Young was born on December 29, 1857, at Farnworth near Widnes, in Lancashire, the third son of Edward Young, a prosperous Liverpool merchant and justice of the Peace for the county of Lancashire. Young spent five years at a private school in Southport and two years at the Royal Institution School in Liverpool. In 1877, after being in business for over two years with his father, he entered Owens College, Manchester, to study chemistry. There he received his training under Henry Enfield Roscoe (1833-1915) and Carl Schorlemmer (1834-1892). At Owens College he befriended Charles William Kimmins (1856-1948), afterwards a well-known lecturer on psychology and education, and chief school inspector for London, Arthur Smithells (1860-1939), and Julius Berend Cohen (1859-1935) (Francis, 1937).
Young obtained his Bachelor of Science in 1880 and his degree of Doctor of Science three years later, while working with William Ramsay (1852-1916) at University College, London. Together with Smithells and Cohen they moved to Strasbourg to work under Rudolf Fittig (1835-1910). Young spent with Fittig the semester of 1881-1882 studying the relation between lactones and the corresponding acids (Young, 1883ab; Francis, 1937).
In 1880 the students at Owens College founded the Chemical Society and Young and Smithells succeeded Cross and Bevan as joint secretaries. It was before this society that at the suggestion of Roscoe Young demonstrated Thomas Carnelley's (1852-1890) discovery that at sufficiently low pressures ice sublimes and cannot be liquefied by the application of heat. His explanation's was the subject of a letter to Nature in 1881 (Young, 1881) and in 1884, together with Ramsay, they provided and published the experimental verification (Ramsay and Young, 1884ab; Francis, 1937). By a curious coincidence, it was his colleague in Dublin, John Joly (1857-1933), who in 1899 showed that it is the converse effect, the liquefaction of ice under pressure-even at temperatures well below 0°C, which renders skating possible (Atkins, 1938) (Note 1).
In 1882 Young was appointed lecturer and demonstrator of Chemistry under Ramsay at University College, Bristol. He had already published some half a dozen papers on miscellaneous chemical subjects, but he now joined Ramsay in a most successful partnership, which lasted till 1887, when Ramsay succeeded Alexander Williamson (1824-1904) in the Chair of Chemistry at University College, London, and Young succeeded him as Professor of Chemistry at University College, Bristol, a position which he occupied for the next fifteen years; this was the most fruitful period of’ his scientific career. In 1903, at the age of 46, he became Professor of Chemistry at Trinity College, Dublin (Atkins, 1938; Timmermans, 1947).
In 1896 Young married Grace Martha Kimmins, the sister of his best friend, Charles William Kimmins, and in 1897 twin sons were born. One of them, Sydney Vernon, studied in the Royal Academy at Woolwich, received a commission in the Royal Engineers, and was killed in action near Ypres, France, in 1915. The second twin, Charles Edgar, served in the war, first in the Army Service Corps and later as a pilot in the Royal Flying Corps. After the war he went to Oxford and eventually became headmaster of Lincoln School and headmaster of Rossall School (Francis, 1937).
In 1903 James Emerson Reynolds (1844-1920) retired from the Chair of Chemistry at Trinity College, Dublin University, and Young was invited to succeed him. He took over early in 1904. Although this new position was not favorable to continued research, Young succeeded in developing the practical applications of his separation techniques. According to Atkins (Atkins, 1938), the students, who regarded every lecture as a joyous social occasion, were at first rather a puzzle to him. He never hid his opinion that they did not work so hard as his Bristol pupils; but he treated them all with courtesy and consideration and his lectures were listened to with great attention. Professor Edward Battersby Bailey (1881-1965) writes of Young's lectures at Trinity College after the war: “When the College halls were once more filled with students, the writer was one among the boisterous crowd who, freed from sterner discipline, flocked into the Department of Chemistry. They found there a Professor who lectured with extreme clarity, who illustrated his lectures by blackboard drawings which were the work of an artist and who, above all, set an example of old-world courtesy which made the deepest impression on those who experienced it” (Francis, 1937).
Occasionally foreign students came to his Dublin laboratory, notably J. E. Mills from the U.S.A., Otto Flaschner from Prague, and Jean Timmermans (1882-1971) from Brussels.
Shortly before his retirement in 1928, after a quarter of a century of service in Dublin, Young was the recipient of an address from over two hundred of his friends, former pupils, and those who were acquainted with his work. The signatures came from all over the world and among those who took a prominent part in this act of recognition were William Ringrose Gelston Atkins (1884-1959) and Timmermans (then at the Chair of Physical Chemistry, Brussels). After retirement, Young and his wife returned to Bristol. A few months before he died he was elected President of the Old Students’ Association of Owens College, Manchester. He passed away in his 79th year, after a very brief illness, on April 9th, 1937, and was survived by his wife and son (Francis, 1937).
Honors and PositionsYoung received many honors for his contribution to science and industry. He was awarded degrees of Doctor of Science Honoris Causa by the University of Dublin (1905) and by the University of Bristol (1921), and the M.A. by the Uni-versity of Dublin (1921). Young was a founder of the Insti-tute of Physics, Fellow of the Institute of Chemistry (1888), and Fellow of the Royal Society (1893). He was President of the Chemical Section of the British Association's Meeting at Cambridge in 1893; chairman of the Chemistry Section of the British Association's Meeting at Cambridge in 1904, Vice-President of the Chemical Society (1917 to 1920), President of the Royal Irish Academy (1921-1926), and member of the Advisory Council of the Department of Scientific and Indus-trial Research (1920-1925). During the War and immediately after, Young was duty-bound to take on an amount of work which world had severely taxed the strength of a much younger man. The medical and engineering schools had in-creased their enrollment very largely and Young was always meticulously careful in the routine work of examinations (Francis, 1937).
Scientific contributionYoung published over 100 papers, some well-known books on distillation and purification of compounds (Young, 1903; 1922), and contributed the articles on Sublimation, Distillation, and Thermometers to Thorpe's Dictionary of Applied Chemistry (Young, 1916, 1922a y 1927). Most of this work was carried during his tenure at Bristol and is related to the study of the thermodynamic properties of and the heterogeneous equilibria between about thirty highly purified organic compounds. The results of these researches appeared in his book Stoichiometry (Young, 1908). To Young also we owe both new experimental methods and new ways of representing the resulting data, which have proved of great practical importance in the laboratory and in industry. He discovered a large numbers of binary and ternary azeotropic mixtures and developed simple analytical procedures for determining their composition. This research led to the industrial production of absolute alcohol by elimination of the water in the form of a ternary azeotropic mixture with benzene (Young, 1922b).
Boiling pointMany different formulas and representations have been developed for the vapor pressure-temperature relationship for pure liquids and their mixtures (Wisniak, 2001a). This is due not only to the importance of this physical property itself but also to its relation to other thermodynamics properties, such as the latent heat of vaporization. For use in thermodynamic calculations an interpolation formula of some kind is essential, particularly since the data are usually fragmentary and located at inconvenient temperatures and pressure intervals (Wisniak, 2001b).
Numerous of the formulas in use have a semi-theoretical background, often based on the Clausius-Clapeyron equation that expresses the variation of the vapor pressure of a pure compound with temperature
where ΔH is heat of vaporization and ΔV the change in volume on vaporization.Between 1885 and 1886 Ramsay and Young (Ramsay and Young, 1885abc; 1886d) developed an expression relating the boiling points of two pure substances, which may be obtained from the integrated Clausius-Clapeyron equation applied to two pure substances 1 and 2:
Equations (2) and (3) are obtained assuming that the heats of vaporization ΔH are constant in the temperature range considered, or have been averaged over the same temperature interval.
Now, if the two substances have the same vapor pressure at the temperatures T1 and T2 respectively, then
so thatSuppose now that both compounds have also the same vapor pressure (different from the previous value) at the temperatures T1 and T2, then it must be that
Subtracting eq (6) from eq (5) gives
where c is a constant given byIn their papers (Ramsay and Young, 1885b; 1886d) Ramsay and Young reported the values of the constant c for 30 different pairs of substances, including such systems as water + ethanol, aniline + water, water + oxygen, and ammonium chloride + water. Their findings indicate not only that c is very small (<2 × 10–4) but also that for chemically similar substances (like water and ethanol) it is almost zero. For the last case we can write
According to eq (10) the ratio of the absolute temperatures at which two substances boil under the same pressure is constant.
Curiously, in all their publications related to the boiling temperature of pure compounds Ramsay and Young made no reference to a very important paper on the subject published by Karl Eugen Dühring (1833-1921), almost ten years before their first work. In 1878 Dühring discovered that plotting the boiling point of a substance against the boiling point of water at the same pressure yielded a straight line. This conclusion was arrived at from a study of about forty substances of greatly different chemical and physical properties, for which Victor Regnault (1810-1878) had published extensive vapor pressure data (Regnault, 1862). Dühring expressed the relationship algebraically, as follows
where T1 and T1′ are the boiling points of one substance at two different pressures, T2 and T2′ are the corresponding boiling points of a second substance (water in this case), and q is a constant that is the slope of the line. This conclusion, known today as Dühring's rule, has been shown to hold remarkably well for single substances over limited ranges of pressure, particularly when the boiling points of the substance in question are plotted against the known boiling points of a chemically similar substance. In the range of several thousands of millimeters of mercury, the deviations rarely amount to more than 10%. Dühring's rule is a valuable tool in the design of evaporators for aqueous solutions of salts (Wisniak, 2001b).It can be shown that the Ramsay-Young equation is somewhat less accurate than Dühring's rule and it is less desirable in that the constant is not the slope of the line (Wisniak, 2001b).
Dühring's rule may be derived from Ramsay-Young's equation as follows. Subtracting the value 1 from each side of eq (10) and rearranging yields
Equation (12) corresponds to Dühring's rule, eq (11).
In a later publication (Young, 1904) Young added the comment that his eq (7) is not valid for the case where the two substances being compared are not closely related or if one or both of them are associated. In this case an additional term must be added
In any case, the value of constant c becomes much higher, as with benzene and ethanol (c = 0.0008030) or sulfur and carbon disulfide (c = 0.0006845).
In 1842 Kopp (Kopp, 1842) concluded that a constant difference in chemical composition is accompanied by a constant difference in boiling point and he adopted the value 19°C as the rise due to the replacement of the methyl by the ethyl group in organic compounds. He further suggested that that this value is the constant difference for an addition of CH2 in any homologous series, and that the observed difference was most regular in the case of fatty acids. Initially he also thought that isomeric compounds with the same composition and the same vapor density have the same boiling point (Young, 1904). Later, after taking a wide survey including many substances such as hydrocarbons and their halogen derivatives, sulfide, and others, he was obliged to admit that the difference was in some cases higher, in others lower, than 19°C, but he still regarded these cases merely as exceptions to the law. In 1867 he admitted that isomeric hydrocarbons have not always the same boiling point and that the addition of CH2 was not always 19°C, but he still believed that the difference for CH2 was constant in any real homologous series.
Young thought that Kopp's wrong conclusions were due to the lack of material of sufficient purity. In practice, the increase in boiling point was not constant for each CH2 added, it was very large for short chain hydrocarbons and became smaller and smaller as the molecular weight increased. Many formulas had been proposed to express this increase and he was not very appreciative of their merits. Young thought that the increase in boiling point was a function only of the absolute temperature, and suggested the formula
where Δ is the difference between the boiling point T of any paraffin and that of its next higher homologue. This equation was also valid for other homologous series, for example, the halogenated alkyls.
Examination of a large number of compounds, associating and non associating, led Young to believe that eq (14) was able to predict the increase of boiling point between any nonassociating compound that contains at least one C-CH2-C group and that of its next higher homologue, with an error rarely exceeding 1.5°C. The formula was applicable to esters, higher fatty acids, ketones, cyanides, and nitro compounds.
In 1916 and 1922 Young published two additional papers (Young, 1916, 1928) in which he claimed that eq (14) in its more general form,
was applicable, as far as data available then, to all the n-paraffins from C3H8 to C35H72, under all pressures from 11 mmHg to 20,000 mmHg. The constants A and B depended on pressure, and in his publications he suggested ways for calculating them.The P-T phase diagram for pure substancesThe fact that arsenic sublimes without melting under atmospheric pressure but melts when the pressure is raised was well documented. Carnelley proved that ice, mercuric chloride, and camphor did not melt below certain pressures peculiar to each substance but above these pressures they melted when heated. This discovery led to the expression hot ice. Carnelley proposed the term critical pressure to denote the pressure under which a solid could not melt.
Preliminary experiments pointed to the possibility of heating a solid above its ordinary melting point without melting, but afterwards additional experiments showed that this was not the case. In 1873, James Thomson (1822-1892) discussed his findings on the behavior of a pure substance in the P-T dominion (Thomson, 1873). Here the three phase change curves, solid-gas, solid-liquid, and liquid-gas, yielded three continuous curves which seemed to cross each other at one common point, which Thomson named triple point. The curve between gas and liquid, which Thomson called the boiling curve, separated the regions of the plane corresponding to the ordinary liquid from those corresponding to the ordinary gaseous state. Thomas Andrews (1813-1885) (Andrews, 1869, 1876) had already demonstrated that this separating boundary came to an end at a point, which he named called the critical point, and that the transition from any liquid state to any gaseous state could be gradually effected by an infinite variety of courses passing round the extreme end of the boiling line. Thomson then proceeded to calculate the value of the slope of each the three phase-change curves using the equation dP/dT = CM, “where C denotes Carnot's function and M the rate of absorption at which heat must be supplied to the substance per unit augmentation of volume.” Since C is a function of the temperature, which has the same value for all substances at the same temperature, then it has the same value for the two cases of steam to liquid water and steam to ice, Hence, the ratio of the slopes of the two curves is
where (′) represents the curve steam-ice curve. Regnault had determined that the latent heat of evaporation and the latent heat of fusion of one pound of water at the freezing point are 606.5 and about 78 or 79 thermal units, respectively, hencea result showing that for any small descent in temperature from the triple point the equilibrium pressure of steam with ice falls off 1.13 times as much as does the equilibrium pressure of steam with liquid water (In today values it is 2375.3 J/kg / 2709 J/kg = 1/1.14) (Thomson, 1873).Using Regnault's experimental data for the variation of pressure with temperature for some changes in state, the numerical value of the left-hand side of eq (17) is 1/1.09, almost the same as that calculated theoretically (Thomson, 1873). The mathematical significance of these numbers is clear: the triple point corresponds to a discontinuity in the curves of phase change and the sublimation curve reaches the triple point with a slope larger than that of the vaporization curve.
The findings of Carnelley and Thomson may be considered the catalyst that catapulted Young, first alone and then with Ramsay, into a vast research of the characteristics of the P-T-V domain of a pure substance and were the subject of most of his publications. On January 1881 Young read a paper before the Chemical Society of the Owens College in which he pointed out that theoretically, at pressures below the triple point of Thomson, water could not exist as a liquid. As mentioned before, Young explanation's was the subject of a letter to Nature in July 14, 1881 (Young, 1881), and in 1884, together with Ramsay, he provided and published the experimental verification of their claim (Ramsay and Young, 1884abc).
A note was published in Chemical News (Young, 1883, 104) describing a simple apparatus built to demonstrate Carnelley's experiment; a further modification was devised in conjunction with Ramsay, which enabled determining the temperature of the ice and calculation of the equilibrium pressure. This new apparatus (Ramsay and Young, 1884c) allowed a very accurate measurement of the vapor pressure of a solid. A barometer tube was nearly filled with freshly distilled and filtered mercury, connected with a triple vacuum pump, and vacuum established. The mercury was then boiled throughout the entire length of the tube, by heating it with a Bunsen burner from below upwards so as to remove air and moisture. After disconnecting the pump some fragments of the solid material were placed on the surface of the mercury and kept in position by means of a coil of platinum gauze. The tube was again exhausted and dry mercury was allowed to flow into the evacuated tube so as to cover the substance and gauze. The tube was then disconnected from the pump and inserted in a trough of dry mercury. This procedure, which allowed complete elimination of air and moisture, was much more convenient than others previously described. The experimental tube was then heated by means of the vapor of substances such as aniline, methyl salicylate, bromonaphthalene, or mercury, to any desired temperature. A very clear drawing of the apparatus appears in the paper by Timmermans (Timmermans, 1947).
Important advantages of the apparatus and its operating method were the fact that temperature was dependent on the pressure, instead of the pressure being dependent on the temperature; the pressure could be easily reduced or increased at will and would remain constant throughout the apparatus. Also, a very large number of observations could be taken simultaneously (Ramsay and Young, 1884c).
The experiments described in the first paper (Ramsay and Young, 1884b) were undertaken in order to ascertain whether solids have definite volatilizing (sublimation) points under different pressures, as liquids have definite boiling points, and whether these pressures are identical with their vapor pressures at those temperatures. Ramsay and Young decided first to study the behavior of ice at low pressures. During freezing the phenomenon of supersaturation was nearly always observed. The temperature fell occasionally as low as –11°C, while the water was still liquid. A sudden formation of ice then occurred and the temperature rose to 0°C. Additional experiments were performed with acetic acid, benzene, naphthalene, and camphor (Ramsay and Young, 1884b).
The results showed clearly that the pressures corresponding to the temperatures of volatilization coincided with the vapor pressure of the solid at the same temperature, that solids have definite temperatures of volatilization, as liquids have definite boiling points, depending on the pressure to which they are subjected, and these are sensibly coincident with those of their vapor pressures. That they cannot be absolutely identical is evident; for there must be a certain excess of pressure to produce a flow of vapor from the evaporating substance to the surrounding space, and consequently the evaporating substance must have a higher temperature corresponding to the higher pressure in its immediate neighborhood (Ramsay and Young, 1884b).
Ramsay and Young provided an interesting explanation of the difference between the evaporation of a liquid and of a solid: When the bottom of a vessel containing a liquid is heated, all the liquid becomes hot owing chiefly to convection currents and evaporation takes place only at its surface. As soon as the temperature reaches the boiling point, either superheating or ebullition must take place. It would thus seem that the surface is not large enough to afford escape for the gaseous molecules hence in the case of supersaturation the temperature of the liquid rises indefinitely whereas in the case of ebullition the liquid surface is increased by the formation of bubbles. Since a solid has a limited surface it might therefore be expected that it will heat up (This was also the explanation given by Carnelley to the existence of hot ice). The rate of evaporation at the surface of a solid can then increase indefinitely and consequently, solids have definite temperatures of volatilization, or volatilizing points, corresponding to definite pressures, as liquids have definite boiling points (Ramsay and Young, 1884b).
In the second paper (Ramsay and Young, 1884c) Ramsay and Young provided an experimental proof of the theory advanced by Thomson (Thomson, 1873) that the pressure exerted by the vapor of a solid substance at a given temperature is less than that of the vapor of the substance in the liquid state at the same temperature. To confirm this theory Thomson used the empirical formulae developed by Regnault to represent the dependence of the vapor pressure with temperature for the equilibrium of water vapor with ice and liquid water, and proved that Regnault's results pointed to a discontinuity in the curve, occurring at a temperature nearly coincident with 0°C, the melting point of ice under normal pressure (Ramsay and Young, 1884c) (the triple point of water is located at 273.16 K and 4.579 mmHg).
Data measured for water, benzene, acetic acid, and water, showed the correctness of Thomson's theory. Since these substances are representative of very different chemical types, the law may be considered to apply to all stable bodies in the liquid and solid states. The results for water, camphor, and benzene showed that the curve representing the vapor pressure of the liquid above the melting point is discontinuous with that of the solid below the melting point. The data for acetic acid were not sufficiently exact to enable a similar comparison (Ramsay and Young, 1884c; 1885d).
For the case of dissociating substances the explanation was more complicated. The abnormal vapor density of many compounds had been ascribed to their dissociating to a greater or less degree while in the gaseous state. The compound molecules yielded, with rise of temperature, a constantly increasing amount of those simpler molecules into which it dissociated. Since dissociation was accompanied by an increase of volume, the vapor density of the mixture of gaseous molecules decreased with an increase in temperature. This phenomenon was not confined to dissociating compounds alone. It was recognized that many, if not all, liquids acquired an abnormal vapor density in the proximity of their point of saturation. The question then arose, for associating liquids, how much abnormality should be attributed to the one cause and how much to the other? In order to answer it Ramsay and Young decided to study and compare the behavior of substances belonging to the four types (a) liquids, the vapor of which are not known to dissociate, (b) liquids, the vapors of which probably dissociate into like molecules, (c) bodies which dissociate gradually in the gaseous state into unlike molecules, (d) bodies which dissociate completely on passage into the gaseous state (Ramsay and Young, 1885e).
Ethanol was chosen as a typical representative of the first class and its behavior fully studied. Measurements were made to establish relations (a) between the volume of the liquid and temperature at various pressures, (b) between the volume of liquid and pressure (compressibility) at various temperatures, and (c) between the volume of unsaturated and saturated vapor, temperature, and pressure. The heats of vaporization were calculated from these data in the range of 13° to 246°C and 10 mmHg to 60,000 mmHg. For ethanol for example, the results indicated that the density of the vapor did not seem to increase with a decrease in temperature; that its critical point lies within 0.5°C from 243.6°C and about 48,900 mmHg, and the critical density is approximately 3.5 cm3 (Ramsay and Young, 1885e).
Experiments were now conducted with substances dissociating in different manners, such as chloral hydrate, butyl chlorate hydrate, chloral methyl alcoholate, choral ethyl alcoholate, ammonium carbamate, ammonium chloride, phthalic acid, succinic acid, aldehyde ammonia, paraldehyde and metaldehyde, nitrogen peroxide, and acetic acid (Ramsay and Young, 1886c). The results indicated that these substances could be divided into two groups: those in which the curves representing the temperature of volatilization and vapor pressures are identical, and those in which these curves are distinct. Members of the first class, such as ammonium chloride, nitrogen peroxide, and acetic acid, behaved like ordinary solids and liquids. Ammonium chloride was nearly completely dissociated 60°C below its temperature of volatilization under normal pressure; nitrogen peroxide was dissociated less than 20% at its boiling point, while with acetic acid it was uncertain whether true dissociation took place. The second group, which contains the rest of the substances studied (with the exception of paraldehyde, which is stable) could be divided into two sections, one in which pressure has no apparent influence on the temperature of volatilization, and the other, in which its influence is partial (Ramsay and Young, 1886c).
In an additional work (Ramsay and Young, 1885a) Ramsay and Young discussed the Clausius-Clapeyron equation, which they wrote in the form
where L is the heat of vaporization of a liquid or solid substance, s2 the volume of the liquid or the solid at the same temperature and s1 that of the gas into which one or the other is converted, and J the heat equivalent of work. Their results led to the statement of the following laws: (a) The amount of heat required to produce unit increase of volume in the passage from the liquid to the gaseous state at the normal boiling point is approximately constant for all bodies, orRamsay and Young provided a table of the value of C for 21 completely different substances; the values vary between 0.2453 for phosphorus chloride to 0.3240 for ethanol. The alcohols, water, and acetic acid give nearly 0.32, and benzene and bodies containing halogens and sulfur give lower numbers averaging 0.2564. Their comment was that “these numbers cannot be regarded as experimental deviations from a constant, but that they have significance can hardly be denied.” (b) If the amounts of heat required to produce unit increase of volume in the passage from the liquid to the gaseous state is compared at different pressures for any two bodies, then the ratio of the amount at the boiling point under a pressure P1, to the amount at another pressure P2, is approximately constant for all liquids. Or, L/s1 − s2 at P1 bears a constant proportion to L/s1 − s2 at P2 for all liquids, and probably for all solids (Ramsay and Young, 1885a).
Other projects included the determination of the thermal properties of several liquids and their mixtures (ethyl ether, methyl, ethyl, and propyl alcohols, acetic acid, and a mixture of ether and ethyl alcohol) (Ramsay and Young, S., 1885e, 1886ab; 1887abc; 1890). The results showed that at constant volume the relation between the temperature and vapor pressure of a liquid was well represented by the formula P = bT – a, where b and a are constants depending on the volume. It was found, however, that the relations between pressure and volume are not accurately represented by van der Waals’ equation of state, although the above expression may he deduced from that equation. Later Young found that in most cases the relationship just mentioned was not strictly true except at large and possibly at very small volumes. Additional data were measured for methanol, ethanol, acetic acid, and nitric peroxide and showed the correctness of the relation P = bt – a, for both gases and liquids (Ramsay and Young, 1887d).
An interesting result was that Ramsay and Young proved that the data reported by Regnault for the vapor pressure of mercury (Regnault, 1862) were too low at high temperatures (Young, 1891).
The law of rectilinear diametersIn 1886, Louis Paul Cailletet (1831-1913) and Émile Mathias (1861-1942) reported that they had constructed a very simple apparatus made out of glass, capable of supporting pressures of several hundreds atmospheres, and used it for measuring the density of the vapor and liquid phases of a pure compound as it approaches its critical point (Cailletet and Mathias, 1886; 1887). A plot of their experimental results of the density for N2O, ethylene, and CO2, showed that the mean density of both phases decreased linearly with the temperature and that the straight line drawn through the middle point of the chords went through the critical point. This result suggested employing the line to determine the critical temperature and density of a gas using measurements below the critical point. This work was considered quite an achievement because of the experimental difficulties involved in measuring the critical volume accurately. Cailletet and Mathias believed that their method yielded the value of the critical volume within 1% of the real one.
This finding is known today as the Cailletet-Mathias law of the rectilinear diameters, and may be expressed as
where Dt and D0 are the means of the densities at t° and 0°C, respectively, and α is the slope of the straight line passing through these means.In 1892 Mathias and Young (Mathias, 1892; Young, 1892ab; 1900) demonstrated independently that if van der Waals’ principle of corresponding states is correct, then the value of α should be directly proportional to the critical densities and inversely proportional to the absolute temperatures, that is, for any substance
orAccording to Mathias to test the validity of the law of corresponding states it was only necessary to establish whether a is really a constant.
In a following work (Mathias, 1892b), Mathias wrote that Émile Hilaire Amagat (1841–1915) had also confirmed the validity of the law of rectilinear diameters for carbon dioxide (Amagat, 1892), and that the results of Young (Young, 1892ab) for twelve widely different substances could be used as the definite proof of the validity of the law because they covered the very large distances of 300° and 325°C from the critical temperature. According to Mathias, an important consequence of all the studies regarding the behaviour of the temperature variation of the densities of the saturated liquid and of the saturated vapor was that both curves converged smoothly to a common limit, located at the critical temperature. In other words, at the critical point the system was homogeneous and not heterogeneous as some others claimed.
A second important consequence was that the value of the critical density determined by the law of rectilinear diameters was substantially different from the critical volumes measured directly by Ramsay and Young, reaching 20% for the case of fluorobenzene: 0.4111 according to Young and 0.3514 according to the law. For Mathias, this substantial difference was an additional proof of the difficulties involved in the direct precise measurement of the critical volume.
The above arguments, coupled with his own research on the critical density, led Young to investigate the ability of the law of rectilinear diameters to predict the critical density more accurately that by direct measurement of the critical volume. According to Young (Young, 1900) the law of Cailletet and Mathias had been found to hold good for a considerable number of substances from the boiling-point to the critical point, and Mathias, making the very natural assumption that the law may be relied upon at lower temperatures, had calculated the value of α from the mean densities below the boiling point.
Mathias then discussed the methods available, notably that of Thomas Edward Thorpe (1845-1925) and Arthur William Rücker (1848-1915), for estimating the critical temperature for the cases where it had not been measured directly. According to Thorpe and Wicker, the critical temperature could be estimated according to
where d1 and d2 are the densities at the temperatures T1 and T2, respectively, and A a parameter that Thorpe and Rücker estimated to have the value 1.995 for all substances.According to Mathias if in Thorpe and Rücker's formula A took the value 2, then it followed that a = 1 and it would then be possible to ascertain both the critical density and the critical temperature by a geometrical method. In most cases, however, the value of A was different from 2 and that of a different from unity, making the geometrical method inapplicable.
For these reasons Young decided to undertake a careful examination of the data that he had measured for thirty substances (Young, 1892ab). In every case, except the alcohols, he calculated the critical densities using the method of Cailletet and Mathias for the temperature range between the normal boiling point and the critical temperature. Although the deviations from the formula Dt= D0 + αt differed sometimes considerably, there did not appear to be any definite tendency to curvature and Young attributed the deviations to the experimental error (Young, 1900). Young repeated the experimental measurements, this time measuring the densities of all thirty substances at intervals of ten degrees between 0° and the boiling point, and found that for many of the substances the deviations increased rapidly below the boiling point. Moreover, on plotting all the differences between mean densities and those calculated from the formula Dt= D0 + αt against the temperature, distinct curvature was noticeable in many cases. The results became well correlated by the parabolic equation Dt= D0+αt+βt2, instead of the straight line recommended by Cailletet and Mathias. Of the thirty substances studied, only for n-pentane the mean density was represented by eq (20). For the alcohols the curvature was so pronounced that a fourth term γt3 had to be introduced into the formula to reproduce the data. Interesting enough, although for the whole temperature range investigated the agreement with the three-constants formula was much better than with the simpler one, for the range of temperatures between the normal boiling point and the critical temperature there was no significant difference between both formulae and the critical density could be calculated using the law of rectilinear diameter with an error rarely exceeding 0.25% and generally not exceeding 0.1%. Nevertheless, Young concluded that in order to find the critical density with the greatest possible accuracy it would be best to use all the available data and to employ the formula with three constants (Young, 1900).
According to Young (Young, 1900) there was a definite relation between the ratio Dc/Dcalc (where Dc= Pc/RTc and Dcalc is the calculated density) and the value of β in the modified Cailletet-Mathias law. The curvature of the curve of the mean densities changes in such a manner that α passes from a positive value, through zero, to a negative value while α and Dc/Dcalc increase monotonously. According to van der Waals Dc/ Dcalc should be equal to 2.67 while the actual values ranged from 3.68 to 3.86 for the normal substances studied.
According to H. Davies, the molecular inductive and refractive powers should be related to the critical constants; for example, Phillipe Auguste Eugène Guye (1862-1922) (Guye, 1890) had shown that for some gases and liquids the molecular refractive power is 1.8 times the critical coefficient Tc/Pc. Although no theoretical basis was known for this relationship, one could be obtained using the fact that Young had calculated the value of Dc/ Dcalc for many substances and ’ found that its average value was 3.7. Calling υc the ideal critical molar volume
so thatThe molecular inductive power is then given by
where Pc is measured in atmospheres. The molecular refractive power therefore has a constant ratio of 2.3 to the critical coefficient. Davies used these relations to calculate the molecular inductive power for benzene, carbon disulfide, carbon tetrachloride, cymene, toluene, naphthalene, o-xylene and aniline, and showed that the mean value was 2.43, that is 5% above the theoretical one (Davies, 1912).Davies also used Young's data on the covolume to derive the following expression:
This equation enables π to be calculated from the known values of vc, π, and R, Substituting α for its value 1/(2Tc– T) we get
The value of π at absolute zero is thus given by 8RTc/υc If Young's value of the ratio of the ideal to the actual critical volume is taken this reduces at once to 29.6Pc. Apparently π should vanish at the temperature T = 2Tc. This formula can, however, only be approximate as P approaches Pc:
a very simple relation (Davies, 1912).DistillationDiscovery of the American oil fields and the beginning of their exploitation in the second half of the nineteenth century led to the search for better methods of separation of the different fractions. Young's work with Ramsay on the critical constants of pure compounds stressed the importance of dealing with pure substances, so special attention was devoted to methods of purification. Young undertook a systematic study of the behavior of mixed liquids when distilled and the design of better fractionation columns. Together with G. L. Thomas in 1897 he devised a dephlegmator based on principle of the Aeneas Coffey still (Note 2). This new device, coupled with a regulated temperature still head, enabled them to separate and prepare for the first time pure specimens of n-pentane (boiling point 34.5°C) and isopentane (boiling point 29.0°C), both of which are present in light petroleum.
Fractional distillation of American petroleum showed that its composition was very similar to the oils extracted from the Russian and Galician fields, the only difference being the relative proportions of paraffins, polymethylenes, and aromatic hydrocarbons present. The thermal constants of hexamethylene, di-isopropyl and di-isobutyl were determined with Emily C. Fortey in 1899 and 1900 (Young and Fortey, 1899, 1900). n-Hexane, prepared from the fractionation of benzene-free petroleum, cannot be separated from isohexane and methylpentamethylene by fractional distillation. In 1898, however, Young and Francis Ernest Francis used fuming nitric acid to remove isohexane and methylpentamethylene and separate pure n-hexane isolated from petroleum for the first time (Young and Francis, 1898).
In 1933 the Petroleum Division of the American Chemical Society wrote to Young expressing their high appreciation of his work on distillation, on the composition of petroleum, and on the determination of the physical properties of numerous hydrocarbons (Francis, 1937).
The series of studies of the vapor pressures and boiling points of mixed liquids began in 1902 led to the discovery of new binary and ternary azeotropic mixtures not reported by Lecat (Lecat, 1918). The most important of these findings was the existence of ternary azeotropic mixtures of the lower alcohols, except methanol, with benzene or n-hexane and water. Particularly interesting was the ternary azeotrope formed by ethanol, water, and benzene. The system ethanol + water has a minimum temperature azeotrope (78.15°C) that cannot be separated by distillation. Young found that addition of benzene resulted in the formation of a minimum temperature ternary azeotrope (64.85°C). The components could then be separated using the fact that benzene and water have a very small mutual solubility. This discovery led to the development of a commercial process for manufacturing anhydrous ethanol, which was first adopted by the firm of C.A.F. Kahlbaum, Chemische Fabrik, Berlin, and later by others. Young's method has since been applied to other liquids, and to the preparation of anhydrous solids; it is widely used in analytical practice for the determination of water in solids (Young and Fortey, 1902; Young, 1922).
Notes1. It is often claimed that one can skate on ice because the pressure of the skate causes the ice to melt, thus dramatically reducing the friction between skate and ice. However, the effect is a small one, using eq (1) we can calculate that to lower the melting point of ice from 0° to –1°C requires application of a pressure of near 121 atmospheres (1.22 MPa). A skater weighing 75 kg and wearing a skate 3 mm wide and 20 cm long, will exert only a pressure of about 12 atmospheres, shifting he melting temperature of the ice by a few tenths of a degree. Since common experience is that ice-skating is possible even when the ambient temperature is well below the normal freezing point, the pressure induced lowering of the melting point clearly does not explain this every day observations.
Van Hove et al. (Matterer et al., 1997; Van Hove, 2004), claim that the phenomena is due to the fact that ice is intrinsically slippery, it has a quasi-fluid layer that coats the surface and provides a permanent lubricant. When pressure is applied, the molecules in the layer compact into underlying interstices, or spaces in the ice structure, and create a smooth surface for easy gliding. The ‘quasi-fluid layer’ is not actually liquid water but ice molecules vibrating very rapidly. The surface ice molecules have an unusually high degree of vibrational motion, several times that of the molecules deeper in the bulk of the ice, which is only in the up and down direction. The quasi-fluid layer may be thicker or thinner depending on the temperature. Lower temperatures give rise to fewer layers whereas if the ice is warmer, the number of slippery layers increases. At around –20°C the ice drastically decreases in slipperiness so it just about resembles any other solid. Under –160°C, the layer is as little as one molecule thick.
Others claim that frictional heating provides the slippery property. Like snow skis, ice skates are warmed by sliding and then cool when the sliding stops. The temperature increases with speed and with thermal insulation. Another reason to reject the pressure melting mechanism is that the pressure needed to reach the melting temperature is above the compressive failure stress and, if it did occur, high squeeze losses would result in very thin films. Pure liquid water cannot coexist with ice much below -200C at any pressure and friction does not increase suddenly in that range. If frictional heating and pressure melting contribute equally, the length of the wetted contact could not exceed 15 μ at a speed of 5 m/s, which seems much too short. If pressure melting is the dominant process, the water films are less than 0.08 μ thick because of the high pressures (Matterer et al., 1997; Van Hove, 2004).
2. The Coffey still (also know as the Patent Still) was invented in 1830 by Aeneas Coffey, a retired government excise Inspector in Ireland. This still made possible the continuous distilling of grain alcohol. In the original patent it was described as a kind of “warmth exchanger made of two columns called respectively the analyzer and the rectifier”. The Coffey still made possible for the scotch industry to put on the market a product able to compete with the French cognac, which at that time was in a very bad situation due to the catastrophe of the phylloxera. The Coffey still produces whiskey faster and more cost efficiently than a pot still.
Modern variations of the original Coffey still are more efficient and are generally called column stills.