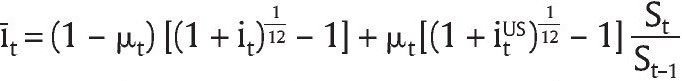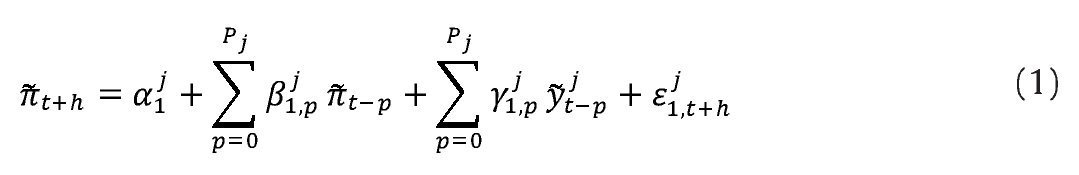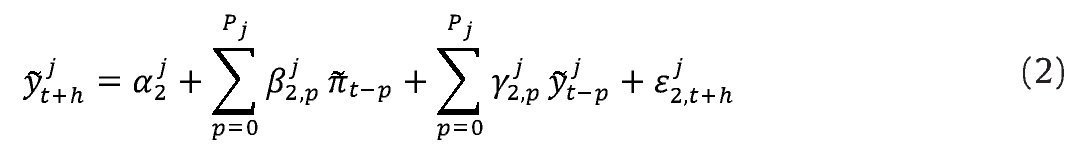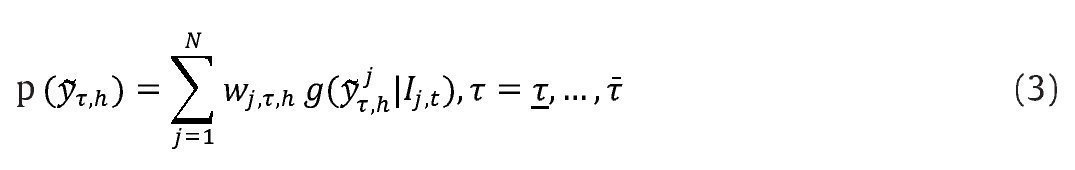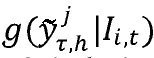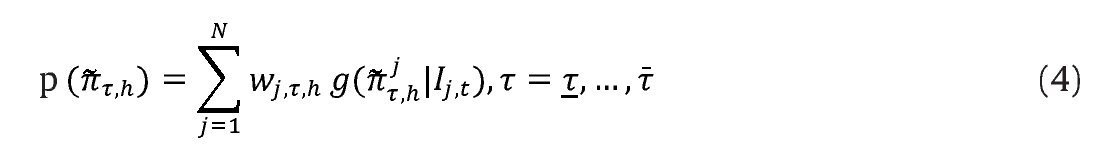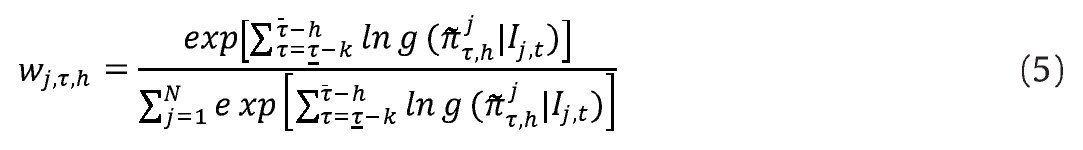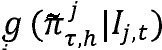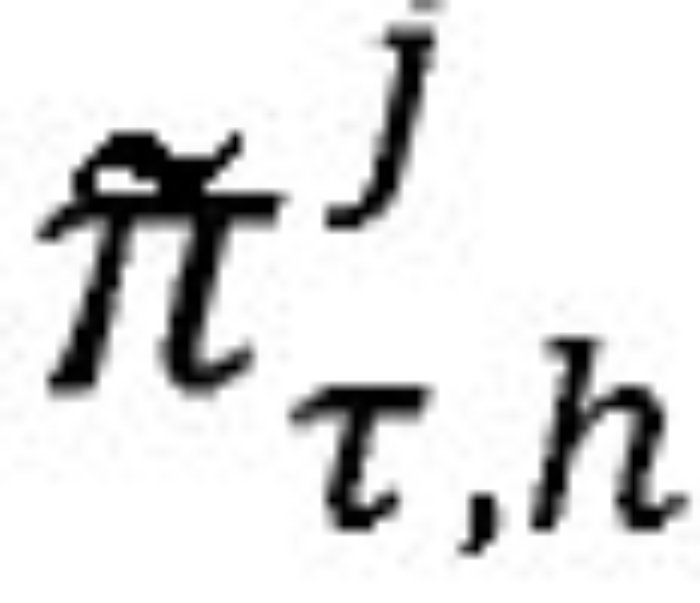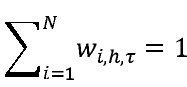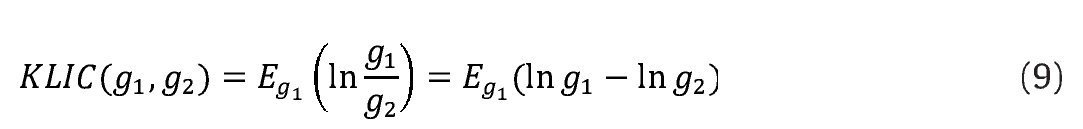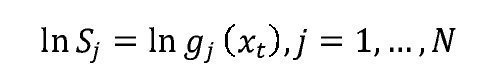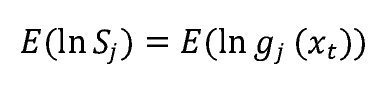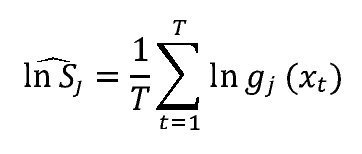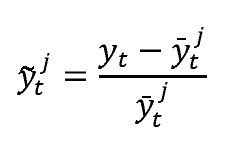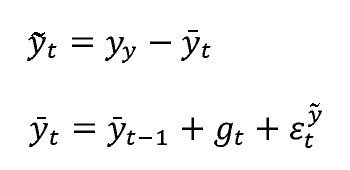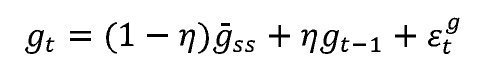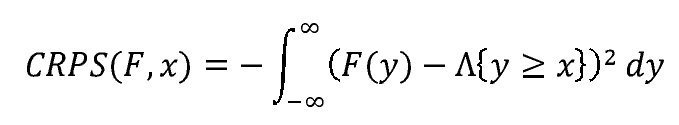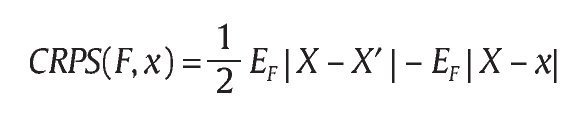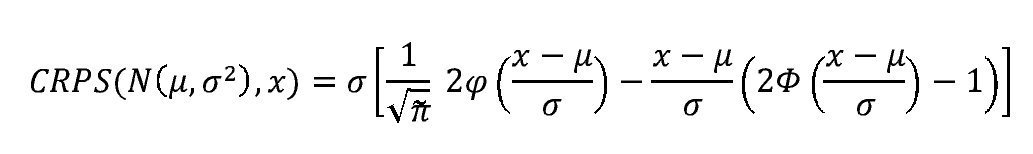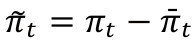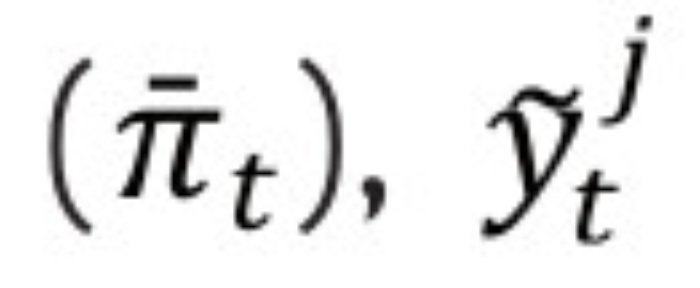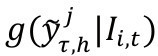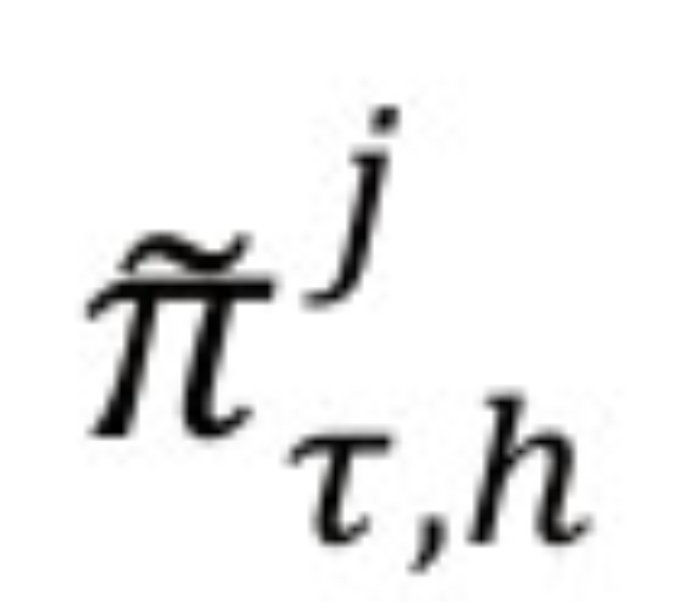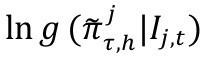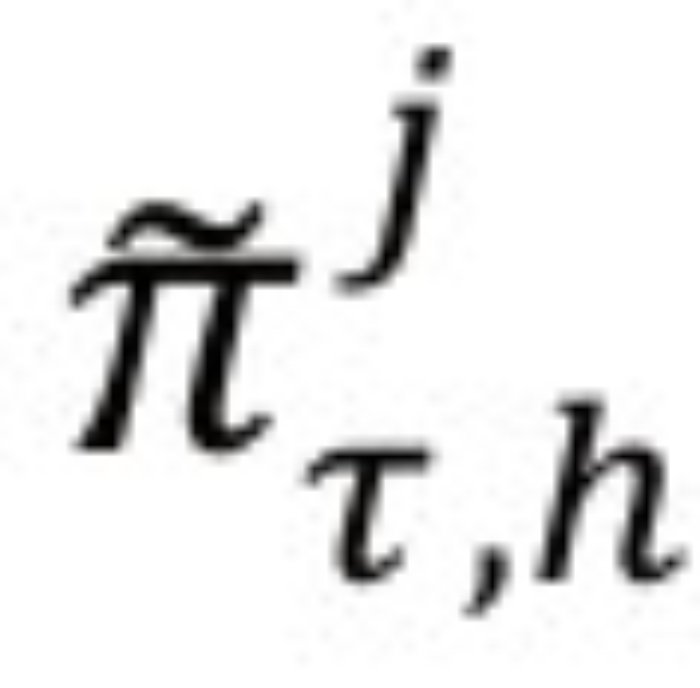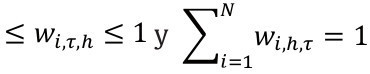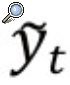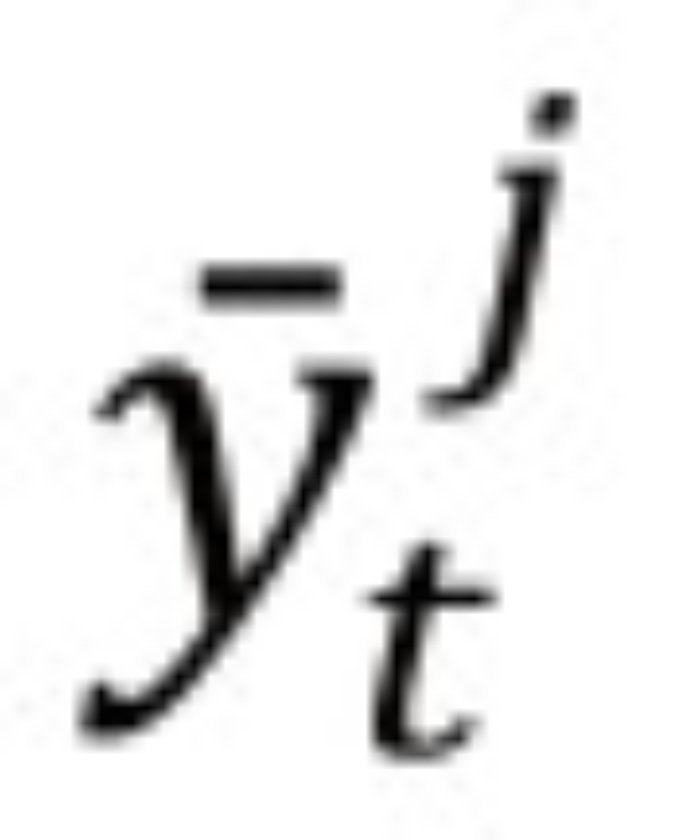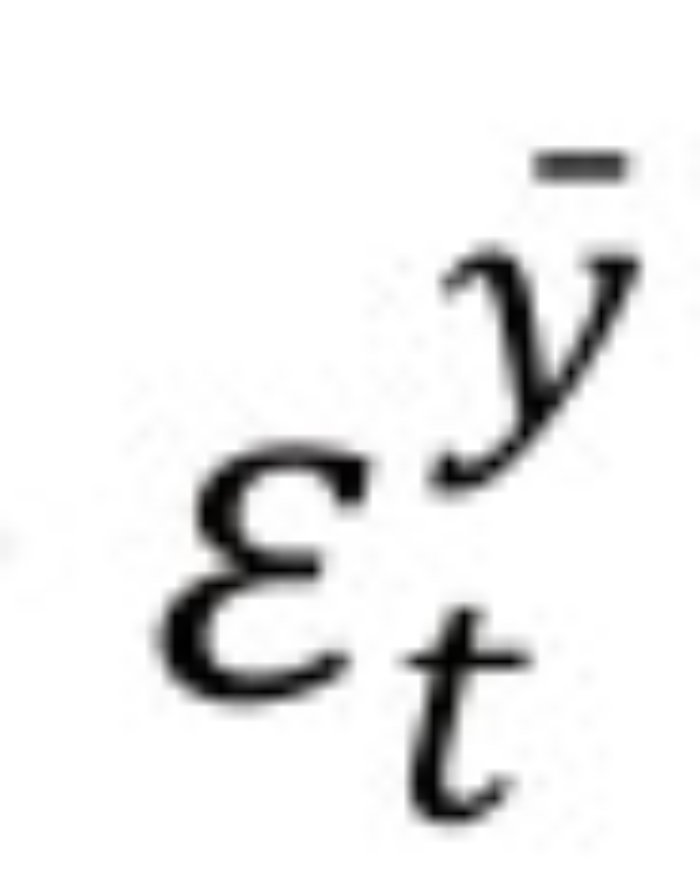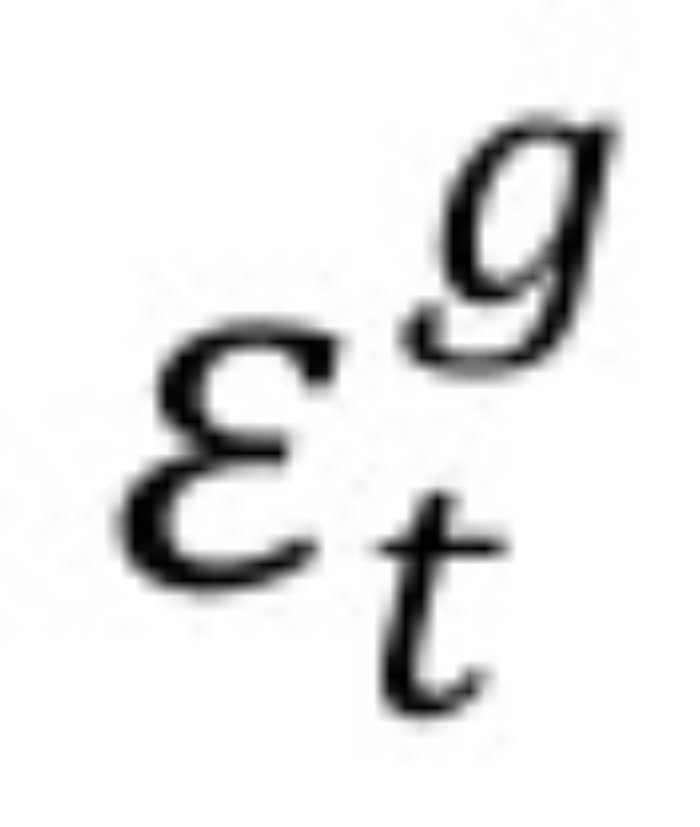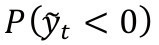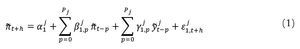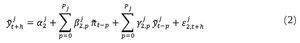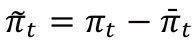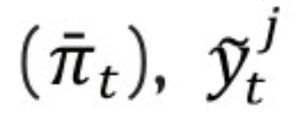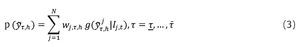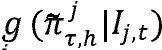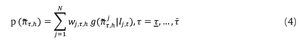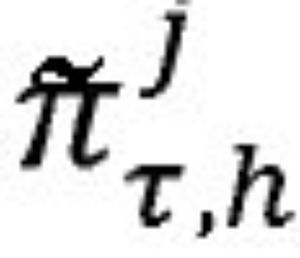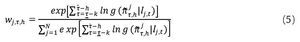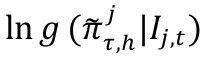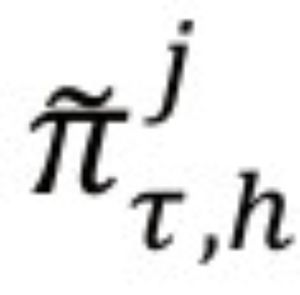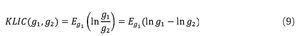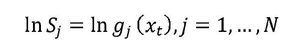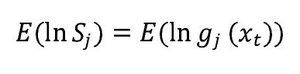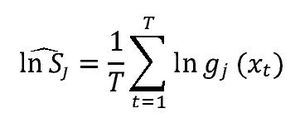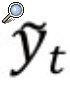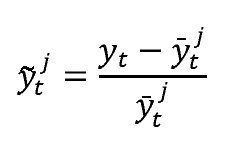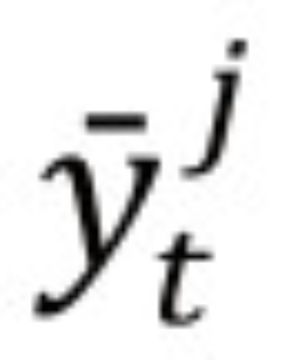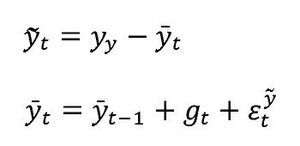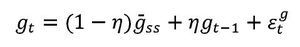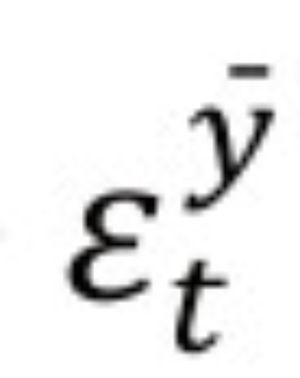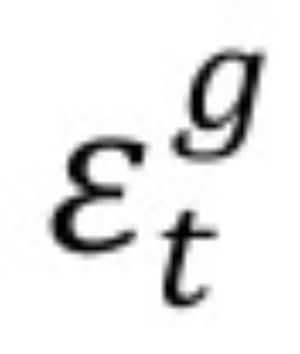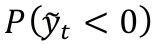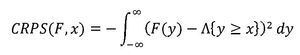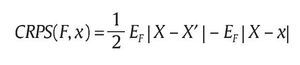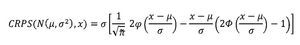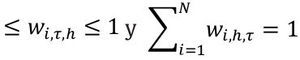Este documento combina estimaciones de 8 metodologías de la brecha del producto colombiano para el período comprendido entre el primer trimestre de 1994 y el tercer trimestre de 2012. A partir de modelos vectoriales autorregresivos que incluyen las diferentes brechas y la inflación, se construyen las densidades combinadas de pronósticos de la brecha mediante el uso de 3 esquemas de ponderación: logarítmicos, basados en puntuaciones de rango de probabilidad continuo y en el error cuadrático medio; estas densidades de la brecha resultan útiles porque proveen indicios de su tendencia central a la vez que caracterizan su incertidumbre. Los resultados sugieren que las densidades combinadas bajo estos 3 esquemas con horizontes de pronóstico de 1, 2, 3 y 4 trimestres adelante están bien especificadas. Adicionalmente, las puntuaciones logarítmicas calculadas sobre estas densidades muestran que las metodologías basadas en ponderadores logarítmicos son las que presentan mejor desempeño, y para horizontes de pronóstico de 2 y 3 trimestres, tienen significativamente una mayor puntuación que las calculadas por los ponderadores basados en puntuaciones de rango de probabilidad continuo y error cuadrático medio.
This paper combines eight estimations of the Colombian output gap for the time period between the first quarter of 1994 and the third quarter of 2012. The combined forecast densities of the gap are obtained by using bivariate VAR models that include the different gaps and inflation, and using three weighting schemes: logarithmic scores, continuous probability range scores (CRPS) and mean square error criteria (MSE), these output gap densities are useful because they provide an insight of the gap's central tendency, while characterizing the uncertainty. The results suggest that the combined densities under these three schemes for one, two, three and four quarters ahead are not miss-specified. Additionally, the combined density based on logarithmic weights has the best performance for all horizons. For two and three quarters ahead there are significant higher scores for the logarithmic weights methodology that those calculated by CRPS and MSE weights.
1. Introducción
La formulación de la política monetaria exige tener información adecuada acerca del estado de la economía, en particular, sobre la brecha del producto. Adicionalmente, se debe tener en cuenta que esta variable no es observable y que aun contando con diferentes estimaciones de la misma, estas nunca podrán ser contrastadas con valores observados. Esto genera un costo adicional para los encargados de la política económica puesto que tiene asociado un mayor grado de incertidumbre en la toma de decisiones.
Dada la característica de no observabilidad y las múltiples metodologías de estimación de la brecha, una pregunta relevante es cómo se pueden combinar dichas estimaciones para obtener una sola que contenga la información de todas las estimaciones consideradas. Es importante notar que este documento se centra en el análisis de los pronósticos de la brecha, ya que estos tienen mayor relevancia para la toma de decisiones. Adicionalmente, no se consideran los pronósticos puntuales, sino los de densidad, los cuales proveen mayor información puesto que a través de estos se puede obtener una descripción completa de la incertidumbre asociada a dichos pronósticos (Hall y Mitchell [2007] y Tay y Wallis [2000]).
Los pronósticos de densidad de la brecha del producto permiten la construcción de gráficos de concentración de la masa de probabilidad de la brecha combinada, a la vez que el cálculo de la pro babilidad de que esta sea negativa a lo largo de un período particular. Estos elementos ayudan a entender la dinámica pasada y futura de la brecha, lo cual es útil para definir el direccionamiento de la política monetaria.
Diferentes estudios muestran que la combinación de pronósticos de densidad brinda mayor información y mejor desempeño que las densidades individuales de pronóstico. McDonald y Anders (2011) encuentran que combinar densidades de pronóstico del producto interior bruto y la tasa de cambio en Nueva Zelanda tiene un mejor desempeño comparado con las densidades de pronóstico individuales para las mismas variables. Este mismo resultado es obtenido por Hall y Mitchell (2007) al combinar los pronósticos de densidad de inflación del Banco Central de Inglaterra y el National Institute of Economic and Social Research y compararlos con los pronósticos individuales.
Este trabajo se compone de 4 secciones, siendo la primera esta introducción. En la segunda se presenta la metodología que se debe utilizar para la combinación y obtención de los pronósticos de densidad. La tercera sección muestra la aplicación para las series de la brecha del producto colombiano. Finalmente, en la cuarta se presentan las conclusiones.
2. Metodología
2.1. Modelo
Los métodos de combinación de densidades de pronóstico suponen que se tiene información sobre el pronóstico y el error de pronóstico1.Sin embargo, para una serie no observable como la brecha del producto, no se tiene lo segundo. Para evitar este inconveniente, Garratt, Mitchell y Vahey (2009) y Orphanides y van Norden (2002) proponen utilizar el siguiente modelo que relaciona la brecha con una variable observada, en nuestro caso, la brecha inflacionaria2:
Donde
denota la brecha entre inflación (πt) y la meta fijada por el Banco de la República
denota las diferentes medidas de la brecha del producto, h el horizonte de pronóstico y j = 1,2, ... , N indica el método utilizado para extraer la brecha del producto. En conjunto, las ecuaciones (1) y (2) conforman un modelo vectorial autorregresivo (VAR), el cual facilita el cálculo de las densidades de pronóstico.3
Nótese que la anterior representación implica que para cada brecha del producto en consideración hay un modelo VAR diferente; en particular, el número de rezagos puede variar. Cada modelo VAR es utilizado para pronosticar h pasos adelante tanto la brecha de inflación como la del producto, y para calcular las varianzas de los errores de pronóstico generados.
Una vez estimado el modelo VAR descrito en las ecuaciones (1) y (2), se construyen los ponderadores para calcular la combinación de las brechas del producto a partir de las funciones de densidad de pronóstico de la brecha de inflación. Este procedimiento se describe en detalle en las secciones posteriores.
2.2. Combinación y ponderación
Dados los N modelos VAR indicados en (1) y (2) y sus respectivas densidades de pronóstico, la densidad combinada se calcula por medio de una combinación lineal convexa4 definida de la siguiente forma:
Donde
es la densidad de pronóstico h-pasos adelante del modelo j de la brecha del producto, yτ denota el período de evaluación.
De manera análoga para las densidades de pronóstico de la brecha de inflación, podemos definir la combinación lineal como:
Donde
son los pronósticos de la brecha de inflación h pasos adelante, obtenidos a partir de una representación VAR en la que se ha utilizado la serie de la brecha del producto.
El anterior esquema de combinación, basado en el trabajo pionero de Stone (1961)5, presenta la característica de que aunque se combinen densidades de pronóstico gausianas, la densidad combinada no necesariamente es normal y puede ser multimodal, Kascha y Ravazzolo (2010).
Dentro de este tipo de esquemas, la densidad combinada es determinada por los ponderadores wj,τ,h. Siguiendo trabajos como los de Bache, Jore, y Mitchell (2001); Jore, Mitchell y Vahey (2010); Garratt et al. (2009) y Garratt, Mitchell Y Vahey (2011), una alternativa usual en la literatura es suponer que las ponderaciones están basadas en el esquema de ponderación logarítmico (o recursivo logarítmico), el cual se deriva de una perspectiva bayesiana emulando el concepto de Bayesian Model Averaging y, en particular, de las probabilidades a posteriori de los modelos que se han de combinar6:
Donde k representa un período a través del cual se inicializan los ponderadores y
es el logaritmo de la función de densidad evaluada en
El logaritmo de la función de densidad evaluada en el valor observado de la variable se conoce en la literatura como puntuación logarítmica y, en general, brinda valores numéricos a través de los cuales se puede evaluar la calidad de un pronóstico de densidad, Gneiting y Raftery (2007). En particular, la puntuación logarítmica ofrece ventajas conceptuales y eventualmente puede facilitar la comparación entre diferentes densidades de pronóstico.
Garratt et al. (2009) comentan que el uso del esquema de ponderación basado en las puntuaciones logarítmicas es apropiado puesto que asigna una alta puntuación a un pronóstico de densidad asociado a probabilidades altas de los valores observados. Sin embargo, por la naturaleza de las puntuaciones logarítmicas, las ponderaciones podrían llegar a tener comportamientos extremos y ser sensibles a valores atípicos.
De manera alternativa al esquema de ponderación logarítmico, en la literatura se ha identificado el uso de otros esquemas diferentes. Por ejemplo, el esquema de ponderación basado en puntuaciones de rango de probabilidad continuo (CRPS, en inglés continuous ranked probability score), donde los ponderadores están dados por7:
El esquema de combinación CRPS, desarrollado en Bjorland, Gerdrup, Jore y Smith (2011), utiliza puntuaciones con rango de probabilidad continuo en lugar de puntuaciones logarítmicas. Estas puntuaciones son menos extremas ante la presencia de datos atípicos.
Otro método de ponderación se basa en los errores cuadráticos medios, (Kascha y Ravazzolo, 2010). En esta metodología, los ponderadores para la densidad j en el horizonte h y el período τ están dados por:
Garratt et al. (2009) y Garratt et al. (2011) proponen calcular las ponderaciones wj,τ,h utilizando el método de ponderación logarítmico sobre las densidades de pronóstico de la brecha de inflación y, posteriormente, utilizar estos ponderadores en la combinación de las densidades de la brecha del producto.
2.3. Evaluación de las densidades de pronóstico
La evaluación de las densidades de pronóstico se puede realizar por medio de diversos métodos. Como primer paso, se debe verificar si las densidades están correctamente especificadas (Berkowitz, 2001 y Diebold, Gunther y Tay, 1998).
Las pruebas utilizadas para verificar si las densidades están especificadas de forma correcta se fundamentan en el concepto de la transformación integral de probabilidad (PIT en inglés probability integral transform), la cual está definida de la siguiente forma:
Donde gh (u) es la función de densidad de pronóstico para horizonte h y
es la brecha de inflación en el período τ. Se considera que una densidad de pronóstico está correctamente especificada si la serie zτ,h se distribuye uniforme en el intervalo [0,1] y si para los pronósticos, un paso adelante es i.i.d, Diebold et al. (1998).Otra prueba de evaluación sugerida en Mitchell y Hall (2005), Bao, Lee, y Saltouglu (2007) y Amisano y Giacomini (2007) se basa en la pseudodistancia8 o medida de divergencia Kullback-Leibler, la cual compara 2 densidades de la siguiente forma:
Siendo g1=g1(χt) y g2=g2(χt) funciones de densidad de pronóstico continuas, y E el valor esperado.
El análisis de las estadísticas de la medida de divergencia Kull-back-Leibler con respecto a la función de densidad verdadera se puede realizar a través de puntuaciones logarítmicas, definidas de la siguiente forma:
Tomando el valor esperado en la anterior expresión, se tiene como resultado:
Y bajo ciertas condiciones de regularidad, este valor esperado puede ser estimado consistentemente por el siguiente estadístico:
Las puntuaciones logarítmicas tienen la característica de que su función de divergencia es la pseudodistancia Kullback-Leibler, Gneiting y Raftery (2007). Además, observando la ecuación (9), se puede deducir que si E(ln g1) > E(ln g2) entonces KLICg1 < KLICg2, siempre y cuando la medida de divergencia Kullback-Leibler haya sido medida con respecto a la densidad verdadera, la cual es común a g1 y g2. Interpretando lo anterior, se puede afirmar que si la puntuación logarítmica de g1 es más grande que la de g2 entonces hay una menor divergencia de g1 con respecto a la densidad verdadera. Por lo tanto, se concluye que funciones de densidad con puntuaciones logarítmicas más altas implican una menor divergencia con respecto a la densidad verdadera y, por consiguiente, son una mejor aproximación a esta última.
Es importante notar que dado que no se conoce la brecha observada del producto, el uso de las pruebas anteriormente sugeridas se limita a la evaluación de las densidades de pronóstico de la inflación.
3. Ejercicio empírico
El ejercicio empírico utiliza diferentes estimaciones de la brecha del producto colombiano para construir la combinación de densidades de pronóstico para el período trimestral comprendido entre 1994:1 y 2012:3. A continuación se describen las brechas utilizadas.
3.1. Medidas de la brecha del producto
La brecha del producto,
es definida como la diferencia porcentual entre el producto observado y el producto potencial, como sigue:Donde yt es el producto observado en el momento t y
denota su tendencia o nivel potencial extraído por el método j. Con base en los trabajos de Cobo (2007), González, Ocampo, Pérez, y Rodríguez (2012) y Rodríguez, Torres y Velasco (2006), se consideran las siguientes estimaciones de la brecha del producto:
1.Filtro de Hodrick-Prescott: se utiliza la metodología propuesta por Hodrick y Prescott (1997), utilizando un parámetro de suavización λ = 1600.
2. Filtro de Hodrick-Prescott con restricciones: la metodología de Hodrick-Prescott con restricciones sigue los mismos lineamientos que la metodología de Hodrick y Prescott (1997). Sin embargo, bajo este enfoque el problema de minimización está sujeto a un conjunto de restricciones en algunos períodos específicos de acuerdo con el consenso de expertos sobre el comportamiento de la brecha. Para mayores detalles, véase Cobo (2007).
3.Brecha adaptativa: este modelo supone que el producto potencial se comporta de acuerdo con un modelo de tendencia local lineal (Harvey y Proietti [2005]) e incluye un conjunto de ecuaciones basadas en teoría económica donde se asume que las expectativas se forman de manera adaptativa. La brecha del producto es extraída usando el filtro de Kalman a partir de las ecuaciones del modelo. Algunos parámetros del modelo son fijos y determinados de acuerdo con consideraciones de expertos, mientras que otros son estimados por medio de técnicas bayesianas. El modelo de tendencia local lineal en su forma básica se compone de las siguientes ecuaciones:
Siendo gt la tasa de crecimiento del componente tendencial de la brecha del producto, el cual a su vez sigue la siguiente dinámica:
Donde
y
son perturbaciones gausianas i.i.d. Las anteriores ecuaciones son complementadas con una curva IS, una curva de Phillips, una condición de la paridad de la tasa de interés y un conjunto de ecuaciones que describen la dinámica de la tasa de interés y de cambio reales. Esta metodología es descrita en detalle en González et al. (2012).
4.Brecha racional: se considera un conjunto de ecuaciones similar al construido en el ítem anterior. Sin embargo, la principal diferencia de este modelo radica en el supuesto que se asume para la formación de las expectativas, las cuales ahora se consideran racionales. Esta metodología también es descrita en González et al. (2012).
5. Componentes principales: en esta metodología, se estima un indicador de la brecha del producto utilizando componentes principales, los cuales resumen de manera eficiente la información disponible sobre la actividad económica. Para mayor detalle, véase Rodríguez et al. (2006).
6.Promedio móvil del filtro de Hodrick-Prescott con restricciones: bajo esta metodología se calcula un promedio móvil de orden 4 sobre la brecha de producto calculada por medio del filtro de Hodrick-Prescott con restricciones.
7.Función de producción: este método modela la tecnología productiva mediante una función Cobb-Douglas que incorpora información sobre el tamaño de la fuerza laboral, el acervo de capital y sus niveles de utilización. Finalmente, se calculan las versiones no inflacionarias de estas variables mediante diferentes tipos de filtros con el objetivo de estimar un producto interior bruto potencial no inflacionario consistente con los niveles de los factores productivos de la economía. Véase Cobo (2007).
Adicionalmente, se utiliza la media aritmética de las 7 medidas de la brecha del producto anteriormente mencionadas. La figura A1 del Anexo A presenta la evolución de las brechas del producto durante el período de análisis. Esta gráfica muestra que aunque se presenta un comportamiento común, las medidas difieren considerablemente entre sí en ciertos períodos. De las diferentes medidas en consideración se observa que las brechas del producto calculadas por medio del filtro de Hodrick-Prescott restringido y la función de producción son las que presentan mayor variabilidad. Por otro lado, la brecha del filtro de Hodrick-Prescott presenta un comportamiento un poco diferente a las demás estimaciones al inicio del período de análisis; sin embargo, este patrón no se cumple al final de la muestra.
3.2. Pronósticos de densidad
Los pronósticos de densidad se basan en los pronósticos directos del modelo VAR especificado en (1) y (2). El número de rezagos de estos modelos fue seleccionado de acuerdo con el criterio de información de Schwartz. Los modelos son estimados inicialmente con información hasta el segundo trimestre de 2002. Posterior a la estimación se realizan pronósticos a 1, 2, 3 y 4 trimestres adelante y se calculan las varianzas de los errores de pronóstico. Tras haber realizado los pronósticos, se adiciona un trimestre de información y se reestiman los parámetros de los modelos para obtener de nuevo pronósticos hasta 4 trimestres adelante y las varianzas de sus errores asociados. El ejercicio continúa de forma recurrente hasta el final del período de evaluación que corresponde al tercer trimestre de 2012.
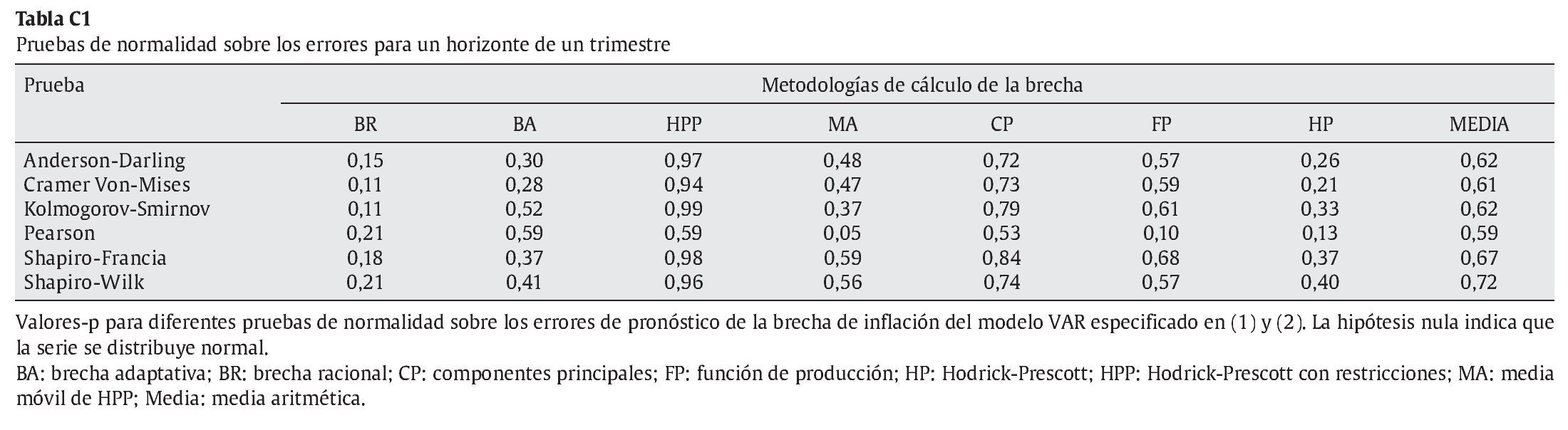
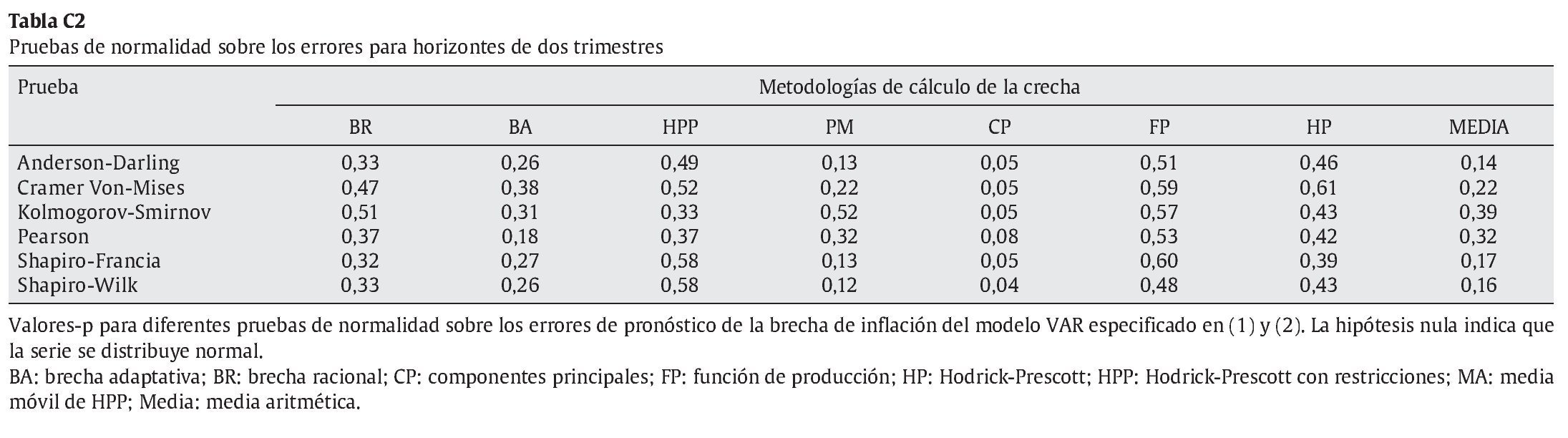
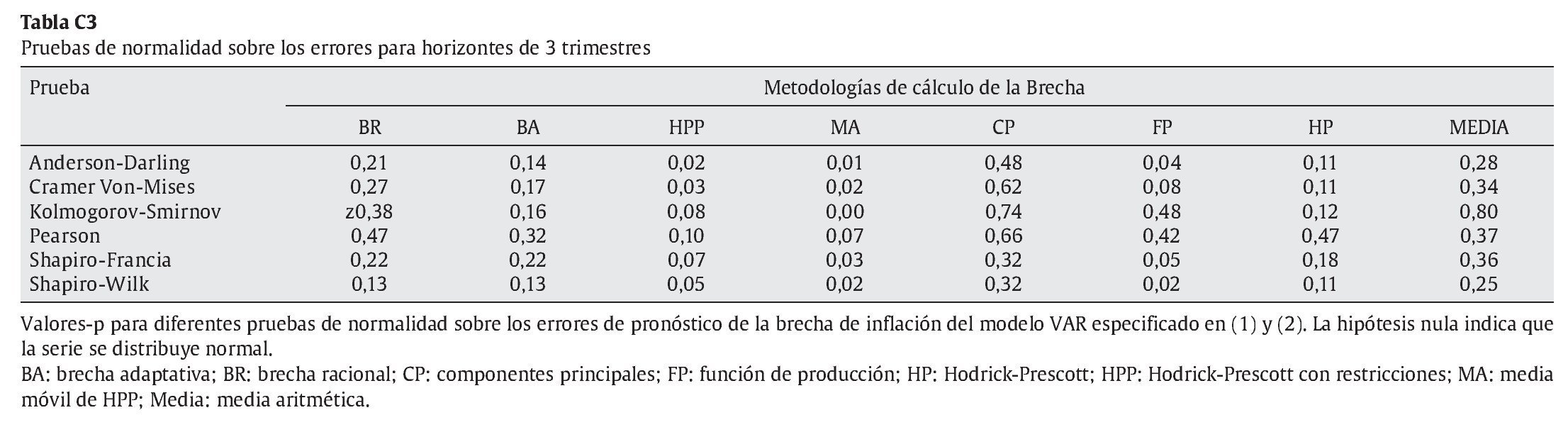
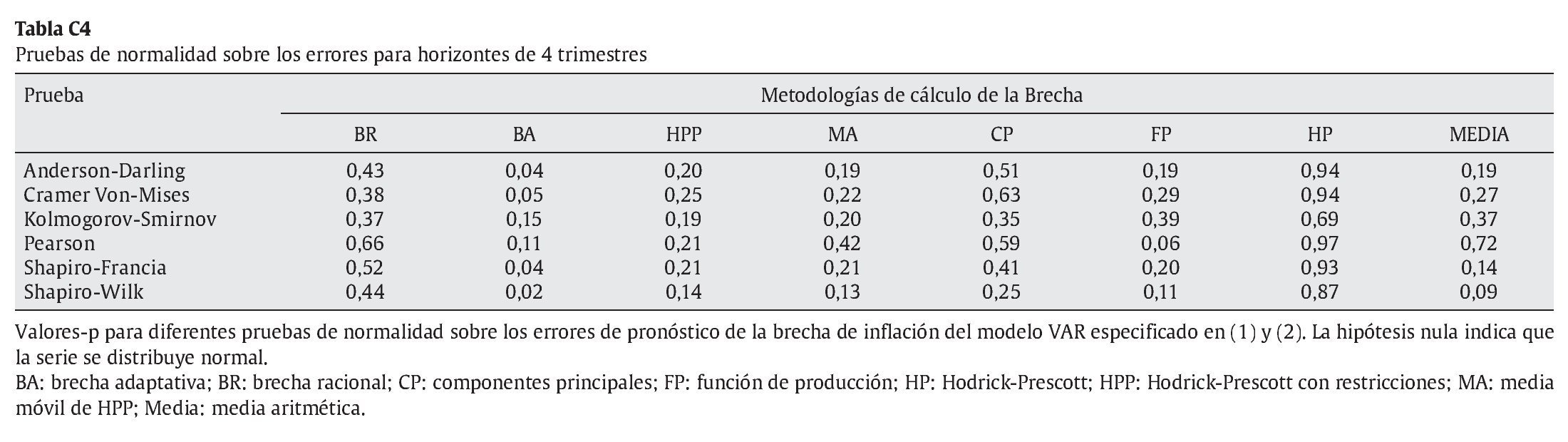
Bajo el supuesto de normalidad, los pronósticos de densidad son obtenidos a partir de las predicciones y las varianzas de los errores de pronóstico calculados en la estimación recurrente del modelo VAR indicado en el párrafo anterior. En el anexo C (tablas C1, C2, C3 y C4) se muestran los resultados de diferentes pruebas sobre los errores de pronóstico de los modelos VAR para verificar el supuesto de normalidad. Estos resultados no dan indicio de violación de dicho supuesto.
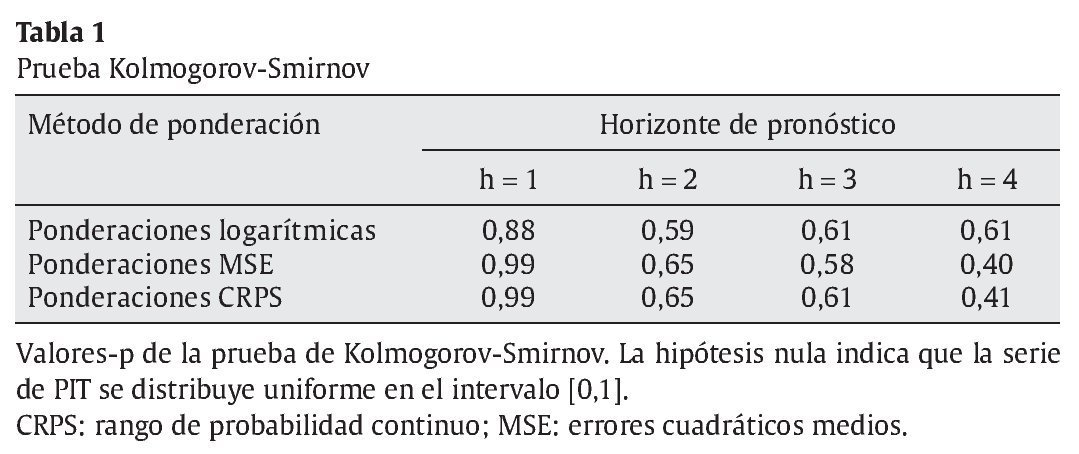
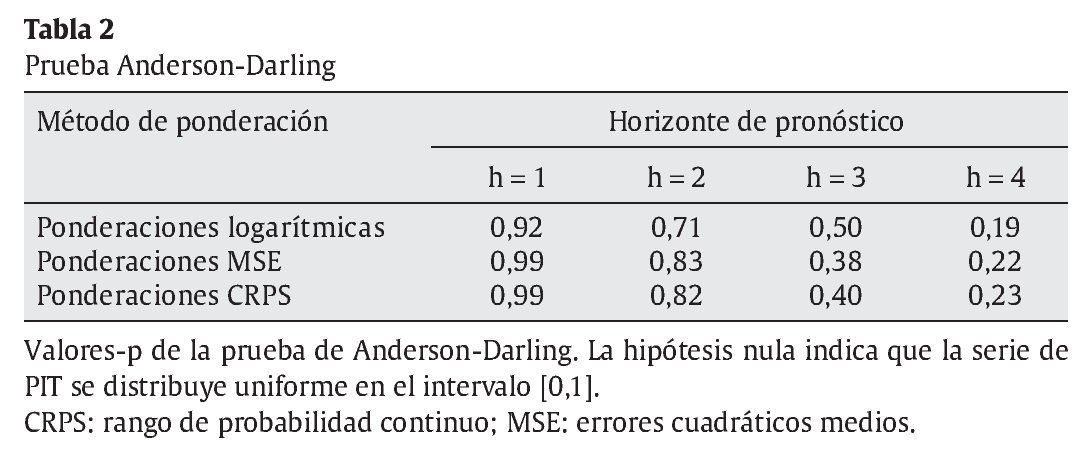
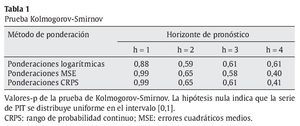
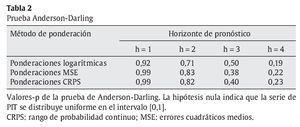
3.2.1. Densidades combinadas de pronósticos de la brecha de inflación En tablas 1 y 2 se muestran los valores-p de las pruebas de bondad de ajuste de Kolmogorov-Smirnov y Anderson-Darling sobre las series de PIT para los métodos de ponderación considerados. Si los modelos están bien especificados, estas series se deben distribuir de manera uniforme en el intervalo [0,1], tal como se menciona en la sección 2.3. Los resultados de ambas pruebas indican que no existe evidencia de mala especificación.
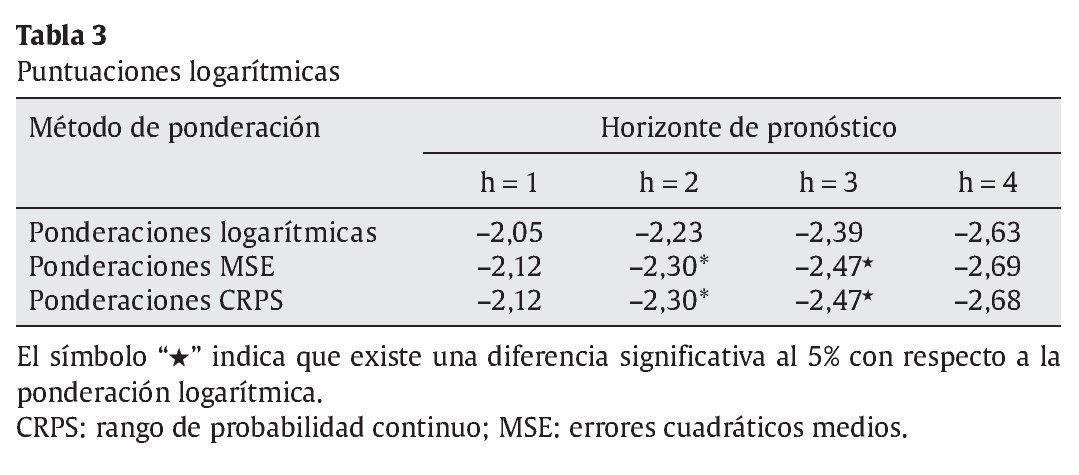
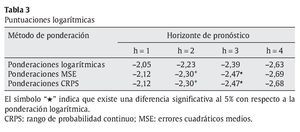
La tabla 3 presenta las puntuaciones logarítmicas sobre las densidades combinadas bajo los diferentes esquemas de ponderación considerados para el período de evaluación comprendido entre el tercer trimestre de 2002 y el tercer trimestre de 20129. Las estimaciones con el símbolo "¡ï" indican que dicha puntuación es menor que la obtenida bajo ponderadores logarítmicos a un nivel de significancia del 5%.10 Los resultados mostrados en esta tabla sugieren que el método de combinación basado en ponderaciones logarítmicas tiene puntuaciones mayores indicando que es la metodología con mejor desempeño. Adicionalmente, para horizontes de 2 y 3 trimestres, estas puntuaciones son significativamente mayores con respecto a los otros métodos de combinación. Teniendo en cuenta estos resultados, en lo que sigue del documento solo se considerarán las densidades obtenidas por este método.
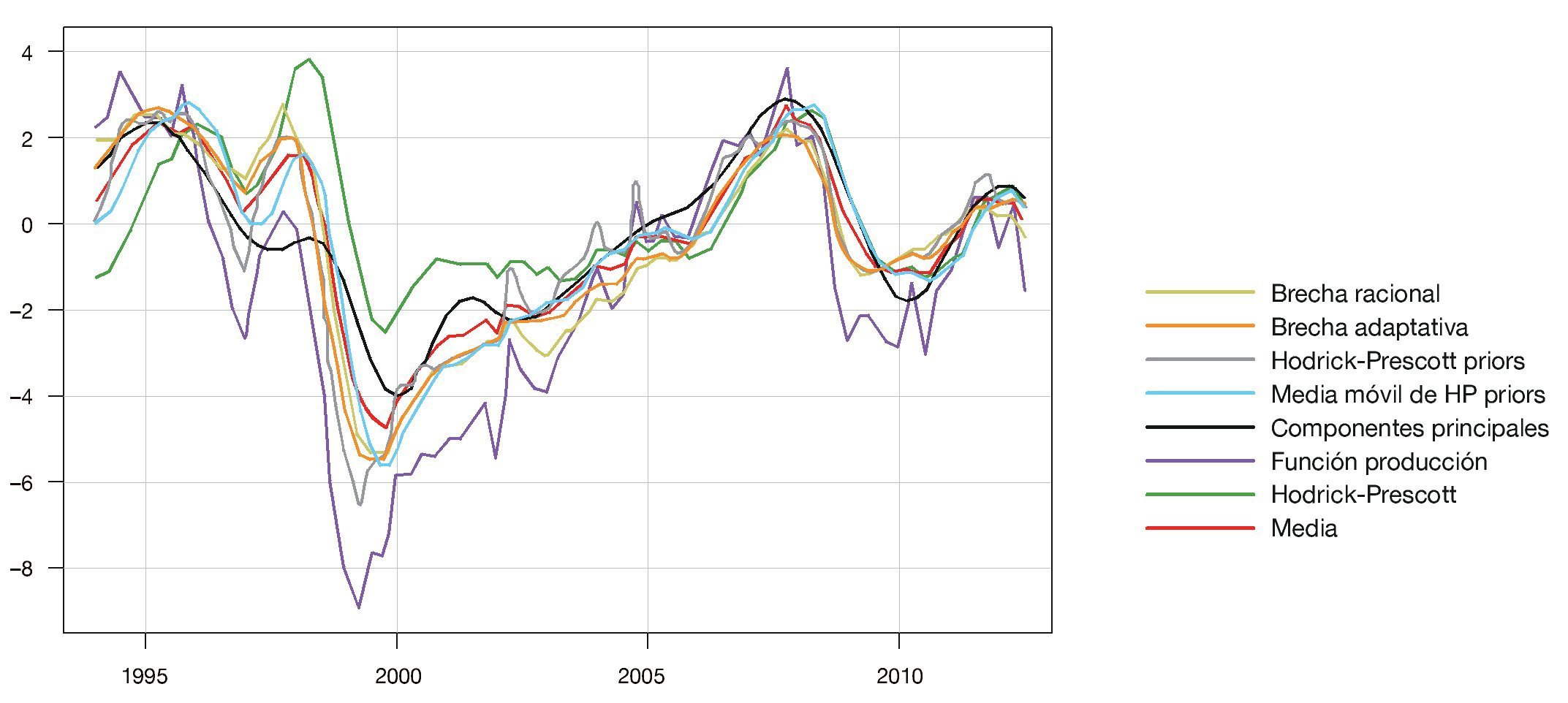
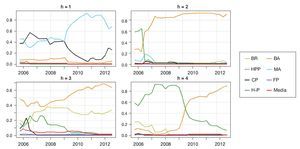
La figura A2 del Anexo A muestra la evolución de las ponderaciones basadas en el método logarítmico a lo largo del período de evaluación para los 8 métodos de estimación de la brecha y para los 4 horizontes de pronóstico considerados. En este gráfico se observa que las densidades asociadas al método de brecha adaptativa presentan una alta ponderación para horizontes de 2, 3 y 4 trimestres adelante; sin embargo, las ponderaciones de las distintas densidades son diferentes de acuerdo con el horizonte de pronóstico considerado. Las densidades generadas por medio del promedio móvil del filtro de Hodrick-Prescott restringido y por componentes principales tienen las ponderaciones más altas para el horizonte de pronóstico de un trimestre. Por otro lado, los métodos de brecha racional y Hodrick-Prescott sin restricciones presentan ponderaciones altas en los horizontes de 3 y 4 trimestres adelante, respectivamente.
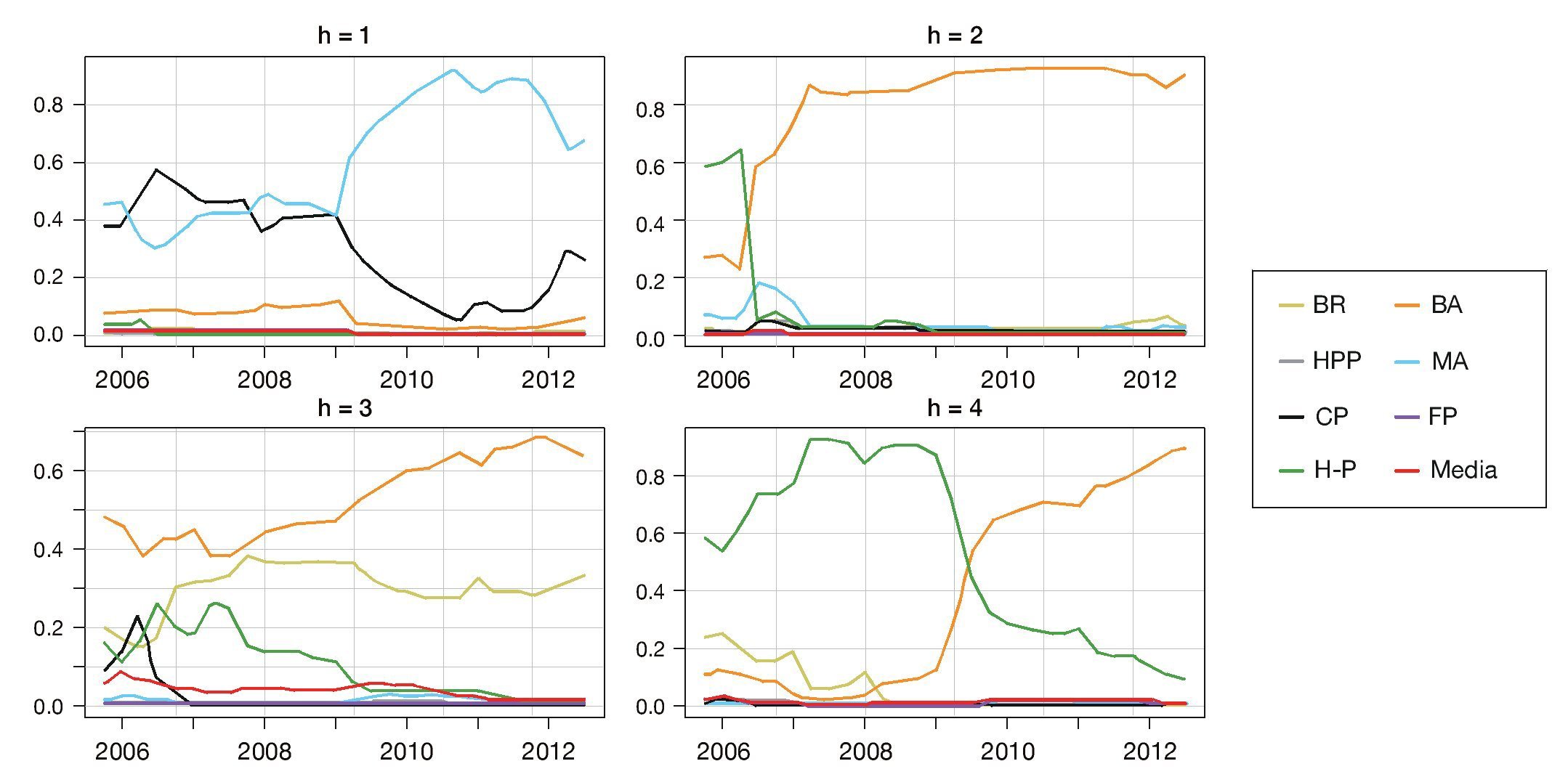
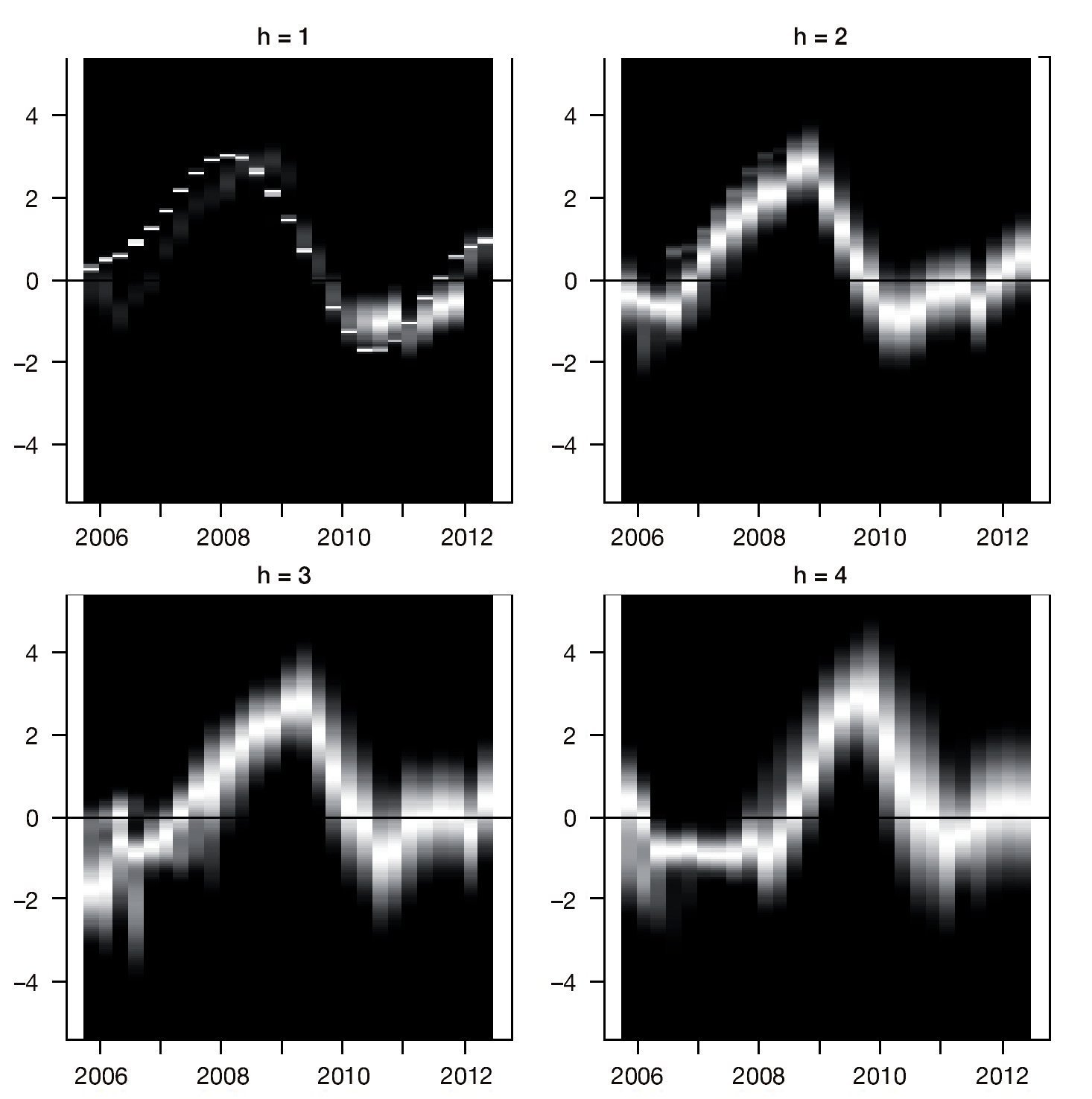
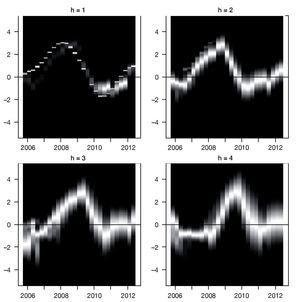
3.2.2. Densidades combinadas de pronósticos de la brecha del producto La figura A3 del Anexo A presenta las densidades combinadas utilizando el método de ponderadores logarítmicos de la brecha para los 4 horizontes de pronóstico. Este gráfico muestra la concentración de masa de probabilidad, la cual es mayor a medida que la región es más clara. El eje vertical mide la brecha del producto, mientras que el horizontal está asociado al tiempo. Se observa que las densidades combinadas presentan algunos comportamientos multimodales; por otro lado, como era de esperar, la dispersión de las densidades estimadas aumenta a medida que el horizonte de pronóstico es mayor.
Puesto que las densidades combinadas pueden tener comportamientos multimodales (Kascha y Ravazzolo, 2010), no es completamente pertinente mostrar medidas de tendencia central. En lugar de ello, se analiza la probabilidad de un evento en particular sobre la brecha del producto.
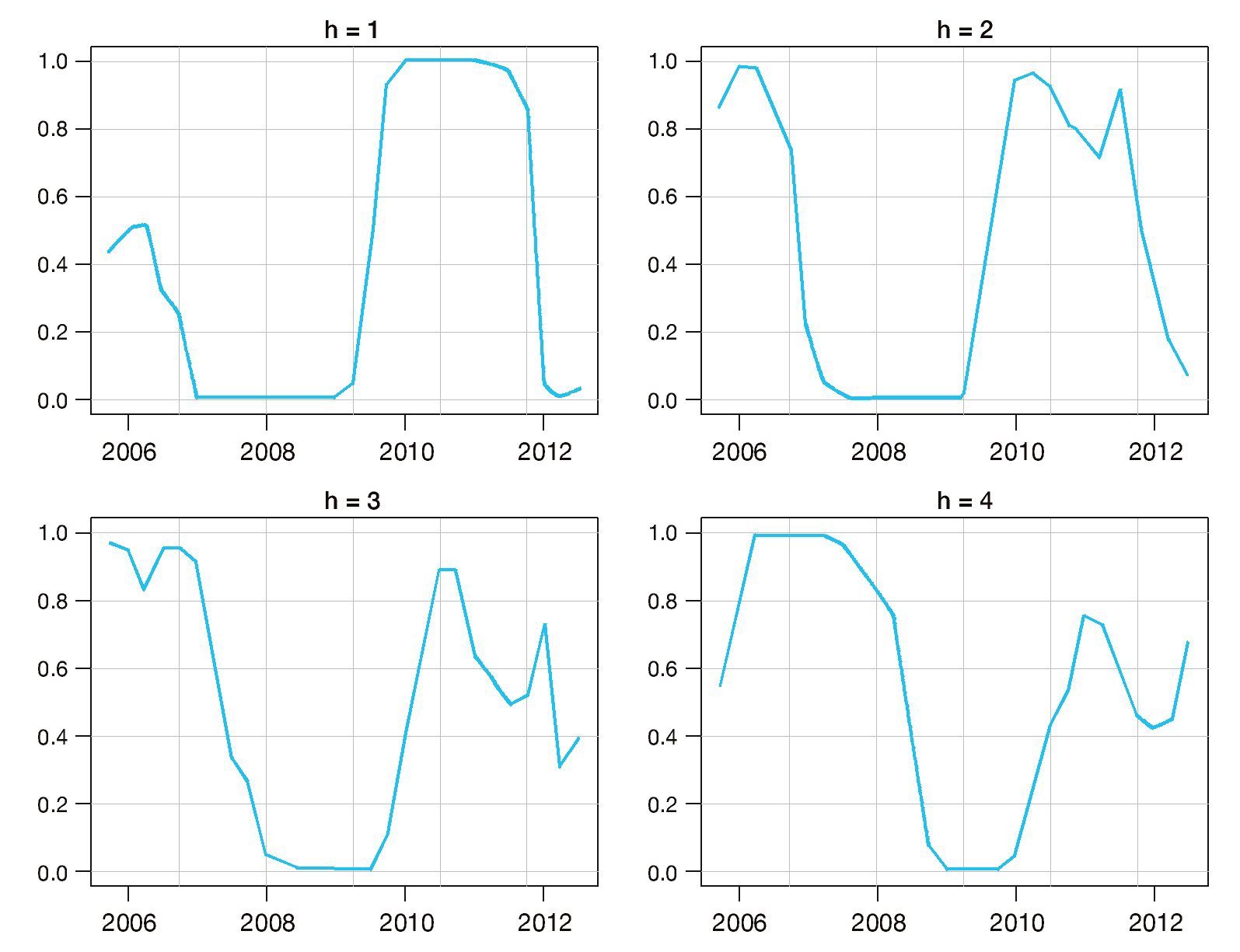
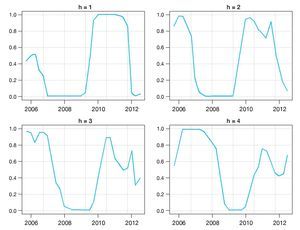
La figura A4 del anexo A muestra la probabilidad de que la brecha del producto sea negativa
a lo largo del período de evaluación para los 4 horizontes de pronóstico. Se observa que las probabilidades de las densidades obtenidas siguen patrones de comportamiento similares para los diferentes horizontes de pronóstico.
Es de resaltar que para el horizonte de pronóstico de un trimestre, los valores de probabilidad tienden a ser extremos (cercanos a 0 o a 1) y menos volátiles. Por otro lado, todos los gráficos indican un aumento en la probabilidad de que la brecha sea negativa a partir de 2009 con un descenso al final de la muestra; sin embargo, para los horizontes de 3 y 4 trimestres, se muestra un leve repunte de esta probabilidad al final del período analizado.
4. Comentarios finales
Este documento combina estimaciones de 8 metodologías de la brecha del producto colombiano para el período comprendido entre el primer trimestre de 1994 y el tercer trimestre de 2012. Utilizando la metodología sugerida por Garratt et al (2009) y Garratt et al. (2011) se construyen las densidades combinadas de pronósticos de la brecha mediante el uso de 3 esquemas de ponderación: ponderadores logarítmicos, CRPS y errores cuadráticos medios. Los resultados sugieren que las densidades combinadas bajo estos 3 esquemas con horizontes de pronóstico de 1, 2, 3 y 4 trimestres adelante están bien especificadas. Por otro lado, las puntuaciones logarítmicas calculadas sobre estas densidades muestran que la metodología basada en ponderadores logarítmicos presenta el mejor desempeño. Adicionalmente, estas ponderaciones tienen un desempeño significativamente mejor que las calculadas por los ponderadores CRPS y errores cuadráticos medios para horizontes de pronóstico de 2 y 3 trimestres.
La densidad combinada resultante puede ser utilizada de diferentes formas, por ejemplo, para estimar dichas densidades en períodos pasados. Esto no solamente provee indicios de la tendencia central de la brecha, sino que también caracteriza su incertidumbre. Además, se pueden estimar dichas densidades para períodos futuros, lo cual es de gran interés para las autoridades económicas. Finalmente, se puede obtener la probabilidad de que la brecha sea negativa para diferentes períodos en el tiempo y horizontes de pronóstico.
Agradecimientos
Los autores agradecen los valiosos comentarios y sugerencias de Juan Sebastián Amador.
Anexo A
Figura A1 Brechas del producto colombiano estimadas por diferentes metodologías.
Figura A2 Ponderadores logarítmicos para el período 2005:4-2012:3. BA: brecha adaptativa; BR: brecha racional; CP: metodología de componentes principales; FP: función de producción; HP: metodología de Hodrick-Prescott; HPP: metodología de Hodrick-Prescott con restricciones; MA: media móvil de HPP; Media: media aritmética de las brechas.
Figura A3 Densidades combinadas de la brecha bajo el esquema de ponderación logarítmico para horizontes de pronósticos de 1, 2, 3 y 4 trimestres adelante.
Figura A4 Probabilidad de que la brecha del producto sea negativa para horizontes de pronósticos de 1, 2, 3 y 4 trimestres adelante. Estas estimaciones son calculadas a partir de la densidad combinada de la brecha bajo el esquema de ponderación logarítmico.
Anexo B. Puntuaciones de rango de probabilidad continuo
Sea P un conjunto de medidas de probabilidad de Borel sobre la línea real ℜ. Todo miembro de P se identifica como un pronóstico de probabilidad y se caracteriza por medio de su función de distribución acumulada, denominada por F.
La puntuación de CRPS se define como:
Siendo Λ {•} una función indicadora. Gneiting y Raftery (2007) argumentan que la aplicación de las puntuaciones CRPS está limitada por dificultades analíticas en el cálculo de la integral. Alternativamente, las puntuaciones se pueden calcular por medio de la siguiente expresión:
Donde X y X′ son copias independientes de una variable aleatoria con distribución F y momento de primer orden finito. Si en particular la densidad de pronóstico es normal con media μ y varianza σ2, las puntuaciones se pueden calcular como:
Siendo φ{•} y Φ{•} la función de densidad y la función de distribución acumulada de una variable normal estándar, respectivamente.
Anexo C. Pruebas de normalidad sobre los errores de pronóstico de los modelos vectoriales autorregresivos
1. En normalidad, solo se requiere estos 2 momentos para identificar la función de densidad de los pronósticos.
2. Este modelo está diseñado para realizar pronósticos directos. Una descripción de los mismos se encuentra, entre otros, en Marcellino, Stock, y Watson (2006) y González, Melo y Grajales (2007).
3. Dado que durante la mayor parte del periodo analizado opera el régimen de inflación objetivo, las presiones inflacionarias relevantes son aquellas que alejen la inflación observada de la meta del Banco de la República. La meta de inflación fue trimestralizada usando la metodología utilizada en González et al. [2012].
4. Con
Estas restricciones son necesarias para asegu rar que la densidad combinada es no-negativa e integra a la unidad, Timmer mann [2006].
5. Un análisis de la combinación de densidades de pronóstico desde un punto de vista bayesiano puede encontrarse en Hall y Mitchell (2004).
6. Para una mayor descripción de Bayesian Model Averaging,véase Kop (2003).
7. La definición y una descripción de las puntuaciones de rango de probabilidad continuo se encuentra en el anexo B.
8. Para mayores detalles de Pseudo-Distancias o divergencias véase Ullah [1996].
9. En este ejercicio se utilizaron 10 observaciones como período de entrenamiento de los ponderadores. Es decir, en el contexto de la expresión (5), k es igual a 10.
10. Esta prueba se realiza de acuerdo a la metodología presentada en Hall y Mitchell [2007] McDonald y Anders [2011].
INFORMACIÓNDEL ARTÍCULO
Historia del artículo:
Recibido el 12 de septiembre de 2013
Aceptado el 5 de noviembre de 2013
*Los resultados y opiniones son responsabilidad exclusiva de los autores, y su contenido no compromete al Banco de la República ni a su Junta Directiva.
* Autor para correspondencia.
Correo electrónico:paulo.sanchez@mail.escuelaing.edu.co (P. M. Sánchez).
Referencias
Amisano, G. y Giacomini, R. (2007). Comparing Density forecasts via weighted likelihood ratio tests. Journal of Business and Economic Statistics, 25, 177-190.
Bache, J., Jore, A. y Mitchell, J. (2001). Combining VAR and DSGE forecast densities. Journal of Economics dynamics and control, 35, 1659-1670.
Bao, Y., Lee T. y Saltouglu, B. (2007). Comparing Density forecasts Models. Journal of Forecasting, 26, 203-225.
Berkowitz, J. (2001). Testing density forecasts, with applications to risk management. Journal of business and economic statistics, 19, 465-474.
Bjorland, H., Gerdrup K., A. Jore, A. y Smith, C. (2011). Weights and pools for a Norwegian density combination. North American Journal of Economics and Finance, 22, 61-76.
Cobo, A. (2007). Output gap in Colombia: an eclectic approach. Borradores de economía, 327. Banco de la República.
Diebold, F., Gunther, T. y Tay, A. (1998). Evaluating density forecasts: with applications to financial risk management. International Economic Review, 39, 863-883.
Garratt, A., J. Mitchell, J. y Vahey, S. (2009). Measuring Output Gap Uncertainty. NIESR Discussion paper, 342. National Institute of Economic and Social Research.
Garratt, A., Mitchell, J. y Vahey, S. (2011). Measuring output gap nowcast uncertainty. CAMA Working paper, 16. Center for Applied Macroeconomic Analysis, The Australian National University.
Gneiting, T., y Raftery, A. (2007). Strictly proper scoring rules, prediction and estimation. American statistical association, 102, 359-378.
González, A., Ocampo, S., Pérez, J. y Rodríguez, D. (2012). Output gap and neutral interest measures for Colombia. Borradores de economía, 726. Banco de la República.
González, E., Melo, L. y Grajales, A. (2007). Pronósticos directos de la inflación colombiana. Borradores de economía, 458. Banco de la República.
Hall, S., y Mitchell J. (2004). Density Forecast combination. Discussion paper, 249. National Institute of Economic and Social Research.
Hall, S. y Mitchell, J. (2007). Combining Density Forecasts. Journal of forecasting, 22, 1-13.
Harvey, A., y Proietti, T. (2005). Readings in unobserved components models. Oxford: Oxford University Press.
Hodrick, R. y Prescott, E. (1997). Post war business cycles: An empirical investigation. Journal of money, credit and banking, 29, 1-16.
Jore, A., Mitchell, J. y Vahey, S. (2010). Combining forecast densities from VARs with uncertain instabilities. Journal of Applied Econometrics, 25, 621-634.
Kascha, C. y Ravazzolo, F. (2010). Combining inflation density forecasts. Journal of forecasting, 29, 231-250.
Kop, G. (2003). Bayesian Econometrics. Wiley: Chichester.
Marcellino, M., Stock, J. y Watson M. (2006). A comparison of direct and iterated multistep AR methods for forecasting macroeconomic time series. Journal of Econometrics, 135, 499-526.
Mcdonald, C. y Anders, L. (2011). Evaluating density forecasts: model combination strategies vs. the RBNZ. Discussion paper, 3. National Institute of Economic and Social Research.
Mitchell, J. y Hall S. (2005). Evaluating, comparing and combining density forecasts using the KLIC with an application to the bank of England and NIESR fan charts of inflation. Oxford bulletin of economics and statistics, 67, 995-1033.
Orphanides, A. y van Norden, S. (2002). The reliability of inflation forecasts based on output-gap estimates in real time. Journal of Money Credit and Banking, 37-3, 583-601.
Rodríguez, N., Torres, J. y Velasco, A. (2006). La estimación de una brecha del producto a partir de encuestas y datos reales. Borradores de economía, 392. Banco de la República.
Stone, M. (1961). The opinion pool. Annals of mathematical statistics, 32, 1339-1342. Tay, A. y Wallis, K. (2000): Density forecasting: a survey. Journal of Forecasting, 19, 235-254.
Timmermann, A. (2006. Forecast combinations. In Handbook of Economic Forecasting, Vol. 1, Elliott G, Granger CWJ, Timmermann A (eds). North-Holland: Amsterdam; 135-196.
Ullah, A. (1996). Entropy, divergence, and distance measures with econometric applications. Journal of Statistical Planning and Inference, 49, 137-162.