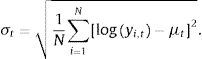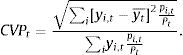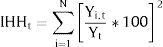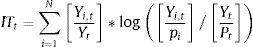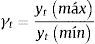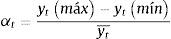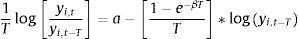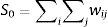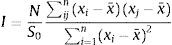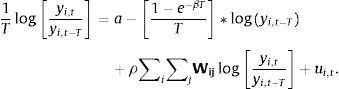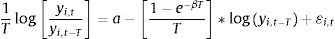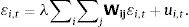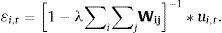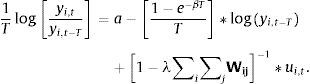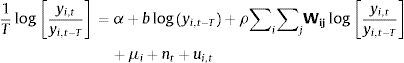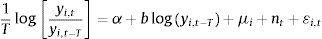Este documento analiza la convergencia del producto interno bruto per cápita (PIB pc) en Colombia durante el periodo de 1990 a 2013. Los resultados muestran un proceso de convergencia para los años de 1999 a 2006, mostrando evidencia estadística a favor de la existencia de dependencia de error espacial. Para estos años, los choques aleatorios en un departamento determinan el movimiento de las economías y la interacción sobre estas no está sujeta a los límites administrativos. Se puede observar un proceso de crecimiento para la región Andina y Caribe, caso contrario lo que pasa en algunas zonas de la región Orinoquia y Amazonas, lo cual permite concluir que el proceso de convergencia es causado por un proceso de factores espaciales no observables los cuales dieron una transición hacia el crecimiento de la región Caribe y Andina. Además, se mantienen constantes en el tiempo los departamentos con PIB pc alto y bajo. El principal aporte de este trabajo a la literatura sobre convergencia en Colombia es la incorporación en el análisis de los factores espacio y tiempo simultáneamente, así como la validación de la existencia de convergencia para el periodo señalado.
This paper analyzes the convergence of Gross Domestic Product per capita (GDP pc) during the period 1990-2013 in Colombia. Results show a convergence process for the 1999-2006 period and statistical evidence for the existence of spatial error dependence. For these years, random shocks determine the movement of the economies and their interaction are not defined by administrative boundaries. A growth process for the Andean and Caribbean region is observed, contrary to what happens in Orinoquia and Amazon region. That convergence process occurred due to a process of unobservable spatial factors which gave a transition to the growth of the Caribbean and the Andean region. Besides, over time departments with high and low GDP pc remain constant. The main contribution of this work is the analysis on convergence that includes space and time factors simultaneously, as well as validation of the existence of convergence.
En Colombia se han realizado diversos trabajos de investigación sobre convergencia económica entre sus regiones. Estos trabajos aplican el modelo neoclásico planteado por Barro y Sala-i-Martin (1991) en el cual se expone cómo economías similares que contienen instituciones, individuos y empresas que se enfrentan a las mismas funciones de utilidad y producción, respectivamente, convergen hacia un mismo estado estacionario de crecimiento. Sin embargo, en su gran mayoría, estos trabajos no han tenido en cuenta todas las regiones de Colombia debido a la dificultad de encontrar o formar los datos para todas las regiones antes de 1990. Los resultados de estos trabajos muestran que existe convergencia para los años previos a 1980 y divergencia a partir de 1990.
El presente trabajo introduce un enfoque diferente llamado análisis espacial. Este incluye los efectos producidos por la distancia que hay entre las regiones y su ubicación geográfica. Islam (1995) demuestra que al no tener en cuenta estas diferencias inherentes entre regiones se pueden estar subestimando o sobrestimando la convergencia o divergencia. Para ello, el presente documento se basa en 3 aproximaciones: la primera es el análisis de la dispersión del ingreso per cápita entre las regiones (convergencia σ); la segunda es la determinación de la dependencia espacial que existe en un modelo de convergencia, y la última presenta no solo la dinámica de tiempo, sino también la dinámica que genera la distancia entre las regiones, análisis planteado por Anselin, Le Gallo y Jayet (2008). De esta forma, el objetivo del presente documento es analizar cómo convergen o divergen las regiones en Colombia, tomando en cuenta la autocorrelación entre regiones usando econometría espacial. Con esto se busca responder a la pregunta: ¿hay convergencia económica en las regiones de Colombia tomando en cuenta los factores de espacio y tiempo dentro del modelo, en el periodo 1990-2013?
El trabajo se divide en 5 partes. La segunda sección presenta una revisión de la literatura y el estado del debate acerca de la convergencia regional en Colombia. A partir de esta revisión es evidente que el principal aporte del documento es la incorporación de los factores espacio y tiempo simultáneamente en el análisis, así como la validación de la existencia de convergencia para el periodo señalado. La tercera sección presenta la metodología a utilizar, la cual se divide en el cálculo de indicadores de diagnóstico de dispersión de la renta y la estimación de modelos que incorporan la variable espacial. La cuarta sección muestra los resultados de las estimaciones y la quinta, algunas conclusiones.
2Revisión de la literaturaLos análisis de crecimiento económico cobraron notoriedad a partir de la década de los cincuenta y tenían como objetivo explicar el crecimiento de la renta per cápita mediante su relación con otras variables. El principal modelo de este periodo es el desarrollado por Solow (1956) y Swan (1956), en el cual se describe una economía donde las familias consumen una fracción de su producto y ahorran la restante. Esta fracción es destinada a acumulación de capital, el cual tiene una tasa de depreciación. El desarrollo del modelo concluye que a mayor stock de capital, menor es la tasa de crecimiento del producto, por lo que economías con diferentes niveles de acumulación de capital tienden a converger en su tasa de crecimiento a largo plazo. Este análisis de convergencia plantea, por tanto, una relación lineal negativa entre el logaritmo del producto interno bruto per cápita (PIB pc) y la tasa de crecimiento. Esta relación es confirmada por Case (1965) y Koopmans (1965), quienes muestran que la relación de las disparidades del ingreso per cápita tiende a reducirse con el paso del tiempo. Este modelo fue refutado por trabajos como el de Summers y Heston (1991), en el cual se expone la relación del crecimiento del PIB pc y su tasa de crecimiento para más de 130 países, en el cual no se encuentra evidencia de la convergencia tradicional.
En los años noventa Barro y Sala-i-Martin (1991), basados en el trabajo de Barro (1991), afirmaron que puede haber convergencia entre economías o grupos similares si contienen instituciones similares, población, individuos y empresas que se enfrenten a las mismas funciones de producción, análogas entre todos los conjuntos. Los resultados hallados por Barro y Sala-i-Martin corroboraron la hipótesis de convergencia entre economías, encontrando la velocidad de convergencia para estos grupos.
Una de las principales críticas contra este modelo fue el uso de sección cruzada para la estimación, pues se argumenta la necesidad de trabajar con series temporales. Esta crítica fue planteada por Quah (1993) en su trabajo Galton's fallacy and test of the convergence hypothesis, quien determinó que la hipótesis de convergencia sufre de la denominada falacia de Galton, en la que, al tomar el ingreso invariante durante la estimación, la correlación negativa entre el nivel inicial del ingreso y la tasa promedio de crecimiento no existe. Las implicaciones dinámicas del comportamiento estocástico de la distribución en el tiempo para las economías dan como resultado que estas no convergen. Al contrario, las economías ricas cada vez serán más ricas y las economías pobres serán cada vez más pobres.
¿Cómo tener en cuenta la dinámica del tiempo y las diferencias de las economías para el modelo de convergencia? Uno de los trabajos pioneros con respecto a este tema fue realizado por Islam (1995), el cual hace un enfoque de datos panel. Una de las principales razones que llevaron a plantearse esta pregunta fue el determinar los efectos inobservables de cada individuo en el estudio. Este estudio encuentra resultados que explican la corrección de la omisión de variables relevantes, el cual genera sesgo en un modelo de sección cruzada.
Al analizar las diferencias inobservables entre las regiones surge otra pregunta: ¿existe alguna relación entre la ubicación de las regiones que intervenga en el crecimiento regional? A la existencia de una relación de una región con el crecimiento de su vecino se le denomina dependencia espacial. Uno de los primeros trabajos al respecto fue realizado por Moreno Serrano y Vayá Valcarce (2000) para las regiones europeas en el modelo de convergencia. Esta visión generó nuevas investigaciones acerca de la dinámica espacial y su influencia en el crecimiento. La creciente literatura e investigaciones acerca de la dinámica espacial han llegado a abordar temas como los modelos espacio y tiempo, tal como lo plantean Anselin et al. (2008) y Elhorst (2014). Una de las mejores formas de abordar los modelos espacio y tiempo es a partir de los datos longitudinales. Estudios posteriores como el de Elhorst, Piras y Arbia (2010) prueban la importancia de la ubicación relativa de una economía y su efecto en el crecimiento y en el bienestar económico incorporando las dinámicas espaciotemporales.
El modelo de convergencia es usado más allá del estudio acerca del PIB. Un ejemplo es el de Adhikari y Chen (2014), donde utilizan este modelo para determinar la convergencia de la producción de energía para 35 países de Asia en el periodo 1993-2010, mostrando evidencia a favor de la convergencia beta para algunos países. También muestran que al utilizar panel espacial mejora la precisión de sus resultados y así mismo permite eliminar los efectos cíclicos de la producción de energía.
Un análisis previamente realizado sobre convergencia espacial con datos de panel dinámicos fue realizado por Montero y del Río Rivera (2013), donde los resultados obtenidos indican una velocidad de convergencia de 4% y 7% para las regiones de Bolivia, con evidencia estadística de que no existe dependencia espacial.
El caso colombiano también ha sido objeto de estudio. El primer trabajo realizado fue hecho por Cárdenas y Pontón (1995), quienes encontraron convergencia beta no condicional entre las regiones colombianas y un valor cercano de la velocidad de convergencia del 4% para el periodo 1950-1989, y de aproximadamente 3% para el periodo 1960-1989. Este trabajo generó nuevas investigaciones como la realizada por Bonet y Meisel (1999), quienes muestran la contraposición del análisis planteado por Barro y Sala-i-Martin (1991) para el caso colombiano, donde se fundamentan en la dinámica distributiva planteada por Quah (1996). Esta metodología permite mirar internamente cómo evoluciona la distribución del ingreso en cada economía regional y permite extraer las propiedades dinámicas y no estáticas del modelo de convergencia. Adicionalmente, otros trabajos como el de Birchenall y Murcia (1997) utilizando estimadores de kernel estocástico muestran el aumento de la desigualdad en los ingresos regionales; en ambos trabajos los resultados encontrados muestran que, para Colombia, no existe convergencia entre regiones.
No solo se han generado investigaciones de la metodología de sección cruzada, sino que también se ha utilizado la predeterminación bayesiana, como en el trabajo realizado por Rocha y Vivas (1998) en el cual se analiza la importancia de la heterogeneidad incorporando las disparidades existentes entre regiones, como las dotaciones de capital humano y la política fiscal, entre otras. Llegan a la conclusión de la existencia de divergencia, lo que indica una persistencia en la desigualdad regional. Además, Bonet y Meisel (1999) usaron depósitos bancarios como variable proxy del PIB, y mostraron que la convergencia beta β y sigma σ son significativas para los periodos comprendidos entre 1926-1960, pero para años posteriores a 1960 afirman que no existe convergencia. Este resultado reafirma la hipótesis de persistencia en la desigualdad regional. Posteriormente, el trabajo realizado por Aguirre Tobón (2006) ilustra una revisión sobre la literatura acerca de la convergencia económica para Colombia antes del 2006. Analizando 18 documentos, encuentra que hay un relativo consenso con respecto a la existencia de una persistencia en las tasas de crecimiento de los departamentos colombianos, acentuada en la última década del siglo, lo que indica un incremento sobre las disparidades regionales.
Un nuevo análisis sobre la distribución del ingreso a nivel espacial de las regiones hecho por Bonet y Meisel (2006) muestra a Bogotá con una evidente supremacía en la participación del ingreso nacional en el tiempo, lo que indica un nivel de polarización. Otros documentos, como el de Franco y Raymond (2009), muestran una nueva metodología al organizar clubes de convergencia en Colombia con un análisis de datos panel y efectos fijos para los años 1975-2005. En este trabajo se encuentra que no existe convergencia beta no condicional, pero existe convergencia condicionada a los «fundamentos» departamentales. Este trabajo también demuestra un punto importante al combinar series de tiempo con datos de corte transversal, dando una idea de la relación de las variables a través del tiempo. Para el mismo periodo Royuela y García (2013), implementando la metodología de Barro y Sala-i-Martin (1991), realizan el análisis espacial para los 24 departamentos enfatizando en los indicadores sociales y económicos. Se estiman las interacciones de rezago espacial y encuentran que al incluir estas variables se refuerza la evidencia a favor de la convergencia en los indicadores sociales, pero no a favor de la convergencia a nivel del PIB pc.
Giraldo (2011) ha apoyado la tesis de que la estimación con datos panel ofrece resultados que muestran que hay convergencia para todos los países de América Latina una vez se han controlado los efectos regionales individuales, es decir, la heterogeneidad en los niveles iniciales de tecnología. Un resultado importante es la incorporación de la heterogeneidad espacial que existe entre los países, lo cual es un planteamiento inicial para el análisis de panel espacial.
El análisis de convergencia, teniendo en cuenta los efectos espaciales y los municipios de Colombia, fue realizado por Moncada y Loiza (2013), quienes encuentran convergencia no condicional explicada por un esquema de autocorrelación espacial residual. Pero este no fue el único trabajo de este tipo. Galvis y Meisel (2012) analizan la convergencia y las trampas de pobreza usando econometría espacial y encuentran que no se han reducido las disparidades del ingreso regional a pesar de las políticas de descentralización, donde persiste la dinámica de desigualdad regional y la dependencia espacial en los índices de pobreza. Lo anterior indicaría la existencia de trampas de pobreza en el país.
Por último, uno de los trabajos más recientes sobre convergencia en Colombia es el de Ramírez y Ayala (2014), quienes utilizan diferentes metodologías de análisis econométrico. De su estudio se concluye que no existe evidencia empírica clara a favor de la existencia de convergencia regional en Colombia. Este documento permite ver cómo son los efectos que se incorporan al utilizar panel espacial, analizando no solo la dinámica espacial, sino la temporal al mismo tiempo.
3MetodologíaComo se ve anteriormente, los análisis empíricos sobre convergencia en Colombia, en su gran mayoría, han mostrado una mayor disparidad regional y divergencia. Para complementar esta discusión se introduce un análisis poco estudiado y bastante importante para Colombia: el análisis espacial, que se encarga de estudiar los fenómenos económicos con énfasis en su localización. La necesidad de entender mejor las dinámicas de espacio y tiempo, incorporadas dentro del modelo, fue postulada como un reto a superar por Anselin (2009), quien afirma que aunque los modelos y estimadores de kernel son formas elegantes y muy generales de incorporar interacciones espacio-tiempo, no ayudan completamente a entender cómo y por qué estas interacciones ocurren.
La metodología implementada para el presente documento se deriva de los documentos realizados por Anselin et al. (2008) y Elhorst (2014), los cuales analizan el comportamiento de las variables en el tiempo, implementando la matriz de pesos espaciales para determinar la relación de crecimiento de un departamento frente a su vecino. Se determina la relación sobre el tipo de efectos que tiene este modelo (efectos fijos o aleatorios) controlando la heterogeneidad y dependencia espacial que pueda tener este modelo. Para los modelos de panel espacial se seguirá con la línea propuesta por Adhikari y Chen (2014), en el cual se utilizan los modelos de retardo espacial (SAR)1 y modelos de dependencia residual (SEM)2 para determinar el tipo de convergencia. Una primera aproximación a este análisis es el uso de indicadores que diagnostiquen la evolución de la disparidad de la renta entre regiones y permitan describir el comportamiento convergente o divergente del PIB pc. A continuación se presentan estos indicadores seguidos de una presentación de los modelos de análisis espacial. La variable PIB pc utilizada para este estudio proviene de los datos del DANE. Se empalmaron las series disponibles antes y después del año 2000 y se usó el 2005 como año base para mantener la serie con precios constantes.
3.1Dispersión de la renta regionalAl analizar la convergencia entre regiones, toca tener en cuenta los diferentes tipos de convergencia, convergencia σ y convengencia β, donde puede haber convergencia β sin existir convergencia σ, pero si existe convergencia σ existirá convergencia β (Barro y Sala-i-Martin, 1991). Por esta razón se analizará inicialmente la convergencia σ.
3.1.1Convergencia σLa convergencia de tipo σ es una medida de dispersión de la renta de las regiones en el tiempo y muestra cómo, a medida que pasa el tiempo, la dispersión en el PIB pc tiende a disminuir. Lo anterior significa que la dispersión de las economías tenderá a reducirse y las economías se estarán acercando hacia un mismo estado estacionario. Siguiendo la metodología de Barro y Sala-i-Martin (1991) la estimación de esta será:
Esta es medida como la desviación estándar de logaritmo del PIB per cápita (log(yi,t)), donde i indica el departamento y t el tiempo; μt indica el promedio del logaritmo del PIB per cápita en el tiempo t.
3.1.2Coeficiente de variación ponderadaBonet y Meisel (1999) argumentan que una de las limitaciones que presenta el análisis tradicional de convergencia tipo σ es que pondera las diferentes unidades territoriales igualmente sin contemplar el tamaño de la población. Tendría, de esta forma, el mismo peso el avance en materia de convergencia de un departamento escasamente poblado al de uno con mucha más población. Para corregir esto se calcula el coeficiente de variación ponderada (CVP) el cual está estimado de la siguiente manera:
En este modelo yt¯ es el promedio del PIB pc en el tiempo t, pi,t la población del departamento i en el tiempo t y finalmente Pt es la población total de los departamentos en el tiempo t.
3.1.3Índice de concentración de Herfindahl-HirschmanEl índice de Herfindahl-Hirschman mide el nivel de concentración del ingreso y busca conocer la evolución de los desequilibrios a un nivel espacial. Está medido como:
donde Yt es el PIB nacional y Yi,t el PIB departamental. Cuanto más se acerque a cero indica una baja concentración, y cuanto más se aleje de cero indica mayor concentración, siendo 10.000 el nivel máximo en el cual todo el PIB nacional lo concentra un solo departamento.3.1.4Índice de TheilMide el nivel de desigualdad y posee las propiedades de ser invariante con respecto a la escala de medición y de ser sensible a las transferencias de ingresos entre los individuos de diferentes niveles de ingreso. Además, este índice es una aproximación de desigualdad relativa: cuando sea igual a cero no habrá desigualdad.
3.1.5Indicadores gamma y alfaEl índice gamma representa una medida de disparidad regional. Si este indicador se aproxima a 1, los departamentos son relativamente iguales. Si se aleja de este valor, los valores de la muestra se encuentran dispersos.
El indicador alfa es la relación de los valores máximo y mínimo del PIB pc departamental sobre el promedio nacional.
3.1.6Convergencia betaEl análisis de convergencia en beta planteado por Barro y Sala-i-Martin (1991) muestra un modelo neoclásico en donde el proceso de crecimiento y transición hacia el estado estacionario puede ser expresado de la siguiente manera:
donde yi,t es el PIB per cápita, T es el número de años en el intervalo de análisis y β es la velocidad de convergencia.La estimación del modelo se debe realizar con métodos no lineales para obtener directamente la velocidad de convergencia donde, al estimar las regresiones, β debe ser positivo y significativo mostrando como las regiones que inicialmente tenían menores valores de ingreso per cápita son las que presentan tasas de crecimiento más altas, generando que las regiones o economías lleguen hacia un mismo estado estacionario.
El interés principal de este documento es hacer énfasis en las estimaciones teniendo en cuenta la existencia de algún tipo de autocorrelación espacial que deba ser considerada explícitamente. Por esta razón se realiza un análisis exploratorio en el cual se revisa inicialmente la I de Moran para determinar la existencia de dependencia espacial en el intervalo de tiempo analizado, seguido de las pruebas referentes a los contrastes sobre dependencia espacial en los modelos de regresión, tales como la sustantiva y residual basada en los multiplicadores de Lagrange.
3.2Análisis espacial3.2.1I de MoranEste índice consiste en contrastar si la variable se encuentra distribuida en forma totalmente aleatoria en el espacio, o si existe una asociación significativa de valores similares o disimiles entre los departamentos vecinos (Moran, 1948). Se representa de la siguiente manera:
donde xi es el valor de la variable cuantitativa, para nuestro estudio es el PIB pc de la región i; x¯ es el promedio del PIB pc, y wij es la matriz de pesos de tamaño n×n. Cabe resaltar que existen diferentes tipos de construcción de esta matriz: la primera es la matriz de contigüidad, la cual toma valores iguales a 0 si no existe relación espacial de vecindad y 1 si existe contigüidad de una región i con una j; la segunda es una matriz que toma la distancia, dependiendo de la especificación del investigador; la tercera es una matriz socioeconómica, la cual tiene que ser creada con una variable exógena al modelo, y finalmente existe la matriz del k-enésimo vecino, una matriz asimétrica, que toma la relación espacial que existe entre el número especificado de vecinos más cercanos (Anselin et al., 2008).La elección de la matriz se hizo con base en la especificación para modelos de panel espacial, que serán explicados más adelante, debido a que esta matriz tiene que ser invariante en el tiempo. Anselin et al. (2008) descartan la utilización de las matrices de distancias y socioeconómicas, las cuales pueden estar variando a través del tiempo. Así mismo descartan la matriz del k-enésimo vecino debido a la relación que obliga a una variable a ser vecina de otra, dependiendo de la especificación del número de vecinos, el cual es un análisis poco conveniente para los departamentos pero bastante útil para los municipios (Galvis Aponte y Hahn-de-Castro, 2015).
Un índice de Moran positivo y significativo indica que existe una relación espacial, es decir, la presencia de concentración de valores similares del PIB pc entre sus regiones vecinas. En caso de que este sea negativo y significativo indica que existe una relación de valores disímiles del PIB pc entre sus regiones vecinas, o dicho de otra manera, indica que las regiones pobres están cerca de las ricas y viceversa.
3.2.2Test para la detección de dependencia espacial en el modelo de regresión linealLos test para la detección de dependencia espacial se realizan sobre los modelos de mínimos cuadrados ordinarios (MCO) para la elección del mejor modelo entre SAR y SEM. Dado que estos modelos son estimados por máxima verosimilitud, se hacen pruebas basadas en los multiplicadores de Lagrange (LM): si solo uno de los test simples LM (LAG para el modelo SAR o error para el modelo SEM) es significativo, se elige el modelo que rechaza la hipótesis nula de no correlación espacial; si ambos test son significativos, se consideran las formas robustas; si solamente uno de los estadísticos robustos es significativo, ese modelo debe ser elegido, y por último, si ambos test LM robustos son significativos, se elige el modelo con el estadístico de mayor valor. También se puede revisar la especificación en Anselin (2001) y Moreno Serrano y Vayá Valcarce (2000).
3.2.3Modelo de convergencia en beta, dependencia con retardo espacialUno de los modelos más utilizados en econometría espacial es el modelo de retardo espacial en el cual se incorpora una nueva variable igual a la multiplicación de la matriz de pesos con la variable dependiente, en este caso la tasa de crecimiento del PIB pc, para los periodos determinados. Este modelo puede reescribirse de la siguiente manera:
En este caso ui,t es el término de error de la regresión y el coeficiente ρ es el crecimiento sistemático de las regiones vecinas el cual contribuye al crecimiento en cada región. En este modelo, el crecimiento presenta un efecto contagio, por el que la tasa de crecimiento es mayor cuando los vecinos están creciendo a tasas elevadas y menor cuando las regiones vecinas crecen lentamente. Si este parámetro es positivo, podría considerarse como una externalidad de oferta. En esta situación la tecnología o los costos de producción dependerán del nivel de tecnología de los vecinos, en los cuales se podrían presentar economías de aglomeración más allá de la región. En caso contrario y que el parámetro sea negativo, la variable explicativa indicaría la existencia del modelo neoclásico acerca de rendimientos decrecientes. En este sentido, la tasa de crecimiento en una región puede estar relacionada negativamente con la cantidad de factores existentes, no solo en su economía, sino también en sus regiones vecinas (Moreno Serrano y Vayá Valcarce, 2000).
3.2.4Modelo de convergencia en beta, dependencia con error espacialEste modelo también es normalmente utilizado debido a la importancia que tiene incluir una estructura de dependencia espacial en términos del error. Este modelo se puede representar como:
Se puede reducir la expresión a:
Llegando así a la siguiente expresión:
En este modelo ui,t representa los residuales del modelo sin el término del error espacial, y ¿i,t son los residuales que incorporan el término del error espacial. La importancia de este modelo es determinar la existencia de efectos provenientes de algún choque aleatorio o imposible de anticipar en las regiones vecinas, lo cual indica que un choque aleatorio en una región específica se propaga a todas las regiones de la muestra. De esta expresión, se deduce que un choque aleatorio en una región específica no afecta tan solo a la tasa de crecimiento de esta región, sino que, a través de la transformación espacial 1−λ∑i∑jWij−1, tiene además un impacto sobre las tasas de crecimiento de las otras regiones. Los modelos econométricos espaciales se revelan, por tanto, útiles para modelar los efectos de desbordamiento o de difusión espacial del crecimiento como lo revela el trabajo realizado por Rey y Montouri (1999).
3.2.5Convergencia en beta utilizando panel espacialEl creciente número de trabajos y teorías que se han visto en los últimos años sobre la econometría espacial han llevado al planteamiento de nuevos modelos, en los cuales se ha dado la inclusión de los efectos temporales, en especial por la posibilidad de encontrar bases de datos a través del tiempo. Cabe aclarar que estos modelos son una extensión de la econometría espacial, mas no de la econometría en series de tiempo (Elhorst, 2014; Anselin et al., 2008). En este sentido, debido a que las unidades de observación geográfica que estamos analizando son las mismas en el tiempo, el análisis del panel espacial resulta pertinente.
Los modelos de panel espacial tienen varias ventajas: primero, al estudiar las mismas observaciones a través del tiempo permiten eliminar los efectos cíclicos, lo cual es útil para probar modelos de largo plazo; segundo, permiten tener en cuenta en mejor medida los efectos espaciales, los choques que surgen en un departamento y que afectan a otros sea de manera residual o rezagada, y, finalmente, al tener en cuenta la dinámica interregional en el tiempo se puede mejorar el modelo solucionando una de las principales críticas: la falacia de Galton, expuesta para el modelo de convergencia por Quah (1993,1996). El trabajo empleará los modelos SAR y SEM en panel de datos con el fin de hacer comparaciones más precisas sobre los modelos anteriormente estimados.
3.2.5.1Modelos de rezago espacial en panel de datosToma en cuenta los efectos entre grupos: variables de individuos que no varían, ya sean en el tiempo (efectos fijos individuales); un efecto temporal que no varía con los individuos (efectos fijos temporales); rasgos comunes en toda la muestra que cambian a lo largo del tiempo (efectos fijos individuales y temporales), y efectos aleatorios.
El modelo de especificación para los modelos SAR panel considera no solo los ítems anteriores de efectos fijos o aleatorios, sino que también incluye el modelo especificado en la ecuación número 10, que se puede ver como:
donde ρ es el componente del rezago espacial, μi y nt representan los efectos fijos individuales y los efectos fijos temporales, respectivamente, y el ui,t que representa el ruido. La descripción y taxonomía de este modelo se pueden encontrar en Elhorst (2014) y Anselin et al. (2008).3.2.5.2Modelo con rezago espacial en el término del error en panel de datosAl igual que el modelo anterior, en este se incluyen efectos fijos y efectos aleatorios que también incluye el modelo especificado en la ecuación número 14, el cual se puede ilustrar como:
La descripción y taxonomía de este modelo se pueden encontrar en Elhorst (2014) y Anselin et al. (2008)3.
4Resultados4.1Dispersión en la renta regionalEn el contexto del análisis de convergencia existen 2 tipos de medidas diferentes: convergencia beta y convergencia sigma. La existencia de convergencia beta, aunque es una condición necesaria, no es suficiente para la existencia de convergencia sigma, pero siempre que exista convergencia sigma existirá convergencia beta (Barro y Sala-i-Martin, 1991).
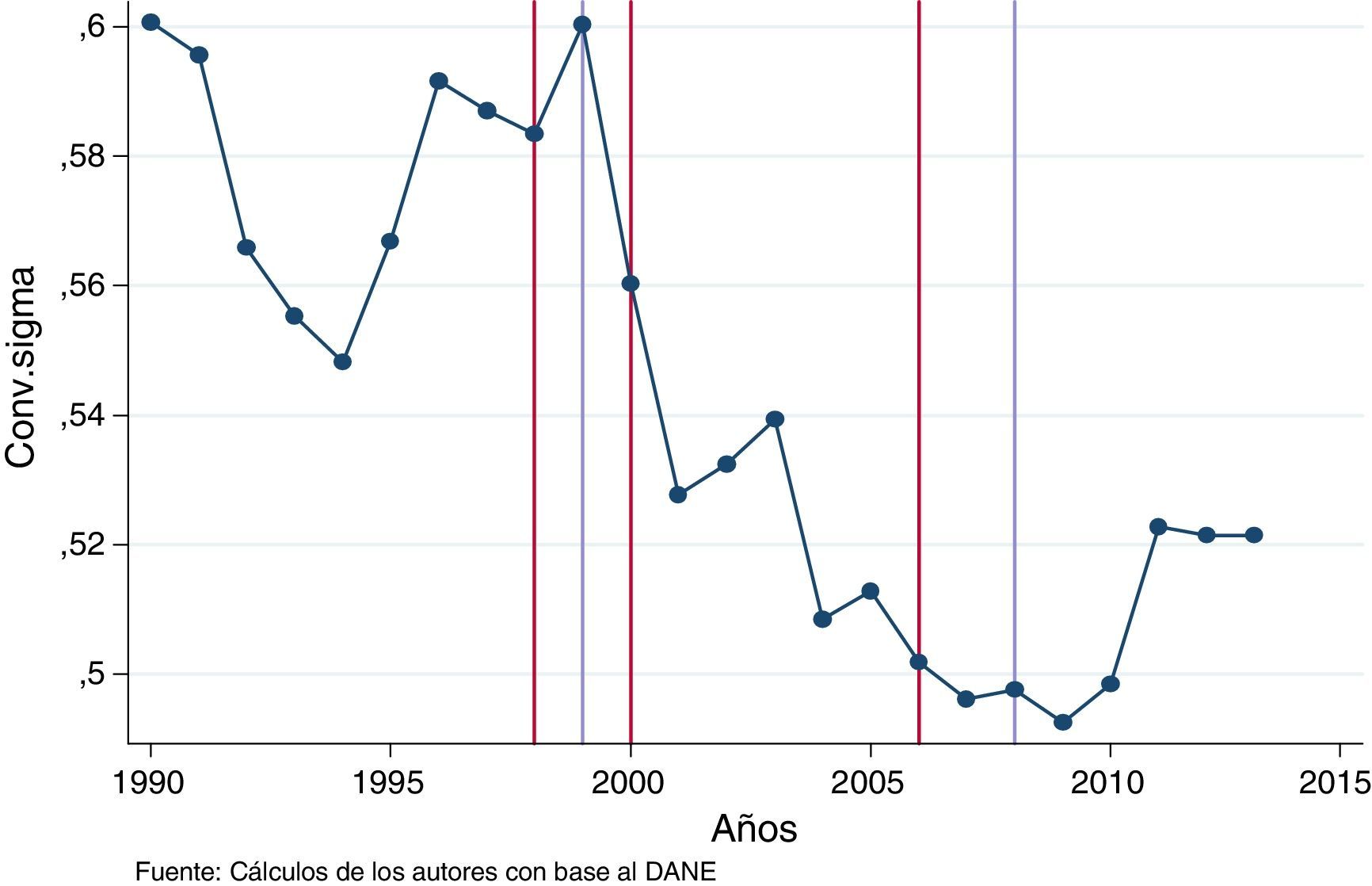
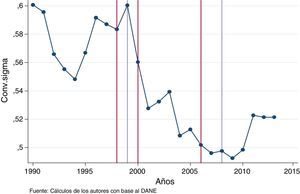
La convergencia sigma mide la desviación estándar del logaritmo del PIB pc. La evolución de este indicador muestra que durante el periodo 1990-1995 hubo una disminución en la dispersión de PIB pc, seguido de un aumento hasta 1999. Posterior a este año se presenta una tendencia a la baja hasta el 2007 y finalmente se presenta un aumento en la dispersión hasta el 2013, como se ilustra en la figura 1.
La figura 1 muestra la evolución de la dispersión en el PIB pc. Las líneas rojas son años de corte para el análisis de convergencia beta basado en la convergencia sigma. Los intervalos de tiempo seleccionados fueron 1990-2013, 2001-2013, 1990-1998, 1999-2006 y 2007-2013, tomando como línea de referencia el último año de cada intervalo, mientras que las líneas de color lavanda muestran los años de crisis internacionales para el periodo analizado 1999 y 2008. Como previamente se había mencionado, el análisis de convergencia en sigma pondera de igual manera las unidades departamentales sin tener en cuenta el tamaño de la población en cada una de ellas.
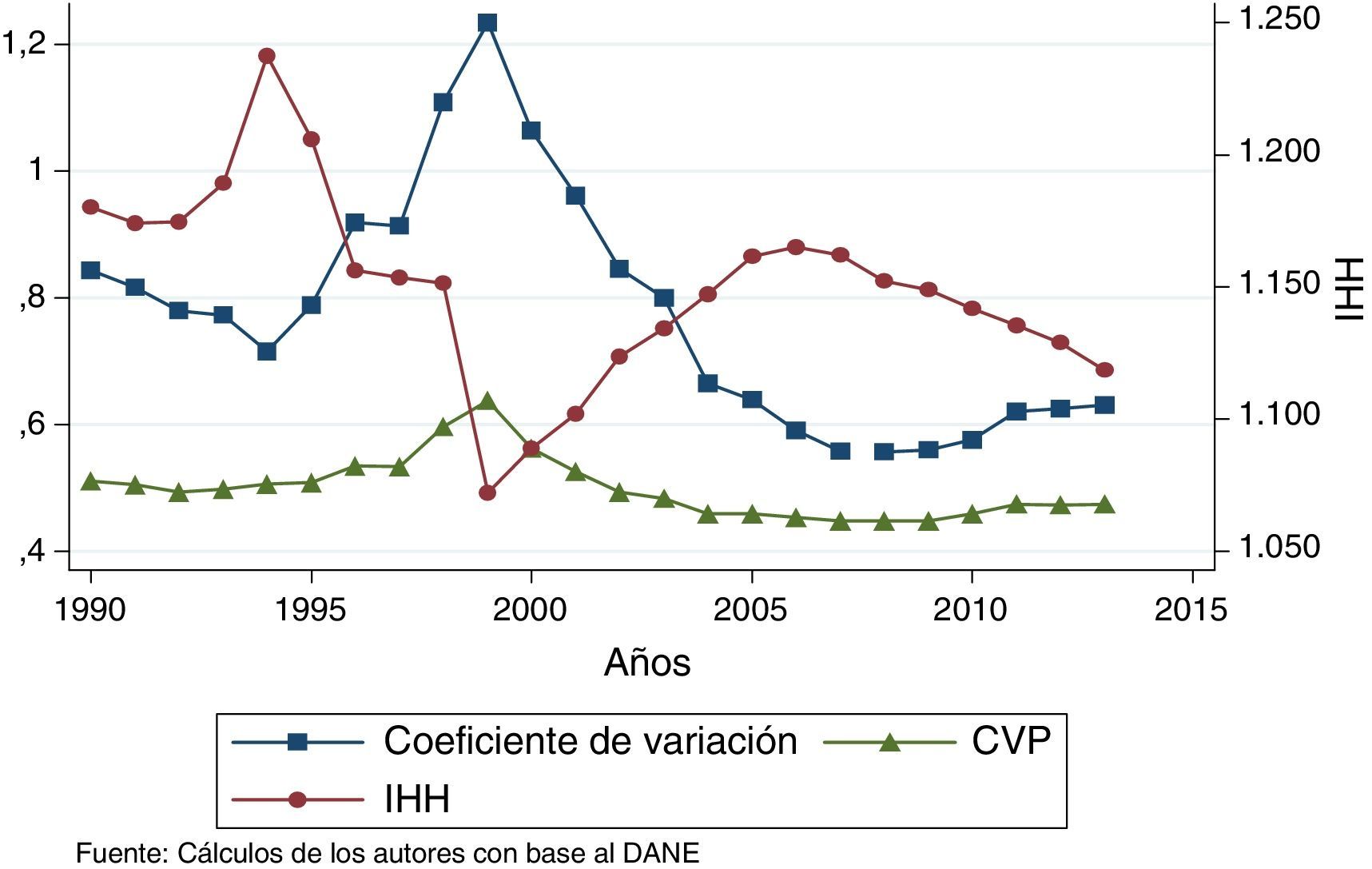
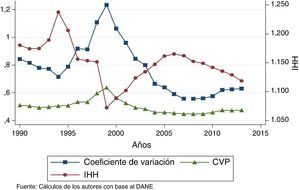
En la figura 2 se emplean 3 tipos de medidas para determinar la dispersión en el ingreso per cápita: la primera es el coeficiente de variación, la segunda es el coeficiente de variación ponderada, el cual toma en cuenta el tamaño relativo de la población en los departamentos, y finalmente el índice de Herfindahl-Hirschman, el cual mide el nivel de concentración del ingreso.
La figura 1, al igual que la figura 2, muestra un proceso de aumento en la dispersión desde 1990 hasta 1999 y a partir de 1999, un proceso de reducción. Una posible explicación a esto puede encontrarse en la crisis asiática de 1999 que afectó considerablemente a la economía colombiana debido a la mayor vulnerabilidad a los ciclos económicos mundiales resultado de la apertura económica de los años noventa (Kalmanovitz, 2010). Adicionalmente, la crisis del sector inmobiliario pudo ocasionar estos descensos en la disparidad regional. El índice de concentración de Herfindahl-Hirschman muestra una relación contracíclica con respecto al coeficiente de variación ponderada, lo cual indica que hay un aumento en la concentración espacial hasta 1994 que luego tiende a disminuir hasta 1999, y vuelve a crecer para años posteriores. Estos resultados coinciden con los de Galvis y Meisel (2012).
Los valores del PIB pc, como los de Arauca, Casanare y Bogotá, se vieron beneficiados por la apertura económica en la década de los noventa; especialmente Arauca y Casanare que, a pesar de tener actividades económicas como la ganadería y la agricultura, descubrieron campos petroleros en Cusiana y Cupiagua a principios de 1990. Estos departamentos concentraron así gran parte del ingreso nacional como participación en el PIB. Debido a la poca población en términos comparativos y a los altos niveles de regalías, se generó que el PIB pc de estos departamentos sea de los más altos del país.
Dentro de los efectos de la crisis asiática estuvo una caída en tasa de cambio, por la salida de capitales, así mismo como el aumento de la tasa de interés. Esto generó el colapso del sector inmobiliario y causó que los departamentos con mayores PIB pc desaceleraran su crecimiento, lo que a su vez ocasionó una menor participación de estos departamentos en el ingreso nacional.
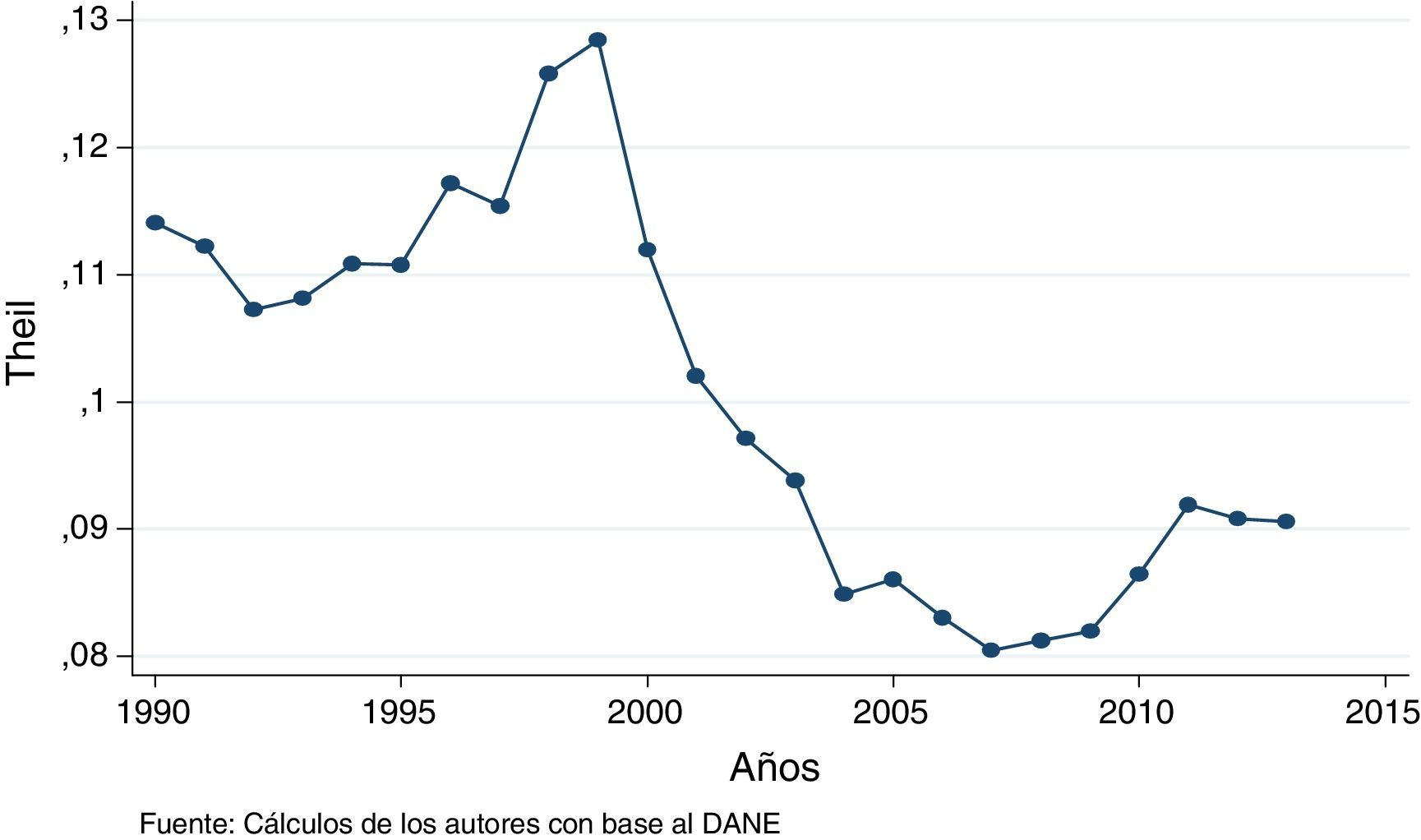
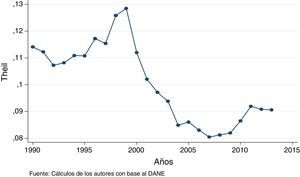
Estos resultados son corroborados por el índice de Theil, el cual muestra un aumento desde la apertura económica hacia un sistema desigual y a partir del 1999 evoluciona hacia un sistema igualitario (fig. 3).
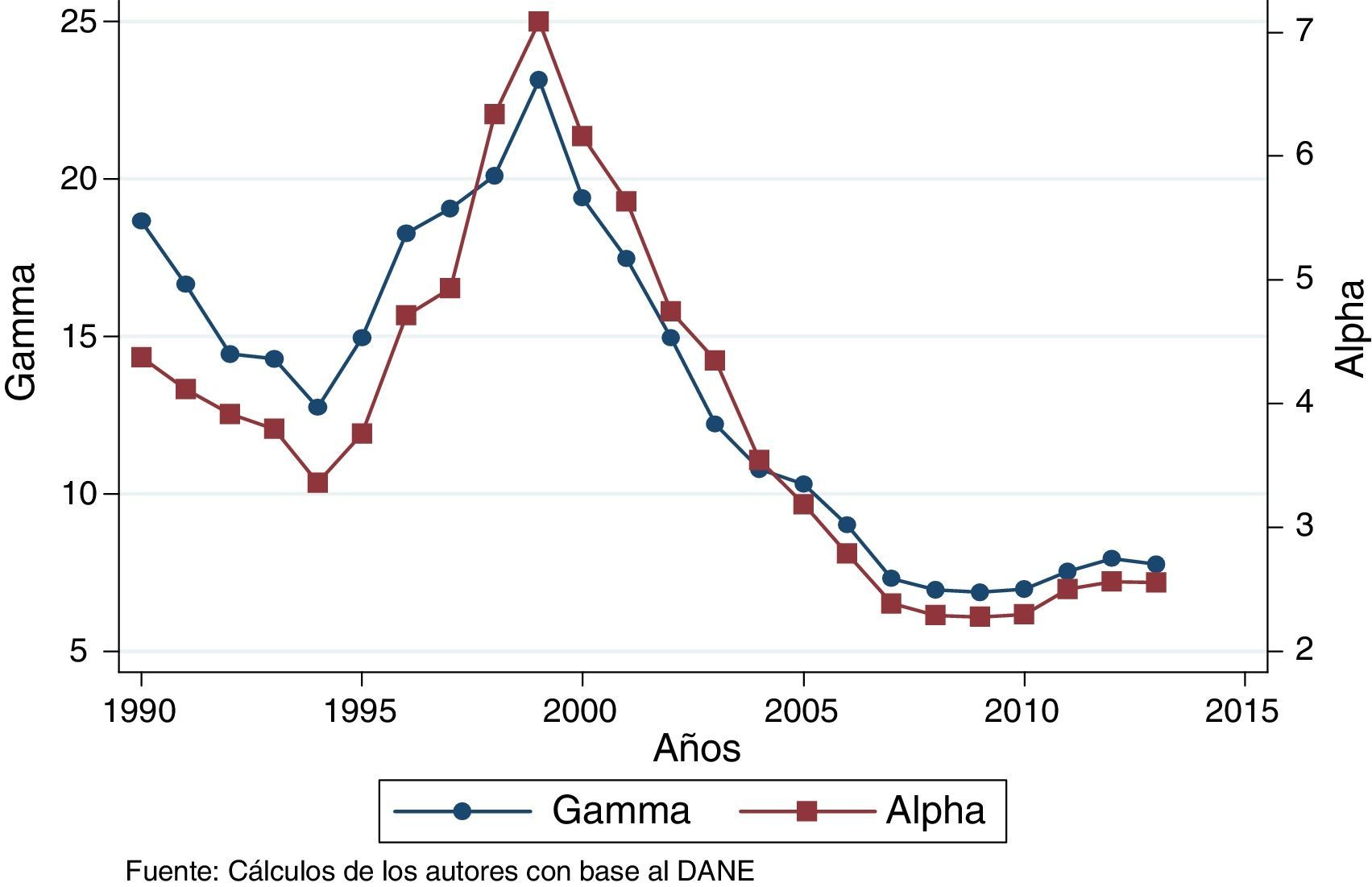
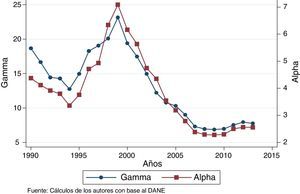
Finalmente, para el estudio de convergencia sigma, los indicadores alfa y gamma reafirman la hipótesis de que el aumento en las disparidades del PIB pc regional desde 1990 y su reducción a partir de 1999, se vieron influenciados por la reducción de los valores más altos, es decir, Arauca y Casanare, posiblemente debido al aumento por la apertura económica en 1990 y una disminución a la crisis de 1999, como lo muestra la figura 4.
En conclusión, la apertura de la economía en los años noventa y la crisis de 1999 son los choques en la economía que pueden haber influido en el crecimiento y reducción de las disparidades regionales. Los resultados son robustos debido a que casi todos los indicadores muestran las mismas tendencias.
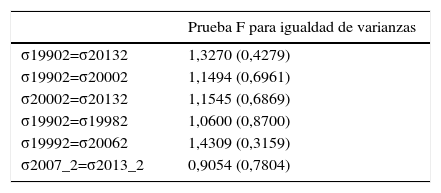
Finalmente, el análisis de la desviación estándar encontró que son estadísticamente no significativos para los intervalos de tiempo seleccionados, como lo muestra la tabla A.1 del Anexo, lo cual quiere decir que las desviaciones estándar son estadísticamente iguales. De esta forma, pueden escogerse los periodos relevantes para el análisis de convergencia en beta.
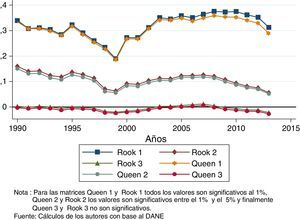
4.2I de Moran para el producto interno bruto per cápitaEl análisis de la I de Moran muestra la relación espacial de la variable en estudio usando la matriz de correlación espacial. Si bien hoy en día aún no hay un consenso acerca de cuál matriz es la que mide mejor la dependencia espacial, los principios que se deben incluyen que la matriz cuente con una diagonal de ceros y que la relación de la mayoría de valores en el espacio sean reales y positivos (Anselin, 2009). Como previamente se ha argumentado se hará inferencia sobre las matrices de contigüidad tanto queen como rook, estandarizadas para su mejor interpretación.
La matriz se hizo relacionando solo 32 de las 33 regiones, excluyendo a San Andrés y Providencia, debido a que no existe una relación claramente definida de contigüidad con alguna otra región. Como anteriormente se describía, el principal objetivo es determinar la relación espacial de las variables y su influencia en el crecimiento, ya sea por derrame o por una relación de empuje por aglomeración, y esta relación no se encuentra claramente definida para San Andrés y Providencia. Por esta razón se decide excluirla del estudio y por eso la matriz n×n será de tamaño 32×32.
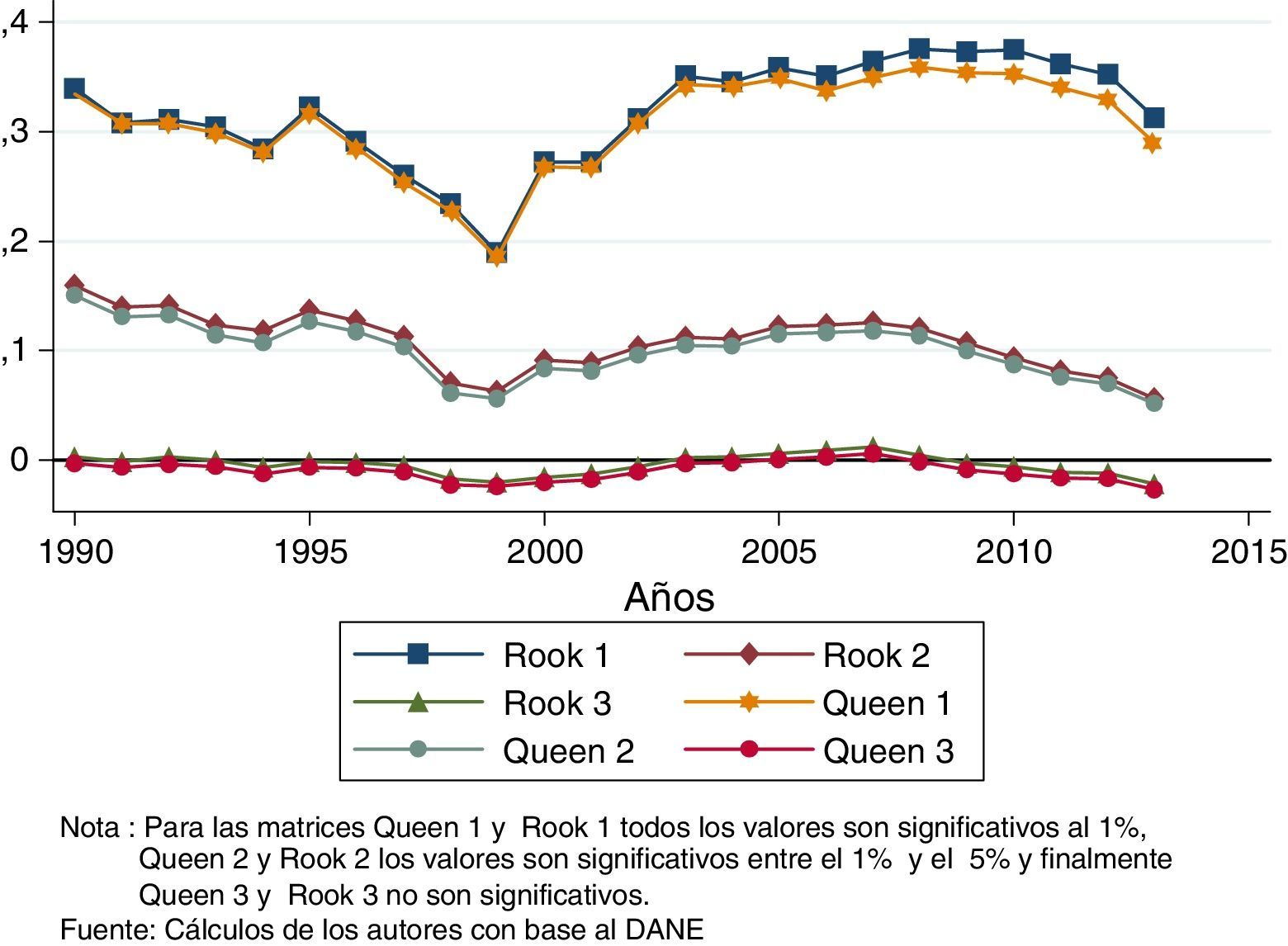
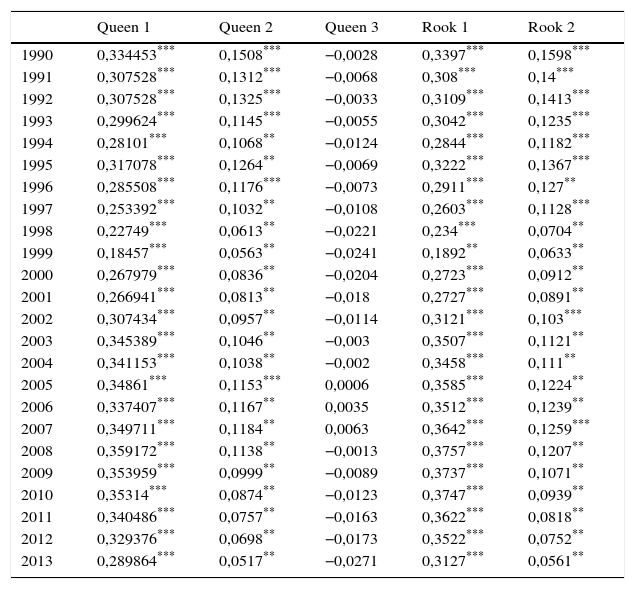
En la figura 5 se observan los resultados de las diferentes especificaciones de las matrices de contigüidad queen y rook. La inferencia de la I de Moran se realiza por simulaciones de Monte Carlo usando el programa GeoDa. Los resultados se muestran en la figura 5, donde se realizan 999 permutaciones para determinar si la correlación encontrada es significativa o no.
En la figura 5 encontramos una relación positiva de la I de Moran, lo que indica que los valores similares se encuentran cercanos unos a otros, es decir, las regiones con PIB pc altos se encuentran cercanas entre sí al igual que las regiones con PIB pc bajos con sus similares. El primer análisis que se puede hacer acerca de este indicador es que no existe ninguna diferencia significativa entre usar la matriz rook o queen, debido a la irregularidad geográfica existente en los departamentos de Colombia. Segundo, al aumentar el grado de contigüidad (queen y rook 2 y 3, las cuales relacionan regiones adyacentes de orden 2 y 3 respectivamente) disminuye la magnitud del índice. Esto es debido a que regiones de ingresos altos se relacionan con regiones de ingresos medios, y en la segunda relación de contigüidad, con regiones de valores bajos en el ingreso.
Por esto es que las matrices queen y rook 3 son no significativas y no existe relación espacial claramente definida. Por último, cabe anotar que la dependencia espacial tiende a reducirse hasta 1999 y en adelante tiende a aumentar, lo cual coincide con la relación encontrada en el índice de Herfindahl-Hirschman.
El indicador Herfindahl-Hirschman muestra la posible relación espacial que existe entre las variables y el crecimiento económico con lo cual se concluye el análisis exploratorio espacial, que hasta el momento muestra una relación clara de los departamentos y el PIB pc, con lo cual podemos proseguir al análisis de convergencia.
4.3Modelos de convergencia usando econometría espacialEl análisis se realizará para la ecuación número 7, estimada por mínimos cuadrados ordinarios (MCO) y métodos no lineales (NL). Esto debido a que los diagnósticos espaciales solo se pueden realizar sobre los residuos estimados para MCO. Sin embargo, también se empleará la metodología de la estimación por métodos NL descrita por Barro y Sala-i-Martin (1991) para determinar directamente la velocidad de convergencia β, demostrando que no difiere el coeficiente estimado del logaritmo natural del PIB pc con respecto al método de estimación.
Las estimaciones MCO y NL se hacen para los siguientes periodos:
- 1.
1990-2013 (todo el intervalo analizado).
- 2.
1990-2000.
- 3.
2001-2013.
- 4.
1990-1998.
- 5.
1999-2006.
- 6.
2007-2013.
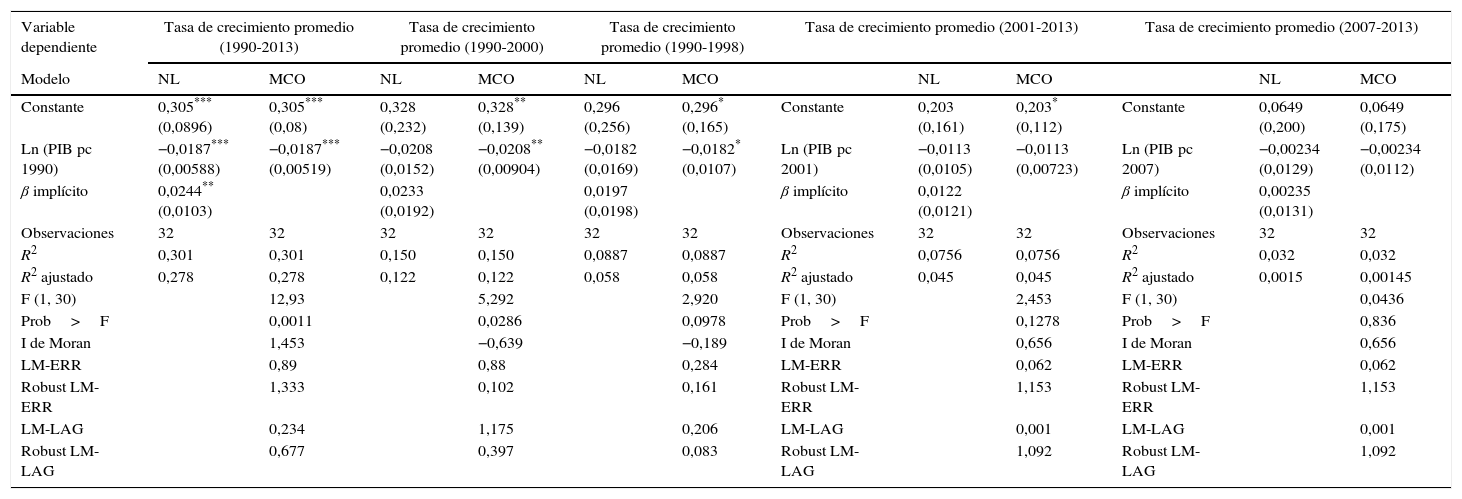
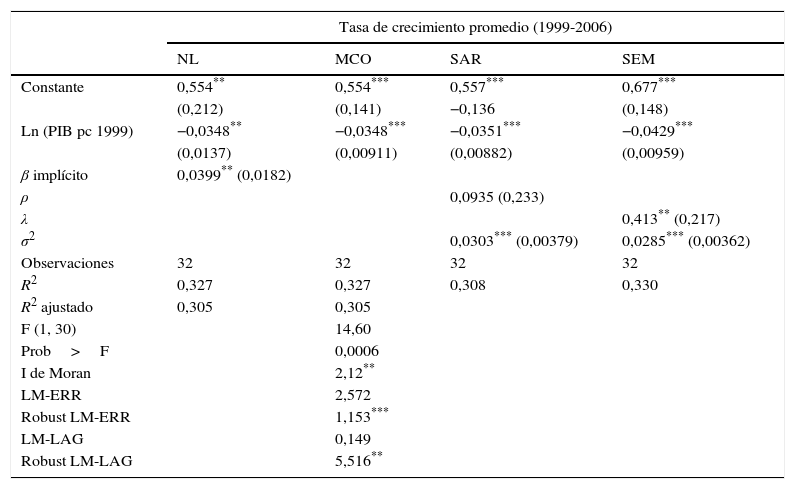
Esta división se realiza con el fin de detectar convergencia en diferentes periodos dentro de todo el intervalo estudiado. Con los resultados anteriores puede hacerse inferencia sobre los diagnósticos espaciales para determinar la existencia de algún tipo de dependencia espacial, ya sea de rezago (SAR) o residual (SER). Los resultados se exponen en la tabla 1, para los cuales no se encuentra evidencia de algún tipo de dependencia espacial en las regresiones, exceptuando el intervalo de 1999-2006 (ver tabla 2) para el cual se encuentran resultados favorables acerca de una correlación espacial dentro del modelo. Además, se observa que el coeficiente estimado que acompaña la variable del logaritmo del PIB pc no difiere entre la estimación por MCO y NL. Así mismo, la tabla 2 muestra los resultados para el modelo de convergencia en el periodo de tiempo 1999-2006 que arrojan la dependencia espacial señalada tanto en términos del error como de rezago espacial.
Resultados convergencia β usando la matriz de contigüidad queen 1
| Variable dependiente | Tasa de crecimiento promedio (1990-2013) | Tasa de crecimiento promedio (1990-2000) | Tasa de crecimiento promedio (1990-1998) | Tasa de crecimiento promedio (2001-2013) | Tasa de crecimiento promedio (2007-2013) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Modelo | NL | MCO | NL | MCO | NL | MCO | NL | MCO | NL | MCO | ||
| Constante | 0,305*** (0,0896) | 0,305*** (0,08) | 0,328 (0,232) | 0,328** (0,139) | 0,296 (0,256) | 0,296* (0,165) | Constante | 0,203 (0,161) | 0,203* (0,112) | Constante | 0,0649 (0,200) | 0,0649 (0,175) |
| Ln (PIB pc 1990) | −0,0187*** (0,00588) | −0,0187*** (0,00519) | −0,0208 (0,0152) | −0,0208** (0,00904) | −0,0182 (0,0169) | −0,0182* (0,0107) | Ln (PIB pc 2001) | −0,0113 (0,0105) | −0,0113 (0,00723) | Ln (PIB pc 2007) | −0,00234 (0,0129) | −0,00234 (0,0112) |
| β implícito | 0,0244** (0,0103) | 0,0233 (0,0192) | 0,0197 (0,0198) | β implícito | 0,0122 (0,0121) | β implícito | 0,00235 (0,0131) | |||||
| Observaciones | 32 | 32 | 32 | 32 | 32 | 32 | Observaciones | 32 | 32 | Observaciones | 32 | 32 |
| R2 | 0,301 | 0,301 | 0,150 | 0,150 | 0,0887 | 0,0887 | R2 | 0,0756 | 0,0756 | R2 | 0,032 | 0,032 |
| R2 ajustado | 0,278 | 0,278 | 0,122 | 0,122 | 0,058 | 0,058 | R2 ajustado | 0,045 | 0,045 | R2 ajustado | 0,0015 | 0,00145 |
| F (1, 30) | 12,93 | 5,292 | 2,920 | F (1, 30) | 2,453 | F (1, 30) | 0,0436 | |||||
| Prob>F | 0,0011 | 0,0286 | 0,0978 | Prob>F | 0,1278 | Prob>F | 0,836 | |||||
| I de Moran | 1,453 | −0,639 | −0,189 | I de Moran | 0,656 | I de Moran | 0,656 | |||||
| LM-ERR | 0,89 | 0,88 | 0,284 | LM-ERR | 0,062 | LM-ERR | 0,062 | |||||
| Robust LM-ERR | 1,333 | 0,102 | 0,161 | Robust LM-ERR | 1,153 | Robust LM-ERR | 1,153 | |||||
| LM-LAG | 0,234 | 1,175 | 0,206 | LM-LAG | 0,001 | LM-LAG | 0,001 | |||||
| Robust LM-LAG | 0,677 | 0,397 | 0,083 | Robust LM-LAG | 1,092 | Robust LM-LAG | 1,092 | |||||
El nivel de significación estadística de los coeficientes está representado como (*) significativo al 10%; (**) significativo al 5% y (***) significativo al 1%; los resultados entre paréntesis son las respectivas desviaciones estándar de cada coeficiente.
Fuente: cálculos realizados por los autores con base al DANE.
Resultados convergencia β usando la matriz de contigüidad queen 1
| Tasa de crecimiento promedio (1999-2006) | ||||
|---|---|---|---|---|
| NL | MCO | SAR | SEM | |
| Constante | 0,554** | 0,554*** | 0,557*** | 0,677*** |
| (0,212) | (0,141) | −0,136 | (0,148) | |
| Ln (PIB pc 1999) | −0,0348** | −0,0348*** | −0,0351*** | −0,0429*** |
| (0,0137) | (0,00911) | (0,00882) | (0,00959) | |
| β implícito | 0,0399** (0,0182) | |||
| ρ | 0,0935 (0,233) | |||
| λ | 0,413** (0,217) | |||
| σ2 | 0,0303*** (0,00379) | 0,0285*** (0,00362) | ||
| Observaciones | 32 | 32 | 32 | 32 |
| R2 | 0,327 | 0,327 | 0,308 | 0,330 |
| R2 ajustado | 0,305 | 0,305 | ||
| F (1, 30) | 14,60 | |||
| Prob>F | 0,0006 | |||
| I de Moran | 2,12** | |||
| LM-ERR | 2,572 | |||
| Robust LM-ERR | 1,153*** | |||
| LM-LAG | 0,149 | |||
| Robust LM-LAG | 5,516** | |||
El nivel de significación estadística de los coeficientes está representado como (*) significativo al 10%; (**) significativo al 5% y (***) significativo al 1%. Los valores entre paréntesis representan la desviación estándar correspondiente a cada coeficiente.
Fuente: cálculos propios de los autores con base al DANE.
Los resultados muestran un proceso de convergencia beta para el intervalo temporal comprendido entre 1990-2013. No existe evidencia estadística que compruebe la existencia de algún tipo de dependencia espacial. Para los valores de 1990 y 2013 la I de Moran es casi igual, de lo que se infiere que, al mantenerse las mismas relaciones del PIB pc, no existen cambios en el periodo. Esto se debe a que existe una relación espacial en el nivel del PIB pc, pero no existe evidencia a favor sobre dependencia en su tasa de crecimiento.
Para los intervalos de tiempo 1990-1998; 2001-2013, y 2007-2013 no existe evidencia estadística a favor de convergencia beta. Para el periodo comprendido entre 1990-2000 existe evidencia estadística débil de un proceso de convergencia debido a que la estimación MCO arroja resultados estadísticamente favorables, mientras que la NL no muestra tal evidencia. Por lo tanto, solo se encuentra evidencia clara a favor de convergencia beta para las regiones de Colombia entre los años 1990 a 2013 y 1999 a 2006 con una velocidad de convergencia de 2,44% y 3,99% respectivamente, encontrando solo para los años 1999 a 2006 evidencia a favor de dependencia espacial.
La tabla 2 muestra esta relación. Para los estimadores robustos del multiplicador de Lagrange se acepta la dependencia del rezago como la dependencia residual, encontrando evidencia a favor del modelo SEM. El modelo SAR muestra un coeficiente rho positivo pero no significativo, lo cual nos lleva a rechazar una dependencia espacial sustantiva, es decir, el crecimiento económico de un departamento en Colombia no es debido a un efecto contagio o de derrame. Para el modelo SEM se encuentra un valor de lambda positivo y significativo, de lo cual se deduce que la relación de crecimiento se ve impulsada o traslapada debido a choques o externalidades aleatorias no observables. Lo anterior significa que la relación de una región con sus vecinos no corresponde a una relación de crecimiento económico, sino a fenómenos de choques aleatorios e impredecibles de un departamento con otro que puede no ser su vecino inmediato. Así mismo, existe evidencia en contra de las economías regionales de aglomeración y relaciones económicas fuertes fuera de las fronteras administrativas.
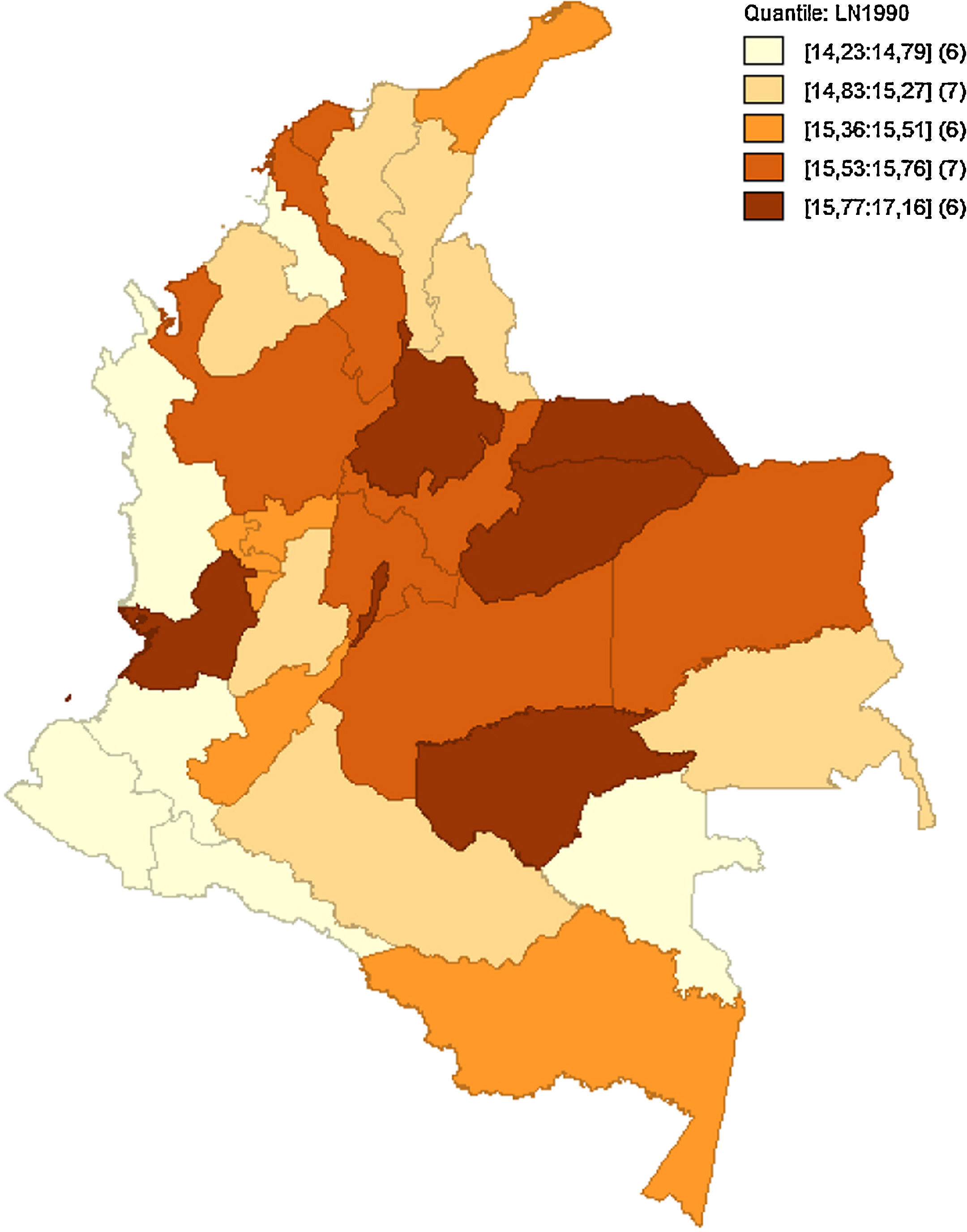
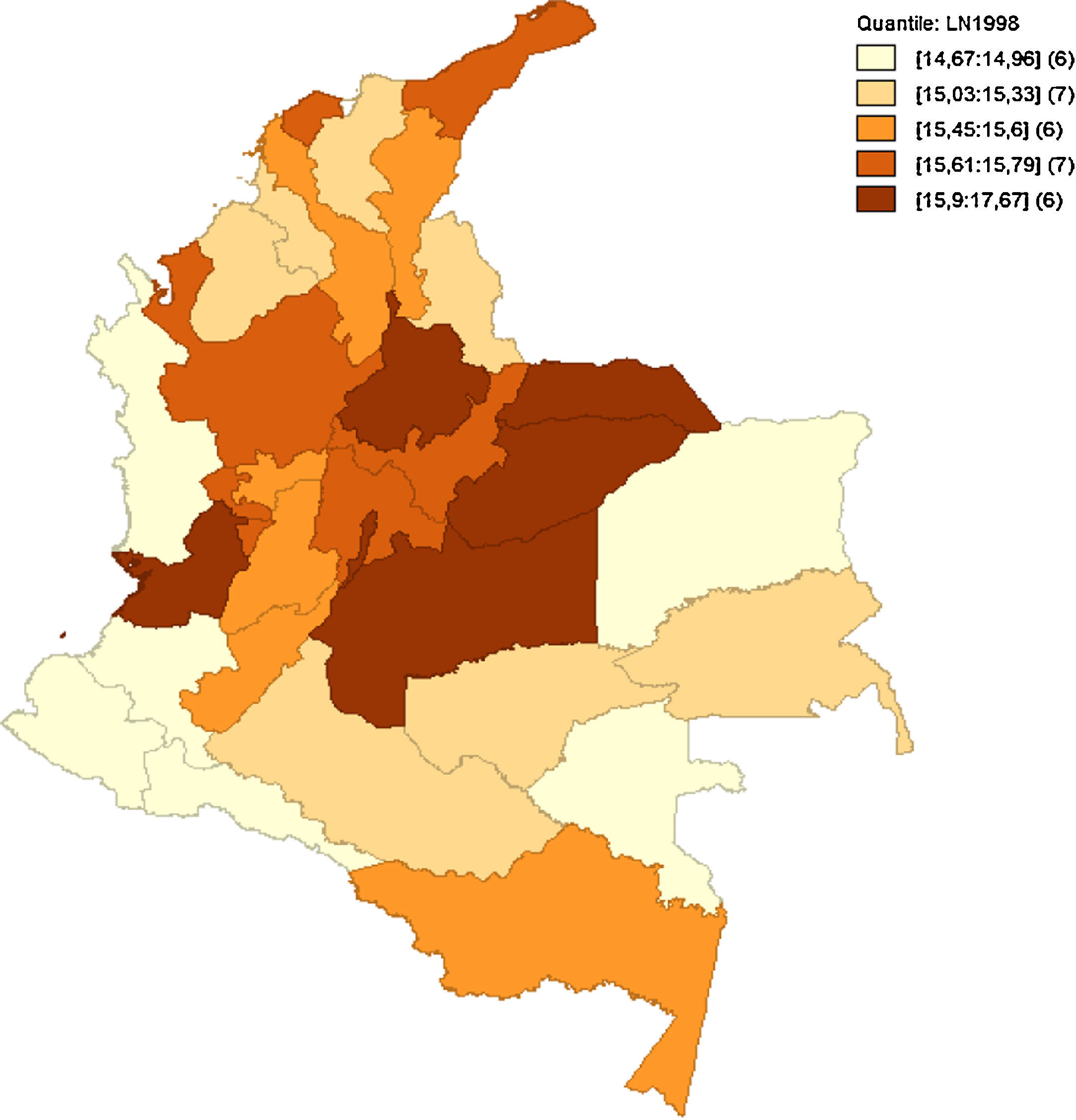
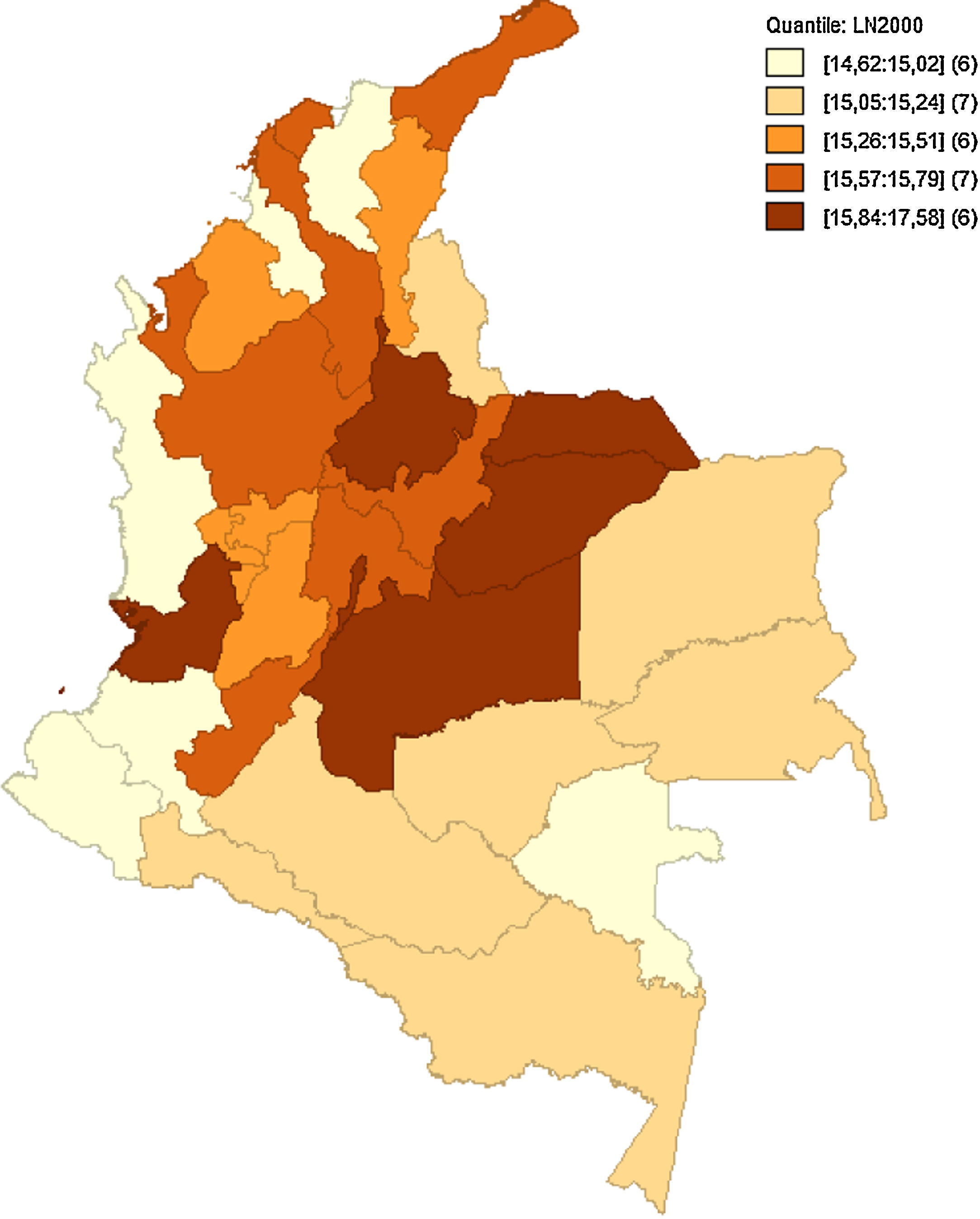
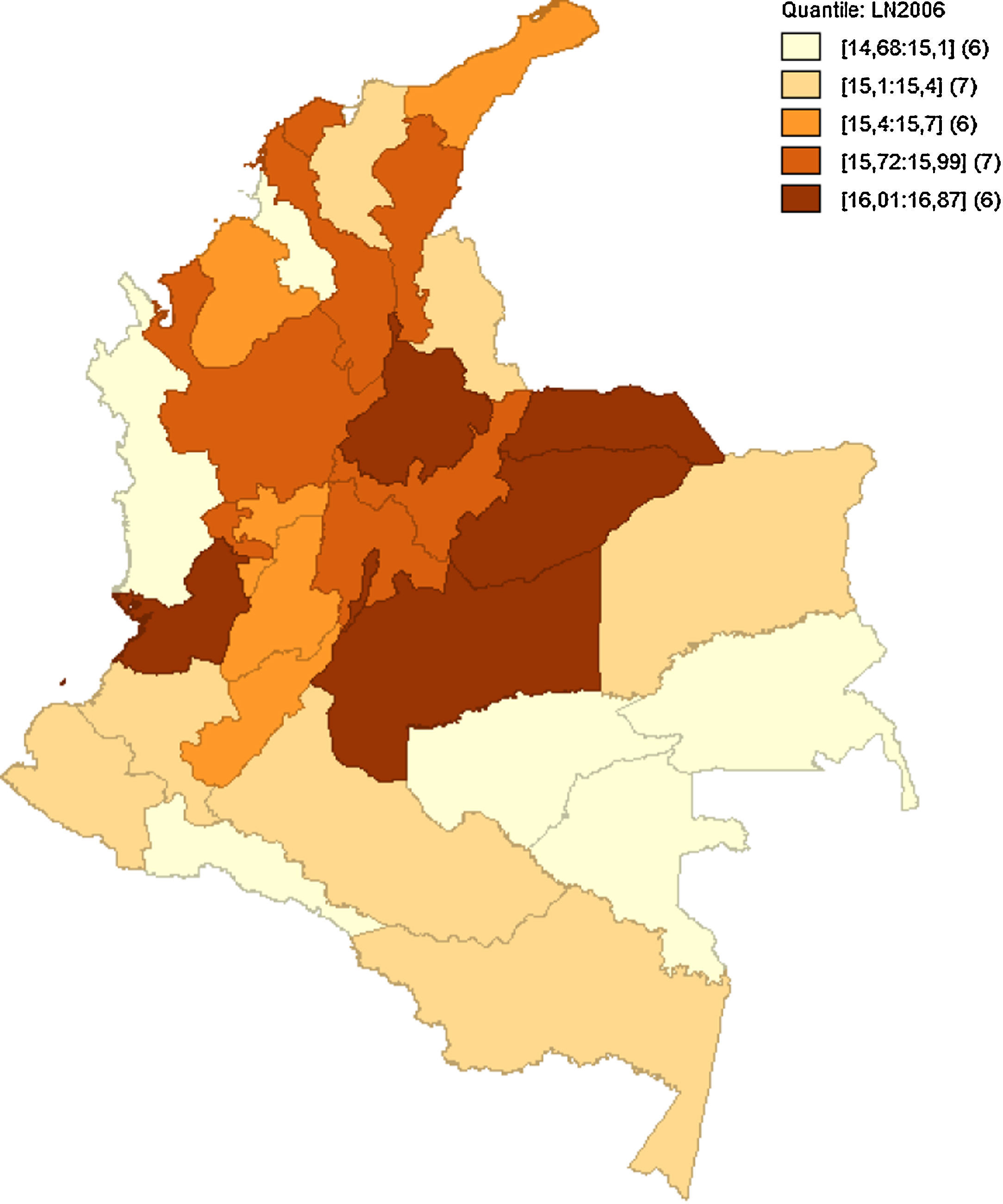
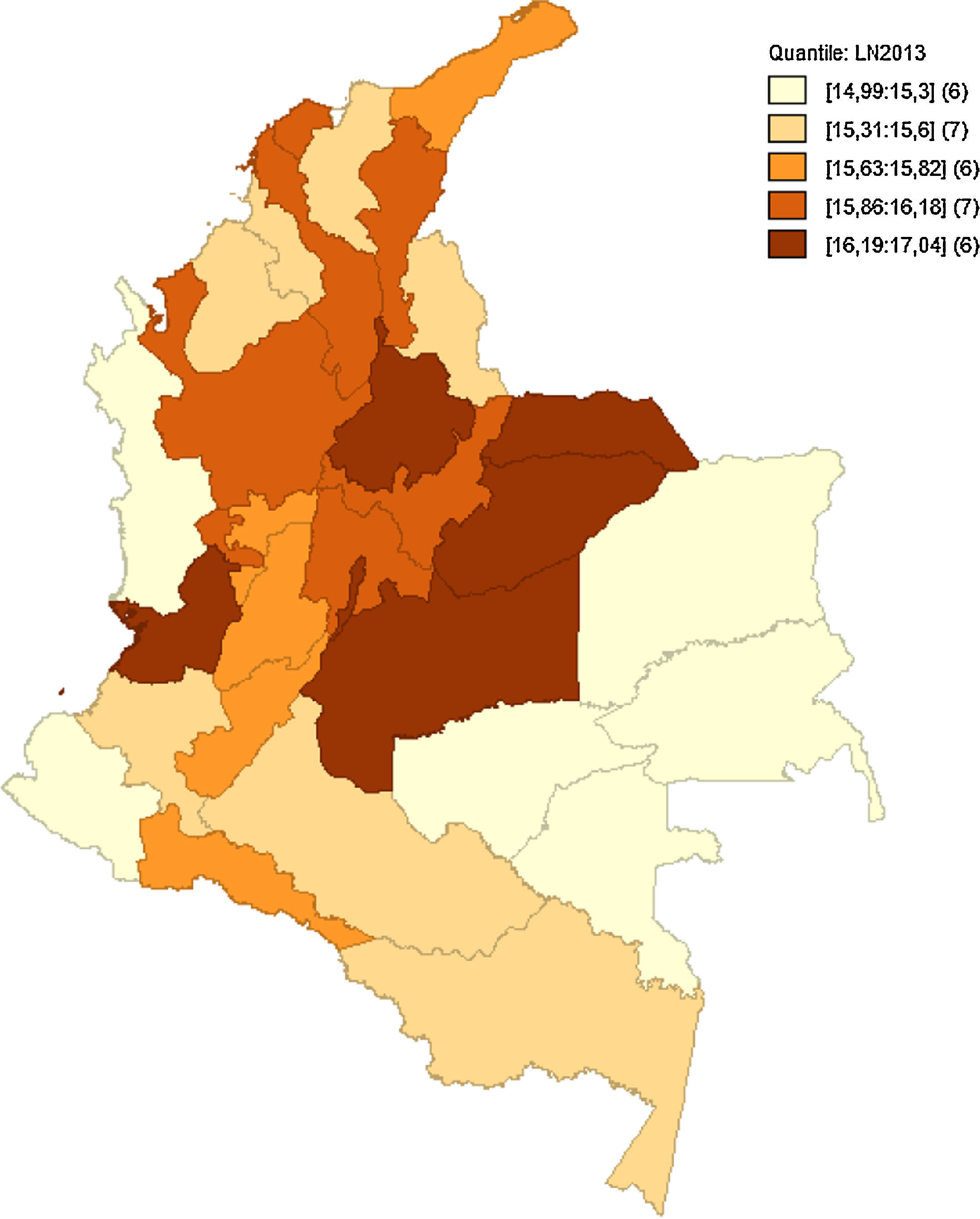
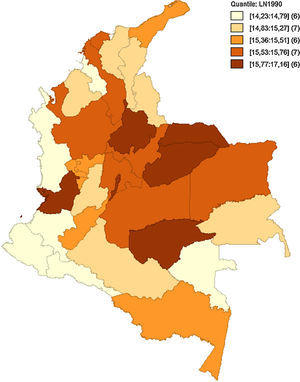
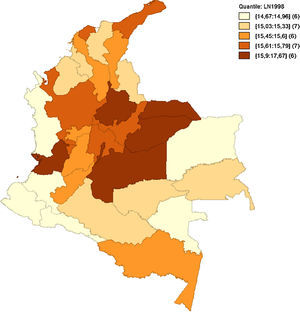
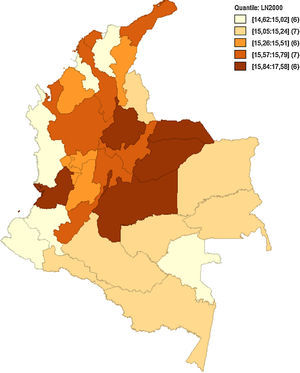
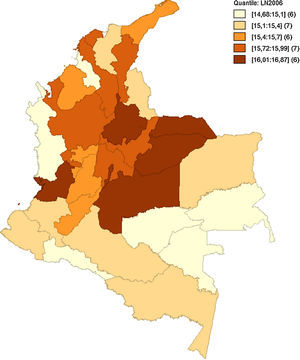
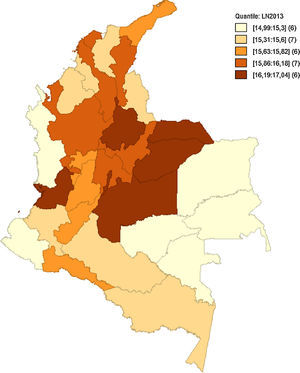
Como hace mención Quah (1993, 1996), el análisis implementado de forma estática no permite observar bien los efectos en el tiempo de las interacciones regionales y sus cambios. Como anteriormente se hacía referencia en la figura 5, las medidas de dependencia espacial no alcanzan a captar el posible relevo de unas regiones consideradas pobres a regiones de ingresos medios, o si bien las regiones de ingresos medios están desapareciendo para convertirse en regiones de ingresos altos o ingresos bajos. Las figuras 6–10 reflejan como ha sido la dinámica del ingreso en los departamentos respecto al tiempo, utilizando como indicador el logaritmo del PIB pc para suavizar las series.
Estos mapas muestran la transición del logaritmo del PIB pc, los cuales son agrupados por quintiles. Es notoria la transición de departamentos que anteriormente se consideraban de ingreso medio a ingreso bajo, como el caso de Amazonas, Guainía y Vichada, que para 1990 estaban entre los departamentos de ingreso medio y pasaron a ser regiones de ingreso bajo en 2013. Caso contrario son Putumayo, Cesar y Tolima. Esto puede haber sucedido por las políticas de fortalecimiento de regiones como el Eje Cafetero, región Andina y región Caribe. Esto fomenta la generación de clústeres en el centro y periferia del país, tal como se aprecia en el figura 10, dejando de lado las regiones limítrofes a Brasil y Perú.
En la región pacífica sobresale solo Valle del Cauca. Un factor adicional muy importante que explica este fenómeno es el conflicto armado. Regiones como Putumayo, Guaviare, Caquetá, Cauca y Nariño se han visto afectadas por violencia y desplazamiento de poblaciones campesinas, lo que genera a la vez una destrucción del capital humano. Hay regiones que se mantienen en el tiempo como regiones de PIB pc alto, como lo es Bogotá, Valle del Cauca, Santander, Casanare y Arauca, e incorporándose Meta a mediados de los noventa. Esto conduce a plantear un modelo que tenga en cuenta las implicaciones dinámicas y las variaciones de los posibles efectos, que tenga una mayor integración económica en la región, concentrándose principalmente en regiones como la Andina y la Caribe.
4.4Modelos de panel espacial con rezago espacial en la variable dependiente y en el términoSe estima finalmente el modelo de panel espacial planteado por Anselin et al. (2008) y Elhorst (2014). Este tiene varias ventajas sobre las estimaciones por MCO y NL: el modelo de panel espacial plantea una función con estimadores consistentes y asintóticamente insesgados; aumenta el número de observaciones, y permite eliminar los efectos cíclicos de las variables, lo cual es determinante para estimar los modelos de crecimiento a largo plazo.
Se estiman 2 conjuntos de modelos: el primero con intervalos de 10 años, en donde se compara el nivel inicial del PIB pc en el momento t y el crecimiento entre t y t+10 (por ejemplo el nivel de 1990 contra el crecimiento en el periodo 1900-2000); el segundo conjunto utiliza intervalos de 7 años (nivel inicial del PIB pc en el momento t y el crecimiento entre t y t+7). En cada uno de estos 2 conjuntos se estima un modelo de efectos fijos espaciales, uno de efectos fijos temporales y uno de efectos fijos espaciotemporales. El primer conjunto de modelos con intervalos de 10 años abarca todo el periodo 1990-2013. El segundo conjunto con intervalos de 7 años abarca 1999-2013. Esta división se realiza con el fin de analizar más detalladamente los resultados de los modelos MCO y NL anteriores que mostraban convergencia en los periodos 1990-2013 y 1999-2006.
Los resultados de las regresiones se encuentran en las tablas 3 y 4.
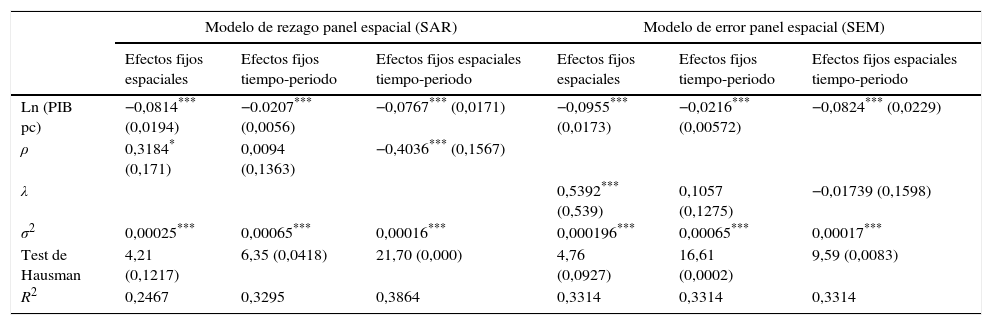
Modelo con tasas de crecimiento promedio a 10 años (1990-2013)
| Modelo de rezago panel espacial (SAR) | Modelo de error panel espacial (SEM) | |||||
|---|---|---|---|---|---|---|
| Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | |
| Ln (PIB pc) | −0,0814*** (0,0194) | −0.0207*** (0,0056) | −0,0767*** (0,0171) | −0,0955*** (0,0173) | −0,0216*** (0,00572) | −0,0824*** (0,0229) |
| ρ | 0,3184* (0,171) | 0,0094 (0,1363) | −0,4036*** (0,1567) | |||
| λ | 0,5392*** (0,539) | 0,1057 (0,1275) | −0,01739 (0,1598) | |||
| σ2 | 0,00025*** | 0,00065*** | 0,00016*** | 0,000196*** | 0,00065*** | 0,00017*** |
| Test de Hausman | 4,21 (0,1217) | 6,35 (0,0418) | 21,70 (0,000) | 4,76 (0,0927) | 16,61 (0,0002) | 9,59 (0,0083) |
| R2 | 0,2467 | 0,3295 | 0,3864 | 0,3314 | 0,3314 | 0,3314 |
El nivel de significación estadística de los coeficientes está representado como (*) significativo al 10%; (**) significativo al 5% y (***) significativo al 1%. Los valores entre paréntesis representan la desviación estándar correspondiente a cada coeficiente.
Para el test de Hausman se utilizó una distribución chi cuadrado con 2 grados de libertad y el valor entre paréntesis es su p-valor correspondiente.
Fuente: cálculos realizados por los autores con base al DANE.
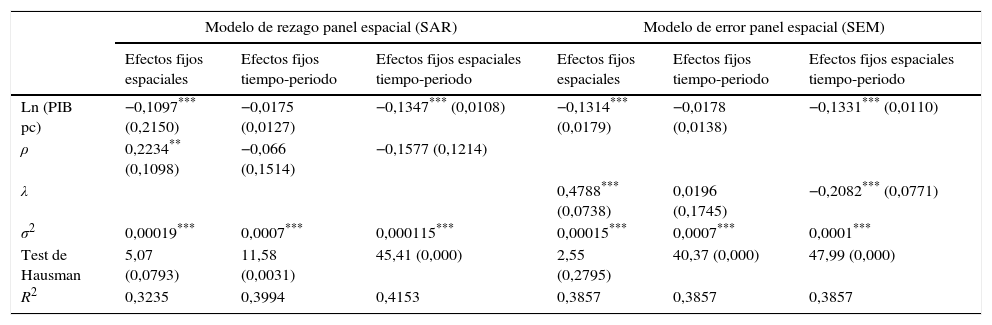
Modelo con tasas de crecimiento promedio a 7 años (1999-2013)
| Modelo de rezago panel espacial (SAR) | Modelo de error panel espacial (SEM) | |||||
|---|---|---|---|---|---|---|
| Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | |
| Ln (PIB pc) | −0,1097*** (0,2150) | −0,0175 (0,0127) | −0,1347*** (0,0108) | −0,1314*** (0,0179) | −0,0178 (0,0138) | −0,1331*** (0,0110) |
| ρ | 0,2234** (0,1098) | −0,066 (0,1514) | −0,1577 (0,1214) | |||
| λ | 0,4788*** (0,0738) | 0,0196 (0,1745) | −0,2082*** (0,0771) | |||
| σ2 | 0,00019*** | 0,0007*** | 0,000115*** | 0,00015*** | 0,0007*** | 0,0001*** |
| Test de Hausman | 5,07 (0,0793) | 11,58 (0,0031) | 45,41 (0,000) | 2,55 (0,2795) | 40,37 (0,000) | 47,99 (0,000) |
| R2 | 0,3235 | 0,3994 | 0,4153 | 0,3857 | 0,3857 | 0,3857 |
El nivel de significación estadística de los coeficientes está representado como (*) significativo al 10%; (**) significativo al 5% y (***) significativo al 1%. Los valores entre paréntesis representan la desviación estándar correspondiente a cada coeficiente.
Para el test de Hausman se utilizó una distribución chi cuadrado con 2 grados de libertad y el valor entre paréntesis es su p-valor correspondiente.
Fuente: cálculos realizados por los autores con base al DANE.
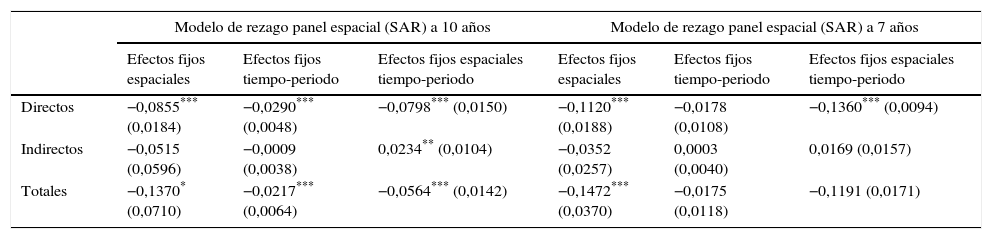
Se estimaron modelos de efectos fijos dado que el test de Hausman muestra la existencia de efectos fijos espaciotemporales y no efectos aleatorios. Para los modelos con intervalo de 10 años, este test ratifica como modelos de efectos fijos al SAR con efecto espaciotemporal, y a los SEM con efectos temporales y espaciotemporales. Sin embargo, en los modelos SEM el valor de lambda no es significativo ni para efectos fijos espaciales ni para efectos fijos temporales. En cambio, hay un valor significativo del rho en el modelo SAR, lo que concluye que el tipo de proceso de convergencia en este periodo es autorregresivo espacial con efectos fijos espaciotemporales. El valor de convergencia absoluta de este modelo es –0,0767 y altamente significativo. Por lo tanto, el proceso de convergencia para este periodo se dio gracias a que la tasa de crecimiento en un departamento pudo estar relacionada negativamente con la cantidad de factores existentes no solo en su economía, sino también en la de los departamentos vecinos, lo cual nos indica que el crecimiento experimentado tiene una dependencia espacial entre departamentos con efecto de contagio, tipo de efecto indirecto, directo y total (ver la tabla A.6 del Anexo). Como muestran los resultados, y debido a que todos estos efectos son diferentes entre sí y además significativos, se concluye que el crecimiento es mayor cuando sus vecinos crecen también a tasas elevadas, y menor cuando las regiones vecinas crecen lentamente. Todo esto nos lleva a deducir que los departamentos con PIB pc altos se mantienen en el tiempo (Bogotá, Santander, Arauca, Casanare, Meta y Valle del Cauca) y los departamentos con PIB pc bajos permanecen también (Chocó, Vaupés, Guainía y Vichada), lo cual muestra un proceso de convergencia gracias a la transición principalmente de departamentos en la región Andina y Caribe de ingresos bajos a medios, y de departamentos situados en la región Amazonas y Orinoquia de ingresos medios a bajos, tal como lo muestran los mapas de la sección 4.3.
Como se mencionaba anteriormente, la dinámica de rezago espacial muestra que la relación y la dinámica de crecimiento en los departamentos son positivas si se encuentran en las regiones Andina y Caribe, siendo negativas si se encuentran en la región Amazonas y parte Orinoquia. Esto nos muestra una relación hacia el crecimiento basado en las desigualdades departamentales que van creciendo y manteniéndose en el tiempo. Los departamentos con PIB pc alto y bajo se mantienen en el tiempo y tienen un impacto con sus vecinos. No hay evidencia de convergencia en el sentido tradicional, según la cual la renta de los departamentos pobres se acerca a la de los departamentos más ricos en todo el país, sino por el contrario un tipo de convergencia regional, en que las zonas Andina y Caribe concentraron en este periodo gran parte del ingreso nacional per cápita junto con departamentos como Meta, Arauca y Casanare que se mantienen con PIB pc altos por las regalías que producen la explotación petrolera y minera.
La tabla 4 muestra el proceso de convergencia en beta para los años posteriores a 1999. Al igual que en el modelo anterior que seleccionamos se realiza el test de Hausman, donde el estadístico ratifica efectos fijos en SAR con efectos espaciotemporales, SEM con efecto temporal y SEM con efecto espaciotemporal. Sin embargo, contrario al conjunto de modelos con intervalos de 10 años, el rho del modelo SAR no fue significativo, escogiendo los modelos SEM que sí tienen un lambda diferente de cero. Se observa un proceso de convergencia del PIB pc con un valor de convergencia absoluta de –0,1314, –0,0178 y –0,1331 para efectos fijos espaciales, temporales y espaciotemporal respectivamente, siendo significativos solo para el primero y tercero al 1%.
Lo anterior muestra que el proceso de convergencia absoluta para el periodo de 1999-2013, con un coeficiente estimado para el logaritmo del PIB pc de –0,1331 significativo al 1%, se da fuera de las fronteras administrativas, lo cual indica un proceso de crecimiento debido a choques aleatorios o imposibles de anticipar en los departamentos vecinos. Estos efectos se pueden dar para el caso de Colombia debido a varios factores: primero, el desplazamiento forzado debido al conflicto armado, lo cual ocasiona una pérdida de capital humano donde poblaciones que subsistían a partir de cultivos que solo se puedan plantar en una zona y clima en particular, al verse desplazadas, estas habilidades se vuelven obsoletas en otras regiones. Segundo, las políticas económicas a favor de un aumento en el gasto público o inversiones inesperadas por el hallazgo de recursos naturales, es decir, aumentos impredecibles para los departamentos vecinos del PIB regional son los que generan la dinámica hacia el crecimiento. Finalmente, como se muestra en Kalmanovitz (2010), hay un aumento en la inversión a partir del 2001 gracias a la recuperación de la confianza en la seguridad nacional. En conclusión, la dinámica que incentiva el crecimiento a partir de 1990 se da fuera de las interacciones económicas de un departamento junto con sus vecinos, además de choques aleatorios que aumentan o disminuyen el crecimiento de un departamento.
5ConclusionesEl presente documento responde a la pregunta: ¿hay convergencia económica en las regiones de Colombia tomando en cuenta los factores de espacio y tiempo dentro del modelo en el periodo 1990-2013? Para ello usa el análisis de dispersión de la renta y la estimación de modelos de econometría espacial. Los resultados confirman la hipótesis de convergencia departamental para los periodos 1990-2013 y 1999-2006 en Colombia, con velocidades de 2,44% y 3,99% respectivamente. Por un lado, al incorporar los efectos espaciales en el modelo de convergencia, se encontró evidencia de dependencia espacial en términos del error para el periodo 1999 a 2013, y la existencia de rezago espacial en el modelo de panel de 1990 a 2003. Así mismo, se infiere que se ha generado un grupo de departamentos con ingresos altos relacionándose entre sí (como es el caso de la región Andina y Caribe junto con departamentos como Meta, Arauca, Casanare y Valle del Cauca), y la convergencia se ha dado hacia estas regiones (Andina y Caribe) debido a un proceso de mayores políticas económicas y efectos de choques aleatorios como relación espacial, la cual afecta de forma tanto directa como indirecta a los departamentos vecinos. Por otro lado, los grupos de departamentos con PIB pc bajos se han mantenido y agrupado. Esto coincide con la hipótesis de clubes de convergencia, pues los mapas presentados en el trabajo muestran cómo se han mantenido y concentrado estas regiones de PIB pc alto y bajo. Los resultados de los modelos panel muestran cómo desde 1990 esta convergencia regional se da por un efecto de contagio, pero luego de 1999 tiene que ver con efectos económicos no observables.
Se propone hacer nuevas investigaciones usando esta metodología que muestren la dinámica espacial dentro y fuera de las regiones, utilizando como variables de control índices de pobreza para determinar cómo influyen y qué tipo de efectos generan tales variables en el crecimiento. Además, pueden realizarse estudios usando esta metodología alrededor de variables microeconómicas como el proceso de aglomeración de empresas entre regiones. Finalmente, se proponen políticas de integración económica enfocadas en las regiones Amazonas y Orinoquía, las cuales han sido las principales afectadas en este proceso de convergencia, en donde se podría incentivar el crecimiento económico a partir de factores medioambientales y llevar a una integración económica y un crecimiento sostenible.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Prueba para la hipótesis de convergencia sigma
| Prueba F para igualdad de varianzas | |
|---|---|
| σ19902=σ20132 | 1,3270 (0,4279) |
| σ19902=σ20002 | 1,1494 (0,6961) |
| σ20002=σ20132 | 1,1545 (0,6869) |
| σ19902=σ19982 | 1,0600 (0,8700) |
| σ19992=σ20062 | 1,4309 (0,3159) |
| σ2007_2=σ2013_2 | 0,9054 (0,7804) |
La tabla anota los valores del estadístico F; los valores entre paréntesis son la probabilidad del estadístico F bajo la hipótesis nula de igualdad entre varianzas.
Fuente: cálculos realizados por los autores con base al DANE.
Índice de Moran
| Queen 1 | Queen 2 | Queen 3 | Rook 1 | Rook 2 | |
|---|---|---|---|---|---|
| 1990 | 0,334453*** | 0,1508*** | −0,0028 | 0,3397*** | 0,1598*** |
| 1991 | 0,307528*** | 0,1312*** | −0,0068 | 0,308*** | 0,14*** |
| 1992 | 0,307528*** | 0,1325*** | −0,0033 | 0,3109*** | 0,1413*** |
| 1993 | 0,299624*** | 0,1145*** | −0,0055 | 0,3042*** | 0,1235*** |
| 1994 | 0,28101*** | 0,1068** | −0,0124 | 0,2844*** | 0,1182*** |
| 1995 | 0,317078*** | 0,1264** | −0,0069 | 0,3222*** | 0,1367*** |
| 1996 | 0,285508*** | 0,1176*** | −0,0073 | 0,2911*** | 0,127** |
| 1997 | 0,253392*** | 0,1032** | −0,0108 | 0,2603*** | 0,1128*** |
| 1998 | 0,22749*** | 0,0613** | −0,0221 | 0,234*** | 0,0704** |
| 1999 | 0,18457*** | 0,0563** | −0,0241 | 0,1892** | 0,0633** |
| 2000 | 0,267979*** | 0,0836** | −0,0204 | 0,2723*** | 0,0912** |
| 2001 | 0,266941*** | 0,0813** | −0,018 | 0,2727*** | 0,0891** |
| 2002 | 0,307434*** | 0,0957** | −0,0114 | 0,3121*** | 0,103*** |
| 2003 | 0,345389*** | 0,1046** | −0,003 | 0,3507*** | 0,1121** |
| 2004 | 0,341153*** | 0,1038** | −0,002 | 0,3458*** | 0,111** |
| 2005 | 0,34861*** | 0,1153*** | 0,0006 | 0,3585*** | 0,1224** |
| 2006 | 0,337407*** | 0,1167** | 0,0035 | 0,3512*** | 0,1239** |
| 2007 | 0,349711*** | 0,1184** | 0,0063 | 0,3642*** | 0,1259*** |
| 2008 | 0,359172*** | 0,1138** | −0,0013 | 0,3757*** | 0,1207** |
| 2009 | 0,353959*** | 0,0999** | −0,0089 | 0,3737*** | 0,1071** |
| 2010 | 0,35314*** | 0,0874** | −0,0123 | 0,3747*** | 0,0939** |
| 2011 | 0,340486*** | 0,0757** | −0,0163 | 0,3622*** | 0,0818** |
| 2012 | 0,329376*** | 0,0698** | −0,0173 | 0,3522*** | 0,0752** |
| 2013 | 0,289864*** | 0,0517** | −0,0271 | 0,3127*** | 0,0561** |
El nivel de significación estadística de los coeficientes está representado como (*) significativo al 10%; (**) significativo al 5% y (***) significativo al 1%.
Fuente: cálculos realizados por los autores con base al DANE.
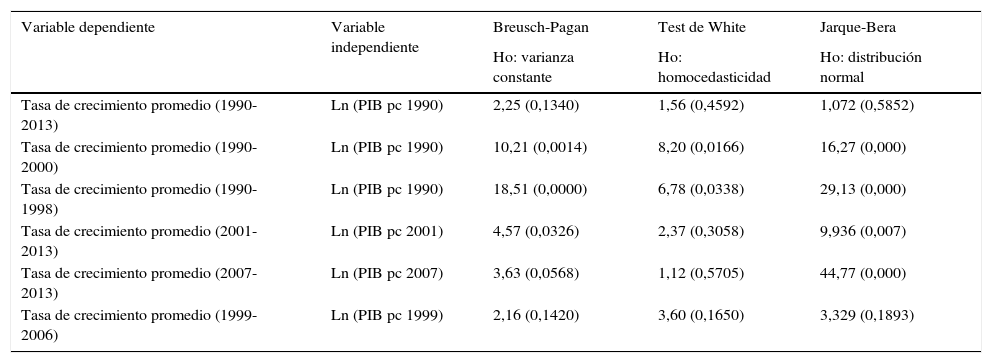
Pruebas para las regresiones MCO para convergencia β usando la matriz de contigüidad queen 1
| Variable dependiente | Variable independiente | Breusch-Pagan | Test de White | Jarque-Bera |
|---|---|---|---|---|
| Ho: varianza constante | Ho: homocedasticidad | Ho: distribución normal | ||
| Tasa de crecimiento promedio (1990-2013) | Ln (PIB pc 1990) | 2,25 (0,1340) | 1,56 (0,4592) | 1,072 (0,5852) |
| Tasa de crecimiento promedio (1990-2000) | Ln (PIB pc 1990) | 10,21 (0,0014) | 8,20 (0,0166) | 16,27 (0,000) |
| Tasa de crecimiento promedio (1990-1998) | Ln (PIB pc 1990) | 18,51 (0,0000) | 6,78 (0,0338) | 29,13 (0,000) |
| Tasa de crecimiento promedio (2001-2013) | Ln (PIB pc 2001) | 4,57 (0,0326) | 2,37 (0,3058) | 9,936 (0,007) |
| Tasa de crecimiento promedio (2007-2013) | Ln (PIB pc 2007) | 3,63 (0,0568) | 1,12 (0,5705) | 44,77 (0,000) |
| Tasa de crecimiento promedio (1999-2006) | Ln (PIB pc 1999) | 2,16 (0,1420) | 3,60 (0,1650) | 3,329 (0,1893) |
Para el test de Breusch-Pagan se utilizó una distribución chi cuadrado con un grado de libertad; para el test de White, una distribución chi cuadrado con 2 grados de libertad al igual que para la prueba de Jarque-Bera; el valor entre paréntesis es la prob>chi.
Fuente: cálculos realizados por los autores con base al DANE.
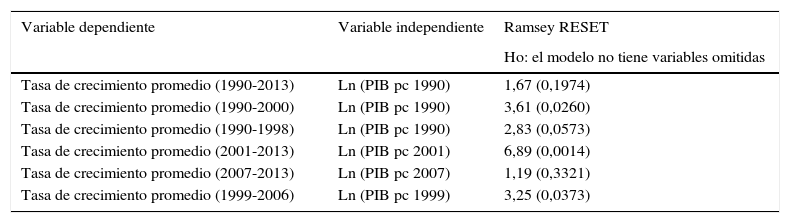
Pruebas para las regresiones MCO para convergencia β usando la matriz de contigüidad queen 1
| Variable dependiente | Variable independiente | Ramsey RESET |
|---|---|---|
| Ho: el modelo no tiene variables omitidas | ||
| Tasa de crecimiento promedio (1990-2013) | Ln (PIB pc 1990) | 1,67 (0,1974) |
| Tasa de crecimiento promedio (1990-2000) | Ln (PIB pc 1990) | 3,61 (0,0260) |
| Tasa de crecimiento promedio (1990-1998) | Ln (PIB pc 1990) | 2,83 (0,0573) |
| Tasa de crecimiento promedio (2001-2013) | Ln (PIB pc 2001) | 6,89 (0,0014) |
| Tasa de crecimiento promedio (2007-2013) | Ln (PIB pc 2007) | 1,19 (0,3321) |
| Tasa de crecimiento promedio (1999-2006) | Ln (PIB pc 1999) | 3,25 (0,0373) |
Para el test de Ramsey RESET se utilizó una distribución F (3,27); el valor entre paréntesis es la prob>F (3,27).
Fuente: cálculos realizados por los autores con base al DANE.
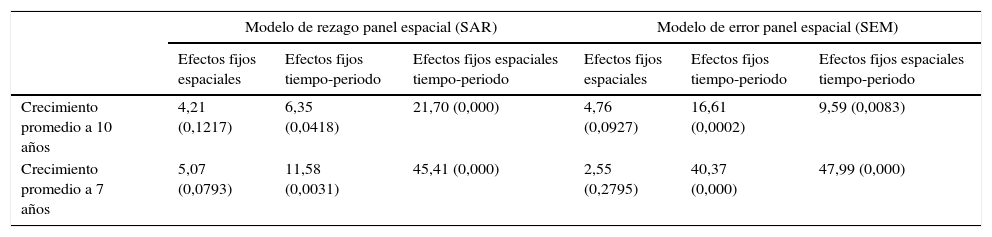
Test de Hausman para los modelos de panel espacial
| Modelo de rezago panel espacial (SAR) | Modelo de error panel espacial (SEM) | |||||
|---|---|---|---|---|---|---|
| Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | |
| Crecimiento promedio a 10 años | 4,21 (0,1217) | 6,35 (0,0418) | 21,70 (0,000) | 4,76 (0,0927) | 16,61 (0,0002) | 9,59 (0,0083) |
| Crecimiento promedio a 7 años | 5,07 (0,0793) | 11,58 (0,0031) | 45,41 (0,000) | 2,55 (0,2795) | 40,37 (0,000) | 47,99 (0,000) |
Para el test de Hausman se utilizó una distribución chi cuadrado con 2 grados de libertad.
Fuente: cálculos realizados por los autores con base al DANE.
Efectos directos, indirectos y totales para los modelos SAR panel espacial
| Modelo de rezago panel espacial (SAR) a 10 años | Modelo de rezago panel espacial (SAR) a 7 años | |||||
|---|---|---|---|---|---|---|
| Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | Efectos fijos espaciales | Efectos fijos tiempo-periodo | Efectos fijos espaciales tiempo-periodo | |
| Directos | −0,0855*** (0,0184) | −0,0290*** (0,0048) | −0,0798*** (0,0150) | −0,1120*** (0,0188) | −0,0178 (0,0108) | −0,1360*** (0,0094) |
| Indirectos | −0,0515 (0,0596) | −0,0009 (0,0038) | 0,0234** (0,0104) | −0,0352 (0,0257) | 0,0003 (0,0040) | 0,0169 (0,0157) |
| Totales | −0,1370* (0,0710) | −0,0217*** (0,0064) | −0,0564*** (0,0142) | −0,1472*** (0,0370) | −0,0175 (0,0118) | −0,1191 (0,0171) |
El nivel de significación estadística de los coeficientes está representado como (*) significativo al 10%; (**) significativo al 5% y (***) significativo al 1%; los resultados entre paréntesis son las respectivas desviaciones estándar de cada coeficiente.
Fuente: cálculos realizados por los autores con base al DANE.
Por sus siglas en inglés Spatial Autoregressive.
Modelos de error espacial por sus siglas en inglés Spatial Error Model.
Debido a que se toma al PIB per cápita como variable dependiente e independiente, no se usa el modelo SLX, más apropiado para determinar convergencia condicional. Al estimar los modelos SAR y SEM, se realizaron las pruebas que descartaron la utilización de los modelos Durbin espaciales.