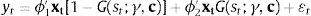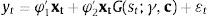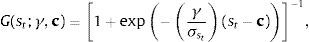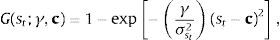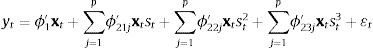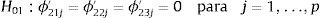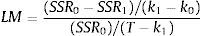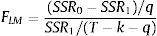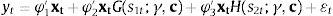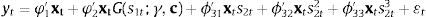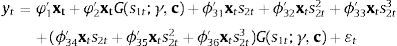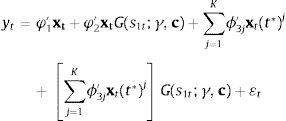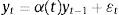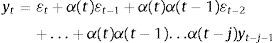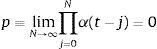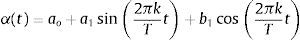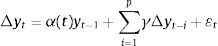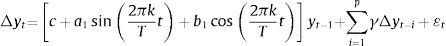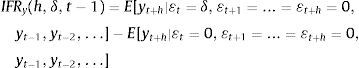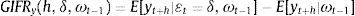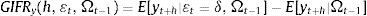En este documento se estima el impacto de los fenómenos climáticos sobre el crecimiento de la inflación de alimentos. Para ello se utilizan funciones de impulso-respuesta generalizadas de un modelo no lineal de transición suave para la inflación de alimentos y las anomalías del índice de la temperatura superficial del mar 3,4 (ENSO). Este análisis se realiza para el periodo mensual comprendido entre junio de 1955 y mayo del 2015. Los resultados obtenidos indican que estos choques son transitorios y asimétricos. En particular, un choque positivo y fuerte sobre ENSO tiene un efecto significativo sobre el crecimiento de la inflación de alimentos y la incrementa en 72,5 y 100 puntos básicos en el cuarto y quinto mes después de la perturbación, respectivamente.
This paper estimates the impacts of weather conditions on Colombian food inflation growth. Generalized impulse response functions were used for a smooth transition non-linear model that includes food inflation and the sea surface temperature index (SST v3.4). In this study, data were obtained from the monthly period between June 1995 and May 2015. Results suggest that the weather shocks are transitory and asymmetric. In particular, a strong and positive shock has a significant effect on the food inflation growth and produces a 72,5 and 100 bases points increment four and five months later, respectively.
El clima es una variable que ha impactado de diversas formas la historia de la humanidad. Los cambios climáticos han generado efectos en ámbitos sociales y económicos, en la producción y en la salud pública, en especial ante la presencia de eventos adversos. Existen muchos fenómenos climáticos que pueden afectar diversos aspectos de la sociedad en un momento determinado;en este trabajo se aborda en particular el fenómeno de El Niño y el de La Niña, siendo el primero el que concentra la mayor atención de la literatura académica. Ambos son eventos de naturaleza oceánica y atmosférica que afectan principalmente a la región del océano Pacífico ecuatorial, cuyas manifestaciones surgen a través de variaciones anómalas de la presión atmosférica (oscilación del Sur) y de la temperatura en la superficie del mar (El Niño en la fase cálida o La Niña en la fase fría) en el océano Pacífico. En general, este fenómeno es conocido como El Niño Southern Oscillation (ENSO).
Para el seguimiento periódico del ENSO, se utilizan usualmente indicadores como el índice de oscilación del Sur (The Southern Oscillation Index [SOI]) y el índice de temperatura superficial del mar (Sea Surface Temperature [SST])1, los cuales se describirán brevemente en la siguiente sección. Durante un episodio de El Niño, la contracorriente ecuatorial se acentúa y produce que la temperatura máxima superficial del mar que había en la zona occidental del Pacífico se desplace gradualmente hacia el Este y, alrededor de 6 meses después, alcance la costa de América del Sur. Para ello se pueden monitorear los diversos indicadores antes mencionados, con la salvedad de que no existe una única medida oficial para identificar el ciclo del ENSO en un momento determinado del tiempo.
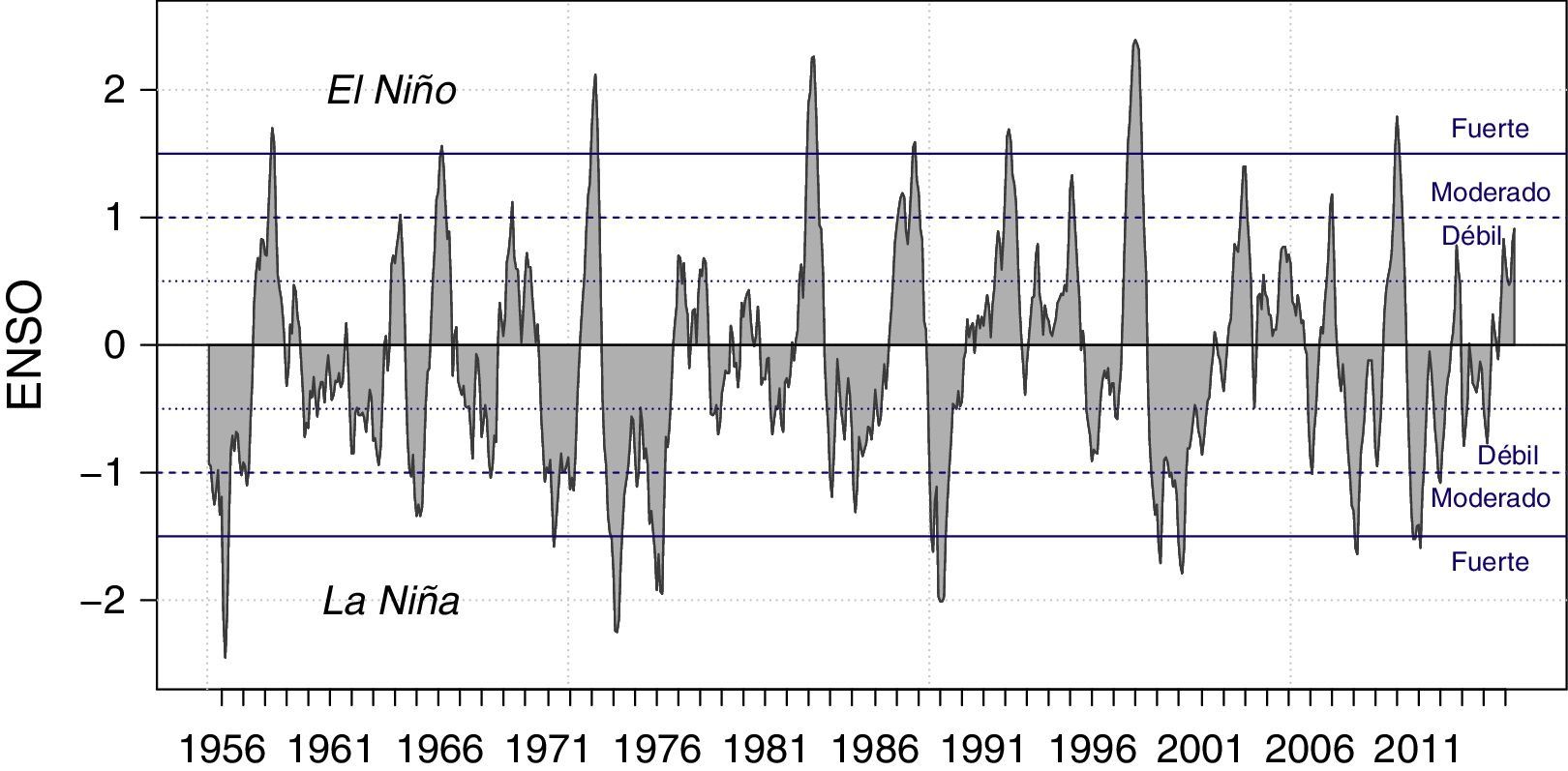
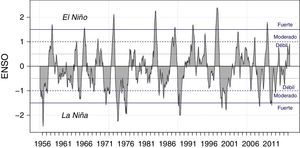
Cuando las anomalías son extremas puede provocar alteraciones en la circulación marina y atmosférica a escala global que pueden intensificar el desarrollo de precipitaciones torrenciales. Esto a su vez puede conllevar a inundaciones, avalanchas, tormentas y ciclones tropicales, como también a sequías que terminan afectando a más de la mitad del planeta Tierra (Wang, 2002). Así, estos fenómenos generan alteraciones significativas en diversos tipos de ecosistemas, tanto terrestres como marinos. En el caso de El Niño, de acuerdo con instituciones internacionales como la NOAA2, se estima que su duración promedio está alrededor de 12 meses, con eventos desde los 7 meses hasta más de 30 meses. Aunque el calentamiento del mar por dicho fenómeno es recurrente, no es periódico y, en términos generales, se presenta cada 2 a 7 años (figura 6 y tabla 3 del anexo A).
Davis (2002) analiza algunos de dichos eventos extremos, los cuales provocaron fuertes sequías globales de los años 1876-1878, 1888-1891 y 1896-1902 relacionadas con el fenómeno climático de El Niño. El estudio encuentra que las consecuencias del colonialismo y la introducción del capitalismo junto con las condiciones climáticas en India, China, Brasil, Etiopía, Corea y Vietnam contribuyeron a incrementar la pobreza del campesinado en dichos periodos, lo que a su vez generó hambrunas y la muerte de millones de personas3. Algo similar se aprecia en la recopilación de estudios del libro de Grove y Chappell (2000), donde se describe una cronología de eventos climáticos de El Niño y se estudian sus consecuencias a nivel de la salud pública y las secuelas epidemiológicas en algunos países del Este Asiático, sequías y hambrunas en Nueva Guinea (1997-1998), e impactos en la productividad agrícola en la India, entre otros.
En Colombia, dichos fenómenos también afectan significativamente al medio ambiente y el ciclo hidrológico (Restrepo y Kjerfve, 2000). En particular, El Niño de 1997-1998 ocasionó condiciones de sequía que dominaron en cerca del 90 % del territorio colombiano y numerosos ríos presentaron una disminución de los caudales en relación con los promedios mensuales multianuales con récord histórico de los últimos 50 años (CAF, 2000). En el caso colombiano, el análisis del ENSO se complica ya que su impacto no es fácil de predecir por diversas razones: i) los efectos climáticos dependen principalmente de la extensión, la intensidad y la duración de las anomalías en el océano y la atmósfera (las cuales varían para cada evento del ENSO), y ii) los planes de contingencia del gobierno para moderar los impactos socioeconómicos en una región particular.
Puertas y Carvajal (2008) encontraron que para el caso colombiano, El Niño se caracteriza por el incremento del SST y una reducción del SOI; de igual manera, concluyen que para el centro, norte y occidente del país este fenómeno ocasiona la disminución en la precipitación e incrementa la temperatura del aire. Durante La Niña ocurre lo contrario. Así mismo, la evidencia estadística del estudio indica que el ENSO tiene mayor incidencia sobre la variabilidad intra-anual de la precipitación y la temperatura media del aire, principalmente en el trimestre determinado por los meses diciembre-enero-febrero4.
Los efectos de dichos fenómenos climáticos también resultan perjudiciales a nivel macroeconómico, ya sea a través del impacto en los precios o en la actividad económica. Desde el punto de vista de la inflación, objeto del presente estudio, las menores precipitaciones producidas por El Niño generan una reducción de la oferta agrícola, la cual repercute en la dinámica de los precios de los alimentos al alza de forma transitoria. Esto ocurre principalmente cuando la incidencia de El Niño es fuerte, ya que el impacto es limitado en eventos moderados o débiles del fenómeno.
Por otra parte, aunque el presente estudio se concentra únicamente en los efectos sobre la inflación, también existen otros impactos sobre la actividad económica. Por ejemplo, una caída en los niveles de embalses y represas disminuye la generación de energía eléctrica e incrementa las tarifas. Adicionalmente, en un entorno de condiciones climáticas desfavorables se puede observar una reducción de los volúmenes de pesca marítima y de transporte de carga a través de ríos. En general, los efectos climáticos principalmente recaerían sobre el sector agrícola ya que lo anterior se refleja en una caída de la productividad de las tierras.
De acuerdo con MinAgricultura (2006), se estima que ante la presencia de dicho fenómeno el rendimiento agrícola se reduce alrededor del 5%, donde los cultivos permanentes (5,5%) son más impactados que los transitorios (4,4%). Caicedo (2007) analiza las series históricas de los precios y encuentra que El Niño genera aumentos significativos en los precios de los alimentos, especialmente en los perecederos. Asimismo, muestra que en presencia de El Niño los alimentos explicaron en promedio el 30,6% de la inflación total causada en dichos años y que los efectos sobre los aumentos en los precios tienden a concentrarse esencialmente en la primera mitad del año.
El interés en la medición del impacto de dicho fenómeno sobre variables económicas ha crecido a nivel internacional en la última década. Brunner (2002) examina el efecto del ENSO sobre los precios y la actividad a nivel global, concentrándose en el crecimiento conjunto de la inflación y el PIB de los países del G7 y de los precios mundiales de bienes básicos (commodities). Entre los resultados más sobresalientes, el autor encontró que ante un choque positivo de una desviación estándar en el ENSO, medido a través del indicador SOI5, se genera un incremento en la inflación real de los bienes básicos de entre un 3,5 y un 4%, que a su vez explica alrededor del 20% de los movimientos de dichos precios en el periodo de estudio. En términos de la inflación y el crecimiento de PIB, la evidencia estadística indica que el ENSO explica aproximadamente entre el 10% y el 20% de la variabilidad de dichas series para los países del G7.
A diferencia de Brunner (2002), que examina un agregado de las tasas de crecimiento y la inflación de los países desarrollados del G7, Laosuthi y Selover (2007) estudian los efectos de El Niño en distintos países, especialmente en los países en desarrollo más vulnerables al fenómeno. Entre los resultados más sobresalientes del trabajo se encuentra que: i) los efectos de los episodios de El Niño pueden ser relativamente pequeños de acuerdo con el tamaño de las economías6, y ii) el conocimiento del fenómeno ha permitido a los países prepararse y responder de mejor manera a sus efectos negativos 7. Otros estudios que se destacan son los de Berry y Okulicz-Kozaryn (2008) y Chimeli, de Souza, Holanda, y Petterini (2008). El primero evaluó la coordinación de los ciclos climáticos y las variables macroeconómicas (inflación y PIB) encontrando que no hay prociclicidad para el caso de Estados Unidos (EE. UU.). Así los autores concluyen que a pesar de que pueden existir efectos locales, estos desaparecen con la persistencia de las tendencias macroeconómicas de una economía tan grande y compleja como la de los EE. UU.8. El segundo investigó la relación entre las anomalías en el clima y la actividad agrícola del maíz en Brasil encontrando una correlación negativa del ENSO con la producción de maíz y positiva con los precios.
Los estudios mencionados en los párrafos anteriores utilizaban modelos lineales para las estimaciones que no tenían en cuenta que el efecto de las anomalías climáticas también varía en el tiempo debido al cambio climático y dan lugar a una literatura que trata de incorporar esto en el análisis mediante el modelamiento de no linealidades y asimetrías. Hall, Skalin, y Teräsvirta (2001) muestran cómo un modelo autorregresivo de transición suave logístico se ajusta mejor que un modelo autorregresivo lineal para describir los periodos de turbulencia climática observados en indicadores como el SOI, demostrando la existencia de una dinámica no lineal. Ubilava (2012b) investiga la dinámica, potencialmente no lineal, de la relación entre el precio de la soya y el maíz aplicando modelos de transición suave (Smooth Transition AutoRegression [STAR]) sobre los precios de derivados financieros de dichos bienes. El modelo estimado demuestra la existencia de una dinámica no lineal, dando lugar a asimetrías en el ajuste al equilibrio de largo plazo de la relación del precio de la soya y el maíz.
Ubilava (2012a), utilizando la misma familia de modelos STAR, incorporó al análisis el modelo multivariado (Smooth Transition Vector Error Correction [STVEC]) para modelar un sistema de cuatro precios de variedad de café y su interrelación con el ENSO. El estudio muestra que existen asimetrías generadas por el ENSO que se transmiten a los precios del café. El autor encuentra que debido a las diferencias existentes en la geografía de los países donde se producen las variedades de café, los eventos del ENSO tiende a afectar de manera diferente a los precios. Por ejemplo, un choque positivo del ENSO (fenómeno de El Niño) tiene un impacto positivo en los precios de la variedad Robusta pero negativo en la variedad Arábica. Adicionalmente, los efectos de El Niño y La Niña no son simétricos, y el impacto final de dichas asimetrías depende del régimen específico en el que se encuentre el ENSO.
Algo similar se aprecia en el trabajo de Ubilava y Holt (2013), donde los autores demuestran no linealidades entre los precios del aceite vegetal y el ENSO; en este caso, los efectos de los choques sobre la dinámica del ENSO tienen impactos diferenciados sobre los precios del aceite vegetal dependiendo del régimen en el que se encuentre el ENSO. En general, los autores encuentran que las desviaciones positivas del ENSO (El Niño) resultan en el aumento de precio de aceite vegetal, mientras que las desviaciones negativas (La Niña) dan como resultado la disminución de dichos precios.
Este documento realiza un aporte a la literatura colombiana al cuantificar los impactos del clima en la inflación de alimentos, lo que podría ser de utilidad para el Banco Central en la toma de decisiones de política u otras instituciones en la elaboración de políticas agrícolas, medio ambiente y cambio climático. El presente estudio encontró que después de presentarse un choque en el clima (sea El Niño o La Niña), el crecimiento de la inflación de los alimentos reacciona significativamente en mayor medida entre 4 y 5 meses después, y su respuesta es asimétrica, dependiendo del signo y el tamaño del choque. Las estimaciones indican que los impactos de El Niño sobre la inflación de alimentos, dependiendo de si es una fase fuerte o moderada del fenómeno, son aproximadamente de 100 puntos básicos (p.b.) y 65 p.b. para el quinto mes, respectivamente. Por su parte, en el caso de La Niña, su impacto se sitúa entre −80 p.b. y −55 p.b.
Este escrito se divide en 3 secciones adicionales. La primera describe la información utilizada para las estimaciones, la segunda enuncia la metodología propuesta para abordar la estimación de los efectos de los fenómenos climáticos en los precios de los alimentos en Colombia y la tercera muestra los resultados encontrados. Para finalizar, se presentan las principales conclusiones.
2Descripción de los fenómenos climáticos y su mediciónLos fenómenos climáticos de El Niño y de La Niña se dan como resultado de fluctuaciones periódicas de la presión del aire en la atmósfera y de la temperatura superficial del mar. Para medir la primera se utiliza el SOI, mientras que para la segunda se recurre al SST.
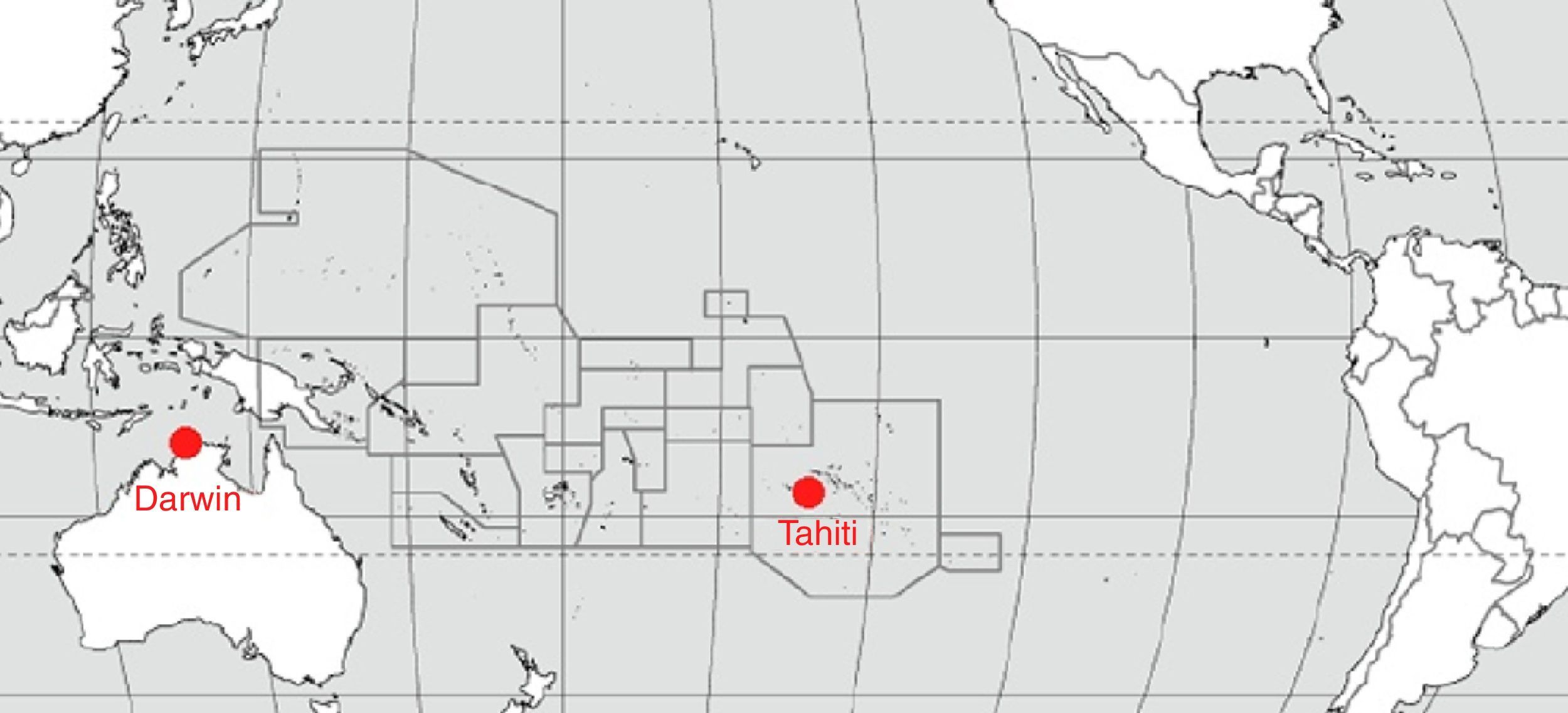
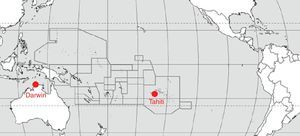
2.1El índice de oscilación del SurLos cambios en la circulación de los vientos alisios debidos a perturbaciones de la dinámica atmosférica relacionados con cambios en los sistemas de presión a nivel del mar se conoce como oscilación del Sur. El SOI es un índice estandarizado sobre la base de las diferencias observadas en la presión a nivel del mar entre Tahití (Polinesia Francesa) y Darwin (Norte de Australia) tal como se aprecia en la figura 1.
En general, al suavizar con promedios móviles las series de tiempo del SOI se encuentra una alta correspondencia con los cambios en la temperatura del océano en todo el Pacífico tropical oriental. La fase negativa del SOI se tiene cuando la presión de aire en Tahití está debajo de lo normal y por encima de lo usual en Darwin. Periodos prolongados de valores negativos (positivos) del indicador SOI coinciden con aguas anormalmente cálidas (frías) a lo largo del océano Pacífico tropical oriental, lo que es típico de un episodio de El Niño (La Niña)9.
2.2El índice de temperatura superficial del marPara el monitoreo de las condiciones del ENSO la mayoría de las instituciones se centra principalmente en las anomalías en la temperatura superficial del mar. Para ello vigilan constantemente cuatro regiones geográficas10 del Pacífico ecuatorial a través de observaciones satelitales. La medición se basa en la amplitud de las radiaciones con longitudes de onda en espectros infrarrojos y microondas que emite el océano, las cuales varían de acuerdo con la temperatura del mismo.
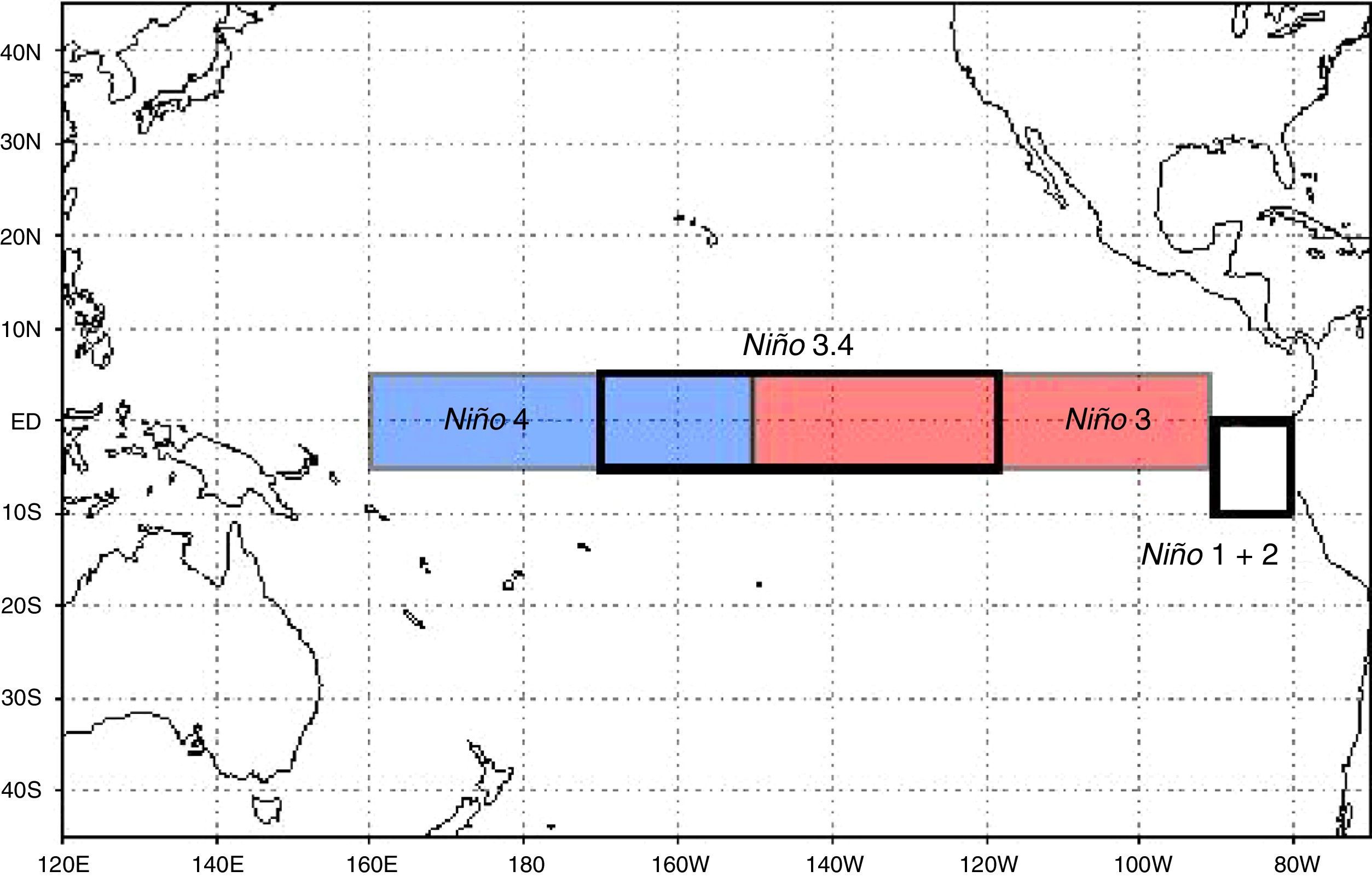
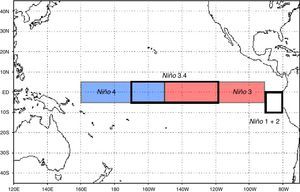
Un caso particular de esta familia de indicadores SST es el índice oceánico El Niño (The Oceanic Niño Index [ONI]), el cual se calcula como la media de 3 meses consecutivos de las anomalías de la temperatura superficial del mar medidas por el sensor ERSST.v3 en la región 3.4 de El Niño (5°N - 5°S, 120° - 170°W). Se consideran episodios cálidos y fríos cuando las anomalías superan el umbral de +/- 0,5°C. Cuando dicho umbral es cubierto durante un mínimo de 5 meses consecutivos se definen como episodios de El Niño(+) o de La Niña(-). En la figura 2 se indican las diferentes zonas en recuadros (azul, rojo y blanco).
Distribución de ENSO según el índice SST
NIÑO1+2 (0-10S, 80-90W). Es la primera región que presenta aumentos significativos en la temperatura al comenzar el fenómeno.
NIÑO3 (5S-5N; 150W-90W). Es la región de del Pacífico tropical que posee la más alta variabilidad en la SST sobre la escala de El Niño.
NIÑO4 (5S-5N: 160E-150W). Región en donde los cambios de la temperatura superficial del mar conducen a los valores totales alrededor de 27,5 C, que se cree que es un umbral importante en la producción de lluvias.
NIÑO3.4 (5S-5N; 170W-120W). Es la región que tiene gran variabilidad en las escalas de tiempo de El Niño, y que está más cerca de la región donde los cambios en la temperatura superficial del mar local son importantes para el desplazamiento de la lluvia normalmente ubicada en el Pacífico occidental.
En esta sección se presenta la metodología econométrica utilizada para analizar las dinámicas no lineales entre el ENSO y el precio de los alimentos en Colombia. Siguiendo a Teräsvirta (1994), Teräsvirta (1998) y Hall et al. (2001), se utilizan los modelos de transición suave (Smooth Transition Regression models [STR]). Un modelo regresivo con transición suave asume que existen estados de la economía o regímenes que influyen en el comportamiento de un determinado indicador económico. Estos estados de la economía son descritos por el comportamiento de una variable que se denomina de transición. En este documento, los modelos regresivos con transición suave pueden ser utilizados para estudiar la no linealidad del efecto del clima sobre los precios de los alimentos ya que la respuesta de dichos precios dependerá del estado del clima en el cual las temperaturas son frías o cálidas (fenómeno de El Niño y de La Niña). Adicionalmente, el hecho de encontrar asimetrías en los impactos del clima sobre el precio de los alimentos justifica también la elección de dicha metodología.
3.1Modelos de transición suaveTeräsvirta (1994) propone el siguiente modelo no lineal:
donde yt es la variable dependiente de interés; xt=(1, yt−1, …, yt−p, z1,t, …, zm,t)′ es un vector de variables explicativas compuesto por rezagos de la variable dependiente y de otras variables exógenas (zj,t para j=1, …, m), y ϕ1 y ϕ2 son vectores de parámetros a estimar de las variables contenidas en xt.Adicionalmente, G(st;γ, c) es la función de transición definida en el intervalo 0 y 1, que depende de la variable de transición (st) y los parámetros γ y c. La variable de transición se puede definir como un rezago de la variable endógena (yt−d), una función del tiempo (t)11 o una variable exógena (zs). El parámetro de suavizamiento γ indica la velocidad del ajuste, la cual determina qué tan rápido ocurre el cambio de un régimen a otro; y c es un conjunto de parámetros de localización o umbral asociado a la transición definida por la función G. Por último, ¿t∼iid(0, σ2).
La expresión (1) puede ser notada como:
donde φ1=ϕ1 y φ2=ϕ2−ϕ1.En la literatura se han planteado varias especificaciones para la función de transición (Teräsvirta, 1994); (Teräsvirta, 1998); (Hall et al., 2001). Una de ellas es la función logística, que en términos generales puede ser escrita como:
con γ>0, c es un parámetro de localización que corresponde al umbral y σst es la desviación estándar de la variable de transición. Cuando la ecuación (3) es combinada con (2), el modelo resultante es conocido como LSTR (por sus siglas en inglés), el cual es usualmente utilizado en situaciones donde existen asimetrías en las dinámicas de respuesta a (st−c).Otra especificación importante de la función de transición es la representación exponencial, que se puede expresar como:
donde los parámetros y las variables corresponden a los definidos anteriormente. Al reemplazar la ecuación (4) en (2) se obtiene la representación ESTR, la cual es útil para modelar las dinámicas asociadas con la magnitud del valor absoluto de la variable de transición.3.2Prueba para no linealidad (LM)Como paso preliminar a la estimación de este tipo de modelos, se debe verificar si el proceso generador de los datos es no lineal y, posteriormente, si es el caso, identificar la variable de transición. Teniendo en cuenta estos objetivos, Luukkonen, Saikkonen, y Teräsvirta (1988) proponen una expansión de Taylor de tercer orden sobre la función de transición del modelo STR 12, de tal forma que se llegue a la siguiente regresión auxiliar:
En este caso, la hipótesis nula de linealidad y la estadística de prueba están dadas por:
donde SRR0 es la suma de residuales al cuadrado de la ecuación (5) bajo la hipótesis nula y SRR1 expresa la suma de residuales al cuadrado de la regresión auxiliar completa. Bajo la hipótesis nula, el estadístico de la prueba LM se distribuye F con k1−k0 y T−k1 grados de libertad.13. Como se muestra a continuación, este prueba también permite seleccionar la función de transición más apropiada.3.3Elección de los modelosUna vez se rechaza la hipótesis nula de linealidad antes mencionada, se selecciona la variable de transición. El siguiente paso consiste en elegir el tipo función de transición de la familia de modelos (STR). Teräsvirta (1994) propone hacerlo a través de una secuencia de pruebas anidadas; así:
- •
H04:ϕ23j′=0j=1,…,p
- •
H03:ϕ22j′=0|ϕ23j′=0j=1,…,p
- •
H02:ϕ21j′=0|ϕ22j′=ϕ23j′=0j=1,…,p
Si el p-valor asociado a la hipótesis H03 es el más pequeño de las 3 pruebas de hipótesis anteriormente reseñadas (H02, H03, H04), se selecciona el modelo ESTR; en otro caso, se escoge el modelo LSTR. Por otra parte, como lo señalan van Dijk, Teräsvirta, y Franses (2002) se pueden estimar ambas especificaciones (LSTR o ESTR) y elegir la más adecuada de acuerdo con los resultados de las pruebas de diagnóstico descritas en el anexo B.
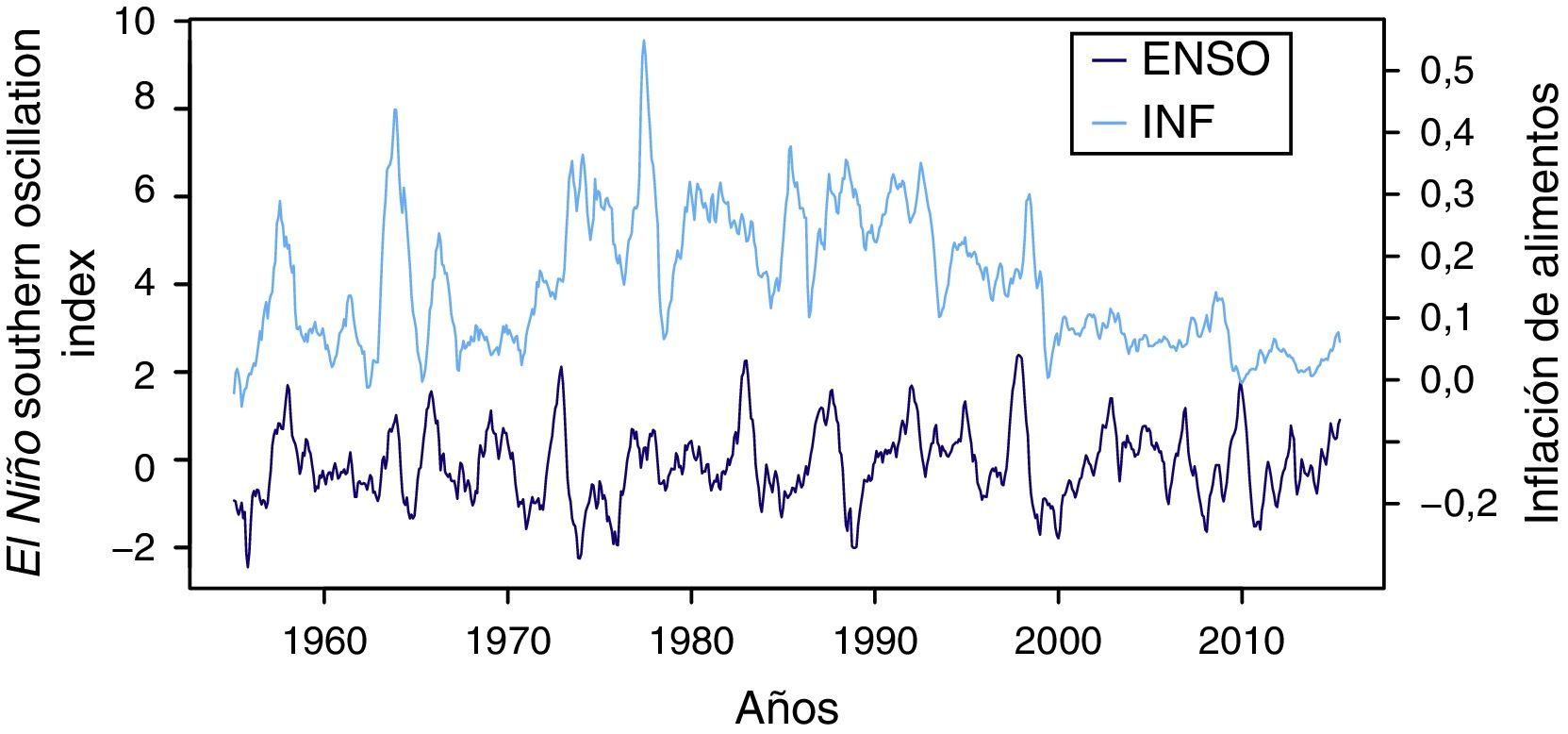
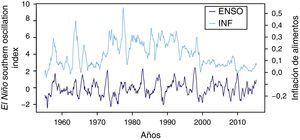
4Estimación y ResultadosEn este documento la variable endógena a modelar es la inflación de alimentos, calculada como la variación anual porcentual del índice mensual de precios al consumidor de la canasta de alimentos divulgada por el Departamento Administrativo Nacional de Estadística (DANE). El periodo de estudio está comprendido entre junio de 1955 y mayo del 2015. Por su parte, para incorporar en el análisis los impactos de los fenómenos climáticos (ENSO) sobre la inflación de alimentos se utilizaron las anomalías14 del (SST) para la región 3.4 del Pacífico Central publicada por el Centro de Predicción Climática de la NOAA. Esta variable es tratada como exógena en la modelación y similar al IPC de alimentos, se cuenta con cifras mensuales para el mismo periodo de tiempo (figura 3).
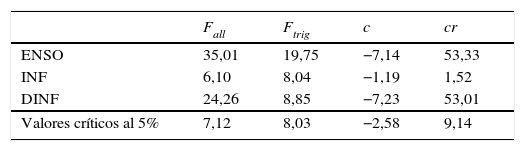
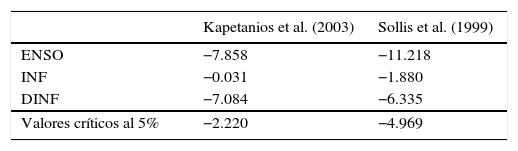
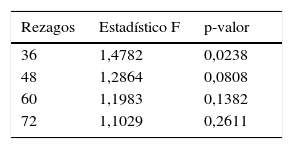
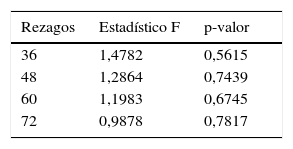
Inicialmente, se realizan las pruebas de raíz unitaria propuestas por Enders y Ludlow (2002) para procesos no lineales ya que la metodología que se desarrolla a continuación requiere del supuesto de estacionariedad. La tabla 1 resume los estadísticos F y t de dichas pruebas15, donde los valores entre paréntesis representan los respectivos valores críticos correspondientes a un nivel de significancia del 5%. Los resultados obtenidos muestran que la serie del ENSO es estacionaria, mientras que la inflación anual de alimentos (INF) sí presenta una raíz unitaria. Estos resultados son confirmados al utilizar las pruebas de raíz unitaria de Kapetanios, Shin, y Snell (2003) y Sollis, Leybourne, y Newbold (1999), tal como se muestran en la tabla 2. Por lo tanto, se utiliza la primera diferencia de la inflación anual de alimentos (DINF), que corresponde al crecimiento de la inflación anual de los alimentos.
Prueba de raíz unitaria de Enders y Ludlow (2002)
| Fall | Ftrig | c | cr | |
|---|---|---|---|---|
| ENSO | 35,01 | 19,75 | −7,14 | 53,33 |
| INF | 6,10 | 8,04 | −1,19 | 1,52 |
| DINF | 24,26 | 8,85 | −7,23 | 53,01 |
| Valores críticos al 5% | 7,12 | 8,03 | −2,58 | 9,14 |
La hipótesis nula indica la existencia de raíz unitaria.
Otras pruebas de raíz unitaria
| Kapetanios et al. (2003) | Sollis et al. (1999) | |
|---|---|---|
| ENSO | −7.858 | −11.218 |
| INF | −0.031 | −1.880 |
| DINF | −7.084 | −6.335 |
| Valores críticos al 5% | −2.220 | −4.969 |
La hipótesis nula indica la existencia de raíz unitaria.
Para la modelación se asume, siguiendo a Brunner (2002), que la inflación de alimentos está correlacionada contemporáneamente con el ENSO y con sus rezagos. Para ello, primero se estima una ecuación para el ENSO como un proceso univariado no lineal como lo indica la literatura. De esta manera, se pretende incorporar en el análisis que los efectos del clima tienen una dinámica propia. En otras palabras, si hoy se observa un choque en el clima (El Niño o La Niña), este puede perdurar unos meses, lo que se modela a través de la estructura de rezagos de la ecuación del ENSO. Adicionalmente, este modelo hace parte de los insumos de la metodología que se utiliza para estimar la respuesta de la inflación de alimentos a choques en ENSO, tal como se explica en la Sección 4.3 y en el anexo D.
Posteriormente, esta variable se incorpora en la ecuación de los precios, ya que los eventos climáticos afectarían el comportamiento de los precios de los alimentos no sólo una vez, sino por el tiempo en el que perdure el efecto del fenómeno climático.
Como paso siguiente, se procede a ajustar un modelo para la inflación de alimentos incluyendo el ENSO como una variable regresora exógena. Así, el sistema de ecuaciones a estimar es el siguiente:
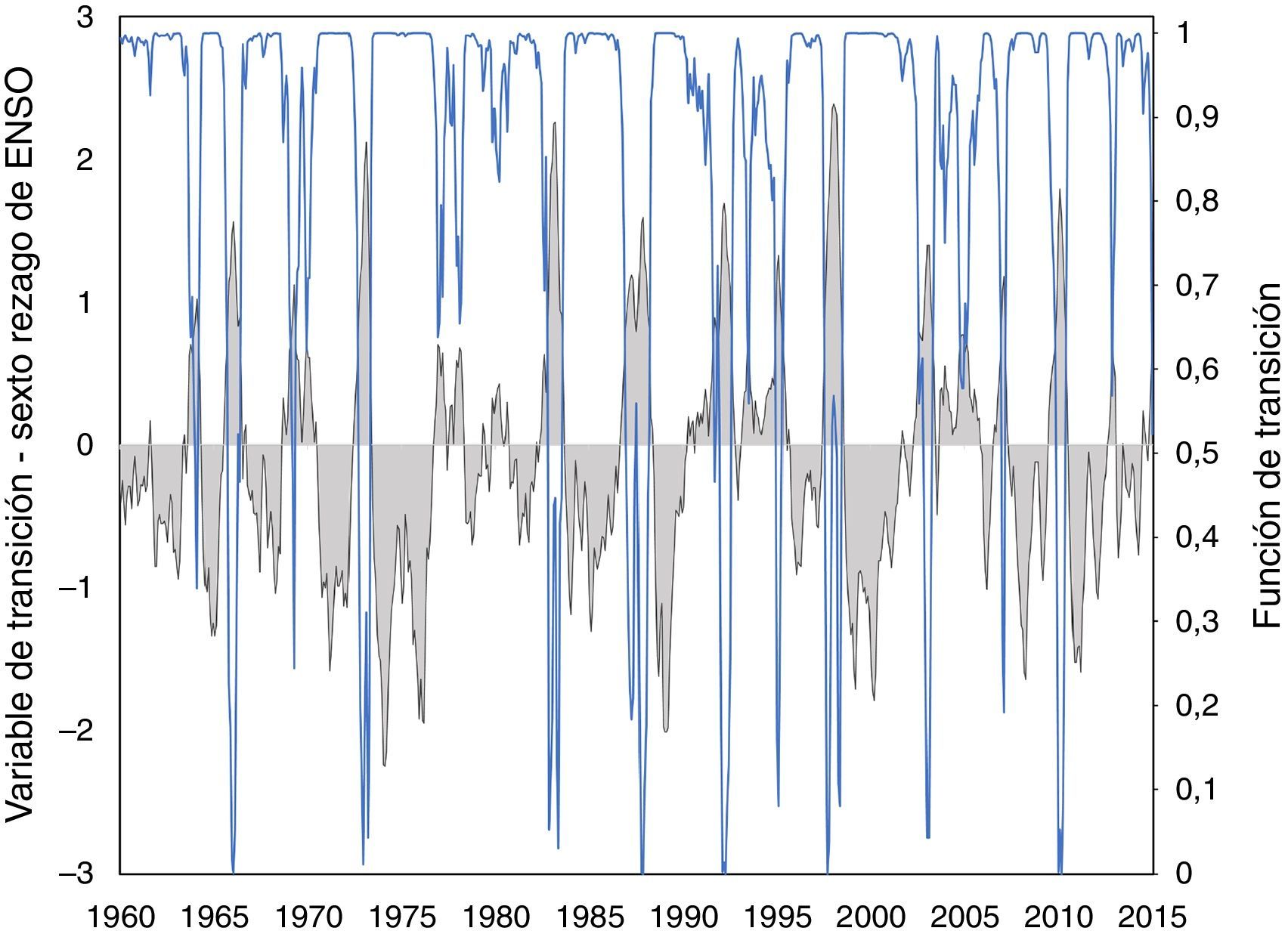
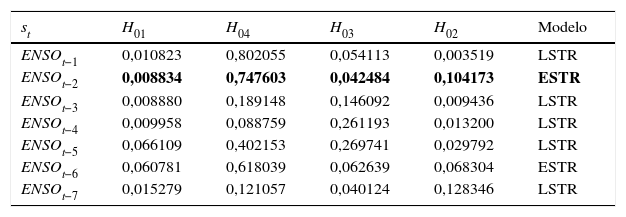
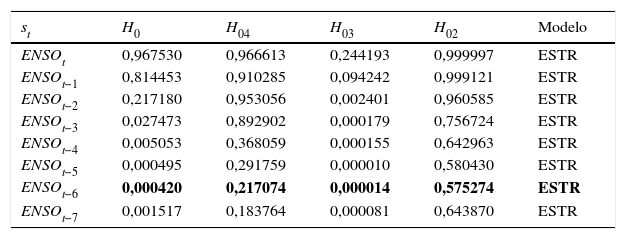
donde p1, p2 y p3 son los rezagos máximos utilizados para ENSO, inflación y ENSO como exógena, respectivamente. Teniendo en cuenta el anterior sistema de ecuaciones, el presente trabajo pretende cuantificar el impacto de choques en el ENSO sobre la inflación de alimentos (DINF) mediante el uso de funciones de impulso respuesta generalizada. A continuación, se describe la especificación de estas 2 ecuaciones.4.1Ecuación del ENSOInicialmente, se especifica el modelo STR para la serie de tiempo del ENSO de acuerdo con los procedimientos descritos en las secciones 3.2 y 3.3. Se realiza la prueba de no linealidad LM, cuyos resultados se presentan en la segunda columna de la tabla 4 (H01) del anexo E. Allí, se puede observar que no se rechaza la especificación no lineal de tipo STR y que la variable de transición elegida corresponde a ENSOt−216. Para completar la especificación, el tipo de función de transición seleccionada fue la exponencial, de acuerdo con los resultados obtenidos para las hipótesis H02, H03 y H04.
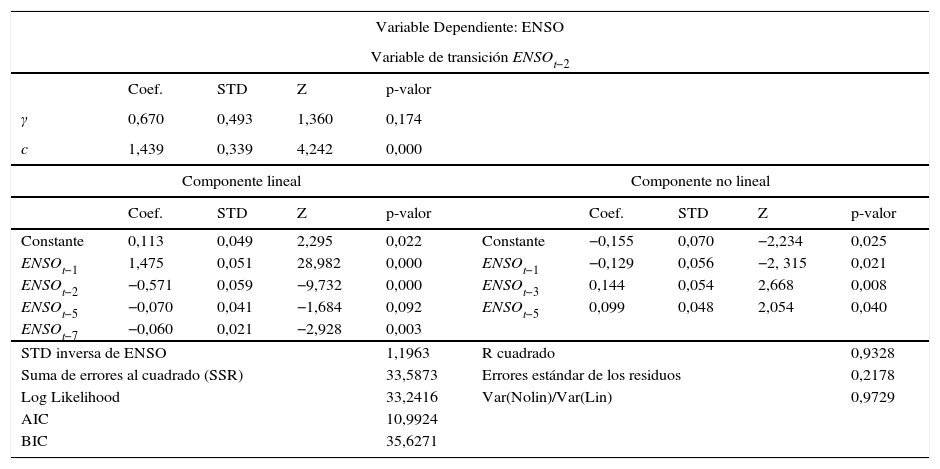
Luego, se estima la ecuación (8) para la variable ENSO, cuyos resultados se muestran en la tabla 5 del anexo E. Se puede apreciar que los coeficientes estimados son significativos al 10%17. El parámetro de localización (cˆ) indica que las variaciones de la función de transición ocurren cuando ENSO se encuentra alrededor de 1.439 (asociado al fenómeno de El Niño en fase moderado). Por su parte, el parámetro de suavizamiento (γˆ) indica una transición suave, aunque similar a lo que ocurre en la mayoría de las aplicaciones empíricas este no es significativo (van Dijk et al., 2002). Finalmente, en las tablas 6, 7 y 8 del anexo E se presentan los resultados de las pruebas de diagnóstico del modelo estimado. Estas indican que no existen problemas de especificación18.
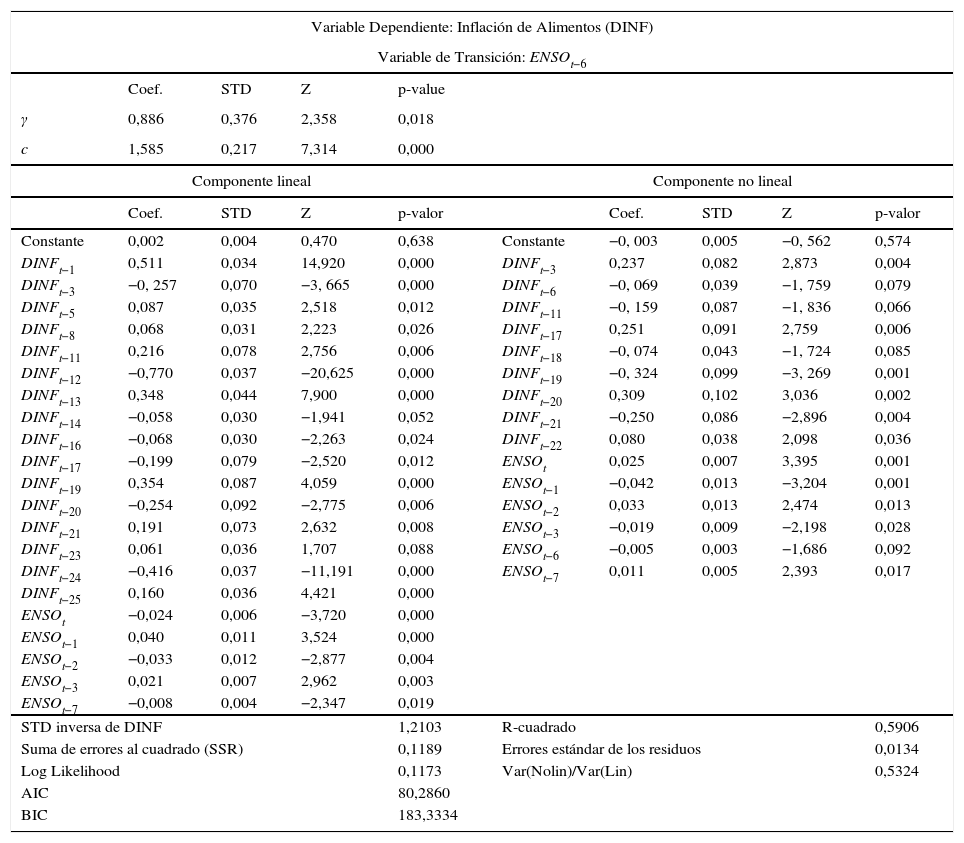
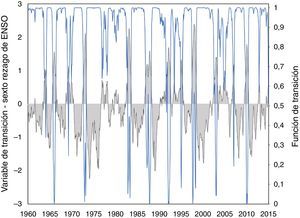
4.2Ecuación de DINFSimilar a lo anterior, en la tabla 9 del anexo E se muestran los resultados para la inflación de alimentos (DINF). Allí, se aprecia que la especificación no lineal tipo STR es adecuada, la variable de transición seleccionada corresponde a ENSOt−6 y la función de transición es exponencial. Posteriormente, se realiza la estimación de la ecuación (9), la cual incluye el ENSO y sus rezagos como variables exógenas. La tabla 10 del anexo E muestra que las estimaciones de estos parámetros son significativas al 10%. Como resultado se destaca que el parámetro de localización (cˆ) es 1.585, el cual indica que las variaciones de la función de transición del modelo se presentan en periodos donde el fenómeno de El Niño tiene una fase fuerte. También se observa que dicha transición obtenida es suave (γˆ = 0,886). Cabe señalar que las pruebas de diagnóstico presentadas en las tablas 11–13 del anexo Eindican que las especificaciones y el modelo utilizado son apropiados.
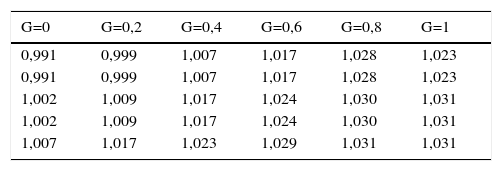
En la figura 7 del anexo F se presentan la función y la variable de transición para la muestra analizada. Allí se puede apreciar qué valores de la función de transición cercanos a cero están asociados a altas magnitudes de ENSO, que a su vez, corresponden a un fenómeno fuerte de El Niño. Adicionalmente, en la tabla 14 del mismo anexo se encuentran los módulos de las raíces dominantes del polinomio característico del modelo STR de DINF para distintos valores de la función de transición (G). Se observa un comportamiento local explosivo (módulos menores que uno) para magnitudes cercanas a cero de G, es decir, cuando ocurre un fenómeno de El Niño de intensidad fuerte. Sin embargo, para la gran parte de los valores de la función de transición se tiene un comportamiento estacionario (módulos mayores que uno)19.
4.3Análisis de impulso respuesta generalizado (GIRF)Para cuantificar la respuesta en el crecimiento de la inflación anual de alimentos (DINF) ante choques relacionados con fenómenos climáticos (ENSO), se implementa un GIRF propuesto por Koop, Pesaran, y Potter (1996) que se describe de manera detallada en anexo D. La ventaja de dicha metodología consiste en incorporar al análisis de impulso respuesta las características de los modelos no lineales como el STR. En particular, permite asimetrías asociadas al signo y al tamaño del choque, y sus resultados pueden depender del tiempo en el que ocurra dicha perturbación20.
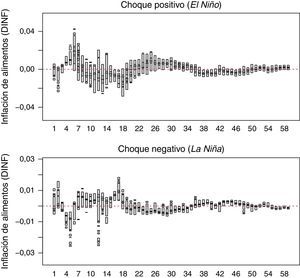
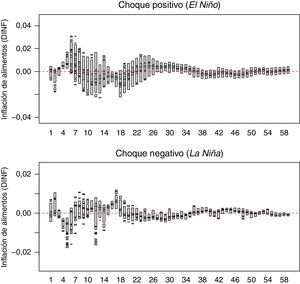
La estimación de la GIRF incluye todas las observaciones disponibles en la muestra como parte de la historia a analizar y cuatro choques sobre el ENSO (positivo moderado, negativo moderado, positivo fuerte y negativo fuerte). Los choques positivos se asocian al fenómeno de El Niño, mientras que los negativos al de La Niña. Los choques fueron definidos así: positivo fuerte como el promedio de los valores de ENSO cuando es mayor a 1,5, positivo moderado como la media de los valores de esta variable que se encuentran entre 1 y 1,5, negativo fuerte como la media de valores menores al umbral -1,5 y negativo moderado a la media del intervalo entre −1 y −1,5 (figura 6 del anexo A)21. Para cada combinación de la historia y choques, se calculó la GIRF con horizontes de 60 periodos y 100 replicaciones.
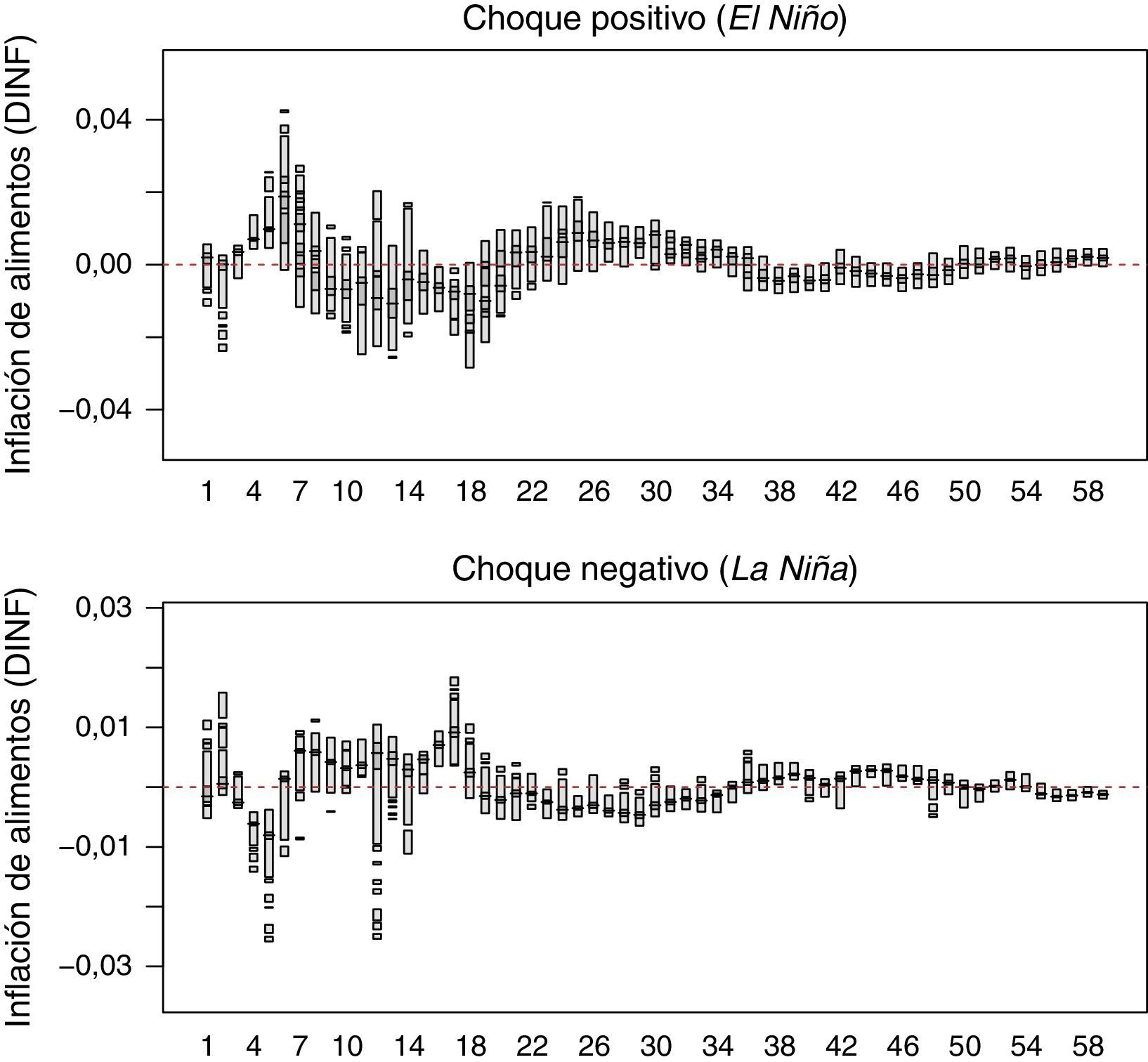
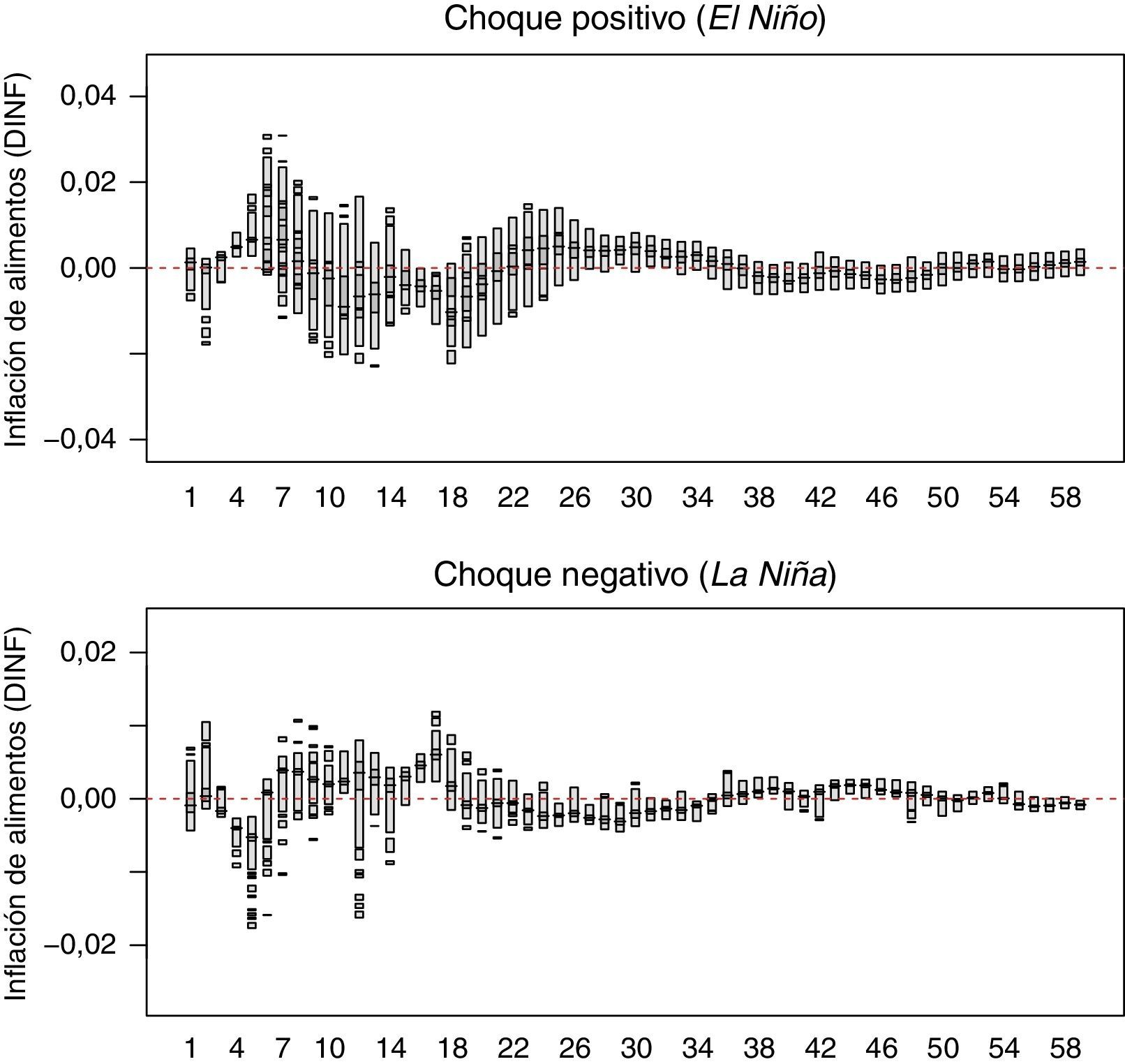
En las figuras 4 y 5 se muestran las respuestas de los precios de alimentos (DINF) ante choques fuertes y moderados del ENSO, respectivamente. El panel superior de cada figura tiene la GIRF para choques positivos (fenómeno de El Niño), mientras el panel inferior presenta las respuestas a choques negativos (fenómeno de La Niña). Dado que la significación de la GIRF no se puede analizar con intervalos de confianza debido a sus comportamientos multimodales, es necesario utilizar regiones de alta densidad (HDR por sus siglas en inglés). La figura de la respuesta para cada mes tiene dos regiones, una al 50% (gris oscuro) y otra al 95% (gris claro)22.
Se observa que la respuesta de DINF ante choques de ENSO es transitoria y solo es significativa para dos periodos que corresponden al cuarto y quinto mes después del choque. También se destaca que los choques positivos tienen mayores efectos que los choques negativos, es decir, el impacto del fenómeno de El Niño es superior al de La Niña. Así, en este trabajo se encuentra evidencia estadística que soporta la respuesta asimétrica en el crecimiento de la inflación de alimentos ante choques en el ENSO. Sobre la base de las medianas asociadas a la GIRF se tiene que la respuesta de DINF ante choques positivos fuertes (fenómeno de El Niño fuerte) de ENSO es aproximadamente de 72,5 y 100 p.b. para el cuarto y quinto mes después del choque, mientras que para un fenómeno de El Niño moderado el efecto es cercano a 51 y 65 p.b. para el mismo número de periodos adelante. De esta manera, se tendría un efecto medio acumulado de 172,5 p.b. en los fenómenos de El Niño fuertes y de 116 p.b. en los moderados. Es importante mencionar que estas estimaciones son los valores medios del impacto, pero como se aprecia en la figura de impulso respuesta, el intervalo encontrado indica que en algunos episodios el impacto puede ser más elevado. Por ejemplo, para el cuarto mes el impacto podría estar contenido entre 42,5 y 140 p.b. y para el quinto mes entre 47,5 y 272,5 p.b. En el caso choques negativos, cuando son fuertes (La Niña fuerte) el impacto sobre DINF es −60 y −80 p.b., mientras que cuando son moderados su efecto es −37,5 y −55 p.b. (figura 4 y figura 5)23.
Teniendo en cuenta que el ENSO tiene una mayor incidencia en la variabilidad intra-anual de la precipitación y la temperatura media del aire en el trimestre diciembre-enero-febrero (véase Puertas y Carvajal (2008)), el modelo estimado en este documento indica que una vez observado el choque en dicho trimestre el impacto sobre el crecimiento de la inflación de alimentos se observaría de forma significativa hacia mitad del año (mayo-junio-julio); este hecho es coherente con lo que se ha observado en los últimos episodios del fenómeno de El Niño en Colombia.
5Comentarios finalesLos cambios climáticos han generado efectos en ámbitos sociales y económicos, en la producción y en la salud pública, en especial ante la presencia de eventos adversos. Son muchos los fenómenos climáticos que pueden repercutir en la sociedad en un momento determinado, pero en este trabajo se abordaron el fenómeno de El Niño y el de La Niña. En términos de la inflación, el estudio del tema toma relevancia ya que dichos eventos impactan los precios de los alimentos y con ello el poder adquisitivo de los hogares colombianos.
La evidencia estadística encontrada en el presente trabajo indica que existen no linealidades en la evolución de la variable climática que mide el ENSO, lo que es coherente con el cambio climático y con la presencia de fenómenos (El Niño o La Niña) cuya intensidad puede variar en el tiempo entre débil, moderada y fuerte de manera no lineal. Esto ratificó la implementación de los modelos de transición suave (STR), utilizados en esta investigación, para cuantificar el impacto de los fenómenos climáticos sobre la inflación de alimentos.
Entre los principales resultados encontrados en las estimaciones se destacan que los choques climáticos impactan el crecimiento de la inflación de alimentos de manera transitoria y que una vez se presenta el choque en el clima (sea El Niño o La Niña) los precios reaccionan significativamente entre cuatro y cinco meses después cuando el fenómeno es de carácter moderado y fuerte. En el caso de fenómenos climáticos catalogados como débiles, se encontró que no tienen un impacto significativo sobre los precios en ningún periodo de tiempo. De acuerdo con Puertas y Carvajal (2008) estos fenómenos climáticos se presentan con mayor intensidad, en promedio, en el trimestre conformado por los meses de diciembre-enero-febrero, de tal manera que el modelo estimado en el presente trabajo indica que el impacto sobre el crecimiento de la inflación de alimentos se observaría de forma significativa hacia mitad del año (mayo-junio-julio).
La evidencia estadística muestra que la respuesta en la inflación de alimentos ante la presencia de dichos fenómenos es asimétrica, y depende de manera importante del signo y el tamaño del choque. Las estimaciones indican que los impactos de un fenómeno de El Niño fuerte sobre el crecimiento de la inflación de alimentos es aproximadamente 72,5 y 100 puntos básicos (p.b.) para el cuarto y quinto mes después del choque, mientras que para un fenómeno de El Niño moderado el efecto es cercano a 51 y 65 p.b. para el mismo número de periodos adelante. Así, el efecto acumulado de un fenómeno de El Niño fuerte y moderado es 172,5 y 116 p.b. en promedio, respectivamente. No obstante, los impactos máximos para El Niño fuerte podrían alcanzar niveles alrededor de 140 y 272,5 para el cuarto y quinto mes, es decir, un efecto acumulado de 412,5 p.b. Por su parte, en el caso del fenómeno de La Niña, fuerte y moderado, su impacto 4 meses después del choque se sitúa en −60 y −37,5 p.b., respectivamente. Para el quinto mes las estimaciones indican −80 y −55 p.b..
Aunque el modelo presentado en este documento es de carácter econométrico y no tiene en cuenta otros aspectos económicos en el análisis, a continuación se comentan algunas posibles implicaciones de política, así como potenciales investigaciones futuras.
En el caso de la política monetaria, tradicionalmente en un esquema de inflación objetivo, el hacedor de política no debería intervenir ante choques de oferta como el fenómeno de El Niño y menos aun cuando su naturaleza es transitoria como se encontró en este documento. No obstante, trabajos como BIS (2009) y González, Jalil, y Romero (2010) muestran que la respuesta de la política monetaria a los choques de oferta en Colombia dista de ser un tema trivial. De hecho, en estos trabajos se indica que si dichos choques tienen gran magnitud, su efecto puede propagarse a la inflación básica y a las expectativas de inflación, y es allí donde el Banco Central debe transmitir a los agentes que no permitirá mayores niveles de inflación, garantizando la estabilidad de la inflación y el producto, objetivos fundamentales de la política monetaria en Colombia.
Teniendo en cuenta esto, una forma de mitigar los impactos del fenómeno de El Niño sobre los precios requiere de políticas públicas adicionales diseñadas para disminuir las consecuencias negativas del cambio climático, lo cual se vería reflejado no solo en los precios sino en general sobre el bienestar de la sociedad. Por ejemplo, Cano (2014) propone los siguientes retos: i) el desarrollo de una agricultura menos costosa y de reducida intensidad en emisiones de gases de efecto invernadero a través del menor uso de agroquímicos; ii) el desarrollo de una segunda generación de biocombustibles basada en materias primas que no compitan con la alimentación humana y animal, y iii) la ampliación de la frontera agrícola ambientalmente sostenible mediante el desarrollo de nuevos materiales genéticos resistentes a la sequía y tolerantes a la salinidad y a la acidez de los suelos. Esto en un entorno institucional y una inversión en ciencia y tecnología que deberían fortalecerse con objetivos de largo plazo en busca del desarrollo sostenible de la economía colombiana.
Por otra parte, cabe señalar que una alternativa de corto plazo frente a las alzas transitorias en los precios pero cuyas implicaciones no han sido exploradas a profundidad, sería contemplar la importación de alimentos. Asimismo, se podrían reducir los aranceles de aquellos alimentos cuyos precios se disparan en situaciones como las actuales. Aunque en este documento no se aborda esta cuestión, valdría la pena sostener el debate para el caso de algunos productos, pero para ello es necesario que tanto los productores nacionales como el gobierno generen los espacios de discusión sobre políticas de largo plazo y la sostenibilidad alimentaria del país.
Hacia adelante, de este estudio se desprenden algunas interrogantes que podrían ser analizadas en agendas de investigación futuras. Por ejemplo, el impacto del fenómeno de El Niño sobre los diferentes productos de la canasta de alimentos puede ser heterogéneo, ya que algunos de los bienes son de carácter perecedero mientras que otros son procesados. Algo similar ocurre si la clasificación que proviene de la oferta agrícola, pues ésta se compone de cultivos permanentes y cultivos transitorios. Por otra parte, las características geográficas de Colombia hacen relevante el estudio del impacto a nivel regional, ya que en el país los patrones climáticos también cambian según el piso térmico y con ello el tipo de cultivo.
Conflicto de interesesLos autores son, en su orden, Estudiante de Maestría en Estadística de la Universidad Nacional, Econometrista Principal de la Unidad de Econometría y Profesional Experto del Departamento de Programación e Inflación del Banco de la República. Los resultados y opiniones son responsabilidad exclusiva de los autores y su contenido no compromete al Banco de la República ni a su junta directiva.
Los autores agradecen los comentarios y sugerencias de Carlos Gustavo Cano, Edgar Caicedo y de 2 evaluadores anónimos, e igualmente dan las gracias por la colaboración de Santiago Aldana.
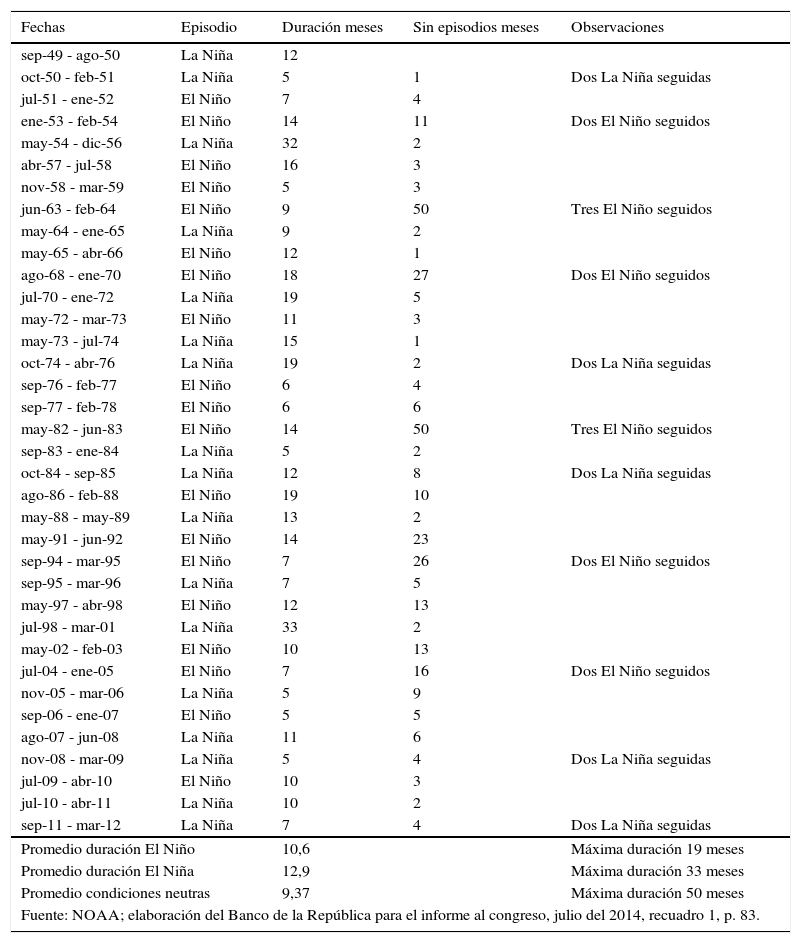
Cronología de eventos en Colombia
| Fechas | Episodio | Duración meses | Sin episodios meses | Observaciones |
|---|---|---|---|---|
| sep-49 - ago-50 | La Niña | 12 | ||
| oct-50 - feb-51 | La Niña | 5 | 1 | Dos La Niña seguidas |
| jul-51 - ene-52 | El Niño | 7 | 4 | |
| ene-53 - feb-54 | El Niño | 14 | 11 | Dos El Niño seguidos |
| may-54 - dic-56 | La Niña | 32 | 2 | |
| abr-57 - jul-58 | El Niño | 16 | 3 | |
| nov-58 - mar-59 | El Niño | 5 | 3 | |
| jun-63 - feb-64 | El Niño | 9 | 50 | Tres El Niño seguidos |
| may-64 - ene-65 | La Niña | 9 | 2 | |
| may-65 - abr-66 | El Niño | 12 | 1 | |
| ago-68 - ene-70 | El Niño | 18 | 27 | Dos El Niño seguidos |
| jul-70 - ene-72 | La Niña | 19 | 5 | |
| may-72 - mar-73 | El Niño | 11 | 3 | |
| may-73 - jul-74 | La Niña | 15 | 1 | |
| oct-74 - abr-76 | La Niña | 19 | 2 | Dos La Niña seguidas |
| sep-76 - feb-77 | El Niño | 6 | 4 | |
| sep-77 - feb-78 | El Niño | 6 | 6 | |
| may-82 - jun-83 | El Niño | 14 | 50 | Tres El Niño seguidos |
| sep-83 - ene-84 | La Niña | 5 | 2 | |
| oct-84 - sep-85 | La Niña | 12 | 8 | Dos La Niña seguidas |
| ago-86 - feb-88 | El Niño | 19 | 10 | |
| may-88 - may-89 | La Niña | 13 | 2 | |
| may-91 - jun-92 | El Niño | 14 | 23 | |
| sep-94 - mar-95 | El Niño | 7 | 26 | Dos El Niño seguidos |
| sep-95 - mar-96 | La Niña | 7 | 5 | |
| may-97 - abr-98 | El Niño | 12 | 13 | |
| jul-98 - mar-01 | La Niña | 33 | 2 | |
| may-02 - feb-03 | El Niño | 10 | 13 | |
| jul-04 - ene-05 | El Niño | 7 | 16 | Dos El Niño seguidos |
| nov-05 - mar-06 | La Niña | 5 | 9 | |
| sep-06 - ene-07 | El Niño | 5 | 5 | |
| ago-07 - jun-08 | La Niña | 11 | 6 | |
| nov-08 - mar-09 | La Niña | 5 | 4 | Dos La Niña seguidas |
| jul-09 - abr-10 | El Niño | 10 | 3 | |
| jul-10 - abr-11 | La Niña | 10 | 2 | |
| sep-11 - mar-12 | La Niña | 7 | 4 | Dos La Niña seguidas |
| Promedio duración El Niño | 10,6 | Máxima duración 19 meses | ||
| Promedio duración El Niña | 12,9 | Máxima duración 33 meses | ||
| Promedio condiciones neutras | 9,37 | Máxima duración 50 meses | ||
| Fuente: NOAA; elaboración del Banco de la República para el informe al congreso, julio del 2014, recuadro 1, p. 83. | ||||
Para verificar que se cumplen los supuestos sobre el residual y los parámetros del modelo no lineal STR, se realizan las siguientes pruebas de diagnóstico.
Prueba de no autocorrelación de errores: esta prueba desarrollada en Teräsvirta (1998) es un caso especial de la prueba de autocorrelación propuesta por Godfrey (1979). El procedimiento parte de una regresión de los residuos ¿ˆt en función de sus valores rezagados ¿ˆt−1...¿ˆt−q y las derivadas parciales de la función log-verosimilitud con respecto a los parámetros del modelo obtenidos en la regresión auxiliar. El estadístico de prueba es:
donde k es el número de parámetros del modelo, q es el número de rezagos de los residuos, SSR0 es la suma de los residuos al cuadrado del modelo STR y SSR1 es la suma de los residuos al cuadrado de la regresión auxiliar.Prueba de no linealidad remanente: una vez el modelo STR ha sido estimado, se debe verificar que no existan no-linealidades adicionales. La alternativa propuesta por Eitrheim y Teräsvirta (1996) se define como:
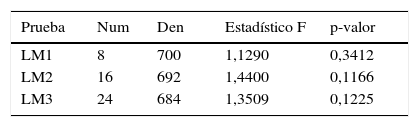
donde G y H son funciones de transición asociadas a las variables de transición s1t y s2t. Adicionalmente, ¿t∼iid(0,σ2). Para evaluar esta alternativa se utiliza la siguiente regresión auxiliar:El estadístico de prueba parte de una regresión de ¿ˆt en función de (xˆt′s2t,xˆt′s2t2,xˆt′s2t3)′ y las derivadas parciales de la función log-verosimilitud con respecto a los parámetros del modelo. La hipótesis nula ϕ31=ϕ32=ϕ33=0 representa la ausencia de no linealidades remanentes. Los estadísticos F asociados a esta prueba están dados de la misma forma que para el test de linealidad.
Posteriormente, van Dijk y Franses (1999) proponen una alternativa a la metodología de Eitrheim y Teräsvirta (1996) que busca comparar un modelo STR de dos regímenes respecto a una posibilidad de multi-régimen (MRSTR). Aunque la idea de esta prueba es similar a la anterior (ecuación (11)), su representación es de la siguiente manera:
donde la hipótesis nula es formulada como H0:ϕ3i=0, i=1, …, 6.Prueba de parámetros constantes: con el objeto de contrastar la hipótesis nula de parámetros constantes frente a cambios suaves y continuos en los parámetros, se parte de la regresión presentada en la ecuación (13) con s2t=t* donde t*=tT−12:
La hipótesis nula es H0:ϕ3j=0, j=1, …, K donde los estadísticos LM1, LM2 y LM3 están asociados a diferentes valores de K. Lin y Teräsvirta (1994) muestran que la distribución estadística de la prueba (F) se mantiene.
Enders y Ludlow (2002) proponen una prueba de raíz unitaria que incorpora un modelo autorregresivo que es una función determinística del tiempo:
donde ¿t es un proceso ruido blanco con varianza constante y α(t) es una función en el tiempo que puede ser no lineal. Aplicando una recursión sobre yt, la ecuación (15) se puede representar como:en donde el decaimiento de la secuencia yt requiere que2424La forma de α(t) puede ser representada, bajo condiciones muy generales, mediante una serie de Fourier lo suficientemente larga.
De acuerdo con los autores, con el fin de lograr parsimonia, se puede realizar la siguiente aproximación paramétrica:
donde T corresponde al número total de observaciones y k es un número entero entre 1 y T/2. De este modo, sólo se deben encontrar valores apropiados para a0, a1, b1, y k. Generalizando la expresión (15) se tiene el siguiente proceso:Luego, reemplazando la ecuación (18) en (19) se obtiene:
En este caso, se puede estimar k minimizando la suma de residuos al cuadrado asociados a la ecuación (20). Después se estiman los parámetros a1, b1 y c=a0−1. El siguiente paso es determinar si estos son significativos, mediante una serie de pruebas anidadas, como lo indicaEnders y Ludlow (2002)2525 Las estadísticas asociadas a estas pruebas de hipótesis son calculadas de la forma usual mediante las distribuciones F o t.
Si el proceso que genera la serie tiene una raíz unitaria, se acepta la hipótesis nula asociada a las estadísticas Fall, Ftrig y c. En caso contrario, cuando no existe una raíz unitaria, las estadísticas Ftrig y c servirán para especificar si se tienen decaimientos lineales (a1=b1=0) o no lineales (a1≠0 ó b1≠0). La aceptación de la hipótesis nula asociada a la estadística cr indica que el proceso que genera la serie no cumple la condición |a0|<1+r2/4 y r<22626 Una descripción detallada de esta prueba se encuentra en Enders y Ludlow (2002) y Jalil y Melo (2000).
Una forma de considerar el comportamiento dinámico de un modelo no lineal como el STR es examinando los efectos de choques ¿t sobre valores futuros de la serie de tiempo yt. Este análisis se puede realizar mediante el uso de funciones de impulso respuesta. Los impulsos respuesta se definen como la diferencia entre 2 pronósticos de yt. En el primer pronóstico, el proceso es afectado por un choque de tamaño δ en el momento t, mientras que en el segundo, el choque no ocurre. Los choques en los periodos intermedios entre t y t+h son cero en ambas realizaciones. Así, la función tradicional impulso respuesta IRF está dada por:
Para h=0, 1, 2, ... esta función tiene algunas propiedades cuando el modelo subyacente es lineal. En primer lugar, la función IRF es simétrica, lo que implica que un choque de tamaño −δ tiene exactamente un efecto opuesto pero de igual magnitud al de un choque de tamaño +δ. Adicionalmente, es lineal pues la respuesta es proporcional al tamaño del choque. Por último, el impulso respuesta es independiente en su historia ya que no depende del periodo de tiempo donde se realice el choque2727 Por ejemplo, en un modelo AR(1) yt=ϕ0+ϕ1yt−1+¿t, el impulso respuesta está dado por IRFy(h,δ,t−1)=ϕ1hδ, para h=0, 1, 2..., el cual no depende de t.
En contraste con lo anterior, en modelos como el STR, el impacto de un choque depende de la historia del proceso, del signo y de la magnitud del choque. Por lo tanto, el enfoque tradicional de impulso respuesta no es adecuado para dicha modelación. Una alternativa metodológica, introducida por Koop et al. (1996), es la función impulso respuesta generalizada (GIRF) en el contexto de modelos no lineales. La GIRF para un choque específico ¿t=δ con historia ωt−1 está definida como:
Para h=0, 1, 2, …, donde ωt−1 representa la historia del proceso en el periodo t. En esta definición el valor esperado está condicionado tanto al choque (δ) como a la historia particular o periodo de tiempo donde ocurre el choque (ωt−1).
La GIRF es una función de h, δ y ωt−1. Es importante notar que δ y ωt−1 son realizaciones de variables aleatorias ¿t y Ωt−1. Koop et al. (1996) destacan que la GIRFy(h, δ, ωt−1) es en sí misma una realización de una variable aleatoria definida como:
La definición anterior permite diferentes versiones condicionales de interés potencial. Por ejemplo, se puede considerar solamente una historia particular ωt−1 y tratar la GIRF como una variable aleatoria en términos de ¿t. También se puede considerar la GIRF como variable aleatoria condicionada a subconjuntos S y H de choques e historias, respectivamente (GIRFy[h, S, H]). Así, se puede condicionar a todas las historias en un régimen particular y considerar solamente choques negativos2828 Véase Koop et al. (1996) para una descripción detallada de las técnicas relevantes y Potter (2000) para más discusiones sobre la GIRF y sus posibles usos.
El choque asociado a la GIRF se puede realizar sobre variables endógenas y exógenas2929 En el caso lineal para modelos VAR, este análisis se encuentra desarrollado en detalle en Lütkepohl (2007), con el nombre de análisis de multiplicadores.
tablas 4–13
Prueba de no linealidad (LM) para ENSO
| st | H01 | H04 | H03 | H02 | Modelo |
|---|---|---|---|---|---|
| ENSOt−1 | 0,010823 | 0,802055 | 0,054113 | 0,003519 | LSTR |
| ENSOt−2 | 0,008834 | 0,747603 | 0,042484 | 0,104173 | ESTR |
| ENSOt−3 | 0,008880 | 0,189148 | 0,146092 | 0,009436 | LSTR |
| ENSOt−4 | 0,009958 | 0,088759 | 0,261193 | 0,013200 | LSTR |
| ENSOt−5 | 0,066109 | 0,402153 | 0,269741 | 0,029792 | LSTR |
| ENSOt−6 | 0,060781 | 0,618039 | 0,062639 | 0,068304 | ESTR |
| ENSOt−7 | 0,015279 | 0,121057 | 0,040124 | 0,128346 | LSTR |
Estimación STR para ENSO
| Variable Dependiente: ENSO | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable de transición ENSOt−2 | |||||||||
| Coef. | STD | Z | p-valor | ||||||
| γ | 0,670 | 0,493 | 1,360 | 0,174 | |||||
| c | 1,439 | 0,339 | 4,242 | 0,000 | |||||
| Componente lineal | Componente no lineal | ||||||||
| Coef. | STD | Z | p-valor | Coef. | STD | Z | p-valor | ||
| Constante | 0,113 | 0,049 | 2,295 | 0,022 | Constante | −0,155 | 0,070 | −2,234 | 0,025 |
| ENSOt−1 | 1,475 | 0,051 | 28,982 | 0,000 | ENSOt−1 | −0,129 | 0,056 | −2, 315 | 0,021 |
| ENSOt−2 | −0,571 | 0,059 | −9,732 | 0,000 | ENSOt−3 | 0,144 | 0,054 | 2,668 | 0,008 |
| ENSOt−5 | −0,070 | 0,041 | −1,684 | 0,092 | ENSOt−5 | 0,099 | 0,048 | 2,054 | 0,040 |
| ENSOt−7 | −0,060 | 0,021 | −2,928 | 0,003 | |||||
| STD inversa de ENSO | 1,1963 | R cuadrado | 0,9328 | ||||||
| Suma de errores al cuadrado (SSR) | 33,5873 | Errores estándar de los residuos | 0,2178 | ||||||
| Log Likelihood | 33,2416 | Var(Nolin)/Var(Lin) | 0,9729 | ||||||
| AIC | 10,9924 | ||||||||
| BIC | 35,6271 | ||||||||
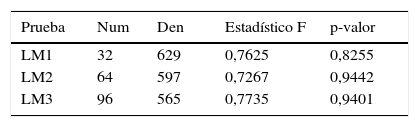
Prueba de no linealidad remanente para ENSO
| Prueba | Num | Den | Estadístico F | p-valor |
|---|---|---|---|---|
| Eitrheim y Teräsvirta (1996) | 12 | 694 | 0,4190 | 0,9564 |
Ho: no hay no linealidades remanente del tipo STR.
Prueba de no linealidad (LM) para DINF
| st | H0 | H04 | H03 | H02 | Modelo |
|---|---|---|---|---|---|
| ENSOt | 0,967530 | 0,966613 | 0,244193 | 0,999997 | ESTR |
| ENSOt−1 | 0,814453 | 0,910285 | 0,094242 | 0,999121 | ESTR |
| ENSOt−2 | 0,217180 | 0,953056 | 0,002401 | 0,960585 | ESTR |
| ENSOt−3 | 0,027473 | 0,892902 | 0,000179 | 0,756724 | ESTR |
| ENSOt−4 | 0,005053 | 0,368059 | 0,000155 | 0,642963 | ESTR |
| ENSOt−5 | 0,000495 | 0,291759 | 0,000010 | 0,580430 | ESTR |
| ENSOt−6 | 0,000420 | 0,217074 | 0,000014 | 0,575274 | ESTR |
| ENSOt−7 | 0,001517 | 0,183764 | 0,000081 | 0,643870 | ESTR |
Los valores en negrita indican el rezago en el que se presenta el menor p-valor asociado a la prueba LM.
Estimación STR para el crecimiento de la inflación de alimentos (DINF)
| Variable Dependiente: Inflación de Alimentos (DINF) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Variable de Transición: ENSOt−6 | |||||||||
| Coef. | STD | Z | p-value | ||||||
| γ | 0,886 | 0,376 | 2,358 | 0,018 | |||||
| c | 1,585 | 0,217 | 7,314 | 0,000 | |||||
| Componente lineal | Componente no lineal | ||||||||
| Coef. | STD | Z | p-valor | Coef. | STD | Z | p-valor | ||
| Constante | 0,002 | 0,004 | 0,470 | 0,638 | Constante | −0, 003 | 0,005 | −0, 562 | 0,574 |
| DINFt−1 | 0,511 | 0,034 | 14,920 | 0,000 | DINFt−3 | 0,237 | 0,082 | 2,873 | 0,004 |
| DINFt−3 | −0, 257 | 0,070 | −3, 665 | 0,000 | DINFt−6 | −0, 069 | 0,039 | −1, 759 | 0,079 |
| DINFt−5 | 0,087 | 0,035 | 2,518 | 0,012 | DINFt−11 | −0, 159 | 0,087 | −1, 836 | 0,066 |
| DINFt−8 | 0,068 | 0,031 | 2,223 | 0,026 | DINFt−17 | 0,251 | 0,091 | 2,759 | 0,006 |
| DINFt−11 | 0,216 | 0,078 | 2,756 | 0,006 | DINFt−18 | −0, 074 | 0,043 | −1, 724 | 0,085 |
| DINFt−12 | −0,770 | 0,037 | −20,625 | 0,000 | DINFt−19 | −0, 324 | 0,099 | −3, 269 | 0,001 |
| DINFt−13 | 0,348 | 0,044 | 7,900 | 0,000 | DINFt−20 | 0,309 | 0,102 | 3,036 | 0,002 |
| DINFt−14 | −0,058 | 0,030 | −1,941 | 0,052 | DINFt−21 | −0,250 | 0,086 | −2,896 | 0,004 |
| DINFt−16 | −0,068 | 0,030 | −2,263 | 0,024 | DINFt−22 | 0,080 | 0,038 | 2,098 | 0,036 |
| DINFt−17 | −0,199 | 0,079 | −2,520 | 0,012 | ENSOt | 0,025 | 0,007 | 3,395 | 0,001 |
| DINFt−19 | 0,354 | 0,087 | 4,059 | 0,000 | ENSOt−1 | −0,042 | 0,013 | −3,204 | 0,001 |
| DINFt−20 | −0,254 | 0,092 | −2,775 | 0,006 | ENSOt−2 | 0,033 | 0,013 | 2,474 | 0,013 |
| DINFt−21 | 0,191 | 0,073 | 2,632 | 0,008 | ENSOt−3 | −0,019 | 0,009 | −2,198 | 0,028 |
| DINFt−23 | 0,061 | 0,036 | 1,707 | 0,088 | ENSOt−6 | −0,005 | 0,003 | −1,686 | 0,092 |
| DINFt−24 | −0,416 | 0,037 | −11,191 | 0,000 | ENSOt−7 | 0,011 | 0,005 | 2,393 | 0,017 |
| DINFt−25 | 0,160 | 0,036 | 4,421 | 0,000 | |||||
| ENSOt | −0,024 | 0,006 | −3,720 | 0,000 | |||||
| ENSOt−1 | 0,040 | 0,011 | 3,524 | 0,000 | |||||
| ENSOt−2 | −0,033 | 0,012 | −2,877 | 0,004 | |||||
| ENSOt−3 | 0,021 | 0,007 | 2,962 | 0,003 | |||||
| ENSOt−7 | −0,008 | 0,004 | −2,347 | 0,019 | |||||
| STD inversa de DINF | 1,2103 | R-cuadrado | 0,5906 | ||||||
| Suma de errores al cuadrado (SSR) | 0,1189 | Errores estándar de los residuos | 0,0134 | ||||||
| Log Likelihood | 0,1173 | Var(Nolin)/Var(Lin) | 0,5324 | ||||||
| AIC | 80,2860 | ||||||||
| BIC | 183,3334 | ||||||||
Prueba de no linealidad remanente para DINF
| Prueba | Num | Den | Estadístico F | p-valor |
|---|---|---|---|---|
| Eitrheim y Teräsvirta (1996) | 45 | 614 | 1,3712 | 0,0577 |
Ho: no hay no linealidades remanente del tipo STR.
Módulos de las raíces dominantes del polinomio característico del modelo STR de DINF para diferentes regímenes
| G=0 | G=0,2 | G=0,4 | G=0,6 | G=0,8 | G=1 |
|---|---|---|---|---|---|
| 0,991 | 0,999 | 1,007 | 1,017 | 1,028 | 1,023 |
| 0,991 | 0,999 | 1,007 | 1,017 | 1,028 | 1,023 |
| 1,002 | 1,009 | 1,017 | 1,024 | 1,030 | 1,031 |
| 1,002 | 1,009 | 1,017 | 1,024 | 1,030 | 1,031 |
| 1,007 | 1,017 | 1,023 | 1,029 | 1,031 | 1,031 |
G corresponde a la función de transición. Las filas están asociadas a los módulos de las 5 raíces mayor dominantes.
Un caso particular de la familia de indicadores SST, es el índice oceánico El Niño (The Oceanic Niño Index [ONI]).
The National Oceanic and Atmospheric Administration (NOAA).
El autor estima que la cifra de muertos por hambre durante el periodo de 26 años de estudio fue de entre 30 y 60 millones de personas.
En Colombia, la precipitación intra-anual presenta dos regímenes: i) bimodal en la zona andina, cuyos trimestres diciembre-enero-febrero y junio-julio-agosto son de baja pluviosidad, frente a marzo-abril-mayo y septiembre-octubre-noviembre, que son de alta pluviosidad, y ii) unimodal en la parte oriental. En la región andina se presentan diversos pisos térmicos y en promedio por cada 100 metros sobre el nivel del mar disminuye la temperatura en 0,065 grados Celsius (GC), mientras que en el resto del país la temperatura promedio oscila entre 24 GC y 30 GC (Pabón et al., 2001).
The Southern Oscillation Index.
Cuando la participación de los sectores agrícola y de pesca de la economía es baja entonces dichos países son menos vulnerables a las fluctuaciones climáticas.
Con el creciente conocimiento de la existencia del ENSO y los avances tecnológicos que permiten ampliar la capacidad de medir y predecir El Niño, algunos de los efectos negativos del ENSO podrían ser contrarrestados mediante respuestas de política apropiadas para el sector agrícola a través de la mejora de las estrategias de riego, el almacenamiento de agua, la construcción y la preparación de mecanismos de defensa frente a posibles incendios forestales, entre otros.
Los autores argumentan que los efectos negativos que el clima tiene sobre algunas actividades es contrarrestado por otras tales como la industria manufacturera, los servicios financieros, entre otros. Así, a nivel agregado los choques del clima no son significativos para el PIB total o la inflación total del país.
Para conocer la metodología de cálculo se puede consultar: https://www.ncdc.noaa.gov/teleconnections/enso/indicators/soi/
Las estadísticas de los sensores disponibles para las 4 regiones se pueden encontrar en: http://www.cpc.ncep.noaa.gov/data/indices/ersst3b.nino.mth.ascii
Este tipo de especificación ha sido trabajada en Lin y Teräsvirta (1994).
La propuesta de Luukkonen et al. (1988) permite solucionar el problema planteado por Davies (1987), en el cual se tenía un problema de identificación debido a que este modelo se puede reducir a uno lineal en 2 casos: cuando γ=0 o al asumir que todos los coeficientes asociados a φ2 son cero.
k0 y k1 representan el número de variables regresoras bajo la hipótesis nula y la regresión auxiliar completa, respectivamente.
Estas anomalías corresponden a las desviaciones mensuales de El Niño 3.4 respecto a su promedio histórico. De acuerdo con el Centro de Predicción Climática de la NOAA, la región SST v3.4 es la más frecuentemente utilizada para hacer análisis de los fenómenos climáticos de El Niño y La Niña. Al realizar cálculos con otras regiones se encontró como resultado que la mayor correlación con los precios de los Alimentos en Colombia se encontraba con dicha variable.
La descripción de esta prueba se encuentra en el anexo C.
El número de rezagos máximo de ENSO presentado en la tabla 4 del anexo E fue seleccionado a partir del criterio de información de Akaike (AIC).
En este documento, las estimaciones de los parámetros que no fueron significativos han sido eliminadas a excepción de las constantes y los parámetros de suavizamiento y localización.
Estas pruebas son descritas en el anexo B.
Tal como ocurre en este caso, es de notar que en contextos no lineales se pueden presentar comportamientos locales explosivos a pesar que el proceso sea globalmente estacionario. Las pruebas de raíz unitaria sobre DINF, presentadas en las tablas 1 y 2, confirman que esta serie es globalmente estacionaria.
El impulso respuesta tradicional (IRF) para modelos lineales exhibe 2 características: simetría e independencia en el tiempo. La primera implica que un choque de magnitud −δ produce el mismo efecto que un choque de magnitud δ. La segunda implica que la respuesta de un choque no depende del periodo en el que se realice.
Los valores de la variable ENSO entre −1 y 1 definen fenómenos de El Niño y La Niña débiles. Los impulsos respuesta de los fenómenos climáticos de carácter débil sobre los precios de los alimentos no tuvieron significación estadística, por lo que no se muestran en el documento.
La mediana se incorpora en la figura como una linea horizontal negra para cada momento de tiempo.
Es importante notar que la escala de las figuras 4 y 5 de los GIRF están en términos porcentuales. Por ejemplo, 0,04 equivale a 4% o 400 puntos básicos.
La forma de α(t) puede ser representada, bajo condiciones muy generales, mediante una serie de Fourier lo suficientemente larga.
Las estadísticas asociadas a estas pruebas de hipótesis son calculadas de la forma usual mediante las distribuciones F o t.
Una descripción detallada de esta prueba se encuentra en Enders y Ludlow (2002) y Jalil y Melo (2000).
Por ejemplo, en un modelo AR(1) yt=ϕ0+ϕ1yt−1+¿t, el impulso respuesta está dado por IRFy(h,δ,t−1)=ϕ1hδ, para h=0, 1, 2..., el cual no depende de t.
Véase Koop et al. (1996) para una descripción detallada de las técnicas relevantes y Potter (2000) para más discusiones sobre la GIRF y sus posibles usos.
En el caso lineal para modelos VAR, este análisis se encuentra desarrollado en detalle en Lütkepohl (2007), con el nombre de análisis de multiplicadores.