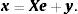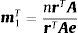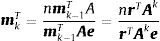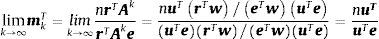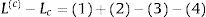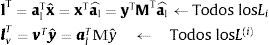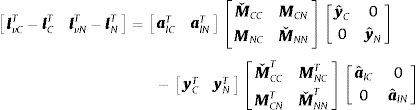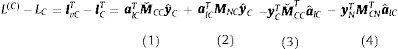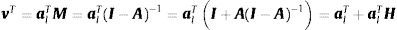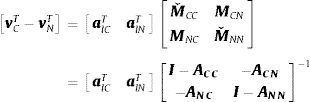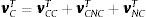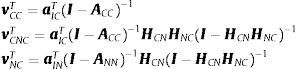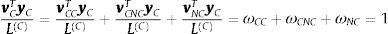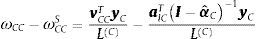Conocer de manera profunda las relaciones de interdependencia de la estructura económica es de gran importancia en el ejercicio de diseño de políticas económicas. Este trabajo usa el modelo insumo-producto para el análisis económico. Se aplican 2 enfoques no usados tradicionalmente para la economía colombiana: análisis de descomposición espectral (Dietzenbacher, 1992) e identificación de clústeres (Garbellini y Wirkierman, 2014). El resultado es la construcción de indicadores de encadenamientos sin sesgo de sobrestimación o subestimación, y la identificación de clústeres de manera endógena. Adicionalmente se derivan los flujos de trabajo incorporado que se propagan a través de la red productiva. Cada uno de estos flujos se descompone en indicadores que permiten caracterizar los clústeres de acuerdo a su cercanía con la demanda final, su grado de cohesión con la red y su importancia para el resto del sistema.
To design economic policy, it is very important to know in depth the interdependence of the economic structure. This work uses the input-output (I/O) model for economic analysis. Two approaches, not traditionally used, are applied to analyse the Colombian economy: spectrum of different I/O coefficient matrices (Dietzenbacher, 1992) and clustering techniques (Garbellini y Wirkierman, 2014). As a result, indicators of linkages are obtained without bias of overestimation or underestimation. Additionally, clusters are identified endogenously. Furthermore, embodied labour flows that spread through the network-production are calculated. Each of these flows is broken down into indicators that characterise the clusters according to their proximity to final demand, to their degree of cohesion to the network, and to their importance for the rest of the system.
El principal objetivo de la política industrial consiste en crear ambientes propicios para el aumento de la competitividad industrial, favoreciendo el crecimiento de la productividad, el empleo y la producción. De forma concreta, las políticas industriales buscan revitalizar las relaciones interindustriales, incentivar la migración hacia nuevas tecnologías y, mediante la intervención sobre sectores, aprovechar las capacidades inherentes del sistema productivo.
Estas políticas cobran mayor importancia para una economía inserta en el mundo globalizado. Es claro que la competencia en el mercado internacional obliga a la industria a ofrecer productos a precios competitivos y con altos estándares de calidad. En este sentido, es cada vez más importante conocer en profundidad el sistema productivo de una economía, identificar los sectores que puedan generar fuertes impulsos productivos al resto de la economía y buscar posibles sinergias entre ellos.
Tradicionalmente, estas medidas, que apuntan a lograr desarrollos productivos, se enfocan principalmente en el ámbito macroeconómico. Según Porter (1990), esto le ha otorgado a la educación un papel primordial como instrumento para el desarrollo económico y social. Pero además ha permitido que se avance en la eliminación de las barreras que restringen la competencia industrial.
Sin embargo, tal enfoque puede quedarse corto si se deja de lado la información microeconómica del sistema. Como se dijo arriba, es fundamental entender las relaciones interindustriales y el comportamiento de la firma en su entorno; establecer cuáles son los principales flujos comerciales entre industrias, y determinar las fortalezas del sistema para la innovación y el crecimiento. Un resultado destacado de este análisis es la construcción de una topología relevante de la red productiva en la economía.
El análisis input-output es precisamente una aproximación a la construcción de esta red de insumos y productos de una economía. La robustez de su estructura permite simular escenarios de forma intuitiva y obtener respuestas de fácil interpretación. Además, cuenta con un número importante de herramientas adecuadas para extraer gran cantidad de información propia de la red productiva.
Entre estas herramientas, las más utilizadas son los indicadores de encadenamientos. Con estos es posible calcular los cambios en las actividades productivas que se generan por choques a la demanda final de algún producto dado. De esta manera, se obtienen medidas normalizadas de la dependencia, directa o indirecta, de un sector industrial en los demás sectores. O, en la otra vía, medir la dependencia de los demás sectores en un sector particular.
Otro de los enfoque es el análisis de clústeres, que permite sintetizar las relaciones industriales en redes agregadas de información. Desde principios de los noventa, esta herramienta ha sido ampliamente usada para promover el desarrollo económico, ya sea regional o sectorial (Titze, Brachert y Kubis, 2010).
Si bien no existe un consenso acerca de la definición de clúster1, según Benneworth y Henry (2004) tiene la ventaja de que reúne múltiples perspectivas, teóricas y prácticas, sobre la aglomeración industrial. En este sentido, define los clústeres como: «…compañías interconectadas, proveedores especializados, servicios, firmas en industrias conectadas e instituciones asociadas (por ejemplo: universidades, agencias de estándares, asociaciones de comercio) en un sector en particular que compiten, pero que también cooperan».
De manera más general, el clúster es un concepto que pretende estudiar los cambios de la productividad derivados del aprovechamiento de sinergias y economías de escala y la aglomeración.
Para Colombia existen 2 estudios relevantes para la identificación de clústeres productivos: Hausmann y Klinger (2007) y Duque, Rey y Gómez (2009). En el primer estudio el objetivo principal de los autores es diagnosticar el desempeño exportador de Colombia. Así, establecen cuáles son las posibles oportunidades para procurar un crecimiento a partir de las exportaciones. La evaluación de los autores concluye que la actual canasta exportadora no le brinda a Colombia suficientes opciones para impulsar el crecimiento productivo. A partir de sus resultados, los autores determinan cuáles serían los sectores más próximos a la cesta producida actualmente en el país, y que otorgan las mayores opciones de crecimiento: medicamentos, productos metálicos fabricados, confecciones textiles, reparaciones y construcción naval, vehículos a motor y electrodomésticos y aparatos eléctricos.
Por su parte, el estudio de Duque et al. (2009) usa la metodología de Duque y Rey (2008) (clústeres industriales basados en redes [NBIC]) para identificar clústeres. Los autores inician tomando la descripción de producción y transacción de insumos planteada en matriz insumo-producto (IP, en adelante) para Colombia 2005. Luego, con la ayuda de un algoritmo de reducción y partición de la red productiva, encuentran los sectores centrales a la economía junto con los flujos interindustriales más fuertes. El resultado es la identificación de 12 clústeres industriales en la economía colombiana: construcción, industria petroquímica, transporte, comida, comercio (mayorista y minorista), servicios de educación, restaurantes, energía para industrias, banca, agricultura, energía para uso residencial y comercial, y servicios públicos.
El presente trabajo es una aproximación al estudio de las relaciones interindustriales para Colombia usando las 2 herramientas mencionadas arriba. Primero, se miden los encadenamientos sectoriales usando la metodología de descomposición espectral desarrollada por Dietzenbacher (1992). Como segunda herramienta se realiza la identificación de clústeres industriales para la economía colombiana usando la metodología planteada por Garbellini y Wirkierman (2014), basada en el algoritmo de partición espectral (APE, en adelante) de Newman (Leicht y Newman, 2008; Newman, 2006). Bajo esta metodología, los clústeres agrupan las industrias de acuerdo con su grado de interacción, es decir, según el grado de encadenamientos que tengan entre ellas mismas. En este sentido, se constituyen como subconjuntos de actividades que comparten interacciones más fuertes que el promedio en la red productiva, donde cada subconjunto se reúne en una estructura significativa con características particulares (Garbellini y Wirkierman, 2014).
Para el año 2005, con los 2 enfoques utilizados, se logran identificar 11 clústeres en los 61 sectores de las cuentas nacionales de la economía colombiana. A partir del cálculo ponderado y recursivo de los encadenamientos, hacia delante y hacia atrás, de estos 61 sectores se destacaron 11 sectores clave. De esta manera, se logró construir una red sintetizada del sistema productivo colombiano, con información suplementaria obtenida del cálculo de los indicadores de jerarquía, circularidad e independencia (Garbellini y Wirkierman, 2014).
Haciendo un paralelo con el estudio metodológicamente más semejante, el de Duque et al. (2009), se presentan algunas similitudes. En ambas investigaciones se parte del uso de matrices IP y de la teoría de grafos para el análisis de redes. Sin embargo, la metodología particular adoptada en este trabajo permite detectar clústeres usando toda la información contenida en la red productiva representada por la matriz IP, incluyendo aquellos flujos que van en doble dirección (Leicht y Newman, 2008). Además, es posible establecer interacciones intra y extra clúster: efectos spillover (efectos derrame) y feedback (efectos de retroalimentación) ante choques sobre la demanda final; jerarquías de clústeres de acuerdo a su cercanía con la demanda final, y grado de independencia (clústeres más o menos cohesionados) dentro de la red productiva.
El documento se organiza como sigue: a continuación, en la sección 2, se presentan las metodologías para el cálculo de los encadenamientos, sectores clave y para la identificación de clústeres de la economía. En la sección 3 se realiza el ejercicio empírico aplicando las 2 metodologías para las cuentas nacionales de Colombia. A partir de estos resultados se realiza una descripción sectorial y a nivel de clúster. Finalmente, en la secciones 3 y 4 se hace la caracterización de los clústeres de la economía de acuerdo al rol que podrían desempeñar en el diseño de una política de desarrollo industrial.
2MetodologíaUno de los desafíos de política para el crecimiento económico es identificar sectores clave en la estructura productiva de un país. Alcanzar este propósito permite realizar políticas diferenciadas, pero logrando efectos integrales a la economía.
Aunque caracterizar sectores puede ser una tarea difícil de llevar a cabo, el modelo IP es una herramienta que permite hacerlo de forma más o menos sencilla. El eje central de este modelo son las matrices IP. En estas se presentan de forma contable la oferta y demanda de cada uno de los sectores de una economía, así como las transacciones de insumos intermedios entre ellos. Adicionalmente, existe gran cantidad de instrumentos teóricos para la síntesis y extracción de la información contenida en ellas.
Una primera aproximación al problema de identificar sectores clave es calcular índices de encadenamientos de las actividades productivas. Esto es, llevar a cabo el cálculo del impacto de un sector sobre el resto de la economía desde 2 ángulos distintos: a)hacia atrás: la capacidad de un sector de arrastrar a otros sectores que le proveen los insumos intermedios para su proceso de producción, y b)hacia delante: la capacidad del sector de impulsar otros sectores proporcionando los insumos intermedios necesarios.
Con los resultados de encadenamientos es posible clasificar las actividades de la economía en sectores clave (que tienen fuertes encadenamientos hacia atrás y hacia a delante), sectores de arrastre (que tienen fuertes encadenamientos solo hacia atrás), sectores impulsores (que tienen fuertes encadenamientos solo hacia delante) y el resto de sectores (que tienen encadenamientos débiles).
Diferentes trabajos han aplicado este enfoque para caracterizar el sistema productivo colombiano. Ya sea que tomen a la economía en su conjunto2 o se limiten a un sector específico3, las 2 metodologías usadas son las de Chenery y Watanabe (1958) para la identificación de los requerimientos directos de producción, y la de Rasmussen (1957) para la identificación de los requerimientos directos e indirectos de producción.
El presente trabajo hace uso de la metodología alternativa, planteada por Dietzenbacher (1992) para la identificación de requerimientos directos e indirectos de producción. Bajo esta perspectiva los encadenamientos de un sector se calculan como los requerimientos directos e indirectos ponderados de acuerdo al grado de interconexión con cada una de las demás industrias. De esta manera, en el cálculo del indicador de encadenamientos hacia atrás de cierta industria el mayor peso le será asignado a su proveedor que tenga mayores encadenamientos hacia atrás. El cálculo se realiza recursivamente en infinitas rondas sucesivas del proceso productivo. De este modo, el indicador de encadenamientos de Dietzenbacher logra sintetizar de manera ponderada los flujos de insumos entre industrias.
En la tabla 1 se presenta una matriz IP de forma general, donde x representa el vector de producción bruta total. Verticalmente la producción se obtiene como la suma de los insumos intermedios, X, más el valor agregado (factores) f′. Por filas, la producción se distribuye hacia el consumo intermedio X y hacia la demanda final y.4
Matriz insumo-producto
| Sectores | Demanda Final | Totales | |
|---|---|---|---|
| Sectores productivos | X | y | x |
| Factores | f' | d | v'e+d |
| Totales | x′ | e'y+d |
Fuente: Dietzenbacher (1992).
La identidad IP está dada por:
Donde e representa el vector columna e=1,…,1T.
En la matriz X se representan los flujos interindustriales del sistema. Este es el punto de partida para el análisis IP de encadenamientos y clústeres, como se expone a continuación.
2.1Encadenamientos sectoriales2.1.1Chenery-Watanabe y RasmussenLos trabajos de Chenery y Watanabe (1958), Rasmussen (1957) y Hirschman (1961) usan la matriz X transformada de donde derivan los indicadores de encadenamientos (tabla 2). Para evitar realizar supuestos poco realistas, los encadenamientos hacia atrás se calculan a partir del enfoque de demanda de Leontief y los encadenamientos hacia delante a partir del enfoque de oferta de Ghosh (Miller y Blair, 2009)5.
Transformaciones de la matriz IP
| Representación Matricial | ||
|---|---|---|
| Enfoque de Leontief | Matriz de coeficientes técnicosa | A=Xxˆ−1 |
| Inversa de Leontief | M=I−A−1 | |
| Enfoque de Ghosh | Matriz de coeficientes de asignaciones | B=xˆ−1X |
| Inversa de Ghosh | G=I−B−1 |
Los símbolos con acento circunflejo (^) representan matrices diagonales, con los elementos del vector correspondiente en la diagonal. es la matriz identidad.
Fuente: Miller y Blair (2009).
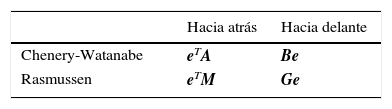
En la tabla 3 se muestran los 2 tipos de indicadores de encadenamientos tradicionalmente usados. Los indicadores de Chenery-Watanabe miden los requerimientos directos de insumos; es decir, la cantidad de insumos contratados directamente por algún sector para producir una unidad de su propio producto.
Encadenamientos: Chenery-Watanabe y Rasmussen
| Hacia atrás | Hacia delante | |
|---|---|---|
| Chenery-Watanabe | eTA | Be |
| Rasmussen | eTM | Ge |
Fuente: Miller y Blair (2009).
Los indicadores de Rasmussen no solo miden los requerimientos directos, sino que también cuantifican los requerimientos indirectos de producción. Estos últimos se refieren a los insumos contratados indirectamente por cierto sector para producir una unidad de su propio bien (para su producción, el sector i demanda insumos directamente al sector j; para satisfacer esta demanda, el sector j demanda insumos al sector k; en este proceso, el sector i demandó indirectamente insumos al sector k). En otras palabras, los requerimientos indirectos se refieren a la demanda acumulada que ejerce un sector sobre cierto insumo, y que se calcula de forma agregada en infinitas rondas sucesivas del proceso productivo6.
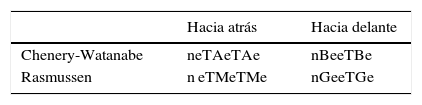
Adicionalmente, Hirschman introdujo el concepto de sectores clave a partir de los indicadores normalizados de encadenamientos. De esta manera, un sector clave es aquel cuyos indicadores de encadenamientos normalizados son mayores que uno: E.Atrás>1 y E.Adelante>1. En la tabla 4 se muestran los indicadores normalizados de encadenamientos; en dicha tabla, n es el número de sectores de la economía.
Encadenamientos normalizados: Chenery-Watanabe y Rasmussen
| Hacia atrás | Hacia delante | |
|---|---|---|
| Chenery-Watanabe | neTAeTAe | nBeeTBe |
| Rasmussen | n eTMeTMe | nGeeTGe |
Fuente: Miller y Blair (2009).
Una tercera aproximación para estimar indicadores de encadenamientos es la planteada por Dietzenbacher. En este enfoque los encadenamientos son calculados con el uso de los vectores propios correspondientes al autovalor dominante de las matrices A y B (Dietzenbacher, 1992).
Partiendo de una generalización de los indicadores directos de Chenery-Watanabe ponderado por el vector de pesos rT(>0):
Dado que m1T es el vector de indicadores de encadenamientos, se puede usar como ponderador. Y recursivamente se llega a que:
Finalmente, aceptando que A es una matriz primitiva y cuyo autovalor dominante es λ>0, se llega a que:
Donde w es el autovector por derecha y u es el autovector por izquierda asociados al autovalor λ.
Pero esto, sencillamente, es el autovector por izquierda normalizado7.
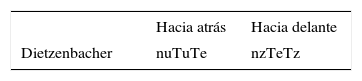
En la tabla 5 se muestran los indicadores de encadenamientos con la metodología de descomposición espectral, donde u es el autovector por izquierda asociado al autovalor dominante de la matriz A, y z es el autovector por derecha asociado al autovalor dominante de la matriz B (véase Dietzenbacher (1992) para una descripción más amplia de la obtención de los indicadores).
Encadenamientos Normalizados: Dietzenbacher
| Hacia atrás | Hacia delante | |
|---|---|---|
| Dietzenbacher | nuTuTe | nzTeTz |
Fuente: Dietzenbacher (1992).
La ventaja de estos indicadores de encadenamientos con respecto a los calculados con el método de Rasmussen o de Chenery-Watanabe es que permiten medir ponderadamente en infinitas rondas sucesivas los encadenamientos de cada sector, ya sea hacia delante o hacia atrás. De esta manera no se sobreestiman sectores con bajos encadenamientos, ni se subestiman sectores con altos encadenamientos.
2.2ClústeresUna segunda aproximación consiste en la caracterización de clústeres productivos a partir de la matriz IP. El estudio de Duque et al. (2009) es un ejemplo de la aplicación de esta técnica para Colombia. En el presente trabajo se hace uso del algoritmo de partición espectral (APE) para redes propuesto por Newman (2006) y Leicht y Newman (2008). Esta metodología logra dividir la red en comunidades, no superpuestas, de industrias cuyas interacciones están por encima del promedio.
Si bien un estudio de las relaciones interindustriales debe incluir los aspectos geográfico e institucional, el análisis IP tiene la ventaja de que permite construir nuevas redes sintéticas, en las cuales se condensan las interacciones de todo el sistema. Particularmente, la metodología propuesta por Garbellini y Wirkierman (2014) permite cuantificar y clasificar los efectos que tienen estímulos a la demanda final sobre los clústeres identificados. Los autores construyen una serie de indicadores para medir tales efectos:
- •
Jerarquía: mide la cercanía de un clúster (o sector) con la demanda final.
- •
Circularidad: mide la distribución de trabajo incorporado intra y extra cluster.
- •
Independencia: mide los efectos spillover y feedback que puedan resultar.
A continuación se expone de manera más detallada la metodología usada para realizar el análisis IP del sistema productivo de una economía.
2.2.1Algoritmo de partición espectral (APE)La identificación de divisiones naturales de sectores en clústeres (comunidades) no superpuestos se hace a partir del APE planteado en Newman (2006) y Leicht y Newman (2008), con la ventaja adicional de que no es necesario conocer a priori el tamaño ni el número de las dichos clústeres (Newman, 2006).
La idea central de este algoritmo es que una forma altamente eficiente de identificar comunidades es organizar la red en grupos cuyas conexiones internas sean mucho más altas de las que se esperarían por el puro azar. En lenguaje formal, esto se traduce en maximizar la modularidad Q de la red, encontrar s de manera que se maximice Q para un R˜ dado (Newman, 2006):
Donde: R˜=R+RT, R=Dij−kiinkjoutm es la matriz de modularidad8; D muestra las conexiones entre cada par de nodos (en este caso la matriz IP: X); m es el peso total de todas las conexiones de la red; kin es el peso total de los links que salen de un vértice; kout es el peso total de los links que entran a un vértice, y en s se encuentra la pertenencia de un sector a un clúster u otro.
El algoritmo para dividir una red dirigida9 se puede resumir en los siguientes 3 pasos:
- i.
A partir de la red dirigida se construye la matriz de modularidad, R.
- ii.
Se separa la red en 2 clústeres, de modo que se maximice la modularidad (Q) de la red (grado de conexiones excepcionales entre los nodos) al interior de las clústeres. En otras palabras, se busca construir comunidades de sectores que comparten un número de conexiones inesperadamente alto. Según Newman (2006), la forma más eficiente de hacer esto es agrupar los sectores de acuerdo al signo del elemento correspondiente en el autovector asociado al autovalor dominante de la matriz R˜, los positivos en una comunidad y los negativos en la otra.
- iii.
De manera recursiva se regresa al paso ii, y se subdividen los clústeres encontrados, cada uno en 2 nuevos clústeres. El proceso continúa hasta el punto en el que subdivisiones adicionales resulten particiones triviales: un conjunto con todos los nodos del clúster y otro grupo con cero nodos. Es decir, hasta el punto en el que la actual subdivisión maximice el grado de conexiones excepcionales.
El componente de partición espectral se lleva a cabo en el paso ii. Allí, los sectores se clasifican de acuerdo al signo que tienen los elementos del autovector asociado al autovalor dominante; aquellos sectores cuyos elementos correspondientes en el autovector son positivos se asignan a una comunidad y los que son negativos a la otra comunidad. Newman (2006) muestra que esta sencilla aproximación es efectiva y eficiente para identificar clústeres (comunidades, como suele denominarse a dichos conjuntos de nodos en la literatura de redes complejas; véase, por ejemplo, Newman, 2006).
Este algoritmo tiene 2 ventajas con respecto a algoritmos similares y ampliamente usados. Primero, permite usar la información completa de una red dirigida: no se eliminan los flujos en doble vía. Y segundo, no es necesario conocer a priori el tamaño ni el número de los clústeres, se identifican endógenamente.
Una vez identificados los clústeres es posible sintetizar la información sobre los flujos de trabajo incorporado en 3 tipos de indicadores (Garbellini y Wirkierman, 2014). A continuación se expone la construcción de tales indicadores y la forma como estos sirven para clasificar los clústeres.
2.2.2Indicadores de jerarquíaEl indicador de jerarquía mide la cercanía de un clúster (o sector) con la demanda final. Se define como la relación entre el trabajo necesario (directa e indirectamente) para producir una unidad del bien final i y el requerimiento técnico de trabajo en sector i.
Para entender mejor este concepto es útil explicar previamente la noción de subsistemas de demanda final. En palabras sencillas, estos se definen como estructuras funcionales que producen únicamente un bien final. Reúnen el conjunto de sectores que contribuyen, directa e indirectamente, a la producción del bien10. De esta manera, en una economía, existe un subsistema por cada bien final que se produce (Garbellini y Wirkierman, 2014).
Siendo esto así, un indicador de jerarquía se puede definir como la resta entre el trabajo que necesita el subsistema i para producir una unidad del bien final y el trabajo que la industria i requiere para su producción bruta: L(i)−Li. Donde:
Li=alTxˆei=alixi ← Requerimientos directos de trabajo de cada industria i para producir el producto bruto xi
Li=alTxˆi=alTMyi=viyi ← Requerimientos de trabajo del subsistema asociado para producir la demanda final yi.
Nótese que si L(i)−Li>0, el sector i requiere, indirectamente, de mucho más trabajo para producir su bien final de aquel que le aporta a la producción de otros subsistemas. En otras palabras, los esfuerzos del sector están más encaminados hacia la demanda final. Para el caso en el que L(i)−Li<0, el análisis es similar (Garbellini y Wirkierman, 2014).
A nivel de clúster, el indicador de jerarquía se define de manera análoga: L(c)−Lc. En este caso, se dice que el clúster se encuentra más o menos cercano a la demanda final.
2.2.3Indicadores de circularidadLos indicadores de circularidad miden la persistencia del trabajo dentro del clúster o su propagación hacia otros clústeres. Esta distribución se puede clasificar en 4 componentes para cada clúster:
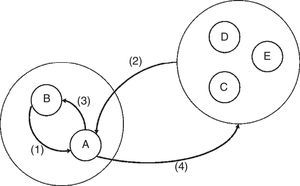
La figura 1 muestra cada uno de los componentes de la distribución de trabajo: 1)trabajo absorbido por cada subsistema del clúster desde otras industrias del mismo clúster; 2)trabajo absorbido por cada subsistema del clúster desde otras industrias fuera del clúster; 3)trabajo contratado directamente en cada industria del clúster que contribuye a la producción de subsistemas del mismo clúster, y 4)trabajo contratado directamente en cada industria del clúster que contribuye a la producción de subsistemas fuera del clúster.
Distribución del trabajo incorporado.
Fuente: Garbellini y Wirkierman (2014).
En la tabla 6 se describen las expresiones algebraicas de cada uno de los 4 indicadores de circularidad. Además se indica la fuente y el destino de los flujos de empleo, ya sea dentro del mismo clúster (intra-C) o fuera del clúster (extra-C). Donde a es el vector de coeficientes directos de trabajo, M es la inversa de Leontief y y es el vector de demandas finales (véase el Apéndice A para una descripción más amplia del cálculo de indicadores).
Indicadores de circularidad
| Flujo | Indicador | Empleo proveniente de industrias | Trabajo que va a subsistemas | Como proporción del total de |
|---|---|---|---|---|
| (1) | φCC=alCTMˇCCyˆC/LC | intra-C | intra-C | Trabajo del subsistema |
| (2) | φNC=alCTMNCyˆC/LC | extra-C | intra-C | Trabajo del subsistema |
| (3) | ψCC=yCTMˇCCTaˆlC/LC | intra-C | intra-C | Empleo de la Industria |
| (4) | ψCN=yNTMCNTaˆlC/LC | intra-C | extra-C | Empleo de la Industria |
Fuente: Garbellini y Wirkierman (2014).
Los indicadores de independencia permiten establecer la importancia que tiene la red productiva para cada uno de los clústeres. De forma recíproca, se puede establecer la importancia que tiene cada clúster para la red productiva. En otras palabras, los indicadores de independencia miden el grado de cohesión de los clústeres con el resto de la red. Estos indicadores señalan 3 efectos:
- 1.
Sinergias propias: efectos autoinducidos que no circulan por la red productiva.
- 2.
Efectos spillover: efectos inducidos sobre los demás clústeres de la red productiva.
- 3.
Efectos feedback: efectos de retroalimentación a través de la red productiva.
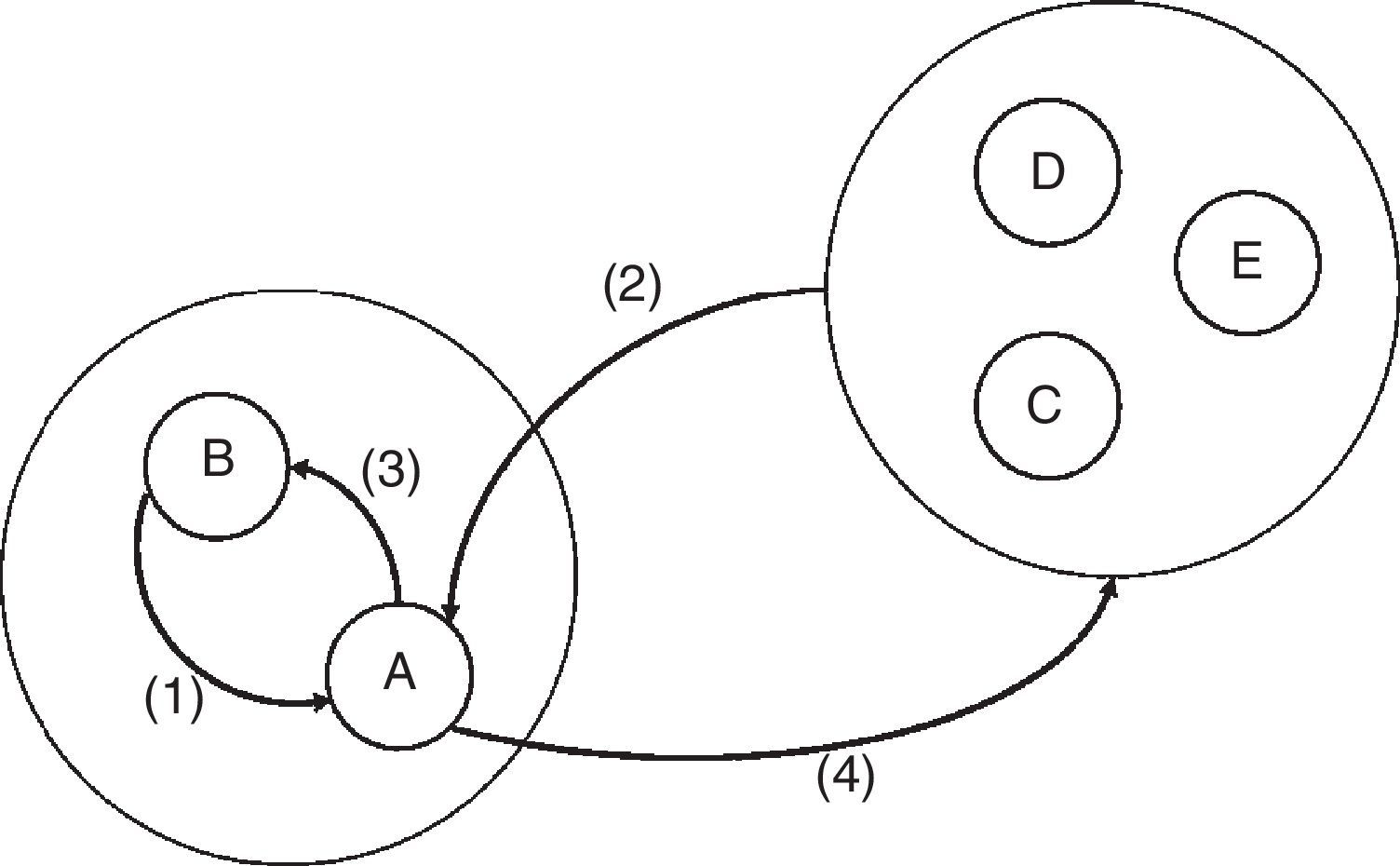
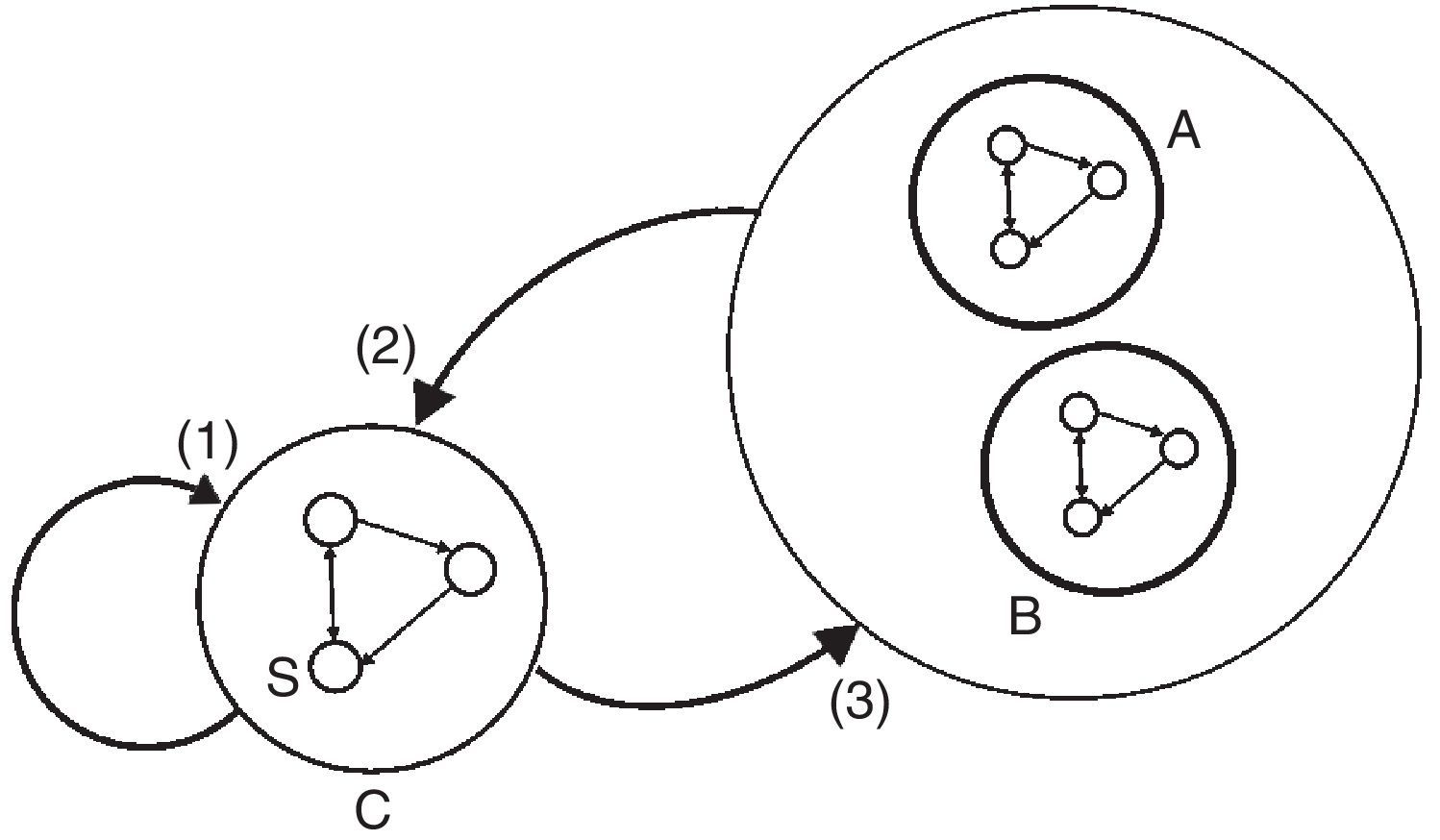
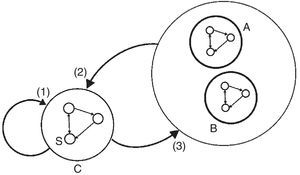
En la figura 2 se muestran estos 3 efectos generados por un choque sobre la demanda final del sector s del clúster C. En el primer paso la industria s demanda los insumos requeridos dentro del mismo clúster. Para lograr esta producción las industrias del clúster también necesitan insumos de otros clústeres, lo que deriva en un efecto spillover sobre la red productiva. Finalmente, el estímulo inicial se retroalimenta cuando el resto de la red productiva demanda insumos del mismo clúster C.
Sinergias, feedbacks y spillovers.
Las flechas indican la dirección de los insumos de producción.
Fuente: Garbellini y Wirkierman (2014).
La tabla 7 resume las expresiones matriciales de los indicadores de independencia. La columna Empleo señala en dónde se genera el efecto final del flujo de trabajo. Finalmente, en la última columna se describe las características de los efectos generados.
Indicadores de independencia
| Flujo | Indicador | Empleo | Generado por |
|---|---|---|---|
| (1) | ωCC−ωCCS=vCCTyCLC−alCTI−αˆC−1yCLC | intra-C | Sinergias entre industrias dentro del clúster |
| (2) | ωCNC=vCNCTyCLC | intra-C | Feedbacks, efectos que retornan luego de atravesar la red |
| (3) | ωNC=vNCTyCLC | extra-C | Spillovers, efectos que se propagan al resto de la red |
Fuente: Garbellini y Wirkierman (2014).
En la tabla, v son los coeficientes de trabajo de cada subsistema y cuantifican requerimientos directos e indirectos. αˆ es la matriz A en la que todos sus elementos, a excepción de la diagonal, son 0 (véase el Apéndice A para una descripción más amplia del cálculo de indicadores).
3Análisis de resultadosPara el análisis de la estructura económica colombiana se utilizó la matriz IP de cuentas nacionales base 2005 (60 sectores)11 y el vector de empleo para el mismo año, ambos elaborados por el DANE. El ejercicio se divide en 3 secciones: 1)cálculo de los indicadores de encadenamientos con la matriz de componente nacional de los insumos intermedios; 2)identificación de clústeres del sistema productivo de cuentas nacionales, y 3)cálculo de los indicadores de jerarquía, circularidad e independencia.
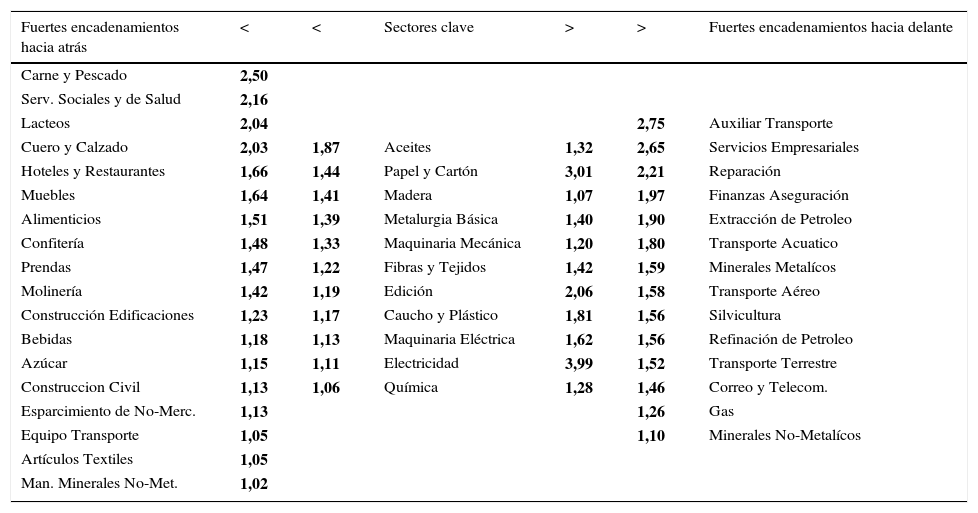
3.1Encadenamientos sectoriales para ColombiaLos indicadores de encadenamientos se calcularon teniendo en cuenta los requerimientos directos e indirectos de insumos. En la tabla 8 se muestran los indicadores calculados con el método de Dietzenbacher12. Se identificaron 60 sectores: 11 sectores clave (18%), 18 con fuertes encadenamientos solo hacia atrás (23%), 14 con fuertes encadenamientos solo hacia delante (30%) y 17 con encadenamientos débiles (28%).
Indicadores de encadenamientos: sectores en la economía colombiana. Método de descomposición espectral
| Fuertes encadenamientos hacia atrás | < | < | Sectores clave | > | > | Fuertes encadenamientos hacia delante |
|---|---|---|---|---|---|---|
| Carne y Pescado | 2,50 | |||||
| Serv. Sociales y de Salud | 2,16 | |||||
| Lacteos | 2,04 | 2,75 | Auxiliar Transporte | |||
| Cuero y Calzado | 2,03 | 1,87 | Aceites | 1,32 | 2,65 | Servicios Empresariales |
| Hoteles y Restaurantes | 1,66 | 1,44 | Papel y Cartón | 3,01 | 2,21 | Reparación |
| Muebles | 1,64 | 1,41 | Madera | 1,07 | 1,97 | Finanzas Aseguración |
| Alimenticios | 1,51 | 1,39 | Metalurgia Básica | 1,40 | 1,90 | Extracción de Petroleo |
| Confitería | 1,48 | 1,33 | Maquinaria Mecánica | 1,20 | 1,80 | Transporte Acuatico |
| Prendas | 1,47 | 1,22 | Fibras y Tejidos | 1,42 | 1,59 | Minerales Metalícos |
| Molinería | 1,42 | 1,19 | Edición | 2,06 | 1,58 | Transporte Aéreo |
| Construcción Edificaciones | 1,23 | 1,17 | Caucho y Plástico | 1,81 | 1,56 | Silvicultura |
| Bebidas | 1,18 | 1,13 | Maquinaria Eléctrica | 1,62 | 1,56 | Refinación de Petroleo |
| Azúcar | 1,15 | 1,11 | Electricidad | 3,99 | 1,52 | Transporte Terrestre |
| Construccion Civil | 1,13 | 1,06 | Química | 1,28 | 1,46 | Correo y Telecom. |
| Esparcimiento de No-Merc. | 1,13 | 1,26 | Gas | |||
| Equipo Transporte | 1,05 | 1,10 | Minerales No-Metalícos | |||
| Artículos Textiles | 1,05 | |||||
| Man. Minerales No-Met. | 1,02 |
Encadenamientos débiles: Manufactura NCP, Ganadería, Tabaco, Manufactura de Café, Esparcimiento de Mercado, Administración Pública, Pesca, Comercio, Agua, Eduación de Mercado, Alcantarillado-Desperdicios, Agro, Carbón, Eduación de No-Mercado, Café, Sevicios Inmobiliarios y Servicio Doméstico
Fuente: DANE, Matrices de oferta y utilización, y GEIH, cálculos DNP-DEE.
A diferencia del método de Rasmussen, el método de descomposición espectral resulta más restrictivo. Con este último, sectores como los de Molinería y Manufacturas de minerales no metálicos dejan de ser sectores clave para clasificarse como sectores solo con fuertes encadenamientos hacia atrás. Actividades del sector primario como Ganadería, Tabaco, Café y Pesca ahora se clasifican como sectores con débiles encadenamientos. En resumen, con el método de Dietzenbacher se identifican menos sectores clave, pero más sectores con débiles encadenamientos (en el Apéndice B se hace una comparación completa de los indicadores de encadenamientos con los 2 métodos).
La tabla 8 muestra los indicadores de encadenamientos de cada sector obtenidos por el método de Dietzenbacher. En la tabla solo se muestran los indicadores mayores a 1. De ese modo, en el caso de los sectores clave se muestran los 2 indicadores de encadenamientos13.
Clasificar sectores de esta forma permite obtener información valiosa para el diseño de la política industrial. Por ejemplo, estimular la demanda final de un sector con fuertes encadenamientos hacia atrás como el de Lácteos va a tener un efecto más provechoso para la economía que si el mismo estímulo se hace sobre el sector Café. La intuición de este resultado es que una mayor producción en el sector de Lácteos genera una mayor demanda intermedia sobre más sectores en la economía.
Similarmente, estimular un sector con fuertes encadenamientos hacia delante, como el de Servicios empresariales, va a generar un efecto mucho mayor sobre la economía que si el mismo estímulo se hace sobre el sector de Servicios inmobiliarios. Una mayor oferta de productos de este último sector va a afectar en menor proporción a los sectores a los cuales les provee sus servicios.
Un estímulo preferible se debe hacer sobre sectores clave como los de Aceites y Papel y cartón. En este caso se tienen las 2 ventajas de un incremento en la producción de bienes finales. Por un lado, la demanda por bienes intermedios se propaga a más sectores; por otro lado, la mayor oferta de bienes beneficia a muchos más sectores en la red (Miller y Blair, 2009).
3.2Clústeres productivos en ColombiaLa anterior es la forma tradicional de clasificar la economía por sector o industria individual bajo el análisis IP. En adelante, el análisis se centra en la caracterización de grupos o clústeres de sectores que conforman una red sintética estructural.
En la tabla 9 se muestran los 9 clústeres identificados a partir de los 60 sectores de las matrices IP de cuentas nacionales: Agricultura-alimentos; Industria médica-química; Cuero y calzado; Industria manufacturera-construcción; Electricidad; Confecciones y textiles; Servicios; Café, e Industria minero-energética. Los nombres adoptados son etiquetas para denominar los clústeres, y de ningún modo reflejan importancia de algún sector sobre los demás.
Clústeres identificados para la economía colombiana
| Clústera | N.o de sectores | Participación sobre el PIB | Sectores involucrados | |
|---|---|---|---|---|
| Servicios | 17 | 40,7% | Papel y cartón, Edición, Manufactura ncp, Agua, Comercio, Transporte aéreo, Servicios complementarios de transporte, Correo y telecomunicaciones, Servicios de finanzas y seguros, Servicios inmobiliarios, Servicios empresariales, Administración pública, Educación de mercado, Educación de no mercado, Desperdicios, Esparcimiento de mercado y Esparcimiento de no mercado. | |
| Agricultura-alimentos | 13 | 17,3% | Agricultura, Ganadería, Pesca, Carne y pescado, Procesado, Aceites, Lácteos, Molinería, Azúcar, Confitería, Alimenticios, Bebidas, Tabaco y Hoteles y restaurantes | |
| Industria manufacturera- construcción | 13 | 16,0% | Silvicultura, Carbón, Mineral metálicos, Minerales no metálicos, Madera, Manufacturas no metálicas, Metalurgia básica, Maquinaria y equipo, Maquinaria eléctrica, Equipo de transporte, Muebles, Edificaciones y Obras civiles | |
| Industria minero- energética | 6 | 10,8% | Extracción y refinación de petróleo, Gas, Reparación de automotores, Transporte terrestre y Transporte acuático | |
| Industria médica-química | 3 | 7,6% | Industria química, Caucho y plástico, Servicios sociales y de salud | |
| Electricidad | 1 | 2,7% | Energía eléctrica | |
| Confecciones-textiles | 3 | 2,5% | Fibras textiles, Artículos textiles y Prendas de vestir | |
| Café | 2 | 1,4% | Café y Trilla de café | |
| Cuero-calzado | 1 | 0,5% | Cuero y calzado | |
Fuente: Dane, Matrices de oferta y utilización, y GEIH, cálculos DNP-DEE.
Es importante aclarar que el único criterio para ordenarlos en la tabla es la participación de cada clúster en el PIB. Los 3 clústeres denominados Servicios, Agricultura-alimentos e Industria manufacturera-construcción reúnen entre ellos tres cuartas partes de la producción bruta de la economía colombiana. Para lograr clasificar los clústeres se recurre a los indicadores calculados en la siguiente sección.
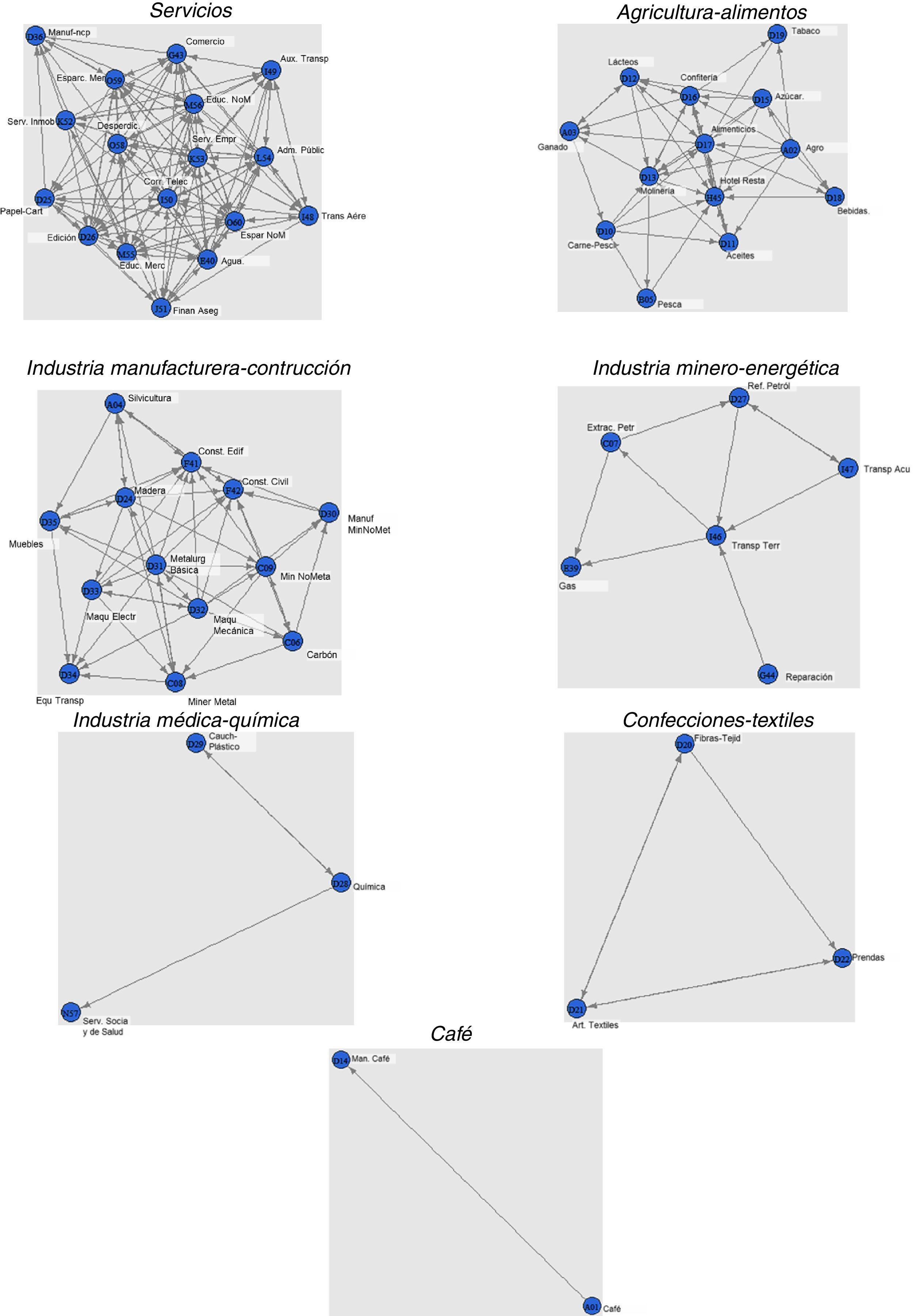
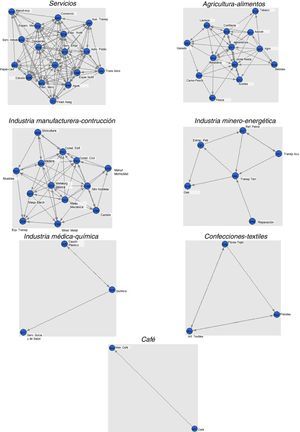
En la figura 3 se hace un esquema de todos lo clústeres con más de un sector, junto con sus conexiones relevantes. Es decir, se señalan aquellas conexiones particularmente fuertes o que se encuentran por encima del promedio.
Grafos de los clústeres identificados.
Fuente: elaboración a partir del paquete IOUNBogota en R (Garbellini y Wirkierman, 2014).
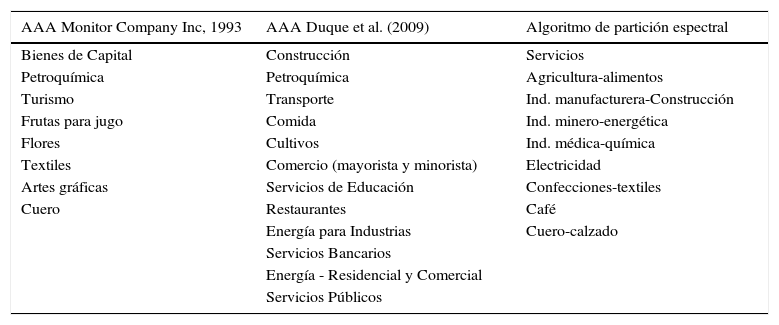
En la tabla 10 se muestran resultados de identificación de clústeres en estudios anteriores. Si bien, como señalan Duque et al., 2009, dadas las metodologías y bases de datos utilizadas es difícil realizar una comparación, se puede observar la presencia de algunos clústeres similares: Agricultura-alimentos, Industria médica-química, y Electricidad.
Resultados en estudios anteriores
| AAA Monitor Company Inc, 1993 | AAA Duque et al. (2009) | Algoritmo de partición espectral |
|---|---|---|
| Bienes de Capital | Construcción | Servicios |
| Petroquímica | Petroquímica | Agricultura-alimentos |
| Turismo | Transporte | Ind. manufacturera-Construcción |
| Frutas para jugo | Comida | Ind. minero-energética |
| Flores | Cultivos | Ind. médica-química |
| Textiles | Comercio (mayorista y minorista) | Electricidad |
| Artes gráficas | Servicios de Educación | Confecciones-textiles |
| Cuero | Restaurantes | Café |
| Energía para Industrias | Cuero-calzado | |
| Servicios Bancarios | ||
| Energía - Residencial y Comercial | ||
| Servicios Públicos |
Fuente: Duque et al. (2009, tabla 6).
Además de verificar la importancia de los clústeres a partir de su peso en la producción, es posible llevar a cabo el análisis partiendo del empleo que cada clúster es capaz de absorber (o proveer) de las demás cadenas de producción. Para esto se hace uso del concepto de trabajo incorporado en el proceso productivo. Esto es, la producción de cada industria no está asociada únicamente al trabajo directo contratado en el mismo sector, sino que también está relacionada con el trabajo que es necesario en la producción de otros sectores que le proveen sus insumos. De esta manera, del trabajo contratado en cada sector, una parte está involucrada en la producción de bienes finales (trabajo incorporado que sale inmediatamente de la cadena productiva) y la restante está involucrada en la producción de insumos que sirven para la producción de otros sectores (trabajo incorporado que continúa en la cadena productiva).
La tabla 11 muestra los indicadores de jerarquía. Es decir, la comparación entre el empleo incorporado absorbido por cada clúster frente al empleo realmente contratado. El clúster de servicios, por ejemplo, necesita un 35,2% del trabajo incorporado para producir su bien final, pero contrata el 41,2% del total del trabajo. En términos netos este sector provee más trabajo hacia la red productiva del que absorbe de la misma. Estos casos, donde el valor de la columna 3 es negativo (Servicios, Industria minero-energética y Café), hacen referencia a aquellos clústeres que son proveedores netos de trabajo a través de los insumos que le suministran a los demás sectores.
Indicadores de Jerarquía: empleo contratado y empleo incorporado absorbido
| Participación sobre el total del empleoa | Jerarquía | ||
|---|---|---|---|
| Empleo contratado (sobre el total del empleo) (1) | Empleo incorporado absorbido (sobre el total del empleo) (2) | Diferencia (2) - (1)=(3) | |
| Servicios | 41,2% | 35,2% | −5,9 |
| Agricultura-alimentos | 26,2% | 28,8% | 2,7 |
| Ind. manufacturera-construc. | 8,8% | 11,8% | 3,0 |
| Industria minero-energética | 5,8% | 4,0% | −1,8 |
| Industria médica-química | 4,1% | 5,4% | 1,4 |
| Electricidad | 0,3% | 0,3% | 0,1 |
| Confecciones-textiles | 2,8% | 3,3% | 0,5 |
| Café | 5,0% | 4,9% | −0,1 |
| Cuero-calzado | 0,3% | 0,5% | 0,2 |
Fuente: Cálculos DNP-DEE; Matrices oferta y utilización y GEIH-Dane.
Otra forma de ver este resultado es asociar la columna 3 con la cercanía de cada clúster a la demanda final. Nótese que, para producir su bien final, un clúster como el de Industria manufacturera-construcción absorbe el 11,8% del trabajo incorporado, pero solo contrata el 8,8% del total del trabajo en la economía. En términos netos se puede afirmar que este clúster dedica su esfuerzo productivo más hacia la demanda final que hacia producción de insumos intermedios. De esta manera, un clúster cuyo valor de la columna 3 es positivo (que absorbe más trabajo de la red productiva del que le provee) es más cercano a la demanda final.
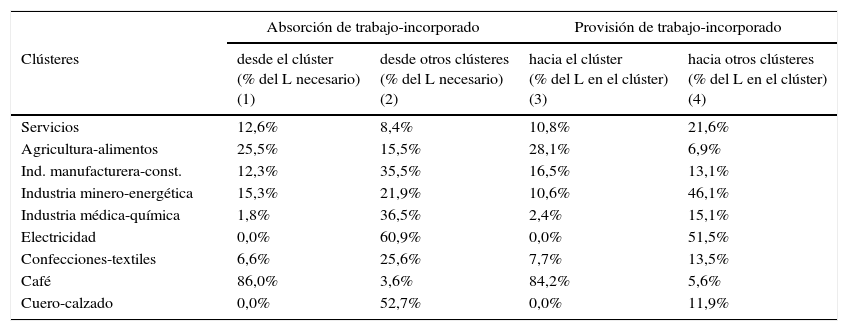
Dentro de la red de clústeres construida se pueden identificar los flujos de trabajo incorporado desde y hacia los sectores dentro del clúster14. De acuerdo a las columnas 2 y 4 de la tabla 12, es claro que los clústeres Electricidad e Industria minero-energética son bastante abiertos. Es decir, que comparten bastantes flujos de trabajo con otros clústeres. En el caso del Café se observa lo contrario; la mayor parte del trabajo requerido proviene del mismo clúster (86,0%). Además, este clúster no participa mucho con insumos para la elaboración de otros productos finales, por lo que solo provee trabajo dentro del clúster (84,2%). De esta manera se puede caracterizar cuáles son los sectores que pueden ser más dinámicos en la absorción y suministro de empleo.
Indicadores de circularidad: flujos de trabajo incorporado
| Absorción de trabajo-incorporado | Provisión de trabajo-incorporado | |||
|---|---|---|---|---|
| Clústeres | desde el clúster (% del L necesario) (1) | desde otros clústeres (% del L necesario) (2) | hacia el clúster (% del L en el clúster) (3) | hacia otros clústeres (% del L en el clúster) (4) |
| Servicios | 12,6% | 8,4% | 10,8% | 21,6% |
| Agricultura-alimentos | 25,5% | 15,5% | 28,1% | 6,9% |
| Ind. manufacturera-const. | 12,3% | 35,5% | 16,5% | 13,1% |
| Industria minero-energética | 15,3% | 21,9% | 10,6% | 46,1% |
| Industria médica-química | 1,8% | 36,5% | 2,4% | 15,1% |
| Electricidad | 0,0% | 60,9% | 0,0% | 51,5% |
| Confecciones-textiles | 6,6% | 25,6% | 7,7% | 13,5% |
| Café | 86,0% | 3,6% | 84,2% | 5,6% |
| Cuero-calzado | 0,0% | 52,7% | 0,0% | 11,9% |
Fuente: Dane, Matrices de oferta y utilización, y GEIH, cálculos DNP-DEE.
De la columna 4 de la misma tabla 12 se destacan 3 clústeres dedicados principalmente a la producción de intermedios: Electricidad, Industria minero-energética y Servicios. En los 2 primeros alrededor del 50% del trabajo es dedicado a la producción de insumos para sectores en otros clústeres. Además, de la columna 3 de la tabla 10 se identifican los sectores más cercanos a la demanda final: Industria manufacturera-construcción, Agricultura-alimentos e Industria médica-química.
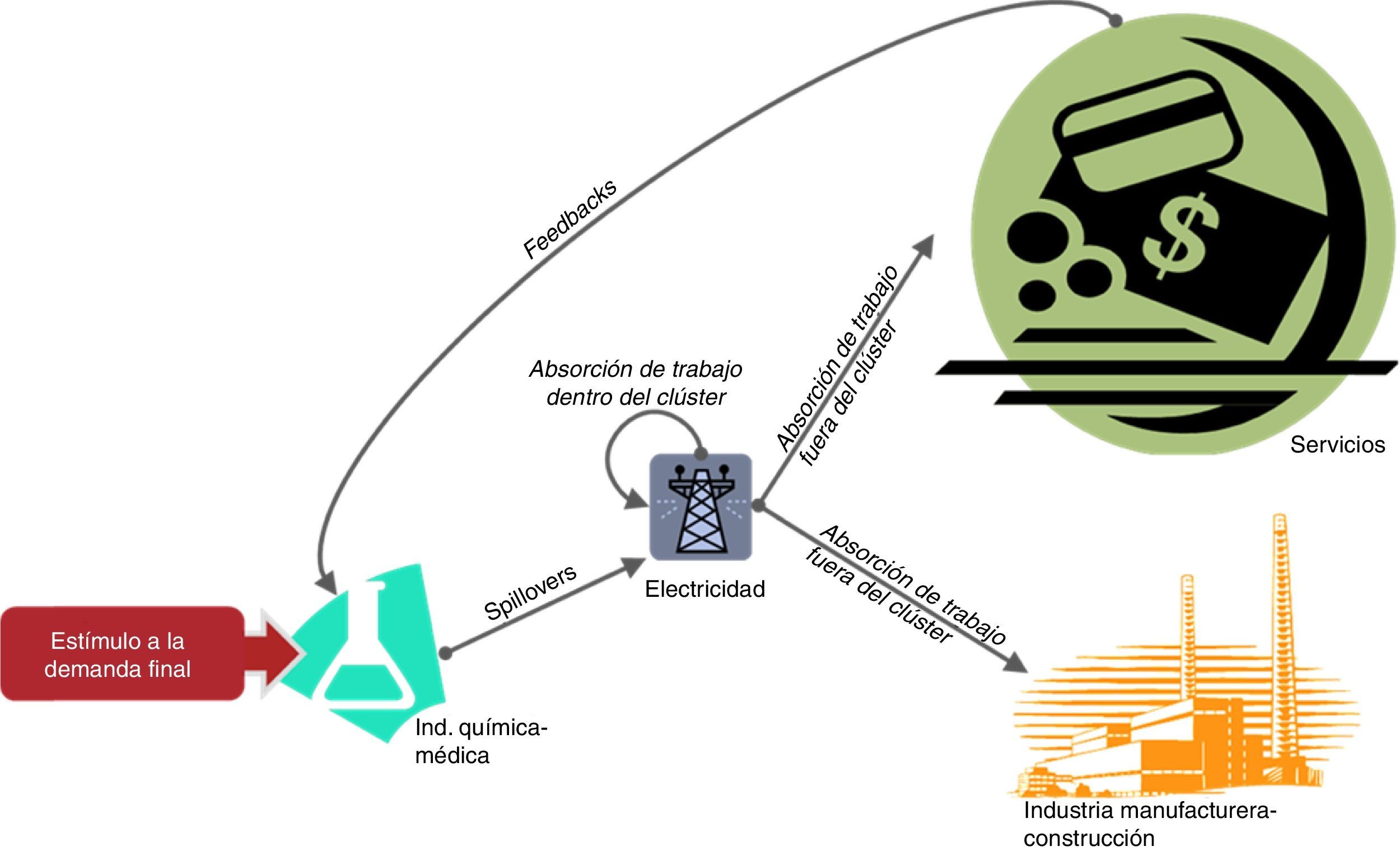
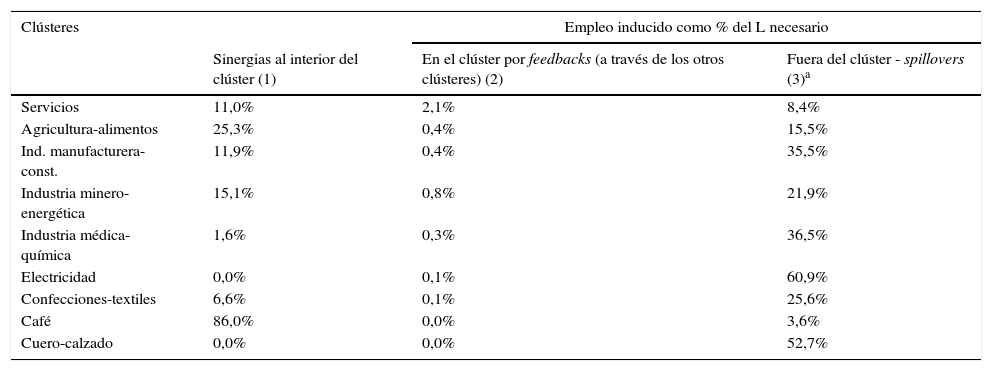
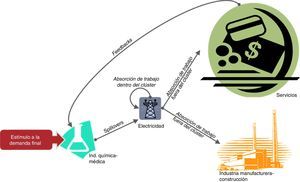
En la tabla 13 se muestran los indicadores de independencia, que reflejan el grado de cohesión de un clúster con la red. Una política de estímulo a la demanda de los sectores con mayores spillover puede generar efectos amplificados sobre la estructura productiva, especialmente para los clústeres que son proveedores netos de insumos. En el ejemplo representado por la figura 4 se destaca una pequeña fracción de la red creada a partir del análisis de clústeres. Dentro de los clústeres cercanos a la demanda final, el de la Industria médica-química es el que presenta mayores efectos spillover (columna 3 de la tabla 13), de modo que un estímulo a la demanda final de sus productos finales se propaga ampliamente a lo largo de la red productiva, por ejemplo sobre el clúster de Electricidad. Este, a su vez, como presenta una gran absorción de trabajo (a través de los insumos que demanda) de otros clústeres (columna 2 de la tabla 12), multiplica el estímulo inicial afectando de manera amplificada a unos terceros clústeres, en este caso Servicios e Industria manufacturera-construcción. Finalmente un efecto feedback se genera cuando el clúster de Servicios absorbe trabajo desde el clúster de Industria médica-química. Si bien estas estructuras de red productiva son disipativas (los choques a la demanda final tienden a desaparecer a lo largo de la red), es posible generar efectos multiplicativos que permeen muchos más rincones de la cadena productiva si se aplica un estímulo a un clúster cercano a la demanda final y con fuertes efectos spillover.
Indicadores de independencia: grado de cohesión de los clústeres
| Clústeres | Empleo inducido como % del L necesario | ||
|---|---|---|---|
| Sinergias al interior del clúster (1) | En el clúster por feedbacks (a través de los otros clústeres) (2) | Fuera del clúster - spillovers (3)a | |
| Servicios | 11,0% | 2,1% | 8,4% |
| Agricultura-alimentos | 25,3% | 0,4% | 15,5% |
| Ind. manufacturera-const. | 11,9% | 0,4% | 35,5% |
| Industria minero-energética | 15,1% | 0,8% | 21,9% |
| Industria médica-química | 1,6% | 0,3% | 36,5% |
| Electricidad | 0,0% | 0,1% | 60,9% |
| Confecciones-textiles | 6,6% | 0,1% | 25,6% |
| Café | 86,0% | 0,0% | 3,6% |
| Cuero-calzado | 0,0% | 0,0% | 52,7% |
Fuente: Dane, Matrices de oferta y utilización, y GEIH, cálculos DNP-DEE.
En líneas generales, los clústeres más cercanos a la demanda final son los de Industria manufacturera-construcción, Agricultura-alimentos e Industria médica-química. Si se realiza algún estímulo sobre la demanda de los productos finales de estos clústeres se va a generar una mayor absorción del trabajo, no solo dentro de cada clúster, sino en el sistema productivo en general. El efecto se refuerza si existen conexiones fuertes con clústeres proveedores netos de insumos, tales como el de Servicios o el de Industria minero-energética. A partir de este tipo de análisis es posible realizar un diagnóstico de las posibilidades que afronta cada clúster.
3.4Caracterización de los clústeres3.4.1ServiciosEs el clúster con mayor número de sectores y con la mayor participación en la economía (40,7%). Aunque la mayoría de sus sectores involucrados presentan fuertes encadenamientos hacia delante, también tiene 2 sectores clave, los de Papel-Cartón y el de Edición (tablas 8 y 9). Según la tabla 11, este es el clúster más enfocado hacia la producción de intermedios. Esto se refuerza con el hecho de que el 21,6% del trabajo en este clúster es usado para producir insumos para otros clústeres.
Lo anterior hace pensar que la actividad de los servicios se debe más al dinamismo de sectores externos, demandantes de sus productos, que a su propio impulso. Esto refuta en cierta medida la tesis de la tercerización de la economía. De acuerdo al análisis de independencia (tabla 13), un estímulo a la demanda final de este clúster puede generar sinergias internas que incentiven el empleo dentro del mismo clúster. Sin embargo, debido a sus bajos efectos spillover, es difícil que tal estímulo afecte de manera importante los demás clústeres del sistema (columna 3 de la tabla 13).
La importancia de este clúster radica en su capacidad de apoyar, a través de sus productos, todo el sistema productivo. Sus fuertes encadenamientos hacia delante son claves para apoyar medidas emprendidas sobre la demanda de otros clústeres con encadenamientos más fuertes hacia atrás. Un aspecto importante de este clúster es que genera los mayores efectos de feedback.
3.4.2Agricultura-alimentosEste clúster tiene la segunda participación más alta dentro de la economía y cuenta con 13 sectores, dentro de los cuales aquellos que están más cerca de la actividad primaria (Ganadería, Agricultura, Tabaco y Pesca) presentan encadenamientos muy débiles. Sin embargo, cuenta con sectores más industrializados, como los de Carne y Pescado, Lácteos y Productos alimenticios, que presentan muy fuertes encadenamientos hacia atrás. La industria de Aceites se destaca por tener fuertes conexiones hacia delante y hacia atrás de la red productiva (tablas 8 y 9).
Precisamente, el hecho de que incluya estos sectores de alimentos procesados lo hace muy cercano a la demanda final (alto valor positivo en la columna 3 de la tabla 11). A pesar de lo anterior, es un clúster muy poco cohesionado con la demás red productiva: tiene un alto grado autonomía intra-clúster y muy bajos spillovers (columnas 1 y 3 de la tabla 13). Además, los flujos de trabajo hacia otros clústeres y provenientes de otros clústeres son muy bajos. Del trabajo necesario para su producción final solo el 16% lo absorbe desde otros clústeres, y del trabajo que contrata actualmente, solo destina el 6,9% para la producción de insumos para otros clústeres.
Siendo un clúster con alta independencia, es poco adecuado para impulsar el trabajo en otros sectores de la economía. Pero dada la gran proporción del trabajo total que contrata (26,2%), frente a la participación de su producción en el PIB (17,3%), es de fundamental importancia una política de estímulo a sus sectores. Para lograrlo se debe contar con medidas diferenciadas dirigidas exclusivamente a incentivar la demanda por los bienes finales del clúster.
3.4.3Industria manufacturera-construcciónEn cuanto a la participación en el producto interno y el número de sectores, este clúster es muy similar al de Agricultura-alimentos. Sin embargo, su estructura de encadenamientos difiere mucho del anterior. Incluye sectores con fuertes encadenamientos hacia delante (Silvicultura, Minerales no-metálicos y Minerales metálicos), otros con fuertes encadenamientos hacia atrás (Muebles, Construcción de edificaciones, Construcción civil…) y un gran número de sectores clave (Madera, Metalurgia básica, Maquinaria mecánica y Maquinaria eléctrica).
Este clúster reúne varias características que le dan gran importancia: a) es el clúster más cercano a la demanda final (valor más alto en la columna 3 de la tabla 11); b) se encuentra muy cohesionado a la red productiva (columnas 2 y 4 de la tabla 12); c) dentro de los clústeres cercanos a la demanda final, presenta muy altos efectos spillover (columna 3 de la tabla 13), y d) tiene un alto grado de sinergias internas (columna 1 de la tabla 13).
Lo que estos indicadores muestran es la capacidad que tiene el clúster de la Industria manufacturera-construcción para generar externalidades positivas dentro del sistema productivo. Los estímulos que se hagan a los sectores del clúster van a generar potentes dinámicas sobre los demás clústeres de la economía y sobre él mismo. Si además se tiene en cuenta que el clúster tiene 4 sectores clave, cobran más importancia las medidas de fomento a la demanda por bienes finales de este clúster.
Si un clúster como este, cercano a la demanda final y con altos encadenamientos hacia atrás, se conecta con uno de las características del de servicios (proveedor neto de insumos, con altos encadenamientos hacia delante y efectos de retroalimentación), los estímulos al primero se amplifican a través de los encadenamientos del segundo. Una política eficiente de estímulo a la economía puede partir del fortalecimiento de las conexiones entre estos 2 clústeres.
3.4.4Industria minero-energéticaEsta industria contribuye en un 10,8% a la producción total de la economía, pero solo se le atribuye el 5,8% del total del trabajo contratado. Todos sus sectores presentan fuertes encadenamientos solo hacia delante (tablas 8 y 9).
Es un clúster proveedor neto de insumos hacia los demás clústeres; después de Servicios, es el clúster más alejado de la demanda final (columna 3 de la tabla 11). No obstante, es de los sectores más enlazados en la cadena de producción (columnas 2 y 4 de la tabla 12). Además, cuenta con un alto grado de sinergias internas que refuerzan los estímulos externos.
Este clúster es un nodo de amplificación dentro de la red productiva. Su alta conectividad con el sistema y las sinergias internas de sus sectores traducen los estímulos exógenos en efectos aumentados que se propagan a más rincones de la cadena productiva. Por tal razón, es importante que cualquier política sectorial se apoye en sus cualidades para lograr impactos más eficientes.
3.4.5Industria médica-químicaAunque esta es una industria relativamente pequeña (la producción de sus 3 sectores tiene una participación del 7,6% en el PIB), se destaca por las particularidades de su estructura productiva. Cuenta con el sector de Servicios sociales y de salud, que es el segundo sector con más fuertes encadenamientos hacia atrás. Además, sus otros 2 sectores, Caucho-plástico y Química, son sectores claves.
Es el clúster cercano a la demanda final que genera más efectos spillover sobre el sistema productivo (columna 3 de la tabla 11 y columna 3 de la tabla 13); si bien las dinámicas internas al clúster no son muy significativas, su alta conectividad con los demás clústeres puede ser usada para generar efectos de grandes impactos.
Al igual que en el caso de la Industria manufacturera-construcción, la conexión de este clúster con clústeres proveedores netos de insumos, como el de Industria minero-energética, produce efectos ampliados con mayor impacto sobre el empleo y sobre la producción agregada. Mucho más, si se trata de estas 2 industrias que comparten bastantes aspectos de sus cadenas productivas.
3.4.6ElectricidadEste clúster solo cuenta con un sector, el de Electricidad, que dentro del análisis de encadenamientos se clasifica como sector clave. Su participación en el PIB es del 2,7%, pero solo contrata el 0,3% del total del trabajo. De este clúster no se puede decir que esté más cerca o más lejos de la demanda final, y la cantidad de empleo que contrata es casi igual a la que necesita para realizar su producto final (tabla 11).
Sin embargo, este es el sector más cohesionado con la red productiva, pues absorbe una gran cantidad de trabajo desde otros clústeres, e igualmente les provee gran cantidad de trabajo (columnas 2 y 4 de la tabla 12). Estos resultados no deben ser extraños, dada la transversalidad de este clúster en la cadena productiva de todos los sectores de la economía.
3.4.7Confecciones-textilesEste es un clúster pequeño, en número (3 sectores) y en tamaño (2,5% del PIB), pero con indicadores muy buenos, similares a los del clúster de Industria médica-química. Al igual que este último, el rol que desempeñan las confecciones y textiles dentro de la cadena productiva es el de generar impactos fuertes ante un estímulo a la demanda final de sus productos.
3.4.8CaféEl clúster incluye 2 sectores con encadenamientos muy débiles, el sector de Café y el sector de Manufactura de café (tablas 8 y 9). Tiene una participación en el PIB del 1,4%, pero contrata el 5,0% del total de trabajo en la economía. Precisamente en este último punto radica su importancia, en el estímulo al empleo rural. El inconveniente es que este es el clúster con mayor grado de autonomía, sus conexiones débiles impiden que se beneficie de las externalidades generadas en otros lugares de la red productiva. De modo que se hacen necesarias políticas especiales que se dirijan únicamente al impulso de la industria cafetera. Un punto a favor de una medida, en este sentido, es que este clúster presenta los mayores efectos positivos por las sinergias internas al clúster (columna 1 de la tabla 13).
3.4.9Cuero-calzadoLa industria del cuero y calzado es la más pequeña en este sistema de clústeres. Es un sector que tiene fuertes encadenamientos hacia atrás (tabla 8 y columna 3 de la tabla 13). Sin embargo, la baja provisión de trabajo hacia otros sectores (columna 4 de la tabla 12) restringe las políticas de estímulo solo a aquellas más enfocadas a aumentar la demanda final de cueros y de calzado.
4ConclusionesEn este estudio se presentaron 2 métodos con los que se analizó el sistema productivo de cuentas nacionales base 2005 para Colombia. El primero consistió en cálculo de los indicadores de encadenamientos con el enfoque de descomposición espectral planteado por Dietzenbacher. La ventaja de este enfoque es que el cálculo se realiza de manera ponderada en infinitas rodas. De esta manera, no se sobreestiman (subestiman) sectores con bajos (altos) encadenamientos.
La clasificación de los sectores por encadenamientos a partir de este enfoque fue: el 18% de los sectores son sectores clave, el 23% de los sectores tienen fuertes encadenamientos solo hacia atrás, el 30% de los sectores tienen fuertes encadenamientos solo hacia delante y el restante 28% de los sectores tienen débiles encadenamientos. En comparación, el método de Rasmussen resulta más flexible para la identificación de sectores clave (25% sectores clave, 32% fuertes encadenamientos hacia atrás, 25% fuertes encadenamientos hacia delante y 18% encadenamientos débiles).
Los 11 sectores clave que se encontraron con el enfoque de Dietzenbacher pertenecen a industrias con grados de tecnificación medio o alto: Aceites, Papel y cartón, Madera, Metalurgia básica, Maquinaria mecánica, Fibras y tejidos, Edición, Caucho y plástico, Maquinaria eléctrica, Electricidad y Química. Por otro lado, las actividades del sector primario agrícola, en su mayoría, pertenecen al grupo de los sectores con encadenamientos débiles: Ganadería, Tabaco, Pesca, Agro y Café.
La segunda aproximación para el análisis IP fue la identificación de clústeres a partir de la metodología de Garbellini y Wirkierman (2014), basada en el algoritmo de partición espectral propuesto por Newman (2006) y Leicht y Newman (2008). Esta metodología permite obtener endógenamente clústeres presentes en la estructura productiva de una economía, identificando los flujos de trabajo incorporado intra y extra clúster.
El resultado fue la identificación de 9 clústeres en la economía colombiana: Servicios, Agricultura-alimentos, Industria manufacturera-construcción, Industria minero-energética, Industria médica-química, Electricidad, Confecciones-textiles, Café y Cuero-calzado.
En líneas generales, los clústeres más cercanos a la demanda final son los de Industria manufacturera-construcción, Agricultura-alimentos e Industria médica-química. Si se realiza algún estímulo sobre la demanda de los productos finales de estos clústeres se va a generar una mayor absorción del trabajo, no solo dentro de cada clúster, sino en el sistema productivo en general. El efecto se refuerza si existen conexiones fuertes con clústeres proveedores netos de insumos, tales como el de Servicios o el de Industria minero-energética.
Aunque la descripción del sistema productivo colombiano hecha en este trabajo provee una gran cantidad de información, un análisis más riguroso puede hacerse a partir de matrices IP más desagregadas y para distintos años de elaboración. Los futuros desarrollos incluyen la realización de ejercicios de simulación de choques de la demanda final y sus efectos a partir de los indicadores calculados. También se pretende realizar el mismo análisis para las cuentas nacionales de 2010, para lo que necesita construir un vector de empleo a 61 sectores para el mismo año.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
AgradecimientosLos autores agradecen los comentarios de Jesús Otero, Gabriel Piraquive, Néstor González y Carolina Lozano, del DNP, e Isabella Muñoz; y especialmente a Ariel Wirkierman, de la Università Cattolica del Sacro Cuore, y Nadia Garbellini, de la Università degli studi Bergamo, por el material aportado para la elaboración de este documento. Los comentarios y errores son responsabilidad de los autores y no comprometen a la institución en que trabajan.
Siguiendo la metodología de Garbellini y Wirkierman (2014), se parte de la identidad IP: x=Xe+y, para llegar a: x=I−A−1y=My.
De esta manera, se puede hacer una partición de x para hacer una aproximación al concepto de subsistema: xi=Myi, i=1,…,n.
Donde yi=eiyi1515 ei es un vector cuyo único elemento distinto de cero es el elemento i: eiT=0,⋯,1i,⋯,0T.
Para poder construir indicadores sintéticos todos los flujos entre sectores se traducen a una única unidad. De esta manera, el análisis se centra en los requisitos directos e indirectos de trabajo. Siendo los coeficientes directos de trabajo: alT=lTxˆ−1 1616 Los símbolos con acento circunflejo (^) representan matrices diagonales, con los elementos del vector correspondiente en la diagonal.
Donde lT es el vector de empleo de la industria. Se puede calcular:
Li=alTxˆei=alixi ← Requerimientos directos de trabajo de cada industria i para producir el producto bruto xi
Li=alTxˆi=alTMyi=viyi ← Requerimientos de trabajo del subsistema asociado para producir la demanda final yi
Así, se tiene que: vT=alTM mide los requerimientos directos e indirectos de trabajo por unidad de demanda final. En resumen:
El indicador de jerarquía se define como la cercanía relativa de un sector (o clúster) a la demanda final: LC−LC. Y, para cada sector:
lvT−lT.
Analizando todos los flujos de trabajo incorporado:
lvT−lT=alTM yˆ−yTMTalˆ=alTMˇyˆ+alTμˆ yˆ−yTMˇTalˆ−yTμˆTalˆ=alTMˇyˆ−yTMˇTalˆ1717 alTμˆ yˆ=yTμˆTalˆ
En esta última ecuación la matriz M se fracciona de modo que: M=Mˇ+μˆ. Donde Mˇ es la matriz M con los elementos de la diagonal iguales a 0 y μˆ es la matriz M en la que todos sus elementos, a excepción de la diagonal, son 0.
Como ya se dijo en el Apéndice B, el APE identifica clústeres no sobrepuestos. Entonces, la ecuación anterior se puede expresar en forma de matrices particionadas, separando las industrias pertenecientes al clúster C y las que no pertenecen al clúster (N):
Ahora bien, como el centro del análisis es el clúster, se puede simplemente ignorar el segundo elemento del vector y computar:
Partiendo de:
Donde H=AI−A−1. Es la matriz de capacidades productivas. Dada la redistribución no superpuesta de sectores en clústeres:
Aplicando la fórmula de inversión de Banachiewicz (véase Garbellini y Wirkierman (2014); Apéndice B):
Donde: HCN=ACNI−ANN−1 y HNC=ANCI−ACC−1
En este caso vCCT contiene los efectos que permanecen al interior del clúster, vCNCT contiene los efectos spillover y vNCT contiene los efectos feedback.
Sabiendo que lvT=vTyˆ y calculando sobre subsistemas: LC=vCTyC. De esta manera:
Sin embargo, el primer indicador, ωCC, se debe corregir para eliminar el componente de autoconsumo de cada sector. De esta manera, se plantea:
Aquí, ωCCS mide los efectos de autoconsumo. αˆ es la matriz A a la que todos sus elementos, a excepción de la diagonal, son 0 (véase Garbellini y Wirkierman (2014, p. 67). Entonces, el término I−αˆC−1 mide únicamente los requerimientos del consumo propio de un sector en particular.
Vega (2008), por ejemplo, encuentra poca transformación de la estructura productiva, durante la apertura económica con precarios encadenamientos productivos y con ausencia de sectores clave. Flórez (2012) encuentra que la agenda de competitividad del Valle del Cauca está enfocada en sectores de fuerte arrastre, lo que es compatible con las metas planteadas por el gobierno a 2032. Hernandez (2012) construye una matriz insumo-producto para 2007 utilizando una transformación de las cuentas nacionales por medio de la estructura de costos para corregir inconsistencias sobre la clasificación de los sectores. Observa fuertes encadenamientos entre sectores como petróleo, químicos, plásticos, electricidad y gas, transporte y comunicaciones.
Para el sector minero, Martínez y Aguliar (2013) encuentran que, aunque es un sector altamente intensivo en capital y con débiles encadenamientos, es una actividad que está lejos de ser un enclave, dados sus efectos sobre producción y empleo. Ramírez y Lesmes (2012) destacan a la industria metalmecánica como un gran motor de la producción de otros sectores económicos. Sus fuertes encadenamientos reflejan su capacidad para demandar gran cantidad de insumos de otras industrias y como proveedor de bienes intermedios para la producción de una gran gama de bienes finales elaborados por otros sectores. Finalmente, Arbeláez y Sandoval (2008) encuentran mayor importancia de los encadenamientos indirectos en la relación de Bavaria con el resto de sectores.
Los símbolos en negrita se refieren a matrices o vectores.
Tradicionalmente se usa el enfoque de Leontief para calcular los 2 tipos de encadenamientos. Sin embargo, para evitar hacer el supuesto de aumentos simultáneos e iguales a una unidad en la demanda final de todos los sectores, los encadenamientos hacia delante se calculan a partir del enfoque de Ghosh (véase Miller y Blair, 2009, p. 558).
Matricialmente esto se tiene porque: M=I−A−1=I+A+A2+A3+⋯. Cada término en la serie de potencias simplemente representa las magnitudes de los efectos ronda a ronda. De esta manera, M=I−A−1 representa la suma de los efectos de infinitas rondas (véase Miller y Blair, 2009, pp. 31-34).
Nótese que el indicador de encadenamientos hacia atrás no depende de rT. De manera que este vector de ponderaciones iniciales se puede escoger arbitrariamente.
Para poder usar la información completa de la dirección de los flujos en una red dirigida se usa la matriz simétrica generalizada: R˜=R+RT (Leicht y Newman, 2008).
En una red dirigida las conexiones entre 2 puntos tienen un sentido definido. No basta con que exista la relación entre 2 puntos, sino que además debe mencionarse la dirección de la relación.
En una red suficientemente interconectada todos los sectores contribuyen directa o indirectamente para la producción de cualquiera de los bienes finales.
Debido a la ausencia de valores positivos en la columna correspondiente al sector 37 (Desperdicios y desechos), este se excluyó análisis.
En el Apéndice B se hace una comparación entre los indicadores calculados con el método de Rasmussen y con el método de Dietzenbacher.
Nótese que para los sectores con fuertes encadenamientos hacia atrás y hacia delante solo se muestra uno de los indicadores, y para los sectores con encadenamientos débiles no se muestra ninguno (véase el Apéndice B).
El clúster Electricidad, que solo está compuesto del sector Electricidad, puede absorber y proveer trabajo únicamente desde y hacia sectores de otros clústeres. Nótese que para este clúster las columnas 1 y 3 de la tabla 12 son ambas cero. De igual manera sucede con el clúster Cuero-calzado.