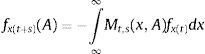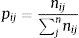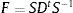Este artículo pretende estudiar las desigualdades regionales en materia del rendimiento educativo a nivel de básica secundaria, para el periodo 2007-2012, en los municipios colombianos. La calidad educativa municipal se mide a través de los resultados de la prueba Saber11, aplicada a estudiantes de último grado. Para tal efecto, se utiliza un enfoque de convergencia, pero a diferencia de la literatura convencional, se vincula al análisis el componente espacial o geográfico como determinante del rendimiento educativo, y variable explicativa de las altas desigualdades educativas del país. Los resultados muestran que el rendimiento educativo de los municipios no presenta un proceso de convergencia en todas las áreas del conocimiento, sino que, por el contrario, los municipios se agrupan (conforman clústeres) de acuerdo a su nivel de calidad educativa. Además, se encuentra que el nivel de calidad educativa del vecindario tiene una fuerte influencia sobre las probabilidades que tiene un municipio de escalar o descender en la distribución de la calidad educativa.
This article studies regional gaps in education quality at the senior high school level, for the period 2000-2012, in Colombia's municipalities. Municipal education quality is measured using a test called Saber11, applied to high school students in their last year. With the aforementioned aim in mind, a non-parametric convergence analysis is carried out, in which the geographical element is taken into account as a factor influencing education quality and explaining regional gaps. Results suggest that there is no evidence of convergence and, on the contrary, it is found that municipalities cluster together in space according to their education quality level. Moreover, it is found that neighbourhoods education quality level has a large influence in the likelihood that a municipality has of moving up or down the distribution.
En los últimos años la educación ha jugado un importante papel como rama y campo de estudio de la teoría económica, y la llamada «economía de la educación» concentra hoy el interés de investigadores e instituciones, convirtiéndose en uno de los campos mayormente tratados y con importantes implicaciones de política. Un fenómeno que ejemplifica la alta importancia de este campo de la economía ha sido la relación entre educación y crecimiento económico. La mayoría de trabajos dedicados al respecto encuentran que existe una relación positiva entre ambas variables, relación tan estrecha que en momentos las indagaciones sobre la causalidad se tornan significativamente complejas (Tolley y Olson, 1971).
Con frecuencia se constata en la literatura que los países con mayores ingresos tienen altos niveles de educación (Gennaioli, la Porta, Lopez-de-Silanes y Shleifer, 2013). De igual manera se ubica al nivel de educación como uno de los determinantes más importantes de las diferencias salariales de los individuos, (Azzoni y Servo, 2002), y los países que invierten más en educación experimentan tasas de crecimiento económico más altas, (Cárdenas y Pontón, 1995). Este acuerdo en la literatura puede verse reflejado en conceptos como «Skilled cities» y «Smart cities» (Glaeser y Saiz, 2004; Shapiro, 2006).
A pesar de esta señalada y documentada relación, existe un aspecto de la literatura donde las indagaciones y estudios sobre el tema de la educación son relativamente escasos comparados con los referentes al crecimiento del ingreso: el tema de la convergencia. A la luz de la citada relación, saber si los países, departamentos o municipios de menores niveles de educación se están acercando a sus correspondientes más educados es quizá tan importante como saber si lo están haciendo en términos de ingreso. Por esta razón, la investigación pretende responder una serie de interrogantes que infortunadamente no han tenido un tratamiento generalizado en la literatura nacional, y cuyas respuestas pueden ayudar de manera importante a orientar la política pública en educación:
¿En el periodo 2000-2012 se ha dado en Colombia un proceso de convergencia en materia de calidad educativa entre los municipios? ¿Cuáles son las probabilidades que tienen los municipios de mejorar o empeorar su posición en la distribución regional de la calidad educativa? ¿Cuáles son las probabilidades que tienen los municipios de mejorar o empeorar su posición en la distribución regional de la educación del país, según la posición de sus vecinos? ¿Existen clústeres de convergencia en el país para la calidad de la educación?
En vista de la crítica de Quah (1996) a las técnicas de regresión usualmente utilizadas en el análisis de convergencia, el presente trabajo pretende dar respuesta a los interrogantes precedentes por medio del uso de un conjunto de técnicas no paramétricas.
De acuerdo con Quah (1996, 1993), la relación negativa que delata un posible proceso de convergencia en un modelo de regresión lineal no necesariamente se deriva del hecho de que en efecto las unidades en un lugar inferior de la distribución estén acercándose a aquellas en la parte superior. Tal resultado puede ser simplemente una manifestación de la falacia de Galton, «originada por derivar implicaciones dinámicas del comportamiento estático de una distribución» (Mora, 2003).
Teniendo en cuenta lo anterior, el presente trabajo se inclina por la implementación de técnicas no paramétricas, como el análisis distribucional a través de kernel estocásticas y la estimación de matrices de Markov o matrices de probabilidad de transición entre rangos de calidad educativa. La implementación de estas técnicas es suplementada por evidencia complementaria proveída a través del análisis exploratorio de datos espaciales (AEDE). El AEDE será especialmente útil para analizar la dimensión geográfica de la evolución de las brechas en calidad educativa detectadas por las kernel estocásticas, y además sirve de antesala para justificar la pertinencia de introducir un condicionante espacial en la estimación de las matrices de Markov. En particular, a través de las matrices de Markov espacialmente condicionadas es posible considerar el efecto del vecindario en la calidad educativa de un municipio. De esta manera, el estudio será pionero en el uso de estas técnicas para el análisis de la economía de la educación en el país, y sus resultados serán especialmente útiles para el direccionamiento de la política pública en educación.
En la siguiente sección se expone una breve revisión de la literatura. Luego se expone la metodología, seguida de la sección de resultados. En este respecto es pertinente señalar que la calidad educativa municipal es medida como el puntaje medio de los estudiantes que tomaron las pruebas ICFES Saber11 en cada año en los exámenes de Lenguaje y Matemática. Finalmente, se cierra el artículo con una sección de conclusiones.
2Revisión de la literaturaTal como se ha enunciado, la literatura referente a la convergencia educativa es escasa tanto a nivel internacional como nacional, y más escasa se torna cuando se considera un enfoque espacial, ya que usualmente es en el caso del estudio del ingreso donde se acepta la influencia de la geografía (Elias y Rey, 2011). El análisis de convergencia se desprende del modelo de crecimiento económico neoclásico para el examen del crecimiento económico regional (Sala-i-Martin, 1994). Posteriormente, su análisis se hizo extensivo a distintos campos.
Dentro de los trabajos que estudian la convergencia tanto de la educación como del ingreso, se destacan los de Berry y Glaeser (2005), quienes encuentran que los niveles de educación de las ciudades de Estados Unidos divergen y que esto está relacionado a un proceso de declive de la convergencia del ingreso. Wolff (2000), por su parte, encuentra convergencia en los niveles de escolaridad de los países de la OECD, hecho que corresponde a su vez con un proceso de convergencia en los niveles de productividad laboral. Tales trabajos permitirían en principio conjeturar como posible la hipótesis de convergencias estrechamente relacionadas y condicionadas.
En la mayoría de estos trabajos, se apela regularmente al análisis tradicional de convergencia, mientras que la técnica alternativa propuesta por Quah (1996) no tiene en este caso un tratamiento generalizado (Rattsø y Stokke, 2012). Una razón para esta situación reside en las características mismas de la técnica del llamado análisis de «dinámica de distribución». En efecto, al pretender dar cuenta de la evolución al interior y al exterior de una distribución, esta técnica encuentra una mayor utilidad a una escala regional menor, caracterizada por mayores dinamismos (por ejemplo, al interior de un país).
Siguiendo el derrotero trazado por Quah (1993), Rattsø y Stokke (2012) realizan un análisis de convergencia tanto del nivel de educación (medido como la población que tiene educación universitaria) como del ingreso, utilizando la técnica de densidades de kernel y matrices de Markov, para 89 regiones NUTS-4 de Noruega, en el que adicionan un test para las probabilidades de transición de acuerdo al concepto de estacionariedad de una serie de tiempo, con el fin de determinar qué tan relacionados estadísticamente se encuentran los procesos de convergencia en ambas variables. Los autores encuentran que hay convergencia tanto en materia educativa como en ingresos. Sin embargo, la aplicación del test indica que ambos procesos no están relacionados.
El hallazgo de Rattsø y Stokke (2012) resulta aleccionador toda vez que de él, por un lado, pueden desprenderse implicaciones de política centradas en los verdaderos determinantes del nivel de educación y, por otro lado, pueden mostrarse resultados importantes que contrastan con aquellos correspondientes a la aplicación de la técnica empleada en el análisis tradicional de convergencia. Sin embargo, algunas consideraciones sobre este trabajo merecen mención: en primer lugar, los autores no desarrollan la técnica conocida como kernel estocástica para complementar sus análisis de convergencia; en segundo lugar, precisamente la kernel estocástica puede, mediante un adecuado esquema sugerido en Quah (1996) y Magrini (2007), determinar si un conjunto dado de variables o indicadores explica el comportamiento de convergencia encontrado.
Por otro lado, distintos estudios se han realizado para analizar el rendimiento educativo manteniendo una perspectiva espacial. Son de destacar los trabajos de Elias y Rey (2011), Naidoo, van Eeden y Munch (2014); Aomar y Jabrane (2014); Gordon y Monastiriotis (2006), entre otros. Estos trabajos analizan el rendimiento educativo de países y municipios, utilizando técnicas de estadística espacial para dilucidar el efecto de distintas variables de orden socioeconómico sobre dicho rendimiento. El trabajo de Gordon y Monastiriotis (2006) toma en cuenta los efectos locales de la variación en la clase social, el nivel de ingresos, junto con la selección de escuelas, como variables de significativa influencia sobre el rendimiento educativo tanto a escala de colegios como de subregiones para Inglaterra. Los autores concluyen que, a escala de colegio, los efectos de «ubicación» inciden significativamente sobre el resultado educativo cuando se tiene en cuenta su correlación con variables socioeconómicas, como la combinación entre etnia y clase social.
En línea con la hipótesis de convergencia, el trabajo de Elias y Rey (2011) presenta un análisis de convergencia espacial del rendimiento educativo de los municipios de Perú desde 1993 a 2005. Para tal propósito, los autores redefinen una versión espacial de la tradicional ecuación de convergencia, bajo la consideración de modelos de error espacial y de rezago espacial. Los autores encuentran convergencia absoluta para estos modelos espaciales.
Si bien estos trabajos, al igual que otros como los de Dall’erba y le Gallo (2008) para el caso de crecimiento económico e inversión pública, aplican técnicas de econometría espacial para testear la hipótesis de convergencia a través de un método paramétrico, es preciso indicar, como lo hace Anselin (1988, 2003), que dichas metodologías se enfrentan a importantes problemas en relación con la influencia de la heterogeneidad espacial sobre las estimaciones y los problemas de la elección del tipo de efectos spillovers que se pretenda analizar. Por esta razón, y habida cuenta de que las disparidades regionales tanto del nivel de ingresos como del nivel de rendimiento educativo en Colombia son significativamente amplias, en este trabajo se opta por seguir un análisis no paramétrico de convergencia espacial. Es decir, el análisis de convergencia a la usanza de Quah (1996) se complementa con la estimación de matrices de Markov condicionadas espacialmente; de esta manera, el análisis de convergencia incluye el elemento espaciotemporal sin incurrir en los riesgos, ampliamente documentados, que involucran el empleo de las metodologías paramétricas tradicionales.
2.1El caso colombianoLa escasez relativa de la literatura internacional sobre este tema también tiene lugar en el escenario colombiano, con el agravante de ser uno de los países con más bajos niveles de calidad educativa y con considerables desigualdades tanto en la educación como en el ingreso de sus regiones (Gamboa, 2012; Galvis y Meisel, 2010).
Barrera-Osorio, Maldonado y Rodríguez (2012), a partir de datos de las pruebas PISA y Saber11, encuentran que los estudiantes colombianos, comparados con los de países desarrollados de la OCDE, presentan en promedio un nivel de calificación de 2, en una escala de 1 a 6, y concluye que: Este resultado muestra que la inversión en educación y el cambio en la forma en que se está ofreciendo la educación en Colombia son temas urgentes. De acuerdo con PISA, una proporción muy alta de los jóvenes escolarizados que tienen 15 años en Colombia carece de conocimientos y competencias básicas para desenvolverse en una sociedad moderna. Son jóvenes que no están en capacidad de entender un texto (47%), no son capaces de tomar resultados científicos simples y relacionarlos con su cotidianidad (55%) y que no son capaces de hacer inferencias simples a partir de resultados matemáticos (71%).
Asimismo, a partir de un análisis de las pruebas PISA y Saber11, Gamboa (2012) encuentra, por su parte, que uno de los factores que mayor inequidad genera es el colegio, a diferencia de las condiciones de género, pero no avanza en un estudio de convergencia para saber cómo ha cambiado la distribución en los últimos años.
En cuanto a la aplicación misma del análisis de convergencia, Galvis y Meisel (2010) reportan la existencia de significativas trampas de pobreza estrechamente relacionadas con disparidades regionales en los niveles de educación (medidos por las tasas de analfabetismo y cobertura en educación primaria y secundaria) a partir de un análisis de convergencia tradicional-convergencia tipo beta y convergencia sigma.
Royuela y García (2010) realizan un análisis de convergencia del ingreso y de un conjunto de indicadores sociales entre los cuales se encuentra la tasa de alfabetismo a nivel departamental. Los autores reportan la existencia de un proceso de convergencia tipo sigma de esta variable, que se ve confirmado a su vez por la aplicación de la kernel estocástica. Los autores también realizan un análisis espacial, bajo la propuesta de una relación entre convergencia y autocorrelación espacial, y encuentran que la tasa de alfabetismo ha experimentado un proceso de autocorrelación espacial para 1975 a 2005, lo cual confirma la necesidad de aceptar el rol del espacio para el análisis de variables educativas y sociales.
La literatura consultada acepta en general la existencia de desigualdades en materia educativa en el país (Gamboa, 2012; Barrera-Osorio et al., 2012). Incluso algunos autores, como Aguirre (2005), reportan que no hay existencia de convergencia en la tasa de analfabetismo en Colombia a nivel departamental para el periodo 1985-2000. Aunque cabe señalar que todos estos resultados pueden verse explicados por los aumentos de cobertura que ha experimentado el país en los últimos años. Ahora bien, los trabajos reseñados que abordan el tema de la evolución de las brechas en materia educativa utilizan indicadores que no dan cuenta necesariamente de su calidad (como tasas de analfabetismo y cobertura educativa), mientras que los otros estudios interesados en analizar la desigualdad en materia educativa, aunque utilizan variables proxy de la calidad como los puntajes en las pruebas PISA y Saber11, no abordan la dinámica temporal, pues se trata de análisis de sección cruzada. Sin embargo la temática de la convergencia en la calidad educativa debe también ser objeto de un interés equiparable, y esta investigación generaría resultados pioneros en Colombia.
3Metodología: análisis espaciotemporal de datosEn razón de que se pretenden estudiar las disparidades regionales, a escala municipal, de la calidad educativa para el periodo de estudio (2000-2012), la hipótesis de convergencia de dicho rendimiento debe ser testeada. En tal sentido, este trabajo opta por la aplicación de las metodologías no paramétricas para el estudio de la convergencia. En concreto se hace uso del análisis de distribuciones (o kernel estocástica) y de las matrices de Markov. Además, para revelar el alcance geográfico de las brechas municipales en calidad educativa se recurre a algunas herramientas básicas del análisis exploratorio de datos espaciales (AEDE), que además sirven de material de apoyo para la interpretación de las matrices de Markov.
3.1Análisis exploratorio de datos espaciales y mapas de persistenciaEl AEDE es un conjunto de herramientas estadísticas encaminadas a conocer y describir la distribución en el espacio de un conjunto de datos. En particular aquí se hace uso de los indicadores locales de asociación espacial (LISA), los cuales permiten identificar patrones en la distribución espacial de una variable, y proporcionan un criterio estadístico para identificar cuáles de esos patrones son significativos (Anselin, 1994). En el presente contexto, esto se traduce en identificar en el espacio posibles conglomerados o clústers de municipios que poseen determinado desempeño en las pruebas ICFES (por ejemplo, un clúster con buen desempeño en las pruebas ICFES), dando así una idea más precisa del alcance geográfico de las brechas en materia educativa. Además, es posible cruzar las variables relacionadas con el desempeño en las pruebas Saber11 con otras que se presuma tengan alguna incidencia sobre el desempeño por medio del análisis LISA bivariado.
Con el fin de ofrecer un mapa resumen que recoja los resultados de los indicadores locales de asociación espacial, se reportan lo que aquí se denominan «mapas de persistencia». Dado que se tiene información acerca de la calidad educativa municipal para un conjunto de años, se calculan para cada año los indicadores locales de asociación espacial y se identifica el número de veces que un municipio es clasificado en un clúster estadísticamente significativo. Finalmente, esta información es representada en un mapa que permite visualizar en qué regiones se ubican los clústeres más persistentes y robustos, es decir, los conjuntos de municipios que aparecen clasificados la mayoría del tiempo en un clúster estadísticamente significativo. En este sentido, dicho mapa proporciona información indicativa acerca de la persistencia en las diferencias regionales en materia de calidad educativa.
En este punto, conviene mencionar que el cálculo de los LISA y de las matrices de Markov espacialmente condicionadas (que se explican más abajo) tiene como uno de sus insumos críticos una matriz de pesos espaciales, cuya función es reflejar la posición relativa en el espacio de la unidad de análisis. La matriz de pesos espaciales en cierta medida se puede interpretar como un constructo que capta las interacciones espaciales. Puesto que la primera ley de la geografía, o ley de Tobler, establece que la cercanía o proximidad condiciona el nivel de interacción entre 2 o más unidades geográficas (Tobler, 1970), una práctica común en la literatura consiste en construir la matriz de pesos espaciales a partir de un criterio de vecindad. El más utilizado es el criterio tipo Queen, a través del cual se considerarían como vecinos aquellas municipalidades que comparten fronteras administrativas (Anselin, 2010). El criterio de vecindad aquí utilizado es del tipo «spheres of influence» (Bivand, Pebesma y Gómez-Rubio, 2008, p. 46). Este criterio procede a través de un algoritmo que traza un círculo alrededor del centroide municipal, cuyo radio está dado por la distancia euclidiana al municipio más cercano. Finalmente, son considerados vecinos aquellos municipios para los cuales estos círculos se intersectan.
3.2Kernel estocásticasEl análisis distribucional por medio de las kernel estocásticas como herramienta para analizar las brechas entre regiones fue propuesto por Quah (1996) en razón de sus críticas a las prácticas tradicionales para determinar convergencia. Esta técnica se basa en la aproximación de la distribución de probabilidad empírica del ingreso, o de la educación en este caso, considerando si una unidad o economía en el periodo t se encuentra en una posición de la distribución y en el periodo t+s cambia o se mantiene en la misma posición. En otras palabras, se trata de conocer el valor esperado de una distribución de datos condicionado a la información que toma en el presente. Con el fin de capturar las fuerzas internas de la distribución, Quah propone dividir la variable de interés por el valor de su promedio. La función de distribución adquiere entonces la forma siguiente:
donde x es la variable de interés (en este caso, el rendimiento educativo municipal), A se refiere al conjunto sobre el cual la matriz se evalúa (el conjunto de los municipios colombianos) y Mt,s(x, A) es una matriz de transición cuyos elementos representan las probabilidades de que una unidad de análisis que en el periodo t se ubica en una determinada posición de la distribución, en el periodo t+s se ubique en la misma posición o una distinta (Quah, 1995, 1996).
Las kernel estocásticas o kernel bidimensionales ofrecen una representación de los movimientos al interior de la distribución que permite discernir si hay un cerramiento o no en las brechas municipales en educación. Por su parte, las kernel clásicas o unidimensionales señalan el perfil de la distribución en un momento en el tiempo. Al comparar 2 cortes temporales, los perfiles permiten entonces discernir el movimiento general de la distribución. Estos movimientos ofrecen indicios acerca de la evolución de las brechas municipales en educación, pero no permiten establecer, por ejemplo, en caso de encontrarse una mejora generalizada del rendimiento educativo, si existen municipios que permanecen estancados, pues este hecho se opaca por los movimientos generales de la distribución.
Los mapas de curvas de nivel de las kernel estocásticas o bidimensionales proveen mayor información, porque permiten visualizar la posición de la masa de la distribución en los 2 cortes temporales considerados y, de esta manera, por ejemplo, determinar si los municipios que presentaban bajo rendimiento educativo presentan un incremento en este, y determinar sus movimientos respecto a los municipios de alto rendimiento educativo. Por tanto, se obtiene un panorama más detallado de la evolución de las brechas en materia educativa. De esta forma, los movimientos generales de la distribución no ocultan los movimientos al interior de esta. Es decir, las kernel bidimensionales exhiben tanto la información interdistribucional como la intradistribucional.
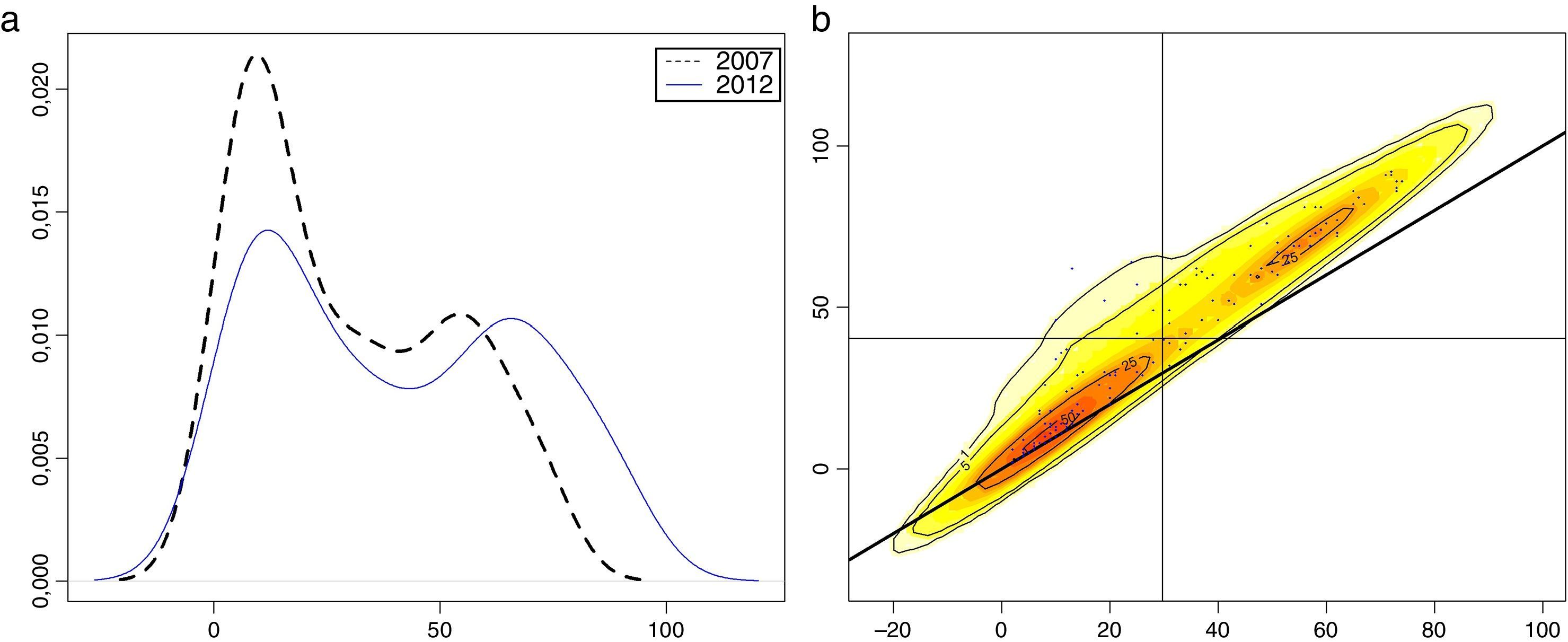
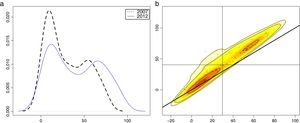
Las kernel estocásticas se pueden representar a través de un gráfico tridimensional, donde los ejes x e y representan la variable de interés en t=0 y t=1, respectivamente, es decir, se refieren a 2 cortes temporales de la variable, mientras el eje z muestra las frecuencias o probabilidades de cada par (x,y) representado. Sin embargo, aquí se elige, por su facilidad de visualización e interpretación, ilustrar las kernel bidimensionales o estocásticas a través de un gráfico de contornos. El gráfico de contornos es una representación bidimensional donde el eje horizontal se refiere a la variable en el periodo inicial, y el eje vertical se refiere a la variable en el periodo final. En este plano bidimensional, la distribución o masa de probabilidad se representa a través de curvas de nivel. Cada curva de nivel se refiere a un nivel distinto de probabilidad. La figura 1b muestra un mapa de contornos donde la curva de nivel exterior representa un nivel de probabilidad o una frecuencia del 1%, mientras los contornos interiores representan probabilidades o frecuencias del 5, del 25 y del 50%, respectivamente. Los contornos dan una idea acerca de dónde se concentra la masa de la distribución. Su interpretación es facilitada por la línea diagonal, la cual representa una recta con una pendiente de 45 grados. Esta línea representa la situación de estabilidad: si un punto se encuentra sobre la diagonal, significa que este no ha cambiado de posición. Si un punto se encuentra por encima de la diagonal, significa que ha mejorado su posición. Si está por debajo, se tiene la situación contraria.
Gráfico ejemplo.
a) Kernel clásica o unidimensional.
b) Kernel estocástica o bidimensional.
Nota: El gráfico a compara el perfil de la distribución el año inicial (línea punteada) y en el año final (línea continua). El gráfico b muestra los contornos de la distribución, como estrategia para determinar los tipos de movimientos que se dan entre el año inicial (representado en el eje horizontal) y el año final (en el eje vertical). Por ejemplo, los contornos en el cuadrante superior derecho representan municipios que tanto al principio como al final del periodo se encontraban por encima del promedio, mientras que los contornos ubicados en el cuadrante superior izquierdo representan municipios que en el periodo inicial estaban por debajo del promedio y en el periodo final se ubican por encima.
Además, las líneas vertical y horizontal representan el promedio que toma la variable en el periodo inicial y final, respectivamente. En el presente caso, el cuadrante superior derecho dibujado por ambas rectas recogería aquellos municipios cuyo desempeño educativo está por encima del promedio tanto al inicio como al final del periodo. El cuadrante inferior izquierdo manifiesta la situación opuesta. El cuadrante superior izquierdo encapsula los municipios que tenían un rendimiento por debajo del promedio en el año inicial, y que en el año final tienen un rendimiento educativo que supera el promedio (es decir, hay un avance). El cuadrante inferior derecho se refiere a la situación opuesta (retroceso).
En la figura 1b, que muestra una situación hipotética, se tienen 2 contornos interiores que representan 2 modas en la distribución. La moda en el cuadrante superior derecho representaría municipios de alto rendimiento educativo, mientras la moda en el cuadrante inferior derecho, que es la más importante en cuanto a masa de probabilidad, representa a los de bajo desempeño.
Como la masa de contornos de los municipios de bajo desempeño educativo se ciñe a la línea diagonal, se puede hablar de una situación de persistencia. Es decir, los municipios de bajo desempeño educativo no incrementaron su desempeño. Por el contrario, la masa de contornos correspondiente a los municipios de alto rendimiento educativo se ubica por encima de la diagonal, lo cual manifiesta una situación de aumento de su desempeño. De esta manera, se tendría una situación de ampliación de las brechas de rendimiento educativo. Otra lectura que puede conducir a esta conclusión es analizar la pendiente de la masa de contornos. Nótese que al observar el conjunto de la masa de contornos en el gráfico, esta es más inclinada (o de mayor pendiente) que la línea diagonal. Esta es otra característica saliente de una distribución que manifiesta aumento de las diferencias entre municipios.
Finalmente, note el lector que, a partir de la kernel clásica o unidimensional en la figura 1a, se pueden extraer algunas conclusiones generales acerca del movimiento de la distribución, como su carácter bimodal y el desplazamiento entre años. No obstante, la kernel unidimensional no permite discernir los movimientos interiores que sí devela la kernel estocástica, tales como establecer si los municipios de baja calidad educativa son los mismos al inicio y al final del periodo.
3.3Matrices de Markov para el rendimiento educativo promedio: matrices con probabilidades de transición municipalLas matrices de Markov para las probabilidades de transición distribucional están relacionadas con las kernel estocásticas por el término Mt,s(x, A) en la ecuación (2). El término Mt,s(x, A) se puede interpretar como una matriz de Markov con dimensionalidad muy grande (es decir, su número de filas y columnas tiende a infinito). Evidentemente la estimación de una matriz de tal dimensionalidad es impráctica, por lo cual una matriz de Markov se ciñe a estudiar las transiciones de entre un conjunto finito de estados. Es pertinente su utilización, ya que tienen la ventaja de poder arrojar conclusiones sobre la secuencia de las distribuciones en el largo plazo, además de estudiar la dinámica intradistribucional más allá de determinar un proceso de convergencia. La construcción de estas se fundamenta en determinar la probabilidad de estar en un estado k en el periodo t+s, a partir de la información suministrada por la distribución en el periodo t. Estas probabilidades se calculan de acuerdo a la siguiente expresión (Rattsø y Stokke, 2012):
donde nij indica el número de transiciones empíricamente observadas del nivel i al j, las cuales cumplen las siguiente propiedades, primero, pij≥0 ∀ i y j, y segundo, ∑jkpij = 1 ∀ i=1, 2,…,k (Valdivia, 2008).
De esta forma las probabilidades se asumen invariantes en el tiempo. Bajo esta hipótesis, es posible obtener una distribución de largo plazo (o ergódica) mediante el proceso markoviano, donde se muestra el hipotético estado de equilibrio. La distribución ergódica para un proceso markoviano regular de primer orden se calcula como F=Mtu con t→∞, y donde F es un vector que hace referencia a la distribución de estado estable o de largo plazo, u es un vector que contiene el estado inicial del proceso y M es la matriz de probabilidad o matriz de Markov. Ahora bien, este procedimiento implica elevar la matriz M a una potencia muy grande, lo cual es impráctico. Sin embargo, si la matriz de probabilidad es diagonalizable, solo se requiere calcular las potencias de la matriz diagonal resultante (Restrepo, Franco y Muñoz, 2010):
siendo D una matriz diagonal que contiene los eigenvalores asociados a la matriz M, y S una matriz que contiene los eigenvectores de M.
Cabe aclarar que para la elaboración de las matrices de Markov, o probabilidad, se consideraron 5 categorías de rendimiento educativo municipal, yendo desde muy bajo hasta muy alto. Estas se definieron mediante 5 cuantiles tiempo invariantes, hallados sobre los datos agrupados, para garantizar la comparabilidad intertemporal de las 5 categorías de rendimiento educativo.
Finalmente, para dar cuenta de los posibles fenómenos de dependencia espacial en la distribución del desempeño educativo municipal, es posible condicionar las matrices markovianas con el rezago espacial de esa variable (Rey, 2001). El rezago espacial de una variable se puede interpretar como el valor promedio que toma la misma en el vecindario de una determinada unidad espacial. En el presente caso correspondería a la calidad educativa promedio de las poblaciones vecinas de cada municipio. Para diferenciar las matrices markovianas espacialmente condicionadas de las que no lo están, se denominará a las últimas como matrices de Markov clásicas.
Por medio de las matrices de Markov espacialmente condicionadas es posible considerar el efecto del vecindario en la calidad educativa de un municipio. En concreto, se espera que las probabilidades que tiene un municipio de escalar o descender en materia de calidad educativa estén relacionadas con el nivel que tienen sus poblaciones vecinas. Adicionalmente, las distribuciones ergódicas que se derivan de estas matrices pueden dar una idea de la posible evolución de las brechas en materia de calidad educativa, de mantenerse vigentes las condiciones que subyacen a la estructura de probabilidades que releven las matrices de Markov condicionadas espacialmente.
4Resultados4.1Las pruebas ICFES Saber 11El rendimiento educativo municipal es medido como el puntaje promedio que obtienen los estudiantes en cada prueba de núcleo común en el municipio considerado, práctica que es seguida por referentes internacionales como las pruebas PISA para el análisis comparativo de ciudades. Además, puesto que la prueba Saber11 se aplica a toda la población estudiantil próxima a graduarse en cada año, esto implica que la media poblacional puede establecerse sin o con poca incertidumbre.
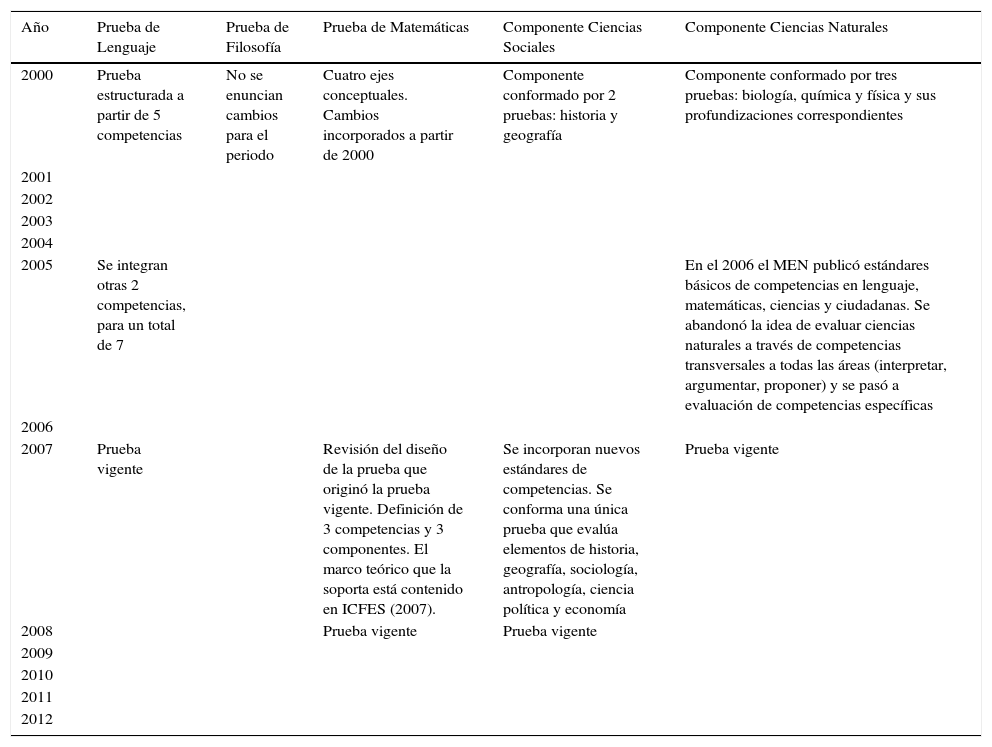
De acuerdo a ICFES (2013), la prueba Saber11 ha experimentado distintos cambios metodológicos que pueden afectar su comparabilidad intertemporal (2000-2012). En particular, se encuentra que entre 2005 y 2006 se suceden una serie de modificaciones que afectan la estructura de las pruebas ICFES Saber11, concretamente de las áreas de evaluación común, como se observa en la tabla 1. En 2006, las pruebas de Historia y Geografía se integran en una única prueba de Ciencias Sociales. En el campo de las Ciencias Naturales se mutan las competencias evaluadas, situación que también padece la prueba de Lenguaje. Finalmente, estos cambios en las metodologías hacen que los resultados de las pruebas no sean directamente comparables entre sí, es decir, el indicador de rendimiento educativo computado para los años en que fueron realizados los cambios explican características distintas del rendimiento educativo de los estudiantes. En el caso del área de Matemática, el conjunto de competencias evaluadas es cambiado en 2007. Además, en el año 2005 se reduce el tiempo que toma el examen a 2 sesiones de medio día, ocasionando que se reduzca el número de preguntas para todas las áreas objeto de evaluación.
Cambios en las pruebas ICFES Saber 11
| Año | Prueba de Lenguaje | Prueba de Filosofía | Prueba de Matemáticas | Componente Ciencias Sociales | Componente Ciencias Naturales |
|---|---|---|---|---|---|
| 2000 | Prueba estructurada a partir de 5 competencias | No se enuncian cambios para el periodo | Cuatro ejes conceptuales. Cambios incorporados a partir de 2000 | Componente conformado por 2 pruebas: historia y geografía | Componente conformado por tres pruebas: biología, química y física y sus profundizaciones correspondientes |
| 2001 | |||||
| 2002 | |||||
| 2003 | |||||
| 2004 | |||||
| 2005 | Se integran otras 2 competencias, para un total de 7 | En el 2006 el MEN publicó estándares básicos de competencias en lenguaje, matemáticas, ciencias y ciudadanas. Se abandonó la idea de evaluar ciencias naturales a través de competencias transversales a todas las áreas (interpretar, argumentar, proponer) y se pasó a evaluación de competencias específicas | |||
| 2006 | |||||
| 2007 | Prueba vigente | Revisión del diseño de la prueba que originó la prueba vigente. Definición de 3 competencias y 3 componentes. El marco teórico que la soporta está contenido en ICFES (2007). | Se incorporan nuevos estándares de competencias. Se conforma una única prueba que evalúa elementos de historia, geografía, sociología, antropología, ciencia política y economía | Prueba vigente | |
| 2008 | Prueba vigente | Prueba vigente | |||
| 2009 | |||||
| 2010 | |||||
| 2011 | |||||
| 2012 |
En las columnas se relacionan las pruebas de núcleo común del examen ICFES Saber 11 y en las filas los años en los que se realizaron cambios sustanciales a cada una.
Habida cuenta de estas modificaciones, que ocasionan que la estructura de las pruebas Saber11 sea distinta para las aplicaciones previas al año 2004 con respecto a las posteriores a 2007, con el ánimo de garantizar la comparabilidad intertemporal de los resultados obtenidos se decide fraccionar el periodo de estudio en 2: 2000-2004 y 2007-2012. Sin embargo, para el caso particular del test de Matemáticas, el segundo subperiodo abarca los años 2007-2012, puesto que esta fue la última prueba en experimentar un cambio en su estructura.
Cabe mencionar que, por razones de espacio, el presente documento se concentra en describir los resultados obtenidos a partir del análisis de las pruebas de matemática y lenguaje.
4.2Análisis kernel estocástica y matrices de Markov clásicasTal como se señaló en la metodología, la técnica no paramétrica denominada kernel estocástica pretende fundamentalmente capturar los movimientos al exterior y al interior que experimenta una distribución en un periodo de tiempo y, al hacerlo, permite determinar la existencia de procesos de convergencia entre las unidades regionales analizadas. En la figura 2d puede verse esta kernel estocástica. La masa de contornos, en amarillo y naranja, constituye la densidad o distribución condicional de las distintas partes de la distribución del rendimiento educativo (parte menor al promedio, igual al promedio, parte mayor al promedio). Cuando esta masa de contornos se superpone a la línea de 45 grados, ello quiere decir que los distintas partes de la distribución del rendimiento educativo, al cabo del periodo o para el año final, no experimentan cambios.
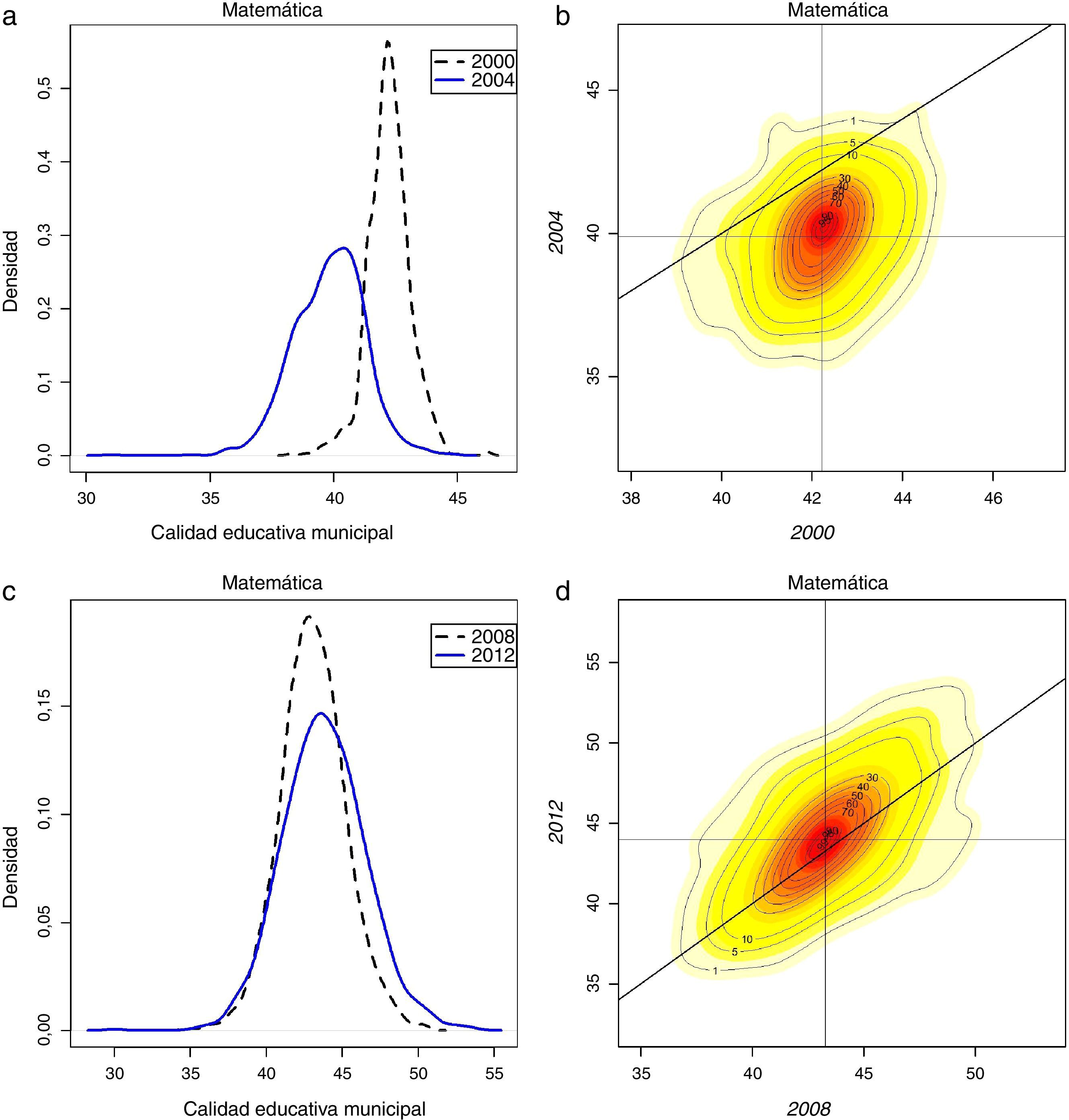
Prueba matemática: kernel estocásticas.
a) Subperiodo 1: Kernel unidimensional.
b) Subperiodo 1: Kernel bidimensional.
c) Subperiodo 2: Kernel unidimensional.
d) Subperiodo 2: Kernel bidimensional.
Notas: Cálculos propios con base en los datos del examen ICFES Saber 11. En la columna izquierda se representan los cambios en el perfil de la distribución. En la columna derecha se representan muestran los mapas de contornos que ilustra el tipo de movimientos acaecidos en los periodos considerados.
De otra parte, si la masa correspondiente a una parte de la distribución se encuentra por debajo de la línea de 45 grados, entonces dicha distribución disminuye su rendimiento educativo, y si por el contrario se encuentra por encima de la línea de 45 grados, ello indicará que dicha distribución presenta un crecimiento promedio de su rendimiento. De esta manera, ¿cuándo hay un proceso de convergencia en el rendimiento? Cuando la masa de contornos presenta, con respecto a la línea de 45 grados, un proceso en el sentido de las manecillas del reloj, en donde la parte baja de la distribución se encuentra por encima de la línea de 45 y la parte alta de la distribución se encuentra por debajo. Ello indicará que los municipios de menor rendimiento educativo se están acercando a sus correspondientes más educados, esto es, habría evidencia estadística de un proceso de convergencia.
4.3Prueba de MatemáticasEn la figura 2 se presentan tanto las kernel unidimensional o clásica como la kernel bidimensional, referida por algunos como kernel estocástica. En la figura 2a se presenta la kernel clásica correspondiente a la prueba de Matemáticas en el subperiodo 2000-2004, mientras la figura 2b presenta la kernel bidimensional respectiva. Para el primer subperiodo, puede notarse que el rendimiento educativo municipal promedio decae en esta prueba, pues en la figura 2a la línea continua se ubica a la izquierda de la línea punteada. Asimismo, la distribución presenta un achatamiento que manifiesta un incremento en la dispersión del rendimiento educativo. La kernel bidimensional en la figura 2b ratifica este proceso, puesto que se observa que la masa de contornos en general se ubica por debajo de la línea diagonal, manifestando que con respecto al periodo inicial hubo un retroceso en la calidad educativa municipal, retroceso que parece ser más evidente en la parte inferior de la distribución (cuadrante inferior izquierdo del mapa de contornos), pues allí la distancia con respecto a la diagonal es mayor.
Por otro lado, en el subperiodo 2008-2012 tiene lugar un ligero crecimiento en la calidad educativa promedio, como lo indica el leve desplazamiento de la distribución hacia la derecha en la figura 2c. Sin embargo, este leve desplazamiento positivo es acompañado de un achatamiento de la distribución, lo cual refleja un incremento de la dispersión y confiere un mayor peso a las colas, síntoma inequívoco de un proceso de divergencia. El movimiento general hacia la derecha sugiere que este proceso de divergencia se debe principalmente al alejamiento de un grupo de municipios que están mejorando su desempeño en la prueba de matemáticas. La kernel bidimensional en la figura 2d ofrece respaldo a los anteriores hallazgos. En efecto, como muestra el mapa de contornos para este subperiodo, los municipios de la parte alta de la distribución experimentan una mejora en su rendimiento, hecho que se refleja en que la parte de la distribución en el cuadrante superior derecho está por encima de la línea diagonal. En contraste, los municipios de bajo rendimiento educativo mantienen su posición relativa, como lo manifiesta el hecho de que los contornos en la parte inferior izquierda parecen seguir la pendiente de la diagonal. De esta manera, no se puede determinar que en este segundo subperiodo la prueba de matemáticas presente un proceso global de convergencia.
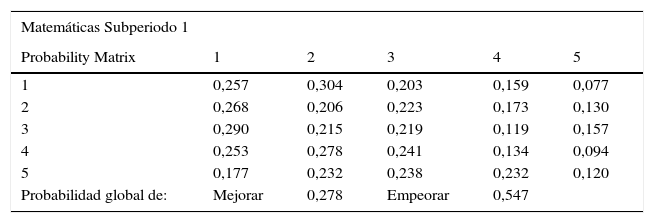
En la tabla 2 se muestra la matriz de Markov clásica que da cuenta de la estructura de probabilidades de transición de los municipios en términos del rendimiento educativo de la prueba de Matemáticas en el subperiodo1. En primer lugar, las probabilidades de la diagonal principal son bajas, lo cual indica que los municipios no mostraron persistencia en dicho subperiodo en su ubicaciones en la distribución y, en segundo lugar, las probabilidades de la submatriz triangular inferior son en promedio mayores a las de la triangular superior, hecho que se traduce en que la probabilidad global de retroceder excede a la de avanzar, lo cual corrobora que la distribución tiende a mostrar un retroceso en la calidad educativa municipal. De hecho, en general la probabilidad de empeorar en el periodo 2000-2004 es del 55,7%, mientras que la probabilidad de mejorar es del 27,8%. Esto respalda, en efecto, los resultados de las distribuciones kernel para el primer subperiodo.
Matriz de Markov clásica para Matemáticas (2000-2004)
| Matemáticas Subperiodo 1 | |||||
|---|---|---|---|---|---|
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,257 | 0,304 | 0,203 | 0,159 | 0,077 |
| 2 | 0,268 | 0,206 | 0,223 | 0,173 | 0,130 |
| 3 | 0,290 | 0,215 | 0,219 | 0,119 | 0,157 |
| 4 | 0,253 | 0,278 | 0,241 | 0,134 | 0,094 |
| 5 | 0,177 | 0,232 | 0,238 | 0,232 | 0,120 |
| Probabilidad global de: | Mejorar | 0,278 | Empeorar | 0,547 |
Cálculos propios con base en los datos del examen ICFES Saber 11. Las filas representan las 5 categorías de desempeño educativo en el año inicial, y las columnas representan estas 5 categorías en el año final. Por tanto, cada entrada representa la probabilidad de transicionar de una categoría a otra dentro del periodo de estudio.
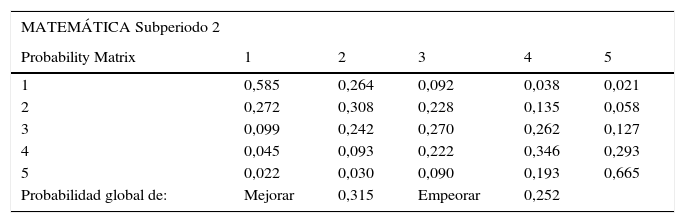
En la tabla 3 se presenta la matriz de Markov correspondiente al subperiodo 2008-2012. En relación con la matriz de Markov en la tabla 2, esta manifiesta un mayor nivel de persistencia: como puede notarse, en la diagonal principal las probabilidades más altas corresponden a los extremos de la distribución, los cuantiles1 y 5. De esta manera, la probabilidad de que los municipios del cuantil1 se queden en el mismo rango de la distribución es del 58,5%, mientras que la probabilidad de que los municipios de más alto rendimiento educativo sigan manteniéndolo es del orden del 66,5%. Este resultado establece indicios de una tendencia a la permanencia en las disparidades del rendimiento. Por otro lado, se puede ver el proceso contrario al anterior: las probabilidades son levemente mayores en la submatriz triangular superior que en la inferior, lo que refleja una tendencia de la distribución hacia el aumento promedio del rendimiento.
Matriz de Markov clásica para matemáticas (2008-2012)
| MATEMÁTICA Subperiodo 2 | |||||
|---|---|---|---|---|---|
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,585 | 0,264 | 0,092 | 0,038 | 0,021 |
| 2 | 0,272 | 0,308 | 0,228 | 0,135 | 0,058 |
| 3 | 0,099 | 0,242 | 0,270 | 0,262 | 0,127 |
| 4 | 0,045 | 0,093 | 0,222 | 0,346 | 0,293 |
| 5 | 0,022 | 0,030 | 0,090 | 0,193 | 0,665 |
| Probabilidad global de: | Mejorar | 0,315 | Empeorar | 0,252 |
Cálculos propios con base en los datos del examen ICFES Saber 11.
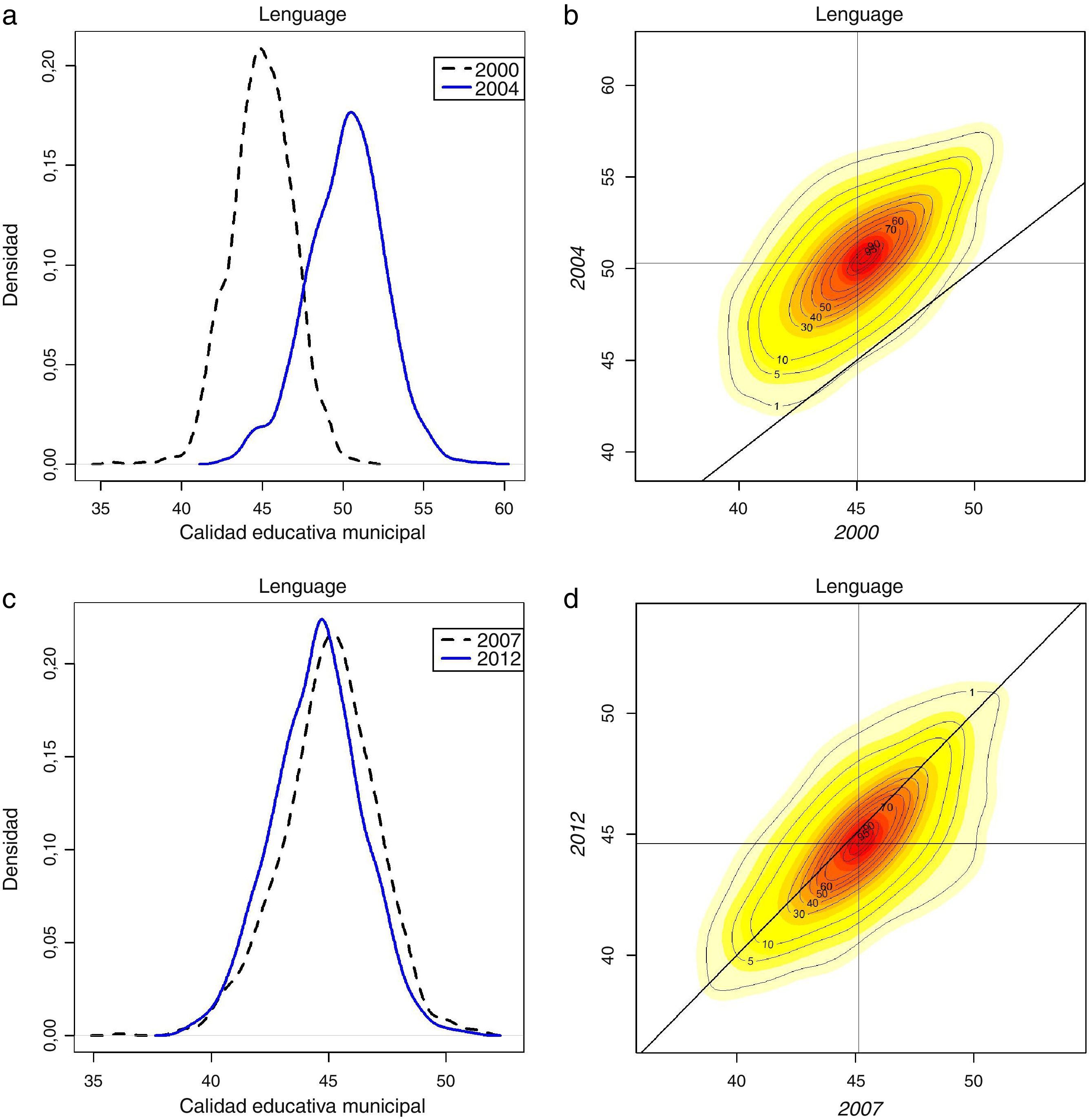
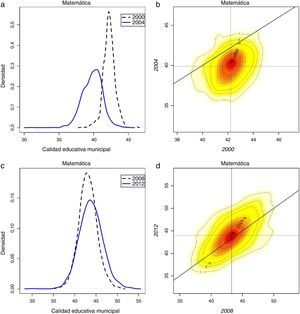
En la figura 3 se ilustran las kernel unidimensional y bidimensional correspondientes al primer subperiodo de la prueba de Lenguaje. Contrario a la prueba de Matemáticas, los estudiantes de los municipios experimentaron un crecimiento importante de su rendimiento en el primer subperiodo. La kernel bidimensional lo confirma en el sentido en que la masa de contornos en buena medida está por encima de la línea de 45 grados; pero en la medida en que la masa de contornos corre de manera relativamente paralela a esta línea diagonal, se colige que las brechas relativas entre municipios en términos de calidad educativa no se han cerrado, a pesar de que se evidencia un aumento generalizado del puntaje medio en la prueba de lenguaje.
Prueba de Lenguaje: kernel estocásticas.
a) Subperiodo 1: Kernel unidimensional.
b) Subperiodo 1: Kernel bidimensional.
c) Subperiodo 2: Kernel unidimensional.
d) Subperiodo 2: Kernel bidimensional.
Notas: Cálculos propios con base en los datos del examen ICFES Saber 11. En la columna izquierda se representan los cambios en el perfil de la distribución. En la columna derecha se representan muestran los mapas de contornos que ilustra el tipo de movimientos acaecidos en los periodos considerados.
En el subperiodo 2007-2012, los municipios presentaron un leve retroceso en su calidad educativa promedio en la prueba de lenguaje (fig. 3c), de manera que el ritmo de avance del primer subperiodo se frenó de manera significativa. Adicionalmente, cuando se observa la figura 3d se nota que la kernel estocástica o bidimensional ligeramente se superpone a la línea de 45 grados, indicando que durante este periodo los cambios distribucionales no son significativos, es decir, se tiene una situación general de persistencia de las brechas existentes.
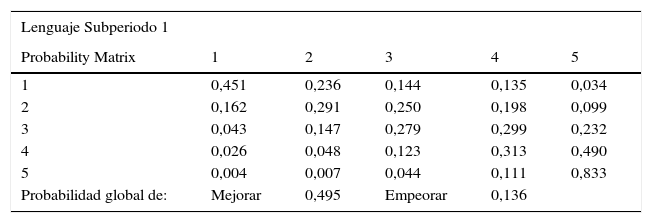
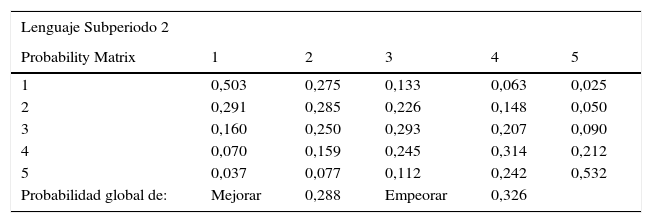
Adicionalmente, en las tablas 4 y 5 se presentan las matrices de Markov clásicas correspondientes a la prueba de Lenguaje. En el primer subperiodo, la probabilidad de permanecer en el cuantil superior es del 83,3%, frente a una probabilidad de permanecer en el primer cuantil del 45,1%. Estas probabilidades disímiles en los extremos son un síntoma del proceso de aumento de la calidad educativa municipal manifestado a través de las distribuciones kernel. En particular, de acuerdo con la tabla 4, se tiene que la probabilidad de escalar en la distribución de la calidad educativa es del 49,5%, frente a una probabilidad de descender del 13,6%.
Matriz de Markov Clásica para Lenguaje (2000-2004)
| Lenguaje Subperiodo 1 | |||||
|---|---|---|---|---|---|
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,451 | 0,236 | 0,144 | 0,135 | 0,034 |
| 2 | 0,162 | 0,291 | 0,250 | 0,198 | 0,099 |
| 3 | 0,043 | 0,147 | 0,279 | 0,299 | 0,232 |
| 4 | 0,026 | 0,048 | 0,123 | 0,313 | 0,490 |
| 5 | 0,004 | 0,007 | 0,044 | 0,111 | 0,833 |
| Probabilidad global de: | Mejorar | 0,495 | Empeorar | 0,136 |
Cálculos propios con base en los datos del examen ICFES Saber 11. Las filas representan las 5 categorías de desempeño educativo en el año inicial, y las columnas representan estas 5 categorías en el año final. Por tanto, cada entrada representa la probabilidad de transicionar de una categoría a otra dentro del periodo de estudio.
Matriz de Markov clásica para Lenguaje (2007-2012)
| Lenguaje Subperiodo 2 | |||||
|---|---|---|---|---|---|
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,503 | 0,275 | 0,133 | 0,063 | 0,025 |
| 2 | 0,291 | 0,285 | 0,226 | 0,148 | 0,050 |
| 3 | 0,160 | 0,250 | 0,293 | 0,207 | 0,090 |
| 4 | 0,070 | 0,159 | 0,245 | 0,314 | 0,212 |
| 5 | 0,037 | 0,077 | 0,112 | 0,242 | 0,532 |
| Probabilidad global de: | Mejorar | 0,288 | Empeorar | 0,326 |
Cálculos propios con base en los datos del examen ICFES Saber 11.
Por su parte, en el segundo subperiodo (2007-2012) esta característica de alta probabilidad de los municipios del cuantil superior de permanecer en esa misma posición se reduce ostensiblemente, pasando a un 53,2%, y la probabilidad del cuantil inferior aumenta significativamente al 50,3%, lo cual ratifica el proceso de retroceso que los municipios experimentaron en esta prueba, tal como lo ilustra la kernel respectiva de la figura 3.
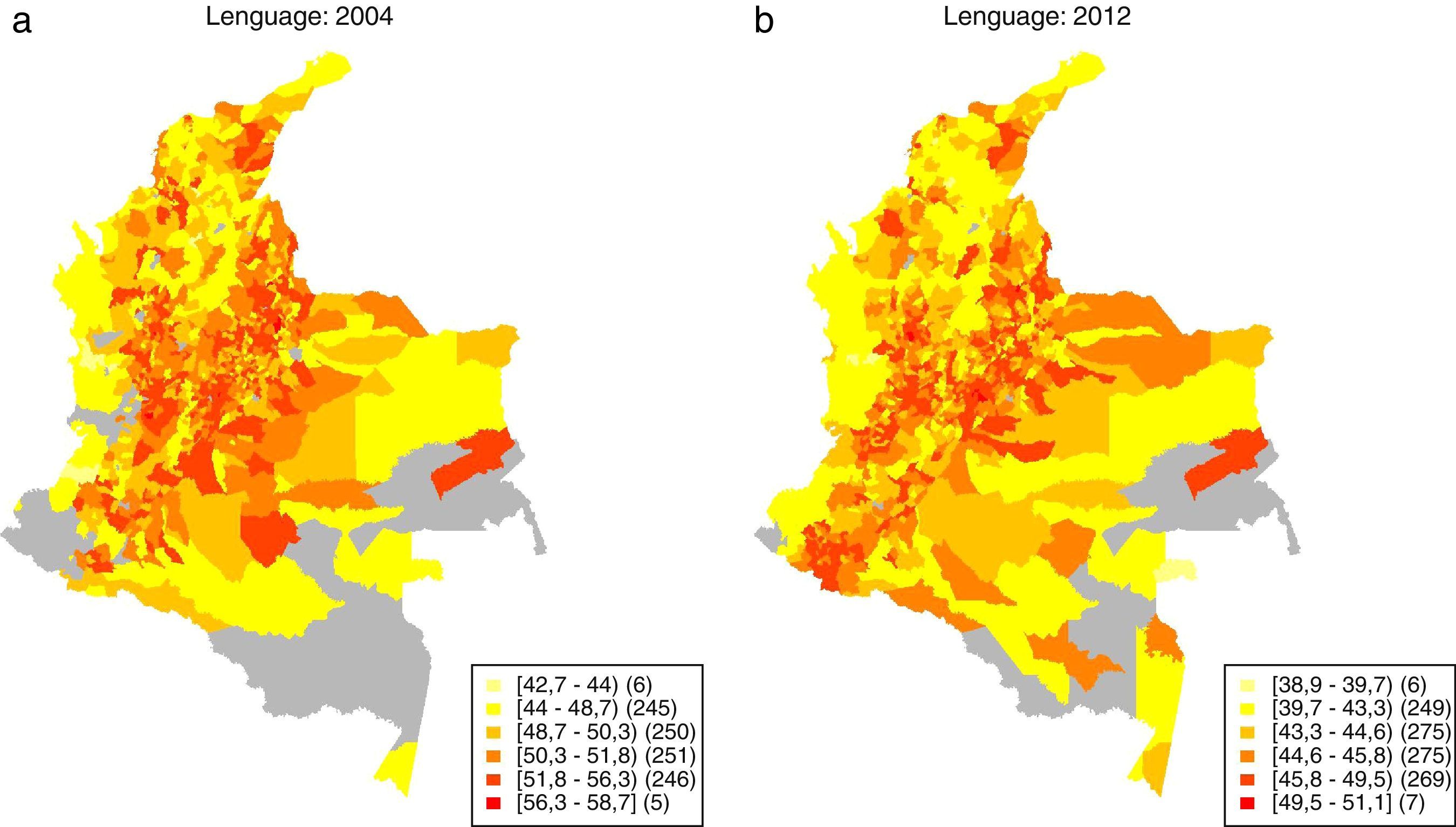
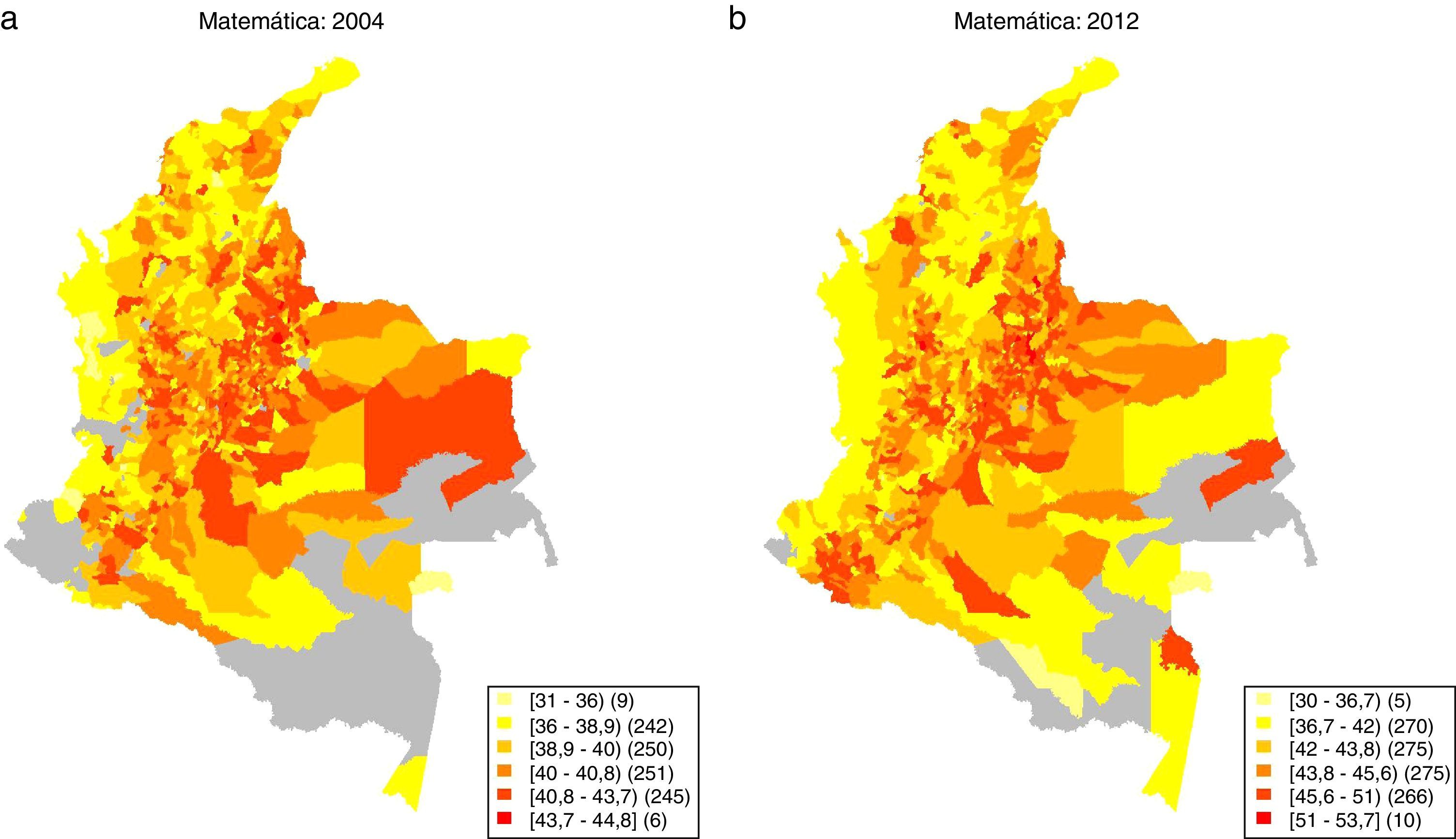
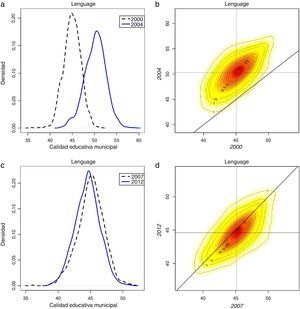
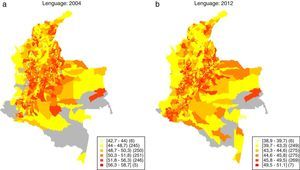
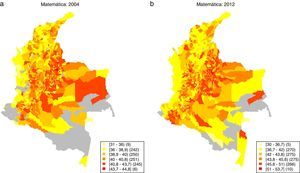
4.5Análisis de clústers de rendimiento educativoEn este apartado se recurre al análisis exploratorio de datos espaciales (AEDE) para determinar si la distribución del rendimiento educativo municipal exhibe patrones particulares en el espacio. Para ilustrar la distribución espacial del rendimiento educativo municipal se elaboran un conjunto de mapas de caja, o boxmaps, los cuales se generaron para cada prueba y para cada año. Por brevedad, solo se reproducen los boxmaps para los años 2004 y 2012, los cuales se presentan entre las figuras 4 y 5. Los municipios con un mayor rendimiento educativo se representan a través del color más oscuro (rojo oscuro).
En el caso de la prueba de Matemáticas se evidencia que las zonas de menor desempeño educativo se localizan sobre el Pacífico (en el occidente) y la región atlántica (al norte). Estas regiones son escoltadas en su bajo desempeño por las zonas más al sur de Colombia y el oriente. Este patrón general se repite en las demás pruebas.
Asimismo, en términos generales los municipios con un mejor desempeño educativo parecen ubicarse sobre la región andina. En algunos casos se adhieren a este club algunos municipios del Piedemonte Llanero y de Nariño.
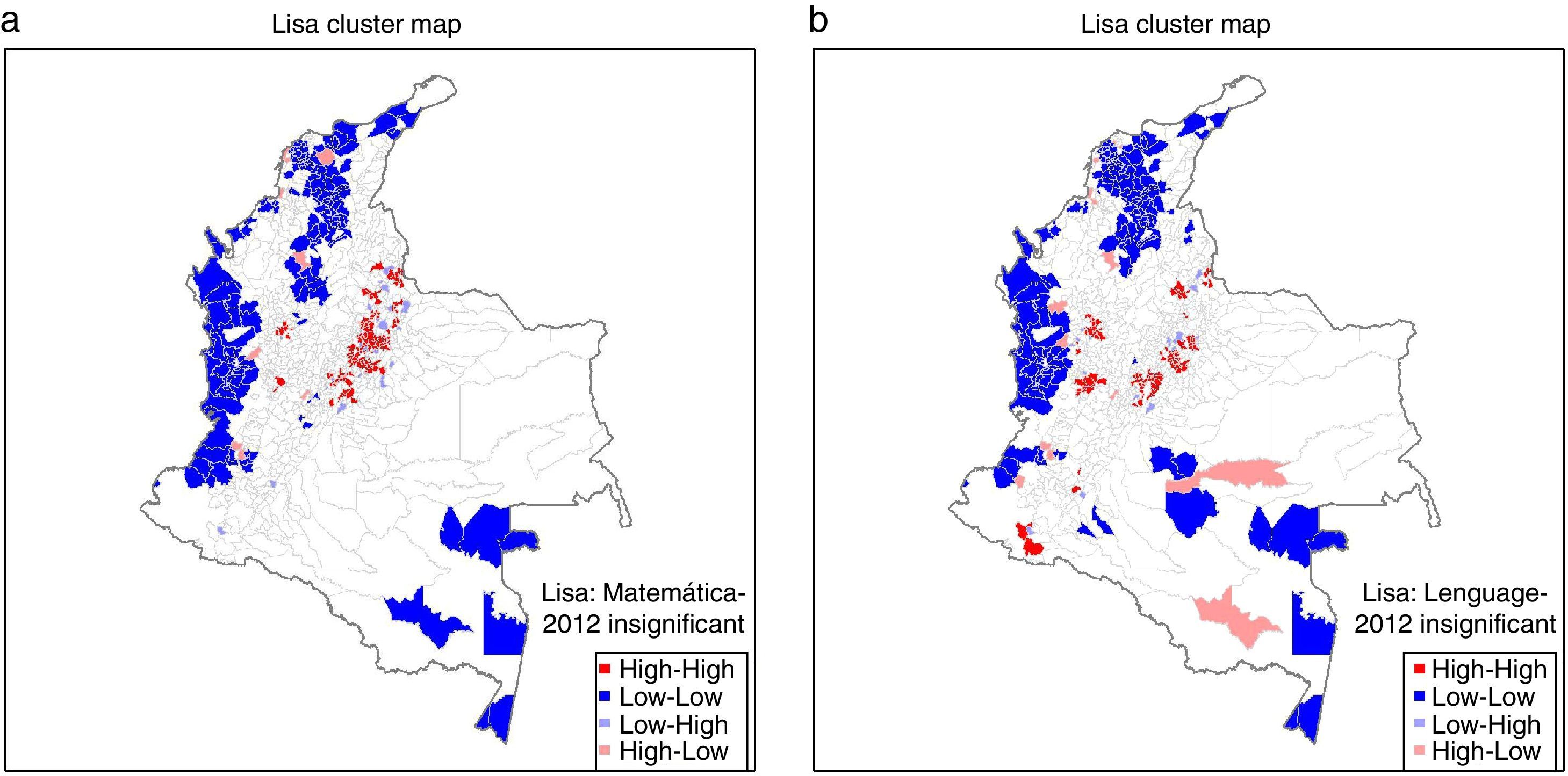
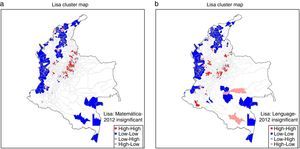
A través de los patrones de distribución espacial sugeridos por los mapas de cajas en las figuras 4 y 5, es dable pensar que existen bolsillos de asociación espacial positiva. Es decir, que se tienen conglomerados de municipios de bajo desempeño educativo, o conglomerados de alto desempeño educativo. Los indicadores espaciales de asociación positiva (LISA) permiten identificar tales conglomerados y representarlos a través de un mapa de clústers. Los mapas de clústers en la figura 6 muestran aquellos municipios para los cuales los LISA calculados son significativos, esto es, son estadísticamente distintos de cero, y los clasifican de acuerdo al tipo de clúster al que pertenecen. Para determinar la significancia de los LISA se empleó un test no paramétrico, llamado test de permutaciones, utilizando un umbral de significancia del 5%.
Matemática y Lenguaje: mapas de clústers, 2012.
a) Matemática.
b) Lenguaje.
Notas: Cálculos propios con base en los datos del examen ICFES Saber 11. Para elaborar los presentes mapas de clústers se calculó la significancia estadística de los LISA por medio de un test de permutaciones, utilizando un umbral de significancia del 5% y 1.000 permutaciones.
Los mapas de clústers mencionados se generaron para cada prueba y para cado año. Sin embargo, dada la estabilidad de los clústers, solo se reproducen los mapas correspondientes al año 2012. Por ejemplo, en el caso de la prueba de matemática en la figura 6a, se observa que el clúster bajo-bajo (color azul oscuro), que representa los municipios en vecindarios de bajo desempeño educativo, coincide con el departamento de Chocó y se extiende hacia el sur sobre la región del Pacífico, e incluye una gran parte de la costa atlántica. Por el contrario, los conglomerados en el clúster alto-alto (color rojo oscuro), que representa los municipios en vecindarios de alto desempeño educativo, se ubican sobre la cordillera oriental, comprendiendo el norte del área metropolitana de Bogotá y varios municipios de Boyacá. También se incluyen el área metropolitana de Bucaramanga y varios municipios de norte de Santander en los alrededores de Pamplona. El sur del área metropolitana de Medellín y algunos municipios cercanos hacia el oriente de dicha ciudad completan este clúster.
En la prueba de Lenguaje, según la figura 6b, otro clúster importante de alto rendimiento educativo se ubica en el eje cafetero, el cual comprende municipios de Quindío, Risaralda y Caldas.
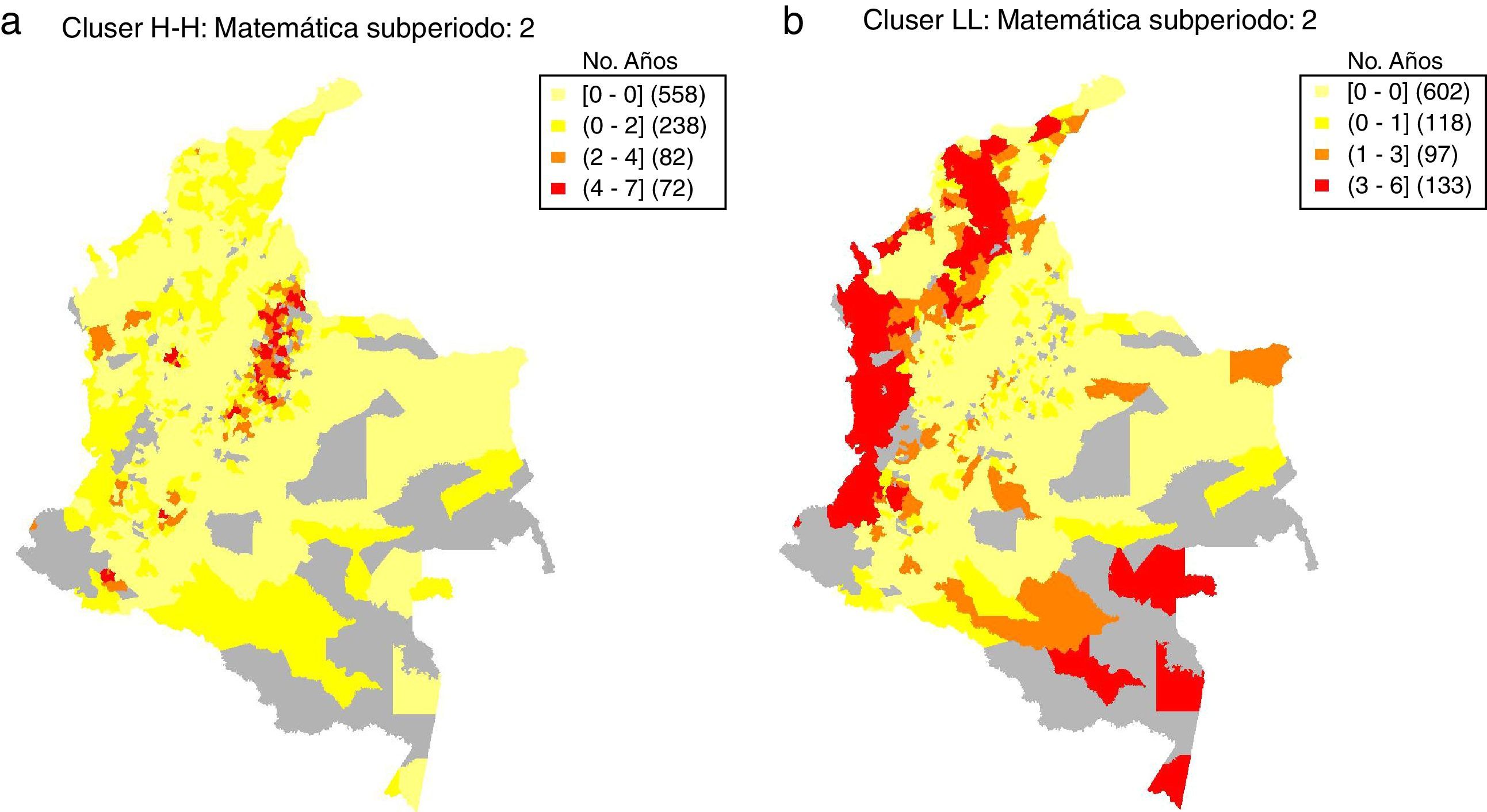
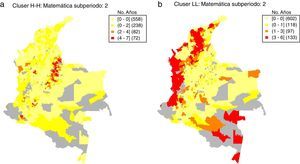
Para corroborar el patrón de estabilidad en las agrupaciones de municipios de acuerdo a su nivel de calidad educativa, se elaboran mapas que ilustran el nivel de persistencia a través del tiempo de los clústeres de municipios identificados. Los mapas de persistencia en las figuras 7 y 8 ofrecen otra mirada a los mapas de clústers elaborados con base en los LISA. Los mapas de persistencia muestran el número de años en los cuales un municipio fue clasificado en un clúster estadísticamente significativo, de alto o de bajo rendimiento educativo. Los mapas de persistencia en las figuras 7 y 8 corresponden solo al segundo subperiodo, para el cual se tienen más datos.
Matemática: mapas de persistencia.
a) Persistencia clústeres alto-alto.
b) Persistencia clústeres bajo-bajo.
Notas: Cálculos propios con base en los datos del Examen ICFES Saber 11. Los mapas de persistencia están basados en los mapas de clústers. En particular, los mapas de persistencia muestran el número de años que un municipio es clasificado en un clúster estadísticamente significativo de acuerdo a los LISA, utilizando en cada año un umbral de significancia del 5% y 1.000 permutaciones.
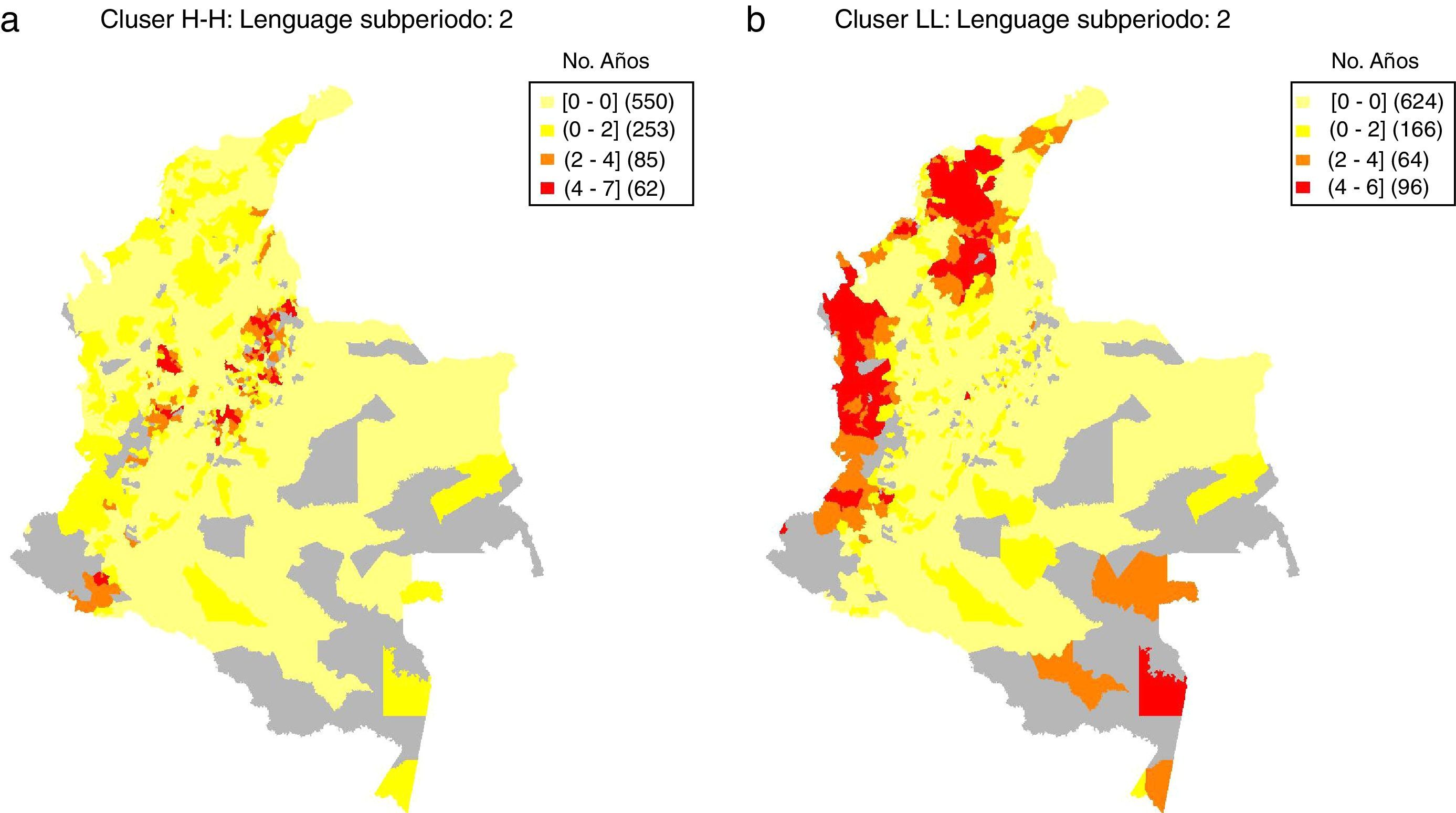
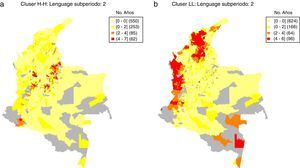
Lenguaje: mapas de persistencia.
a) Persistencia clústers alto-alto.
b) Persistencia clústers bajo-bajo.
Notas: Cálculos propios con base en los datos del examen ICFES Saber 11. Los mapas de persistencia están basados en los mapas de clústers. En particular, los mapas de persistencia muestran el número de veces que un municipio es clasificado en un clúster estadísticamente significativo de acuerdo a los LISA, utilizando en cada año un umbral de significancia del 5% y 1.000 permutaciones.
Por ejemplo, para el caso de la prueba de Lenguaje, en la figura 8a se muestra el mapa de persistencia de los clústers alto-alto, es decir, de los conglomerados de alto rendimiento educativo. Los municipios en rojo corresponden a aquellos que fueron clasificados en dicho clúster en 4 o más años (el subperiodo comprende 6 años, desde 2007 hasta 2012), es decir, más de la mitad de las veces. Resalta que en este caso se observa que el clúster de alto desempeño identificado en el eje cafetero pierde la dimensión que sugería el mapa de clústeres en la figura 6b; posiblemente este sea un clúster en formación. Por el contrario, la figura 8a confirma los demás clústers señalados: el norte del área metropolitana de Bogotá, el área metropolitana de Medellín y algunos municipios cercanos hacia el oriente de esa zona, el área metropolitana de Bucaramanga y algunos municipios cercanos a Pamplona.
El mapa de persistencia del clúster alto-alto en la prueba de Matemáticas en términos generales exhibe patrones similares (fig. 7a). No obstante, llama la atención el caso de Nariño (particularmente Pasto), donde se identifican uno o más municipios en un clúster persistente de alto rendimiento educativo.
En lo que concierne a los mapas de persistencia del clúster bajo-bajo, es decir, de las agrupaciones de bajo rendimiento educativo, la figura 8b muestra, para el caso de la prueba de Lenguaje, que la periferia en términos de calidad educativa municipal se corresponde claramente con el Pacífico colombiano y gran parte de la región caribe o atlántica. Estas zonas son clasificadas más de la mitad del tiempo como clústers de bajo desempeño educativo.
Es visible que los mapas de persistencia dan una mirada un poco más detallada de las diferencias regionales en el desempeño educativo municipal. De hecho, permiten traducir de manera directa las disparidades regionales en ese respecto a su dimensión geográfica o espacial. Es notorio que los municipios se agrupan en el espacio de acuerdo a su nivel de desempeño educativo, lo cual sugiere que el vecindario en el cual se encuentra un municipio puede tener algún tipo de incidencia sobre el nivel de desempeño educativo que puede alcanzar. Es posible que los patrones de distribución espacial del rendimiento educativo sean el resultado de otras causas subyacentes que comparten los territorios clasificados en uno u otro clúster. Y es claro también, de acuerdo a lo arrojado por los mapas de persistencia, que estos clústeres son estables en el tiempo, situación preocupante especialmente con respecto a las poblaciones de bajo rendimiento educativo. Por tanto, conviene analizar el grado en el cual la ubicación relativa de un municipio, dada por las características de su vecindario, afecta sus chances de escalar en términos de calidad educativa. Con este fin, se utilizan las matrices de Markov condicionadas espacialmente, cuyos resultados se exponen a continuación.
4.6Matrices de Markov espaciales y distribuciones ergódicasEn este apartado se exponen los resultados proporcionados por las matrices de Markov espacialmente condicionadas. El cálculo de estas matrices implica conocer el rendimiento promedio del vecindario de cada municipio. Con tal propósito se emplea una matriz de pesos espaciales estandarizada por filas, construida a través del criterio de vecindad por esferas de influencia (Spheres of Influence, ver Bivand et al., 2008, p. 246), explicado en la sección metodológica. Con esta matriz es posible calcular el rendimiento promedio del vecindario de cada municipio. El rendimiento promedio de cada vecindario luego es clasificado en 5 cuantiles, que corresponden a las 5 categorías de desempeño educativo empleadas en este artículo (que van desde muy bajo hasta muy alto).
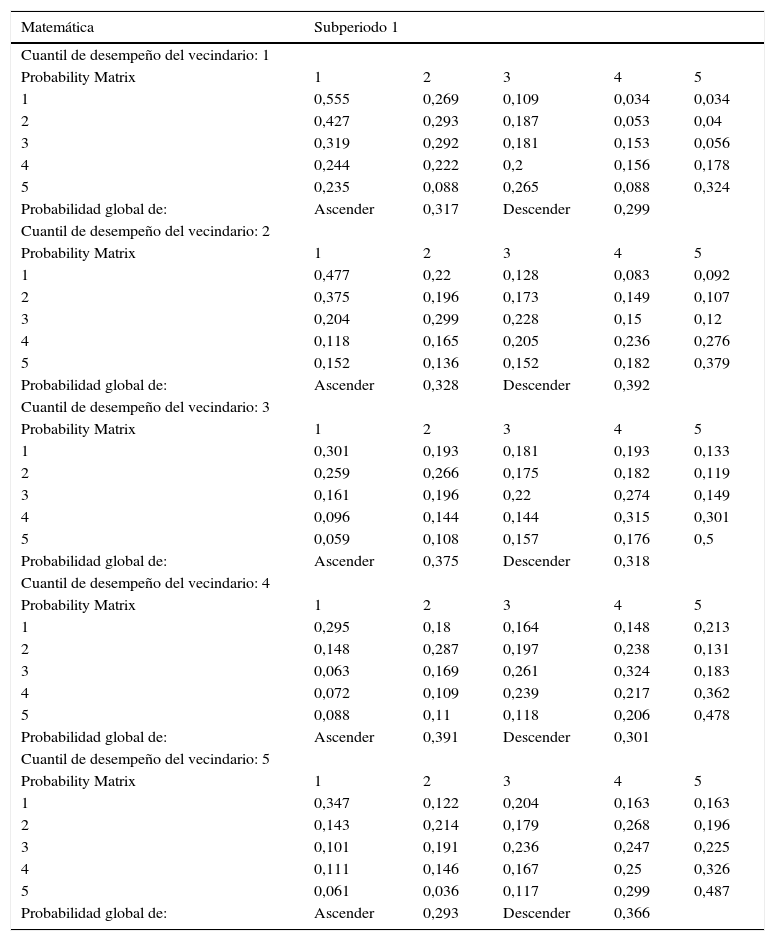
4.7MatemáticasEn consistencia con lo hallado a través de las kernel estocásticas, la matriz de Markov espacial para el primer subperiodo (tabla 6a) manifiesta una tendencia general al descenso del rendimiento educativo municipal. Sin embargo, al tener en cuenta la situación del vecindario surgen ciertas particularidades: para los municipios ubicados en vecindarios de muy bajo desempeño educativo (vecinos en el cuantil 1) se encuentra, por ejemplo, que la probabilidad que tiene un municipio de muy alto rendimiento educativo de descender a los cuantiles inferiores (de muy bajo y bajo desempeño) es del 32,3%. En contraste, un municipio de muy alto desempeño educativo ubicado en un vecindario de la misma característica tiene una probabilidad de descender a los 2 cuantiles inferiores de 9,7%. Es decir, estar ubicado en un vecindario de alto rendimiento corta apreciablemente las chances de retroceder, en tanto que la probabilidad de descender a los 2 cuantiles inferiores es bastante menor en relación con los municipios ubicados en vecindarios con una calidad educativa más baja.
Prueba Matemática: matrices de probabilidad condicionadas espacialmente
| Matemática | Subperiodo 1 | ||||
|---|---|---|---|---|---|
| Cuantil de desempeño del vecindario: 1 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,555 | 0,269 | 0,109 | 0,034 | 0,034 |
| 2 | 0,427 | 0,293 | 0,187 | 0,053 | 0,04 |
| 3 | 0,319 | 0,292 | 0,181 | 0,153 | 0,056 |
| 4 | 0,244 | 0,222 | 0,2 | 0,156 | 0,178 |
| 5 | 0,235 | 0,088 | 0,265 | 0,088 | 0,324 |
| Probabilidad global de: | Ascender | 0,317 | Descender | 0,299 | |
| Cuantil de desempeño del vecindario: 2 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,477 | 0,22 | 0,128 | 0,083 | 0,092 |
| 2 | 0,375 | 0,196 | 0,173 | 0,149 | 0,107 |
| 3 | 0,204 | 0,299 | 0,228 | 0,15 | 0,12 |
| 4 | 0,118 | 0,165 | 0,205 | 0,236 | 0,276 |
| 5 | 0,152 | 0,136 | 0,152 | 0,182 | 0,379 |
| Probabilidad global de: | Ascender | 0,328 | Descender | 0,392 | |
| Cuantil de desempeño del vecindario: 3 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,301 | 0,193 | 0,181 | 0,193 | 0,133 |
| 2 | 0,259 | 0,266 | 0,175 | 0,182 | 0,119 |
| 3 | 0,161 | 0,196 | 0,22 | 0,274 | 0,149 |
| 4 | 0,096 | 0,144 | 0,144 | 0,315 | 0,301 |
| 5 | 0,059 | 0,108 | 0,157 | 0,176 | 0,5 |
| Probabilidad global de: | Ascender | 0,375 | Descender | 0,318 | |
| Cuantil de desempeño del vecindario: 4 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,295 | 0,18 | 0,164 | 0,148 | 0,213 |
| 2 | 0,148 | 0,287 | 0,197 | 0,238 | 0,131 |
| 3 | 0,063 | 0,169 | 0,261 | 0,324 | 0,183 |
| 4 | 0,072 | 0,109 | 0,239 | 0,217 | 0,362 |
| 5 | 0,088 | 0,11 | 0,118 | 0,206 | 0,478 |
| Probabilidad global de: | Ascender | 0,391 | Descender | 0,301 | |
| Cuantil de desempeño del vecindario: 5 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,347 | 0,122 | 0,204 | 0,163 | 0,163 |
| 2 | 0,143 | 0,214 | 0,179 | 0,268 | 0,196 |
| 3 | 0,101 | 0,191 | 0,236 | 0,247 | 0,225 |
| 4 | 0,111 | 0,146 | 0,167 | 0,25 | 0,326 |
| 5 | 0,061 | 0,036 | 0,117 | 0,299 | 0,487 |
| Probabilidad global de: | Ascender | 0,293 | Descender | 0,366 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. La tabla está compuesta de 5 submatrices, cada una de la cuales muestra la probabilidad de transicionar de una categoría en el periodo inicial (en las filas) a una categoría en el periodo final (en las columnas), de acuerdo a la categoría de calidad educativa del vecindario.
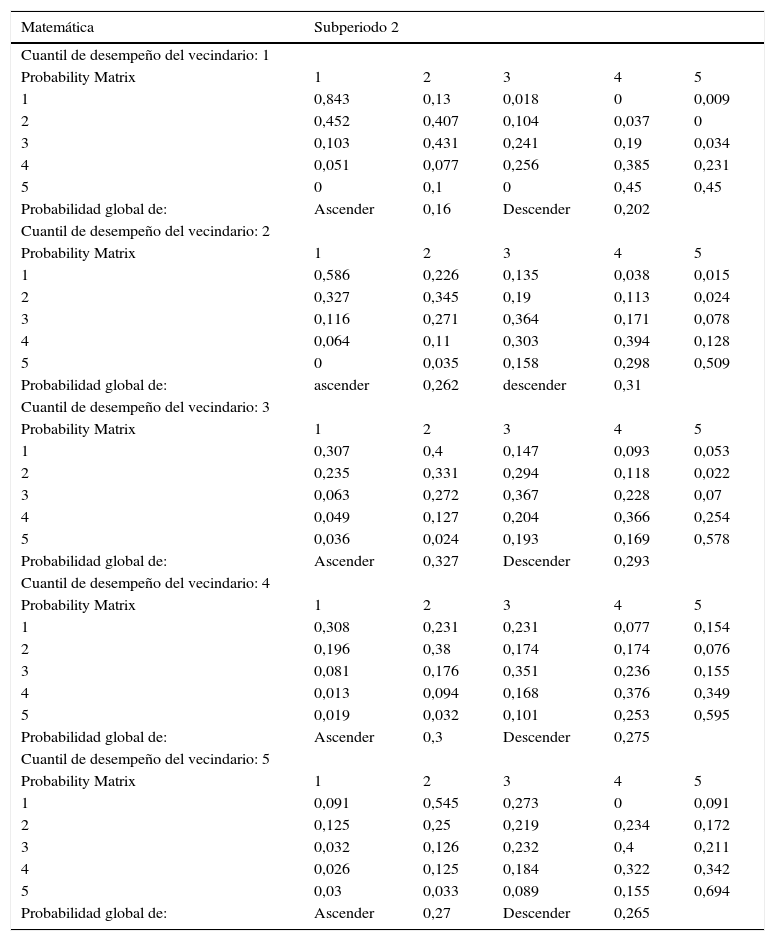
En lo que atañe al segundo subperiodo de análisis, el análisis de las kernel sugería un proceso de divergencia, por un aumento en la dispersión de la distribución. La matriz de Markov espacial respectiva en la tabla 6b añade nuevos detalles: este proceso de divergencia puede estar asociado a un alejamiento de los 2 extremos de la distribución, es decir, a un posible fenómeno de clubes de convergencia. En este sentido, es posible hablar al menos de 2 clubes de convergencia, pues la probabilidad global de descender cuando el vecindario está en uno de los 2 cuantiles inferiores de desempeño supera la probabilidad de ascender: esto es, hay convergencia hacia un desempeño educativo bajo cuando se está cerca de un vecindario de tal característica. Asimismo, cuando se está en un vecindario de desempeño medio o alto, la probabilidad global de ascender supera a la de descender. Por ejemplo, un municipio de calidad educativa intermedia (cuantil 3) ubicado en un vecindario de muy alto desempeño educativo tiene una probabilidad del 21,1% de escalar a este nivel, frente a una probabilidad del 3,4% si ese mismo municipio estuviese en un vecindario del primer cuantil.
Prueba Matemática: matrices de probabilidad condicionadas espacialmente
| Matemática | Subperiodo 2 | ||||
|---|---|---|---|---|---|
| Cuantil de desempeño del vecindario: 1 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,843 | 0,13 | 0,018 | 0 | 0,009 |
| 2 | 0,452 | 0,407 | 0,104 | 0,037 | 0 |
| 3 | 0,103 | 0,431 | 0,241 | 0,19 | 0,034 |
| 4 | 0,051 | 0,077 | 0,256 | 0,385 | 0,231 |
| 5 | 0 | 0,1 | 0 | 0,45 | 0,45 |
| Probabilidad global de: | Ascender | 0,16 | Descender | 0,202 | |
| Cuantil de desempeño del vecindario: 2 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,586 | 0,226 | 0,135 | 0,038 | 0,015 |
| 2 | 0,327 | 0,345 | 0,19 | 0,113 | 0,024 |
| 3 | 0,116 | 0,271 | 0,364 | 0,171 | 0,078 |
| 4 | 0,064 | 0,11 | 0,303 | 0,394 | 0,128 |
| 5 | 0 | 0,035 | 0,158 | 0,298 | 0,509 |
| Probabilidad global de: | ascender | 0,262 | descender | 0,31 | |
| Cuantil de desempeño del vecindario: 3 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,307 | 0,4 | 0,147 | 0,093 | 0,053 |
| 2 | 0,235 | 0,331 | 0,294 | 0,118 | 0,022 |
| 3 | 0,063 | 0,272 | 0,367 | 0,228 | 0,07 |
| 4 | 0,049 | 0,127 | 0,204 | 0,366 | 0,254 |
| 5 | 0,036 | 0,024 | 0,193 | 0,169 | 0,578 |
| Probabilidad global de: | Ascender | 0,327 | Descender | 0,293 | |
| Cuantil de desempeño del vecindario: 4 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,308 | 0,231 | 0,231 | 0,077 | 0,154 |
| 2 | 0,196 | 0,38 | 0,174 | 0,174 | 0,076 |
| 3 | 0,081 | 0,176 | 0,351 | 0,236 | 0,155 |
| 4 | 0,013 | 0,094 | 0,168 | 0,376 | 0,349 |
| 5 | 0,019 | 0,032 | 0,101 | 0,253 | 0,595 |
| Probabilidad global de: | Ascender | 0,3 | Descender | 0,275 | |
| Cuantil de desempeño del vecindario: 5 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,091 | 0,545 | 0,273 | 0 | 0,091 |
| 2 | 0,125 | 0,25 | 0,219 | 0,234 | 0,172 |
| 3 | 0,032 | 0,126 | 0,232 | 0,4 | 0,211 |
| 4 | 0,026 | 0,125 | 0,184 | 0,322 | 0,342 |
| 5 | 0,03 | 0,033 | 0,089 | 0,155 | 0,694 |
| Probabilidad global de: | Ascender | 0,27 | Descender | 0,265 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. La tabla está compuesta de 5 submatrices, cada una de la cuales muestra la probabilidad de transicionar de una categoría en el periodo inicial (en las filas) a una categoría en el periodo final (en las columnas), de acuerdo a la categoría de calidad educativa del vecindario.
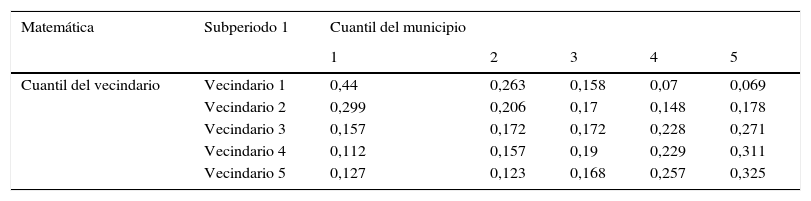
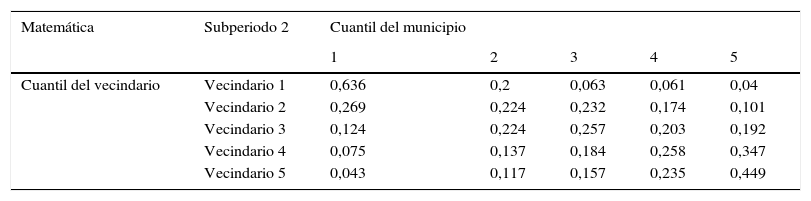
En lo que atañe a las distribuciones ergódicas, si se hubiesen mantenido las condiciones del primer subperiodo, el 70,3% de los municipios en un vecindario del cuantil inferior terminarían ubicados en los 2 cuantiles inferiores (ver primera fila de la tabla 7a). En el segundo subperiodo, la nueva distribución ergódica apunta a que esta cifra se ubicaría en un 83,6% (tabla 7b). Asimismo, bajo las condiciones del primer subperiodo, el 58,2% de los municipios en un vecindario en el cuantil superior se ubicarían en los 2 cuantiles de alto desempeño educativo. Bajo las condiciones del segundo subperiodo, la distribución de largo plazo apunta a que esta cifra pasaría a un 68,4%. De esta manera, se ratifica la sugerencia de clubes de convergencia que plantean las matrices de Markov analizadas.
Matemática: distribución ergódica del proceso markoviano espacial, subperiodo 1
| Matemática | Subperiodo 1 | Cuantil del municipio | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Cuantil del vecindario | Vecindario 1 | 0,44 | 0,263 | 0,158 | 0,07 | 0,069 |
| Vecindario 2 | 0,299 | 0,206 | 0,17 | 0,148 | 0,178 | |
| Vecindario 3 | 0,157 | 0,172 | 0,172 | 0,228 | 0,271 | |
| Vecindario 4 | 0,112 | 0,157 | 0,19 | 0,229 | 0,311 | |
| Vecindario 5 | 0,127 | 0,123 | 0,168 | 0,257 | 0,325 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. Cada fila de la tabla representa las proporciones en las cuales se distribuirían los municipios entre las 5 categorías de desempeño educativo, de acuerdo al vecindario en el que se ubican, de mantenerse vigente la estructura de probabilidades en la tabla 6a.
Matemática: distribución ergódica del proceso markoviano espacial, subperiodo 2
| Matemática | Subperiodo 2 | Cuantil del municipio | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Cuantil del vecindario | Vecindario 1 | 0,636 | 0,2 | 0,063 | 0,061 | 0,04 |
| Vecindario 2 | 0,269 | 0,224 | 0,232 | 0,174 | 0,101 | |
| Vecindario 3 | 0,124 | 0,224 | 0,257 | 0,203 | 0,192 | |
| Vecindario 4 | 0,075 | 0,137 | 0,184 | 0,258 | 0,347 | |
| Vecindario 5 | 0,043 | 0,117 | 0,157 | 0,235 | 0,449 |
Cálculos propios con base en los datos del examen ICFES Saber 11. Cada fila de la tabla representa las proporciones en las cuales se distribuirían los municipios entre las 5 categorías de desempeño educativo, de acuerdo al vecindario en el que se ubican, de mantenerse vigente la estructura de probabilidades en la tabla 6b.
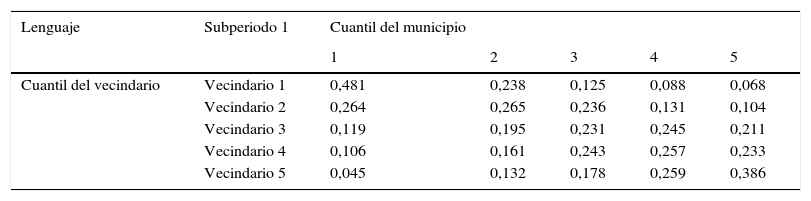
La tabla 8a, para el primer subperiodo, muestra una tendencia general al ascenso para los municipios ubicados en un vecindario de muy bajo desempeño educativo. En los demás casos se halla una leve tendencia al descenso, puesto que las probabilidades de descender tienden a superar a las de escalar. Sin embargo, nuevamente, estar ubicado en un vecindario de alto o muy alto desempeño educativo reduce ostensiblemente las chances de que este descenso se dé hacia las categorías inferiores de desempeño educativo, teniendo entonces un vecindario de buenas características un efecto amortiguador del descenso.
Prueba Lenguaje: matrices de probabilidad condicionadas espacialmente
| Lenguaje | Subperiodo 1 | ||||
|---|---|---|---|---|---|
| Cuantil de desempeño del vecindario: 1 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,747 | 0,193 | 0,036 | 0,018 | 0,006 |
| 2 | 0,39 | 0,353 | 0,147 | 0,081 | 0,029 |
| 3 | 0,116 | 0,275 | 0,319 | 0,203 | 0,087 |
| 4 | 0,093 | 0,093 | 0,302 | 0,326 | 0,186 |
| 5 | 0,091 | 0,273 | 0,091 | 0,091 | 0,455 |
| Probabilidad global de: | Ascender | 0,249 | Descender | 0,181 | |
| Cuantil de desempeño del vecindario: 2 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,611 | 0,236 | 0,104 | 0,042 | 0,007 |
| 2 | 0,269 | 0,352 | 0,269 | 0,077 | 0,033 |
| 3 | 0,096 | 0,32 | 0,4 | 0,128 | 0,056 |
| 4 | 0,038 | 0,152 | 0,253 | 0,291 | 0,266 |
| 5 | 0,038 | 0,132 | 0,094 | 0,302 | 0,434 |
| Probabilidad global de: | Ascender | 0,29 | Descender | 0,285 | |
| Cuantil de desempeño del vecindario: 3 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,431 | 0,294 | 0,098 | 0,078 | 0,098 |
| 2 | 0,135 | 0,302 | 0,317 | 0,175 | 0,071 |
| 3 | 0,101 | 0,264 | 0,331 | 0,236 | 0,068 |
| 4 | 0,047 | 0,121 | 0,235 | 0,356 | 0,242 |
| 5 | 0,03 | 0,051 | 0,111 | 0,283 | 0,525 |
| Probabilidad global de: | Ascender | 0,316 | Descender | 0,311 | |
| Cuantil de desempeño del vecindario: 4 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,5 | 0,211 | 0,237 | 0,026 | 0,026 |
| 2 | 0,129 | 0,318 | 0,294 | 0,2 | 0,059 |
| 3 | 0,072 | 0,209 | 0,331 | 0,295 | 0,094 |
| 4 | 0,042 | 0,091 | 0,273 | 0,327 | 0,267 |
| 5 | 0,017 | 0,057 | 0,085 | 0,284 | 0,557 |
| Probabilidad global de: | Ascender | 0,272 | Descender | 0,323 | |
| Cuantil de desempeño del vecindario: 5 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,238 | 0,238 | 0,238 | 0,19 | 0,095 |
| 2 | 0,132 | 0,338 | 0,324 | 0,118 | 0,088 |
| 3 | 0,046 | 0,241 | 0,287 | 0,241 | 0,185 |
| 4 | 0,026 | 0,066 | 0,212 | 0,391 | 0,305 |
| 5 | 0,004 | 0,043 | 0,047 | 0,236 | 0,669 |
| Probabilidad global de: | Ascender | 0,239 | Descender | 0,282 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. La tabla está compuesta de 5 submatrices, cada una de la cuales muestra la probabilidad de transicionar de una categoría en el periodo inicial (en las filas) a una categoría en el periodo final (en las columnas), de acuerdo a la categoría de calidad educativa del vecindario.
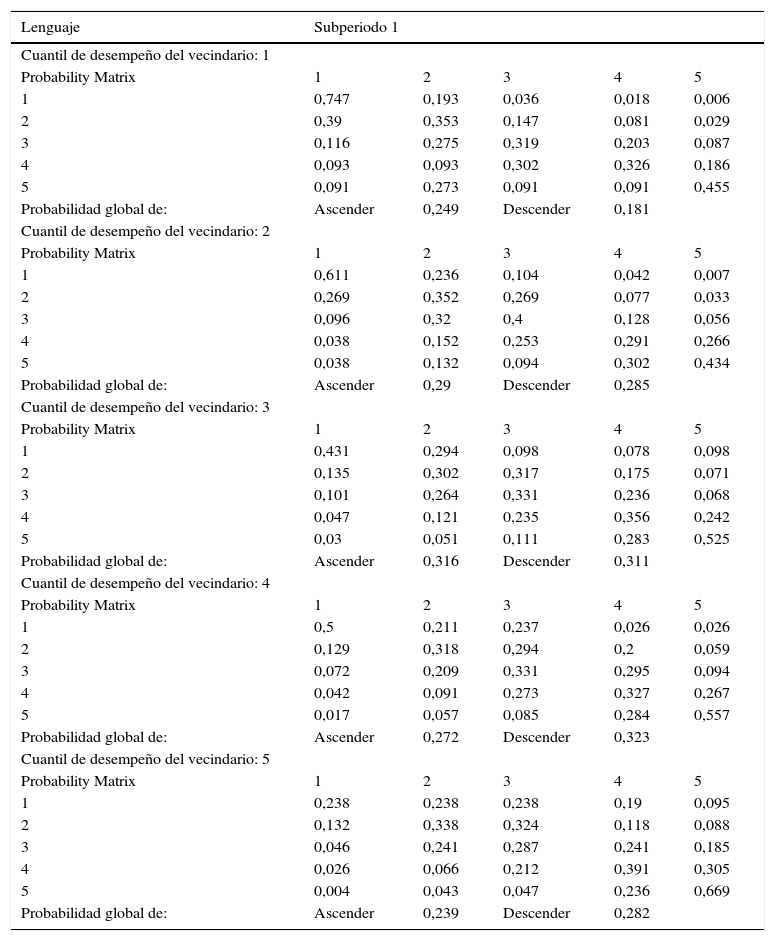
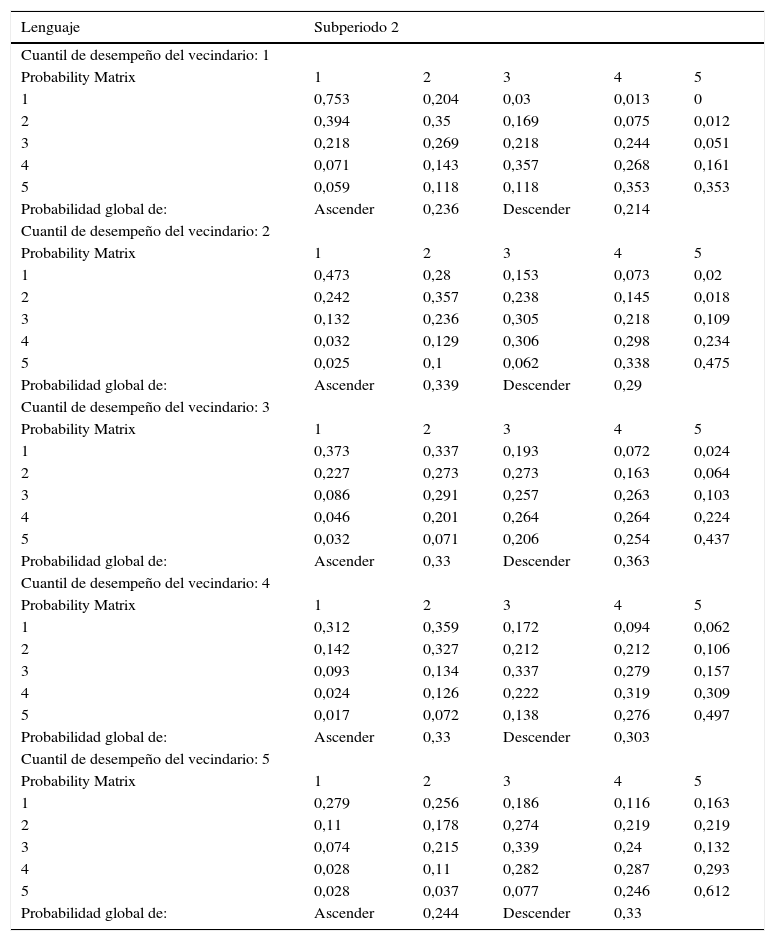
En el segundo subperiodo, en la tabla 8b, no se identifica que predomine una dirección de movimiento en particular, en línea con la situación general de estabilidad que mostraba el análisis de las kernel. Sin embargo, de acuerdo a las distribuciones ergódicas en la tabla 9b correspondientes a esta prueba, se identifica un posible proceso de clubes de convergencia. En efecto, para los municipios ubicados en un vecindario de muy bajo desempeño educativo en el largo plazo se manifiesta una tendencia al predominio de los 2 cuantiles inferiores. En concreto, en el largo plazo el 51,8%+23,8%=75,6% de los municipios se ubicarían en esos 2 cuantiles, si su vecindario está en el cuantil inferior. En contraste, para los vecindarios de muy alto desempeño educativo (cuantil 5) se tiene que el 24,3%+35,4%=59,5% de los municipios se establecerían en los 2 cuantiles superiores (tabla 9a).
Prueba Lenguaje: matrices de probabilidad condicionadas espacialmente
| Lenguaje | Subperiodo 2 | ||||
|---|---|---|---|---|---|
| Cuantil de desempeño del vecindario: 1 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,753 | 0,204 | 0,03 | 0,013 | 0 |
| 2 | 0,394 | 0,35 | 0,169 | 0,075 | 0,012 |
| 3 | 0,218 | 0,269 | 0,218 | 0,244 | 0,051 |
| 4 | 0,071 | 0,143 | 0,357 | 0,268 | 0,161 |
| 5 | 0,059 | 0,118 | 0,118 | 0,353 | 0,353 |
| Probabilidad global de: | Ascender | 0,236 | Descender | 0,214 | |
| Cuantil de desempeño del vecindario: 2 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,473 | 0,28 | 0,153 | 0,073 | 0,02 |
| 2 | 0,242 | 0,357 | 0,238 | 0,145 | 0,018 |
| 3 | 0,132 | 0,236 | 0,305 | 0,218 | 0,109 |
| 4 | 0,032 | 0,129 | 0,306 | 0,298 | 0,234 |
| 5 | 0,025 | 0,1 | 0,062 | 0,338 | 0,475 |
| Probabilidad global de: | Ascender | 0,339 | Descender | 0,29 | |
| Cuantil de desempeño del vecindario: 3 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,373 | 0,337 | 0,193 | 0,072 | 0,024 |
| 2 | 0,227 | 0,273 | 0,273 | 0,163 | 0,064 |
| 3 | 0,086 | 0,291 | 0,257 | 0,263 | 0,103 |
| 4 | 0,046 | 0,201 | 0,264 | 0,264 | 0,224 |
| 5 | 0,032 | 0,071 | 0,206 | 0,254 | 0,437 |
| Probabilidad global de: | Ascender | 0,33 | Descender | 0,363 | |
| Cuantil de desempeño del vecindario: 4 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,312 | 0,359 | 0,172 | 0,094 | 0,062 |
| 2 | 0,142 | 0,327 | 0,212 | 0,212 | 0,106 |
| 3 | 0,093 | 0,134 | 0,337 | 0,279 | 0,157 |
| 4 | 0,024 | 0,126 | 0,222 | 0,319 | 0,309 |
| 5 | 0,017 | 0,072 | 0,138 | 0,276 | 0,497 |
| Probabilidad global de: | Ascender | 0,33 | Descender | 0,303 | |
| Cuantil de desempeño del vecindario: 5 | |||||
| Probability Matrix | 1 | 2 | 3 | 4 | 5 |
| 1 | 0,279 | 0,256 | 0,186 | 0,116 | 0,163 |
| 2 | 0,11 | 0,178 | 0,274 | 0,219 | 0,219 |
| 3 | 0,074 | 0,215 | 0,339 | 0,24 | 0,132 |
| 4 | 0,028 | 0,11 | 0,282 | 0,287 | 0,293 |
| 5 | 0,028 | 0,037 | 0,077 | 0,246 | 0,612 |
| Probabilidad global de: | Ascender | 0,244 | Descender | 0,33 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. La tabla está compuesta de 5 submatrices, cada una de la cuales muestra la probabilidad de transicionar de una categoría en el periodo inicial (en las filas) a una categoría en el periodo final (en las columnas), de acuerdo a la categoría de calidad educativa del vecindario.
Lenguaje: distribución ergódica del proceso markoviano espacial, subperiodo 2
| Lenguaje | Subperiodo 2 | Cuantil del municipio | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
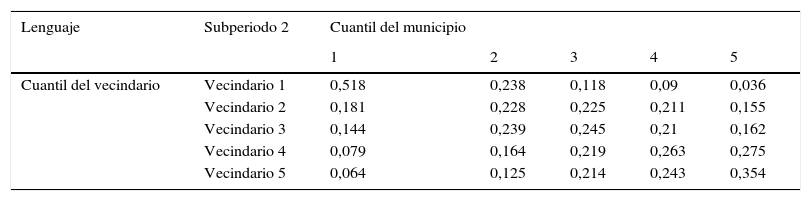
| Cuantil del vecindario | Vecindario 1 | 0,518 | 0,238 | 0,118 | 0,09 | 0,036 |
| Vecindario 2 | 0,181 | 0,228 | 0,225 | 0,211 | 0,155 | |
| Vecindario 3 | 0,144 | 0,239 | 0,245 | 0,21 | 0,162 | |
| Vecindario 4 | 0,079 | 0,164 | 0,219 | 0,263 | 0,275 | |
| Vecindario 5 | 0,064 | 0,125 | 0,214 | 0,243 | 0,354 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. Cada fila de la tabla representa las proporciones en las cuales se distribuirían los municipios entre las 5 categorías de desempeño educativo, de acuerdo al vecindario en el que se ubican, de mantenerse vigente la estructura de probabilidades en la tabla 8b.
Lenguaje: distribución ergódica del proceso markoviano espacial, subperiodo 1
| Lenguaje | Subperiodo 1 | Cuantil del municipio | ||||
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| Cuantil del vecindario | Vecindario 1 | 0,481 | 0,238 | 0,125 | 0,088 | 0,068 |
| Vecindario 2 | 0,264 | 0,265 | 0,236 | 0,131 | 0,104 | |
| Vecindario 3 | 0,119 | 0,195 | 0,231 | 0,245 | 0,211 | |
| Vecindario 4 | 0,106 | 0,161 | 0,243 | 0,257 | 0,233 | |
| Vecindario 5 | 0,045 | 0,132 | 0,178 | 0,259 | 0,386 |
Cálculos propios con base en los datos del Examen ICFES Saber 11. Cada fila de la tabla representa las proporciones en las cuales se distribuirían los municipios entre las 5 categorías de desempeño educativo, de acuerdo al vecindario en el que se ubican, de mantenerse vigente la estructura de probabilidades en la tabla 8a.
La implementación de las distintas técnicas estadísticas arroja resultados que sirven de referente no solo para aportar elementos en el direccionamiento de políticas públicas en torno a la educación, sino para aportar al debate académico sobre economía de la educación en el país, el cual no se muestra prolífico respecto al tema de convergencia en rendimiento educativo.
Con el fin de sortear el problema de la no comparabilidad anual de las pruebas debido a los cambios metodológicos, el análisis se llevó a cabo mediante subperiodos, habiendo un mayor halo de incertidumbre alrededor de los resultados obtenidos para el primer subperiodo de análisis (2000-2004), pues según la entidad encargada de aplicar las pruebas, hay problemas de anclaje en dichos años que afectan la comparabilidad intertemporal. Sin embargo, para el segundo subperiodo (2007-2012) no existe tal problema, por lo cual los resultados obtenidos en relación con el segundo subperiodo gozan de mayor confiabilidad.
En línea con la literatura sobre disparidades regionales del ingreso en Colombia, este trabajo evidencia de igual manera la existencia de unas fuertes disparidades municipales en relación con el rendimiento educativo para las pruebas analizadas. Las kernel estocásticas permitieron concluir que en cada subperiodo los municipios de Colombia no experimentaron convergencia en materia de calidad educativa municipal medida a través de los exámenes de lenguaje y matemática. En estrecha relación con estos resultados, la aplicación de las matrices de Markov clásicas sugieren una persistencia significativa de las disparidades en los rangos extremos. En general, las matrices de Markov, tanto las clásicas como las espacialmente condicionadas, sugieren una alta persistencia en los cuantiles de muy bajo y muy alto desempeño educativo, mientras que hay una alta movilidad en los intervalos interiores, lo cual se puede interpretar como un indicativo de que las mayores barreras a la movilidad están en los extremos, no en el centro de la distribución.
Una de las hipótesis que ha enmarcado el curso de la investigación tiene que ver con la dependencia espacial de la calidad educativa de los municipios, es decir, el rendimiento educativo por prueba de un municipio está explicado por el de sus vecinos. Se calcularon para tal propósito estadísticos de Moran, confirmando que en todas las pruebas existe un patrón espacial significativo que debe ser capturado en el análisis; por otro lado, y dada esta dependencia espacial, fueron realizados mapas de clúster por pruebas (mapas LISA), y mapas de persistencia. En particular, los mapas de persistencia sugieren que los clústeres identificados son estables en el tiempo. Tal estabilidad de los clústeres identificados constituye una pieza de evidencia adicional acerca de ausencia de convergencia en lo que atañe a la calidad de la educación secundaria. En términos generales, los resultados de estos mapas muestran una suerte de patrón centro-periferia en los cuales los conglomerados de municipios de bajo rendimiento educativo se localizan en la región pacífica y la sabana atlántica.
Por su parte, con el fin de capturar el efecto del espacio sobre las probabilidades encontradas en las matrices de Markov, se estiman las matrices espaciales de Markov (Spatial Markov Matrices), como en Rey (2001). Fundamentalmente, los resultados sugieren que la ubicación de un municipio determina las probabilidades de que este escale o descienda en materia de calidad educativa; por ejemplo, se encuentra que tener vecinos de alto rendimiento educativo supone una reducción en las probabilidades de descender en la distribución, así como un aumento en las respectivas probabilidades de ascender. Igualmente, se halla evidencia que sugiere la existencia de clubes de convergencia en lo que atañe a los municipios ubicados en vecindarios de los cuantiles extremos.
Los anteriores resultados dan cuenta de las características de la distribución espacial del rendimiento educativo por prueba para los municipios del país. Entender que el rendimiento educativo de los municipios del país comporta determinantes espaciales claros, como esta investigación muestra, ayuda a la ejecución de políticas públicas plenamente conscientes de la manera en que interactúan los municipios y en la cual puede tratarse el problema de clubes de convergencia de bajo capital humano, o cómo un municipio puede realmente aprovechar las características de su ubicación para establecer mejoras en el rendimiento educativo de sus estudiantes.
Evidentemente, el análisis AEDE y las matrices de Markov espacialmente condicionadas señalan zonas críticas, que presentan factores subyacentes que afectan sus posibilidades de escalar en la distribución del rendimiento educativo, y que en ese sentido una intervención efectiva requiere un esfuerzo proporcionalmente mayor en relación con aquellas zonas ajenas a los vecindarios de bajo desempeño educativo, puesto que las probabilidades de escalar tienen una relación directa con el nivel de desempeño educativo del vecindario y la posición del municipio en la distribución. De esta manera, el presente estudio aporta elementos para: 1)un criterio de priorización de las intervenciones gubernamentales para incrementar el rendimiento educativo, y 2)un criterio para determinar la proporcionalidad de la intervención, puesto que evidentemente en aquellos vecindarios de bajo desempeño educativo la magnitud del esfuerzo para incrementar el desempeño educativo debe ser bastante superior en relación con aquellos municipios ubicados en vecindarios de alto o muy alto desempeño educativo.
FinanciaciónProyecto financiado por el ICFES, en el marco de sus convocatorias a grupos de investigación.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Se extiende un agradecimiento al ICFES y a la Universidad Nacional de Colombia por su apoyo y financiación para la elaboración de la investigación de la cual se deriva este trabajo.