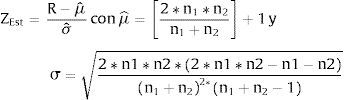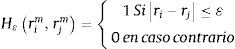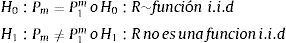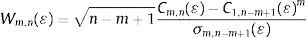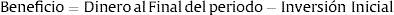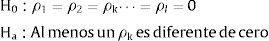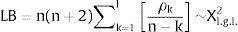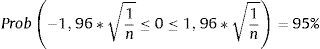El presente trabajo tiene como objetivo comprobar la eficiencia débil en los 5 principales mercados bursátiles de Latinoamérica, usando 2 enfoques; primero se evalúa la normalidad de las series mediante las estadísticas básicas, el test Jarque-Bera y la prueba de bondad de ajuste de la chi-cuadrado; en segundo lugar, se contrasta la caminata aleatoria (RW) de los activos en sus versiones RW1 (test Rachas y test BDS), RW2 (filtros de Alexander con algoritmos genéticos) y RW3 (Test Ljung-Box e Intervalo de Bartlett); encontrando que las 5 principales economías latinoamericanas han experimentado un cambio de no eficiencia a eficiencia en los últimos años de acuerdo con el siguiente orden cronológico: México (2007), Brasil (2008), Colombia (2008), Chile (2011) y Perú (2012).
This paper aims to test weak-form efficiency in the top five Latin American stock markets, using two approaches. Firstly, by evaluating the normality of the series using basic statistics, then by using the Jarque-Bera test and Chi-Square goodness of fit test, contrasting the RW1 (Runs test and BDS test), RW2 (Alexander filters with genetic algorithms) and RW3 (Ljung-Box test and Bartlett Interval) of the random walk (RW) of the assets. It was found that the five major Latin American economies studied have experienced a change from non-efficiency to market efficiency in recent years, according to the following chronological order: Mexico (2007), Brazil (2008), Colombia (2008), Chile (2011) and Peru (2012).
O presente trabalho tem como objectivo comprovar a fraca eficácia nos cinco principais mercados bolsistas da América Latina, usando duas abordagens; primeiro avalia-se a normalidade das séries através das estatísticas básicas, o teste Jarque-Bera e a avaliação da qualidade do ajuste Qui-quadrado; em segundo lugar, contrasta-se o percurso aleatório (RW) dos activos e suas versões RW1 (teste Rachas e teste BDS), RW2 (filtros de Alexander com algoritmos genéticos) e RW3 (Test Ljung-Box e Intervalo de Bartlett); economias latino-americanas experimentaram uma mudança de não eficácia a eficácia nos últimos anos de acordo com a seguinte ordem cronológica: México (2007), Brasil (2008), Colômbia (2008), Chile (2011) e Peru (2012).
La definición de mercado eficiente está asociado al concepto de igualdad de condiciones planteado por el matemático italiano Cardano (1565) en su obra The book on games of chance, como un principio fundamental de los juegos de azar. Trasladando este concepto a los mercados bursátiles, podría decirse que es la idea subyacente de la teoría de mercados bursátiles eficientes, en el sentido de que la igualdad de condiciones de tipo informacional es lo que hace que el mercado de valores sea «un juego justo», en el cual ningún agente pueda sistemáticamente obtener ganancias extraordinarias a partir de cualquier tipo de información. La definición moderna de mercado eficiente está fundamentada en los aportes de autores como Bachelier (1900), Samuelson (1965), Mandelbrot (1963a, 1963b, 1966); Malkiel (1992) y Fama (1965, 1991, 1998), quienes en términos generales plantean que un mercado es eficiente cuando en él se cuenta con la suficiente liquidez y racionalidad económica por parte de los agentes, como para que cualquier tipo de información relevante sea absorbida por los precios de los activos en forma instantánea, generando un comportamiento aleatorio en ellos, lo que hace imposible su pronóstico sistemático.
En los últimos años, se ha experimentado en América Latina un considerable incremento de la inversión directa extranjera, originado principalmente por 2 sinergias; por un lado, el fuerte crecimiento de la explotación de recursos naturales e infraestructura en la región por parte de países como Estados Unidos (17%), Holanda (13%), China (9%), Canadá (4%) y España (4%), tal como lo revela la CEPAL (2011); por otro lado, la crisis económica actual originada por la caída de las subprimes en Estados Unidos en el 2008, ha propiciado que inversionistas internacionales vean en Latinoamérica un escenario prometedor de generación de riqueza (FMI, 2010). Como consecuencia de este auge económico, se han incrementado los flujos brutos de capital, experimentando en la región una profundización del proceso bidireccional de integración en el mercado financiero internacional (Banco Mundial, 2012).
Esta dinámica bursátil en Latinoamérica justifica la pregunta ¿cuál ha sido el comportamiento de la eficiencia de los mercados bursátiles de América Latina en la última década?, teniendo en cuenta que los modelos de valoración de activos como el Capital Asset Pricing Model y el Arbitrage Pricing Theory, parten del supuesto de que los mercados son eficientes. Para responder esta pregunta, se realiza inicialmente una revisión de la literatura a nivel de Latinoamérica, encontrando que se han realizado estudios de eficiencia en los índices generales de los mercados, mas no de los principales activos en el interior de ellos; además, en dichos estudios solo se evalúan periodos completos de estudio o subperiodos iguales, sin analizar la eficiencia de los mercados en periodos al alza (Bull) y a la baja (Bear), tal como lo hacen Fernández, Sosvilla y Dolores (1999) al evaluar la predictibilidad del índice Nikkei de Tokio para el periodo 1986 a 1997.
El trabajo está organizado en 5 secciones; en la primera, se presenta la introducción, la segunda expone la revisión de la literatura de mercados eficientes, la tercera presenta la metodología, la cuarta presenta los resultados y, por último, se exponen las conclusiones y las recomendaciones más importantes del estudio.
2Revisión de la literaturaCowles (1933) fue uno de los primeros en estudiar la eficiencia de los mercados de forma empírica al evaluar el nivel de asertividad de los analistas de bolsa de su tiempo, concluyendo que sus recomendaciones no predecían sistemáticamente el mercado, reforzando así la teoría de que el mercado americano era eficiente para esa época. Posteriormente, Kendall (1953) detecta aleatoriedad y estacionalidad en las series de precios de 22 compañías norteamericanas. Años más tarde, Roberts (1959) demuestra que las series financieras son semejantes al paseo aleatorio, mientras que Osborne (1959) asocia el comportamiento de los precios de los activos al movimiento browniano.
En los años sesenta, Mandelbrot (1963a) y Samuelson (1965) relacionaron las series bursátiles con modelos matemáticos como la martingala, mientras que Fama (1965, 1970) compiló en sus publicaciones los fundamentos empíricos y teóricos desarrollados hasta la fecha, analizando el modelo de recorrido aleatorio como herramienta para describir los mercados bursátiles, resaltando el reto que enfrentan los chartistas al intentar predecir los precios de las acciones en presencia de aleatoriedad.
Estrictamente hablando, la hipótesis de eficiencia del mercado no es posible comprobarla, tal como lo exponen Granger (1992) y Fama (1970); sin embargo, existen aproximaciones empíricas para su contrastación; es así como, a partir de la búsqueda en la base de datos ScienceDirect1, se caracterizan 179 trabajos de investigación realizados desde 1997 hasta inicios del 2013, a partir de las cuales se encuentra que Estados Unidos es el mercado más testeado; sin embargo, al consolidar las estadísticas de eficiencia de mercado de China Continental, Hong Kong y Taiwán en la República Popular China, este país se convierte en el más estudiado en los últimos 15 años, lo que reflejaría el interés académico por dicho mercado dado su reciente crecimiento económico.
En cuanto al interrogante de si los mercados financieros son o no eficientes, se verifica que el 60% de los trabajos consultados niegan la eficiencia del mercado, el 35% no rechazan la hipótesis del mercado eficiente, mientras que en el restante 5% se encuentra mejora de la eficacia concentrada principalmente en las economías asiáticas a finales de la década de los 90, mejora que es motivada por varios factores, como son: las reformas económicas (Kawakatsu y Morey, 1999); la mayor velocidad en el flujo de la información posibilitado por la Internet (Lee, Park, Jo, Yang y Moon, 2009); la introducción al mercado de productos financieros como las opciones y los futuros (Mazouz y Bowe, 2006), y las correcciones de asimetrías del mercado en periodos poscrisis económicas (Lim, Brooks y Kim, 2008).
Adicionalmente, al analizar la trayectoria de la eficiencia de un determinado mercado se encuentran resultados contradictorios por parte de diferentes autores, principalmente en las economías desarrolladas, hallazgo que es explicado por Majumder (2012), quien argumenta que la eficiencia del mercado no es continua, sino que los mercados bursátiles presentan periodos de eficiencia y no eficiencia; es así que mercados generalmente aceptados como eficientes pueden presentar periodos de ineficiencia motivados por diferentes factores.
De la búsqueda en las bases de datos se caracterizan 371 pruebas y metodologías usadas para verificar la eficiencia débil, semifuerte y fuerte en los mercados bursátiles a nivel mundial, encontrándose que la forma débil de eficiencia del mercado es la más comprobada empíricamente (85,71%), hallazgo que estaría en la misma dirección de lo planteado por Grossman y Stiglitz (1980), quienes cuestionan la eficiencia fuerte mas no la débil y semifuerte. Adicionalmente, se verifica que el 59,1% de las pruebas utilizadas para contrastar la eficiencia débil de los mercados son basadas en el recorrido aleatorio, principalmente en sus versiones Random Walk 1 (RW1) y 3 (RW3); por tal motivo, en el presente trabajo se acude a esta metodología para evaluar la eficiencia de los mercados bursátiles de Latinoamérica.
En cuanto a los estudios sobre la eficiencia de Latinoamérica durante la última década y media, Urrutia (1995) fue uno de los primeros en evaluar los mercados de Argentina, Chile y México para el periodo 1975 a 1991, mediante pruebas de rachas y razón de variancias, llegando a la conclusión de que estos mercados no cumplen con el recorrido aleatorio. Años más tarde, Harvey y Viscanta (1997) rechazan el comportamiento de recorrido aleatorio para el índice de la Bolsa de Valores de Medellín de Colombia en el periodo 1987 a 1994, usando como criterio de decisión la correlación serial y la prueba de rachas.
Posteriormente, Ojah y Karemera (1999), usando la razón de variancia y promedios móviles integrados, no rechazan la eficiencia en los mercados de Argentina, Brasil, Chile y México, para el periodo 1987 a 1997. En el nuevo milenio, Delfiner (2002) comprueba la eficiencia relativa de los mercados de Argentina vs. Estados Unidos, en el periodo de 1993 a 1998, usando la prueba del cociente de variancias, el test rango reescalado (R/S) modificado, análisis de autocorrelación y prueba de rachas, detectando cierto nivel de dependencia de los retornos de Argentina; adicionalmente, mediante filtros de Alexander, plantea una estrategia de trading, concluyendo que, efectivamente, en el caso de Argentina se pueden tener rentabilidades extra, pero que al incluir las comisiones estas se pierden. En su tesis, Valdivieso (2004) analiza, entre otros estudios, la eficiencia del mercado de México en el periodo 1994 a 1999, usando herramientas estadísticas como correlogramas, test Q de Box-Pierce, test Ljung-Box y test de rachas, encontrando rechazo al recorrido aleatorio. En el mismo año, Maya y Torres (2004) llevan a cabo un estudio similar al de Harvey y Viscanta (1997) para el mercado de Colombia, solo que para el año 1999, encuentran aceptación del recorrido aleatorio en este mercado. Además, Guardia (2005) estudia el gobierno corporativo y la eficiencia de los mercados de Argentina, Brasil, Chile, México y Perú, dividiendo su análisis en diferentes subperiodos iguales desde el año 1990 hasta el 2005, aceptando el comportamiento aleatorio de los rendimientos, mediante el uso del test Q de Ljung y Box y autorregresión del orden 1. Por otro lado, en la base ScienceDirect se encontraron 2 trabajos de investigación de Tabak (2007) y Freitas, de Souza y de Almeida (2009) que evalúan el mercado de Brasil en cuanto a su eficiencia mediante raíces unitarias y modelos de predicción, respectivamente, revelando que este mercado no es eficiente en su forma débil para el periodo entre 1998 y 2007. Además, los mercados de México y Estados Unidos son evaluados entre 1996 y 2000 por Mansilla (2001), quien mediante un algoritmo de complejidad física halla aleatoriedad en los retornos de ambos mercados, lo cual es normal teniendo en cuenta la dependencia del mercado mexicano con respecto al de Estados Unidos. Igualmente, Hatgioannides y Mesomeris (2007) encuentran eficiencia mediante el análisis técnico en los mercados de Argentina, Brasil, Chile y México, mas no en Indonesia, Filipinas, Taiwán y Tailandia; después de tener en cuenta los costes de transacción para el periodo entre 1988 y 2002.
3MetodologíaLa metodología utilizada para la comprobación empírica de la eficiencia de los mercados inicia con la descripción de los criterios que se tienen en cuenta para la delimitación del marco muestral, así como la definición del espacio temporal y la variable objeto de estudio de la investigación. Posteriormente, se definen las fechas críticas en donde se presentan cambios de tendencia de largo plazo al alza y a la baja mediante el análisis gráfico y el test de Chow para cada uno de los diferentes mercados, para luego realizar un análisis exploratorio de las series financieras seleccionadas, buscando evaluar su aproximación a la distribución normal a partir de: los estadísticos básicos, la prueba Jarque-Bera y el test de bondad de ajuste de la chi-cuadrado. Finalmente, se comprueba la eficiencia débil de los mercados bursátiles latinoamericanos mediante el recorrido aleatorio, utilizando la prueba de rachas de Wald y Wolfowitz (1940) y el estadístico BDS de Brock, Dechert, Scheinkman y LeBaron (1996) para verificar ramdom walk 1 (RW1), los filtros de Alexander (1961) con algoritmos genéticos para Random Walk 2 (RW2), además del test LB de Ljung y Box (1978) y la prueba de Bartlett (1946) para RW3. A continuación, se describen los test estadísticos utilizados.
3.1Test de rachasEste test analiza el número total de rachas (R) que se presentan en una serie financiera, con el fin de contrastar si existen cantidades muy pequeñas o muy grandes de R, lo cual reflejaría no aleatoriedad en los datos. El proceso para la estimación del test consiste en determinar el número de rachas mayores y menores al retorno medio del activo financiero, cuya suma genera el número total de rachas R, variable que se comporta asintóticamente como una distribución normal, que al ser estandarizada genera el estadístico ZEst descrito como:
donde n1 y n2 son el número de retornos mayores y menores a la media, respectivamente. Se rechaza la hipótesis de retornos independientes e idénticamente distribuidos (i.i.d), si el p-valor es inferior a un nivel de confianza generalmente aceptado del 5 o el 10%.3.2Test BDSLa prueba BDS detecta todo tipo de estructura lineal y no lineal. El proceso de estimación inicia cuando de la serie financiera, se extraen al azar subconjuntos de m-historias de retornos r, tal que rtm≡{rt,rt−τ,rt−2τ,…,rt−(m−1)τ}, donde m es la dimensión de inmersión y τ el tiempo de desfase de los datos que por literatura generalmente se toma 1. Posteriormente, se toman de a 2 m-historias para determinar su proximidad, condición que se cumple si la máxima diferencia (en valor absoluto) entre sus miembros es inferior a un épsilon (¿) determinado, llevándose el registro de las veces que se cumple la proximidad mediante la función H¿, definida como
La hipótesis formal del test está determinada por la función de la probabilidad de proximidad entre las m-historias:Es decir, la hipótesis busca evaluar si la probabilidad de proximidad de una muestra de dimensión m es igual a la probabilidad de dimensión 1 elevada a la m. El estadístico mediante el cual se evalúa dicha probabilidad está definido por la ecuación:Asintóticamente, el estadístico Wm,n se comporta como una distribución normal con media cero y desviación típica 1, de tal forma que se rechaza la hipótesis nula si el p-valor del estadístico es inferior al nivel de confianza determinado.3.3Filtros de AlexanderAunque es una técnica que no aplica rigurosa inferencia estadística, tiene aceptación porque genera una dinámica en donde es interesante comparar los resultados de gestión activa y pasiva en series financieras. La gestión activa se realiza mediante filtros de Alexander y consiste en invertir y desinvertir durante un determinado periodo sobre la base de la regla de comprar el activo cuando su precio se incrementa x% y venderlo cuando su precio cae x%, mientras que la gestión pasiva radica en comprar el activo al inicio del periodo de estudio y venderlo al final del mismo, lo que se conoce como comprar y mantener.
Para el presente trabajo no se utiliza un número discreto de filtros, como en Fama y Blume (1965), sino que se centra en determinar los filtros para los cuales el beneficio se maximiza haciendo uso de algoritmos genéticos, para 3 escenarios diferentes, como son:
- –
Filtros sin costes de transacción: este escenario de negociación realmente es el ideal, mas no real, ya que toda operación de compra y venta de activos tiene adosado un coste mínimo; sin embargo, se tiene en cuenta porque aporta elementos de análisis al estudio.
- –
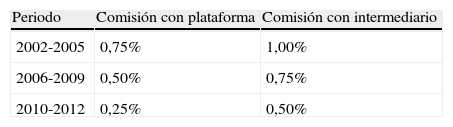
Filtros con comisión usando plataformas por Internet: esta opción tiene en cuenta costes e impuestos por transacción que son inferiores a los de un intermediario, pero requiere de tiempo por parte del inversionista para realizar las operaciones por vía Internet; los costes por operación mediante plataforma para el periodo de estudio, se presentan en la tabla 1.
Tabla 1.Comisiones en la compra y venta de activos financieros
Periodo Comisión con plataforma Comisión con intermediario 2002-2005 0,75% 1,00% 2006-2009 0,50% 0,75% 2010-2012 0,25% 0,50% Fuente: datos estimados por intermediario financiero y costes publicados en la plataformas de Internet Correval.
- –
Filtros con comisión mediante un intermediario: este escenario asume que el inversionista delega en una compañía administradora de portafolios la gestión del filtro de un activo determinado, por lo cual su coste es mayor al de la gestión activa mediante plataforma, tal como se distingue en la tabla 1.
La verificación del recorrido aleatorio mediante filtros de Alexander se fundamenta en el hecho de que si los precios son independientes, la gestión mediante esta técnica no produce beneficios superiores a los de comprar y mantener, por lo que se generan 15.000 simulaciones aleatorias usando filtros entre 0 y 10%, con el fin de obtener el máximo y mínimo beneficio para cada uno de los 3 escenarios, determinando si algún filtro genera mayores beneficios a la estrategia de comprar y mantener; el beneficio está dado por:
3.4Test de Ljung BoxEste test busca comprobar la hipótesis conjunta de que todos los coeficientes de autocorrelación ρι de una serie, son simultáneamente cero, es decir:
El estadístico LB tiende a una distribución de chi-cuadrado con l grados de libertad.Donde n es el tamaño de la muestra y l la longitud del retardo. Se rechaza la hipótesis nula si el estadístico LB>Xmg.l.2, o si su p-valor es inferior al nivel de significación dado.3.5Prueba de BartlettDebe tenerse en cuenta que el test LB prueba la hipótesis conjunta de que todas las autocorrelaciones son significativamente iguales a cero; sin embargo, es importante analizar la hipótesis individual de que alguna(s) de las autocorrelaciones son diferentes de cero, para ello se acude a la prueba de Bartlett, en el sentido de que si una serie de tiempo es puramente aleatoria (ruido blanco), los coeficientes de autocorrelación asintóticamente se comportan como una distribución normal con media cero y variancia 1/n, en cuyo caso el intervalo de confianza del 95% para cada autocorrelación estimada ρˆk es [0±1,96(σ2)]. El intervalo de confianza está dado por:
Si el intervalo de confianza no incluye el valor ρˆk, se rechaza la hipótesis nula de que el verdadero valor ρk es cero, y viceversa.3.6Evaluación conjunta del recorrido aleatorioCon el fin de obtener una evaluación total de la aleatoriedad para cada uno de los activos y sus respectivos subperiodos, se acude a consolidar los resultados de las 5 pruebas analizadas, lo que permite evaluar la consistencia de la aleatoriedad en el tiempo, en una escala de cero (todas las pruebas rechazan la aleatoriedad) a 5 (ninguna de las pruebas rechaza aleatoriedad). En general, se considera que una serie es aleatoria si 3 o más de las 5 pruebas empleadas no rechazan el comportamiento de recorrido aleatorio.
4Resultados de la comprobación empíricaLos resultados derivados del presente trabajo se estructuran en 3 etapas; inicialmente, determinación de los cambios de tendencia; evaluación de normalidad; contrastación de la eficiencia mediante la comprobación del recorrido aleatorio en sus versiones RW1, RW2 y RW3 de las principales series bursátiles de la región y Estados Unidos.
4.1DatosPara cada uno de los países de la muestra, se toman sus principales índices bursátiles como son Ibovespa (Brasil), IPSA (Chile), IGBC (Colombia), IPC (México) e IGBVL (Perú); además, para estos mercados se seleccionan las 5 empresas más representativas que cumplan con 2 criterios: en primer lugar, se eligen aquellas organizaciones que presenten el mayor peso en el cálculo del índice respectivo, y en segundo lugar, se toman las compañías que hayan cotizado preferiblemente durante todo el periodo de estudio.
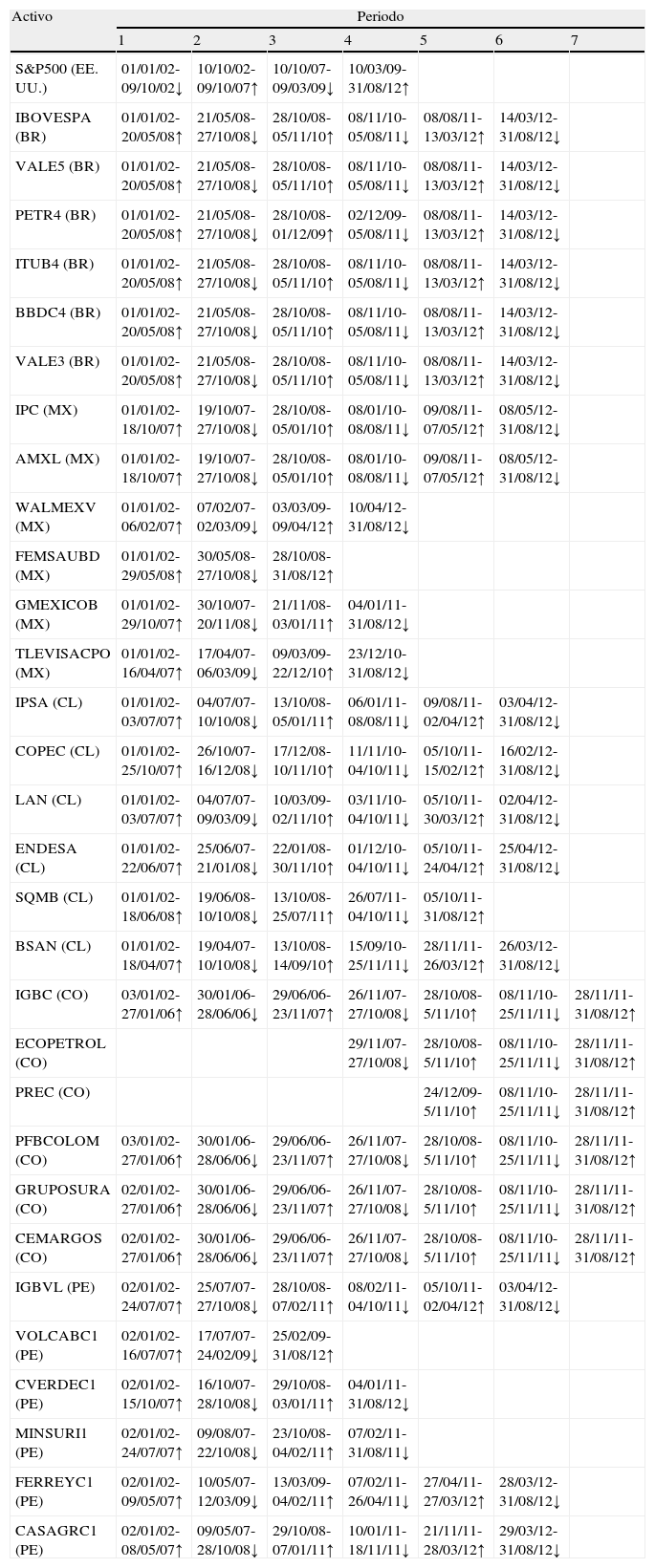
El periodo para el cual se analizan los datos inicia el 1 enero del 2002 y finaliza el 31 de agosto del 2012 para la mayoría de los activos analizados, con excepción de Ecopetrol y Pacific Rubiales de Colombia, que aunque inician cotizaciones desde los años 2007 y 2009, respectivamente, tienen una alta participación en dicho mercado. Por otro lado, autores como French (1980) y otros en sus trabajos dividen el periodo total de estudio en subperiodos iguales, con el fin de analizar la evolución del mercado en el tiempo; sin embargo, el presente trabajo toma divisiones del periodo total de estudio de acuerdo con la tendencia del mercado, ya sea al alza o a la baja, como lo hacen Vayanos y Woolley (2008), con el objeto de evaluar el comportamiento aleatorio de los activos en dichos subperiodos, sin perder de vista la evolución del mercado y el comportamiento aleatorio a través del tiempo. Con el propósito de definir las tendencias de cada activo, se inicia con una identificación gráfica de los cambios de pendiente en las diferentes series; posteriormente, se estiman los puntos máximos o mínimos locales que delimitan cada subperiodo, finalmente el cambio estructural se verifica mediante la prueba «breakpoint» de Chow (1960). En la tabla A.1 del anexo se definen los respectivos subperiodos para cada mercado.
Al definir los puntos de quiebre de tendencia en los diferentes activos se encuentra una gran disparidad, tanto al interior de cada país como entre países, lo cual, según Lee, Lee y Lee (2010) se debe a variables exógenas y endógenas de cada economía y empresa; sin embargo, al analizar las fechas de corte de los subperiodos para los diferentes países, se observan 4 cambios estructurales de tendencia que coinciden para la mayoría de los activos bajo estudio, con eventos mundiales como son: crisis subprime (noviembre del 2007); guerra de divisas (noviembre del 2010); recesión en países de la Unión Europea (entre febrero y abril del 2012). Estos 3 acontecimientos que inciden generalizadamente sobre los cambios de tendencias en los mercados latinoamericanos realmente pueden ser el resultado de una crisis financiera extendida a nivel mundial motivada por la correlación de sus economías, que ha generado coletazos sistemáticos a lo largo de los últimos 4 años, es decir, es un solo problema que ha sido retransmitido a diferentes partes del mundo como consecuencia de reajustes en economías correlacionadas.
4.2Variable de comprobaciónCampbell, Lo y Mackinley (1997) resaltan al menos 2 razones por las cuales se debe preferir los retornos como variable de estudio sobre los precios de los activos; en primer lugar, para el inversor promedio, el retorno es un resumen completo de la oportunidad de inversión que está libre de escala (no dimensional); en segundo lugar, los retornos tienen propiedades estadísticas más atractivas que los precios. Por tal motivo, se toma como variable los rendimientos compuestos continuamente definidos como Rt=Ln[Pt/Pt−1].
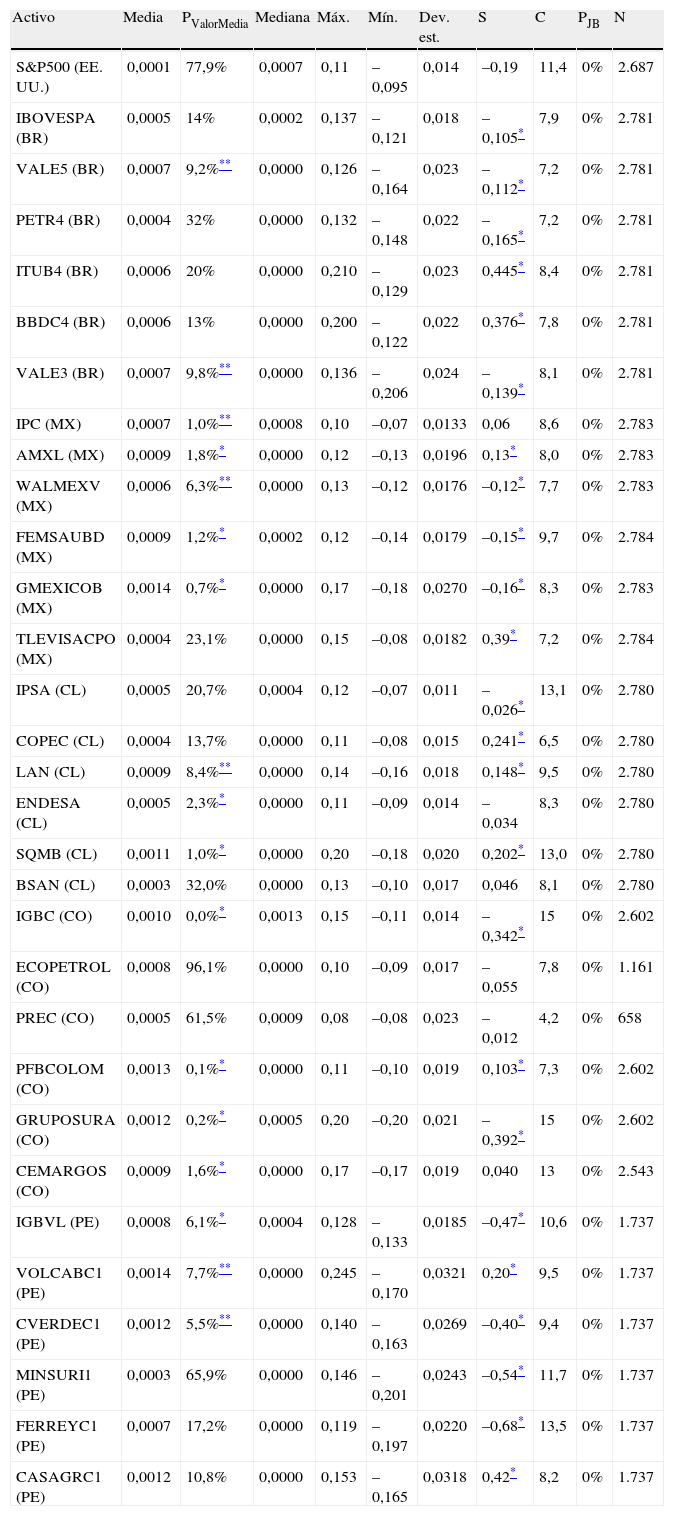
4.3Análisis preliminarUna vez definida la variable de estudio, se procede a indagar preliminarmente sobre la distribución de las series financieras mediante estadísticos básicos como: media, mediana, valor máximo, valor mínimo, coeficiente de asimetría y curtosis; además, se usa el test estadístico Jarque-Bera para evaluar la hipótesis de que los rendimientos de estas series financieras siguen el comportamiento de una distribución normal. Los resultados se observan en la tabla A2 de los anexos.
De las estadísticas de la tabla A.2 del anexo, se observa que, en general, los mercados latinoamericanos presentan retornos superiores a los del S&P500, lo que se explica teniendo en cuenta el mayor riesgo país que representa la región con respecto a Estados Unidos. En cuanto al comportamiento de la desviación estándar promedio para cada país, se encuentra que México, Chile y Colombia experimentan volatilidades promedio cercanas a la del S&P500, siendo Perú el país que mayor similitud muestra con el índice americano, mientras que Brasil, por el contrario, es el mercado que presenta mayor variancia con respecto a la del S&P500, motivado posiblemente por inversiones foráneas de corto plazo que buscan rendimientos superiores a los obtenidos en países desarrollados, produciendo fuertes volatilidades en el mercado. Estos comportamientos pueden ser explicados por los hallazgos de Sarmiento, Duarte y Mascareñas (2012), en donde mediante la prueba de Granger se verifica la fuerte causalidad del S&P500 sobre Perú, México, Chile y Colombia, mientras que con Brasil la causalidad del índice americano es débil.
Por otro lado, al analizar la asimetría, la curtosis y el test de bondad de ajuste de la chi-cuadrado, se observa que tanto los activos latinoamericanos como el S&P500 presentan comportamientos asimétricos, alta curtosis y colas pesadas, propiedades no características de una distribución normal, lo cual es corroborado con la prueba de bondad de ajuste de los datos empíricos, mediante la cual se detecta que el primer lugar de ajuste es ocupado por las distribuciones teóricas: logistic (76,7%), log-logistic (20%) y normal (3,3%). En cuanto a la distribución normal, se encuentra que ocupa el segundo (53,3%) y el tercer (3,3%) lugar de ajuste, resultados que no coinciden con los hallazgos de Bachelier (1900), Kendall (1953), Osborne (1959) y Moore (1962), quienes exponen que los retornos de los activos financieros deberían aproximarse a un comportamiento normal; no obstante, otros autores, como Mandelbrot (1963a) y Fama y Blume (1965), han observado en mercados desarrollados características similares a las halladas en el presente trabajo, lo cual haría pensar que los mercados latinoamericanos vienen evolucionado hacia distribuciones como la logistic y log-logistic, con alta concentración de sus retornos alrededor de la media, derivado posiblemente por la fuerte competencia entre los agentes del mercado. Además, al analizar las 2 distribuciones teóricas que mejor describen los activos financieros de Latinoamérica, se encuentra que las series que se ajustan a la logistic presentan en su mayoría simetría negativa o cero (82%), mientras que aquellos activos con distribución log-logistic muestran sesgo positivo (83%), es decir, estas 2 distribuciones prevalecen sobre la normal por captar mejor la asimetría y la leptocurtosis de los datos empíricos, hallazgo que es relevante dado que la asunción de no normalidad en los activos financieros es importante al modelar procesos de volatilidad con memoria de largo plazo, tal como lo resaltan Kang, Cheong y Yoon (2010).
Por último, el 53% de los activos latinoamericanos presentan retornos medios significativos y mayores a cero, de los cuales el 25% (FEMSAUBD, GMEXICOB, IGBC y Gruposura) muestran variancias menores o iguales al promedio, sesgo significativamente negativo y alta curtosis (superior a 8,3); características que podrían hacer atractivos a estos activos, dada su concentración de retornos al lado derecho de la distribución; sin embargo, no se encuentra evidencia de que, a partir del análisis de los primeros 4 momentos de estas series sea posible batir el mercado usando la técnica de Alexander.
4.4Comprobación de la eficiencia débilA continuación, se presentan para el S&P500 y los 5 países latinoamericanos los resultados de las pruebas empíricas de recorrido aleatorio los 3 tipos de recorrido aleatorio y el análisis de la evaluación conjunta de las pruebas realizadas para el periodo total de estudio, que inicia el 2 de enero del 2002 y finaliza el 31 de agosto del 2012, y los subperiodos de la tabla A.1.
4.4.1Random Walk 1Al comparar los resultados obtenidos mediante la prueba de rachas y el test BDS, se observa que el primer estadístico tiende a no rechazar la hipótesis i.i.d., mientras que el test BDS la rechaza con mayor frecuencia, lo cual llevaría a pensar que cuando la serie no es aleatoria, la prueba de rachas detecta mejor su comportamiento, mientras que cuando el test BDS encuentra aleatoriedad en un activo es porque este sigue un recorrido aleatorio, de ahí que se haya preferido la evaluación de la eficiencia de los mercados latinoamericanos mediante ambas pruebas, dada su complementariedad. Por ejemplo, el test de rachas detecta aleatoriedad para Brasil y México desde 2002 y para Colombia desde 2006, mientras que la prueba BDS solamente verifica aleatoriedad desde 2010 para Brasil y Colombia, y desde 2011 para México. Sin embargo, en términos generales, las pruebas de RW1 detectan mejora de la eficiencia del mercado en los últimos años para Brasil, México y Colombia, y baja aleatoriedad en Chile y Perú.
4.4.2Random Walk 2Así mismo, mediante el modelo de optimización de algoritmos genéticos en los filtros de Alexander, se verifica para Latinoamérica que el escenario de inversión sin costos de transacción ofrece beneficios extraordinarios, pero al incluir los costes por trading, ya sea mediante plataforma o intermediario financiero, los beneficios no son mejores que la estrategia de comprar y mantener, tal como también es comprobado en el mercado chino por Chong, Lam y Yan (2012). Además, se observa que para algunos activos en periodos al alza, esta técnica permite obtener beneficios superiores a la estrategia comprar y mantener; sin embargo, los filtros óptimos se caracterizan por ser valores puntuales e inconsistentes en los diferentes subperiodos, propiedades que dificultan la elección del filtro a usar con el fin de obtener beneficios sistemáticos hacia el futuro, implicando un alto riesgo de tomar un valor porcentual que pueda generar grandes pérdidas respecto a la opción de comprar y mantener. Por otro lado, pareciera que en subperiodos a la baja, la técnica de Alexander diera excelentes rendimientos marginales, aunque realmente no se trata de mayores beneficios, sino de menores pérdidas con relación a comprar y mantener; por consiguiente, en periodos a la baja la mejor opción sería desinvertir o acudir a activos refugio. Por último, Perú es el único país donde 3 de sus activos (CASAGRC1, CVERDEC1 y MINSURI1) producen márgenes extraordinarios mediante el uso de filtros, al indagar sobre su origen se encuentra que dicha ganancia es causada por la fuerte variación de sus precios durante el mes de abril del año 2006, como consecuencia del crecimiento económico de este país, originado por el boom de las materias primas como el cobre, el estaño y el petróleo; a pesar de esto, se enfatiza que dichos filtros no son fácilmente predecibles a la hora de usar esta estrategia en la inversión bursátil, ya que al utilizar las mismas reglas en diferentes periodos, el criterio a menudo no funciona, tal como es verificado por Fritsche (2001).
4.4.3Random Walk 3El test LB identifica autocorrelación en Estados Unidos desde octubre del 2002, contrariamente en Latinoamérica se observa una disminución de las autocorrelaciones desde 2007 (Colombia), 2008 (México y Brasil) y 2011 (Chile y Perú); de tal manera que mientras en Estados Unidos se ha observado un aumento de las dependencias lineales, en Latinoamérica estas han disminuido a través del tiempo. Por medio de este test, también se verifica que Chile es el país con mayores autocorrelaciones en las series de sus activos y Perú es el único país que presenta mayor correlación serial en periodos a la baja.
Adicionalmente, los resultados del test de Bartlett evidencian que las autocorrelaciones más significativas se presentan principalmente en el primer retardo, seguido por el tercero, cuarto y segundo retardo, lo que indica que en el mercado latinoamericano los retornos podrían ser modelados mediante procesos autorregresivos de primer orden (AR1). Esta prueba también identifica Perú y Chile como los países con el mayor número de autocorrelaciones significativas, mientras que Brasil, Colombia y México son los países con menor correlación serial, ratificando lo encontrado con el análisis conjunto respecto a la mayor eficiencia de estos 3 países.
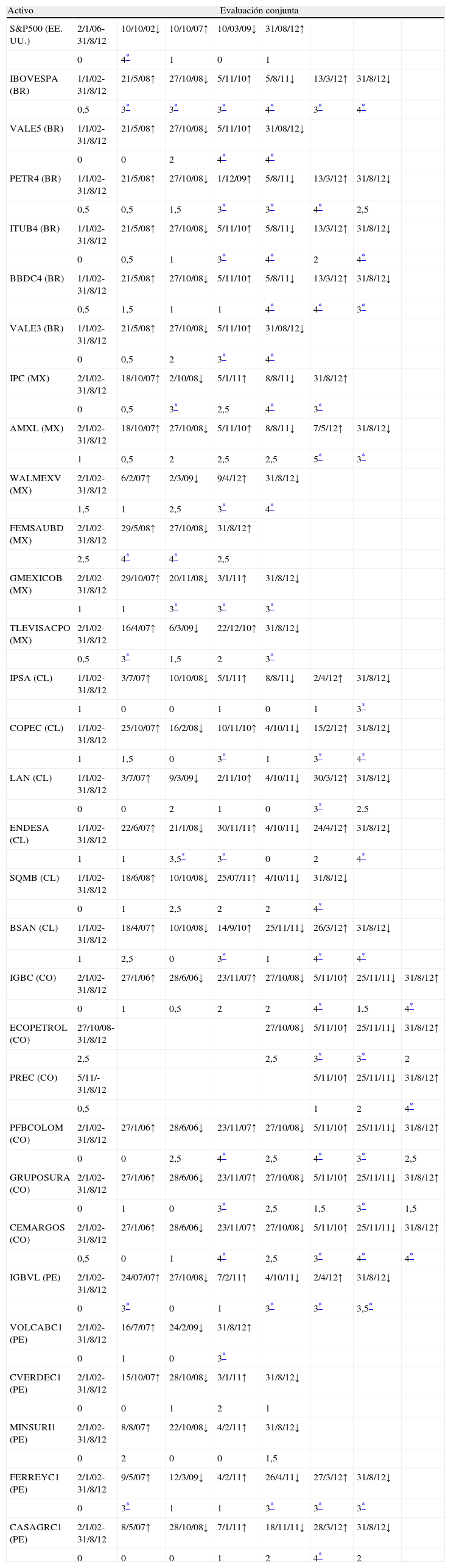
4.4.4Evaluación conjunta de Random WalkPara cada uno de los activos y periodos estudiados se consolidan los resultados de las 5 pruebas analizadas con el fin de realizar la evaluación total de la aleatoriedad presentada en la tabla A.3 del anexo, para lograrlo se asigna el valor de 1 si el test cumple acepta la hipótesis de aleatoriedad, 0 en el caso contrario o 0,5 en resultados no concluyentes, al sumar los resultados de los 5 test se obtiene el valor de la evaluación conjunta en una escala de cero a 5 (0-5) indicando el rechazo de la aleatoriedad en todas las pruebas (0) o la aceptación de la misma en los 5 test analizados (5). En general, se considera que una serie es aleatoria, si su evaluación conjunta es igual o mayor a 3.
De los resultados conjuntos de las pruebas de recorrido aleatorio, se extrae que el nivel de eficiencia relativa en orden descendente está dado por México, Brasil, Colombia, Chile y Perú; esta categorización está correlacionada en un 65% con los volúmenes de capitalización bursátil para los últimos 11 años en estos 5 mercados (World Federation of Exchanges, 2012).
Además, de la investigación se extrae que para los países donde se detectó mayor nivel de eficiencia (México, Brasil y Colombia), la relación entre tendencia y aleatoriedad es inversa, mientras que en los países con menores niveles de eficiencia (Chile y Perú) se verifica una relación directa entre tendencia y aleatoriedad, hallazgo que iría en la misma dirección de lo planteado por Peters (1994), en el sentido de que cuando los inversores de largo plazo detectan variables económicas que cambian sus expectativas de crecimiento del mercado, dejan de participar en él, e inician operaciones de corto plazo que fuerzan al mercado a caer, produciendo un comportamiento más aleatorio en los precios de los activos financieros. Además, según Coakley (2006), en periodos alcistas los precios presentan desviaciones pronunciadas y duraderas respecto a su valor intrínseco, mientras que en periodos bajistas los precios se mueven hacia su nivel de equilibrio o fundamental, ratificando los hallazgos en el presente trabajo respecto al comportamiento aleatorio de los mercados al alza y a la baja.
Por otro lado, mediante los diferentes test se verifica no aleatoriedad en el S&P500 para el periodo total de estudio, como también para el subperiodo que inicia el 10 de octubre del 2007 y finaliza el 09 de marzo del 2009 (a la baja), hallazgo que coincide en primera instancia con el inicio de la crisis económica generada por la subprime en Estados Unidos; en segundo lugar, con el mejoramiento de la eficiencia del mercado de México (2007), Brasil (2008), Colombia (2008), Perú (2011) y Chile (2012), y además con el aumento significativo de la capitalización bursátil en los mercados bajo estudio a partir de 2007. Estos 3 eventos parecen relacionarse entre sí, en el sentido de que ante el problema estructural presentado en Estados Unidos, los inversionistas optan por la movilización de sus capitales hacia mercados como los latinoamericanos explicando el mejoramiento de su eficiencia en los últimos años; esta misma evolución bursátil es verificada por Yu, Nartea, Gan y Yao (2013) en los mercados emergentes de Malasia y Tailandia, y por Montagnoli y deVries (2010) en el mercado del CO2 en Europa.
5ConclusionesDe los resultados de la investigación se extrae que, en general, las 5 principales economías latinoamericanas estudiadas han experimentado una mejora de su eficiencia del mercado en los últimos años; al matizar este mejoramiento se verifica que es mayor la eficiencia de los mercados de México, Brasil y Colombia a partir de los años 2007 y 2008, mientras que en Chile y Perú el incremento de su eficiencia se detecta a partir del 2011 y 2012, respectivamente. Es decir, desde el punto de vista de la madurez de la eficiencia del mercado, los 3 primeros países han experimentado un mayor periodo de aleatoriedad en sus activos, sin que ello demerite la evolución positiva hacia la transparencia bursátil en los mercados de Chile y Perú.
Este hallazgo de mejora en la eficacia del mercado es congruente con el verificado a finales de la década de los 90 en los mercados asiáticos por autores como Kawakatsu y Morey (1999) y Lee et al. (2009), lo que significa que Latinoamérica está recorriendo un camino similar al de los países orientales hace 15 años en cuanto a la eficiencia de sus mercados se refiere. En los estudios de Mazouz y Bowe (2006); Kasman y Kasman (2008) y Lim et al., 2008, los autores identifican como causas del mejoramiento de la eficiencia de los mercados bursátiles varios factores, entre ellos: las aperturas económicas; la introducción al mercado de nuevos activos financieros, como las opciones y futuros; el mayor flujo de la información debido al auge de la Internet, y las correcciones de asimetrías del mercado motivadas por crisis económicas sufridas por los países orientales en 1997. Sin embargo, para el caso de Latinoamérica, estos factores no son los responsables del reciente comportamiento aleatorio de sus mercados, sino posiblemente al aumento en la capitalización de estos mercados debido al crecimiento de la inversión directa extranjera a partir del 2007 (CEPAL, 2011), motivado por 2 sinergias positivas para la región, como son en primera instancia las inversiones en infraestructura y explotación de materias primas por parte de países como Estados Unidos, Holanda, China, Canadá y España, y en segundo lugar, por la movilización de capitales desde las económicas desarrolladas hacia mercados emergentes como consecuencia de la crisis económica originada en los Estados Unidos en noviembre del 2007.
Además, en los 3 países con mayor nivel de eficiencia (México, Brasil y Colombia) se encuentra que la relación entre la tendencia del mercado y la aleatoriedad es inversa, es decir, en subperiodos con tendencias a la baja los mercados presentan mayor aleatoriedad que al alza, por el contrario, en los 2 países que se verifica menor eficiencia (Chile y Perú), se presenta mayor aleatoriedad cuando la tendencia es al alza que cuando es a la baja; hallazgos que van en la misma dirección a lo planteado por Peters (1994) y (Coakley, 2006), quienes respaldan la premisa de que los mercados deberían ser más eficientes a la baja que al alza.
Al concluir el presente trabajo, se recomienda indagar sobre el papel que deben cumplir los agentes reguladores del mercado con miras a responder la pregunta ¿cuál es el nivel de control «adecuado» que se debe ejercer sobre los mercados para que sean eficientes?
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
Espacio temporal con subperiodos al alza y a la baja de los activos seleccionados
| Activo | Periodo | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| S&P500 (EE. UU.) | 01/01/02-09/10/02↓ | 10/10/02-09/10/07↑ | 10/10/07-09/03/09↓ | 10/03/09-31/08/12↑ | |||
| IBOVESPA (BR) | 01/01/02-20/05/08↑ | 21/05/08-27/10/08↓ | 28/10/08-05/11/10↑ | 08/11/10-05/08/11↓ | 08/08/11-13/03/12↑ | 14/03/12-31/08/12↓ | |
| VALE5 (BR) | 01/01/02-20/05/08↑ | 21/05/08-27/10/08↓ | 28/10/08-05/11/10↑ | 08/11/10-05/08/11↓ | 08/08/11-13/03/12↑ | 14/03/12-31/08/12↓ | |
| PETR4 (BR) | 01/01/02-20/05/08↑ | 21/05/08-27/10/08↓ | 28/10/08-01/12/09↑ | 02/12/09-05/08/11↓ | 08/08/11-13/03/12↑ | 14/03/12-31/08/12↓ | |
| ITUB4 (BR) | 01/01/02-20/05/08↑ | 21/05/08-27/10/08↓ | 28/10/08-05/11/10↑ | 08/11/10-05/08/11↓ | 08/08/11-13/03/12↑ | 14/03/12-31/08/12↓ | |
| BBDC4 (BR) | 01/01/02-20/05/08↑ | 21/05/08-27/10/08↓ | 28/10/08-05/11/10↑ | 08/11/10-05/08/11↓ | 08/08/11-13/03/12↑ | 14/03/12-31/08/12↓ | |
| VALE3 (BR) | 01/01/02-20/05/08↑ | 21/05/08-27/10/08↓ | 28/10/08-05/11/10↑ | 08/11/10-05/08/11↓ | 08/08/11-13/03/12↑ | 14/03/12-31/08/12↓ | |
| IPC (MX) | 01/01/02-18/10/07↑ | 19/10/07-27/10/08↓ | 28/10/08-05/01/10↑ | 08/01/10-08/08/11↓ | 09/08/11-07/05/12↑ | 08/05/12-31/08/12↓ | |
| AMXL (MX) | 01/01/02-18/10/07↑ | 19/10/07-27/10/08↓ | 28/10/08-05/01/10↑ | 08/01/10-08/08/11↓ | 09/08/11-07/05/12↑ | 08/05/12-31/08/12↓ | |
| WALMEXV (MX) | 01/01/02-06/02/07↑ | 07/02/07-02/03/09↓ | 03/03/09-09/04/12↑ | 10/04/12-31/08/12↓ | |||
| FEMSAUBD (MX) | 01/01/02-29/05/08↑ | 30/05/08-27/10/08↓ | 28/10/08-31/08/12↑ | ||||
| GMEXICOB (MX) | 01/01/02-29/10/07↑ | 30/10/07-20/11/08↓ | 21/11/08-03/01/11↑ | 04/01/11-31/08/12↓ | |||
| TLEVISACPO (MX) | 01/01/02-16/04/07↑ | 17/04/07-06/03/09↓ | 09/03/09-22/12/10↑ | 23/12/10-31/08/12↓ | |||
| IPSA (CL) | 01/01/02-03/07/07↑ | 04/07/07-10/10/08↓ | 13/10/08-05/01/11↑ | 06/01/11-08/08/11↓ | 09/08/11-02/04/12↑ | 03/04/12-31/08/12↓ | |
| COPEC (CL) | 01/01/02-25/10/07↑ | 26/10/07-16/12/08↓ | 17/12/08-10/11/10↑ | 11/11/10-04/10/11↓ | 05/10/11-15/02/12↑ | 16/02/12-31/08/12↓ | |
| LAN (CL) | 01/01/02-03/07/07↑ | 04/07/07-09/03/09↓ | 10/03/09-02/11/10↑ | 03/11/10-04/10/11↓ | 05/10/11-30/03/12↑ | 02/04/12-31/08/12↓ | |
| ENDESA (CL) | 01/01/02-22/06/07↑ | 25/06/07-21/01/08↓ | 22/01/08-30/11/10↑ | 01/12/10-04/10/11↓ | 05/10/11-24/04/12↑ | 25/04/12-31/08/12↓ | |
| SQMB (CL) | 01/01/02-18/06/08↑ | 19/06/08-10/10/08↓ | 13/10/08-25/07/11↑ | 26/07/11-04/10/11↓ | 05/10/11-31/08/12↑ | ||
| BSAN (CL) | 01/01/02-18/04/07↑ | 19/04/07-10/10/08↓ | 13/10/08-14/09/10↑ | 15/09/10-25/11/11↓ | 28/11/11-26/03/12↑ | 26/03/12-31/08/12↓ | |
| IGBC (CO) | 03/01/02-27/01/06↑ | 30/01/06-28/06/06↓ | 29/06/06-23/11/07↑ | 26/11/07-27/10/08↓ | 28/10/08-5/11/10↑ | 08/11/10-25/11/11↓ | 28/11/11-31/08/12↑ |
| ECOPETROL (CO) | 29/11/07-27/10/08↓ | 28/10/08-5/11/10↑ | 08/11/10-25/11/11↓ | 28/11/11-31/08/12↑ | |||
| PREC (CO) | 24/12/09-5/11/10↑ | 08/11/10-25/11/11↓ | 28/11/11-31/08/12↑ | ||||
| PFBCOLOM (CO) | 03/01/02-27/01/06↑ | 30/01/06-28/06/06↓ | 29/06/06-23/11/07↑ | 26/11/07-27/10/08↓ | 28/10/08-5/11/10↑ | 08/11/10-25/11/11↓ | 28/11/11-31/08/12↑ |
| GRUPOSURA (CO) | 02/01/02-27/01/06↑ | 30/01/06-28/06/06↓ | 29/06/06-23/11/07↑ | 26/11/07-27/10/08↓ | 28/10/08-5/11/10↑ | 08/11/10-25/11/11↓ | 28/11/11-31/08/12↑ |
| CEMARGOS (CO) | 02/01/02-27/01/06↑ | 30/01/06-28/06/06↓ | 29/06/06-23/11/07↑ | 26/11/07-27/10/08↓ | 28/10/08-5/11/10↑ | 08/11/10-25/11/11↓ | 28/11/11-31/08/12↑ |
| IGBVL (PE) | 02/01/02-24/07/07↑ | 25/07/07-27/10/08↓ | 28/10/08-07/02/11↑ | 08/02/11-04/10/11↓ | 05/10/11-02/04/12↑ | 03/04/12-31/08/12↓ | |
| VOLCABC1 (PE) | 02/01/02-16/07/07↑ | 17/07/07-24/02/09↓ | 25/02/09-31/08/12↑ | ||||
| CVERDEC1 (PE) | 02/01/02-15/10/07↑ | 16/10/07-28/10/08↓ | 29/10/08-03/01/11↑ | 04/01/11-31/08/12↓ | |||
| MINSURI1 (PE) | 02/01/02-24/07/07↑ | 09/08/07-22/10/08↓ | 23/10/08-04/02/11↑ | 07/02/11-31/08/11↓ | |||
| FERREYC1 (PE) | 02/01/02-09/05/07↑ | 10/05/07-12/03/09↓ | 13/03/09-04/02/11↑ | 07/02/11-26/04/11↓ | 27/04/11-27/03/12↑ | 28/03/12-31/08/12↓ | |
| CASAGRC1 (PE) | 02/01/02-08/05/07↑ | 09/05/07-28/10/08↓ | 29/10/08-07/01/11↑ | 10/01/11-18/11/11↓ | 21/11/11-28/03/12↑ | 29/03/12-31/08/12↓ | |
Fuente: elaboración propia.
BR: Brasil; CL: Chile; CO: Colombia; MX: México; PE: Perú.
Estadísticas básicas y prueba Jarque-Bera
| Activo | Media | PValorMedia | Mediana | Máx. | Mín. | Dev. est. | S | C | PJB | N |
| S&P500 (EE. UU.) | 0,0001 | 77,9% | 0,0007 | 0,11 | –0,095 | 0,014 | –0,19 | 11,4 | 0% | 2.687 |
| IBOVESPA (BR) | 0,0005 | 14% | 0,0002 | 0,137 | –0,121 | 0,018 | –0,105* | 7,9 | 0% | 2.781 |
| VALE5 (BR) | 0,0007 | 9,2%** | 0,0000 | 0,126 | –0,164 | 0,023 | –0,112* | 7,2 | 0% | 2.781 |
| PETR4 (BR) | 0,0004 | 32% | 0,0000 | 0,132 | –0,148 | 0,022 | –0,165* | 7,2 | 0% | 2.781 |
| ITUB4 (BR) | 0,0006 | 20% | 0,0000 | 0,210 | –0,129 | 0,023 | 0,445* | 8,4 | 0% | 2.781 |
| BBDC4 (BR) | 0,0006 | 13% | 0,0000 | 0,200 | –0,122 | 0,022 | 0,376* | 7,8 | 0% | 2.781 |
| VALE3 (BR) | 0,0007 | 9,8%** | 0,0000 | 0,136 | –0,206 | 0,024 | –0,139* | 8,1 | 0% | 2.781 |
| IPC (MX) | 0,0007 | 1,0%** | 0,0008 | 0,10 | –0,07 | 0,0133 | 0,06 | 8,6 | 0% | 2.783 |
| AMXL (MX) | 0,0009 | 1,8%* | 0,0000 | 0,12 | –0,13 | 0,0196 | 0,13* | 8,0 | 0% | 2.783 |
| WALMEXV (MX) | 0,0006 | 6,3%** | 0,0000 | 0,13 | –0,12 | 0,0176 | –0,12* | 7,7 | 0% | 2.783 |
| FEMSAUBD (MX) | 0,0009 | 1,2%* | 0,0002 | 0,12 | –0,14 | 0,0179 | –0,15* | 9,7 | 0% | 2.784 |
| GMEXICOB (MX) | 0,0014 | 0,7%* | 0,0000 | 0,17 | –0,18 | 0,0270 | –0,16* | 8,3 | 0% | 2.783 |
| TLEVISACPO (MX) | 0,0004 | 23,1% | 0,0000 | 0,15 | –0,08 | 0,0182 | 0,39* | 7,2 | 0% | 2.784 |
| IPSA (CL) | 0,0005 | 20,7% | 0,0004 | 0,12 | –0,07 | 0,011 | –0,026* | 13,1 | 0% | 2.780 |
| COPEC (CL) | 0,0004 | 13,7% | 0,0000 | 0,11 | –0,08 | 0,015 | 0,241* | 6,5 | 0% | 2.780 |
| LAN (CL) | 0,0009 | 8,4%** | 0,0000 | 0,14 | –0,16 | 0,018 | 0,148* | 9,5 | 0% | 2.780 |
| ENDESA (CL) | 0,0005 | 2,3%* | 0,0000 | 0,11 | –0,09 | 0,014 | –0,034 | 8,3 | 0% | 2.780 |
| SQMB (CL) | 0,0011 | 1,0%* | 0,0000 | 0,20 | –0,18 | 0,020 | 0,202* | 13,0 | 0% | 2.780 |
| BSAN (CL) | 0,0003 | 32,0% | 0,0000 | 0,13 | –0,10 | 0,017 | 0,046 | 8,1 | 0% | 2.780 |
| IGBC (CO) | 0,0010 | 0,0%* | 0,0013 | 0,15 | –0,11 | 0,014 | –0,342* | 15 | 0% | 2.602 |
| ECOPETROL (CO) | 0,0008 | 96,1% | 0,0000 | 0,10 | –0,09 | 0,017 | –0,055 | 7,8 | 0% | 1.161 |
| PREC (CO) | 0,0005 | 61,5% | 0,0009 | 0,08 | –0,08 | 0,023 | –0,012 | 4,2 | 0% | 658 |
| PFBCOLOM (CO) | 0,0013 | 0,1%* | 0,0000 | 0,11 | –0,10 | 0,019 | 0,103* | 7,3 | 0% | 2.602 |
| GRUPOSURA (CO) | 0,0012 | 0,2%* | 0,0005 | 0,20 | –0,20 | 0,021 | –0,392* | 15 | 0% | 2.602 |
| CEMARGOS (CO) | 0,0009 | 1,6%* | 0,0000 | 0,17 | –0,17 | 0,019 | 0,040 | 13 | 0% | 2.543 |
| IGBVL (PE) | 0,0008 | 6,1%* | 0,0004 | 0,128 | –0,133 | 0,0185 | –0,47* | 10,6 | 0% | 1.737 |
| VOLCABC1 (PE) | 0,0014 | 7,7%** | 0,0000 | 0,245 | –0,170 | 0,0321 | 0,20* | 9,5 | 0% | 1.737 |
| CVERDEC1 (PE) | 0,0012 | 5,5%** | 0,0000 | 0,140 | –0,163 | 0,0269 | –0,40* | 9,4 | 0% | 1.737 |
| MINSURI1 (PE) | 0,0003 | 65,9% | 0,0000 | 0,146 | –0,201 | 0,0243 | –0,54* | 11,7 | 0% | 1.737 |
| FERREYC1 (PE) | 0,0007 | 17,2% | 0,0000 | 0,119 | –0,197 | 0,0220 | –0,68* | 13,5 | 0% | 1.737 |
| CASAGRC1 (PE) | 0,0012 | 10,8% | 0,0000 | 0,153 | –0,165 | 0,0318 | 0,42* | 8,2 | 0% | 1.737 |
Fuente: elaboración propia.
BR: Brasil; C: curtosis: CL: Chile; CO: Colombia; MX: México; PE: Perú; S: sesgo.
Resultados evaluación conjunta de pruebas de aleatoriedad
| Activo | Evaluación conjunta | |||||||
| S&P500 (EE. UU.) | 2/1/06-31/8/12 | 10/10/02↓ | 10/10/07↑ | 10/03/09↓ | 31/08/12↑ | |||
| 0 | 4* | 1 | 0 | 1 | ||||
| IBOVESPA (BR) | 1/1/02-31/8/12 | 21/5/08↑ | 27/10/08↓ | 5/11/10↑ | 5/8/11↓ | 13/3/12↑ | 31/8/12↓ | |
| 0,5 | 3* | 3* | 3* | 4* | 3* | 4* | ||
| VALE5 (BR) | 1/1/02-31/8/12 | 21/5/08↑ | 27/10/08↓ | 5/11/10↑ | 31/08/12↓ | |||
| 0 | 0 | 2 | 4* | 4* | ||||
| PETR4 (BR) | 1/1/02-31/8/12 | 21/5/08↑ | 27/10/08↓ | 1/12/09↑ | 5/8/11↓ | 13/3/12↑ | 31/8/12↓ | |
| 0,5 | 0,5 | 1,5 | 3* | 3* | 4* | 2,5 | ||
| ITUB4 (BR) | 1/1/02-31/8/12 | 21/5/08↑ | 27/10/08↓ | 5/11/10↑ | 5/8/11↓ | 13/3/12↑ | 31/8/12↓ | |
| 0 | 0,5 | 1 | 3* | 4* | 2 | 4* | ||
| BBDC4 (BR) | 1/1/02-31/8/12 | 21/5/08↑ | 27/10/08↓ | 5/11/10↑ | 5/8/11↓ | 13/3/12↑ | 31/8/12↓ | |
| 0,5 | 1,5 | 1 | 1 | 4* | 4* | 3* | ||
| VALE3 (BR) | 1/1/02-31/8/12 | 21/5/08↑ | 27/10/08↓ | 5/11/10↑ | 31/08/12↓ | |||
| 0 | 0,5 | 2 | 3* | 4* | ||||
| IPC (MX) | 2/1/02-31/8/12 | 18/10/07↑ | 2/10/08↓ | 5/1/11↑ | 8/8/11↓ | 31/8/12↑ | ||
| 0 | 0,5 | 3* | 2,5 | 4* | 3* | |||
| AMXL (MX) | 2/1/02-31/8/12 | 18/10/07↑ | 27/10/08↓ | 5/11/10↑ | 8/8/11↓ | 7/5/12↑ | 31/8/12↓ | |
| 1 | 0,5 | 2 | 2,5 | 2,5 | 5* | 3* | ||
| WALMEXV (MX) | 2/1/02-31/8/12 | 6/2/07↑ | 2/3/09↓ | 9/4/12↑ | 31/8/12↓ | |||
| 1,5 | 1 | 2,5 | 3* | 4* | ||||
| FEMSAUBD (MX) | 2/1/02-31/8/12 | 29/5/08↑ | 27/10/08↓ | 31/8/12↑ | ||||
| 2,5 | 4* | 4* | 2,5 | |||||
| GMEXICOB (MX) | 2/1/02-31/8/12 | 29/10/07↑ | 20/11/08↓ | 3/1/11↑ | 31/8/12↓ | |||
| 1 | 1 | 3* | 3* | 3* | ||||
| TLEVISACPO (MX) | 2/1/02-31/8/12 | 16/4/07↑ | 6/3/09↓ | 22/12/10↑ | 31/8/12↓ | |||
| 0,5 | 3* | 1,5 | 2 | 3* | ||||
| IPSA (CL) | 1/1/02-31/8/12 | 3/7/07↑ | 10/10/08↓ | 5/1/11↑ | 8/8/11↓ | 2/4/12↑ | 31/8/12↓ | |
| 1 | 0 | 0 | 1 | 0 | 1 | 3* | ||
| COPEC (CL) | 1/1/02-31/8/12 | 25/10/07↑ | 16/2/08↓ | 10/11/10↑ | 4/10/11↓ | 15/2/12↑ | 31/8/12↓ | |
| 1 | 1,5 | 0 | 3* | 1 | 3* | 4* | ||
| LAN (CL) | 1/1/02-31/8/12 | 3/7/07↑ | 9/3/09↓ | 2/11/10↑ | 4/10/11↓ | 30/3/12↑ | 31/8/12↓ | |
| 0 | 0 | 2 | 1 | 0 | 3* | 2,5 | ||
| ENDESA (CL) | 1/1/02-31/8/12 | 22/6/07↑ | 21/1/08↓ | 30/11/11↑ | 4/10/11↓ | 24/4/12↑ | 31/8/12↓ | |
| 1 | 1 | 3,5* | 3* | 0 | 2 | 4* | ||
| SQMB (CL) | 1/1/02-31/8/12 | 18/6/08↑ | 10/10/08↓ | 25/07/11↑ | 4/10/11↓ | 31/8/12↓ | ||
| 0 | 1 | 2,5 | 2 | 2 | 4* | |||
| BSAN (CL) | 1/1/02-31/8/12 | 18/4/07↑ | 10/10/08↓ | 14/9/10↑ | 25/11/11↓ | 26/3/12↑ | 31/8/12↓ | |
| 1 | 2,5 | 0 | 3* | 1 | 4* | 4* | ||
| IGBC (CO) | 2/1/02-31/8/12 | 27/1/06↑ | 28/6/06↓ | 23/11/07↑ | 27/10/08↓ | 5/11/10↑ | 25/11/11↓ | 31/8/12↑ |
| 0 | 1 | 0,5 | 2 | 2 | 4* | 1,5 | 4* | |
| ECOPETROL (CO) | 27/10/08-31/8/12 | 27/10/08↓ | 5/11/10↑ | 25/11/11↓ | 31/8/12↑ | |||
| 2,5 | 2,5 | 3* | 3* | 2 | ||||
| PREC (CO) | 5/11/-31/8/12 | 5/11/10↑ | 25/11/11↓ | 31/8/12↑ | ||||
| 0,5 | 1 | 2 | 4* | |||||
| PFBCOLOM (CO) | 2/1/02-31/8/12 | 27/1/06↑ | 28/6/06↓ | 23/11/07↑ | 27/10/08↓ | 5/11/10↑ | 25/11/11↓ | 31/8/12↑ |
| 0 | 0 | 2,5 | 4* | 2,5 | 4* | 3* | 2,5 | |
| GRUPOSURA (CO) | 2/1/02-31/8/12 | 27/1/06↑ | 28/6/06↓ | 23/11/07↑ | 27/10/08↓ | 5/11/10↑ | 25/11/11↓ | 31/8/12↑ |
| 0 | 1 | 0 | 3* | 2,5 | 1,5 | 3* | 1,5 | |
| CEMARGOS (CO) | 2/1/02-31/8/12 | 27/1/06↑ | 28/6/06↓ | 23/11/07↑ | 27/10/08↓ | 5/11/10↑ | 25/11/11↓ | 31/8/12↑ |
| 0,5 | 0 | 1 | 4* | 2,5 | 3* | 4* | 4* | |
| IGBVL (PE) | 2/1/02-31/8/12 | 24/07/07↑ | 27/10/08↓ | 7/2/11↑ | 4/10/11↓ | 2/4/12↑ | 31/8/12↓ | |
| 0 | 3* | 0 | 1 | 3* | 3* | 3,5* | ||
| VOLCABC1 (PE) | 2/1/02-31/8/12 | 16/7/07↑ | 24/2/09↓ | 31/8/12↑ | ||||
| 0 | 1 | 0 | 3* | |||||
| CVERDEC1 (PE) | 2/1/02-31/8/12 | 15/10/07↑ | 28/10/08↓ | 3/1/11↑ | 31/8/12↓ | |||
| 0 | 0 | 1 | 2 | 1 | ||||
| MINSURI1 (PE) | 2/1/02-31/8/12 | 8/8/07↑ | 22/10/08↓ | 4/2/11↑ | 31/8/12↓ | |||
| 0 | 2 | 0 | 0 | 1,5 | ||||
| FERREYC1 (PE) | 2/1/02-31/8/12 | 9/5/07↑ | 12/3/09↓ | 4/2/11↑ | 26/4/11↓ | 27/3/12↑ | 31/8/12↓ | |
| 0 | 3* | 1 | 1 | 3* | 3* | 3* | ||
| CASAGRC1 (PE) | 2/1/02-31/8/12 | 8/5/07↑ | 28/10/08↓ | 7/1/11↑ | 18/11/11↓ | 28/3/12↑ | 31/8/12↓ | |
| 0 | 0 | 0 | 1 | 2 | 4* | 2 | ||
Fuente: elaboración propia.
BR: Brasil; CL: Chile; CO: Colombia; MX: México; PE: Perú.