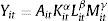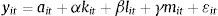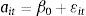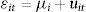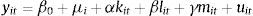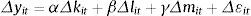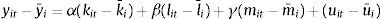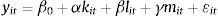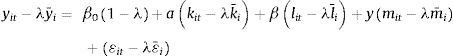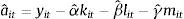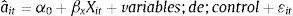En el presente artículo se analiza la producción del sector de innovación global en mercados locales en España durante el periodo 1990-2005 mediante la estimación de una función de producción por mínimos cuadrados ordinarios y efectos fijos y aleatorios, utilizando factores tradicionales. Este artículo tiene como objetivos realizar una descripción del sector, estimar una función de producción a nivel de empresa y, finalmente, estudiar la productividad total de los factores (PTF) y su relación con las exportaciones e innovación tecnológica. Como principales conclusiones se obtiene que la PTF presenta un patrón de crecimiento a lo largo del periodo y se encuentra evidencia a favor de una relación positiva entre la PTF y la actividad exportadora e innovadora de las empresas.
This paper analyzes the production of the sector of global innovation in local markets in Spain during the period 1990-2005, by estimating a function of production by Ordinary Least Squares and fixed and random effects, using traditional factors. This article aims at making a description of the sector, estimating a production function at firm level and, finally, studying the total factor productivity (TFP) and its relationship with exports and technological innovation. The main conclusions are that TFP presents a pattern of growth throughout the period and there is evidence in favor of a positive relationship between TFP and exports and innovative activities of the companies.
Este artigo analisa a produção do setor de inovação global nos mercados locais em Espanha durante o período 1990-2005, por meio da estimação de uma função de produção por mínimos quadrados ordinários e efeitos fixos e aleatórios usando fatores tradicionais. Este artigo tem como objetivo fazer uma descrição do setor, estimar uma função de produção no nível da empresa e, finalmente, estudar a produtividade total dos fatores (PTF) e sua relação com as exportações e a inovação tecnológica. As principais conclusões são que a PTF apresenta um padrão de crescimento ao longo do período e há evidências a favor de uma relação positiva entre a PTF e a atividade de exportação e inovação das empresas.
El estudio de las manufacturas a nivel mundial es un tema que se está retomando con mayor intensidad por la crisis económica del año 2008, que afectó a las principales economías, y porque podría ser una vía de salida a los problemas de mercado desde la producción, la productividad y la capacidad de mejora en los diferentes factores de producción de los sectores manufactureros que componen un país. Además, la visión de estudio de las manufacturas y las alternativas de mejora en cada uno de los sectores que lo componen generan una herramienta muy útil a los responsables de políticas públicas y empresariales.
La importancia de las manufacturas es notable al momento de observar ciertas cifras; por ejemplo, las manufacturas representaron para los países miembros de la Unión Europea el 15% del valor añadido bruto en 2012, el 67% de las exportaciones, el 65% del gasto en investigación y desarrollo (I+D) y el 14% del empleo (Veugelers, 2013). En el caso de España, las manufacturas contribuyeron al crecimiento y a la productividad, con un 26% entre los años 2010 y 2012, un 47% a los gastos de I+D en 2012, un 75% a las exportaciones en 2013, y realizaron un aporte del 13% al total del valor añadido bruto en 2013 (Fariñas, 2015).
Por otra parte, el sector manufacturero en España está conformado por 23 sectores1, donde cada sector se diferencia por ser intensivo en capital, trabajo y/o innovación tecnológica, que son los factores de producción tradicionales de la economía. De esta forma, dependiendo del sector y de su intensidad en alguno de los factores de producción mencionados, se puede determinar el grado de eficiencia de cada uno de ellos.
La segmentación de los sectores industriales y manufactureros se ha venido estudiando desde décadas atrás. Pavitt (1984) propone la agrupación de sectores industriales y manufactureros, y los clasifica en dominados por la oferta, intensivos en producción y basados en ciencia. Por otro lado, estudios más recientes de la Organización para la Cooperación y el Desarrollo Económico - OCDE (2001) clasifican a los sectores por su intensidad en I+D, calculadas a partir de dos medidas de la producción (valor de la producción y valor añadido). Esta clasificación divide a los sectores en: sectores de alta tecnología, sectores de media-alta tecnología, sectores de media baja tecnología y sectores de baja tecnología.
En la última década, el estudio del sector manufacturero ha tomado diferentes formas, especialmente por la agregación y conglomeración de sectores industriales que son intensivos en algún factor de producción tradicional y/o factores endógenos que ayudan especialmente a la eficiencia de cada industria, para lo cual a estos sectores se les podría realmente denominar subsectores de grandes segmentos, que acumulan las industrias intensivas en factores específicos que les generan cierta ventaja competitiva frente a otros segmentos.
En este trabajo se utiliza la clasificación del sector manufacturero propuesta por el McKinsey Global Institute (2012). Esta clasificación agrupa a las manufacturas en cinco grandes sectores y constituye una clasificación alternativa y útil para observar de manera global las diferencias entre industrias aunque se parezcan mucho. Estos cinco grandes sectores son: 1)sector de innovación global en mercados locales; 2)sector con fabricación orientada a mercados regionales; 3)sector intensivo en energía y recursos naturales; 4)sector de tecnología y mercados globales, y 5)sector intensivo en trabajo.
Esta clasificación hace hincapié en la importancia de la innovación en las industrias y es una clasificación útil para delimitar la intensidad en los factores de producción. Además, la clasificación propuesta por el McKinsey señala que el sector manufacturero es muy diverso y que cada subsector puede ser intensivo en los factores de producción tradicionales, pero también en factores endógenos tales como la intensidad del comercio que puede ser medida a partir de las exportaciones, intensidad de uso de energía y cadena de valor.
En este sentido, el objetivo de este trabajo es analizar el sector de innovación global en mercados locales en España. Este análisis se centra en tres aspectos: en primer lugar, en la descripción del sector de innovación global en mercados locales; en segundo lugar, en la estimación de una función de producción para las empresas de este sector; en tercer lugar, en el estudio de la productividad total de los factores (PTF) y su relación con las exportaciones e innovación tecnológica.
Para la estimación de la función de producción y análisis de la PTF y su relación con las exportaciones e innovación tecnológica se desarrolla un marco empírico simple como es una función al estilo Cobb Douglas con los insumos tradicionales. A partir de lo anterior, se estiman cuatro funciones de producción y se realizan dos estimaciones de productividad con datos de panel no balanceado para las empresas manufactureras españolas, agrupadas según el estudio del McKinsey Global Institute (2012).
Según el autor del presente artículo, recientemente no se han realizado estudios académicos sobre esta nueva forma de clasificación de las manufacturas y la estimación de funciones de producción en España. En el caso del presente trabajo, este se centra en uno de los sectores propuestos por el McKinsey Global Institute (2012): el sector de innovación global en mercados locales en España. Este sector está compuesto a su vez por cinco industrias (o subsectores): industria química y productos farmacéuticos; máquinas agrícolas e industriales; maquinaria y material eléctrico; vehículos de motor, y otro material de transporte. Esta agrupación es interesante, ya que es altamente intensiva en I+D y su competencia dentro del mercado se basa en innovaciones y nuevos modelos.
El presente trabajo está organizado de la siguiente manera. La sección 2 presenta una descripción del sector de innovación global en mercados locales en España y principales referencias teóricas sobre la PTF. La sección 3 se centra en la estimación de una función de producción y la PTF. La sección 4 muestra los principales resultados y, finalmente, la sección 5 presenta las principales conclusiones.
2Marco teóricoEn esta sección se presenta una descripción del sector de innovación global en mercados locales en España propuesto por el McKinsey Global Institute (2012), además de las principales características que posee esta nueva agrupación industrial. Por otro lado, se conceptualiza la PTF, sus diferentes formas de cálculos y los factores asociados a la productividad, de tal manera que se conozca qué actividades pueden influir en su rendimiento.
2.1El sector de innovación global en mercados locales en EspañaLa agrupación de segmentos propuesta por el McKinsey Global Institute (2012) responde a las continuas modificaciones industriales comprendidas especialmente desde la perspectiva de la especialización y competitividad en la producción. Son las economías avanzadas las que lideran la producción intensiva en I+D y las economías en vías de desarrollo las que lideran la producción intensiva en trabajo. Teniendo en cuenta la especialización en ciertos factores de producción dentro de las manufacturas, la clasificación propuesta por el McKinsey Global Institute (2012) divide a las manufacturas en los siguientes sectores: 1)sector de innovación global en mercados locales; 2)sector con fabricación orientada a mercados regionales; 3)sector intensivo en energía y recursos naturales; 4)sector de tecnología y mercados globales, y 5)sector intensivo en trabajo.
El estudio del McKinsey Global Institute (2012) utiliza la base de datos EU Klems growth and Productivity accounts2, que es un proyecto financiado por la Comisión Europea, específicamente por la Dirección General de Investigación como parte del Sexto Programa Marco, Prioridad 8, «Apoyo a las políticas y previsión de la ciencia y necesidades tecnológicas». La base de datos EU Klems contiene una muestra del periodo 1970-2007, y los datos usados son obtenidos de los institutos nacionales de estadísticas de cada país; la muestra de países comprende los miembros de la Unión Europea, Euro Zona, Australia, Canadá y Estados Unidos. En el caso del presente trabajo, para realizar la descripción del sector innovación global en mercados locales en España se utilizan datos de EU Klems para el periodo 1990-2007.
Para el caso de España, por ser considerada una economía desarrollada y en lo esencial un país muy competitivo en manufactura, se estudia el sector de innovación global en mercados locales, ya que es altamente intensivo en I+D. Adicionalmente, es importante mencionar que en la década de los noventa España ocupaba el puesto 9 en el ranking de países con mayor participación de las manufacturas como porcentaje del valor añadido bruto, luego en el año 2000 pasó a la posición 11 y en 2010 pasó a ocupar el puesto número 143.
El sector que se analiza tiene ciertas características muy relevantes; es muy intensivo en I+D, la competencia de sus productos está basada en la calidad y creación de nuevos productos para los mercados, posee productos intensivos en exportaciones, acceso a la cadena de valor, es muy próximo a la demanda (localización), es altamente regulado e intervenido gubernamentalmente y cuenta con mano de obra altamente calificada.
Se considera un sector muy próximo a la demanda, ya que los productos producidos por las empresas de este sector son ensamblados en la misma región donde se venden, debido a su alto coste de transporte y políticas de entrega a tiempo; además, generan economías de escala y de ámbito, optimizando los recursos.
Por otra parte, este sector posee políticas de regulación que ayudan a su desarrollo y se encuentra altamente intervenido. Este es otro motivo por el cual su producción y la comercialización de los diferentes productos se realizan dentro de la misma región. Por tanto, producir y comercializar sus productos dentro de una misma región genera una proximidad a la demanda que le da una ventaja al conocer rápidamente las necesidades del mercado y estar en constante innovación.
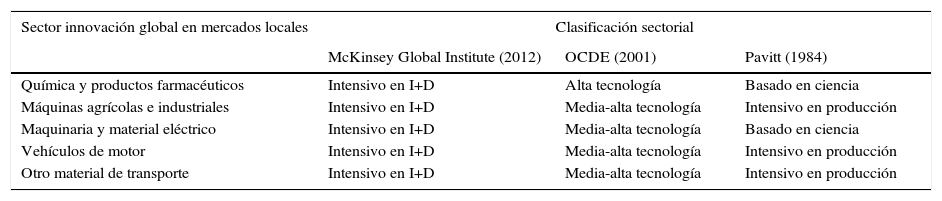
El sector de innovación global en mercados locales está compuesto por 5 industrias: industria química y productos farmacéuticos, máquinas agrícolas e industriales, maquinaria y material eléctrico, vehículos de motor, y otro material de transporte. En la tabla 1 se puede observar la clasificación sectorial de cada industria del sector innovación global en mercados locales propuesto por los diferentes estudios mencionados anteriormente, a partir de lo cual se puede concluir que entre las tres clasificaciones que se comparan no existen muchas diferencias en lo que respecta a la tecnología. En las clasificaciones del McKinsey Global Institute (2012) y de la OCDE (2001) los sectores se encuentran entre intensivos en innovación y media y alta tecnología, dado que son sectores que constantemente innovan y su producción se caracteriza por avances tecnológicos para poder ser vendidos en los diferentes mercados locales e internacionales. Por su parte, el estudio de Pavitt (1984) indica que los sectores basados en ciencia son los que más innovan y desarrollan productos más sofisticados.
Clasificación sectorial del sector innovación global en mercados locales
| Sector innovación global en mercados locales | Clasificación sectorial | ||
|---|---|---|---|
| McKinsey Global Institute (2012) | OCDE (2001) | Pavitt (1984) | |
| Química y productos farmacéuticos | Intensivo en I+D | Alta tecnología | Basado en ciencia |
| Máquinas agrícolas e industriales | Intensivo en I+D | Media-alta tecnología | Intensivo en producción |
| Maquinaria y material eléctrico | Intensivo en I+D | Media-alta tecnología | Basado en ciencia |
| Vehículos de motor | Intensivo en I+D | Media-alta tecnología | Intensivo en producción |
| Otro material de transporte | Intensivo en I+D | Media-alta tecnología | Intensivo en producción |
Fuente: elaborado a partir de Pavitt (1984), OCDE (2001), McKinsey Global Institute (2012).
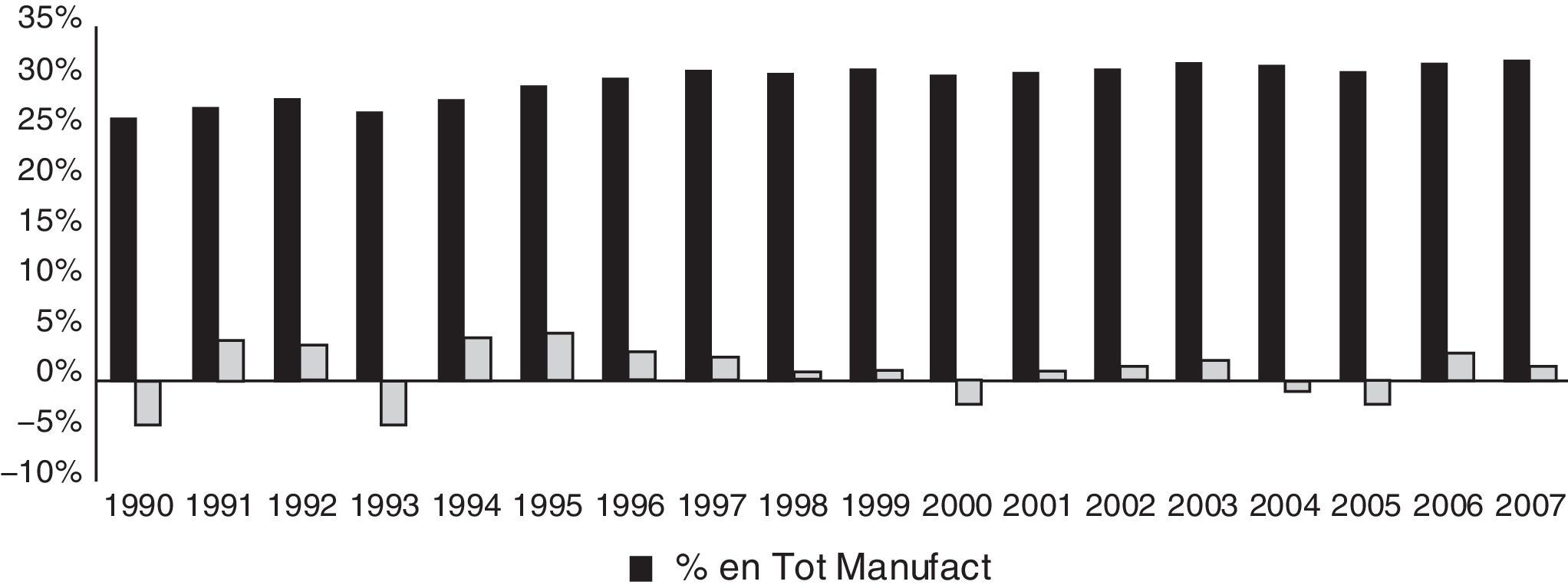
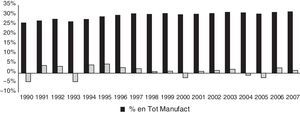
Según la clasificación propuesta por el McKinsey Global Institute (2012), el sector de innovación global en mercados locales aporta alrededor del 31% al valor añadido bruto del total manufacturero español. Además, esta aportación al valor añadido bruto es estable a lo largo del periodo analizado. Para el año 2007 este sector representaba el 31,9% del total del valor añadido bruto de las manufacturas españolas, con una variación interanual del 1,25%. La figura 1 detalla la evolución de la participación de este sector en las manufacturas españolas desde 1990 hasta 2007.
Es importante mencionar que el total de las manufacturas españolas ha presentado tasas interanuales de crecimiento del 5,67% para el año 2006 y del 5,65% para el año 2007; por lo tanto, el aumento de la participación del sector de innovación global en mercados locales no se debe a una disminución del valor añadido bruto de las manufacturas sino más bien al crecimiento de este sector.
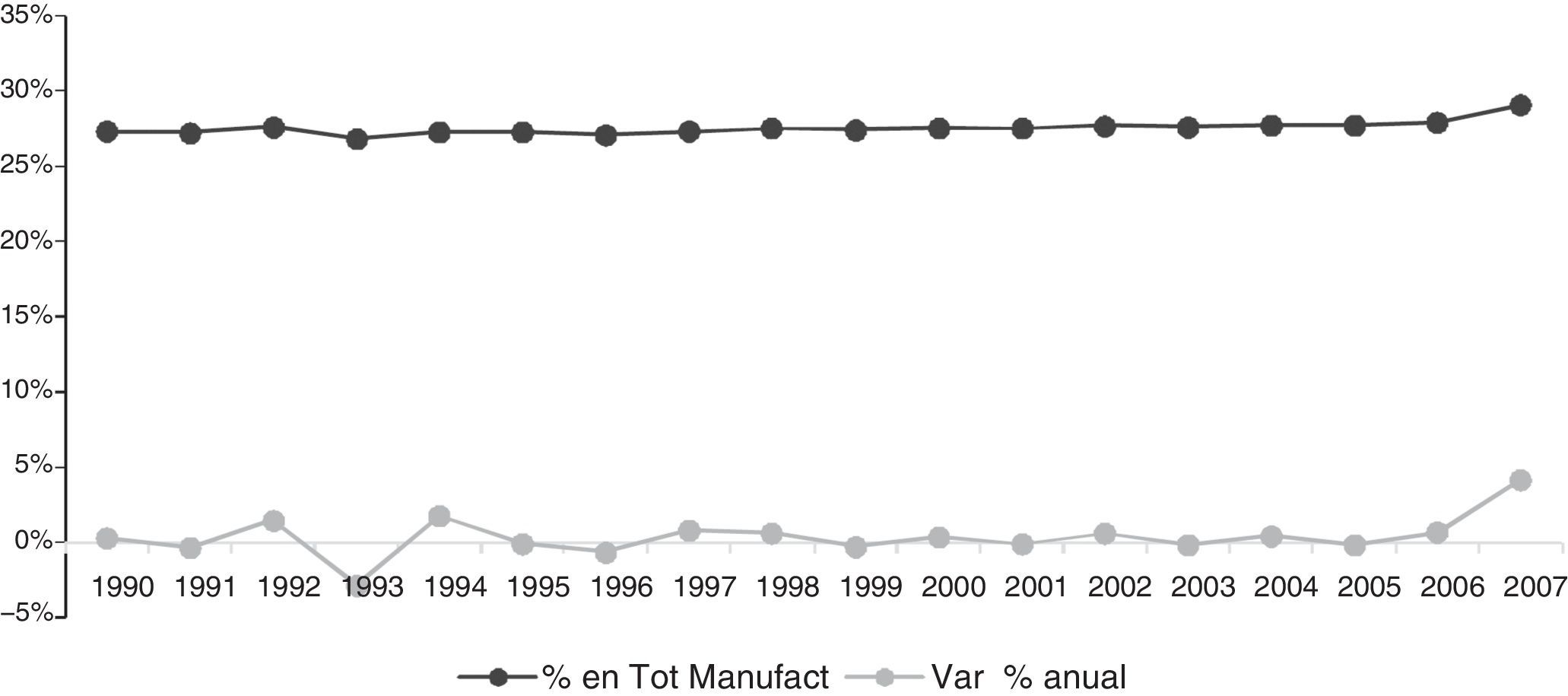
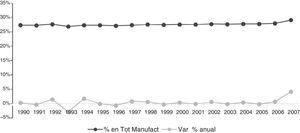
En la figura 2 se puede observar la evolución de la participación del sector en el total de los empleados de las manufacturas españolas desde el año 1990 hasta 2007. Durante la década de los noventa y hasta el año 2006 el sector de innovación global en mercados locales aporta alrededor del 27% de los empleados del total de las manufacturas, mientras que en el año 2007 tiene un pequeño repunte, llegando a aportar el 29% y obteniendo un crecimiento interanual del 4,2%, esto gracias a la época de auge de la economía española.
2.2Productividad total de los factoresLa PTF representa la producción que no es explicada por los factores productivos, lo que en macroeconomía se denomina Residuo de Solow. Para calcular la PTF existen diversas metodologías. Van Biesebroeck (2007) menciona que existen tres enfoques generales para el cálculo de la PTF: 1)el cálculo de la PTF mediante el uso de números índices, que supone que las empresas toman decisiones de inputs de manera óptima pero con algunas restricciones de la naturaleza de las decisiones tecnológicas; 2)la estimación mediante fronteras no paramétricas, tales como el análisis envolvente de datos (DEA), que construye para cada observación una combinación lineal de todas las demás observaciones (normalizado por output) para la comparación explícita, donde la tecnología sigue siendo específica en cada empresa, y, por último, 3)la estimación de funciones de producción mediante métodos paramétricos o semiparamétricos. En este trabajo se calcula (o estima) la PTF mediante la estimación de funciones de producción aplicando un método paramétrico.
En general, el estudio de la PTF y de los factores que la determinan es muy importante para explicar las diferencias de productividad entre empresas, sectores industriales y, por lo tanto, para tomar decisiones de política económica.
Existe una amplia literatura que analiza los factores asociados a la PTF de las empresas. Una lista (no exhaustiva) de estos factores es: exportaciones, innovación tecnológica, gasto en I+D, subcontratación de personal, aprender haciendo (learning by doing), tamaño de la empresa, capital humano, uso de tecnologías de la información y la comunicación (TIC), innovación organizativa.
En este orden de ideas, que una empresa tenga una mayor PTF que otra puede llevar a dos conclusiones: que produce más con la misma cantidad de inputs, o para producir la misma cantidad de output necesita una menor cantidad de factores productivos. El estudio realizado por Syverson (2011) es una importante contribución al estudio sobre los determinantes de la productividad, y por qué es importante su estudio para los economistas y responsables de política económica. Muchas veces se suele considerar la productividad como un concepto de la oferta, pero la demanda también influye en la productividad cuando se conocen las variaciones de los precios dentro de una industria; además de las causas sobre las diferencias de la productividad que se mencionan en el párrafo anterior, se puede mencionar qué factores tanto internos como externos de las empresas cambian la distribución de la productividad.
El análisis de la PTF y la relación que tiene con las exportaciones es muy importante, ya que a menudo se menciona que las empresas más productivas son las que exportan, pero también se podría mencionar que las empresas que exportan se vuelven más productivas. Por lo tanto, podría existir un efecto de doble vía o causalidad. Wagner (2007) menciona que las empresas exportadoras son más productivas que las no exportadoras, pero que la exportación no mejora necesariamente la productividad. Por lo tanto, existen dos hipótesis alternativas pero no mutuamente excluyentes de por qué son más productivas las empresas exportadoras que las no exportadoras. La primera hipótesis apunta a la libre selección de las empresas más productivas en los mercados de exportación. La razón de esto es que existen costes adicionales de venta de bienes en países extranjeros, y además, el comportamiento de las empresas podría ser prospectivo en el sentido de que el deseo de exportar mañana conduce a una empresa a mejorar el rendimiento hoy para ser competitiva en el mercado exterior. La segunda hipótesis apunta a la función de aprendizaje a través de la exportación. Los flujos de conocimiento de los compradores y de los competidores internacionales ayudan a mejorar el desempeño posterior a la entrada de insumos de exportación. Por otra parte, las empresas que participan en los mercados internacionales están expuestas a una competencia más intensa y deben mejorar más rápidamente que las empresas que venden sus productos únicamente a nivel nacional. En este sentido, exportar haría que las empresas sean más productivas.
Por otro lado, Syverson (2011) estudia la competencia comercial de las empresas y concluye que los exportadores son casi inevitablemente más productivos que sus colegas no exportadores de la industria. Sin embargo, la mayoría de los estudios han encontrado que esta correlación refleja en gran medida la relación en lugar de un efecto causal de la exportación sobre la productividad. En realidad, las empresas que eligen comenzar la exportación ya eran más productivas antes del comercio internacional. Esto es sorprendente, aunque solo sea porque las empresas exportadoras pueden aprovechar los beneficios de las ganancias de productividad en los mercados más grandes, aumentando el incentivo de participar en actividades innovadoras.
No obstante, la gama de los costes adicionales a la producción en el caso de las empresas exportadoras incluye costes de transporte, costes de distribución o comercialización, personal con habilidades para gestionar redes extranjeras, o costes de producción en la modificación de los productos nacionales actuales para el consumo extranjero. Estos costes proporcionan una barrera de entrada que las empresas menos exitosas no podrían superar.
Otro de los factores importantes que se estudian al momento de analizar los elementos que determinan la PTF es la innovación tecnológica (innovación de producto o de proceso). La innovación tecnológica ayuda en muchas ocasiones a mejorar los procesos productivos, logrando una mayor eficiencia y eficacia, además de mejorar la calidad del producto, lo que generaría un aumento en ventas y un aumento de productividad. En este sentido, existen numerosos estudios que mencionan la importancia de la innovación en la mejora de la PTF, tales como Hall (2011), Mohnen y Hall (2013), Wieser (2005), entre otros.
Por su parte, Syverson (2011) manifiesta que las innovaciones en la calidad de los productos algunas veces no aumentan la cantidad producida, y lo que normalmente hacen es aumentar el precio del producto y, como consecuencia, la empresa aumenta los ingresos por venta de unidad. Si se piensa en la productividad como unidades de calidad entregada por venta de unidad, la innovación de productos puede mejorar la productividad; pero muchas veces la innovación de producto va direccionada a entrar en nuevos mercados o a la entrada en segmentos con demanda en crecimiento.
3MetodologíaLa economía industrial ha experimentado muchos cambios desde finales de los ochenta, donde se han propuesto nuevos modelos empíricos para analizar situaciones de competencia y organización de los mercados. Estos resultados de las estimaciones de los modelos empíricos son usados por las empresas, organizaciones gubernamentales y responsables de políticas públicas para poder comprender cómo se organizan y operan las firmas, y además para que a partir de la información obtenida se puedan tomar decisiones por el lado de la demanda y/o la oferta. En este sentido, la estimación de una función de producción ha tomado relevancia, ya que sirve para evaluar la eficiencia de una industria, sector o segmento de la economía, observando cómo es el comportamiento de sus rendimientos a escala, si sus factores de producción son sustituibles entre sí, costes de regulación, fusiones, economías de alcance y el aprendizaje con la experiencia (learning by doing). Además, la estimación de funciones de producción es una de las vías para el cálculo de la PTF.
Dado lo anterior, en esta sección se presenta el método y modelo empírico que se utiliza para analizar la función de producción y de PTF del sector de innovación global en mercados locales en España; adicionalmente, se indican los datos empleados para dicho análisis, desagregados por subsector económico.
3.1Método y modelo empíricoExisten algunos autores que han estimado funciones de producción para luego estudiar la productividad en los diferentes sectores de una economía; entre los más destacados y que han utilizado el modelo propuesto para esta investigación se encuentran Van Biesebroeck (2007), Van Beveren (2012) y Syverson (2011). Siguiendo a estos mismos autores, el modelo propuesto supone que la empresa i produce un solo output en el tiempo t con una función de producción Cobb-Douglas.
donde Y representa la producción real, A es un índice de progreso técnico Hicks-Neutral y proporciona una medida de la PTF, K representa el stock de capital real, L representa el factor trabajo y M representa los consumos intermedios (o materias primas). Aplicando logaritmos neperianos en la ecuación1 se obtiene una expresión lineal de la función de producción. Además, realizando esta transformación, los parámetros α, β, γ se convierten en las elasticidades de los factores productivos respecto del output. La suma de estos tres parámetros indicaría el tipo de rendimientos a escala que presentan la función de producción.
donde y representa el logaritmo neperiano de la producción real, las letras minúsculas k, l, m representan los logaritmos neperianos de los inputs y a representa la PTF (en logaritmos). En este trabajo se supone que este último término se puede descomponer en β0, que puede interpretarse como el nivel de eficiencia media de las empresas a través del tiempo, y εit, que puede interpretarse como la desviación de esa media para la empresa i en el periodo t. A su vez, también se supone que el término εit tiene dos componentes: μiyuit. En primer lugar μi, representa la heterogeneidad inobservable. Este término recoge la productividad no observada por los analistas pero observada por las empresas (por ejemplo, intuitivamente, μi puede estar asociado a la capacidad de gestión en la empresa). En este trabajo se supone que μi es constante en el tiempo. En segundo lugar, el término uit no es observado ni por la empresa ni por los analistas (es un error aleatorio). Por tanto, la ecuación2 se puede reescribir de la siguiente forma:
La ecuación 3 se puede estimar por el método de mínimos cuadrados ordinarios (MCO), pero se conoce desde las primeras estimaciones de funciones de producción que este método presenta problemas. Uno de los problemas es que si las empresas eligen sus inputs después de conocer su productividad μi, es muy probable que estas decisiones estén correlacionadas con μi y, por tanto, se genera un problema de endogeneidad. En este caso, los estimadores MCO serán sesgados y los estadísticos t no serían válidos para probar hipótesis. Por lo tanto, es necesario corregir el problema de endogeneidad generado por la correlación entre la productividad y los inputs variables para poder obtener estimaciones consistentes.
En este trabajo se utilizan tres alternativas a la estimación por MCO: dos estimadores de efectos fijos (estimación en primeras diferencias y estimador intragrupos) y el estimador de efectos aleatorios. El primero de los estimadores en primeras diferencias logra eliminar el efecto fijo. En la ecuación3 existe un efecto fijo (μi) (heterogeneidad inobservable) que se puede eliminar si a cada empresa se le resta su observación del periodo anterior, es decir, se realiza una estimación en primeras diferencias y se obtiene que el efecto fijo es eliminado del residual (Δεit=εit−εit−1), obteniendo la siguiente expresión:
Donde Δyit, Δkit, Δlit, Δmit son, respectivamente, primeras diferencias de logaritmos del output, capital, trabajo y consumos intermedios.
Por otra parte, el estimador de intragrupos elimina el efecto fijo calculando para cada individuo las diferencias respecto a la media. Entonces se calcula la media de cada variable para cada individuo, así yi¯=∑Tt=1yitT, y entonces μi¯=μi. La productividad no observada en la función de producción μi es constante para cada empresa, y este supuesto permite estimar consistentemente los parámetros utilizando cualquier método basado en primeras diferencias o diferencias con respecto a la media.
Por tanto, el modelo de la ecuación3 se puede transformar, ya que las diferencias serían respecto a la media de cada parámetro, por lo que se necesita que los errores y los regresores no estén correlacionados; además, no se puede estimar el efecto con variables constantes en el tiempo, ya que solo se usa variación intragrupos y no entre individuos. Entonces la ecuación3 se puede re escribir de la siguiente forma:
No obstante, el principal problema de la estimación por efectos fijos intragrupos es el supuesto que μi es constante en el tiempo, en paneles largos; pero si el periodo de estudio contiene importantes cambios macroeconómicos, esto es difícil de asumir.
Por último, el estimador de efectos aleatorios supone que el efecto inobservable μi no se correlaciona con ninguna variable explicativa, es decir, Covxitj,μi=0,t=1,2,…,T;j=1,2,…,k, y se puede estimar por el método de mínimos cuadrados generalizados (MCG), ya que de esta manera se mejora la eficiencia y se asume que no existe correlación entre los errores y los regresores.
De esta forma, el supuesto de efectos aleatorios reúne todos los supuestos de efectos fijos más el requisito adicional que μi es independiente de todas las variables explicativas en todos los periodos. En este sentido, se puede definir el término de error compuesto como εit=μi+uit. Por lo tanto, se puede escribir la fórmula como:
Como μi está en el error compuesto en cada periodo, los εit se correlacionan serialmente en cada periodo de tiempo, bajo los supuestos de efectos aleatorios, de tal manera que Covεit,εis=σa2σa2+σu2, t≠s, donde σa2=Varai y σu2=Varuit. Dado lo anterior, es posible usar el modelo de MCG para resolver los problemas de correlación serial. Sin embargo, se debe tener una N grande y una T relativamente pequeña. Finalmente, el método de efectos aleatorios puede asumir que λ=1−σu2σu2+Tσa21/2 y que está entre 0 y 1; dado este supuesto, el modelo de MCG puede transformarse en un modelo de MCO y podría estimarse de la siguiente manera:
La barra superior en las variables indica los promedios a lo largo del tiempo. La ecuación6 permite variables explicativas constantes en el tiempo, lo que representa una ventaja sobre los efectos fijos en primeras diferencias e intragrupos, ya que supone que el efecto inobservable no está correlacionado con ninguna de las variables explicativas, ya sea que estas estén fijas en el tiempo o no.
En resumen, se realizan las estimaciones de efectos fijos (intragrupos) ya que este estimador es consistente, tanto si los efectos individuales están correlacionados con los factores productivos como si no lo están. Además, se estima el modelo de efectos aleatorios ya que es más eficiente que el estimador intragrupos en el caso que los efectos individuales estén incorrelacionados con los regresores, es decir, sean puramente aleatorios. Si los efectos individuales están correlacionados con los regresores (factores productivos) el estimador de efectos aleatorios es inconsistente; por lo tanto, se sugiere utilizar el estimador de efectos fijos (intragrupos). Esta solución de qué estimador utilizar lo indica el cálculo del test de Hausman.
Las limitaciones de los métodos de estimación analizados en este trabajo es que a menudo al usar el estimador intragrupos o de efectos aleatorios y suponer que μi es invariante en el tiempo y solo cambia con las empresas, conduce a estimaciones irrazonablemente bajas del coeficiente del capital; además, el estimador de efectos fijos impone estricta exogeneidad de los inputs condicionada a la heterogeneidad de las empresas. En términos económicos esto significa que los insumos no pueden ser elegidos como reacción a los choques de productividad, un supuesto que no es probable que se mantenga en la práctica (Van Beveren, 2012). Desde inicios del 2000, para relajar estas limitaciones se utilizan métodos más sofisticados, como la estimación del método de momentos generalizados (GMM, pos sus siglas en inglés) propuesto por Blundell y Bond (2000), y métodos semiparamétricos, como el propuesto por Olley y Pakes (1992). Sin embargo, la utilización de estos métodos de estimación excede los objetivos de este trabajo.
Por lo tanto, una vez estimadas las funciones de producción para el sector de innovación global en mercados locales de España, se utilizan los coeficientes estimados de cada uno de los inputs en primeras diferencias, ya que estos coeficientes, según la literatura sobre funciones de producción, son los más utilizados. Dado lo anterior, se obtiene:
Cuando se estima la PTF de la ecuación7, se puede relacionar la PTF con otras variables y de esta manera observar si existe una asociación positiva o negativa. En este trabajo se analiza la relación con las exportaciones e innovación tecnológica por separado, y para realizar esta modelización la ecuación que se estima es la siguiente:
donde Xit es una variable dummy que representa alternativamente la actividad exportadora de la empresa y si la empresa ha obtenido innovaciones tecnológicas (producto o proceso). En la estimación de la ecuación8 también se incluyen variables de control de tamaño y año4.
Es este sentido, lo que busca esta estimación es analizar si existe una relación positiva entre la PTF de las empresas y las dos actividades analizadas. El marco propuesto en este trabajo no permite obtener conclusiones sobre la dirección del efecto (es decir, sobre la causalidad).
3.2Materiales: descripción de los datos y variablesEn este análisis se utilizan datos de la Encuesta sobre Estrategias Empresariales (ESEE). La ESEE es una encuesta de panel a empresas industriales manufactureras que, iniciada con los datos correspondientes a 1990, se ha venido realizando hasta el año 2015. Se basa en una muestra dinámicamente representativa (articulada en dos grandes submuestras, empresas con más y menos de 200 trabajadores) a la que se ha investigado en un conjunto muy amplio de aspectos relacionados con temas de economía industrial. En este sentido, Fariñas y Jaumandreu (1999) constituyen una introducción a la ESEE y a su empleo para quien desee trabajar con la misma.
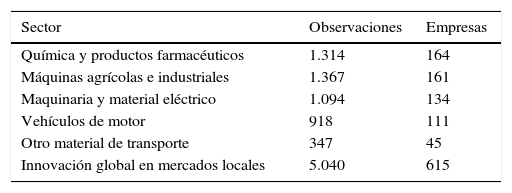
Para este trabajo se dispone de un panel no balanceado (panel incompleto) de 615 empresas y 5.040 observaciones pertenecientes solo al sector de innovación global en mercados locales para el período 1990-2005. En la tabla 2 se muestra la distribución de las empresas y observaciones de todo el sector que se estudia y de las 5 industrias que lo componen: química y productos farmacéuticos, máquinas agrícolas e industriales, maquinaria y material eléctrico, vehículos de motor y otro material de transporte.
Distribución de empresas y observaciones de cada sector
| Sector | Observaciones | Empresas |
|---|---|---|
| Química y productos farmacéuticos | 1.314 | 164 |
| Máquinas agrícolas e industriales | 1.367 | 161 |
| Maquinaria y material eléctrico | 1.094 | 134 |
| Vehículos de motor | 918 | 111 |
| Otro material de transporte | 347 | 45 |
| Innovación global en mercados locales | 5.040 | 615 |
Fuente: elaboración propia con base en los datos de la ESEE.
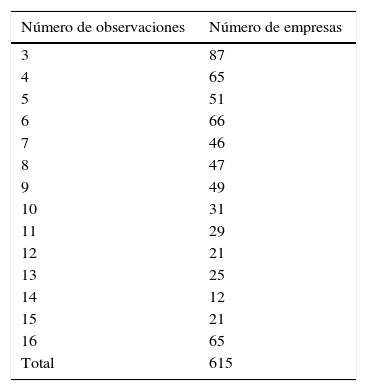
En la tabla 3 se describe cómo está clasificado el número de empresas de acuerdo al número de años consecutivos para los que la ESEE posee información disponible de las empresas. Además, en los anexos (tabla A1) se muestra el número de observaciones por sectores y por años que componen el segmento a estudiar.
Número de empresas clasificadas por el número de años consecutivos para los que la empresa tiene información disponible
| Número de observaciones | Número de empresas |
|---|---|
| 3 | 87 |
| 4 | 65 |
| 5 | 51 |
| 6 | 66 |
| 7 | 46 |
| 8 | 47 |
| 9 | 49 |
| 10 | 31 |
| 11 | 29 |
| 12 | 21 |
| 13 | 25 |
| 14 | 12 |
| 15 | 21 |
| 16 | 65 |
| Total | 615 |
Fuente: elaboración propia con base en los datos de la ESEE.
Una de las principales ventajas de la ESEE es que proporciona información sobre precios del output y precio de los consumos intermedios, lo que logra transformar ciertas variables de nominales a reales de tal manera que las variaciones de los insumos y de la producción no se encuentren influenciadas por las variaciones de los precios; de esta manera también se disminuye el sesgo en la estimación de la PTF. En concreto, si la empresa es capaz de negociar precios más bajos para una entrada dada, el uso de los precios a nivel de la industria en lugar de precios de los insumos a nivel de empresa dará lugar a una subestimación de su uso de insumos, causando que la PTF esté sesgada hacia arriba (Van Beveren, 2012).
De esta forma, varios trabajos utilizan la ESEE para la estimación de funciones de producción de sectores manufactureros en España; por ejemplo, Martín-Marcos y Suárez (1997). Por otro lado, existen también algunos estudios más profundos sobre la estimación de funciones de producción en el sector manufacturero pero agregándole variables como la subcontratación, la localización de empresas y las exportaciones (Fariñas y Martín-Marcos, 2007; Fariñas, López y Martín-Marcos, 2014; López, 2014).
Debido a que se estudia la relación entre la PTF y las exportaciones, la tabla 4 muestra el porcentaje de empresas que exportan por industria del sector de innovación global en mercados locales durante el periodo 1990-2005 en España. En dicha tabla 4 se observa que la industria de vehículos de motor es la que más exporta, mientras que la industria de otro material de transporte es la que menos lo hace.
Porcentaje de empresas que exportan del total de cada industria
| Sector | Exportan (%) |
|---|---|
| Química y productos farmacéuticos | 73,36 |
| Máquinas agrícolas e industriales | 70,15 |
| Maquinaria y material eléctrico | 73,12 |
| Vehículos de motor | 82,13 |
| Otro material de transporte | 68,87 |
| Innovación global en mercados locales | 73,73 |
Fuente: elaboración propia con base en los datos de la ESEE.
Por otra parte, la tabla 5 muestra el porcentaje de empresas en España que introdujeron alguna innovación tecnológica por industria del sector de innovación global en mercados locales durante el periodo 1990-2005. La industria que más innovó fue la de maquinaria y material eléctrico, mientras que la que menos lo hizo fue la de maquinarias agrícolas e industriales.
Porcentaje de empresas que innovan del total de cada industria
| Sector | Innovan (%) |
|---|---|
| Química y productos farmacéuticos | 52,35 |
| Máquinas agrícolas e industriales | 47,91 |
| Maquinaria y material eléctrico | 57,95 |
| vehículos de motor | 57,51 |
| Otro material de transporte | 53,60 |
| Innovación global en mercados Locales | 53,39 |
Fuente: elaboración propia con base en los datos de la ESEE.
En esta sección se presentan los principales resultados de la estimación de las ecuaciones3, 4, 5 y 6 realizadas al sector de innovación global en mercados locales de España. En los anexos (tabla A2) se muestra la definición de cada una de las variables que se han utilizado para la estimación de las ecuaciones mencionadas.
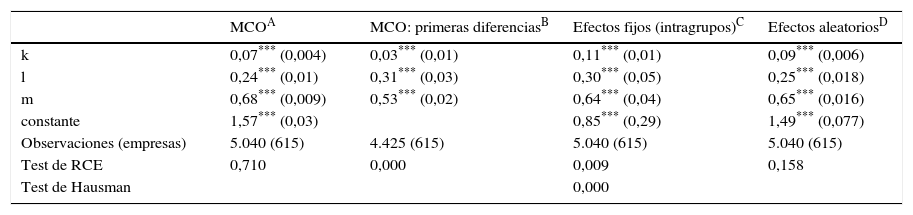
En la tabla 6 se presenta la estimación de la función de producción por diferentes métodos: MCO, MCO en primeras diferencias, MCO efectos fijos intragrupos y MCG efectos aleatorios. En este caso, la muestra es el conjunto de empresas que forman el sector de innovación global en mercados locales de España.
Estimación de la función de producción del sector innovación global en mercados locales de España
| MCOA | MCO: primeras diferenciasB | Efectos fijos (intragrupos)C | Efectos aleatoriosD | |
|---|---|---|---|---|
| k | 0,07*** (0,004) | 0,03*** (0,01) | 0,11*** (0,01) | 0,09*** (0,006) |
| l | 0,24*** (0,01) | 0,31*** (0,03) | 0,30*** (0,05) | 0,25*** (0,018) |
| m | 0,68*** (0,009) | 0,53*** (0,02) | 0,64*** (0,04) | 0,65*** (0,016) |
| constante | 1,57*** (0,03) | 0,85*** (0,29) | 1,49*** (0,077) | |
| Observaciones (empresas) | 5.040 (615) | 4.425 (615) | 5.040 (615) | 5.040 (615) |
| Test de RCE | 0,710 | 0,000 | 0,009 | 0,158 |
| Test de Hausman | 0,000 | |||
RCE: rendimientos constantes a escala.
indica la significancia al 1% de nivel de confianza.
Las estimaciones A, B, C y D corresponden a las ecuaciones 3, 4, 5, 6, respectivamente, de la sección 3.
Errores estándar robustos a heterocedasticidad de coeficientes estimados se encuentran entre paréntesis.
Fuente: elaboración propia con base en los datos de la ESEE.
Los resultados de la tabla 6 muestran valores plausibles en las estimaciones de los coeficientes de los factores de producción tradicionales. Cuando se estima esta función de producción los resultados de los coeficientes son estimaciones de las elasticidades y, como se ha mencionado anteriormente, existen diferencias en el cálculo del coeficiente del capital; esto sucede específicamente por las limitaciones del uso de los estimadores intragrupos y efectos aleatorios. Por otro lado, se rechaza la existencia de rendimientos constantes a escala en el estimador de efectos fijos en primeras diferencias e intragrupos.
Es importante señalar también que el sector de innovación global en mercados locales de España prefiere la estimación por efectos fijos (intragrupos) una vez contrastado el test de Hausman entre efectos fijos (intragrupos) y efectos aleatorios. Por lo tanto, esto indica que el supuesto clave de efectos aleatorios es falso (Covxitj,μi=0,t=1,2,…,T;j=1,2,…,k); de esta manera, los efectos individuales (ineficiencia) están correlacionados con los regresores (factores productivos).
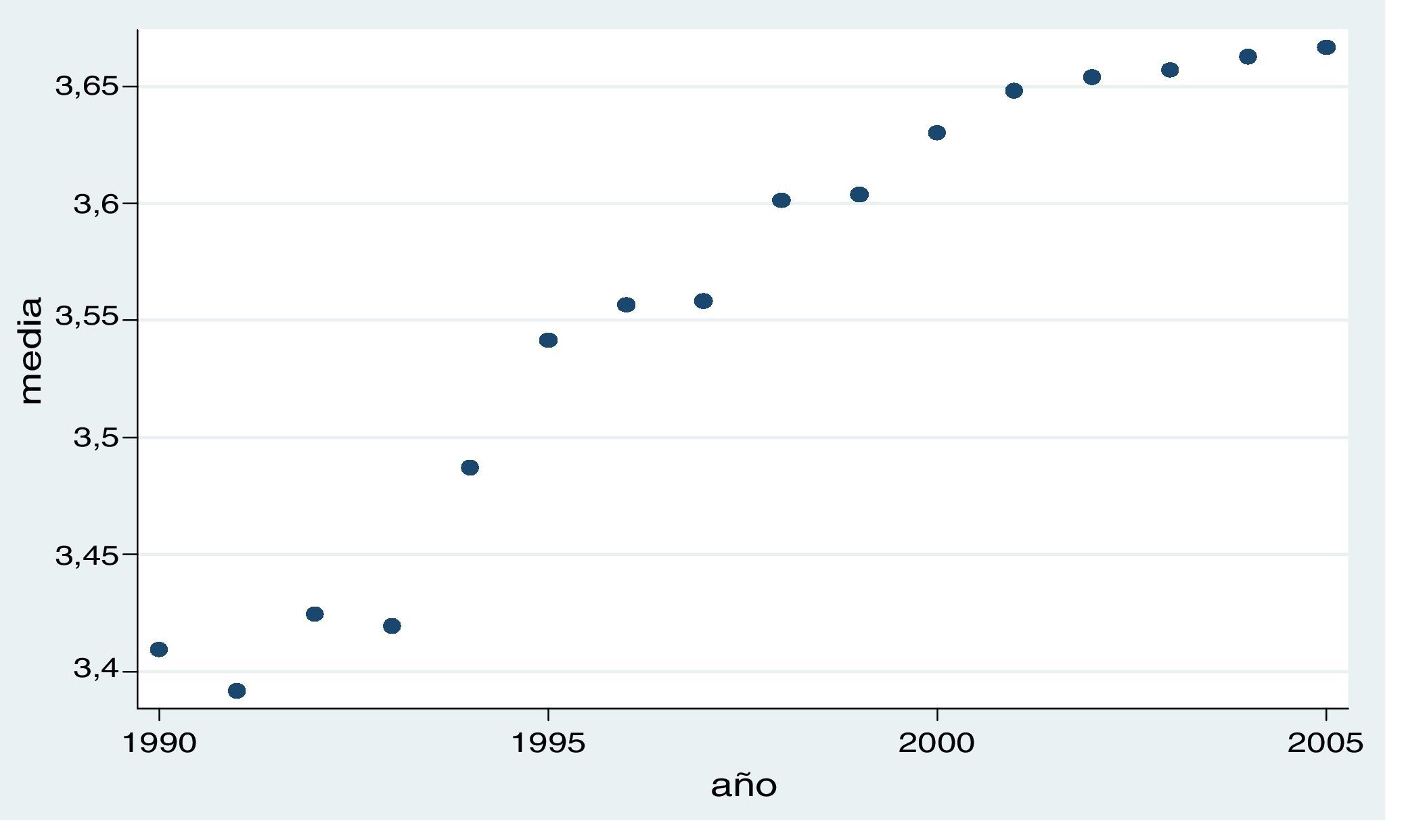
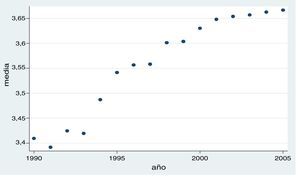
Una vez estimada la función de producción para el sector de innovación global en mercados locales se puede calcular la PTF mediante la ecuación7. De esta manera, la figura 3 muestra la evolución de la media de la PTF en el sector de innovación global en mercados locales. A partir de este cálculo, se observa una evolución positiva de la PTF a lo largo del periodo analizado.
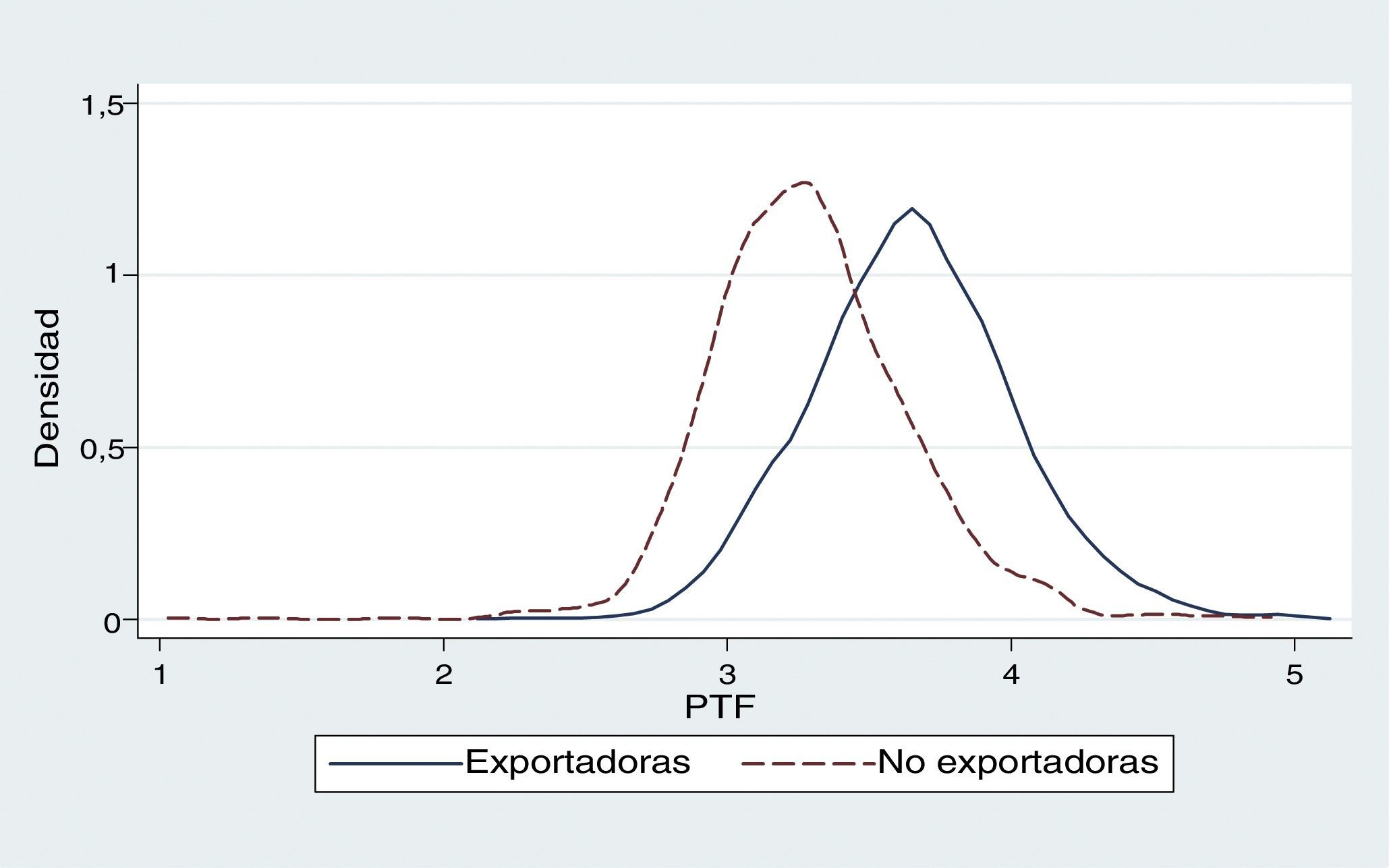
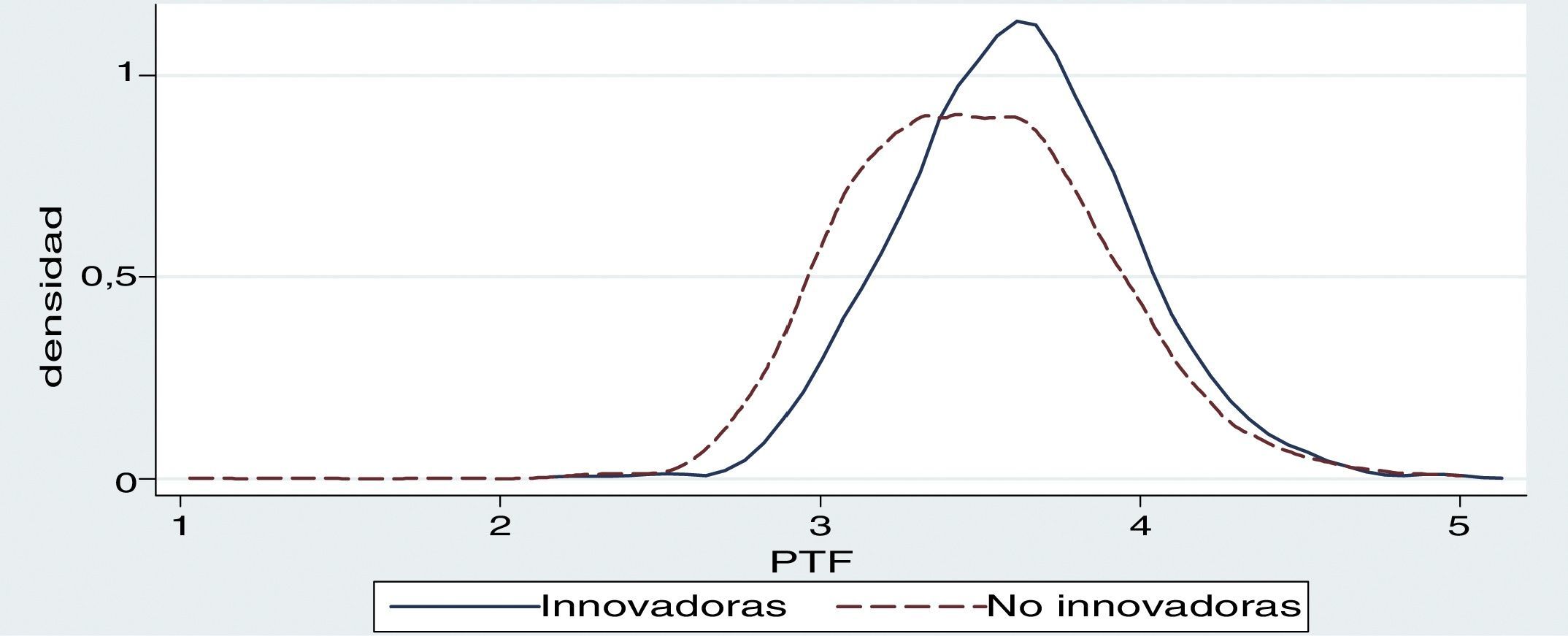
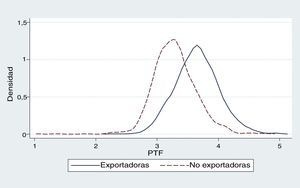
Por otro lado, uno de los objetivos de este estudio es determinar la relación que existe entre las exportaciones y la PTF. De esta forma, en la figura 4 se muestra cómo la media de la PTF es mayor cuando las empresas del sector de innovación global en mercados locales exportan en comparación con las que no exportan, donde la distribución de las empresas exportadoras está desplazada a la derecha de las no exportadoras. Este análisis gráfico es una primera señal de que existe una relación positiva entre PTF y exportaciones.
Para corroborar esta información proporcionada por la figura 4 se procede a estimar la relación entre la PTF y la actividad exportadora de las empresas utilizando la ecuación8. En este caso, la variable Xit en la ecuación8 es una variable dummy que captura si la empresa exporta o no (esta variable es igual a 1 cuando la empresa exporta y es 0 si no lo hace).
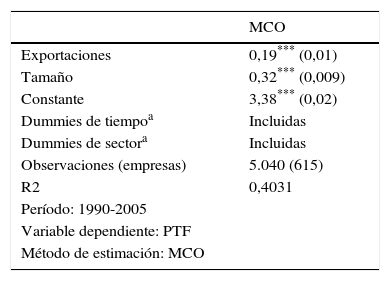
En la tabla 7 se estima la ecuación8 por MCO, a partir de la cual se puede observar que existe una relación positiva entre la PTF y las exportaciones, ya que la variable exportaciones es significativa y positiva; por lo tanto, las empresas que exportan en el segmento de innovación global en mercados locales poseen una PTF aproximadamente de un 20,92% más que las que no son exportadoras, manteniendo constante los demás factores5.
Estimación de la PTF del sector innovación global en mercados locales de España a nivel de empresa relacionada con las exportaciones
| MCO | |
|---|---|
| Exportaciones | 0,19*** (0,01) |
| Tamaño | 0,32*** (0,009) |
| Constante | 3,38*** (0,02) |
| Dummies de tiempoa | Incluidas |
| Dummies de sectora | Incluidas |
| Observaciones (empresas) | 5.040 (615) |
| R2 | 0,4031 |
| Período: 1990-2005 | |
| Variable dependiente: PTF | |
| Método de estimación: MCO |
Las estimaciones corresponden a la ecuación 8.
La tabla 7 también muestra que existe una relación positiva entre la PTF y la variable tamaño de la empresa, ya que es significativa y positiva; esto quiere decir que cuando una empresa posee más de 200 trabajadores posee una PTF aproximadamente de un 37,71% más que una que tiene menos de 200 trabajadores.
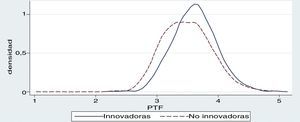
Por otro lado, en la figura 5 se puede observar que la media de la PTF es ligeramente mayor cuando las empresas del sector de innovación global en mercados locales realizan innovación tecnológica en comparación con las que no la realizan; esta es una primera señal de que existe una relación positiva entre PTF e innovación tecnológica.
Para corroborar esta información proporcionada por la figura 5 se procede a estimar la relación entre la PTF y la innovación tecnológica de las empresas utilizando la ecuación8. En este caso la variable Xit en la ecuación8 es una variable dummy que captura si la empresa realiza innovación tecnológica o no (esta variable es igual a 1 cuando la empresa innova y es 0 si no lo hace).
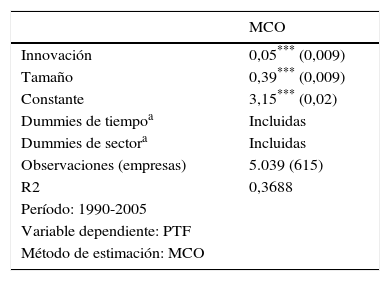
En la tabla 8 se muestra la estimación de la ecuación8 por MCO. En esta se puede observar que existe una relación positiva entre la PTF e innovación tecnológica, ya que la variable innovación es significativa y positiva. Por lo tanto, las empresas que realizan innovación tecnológica en el sector de innovación global en mercados locales poseen una PTF aproximadamente de un 5,12% más que aquellas que no realizan innovación tecnológica, manteniendo constante los demás factores.
Estimación de la PTF del sector innovación global en mercados locales de España a nivel de empresa relacionada con la innovación tecnológica
| MCO | |
|---|---|
| Innovación | 0,05*** (0,009) |
| Tamaño | 0,39*** (0,009) |
| Constante | 3,15*** (0,02) |
| Dummies de tiempoa | Incluidas |
| Dummies de sectora | Incluidas |
| Observaciones (empresas) | 5.039 (615) |
| R2 | 0,3688 |
| Período: 1990-2005 | |
| Variable dependiente: PTF | |
| Método de estimación: MCO |
La tabla 8 también muestra que existe una relación positiva entre la PTF y la variable tamaño de la empresa, ya que es significativa y positiva. Esto quiere decir que cuando una empresa tiene más de 200 trabajadores posee una PTF aproximadamente de un 47,7% más que una que tiene menos de 200 trabajadores, manteniéndose constante el resto de los factores.
Por otra parte, la PTF tiene una mejor relación con la variable exportación, ya que los coeficientes que se muestran en la tabla 8 son inferiores a los que resultan en la tabla 7. En las figuras 4 y 5 de densidad (Kernel), en las que se muestra la relación de la media de la PTF con las exportaciones e innovación tecnológica, también se confirma que la variable exportación presenta una relación positiva más fuerte que la variable innovación tecnológica.
5ConclusionesEl sector manufacturero es un sector estratégico que se caracteriza por dinamizar la economía a través de mecanismos como la generación de empleo, aportes al valor añadido bruto, etc. En ese sentido, analizar su producción y su productividad resulta de gran importancia para todos los países en general. España no es la excepción y, según la propuesta del McKinsey Global Institute en su nueva agrupación de sectores por intensidad de uso de factores de producción, el sector de innovación global en mercados locales en España representa alrededor del 31% de valor añadido bruto del total manufacturero y esta aportación es estable a lo largo del periodo analizado, y además representa alrededor del 27% de los empleados del total de las manufacturas. Dado lo anterior, en este trabajo se ha estimado una función de producción y se ha analizado a partir de esta estimación la relación que tiene la PTF con la actividad exportadora e innovación tecnológica en el sector de innovación global en mercados locales. Esta nueva agrupación industrial es utilizada por primera vez en un estudio para las manufacturas españolas, por lo que los resultados obtenidos son los primeros usando la metodología propuesta por el McKinsey, el cual ofrece una nueva perspectiva de análisis sobre la intensidad en la que los sectores económicos utilizan sus factores productivos. Además, se han obtenido estimaciones plausibles de las elasticidades de la producción respecto de los diferentes factores de producción y todos los inputs utilizados fueron estadísticamente significativos y con el signo esperado, lo que muestra que un aumento de alguno de los factores productivos generaría un aumento de la producción.
Respecto de la PTF, esta muestra un patrón de crecimiento a lo largo del periodo analizado; sin embargo, cuando se analiza la media de la PTF entre 1990 y 2005, se obtiene que ha crecido tan solo un 7,8% en 15años; además, entre 2000 y 2005 creció apenas un 1%, lo cual muestra un crecimiento más lento en los últimos cinco años de estudio. El anterior resultado va en línea con Gonçalves y Martins (2016), quienes encontraron que la PTF ha disminuido constantemente desde finales de los noventa para algunos países del sur de Europa, como España, Italia y Portugal. Este efecto de disminución de la productividad se viene dando en las principales economías desarrolladas como un problema de competitividad y poco dinamismo económico.
Por otro lado, se obtiene evidencia a favor de una relación positiva entre la PTF y la actividad exportadora. Gonçalves y Martins (2016) encontraron que existe un premio del 5,9% en aumento de la productividad para las empresas manufactureras portuguesas que exportan, resultado que concuerda con el signo pero no con la magnitud del resultado de este estudio, ya que para las empresas manufactureras españolas que operan en el sector de innovación global en mercados locales existe un premio en productividad por exportar del 20,92% frente a aquellas que no exportan; esto podría deberse a que España es una economía que exporta más del 60% de los bienes manufactureros producidos, a diferencia de Portugal. En este sentido, Wagner (2007) encuentra, en 33 países entre 1995 y 2004, que las empresas exportadoras son más productivas que las no exportadoras, pero que la exportación no mejora necesariamente la productividad, ya que esta puede depender de otras variables como la innovación, el tiempo de la empresa en el mercado y tamaño de la empresa, entre otras. Sin embargo, Delgado, Fariñas y Ruano (2002) encuentran niveles claramente superiores de productividad para las empresas exportadoras en comparación con las empresas no exportadoras del sector manufacturero español. De esta forma, las diferencias en el premio de productividad para las empresas que exportan dependerá en general de la capacidad de comercio internacional que tengan los bienes manufactureros producidos en ese país. Sin embargo, es posible a su vez que esto dependa de otros factores, como la innovación tecnológica, la capacitación, el tamaño de la empresa y el sector económico.
También se encuentra evidencia a favor de una relación positiva entre la PTF y la capacidad innovadora de las empresas. La innovación tecnológica juega un rol importante en el aumento de la productividad. En este estudio se obtiene evidencia que una empresa que gasta en innovación aumentaría su PTF un 5,12% más que las que no gastan en ese rubro. Al respecto, Grossman y Helpman (1993) mencionan que existe un efecto positivo y sostenido en el tiempo, y que el gasto en innovación incrementa la producción y la PTF; así mismo, Grossman y Helpman (1990) consideran que la innovación tecnológica acelera la tasa de crecimiento de un país. En esa línea, y al analizar las manufacturas, se conoce que este sector tiene una estrecha relación con el empleo y con la tasa de crecimiento del PIB, por lo que buscar mejorar el efecto del premio por innovar en las empresas manufactureras que lo realizan debería ser más importante. De esta manera, las políticas públicas como incentivos fiscales, alianzas público-privadas, alianzas universidad-empresa, financiamiento público y/o privado de proyectos de innovación tecnológica, que busquen incentivar a las empresas que gastan en innovación de producto o proceso, ayudarían a impulsar y mejorar esta relación en el largo plazo.
Este trabajo también posee ciertas limitaciones, principalmente que los datos utilizados corresponden de 1990 a 2005, por lo que los resultados en la actualidad pueden variar y deben ser tomados con cautela; también, por el método utilizado, no es posible establecer una relación causa-efecto entre las variables estudiadas; finalmente, no se analiza una relación entre la PTF y las exportaciones e innovación tecnológica al mismo momento, por lo que además se desprenden posibilidades de futuras investigaciones que encuentren asociaciones en el mismo instante entre la actividad exportadora y el gasto en innovación, así como también con la relación con otras variables de interés empresarial, como I+D, capacitación, outsourcing, importaciones, crédito público o privado, localización, entre otros, usando la metodología propuesta por el McKinsey Global Institute.
Finalmente, en este estudio la actividad exportadora es la que se relaciona en mayor magnitud con la productividad, ya que el premio por realizar dicha actividad es mayor que por realizar innovación tecnológica. Por ello, los hacedores de política pública podrían generar propuestas que busquen mejorar el comercio internacional en los sectores que constituyen el sector de innovación global en mercados locales, tales como incentivos fiscales que estimulen la participación en mercados internacionales: devolución y exención de impuestos en la venta de productos de este sector, acompañamiento y capacitación en la inserción en mercados internacionales no tradicionales, entre otros.
Conflicto de interesesEl autor declara no tener conflicto de intereses.
El autor agradece a Alberto López Sebastián y Grace Armijos Bravo por sus importantes sugerencias y discusión durante su estancia en la Universidad Complutense de Madrid. También agradece los comentarios que recibió la presentación de este trabajo por parte de los asistentes del IIICongreso Internacional de Ciencia, Tecnología, Innovación y Emprendimiento de la Universidad Estatal de Bolívar (2015), Ecuador. Finalmente, el autor agradece a Natalia Solano, Directora Editorial de Estudios Gerenciales, por sus importantes sugerencias y comentarios.
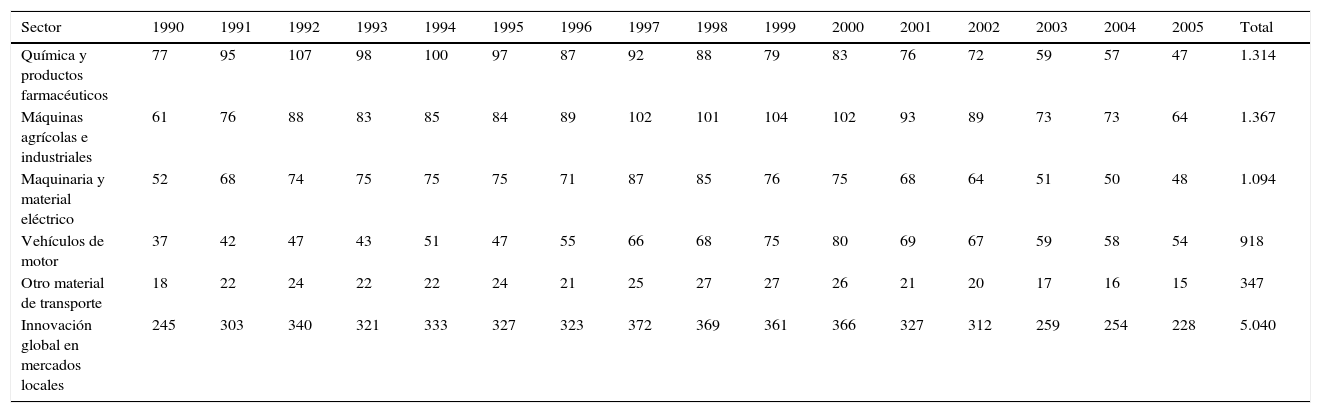
Tabla A1. Total de observaciones clasificadas por sector manufacturero y por año
| Sector | 1990 | 1991 | 1992 | 1993 | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | Total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Química y productos farmacéuticos | 77 | 95 | 107 | 98 | 100 | 97 | 87 | 92 | 88 | 79 | 83 | 76 | 72 | 59 | 57 | 47 | 1.314 |
| Máquinas agrícolas e industriales | 61 | 76 | 88 | 83 | 85 | 84 | 89 | 102 | 101 | 104 | 102 | 93 | 89 | 73 | 73 | 64 | 1.367 |
| Maquinaria y material eléctrico | 52 | 68 | 74 | 75 | 75 | 75 | 71 | 87 | 85 | 76 | 75 | 68 | 64 | 51 | 50 | 48 | 1.094 |
| Vehículos de motor | 37 | 42 | 47 | 43 | 51 | 47 | 55 | 66 | 68 | 75 | 80 | 69 | 67 | 59 | 58 | 54 | 918 |
| Otro material de transporte | 18 | 22 | 24 | 22 | 22 | 24 | 21 | 25 | 27 | 27 | 26 | 21 | 20 | 17 | 16 | 15 | 347 |
| Innovación global en mercados locales | 245 | 303 | 340 | 321 | 333 | 327 | 323 | 372 | 369 | 361 | 366 | 327 | 312 | 259 | 254 | 228 | 5.040 |
Fuente: elaboración propia con base en a los datos de la ESEE.
Tabla A2. Definición de variables
| Consumos intermedios | Suma de compras y servicios exteriores menos la variación de existencias de compras. Los consumos intermedios nominales se deflactan a través del índice de precios (de los consumos intermedios) específico de cada empresa |
| Exportaciones | Variable artificial que toma el valor 0 cuando la empresa no exporta y 1 cuando la empresa exporta |
| Horas de trabajo | Horas efectivas totales de trabajo. Se calcula multiplicando la jornada efectiva por el número de trabajadores. La jornada efectiva se define como las horas efectivamente trabajadas en el año por el trabajador, y es igual a la suma de la jornada normal y las horas extraordinarias menos las horas no trabajadas |
| Innovación tecnológica | Variable artificial que toma el valor 0 cuando la empresa no gasta en innovación tecnológica y 1 cuando la empresa gasta en innovación tecnológica |
| Precio del output | Índice de precios tipo Paasche calculado a partir de las variaciones porcentuales en los precios aportados por la empresa en los mercados en los que opera |
| Precio de los consumos intermedios | Índice de precios tipo Paasche calculado a partir de las variaciones porcentuales en los precios de las materias primas, energía y servicios aportados por la empresa |
| Producción de bienes y servicios | Suma de las ventas y de la variación de existencias de ventas, deflactada a través del índice de precios (del output) específico de cada empresa |
| Stock de capital | El capital a valores corrientes de reposición se calcula recursivamente a partir de una estimación inicial y de los datos de inversión de las empresas en bienes de equipo (exceptuando construcciones y activos financieros), actualizados a través de la media de un índice de precios de bienes de capital y usando estimaciones sectoriales de las tasas de depreciación. El capital real se obtiene deflactando el valor corriente de reposición. Para una mayor información sobre el cálculo de esta variable, véase Martín-Marcos y Suárez (1996) |
| Tamaño | Variable artificial que toma el valor 0 cuando la empresa posee 200 y menos trabajadores y 1 cuando la empresa posee más de 200 trabajadores |
Fuente: elaboración propia con base en los datos de la ESEE.
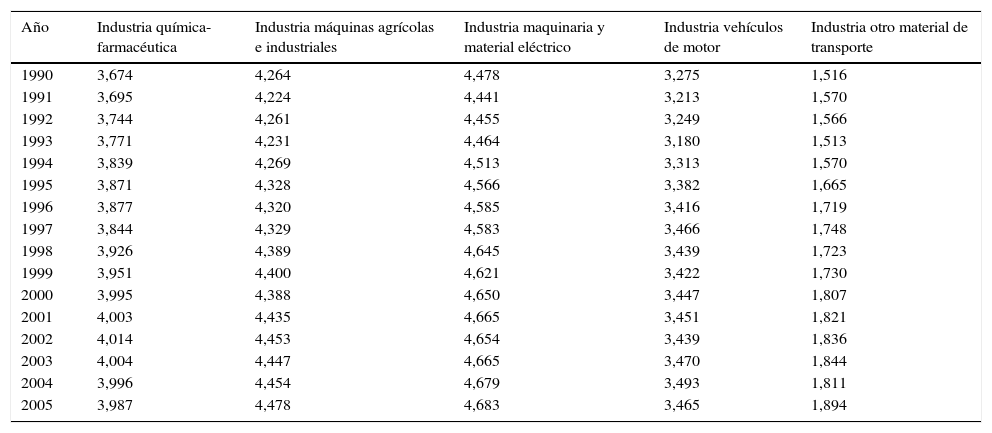
Tabla A3. Evolución de la media de la PTF de las industrias que conforman el sector de innovación global en mercados locales de España
| Año | Industria química-farmacéutica | Industria máquinas agrícolas e industriales | Industria maquinaria y material eléctrico | Industria vehículos de motor | Industria otro material de transporte |
|---|---|---|---|---|---|
| 1990 | 3,674 | 4,264 | 4,478 | 3,275 | 1,516 |
| 1991 | 3,695 | 4,224 | 4,441 | 3,213 | 1,570 |
| 1992 | 3,744 | 4,261 | 4,455 | 3,249 | 1,566 |
| 1993 | 3,771 | 4,231 | 4,464 | 3,180 | 1,513 |
| 1994 | 3,839 | 4,269 | 4,513 | 3,313 | 1,570 |
| 1995 | 3,871 | 4,328 | 4,566 | 3,382 | 1,665 |
| 1996 | 3,877 | 4,320 | 4,585 | 3,416 | 1,719 |
| 1997 | 3,844 | 4,329 | 4,583 | 3,466 | 1,748 |
| 1998 | 3,926 | 4,389 | 4,645 | 3,439 | 1,723 |
| 1999 | 3,951 | 4,400 | 4,621 | 3,422 | 1,730 |
| 2000 | 3,995 | 4,388 | 4,650 | 3,447 | 1,807 |
| 2001 | 4,003 | 4,435 | 4,665 | 3,451 | 1,821 |
| 2002 | 4,014 | 4,453 | 4,654 | 3,439 | 1,836 |
| 2003 | 4,004 | 4,447 | 4,665 | 3,470 | 1,844 |
| 2004 | 3,996 | 4,454 | 4,679 | 3,493 | 1,811 |
| 2005 | 3,987 | 4,478 | 4,683 | 3,465 | 1,894 |
Fuente: elaboración propia.
Para un mayor detalle sobre la conformación de cada uno se debe revisar la Clasificación Nacional de Actividades Económicas: CNAE (2009).
Para una descripción resumida de la metodología y construcción de la base de datos EU Klems growth and productivity accounts, véase O’Mahony y Marcel (2009).
Estudio fundamentado en la base de datos de Information Handling Services (IHS) Global Insight con una muestra de 75 economías, publicado por el McKinsey Global Institute (2012).
Para el sector de innovación global en mercados locales se realiza una regresión con variables de control de tamaño, año y sectores.
El cálculo de la aproximación del aumento de la PTF cuando una empresa exporta se ha realizado con la siguiente expresión: %Δaˆit=100exp βˆx−1 (Wooldridge, 2006).