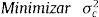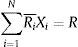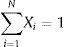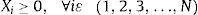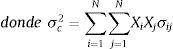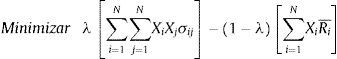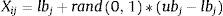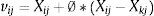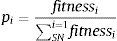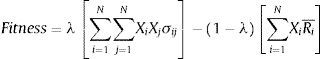El presente artículo resuelve el problema clásico de optimización de carteras de inversión, usando el modelo de media-varianza y proponiendo una forma de calcular la volatilidad a través de los modelos generalizados autorregresivos condicionalmente heterocedásticos (GARCH). El problema es resuelto a través de una metaheurística bioinspirada, llamada colonia artificial de abejas (artificial bee colony [ABC]), cuyo objetivo es reducir los tiempos de ejecución computacionales presentes en otras soluciones. Los resultados fueron contrarrestados con un trabajo anterior, resuelto con multiplicadores de Lagrange, encontrando una frontera de inversión similar, pero con una reducción del tiempo de ejecución notablemente inferior. Finalmente, se hace referencia a futuros trabajos dentro del área de las finanzas computacionales.
The present article solves the classic problem of optimization of investment portfolios, using the model of average-variance and proposing a way to calculate the volatility through the generalized autoregressive conditional heteroskedasticity (GARCH) models. The problem is solved through a bio-inspired metaheuristic, called artificial bee colony (ABC), whose objective is to reduce the computational execution times present in other solutions. The results were counteracted by a previous work, solved with Lagrange multipliers, finding a similar investment boundary, but with a notably lower reduction in execution time. Finally, reference is made to future work within the area of computer finance.
O presente artigo resolve o problema clássico da otimização das carteiras de investimentos, utilizando o modelo de variância-média e propondo uma maneira de calcular a volatilidade através dos modelos generalizados autoresgresivos condicionalmente heterocedasticos (GARCH). O problema é resolvido através de uma metaheurística bio-inspirada, chamada colônia de artificial de abelhas (artificial bee colony [ABC]), cujo objetivo é reduzir os tempos de execução computacional presentes em outras soluções. Os resultados foram neutralizados por um trabalho anterior, resolvido com multiplicadores de Lagrange, encontrando um limite de investimento similar, mas com uma redução notadamente menor no tempo de execução. Finalmente, referência ao trabalho futuro na área de finanças informáticas é feita.
En el campo de la teoría de selección de carteras ocupa un lugar destacado Harry Markowitz, quien publicó en el Journal of Finance el artículo de selección de carteras de inversión, donde planteó un modelo que es considerado un gran aporte a nivel teórico-práctico y referencia fundamental para todas las investigaciones realizadas posteriormente.
Una de las variaciones del modelo de Markowitz es considerar la volatilidad de una serie financiera, suponiendo homocedasticidad. Para abordar dicho problema se han propuesto modelos, entre los que se encuentran la familia de modelos generalizados autorregresivos condicionalmente heterocedásticos (GARCH), que tienen como finalidad predecir la volatilidad. Sin embargo, no se considera la eficiencia computacional, aspecto crucial, pues se trata de un problema de optimización combinatorial, conocido como el «problema de la mochila»1, que está clasificado como un problema NP hard, es decir, intratable desde el punto de vista computacional, pues tiene un alto costo de tiempo de ejecución.
Por otro lado, han surgido algunas propuestas para resolver el problema —encontrando una solución subóptima, pero con costos de tiempos muy inferiores— conocidas como «metaheurísticas», entre las cuales están las bioinspiradas, que tienen como referencia la inteligencia colectiva y la teoría de la evolución y genética.
Una revisión de metaheurísticas aplicadas a la empresa de inteligencia colectiva se puede ver en Toca (2014), y de algoritmos evolutivos, más específicamente en finanzas, en Chen y Kou (2002). Por otra parte, se destacan Yang (2002), el cual construyó una red neuronal para un problema de subasta doble; Chen, Yeh y Liao (2002), quienes desarrollaron un software basado en programación genética que realiza simulaciones de una bolsa de valores; Gutiérrez, Torres, Gálvez y Poo (2007), quienes resolvieron el problema de optimización de carteras a través de un algoritmo microgenético.
En este trabajo se implementa un algoritmo basado en la colonia artificial de abejas (ABC, por su sigla en inglés de artificial bee colony) para resolver la variante Markowitz-GARCH, el cual es aplicado en el mercado de valores chileno, comparando sus resultados con el problema resuelto con los multiplicadores de Lagrange.
Dado lo anterior, el artículo está organizado en 4 secciones. A la introducción le sigue el marco teórico, que incluye los modelos de optimización de carteras y las bases de la metaheurística de colonia artificial de abejas. En la tercera sección se estudia el caso de la aplicación en el mercado de valores de Chile y, finalmente, se realiza el análisis de los resultados, presentando las conclusiones y trabajos futuros.
2Marco teóricoEl problema de optimización del portafolio corresponde a una de las interrogantes más conocidas en el rubro de gestión económica y financiera. Este problema consiste en encontrar la asignación ideal a invertir en los distintos activos que conforman una cartera de inversiones, donde existen activos tales como bonos, acciones, seguros o incluso derivados financieros.
Uno de los pioneros en la investigación del problema del portafolio fue Markowitz, quien a través de sus investigaciones propuso el modelo cuantitativo de media-varianza (Markowitz, 1952). Este modelo plantea que los inversionistas tienen una conducta racional a la hora de seleccionar su cartera de inversión y, por lo tanto, siempre buscan obtener la máxima rentabilidad al menor riesgo posible.
En la práctica, este problema se transforma en un problema de optimización muy difícil de resolver, dado que sus características de tamaño, requerimientos de la vida real, el tiempo computacional permitido, y las distintas restricciones, no generan resultados satisfactorios a través de los métodos y técnicas tradicionales (Di Tollo y Roli, 2008).
Para la resolución del problema de selección del portafolio existen distintas maneras de plantearlo y modelarlo. No obstante, este problema de optimización es uno de los problemas más difíciles tratados en las finanzas, debido a lo cual ha sido estudiado y resuelto a través de distintas técnicas y métodos (Bacanin, Pelevic y Tuba, 2013), como por ejemplo: programación paramétrica cuadrática (Wu y Liu, 2012), programación lineal (Lang, Lv y Zhang, 2007) y programación entera (Cooper y Farhangian, 1982).
Uno de los desafíos principales de este artículo es resolver el problema de optimización de carteras de inversión, mediante estas técnicas de programación. Así, de acuerdo a los estudios presentados por Markowitz (1952), su modelo estándar de media-varianza se puede formular de la siguiente manera:
Sujeto a las siguientes restricciones:
De acuerdo a lo anterior, se puede definir:
σc2: corresponde al riesgo del portafolio de inversión medido a través de la varianza de este.
Ri:¯ corresponde al retorno promedio del activo financiero i.
Xi: corresponde a la cantidad invertida en el portafolio del activo financiero i.
R: corresponde al nivel de rentabilidad deseado por parte del portafolio de inversión.
σij: corresponde a la covarianza que existe entre el activo financiero i y el activo financiero j, en caso de que i=j, entonces corresponde a la varianza del activo financiero i.
N: corresponde al número de posibles activos financieros en el mercado.
Para este modelo, dado que el problema se puede analizar como un problema de maximización de rentabilidad de una cartera para un nivel de riesgo o minimización de la varianza para un nivel de rentabilidad dado, se trabajará con el segundo caso.
Este modelo es utilizado en la literatura para el análisis y estudio del problema del portafolio. Básicamente, consiste en dos submodelos, frontera eficiente e índice de Sharpe2 (Zhou, Gao, Gao y Zhang, 2003; Chen, Lian y Liu, 2012), donde se incluye un parámetro de aversión al riesgo, el cual se representa a través del símbolo λ, cuyos valores oscilan entre 0 y 1, situación que se plantea en la ecuación 2.
Sujeto a las siguientes restricciones:
A diferencia del modelo estándar de Markowitz, en este caso, una de las restricciones se incorpora dentro de la función objetivo. Todas las variables y parámetros se mantienen, pero incorporando λ, tal como se mencionó anteriormente. Dicho lo anterior, dado que λ corresponde al grado de aversión al riesgo, se pueden tener dos casos extremos. Cuando λ=1, se dice que el grado de aversión es total, es decir, el objetivo del problema de portafolio es minimizar la varianza de este y así obtener la composición del portafolio. Por otra parte, si λ=0, no existe grado de aversión al riesgo, de manera que el individuo busca maximizar el retorno del portafolio sin considerar la varianza; de acuerdo a esto, el portafolio estará conformado con aquellos activos que experimentan los mayores retornos.
Respecto a la complejidad computacional, esta corresponde a la rama de la teoría de la computación que tiene como objetivo clasificar los problemas de acuerdo a su complejidad computacional; en otras palabras, su objetivo es medir la cantidad de recursos computacionales que se necesitan para solucionar un problema.
En este sentido, interesa saber la complejidad computacional de los problemas para poder identificar cómo resolverlos; por ejemplo, en el caso del problema de optimización de portafolio o selección de portafolio, este corresponde a un problema de la mochila o el knapsack problem (KP) con relajación lineal. Por otra parte, el problema del portafolio corresponde a un problema NP-completo (Mansini y Speranza, 1999), es decir, pertenece a uno de los problemas que son difíciles, en el sentido de que los algoritmos que los resuelven, al aumentar el tamaño de la entrada de información, tienen tiempos de procesos inaceptables; es por eso que, en esos casos, es preferible una buena solución, en tiempo razonable.
En relación con las heurísticas y metaheurísticas, Reeves (1996) plantea que una heurística es un método que busca buenas soluciones, es decir, soluciones cercanas al óptimo, pero con un menor costo computacional. No obstante, una de las críticas es que se pueden plantear distintas heurísticas para un mismo problema, sin considerar mecanismos para salir de soluciones subóptimas.
Por su parte, Glover y Laguna (1997) entienden las metaheurísticas como estrategias que guían y modifican heurísticas, para producir soluciones que van más allá de aquellas generadas normalmente, es decir, a partir de una solución de optimalidad local se puede llegar a óptimos globales.
Dentro de las metaheurísticas están las denominadas bioinspiradas, que replican la forma en que la naturaleza se enfrenta a problemas de optimización, emulando la evolución natural de las especies y la respuesta de sistemas sociales a sus desafíos.
Por otra parte, los algoritmos de inteligencia colectiva (swarm intelligence) son técnicas metaheurísticas de inteligencia artificial, basados en el estudio de comportamientos colectivos, presentes en la naturaleza. Dicho comportamiento define los movimientos de las variables de decisión en el espacio de búsqueda y los orienta hacia soluciones óptimas.
Dentro de los algoritmos de inteligencia colectiva, se encuentran aquellos que están asociados al comportamiento de las abejas. Estos corresponden a un comportamiento natural y social de una colonia de insectos, basado en la recolección de información.
Se debe tener presente que las abejas, durante el proceso de exploración y recolección de alimentos, utilizan un mecanismo denominado «danza waggle», a través del cual localizan las mejores fuentes de alimentos. En la mayoría de las colonias, los insectos basan su comportamiento de acuerdo a la división del trabajo, y a partir de este se puede distinguir en el sistema de las abejas distintos componentes clave, por ejemplo:
- •
Fuentes de alimento: para poder seleccionar las fuentes de alimentos, las abejas recolectoras deben primero evaluar distintos parámetros de acuerdo a esta fuente, tales como cercanía con respecto a la colmena, cantidad de comida, delicia del néctar y la facilidad de extraer la comida. Para simplificar estos parámetros, la calidad de la fuente de alimentos se puede representar solo a través de una función que cuantifique todos estos elementos.
- •
Recolector empleado: corresponde a una abeja que se encuentra empleada en una fuente específica de alimentos en la cual se encuentra explotando sus recursos. El empleado posee la información sobre esa fuente de alimento específica y la comparte con las otras abejas que se encuentran esperando en la colmena. Esta información incluye la distancia, la dirección y la rentabilidad de la fuente de alimento.
- •
Recolector desempleado: una abeja recolectora que se encuentra buscando una fuente de alimento para explotar es llamada desempleada. También puede ser una exploradora que se encuentra buscando aleatoriamente una fuente de alimento o una abeja observadora que se encuentra tratando de encontrar una fuente de alimento a través de la información entregada por parte de una abeja empleada.
Como se mencionó anteriormente, el intercambio de información entre las abejas es la ocurrencia más importante en el conocimiento colectivo de la colmena. Al examinar las colmenas es posible distinguir algunas partes que son comunes y repetitivas en las distintas colmenas, pero la que se destaca corresponde al área donde se intercambia la información, que es una zona de danza. Esta danza es la denominada «danza waggle» y contiene toda la información respecto a la fuente de alimento, de manera que una abeja observadora pueda considerarla como su fuente. Dentro de esta zona habrá varias danzas, por lo tanto, se elegirán aquellas fuentes que sean las más rentables.
En este sentido, las abejas elegirán aquellas fuentes más llamativas, dado que existe mayor probabilidad de que las fuentes de alimentos más rentables sean vistas. Una de las razones corresponde a que en la zona de danza se verán varias abejas recolectoras entregando la información de una misma fuente de alimento. Por otra parte, la danza entrega la dirección de la fuente con respecto a la posición del sol, la intensidad del meneo indica qué tan lejos está y, finalmente, la duración de la danza indica la cantidad de alimento disponible para ser recolectado. Por lo tanto, a través de este último factor, nuevamente existe mayor probabilidad de que la abeja empleada sea vista por una abeja desempleada.
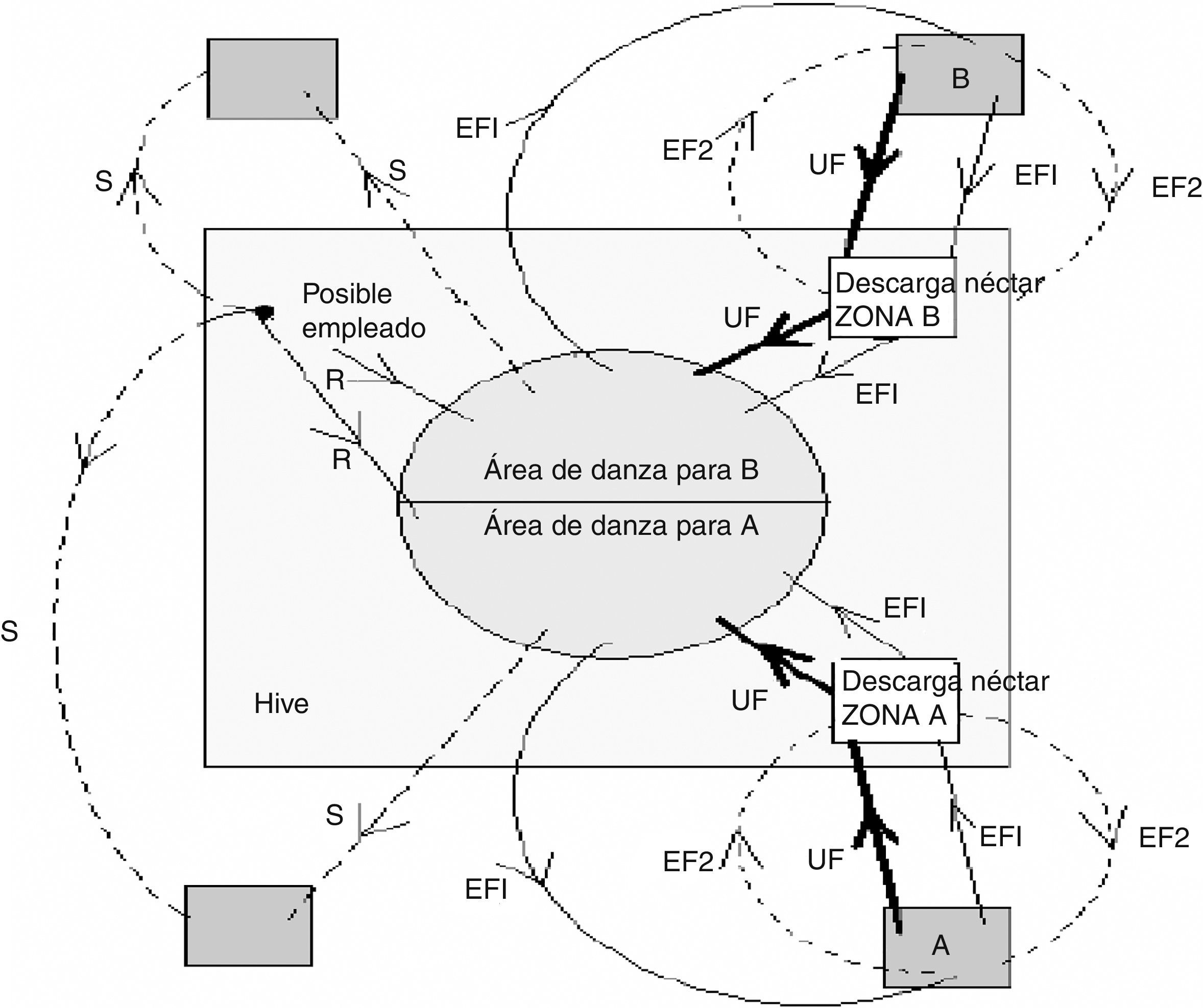
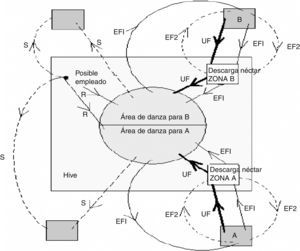
En la figura 1, se muestra el comportamiento básico de las características de las abejas recolectoras. En este caso, se asume que existen dos fuentes de alimentos: A y B. Se debe recordar que en el inicio del proceso las abejas comienzan como desempleadas y no tendrán conocimiento alguno sobre las fuentes de alimentos que hay alrededor de la colmena. De acuerdo a esto, dicha abeja presenta dos opciones:
- 1.
Puede ser una abeja exploradora y comenzar a buscar espontáneamente una fuente de comida alrededor de la colmena, a través de una motivación interna o una posible clave externa (S en la fig. 1).
- 2.
Puede ser una recluta tras observar las danzas waggles y comenzar a buscar fuentes de alimentos (R en la fig. 1).
Luego de ubicar la fuente de alimento, la abeja utiliza su propia capacidad para memorizar la ubicación y comienza inmediatamente a explotar esa fuente. Por lo tanto, esta abeja se transforma en una abeja recolectora empleada.
La abeja exploradora carga el néctar de la fuente y regresa a la colmena para descargar el alimento en la zona de almacenaje. Tras descargar el néctar, la abeja posee tres opciones:
- 1.
Se transforma en un seguidor sin compromiso luego de abandonar la fuente de alimento (UF en la fig. 1).
- 2.
Realiza la danza waggle para que compañeras sean sus reclutas y regresen a la fuente de alimento (EF1 en la fig. 1).
- 3.
Continúa recolectando néctar de la fuente de alimento sin reclutar otras abejas (EF2 en la fig. 1).
Cabe destacar que no todas las abejas comienzan como recolectoras simultáneamente.
El algoritmo colonia artificial de abejas es una de las metaheurísticas más nueva, inspirada en la naturaleza, propuesta y ampliada por Dervis Karaboga en 2005 (Bacanin et al., 2013; Wang, Liu y Kong, 2012; Chen et al., 2012). En la colonia artificial de abejas existen tres tipos de abejas artificiales o agentes: las empleadas, las observadoras y las exploradoras, donde la mitad de la colonia corresponde a abejas empleadas. Las abejas empleadas son las encargadas de explotar las fuentes de alimentos y entregar la información a las observadoras en la colmena. La relación entre las abejas empleadas y las fuentes de alimentos es uno a uno, es decir, solo hay una abeja empleadora por cada fuente de alimento. Cuando el néctar de una fuente de alimento se acaba, la fuente es abandonada y la abeja empleada pasa a ser una abeja exploradora. Apenas encuentre una nueva fuente, inmediatamente se transforma en una abeja empleada.
El algoritmo colonia artificial de abejas corresponde a un algoritmo iterativo que comienza asociando cada abeja empleada con una fuente de alimento aleatoria, que corresponde a una solución del problema. Cada solución Xi corresponde a un vector con D-dimensiones, y además, se tendrán hasta SN soluciones, que corresponde al tamaño de la población, de manera que i puede ir desde 1 hasta SN.
Dado lo anterior, para inicializar la población de empleadas en fuentes de alimentos aleatorias, se utiliza la siguiente expresión:
Donde Xij corresponde al parámetro j de la solución i en la población; lbj se refiere al límite inferior del parámetro j; ubj es el límite superior del parámetro j y rand0,1 corresponde a un número real aleatorio entre 0 y 1.
En cada iteración, cada abeja recolectora empleada encuentra una fuente de alimento cercana a su vecindad. Esta nueva fuente es evaluada en su cantidad de alimento a través de una función fitness, que corresponde a la función objetivo del problema.
Para poder descubrir estas nuevas fuentes de alimentos en la vecindad, se utiliza la siguiente expresión:
Donde vij corresponde a una solución candidata para el parámetro j, con respecto a la vieja solución i; Xij es el parámetro j de la antigua solución i en la población; Xkj; se refiere al parámetro j de la solución vecina k; ∅ es un valor aleatorio entre 0 y 1 y k corresponde a la elección aleatoria de una fuente distinta a i.
Todas las soluciones candidatas de cada abeja empleada son evaluadas en la función fitness, de manera que si esta es mejor que la solución antigua, la abeja empleada se mueve a esta nueva fuente de alimentos, es decir, se reemplaza la solución. En caso contrario, la abeja empleada se mantiene en la fuente de alimento (solución) en que se encontraba.
Luego de completar este proceso de comparar las soluciones actuales con las candidatas y evaluarlas, las abejas recolectoras empleadas comparten la información del fitness de cada fuente de alimento con las abejas desempleadas. Estas últimas seleccionan a qué fuente de alimento ir a través de un proceso probabilístico, es decir, eligen una fuente i con una probabilidad que es proporcional al fitness de la fuente de alimento. Esta probabilidad se calcula de la siguiente manera:
Donde fitnessi corresponde al fitness de la función objetivo para la solución i y SN se refiere al número total de fuentes de alimentos (soluciones).
Esta expresión permite demostrar que aquellas fuentes que presentan un mejor fitness poseen mayor probabilidad de que sean escogidas, con respecto a las otras, por las abejas desempleadas. Una vez que las abejas desempleadas observadoras hayan terminado con el proceso de selección de fuentes a partir del fitness, cada una de ellas buscará otra fuente de alimento en la vecindad de cada una de sus fuentes, a través de la ecuación 5, y evaluará el desempeño que está con la función fitness. Si el fitness de la nueva fuente de alimento o solución candidata por parte de las abejas que se incorporaron es mejor, entonces esta será la nueva ubicación de la fuente de alimento.
En el caso de que una abeja no pueda ir mejorando el fitness de una fuente de alimento, dado cierto número de iteraciones, entonces la fuente es abandonada y la abeja se transforma en una exploradora, buscando otra fuente utilizando la expresión de la ecuación 5. En este caso, es necesario fijar como parámetro el número de iteraciones que se pueden realizar en una misma fuente antes de abandonarla.
3Metodología del estudioEn esta sección se aplicará la metodología a la búsqueda de la frontera eficiente, para una cartera de inversión compuesta por acciones de la Bolsa de Comercio de Santiago de Chile. Posteriormente, se buscarán las mejores combinaciones de rentabilidad y riesgo, mediante el algoritmo de colonia artificial de abejas (ABC), construido especialmente para esta investigación.
3.1Estudio de caso Bolsa chilenaLos datos utilizados para realizar este análisis corresponden a acciones o títulos accionarios que fueron transados en la Bolsa de Comercio de Santiago de Chile durante el período comprendido entre el 2 de enero del año 2005 hasta el 29 de diciembre del año 2010. Respecto al criterio de selección de las empresas para incorporarlas al estudio, fue su presencia bursátil, considerando aquellas acciones que permanecieron durante todo el período de estudio dentro del índice de precios selectivos de acciones (IPSA). Según este criterio, el portafolio de inversión está conformado por:
- •
Sector recursos naturales (COPEC).
- •
Sector industrial (CAP).
- •
Sector servicios (CTC-A).
- •
Sector servicios (ENTEL).
- •
Servicio eléctrico (COLBUN).
- •
Servicio eléctrico (ENDESA).
Por otra parte, para evaluar el desempeño se utiliza como proxy de la tasa libre de riesgo los pagarés descontables del Banco Central (PDBC), con vencimiento en 5 años.
Para poder observar y comparar los distintos resultados obtenidos a través de la heurística colonia artificial de abejas y los obtenidos a través de un software estadístico de optimización (Gutiérrez et al., 2007), es necesario llevar estos valores a un mismo formato para poder compararlos. Es decir, no se pueden comparar dos o más portafolios si estos poseen distinto riesgo y por ende distinta rentabilidad. Debido a esto se calcula el índice de Sharpe que permite medir el exceso de retorno por unidad de riesgo.
3.2Modelo de la frontera eficientePara resolver el problema de optimización de la frontera de inversiones eficiente es necesario encontrar las relaciones óptimas de rentabilidad y riesgo que cumplan las restricciones financieras del modelo, dentro de la frontera eficiente. Este problema puede ser resuelto a través de propuestas de modelos estadísticos complejos y demandantes de altos recursos computacionales. La presente investigación pretende resolver el problema a través de la colonia artificial de abejas, que reduce notablemente los tiempos computacionales. De acuerdo a la literatura, para poder resolver el problema del portafolio a través de una heurística, tal como la metaheurística bioinspirada de la colonia artificial de abejas, se recurre a uno de los modelos matemáticos más utilizado para su resolución, que corresponde al modelo de la frontera eficiente (Bacanin et al., 2013; Chen et al., 2012; Karaboga, 2005).
Este modelo facilita la aplicación de una heurística, dado que incluye una de las restricciones en la función objetivo del problema, como una especie de relajación lagrangiana. De manera que, al momento de realizar una programación y evaluar las distintas posibles soluciones factibles, sea más fácil y requiera de menos complejidad.
3.3Propuesta metaheurística de la colonia artificial de abejas para el problemaPara poder aplicar el pseudocódigo de la colonia artificial de abejas (Bacanin et al., 2013; Chen et al., 2012; Karaboga, 2005), al problema de selección de portafolio, es necesario realizar pequeñas modificaciones que mantengan la esencia del algoritmo, pero que a su vez permitan que sea aplicable a un problema de este estilo. De acuerdo a esto el pseudocódigo queda de la siguiente manera:
- 1.
Begin.
- 2.
Inicializar la población de soluciones o fuentes de alimentos de forma aleatoria, Xi,0, para todo i=1,…, SN.
- 3.
Evaluar cada fuente de alimento generada, es decir, la población, a través de la función fitness.
- 4.
Definir una variable para el ciclo, g=1.
- 5.
Repeat.
- 6.
Fase abeja empleada.
- 7.
Producir nuevas soluciones o soluciones candidatas (Vi,g) para las abejas empleadas generando un vector aleatorio que genere pequeñas variaciones en los componentes de la solución factible inicial, pero que tenga como condición que el sumatorio de los componentes del vector aleatorio sea igual a cero.
- 8.
Evaluar las soluciones candidatas a través de la función fitness del problema (ecuación 6).
- 9.
Conservar las mejores soluciones entre las actuales y las candidatas.
- 10.
Calcular los valores de probabilidad para cada fuente de alimento a partir de la función fitness a través de la ecuación 6.
- 11.
Fase abeja observadora.
- 12.
Asignar las abejas observadoras a las fuentes de alimentos existentes a partir de los valores de las probabilidades.
- 13.
Producir nuevas soluciones o soluciones candidatas (Vi,g) para las abejas observadoras a través del mismo mecanismo del paso 7, permitiendo nuevamente a las abejas poder buscar, alrededor de la vecindad de las fuentes donde fueron asignadas, soluciones candidatas y evaluarlas en la función fitness del problema (ecuación 6).
- 14.
Aplicar el proceso de selección entre la solución nueva y la antigua, observando los valores obtenidos en su función fitness.
- 15.
Fase abeja exploradora.
- 16.
En caso de que una fuente de alimento no mejore luego de cierto número de iteraciones, la fuente de alimento se abandona y la abeja empleada se transforma en una abeja exploradora, generando una nueva solución aleatoria a través de la ecuación 6.
- 17.
Memorizar la mejor solución encontrada hasta el momento.
- 18.
Para los ciclos g=g+1.
- 19.
Until g=MCN, donde MCN corresponde al máximo número de ciclos.
- 20.
End.
Desde el punto de vista computacional, el código para programar la heurística de la colonia artificial de abejas se realizó en Java a través de los programas Netbeans IDE 8.0 y Eclipse. El computador utilizado para ejecutar el código programado corresponde a un equipo Asus R401VJ, con sistema operativo Windows 7 de 64 bits, con 8Gb de memoria RAM DDR3 y procesador Intel Core i5-3230M CPU 2,60GHz. Para la programación se utilizó el pseudocódigo modificado de la heurística colonia artificial de abejas y el modelo de frontera eficiente (Wang et al., 2012); respecto a los datos empleados en el caso práctico, estos provienen de la Bolsa de Comercio de Santiago de Chile. El proceso de selección de carteras demoró 30minutos estableciendo una relación de 1:15 respecto a la programación con multiplicadores de Lagrange.
En esta sección, inicialmente se presentan los resultados obtenidos por medio de los modelos GARCH. Posteriormente, se presentan los resultados para la frontera eficiente considerando solo posiciones largas, mediante el algoritmo colonia artificial de abejas. Finalmente, se construye la frontera eficiente con posiciones cortas y largas, utilizando el algoritmo colonia artificial de abejas.
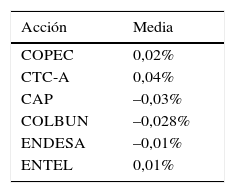
4.1Frontera eficiente modelo GARCH3Inicialmente, para poder observar y analizar los resultados a través de la heurística, es necesario revisar cuáles fueron los obtenidos en el caso práctico de la Bolsa de Comercio de Santiago de Chile. Se debe recordar que en este caso se trabajó con 6 títulos accionarios. De acuerdo a lo anterior, se presentarán algunos datos de estas acciones, tales como el rendimiento promedio de los activos y la matriz de varianza y covarianza (tablas 1 y 2, respectivamente).
Rendimiento promedio de la acción
| Acción | Media |
|---|---|
| COPEC | 0,02% |
| CTC-A | 0,04% |
| CAP | –0,03% |
| COLBUN | –0,028% |
| ENDESA | –0,01% |
| ENTEL | 0,01% |
Fuente: tomado de Gálvez, Salgado y Gutiérrez (2015, p. 45).
Matriz de varianza-covarianza
| COPEC | CTC-A | CAP | COLBUN | ENDESA | ENTEL | |
|---|---|---|---|---|---|---|
| COPEC | 0,038% | 0,020% | 0,017% | 0,014% | 0,019% | 0,017% |
| CTC-A | 0,020% | 0,043% | 0,015% | 0,013% | 0,021% | 0,014% |
| CAP | 0,017% | 0,015% | 0,034% | 0,011% | 0,014% | 0,014% |
| COLBUN | 0,014% | 0,013% | 0,011% | 0,044% | 0,014% | 0,011% |
| ENDESA | 0,019% | 0,021% | 0,014% | 0,014% | 0,040% | 0,014% |
| ENTEL | 0,017% | 0,014% | 0,014% | 0,011% | 0,014% | 0,046% |
Fuente: tomado de Gálvez et al. (2015, p. 45).
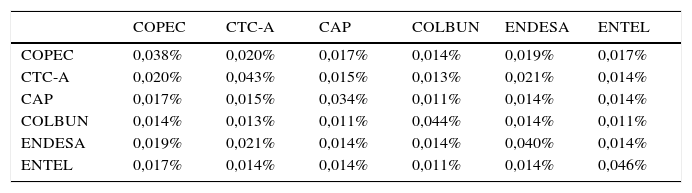
Por otra parte, en la tabla 2, se observa la matriz de varianza y covarianza entre las 6 acciones de la Bolsa de Comercio de Chile.
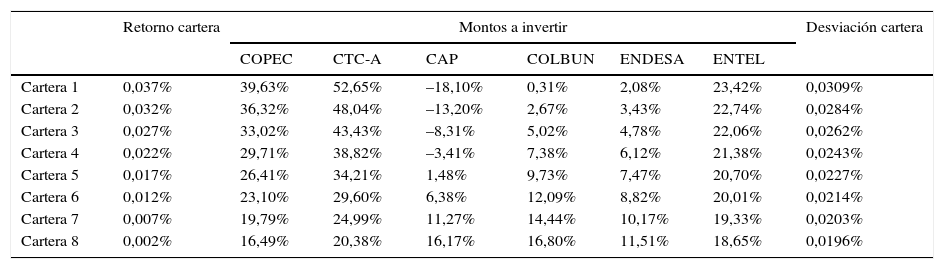
Se debe tener presente que en el modelo de Markowitz se busca minimizar el riesgo de una cartera de inversión para cierto retorno esperado de esta. Dentro de este modelo existen distintas restricciones, donde solo se pueden tener posiciones de compra en las acciones y no ventas cortas, es decir, solo se pueden tener montos a invertir positivos dentro de las acciones. Se puede apreciar en la tabla 3 que, en algunas carteras con su retorno dado, existen posiciones cortas o de venta corta. De acuerdo a esto, se desarrollará una heurística que permita evaluar su desempeño solo con posiciones largas o de compra.
Portafolios eficientes obtenidos del modelo GARCH
| Retorno cartera | Montos a invertir | Desviación cartera | ||||||
|---|---|---|---|---|---|---|---|---|
| COPEC | CTC-A | CAP | COLBUN | ENDESA | ENTEL | |||
| Cartera 1 | 0,037% | 39,63% | 52,65% | –18,10% | 0,31% | 2,08% | 23,42% | 0,0309% |
| Cartera 2 | 0,032% | 36,32% | 48,04% | –13,20% | 2,67% | 3,43% | 22,74% | 0,0284% |
| Cartera 3 | 0,027% | 33,02% | 43,43% | –8,31% | 5,02% | 4,78% | 22,06% | 0,0262% |
| Cartera 4 | 0,022% | 29,71% | 38,82% | –3,41% | 7,38% | 6,12% | 21,38% | 0,0243% |
| Cartera 5 | 0,017% | 26,41% | 34,21% | 1,48% | 9,73% | 7,47% | 20,70% | 0,0227% |
| Cartera 6 | 0,012% | 23,10% | 29,60% | 6,38% | 12,09% | 8,82% | 20,01% | 0,0214% |
| Cartera 7 | 0,007% | 19,79% | 24,99% | 11,27% | 14,44% | 10,17% | 19,33% | 0,0203% |
| Cartera 8 | 0,002% | 16,49% | 20,38% | 16,17% | 16,80% | 11,51% | 18,65% | 0,0196% |
Fuente: tomado de Gálvez et al. (2015, p. 46).
Para el caso de la heurística colonia artificial de abejas, es muy probable que muchas de sus soluciones factibles estén por debajo de esta frontera eficiente.
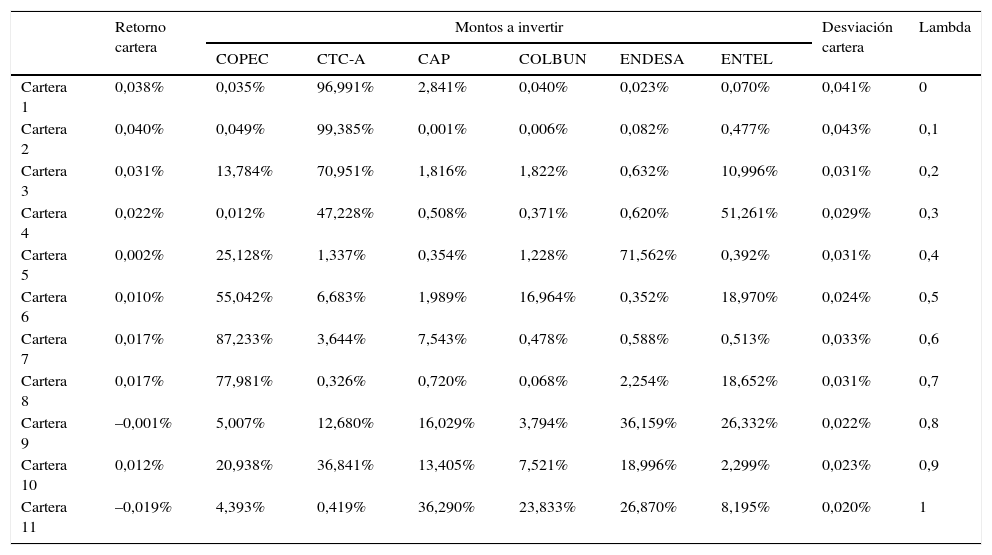
4.2Resultados obtenidos con la heurística colonia artificial de abejas solo con posiciones largasLuego de programar a través de Eclipse y en Java, se logró llegar a los resultados que muestra la tabla 4.
Resultados solo con posiciones largas
| Retorno cartera | Montos a invertir | Desviación cartera | Lambda | ||||||
|---|---|---|---|---|---|---|---|---|---|
| COPEC | CTC-A | CAP | COLBUN | ENDESA | ENTEL | ||||
| Cartera 1 | 0,038% | 0,035% | 96,991% | 2,841% | 0,040% | 0,023% | 0,070% | 0,041% | 0 |
| Cartera 2 | 0,040% | 0,049% | 99,385% | 0,001% | 0,006% | 0,082% | 0,477% | 0,043% | 0,1 |
| Cartera 3 | 0,031% | 13,784% | 70,951% | 1,816% | 1,822% | 0,632% | 10,996% | 0,031% | 0,2 |
| Cartera 4 | 0,022% | 0,012% | 47,228% | 0,508% | 0,371% | 0,620% | 51,261% | 0,029% | 0,3 |
| Cartera 5 | 0,002% | 25,128% | 1,337% | 0,354% | 1,228% | 71,562% | 0,392% | 0,031% | 0,4 |
| Cartera 6 | 0,010% | 55,042% | 6,683% | 1,989% | 16,964% | 0,352% | 18,970% | 0,024% | 0,5 |
| Cartera 7 | 0,017% | 87,233% | 3,644% | 7,543% | 0,478% | 0,588% | 0,513% | 0,033% | 0,6 |
| Cartera 8 | 0,017% | 77,981% | 0,326% | 0,720% | 0,068% | 2,254% | 18,652% | 0,031% | 0,7 |
| Cartera 9 | –0,001% | 5,007% | 12,680% | 16,029% | 3,794% | 36,159% | 26,332% | 0,022% | 0,8 |
| Cartera 10 | 0,012% | 20,938% | 36,841% | 13,405% | 7,521% | 18,996% | 2,299% | 0,023% | 0,9 |
| Cartera 11 | –0,019% | 4,393% | 0,419% | 36,290% | 23,833% | 26,870% | 8,195% | 0,020% | 1 |
Fuente: elaboración propia.
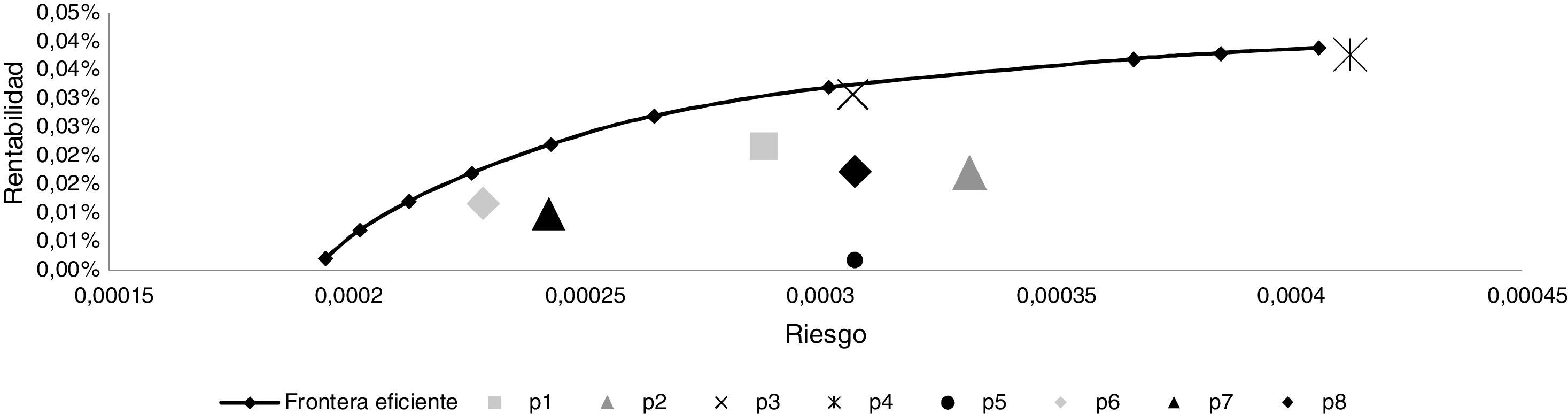
En la tabla 4 se observan los distintos portafolios para cada lambda (λ), de acuerdo al modelo utilizado. Estos resultados no pueden ser comparados directamente con los obtenidos por Gutiérrez y Salgado (2012), de manera que es necesario calcular cuáles fueron los portafolios óptimos para esos mismos niveles de retorno, es decir, cuáles son aquellos que minimizan la varianza y se encuentran en la frontera eficiente.
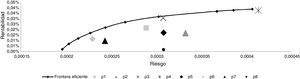
De acuerdo a la figura 2, se puede observar que los portafolios calculados a través de la heurística colonia artificial de abejas no son óptimos, pero algunos de los resultados se acercan a la frontera eficiente. El aporte de la colonia artificial de abejas es encontrar resultados similares, pero con costos computacionales comparativamente menores.
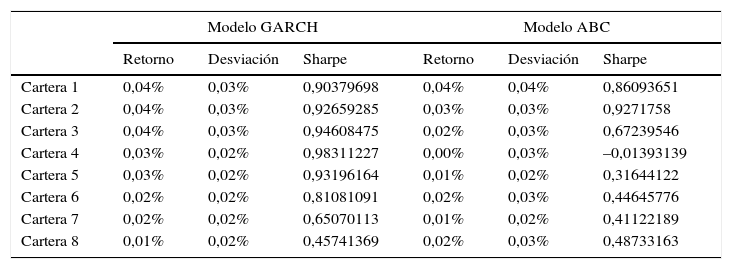
Por otra parte, los índices de Sharpe para los distintos portafolios que pertenecen a la frontera eficiente se presentan en la tabla 5. Los resultados obtenidos por ambos métodos son bastante similares, pero con costos muy diferentes.
Índices de Sharpe frontera eficiente modelo GARCH y colonia artificial de abejas (ABC)
| Modelo GARCH | Modelo ABC | |||||
|---|---|---|---|---|---|---|
| Retorno | Desviación | Sharpe | Retorno | Desviación | Sharpe | |
| Cartera 1 | 0,04% | 0,03% | 0,90379698 | 0,04% | 0,04% | 0,86093651 |
| Cartera 2 | 0,04% | 0,03% | 0,92659285 | 0,03% | 0,03% | 0,9271758 |
| Cartera 3 | 0,04% | 0,03% | 0,94608475 | 0,02% | 0,03% | 0,67239546 |
| Cartera 4 | 0,03% | 0,02% | 0,98311227 | 0,00% | 0,03% | –0,01393139 |
| Cartera 5 | 0,03% | 0,02% | 0,93196164 | 0,01% | 0,02% | 0,31644122 |
| Cartera 6 | 0,02% | 0,02% | 0,81081091 | 0,02% | 0,03% | 0,44645776 |
| Cartera 7 | 0,02% | 0,02% | 0,65070113 | 0,01% | 0,02% | 0,41122189 |
| Cartera 8 | 0,01% | 0,02% | 0,45741369 | 0,02% | 0,03% | 0,48733163 |
Fuente: elaboración propia.
Luego de programar a través de Eclipse y en Java, se logró llegar a los siguientes resultados que aparecen en la tabla 6.
Resultados con ambas posiciones
| Retorno cartera | Montos a invertir | Desviación cartera | Lambda | ||||||
|---|---|---|---|---|---|---|---|---|---|
| COPEC | CTC-A | CAP | COLBUN | ENDESA | ENTEL | ||||
| Cartera 1 | 0,015% | 9,209% | 36,630% | 6,447% | 6,500% | 0,663% | 40,551% | 0,024% | 0 |
| Cartera 2 | 0,024% | 69,065% | 23,918% | –0,063% | 0,042% | 0,701% | 6,336% | 0,030% | 0,1 |
| Cartera 3 | 0,022% | 26,802% | 49,876% | 8,188% | 3,633% | 5,374% | 6,126% | 0,026% | 0,2 |
| Cartera 4 | 0,017% | 0,356% | 51,564% | –0,767% | 10,446% | 28,994% | 9,407% | 0,026% | 0,3 |
| Cartera 5 | 0,016% | 2,738% | 30,248% | –0,614% | 1,211% | 0,924% | 65,493% | 0,031% | 0,4 |
| Cartera 6 | 0,017% | 89,074% | 1,676% | 6,866% | 1,428% | 0,819% | 0,137% | 0,034% | 0,5 |
| Cartera 7 | 0,010% | 2,169% | 25,086% | 4,830% | 9,087% | 0,441% | 58,387% | 0,027% | 0,6 |
| Cartera 8 | 0,025% | 68,633% | 24,620% | –0,738% | –0,431% | 3,983% | 3,933% | 0,030% | 0,7 |
| Cartera 9 | 0,012% | 1,613% | 53,883% | 31,534% | –3,239% | 7,723% | 8,486% | 0,026% | 0,8 |
| Cartera 10 | –0,001% | 0,314% | 26,594% | 39,313% | 1,405% | 0,458% | 31,917% | 0,023% | 0,9 |
| Cartera 11 | 0,023% | 32,093% | 41,794% | 1,293% | 3,286% | 0,555% | 20,979% | 0,025% | 1 |
Fuente: elaboración propia.
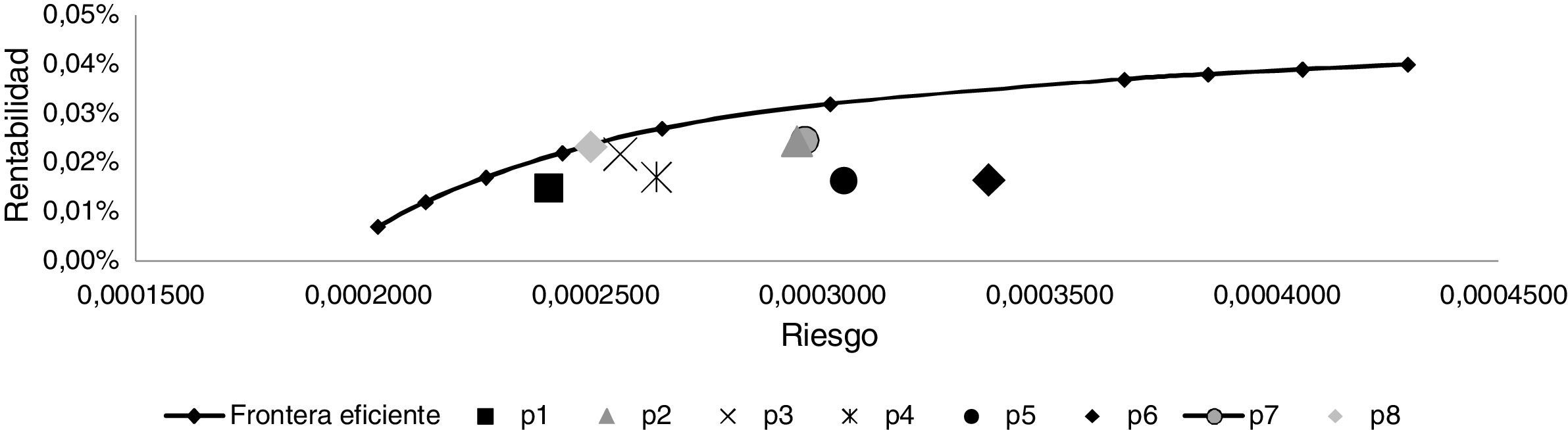
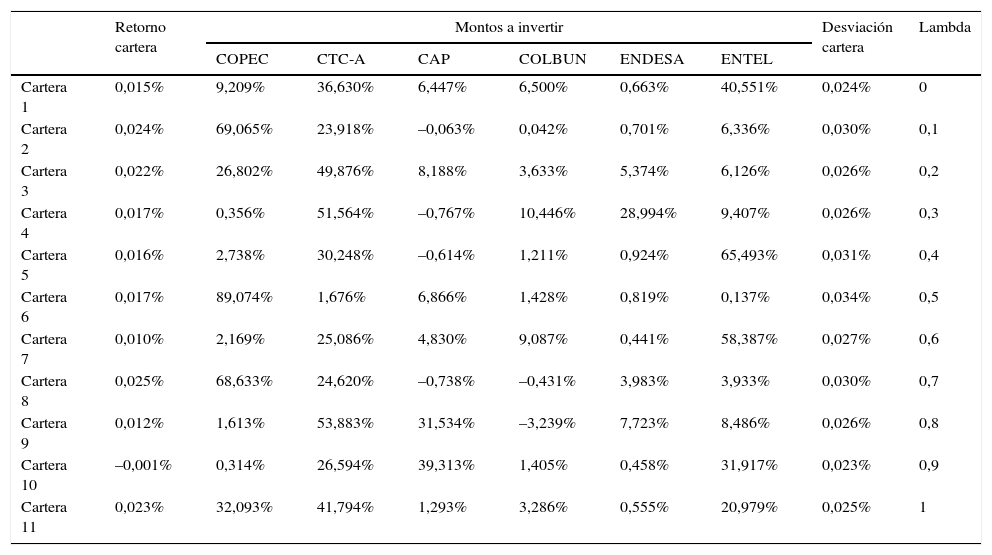
En la tabla 6 se observan los resultados obtenidos de la heurística colonia artificial de abejas permitiendo posiciones largas y cortas sobre los títulos financieros, es decir, ya no existe la restricción de no negatividad de los montos a invertir. Además, al graficar la frontera eficiente y algunos de estos nuevos portafolios con ambas posiciones se obtiene la figura 3.
Una vez más, en la figura 3 se observa que se repite la tendencia anterior, donde los portafolios calculados a través de la heurística colonia artificial de abejas no son óptimos, pero a pesar de esto se observa que algunos de los resultados se acercan a la frontera eficiente.
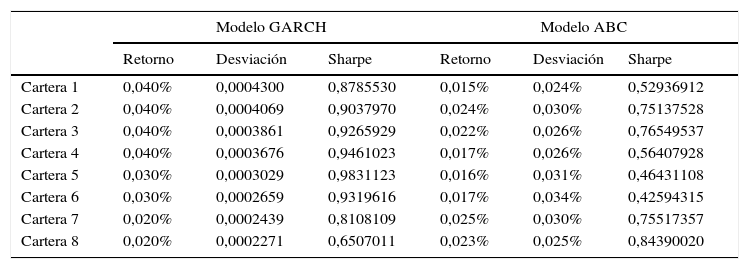
Por otra parte, los índices de Sharpe para los distintos portafolios que pertenecen a la frontera eficiente se presentan en la tabla 7.
Índices de Sharpe frontera eficiente
| Modelo GARCH | Modelo ABC | |||||
|---|---|---|---|---|---|---|
| Retorno | Desviación | Sharpe | Retorno | Desviación | Sharpe | |
| Cartera 1 | 0,040% | 0,0004300 | 0,8785530 | 0,015% | 0,024% | 0,52936912 |
| Cartera 2 | 0,040% | 0,0004069 | 0,9037970 | 0,024% | 0,030% | 0,75137528 |
| Cartera 3 | 0,040% | 0,0003861 | 0,9265929 | 0,022% | 0,026% | 0,76549537 |
| Cartera 4 | 0,040% | 0,0003676 | 0,9461023 | 0,017% | 0,026% | 0,56407928 |
| Cartera 5 | 0,030% | 0,0003029 | 0,9831123 | 0,016% | 0,031% | 0,46431108 |
| Cartera 6 | 0,030% | 0,0002659 | 0,9319616 | 0,017% | 0,034% | 0,42594315 |
| Cartera 7 | 0,020% | 0,0002439 | 0,8108109 | 0,025% | 0,030% | 0,75517357 |
| Cartera 8 | 0,020% | 0,0002271 | 0,6507011 | 0,023% | 0,025% | 0,84390020 |
Fuente: elaboración propia.
La figura 2 muestra, para los distintos niveles de aversión al riesgo, pero con la restricción de no realizar operaciones especulativas de venta corta, que la frontera eficiente y los índices de Sharpe exhiben un mejor desempeño para los modelos GARCH. Los resultados obtenidos a través del algoritmo de colonia artificial de abejas arrojan resultados bastante cercanos a los anteriores, pero con un costo computacional muy inferior. La misma situación se observa en la figura 3, pero esta vez permitiendo que los inversionistas adopten posiciones especulativas de venta corta.
5ConclusionesEn el presente artículo se implementó la metaheurística colonia artificial de abejas para resolver el problema clásico de la selección óptima de carteras de inversión, aplicándose a una muestra de acciones provenientes de la Bolsa de Comercio de Santiago de Chile, logrando resultados que verifican que su eficacia (optimización) y eficiencia (tiempos de ejecución) es mejor, si se compara con trabajos previos que pretenden alcanzar soluciones óptimas, pero utilizando otros modelos.
Para ninguno de los casos, con distintos grados de aversión al riesgo de los individuos, se logró obtener portafolios con mejores resultados que los obtenidos a través de los elaborados por medio de modelos autorregresivos (GARCH). Esto se debe a que las heurísticas son técnicas que permiten llegar a buenos resultados, pero en un tiempo computacional aceptable. El gran aporte de la metaheurística de la colonia artificial de abejas no es encontrar mejores soluciones que los modelos tradicionales, sino más bien encontrar soluciones bastante similares, pero con un costo computacional asociado a tiempo y recursos notablemente menor. En este caso, tanto para carteras sin venta corta como para carteras con venta corta, el tiempo de ejecución para encontrar la solución representa una relación de 1 a 15, es decir, las soluciones utilizando el algoritmo de la colonia artificial de abejas se encontraron en un tiempo máximo de 30minutos.
Dentro de posibles investigaciones futuras se debe tener presente que, dada la versatilidad de las metaheurísticas, estas pueden incorporar nuevas restricciones, que podrían agregarse a los modelos de decisiones de inversión de carteras. Además, desde el punto de vista de la eficiencia, para tener respuestas en tiempo real se podrían paralelizar las metaheurísticas, para de esta forma poder dar respuesta a la toma de decisiones en los mercados financieros dentro del menor tiempo (trading) y tender a la automatización, a través de lo que se ha denominado finanzas computacionales.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.
En algoritmia, el problema de la mochila, comúnmente abreviado por KP (del inglés knapsack problem) es un problema de optimización combinatoria, es decir, que busca la mejor solución entre un conjunto finito de posibles soluciones a un problema. Modela una situación análoga al llenar una mochila, incapaz de soportar más de un peso determinado, con todo o parte de un conjunto de objetos, cada uno con un peso y valor específicos. Los objetos colocados en la mochila deben maximizar el valor total sin exceder el peso máximo.
El índice de Sharpe es una medida del exceso de rendimiento por unidad de riesgo de una inversión.
Una clase más general de modelos, los GARCH (modelos generalizados autorregresivos condicionalmente heterocedásticos), que extiende la clase de los modelos ARCH, fue introducida por Bollerslev, Chou y Kroner (1992). En estos la estructura de la varianza condicional depende, además del cuadrado de los errores retrasados q períodos como en el modelo ARCH(q), de las varianzas condicionales retrasadas p períodos.