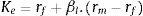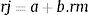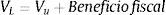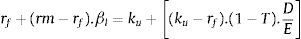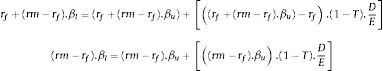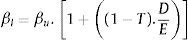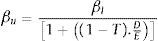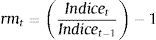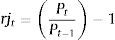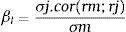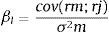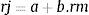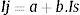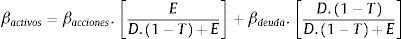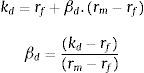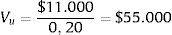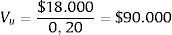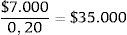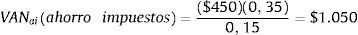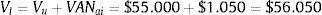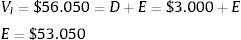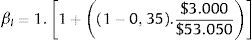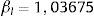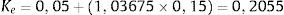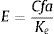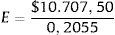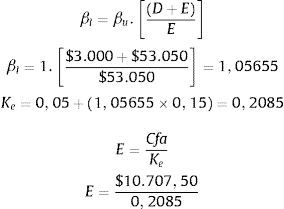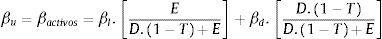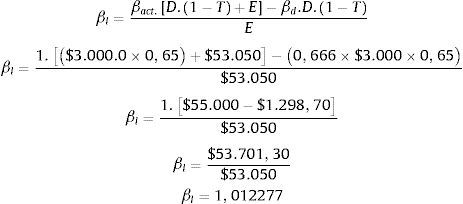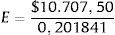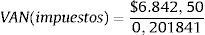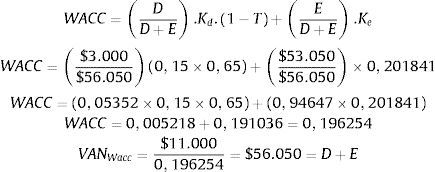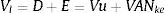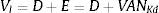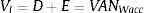Producto de una revisión de la literatura, en el presente trabajo se aplican 4 métodos para el cálculo de las betas de una muestra de 11 compañías que entre 2010 y 2012 cotizaron en el Mercado de Valores de Argentina. Empleando cada método, se identifica aquel que puede ser tomado como referencia para determinar las betas de pequeñas y medianas empresas (Pymes) que no cotizan en la Bolsa de Valores. Se concluye que para calcular los valores de las betas e interpretar el riesgo de cada empresa resulta necesario analizar técnicamente el método utilizado y la variabilidad de las series temporales empleadas, además de conocer las perspectivas futuras tanto de la empresa analizada como del sector al cual pertenece.
Using a literature review, four methods are applied for calculating betas in a sample of eleven companies that, between 2010 and 2012, were listed on the Stock Exchange of Argentina. Using each method, it was identified that one can be relied upon to determinate the betas of Small Business not quoted on the Stock Exchange. It is concluded that to calculate the beta values and interpret the risk of each company, it is technically necessary to analyze the method used and the variability of the time series used, as well as having knowledge of the future prospects of both the company analyzed and the industryto which it belongs.
Produto de uma análise da literatura, no presente trabalho aplicam-se quatro métodos para o cálculo das betas de uma amostra de 11 empresas cotadas na Bolsa de Valores da Argentina entre 2010 e 2012. Empregando cada método, identifica-se aquele que pode ser tomado como referência para determinar as betas de pequenas e médias empresas (PMEs) não cotizadas na Bolsa de Valores. Conclui-se que para calcular os valores das betas e interpretar o risco de cada empresa, é necessário analisar tecnicamente o método utilizado e a variabilidade das séries temporais empregadas, além de conhecer as perspectivas futuras, tanto da empresa analisada como do sector ao qual pertence.
A partir del modelo Capital Asset Pricing Mode (CAPM) (Sharpe, 1964), se puede definir la rentabilidad exigida por los accionistas o inversores como:
Recordando que rf se refiere a la tasa libre de riesgo, βl es la beta leverage o beta apalancada1, rm es la tasa de rentabilidad del mercado y (rm–rf) es la prima de riesgo esperada sobre el mercado.
Así como por definición la beta (β) de una acción mide el riesgo incremental que aporta una acción de una empresa a una cartera de valores diversificada (riesgo sistemático) y se define como la covarianza de las rentabilidades del valor y del mercado, dividida por la varianza de la rentabilidad del mercado (también el coeficiente de correlación entre las rentabilidades del valor y del mercado multiplicado por la volatilidad del valor y dividido por la volatilidad del mercado), la volatilidad mide el riesgo total de dicha acción y es el desvío estándar anualizado de la rentabilidad de la acción (σ). La diferencia entre ambos riesgos es el «riesgo no sistemático», es decir, aquel que puede eliminarse diversificando la cartera.
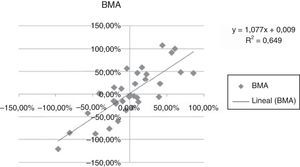
El procedimiento estándar para estimar la beta consiste en correr una regresión entre los rendimientos2 de la acción de una empresa j (rj) y del mercado (rm):
La pendiente de la regresión (b) corresponde a la beta de la acción, y mide el riesgo de la misma. La ordenada en el origen corresponde a la tasa libre de riesgo (rf).
Si la beta está correctamente calculada, el CAPM es el modelo apropiado para medir el riesgo, y una inversión en esa acción arrojaría un rendimiento del Ke anual a largo plazo. Por otro lado, para la compañía j significa que debe ganar, al menos, el Ke como retorno sobre la inversión de capital.
A continuación se realizará un desarrollo de cálculo del riesgo propio de la empresa, a través de la determinación del coeficiente beta del modelo de valoración de activos de capital, o CAPM. En la sección 1.1 se explica cómo es posible eliminar el efecto de apalancamiento de una beta correspondiente a una empresa cotizante, para utilizarla como referencia para el análisis de riesgo de una empresa no cotizante del mismo sector.
1.1Determinación de la beta desapalancada o unleveragedDe acuerdo con Modigliani y Miller (1958), el valor de una empresa con deuda (VL) es igual al valor de mercado de la firma sin deuda (Vu) más el beneficio fiscal producto de la deducción de impuestos de los intereses sobre la deuda, es decir:
Dada esta circunstancia, se puede visualizar la importancia del efecto que tiene para una empresa el uso de la deuda, pues según dichos autores, a medida que aumenta la deuda en la estructura de financiamiento de la empresa, su valor de mercado crece. Sin embargo, esto no es totalmente cierto, pues en la realidad las empresas no solo se financian con deuda, y a medida que van tomando deuda, el costo de la misma aumenta en línea con el incremento del riesgo de repago. Es por ello que Modigliani y Miller (1958) consideran el costo de la deuda (Kd) como constante durante todo su análisis.
Según Hamada (1972), partiendo de este concepto (Modigliani y Miller, 1958) y tomando como referencia el modelo CAPM (Sharpe, 1964) para el costo de capital (con apalancamiento o leverage), se cumple que:
Si se emplea la definición que da el CAPM a Ku y se reemplaza en la ecuación 4:
Reordenando lo anterior, en la ecuación5 se concluye que la beta apalancada de la acción (βl) puede ser calculada como función de la beta sin apalancamiento (βu) y el ratio de endeudamiento (D/E):
Siendo βu la beta sin apalancar, T la tasa de impuesto a las ganancias y D/E el cociente deuda/capital.
Ante esto puede decirse en principio que beta depende, entre otras cosas, del grado de apalancamiento financiero de la empresa. A medida que las empresas toman deuda, tienen mayores costos en concepto de pago de intereses, los cuales aumentan la variabilidad de sus ingresos y, en consecuencia, aumenta la beta.
Reordenando la ecuación 5, se concluye que la beta desapalancada, o beta unleveraged, será:
Ahora bien, existe una serie de supuestos que no necesariamente se presentan en la realidad, como por ejemplo: conforme aumenta el monto de la deuda con relación al capital de la empresa, los costos de su financiamiento en los mercados financieros se incrementan. Esto puede ocasionar, entre otras cosas:
- •
Tasas de interés elevadas.
- •
Falta de financiamiento para diversos proyectos, lo cual disminuye la capacidad de crecimiento de la empresa.
- •
Pérdida de proveedores, por temor a un eventual incumplimiento en los pagos por parte de la firma.
- •
Liquidación de activos productivos para cubrir flujos de deuda.
Para el desarrollo de los métodos de cálculo de las betas de compañías que no coticen en bolsa, como es el caso de la mayoría de las pymes en Argentina, se tomará como referencia información de empresas cotizantes de distintos sectores (energía, industrial y financiero) en el mercado de valores. Asimismo se utilizará esta información para analizar y observar la confiabilidad de los resultados de las betas de las compañías cotizantes que se tomarán como referencia, en función de la volatilidad de los rendimientos observados para cada uno de esos sectores, con el objetivo de establecer si los métodos que se vayan a desarrollar son fiables para el cálculo de las correspondientes betas.
Con el propósito de presentar a los lectores una serie de métodos para aplicar al cálculo de las betas de compañías que no cotizan en el mercado de valores, en el presente trabajo se plantea el análisis aplicado a una muestra de 11 compañías que entre los años 2010 y 2012 cotizaron en el Mercado de Valores (MERVAL) de Argentina, y partiendo de una revisión de los conceptos y diferentes metodologías para el cálculo de las betas (secciones 2.1, 2.2, 2.3 y 2.4) se procede a efectuar las interpretaciones de los resultados brindados al aplicar cada método, identificando las ventajas y desventajas en cuanto a su aplicación (sección 3). A continuación se presentan las conclusiones respecto a la utilidad de cada método en virtud de factores como la información con la cual se cuente, la estructura del sector y el conocimiento técnico, entre otros, para el cálculo de las betas para compañías que no cotizan en el mercado de valores (sección 4). Por último, se brinda una serie de preguntas de discusión y un listado de bibliografía sugerida para profundizar en la comprensión de la temática y su marco teórico de referencia.
2DesarrolloAunque la regresión sea el método más común para calcular la beta de una compañía, no necesariamente brinda como resultado el valor justo, dado que el índice de mercado puede estar definido para un universo reducido de empresas, como ocurre en el Mercado de Valores de Argentina.
Hay muchas fuentes para obtener los datos para la estimación de las betas; entre otras, pueden mencionarse:
- •
New York Stock Exchange (NYSE).
- •
Nasdaq.
- •
MERVAL (Mercado de Valores de Buenos Aires).
- •
Yahoo Finance.
- •
Google Finance.
- •
Bloomberg.
- •
Puentenet.
Dado lo anterior, la rentabilidad de mercado se calcula como:
Por otra parte, la rentabilidad de la acción en forma simplificada, sin incluir dividendos, se calcula así:
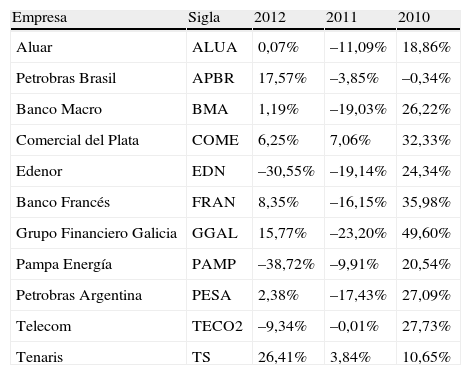
A continuación se presentan las tablas 1–4, en las cuales se demuestran los cálculos de las betas por diferentes métodos para una muestra de 11 empresas que cotizan en MERVAL (Argentina), pertenecientes a los sectores industrial, financiero, comunicaciones y energía, tomando las cotizaciones diarias y mensuales de sus correspondientes acciones entre el 01 de enero de 2010 y el 30 de septiembre de 2012.
Análisis de rentabilidades anuales
| Empresa | Sigla | 2012 | 2011 | 2010 |
| Aluar | ALUA | 0,07% | –11,09% | 18,86% |
| Petrobras Brasil | APBR | 17,57% | –3,85% | –0,34% |
| Banco Macro | BMA | 1,19% | –19,03% | 26,22% |
| Comercial del Plata | COME | 6,25% | 7,06% | 32,33% |
| Edenor | EDN | –30,55% | –19,14% | 24,34% |
| Banco Francés | FRAN | 8,35% | –16,15% | 35,98% |
| Grupo Financiero Galicia | GGAL | 15,77% | –23,20% | 49,60% |
| Pampa Energía | PAMP | –38,72% | –9,91% | 20,54% |
| Petrobras Argentina | PESA | 2,38% | –17,43% | 27,09% |
| Telecom | TECO2 | –9,34% | –0,01% | 27,73% |
| Tenaris | TS | 26,41% | 3,84% | 10,65% |
Fuente: elaboración de los autores con base en los precios de las acciones entre el 01/01/2010 y el 30/09/2012 publicados en www.puentenet.com.
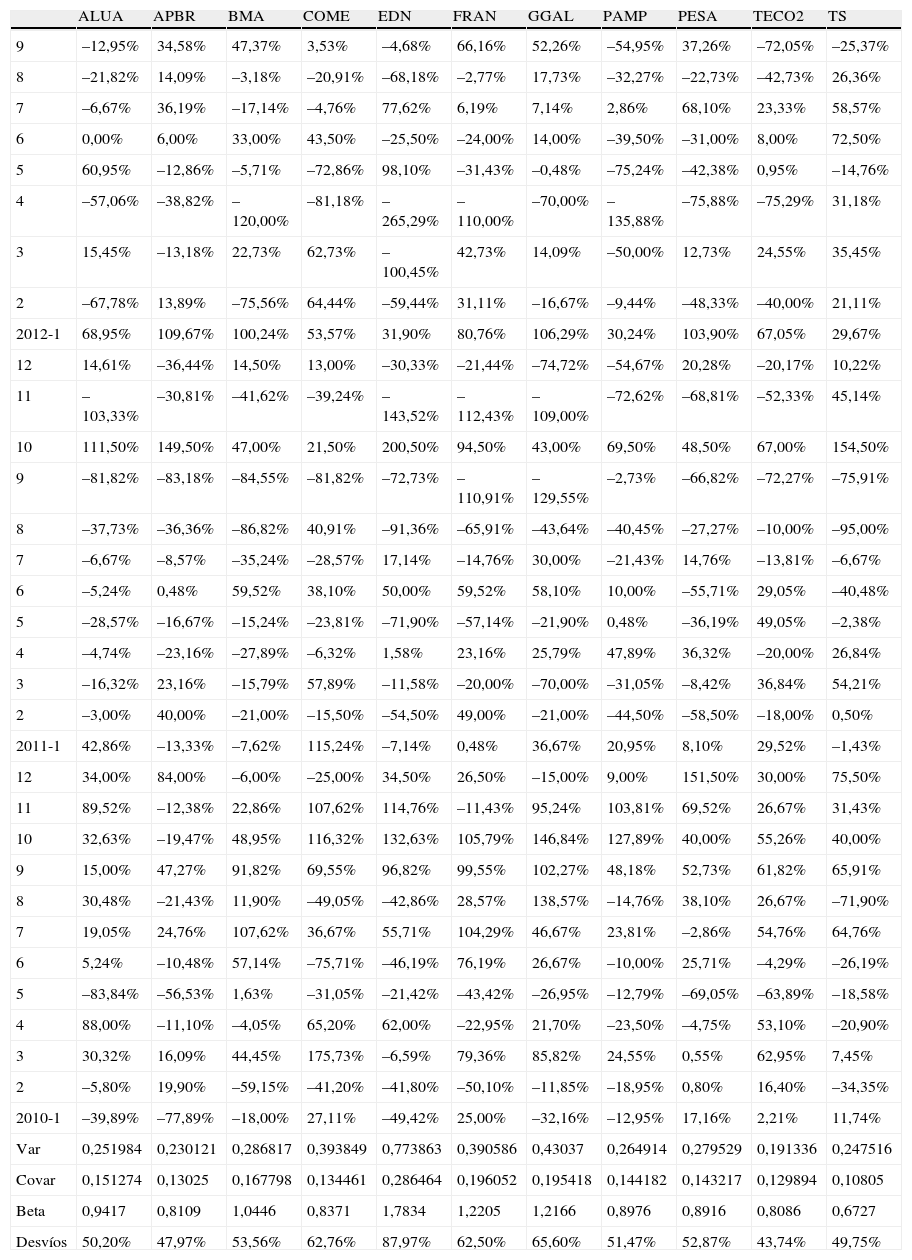
Análisis de rentabilidades mensuales y cálculo de betas con datos mensuales
| ALUA | APBR | BMA | COME | EDN | FRAN | GGAL | PAMP | PESA | TECO2 | TS | |
| 9 | –12,95% | 34,58% | 47,37% | 3,53% | –4,68% | 66,16% | 52,26% | –54,95% | 37,26% | –72,05% | –25,37% |
| 8 | –21,82% | 14,09% | –3,18% | –20,91% | –68,18% | –2,77% | 17,73% | –32,27% | –22,73% | –42,73% | 26,36% |
| 7 | –6,67% | 36,19% | –17,14% | –4,76% | 77,62% | 6,19% | 7,14% | 2,86% | 68,10% | 23,33% | 58,57% |
| 6 | 0,00% | 6,00% | 33,00% | 43,50% | –25,50% | –24,00% | 14,00% | –39,50% | –31,00% | 8,00% | 72,50% |
| 5 | 60,95% | –12,86% | –5,71% | –72,86% | 98,10% | –31,43% | –0,48% | –75,24% | –42,38% | 0,95% | –14,76% |
| 4 | –57,06% | –38,82% | –120,00% | –81,18% | –265,29% | –110,00% | –70,00% | –135,88% | –75,88% | –75,29% | 31,18% |
| 3 | 15,45% | –13,18% | 22,73% | 62,73% | –100,45% | 42,73% | 14,09% | –50,00% | 12,73% | 24,55% | 35,45% |
| 2 | –67,78% | 13,89% | –75,56% | 64,44% | –59,44% | 31,11% | –16,67% | –9,44% | –48,33% | –40,00% | 21,11% |
| 2012-1 | 68,95% | 109,67% | 100,24% | 53,57% | 31,90% | 80,76% | 106,29% | 30,24% | 103,90% | 67,05% | 29,67% |
| 12 | 14,61% | –36,44% | 14,50% | 13,00% | –30,33% | –21,44% | –74,72% | –54,67% | 20,28% | –20,17% | 10,22% |
| 11 | –103,33% | –30,81% | –41,62% | –39,24% | –143,52% | –112,43% | –109,00% | –72,62% | –68,81% | –52,33% | 45,14% |
| 10 | 111,50% | 149,50% | 47,00% | 21,50% | 200,50% | 94,50% | 43,00% | 69,50% | 48,50% | 67,00% | 154,50% |
| 9 | –81,82% | –83,18% | –84,55% | –81,82% | –72,73% | –110,91% | –129,55% | –2,73% | –66,82% | –72,27% | –75,91% |
| 8 | –37,73% | –36,36% | –86,82% | 40,91% | –91,36% | –65,91% | –43,64% | –40,45% | –27,27% | –10,00% | –95,00% |
| 7 | –6,67% | –8,57% | –35,24% | –28,57% | 17,14% | –14,76% | 30,00% | –21,43% | 14,76% | –13,81% | –6,67% |
| 6 | –5,24% | 0,48% | 59,52% | 38,10% | 50,00% | 59,52% | 58,10% | 10,00% | –55,71% | 29,05% | –40,48% |
| 5 | –28,57% | –16,67% | –15,24% | –23,81% | –71,90% | –57,14% | –21,90% | 0,48% | –36,19% | 49,05% | –2,38% |
| 4 | –4,74% | –23,16% | –27,89% | –6,32% | 1,58% | 23,16% | 25,79% | 47,89% | 36,32% | –20,00% | 26,84% |
| 3 | –16,32% | 23,16% | –15,79% | 57,89% | –11,58% | –20,00% | –70,00% | –31,05% | –8,42% | 36,84% | 54,21% |
| 2 | –3,00% | 40,00% | –21,00% | –15,50% | –54,50% | 49,00% | –21,00% | –44,50% | –58,50% | –18,00% | 0,50% |
| 2011-1 | 42,86% | –13,33% | –7,62% | 115,24% | –7,14% | 0,48% | 36,67% | 20,95% | 8,10% | 29,52% | –1,43% |
| 12 | 34,00% | 84,00% | –6,00% | –25,00% | 34,50% | 26,50% | –15,00% | 9,00% | 151,50% | 30,00% | 75,50% |
| 11 | 89,52% | –12,38% | 22,86% | 107,62% | 114,76% | –11,43% | 95,24% | 103,81% | 69,52% | 26,67% | 31,43% |
| 10 | 32,63% | –19,47% | 48,95% | 116,32% | 132,63% | 105,79% | 146,84% | 127,89% | 40,00% | 55,26% | 40,00% |
| 9 | 15,00% | 47,27% | 91,82% | 69,55% | 96,82% | 99,55% | 102,27% | 48,18% | 52,73% | 61,82% | 65,91% |
| 8 | 30,48% | –21,43% | 11,90% | –49,05% | –42,86% | 28,57% | 138,57% | –14,76% | 38,10% | 26,67% | –71,90% |
| 7 | 19,05% | 24,76% | 107,62% | 36,67% | 55,71% | 104,29% | 46,67% | 23,81% | –2,86% | 54,76% | 64,76% |
| 6 | 5,24% | –10,48% | 57,14% | –75,71% | –46,19% | 76,19% | 26,67% | –10,00% | 25,71% | –4,29% | –26,19% |
| 5 | –83,84% | –56,53% | 1,63% | –31,05% | –21,42% | –43,42% | –26,95% | –12,79% | –69,05% | –63,89% | –18,58% |
| 4 | 88,00% | –11,10% | –4,05% | 65,20% | 62,00% | –22,95% | 21,70% | –23,50% | –4,75% | 53,10% | –20,90% |
| 3 | 30,32% | 16,09% | 44,45% | 175,73% | –6,59% | 79,36% | 85,82% | 24,55% | 0,55% | 62,95% | 7,45% |
| 2 | –5,80% | 19,90% | –59,15% | –41,20% | –41,80% | –50,10% | –11,85% | –18,95% | 0,80% | 16,40% | –34,35% |
| 2010-1 | –39,89% | –77,89% | –18,00% | 27,11% | –49,42% | 25,00% | –32,16% | –12,95% | 17,16% | 2,21% | 11,74% |
| Var | 0,251984 | 0,230121 | 0,286817 | 0,393849 | 0,773863 | 0,390586 | 0,43037 | 0,264914 | 0,279529 | 0,191336 | 0,247516 |
| Covar | 0,151274 | 0,13025 | 0,167798 | 0,134461 | 0,286464 | 0,196052 | 0,195418 | 0,144182 | 0,143217 | 0,129894 | 0,10805 |
| Beta | 0,9417 | 0,8109 | 1,0446 | 0,8371 | 1,7834 | 1,2205 | 1,2166 | 0,8976 | 0,8916 | 0,8086 | 0,6727 |
| Desvíos | 50,20% | 47,97% | 53,56% | 62,76% | 87,97% | 62,50% | 65,60% | 51,47% | 52,87% | 43,74% | 49,75% |
Fuente: elaboración de los autores con base en los precios de las acciones entre el 01/01/2010 y el 30/09/2012 publicados en www.puentenet.com.
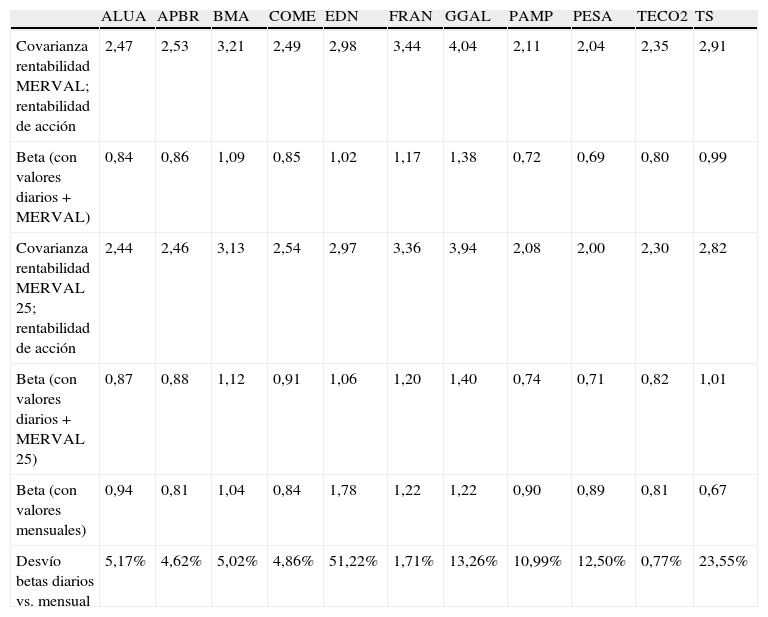
Cálculo de betas con datos diarios
| ALUA | APBR | BMA | COME | EDN | FRAN | GGAL | PAMP | PESA | TECO2 | TS | |
| Covarianza rentabilidad MERVAL; rentabilidad de acción | 2,47 | 2,53 | 3,21 | 2,49 | 2,98 | 3,44 | 4,04 | 2,11 | 2,04 | 2,35 | 2,91 |
| Beta (con valores diarios+MERVAL) | 0,84 | 0,86 | 1,09 | 0,85 | 1,02 | 1,17 | 1,38 | 0,72 | 0,69 | 0,80 | 0,99 |
| Covarianza rentabilidad MERVAL 25; rentabilidad de acción | 2,44 | 2,46 | 3,13 | 2,54 | 2,97 | 3,36 | 3,94 | 2,08 | 2,00 | 2,30 | 2,82 |
| Beta (con valores diarios+MERVAL 25) | 0,87 | 0,88 | 1,12 | 0,91 | 1,06 | 1,20 | 1,40 | 0,74 | 0,71 | 0,82 | 1,01 |
| Beta (con valores mensuales) | 0,94 | 0,81 | 1,04 | 0,84 | 1,78 | 1,22 | 1,22 | 0,90 | 0,89 | 0,81 | 0,67 |
| Desvío betas diarios vs. mensual | 5,17% | 4,62% | 5,02% | 4,86% | 51,22% | 1,71% | 13,26% | 10,99% | 12,50% | 0,77% | 23,55% |
Fuente: elaboración de los autores con base en los precios de las acciones entre el 01/01/2010 y el 30/09/2012 publicados en www.puentenet.com.
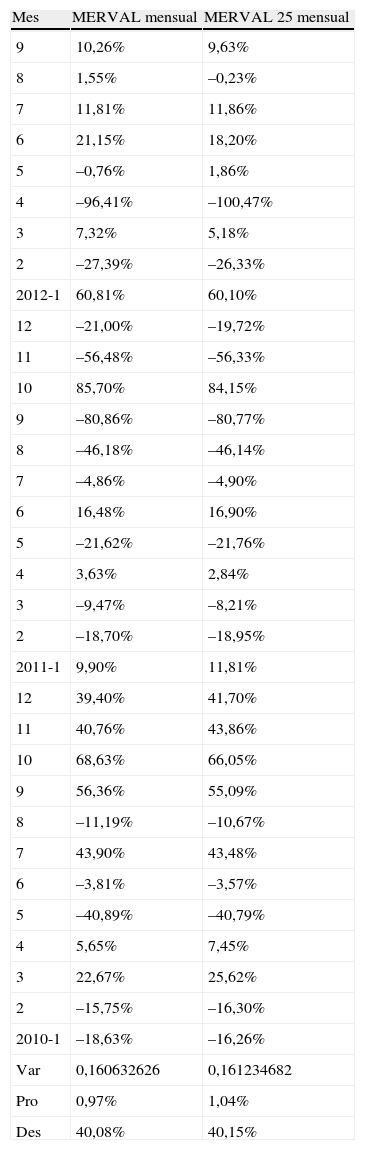
Cálculo de rendimientos mensuales: índices MERVAL y MERVAL 25
| Mes | MERVAL mensual | MERVAL 25 mensual |
| 9 | 10,26% | 9,63% |
| 8 | 1,55% | –0,23% |
| 7 | 11,81% | 11,86% |
| 6 | 21,15% | 18,20% |
| 5 | –0,76% | 1,86% |
| 4 | –96,41% | –100,47% |
| 3 | 7,32% | 5,18% |
| 2 | –27,39% | –26,33% |
| 2012-1 | 60,81% | 60,10% |
| 12 | –21,00% | –19,72% |
| 11 | –56,48% | –56,33% |
| 10 | 85,70% | 84,15% |
| 9 | –80,86% | –80,77% |
| 8 | –46,18% | –46,14% |
| 7 | –4,86% | –4,90% |
| 6 | 16,48% | 16,90% |
| 5 | –21,62% | –21,76% |
| 4 | 3,63% | 2,84% |
| 3 | –9,47% | –8,21% |
| 2 | –18,70% | –18,95% |
| 2011-1 | 9,90% | 11,81% |
| 12 | 39,40% | 41,70% |
| 11 | 40,76% | 43,86% |
| 10 | 68,63% | 66,05% |
| 9 | 56,36% | 55,09% |
| 8 | –11,19% | –10,67% |
| 7 | 43,90% | 43,48% |
| 6 | –3,81% | –3,57% |
| 5 | –40,89% | –40,79% |
| 4 | 5,65% | 7,45% |
| 3 | 22,67% | 25,62% |
| 2 | –15,75% | –16,30% |
| 2010-1 | –18,63% | –16,26% |
| Var | 0,160632626 | 0,161234682 |
| Pro | 0,97% | 1,04% |
| Des | 40,08% | 40,15% |
Fuente: elaboración de los autores con base en los precios de las acciones entre el 01/01/2010 y el 30/09/2012 publicados en www.puentenet.com.
En los siguientes apartados se presentarán los diferentes métodos o alternativas de cálculo de los coeficientes beta del modelo de valoración de activos de capital (CAPM).
2.1Método 1Consiste en la utilización de las estadísticas de los datos de mercado y de la acción (tales como las desviaciones estándar) para calcular la beta a partir de:
- •
La desviación estándar de la rentabilidad del mercado (σm).
- •
La desviación estándar de la rentabilidad de la acción (σj).
- •
El coeficiente de correlación entre la rentabilidad del mercado y de la acción [cor (rm,rj)].
Tomando con referencia la ecuación 9, podrían tomarse las siguientes variantes de cálculos estadísticos:
- •
La covarianza entre la rentabilidad del mercado y de la acción [cov (rm,rj)].
- •
La varianza de la rentabilidad del mercado (σ2m).
En la tabla 2 se presenta el cálculo de las betas con datos mensuales, mientras que en la tabla 3 se presenta dicho cálculo tomando los datos diarios.
Asimismo, otra alternativa sería correr una regresión lineal simple con mínimos cuadrados ordinarios (MCO) entre la rentabilidad del mercado (rm) y la rentabilidad de la acción (rj):
Dicho método implica el cálculo de:
- •
Las estadísticas de la regresión.
- •
El coeficiente de correlación múltiple.
- •
El coeficiente de determinación R2.
- •
El análisis de R2 ajustado.
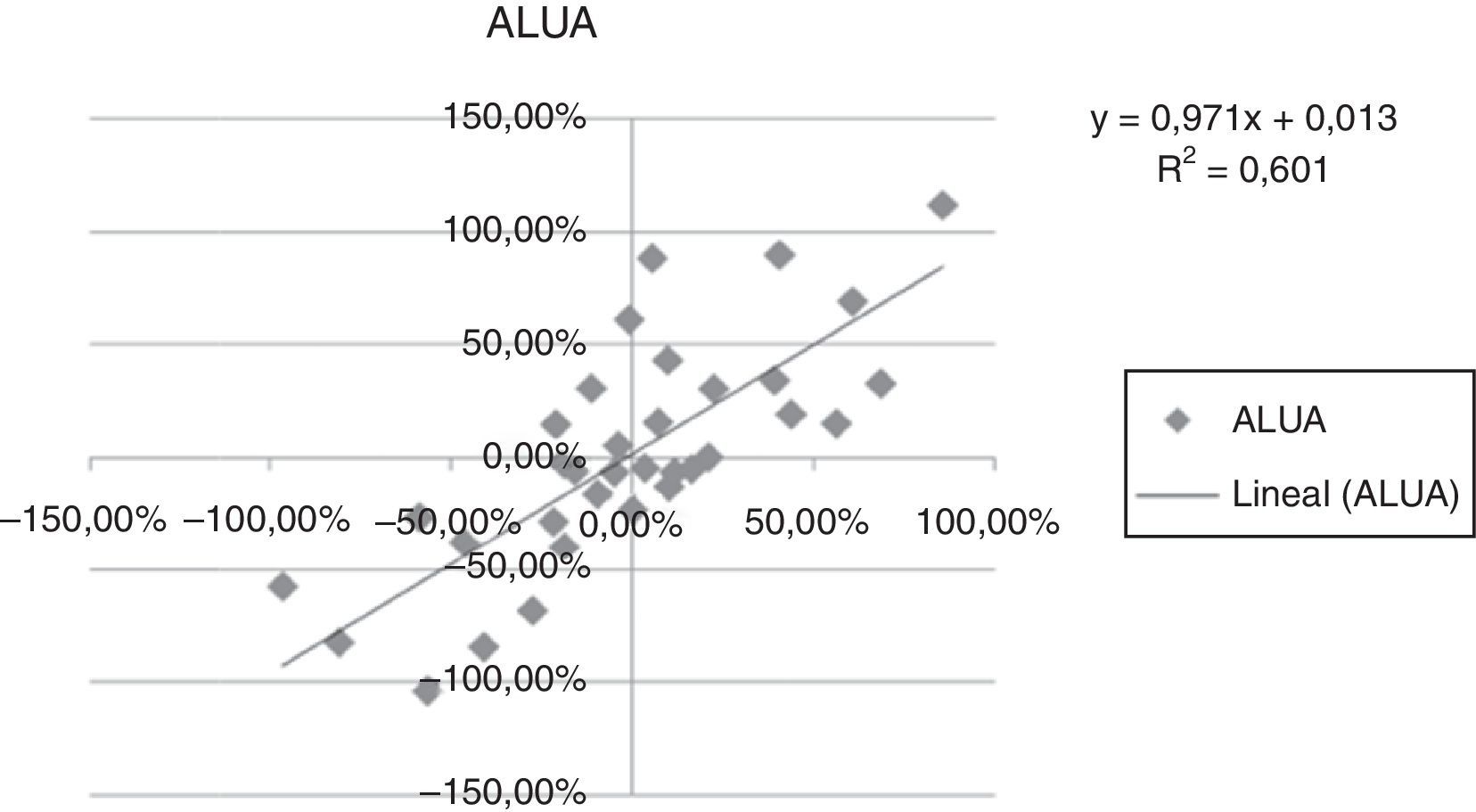
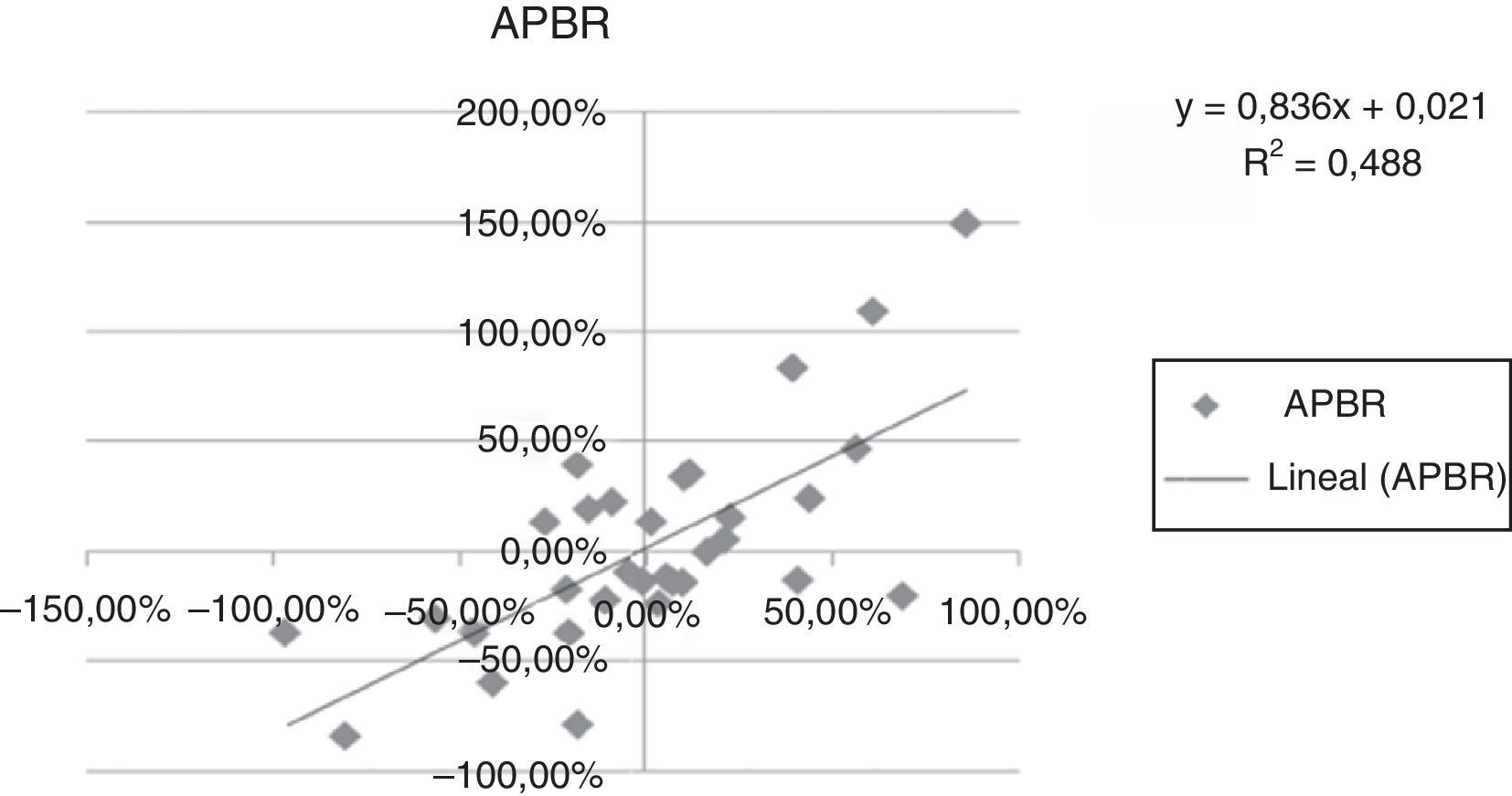
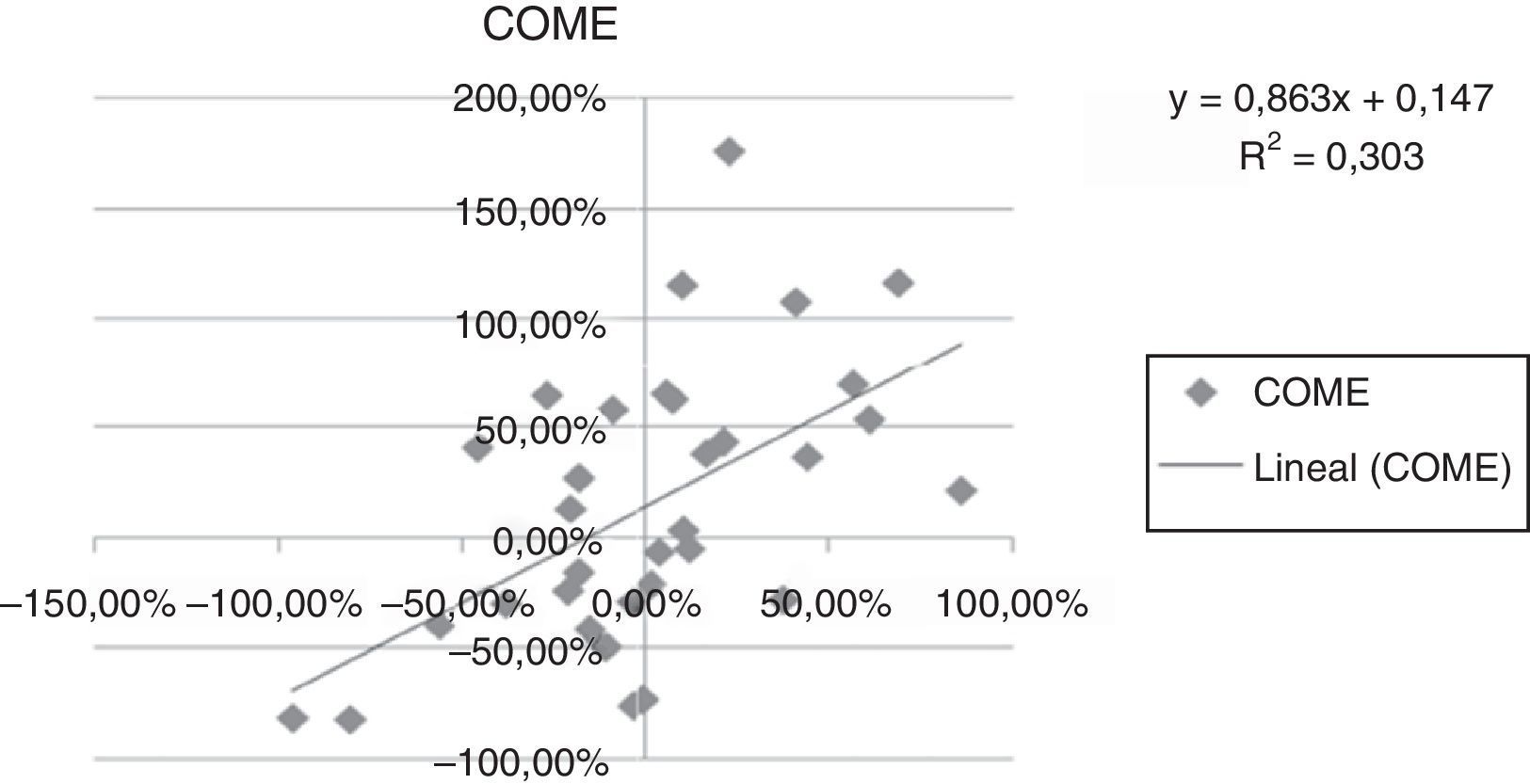
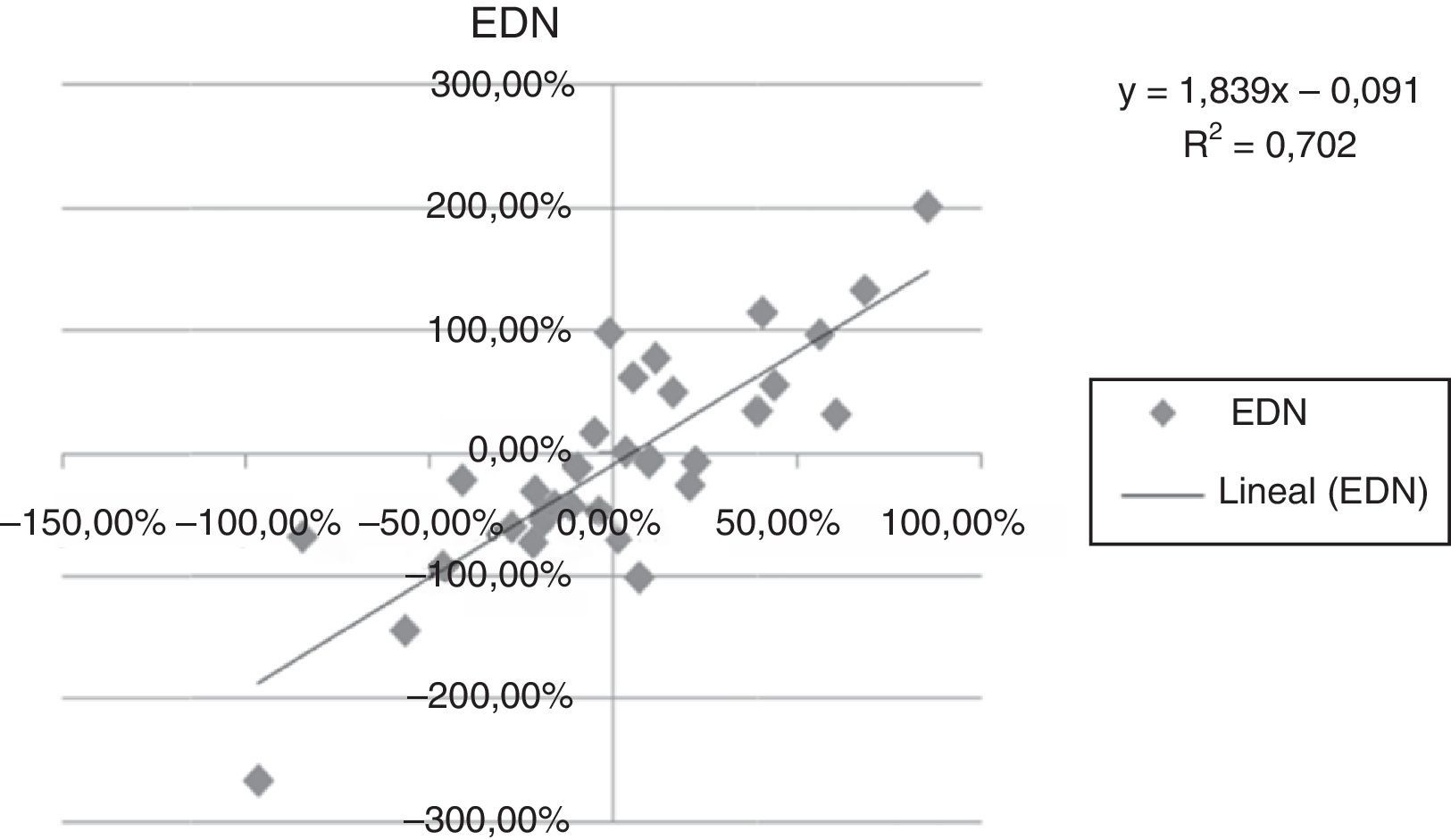
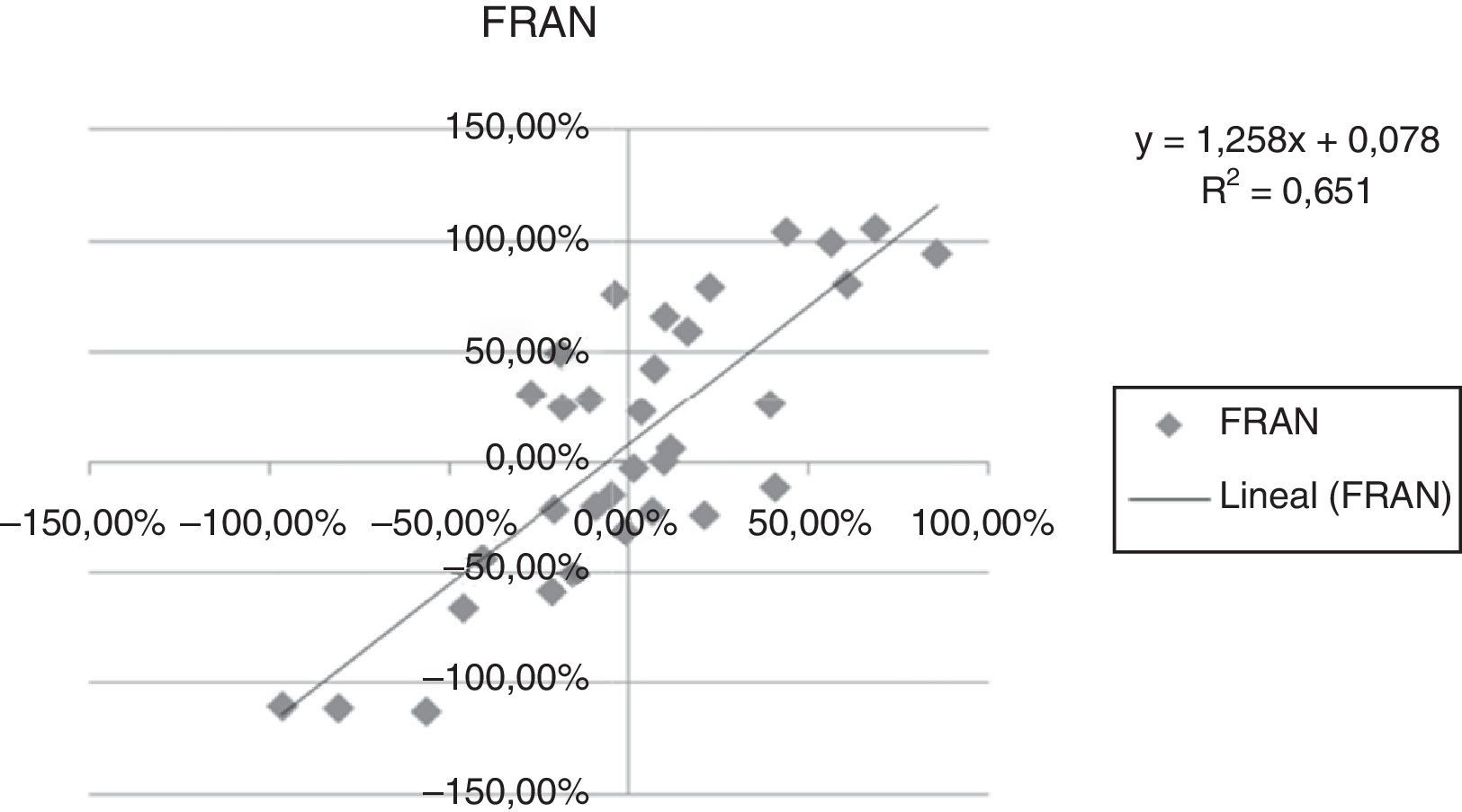
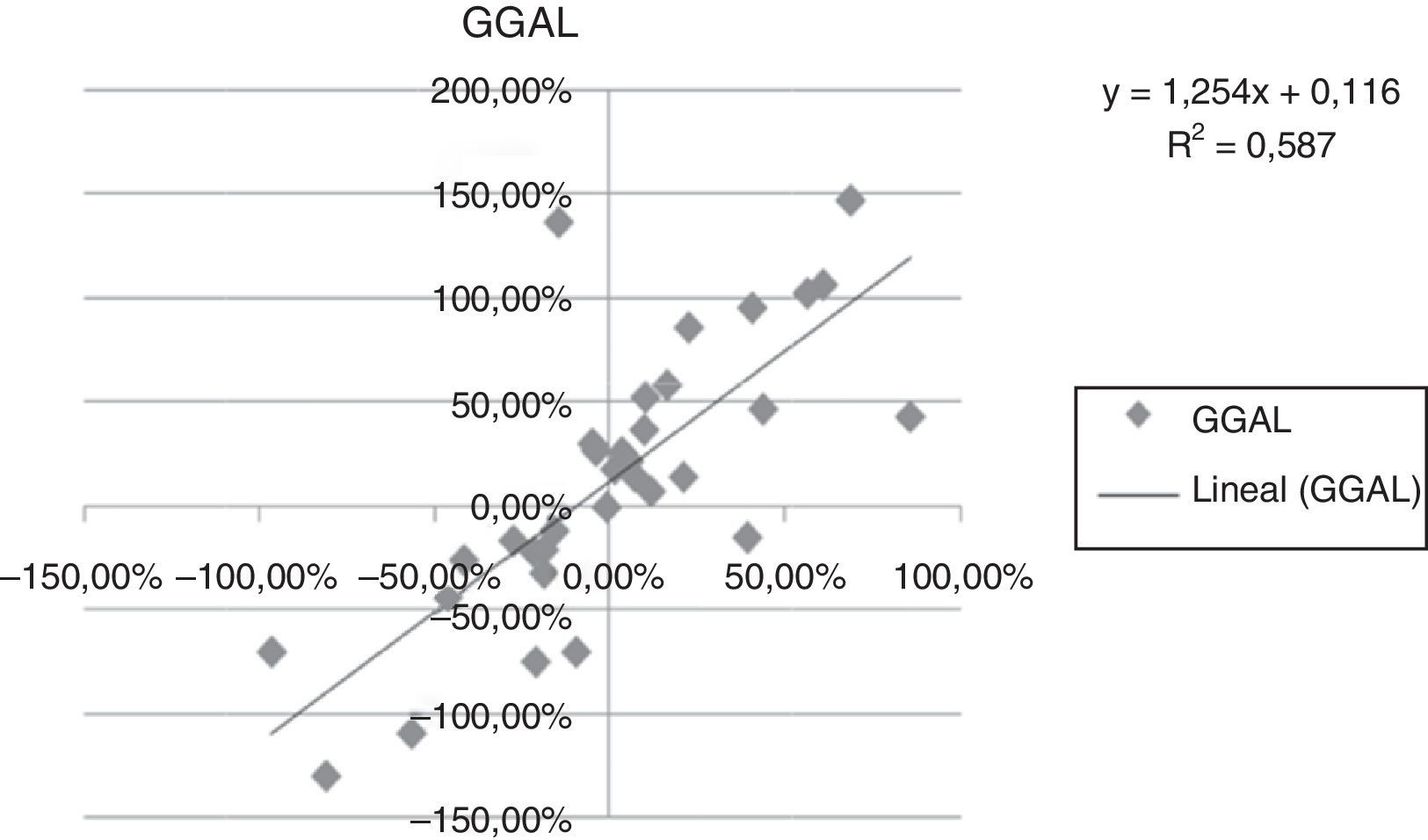
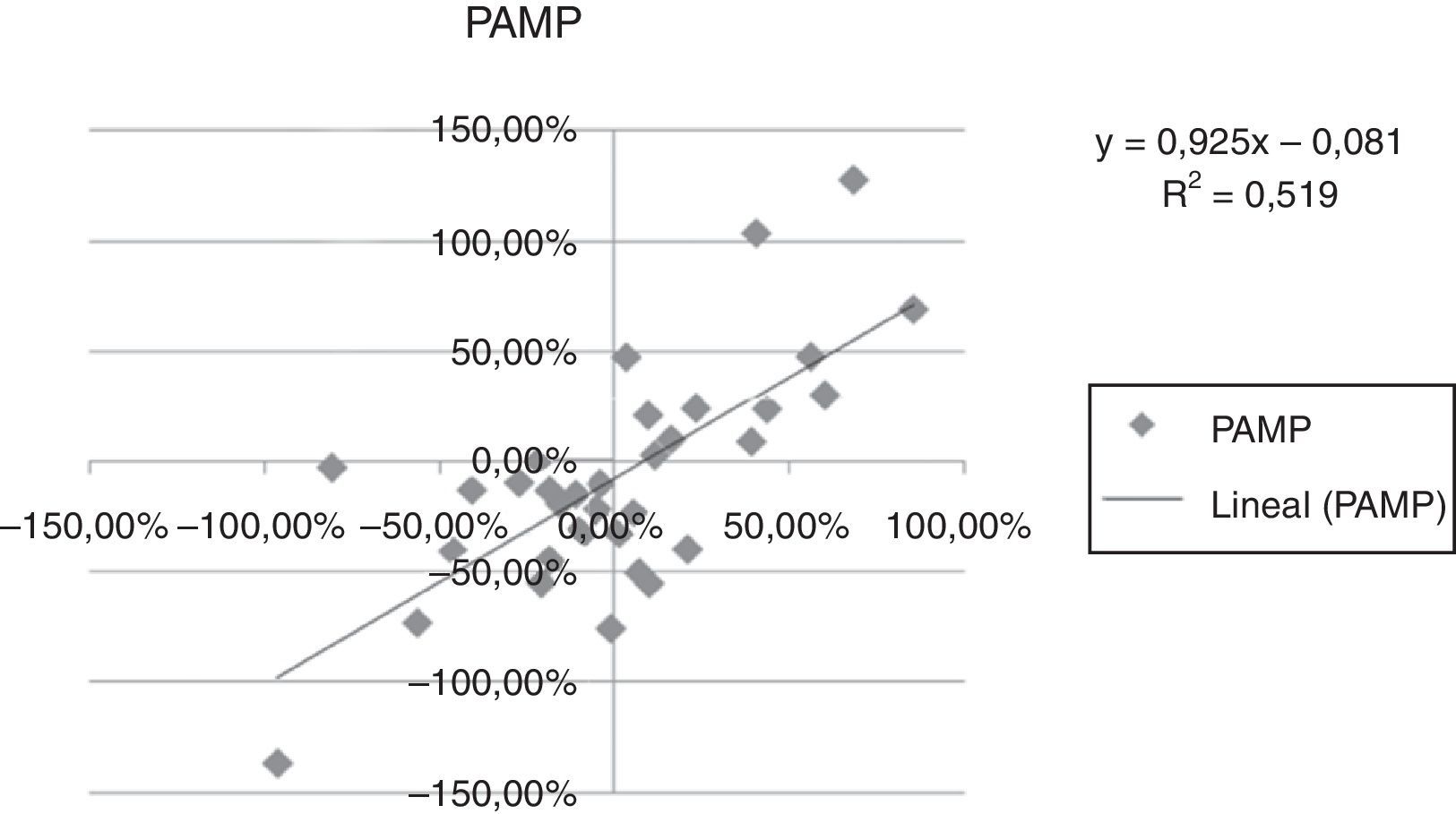
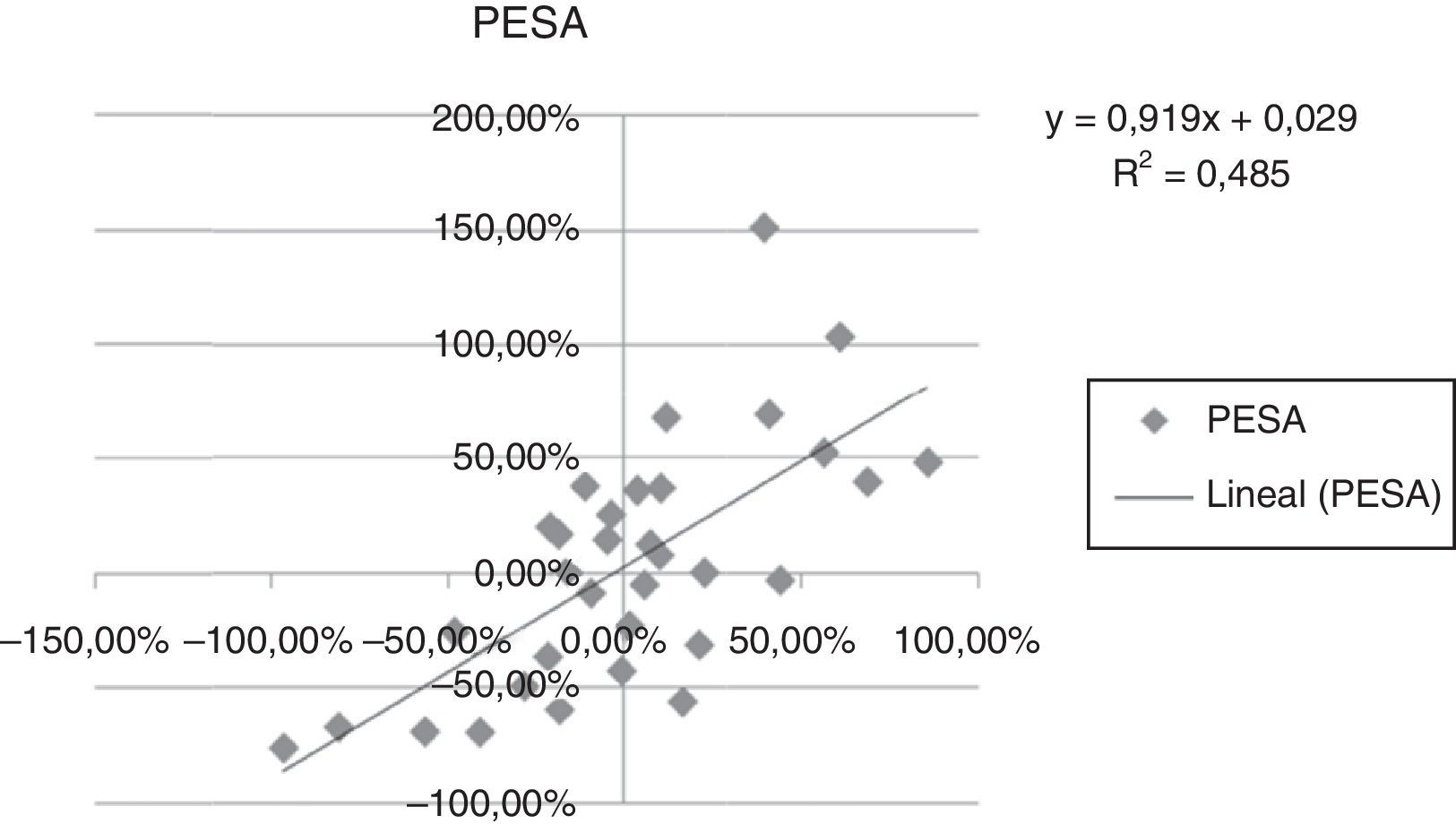
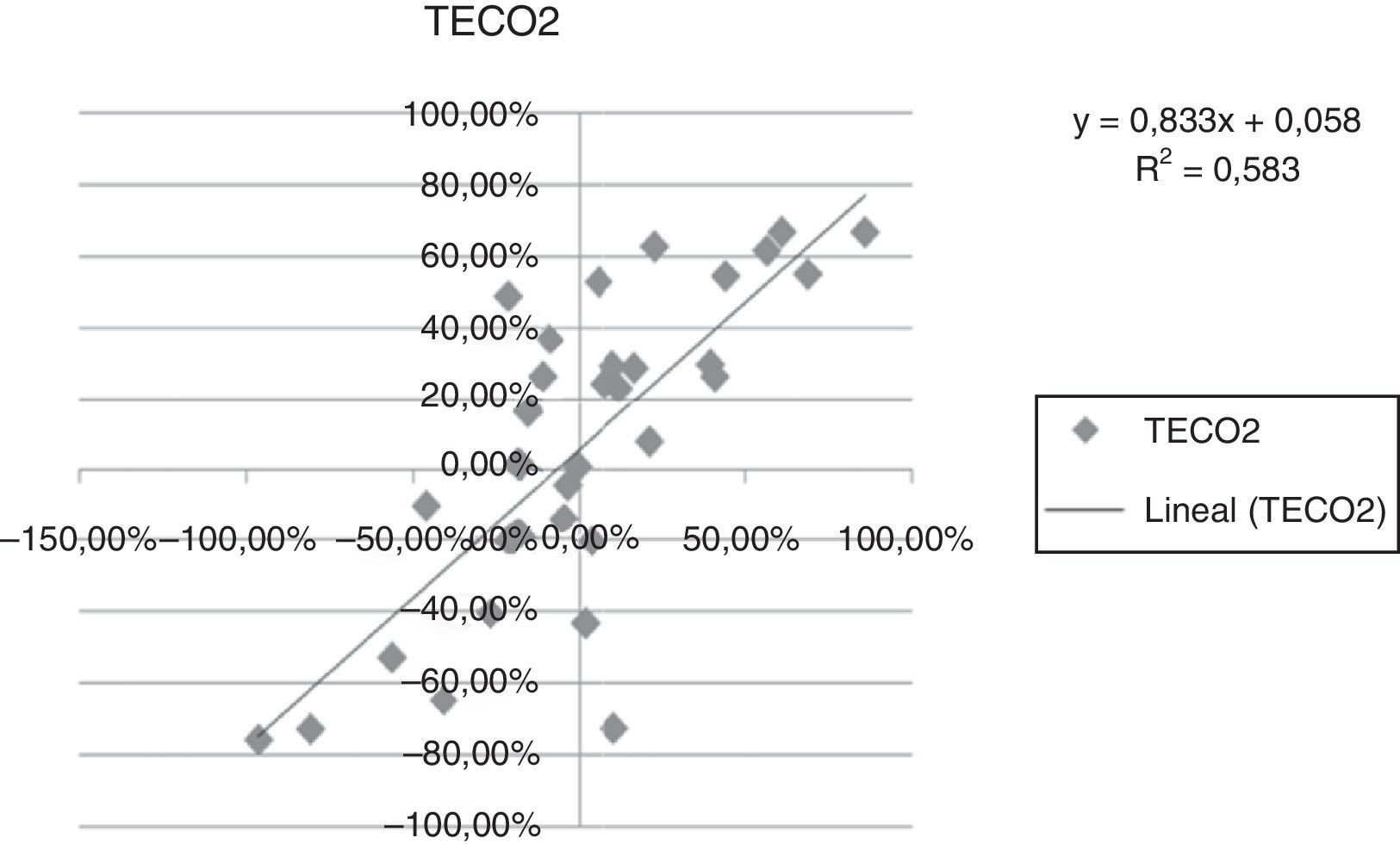
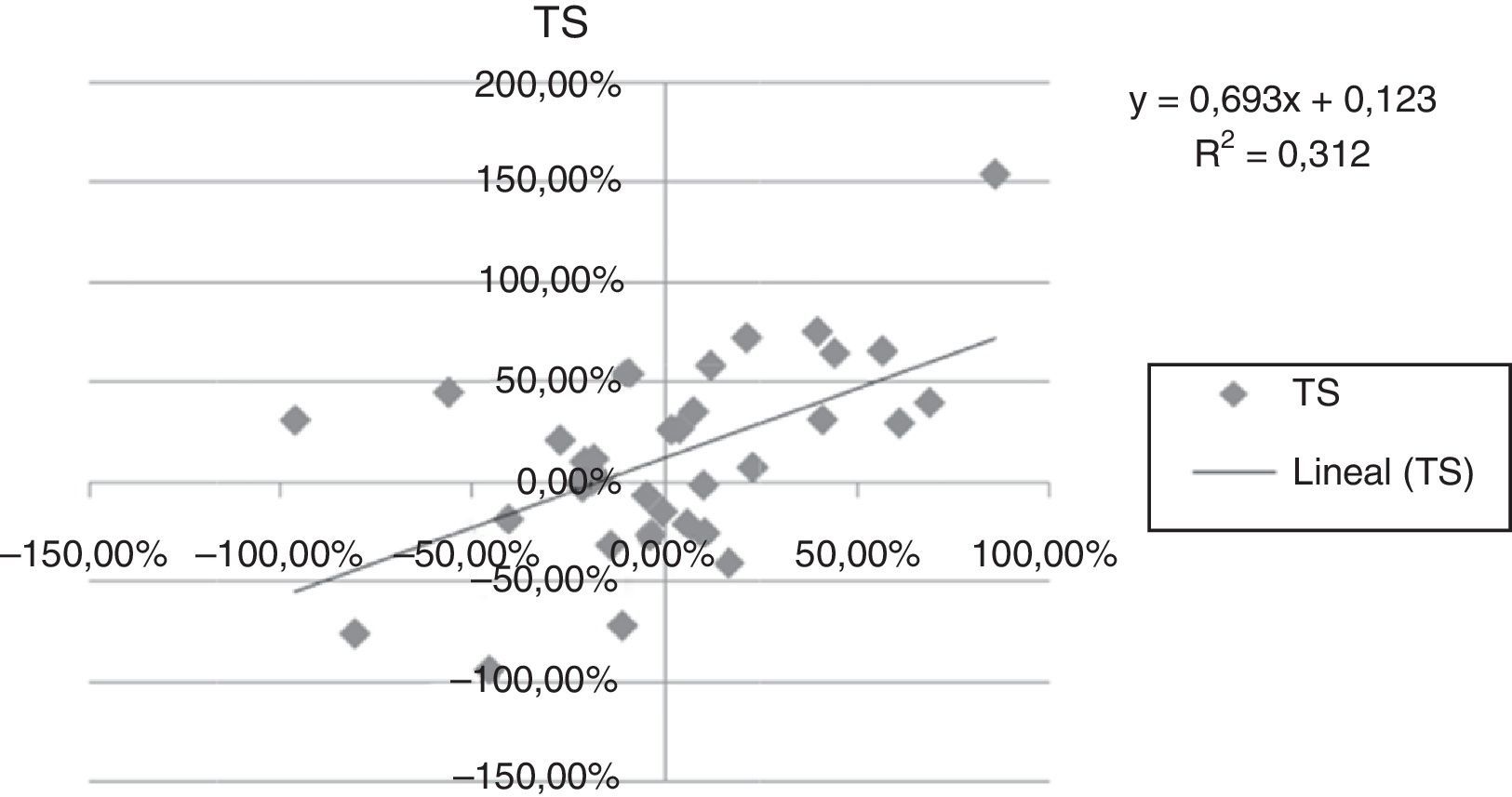
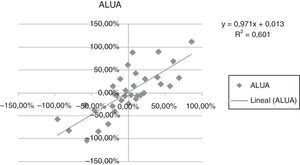
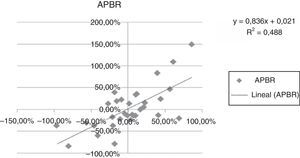
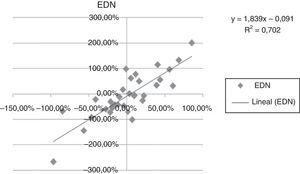
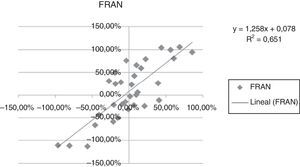
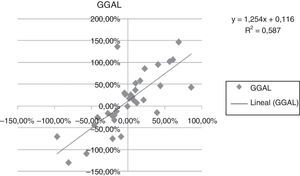
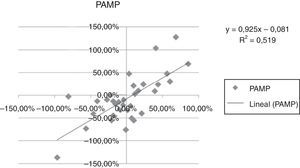
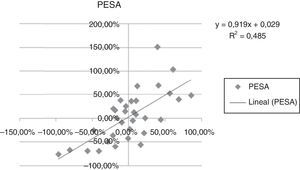
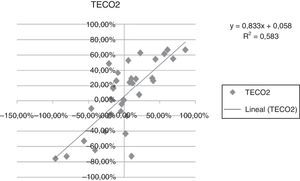
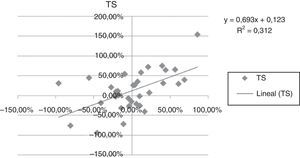
A continuación se presentan las figuras 1–11 con el cálculo de las betas con datos mensuales, utilizando ajustes o regresiones lineales.
2.2Método 2Esta solución consiste en correr una regresión con los ingresos o las ganancias de las compañías que tienen menor varianza que el precio de sus acciones. Aunque este método sea válido para empresas sin cotización pública, sufre de importantes limitaciones de información, lo cual se acentúa en economías emergentes.
En este método se podrían pensar las siguientes modalidades de cálculo:
Donde Ij corresponde a los ingresos de la compañía e Is se refiere a los ingresos del sector en el que se desempeña la compañía.
Donde Gj está relacionado con las ganancias de la compañía y Gs son las ganancias del sector en el que se desempeña la compañía.
2.3Método 3Otra forma de estimar la beta de una empresa consiste en el método denominado Bottom-Up. Si se desea estimar β para una empresa que no cotiza en bolsa, hay que «desapalancar» las betas de la industria y luego realizar un promedio de las mismas, tomando como criterio de ponderación el peso relativo de los ingresos por ventas de cada compañía que compone el sector analizado. Una vez que se tenga la media de la beta sin apalancamiento, se puede utilizar el CAPM para estimar Ku y usar la ecuación (6) para estimar βl por ecuación (5), y finalmente calcular Ke por la ecuación (1).
Los pasos para el cálculo serían:
- •
Identificar el sector o negocio en el que se desempeña la firma.
- •
Calcular las betas sin apalancamiento de las otras empresas en ese sector.
- •
Calcular su promedio, tomando como criterio de ponderación el peso relativo de los ingresos por ventas de cada compañía del sector3.
- •
Agregar finalmente el componente de apalancamiento, utilizando el ratio de endeudamiento de la empresa.
De acuerdo con Fruet (2004), el método Bottom Up —mayormente utilizado en la literatura de la temática— no tiene en cuenta el efecto que tiene la β de la deuda, por lo cual podría ser más exacto calcular la β apalancada a partir de la siguiente expresión:
Una vez calculado el costo de la deuda (kd), la beta de la deuda se puede obtener a partir del modelo CAPM, por lo cual puede plantearse βd:
Luego, partiendo de un determinado valor de la beta de los activos de la empresa, se puede hallar el valor de la beta de las acciones o beta apalancada, de acuerdo con alguno de los métodos expresados en párrafos anteriores.
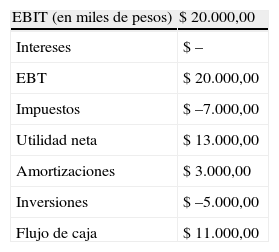
A continuación (tabla 5) se presenta un ejemplo. Suponga que se dispone de los siguientes datos para una empresa no endeudada y sin crecimiento (g=0), es decir, se supone que el flujo de caja de la empresa es el mismo todos los años.
Donde adicionalmente:
- •
Deuda (D)=$ 0.
- •
Beta desapalancado (βu)=1.
- •
Tasa libre de riesgo (rf)=5%.
- •
Premio de mercado (rm–rf)=15%
- •
Ke=rf+βu.rm−rfKe=0,05+(1)(0,15)Ke=0,20=20%
El valor de la empresa sin apalancar (Vu), o el valor de las acciones de la empresa sin deuda, puede obtenerse descontando el flujo de caja para los accionistas al costo del capital propio (Ke) calculado con el modelo CAPM, como se muestra a continuación:
Es importante considerar que si no hubiera impuestos, el flujo de caja para las acciones sería $18.000, con lo cual el valor de las acciones en ese caso sería:
La diferencia entre $90.000 (valor de las acciones sin impuestos) y $55.000 (valor de las acciones con impuestos del 35%) es el valor de los impuestos que se pagan al Estado ($90.000−$55.000=$35.000).
Este valor también puede calcularse como el valor actual neto (VAN) de los impuestos que se pagarán anualmente (7 millones por año).
Por esto, puede decirse que el valor de la empresa (es decir, de sus acciones) antes de impuestos es $90.000, de los cuales $35.000 (el 35%) corresponden al Estado y $55.000 (el 65%) a los propietarios de las acciones o inversores.
Suponiendo que la misma empresa tiene deuda por valor de $3.000 y el costo de la deuda es Kd=15%4 (tabla 6), el valor actual del ahorro de impuestos por intereses será:
De esta manera, Vl, que es el valor de la empresa apalancada (valor de las acciones más valor de la deuda), será:
Con este resultado se comprueba que la empresa aumenta su valor al aumentar el endeudamiento, debido al valor del ahorro de impuestos por los intereses de la deuda.
Adicionalmente, se puede obtener el valor del capital propio (E) como:
Luego se puede calcular βl a partir de la ecuación 5:
E=$ 52.104,62
O también se puede plantear:
E=$ 51.354,91
Dado lo anterior, se puede observar que en ambos casos, a pesar de ser las fórmulas que frecuentemente se utilizan, no son las correctas, ya que se necesitaría un flujo de caja para los accionistas diferente a $10.707,50. Esto es así, dado que este βl ignora el efecto de la βd de la deuda y el efecto de la tasa impositiva.
Por lo tanto, la fórmula que se debería aplicar para obtener la β apalancada es:
En consecuencia, se puede comprobar que:
Ke=0,05+(1,012277×0,15)=0,201841
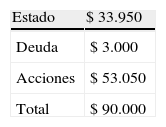
E=$ 53.050,00
Por lo tanto, el VAN de los impuestos es ahora:
VAN (impuestos)=$ 33.950
El valor antes de impuestos de la empresa (90 millones) se compone ahora de la forma expresada en la tabla 7.
Ahora, con los valores de D y E, se puede comprobar que también se verifica que Vl=VANWacc.
Para ello se calcula primero el costo promedio ponderado de los recursos (WACC) y luego se descuenta el flujo de caja libre a dicha tasa para obtener el valor de la empresa:
A través de este ejemplo se verifica que, bajo los supuestos dados, se obtiene el mismo valor para la empresa con cualquiera de las siguientes fórmulas:
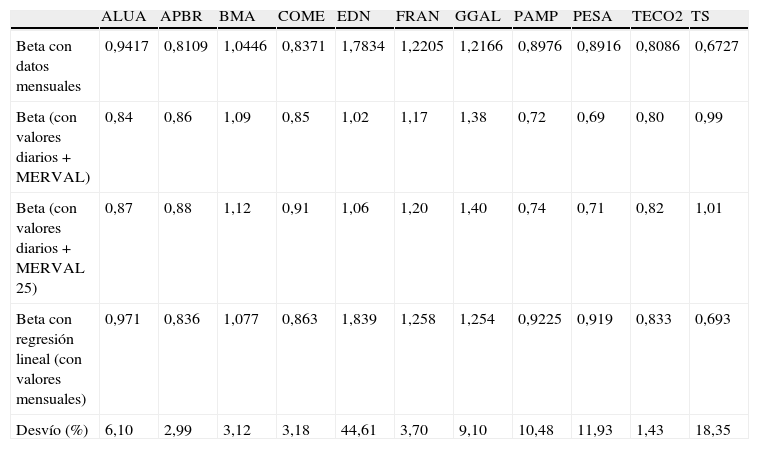
3InterpretacionesLa tabla 1 muestra los rendimientos anuales de 11 empresas que cotizan en el Mercado de Valores de Argentina entre los años 2010 a 2012. En la tabla 2 se muestran los rendimientos mensuales de esas empresas, y se calcula la beta de cada una de ellas (y las volatilidades), utilizando el denominado método1. La tabla 3 muestra los cálculos de las betas a partir de los datos de rendimientos diarios (y las volatilidades), utilizando también el denominado método1. La tabla 4 muestra los rendimientos mensuales de los índices MERVAL y MERVAL25, y se calcularon las volatilidades utilizando rentabilidades mensuales.
En las figuras 1–11 se han calculado las betas utilizando datos de rendimientos mensuales y realizando una regresión o ajuste lineal, es decir, utilizando también el denominado método1.
Una interpretación conjunta de las tablas 1–2 es que en algunas empresas la cotización de su acción no tiene variaciones significativas de un día para otro; sin embargo, es más difícil de observar esto a largo plazo, y este comportamiento se ve reflejado en una volatilidad anual mayor que la volatilidad mensual, y esta última mayor que la diaria. Por el contrario, hay empresas cuya cotización o rendimiento diario oscila más, es decir, que reaccionan más a corto plazo. La evolución del MERVAL se ve afectada por las empresas que no amortiguan la oscilación diaria del precio de su acción. También hay varias empresas de comportamiento más «normal», que son aquellas en las que la beta mensual y la beta diaria no son muy distintas.
Las betas se han calculado de distintas maneras: utilizando las rentabilidades diarias para cada uno de los años, para los 3años (2010-2011-2012) y utilizando datos mensuales de cada uno de los años. El análisis de los resultados de la tabla 8 muestra una relativa inestabilidad de las betas en las empresas vinculadas al sector de energía, y más estable en los sectores industriales y bancarios o financieros.
Comparación de los betas calculados de diferentes formas
| ALUA | APBR | BMA | COME | EDN | FRAN | GGAL | PAMP | PESA | TECO2 | TS | |
| Beta con datos mensuales | 0,9417 | 0,8109 | 1,0446 | 0,8371 | 1,7834 | 1,2205 | 1,2166 | 0,8976 | 0,8916 | 0,8086 | 0,6727 |
| Beta (con valores diarios+MERVAL) | 0,84 | 0,86 | 1,09 | 0,85 | 1,02 | 1,17 | 1,38 | 0,72 | 0,69 | 0,80 | 0,99 |
| Beta (con valores diarios+MERVAL 25) | 0,87 | 0,88 | 1,12 | 0,91 | 1,06 | 1,20 | 1,40 | 0,74 | 0,71 | 0,82 | 1,01 |
| Beta con regresión lineal (con valores mensuales) | 0,971 | 0,836 | 1,077 | 0,863 | 1,839 | 1,258 | 1,254 | 0,9225 | 0,919 | 0,833 | 0,693 |
| Desvío (%) | 6,10 | 2,99 | 3,12 | 3,18 | 44,61 | 3,70 | 9,10 | 10,48 | 11,93 | 1,43 | 18,35 |
Asimismo puede observarse que las betas calculadas con series de datos mensuales o serie de datos diarios, calculadas por métodos distintos, tienden a tener valores cercanos en sectores no vinculados al sector de energía.
4ConclusionesCoherente con los objetivos planteados en la introducción, se puede decir que la inestabilidad de la beta es especialmente importante en el sector de energía, y la determinación de la misma podrá variar según los datos utilizados para su cálculo. Hacer uso de una beta histórica de una acción, sin proceder al análisis de la misma y de las perspectivas futuras de la empresa en este sector, es muy arriesgado, ya que las betas históricas resultan cambiantes según los datos que se empleen. Para el resto de los sectores, cualquier método que se utilice, y cualquier tipo de serie que se tome como insumo (diaria o mensual), producirá valores de beta muy aproximados, con lo que se pueden tomar como referencia para determinar los betas de empresas pymes que no coticen en la Bolsa de Valores, utilizando luego el denominado método 3: Bottom up.
- 1)
Responda las siguientes preguntas de comprensión:
- A.
¿Qué mide beta?
- B.
¿Cómo puede calcularse la beta de una compañía?
- C.
¿Cuál sería la beta del mercado?
- D.
¿Cuál sería la beta de un activo libre de riesgo?
- A.
- 2)
Usted es un asesor financiero contratado por una empresa pyme no cotizante en bolsa que tiene planeado realizar una inversión productiva de la cual quiere evaluar su viabilidad económico-financiera. Para ello necesitaría determinar la tasa de descuento de los flujos futuros del proyecto en estudio. ¿Qué información necesitaría obtener para determinar dicha tasa? Y en este contexto, ¿qué variables utilizaría para la determinación de la beta de la compañía?
- 3)
Indique y justifique si es verdadera o falsa cada una de las siguientes frases:
- a)
La correcta determinación de la beta de las acciones de una empresa es relevante en la determinación de la rentabilidad esperada o el costo de capital de la compañía.
- b)
Si una empresa utilizara el mismo costo del capital (Ke) para evaluar todos los proyectos de inversión, cometería el error de rechazar proyectos con alto beta y aceptar proyectos con bajo beta.
- c)
Una acción con beta mayor a 1 implica que ante un aumento en el rendimiento del 1% del mercado, la acción mostrará un rendimiento mayor, y por lo tanto si su rendimiento es mayor, su riesgo será menor.
- d)
Para la determinación de la beta de una compañía no cotizante se debe tomar como referencia una compañía similar, del mismo sector, que cotice en bolsa, desapalancar su beta, y luego volver a apalancarla con la estructura de capital de la empresa no cotizante.
- e)
La beta no depende del grado de «apalancamiento financiero» de la empresa.
- f)
Se puede determinar la beta apalancada de una compañía cotizante en bolsa, sin tener en cuenta la estructura de capital de la misma, ni la referencia de una tasa libre de riesgo.
- g)
Se puede correr una regresión lineal simple con mínimos cuadrados ordinarios (MCO) entre la rentabilidad del mercado (rm) y la rentabilidad de la acción (rj), presentando los gráficos con el cálculo de las betas, con datos indistintamente diarios o mensuales, para cualquier sector de una economía.
- a)
Para el caso de los lectores que deseen continuar con las lecturas respecto a la temática tratada en este trabajo, se presentan a continuación una serie de publicaciones que permitirá ampliar el marco teórico de referencia:
Brealey, R.A., Myers, S.C. y Allen, F. (2006a). Principios de finanzas corporativas (8.a ed.). Madrid: Mc Graw Hill.
Brealey, R.A., Myers, S.C. y Allen, F. (2006b). Modelo para valorar activos de capital (CAPM). Madrid: Mc Graw Hill.
Mascareñas J. (2007). La beta apalancada. Documento de Investigación. Universidad Complutense de Madrid, España [consultado 1 Oct 2012]. Disponible en: http://www.ucm.es/info/jmas/monograf.htm
Mascareñas J. (2010). Introducción al riesgo en la empresa. Monografía sobre Finanzas Corporativas. Universidad Complutense de Madrid, España [consultado 1 Oct 2012]. Disponible en: http://www.ucm.es/info/jmas/monograf.htm
Vélez-Pareja I. (2011). Estimación de betas y relación entre las betas apalancadas y el coste del capital. Análisis Financiero, 116, 6-13.
Los autores declaran no tener ningún conflicto de intereses.
Vale aclarar que el coeficiente beta (β) es una medida de la volatilidad de un activo relativa a la variabilidad del mercado. Valores altos de beta implican más volatilidad, mientras que un beta 1 significa que el activo sigue los movimientos que tiene el mercado. Así, un valor con beta 1,30 significa que la acción es un 30% más volátil que el mercado, mientras que un valor de beta 0,80 es un 20 % menos volátil que el mercado.
Este artículo es resultado del trabajo de los autores en el marco del proyecto de investigación «Metodología para la determinación de la tasa de descuento en proyectos de inversión productiva para economías emergentes», perteneciente al Departamento de Economía y Administración de la Universidad Nacional de Quilmes, Argentina.
Resulta conveniente aclarar que si se utilizaran datos diarios convendría calcular los rendimientos con logaritmos naturales.
Dado que las compañías de un mismo sector tienen diferentes estructuras y escalas de producción, para el cálculo del promedio de la beta se busca evidenciar dichas diferencias tomando como referencia los ingresos por ventas.
Que el costo de la deuda sea del 15% supone que la beta asignada a la deuda es de 0,666. Por lo tanto: Kd=15%=0,15=0,05+bd es decir 0,15=0,05+(0,666)(0,15).