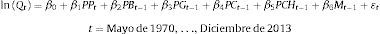El objetivo de este caso es discutir sobre la aproximación adecuada para realizar predicciones cuando se emplea un modelo de regresión lineal con una forma semilogarítmica. Para ello, se contextualiza el problema de una firma que requiere realizar predicciones sobre las cantidades demandadas de su producto estrella. De esta manera, el lector se enfrenta al desafío de cuestionar si una aproximación aparentemente intuitiva genera pronósticos adecuados.
This case discusses a problem that may arise when using a semi-logarithmic linear model to forecast the demand of a given product. This problem is presented using the discussion that emerges in a company that is looking for an approach to forecast the demand of its leading product. The reader faces the challenge of deciding which approach is adequate to the problem.
O objectivo deste caso é discutir a aproximação adequada para realizar previsões quando se emprega um modelo de regressão linear com uma forma semi-logarítmica. Para isto, contextualiza-se o problema de uma firma que requer a realização de previsões sobre as quantidades procuradas do seu produto principal. Desta maneira, o leitor enfrenta o desafio de questionar se uma aproximação aparentemente intuitiva gera prognósticos adequados.
En este caso se discute sobre el uso de un modelo de regresión lineal para realizar predicciones sobre las cantidades demandadas del producto estrella de una empresa cuando se emplea una forma funcional semilogarítmica. En particular, se busca incentivar el debate sobre la aproximación adecuada para realizar predicciones sobre una variable de interés, cuando se estima un modelo de forma semilogarítmica.
Por ello, en este caso se presenta la problemática que enfrenta la firma Panes S.A. para predecir las cantidades demandadas de su producto estrella; después se presenta la aproximación que se toma en una firma consultora para generar pronósticos y el debate que se desarrolla en esta última firma como consecuencia de adoptar esa forma funcional para la generación de un pronóstico.
Así, el lector asume el reto de resolver el debate, de manera que las predicciones para las cantidades demandadas del producto estrella de Panes S.A. sea la más adecuada posible. Teniendo esto en cuenta, este caso se acompaña de datos que permiten replicar los resultados obtenidos y dar respuesta a la pregunta planteada.
Este caso está organizado de la siguiente manera: la segunda sección corresponde al planteamiento de la situación problemática que se presenta al interior de la firma consultora y la tercera sección presenta la pregunta de discusión. Las respuestas sugeridas al caso están disponibles a petición del lector.
2CasoDesde 1971, Panes S.A., la única empresa productora de pan tajado de larga vida de la región, ha utilizado el método Delphi para hacer pronósticos de ventas de una manera más o menos acertada. Sin embargo, en los últimos 2años los errores en las predicciones, especialmente en el pan blanco tajado de 500g (su producto estrella), han generado pérdidas millonarias en la empresa, como consecuencia de excesos en la producción.
En otras palabras, las cantidades que se predicen son mayores que las que realmente se demandan. Por tanto, la firma termina produciendo más unidades de pan blanco tajado de 500g que las que puede colocar en el mercado. Por esta razón, Panes S.A. ha decidido contratar a Estimaciones Ltda., una prestigiosa firma consultora, para realizar sus próximas predicciones de demanda para el pan blanco tajado de 500g.
Como es costumbre en la firma consultora, los consultores líderes se reunieron para discutir la metodología que debían seguir para abordar el problema. Para muchos de los consultores líderes este era un caso rutinario, de manera que rápidamente coincidieron en que debería estimarse la función de demanda de pan utilizando el método de mínimos cuadrados ordinarios. Así, se tendría un modelo en el que las cantidades demandadas de pan dependen de su propio precio, del precio de las galletas, del precio promedio del pan blanco fabricado en las pequeñas panaderías de la región, del precio del café, del precio del chocolate y del ingreso de las personas.
Además, el consultor A argumentó convincentemente que la mejor forma funcional para este tipo de mercados es una semilogarítmica. Teniendo en cuenta este argumento, el equipo a cargo de estimar el modelo decidió estimar el siguiente modelo.
donde Qt son las cantidades demandadas del producto estrella de Panes S.A., en miles de toneladas; PPt es el precio del pan blanco tajado de 500g, en dólares de 2010; PBt es el precio de venta promedio del pan blanco, fabricado en las pequeñas panaderías de la región, en centavos de dólar de 2010 por gramo; PGt es el precio promedio de las galletas de soda de 950g, en dólares de 2010; PCt es el precio promedio del kilogramo de café, en dólares de 2010; PCHt es el precio promedio de la barra de 250g de chocolate de mesa, en dólares de 2010, y Mt es el ingreso per cápita, medido en miles de dólares de 2010.Una vez tomada la decisión sobre cuál modelo estimar, se encargó al nuevo investigador asociado a Estimaciones Ltda. realizar los cálculos pertinentes para pronosticar la demanda de Panes S.A. del próximo mes y calcular los correspondientes intervalos de confianza.
El investigador asociado realizó su tarea. Primero, estimó el modelo que se muestra en la tabla 1 y, al consultar con los encargados de los precios en Panes S.A., se enteró de que el próximo mes el precio del pan blanco tajado de 500g será de 1,26 dólares de 2010.
Resultados de la estimación del modelo (1)
| Variable dependiente: Ln(Qt) | ||
|---|---|---|
| (estadísticos t entre paréntesis) | ||
| Últimos 522 meses | ||
| MCO | ||
| Constante | 1,7053 (1,99) | * |
| PPt | −0,7748 (−2,96) | ** |
| PBt-1 | −2,9540 (−2,24) | * |
| PGt-1 | 0,6211 (2,34) | * |
| PCt-1 | −0,3060 (−3,25) | ** |
| PCHt-1 | −0,5931 (−2,85) | ** |
| Mt-1 | 0,4718 (23,14) | *** |
| R2 | 0,53290 | |
| R2-ajustado | 0,52750 | |
| F | 97,92 | *** |
| # de Obs. | 522 | |
El investigador asociado aseguraba que el modelo que se muestra en la tabla 1 estaba libre de problemas econométricos, por lo que era posible hacer predicciones a partir de él. Como el modelo (1) tiene como variable dependiente lnQt y no Qt, realizó la predicción en los siguientes pasos:
- 1.
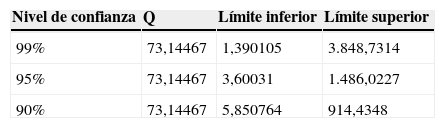
Calculó lnQt+1ˆ=β0ˆ+β1ˆPPt+1ˆ+β2ˆPBt+β3ˆPGt+β4ˆPCt+β5ˆPCHt+β6ˆMt, con sus respectivos intervalos del 95% de confianza para la realización puntual.
- 2.
Usando esta información, y sabiendo que x=elnx, obtuvo las predicciones de las cantidades demandadas de pan, así como de los límites superior e inferior del intervalo de confianza, empleando la siguiente transformación: Qt+1ˆ=elnQt+1ˆ.
Siguiendo el conducto regular de la organización, el investigador asociado le presentó los resultados de la estimación al estadístico del equipo, para que verificara que el procedimiento que había seguido era el adecuado, así como los resultados obtenidos. El investigador asociado le muestra los resultados de las tablas 1 y 2 al estadístico.
Al ver los resultados que le presenta el investigador asociado, el estadístico se muestra bastante preocupado, pues cree que los pronósticos presentados por el investigador asociado son sesgados. De acuerdo con el estadístico, si el error del modelo sigue una distribución normal, es posible conocer la magnitud del sesgo de los resultados presentados por el investigador asociado. Sin embargo, si no se conoce la distribución del término de error, el sesgo será desconocido, aunque muy probablemente diferente de cero.
El investigador asociado argumenta que el término de error del modelo no es relevante al realizar las predicciones de las cantidades demandadas de pan. Argumenta que la distribución del término de error no es relevante para estimar la realización puntual de la variable dependiente. Afirma que «el cálculo de la predicción es bastante simple, lo único que debe hacerse es reemplazar los valores que creemos que van a tomar las variables explicativas en el modelo estimado, y obtenemos la predicción de la variable dependiente. En este caso, dado que nos interesa la predicción para las cantidades vendidas de pan y no para el logaritmo de las cantidades vendidas de pan, es necesario aplicar la definición de logaritmo para obtener las cantidades vendidas. No hay espacio para la equivocación. Es más, si se trata de encontrar un intervalo de confianza para el valor esperado de la producción de pan, entonces la distribución del error no es relevante».
La discusión al interior de la firma se está convirtiendo en un gran problema. La mayoría de los empleados están tomando partida por los diferentes bandos y no parece existir un consenso sobre quién tiene la razón. Esta situación se está tornando inmanejable, y además la fecha para entregar el resultado final de la consultoría está cerca.
Como gerente de la firma consultora, ¿quién cree usted que tiene la razón? ¿Se puede realizar la transformación del logaritmo natural de las cantidades, a las cantidades sin ningún problema estadístico?
3Preguntas de discusión¿Tiene razón el estadístico del equipo? Si tiene la razón, ¿qué deberían hacer en Estimaciones Ltda. para obtener predicciones adecuadas para las cantidades demandadas de pan en el próximo mes?
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.