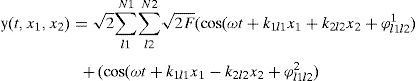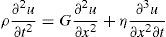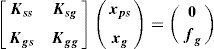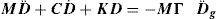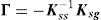En fase de diseño es habitual suponer que los desplazamientos sísmicos del terreno son uniformes entre apoyos de la estructura. Sin embargo, este no es necesariamente el caso para grandes estructuras, como viaductos, cuando existen importantes variaciones topográficas y/o geológicas a lo largo de la traza. En el presente caso se compara la respuesta de un puente continuo de 850m de longitud situado en una zona sísmica de PGA=0,1g, sometido a una serie análisis dinámicos con acelerogramas sintéticos, con y sin variación espacial del sismo, obtenidos por propagación de ondas hacia la superficie de cada apoyo.
In the design phase, seismic ground displacements are usually assumed to be uniform between the structure supports. However, this is not necessarily the case for extended structures, such as bridges, especially when there are different soil and/or topographic conditions along the structure. In the present study, the response of an 850m continuous bridge located in a seismic region of PGA=0.1g, is investigated. A set of synthetic accelerograms is generated from 1D site-response analysis at each bridge support. Furthermore, a number of linear time-history analyses are performed, with and without uniform support excitation, in order to quantify its influence on the bridge performance.
Los recientes terremotos producidos en Ecuador y en Italia en el pasado año son recordatorio del devastador impacto que dicho fenómeno puede causar en nuestro ámbito económico y social, principalmente a causa del daño y colapso estructural de edificaciones e infraestructuras. El diseño de estructuras en zonas sísmicas requiere, por tanto, especial atención al existir cierta probabilidad de colapso a lo largo de la vida útil de la estructura. Aunque las actuales normas de proyecto incorporan varios avances en materia de diseño sismo-resistente, como por ejemplo diseño por capacidad o verificación mediante análisis no lineal, todavía existen ciertos aspectos de controversia e incluso vacío total que dejan con poco criterio al ingeniero proyectista.
Por ejemplo, la definición de la acción sísmica mediante espectros de diseño constituye una forma simplificada de representar la acción sísmica, al dejar de lado aspectos clave como la duración del sismo, el número de ciclos o impulsos locales de aceleración por condiciones de proximidad a la falla, etc., los cuales afectan la respuesta inelástica y la disipación de energía de la estructura. Además, es habitual suponer en proyecto que el movimiento del terreno es uniforme en todos los puntos de apoyo de la estructura. Esto último puede no ser el caso para grandes estructuras, como viaductos o redes de tuberías, sobre todo cuando existen diferentes tipos de estrato o variaciones topográficas importantes a lo largo del eje de la estructura.
En esta línea, el Eurocódigo 8: ParteII proporciona un método simplificado de diseño con excitación variable en los apoyos de la estructura, el cual se basa en la imposición de un perfil de desplazamientos en los apoyos que depende del desplazamiento máximo del terreno, la longitud de la estructura y las condiciones locales de suelo [1]. Al mismo tiempo, para estructuras complejas con importantes variaciones de rigidez y resistencia, ya sea por las características del terreno o por la estructura en sí, y cuya respuesta depende de la participación de varios modos de vibración, la mayoría de normativas recomiendan la realización de análisis dinámicos (modal espectral o integración directa).
En el presente trabajo se presenta un estudio detallado de la respuesta de un puente de tablero continuo de 850m de longitud, situado en una zona sísmica de aceleración 0,1g, en suelo tipoiii[2], donde la acción sísmica se representó en el dominio del tiempo incluyendo su variación espacial a lo largo de la traza del puente. Para ello, primero se simuló la propagación de ondas en la roca base, de donde se obtuvieron las aceleraciones horizontales en roca para cada punto de apoyo del puente. A continuación, cada acelerograma se propagó hacia la superficie a través de las distintas capas del terreno mediante la resolución de un problema unidimensional de propagación de ondas (convolución). Tras definir en detalle el puente mediante un modelo de elementos finitos, cada sismo se definió como input en su correspondiente apoyo para la realización de un análisis dinámico paso a paso en el tiempo. Finalmente, se comparan las envolventes de esfuerzos y desplazamientos de la estructura con y sin variación espacial de la acción sísmica, con el objetivo de cuantificar su importancia en el proyecto de viaductos continuos de grandes longitudes.
2Generación de acelerogramas sintéticos en la roca baseLos acelerogramas sintéticos se generaron mediante el método estocástico de generación de ondas propuesto por Shinozuka et al. [3] y que proporciona los desplazamientos verticales del terreno en un punto de coordenadas (x1, x2) como suma de varios armónicos de distinta amplitud y ángulos de fase (ecuación 1):
donde N1, N2 son el número total de armónicos en cada dirección, F es el espectro de potencia evolutivo, kjli es el número de onda, dado por kjli=li·Δkj, donde Δkj=kju/Nj(j=1,2) y kju son constantes del modelo, ϕjl1l2 son ángulos de fase independientes y uniformemente distribuidos entre 0 y 2π, y ω es la frecuencia angular, dada como ω=c(k1l1+k2l2)0,5, donde c es la velocidad de propagación de onda igual a 2.800m/s. El espectro F es función del tiempo y de las coordenadas x1 y x2, por lo que las características espectrales de y(t,x1,x2) varían en función del tiempo y del espacio (proceso no estacionario no homogéneo). Detalles adicionales sobre el método pueden encontrarse en [3,4]
Para la generación de las ondas se adoptó una malla de referencia de 8,5×8,5km2 discretizada en intervalos de 0,5×0,5km2, de donde se calcularon los desplazamientos verticales en las coordenadas correspondientes a los puntos de apoyo de la estructura, despreciando la curvatura en planta del puente tras comprobar que apenas influía en la variación espacial de la señal.
Las velocidades y aceleraciones finales en cada apoyo se obtuvieron por derivación de los desplazamientos, aplicación de la corrección de base con el objetivo de imponer una velocidad igual a cero al final del registro, y escalado de acuerdo con la aceleración pico en roca, tomada como 0,04g. También se aplicó una envolvente de tipo trapecial con una duración de 20s, para mejorar el ajuste a registros sísmicos reales. Dicho proceso se repitió 14veces para obtener 7 parejas de registros en cada apoyo, esto es, dos componentes horizontales por apoyo, para posteriormente realizar 7 análisis dinámicos de la estructura, generando así un total de 112 registros.
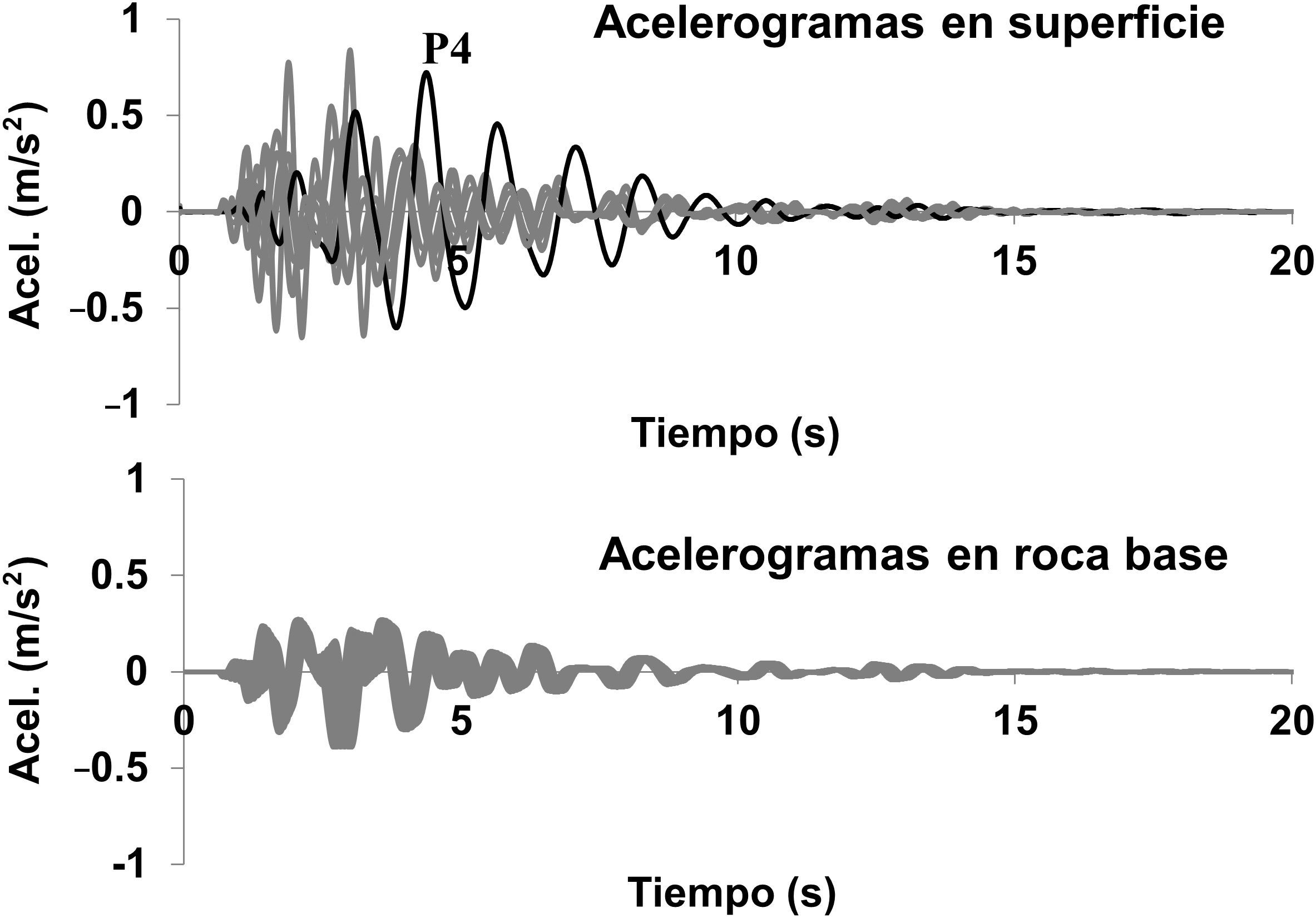
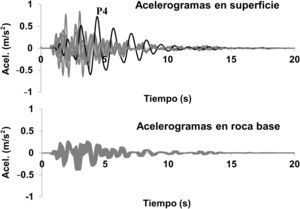
En la figura 1 se muestran los 8 registros obtenidos del primer análisis, desde el estribo E1 hasta el E2, pasando por las pilas P1, P2, etc., de donde se observa que las aceleraciones son muy similares al estar los puntos de apoyo relativamente próximos entre sí. También se muestran las aceleraciones obtenidas en superficie tras propagar las ondas a través de las distintas capas de suelo, tal como se explicará a continuación, de donde se observa que las diferencias entre apoyos ya no son despreciables.
3Propagación de ondas hacia la superficie y espectros de respuestaLos acelerogramas de cálculo en superficie se obtuvieron tras propagar aquellos generados en roca a través de las distintas capas del terreno mediante la resolución de la ecuación de ondas dada como (ecuación 2):
donde ρ es la peso específico, G el módulo de cortante, u el desplazamiento horizontal del terreno y η viene dado como η=2Gξ/ω, donde ξ es el porcentaje de amortiguamiento crítico [4]. En el dominio de la frecuencia, dicha ecuación adquiere la forma de una ecuación diferencial ordinaria homogénea de segundo orden, la cual se puede discretizar en función del número de capas y obtener así un sistema lineal de ecuaciones. De esta forma, conocido el desplazamiento en la roca base y las propiedades del terreno a lo largo de la vertical sobre el eje de la pila, se pueden calcular los desplazamientos en la superficie del terreno, lo cual se conoce como convolución de la señal sísmica. El procedimiento de cálculo se resume en los siguientes pasos:
- 1)
Dado el acelerograma en la roca base en el dominio del tiempo
- 2)
Transformar al dominio de la frecuencia mediante la transformada de Fourier.
- 3)
Multiplicar por 1/ω2 para obtener el espectro de desplazamientos en la roca base.
- 4)
Resolver el problema de convolución y obtener el espectro de desplazamientos en superficie.
- 5)
Aplicar la inversa de la transformada de Fourier para pasar al dominio del tiempo.
- 6)
Derivar para obtener velocidades y aceleraciones.
- 7)
Aplicar corrección de base para imponer velocidades igual a cero al final del registro.
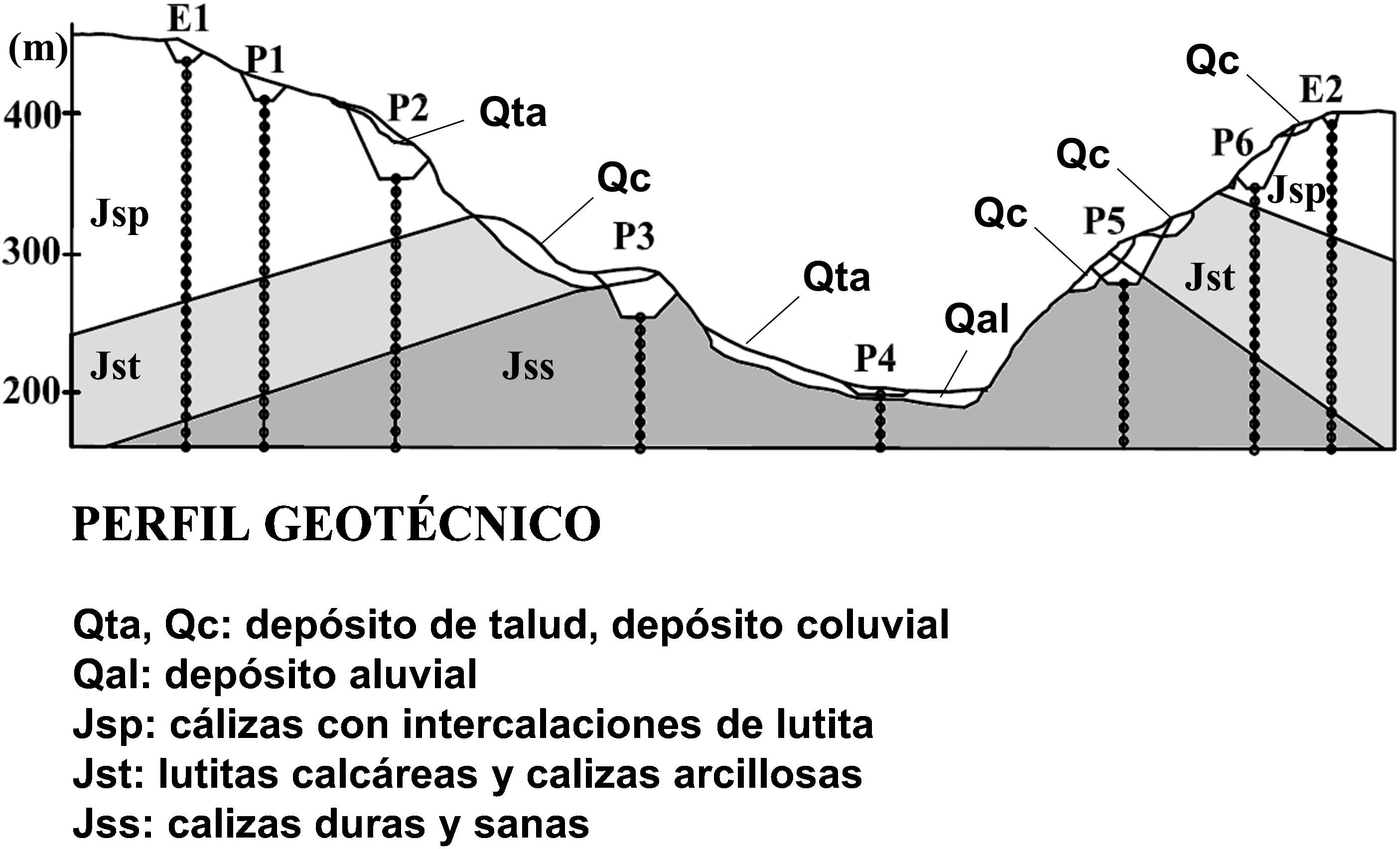
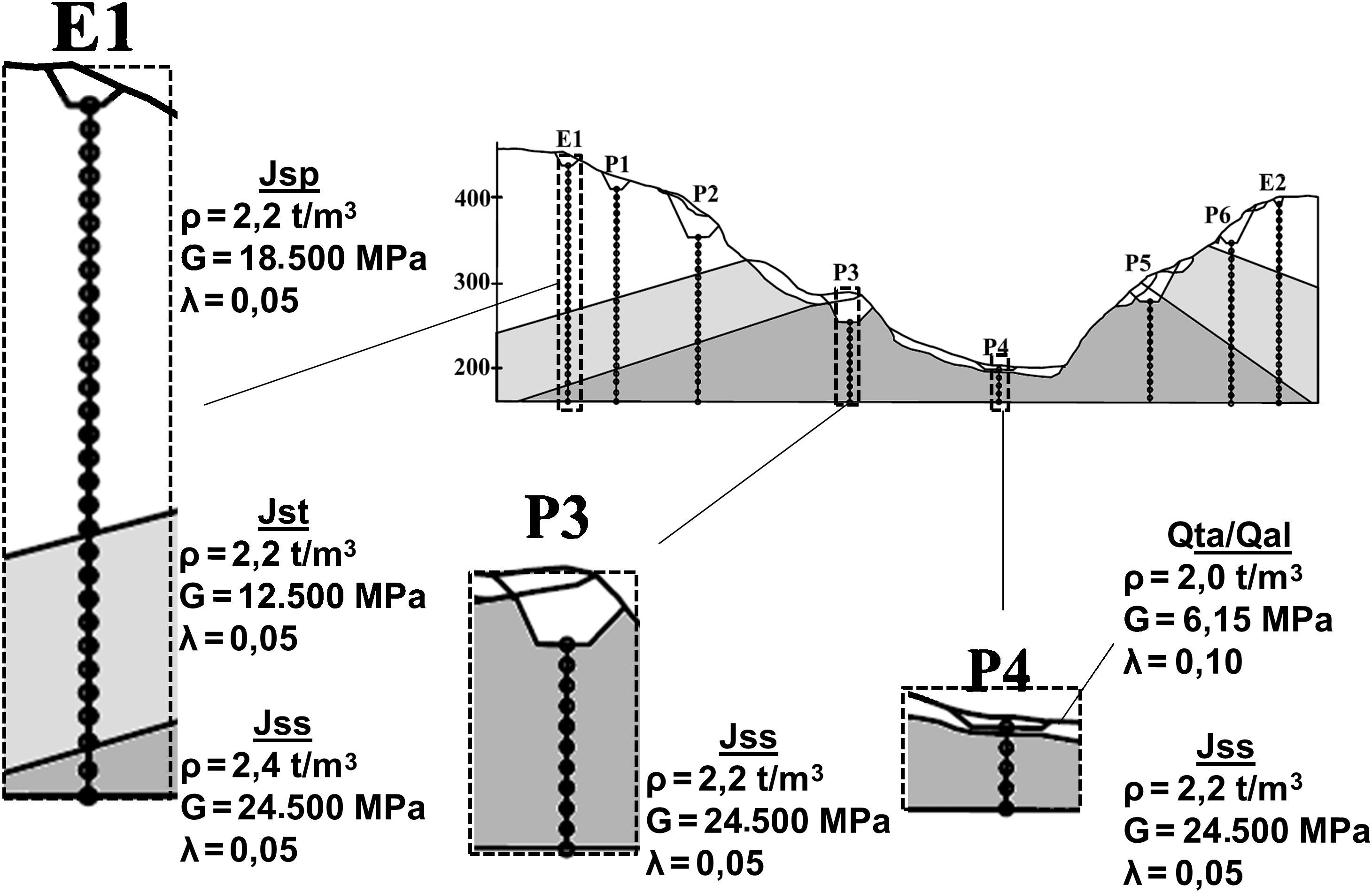
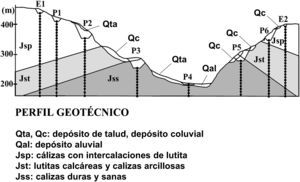
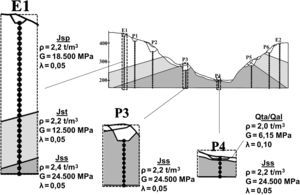
En la figura 2 se representa el perfil geotécnico a lo largo de la traza de la estructura objeto de estudio, con su correspondiente discretización en masas concentradas, y en la figura 3, las propiedades del terreno adoptadas en el análisis. En general, la estructura se asienta sobre estratos competentes de roca caliza, con excepción de la pila4, donde existe una capa superior de unos 10m de depósito aluvial/coluvial con una rigidez a cortante mucho menor, lo cual dará lugar a una amplificación en el rango de periodos largos.
Las aceleraciones de cálculo en superficie para el primer análisis se mostraron en la figura 1, de donde se observa la falta de correlación entre señales y la amplificación de aceleraciones con respecto a la roca base. En la tabla 1 se resumen las máximas aceleraciones pico en cada apoyo obtenidas de los 112 acelerogramas. Los mayores valores se producen en los extremos del valle al existir una columna de suelo de mayor altura, y en la pila4 debido a la presencia de suelos blandos. Además, nótese que dichos valores se encuentran entre 1,2-3,5 veces la aceleración pico en la roca base (0,04g), lo cual es interesante comparar con el factor de amplificación de suelo dado por la norma, el cual es de 2,5.
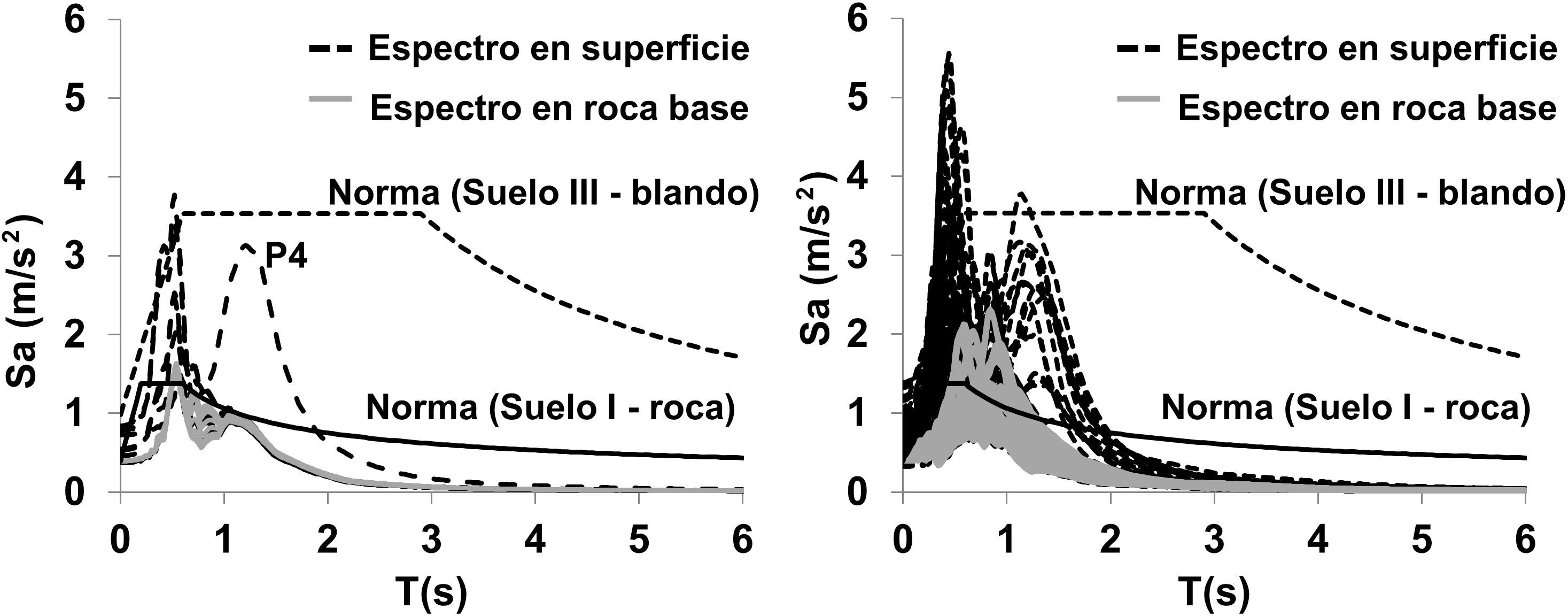
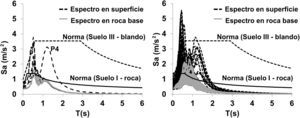
Finalmente, en la figura 4 se comparan los espectros elásticos de aceleraciones para un amortiguamiento crítico del 5%. También aparecen los espectros de diseño de la normativa para un periodo de retorno de 475años, en roca y en superficie. Los espectros calculados casi siempre quedan por debajo de los de diseño en el rango de periodos intermedios y largos (T>1,2s), mientras que en el rango de periodos cortos algunos valores exceden los de diseño. Nótese también el efecto de la variabilidad espacial en los espectros en superficie, y en especial la amplificación de la pila 4 alrededor del periodo T=1,5s.
4Análisis estructural4.1Análisis dinámico con excitación múltipleLos acelerogramas de cálculo obtenidos en el apartado interior se emplearon como input en los análisis dinámicos lineales paso a paso de la estructura con múltiples excitaciones. En este caso, la respuesta estructural viene dada por la suma de efectos inerciales y pseudoestáticos, estos últimos producidos por desplazamientos diferenciales entre apoyos. Esto quiere decir que, por ejemplo, al final del análisis pueden existir esfuerzos remanentes aun estando la estructura en reposo. El vector de desplazamientos de la estructura se puede dividir en desplazamientos pseudoestáticos, xps, y desplazamientos impuestos en los apoyos, xg, quedando la ecuación de equilibrio como (ecuación 3):
donde fg son las fuerzas correspondientes a xg, y Kss, Ksg, Kgs y Kgg, submatrices de la matriz de rigidez global de la estructura [5]. Las ecuaciones de movimiento en coordenadas relativas, y suponiendo una respuesta elástico lineal, vendrían dadas como (ecuación 4):donde M, C y K son las matrices de masas, amortiguamiento y rigidez, respectivamente. D, D˙ y D¨ son los vectores de desplazamiento, velocidad y aceleración causados por efectos inerciales. Γ es la matriz de influencia y D¨g es la matriz de aceleraciones en los apoyos. La matriz Γ, a diferencia del vector de influencias en el caso de excitación uniforme, es función de las submatrices de la matriz de rigidez (ecuación 5):La matriz Γ es, por tanto, la única diferencia respecto de un algoritmo de cálculo con excitación uniforme. La resolución del sistema de ecuaciones dinámicas se realiza de la misma forma, con métodos de integración paso a paso implícitos o explícitos.
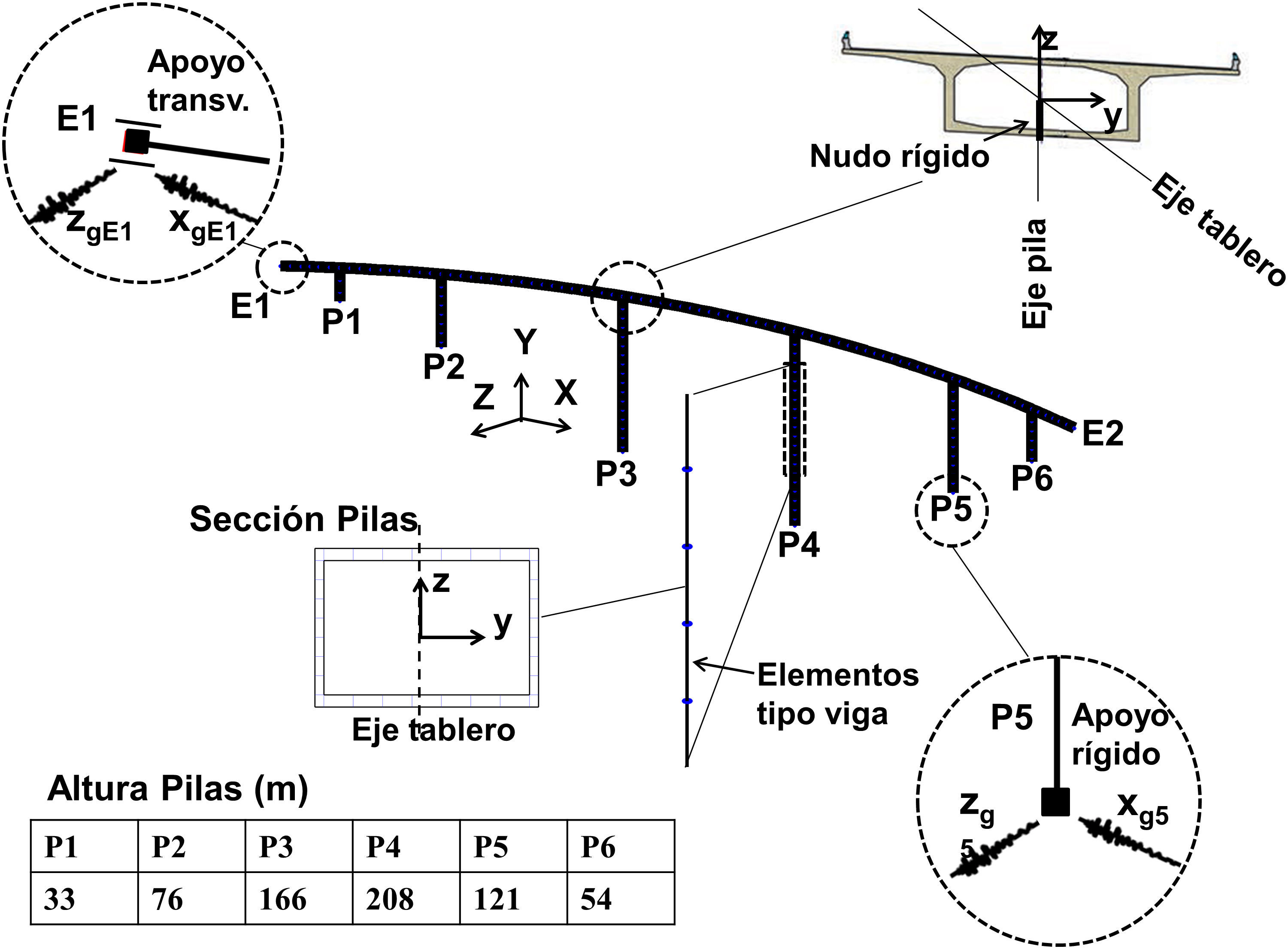
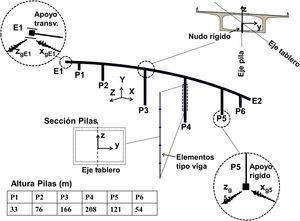
4.2Modelo estructuralLa estructura objeto de estudio se muestra en la figura 5. Se trata de un viaducto continuo de planta curva de radio constante (R=1.150m), con una longitud total de 850m y una distribución de vanos simétrica de 75-90-180-180-180-90-75. Las pilas poseen alturas variables, tal como se muestra en la figura 5, siendo la pila intermedia P4 de 210m de altura. La vinculación pilas-tablero es monolítica en las pilas P2, P3, P4 y P5, quedando el tablero libre longitudinalmente en las pilas extremas (P1 y P6) y estribos. La sección de tablero y pilas es en cajón de canto variable [6].
La estructura se modeló en 3D con elementos finitos de tipo viga, con sus correspondientes secciones, propiedades elásticas de los materiales y vinculaciones pilas-tablero y tablero-estribos. Las pilas y tablero se discretizaron en varios elementos, definiendo elementos rígidos de conexión entre el eje del tablero, coincidente con el centro geométrico de la sección sin fisurar, y las pilas. Las pilas se supusieron perfectamente empotradas en base, sin considerar efectos de suelo. Nótese que el eje globalX se definió en la dirección de los estribos E1 y E2, siendo esta la dirección en la que se aplicó la componente longitudinal del sismo xgi. Para la realización de análisis dinámicos se utilizó la matriz de masas consistente, correspondiente al peso propio de la estructura y una carga muerta de 2kN/m2, y un amortiguamiento de tipo Rayleigh con 5% en el primer y segundo modo de vibración. El programa de análisis utilizado fue IDEEA3D [7].
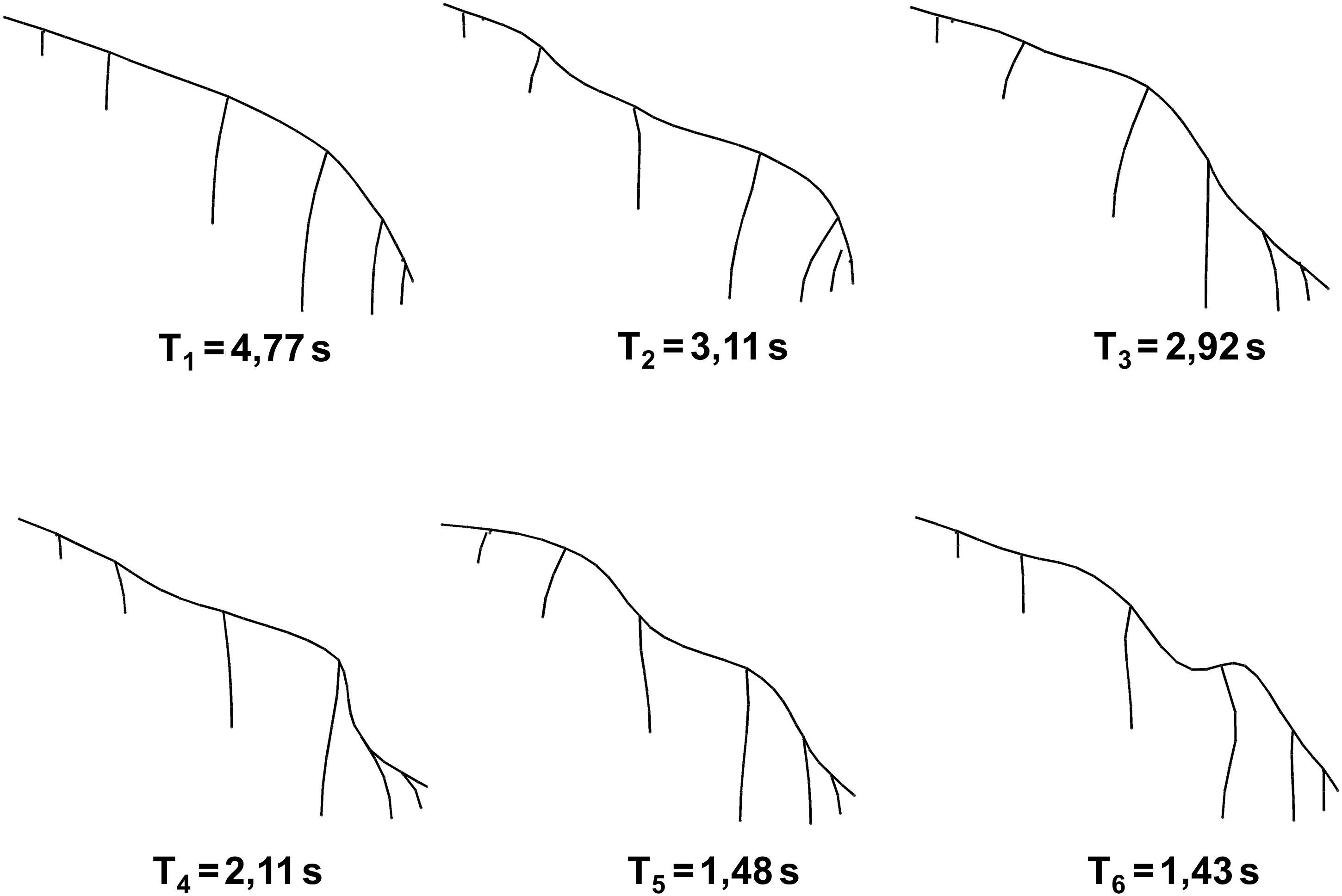
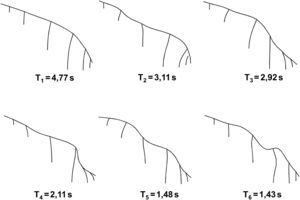
4.3Resultados de análisisEn la figura 6 se resumen los seis primeros modos de vibración. Es de destacar que la mayoría de modos son modos acoplados entre la dirección longitudinal y transversal debido a la irregularidad del puente. En el primer modo, el cual podría considerarse como transversal, participa aproximadamente el 66,1% de la masa total, y en el segundo, solo el 49,8%, lo cual implicaría considerar varios modos en la respuesta en caso de análisis modal espectral. En el caso de integración directa de las ecuaciones dinámicas, todos los modos quedan incluidos en la respuesta [8].
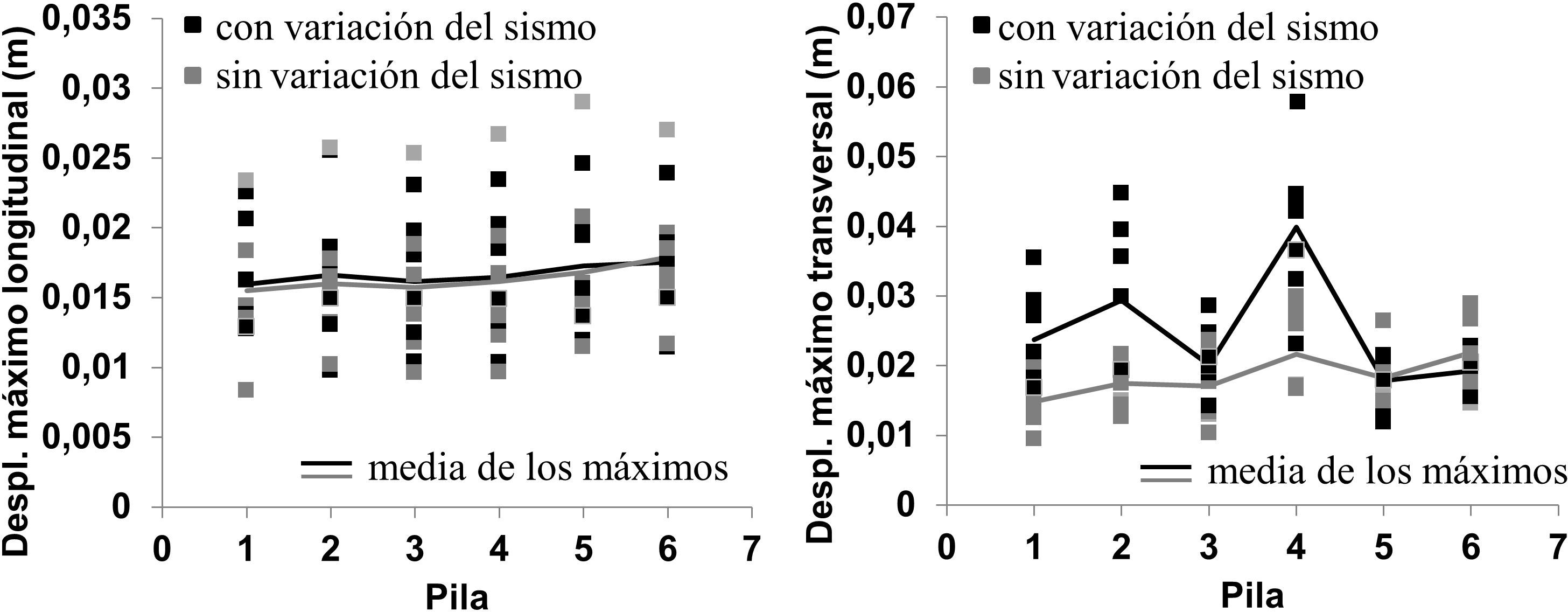
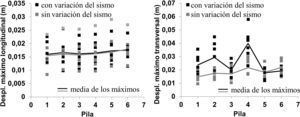
En la figura 7 se muestran los desplazamientos máximos en la dirección longitudinal y transversal en cabeza de pila, con y sin variación de la excitación sísmica entre apoyos. Los desplazamientos máximos fueron 30mm en la dirección longitudinal (P5) y 58mm en la dirección transversal (P4). Es interesante observar que en la dirección longitudinal la variación del sismo apenas influye en términos medios debido a la importante rigidez axial del tablero, mientras que en la dirección transversal se alcanzan mayores valores con variación del sismo debido a la mayor flexibilidad del tablero en dicha dirección. En este último caso, la mayor amplificación de desplazamientos transversales en las pilas P1 y P2 indica la influencia de modos de periodo corto en la respuesta.
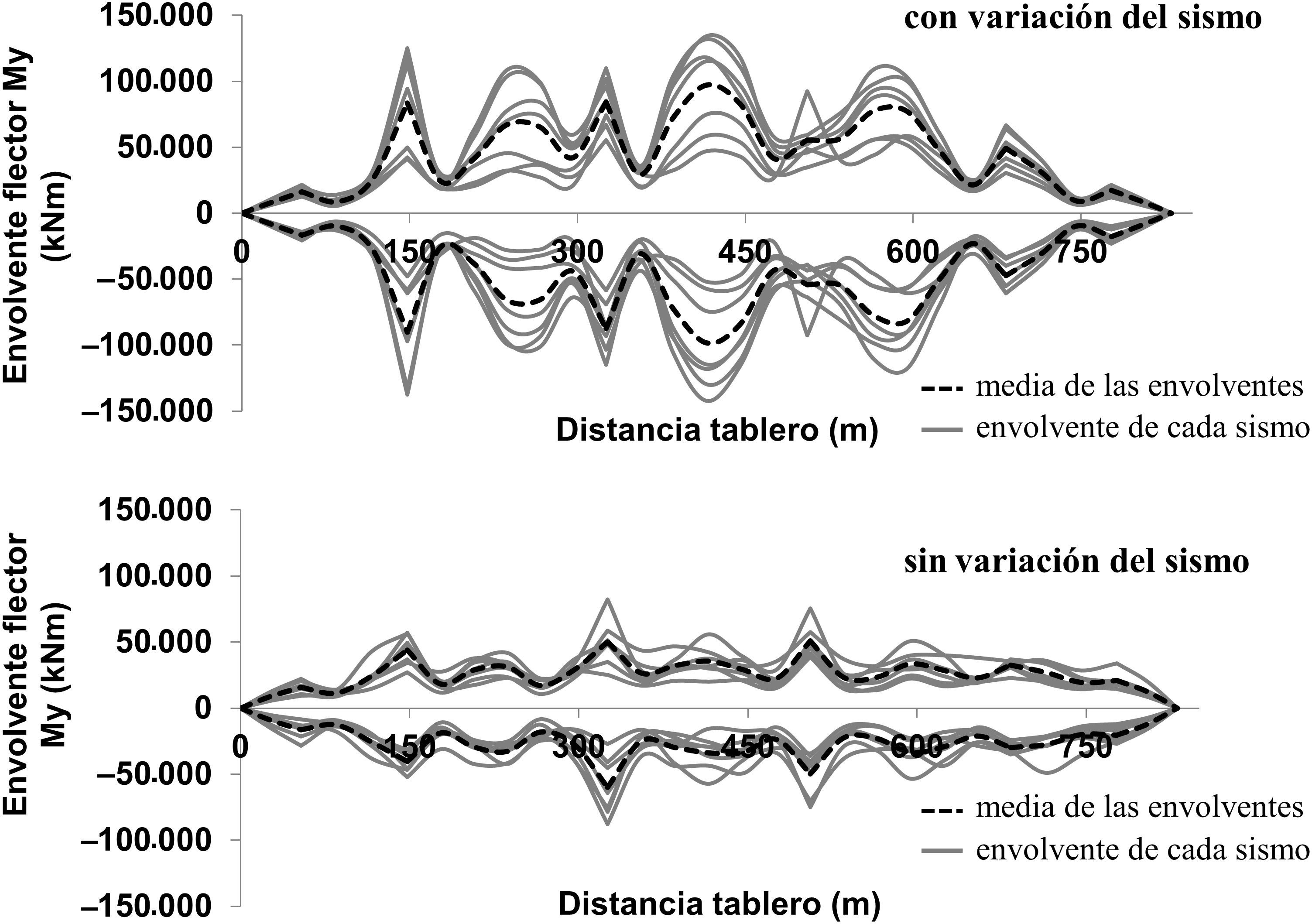
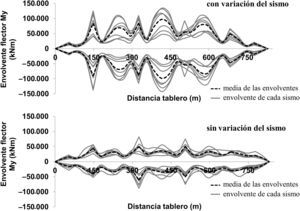
En las figuras 8 y 9 se comparan las envolventes de momentos flectores My (según el eje local y, véase fig. 5) a lo largo del tablero para los 7 análisis realizados, con y sin variación de la excitación sísmica, de donde se aprecia la amplificación causada por la variación de la señal. Nótese que desplazamientos diferenciales entre apoyos de pilas en la dirección longitudinal introducen tanto flexión vertical como transversal del tablero a causa de la curvatura en planta. Los valores máximos fueron del orden de 140MNm en el centro del vano central (entre P3 y P4) y 90MNm sobre pilas (P3 y P4), para el caso con y sin variación de la señal, respectivamente. Nótese que importantes amplificaciones se produjeron sobre las pilas extremas, debido a la mayor influencia de los modos de periodo corto cuando se introduce variación del sismo.
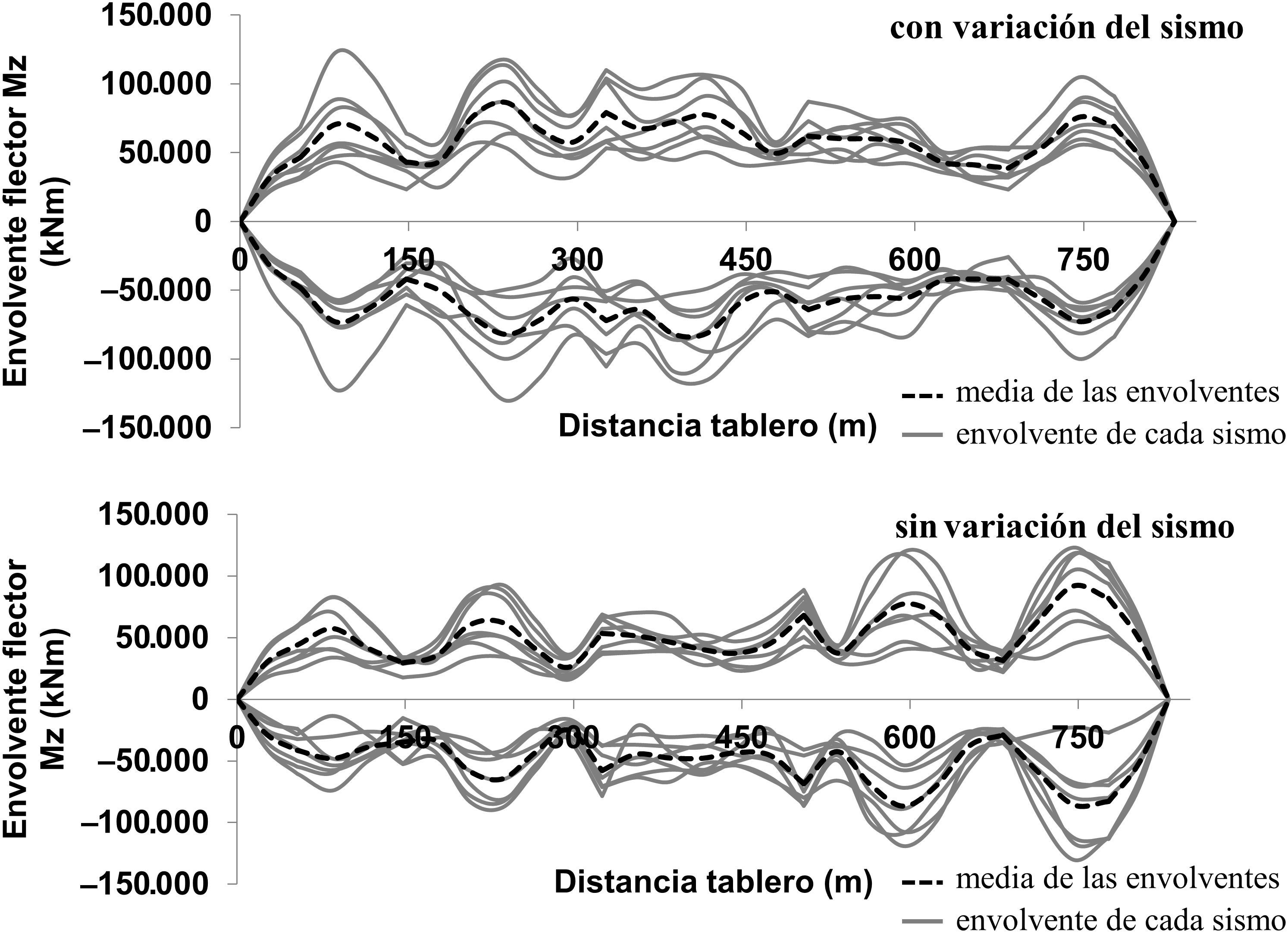
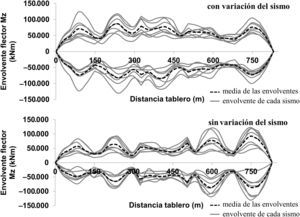
Conclusiones similares se deducen de la figura 9, donde se comparan los flectores transversales Mz, aunque con menor amplificación. Los valores máximos rondan los 120MNm tanto para el caso «con variación» como «sin variación».
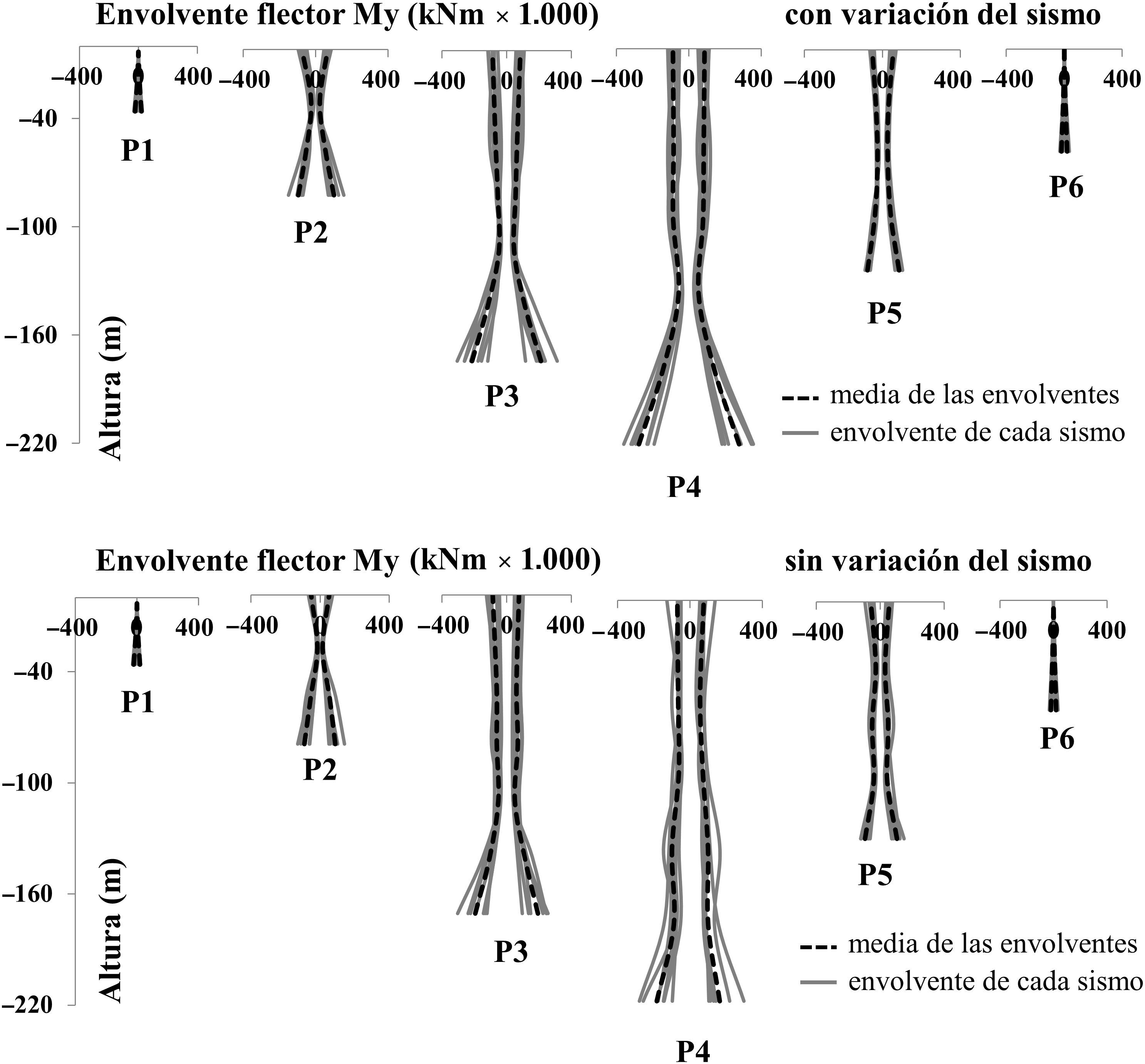
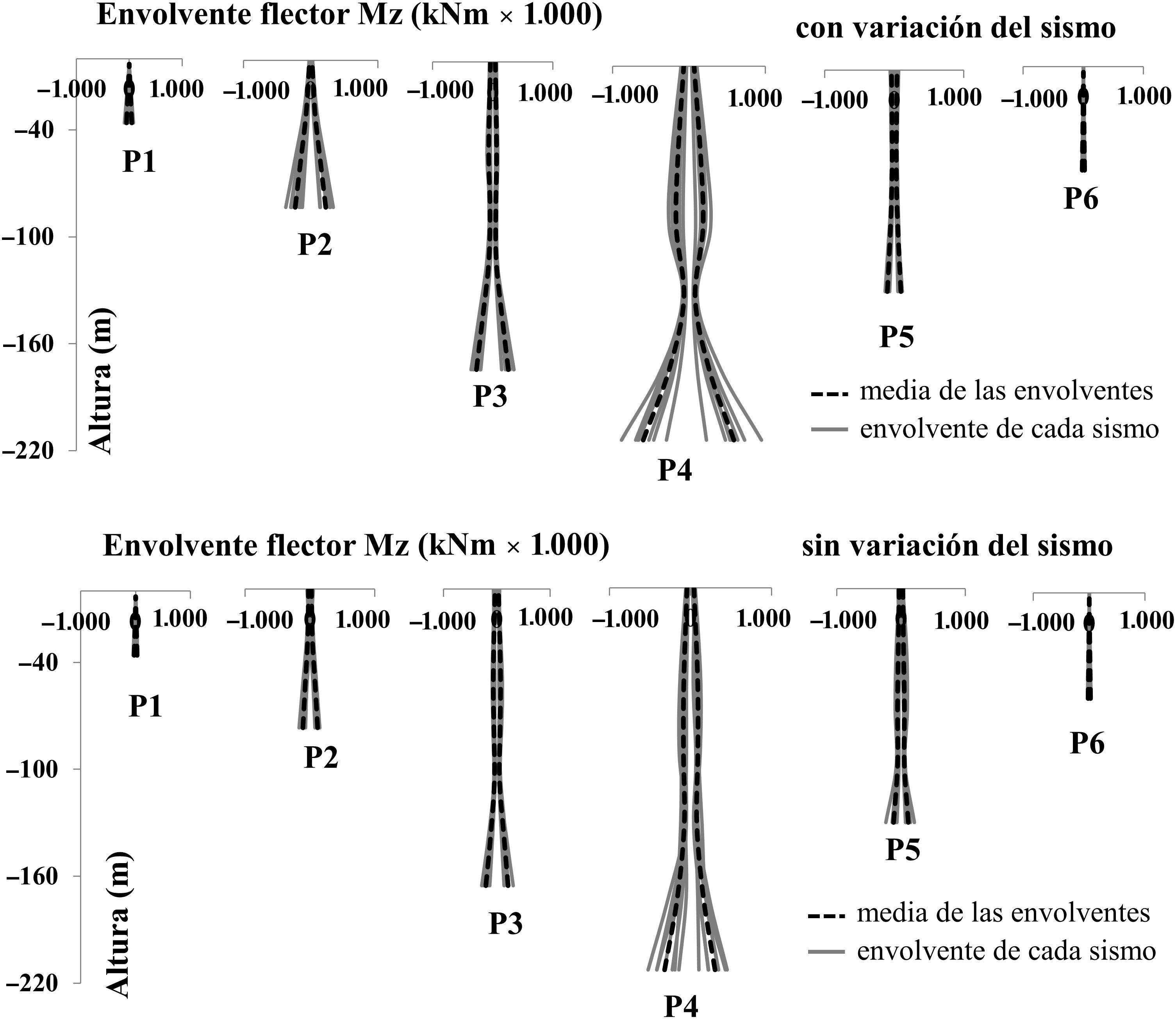
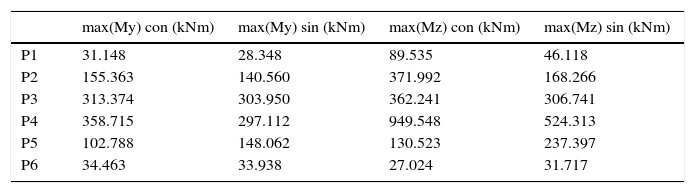
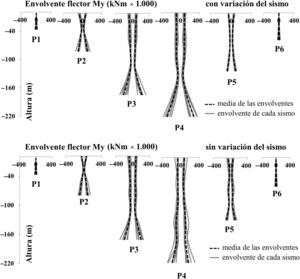
En las figuras 10 y 11 se comparan los flectores en las pilas. De nuevo, mayores esfuerzos se obtienen con variación del sismo, tanto en arranque como en coronación de pilas empotradas al tablero. Es de observar que en las pilas de mayor altura (P3, P4, P5) el segundo valor máximo del flector no se da necesariamente en coronación, sino que importantes esfuerzos aparecen a lo largo de la pila, aproximadamente entre 1/2 y 3/4 la altura, debido a la contribución de múltiples modos de vibración. Los momentos máximos en valor absoluto para cada pila se resumen en la tabla 2.
Máximos flectores en arranque de pilas
| max(My) con (kNm) | max(My) sin (kNm) | max(Mz) con (kNm) | max(Mz) sin (kNm) | |
|---|---|---|---|---|
| P1 | 31.148 | 28.348 | 89.535 | 46.118 |
| P2 | 155.363 | 140.560 | 371.992 | 168.266 |
| P3 | 313.374 | 303.950 | 362.241 | 306.741 |
| P4 | 358.715 | 297.112 | 949.548 | 524.313 |
| P5 | 102.788 | 148.062 | 130.523 | 237.397 |
| P6 | 34.463 | 33.938 | 27.024 | 31.717 |
Los resultados obtenidos en el presente trabajo cuantifican los efectos de la variación espacial de la acción sísmica en el análisis de grandes viaductos de tablero continuo. En general, mayores desplazamientos y esfuerzos se obtienen cuando se consideran dichos efectos, al aparecer esfuerzos «pseudoestáticos» adicionales, además de aquellos debidos a las fuerzas inerciales. La participación de modos de periodo corto (higher-mode effects) también influyó en la respuesta. Recomendaciones para la consideración de dichos efectos mediante análisis estático simplificado aparecen en el Eurocódigo 8: Parte II. En el presente caso se realizaron análisis dinámicos por integración directa utilizando como input acelerogramas sintéticos generados acorde a la geología y topografía del emplazamiento. En estudios posteriores sería interesante comparar estos últimos con los resultados obtenidos de la normativa.
El autor agradece la colaboración del departamento de puentes de FCC en la realización del presente estudio.