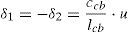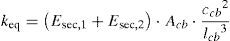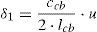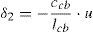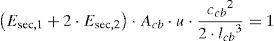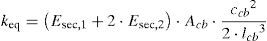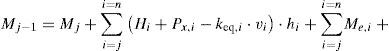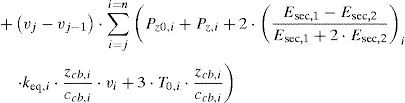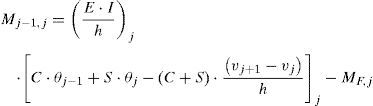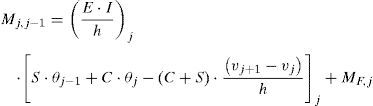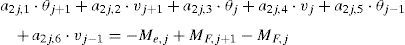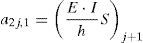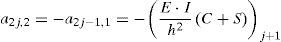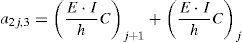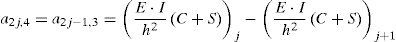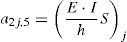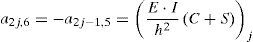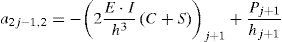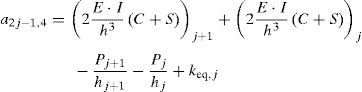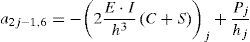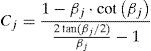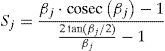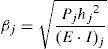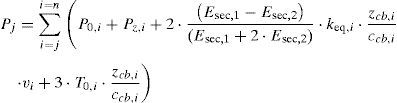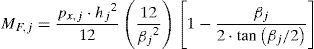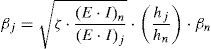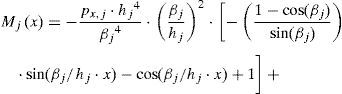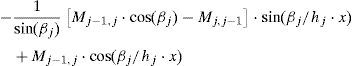En este trabajo se desarrolla una nueva formulación, basada en el método de la viga-columna, para el análisis de mástiles atirantados. El método propone el cálculo de las deformaciones producidas por los efectos de segundo orden a partir de las funciones de estabilidad. A tales efectos, la torre se modela como una viga-columna equivalente, continua, sobre apoyos elásticos no-lineales, cuyas rigideces axial, flexional y de corte se calculan según sea el patrón de construcción de la torre. Los cables son reemplazados por apoyos elásticos no-lineales cuya constante elástica se obtiene a partir de la utilización de módulo de elasticidad secante de los cables. A los efectos de validar el método propuesto se realiza un estudio comparativo analizando un mástil atirantado de 150m de altura mediante el método de los elementos finitos con el programa comercial SAP2000.
Based on the equivalent beam-column method, this paper develops a new formulation for the analysis of guyed towers. The method proposes the calculation of the second order deformation using the stability functions. For this purpose, the tower is modelled as a continuous equivalent beam-column, on non-linear elastic supports, for which the axial stiffness, flexural stiffness, and shear stiffness are calculated depending on the pattern construction of the tower. The guys are replaced by non-linear elastic supports for which the spring constant is obtained from the secant modulus of the cables. In order to validate the proposed method, a comparative study is carried out between the proposed method and the finite element method on a 150metre-high guyed tower using the SAP2000 software.
Las comunicaciones de radio y televisión, así como la telefonía celular, son posibles en el mundo moderno gracias a estructuras que ejercen de soporte para los equipos de transmisión de las señales de un lugar a otro. Las torres de celosía son estructuras con una amplia utilización como soporte de los sistemas de comunicación, debido a su gran resistencia en relación al consumo de material y a su permeabilidad, lo que reduce las fuerzas del viento generadas sobre ellas. Estas estructuras suelen ser elementos esbeltos y ligeros, ubicados en su mayoría en lugares expuestos, por lo que las cargas ambientales prevalecen en el diseño.
Dos tipos de torres de celosía se emplean de acuerdo a la tipología estructural: las torres autoportantes y las torres atirantadas. Cuando se requieren grandes alturas y las condiciones del sitio de implantación lo permiten, estas últimas son las usualmente utilizadas, debido a su menor costo de construcción en relación con las autoportantes.
Para el análisis de torres atirantadas existen varios métodos. La norma TIA222-G [1] especifica tres tipos de análisis. El primero consiste en un análisis donde la torre es modelada como una viga-columna equivalente soportada por cables representados como elementos tipo cable o como apoyos elásticos no-lineales. El segundo consiste en un análisis tridimensional elástico en donde la torre se modela como un reticulado espacial cuyas barras solo pueden tomar fuerza directa. Por último, puede realizarse un análisis elástico tridimensional en donde algunos de los miembros de la torre se modelan como elementos que trabajan a flexión y a fuerza directa, y otros como elementos que trabajan exclusivamente a fuerza directa. En los dos últimos métodos de análisis, los cables se modelan como elementos tipo cable.
Cualquiera que sea el método de análisis utilizado, la complejidad del mismo radica en la inherente no-linealidad que presentan estas estructuras. Por una parte, la no-linealidad de los tirantes —elementos estructurales que se materializan mediante cables de acero pretensado de alta resistencia— y por otra, la no-linealidad geométrica. La esbeltez que presentan estas torres las hace susceptibles al fenómeno de pandeo; en otras palabras, los efectos de segundo orden no pueden ser despreciados. Las acciones horizontales provocan desplazamientos que incrementan el nivel de tensión en los cables y a su vez las fuerzas de compresión sobre la torre. Estas fuerzas de compresión tienden a aumentar el desplazamiento, y así sucesivamente, fenómeno que se denomina comúnmente efecto P-Δ.
Dentro de los métodos del primer tipo, basados en el modelo de la viga-columna, diferentes investigadores han realizado distintas propuestas en más de cincuenta años. Cohen y Perrin [2] propusieron un análisis bidimensional mediante un modelo de viga-columna sobre apoyos elásticos considerando únicamente la rigidez flexional de la viga. En el mismo sentido, Ezra [3] propuso un análisis bidimensional basado en el modelo de la viga-columna sobre apoyos elásticos no-lineales y considerando la torsión de la estructura mediante resortes de torsión. Básicamente, el análisis consiste en calcular los desplazamientos de la estructura en forma iterativa a partir de un conjunto arbitrario de desplazamientos iniciales. Kalha [4] propone un método aproximado para el análisis de mástiles atirantados utilizando para la torre una viga-columna equivalente y para los tirantes elementos tipo cable. Esto es llevado a cabo ensamblando en forma matricial elementos tridimensionales tipo viga para la torre y elementos de cable para los cables. Si bien el método tiene en cuenta el acoplamiento geométrico entre los diferentes grados de libertad y los efectos de segundo orden, es difícil de aplicar, pues requiere un alto grado de programación computacional. Wahba et al. [5] analizaron tres modelos diferentes para torres atirantadas, y uno de ellos consistió en modelar la torre como viga-columna equivalente y elementos no-lineales para los cables. Sus resultados validaron las conclusiones de estudios previos de Kahla y confirmaron la respuesta no-lineal geométrica de estas estructuras frente a las cargas de viento. Margariti y Gantes [6] proponen un método aproximado basado en las expresiones clásicas de pandeo para el cálculo de la carga crítica en torres atirantadas y en pilones de puentes atirantados. Dicho método se basa en un modelo de un solo vano de viga-columna, considerando únicamente la rigidez flexional del mástil o pilón. La no-linealidad de los cables se tiene en cuenta mediante el módulo de elasticidad equivalente obtenido a partir de la fórmula del módulo tangente de los cables.
Importantes han sido las contribuciones de los diferentes autores al problema planteado. Dentro de estas contribuciones los métodos más utilizados hoy en día son los basados en los elementos finitos. Estos métodos son muy precisos. Sin embargo, para que las soluciones converjan se requiere discretizar la estructura en un elevado número de elementos, además de requerir un gran esfuerzo de programación computacional [4,5]. Las contribuciones basadas en los métodos analíticos requieren análisis complejos, y si bien permiten obtener soluciones cuyos resultados son próximos a los obtenidos mediante la utilización de elementos finitos, en general presentan diferencias significativas [2,3,6]. Es por ello que en este trabajo se propone desarrollar un nuevo método analítico para el análisis de mástiles atirantados, basado en el modelo de la viga-columna, que además de mantener la rigurosidad matemática de los métodos analíticos presenten una precisión tal que se obtengan soluciones suficientemente exactas para el diseño de este tipo de estructuras, pero cuya aplicación sea simple, evitando así el alejamiento del ingeniero de la concepción del modelo, y cuyas soluciones puedan obtenerse en un tiempo y con un esfuerzo razonables.
El método propuesto considera la no-linealidad de los cables y los efectos de segundo orden. En este sentido, la torre se modela como una viga-columna equivalente, continua, sobre apoyos elásticos, cuyas rigideces axial, flexional y de corte se calculan según sea el patrón de construcción de la torre [7]. Los cables son reemplazados por apoyos elásticos cuya constante elástica se obtiene a partir de la utilización de módulo de elasticidad secante de los cables [8]. El método propone el cálculo de las deformaciones producidas por los efectos de segundo orden a partir de las funciones de estabilidad[9].
Una de las principales ventajas del método es la reducción del esfuerzo computacional, ya que la estructura no necesita ser discretizada en un número grande de elementos para la convergencia, con lo cual el método puede ser más útil en las etapas de prediseño. Otra ventaja del método analítico propuesto es que utiliza los conceptos básicos y más generales desde el punto de vista de la ingeniería estructural, lo que permiten al ingeniero visualizar rápidamente cuáles son los parámetros que influyen en el diseño.
A los efectos de validar el método propuesto se realizará un estudio comparativo analizando un mástil atirantado a partir de diferentes modelos numéricos mediante el empleo de elementos finitos con el programa comercial SAP2000 [10].
2Las torres atirantadasLas torres están formadas por una serie de barras verticales —en general denominadas montantes—, barras horizontales y barras diagonales que conforman de esta manera un reticulado espacial. La sección transversal de torre frecuentemente utilizada es la triangular equilátera, si bien en algunos casos pueden utilizarse secciones cuadradas. Para las estructuras de menor porte los elementos estructurales que conforman el reticulado son materializados mediante barras circulares macizas de acero, mientras que para estructuras de mayor porte se utilizan tubos circulares de acero, perfiles angulares y perfiles de chapas plegadas.
Los tirantes proporcionan soporte lateral a las torres. Se colocan en general uniformemente distribuidos en la altura y se los pretensa con un valor inicial de tensión. En el caso de torres de sección triangular se colocan tres por cada nivel, y en el caso de sección rectangular se colocan cuatro por nivel. Los tirantes se anclan en el terreno de manera tal que los ángulos que forman los planos constituidos por cada tirante y la torre sean iguales. Las inclinaciones típicas utilizadas para estos, medidas como el ángulo que forma el tirante con la horizontal, están el entorno de los 40° a 60°, pudiendo alcanzar inclinaciones menores para los tirantes del primer nivel.
La tensión inicial de pretensado de los cables es uno de los principales parámetros que afectan la estabilidad de este tipo de estructuras [11]. Este es impuesto durante la construcción del mástil y debe ser verificado periódicamente. La norma TIA222-G recomienda valores medios del 10% de la tensión de rotura del cable, con un rango de variación entre el 7 y el 15% de la tensión de rotura, ya que dentro de este rango pueden ser despreciados los efectos de las vibraciones y de inestabilidad aeroelástica. Por su parte, la norma EN1993-1-11 proporciona lineamientos algo más generales, permitiendo tensiones iniciales de hasta el 45% de la tensión de rotura. No obstante, requiere que sean verificados los fenómenos de vibración e inestabilidad aeroelástica [12].
Este trabajo se centrará en las torres de sección transversal triangular equilátera, si bien la mayoría de los razonamientos expuestos aquí pueden extenderse a torres de sección transversal cuadrada.
3Modelo de la torre: propiedades de la viga-columna equivalenteEl modelo de la torre como una viga-columna equivalente requiere trabajar bajo determinadas hipótesis. El material que constituye la viga presenta un comportamiento elástico lineal, las deformaciones de la viga son pequeñas, y admitamos que las secciones normales al eje de la viga, primitivamente planas, permanecen planas pero no necesariamente normales al eje baricéntrico de la viga, bajo la acción del momento flector y la fuerza cortante.
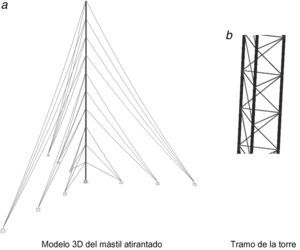
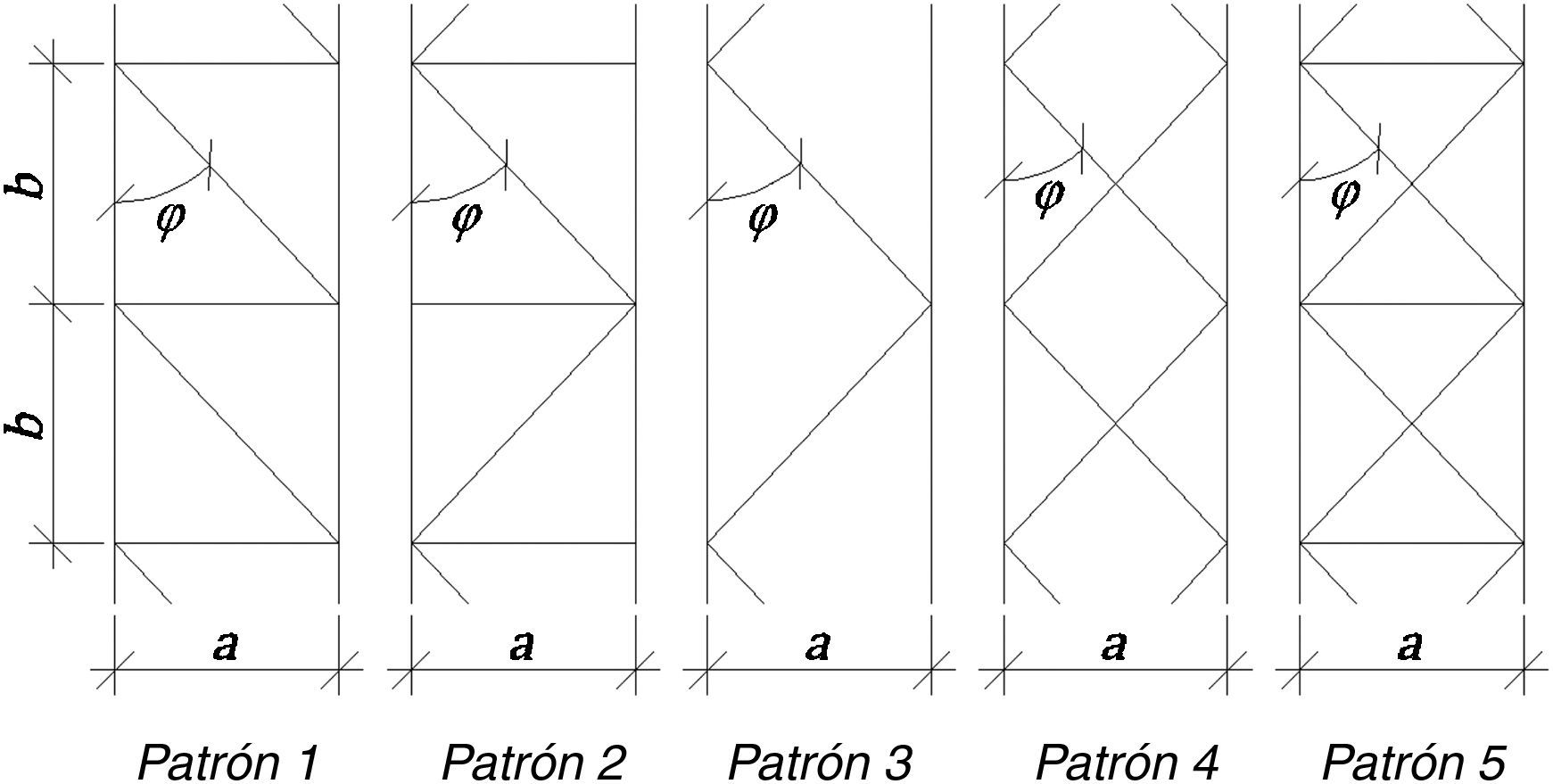
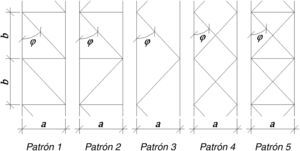
La figura 1 muestra los patrones típicos de reticulado de una de las caras de la torre. Para cada uno de dichos patrones, las propiedades geométricas de la viga-columna equivalente pueden ser obtenidas utilizando el principio de los trabajos virtuales. En la tabla 1 se hallan dichas propiedades para el caso de torres de sección triangular [4,7].
Propiedades geométricas equivalentes de la sección de la viga-columna según el patrón de reticulado de una cara de la torre
| Propiedades equivalentes | Patrón 1 | Patrón 2 y 3 | Patrón 4 | Patrón 5 |
|---|---|---|---|---|
| E·A | 3·E·Am | 3·E·Am | 3·E·Am | 3⋅E⋅Am+Aˆ |
| E·Iy, E·Iz | 12⋅E⋅Am⋅a2 | 12⋅E⋅Am⋅a2 | 12⋅E⋅Am⋅a2 | 12⋅E⋅a2⋅Am+Aˆ |
| G·Ay, G·Az | 321E⋅Ad⋅ψ1+tanφE⋅Ah−1 | 32E⋅Ad⋅ψ1 | 32E⋅Ad⋅ψ1 | 3·E·Ad·ψ1 |
E y G son el módulo de elasticidad y el módulo de corte del material.
E·A es la rigidez axial equivalente de la viga-columna.
E·Iz, E·Iy, G·Az y G·Ay corresponden a la rigidez flexional y a la rigidez de cortante de la viga-columna equivalente con respecto a ejes coordenados baricentros z e y, respectivamente.
Am, Ad y Ah son las áreas de las secciones de las barras de los montantes, las barras diagonales y horizontales que conforman el reticulado.
a y b son la distancia entre las barras montantes y la distancia entre las barras horizontales.
φ es el ángulo que forman las barras montantes con las diagonales.
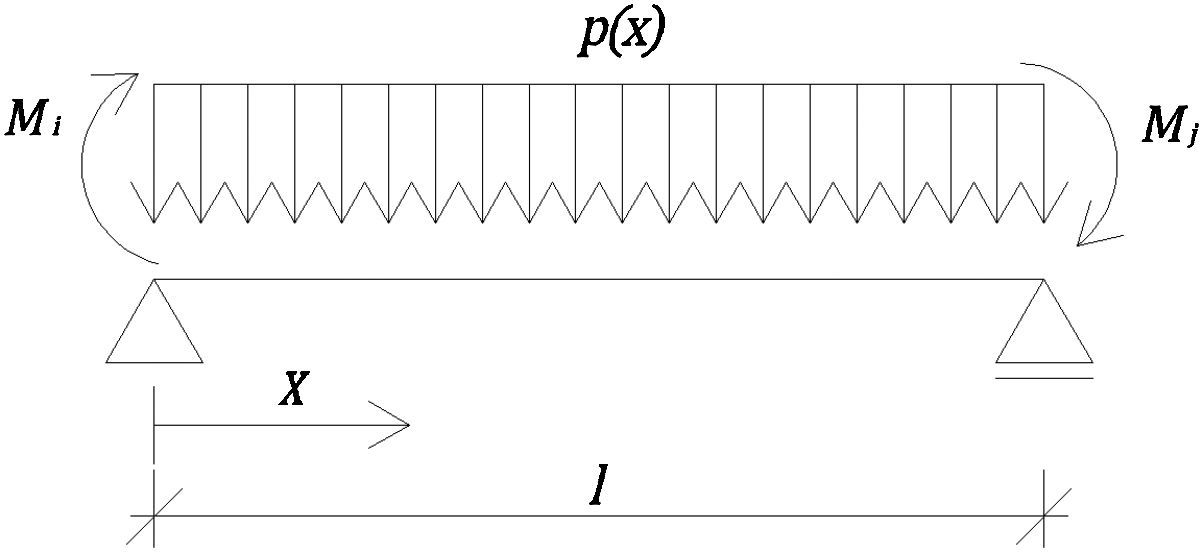
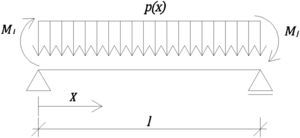
Dedo que en las estructuras reticuladas la deformación por esfuerzo cortante no es despreciable, esta puede ser tenida en cuenta en la viga equivalente considerando un momento de inercia reducido. Para la viga simplemente apoyada de la figura 2, la curvatura puede calcularse por medio de la ecuación 1 [13]:
siendo vx el valor de la elástica a una distancia x del extremo; Mx y Vx son el momento flector y la fuerza cortante para una sección situada a una distancia x del extremo, y Ωred es la sección reducida, cuya expresión viene dada por la ecuación 2:siendo μz el momento estático de primer orden respecto al eje baricéntrico, y bz el ancho de la sección.Tomando Ωred=A, la relación entre la flecha por fuerza cortante, fcor, y la flecha por momento flector en el centro del vano, ffl, es aproximadamente calculada por la ecuación 3:
Por lo tanto, a los efectos de tener en cuenta la deformación por fuerza cortante, puede utilizarse un momento de segundo orden equivalente al valor dado por la ecuación 4:
En este sentido, Williamson y Margolin [14] muestran la importancia de considerar los efectos del corte en el análisis de las torres atirantadas.
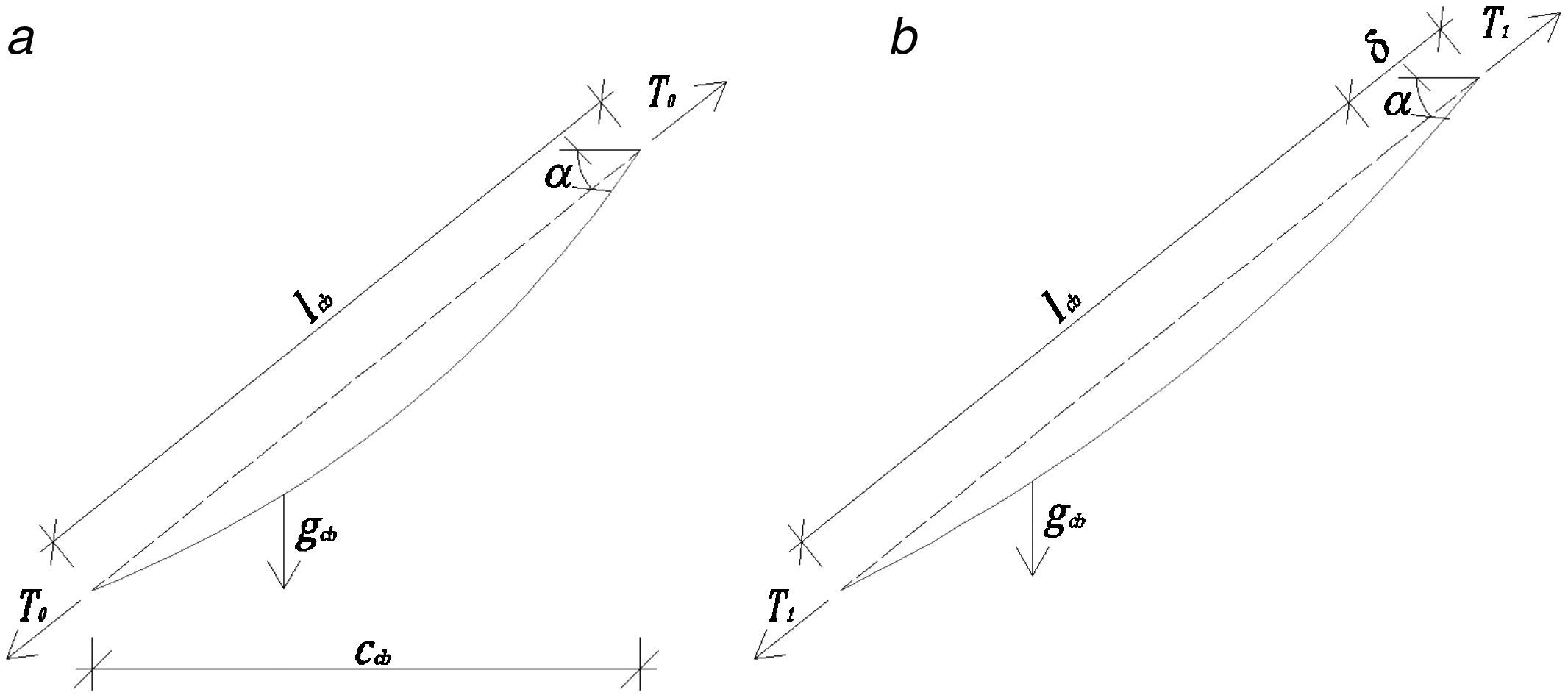
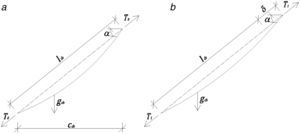
4Modelo de los tirantes4.1El cable elástico: módulo de elasticidad secanteSea un cable inclinado cuya longitud de cuerda sea igual a lcb y su proyección con respecto a la horizontal ccb, sometido a la acción de una fuerza de tracción T0 en el sentido de la cuerda y a la acción de su peso propio gcb (fig. 3). Basados en la configuración catenaria del cable, al aplicar una fuerza de tracción T1 en la dirección de la cuerda, el alargamiento δ del mismo puede expresarse mediante la ecuación 5 [8]:
siendo Ecb el módulo de elasticidad del material del cable, σ1 y σ0 las tensiones en el cable debido a las fuerzas en la dirección en la cuerda T1 y T0, respectivamente, y γcb la densidad del cable.
La no-linealidad existente entre la fuerza de tracción aplicada en la dirección de la cuerda y la deformación debido al cambio en la flecha bajo diferentes condiciones de carga puede ser tenida en cuenta mediante los módulos de elasticidad tangente y secante. De esta manera puede tratarse el fenómeno no-lineal como uno lineal. Sin embargo, el módulo tangente debe utilizarse cuando la relación entre las tensiones σ1 y σ0 es pequeña; de lo contrario, deberá utilizarse el módulo secante cuya expresión viene dada por la ecuación 6 [8]:
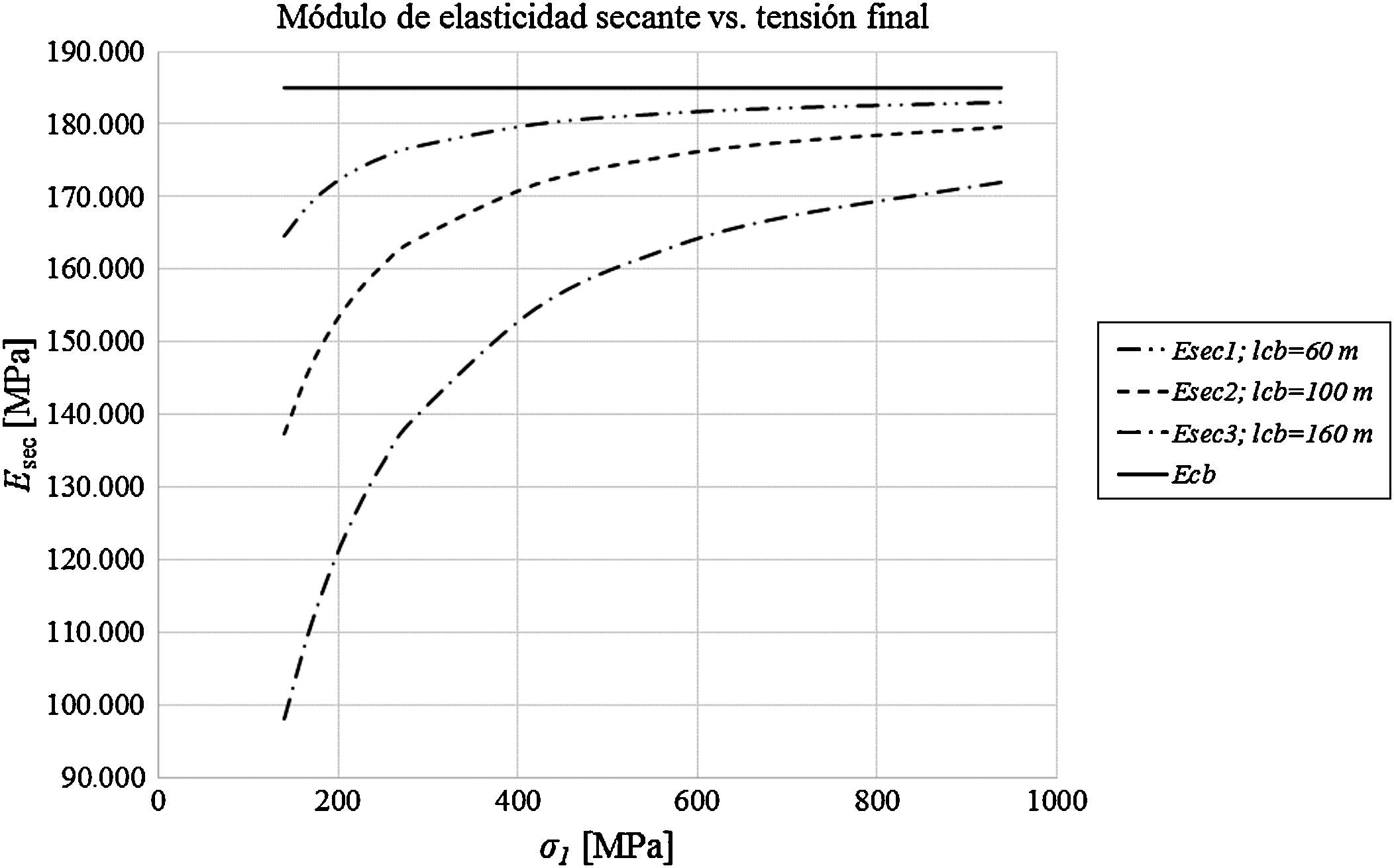
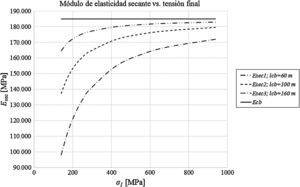
La gráfica de la figura 4 muestra la variación del módulo de elasticidad secante en función de la tensión final σ1 para longitudes de cable de 60, 100 y 160m, cuyo módulo de elasticidad es Ecb=185 GPa y su tensión inicial es σ0=140 MPa, que corresponde al 10% de la tensión de rotura. Podemos ver que para tensiones finales del orden del 50% de la tensión de rotura, la relación entre el módulo de elasticidad del cable y el módulo secante no excede del 10% para una longitud del cable de 160m, ni del 4% para una longitud del cable de 100m.
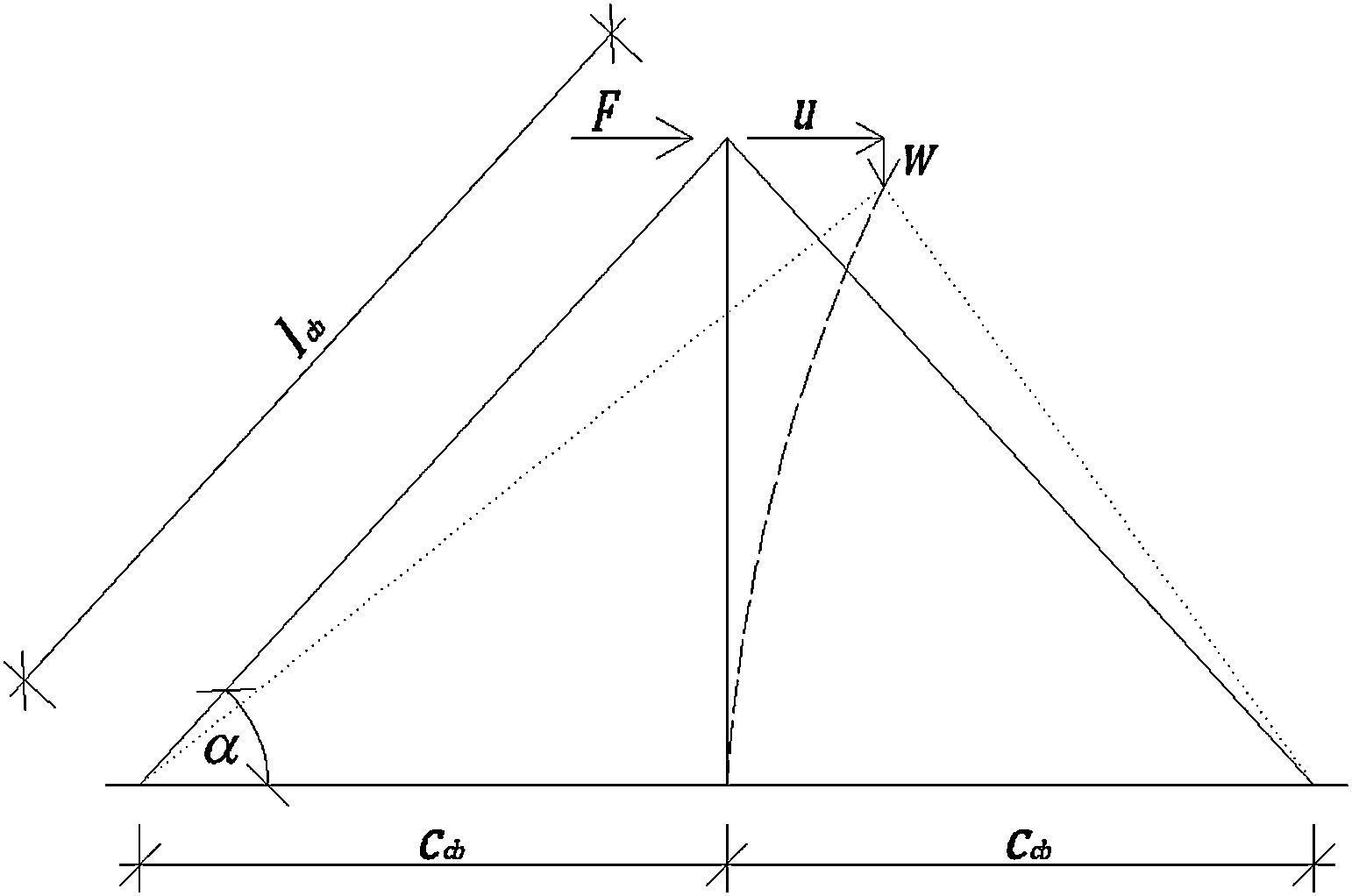
4.2El sistema de cables: constante elástica equivalenteConsideremos en primera instancia el sistema plano simétrico, en equilibrio, formado por el mástil y dos cables (fig. 5). Si aplicamos una fuerza horizontal en el extremo superior del mástil, este se deformará y su posición puede describirse como un desplazamiento horizontal u y uno vertical w, siendo ambas componentes del desplazamiento pequeñas. Dado que el desplazamiento de mástil está compuesto por un movimiento rígido y por la flexión del mismo, puede asumirse que el desplazamiento w es un infinitésimo de segundo orden de u (w∼Ou2) [15].
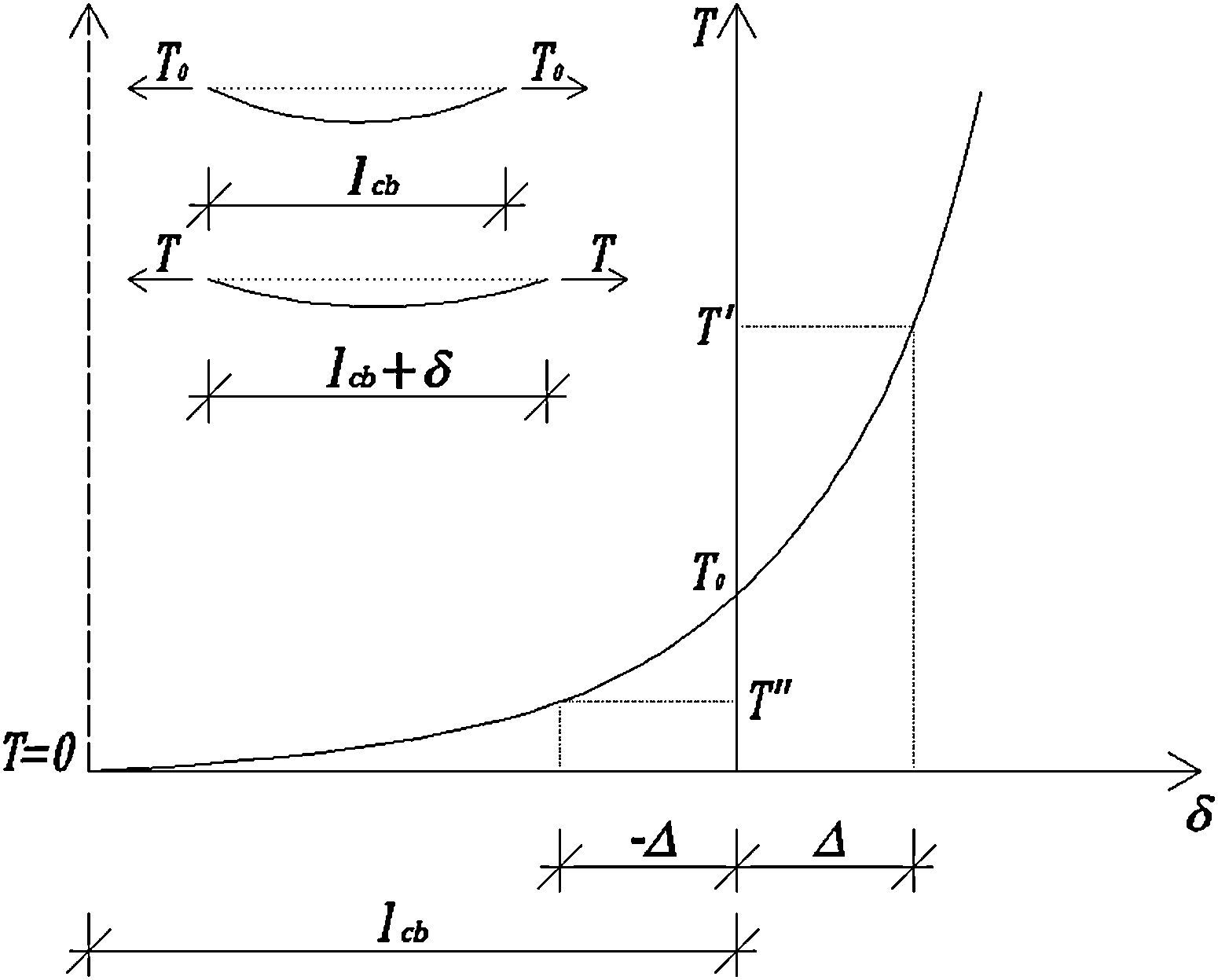
Al desplazarse el mástil, el cable a la izquierda se alargará mientras que el de la derecha se acortará. Si ambos cables están sometidos a una fuerza de tracción inicial T0 en la dirección de la cuerda, el cable de la izquierda experimentará un rápido aumento de la tensión, mientras que el de la derecha un rápido descenso. La figura 6 muestra de manera esquemática el razonamiento precedente.
Curva fuerza vs. desplazamiento del cable con origen en la condición inicial de tensado. Adaptada de [8].
Con relación a la figura 6, el alargamiento δ1 del cable de la izquierda y el acortamiento δ2 del cable de la derecha en función del desplazamiento horizontal u pueden expresarse por medio de la ecuación 7:
Si la fuerza F aplicada es de valor unidad y considerando una relación lineal entre la tensión y la deformación mediante el empleo del módulo de elasticidad secante (ecuación 7), la constante elástica equivalente utilizada para sustituir el sistema de cables es (ecuación 8):
siendo Acb el área de la sección transversal de los cables, Esec,1 y Esec,2 son los módulos de elasticidad secante del cable que se estira y del cable que se acorta, respectivamente, y α es la inclinación de los cables con respecto a la horizontal.
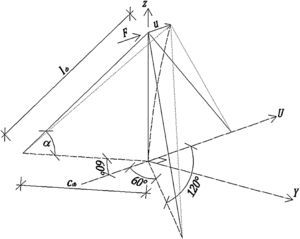
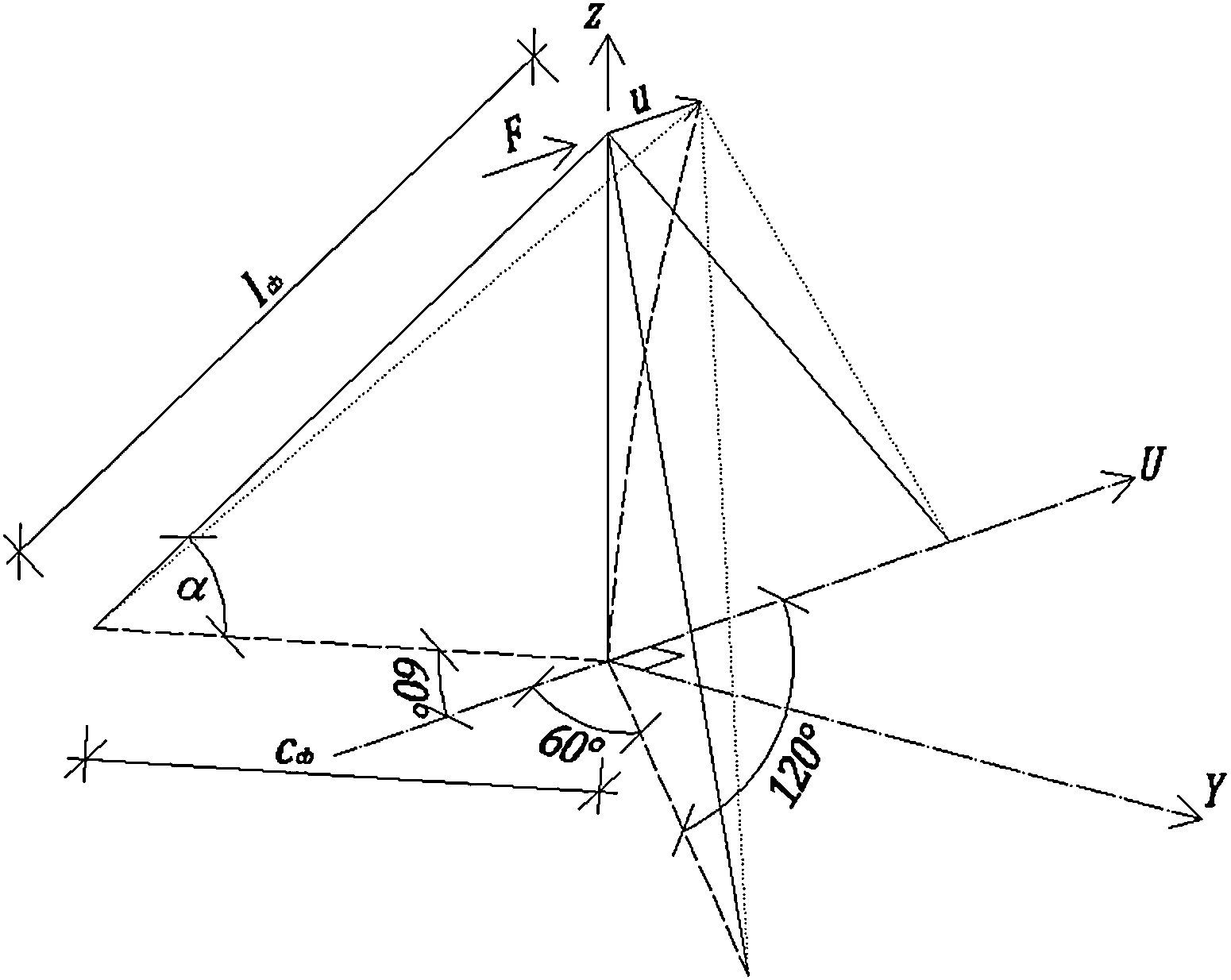
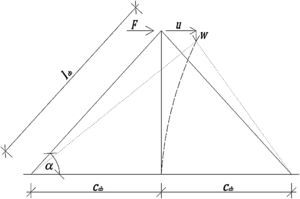
Consideremos ahora el sistema tridimensional constituido por el mástil y tres cables de igual longitud de cuerda lcb, igual inclinación α y tal que los planos formados por cada cable y el mástil equidistan entre sí, al que se aplica una fuerza horizontal F de valor unidad en el extremo superior del mástil en la dirección del eje U (fig. 7). Si la fuerza se aplica en el sentido positivo del eje U (como se muestra en la figura), la relación entre el alargamiento δ1 de los cables a barlovento y el desplazamiento horizontal u, así como la relación entre el acortamiento δ2 del cable a sotavento y el desplazamiento horizontal, puede expresarse mediante las ecuaciones 9:
Planteando equilibrio horizontal, ecuación 10:
Por lo tanto, la constante elástica equivalente utilizada para sustituir el sistema de cables queda determinada por la ecuación 11:
A partir de las ecuaciones 5, 9 y 11 podemos concluir que, bajo las hipótesis planteadas, la estructura de la figura 7 es más flexible en el sentido positivo del eje U que en el sentido negativo.
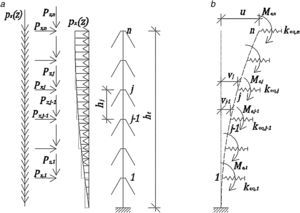
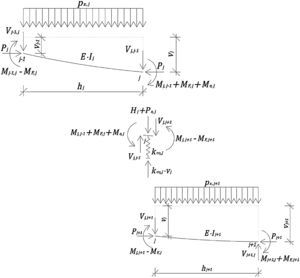
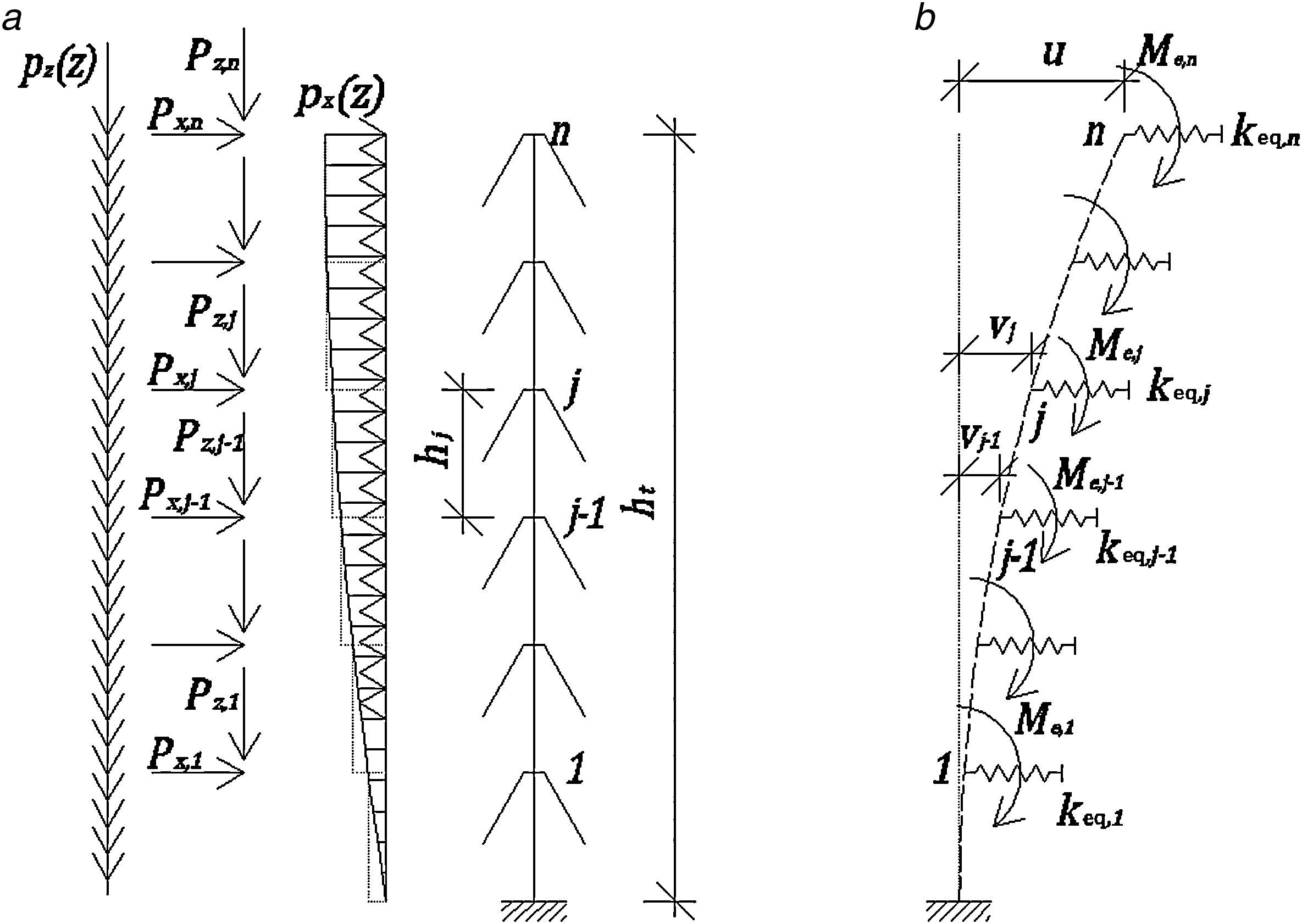
5Método propuestoConsideremos una estructura tipo mástil atirantado, de altura ht, con n niveles de tirantes uniformemente espaciados entre sí una distancia hj. Sin pérdida de generalidad, consideremos que la estructura está empotrada en la base, como se representa en la figura 8a.
La torre estará sujeta a cargas distribuidas verticales pzz como su peso propio; cargas verticales puntuales Pz, debidas por ejemplo al peso de los accesorios, pero en carácter general serán debidas al alargamiento y acortamiento de los cables y a la carga de viento sobre los mismos; y a cargas puntales y distribuidas horizontales, Px y pxz, respectivamente, básicamente debidas a la acción del viento sobre el mástil, los cables y los accesorios.
Planteando equilibrio en la configuración deformada en el nodo j, en referencia a la figura 8b podemos escribir para el momento de continuidad j-1 la ecuación 12:
siendo zcb,j la altura correspondiente al nivel j de tirantes, vj el valor de la elástica para dicho nivel de tirantes, keq,j es el valor de la constante elástica equivalente para el nivel j de tirantes, ccb,j es la distancia horizontal entre el pie de los tirantes del nivel j y la torre, Hj es la fuerza resultante horizontal entre dos niveles de tirantes, obtenida como, Hj=∫zcb,j−hj/2zcb,j+hj/2pxzdz, Pz0,j es la fuerza resultante vertical debida a la carga vertical uniformemente distribuida entre dos niveles de tirantes, obtenida como, Pz0,j=∫zcb,j−hj/2zcb,j+hj/2pzzdz, Pz,j es la fuerza vertical en el nivel de tirantes j debida a la acción del viento sobre estos y Me,j es el momento debido a la excentricidad de los cables en el nivel j de tirantes y viene dado por la ecuación 13:
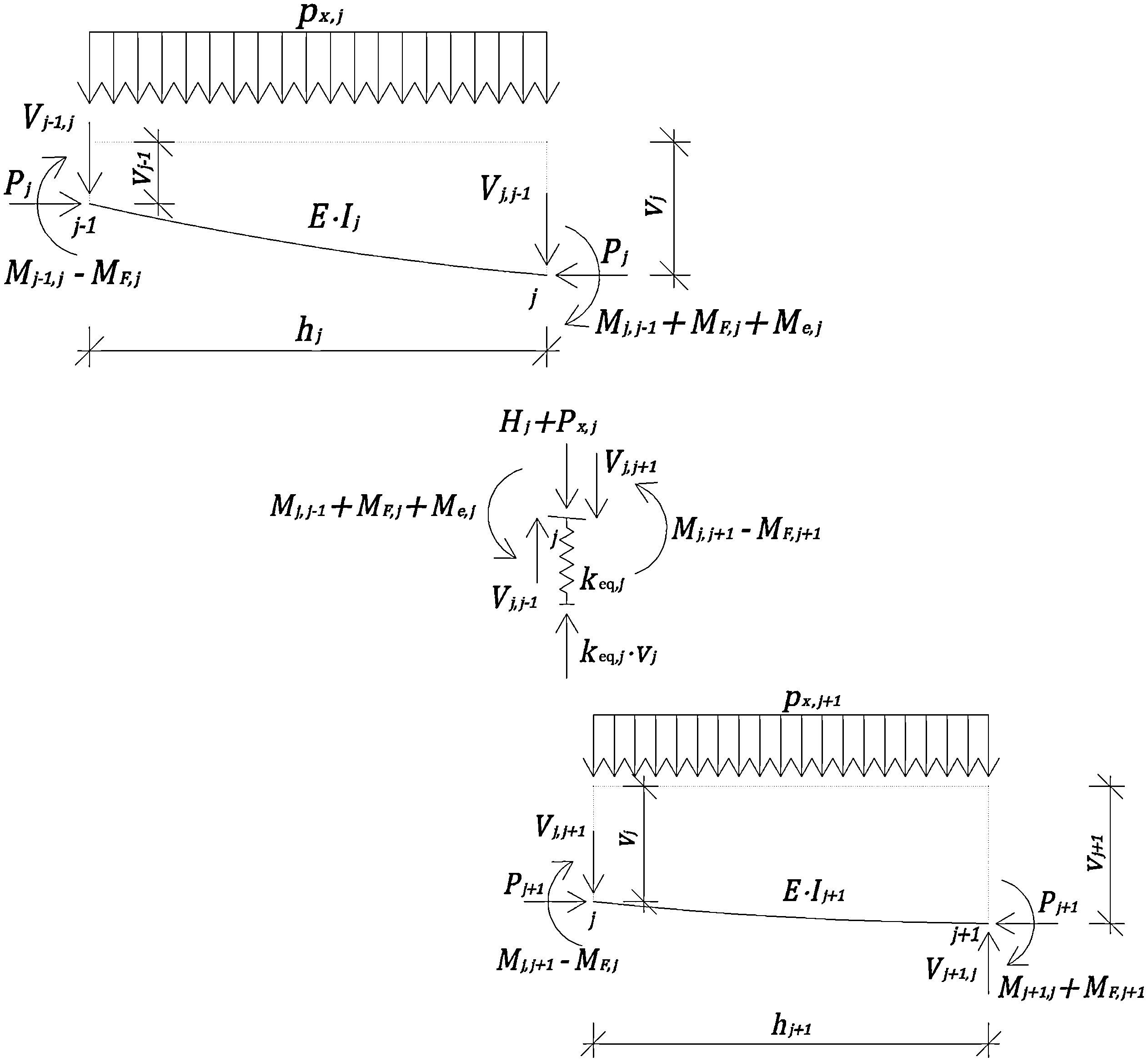
5.1Análisis de la estructuraConsideremos una viga-columna continua sobre apoyos elásticos discretos sometida a la acción de cargas externas para la que son conocidas las propiedades seccionales y de los materiales. Planteando equilibrio en la configuración deformada para las barras entre los nudos j-1, j y j+1 (fig. 9), y aplicando las ecuaciones de slope-deflection con fuerza axial de compresión [9], ecuación 14:
obtenemos las ecuaciones 15:
a2j−1,1⋅θj+1+a2j−1,2⋅vj+1+a2j−1,3⋅θj+a2j−1,4⋅vj+a2j−1,5⋅θj−1+a2j−1,6⋅vj−1=Hj+Px,jen donde los coeficientes aij en la ecuación 15 dependen de las propiedades geométricas de la viga y del material constituyente, de las funciones de estabilidad, de las fuerzas de compresión y de las constantes equivalentes de los resortes. Sus expresiones vienen dadas por la ecuación 16:
Cj y Sj son las funciones de estabilidad para la barra j, ecuación 17:
βj se denomina parámetro de pandeo y su expresión viene dada por la ecuación 18:
De las ecuaciones de equilibrio se deduce la expresión para la fuerza de compresión en la barra j, Pj, ecuación 19:
Los subíndices para las expresiones entre paréntesis indican a la barra que corresponde. Por ejemplo, E⋅IhSj indica que el módulo de elasticidad, el momento de segundo orden, la longitud de vano y la función de estabilidad S son las correspondientes a la barra j.
Mj−1,j y Mj,j−1 son los momentos de extremo en la barra j. MF,j es el momento de empotramiento perfecto para una viga sometida a una fuerza uniformemente distribuida en su plano y a fuerza axial de compresión. Su expresión depende de las condiciones de vínculo de los extremos; para el caso de barras bi-empotradas, su expresión viene dada por la ecuación 20 [16]:
Para una viga-columna de n tramos, a partir de la ecuación 15 se forma un sistema de 2n-1×2n-1 ecuaciones cuyas incógnitas son los giros y los desplazamientos laterales de los nudos θ1⋯θj⋯θn−1 y v1⋯vj⋯vn, respectivamente, ya que, por un lado, el extremo superior de mástil se considera articulado, lo que implica que θn puede escribirse en función de θn−1, y por otro, cuando el extremo inferior está empotrado θ0=v0=0 y cuando está articulado v0=0 y θ0 puede escribirse en función de θ1.
5.2Obtención de la configuración deformada: análisis de segundo orden método iterativoPara resolver el problema de forma simple, el método propuesto supone conocida la forma inicial de la elástica de la torre bajo la acción de las fuerzas externas, considerando para esta una función parabólica y tal que el valor máximo de la elástica sea menor que un valor prefijado vm,i, con vm,i=0,001⋅ht. Las contantes elásticas equivalentes en cada uno de los niveles se calculan a partir de los desplazamientos laterales supuestos. De esta manera puede estimarse de forma razonable la relación entre la fuerza de compresión en la barra j y la fuerza de compresión en la barra n de extremo. Sea ζ el factor de relación entre dichas fuerzas, esto es Pj=ζ·Pn, de esta manera la relación entre los parámetros de pandeo puede escribirse como (ecuación 21):
Los pasos del procedimiento iterativo para la obtención del desplazamiento lateral son:
- 1.
Se calculan los desplazamientos laterales de la torre, esto es, vj para j=1 a n. El método propuesto supone considerar que la curva elástica inicial es una función parabólica.
- 2.
Con los valores de los desplazamientos laterales calculados en el paso 1 se obtienen los módulos de elasticidad Esec,1 y Esec,2 para cada nivel de tirantes.
- 3.
El nuevo desplazamiento lateral de la torre bajo la acción de las cargas actuantes se obtiene resolviendo el sistema de 2n-1×2n-1 ecuaciones, obtenido a partir de la ecuación 15.
- 4.
Si para cada uno de los niveles de tirantes la diferencia entre el desplazamiento obtenido en el paso 3 y el desplazamiento del paso 1 es menor que un valor predeterminado, se da por finalizado el proceso. En caso contrario, con el desplazamiento obtenido en el paso 3 se repite el proceso hasta la convergencia.
- 5.
Si la diferencia entre los desplazamientos en cada nivel de tirantes no puede hacerse menor que un valor predeterminado, la estructura es inestable bajo la acción de las cargas actuantes. Deberá modificarse la rigidez de la viga-columna y/o la rigidez de las contantes elásticas.
Luego, planteando las ecuaciones de equilibrio en la configuración deformada para cualquier sección se obtienen las solicitaciones y se procede al dimensionado de las secciones de los elementos que conforman la torre utilizando los métodos habituales de resistencia de materiales y la norma que se tome como referencia. En relación a la figura 9, para la barra j y para una sección a una distancia x del extremo j-1, el momento en dicha sección viene dado por la ecuación 22:
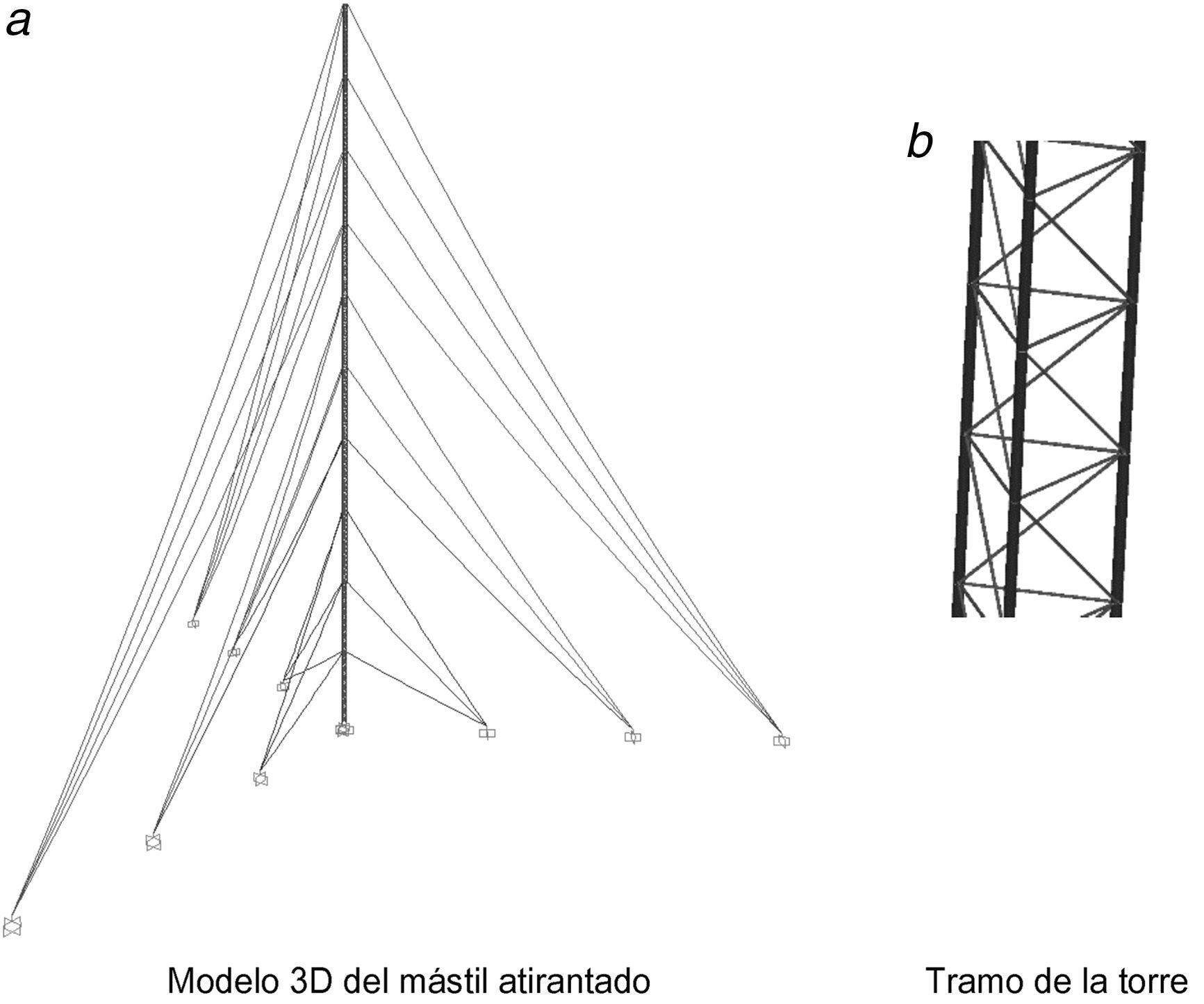
6Caso de estudio: comparación entre el método de elementos finitos y el método propuestoA los efectos de validar el método propuesto (MP), se analiza una estructura tipo mástil atirantado de 150m de altura, con dos condiciones de vínculo externo en su base, empotrado y articulado, utilizando dos modelos diferentes por medio del método de los elementos finitos (FEM) a partir del uso del programa SAP2000. Los resultados se contrastarán con los obtenidos por el MP. En el primer modelo (FEM: retic.) la estructura se modela como un reticulado espacial donde las barras trabajan principalmente a fuerza directa y los cables se modelan como elementos tipo cable (fig. 10). En el segundo modelo (FEM: viga-col.) la estructura se modela como una viga-columna equivalente, mediante elementos que trabajan a flexión y a fuerza directa, y cuyas propiedades geométricas se obtienen a partir del patrón de construcción de una de las caras de la torre (tabla 1). Se tienen en cuenta las excentricidades de los cables en los niveles de tirantes, y estos se modelan como elementos tipo cable. En ambos modelos los efectos de segundo orden se consideran a partir de un análisis no-lineal P-Δ.
La torre es de sección triangular, de 1m de ancho de cara medida eje a eje de las barras verticales. Las barras son materializadas por perfiles tubulares circulares de acero de módulo de elasticidad Ecb =200GPa. Los montantes (barras verticales) son de 73,00mm de diámetro exterior y 5,20mm de espesor, y las barras horizontales y las diagonales de diámetro exterior, de 21,33mm, y 2,77mm de espesor. La inclinación de las diagonales es de 45°.
Los tirantes son de acero EHS, de tensión de rotura 1.400MPa y módulo de elasticidad Ecb =185GPa. Están colocados con espaciamientos de 15m en la altura. Los tirantes cuyas cotas de anclaje a la torre son +15, +30 y +45m se anclan al terreno a una distancia de 30m del eje del mástil y son de diámetro nominal de 6,35mm (Acb =24,632mm2). Los tirantes cuyas cotas de anclaje son +60, +75 y +90m se anclan al terreno a una distancia de 60m y sus diámetros nominales son 6,35, 8,00 y 8,00mm (Acb =38,511mm2), respectivamente. Los restantes tirantes, cuyos niveles de anclaje a la torre son +105, +120, +135 y +150m, se anclan al terreno a una distancia de 90m del eje de la torre y sus diámetros nominales son de 8,00mm.
Las cargas de viento sobre la estructura se calculan a partir de los lineamientos establecidos por la norma TIA222-G, y se considera una velocidad característica de viento de 43,4m/s calculada como la velocidad media del viento en un intervalo de 3segundos a una altura de 10m sobre el nivel de terreno para una categoría de exposiciónC y cuyo período de retorno es de 50años.
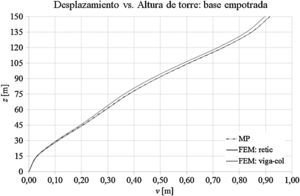
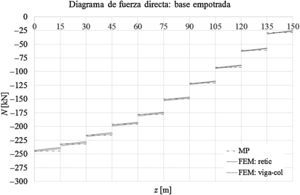
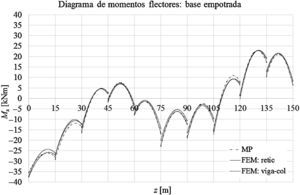
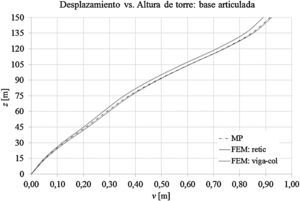
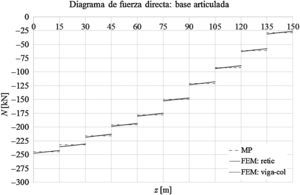
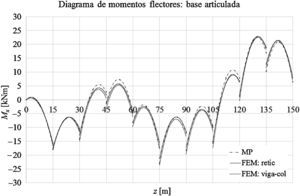
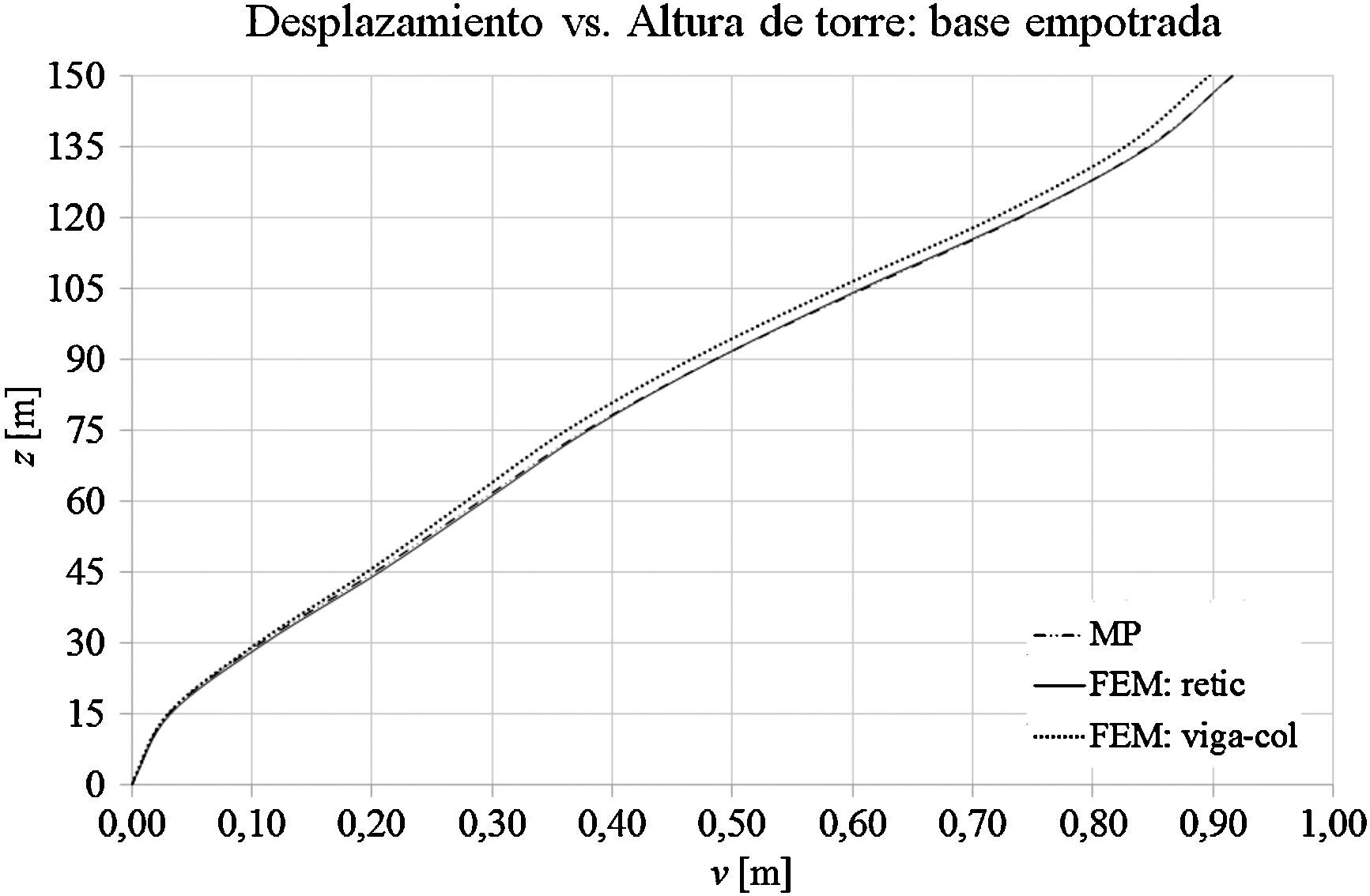
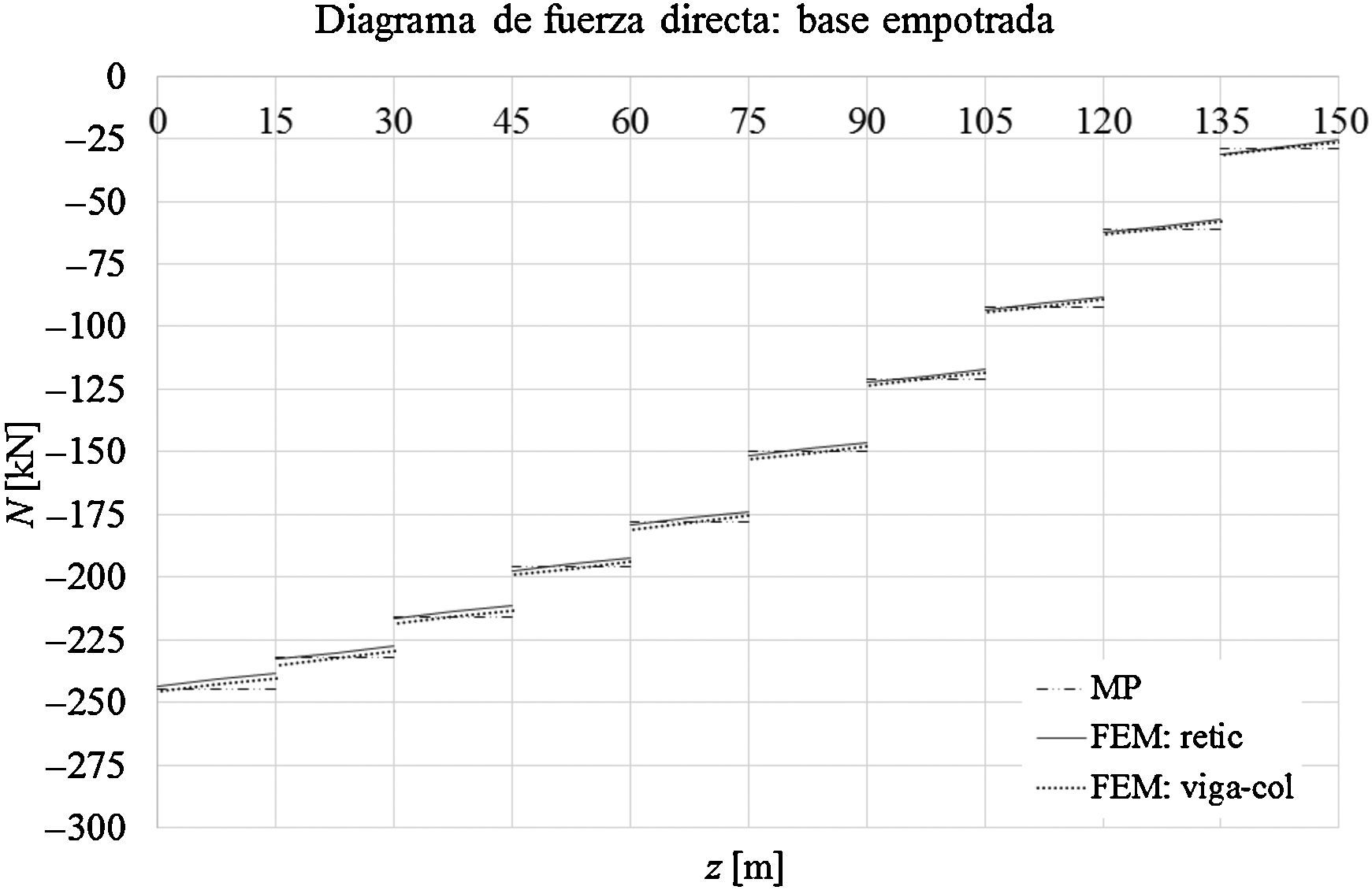
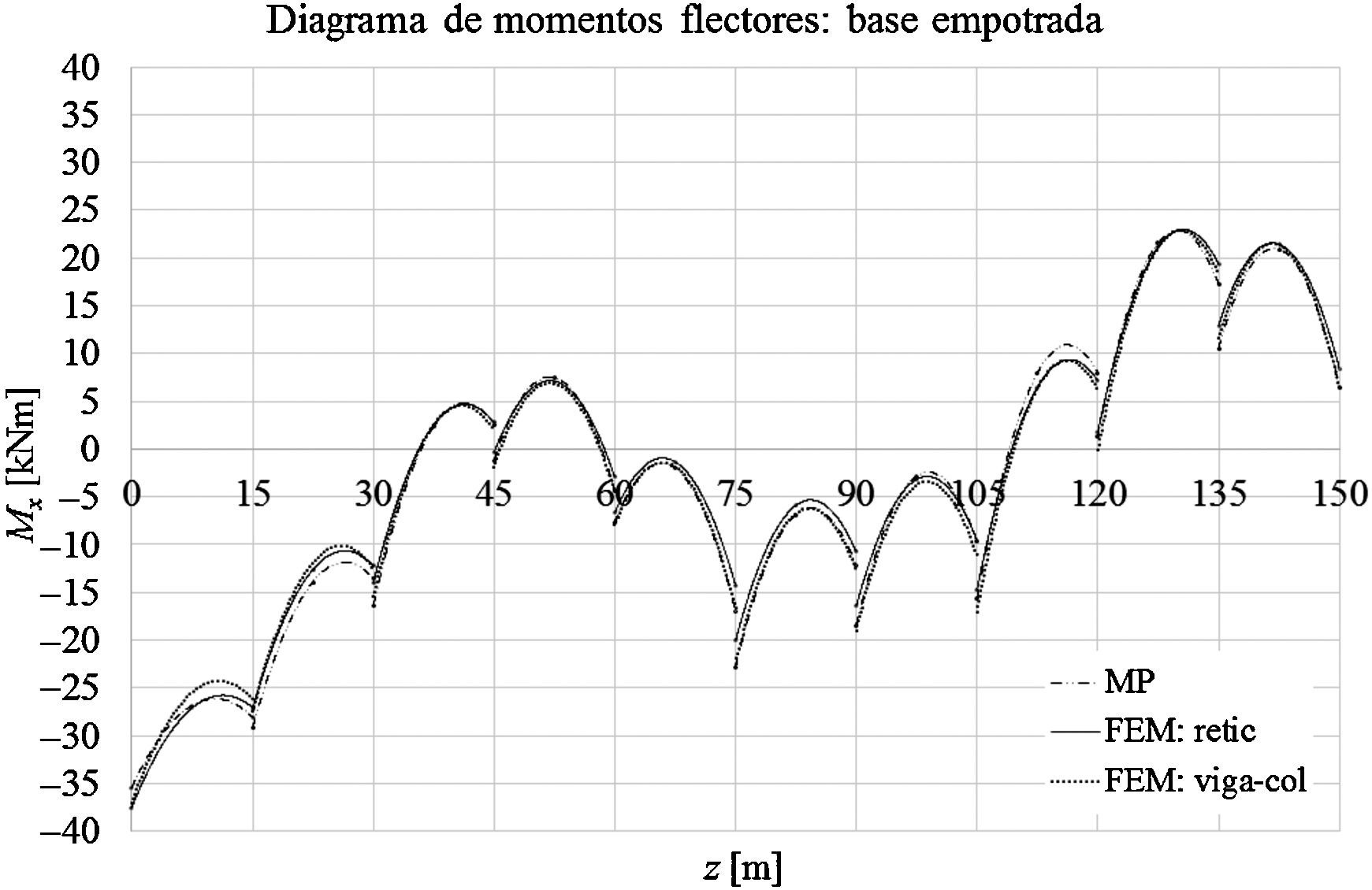
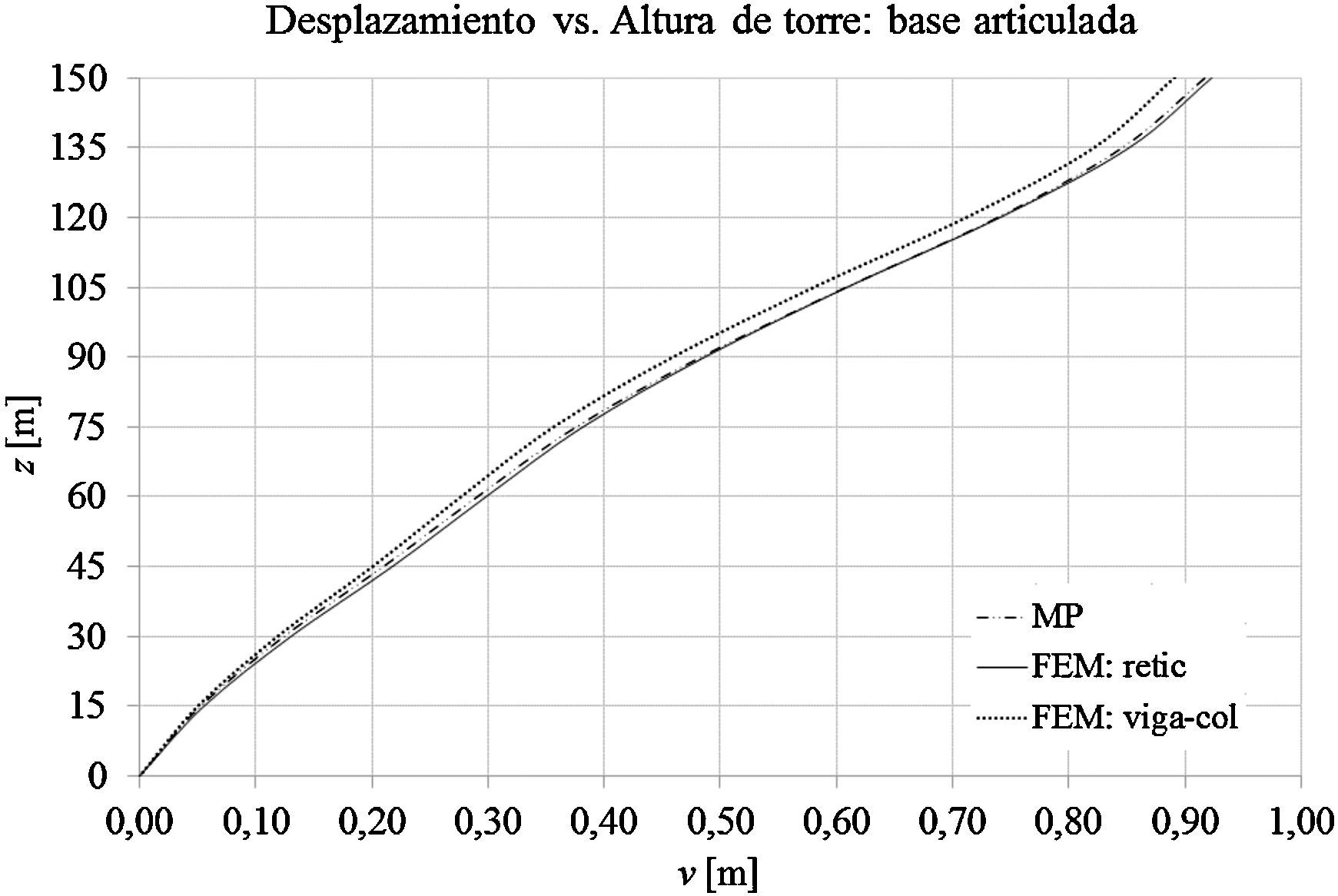
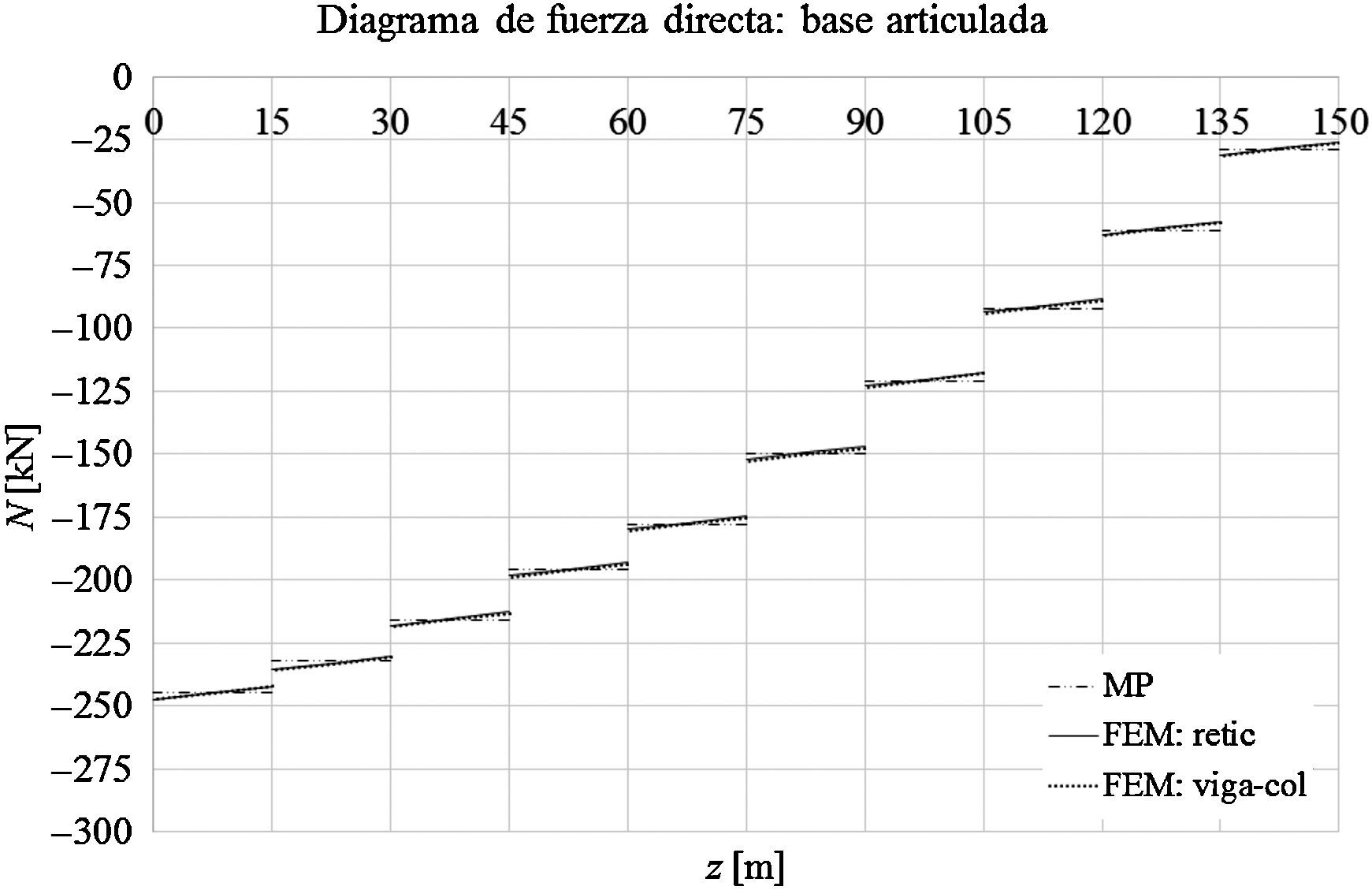
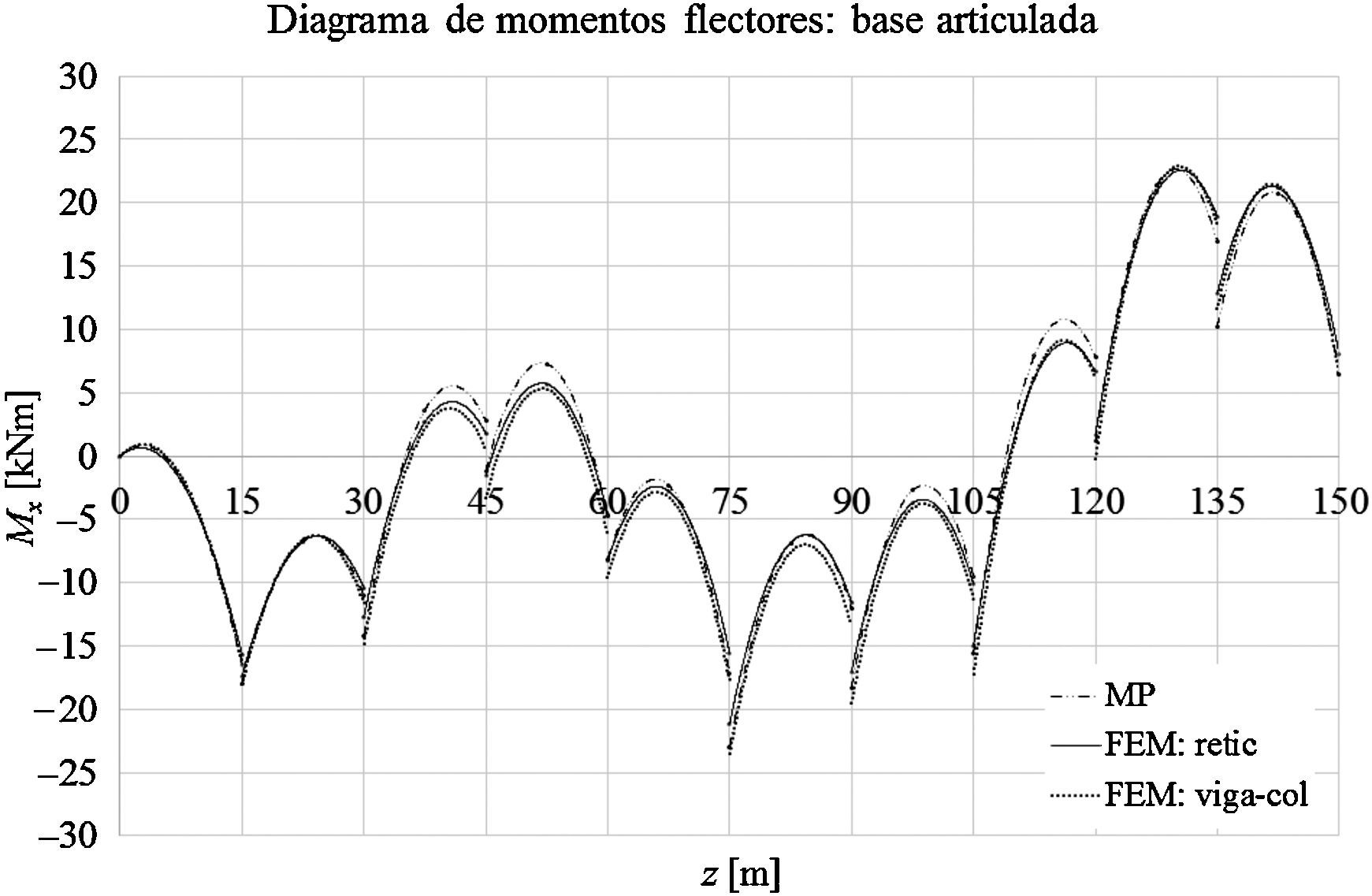
Las gráficas de las figuras 11-13 muestran los desplazamientos laterales, las fuerzas directas y los momentos flectores obtenidos a partir del MP y de los modelos mediante elementos finitos FEM: retic. y FEM: viga-col. en el caso de que la base de la torre esté empotrada. Las figuras 14-16 muestran los desplazamientos laterales, las fuerzas directas y los momentos flectores en el caso de que la base de la torre esté articulada.
Con relación a los desplazamientos máximos de la torre para el modelo cuya base está empotrada, la diferencia entre los modelos MP y FEM: retic. es el orden del 0,06% y la diferencia entre los modelos FEM: retic., y FEM: viga-col. es del orden del 2%. En el caso del modelo con la base articulada, la diferencia entre los modelos MP y FEM: retic. es del orden del 0,70%, y la diferencia entre los modelos FEM: retic. y FEM: viga-col. es del orden del 2,8%.
Para la torre con la base empotrada, la diferencia entre los momentos flectores positivos máximos a partir de los modelo MP y FEM: retic. es del orden de 2,2%, mientras que entre los modelos FEM: retic. y FEM: viga-col. son del orden del 0,2%. En relación a los momentos flectores negativos máximos, la diferencia entre los modelos MP y FEM: retic. es del orden del 5,5%, mientras que entre los modelos FEM: retic. y FEM: viga-col. es del orden del 1,4%.
Para el caso de la base de la torre con vínculo externo tipo articulación, la diferencia entre los momentos flectores positivos máximos a partir de los modelo MP y FEM: retic. es del orden de 2,7%, mientras que entre los modelos FEM: retic. y FEM: viga-col. es del orden del 1,6%. En relación a los momentos flectores negativos máximos, la diferencia entre los modelos MP y FEM: retic. es del orden del 7,8%, mientras que entre los modelos FEM: retic. y FEM: viga-col. es del orden del 10,1%.
Para los dos tipos de vínculo del extremo de la torre, las deformaciones máximas, los momentos flectores positivos máximos y la fuerza directa presentan diferencias muy poco significativas. Sin embargo, para el caso de la torre con la base empotrada el momento negativo máximo ocurre en la base de la misma y es del orden del 77% superior que en el caso de la torre con la base articulada, y por lo tanto también lo es el esfuerzo en los montantes del apoyo. De esta manera podemos establecer que el modelo de la torre con la base articulada es más conveniente como solución estructural.
7ConclusionesEn este trabajo se ha propuesto un método aproximado para el cálculo de las deformaciones producidas por los efectos de segundo orden en torres atirantadas de sección triangular. El método se basa en las funciones de estabilidad. Las propiedades geométricas para la viga-columna equivalente se obtienen según sea el patrón de reticulado de cada una de las caras de la torre. Los tirantes son modelados como constantes elásticas de resortes equivalentes a partir del módulo de elasticidad secante de los cables, y se tienen en cuenta las excentricidades de los mismos en los puntos de anclaje a la torre.
El método propuesto ha sido validado numéricamente mediante un caso de estudio comparándolo con los métodos de elementos finitos. A partir de los resultados expuestos pueden deducirse las siguientes conclusiones:
- 1.
Se observan diferencias poco significativas en el cálculo de los efectos producidos por las deformaciones de segundo orden de la estructura entre el MP y los métodos de elementos finitos. En otras palabras, los valores de las solicitaciones y de los desplazamientos de la estructura obtenidos mediante el método propuesto son suficientemente precisos comparados con los obtenidos mediante el método de elementos finitos, lo que confirma la validez de las hipótesis adoptadas en el desarrollo del método.
- 2.
El MP mantiene la complejidad y la rigurosidad matemática de los métodos analíticos; sin embargo, ha sido concebido como un método de aplicación simple. Utiliza los conceptos básicos y más generales desde el punto de vista de la ingeniería estructural, lo que permite al ingeniero visualizar rápidamente cuáles son los parámetros que influyen en el diseño.
- 3.
El modelo propuesto utiliza directamente las funciones de estabilidad, lo cual permite trabajar con mayor exactitud, sin la necesidad de realizar aproximaciones y/o divisiones de los elementos entre cada tramo entre tirantes. Es muy simple de programar, incluso a partir del uso de planillas electrónicas como se ha realizado en este trabajo, pues no necesita discretizar la estructura en un número grande de elementos para la convergencia. Es por esto que el método puede ser muy útil en las etapas de diseño preliminar o anteproyecto, con un ahorro importante de tiempo en la etapa de diseño. En otras palabras, el método de elementos finitos no presenta en la etapa de anteproyecto mayores ventajas que el método propuesto.
- 4.
En este trabajo también hemos podido establecer que la solución estructural de torre con base articulada es más conveniente desde el punto de vista estructural, ya que mientras que los desplazamientos máximos presentan diferencias poco significativas, las fuerzas máximas en los elementos estructurales de la torre son menores que para el caso de torre con base empotrada.
- 5.
Si bien el trabajo se ha centrado en las torres de sección triangular equilátera, con un arreglo para los tirantes de tres por nivel, el método propuesto puede extenderse a otro tipo de arreglo de los cables y a otro tipo de formas de sección. Por lo tanto, el método propuesto, inicialmente desarrollado para el análisis de torres atirantadas, puede extenderse al análisis de pilones de puentes atirantados.





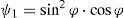
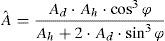
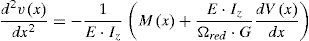
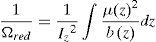
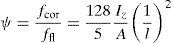
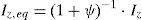
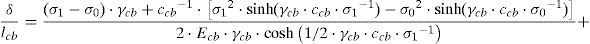
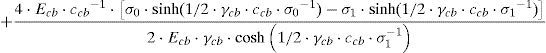
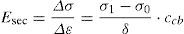
![Curva fuerza vs. desplazamiento del cable con origen en la condición inicial de tensado. Adaptada de [8]. Curva fuerza vs. desplazamiento del cable con origen en la condición inicial de tensado. Adaptada de [8].](https://static.elsevier.es/multimedia/04395689/0000006800000283/v1_201712210820/S0439568917300499/v1_201712210820/es/main.assets/thumbnail/gr6.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)