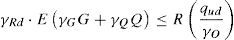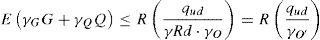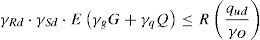Cálculo y control detallado del proceso de construcción del tramo atirantado del Puente de la Constitución de 1812 sobre la Bahía de Cádiz

Resumen

La construcción del puente por voladizos cuasi-simétricos con longitud máxima del voladizo sin más apoyos que la propia torre de 218,5 m, y el izado de dovelas de gran magnitud, en general de longitud 20 m, 34,30 m de ancho y hasta 4.000 kN de peso, estableciendo el proceso constructivo definitivo cuando parte de las torres ya estaban hechas, han hecho del cálculo y control de la construcción un gran desafío.

Ha requerido un análisis detallado de las 1.275 fases del proceso de construcción, con cálculos no lineales geométricos y materiales, comprobando todos los aspectos del tablero, torre y tirantes incluyendo acciones accidentales como la caída de dovela, controlando exhaustivamente todas las cargas presentes en el tablero y los cambios en la secuencia constructiva.

Abstract

The erection of the bridge with an almost symmetrical balanced cantilever, with a maximum length of 218.5 m, with no additional supports apart from the tower itself, and the erection of the truly massive segment of about 20.0 m long, 34.30 m wide, and up to 4,000 kN in weight, establishing the construction sequence when part of the towers were already erected, have made the calculation and control of the construction a significant challenge.

It has required a detailed analysis of the 1275 construction stages using non-linear geometric and material calculations, checking all the cable stays, tower and deck elements, including accidental actions, such as fallen segments, exhaustively controlling all loads on the deck and changes in the construction sequence.

1

Antecedentes

El diseño del proceso de construcción para el proyecto de licitación del puente consideró un izado de dovelas de 10,0 m de longitud en sección metálica. En esas condiciones, el proceso constructivo no era dependiente de la resistencia de las torres, por lo que no se planteó ningún elemento adicional para aumentar la resistencia de estas, como cables inferiores provisionales. Tampoco se realizó un armado ajustado a las necesidades del proceso, ya que los requerimientos de armado durante el servicio de la estructura eran mayores. Lo primero hubiese sido un armado constante, puesto que el momento de desequilibrio a lo largo del fuste es casi constante en el proceso. Lo segundo es un armado que aumenta hasta alcanzar su máximo en la cimentación, con una ley de momentos triangular (fig. 1).

Figura 1.

Fuste de la torre P13 ya construido al cambiar el proceso constructivo.

Con esa configuración del proceso se empezaron a construir las 2 torres. Sin embargo, la UTE Puente de Cádiz (Dragados-Drace) planteó un cambio de proceso constructivo de cara a acelerar y mejorar la construcción. Para minimizar el número de operaciones de izado y soldadura de dovelas en altura, planteó izar dovelas de 20,0 m incluyendo la losa de hormigón. Como consecuencia de este hecho:

• •

  La sección pésima de la torre pasó a ser la superior del fuste único, donde se abre en 2 patas para el paso del tablero. De ahí hacia abajo ya había armadura suficiente para hacer frente a los desequilibrios existentes durante la construcción.

• •

  No se podía añadir de manera sencilla una ayuda adicional al fuste inferior de la torre, en forma de cable inferior para estabilizarla.

Por tanto, hubo que adecuar todo el proceso de construcción a la resistencia de las torres, tomando las siguientes decisiones:

• •

  Para el resto de la torre P13 del muelle se aumentó la armadura lo suficiente para que la sección de control fuese la superior del fuste inferior.

• •

  Se puso la misma armadura en la torre P12 de la bahía, de manera que el proceso finalmente encontrado para la P13 fuese válido igualmente para la P12.

• •

  Se limitó el izado de hormigón con las dovelas a 2 franjas laterales que permitían acelerar el ciclo al tesar la primera pareja de tirantes hormigonando simplemente una junta pequeña entre dovelas con hormigón de alta resistencia y fraguado rápido.

• •

  Se cambió la secuencia de dovelas para limitar el máximo desequilibrio de tablero entre uno y otro voladizo a 10,0 m.

Con estas decisiones se pasó a comprobar todos los estados límites últimos (ELU) y los estados límites de servicio (ELS) del proceso constructivo, en un proceso iterativo con la Dirección Técnica de Dragados donde se comprobaba qué se podía hacer y qué no, buscando la optimización del ciclo constructivo, siempre condicionado por las comprobaciones sobre tablero, torre y tirantes. Además y paralelamente, se establecieron los mecanismos de control necesarios para poder llevarlo a cabo con total garantía de seguridad y finalización. Como consecuencia de todas estas decisiones, las particularidades de este proyecto que más relevancia tuvieron de cara al cálculo fueron [1–5]:

• •

  Izado de dovelas de 34,30 m × 20,0 m, con pesos de hasta 4.000 kN.

• •

  Que el desequilibrio máximo entre voladizos fuese de 10,0 m con izado de dovelas de 20,0 m implicó que la torre nunca estuviese equilibrada, ya que en cualquier configuración durante el proceso había un desequilibrio de 10,0 m como mínimo.

• •

  Voladizo del tablero máximo de 218,5 m hacia el vano principal y 198,0 m hacia el vano de compensación sin apoyos ni ayudas adicionales provisionales durante la construcción.

• •

  Sección de cálculo mixta, con hormigón en la losa superior.

• •

  Un total de 1.275 fases del proceso de construcción del tramo atirantado.

2

Control de la construcción

Debido a todo lo planteado en el apartado anterior y en [6], fue absolutamente fundamental un control riguroso y exhaustivo de todo el proceso constructivo, comprobando los ELU y ELS de todos los elementos de la estructura en todas las fases, ya que debido al proceso seleccionado estuvieron al límite de su capacidad durante la construcción, siempre cumpliendo los límites normativos. Para ello, se utilizaron continuas tomas de datos topográficos en toda la construcción tanto en torre como en tablero y mediciones también continuas mediante instrumentación como clinómetros, células de carga, bandas extensométricas, termómetros dentro y fuera de los materiales, anemómetros, acelerómetros, etc. [7].

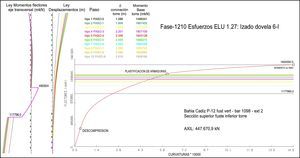
2.1

Control de la secuencia constructiva

Lo primero que se estableció fue el ciclo constructivo [5] de cada voladizo de una torre, con independencia del ciclo constructivo del voladizo contrario de la misma torre. Como se comentará luego, esta secuencia constructiva era inalterable, de manera que no se podía cambiar de ninguna manera el orden de fases, puesto que de otro modo no se cumplían las exigencias ELU y ELS del tablero y/o tirantes (apartados 4.3 y 4.5). En la tabla 1 están las 24 fases de un ciclo constructivo de un voladizo del tablero desde el punto de vista de cálculo.

• •

  La fase de izado (fig. 2a) correspondía al peso de la dovela exclusivamente, colocada 0,50 m alejada de su posición final, introducido a través de las patas del carro. En caso de caída de dovela y considerando un coeficiente de impacto ϕ = 2 (apartado 4.1), esta fase se restaba directamente en vez de sumarla al estado acumulado de todas las fases anteriores.

  
  

  Figura 2.

  Izado y colocación de dovela.
• •

  En la fase de colocación (fig. 2b) se introducía el peso de la dovela en su posición definitiva, junto con un estado de cargas autoequilibrado para representar la cogida de la dovela por el carro; se introducían por un lado 3 cargas verticales sobre la dovela correspondientes a los cables de cogida, y por otro el efecto de dicha cogida en las patas del carro. Esta era la fase utilizada [6] para establecer el posicionamiento teórico de la dovela durante el control geométrico de cada izado.

• •

  Después de la colocación, se avanzaba el carro de soldadura 3,50 m a su posición bajo la junta, se procedía a realizar la soldadura completa de la dovela izada (esta fase no producía ninguna acción en el modelo de cálculo) y se hormigonaba la junta del hormigón de las franjas laterales. A veces incluso se procedió al hormigonado de dichas juntas con una soldadura parcial. A continuación se soltaba la dovela del carro, eliminando entonces las cargas autoequilibradas que simulaban la cogida de la dovela.

• •

  Después del tesado de los tirantes delanteros se retesaban, en caso de ser necesario, las 2 parejas de tirantes de la dovela anterior.

• •

  Se izaban las losas, con el mismo criterio que la fase de cálculo del izado de la dovela, incluyendo la posibilidad de caída del paquete.

• •

  Se colocaban en su sitio y se hormigonaban las juntas, tesando la pareja trasera de tirantes y avanzando 20,0 m el carro de izado y 16,5 m el carro de soldadura.

Tabla 1.

Ciclo constructivo desde el punto de vista del cálculo: ejemplo dovela 13-i torre P13 sobre el muelle

Fase	Descripción
1174	Izado dovela (lateral: con hormigón) + balancín regulación
1175	Colocación dovela
1176	Mov. 1: encofrado juntas + carro soldadura (3,5 m) + plataforma tirantes + bastidor losas + acopio vaina
1185	Hormigonado junta lateral
1186	Peso propio tirantes delanteros
1187	Tesado tirante delantero izquierda
1188	Tesado tirante delantero derecha
1189	Retrasar plataforma de tirantes (1)
1190	Retesado tirante delantero izquierda dovela anterior
1191	Retesado tirante delantero derecha dovela anterior
1192	Retrasar plataforma de tirantes (2)
1193	Retesado tirante trasero izquierda dovela anterior
1194	Retesado tirante trasero derecha dovela anterior
1195	Adelantar plataforma de tirantes (1)
1196	Adelantar plataforma de tirantes (2)
1201	Quitar balancín regulación
1202	Izado losas + balancín losas
1203	Colocación losas + hormigonado juntas
1216	Quitar barandilla + mov. enanos y viga carril
1217	Peso propio tirantes traseros
1218	Tesado tirante trasero izquierda
1219	Tesado tirante trasero derecha
1220	Mov. 2: carro + trolley + retenida + carro soldadura (16,5 m) + pórtico fuerzas extr. dov. + mov. otras sob.
1221	Quitar balancín losas

A continuación, a partir de las indicaciones de la UTE Puente de Cádiz, se estableció una alternancia entre las fases de un voladizo y del contrario, cumpliendo todos los requisitos de ELS y ELU. Sin embargo, durante la construcción y de cara a optimizar el tiempo de ejecución, se plantearon continuamente cambios en el orden de ejecución de la secuencia entre uno y otro lado del voladizo del tablero cumpliendo siempre las siguientes premisas:

• •

  Cualquier cambio en el orden de cualquiera de las 1.275 fases requirió la elaboración del correspondiente informe y autorización por parte del proyectista.

• •

  No se podía cambiar el orden de ejecución de fases dentro de un mismo voladizo.

• •

  Para dicha autorización fue necesario calcular los momentos de desequilibrio en la torre producidos en esa nueva secuencia, teniendo también en cuenta la configuración de las sobrecargas de construcción.

• •

  En concreto, la fase que alteraba más el momento de desequilibrio de la torre era el izado de las losas prefabricadas en una lado antes o después del izado de una dovela en el lado contrario; al mismo tiempo era el cambio más solicitado por la UTE, ya que permitía avanzar mucho en la ejecución de un lado del voladizo.

2.2

Control de pesos

Parte esencial en dicho control del proceso fue la gestión de pesos añadidos a la estructura, fueran sobrecargas provisionales de construcción o los pesos estructurales definitivos.

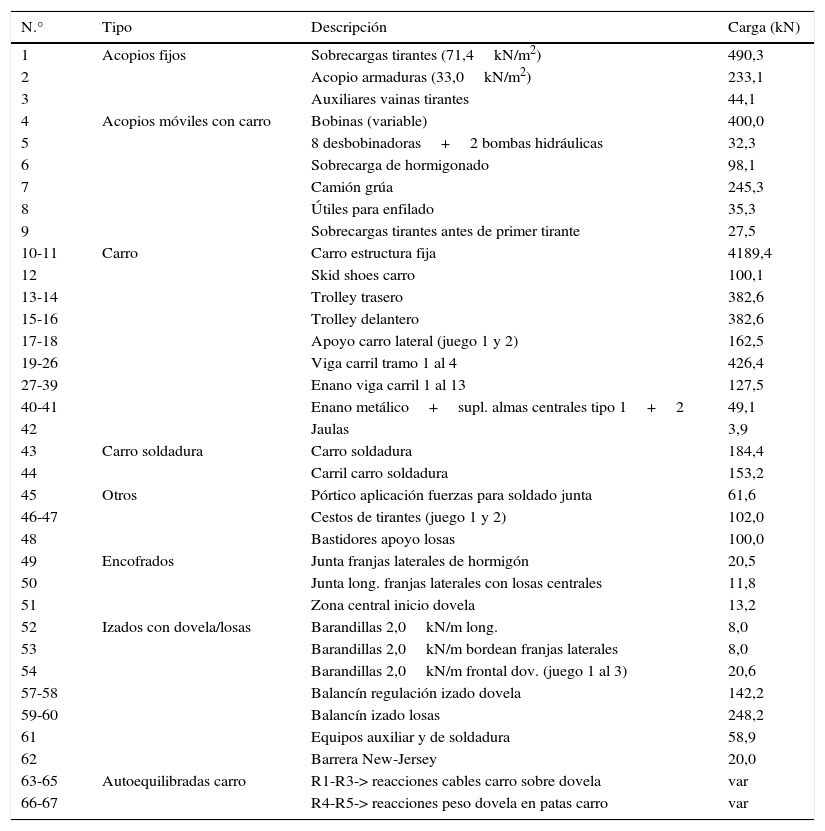
2.2.1

Sobrecargas de construcción

El control de las sobrecargas de construcción tuvo una gran importancia. En primer lugar porque su magnitud era superior a las sobrecargas que actuarán cuando el puente esté ya en servicio y, en segundo lugar, porque alteraban la deformación del tablero de forma muy significativa. Se hizo un esfuerzo muy considerable para concretar con la mayor precisión posible las cargas que estarían en el tablero en las distintas fases constructivas. Se definieron 67 sobrecargas de construcción diferentes, todas ellas con su valor, posición y cinemática: carro de izado de dovelas, carro de soldadura, acopio de bobinas para tirantes, devanadoras, carriles para el desplazamiento del carro, camión grúa, acopios de ferralla, acopios de vainas de tirantes [8], etc., y se incluyeron todas ellas en el modelo de cálculo (tabla 2). Es importante remarcar que no solo se buscaba tener las cargas equivalentes desde el punto de vista de esfuerzos máximos, sino también introducirlas en el modelo de la manera más adecuada para reproducir la deformada del puente en todo instante. Como muestra de lo indicado:

• •

  El valor de las sobrecargas en los 40,0 m delanteros del tablero ejecutado era alrededor de 7.500 kN, valor enorme que ha condicionado desde el punto de vista del ELU y/o del ELS muchísimas decisiones.

• •

  Para tener la deformada exacta en cada situación, las cargas que colgaban del carro se han introducido como un par de fuerzas en la pata delantera y trasera del carro (sobrecargas 10-11, 13-16, 57-60).

• •

  Las sobrecargas 63-67 eran las cargas autoequilibradas que representaban la cogida de la dovela.

Tabla 2.

Resumen de sobrecargas en el tablero

N.°	Tipo	Descripción	Carga (kN)
1	Acopios fijos	Sobrecargas tirantes (71,4 kN/m^2)	490,3
2		Acopio armaduras (33,0 kN/m^2)	233,1
3		Auxiliares vainas tirantes	44,1
4	Acopios móviles con carro	Bobinas (variable)	400,0
5		8 desbobinadoras + 2 bombas hidráulicas	32,3
6		Sobrecarga de hormigonado	98,1
7		Camión grúa	245,3
8		Útiles para enfilado	35,3
9		Sobrecargas tirantes antes de primer tirante	27,5
10-11	Carro	Carro estructura fija	4189,4
12		Skid shoes carro	100,1
13-14		Trolley trasero	382,6
15-16		Trolley delantero	382,6
17-18		Apoyo carro lateral (juego 1 y 2)	162,5
19-26		Viga carril tramo 1 al 4	426,4
27-39		Enano viga carril 1 al 13	127,5
40-41		Enano metálico + supl. almas centrales tipo 1 + 2	49,1
42		Jaulas	3,9
43	Carro soldadura	Carro soldadura	184,4
44		Carril carro soldadura	153,2
45	Otros	Pórtico aplicación fuerzas para soldado junta	61,6
46-47		Cestos de tirantes (juego 1 y 2)	102,0
48		Bastidores apoyo losas	100,0
49	Encofrados	Junta franjas laterales de hormigón	20,5
50		Junta long. franjas laterales con losas centrales	11,8
51		Zona central inicio dovela	13,2
52	Izados con dovela/losas	Barandillas 2,0 kN/m long.	8,0
53		Barandillas 2,0 kN/m bordean franjas laterales	8,0
54		Barandillas 2,0 kN/m frontal dov. (juego 1 al 3)	20,6
57-58		Balancín regulación izado dovela	142,2
59-60		Balancín izado losas	248,2
61		Equipos auxiliar y de soldadura	58,9
62		Barrera New-Jersey	20,0
63-65	Autoequilibradas carro	R1-R3-> reacciones cables carro sobre dovela	var
66-67		R4-R5-> reacciones peso dovela en patas carro	var

2.2.2

Peso propio

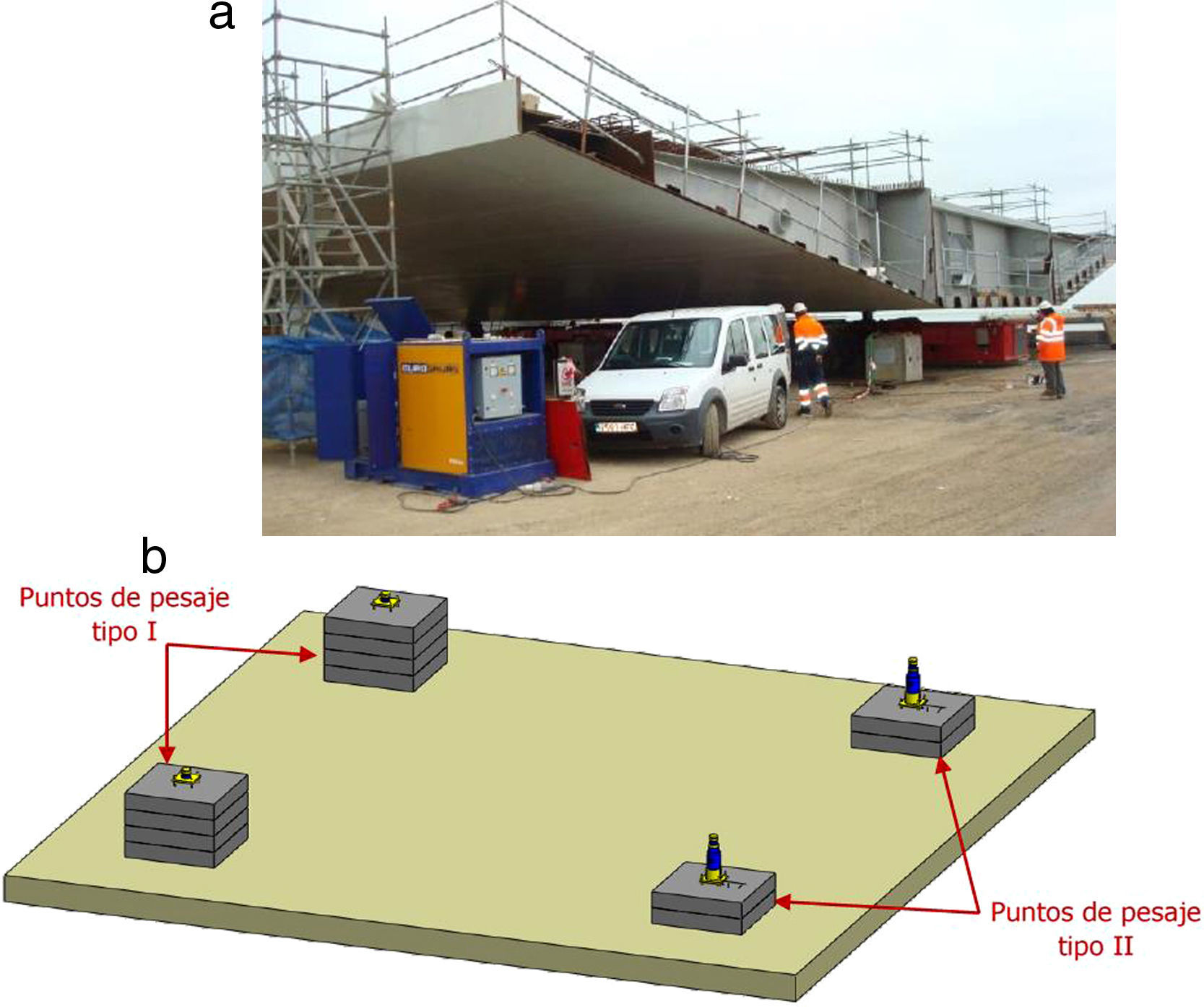
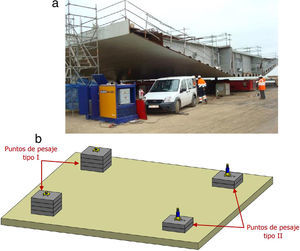
Respecto al peso de cada dovela, y dada la influencia tan determinante que este valor tenía en la flecha en punta del voladizo y en las cargas de los tirantes, tras varias mediciones de contraste se decidió pesar cada dovela antes de proceder al izado. Para ello se construyó una «estación de pesaje» compuesta por 4 puntos formando un cuadrado de 10 m de lado, iguales 2 a 2, con capacidad de 1.500 kN cada uno, ya que el peso estimado de la dovela más pesada era de 4.000 kN. Cada uno de estos puntos estaba dotado de una célula de carga, y en 2 de los 4 (puntos de pesaje tipo ii según la fig. 3) hay gatos hidráulicos conectados entre sí a un mismo circuito, de forma que se asegura el apoyo en 3 puntos, pues los apoyos en gatos funcionan como uno solo. Con este sistema de pesaje se obtenía también la posición del centro de gravedad, valor este muy importante para fijar la posición del balancín de regulación y subir la dovela equilibrada y con la pendiente apropiada.

Figura 3.

Estación de pesaje de dovelas.

En las dovelas tipo el peso de las losas prefabricadas estaba en torno de los 2.000 kN. Sin embargo, para precisar bien este valor, dada la influencia tan importante que tenía en los esfuerzos y deformaciones del tablero, se calculó de forma analítica la densidad real de cada losa, descontando del peso del hormigón el volumen ocupado por las armaduras y añadiendo el peso de estas. El valor de la densidad obtenido dependía del armado de la losa, pero en las zonas más densamente armadas se alcanzaron los 28 kN/m³. Adicionalmente, se comprobó el peso de las losas prefabricadas pesándolas en una báscula.

3

Modelo de cálculo para el proceso

El modelo de cálculo para cada una de las 1.275 fases del proceso constructivo [5] considera el esquema estructural adecuado a cada situación, incluyendo también la configuración evolutiva de los apoyos en cada fase. En este caso fue necesario un modelo no lineal iterativo para mejorar la precisión de los resultados al tener en cuenta que las variaciones en porcentaje de las cargas axiles de los elementos estructurales y tirantes es mucho mayor, considerando por tanto:

• •

  La matriz geométrica «exacta» en pilas y torres en cada fase para considerar la no linealidad geométrica.

• •

  El módulo de Ernst secante en los tirantes a partir de la carga real de cada fase.

• •

  La inercia fisurada, esto es, incluyendo la sección metálica + armadura pasiva en las fases correspondientes.

En este modelo, de acuerdo con el apartado 2, se han incluido:

• •

  Los pesos estructurales definitivos de manera detallada en valor y posición, con introducción en varias fases del hormigón de la losa superior, cada una con su densidad correspondiente.

• •

  Las cargas metálicas izadas provisionalmente, que se eliminan tras varias fases, una vez alejado el extremo del voladizo del tablero respecto la dovela en cuestión.

• •

  La posición y el valor de cada una de las 67 sobrecargas de construcción.

4

Cálculo detallado de los estados límites últimos

4.1

Bases de cálculo

Aparte de las bases de cálculo generales [9], ha habido 2 aspectos fundamentales a considerar. El primero fue la ausencia de coeficientes de seguridad para el desequilibrio de pesos (0,90/1,10) durante el proceso. Tal y como se ha detallado en [6], el sistema era extremadamente flexible, y el control del proceso y de las cargas fue exhaustivo (apartado 2). Para tener un orden de magnitud, introducir un coeficiente de 1,10 en el voladizo del vano principal y 0,90 en el vano lateral antes de llegar a la pila desplazaría la punta del voladizo de 218,5 m aproximadamente 6,5 m. Este valor, e incluso la décima parte del mismo, es claramente incompatible con el control geométrico continuo realizado de tablero y torres [6]. El segundo aspecto fue la caída de dovela y/o carro durante el izado de las dovelas. Se adoptaron los siguientes criterios:

• •

  El izado de las dovelas era una operación en movimiento, con carga hidráulica. En estas condiciones era necesario considerar la caída accidental de la misma durante la operación.

• •

  El carro de izado estaba anclado por medios mecánicos estáticos al tablero. Por tanto, incluso aun cuando se cayese la dovela, no podía caerse. De igual manera que no se consideró la rotura accidental de un tirante durante la construcción, no se tuvo como posible el fallo del anclaje mecánico del carro. En [8] está la descripción de todas las medidas consideradas para que este anclaje fuese plenamente efectivo y controlable.

• •

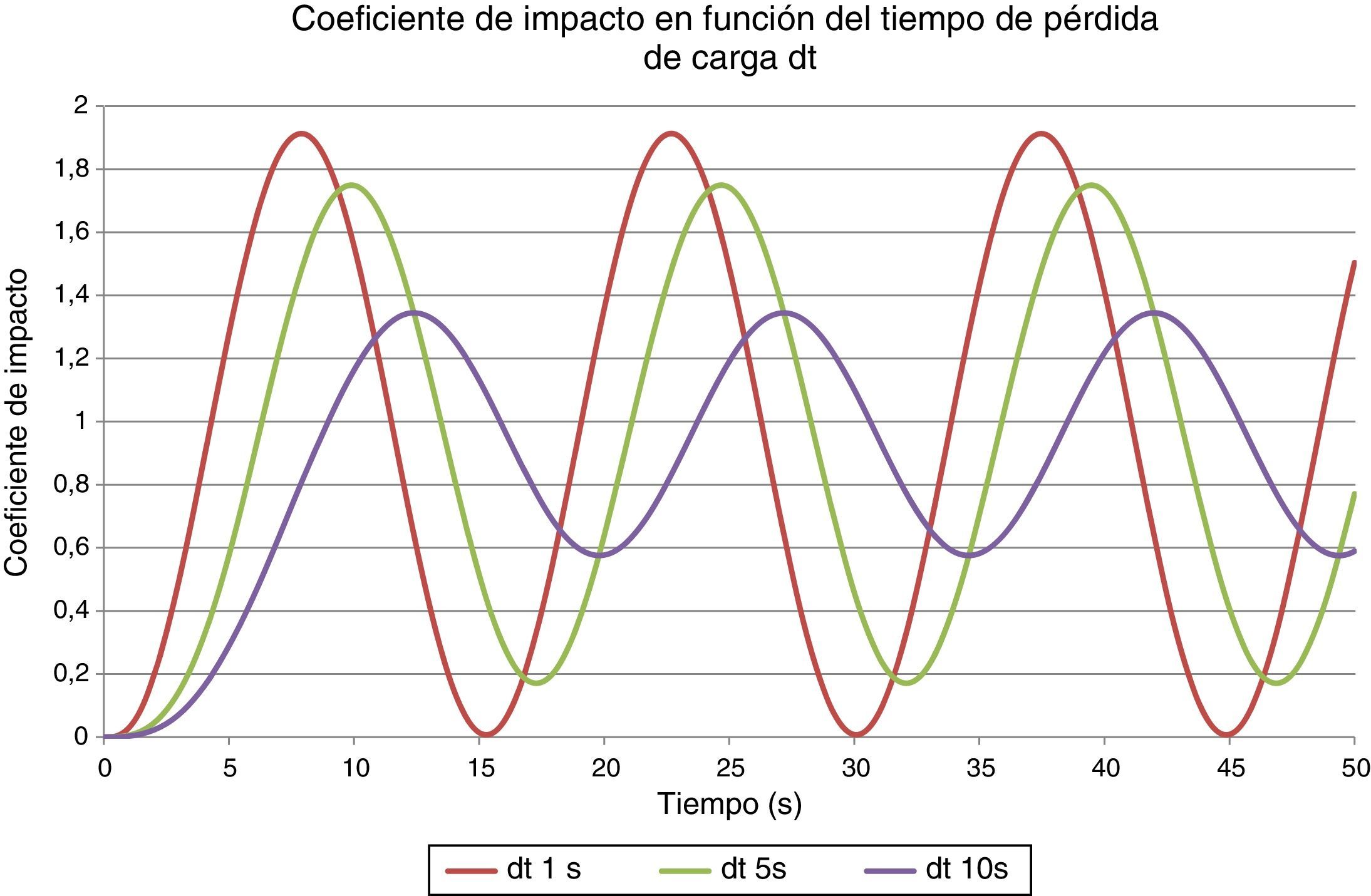
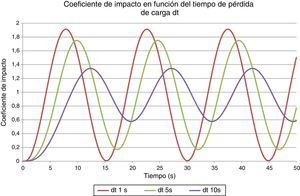
  Para el coeficiente de impacto dinámico de la dovela se consideró ϕ = 2,00. Se intentó disminuir este coeficiente con una aproximación en función del tiempo de caída con un modelo simplificado de 1 grado de libertad (fig. 4). Para un tiempo de desaparición de la carga de la dovela de 1,00 segundo, el coeficiente era de ϕ = 1,92; para un tiempo de 5 segundos, ϕ = 1,75. Como no se podían garantizar tiempos de desaparición de la carga mayores que esos valores, se decidió mantener el coeficiente ϕ = 2,00.

  
  

  Figura 4.

  Coeficiente de impacto en función del tiempo de pérdida de carga de la dovela.

Con todo esto, el resumen de estas bases de cálculo está incluido en la tabla 3.

Tabla 3.

Resumen combinación de acciones en ELU durante el proceso

Situación	Coeficiente mayoración	Carga	Descripción
Transitoria	1,35	Desequilibrio pesos de construcción
	1,35	Sobrecargas de construcción
	1,50	Viento transversal IAP	Ráfaga transversal sobre 1 voladizo
			Transversal tablero + torre + vertical tablero 1 voladizo + tirantes
	1,50	Viento longitudinal IAP	Longitudinal tablero + torre + tirantes
Accidental	1,00	Desequilibrio pesos de construcción
	1,00	Caída de dovela	Coeficiente de impacto 2,00
	1,00	Sobrecargas de construcción
	0,00	No caída de carro
	1,00	Viento 13,9 m/s

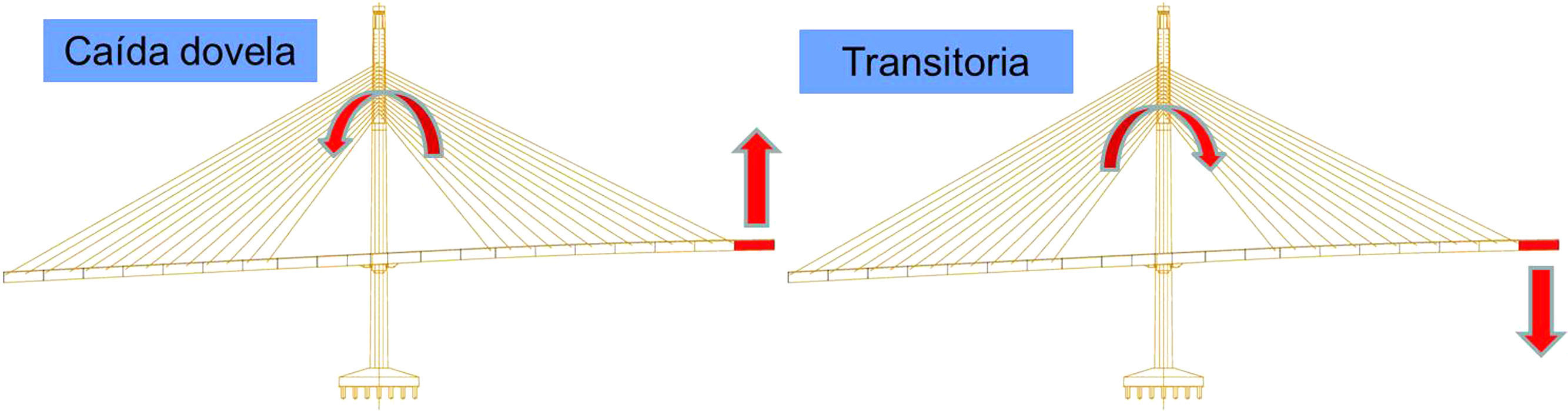
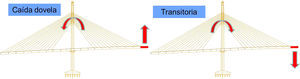
El problema con la caída de dovela es que, tal y como aparece en la figura 5, la situación transitoria y la situación accidental eran opuestas. Si se arreglaba la situación transitoria añadiendo peso en el lado contrario al izado de la dovela se estropeaba la situación de caída. Con el desequilibrio de 10,0 m se disminuía la descompensación en situación transitoria, aunque se estropeaba la caída; con el coeficiente ϕ = 2,00 equivalía a poner una dovela en el lado contrario, lo que equivaldría a un desequilibrio de 30,0 m. Sin embargo, esta era la situación óptima, ya que el viento compatible con el izado era muy pequeño (apartado 4.2), lo que llevaba prácticamente a anular su efecto, y los coeficientes de mayoración de cargas y minoración de resistencia de materiales mejoraban también. Así, con dicho desequilibrio de 10,0 m se llegó a la mejor situación posible.

Figura 5.

Esquema de control de seguridad durante las fases transitoria y accidental.

Sin embargo, dado lo expuesto, la primera consecuencia es que para una configuración del voladizo y una resistencia de la torre dadas, la única solución para resolver ambas situaciones transitoria y accidental era disminuir el peso izado. Así, las primeras dovelas se izaron con la sección metálica y hormigón de las franjas laterales; después, solo con la armadura de dichas franjas, y por último solo con la sección metálica. Tras la llegada del voladizo lateral a la primera pila de retenida se volvieron a subir las dovelas con las franjas laterales de hormigón completas. La segunda consecuencia es que el orden de fases entre uno y otro voladizo, tal y como se mencionó en el apartado 2.1, no podía ser alterado libremente sino que requería una comprobación completa de la nueva situación.

La otra solución posible era haber usado contrapesos temporales. Durante el izado de dovela el viento es muy reducido, por condicionantes del carro. Esto llevaba a que la situación transitoria no era crítica durante el izado, siendo la situación pésima la caída de dovela. Si se añadía un peso en el lado del izado se podía arreglar este punto. Una vez izada y colocada la dovela, esto es, una vez que ya no se podía caer, se podría eliminar ese contrapeso o incluso moverlo al lado contrario. Sin embargo, se consideró ese procedimiento como inconveniente y difícilmente controlable, por lo que fue descartado.

4.2

Consideración del viento

El viento de cálculo en la bahía de Cádiz [9] es de 28 m/s a 10 m de altura, sin incluir ráfaga. Durante la construcción, con menor período de retorno, se podía reducir a 0,84 × 28 m/s. Este viento a la altura del tablero e incluyendo el coeficiente de ráfaga se transformaba en aproximadamente 0,84 × 28 × 1,475 × 1,344 = 46,6 m/s = 168 km/h. Durante el izado, teniendo en cuenta el corto plazo del mismo, la previsión de viento se podía considerar como cierta [10], empezando el izado cuando dicha previsión limitaba el viento a 50 km/h en altura, incluyendo ráfaga. Si además se consideraba un coeficiente de mayoración para dicho viento durante la caída de γ = 1,00 y γ = 1,50 durante la situación transitoria, nos lleva a que el viento en situación accidental es únicamente el (50/168) ^ 2/1,50 = 5,9% del viento durante la situación transitoria. En otras palabras, el viento pasa de ser una acción tan relevante como el desequilibrio de pesos en situación transitoria a una acción con importancia residual en situación accidental.

Para cada una de las fases del proceso constructivo se ha considerado el viento transversal, longitudinal y vertical sobre tablero, torre y tirantes en la estructura existente en ese momento, de acuerdo con los coeficientes de arrastre obtenidos en [11]. Simplificadamente y del lado de la seguridad, se consideró una longitud de ráfaga igual a la longitud del voladizo. Esto, unido a la consideración de un coeficiente de ráfaga de 2,0, daba como resultado que el viento transversal al puente, y el viento vertical asociado a él, podían actuar en un voladizo con su valor característico y en el otro tener valor nulo.

En la sección de control de la torre, que de acuerdo con el apartado 0 es la sección superior del fuste inferior, y para el momento de eje transversal al puente, que era el que se sumaba a los momentos de desequilibrio por pesos, el viento más condicionante era el viento longitudinal al tablero, principalmente debido a la componente del viento sobre la torre. El viento transversal en las fases iniciales daba momento de eje transversal nulo; a medida que avanzaba la construcción, el viento vertical sobre uno de los 2 voladizos, considerando el viento vertical sobre el otro voladizo nulo, se aproximaba al momento por el viento longitudinal al puente hasta dar valores parecidos.

Por otro lado, y para calcular el momento de eje vertical en el empotramiento del tablero en la torre, fundamental para el diseño de las uñas de fijación provisional del tablero contra la torre, se utilizó el procedimiento descrito en [12], para tener en cuenta de manera más ajustada el viento sobre una estructura donde el peor efecto corresponde al viento sobre una parte de la misma, relacionándolo con su frecuencia natural de torsión de la torre de 0,286 Hz en su configuración de máximo voladizo antes de alcanzar la primera pila de retenida. Se consideró para ello un amortiguamiento total de 0,065, suma del decremento logarítmico estructural de 0,05, dato seleccionado para la torre de hormigón, y un amortiguamiento aerodinámico de 0,015, estimado a partir de la formulación. Como resultado más significativo, con este cálculo más depurado se obtuvo un momento de empotramiento de unos 127.000 mkN, frente a los 173.000 mkN obtenidos al aplicar el viento transversal máximo a un voladizo y viento nulo al otro voladizo.

4.3

Tablero

Inicialmente se hizo una comprobación general de todo el tablero en todas las fases. La resistencia del mismo condicionó el proceso en varias secuencias, así como el diseño del carro [8]. Una vez que se resistían correctamente todas las fases, las comprobaciones posteriores durante el proceso fueron sencillas, ya que, como se comentó en el apartado 2.1, no se podía variar nada la secuencia constructiva dentro de un voladizo. Por otro lado, los cambios en la secuencia constructiva de un voladizo no afectan prácticamente al tablero del otro; por tanto, no hizo falta ninguna comprobación adicional debido a cambios en el proceso de construcción seguido finalmente.

El principal problema de cara a la comprobación de los ELU en el tablero fueron las elevadísimas cargas locales transmitidas por el carro. De hecho, hubo que diseñar cuidadosamente todos los apoyos del mismo para poder resistirlos adecuadamente:

• •

  El avance del carro se hizo siempre apoyado en unas vigas carril, apoyadas directamente de diafragma en diafragma a través de enanos metálicos. Por tanto, nunca se apoyó en el hormigón de la losa superior durante el avance.

• •

  Durante el izado, en las secciones iniciales sin tirantes se apoyó el carro sobre las almas centrales. En fases posteriores, el carro se diseñó con un juego de patas que se abrían para apoyarse directamente en los lados de los tirantes.

• •

  Para la retirada del carro, inicialmente estaba prevista sobre la misma viga carril de avance. Sin embargo, para acelerar el proceso, 3 de ellos se retiraron sobre carros multirruedas. Esto cambió totalmente la filosofía de apoyo del carro, llevando la losa superior al límite de su capacidad.

• •

  De hecho, ante la magnitud del peso del carro, se aprovechó su retirada para hacer una primera prueba de carga en cada uno de los 4 voladizos.

4.4

Torre

4.4.1

Etapas

A modo de resumen, hay 3 etapas en las comprobaciones de la torre:

• •

  En el primer tramo, hasta llegar a los primeros tirantes, la limitación estuvo en la resistencia a torsión de la riostra de apoyo del tablero en la torre. El tablero simplemente se apoyaba en la riostra de la torre una vez instalados los 4 primeros tirantes y durante el servicio de la estructura. Sin embargo, en las primeras fases se empotraba en la misma para resistir los desequilibrios de pesos. Esta situación era claramente condicionante durante estas fases, principalmente debido a la gran diferencia de funcionamiento de la misma.

• •

  Durante la fase de voladizo puro, es decir, hasta que el tablero se apoyó en la primera pila de retenida, el proceso constructivo del tablero estuvo condicionado por la resistencia del fuste de la torre; más concretamente, por la resistencia a flexocompresión de la sección de control de la torre. Tal y como se explicó en el apartado 0, debido al hecho de haber construido parte de la torre P13 sobre el muelle cuando se redefinió el proceso, se dimensionó toda la armadura del resto de las torres de manera que controlando la sección superior del fuste inferior se podía asegurar que el resto de secciones cumplían las condiciones estructurales.

• •

  Una vez apoyado el tablero en la primera pila del vano de retenida, a 200,0 m de las torres, configurando entonces un único voladizo máximo sin apoyos de 218,5 m, solo hubo que comprobar la resistencia de los cajones superiores de las torres donde se anclan los tirantes para evitar fisuraciones indeseables y verificar que no había tiro en los apoyos de la pila.

4.4.2

Resistencia a torsión de las riostras de las torres

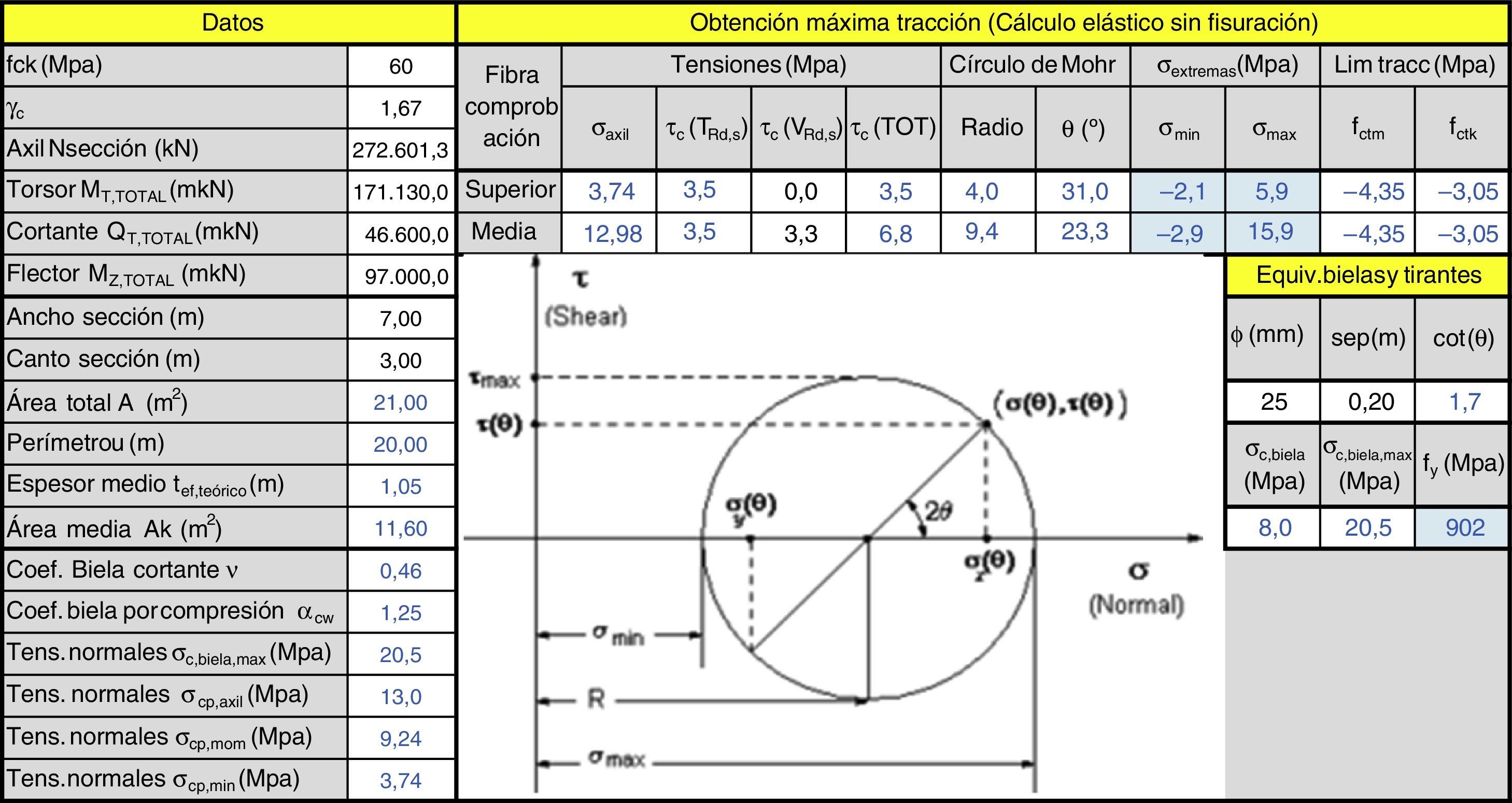
En el primer tramo fue necesario comprobar detalladamente la resistencia de la riostra de la torre, máxime cuando las cargas para las que fue inicialmente diseñada aumentaron, principalmente por el incremento de peso de los medios auxiliares. Normativamente el problema está bien cubierto desde el punto de vista ELU, con la salvedad de que se utilizaron 2 mecanismos de torsión, el primero para una armadura situada en el perímetro de la riostra y el segundo para una armadura cerrada que no llegaba al borde de la misma, comprobando la resistencia de la biela de compresión a torsión como suma de ambos mecanismos. El principal problema fue garantizar la no fisuración de la riostra por torsión en ELS durante estas fases, tal y como se explica posteriormente.

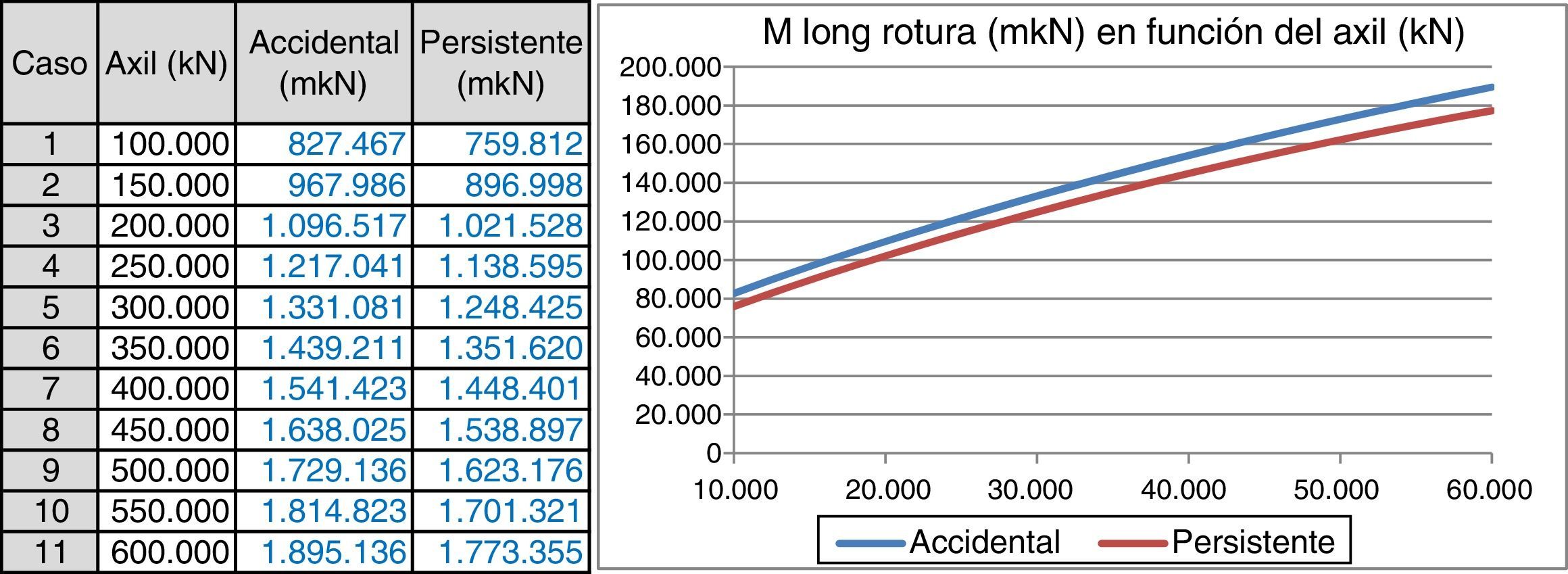
4.4.3

Cálculo no lineal en la fase de voladizo

Como orden de magnitud de los esfuerzos en dicha sección pésima durante las fases de voladizo cuasi-simétrico sin apoyo en la pila del vano de compensación, el esfuerzo axil osciló de 180.000 kN, debido exclusivamente al peso propio de la torre, hasta los 360.000 kN en la fase antes del bloqueo en la pila de retenida. Respecto a los momentos de eje transversal, que eran claramente los que condicionaban la resistencia de la sección, el momento del viento varió poco durante la construcción, ya que condicionaba claramente el viento sobre la torre, unos 290.000 mkN. Debido a los desequilibrio de pesos, el valor del momento fue de hasta ±450.000 mkN. Todos estos valores son característicos, sin mayorar.

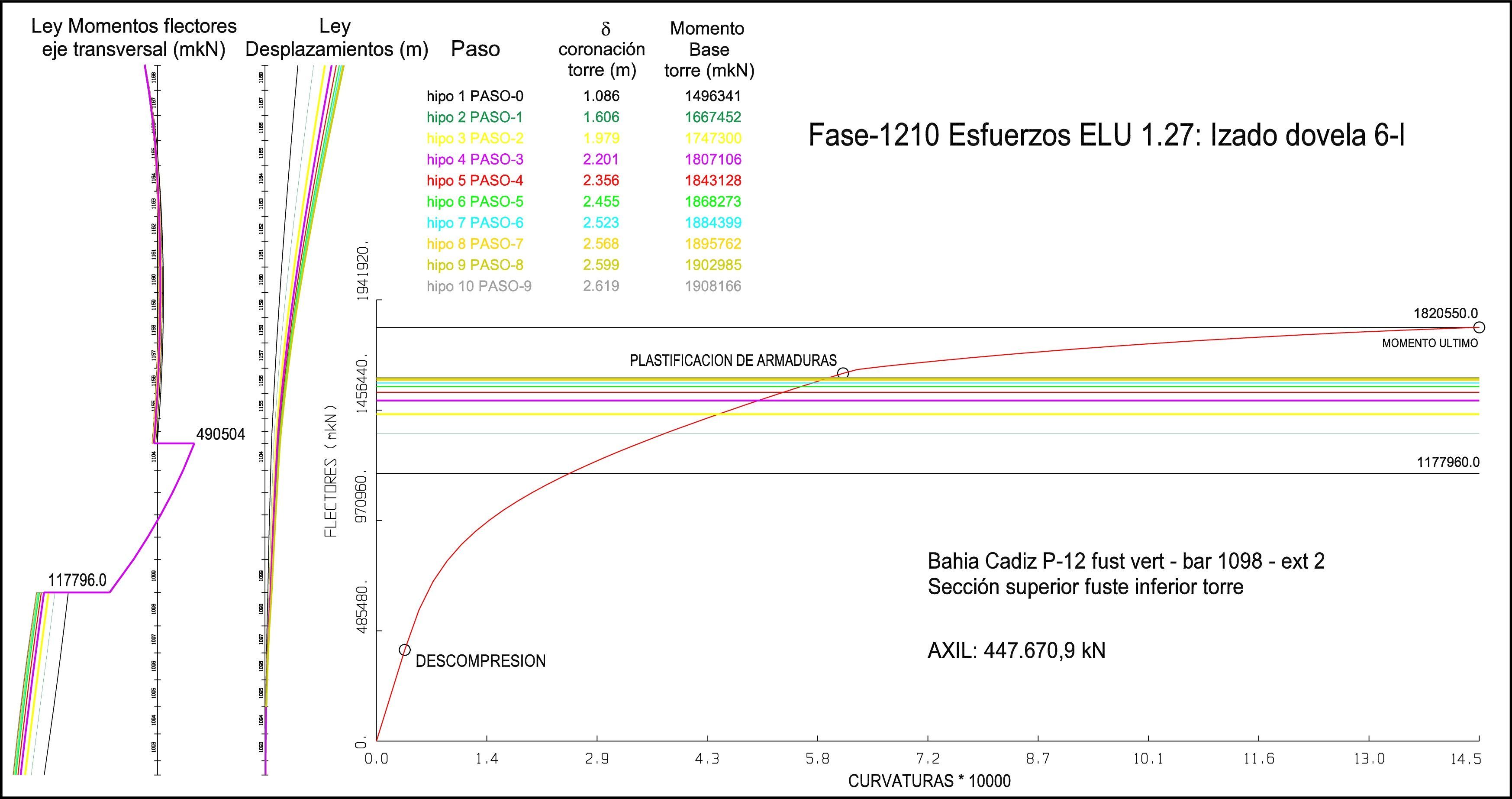
En la figura 6 está la resistencia de la sección de control en función del esfuerzo axil. Se observa que aumenta muchísimo al incrementar el esfuerzo axil, un 40% más entre la situación inicial y la final antes del bloqueo en la pila, lo que indica claramente que el condicionante de la sección fue la armadura y no la resistencia a compresión de la pila. De hecho, del lado de la seguridad, estos momentos resistentes están considerados con el requisito de resistencia a compresión del hormigón de la torre, 60 MPa, en vez de con la resistencia real obtenida, más de 70 MPa, máxime teniendo en cuenta la edad del hormigón de las torres, mayor de 2 años en las fases constructivas pésimas.

Figura 6.

Momento longitudinal de rotura de la sección pésima de la torre en función del axil.

Con todas estas consideraciones, fue necesario realizar un cálculo no lineal geométrico y material completo. Evidentemente, no se podía hacer en las aproximadamente 900 fases antes de apoyar en las pilas del vano de compensación. Por tanto, se hizo en aquellas donde el coeficiente entre el momento resistente y el actuante era menor. Dicho cálculo se hizo con actualización iterativa de la geometría de las torres y diagramas momento curvatura en todas las secciones relevantes (fig. 7). La principal diferencia entre el cálculo lineal estándar y estos cálculos es que estos últimos se hacen con valores característicos de las propiedades del material en vez de utilizar los valores de diseño minorados. Por tanto, hace falta un formato de seguridad especial, para lo que se ha utilizado el establecido en [13], donde existen 3 posibilidades, de acuerdo a las ecuaciones (1), (2) y (3):

Figura 7.

Cálculo no lineal geométrico y material de la torre.

Donde γ_Rd = 1,06 es el coeficiente por la incertidumbre en el modelo de la resistencia de los materiales, γ_Sd = 1,15 es el coeficiente por la incertidumbre en el modelo del efecto de las acciones, γ_o = 1,20 es el coeficiente global de seguridad, G son las acciones permanentes, Q son las acciones variables, E() representa los esfuerzos provocados por las acciones de diseño mayoradas y R(), los esfuerzos provocados por la primera carga que causa el colapso de la estructura. Cuando las incertidumbres en el modelo no son consideradas de manera explícita, esto es, γ_Rd = 1,0 y γ_Sd = 1,0, γ_0′ debe ser 1,27, valor seleccionado en nuestro caso. Para estructuras donde la respuesta de la misma tiene forma cóncava respecto la lineal, o dicho de otro modo, donde un incremento de la carga conlleva un incremento de la respuesta más que proporcional, el formato de la ecuación (2) es el que proporciona resultados más del lado de la seguridad entre las 3 posibilidades, por lo que es el que se ha utilizado.

Como se observa en la figura 7, la amplificación no lineal del momento en la sección crítica de control era en este caso 1,30. Tras un estudio de varios casos de izado, se llegó a la conclusión de que considerando un coeficiente adicional de 1,50 respecto el cálculo lineal, se estaba del lado de la seguridad. Dicho de otro modo, si el cociente entre el momento resistente para ese esfuerzo axil y el momento obtenido mediante cálculo lineal es mayor de 1,50, no habrá problemas cuando se considere la amplificación de los momentos de cálculo por los efectos no lineales. O de otra manera, si con cálculo lineal el coeficiente era de 1,50, se podía garantizar que con un cálculo no lineal completo se cumplirían las ecuaciones (1), (2) y (3).

4.4.4

Cálculo en fases posteriores

Una vez apoyado el tablero en la pila del vano de compensación se acabaron los problemas resistentes del fuste de la torre. Cualquier desequilibrio de pesos era resistido principalmente por un par de fuerzas verticales entre la pila y la torre. Sin embargo:

• •

  Fue necesario garantizar que no iban a existir tracciones en los apoyos de la pila, tanto para verificar la seguridad de la torre como para evitar el levantamiento del tablero. En las primeras fases hubo que hormigonar el contrapeso sobre la pila [14] en varias fases y alterar la secuencia constructiva convenientemente. Cuando se izaron varias dovelas más en el lado del vano lateral la reacción aumentó considerablemente y no hubo que comprobar nada más.

• •

  La maniobra de llegada y paso por la primera pila de retenida constituyó la primera de las maniobras singulares que se acometieron [14], por lo que su duración fue superior el ciclo de una dovela estándar. Para no penalizar el plazo y poder seguir avanzando en la construcción del vano principal, se colocó un lastre adicional sobre la pila, que aseguraba la reacción negativa.

• •

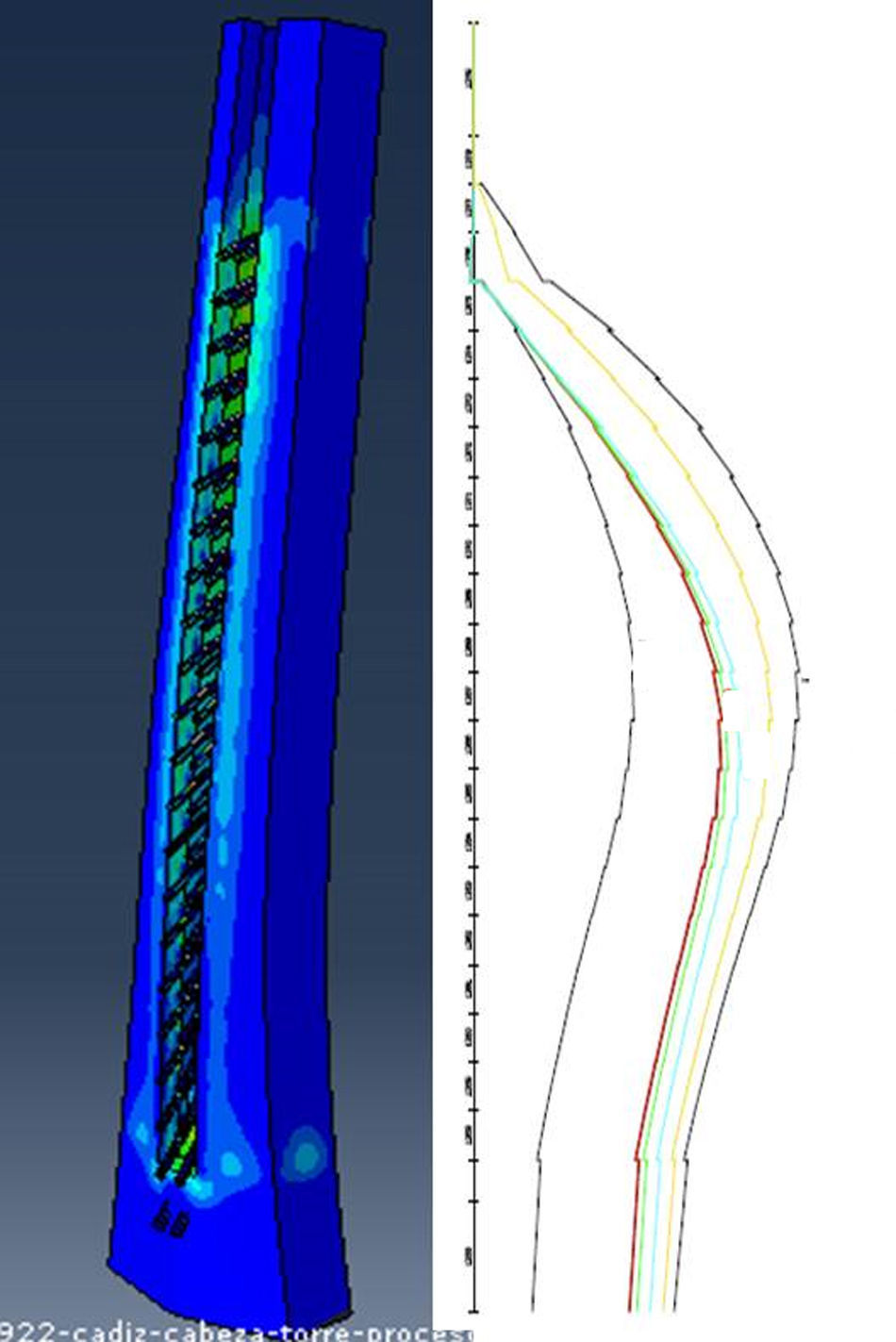
  Sin embargo, al avanzar de esa manera aumentaba el número de tirantes tesados hacia el centro de vano respecto los del vano lateral, aumentando localmente las tracciones en el hormigón del fuste superior de la torre. De manera prudente y para controlar la geometría de la torre, se decidió no permitir situaciones que fisuraran la misma, aunque fuese localmente. Esto se calculó (fig. 8) con un modelo de elementos finitos que incluía el hormigón con elementos tipo sólido y las chapas del armario metálico con elementos tipo lámina. La conclusión de este análisis fue no permitir el desequilibrio de más de una pareja de tirantes a izquierda y derecha del mástil.

  
  

  Figura 8.

  Comprobación local del fuste superior de la torre por desequilibrio de cargas en tirantes: forma ley momentos flectores eje transversal al puente a lo largo del fuste superior.

4.5

Tirantes

Debido al procedimiento seleccionado, se izaban dovelas de 20,0 m de longitud en las que se colocarían 2 parejas de tirantes. Por tanto, en las fases previas a la instalación de dichos cables, la sección del extremo del tablero debía resistir provisionalmente un voladizo muy grande sin ayuda de sus correspondientes tirantes. Además, debido a la configuración resistente de la introducción de las cargas de los mismos en el tablero [4,9], al menos era necesario disponer de 2 franjas laterales de hormigón en la losa superior para transmitir la compresión horizontal de la carga del tirante. Con todo esto, además de fisurar la losa superior en una longitud de 60,0 m, se sobrecargaba mucho la pareja de tirantes extrema, llegando hasta 0,63 × f_pk. Este valor permanecía muy poco tiempo, ya que en cuanto se tesaba la pareja delantera de la dovela izada se relajaba totalmente la situación, desapareciendo la fisuración de la losa y los excesos en la carga de los tirantes. A pesar de que la duración de esta situación de sobrecarga en los tirantes era muy corta en el tiempo, se decidió tomar medidas para cumplir los límites normativos de carga máxima de los tirantes durante la construcción [15]. Para ello:

• •

  En la instalación de la pareja delantera de tirantes de la dovela se redujo la carga de tesado.

• •

  De esta manera, cuando se izaba la siguiente dovela, esos tirantes tenían una carga menor, dentro de los límites aceptables.

• •

  El problema sería entonces en los tirantes y/o tablero posteriores; sin embargo, la fisuración del tablero no aumentaba mucho y los tirantes traseros no tenían problemas de carga máxima.

• •

  Cuando se había tesado el tirante delantero de la siguiente dovela, y la carga en el tirante delantero anterior había bajado, se retesaban estos tirantes hasta llegar a su carga adecuada para alcanzar la carga objetivo al final de la construcción.

Por otro lado, el fuerte descenso del extremo del tablero en esa fase crítica de izado de dovela llevó a fuertes giros de los anclajes de tirantes respecto la recta de unión entre el anclaje de la torre y del tablero. Ello, de nuevo, obligó a comprobar este giro en las 1.275 fases del proceso, verificando que aunque se estaba por debajo del límite de 30 mrad [16], los giros eran muy importantes y estaban cerca de dicho límite. Esta comprobación no fue inmediata, ya que no solo había que comprobar el giro del nudo del tablero, sino que hubo que sumarle con su signo el giro de la barra del tirante; este valor no lo da el modelo, sino que se calculó en cada fase a partir de los desplazamientos del nudo inicial y final de dicha barra.

También se dimensionó el diámetro de los tubos de encofrado de los tirantes teniendo en cuenta esta capacidad de giro, evitando que el cable tocase con los mismos en estas fases.

5

Cálculo detallado de los estados límites de servicio

5.1

Tablero

El tablero estuvo muy solicitado durante toda la construcción. Las consideraciones que permitieron controlar las máximas tensiones en las chapas metálicas y tracciones en el hormigón fueron:

• •

  El hormigón de las bandas laterales de la losa superior era imprescindible antes de tesar, aunque condicionase el ciclo, ya que las chapas metálicas superiores no eran capaces de resistir la compresión de los tirantes.

• •

  El hormigón de la losa superior se fisuró en una longitud considerable, unos 60,0 m del voladizo. No representaba un problema de cálculo desde el punto de vista de la comprobación ELS del tablero, ya que se está del lado de la seguridad si se calculan las tensiones con propiedades de la sección fisurada, esto es, solo con el acero estructural y pasivo. Para las comprobaciones geométricas se tomó la media entre las propiedades fisuradas y bruta sin fisurar.

• •

  Se comprobó que la apertura de fisura en todas las fases era controlada, máxime considerando la corta duración de la fase pésima. Sin embargo, este cálculo condicionó toda la armadura longitudinal del tablero. Durante la ejecución se midieron las aperturas de fisura reales, comprobando que efectivamente estaban dentro de los límites establecidos.

5.2

Torre

5.2.1

Fuste

En el apartado 4.4.3 se explicó detalladamente el cálculo ELU de la torre durante el avance en voladizo cuasi-simétrico. Sin embargo, de cara al control geométrico se consiguió que la torre no fisurase en ninguna de las fases estándar del proceso, considerando el desequilibrio de pesos sin mayorar y con viento reducido a niveles normales. Además, se verificó que la posible fisuración a torsión de los brazos inclinados de la torre no afecta prácticamente nada a la deformabilidad del puente.

5.2.2

Torsión de las riostras de las torres

Como se ha comentado en el apartado 4.4.2, en el primer tramo de ejecución del tablero, hasta llegar a los primeros tirantes, la limitación estuvo en la resistencia a torsión de la riostra de apoyo del tablero en la torre. El principal problema fue garantizar la no fisuración de dicha riostra por torsión en ELS durante estas fases, para evitar movimientos estructurales no previstos y aparición de fisuras que pudiesen comprometer la «sensación» de seguridad. Por ello, en cada fibra de la sección:

• •

  Fibra superior, con compresión mínima por flexión, tensión de torsión y tensión nula por cortante.

• •

  Fibra media, con compresión media por flexión, tensión de torsión y máxima por cortante.

Se calcularon las máximas tracciones en cualquier dirección en el estado bidireccional del perímetro de la riostra (fig. 9), comprobando que eran menores que la resistencia a tracción media e incluso característica del hormigón de la riostra.

Figura 9.

Comprobación ELS de la riostra de las torres.

Esta comprobación se hizo en todas las fases del proceso de construcción hasta el tesado de las 2 primeras parejas de tirantes, añadiéndoles a todas un viento correspondiente a unos 168 km/h a la altura del tablero (ver apartado 4.2).

6

Conclusiones

• •

  La dovela de 20,0 m de longitud, 34,30 m de ancho y peso hasta 4.000 kN ha sido un gran acierto desde el punto de vista constructivo, ya que permitió la construcción de hasta 2 dovelas por torre en un mes.

• •

  Sin embargo, ha sido un reto muy complejo desde el punto de vista ingenieril, ya que:

  • ∘

    El control geométrico se complicó sobremanera al producirse movimientos muy grandes.

  • ∘

    Fue necesario considerar no linealidades más importantes de lo habitual, tanto geométricas como del material.

  • ∘

    Los medios de izado fueron muy potentes y de diseño complicado.

  • ∘

    Toda la armadura longitudinal de la losa superior quedó condicionada por el proceso de construcción.

  • ∘

    Los desequilibrios a izquierda y derecha del mástil fueron muy grandes, y fue preciso verificar continuamente la sección más débil de la torre.

• •

  Estas dificultades requirieron, tal y como se ha hecho, de un control riguroso y exhaustivo:

  • ∘

    Generando programas específicos de control que permitieron automatizar y acelerar los controles de manera que entorpeciesen lo menos posible la marcha de la obra.

  • ∘

    Comprobando todos los elementos, tanto generales como de detalle, puesto que se dieron multitud de situaciones muy diferentes a las situaciones estándar que se puedan dar en otros puentes más convencionales.

• •

  Ha sido necesario un esfuerzo para definir unas bases de cálculo que tuvieran en cuenta todas las particularidades de una construcción de este tipo.

• •

  Fueron necesarios elementos de control y ajuste constante; en este caso han sido sobre todo los tirantes, aunque se han utilizado contrapesos en algunas situaciones constructivas.

• •

  Respecto a los tirantes:

  • ∘

    Se produjeron giros relativos muy importantes entre el anclaje y la recta de unión entre el anclaje de la torre y del tablero; lo cual requirió su comprobación en todas las fases del proceso.

  • ∘

    Respecto a la fase de tesado de la pareja frontal, fueron necesarias al menos unas franjas de hormigón en las bandas para resistir la compresión horizontal de la carga. Además, cuando se tesaban esos tirantes se relajaba la situación de todos los elementos.

• •

  Durante la fase de izado de dovela hubo que tener en cuenta:

  • ∘

    Cargas locales muy elevadas.

  • ∘

    Deformaciones fuertes del frente de dovela a soldar.

• •

  Tracciones en la losa superior elevadas, con 60,0 m fisurados desde el frente de la dovela hacia la torre, condicionando toda la armadura longitudinal de la losa por proceso. Se consideraron las propiedades medias entre la inercia fisurada y la no fisurada para cálculo de la deformada y las propiedades fisuradas para cálculo de tensiones.