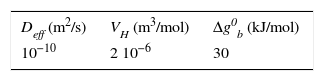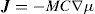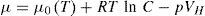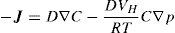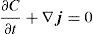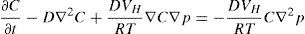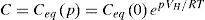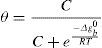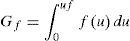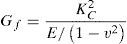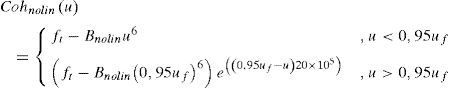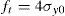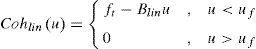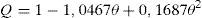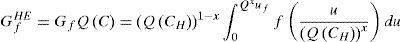La durabilidad de los aceros de alta resistencia en medios agresivos está condicionada por la fragilización por hidrógeno. La fragilización por hidrógeno está presente en muchos de los fallos de estructuras o componentes de acero. En estudios anteriores se ha mostrado el efecto del hidrógeno intersticial dentro de la red de hierro a nivel atómico, y se concluía que el hidrógeno no establece enlace químico con el hierro pero introduce tensiones internas que debilitan los enlaces hierro-hierro y disminuyen la tenacidad de fractura. En el presente trabajo se ha simulado la propagación de una fisura en una matriz de hierro en presencia de hidrógeno. Se han acoplado factores como el transporte de hidrógeno, los gradientes de tensiones y la variación de la tenacidad de fractura en un modelo multifísico de elementos finitos. El comportamiento en fractura se ha simulado mediante dos leyes cohesivas, una lineal y otra polinómica. Los resultados muestran que existe una influencia de la ley cohesiva sobre la propia velocidad de propagación de la fisura y el perfil de concentración de hidrógeno.
The durability of high strength steels in aggressive media is determined by the presence of hydrogen, in particular hydrogen embrittlement processes. Hydrogen embrittlement is present in many of the failures of structures made with steel components. The effect of interstitial hydrogen within the network of iron has been investigated in previous studies at the atomic level. It is concluded that the main role of hydrogen is not to establish chemical bonds with iron atoms, but to introduce internal stresses that weaken the interactions between iron atoms and decrease fracture toughness. In this work, the spread of a crack has been stimulated inside a matrix of iron in the presence of hydrogen. Hydrogen transport, stress distributions, and the evolution of fracture toughness were analysed together in a multi-physics finite element model. The behaviour in the fracture was simulated using two different models for the cohesive law, one lineal and the other polynomial. Results show that the choice for the cohesive law influences the crack propagation rate and the hydrogen concentration profiles.
La fragilización por hidrógeno (FH) es una de las principales causas de fallo en los componentes metálicos expuestos a ambientes agresivos y puede estar asociada a otros tipos de degradación, como es la corrosión o la corrosión bajo tensión [1–3]. Desde el punto de vista teórico, existen diversas aproximaciones al fenómeno de la FH que pueden reproducir en mayor o menor medida el comportamiento de los diferentes metales o aleaciones frente a la FH [4–15]. En el caso del acero ferrítico se ha demostrado que el hidrógeno no establece enlace con los átomos de Fe [16], siendo su papel principal introducir tensiones/distorsiones en la red bcc del hierro (α-Fe) que condicionan el camino de difusión del hidrógeno intersticial [17,18] y debilitan el enlace Fe-Fe [9], o lo que es lo mismo, reduce la energía de fractura del acero [4,6,19,20].
Centrándonos en el caso del acero, existe una amplia bibliografía dedicada al fenómeno de difusión en función del medio y considerando las diferentes trampas existentes y su desorción [21,22], y también el comportamiento mecánico y la reducción en la tenacidad de fractura [2,8,23]. Por otra parte, desde la mecánica de fractura se ha abordado el problema del crecimiento de las fisuras desde diferentes puntos de vista, siendo uno de los más utilizados el modelo de fisura cohesiva cuando se trata de estudiar el crecimiento de una fisura discreta [24–26]. Algunos autores han aplicado esta metodología para el caso de la FH en aceros [10].
El objetivo de este artículo es desarrollar un método de cálculo que permita estimar la velocidad de propagación de la fisura comparando dos curvas de ablandamiento distintas para el caso de un acero ferrítico: una curva lineal [10] y otra tipo escalón de Heaviside (aproximada por un polinomio de grado 6) [27].
2MetodologíaA continuación se presenta la metodología adoptada para simular la propagación de una fisura por FH teniendo en cuenta: a)el transporte de hidrógeno hacia la zona en proceso de fractura donde existe un gradiente de tensiones; b)la generación de hidrógeno en la superficie de la fisura, y por último c)se ha aplicado un modelo de fisura cohesivo que incluye una penalización por la presencia de hidrógeno.
2.1Difusión de hidrógeno en el aceroEn este trabajo se ha considerado únicamente el hidrógeno intersticial presente en la red de hierro, no teniéndose en cuenta el hidrógeno que se encuentra en defectos o en trampas. La base teórica sobre el transporte de hidrógeno en los metales se encuentra ampliamente desarrollada en la literatura [12,13], por lo que solo se mostrarán las ecuaciones básicas. Se parte de la hipótesis de que el flujo de hidrógeno viene definido por el gradiente del potencial químico según la ley de Fick [4]:
donde J es el flujo de hidrógeno, M se corresponde con la movilidad del propio gas, C es la concentración y μ es el potencial químico.El proceso de difusión está relacionado con la tensión a través de la presión hidrostática p=Trσ/3, que a su vez forma parte de la ecuación del potencial químico del hidrógeno [4]:
donde T es la temperatura, R=8.314J/(molK), K es la constante universal de los gases, VH es el volumen molar parcial del hidrógeno y C es la concentración. El coeficiente de difusión viene definido por D=M R T. A partir de las ecuaciones 1 y 2 se obtiene:
A continuación se añade la ecuación de continuidad:
Y finalmente, combinando las ecuaciones 3 y 4, obtenemos la ecuación de difusión que rige este proceso:
2.2Generación de hidrógeno en la superficie de la fisuraLas condiciones de contorno aplicadas en este modelo se basan en la adsorción de hidrógeno en equilibrio con el medio y que a su vez depende de las tensiones mecánicas [10]. Esta condición de contorno se aplica sobre la superficie de la fisura:
donde Ceq(p) es la concentración en equilibrio en la superficie de la fisura a la presión hidrostática correspondiente a 1/3 de la traza del tensor de tensiones, p, y Ceq(0) corresponde con la concentración en equilibrio a la presión hidrostática de valor cero [10].Mediante la ecuación de Langmuir podemos relacionar la adsorción de hidrógeno sobre la superficie de acero con la concentración en equilibrio sobre dicha superficie metálica (temperatura constante):
En esta ecuación se define Δg0b como la diferencia de energía para el hidrógeno sobre la superficie de la fisura y para el hidrógeno dentro de la red de hierro.
2.3Descripción de las leyes cohesivas en presencia de hidrógenoLas técnicas de la mecánica de fractura ofrecen diversas formas para abordar el problema de la propagación de fisuras en los materiales. Una de ellas es la aplicación de la ley cohesiva, en la que se establece que la separación entre dos planos del material (u) está relacionada con la tensión (f) a través de una ecuación o ley, de tal forma que el área que encierra la curva f-u está relacionada con la energía de fractura (Gf):
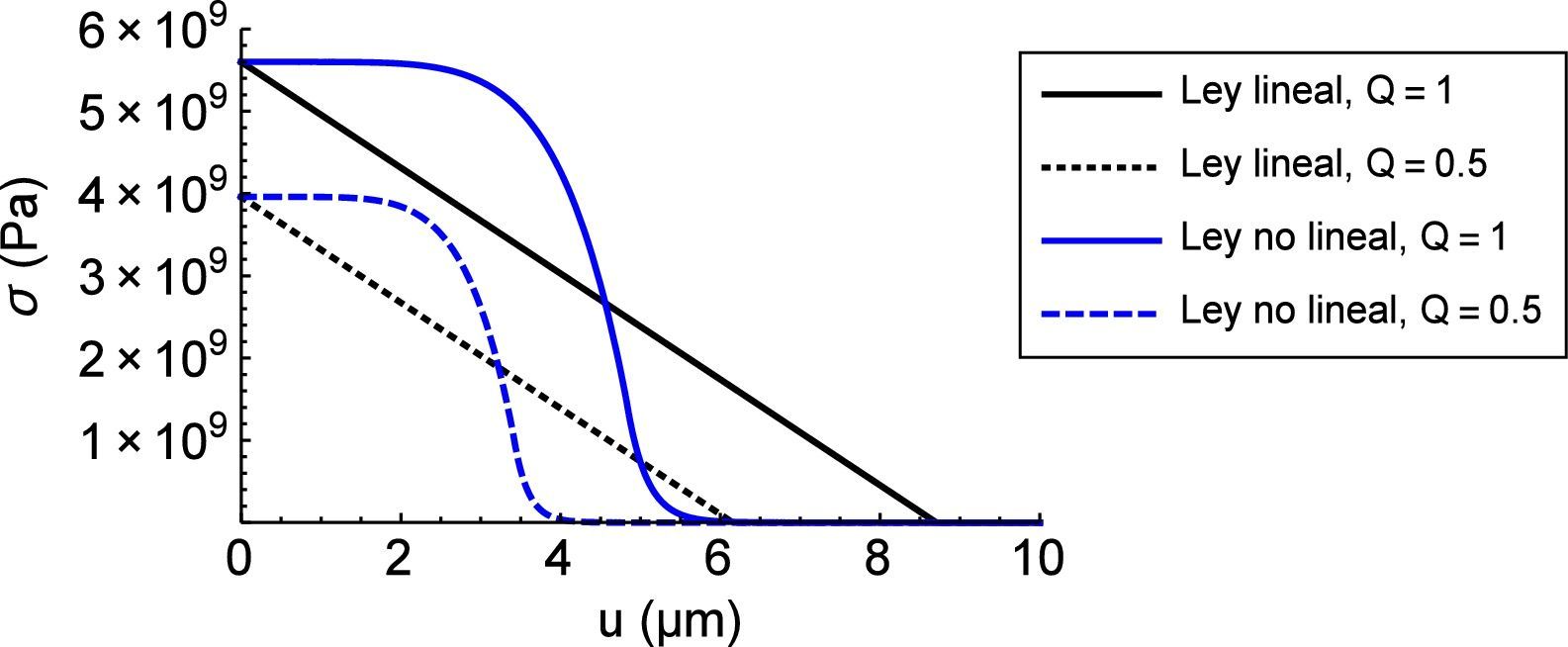
donde uf es la separación crítica a partir de la cual se considera que el material se encuentra completamente descohesionado y ya no transfiere carga. Por otra parte, de acuerdo con la ecuación de Irwin [28], se puede establecer una relación entre la energía de fractura y la tenacidad de fractura, que para el caso de deformación plana es:El comportamiento en fractura se ha simulado mediante dos leyes cohesivas diferentes, f(u): a) una función escalón de Heaviside que describe una transición abrupta, y b)una ley cohesiva lineal que representa una transición gradual. La primera (Cohnolin(u)) está relacionada con la propuesta por Elices et al. [27]. Como aproximación a dicha ley se ha empleado un polinomio de grado 6 y la parte final se ha ajustado con una exponencial para facilitar la convergencia del programa de elementos finitos.
donde Bnolin=ft/uf6 y ft es la tensión inicial cuando u=0, equivalente a la resistencia a tracción del material. Diversos autores proponen que este valor es aproximadamente 4 veces el límite elástico, σy0[10]. En el presente estudio se ha decidido mantener este criterio para poder facilitar la comparación con los resultados de la literatura, aunque puede dar lugar a valores de ft poco realistas. Si se pretende adaptar el modelo a un material de interés en particular, el valor de ft se debería determinar experimentalmente.
La segunda ley cohesiva que se va a utilizar está relacionada con los estudios de Serebrinsky et al. [10] (Cohlin(u)). Esta ley se caracteriza por tener un comportamiento lineal, que responde a las siguientes ecuaciones:
donde Blin=ft/uf.Experimentalmente se ha observado que la tenacidad de fractura en el acero disminuye en presencia de hidrógeno [29]. Cálculos ab initio realizados por Jiang y Carter [19] proponen la siguiente ecuación que relaciona el factor de reducción de la energía de fractura (Q) con el recubrimiento de hidrógeno (θ):
Por lo tanto, en el estudio por elementos finitos del proceso de FH es necesario actualizar la energía de fractura, GfHE, en función de la concentración de hidrógeno, C. Una opción es aplicar el factor Q directamente sobre la energía de fractura, lo cual supone una reducción en la tensión inicial de la curva de ablandamiento ft. Al hacerlo de esta forma no se penaliza la separación crítica uf, únicamente la tensión máxima ft. A escala microestructural, la FH se caracteriza por la aparición de facetas de clivaje, que conllevan una rotura del material con menos deformación que la que le correspondería por una rotura dúctil. Para lograr este efecto, se propone la siguiente ecuación, donde, a través de un cambio de variables, se modifica la ley cohesiva disminuyendo tanto ft como uf en función de la concentración de hidrógeno C:
donde el parámetro x es una constante entre 0 y 1. Las simulaciones se han realizado para x=0,4.
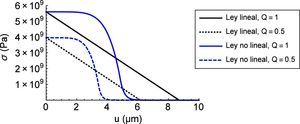
En la figura 1 se muestran las leyes cohesivas empleadas en el estudio para: a)el caso de que no haya hidrógeno (Q=1), y b)el caso en que el hidrógeno actúe reduciendo la energía de fractura por un factor Q=0,5.
3Resultados numéricosA continuación se muestran los resultados obtenidos en las simulaciones de elementos finitos donde se muestra el efecto del gradiente de tensiones sobre la difusión del hidrógeno dentro del acero y el cálculo de la propagación de la fisura debida a la FH.
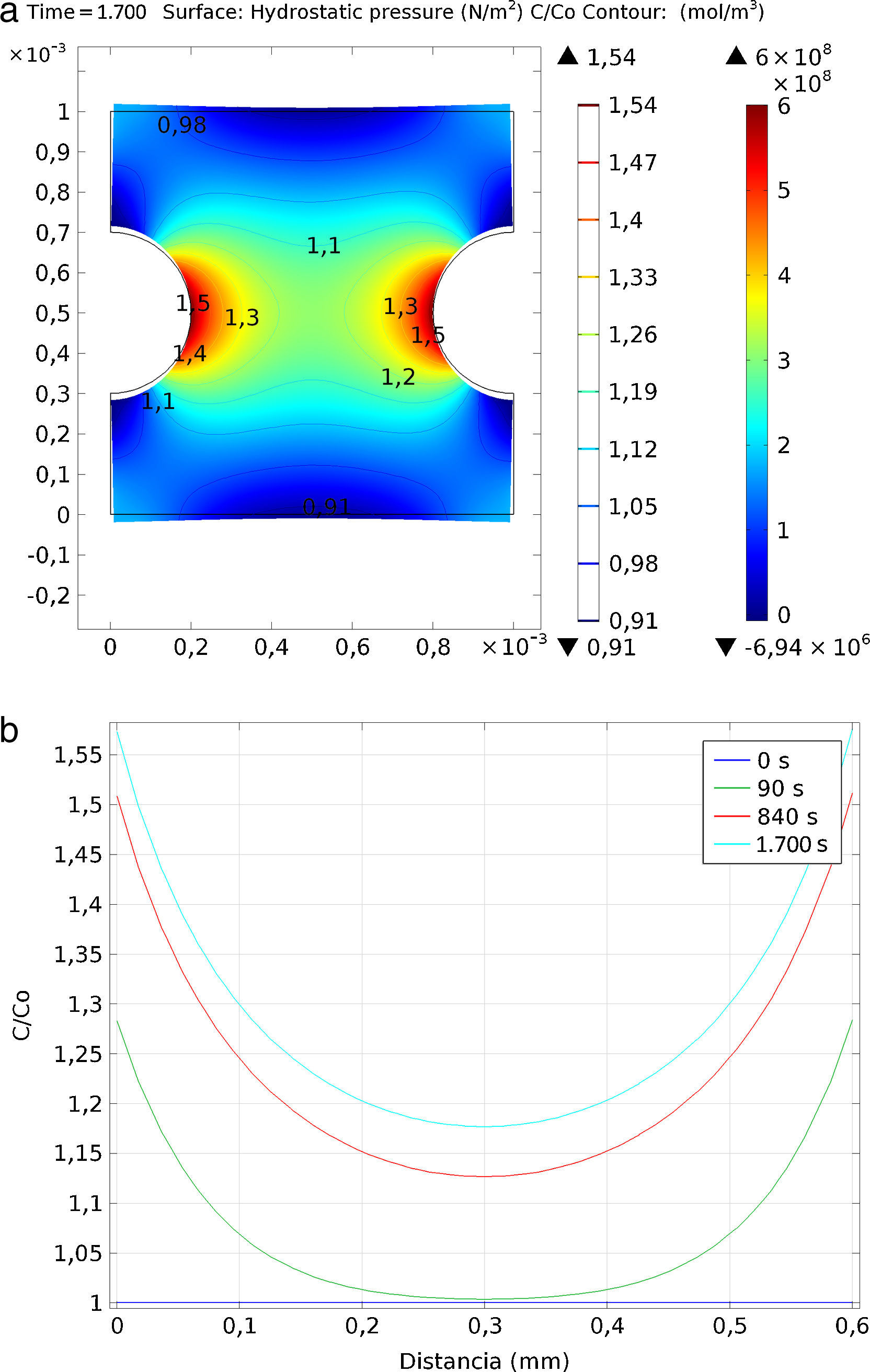
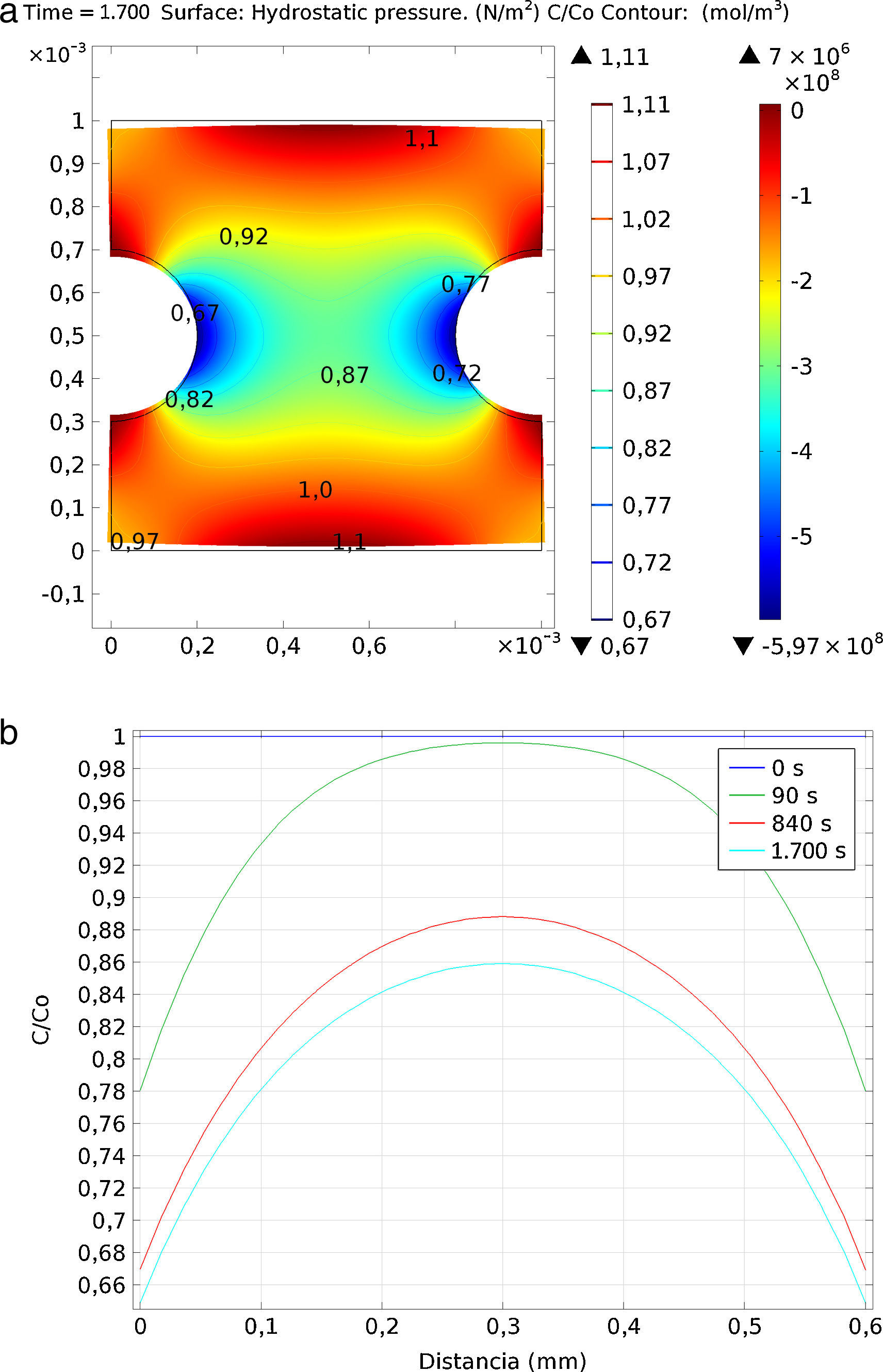
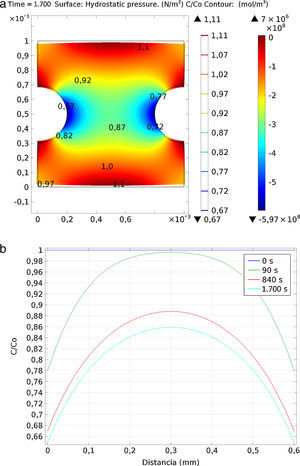
3.1Análisis del efecto del gradiente de tensiones sobre la concentración de hidrógenoEn primer lugar se muestra la variación de la concentración por efecto de las tensiones mecánicas, considerando únicamente el comportamiento elástico-lineal del material. Se ha simulado una placa de dimensiones 1×1mm2 y dos entallas circulares simétricas en la parte central de 0,2mm de radio. Los cálculos se realizaron para dos escenarios distintos, uno de tracción y otro de compresión, a una tensión remota constante de 400MPa.
Respecto al transporte de hidrógeno, se parte de una concentración constante inicial de C0=10−5mol/m3, sin aporte adicional de hidrógeno, y se define el transporte de hidrógeno según la ecuación (5). Se ha empleado un coeficiente de difusión de 10−10 m2/s, dado experimentalmente por diversos autores [10,21] y que, según los cálculos ab initio realizados, se corresponde para unas condiciones de concentración de hidrógeno relativamente alta [17].
Para la resolución mediante el programa COMSOL Multiphysics se ha optado por un solver directo (SPOOLES), con una tolerancia relativa de 10−5, un paso temporal de 10s y un rango de tiempo de 1.700s. La malla se ha realizado con elementos triangulares, empleándose más de 6.500 para estas simulaciones.
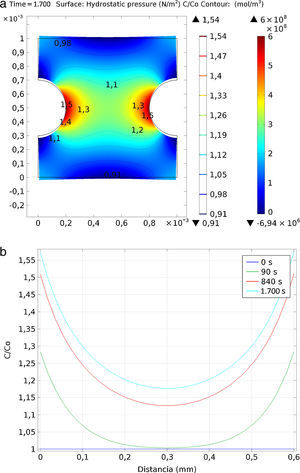
Las figuras 2 y 3 muestran la entalla deformada por la acción del campo de tensiones (presión hidrostática) junto con las líneas de isoconcentración. Los resultados demuestran que existe una acumulación de hidrógeno en las zonas bajo tracción, mientras que en las zonas comprimidas la concentración de hidrógeno disminuye. En el caso del modelo sometido a tracción la máxima tensión se produce en las proximidades de la entalla, alcanzando un valor de tensión de Von Mises de 1.350MPa o una presión hidrostática de 600MPa. En este punto, a los 1.700s se llega a alcanzar una concentración de C/C0=1,57. En la figura 2 b) se muestra la evolución de la concentración de hidrógeno, C/C0, en el ligamento entre las entallas para los tiempos 0, 90, 840 y 1.700s. La concentración aumenta en los primeros momentos y luego tiende a estabilizarse, tanto en el centro como en las zonas más traccionadas.
En la figura 3 se muestra el mismo comportamiento, pero en este caso cuando la muestra se encuentra sometida a esfuerzos de compresión. En el punto de mayor tensión de compresión se produce una migración del hidrógeno que, para el tiempo de 1.700s, es de C/C0=0,65. En el ligamento que une las dos entallas se produce una pérdida de hidrógeno, que es mayor en la zona más próxima a la entalla.
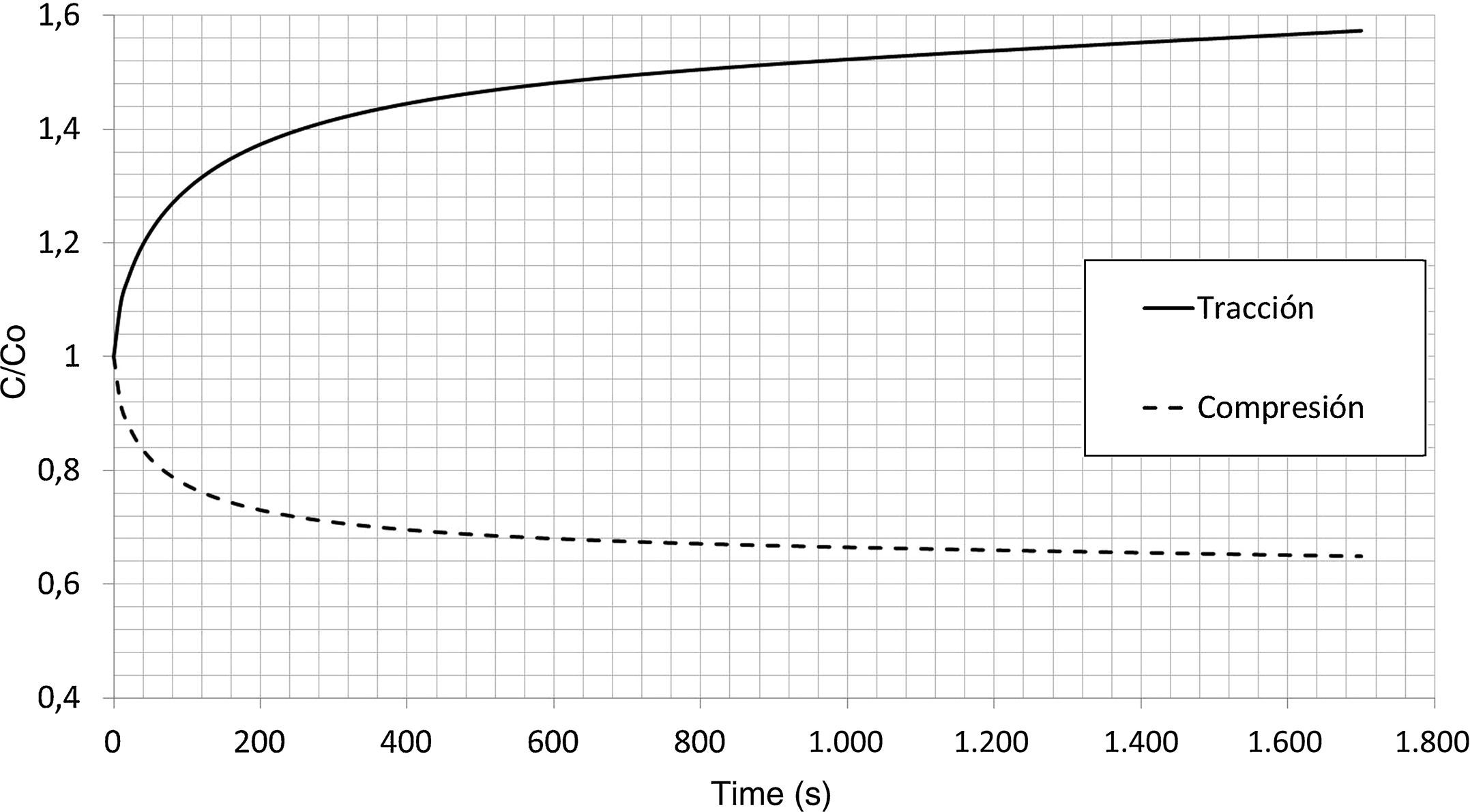
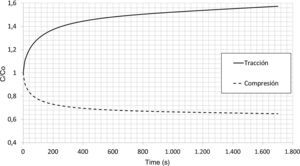
En la figura 4 se muestra la evolución de la concentración de hidrógeno, C/C0, con el tiempo en el punto de mayor tensión de Von Mises. En el caso de la simulación bajo tensión se produce una acumulación de hidrógeno, mientras que cuando se encuentra sometida a compresión, se produce una disminución en la concentración. Para el tiempo de simulación que se ha considerado, se puede observar que el efecto de las tensiones mecánicas influye sobre el transporte de hidrógeno de forma no despreciable, y que es necesario tenerlas en cuenta para simular la propagación de las fisuras por FH.
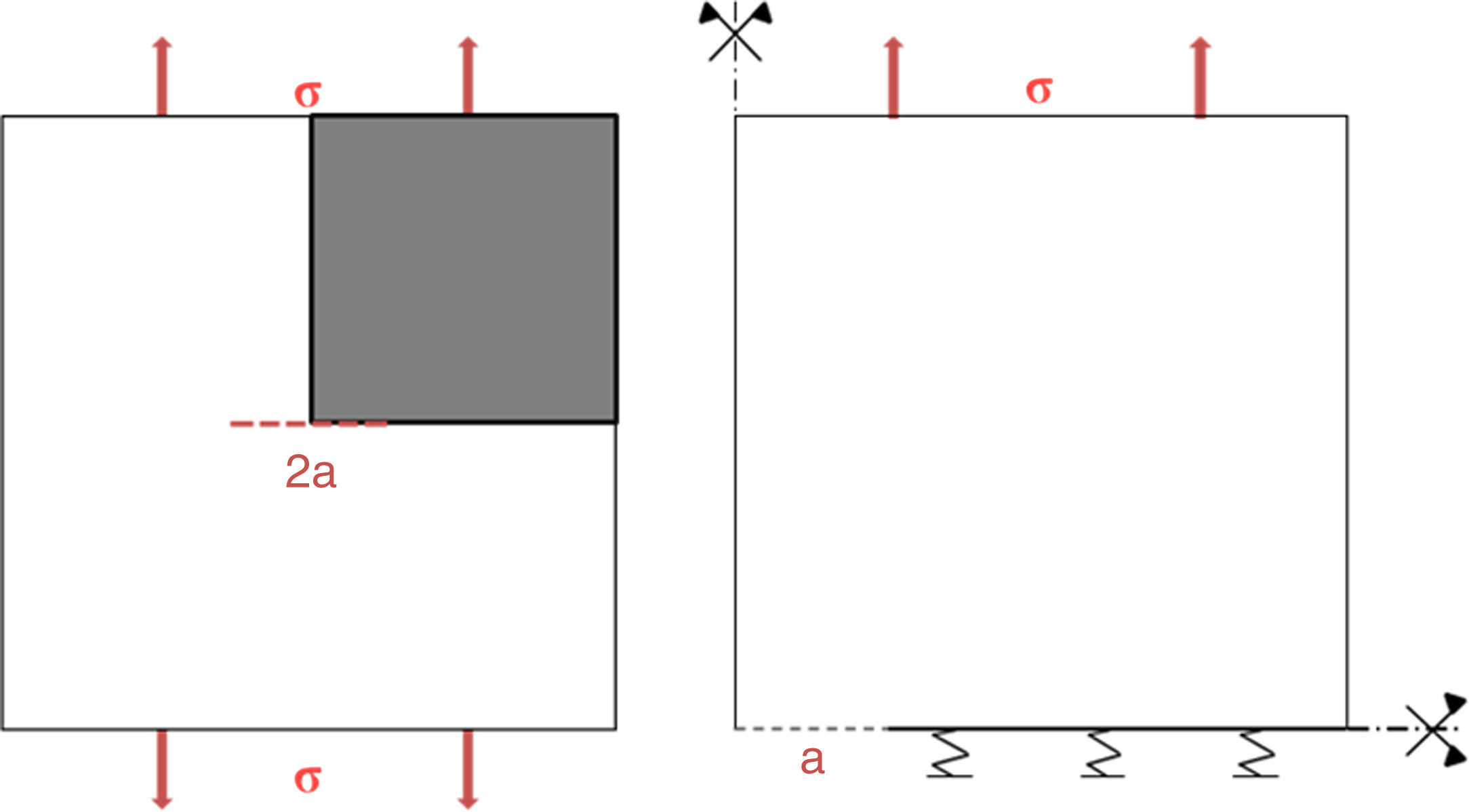
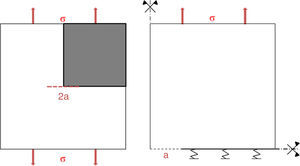
3.2Cálculo de la velocidad de propagación de fisura por fragilización por hidrógenoPara las simulaciones de la propagación de la fisura por FH se ha considerado una placa de acero de 20×20mm2 con una prefisura, 2a=0,8mm. Tanto la parte superior como la inferior están sometidas a una carga distribuida en toda su longitud (fig. 5). Existen dos planos de simetría perpendiculares al eje vertical y horizontal que atraviesan la probeta por su centro, que permite simplificar el cálculo a ¼ de la probeta. Se ha considerado que el camino de propagación de la fisura coincide con el eje x. En este eje se ha introducido la ley cohesiva correspondiente a una condición de contorno tipo muelle no lineal, donde se ha tenido en cuenta el desplazamiento, 2u, como apertura de la fisura en la ley cohesiva.
La tensión remota aplicada (σ) es de 1.400MPa. La concentración inicial de hidrógeno es nula, y se ha considerado que la entrada de hidrógeno se produce en la superficie de la fisura según la ecuación 2. En las tablas 1 y 2 se muestran las constantes mecánicas y de transporte de hidrógeno en el acero.
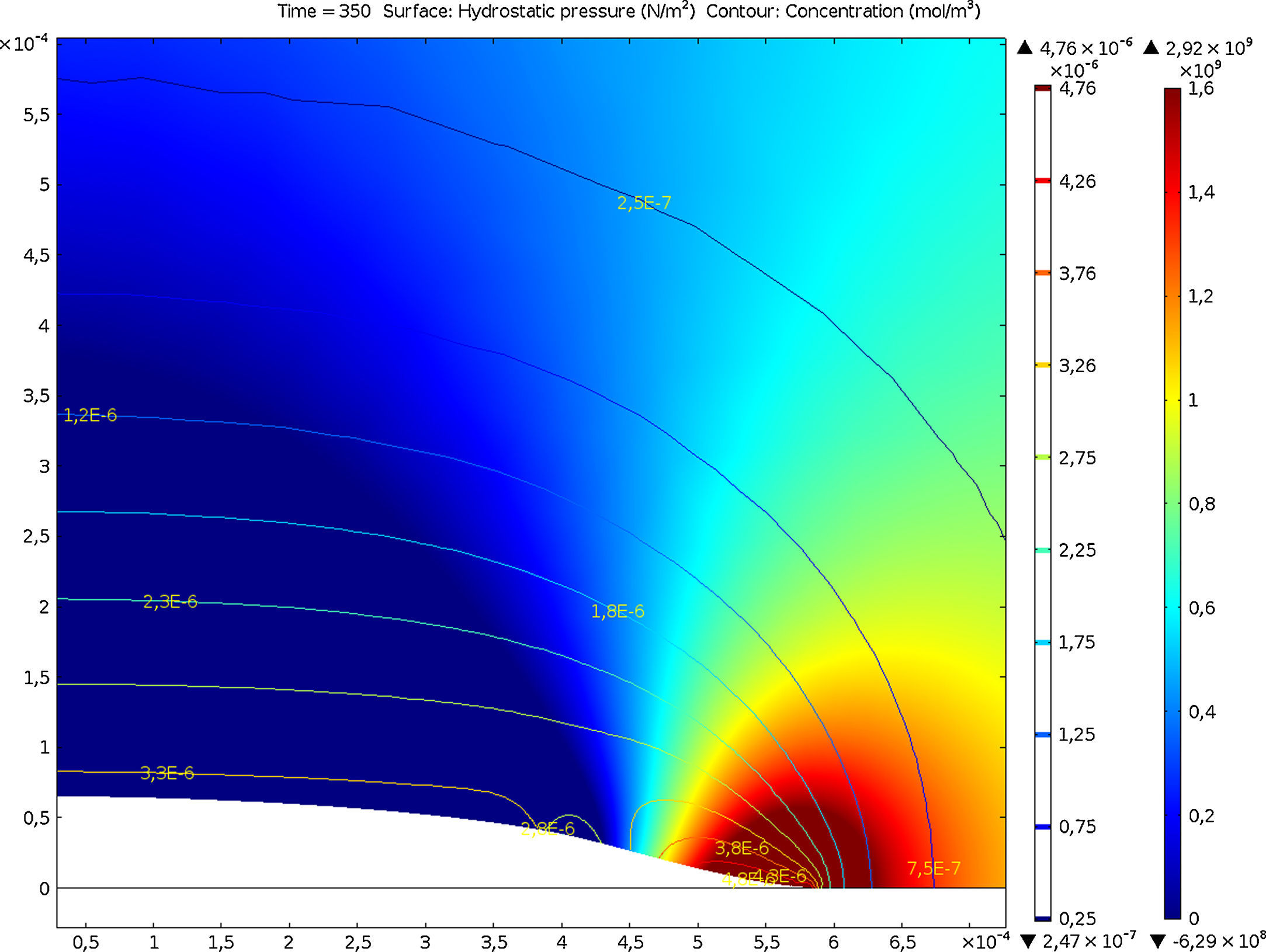
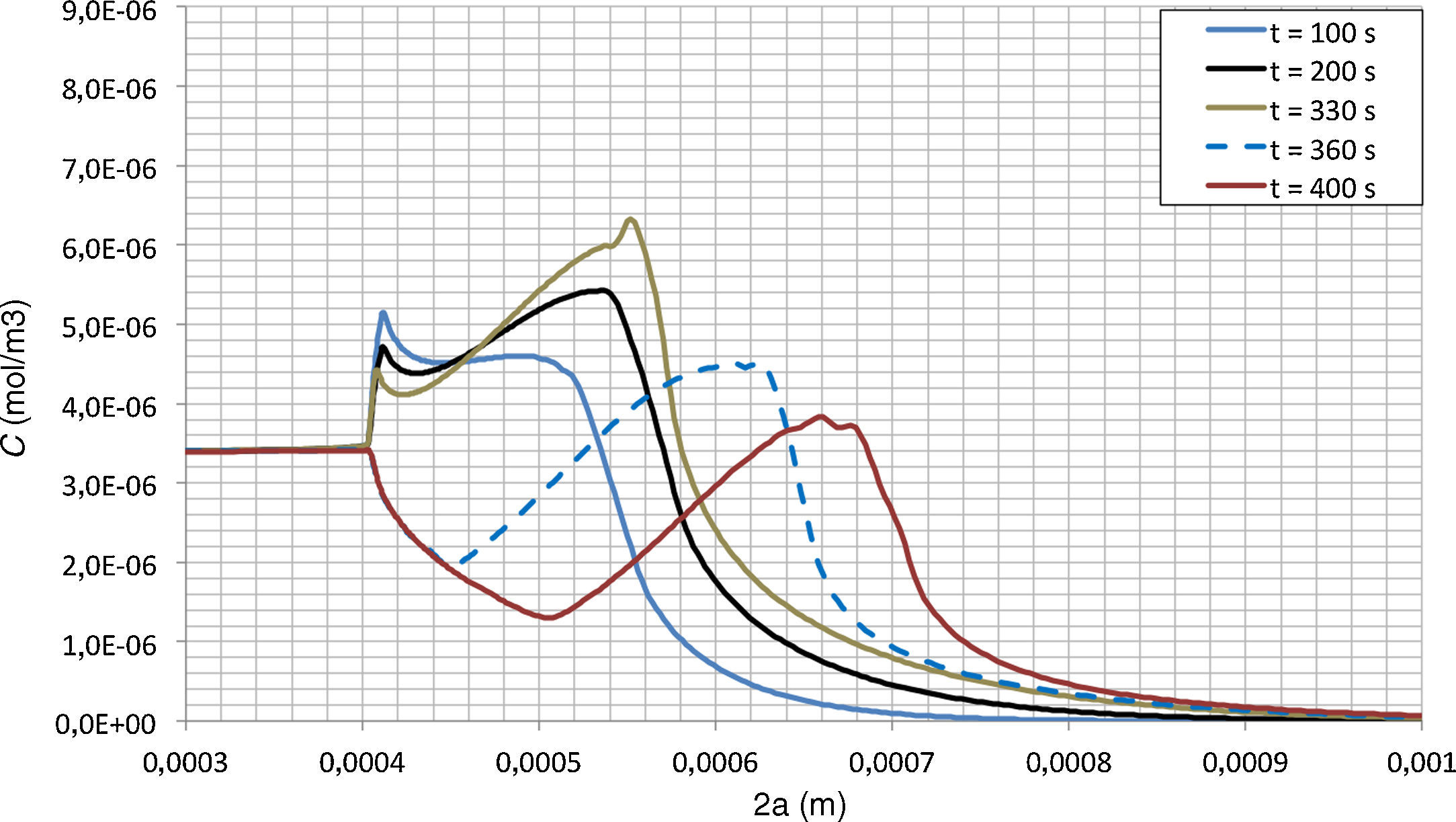
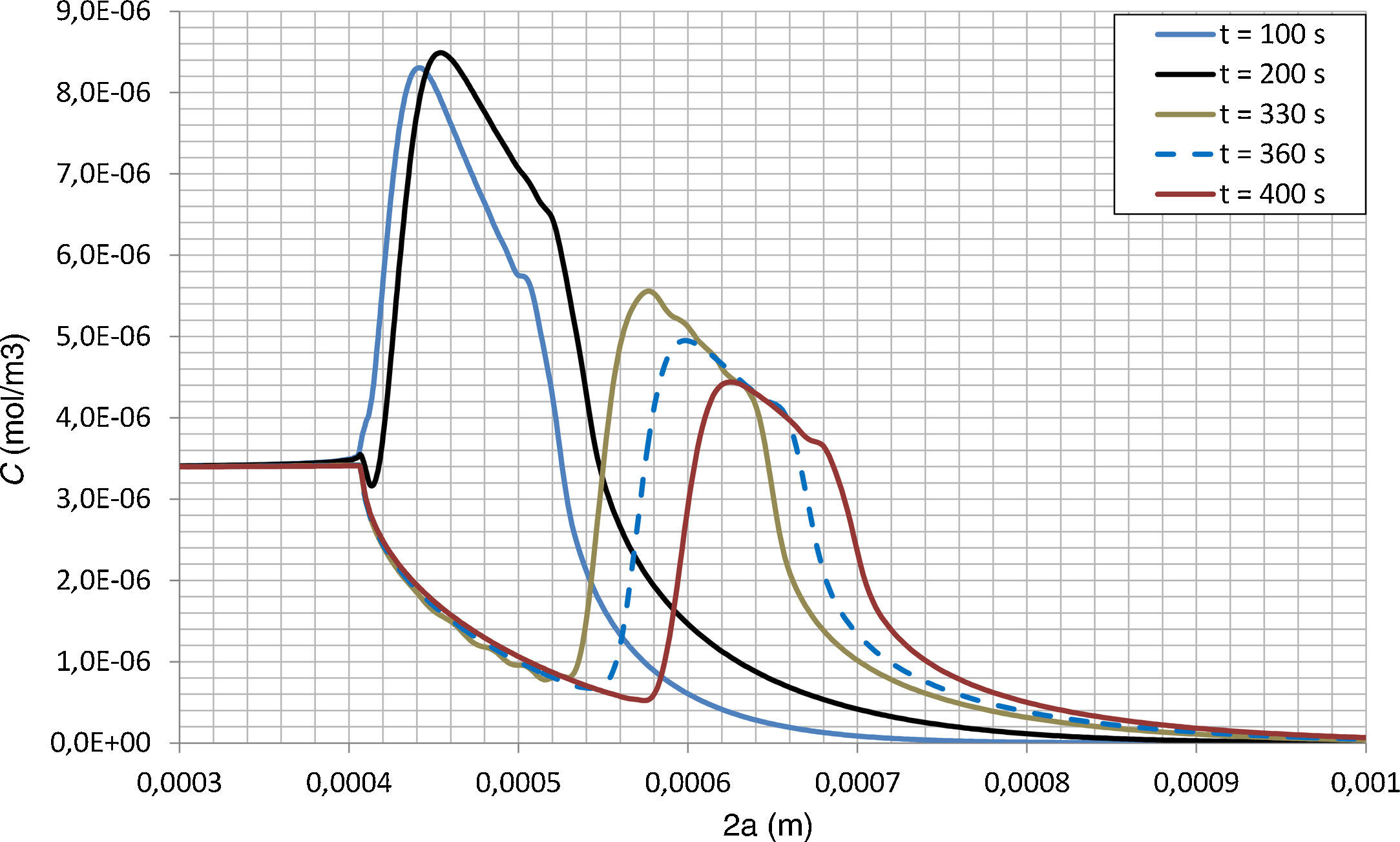
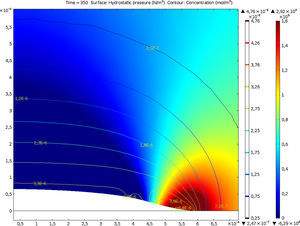
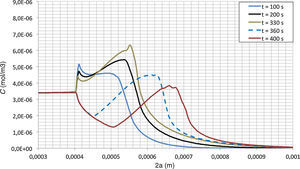
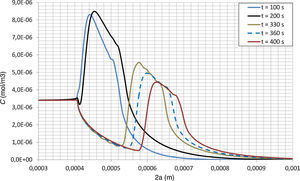
En la figura 6 se muestra el resultado de la simulación para el caso de la ley cohesiva lineal y para un tiempo de 350s. En esta figura se puede observar que la fisura ya ha comenzado a propagarse; se partía de una fisura de 4×10−4m. También se observa que se produce una acumulación de hidrógeno en la zona en proceso de fractura. En las figuras 7 y 8 se muestra la concentración de hidrógeno en el frente de la fisura para diferentes tiempos. Independientemente de la ley cohesiva aplicada, se produce un máximo de la concentración de hidrógeno en el frente de la fisura, que se va desplazando a medida que se produce la propagación de la misma. De forma cualitativa, se observa que la concentración máxima de hidrógeno es más puntual para el caso de la ley lineal (fig. 7), mientras que para el caso de la ley no-lineal se produce una acumulación más distribuida (fig. 8).
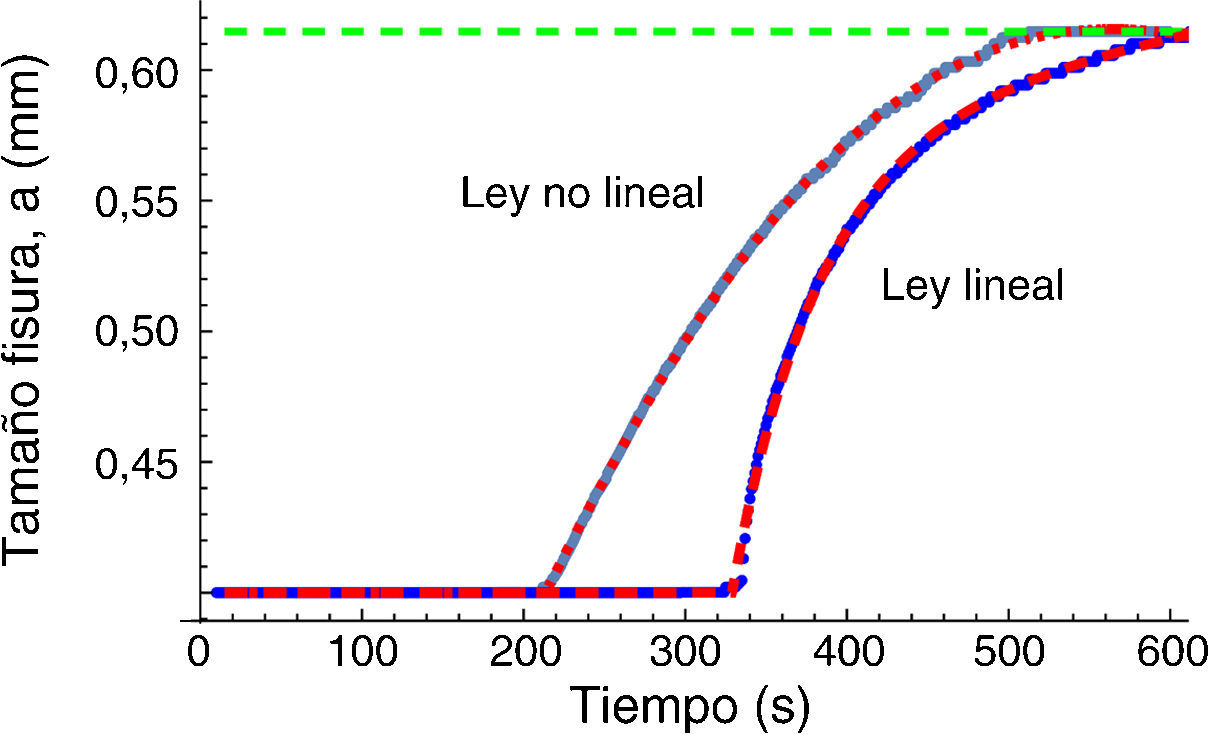
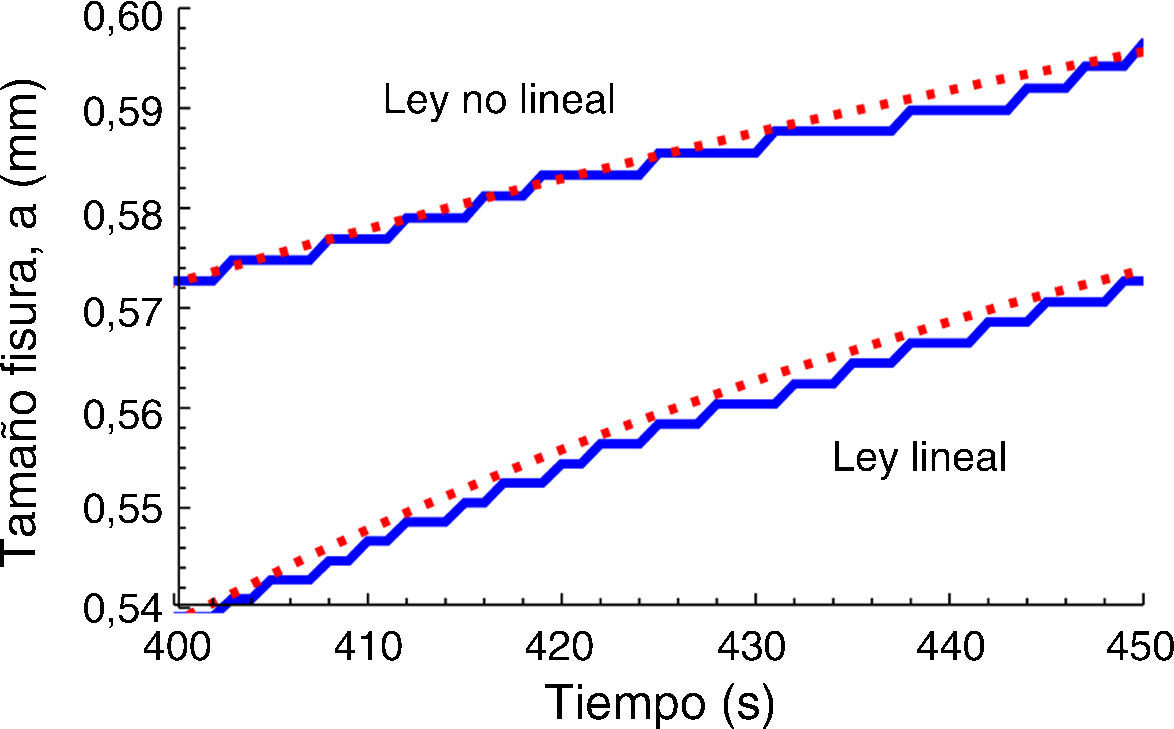
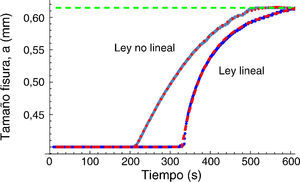
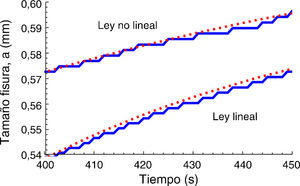
Para analizar la posición del frente de la fisura se ha considerado la posición del punto que alcanza la separación crítica uf. En la figura 9 se muestra la posición del frente de la fisura para ambas leyes cohesivas. En el caso de una ley no-lineal, el comienzo de la propagación se produce para un tiempo inferior, 200s, frente a más de 330s para el caso de la ley lineal. Sin embargo, a los 600s alcanzan el mismo valor en la posición del frente de la fisura. En ambos casos la propagación de la fisura tiene lugar de forma discontinua, con saltos de aproximadamente 2μm (fig. 10). Para el tratamiento de datos se han ajustado las curvas a una función exponencial.
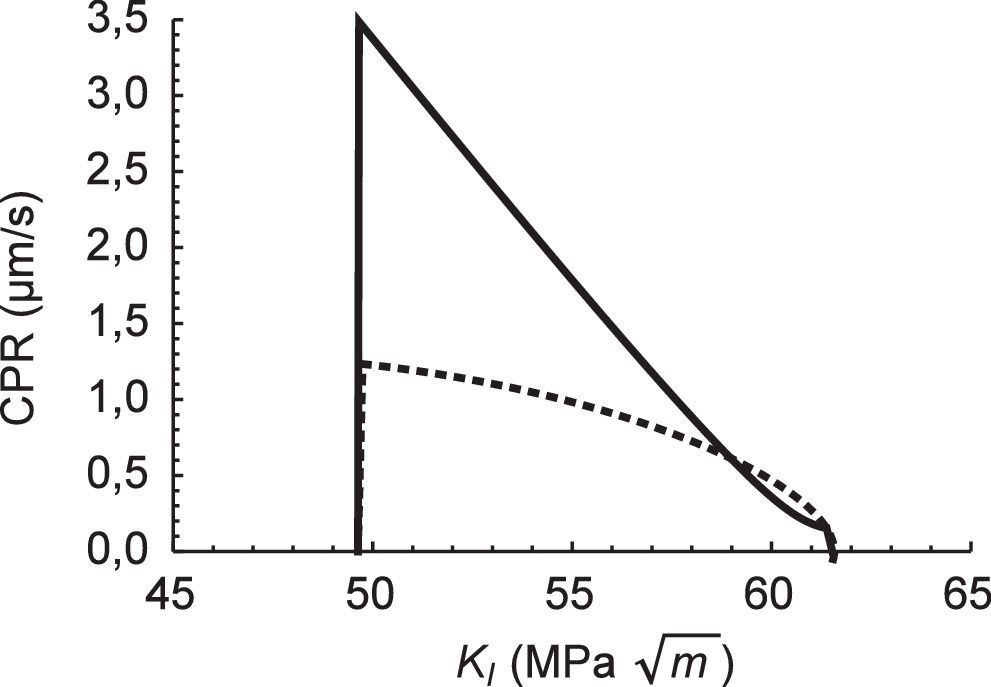
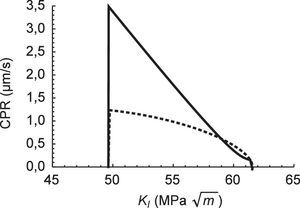
Derivando las curvas anteriores se obtiene la velocidad de propagación de la fisura (Crack Propagation Rate [CPR]). En la figura 11 se muestran los valores de CPR en función del factor de intensidad de tensiones, KI, para ambas leyes cohesivas, obteniéndose valores ligeramente superiores en el caso de la ley lineal. Para estas condiciones de simulación se produce la parada de la fisura. Al aumentar el tamaño de la fisura, a, se produce una mayor concentración de hidrógeno en la sección resistente, no solo en el frente de la fisura. Como consecuencia de un aumento de la concentración de hidrógeno en la zona en proceso de fractura se produce una disminución de la tenacidad de fractura que induce la fractura frágil del componente, que por ser inestable ya no puede ser capturada por la simulación.
4ConclusionesSe ha observado que la velocidad de propagación de la fisura depende de la ley cohesiva empleada. La ley cohesiva influye sobre la distribución de tensiones en el frente de la fisura, y este a su vez modifica la concentración de hidrógeno. De esta forma, la ley cohesiva lineal produce una concentración de tensiones en una región más localizada que la ley no lineal. Del mismo modo, la concentración de hidrógeno en el caso de la ley lineal produce un aumento de la concentración de forma puntual, mientras que en el caso de la ley no lineal se produce una mayor acumulación de hidrógeno en el frente de la fisura.
La ley cohesiva también influye sobre el tiempo de iniciación hasta que se produce la propagación de la fisura. La mayor acumulación de hidrógeno para la ley no lineal produce una mayor reducción de la tenacidad de fractura y, por lo tanto, el inicio más temprano de la propagación de la fisura.
En ambos casos se capta la propagación discontinua de la fisura con saltos aproximadamente de 2μm, lo cual coincide con resultados experimentales [4,10].
Para las condiciones de simulación introducidas se produce una parada de la fisura al crecer el tamaño de la misma hasta que se produce la ruptura frágil del elemento simulado. Este resultado se explica por la acumulación de hidrógeno en el ligamento resistente que compite con la propagación de la fisura debida a la concentración de hidrógeno de forma local en el frente de la fisura.
FinanciaciónLos autores desean agradecer al Ministerio de Ciencia e Innovación por la financiación recibida en el proyecto BIA2013-47892-P.