El hormigón reforzado con fibras metálicas (SFRC por sus siglas en inglés) ha mostrado su eficacia mejorando las propiedades del hormigón. Una aplicación interesante de dicho material es en las estructuras sometidas a impactos. Con el objetivo de caracterizar las propiedades dinámicas del SFRC se ha llevado a cabo una campaña experimental con una máquina de impactos instalada recientemente en el Laboratorio de Estructuras de la Universidad Politécnica de Madrid. Las probetas ensayadas, reforzadas con distintos tipos de fibras metálicas en diferentes dosificaciones, muestran que las mezclas de SFRC presentan mejores propiedades dinámicas y una sensibilidad a la velocidad de carga diferente que el hormigón convencional.
Steel-fibre-reinforced concrete (SFRC) has demonstrated its effectiveness in improving concrete properties. An interesting application of this material may be for structures subject to impact loads. An experimental camping was conducted in order to determine the dynamic properties of SFRC, with a drop weight testing machine recently installed in the UPM Structures Laboratory. The tested specimens, reinforced with different types of steel fibres and fibre content, showed that SFRC mixes have improved mechanical properties and a strain-rate sensitivity different than that of plain concrete.
Las cargas accidentales causadas por catástrofes naturales o por acciones humanas, deliberadas o no, están captando una atención especial, aumentado la concienciación sobre la necesidad de incrementar la seguridad estructural en dichas situaciones. Entre estas cargas pueden resultar especialmente dañinos los impactos de cuerpos rígidos a velocidades moderadas. Estas acciones dinámicas de naturaleza impulsiva están caracterizadas por cargas máximas elevadas, velocidades de deformación considerables y grandes cantidades de energía liberada. Las estructuras de hormigón son especialmente sensibles a estas acciones dinámicas, frente a las que presentan una tendencia a desarrollar una rotura de tipo frágil, por cortante o punzonamiento [1,2]. Un modo interesante de mejorar la resistencia a impacto de las estructuras de hormigón es aumentar su capacidad de absorción de energía mediante la adición de fibras. Sin embargo el comportamiento dinámico del hormigón reforzado con fibras (fibre-reinforced concrete [FRC]) no está bien definido, siendo necesaria una adecuada caracterización para poder utilizarla debidamente a nivel estructural. La investigación experimental es fundamental de cara a dicha caracterización.
La investigación presentada en este artículo trata sobre el comportamiento a impacto del hormigón reforzado con fibras de acero (steel-fibre-reinforced concrete [SFRC]). Se ha realizado una campaña experimental en probetas prismáticas sin entallar, comprendiendo dos tipos de fibras (recta y con anclajes), dos dosificaciones volumétricas (0,5 y 1%) y una serie complementaria de probetas de hormigón en masa convencional (HM) como referencia. Las probetas se ensayaron bajo condiciones cuasi-estáticas y de impacto. Para estos últimos ensayos se ha utilizado una máquina de impactos bien instrumentada, instalada recientemente en el Laboratorio de Estructuras de la Universidad Politécnica de Madrid (UPM). Este estudio forma parte de una campaña experimental más amplia. Los resultados de esta investigación completan los de otro estudio previo [3].
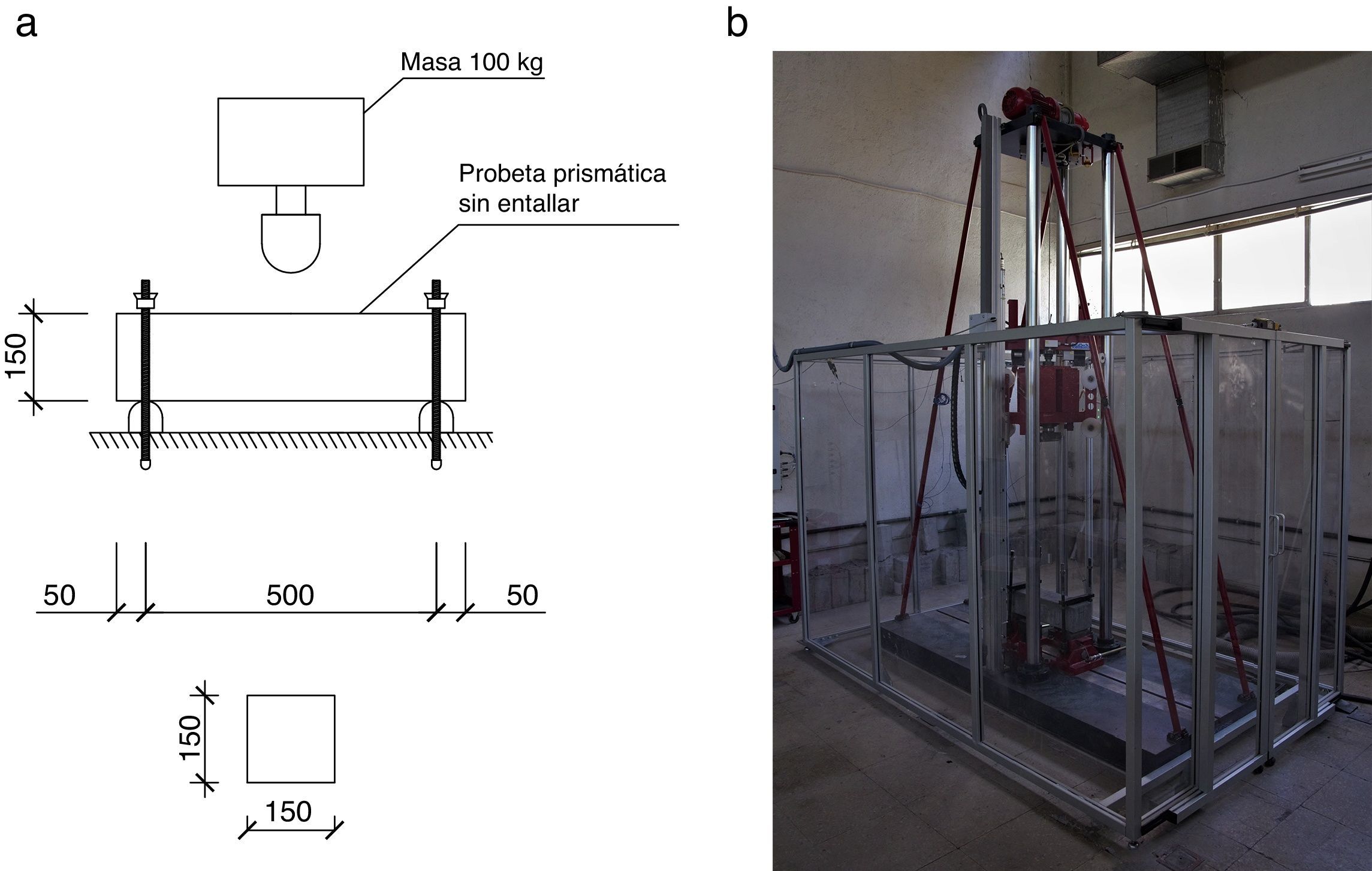
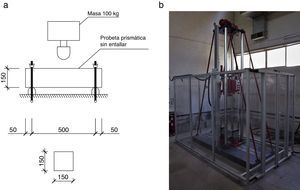
2Metodología experimental2.1Descripción de los ensayosLa campaña experimental comprende 25 ensayos realizados sobre probetas de hormigón sin armadura. Cuatro de las probetas se ejecutaron con HM, mientras que las 21 probetas restantes son de SFRC. En total se ensayaron 5 series diferentes, de las cuales 4 comprenden diferentes tipos de SFRC, tal y como se muestra en la tabla 1. Estos se fabricaron con dos tipos de fibras, rectas o con anclaje, con distintas dosificaciones, 1,0% y 0,5%, para cada tipo de fibra. Para cada una de las series se ensayó una probeta bajo condiciones cuasi-estáticas, como referencia, y el resto de las probetas se ensayaron con una máquina de impactos instalada recientemente en el Laboratorio de Estructuras de la UPM, mostrada en la figura 1b. Esta máquina deja caer una masa rígida en caída libre, con una capacidad de impacto de hasta 3,92kJ, pudiendo variarse tanto la masa como la altura de caída.
La geometría de todas las probetas es idéntica: son probetas prismáticas sin entallar, tal y como se muestra en la figura 1a. Las dimensiones de estas son 600×150×150mm, y se ensayan en flexión en 3 puntos, con una luz entre apoyos de 500mm.
En los ensayos cuasi-estáticos se aplica la carga en centro de vano (CDV) con un gato hidráulico con control de desplazamientos, impuestos a un ritmo de 0,1mm/s. La carga aplicada se midió con una célula de carga integrada en el gato. La instrumentación en las probetas consistió en un transformador diferencial de variación lineal (linear variable differential transformer [LVDT]) midiendo la flecha en CDV respecto a los apoyos, otro LVDT midiendo la apertura de la fisura en CDV, y una galga junto a la cara superior del CDV (a 14,1mm de la cara superior y a 47mm del CDV), evitando su fallo durante la propagación de la fisura.
En los ensayos a impacto, las probetas se disponen con los apoyos a la misma luz, pero fijando tanto en la cara inferior como en la superior evitando el rebote tras el impacto. Una masa en caída libre de 100kg se desprende sobre el CDV desde alturas comprendidas entre 500 y 1.750mm, alcanzando velocidades de 3,1 y 5,9m/s, respectivamente. Por su parte, los apoyos y la cabeza de impacto de la masa son cilíndricos de 58mm de diámetro. Para evitar el levantamiento de las probetas durante el impacto se disponen unas abrazaderas. En caso de ser excesivamente rígidas, estas abrazaderas pueden modificar los mecanismos de fallo al generar registros con reacciones parásitas. Se evitaron estas reacciones parásitas en los apoyos mediante la disposición un elemento tipo foam entre la probeta y las abrazaderas, como se ha descrito detalladamente en [3].
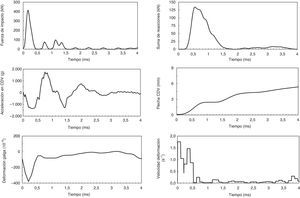
En estos ensayos se registraron las reacciones en ambos apoyos, la fuerza de impacto en CDV y la aceleración vertical en el centro vano a una frecuencia de muestreo de 40kHz. Los desplazamientos del CDV se calcularon mediante la doble integración de la aceleración medida. Las deformaciones se midieron con una galgas extensométricas dispuestas del mismo modo que en el ensayo cuasi-estático. La máxima velocidad de muestreo alcanzada para las galgas fue de 9,6kHz. La velocidad de deformación se obtuvo mediante la derivación de las deformaciones medidas.
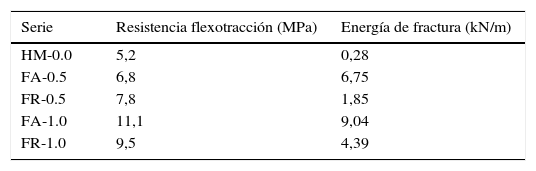
2.2Caracterización de los materialesEn todas las mezclas se utilizó cemento ordinario Portland I 42.5 R/SR (375kg/m3). El amasado se realizó con un ratio agua/cemento de 0,42. Se emplearon áridos silíceos con tamaño máximo de 12,5mm, filler calizo y superplastificante Viscocrete 20HE. Para el SFRC se utilizaron fibras rectas y con anclaje, con un límite elástico de 3.000 y 1.200MPa, respectivamente. La cantidad de fibras dispuesta fue de 39 y 79kg/m3 para las proporciones volumétricas del 0,5 y del 1,0%, respectivamente. Las fibras rectas eran Dramix OL 10/.16 con un ratio de esbeltez de 62,5 (diámetro de 0,16mm y longitud de 10mm). Por su parte, las fibras con anclaje eran Dramix 3D 60/0,75 con un ratio de esbeltez de 80 (diámetro de 0,75mm y longitud de 60mm). Las resistencias medias a compresión y a tracción indirecta (ensayo brasileño) sobre probetas cilíndricas (150×300mm) a la edad de los ensayos se muestran en la tabla 1.
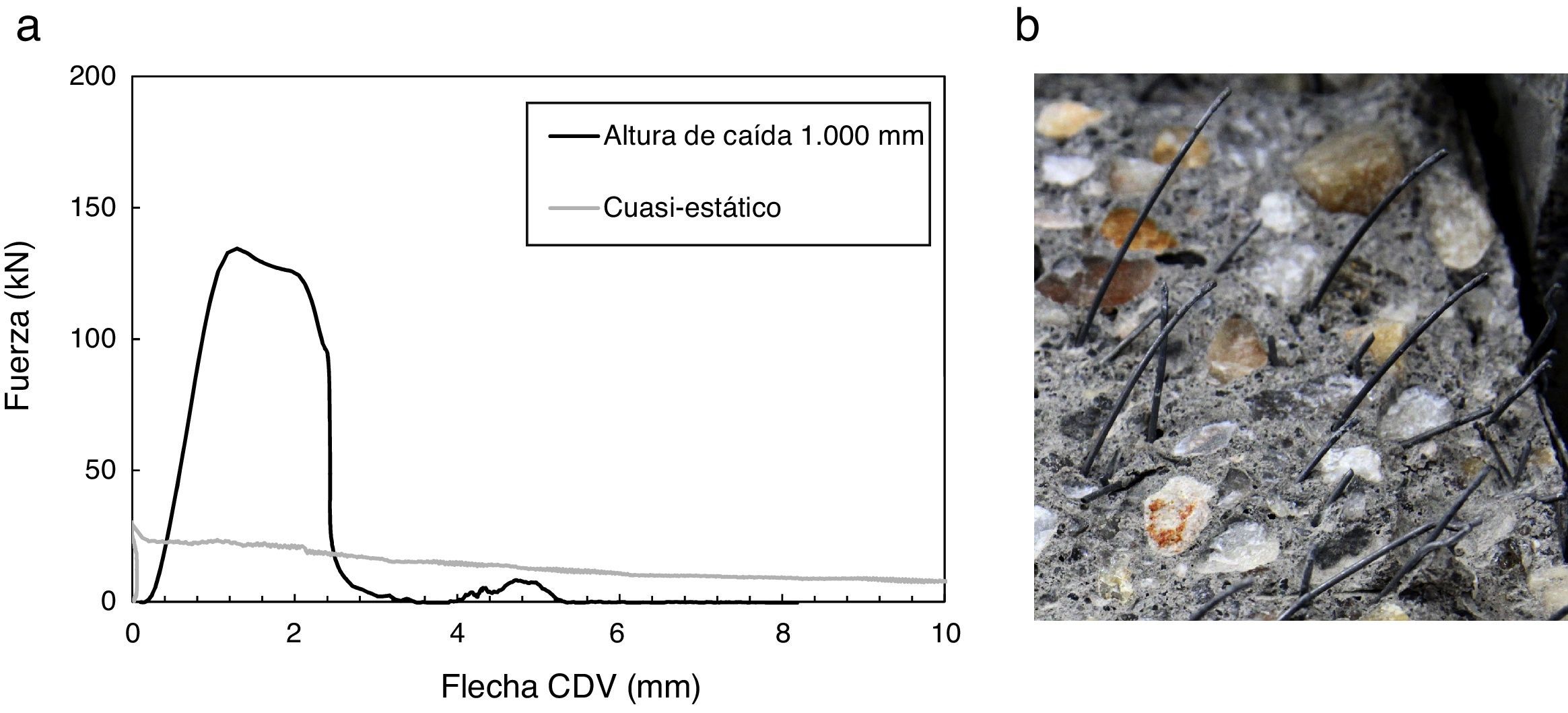
2.3Resultados experimentalesLos resultados de los ensayos, tanto cuasi-estáticos como dinámicos, se estudiarán en términos de tensión equivalente y de la energía de fractura. Ambos términos se han obtenido de los diagramas fuerza-flecha en CDV, equivalentes al mostrado en la figura 2a. La tensión equivalente se ha obtenido como la resistencia a flexotracción del hormigón correspondiente a la carga de colapso registrada, suponiendo que los esfuerzos en rotura son similares a los cuasi-estáticos. La energía de fractura se ha obtenido como el área comprendida bajo las curvas fuerza-flecha en CDV dividido por área de la sección fisurada. Como fuerza se ha asumido la suma de ambas reacciones, puesto que para los ensayos dinámicos resulta más conveniente que la carga de impacto para comparar la resistencia cuasi-estática y dinámica, de acuerdo con estudios previos [2,4,5], ya que así se elimina el efecto de las fuerzas de inercia.
En la tabla 2 se muestra la tensión equivalente que proporciona la resistencia a flexotracción y la energía de fractura de los ensayos cuasi-estáticos de flexión en 3 puntos. Las probetas fallaron por la formación de una sola fisura en CDV. En las fisuras se observaron la rotura de áridos. No se encontraron fibras rotas, y en el caso de las fibras con anclaje se constató que se desarrolló completamente el arrancamiento, al observarse los anclajes enderezados.
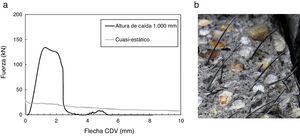
En los ensayos de impacto se produjo la rotura de la probeta por el desarrollo completo de una fisura vertical en CDV. En el análisis de las superficies de fallo se observaron rotura de áridos en todos los casos. En general se observaron algunas pocas roturas de fibras; sin embargo, la distribución de estas indica que por lo general su rotura depende del tipo de fibra utilizado. En el caso de las fibras rectas se observaron muy pocas roturas. En las fibras con anclaje, aunque la mayor parte de las fibras no se rompieron, mostrando su anclaje enderezado, se observaron algunas roturas de fibras, tal y como se muestra en la figura 2b. Además, también se observó la influencia de la velocidad de carga en el incremento de las roturas de fibras.
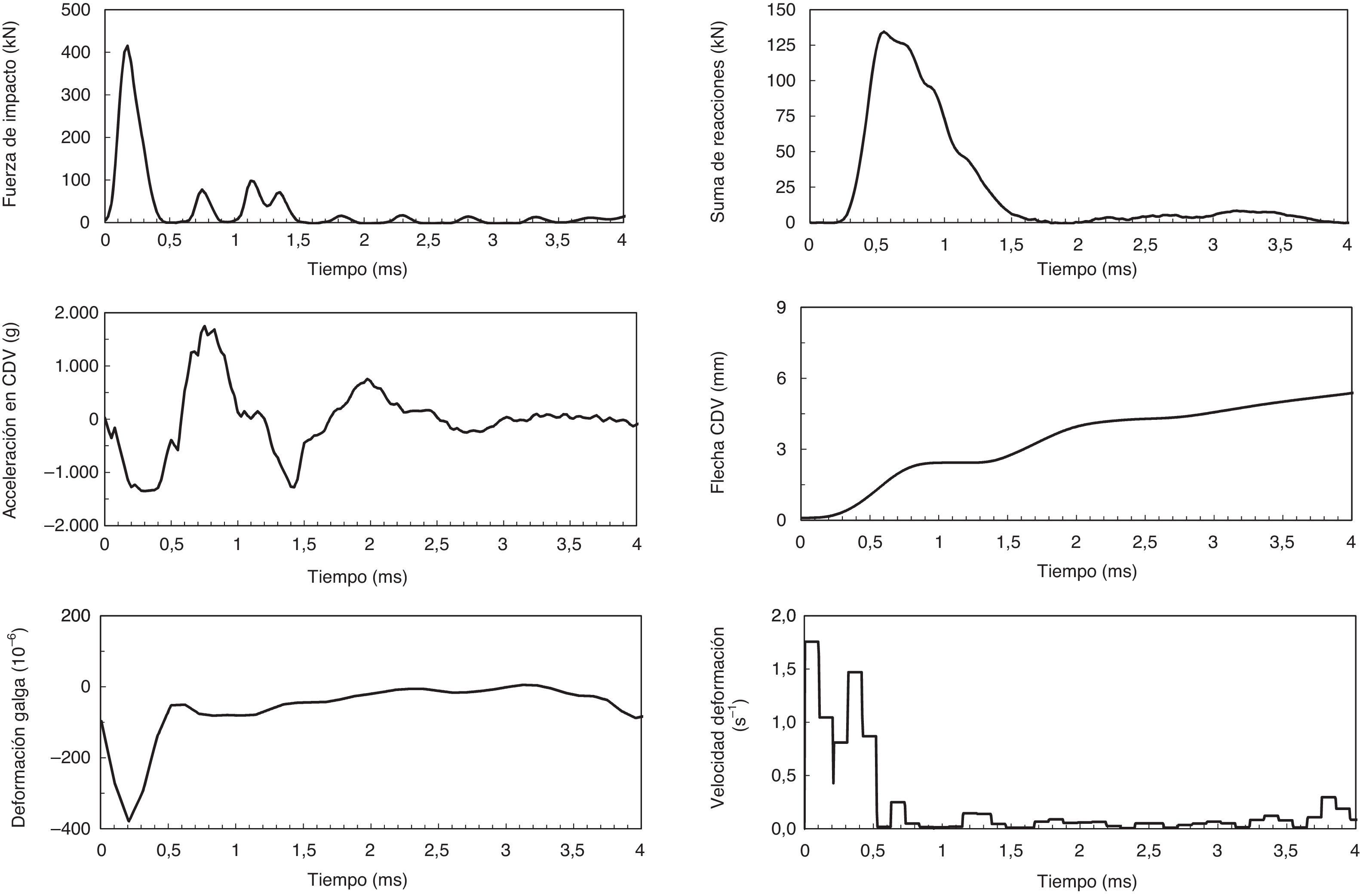
En la figura 3 se muestran los registros a lo largo del tiempo de un ensayo de impacto típico. En este caso la probeta ensayada pertenece a la serie FA-0.5 y fue sometida a un impacto desde una altura de 1,00m. En el momento en el que comienza el impacto se produjo un aumento muy pronunciado de la carga en CDV, presentando un pico muy elevado. La suma de las reacciones presentó un pico menor y un aumento menos abrupto que la fuerza de impacto, que consiste en una onda de menor frecuencia. Se confirmó un desfase de 0,25ms entre el comienzo del impacto y de las reacciones, tal y como ha observado en otros estudios [6]. Según los autores, este desfase se debe al tiempo que tarda la onda de choque en alcanzar los apoyos desde el punto de impacto y la presencia de pequeños huecos entre el apoyo y la probeta.
En la figura 2a se muestra el diagrama fuerza-flecha en CDV del caso discutido en el párrafo anterior (probeta de la serie FA-0.5 sometida a impacto desde una altura de 1,00m) y su correspondiente caso cuasi-estático. En general estas curvas están formadas por una rama de carga ascendente hasta alcanzar la resistencia máxima y una rama de ablandamiento posterior.
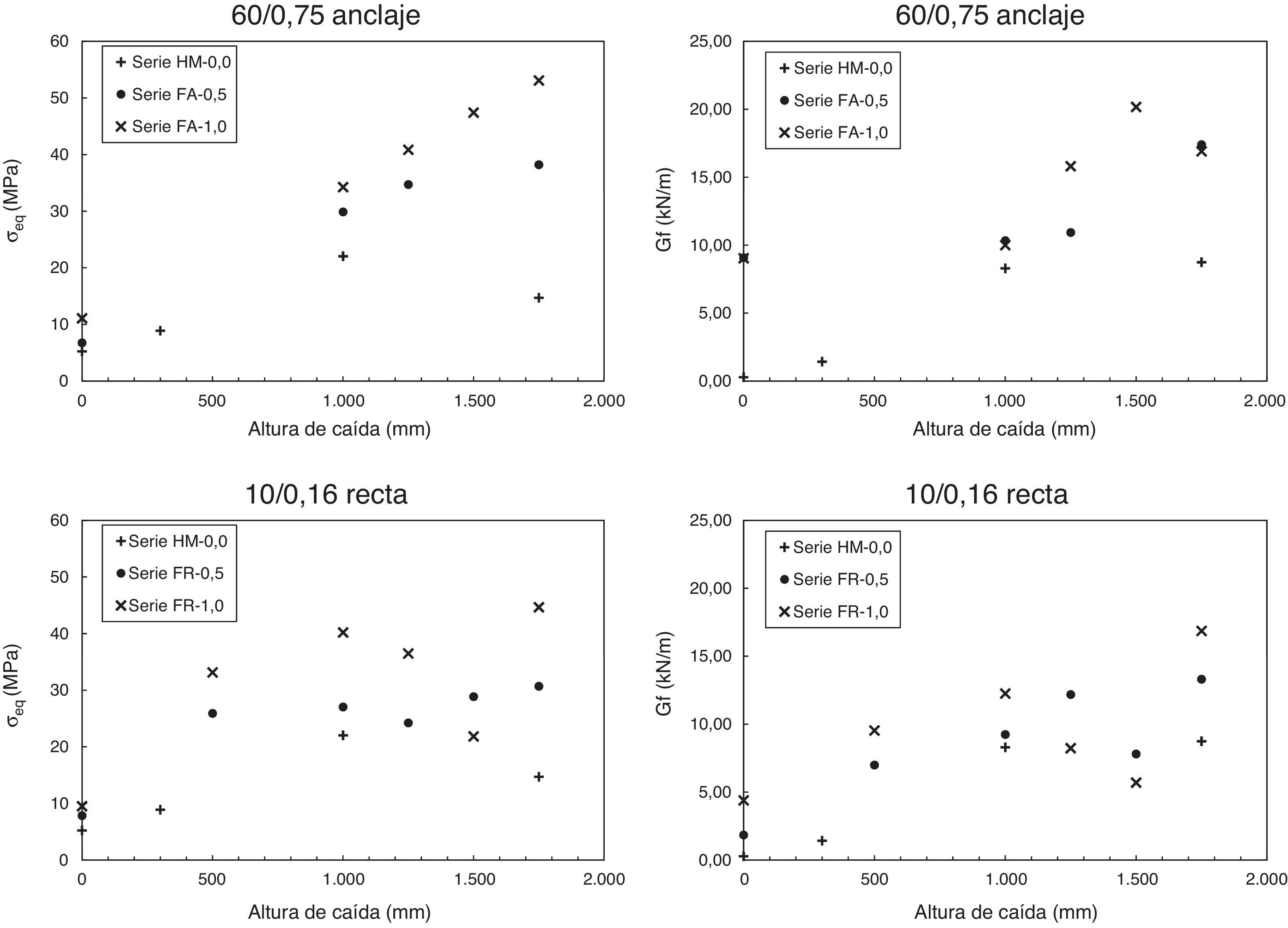
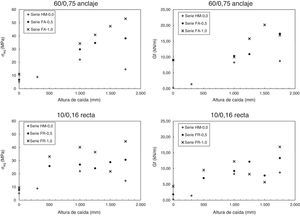
Los resultados extraídos de estos ensayos, tensión de pico equivalente y energía de fractura, se muestran en la figura 4, en función de la altura de caída en el impacto. En cada uno de los gráficos se muestran los resultados para un solo tipo de fibra en diferentes dosificaciones (0,5 y 1,0%), además de los resultados de la serie de HM. Se observa que por lo general tanto la tensión de pico equivalente como la energía de fractura de las probetas aumenta con la altura de caída. No obstante, este crecimiento no se produce del mismo modo en todos los casos. Las probetas de HM presentan un gran aumento de sus propiedades mecánicas según aumenta la altura de caída, alcanzando una tensión de pico equivalente cercana a 20MPa y una energía de fractura superior a 8kN/m. Es destacable que en los ensayos de impacto con una altura de caída mayor a 1.000mm no se observa aumento de las propiedades mecánicas.
En el caso de las fibras con anclaje se observa un crecimiento de la tensión de pico equivalente según se incrementa la altura de caída, llegando hasta casi 55MPa para una altura de caída de 1,750mm con un contenido en fibras del 1,0%. La energía de fractura también aumenta junto a la altura de caída, pero no tan evidente y monótonamente como el crecimiento de la tensión de pico equivalente, incluso existiendo casos aislados en los que se produce un decremento de esta. No obstante, cabe destacar que se alcanzan valores altos de energía de fractura sobrepasando 20kN/m.
Las fibras rectas también aumentan sus propiedades mecánicas junto con la altura de caída. Sin embargo, presentan un comportamiento más irregular que las fibras con anclaje, observándose más casos en los que se producen decrementos tanto de la tensión de pico equivalente como en la energía de fractura, según aumenta la altura de caída. La tensión de pico equivalente sobrepasa los 40MPa y la energía de fractura casi alcanza los 18kN/m en la serie FR-1.0.
3Análisis de los resultadosCon los datos tensión de pico equivalente y energía de fractura (fig. 4) se puede establecer una comparación entre las series ensayadas. Es simple observar que los SFRC estudiados mejoran las prestaciones del HM en las dosificaciones estudiadas. Se observa un incremento significativo tanto de la tensión de pico equivalente como de la energía de fractura. Concretamente, entre las series de SFRC destacan las prestaciones de la serie FA-1.0 (hormigón reforzado con un 1,0% de fibras con anclaje) tanto en régimen dinámico como en régimen cuasi-estático. Las fibras rectas también incrementan las prestaciones del hormigón de una manera notable, aunque presentan un comportamiento más irregular que las fibras con anclaje y unas prestaciones más reducidas. Esto puede deberse a su reducida longitud, que frente a aperturas de fisura crecientes su anclaje es más incierto, ya que según ciertos autores [7,8] estas son especialmente efectivas cosiendo microfisuras, más que controlando la apertura de macrofisuras.
En términos de la dosificación, las series que mejor comportamiento presentan frente a impacto, por lo general, son las que tienen un 1,0% de contenido volumétrico de fibras. Las prestaciones que ofrecen las series con un 0,5% de contenido volumétrico de fibras representa, por lo general, el comportamiento promedio entre las series con un 1% de contenido en fibras y el HM.
Como se ha discutido previamente, bajo condiciones de impacto el hormigón y el SFRC suelen mostrar una resistencia y una energía de fractura mayor que en condiciones cuasi-estáticas, tal y como sugieren la figura 2a y la figura 4. Un modo interesante y muy extendido de comparar ambas situaciones puede ser a través del uso de un factor de incremento dinámico (DIF). Los resultados de los ensayos cuasi-estáticos son tomados como referencia para calcular el DIF. También puede resultar interesante la obtención del DIF de la energía de fractura mediante un procedimiento similar.
El DIF de la resistencia máxima depende de la contribución de cada uno de los mecanismos de rotura movilizados durante el colapso de las probetas. En el caso de la resistencia a flexión de las probetas de hormigón, está determinada por la resistencia a compresión y la resistencia a tracción del hormigón. El DIF de cado uno de estos mecanismos ha sido estudiado por diversos autores en términos de la velocidad de deformación [9–12]. Puesto que los valores del DIF para cada uno de estos mecanismos son diferentes, es previsible que el DIF global difiera respecto a las formulaciones existentes. Entre las series estudiadas hay probetas de SFRC, por lo que podemos esperar una influencia de la velocidad de deformación diferente que en el HM debido a los mecanismos que influyen en el arrancamiento de las fibras [13]. Para ciertos mecanismos ya se ha caracterizado su sensibilidad a la velocidad, como el límite elástico del acero [14], pero hay otros de los que todavía se desconoce su sensibilidad, como la adherencia matriz-fibra.
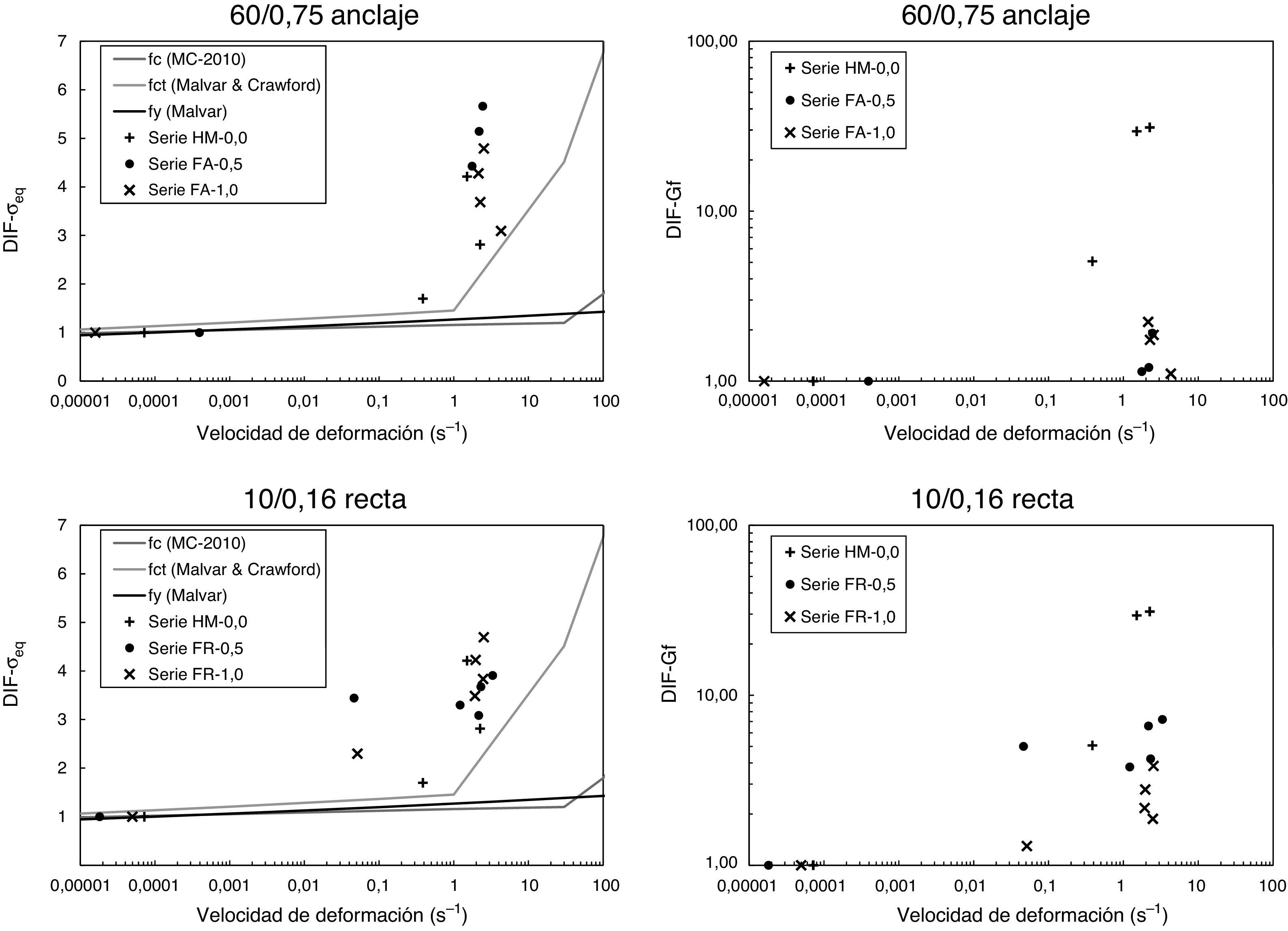
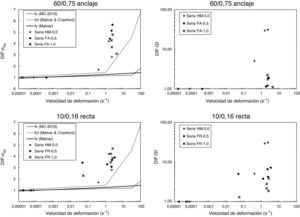
Con los datos previos se puede establecer una comparación entre el DIF, tanto de resistencia como de energía de fractura, para las diferentes series en función de la velocidad de deformación. De cara a entender mejor el comportamiento dinámico puede ser interesante comparar dichos resultados con las formulaciones existentes. Las formulaciones de DIF de resistencia máxima más extendidas para hormigón y acero son las de Malvar [11,14] y la del Código Modelo2010 [10]. El DIF de la energía de fractura no tiene una formulación comúnmente aceptada. Las formulaciones existentes y el DIF se muestran en la figura 5. Se observa una alta la sensibilidad a la velocidad en el DIF de ambos parámetros. Se ha obtenido un DIF para la resistencia comprendido entre 2,0 y 6,0 para las series de SFRC, y algo menor para la serie de HM. Sin embargo, el DIF de la energía de fractura ha destacado en la serie de HM, estando comprendido entre 4.0 y 30.0, siendo bastante menores en las series de SFRC, entre 1,0 y 7,0.
Estudiando los valores teóricos del DIF de resistencia dentro del rango de velocidades de deformación de los ensayos de impacto (generalmente mayores que 1s−1) se puede llegar a dos conclusiones que a priori parecen ciertas. Puesto que el DIF de la resistencia a tracción es mayor que el de compresión, resulta lógico que el DIF en flexión sea menor que en tracción. En el caso del SFRC, siendo el DIF del acero menor que el del hormigón, resulta asimismo lógico que el DIF del SFRC sea menor que el de HM. Sin embargo, ninguna de estas afirmaciones se cumple de acuerdo a los resultados presentados en este artículo y en otros estudios [6,15,16]. Una explicación a ambos fenómenos puede ser debida a la diferencia entre el comportamiento uniaxial y el comportamiento a flexión, y a que el efecto tamaño —muy importante en flexión— difiera en régimen dinámico del estático, como han descrito ciertos autores [17–19]. Así mismo se ha observado que el tipo de fibra tiene cierta influencia, puesto que las fibras rectas aumentan su DIF de resistencia máxima junto con el contenido de fibras, al contrario de las fibras con anclaje, cuyo DIF máximo es con 0,5% de contenido en fibras.
Analizando el DIF de la energía de fractura se observa como disminuye junto con el aumento del contenido de fibras. Este resultado es acorde a otros estudios en la literatura [20] que proponen un modelo analítico para estudiar el comportamiento dinámico del SFRC. El SFRC es un material pseudodúctil con gran capacidad de absorción de energía, gracias a la capacidad que tienen las fibras durante su arrancamiento de transmitir tensiones a través de las fisuras, incluso con aperturas considerables. Los mecanismos de adherencia son los que gobiernan el proceso de arrancamiento. Se ha descrito [20] que la influencia de la velocidad de carga en los mecanismos de adherencia es menor que en el hormigón en tensión, por lo cual el SFRC tendrá unas propiedades mecánicas menos dependientes de la velocidad que en el caso del HM, especialmente en términos de energía de fractura, donde el hormigón presenta un DIF mucho más elevado que el correspondiente a la resistencia, y su contribución a la energía de fractura global de SFRC es poco determinante. Esto explica que la diferencia en el DIF de la energía de fractura entre las series de SFRC y el HM sea tan llamativa, y que el DIF sea mayor en las series con menos fibras.
Así mismo, también se observan divergencias entre los diferentes tipos de fibras. Las fibras con anclajes presentan DIF de energía de fractura especialmente bajos. Según Zanuy et al. [20], el arrancamiento de estas las fibras está muy influenciado por el proceso de enderezamiento del anclaje, gracias al cual se alcanzan tensiones muy altas en las fibras. Sin embargo, dichas tensiones pueden resultar dañinas según se incrementa la velocidad de carga. El hormigón mejora sus propiedades mecánicas con la velocidad de carga considerablemente más que el acero. Esto puede producir, bajo condiciones dinámicas, incrementos considerables de la tensión en las fibras durante su arrancamiento que lleguen a superar a la resistencia del acero, produciéndose roturas de fibras durante el arrancamiento. Esto explica las diferencias del DIF de la energía de fractura entre los distintos tipos de fibras. En la figura 2b se observa como ciertas fibras se han roto, presentando en el extremo una forma de cuello de botella, mientras que otras presentan en el extremo el anclaje enderezado, sugiriendo que se han arrancado. Dicha variabilidad del modo rotura de las fibras, dentro de la misma probeta, puede explicarse por las diferentes orientaciones de esas fibras y las diversas longitudes de anclaje en el arrancamiento.
Hay que remarcar que la energía de fractura es un parámetro más objetivo que la resistencia a flexotracción, en cuanto a influencia del efecto tamaño, por lo que parece lógico que la evolución del DIF de la energía de fractura sea más fácilmente explicable que el DIF de la resistencia a flexión. Así, de cara a futuros trabajos, puede resultar más interesante comparar los resultados experimentales con modelos de arranque de fibras en términos de la energía de fractura, en vez de la resistencia, evitando las incertidumbres asociadas al efecto tamaño.
4ConclusionesEn este artículo, cuyo contenido forma parte y completa un estudio más amplio [3], se presentan los resultados experimentales de 25 probetas sin armadura de HM y SFRC, bajo diferentes velocidades de carga. Específicamente se ha estudiado el comportamiento del SFRC a flexión en 3 puntos en términos de resistencia a flexotracción y energía absorbida, indagando en su dependencia de las diferentes velocidades de carga.
Tanto la resistencia a flexotracción como la energía de fractura del hormigón han mostrado un aumento muy significativo con la adición de fibras. También se ha observado un incremento de estos valores con una mayor dosificación de las fibras. En general se ha mostrado que estos términos son sensibles a la velocidad de carga tanto en el HM como en el SFRC.
El estudio muestra un incremento dinámico de la resistencia a flexotracción muy elevado, especialmente en las probetas de SFRC. Sin embargo, las fibras con anclaje muestran menor DIF con dosificaciones más elevadas, siendo al contrario en las mezclas con fibras rectas. Es destacable que en todos los casos se supera el DIF teórico de tracción uniaxial del hormigón, probablemente debido al efecto tamaño de los ensayos.
La presencia de fibras aumenta la energía de fractura de las mezclas, pero el DIF correspondiente ha resultado ser menor respecto al HM, posiblemente debido a que los mecanismos que gobiernan el arrancamiento son menos sensibles a la velocidad de carga que el hormigón. En el caso de las fibras con anclaje, han mostrado un DIF muy bajo, ya que con velocidades de carga crecientes tiende a producirse un mayor número de roturas.
Se agradece el apoyo financiero recibido por parte del Ministerio de Economía y Competitividad (Ref. BIA2012-30998), así como al programa para los grupos de investigación de la Universidad Politécnica de Madrid (UPM). Asimismo, los autores desean expresar su gratitud a Bekaert por proporcionar amablemente las fibras utilizadas en esta investigación.