En el presente trabajo se propone un modelo analítico basado en Mecánica de Fractura aplicada al hormigón armado que permite estudiar el fallo de secciones sometidas a flexión. Se incorpora una ecuación de compatibilidad que relaciona la apertura de fisura con el alargamiento de la barra de refuerzo; de esta forma la adherencia entre hormigón y acero se incorpora como parámetro al modelo. La formulación propuesta permite obtener la relación entre el momento aplicado en la sección y la apertura de fisura correspondiente. Asimismo, permite evaluar la capacidad de rotación de las secciones de hormigón armado.
An analytical model is presented in order to study the failure of reinforced concrete sections subjected to bending, based on fracture mechanics concepts applied to concrete. It determines the stress in the reinforcement by introducing an additional compatibility equation that relates the crack opening with the stretching of the reinforcement. The proposed formulation assumes a cohesive behaviour of the fractured concrete introducing a force that depends on the cohesive stresses at the crack tip. Model results are validated against several beam tests. The crack opening and the rotational capacity of reinforced concrete sections can be obtained with the model.
El comportamiento de las vigas de hormigón armado frente a esfuerzos de flexión ha sido un tema extensamente estudiado desde el punto de vista del diseño de estructuras de hormigón. Así pues, desde el inicio de la tecnología del hormigón se han ido proponiendo diversos modelos para su análisis [1,2]. Desde un punto de vista práctico, los métodos más utilizados actualmente para determinar el momento último en secciones de hormigón armado son los derivados del uso del método del diagrama rectangular y del método parábola-rectángulo, en los que la ecuación de compatibilidad se establece a través del denominado diagrama de pivotes. Estos métodos asumen que el hormigón no resiste tracciones, que la deformada de la sección es plana y que la adherencia entre el hormigón y el acero de las barras de refuerzo es perfecta, hipótesis que si bien simplifican los modelos para que su uso no sea complejo, tienen el inconveniente de no proporcionar información sobre la apertura de fisura y capacidad de rotación de las secciones, siendo este último aspecto un parámetro cada vez más necesario en el diseño estructural [3–7]. Su interés tiene una conexión directa con el cálculo plástico y el análisis sísmico de estructuras de hormigón armado [8].
En el ámbito de la Mecánica de Fractura se han propuesto diferentes formulaciones para el análisis del comportamiento de una sección sometida a flexión teniendo en cuenta el proceso de fisuración. Desde los trabajos iniciados por Hillerborg, el cual introdujo el concepto de fisura cohesiva [9,10], estos estudios han estado fundamentalmente encuadrados en el estudio de secciones débilmente armadas [11–19]. En todos ellos se pone de manifiesto la necesidad de estudiar el fenómeno de la flexión incluyendo ecuaciones constitutivas que nos permitan relacionar directamente la apertura de fisura con el momento aplicado, reproduciendo de esta forma el fenómeno físico del proceso de fisuración. Aplicando estas metodologías se evita la actual desconexión normativa existente entre la comprobación de capacidad y la de fisuración, proporcionándose un marco teórico que permite unificar las comprobaciones.
En el presente trabajo se propone una metodología para analizar el comportamiento ante esfuerzos de flexión de secciones rectangulares de hormigón armado. El fallo se produce bien por la rotura de la barra de acero o bien porque se alcanza una cierta deformación crítica en la zona de hormigón comprimida. El modelo introduce una ecuación de compatibilidad basada en conceptos de Mecánica de Fractura que relaciona la apertura de fisura con la tensión en la barra de acero, incluyendo como parámetros la adherencia hormigón-acero, la cuantía de armado y propiedades mecánicas de los materiales. De esta forma, complementariamente a la capacidad de la sección, se puede evaluar la apertura de fisura y la capacidad de rotación de la sección.
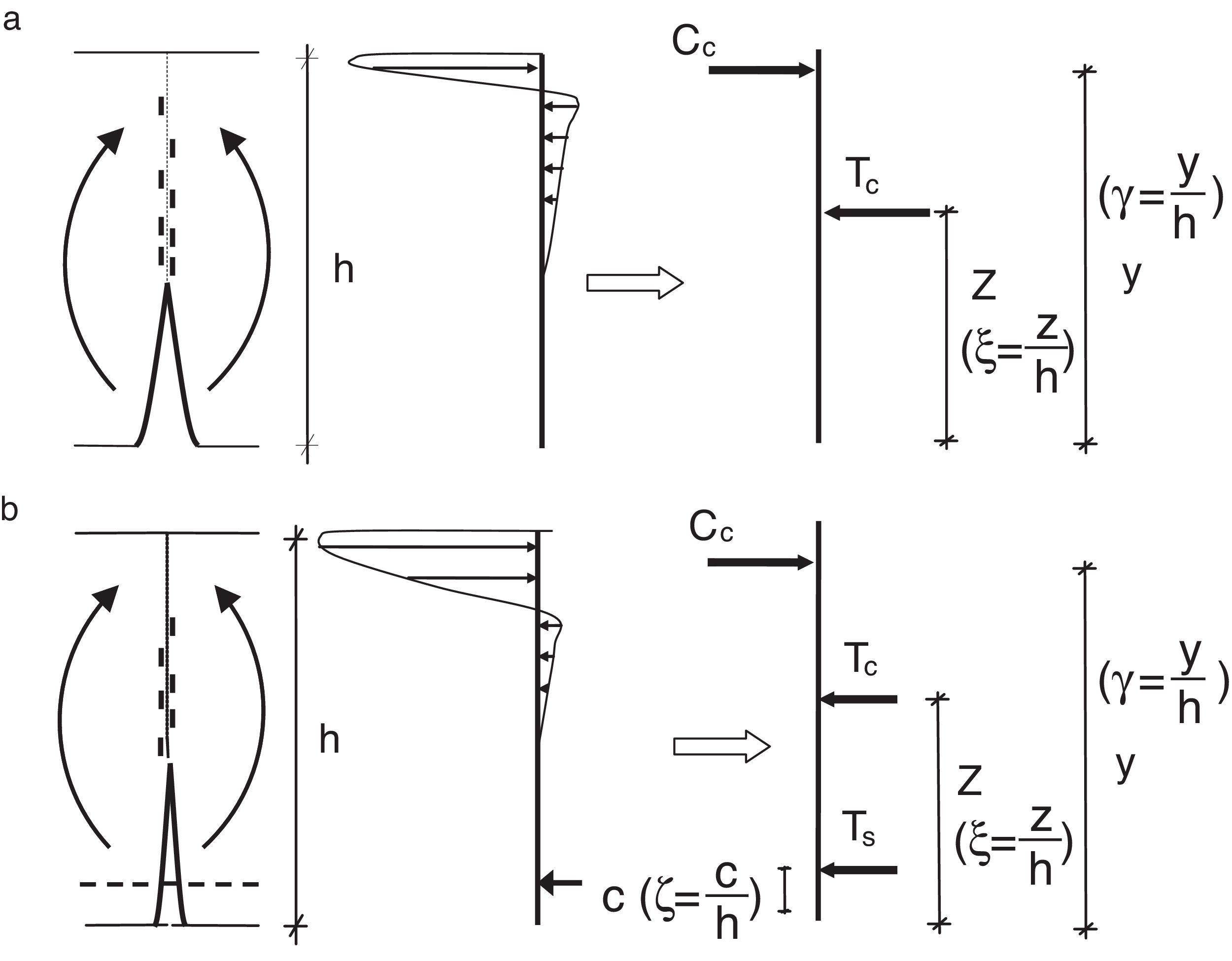
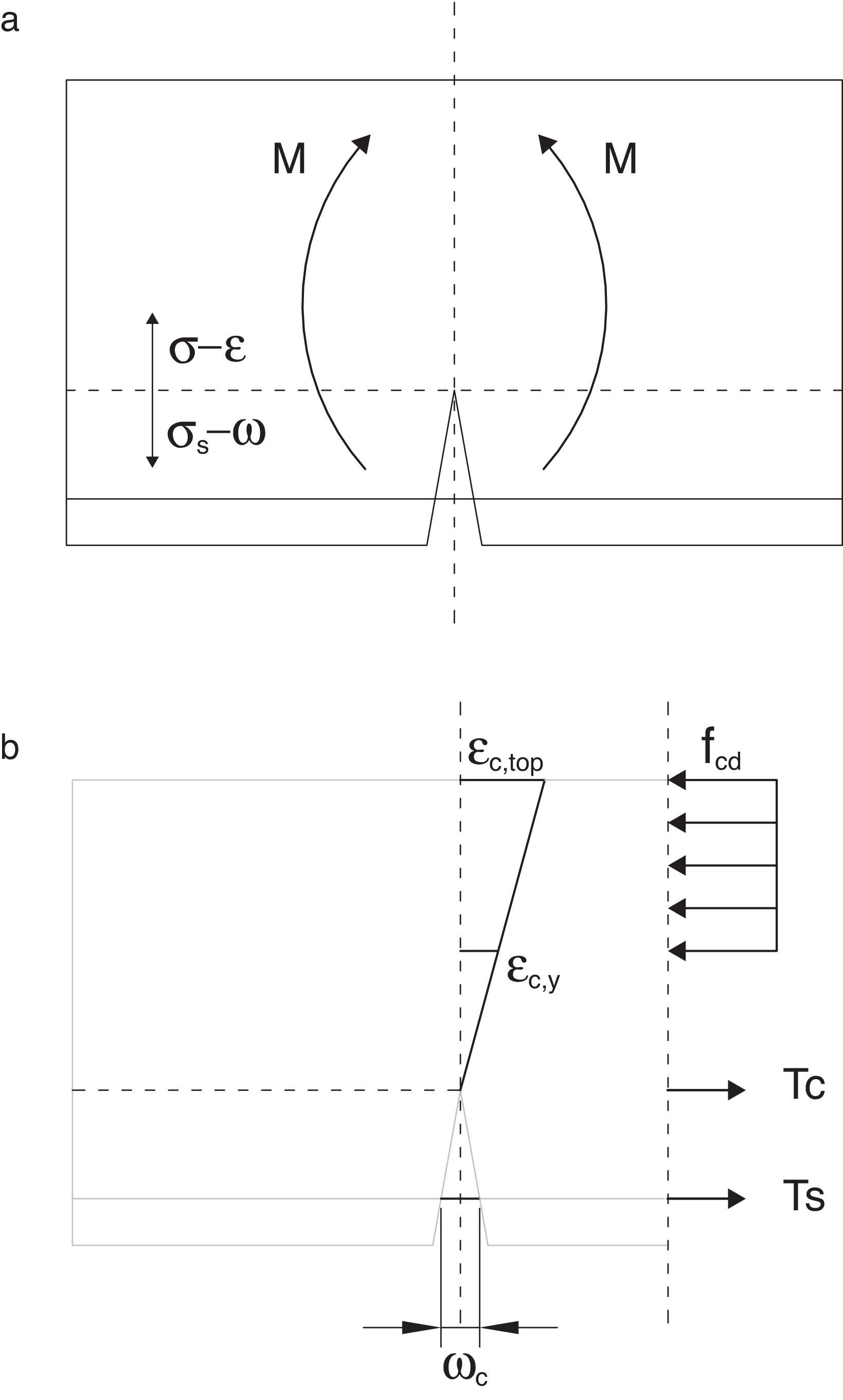
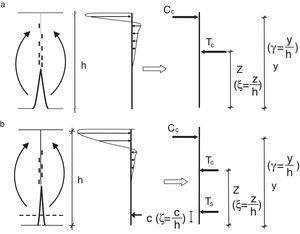
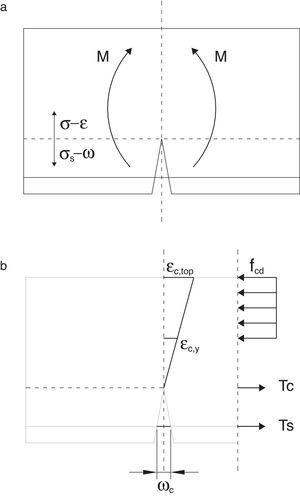
2Modelado del comportamiento de la sección de hormigón armadoSe considera una sección rectangular de hormigón armado en la que va a progresar una fisura. Las diferentes variables geométricas que intervienen en el problema se muestran en la figura 1. La viga tiene un canto h y un ancho b. La profundidad de la fisura viene representada por la letra z, el recubrimiento de las barras de acero por la letra c y la profundidad de la resultante del bloque comprimido con la letra y. Estas dimensiones geométricas pueden adimensionalizarse dividiendo por el canto h. De este modo definimos: ξ=z/h como la profundidad relativa de la fisura adimensionalizada, ζ=c/h como el recubrimiento expresado en forma adimensional y γ=y/h como profundidad de la resultante de las compresiones; estos parámetros tienen un valor comprendido entre 0 y 1.
La profundidad de la resultante del bloque comprimido, y, es evaluada mediante el equilibrio de fuerzas horizontales (véase la fig. 1a):
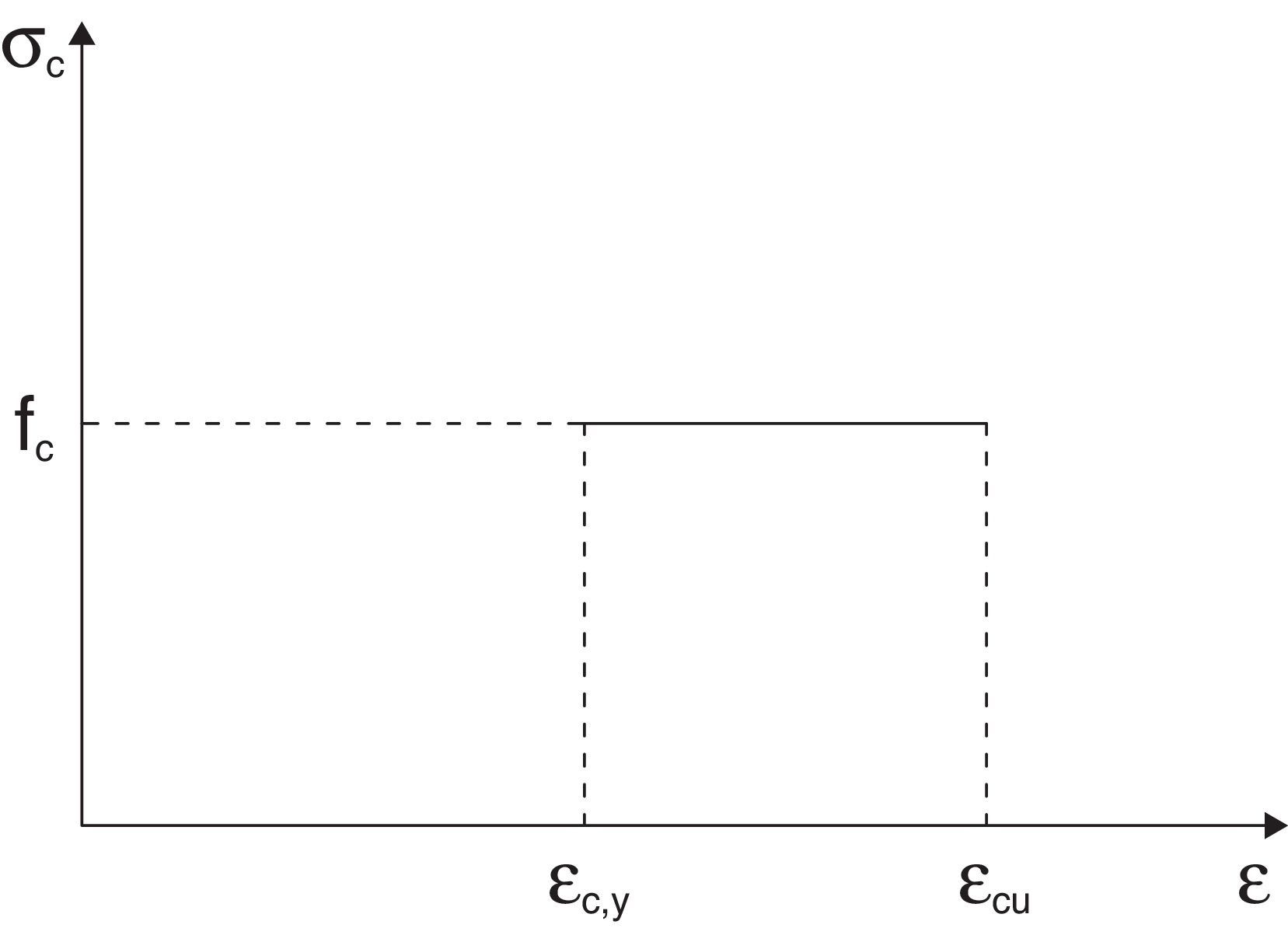
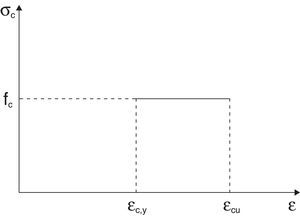
Se asume una distribución rectangular de las tensiones en la zona comprimida, con un valor igual a la resistencia del hormigón, fc. La resultante del bloque comprimido está situada en el centro de gravedad de la distribución de tensiones, de forma que la resultante de las compresiones Cc puede escribirse como:
A partir de las ecuaciones (1) y (2), la profundidad de la resultante del bloque comprimido es igual a:
Las resultantes de compresiones y tracciones se pueden expresar en forma adimensionalizada dividiendo su valor por el área de la sección, bh, multiplicada por la resistencia a tracción del hormigón, fct.
Así pues, la ecuación (3) puede reescribirse de la siguiente forma:
donde nf expresa el cociente entre la resistencia a compresión, fc, y la resistencia a tracción, fct. Durante el progreso de una fisura, el hormigón en su frente va a generar una zona de proceso daño dado el carácter cuasifrágil del material. La resultante adimensional de las tracciones en esa zona, Tc*, puede representarse a través de la ley de Efecto de Escala propuesta por Bažant [19] (véase la ecuación 7).donde βH es el denominado número de fragilidad de Hillerborg [5], que es igual a una dimensión característica del elemento en estudio; en nuestro caso adoptaremos el canto, dividido de la longitud característica del material. Esta longitud se define como, lch=(EcGF)/fct2, donde Ec es el módulo de elasticidad del hormigón, GF es la energía de fractura y fct es la resistencia a tracción del hormigón. βH es un parámetro que nos servirá para comparar elementos escalados entre sí. β0 es una constante relacionada con el tamaño de árido y que se ha tomado igual a 2 veces el tamaño máximo de árido dividido de lch[19]. La fuerza Tc se aplica a la altura z. Obsérvese que z es también la longitud que se toma como referencia en el proceso de crecimiento de la fisura, la cual, para simplificar el problema, se identifica con la profundidad de la fisura. Debe tenerse en cuenta que la posición de la punta de una fisura cohesiva se difumina a lo largo de la zona de proceso de daño [19]. Así pues, el momento en la sección es igual a la tracción, Tc, por el brazo (y-z), que si se expresa de forma adimensionalizada queda como:La existencia de una armadura introduce una nueva fuerza en nuestra sección (véase la fig. 1b). El valor de esta fuerza, Ts, es igual a:
donde As es la cantidad de armadura, ρ la cuantía de armado y σs es la tensión de la barra de armado. Esta tensión se va a expresar de forma adimensionalizada, σ*s dividiéndola por la resistencia a tracción fct del hormigón. Esta nueva fuerza modifica el equilibrio de fuerzas en la sección, quedando este como:Así pues, la profundidad de la resultante de las compresiones es igual a:
El valor del momento durante el progreso de una fisura para una cierta profundidad, ξ, lo podemos expresar como:
Ecuación que, en forma no dimensional, queda como:
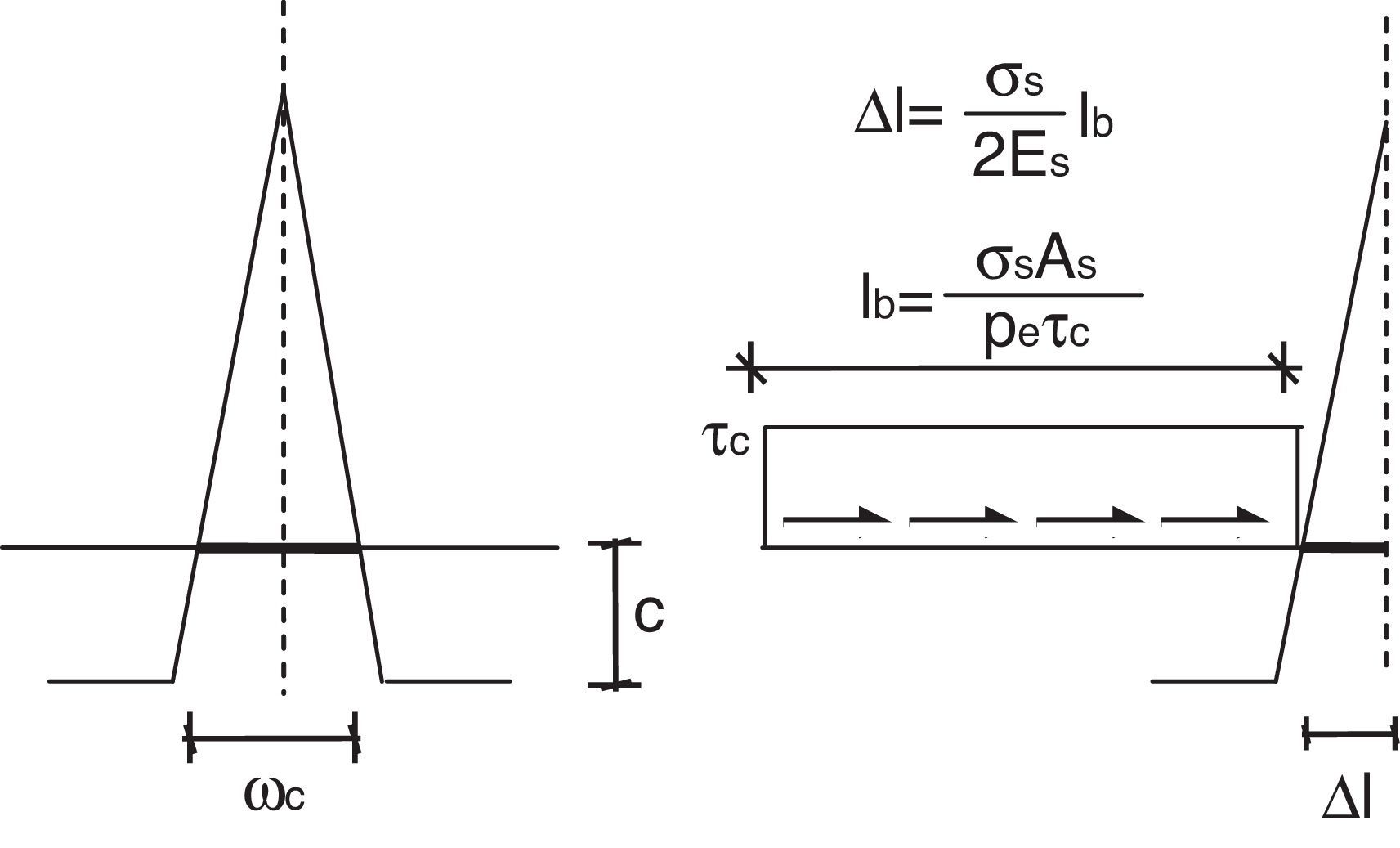
La ecuación (13) refleja que el momento flector durante el progreso de la fisura es la suma de dos términos: uno que depende de las características del hormigón en fractura y otro que depende de la cuantía de armado, tensión de la barra de acero y recubrimiento. Para hallar la tensión en el acero durante el proceso de propagación vamos a tener que plantear una ecuación adicional. Esta se propone de tal forma que compatibilice el alargamiento de la armadura en la fisura con la apertura de la misma. Se va a considerar que el alargamiento de la barra es igual a la mitad de la apertura de fisura (véase la fig. 2 y la ecuación 14).
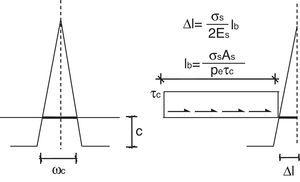
donde w es la apertura de fisura y Δls es el incremento de longitud de la barra de acero respecto del hormigón. Se supone que la tracción en la barra es la misma a ambos lados de la fisura y un crecimiento lineal del esfuerzo axil en la barra en la longitud de anclaje. La ecuación (14) se puede expresar de forma adimensionalizada dividiendo ambos términos por el canto de la pieza:El término correspondiente a la apertura de la fisura, wc, puede ser expresado a partir de la ecuación definida por Tada, Paris e Irwin [20].
donde f(ξ) es igual a:El incremento de longitud de la barra es evaluado (fig. 2) mediante la expresión:
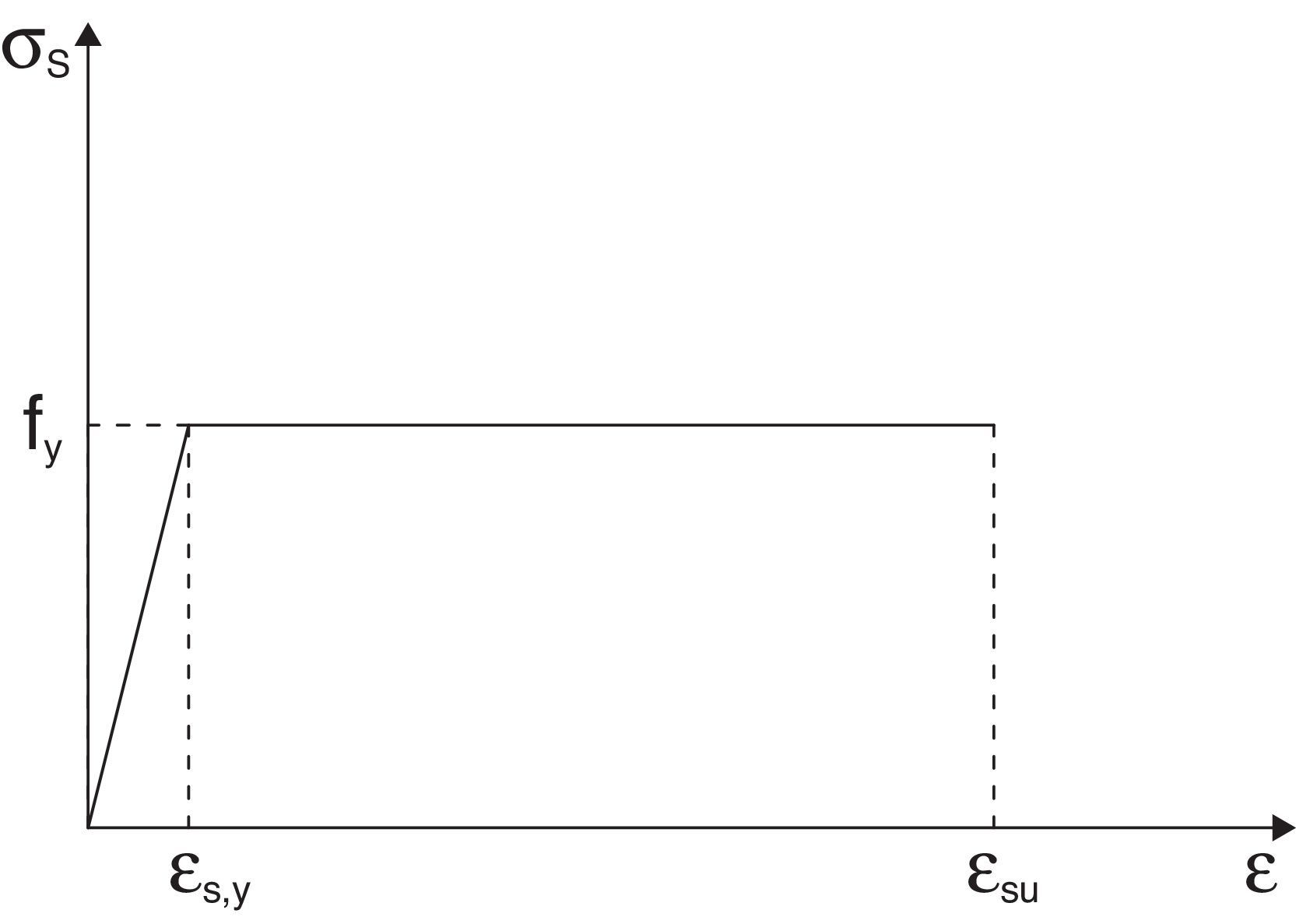
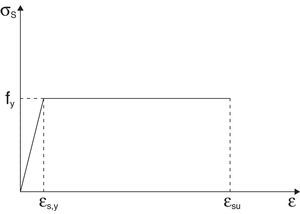
donde τc es la tensión rasante entre el acero y el hormigón y pe es la suma del perímetro de las barras. Sustituyendo las ecuaciones (16) y (18) en la ecuación (15), la tensión en forma adimensional en las barras de acero se puede expresar como:donde η es un parámetro relacionado con la adherencia [11], definido por:nE es el cociente entre el módulo de elasticidad del acero, Es, y el módulo de elasticidad del hormigón, Ec. Se considera un comportamiento elástico-perfectamente plástico para el acero de las armaduras (fig. 3). Es decir, una vez que se alcanza el límite elástico, fy, la tensión en la barra permanece constante.Con todo ello queda un sistema formado por las ecuaciones (11), (13) y (19). Para una cierta profundidad de fisura, ξ, obtendremos el momento asociado a esa profundidad, Mt*, la tensión en el acero, σs*, y la profundidad de la resultante del bloque comprimido, γ. Resuelto el sistema, se puede evaluar la apertura de fisura a partir de la ecuación (16) y la profundidad del bloque comprimido relativa al canto mediante la expresión 2(1-γ).
3Criterios de fallo y rotación plásticaEl modelo presentado reproduce la evolución del momento resistido por una sección según avanza el proceso de fisuración, pero no indica cuándo se produce el fallo. Para fijar los puntos de fallo debemos introducir una serie de criterios adicionales. La rotura de la sección se producirá bien porque se alcance un cierto valor de la deformación en la barra de acero, ¿su (fig. 3), o bien un valor máximo de la deformación en el hormigón, ¿cu (fig. 4). En la zona fisurada (véase la parte inferior de la sección en la fig. 5a) la ecuación de compatibilidad introducida nos permite evaluar la apertura de fisura y la longitud de anclaje movilizada (véase lb en la fig. 2).
De esta forma, la deformación en el acero, teniendo en cuenta el crecimiento lineal del axil en la longitud de anclaje, se puede evaluar mediante la expresión:
Los valores de ¿cu y ¿su vienen determinados en las distintas normativas. Valores comunes para estos parámetros son, por ejemplo, ¿cu=0,0035 y ¿su=0,01. En todo caso se podrían adoptar formulaciones más complejas en las que, por ejemplo, la deformación en el hormigón pueda depender de la profundidad del bloque comprimido, con el fin de tener en cuenta el efecto de tamaño en esa zona. Una vez superado alguno de los límites de deformaciones considerados, la sección falla, y el momento asociado a ese punto será el momento último resistente de la sección.
Complementariamente, el modelo permite determinar la capacidad de rotación de la sección, ya que para cada apertura de fisura se puede asociar un giro de la sección mediante la relación:
Dividiendo el numerador y el denominador de la expresión anterior por el canto del elemento, h, la ecuación (22) se puede expresar de forma adimensional:
Una vez conocida la rotación de las secciones para los diferentes momentos aplicados en la sección, se puede evaluar la rotación plástica de la sección, parámetro de interés para determinar la ductilidad de la sección. La rotación plástica, θpl, será igual a la rotación en el momento del fallo, θu, menos la rotación cuando el acero alcanza el límite elástico, θy.
Así pues, la metodología propuesta permite evaluar en una sola comprobación el momento último, la apertura de fisura para cada momento aplicado y la rotación plástica de una sección de hormigón armado.
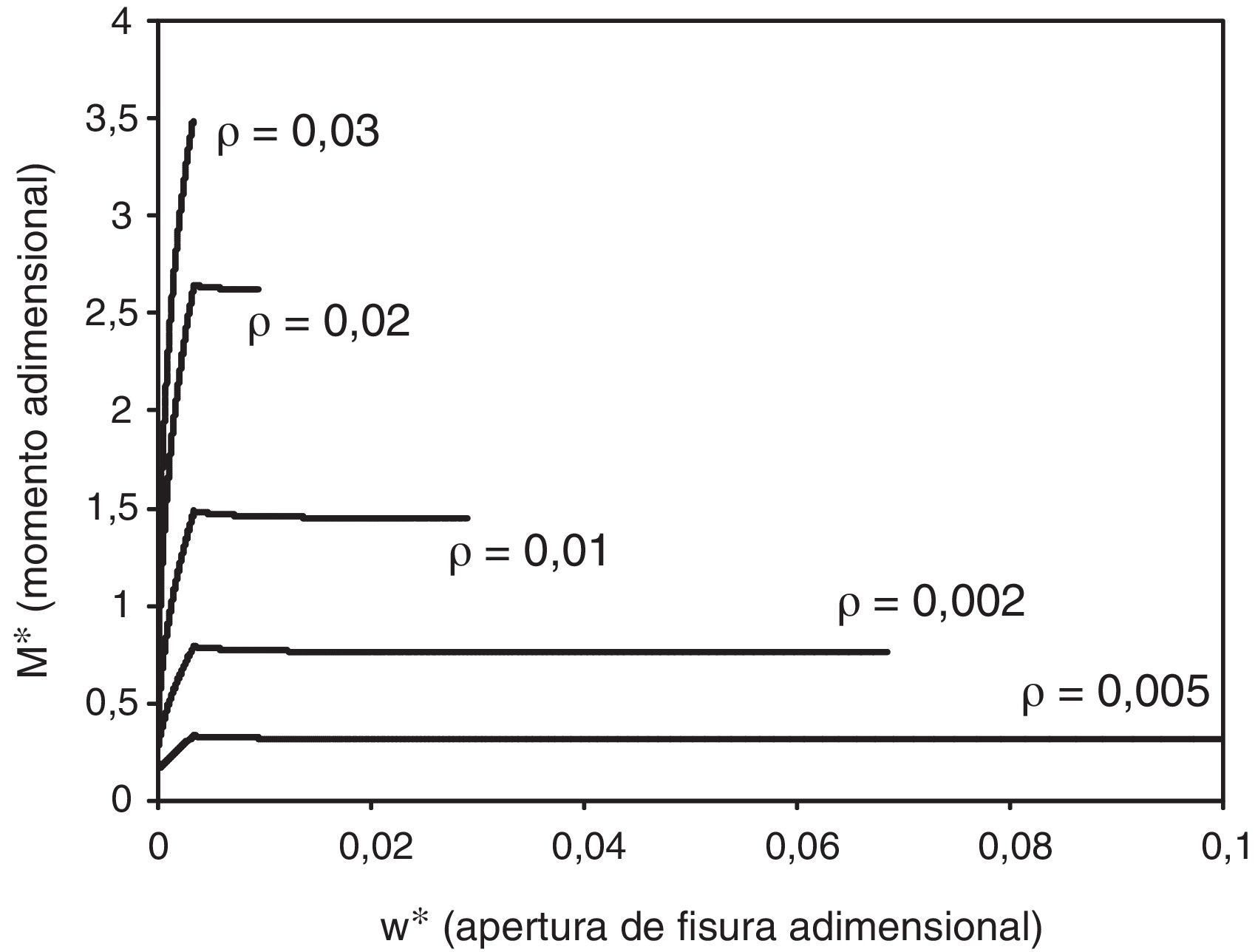
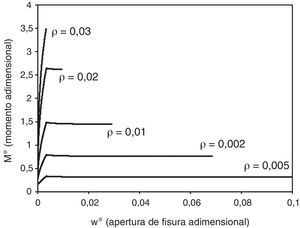
En las siguientes figuras mostramos las gráficas adimensionales momento-apertura de fisura, obtenidas para una sección de hormigón armado con un valor de βH=2. La figura 6 muestra el efecto de la variación de la cuantía. Observamos como el aumento de cuantía provoca una disminución de la apertura de fisura en el momento de fallo, lo cual está relacionado con una disminución de la capacidad de rotación. Para cuantías altas el fallo se produce por compresión, antes de que se produzca la plastificación de las barras de acero.
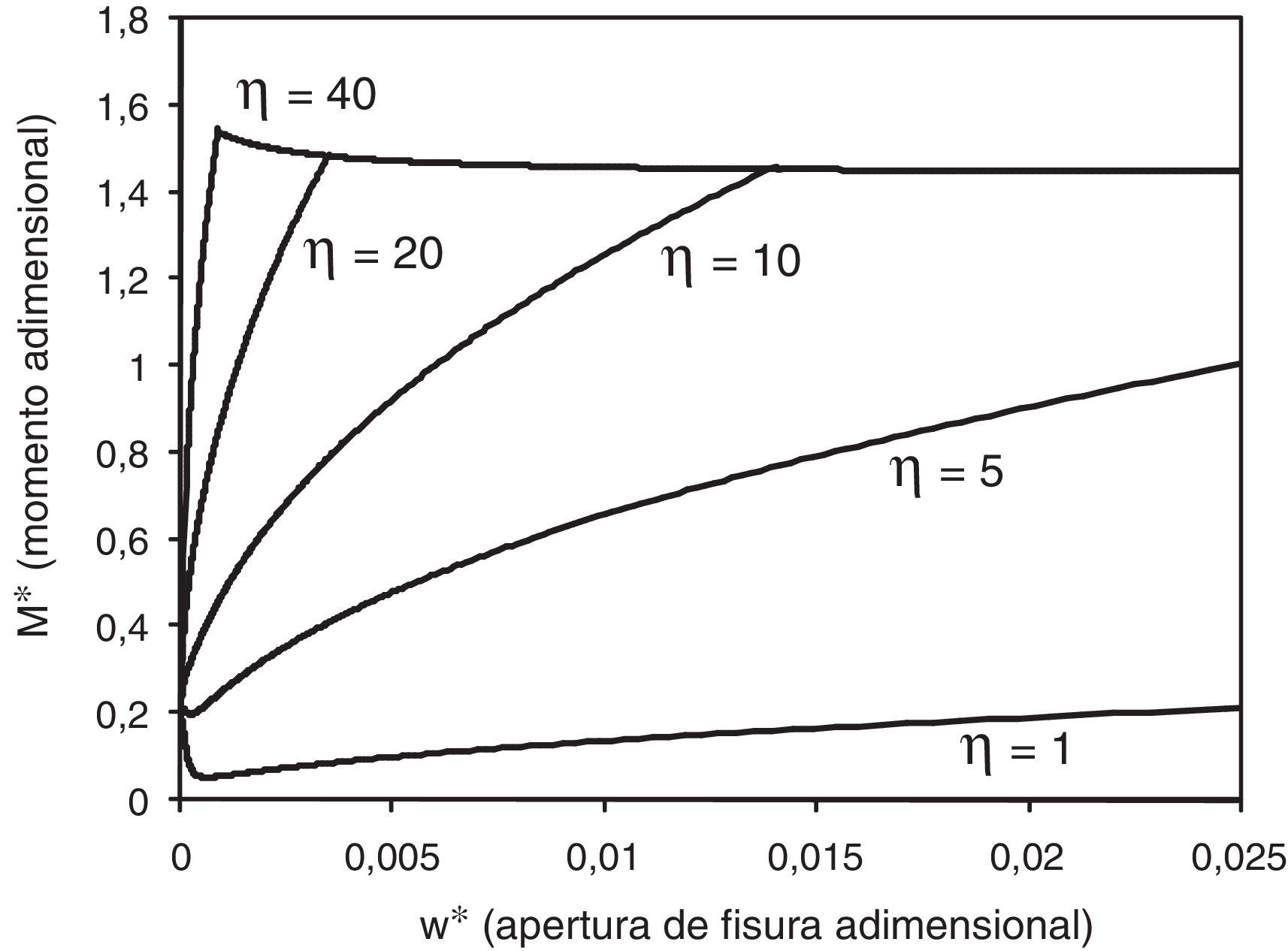
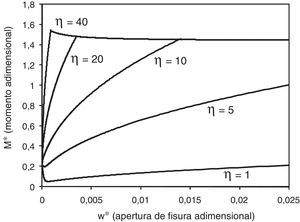
La figura 7 muestra el efecto de la variación de la adherencia no dimensional en la apertura de fisura. Para valores bajos de la adherencia observamos que es necesario que la apertura de fisura sea alta para que el momento aumente; incluso es posible que en algunos casos se llegue al fallo por compresión antes que plastifique la armadura debido a una deformación excesiva de la cabeza comprimida. Para valores altos de la adherencia, se produce la plastificación de la barra. En todo caso, se observa la dependencia de la apertura de la fisura del parámetro que define la adherencia.
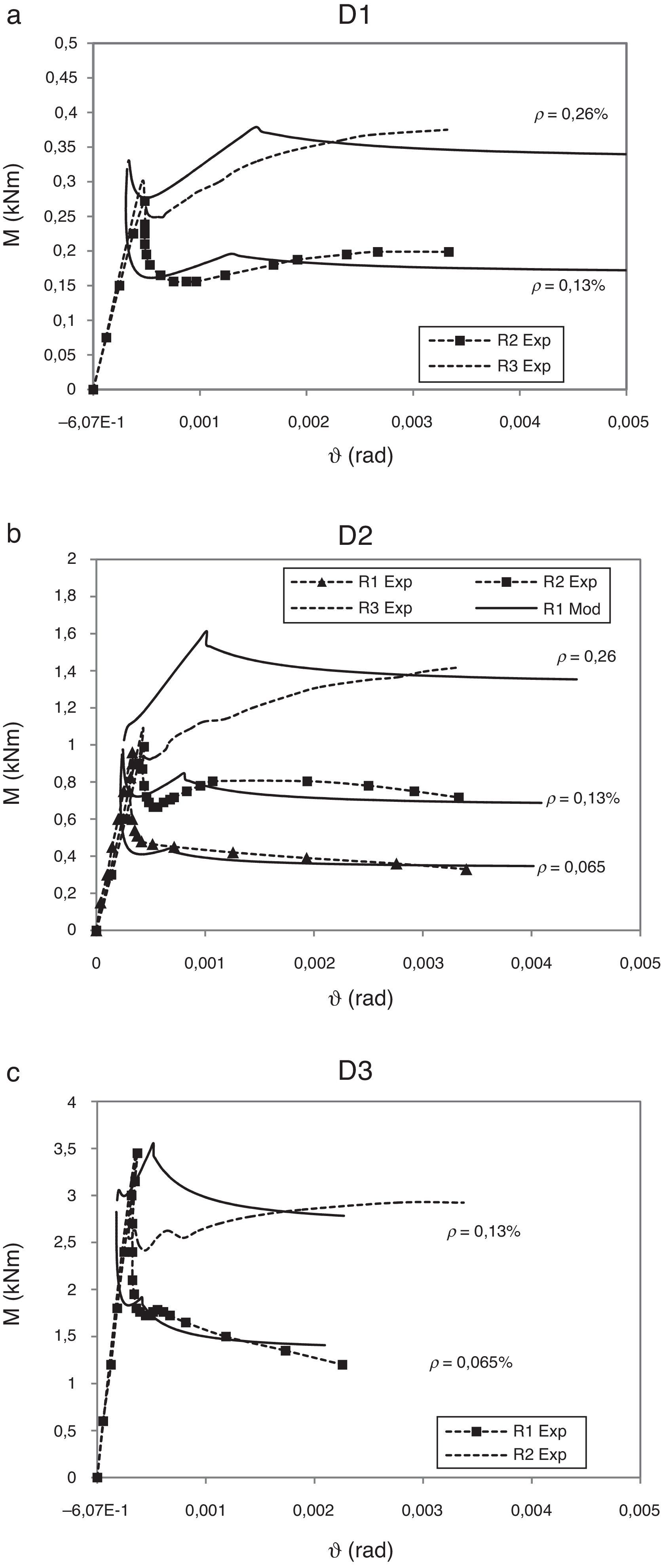
4Contrastación con resultados experimentales y discusión de resultadosCon el fin de contrastar la respuesta del modelo hemos comparado los resultados del mismo con los resultados experimentales obtenidos por Ruiz, Elices y Planas en ensayos a flexión en tres puntos en vigas débilmente armadas [13]. En concreto se han modelado los resultados para vigas con armadura adherente para tres tamaños diferentes: D1, 75mm de canto; D2, 150mm de canto, y D3, 300mm de canto. Estos ensayos se realizaron con cuantías bajas de armadura longitudinal, por lo que únicamente se producía una fisura en la parte central de la viga. Se ha considerado que la rotación de la sección está provocada únicamente por el giro de la sección fisurada, despreciando el giro elástico del resto de secciones. En la figura 6 se muestran los resultados obtenidos.
En la figura 8 se representa en abscisas la rotación de la sección y en ordenadas el momento flector sobre la sección. El modelo reproduce de forma correcta los momentos de fallo y la tendencia en cuanto a los giros últimos de las secciones.
Contrastación experimental. Ensayos Ruiz, Elices y Planas [13].
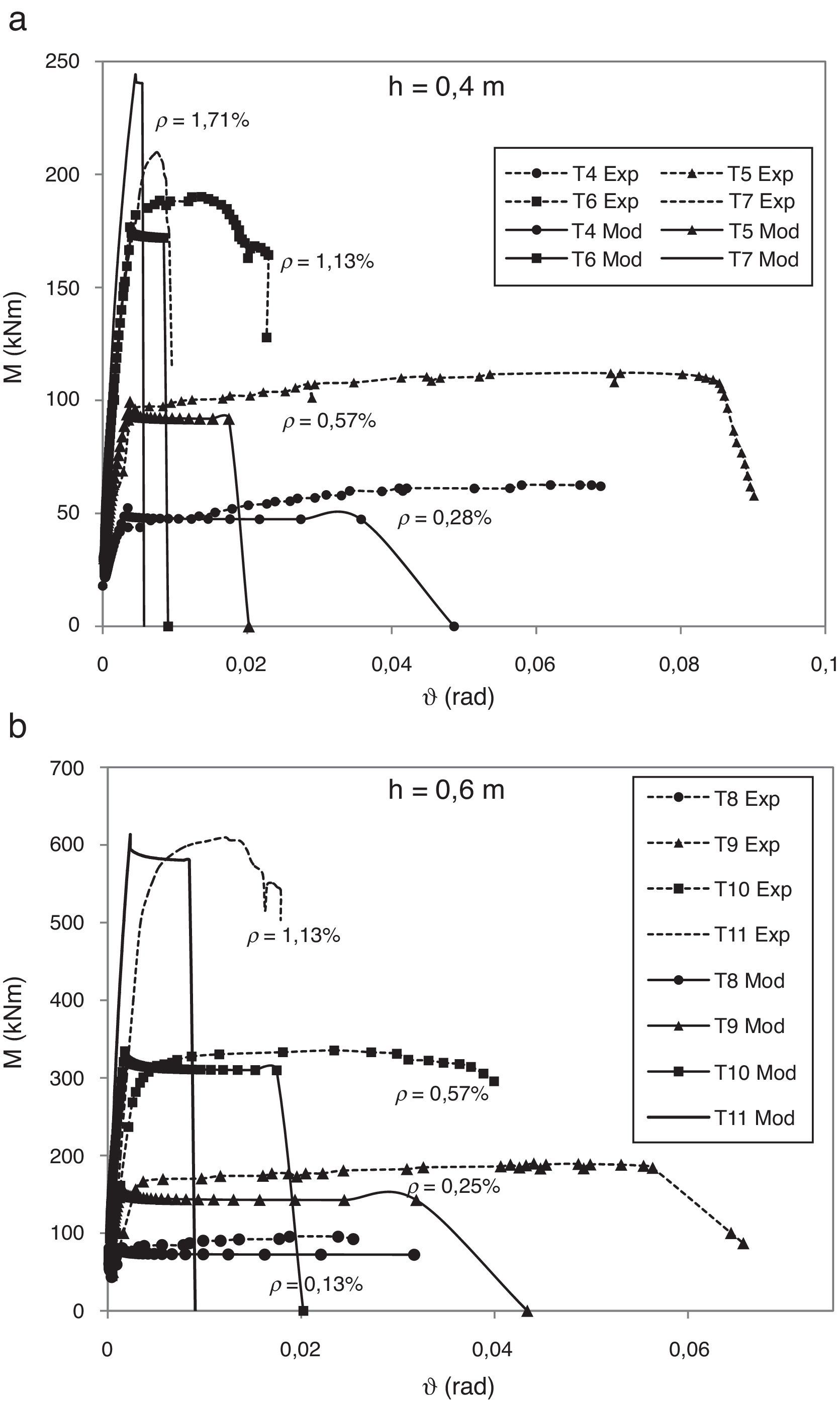
Para cubrir un rango de cuantías de armado mayor se han contrastado los resultados del modelo con una campaña experimental realizada por Bosco y Debernardi en 1992 y cuyos resultados se muestran en la referencia [21]. El rango de cuantías cubre desde secciones débilmente armadas hasta cuantías que inducen un fallo por compresiones excesivas. Se han contrastado los resultados para vigas de 0,4 y 0,6m de canto (fig. 9). En abscisas se representa la rotación de la sección y en ordenadas el momento sobre la sección en el centro de vano.
Contrastación experimental. Ensayos Bosco y Debernardi [21].
También en este caso, los momentos son reproducidos de forma adecuada. En cuanto a la rotación de la sección, en general, los ensayos presentan una rotación mayor en rotura que lo indicado por el modelo. Esto es debido a que en las vigas más armadas aparece más de una fisura y, consecuentemente, la rotación es superior a la calculada. En todo caso, las tendencias observadas experimentalmente son reproducidas por el modelo.
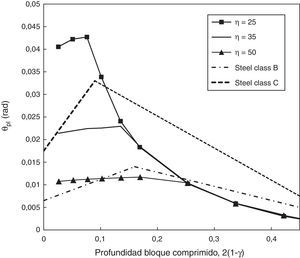
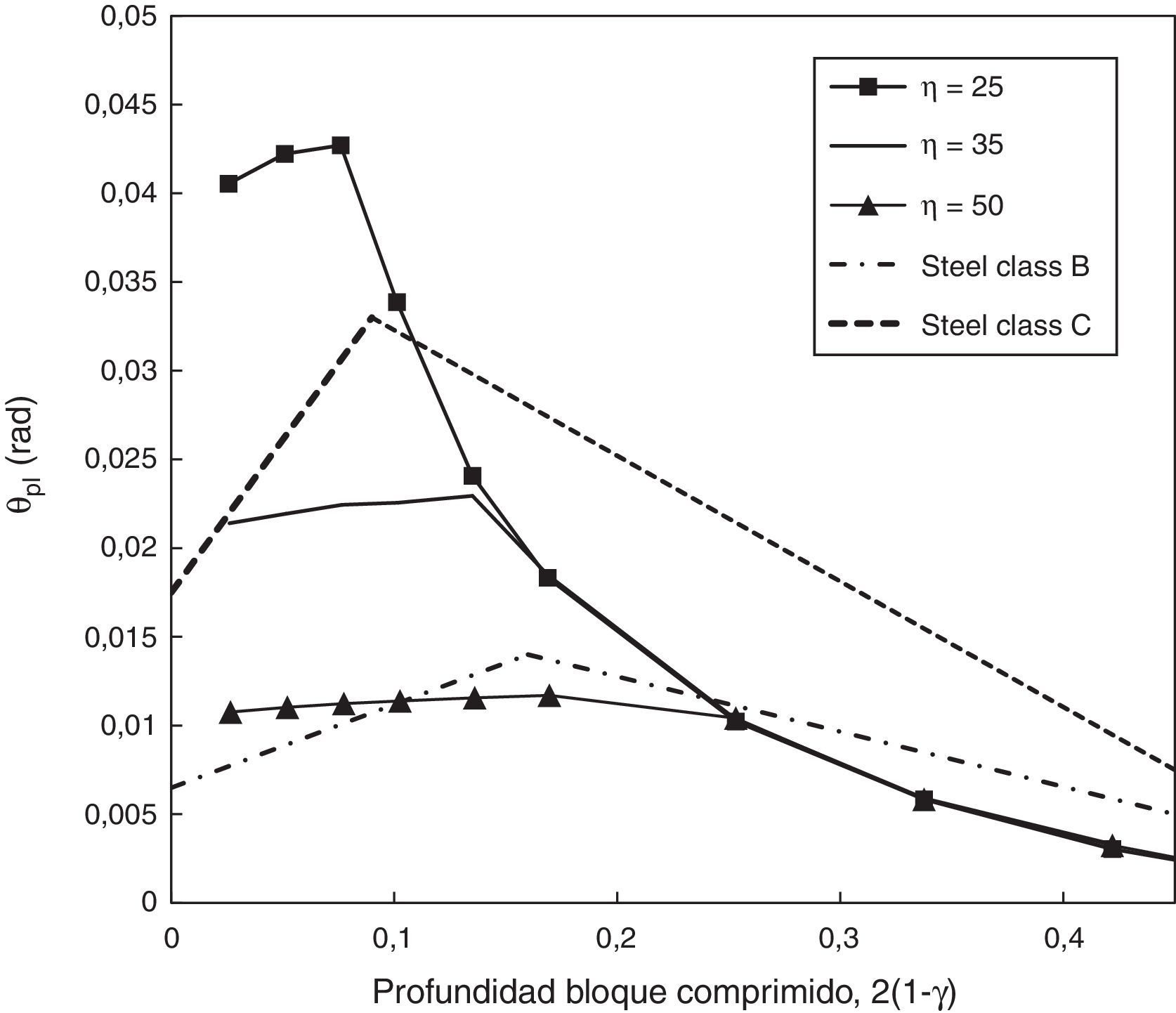
En la figura 10 se muestra la influencia de la adherencia en la rotación plástica para una sección de hormigón armado. En abscisas se representa la profundidad del bloque comprimido y en ordenadas la rotación plástica. Cada curva se ha calculado para una sección manteniendo constante el parámetro que define la adherencia, η. Complementariamente se han dibujado los límites permitidos de giro plástico indicados en el Código Modelo para aceros de clases B y C. Para profundidades bajas, coincidentes en general con cuantías bajas, se observa como el aumento de la adherencia disminuye la capacidad de rotación, ya que en esta zona el fallo se produce por la rotura del acero. Al aumentar la profundidad del bloque comprimido las curvas convergen debido a que el fallo se produce por compresiones excesivas y la influencia de la adherencia desaparece. Los resultados obtenidos se encuentran en el rango establecido por el Código Modelo.
5ConclusionesEl presente trabajo propone una formulación analítica sencilla, basada en conceptos de Mecánica de Fractura, para estudiar el comportamiento de secciones de hormigón armado sometidas a flexión, con especial atención al proceso de avance de una fisura y al modelado de la adherencia hormigón-acero.
Los resultados del modelo se han contrastado con diferentes campañas experimentales, reproduciendo de forma adecuada las tendencias observadas en estas, con especial atención a la transición entre el fallo por plastificación de las barras y el fallo por deformación excesiva en la zona comprimida. Con el modelo se pueden evaluar, en una sola comprobación, el momento último, la apertura de fisura para cada momento aplicado y la rotación plástica de una sección de hormigón armado.
FinanciaciónLos autores agradecen la financiación recibida a través de los proyectos de investigación BIA2015-68678-C2-1-R del Ministerio de Economía y Competitividad, y PEII-2014-016-P de la Junta de Comunidades de Castilla-La Mancha.





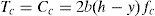
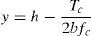
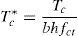
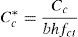
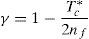
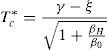
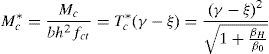
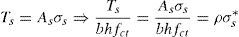
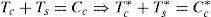
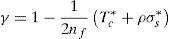
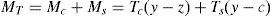
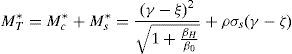
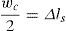
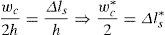
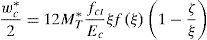
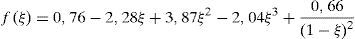
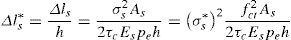
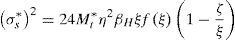
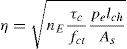
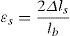
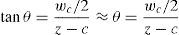
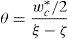
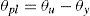
![Contrastación experimental. Ensayos Ruiz, Elices y Planas [13]. Contrastación experimental. Ensayos Ruiz, Elices y Planas [13].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300190/v1_201710110055/es/main.assets/thumbnail/gr8.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
![Contrastación experimental. Ensayos Bosco y Debernardi [21]. Contrastación experimental. Ensayos Bosco y Debernardi [21].](https://static.elsevier.es/multimedia/04395689/0000006800000282/v1_201710110055/S0439568917300190/v1_201710110055/es/main.assets/thumbnail/gr9.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)