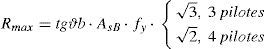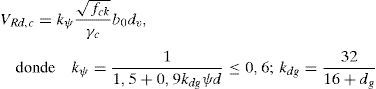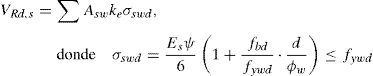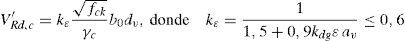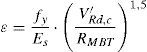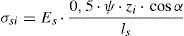Modelos mecánicos para el diseño de encepados de tres y cuatro pilotes solicitados por cargas centradas y excéntricas

Resumen

A partir de los resultados obtenidos de ensayos experimentales propios sobre 30 encepados, solicitados por carga centrada y excéntrica, se proponen dos modelos de bielas y tirantes (MBT) complementarios: uno de descarga directa a los pilotes y otro adicional para captar el efecto de la armadura secundaria horizontal y vertical. Estos MBT definen la carga de plastificación del sistema de armaduras dispuesto, pero el posterior incremento de carga registrado tras la plastificación queda limitado por la rotura por punzonamiento de cada encepado. Se presenta una formulación de punzonamiento basada en la del Código Modelo 2010, adaptando los parámetros que caracterizan la rotura de los encepados de pilotes. Se obtiene así una propuesta de diseño segura, más racional y con un coeficiente de variación menor que el que proporcionan los MBT tradicionales.

Abstract

Using the results obtained from experimental trials on 30 pile caps tested under centric and eccentric loads, two complementary strut-and-tie models (STM) are proposed: the traditional STM by direct load on piles, and the new STM which describes the vertical thrust along sides of the pile caps. These STMs define the yielding load of the reinforcement, but further load increase after yielding is limited by the punching failure of each pile cap. A punching formulation based on Model Code 2010 is presented. Parameters that define the failure surface are adapted to the particular case of deep pile caps. Conservative predictions and a reduced coefficient of variation confirm the good agreement with the proposal.

1

Introducción

Los encepados rígidos se consideran una región D en su totalidad, por lo que actualmente los principales códigos de diseño de estructuras de hormigón [1–3] recomiendan emplear modelos de bielas y tirantes (MBT) para la obtención de la armadura principal en bandas. Se trata de un método basado en el «teorema del límite inferior de la plasticidad», por lo que se asegura que el encepado resistirá la carga de diseño sin alcanzar la rotura. La geometría del modelo para carga centrada es sencilla, pero la definición de zonas nodales congruentes para la comprobación de tensiones puede ser compleja y los factores de eficacia, desarrollados para estados biaxiales de tensiones, pueden resultar inapropiados, tal y como se apunta en el FIB Bulletin 61 [4]. Resulta necesario, por tanto, establecer comprobaciones relativas al fallo del hormigón que limiten la capacidad de estos modelos. De forma simplificada, Adebar et al. [5,6] proponen acotar las tensiones en las secciones de carga y apoyo para evitar de forma indirecta el splitting de las bielas.

El análisis de resultados de la campaña experimental llevada a cabo por los autores [7] sobre encepados de tres y cuatro pilotes, con distintas configuraciones de armado y excentricidades de carga, concluye que los MBT resultan conservadores y además no captan el efecto de la relación vuelo-canto en la resistencia, ni permiten cuantificar la contribución de la armadura secundaria vertical dispuesta. El patrón de fisuración observado revela la existencia de trayectorias de carga hacia las bandas que no quedan bien representadas por los MBT tradicionales, basados en la descarga directa hacia los pilotes. Además, los modos de rotura detectados (una combinación de punzonamiento con plastificación de las armaduras principales) no llegan a ser explicados por estos modelos.

Con el objetivo de identificar el modo de fallo, investigaciones recientes como las de Jensen y Hoang [8] y Simões et al. [9] abordan el análisis de la resistencia de encepados sobre la base del «teorema del límite superior de la plasticidad». Para ello, definen una serie de mecanismos de colapso (punzonamiento, flexión y cortante), de los que se describe su cinemática para evaluar el trabajo producido por las fuerzas exteriores y la energía disipada por las fuerzas interiores en las superficies de rotura definidas. La mínima carga obtenida de cada uno de los mecanismos planteados indica tanto la resistencia como el modo de rotura para la geometría del encepado en cuestión.

2

Objetivos

Se busca completar el análisis de encepados mediante MBT de descarga directa sobre los pilotes, con un modelo complementario que explique las trayectorias de carga hacia las bandas y que permita cuantificar la contribución de las armaduras secundarias.

Para limitar el fallo frágil de estos elementos, se adapta la formulación de punzonamiento del Código Modelo 2010 [10] a las características de la superficie de fallo observada en los especímenes ensayados. El objetivo es hacer una propuesta de diseño de encepados sencilla, extensible a casos complejos con un mayor número de pilotes y válido también para cargas excéntricas.

3

Modelos de bielas y tirantes

Los MBT empleados para el diseño de encepados de pilotes consideran que la carga aplicada a través del pilar se distribuye directamente a los pilotes por bielas inclinadas. Estas son recogidas en el plano inferior por tirantes que las unen, formando una estructura interna tridimensional en equilibrio. Como se trata de un cálculo basado en el «teorema del límite inferior de la plasticidad», la carga de diseño representa un límite inferior de aquellas que causarán la rotura.

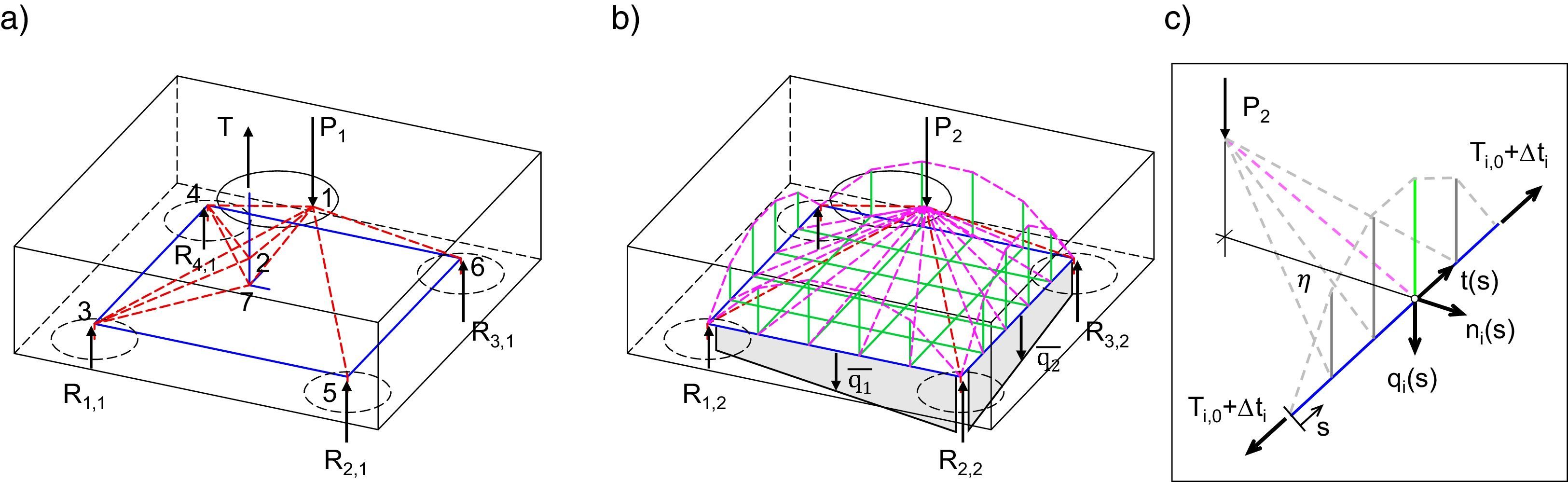
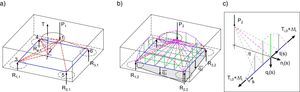
En este apartado se plantea la posibilidad de encontrar un MBT complementario al de descarga directa (en adelante MBT-1, fig. 1a), que proporcione una visión más precisa de los flujos de tensiones desarrollados en el interior del encepado. El segundo modelo presentado (MBT-2, fig. 1b) podrá ser considerado en el dimensionamiento de la armadura secundaria horizontal y vertical, o para evaluación de la resistencia de estructuras existentes en las que resulta complejo justificar la colaboración de estas armaduras.

Figura 1.

MBT complementarios para el diseño de encepados: a) MBT-1; b) MBT-2; c) detalle de transmisión de tracción en las bandas según el MBT-2.

3.1

Modelo de bielas y tirantes-1

El modelo de descarga directa se presenta de forma general para el caso de una flexión compuesta actuando sobre el pilar. La tracción resultante en el pilar (T) se equilibra dentro del encepado en el nudo 2 mediante las bielas 1-2, 2-3 y 2-4. Si en el tramo vertical de esta armadura no se produce la pérdida de su tracción (longitud de anclaje insuficiente), esta debe equilibrarse en el nudo 7 por doblado de la armadura, formándose la biela 1-7. El resto de la componente de compresión (P₁) se reparte hacia los pilotes generando las bielas 1-3, 1-4, 1-5 y 1-6.

Según los resultados obtenidos por los autores en [7], el MBT-1 no capta la influencia de la relación vuelo-canto en la resistencia de los encepados. El aumento de la carga resistida con el canto revela una colaboración de la masa de hormigón en tracción que no se está considerando. Estas tracciones posibilitarían la desviación de las bielas (fig. 2) aumentando su ángulo de inclinación respecto a la horizontal, y con él la reacción máxima (valor de comparación entre encepados con y sin excentricidad de carga) según la ecuación 1. La dirección de estas tracciones explicaría también la inclinación de las fisuras verticales más próximas a los pilotes, que siguen el mismo patrón de fisura crítica que el analizado por Muttoni y Schwartz [11] para el punzonamiento en losas sin armadura de cortante.

Figura 2.

a) Inicio de la fisuración: modelo de descarga directa; b) carga máxima: descarga directa con desvío de compresiones por tirantes de hormigón; c) rotura al formarse la fisura crítica.

3.2

Modelo de bielas y tirantes-2

La disposición de armadura secundaria vertical y horizontal posibilita el desarrollo de mecanismos resistentes secundarios que no se están teniendo en cuenta actualmente con el diseño basado en el MBT-1. Los resultados de la campaña experimental [7] demuestran el incremento de la carga resistida tras la plastificación al añadir armadura secundaria. En los encepados más planos (h = 0,25 m) pasa de un 12,6 a un 32,4% (serie 1, tres pilotes) y de un 5,8 a un 42,2% (serie 2, cuatro pilotes). No ocurre lo mismo en los encepados de mayor canto (h = 0,45 m), en los que la cuantía de armado obtenida para la misma carga de diseño es mucho menor y el porcentaje de carga resistida tras la plastificación se mantiene en torno al 30%, independientemente de la armadura secundaria. En estos casos, tanto la carga de plastificación como la carga última aumentan al disponer armadura secundaria.

El modelo de bielas y tirantes complementario (MBT-2) recoge el concepto de desvío de las bielas directas, presentado en la figura 2, adaptándolo a la posición de las armaduras secundarias para asegurar la transmisión de tracciones. La carga vertical se transmite a las bandas mediante bielas inclinadas. La componente vertical de estas bielas (q_i(s)) es transmitida mediante tirantes a un arco situado en el plano vertical entre pilotes. Este arco solamente genera reacciones verticales porque está atirantado por la armadura de bandas (T_i,0). A esta tracción se le añade un incremento de tracción a lo largo del tirante (Δt_i) debido al apoyo de las bielas en la banda (t(s)). La componente horizontal de las bielas inclinadas (n_i) genera un esfuerzo de membrana sobre el plano inferior del encepado, que requiere un armado perpendicular a la banda. La carga repartida sobre las bandas se determina considerando una distribución lineal que asegure una ley plana de reacciones.

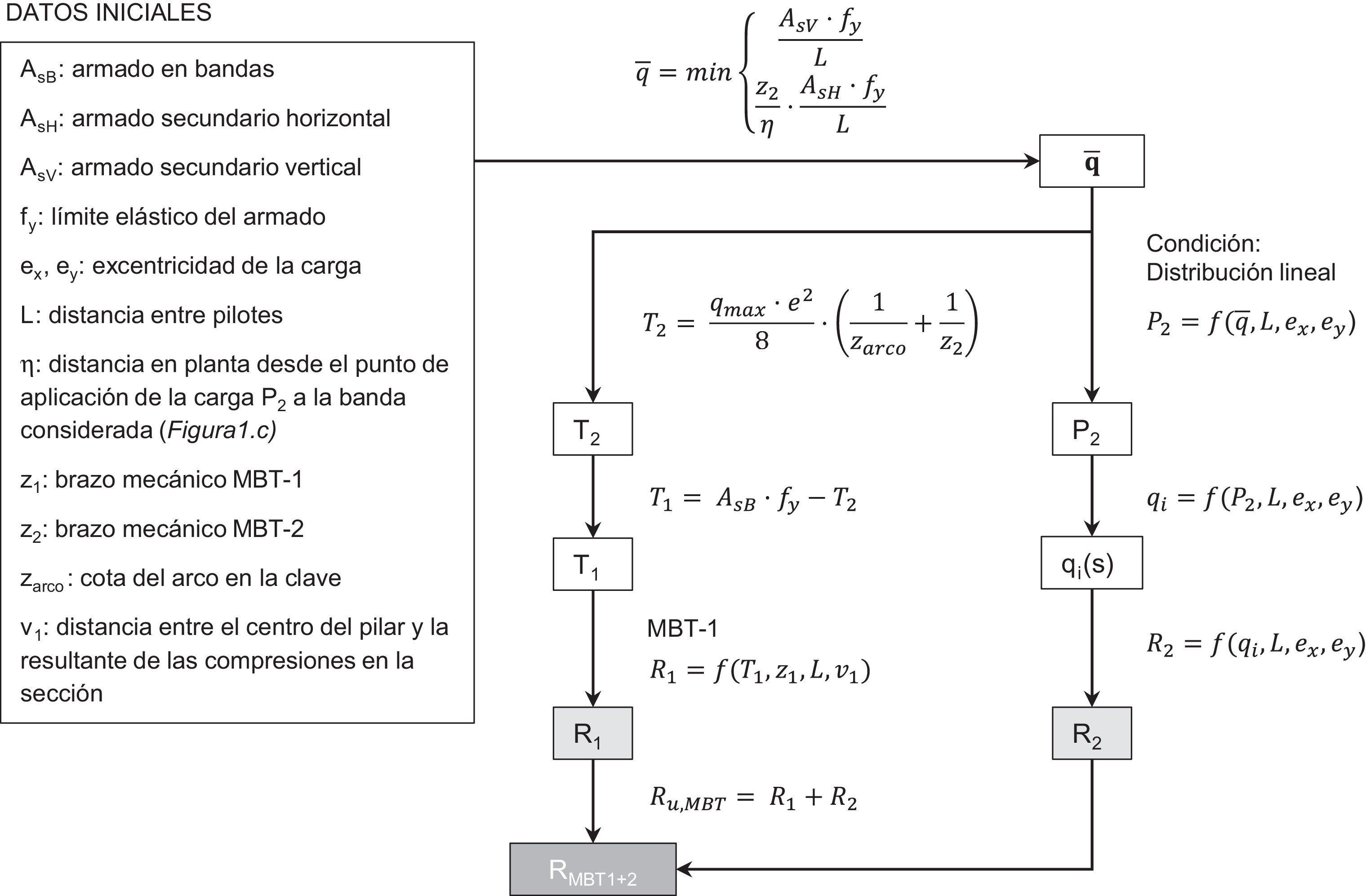
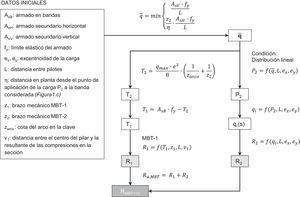
3.3

Reparto de la carga entre los modelos de bielas y tirantes 1 y 2

Como los tirantes principales que unen los pilotes son compartidos por ambos modelos, estos se reparten la proporción de carga resistida (k) y (1 – k) a criterio del proyectista. En una situación de evaluación de la capacidad de un encepado con armaduras secundarias, que haya sido diseñado siguiendo otros criterios, como por ejemplo los establecidos en la EHE-08 [1], el reparto de carga se debe realizar en función de la capacidad de cada MBT, limitado por el área de armadura disponible para cada tirante. En la figura 3 se muestra de forma esquemática el procedimiento a seguir para determinar la carga resistida por cada uno de los MBT planteados (P₁ y P₂).

Figura 3.

Diagrama de cálculo de la carga última considerando MBT-1 y MBT-2, para encepados con armaduras secundarias horizontales y verticales.

En primer lugar se obtiene el valor medio de la carga repartida (q¯) sobre la banda más cargada. Este valor está relacionado con la incidencia de las bielas en las bandas, cuya componente vertical se encuentra limitada por la capacidad del armado secundario vertical (A_sV) y la horizontal por el área del armado secundario distribuido (A_sH).

Tras hallar el valor medio de la carga repartida (q¯) compatible con la distribución de armado dada y conociendo el valor de la excentricidad de la carga aplicada (e_x, e_y), es posible obtener la carga resistida por el MBT-2 (P₂) y la tracción en el tirante principal más solicitado debida al efecto arco y al incremento de tracción por apoyo de las bielas en la banda (T₂ = T_2,0 + Δt₂).

Conocido el valor de P₂ y su excentricidad, se tiene la distribución de carga repartida sobre cada banda (q_i(s)), que en este caso permite hallar la máxima reacción en el pilote debida al MBT-2 (R_2,max) como valor de comparación entre series.

Una vez determinada la tracción T₂, se obtiene la tracción en el tirante principal generada por el apoyo directo de las bandas, que será la diferencia entre la capacidad total y la tracción requerida por el MBT-2 (T₁ = A_sB·f_y – T₂). A partir del valor de T₁ se puede obtener directamente la carga resistida por el MBT-1, en términos de carga aplicada (P₁) o de la reacción en el pilote más solicitado (R_1,max).

Es habitual que al seguir las recomendaciones de la EHE-08 [1] para el cálculo de la armadura distribuida horizontal (50% del armado en bandas) y de los cercos verticales que atan las bandas (carga de diseño entre 1,5 veces el número de pilotes), no se agote la capacidad de los tirantes secundarios verticales u horizontales.

Con esta propuesta es posible justificar una mayor capacidad de carga del encepado, proporcionada por el sistema de armaduras secundarias, que de otra forma está siendo despreciado.

En la tabla 1 se recogen las estimaciones de carga para los encepados de la campaña experimental anteriormente citada, dadas por el MBT-1 y considerando la contribución de las armaduras secundarias horizontales y verticales dada por el MBT-2. Se observa claramente la mejora en la predicción de la carga última al incorporar el MBT-2.

Tabla 1.

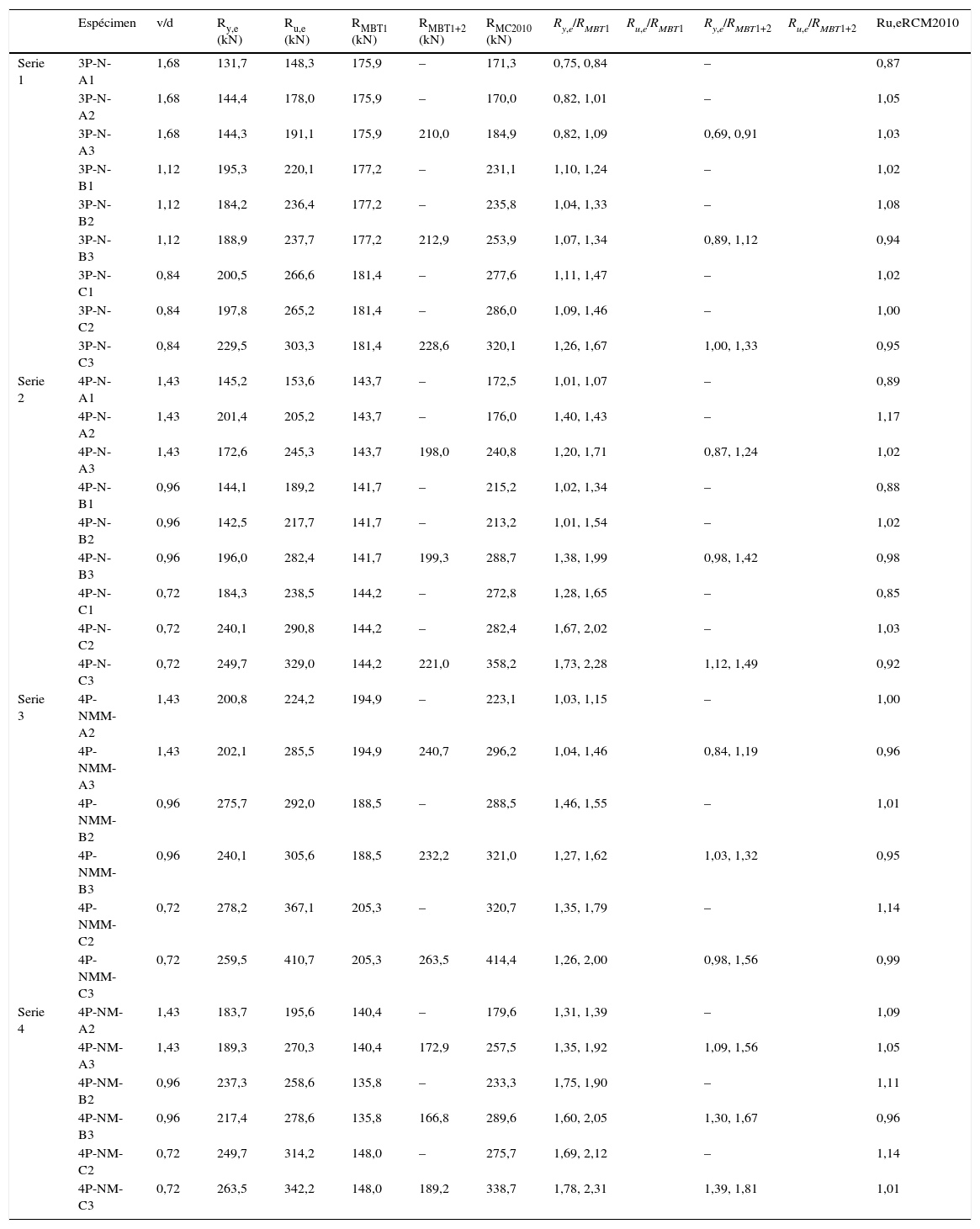
Carga de rotura por pilote y resistencias estimadas por los métodos de bielas y tirantes propuestos y la formulación basada en el Código Modelo 2010

	Espécimen	v/d	Ry,e (kN)	Ru,e (kN)	RMBT1 (kN)	RMBT1+2 (kN)	RMC2010 (kN)	Ry,e/RMBT1 Ru,e/RMBT1	Ry,e/RMBT1+2 Ru,e/RMBT1+2	Ru,eRCM2010
Serie 1	3P-N-A1	1,68	131,7	148,3	175,9	–	171,3	0,75, 0,84	–	0,87
	3P-N-A2	1,68	144,4	178,0	175,9	–	170,0	0,82, 1,01	–	1,05
	3P-N-A3	1,68	144,3	191,1	175,9	210,0	184,9	0,82, 1,09	0,69, 0,91	1,03
	3P-N-B1	1,12	195,3	220,1	177,2	–	231,1	1,10, 1,24	–	1,02
	3P-N-B2	1,12	184,2	236,4	177,2	–	235,8	1,04, 1,33	–	1,08
	3P-N-B3	1,12	188,9	237,7	177,2	212,9	253,9	1,07, 1,34	0,89, 1,12	0,94
	3P-N-C1	0,84	200,5	266,6	181,4	–	277,6	1,11, 1,47	–	1,02
	3P-N-C2	0,84	197,8	265,2	181,4	–	286,0	1,09, 1,46	–	1,00
	3P-N-C3	0,84	229,5	303,3	181,4	228,6	320,1	1,26, 1,67	1,00, 1,33	0,95
Serie 2	4P-N-A1	1,43	145,2	153,6	143,7	–	172,5	1,01, 1,07	–	0,89
	4P-N-A2	1,43	201,4	205,2	143,7	–	176,0	1,40, 1,43	–	1,17
	4P-N-A3	1,43	172,6	245,3	143,7	198,0	240,8	1,20, 1,71	0,87, 1,24	1,02
	4P-N-B1	0,96	144,1	189,2	141,7	–	215,2	1,02, 1,34	–	0,88
	4P-N-B2	0,96	142,5	217,7	141,7	–	213,2	1,01, 1,54	–	1,02
	4P-N-B3	0,96	196,0	282,4	141,7	199,3	288,7	1,38, 1,99	0,98, 1,42	0,98
	4P-N-C1	0,72	184,3	238,5	144,2	–	272,8	1,28, 1,65	–	0,85
	4P-N-C2	0,72	240,1	290,8	144,2	–	282,4	1,67, 2,02	–	1,03
	4P-N-C3	0,72	249,7	329,0	144,2	221,0	358,2	1,73, 2,28	1,12, 1,49	0,92
Serie 3	4P-NMM-A2	1,43	200,8	224,2	194,9	–	223,1	1,03, 1,15	–	1,00
	4P-NMM-A3	1,43	202,1	285,5	194,9	240,7	296,2	1,04, 1,46	0,84, 1,19	0,96
	4P-NMM-B2	0,96	275,7	292,0	188,5	–	288,5	1,46, 1,55	–	1,01
	4P-NMM-B3	0,96	240,1	305,6	188,5	232,2	321,0	1,27, 1,62	1,03, 1,32	0,95
	4P-NMM-C2	0,72	278,2	367,1	205,3	–	320,7	1,35, 1,79	–	1,14
	4P-NMM-C3	0,72	259,5	410,7	205,3	263,5	414,4	1,26, 2,00	0,98, 1,56	0,99
Serie 4	4P-NM-A2	1,43	183,7	195,6	140,4	–	179,6	1,31, 1,39	–	1,09
	4P-NM-A3	1,43	189,3	270,3	140,4	172,9	257,5	1,35, 1,92	1,09, 1,56	1,05
	4P-NM-B2	0,96	237,3	258,6	135,8	–	233,3	1,75, 1,90	–	1,11
	4P-NM-B3	0,96	217,4	278,6	135,8	166,8	289,6	1,60, 2,05	1,30, 1,67	0,96
	4P-NM-C2	0,72	249,7	314,2	148,0	–	275,7	1,69, 2,12	–	1,14
	4P-NM-C3	0,72	263,5	342,2	148,0	189,2	338,7	1,78, 2,31	1,39, 1,81	1,01

4

Limitación de tensiones en el hormigón

Para completar el análisis basado en el método de bielas y tirantes es necesario comprobar el estado tensional en bielas y zonas nodales, de forma que no se produzca la rotura debida al hormigón por compresión o tracciones indirectas (splitting).

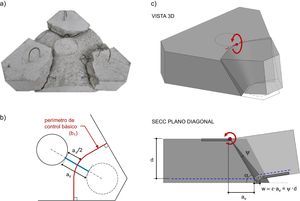
La similitud existente en los modos de rotura de la mayoría de encepados con un fallo por punzonamiento plantea considerar como criterio de limitación de tensiones en el hormigón una comprobación de punzonamiento de losas adaptada a las particularidades de la superficie de rotura observada (fig. 4a). En ese sentido, el artículo 10.4.5 del FIB Bulletin 12 [12] destaca la importancia de la geometría de la superficie de rotura en la resistencia a punzonamiento, especialmente cuando esta difiere de la normalmente considerada. Los ensayos sobre losas realizados por Regan [13], con variaciones en su geometría y en la distancia pilar-apoyos, lo constatan. Posteriormente Regan [14] propone un cambio en el perímetro crítico propuesto por el Código Modelo 90 [15] (precursor del actual Eurocódigo 2), pasando de 2 d a d/4, para la comprobación de punzonamiento en losas bajo cargas muy concentradas.

Figura 4.

a) Superficie de rotura por punzonamiento (espécimen 3P-N-A3); b) perímetro de control básico (b₁); c) cinemática de la rotura por punzonamiento de encepados rígidos.

4.1

Código Modelo 2010: punzonamiento de losas

La formulación de punzonamiento que presenta el Código Modelo 2010 [10] se basa en la Teoría de la fisura crítica (CSCT por sus siglas en inglés) propuesta por Muttoni y Schwartz [11], tal y como se describe en el artículo de Fernández Ruiz et al. [16]. El concepto de fisura crítica se desarrolla para explicar el fallo por cortante en vigas sin armadura de cortante, en las que resulta necesario admitir la colaboración del hormigón en tracción para completar una celosía de transmisión de tensiones, y se extiende al fallo por punzonamiento de losas. Esta fisura crítica es responsable de la reducción de la carga última, y su abertura (proporcional a la rotación de la losa [ψ] y al canto útil [d]) y su rugosidad (función del tamaño máximo de árido [d_g]) se relacionan con la resistencia a punzonamiento. Admitiendo además que la resistencia a cortante es proporcional a la raíz cuadrada de la resistencia a compresión del hormigón, resulta la formulación que ha sido adoptada por el Código Modelo 2010 (ecuación 2).

El valor de la rotación de la losa en torno al pilar se puede determinar según distintos niveles de aproximación que aumentan en complejidad y precisión: desde fórmulas simplificadas basadas en ecuaciones analíticas (nivel de aproximación i) hasta modelos no lineales de elementos finitos (nivel de aproximación iv).

La ecuación 3 permite evaluar la contribución del armado de punzonamiento (A_sw) a la resistencia. La tensión en la armadura (σ_swd) se obtiene a partir de la expresión general propuesta por Fernández Ruiz y Muttoni [17] para la cinemática de la fisura crítica. La ecuación simplificada recogida en el Código Modelo 2010 [10] asume una tensión media para las armaduras de punzonamiento igual a la del armado situado a 0,5 d del área de apoyo o carga puntual. Además considera de forma implícita que el ángulo de inclinación de la fisura crítica (α) es 45°.

4.2

Teoría de la fisura crítica adaptada a encepados de pilotes

A partir de los resultados de la campaña experimental de referencia [7] se revisan los parámetros clave de la formulación de punzonamiento del Código Modelo 2010 [10], basada en la teoría de la fisura crítica, para adaptarla a la comprobación de encepados de pilotes. La estimación de carga de la propuesta final (R_CM2010 = V_Rd,c’ + V_Rd,s) se recoge también en la tabla 1.

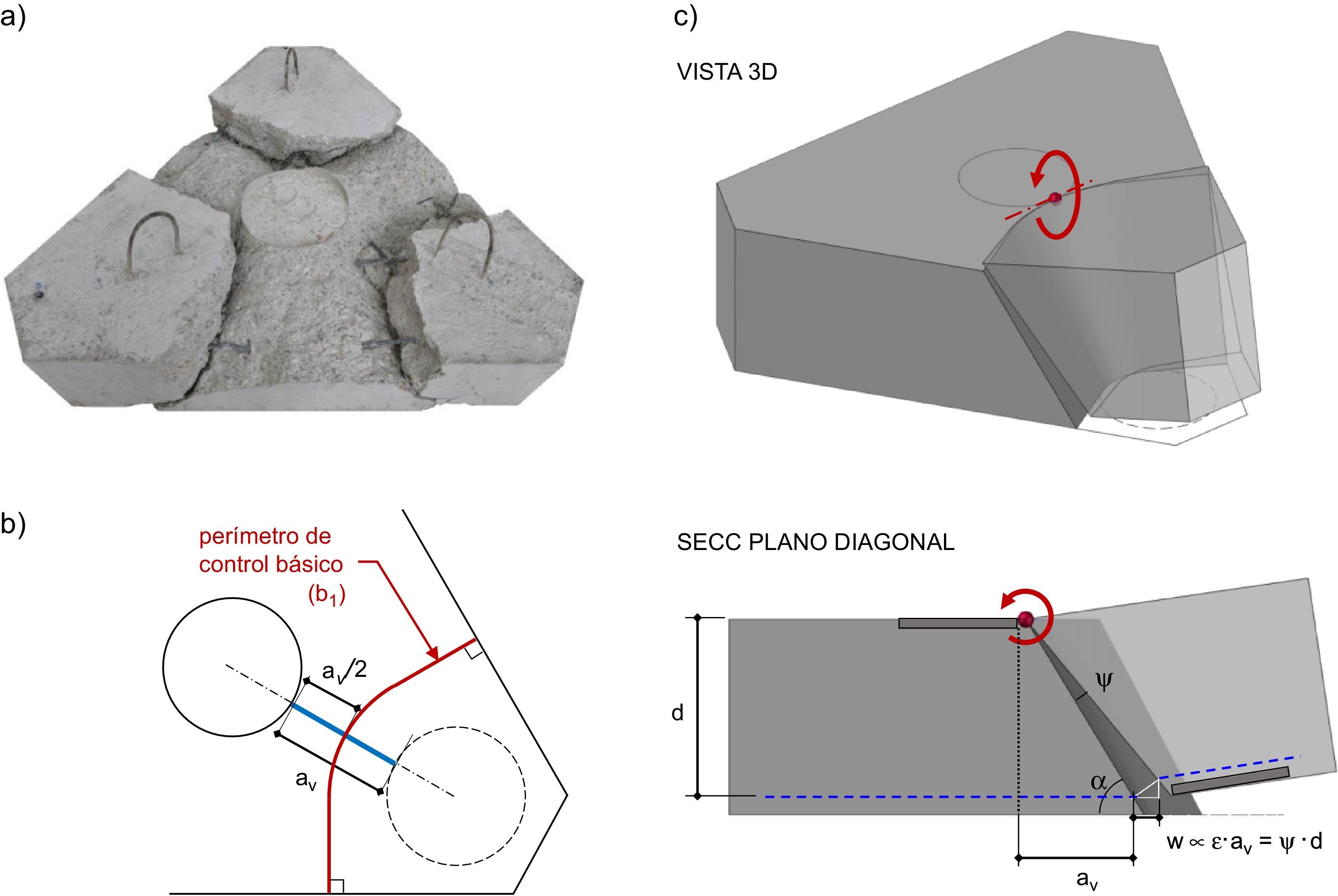
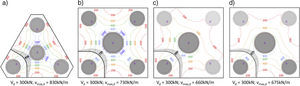
4.2.1

Perímetro de control básico (b₁) para encepados rígidos

La superficie de rotura por punzonamiento observada en los encepados (fig. 4a) viene condicionada por la proximidad entre carga y apoyos. Si la carga es centrada, la rotura divide al encepado en sólidos, uno sobre cada pilote y otro sólido central bajo el pilar. Si el encepado se halla solicitado a flexión esviada, se separa únicamente el pilote que soporta mayor carga. Si el encepado se halla solicitado a flexión recta se mantiene este comportamiento en los dos pilotes más cargados, sin que se aprecie la formación de un plano de corte que atraviese la pieza. Cada uno de los sólidos sobre los pilotes puede simplificarse como tronco de cono (fig. 4c), cuya directriz resulta de unir en diagonal los bordes de pilar y pilote. La distancia entre los bordes de la carga aplicada y los apoyos (a_v, función del canto y de la separación de apoyos) será la que condicione la geometría de este sólido y, por tanto, la superficie de rotura. De forma análoga a la descrita en el Código Modelo 2010 [10], se considera que el perímetro de control básico (b₁) se sitúa en el plano medio de la superficie de rotura (vista en planta en la fig. 4b).

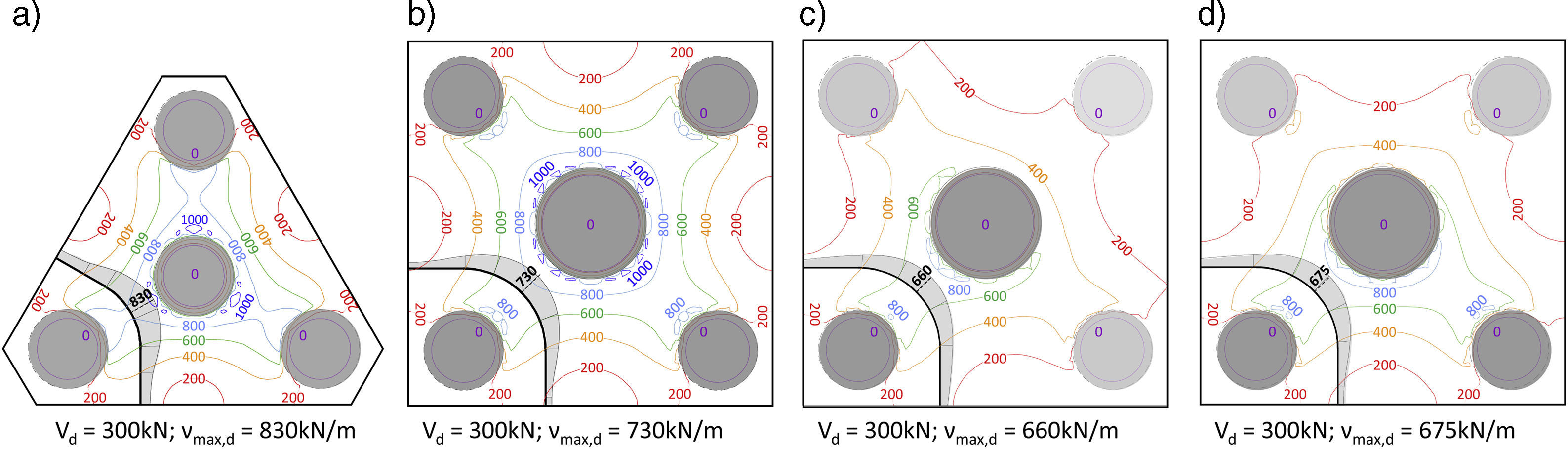
4.2.2

Coeficiente de excentricidad

Cuando la distribución de esfuerzos cortantes no es uniforme a lo largo del perímetro básico, es necesario definir un perímetro de control de cortante (b₀) equivalente, sobre el que sea posible considerar la resistencia a punzonamiento por unidad de longitud uniforme. Vaz Rodrigues et al. [18] plantean una metodología general para la determinación de este perímetro de control que consiste en hallar el valor máximo del esfuerzo cortante principal por unidad de longitud (v_max,d) perpendicular al perímetro de control básico (b₁), a partir de un modelo de elementos finitos elástico y lineal. El perímetro de control (b₀) se obtiene dividiendo la carga puntual (V_d) entre v_max,d. El coeficiente de excentricidad (k_e) relaciona ambos perímetros de control: k_e = b₁/b₀. En la figura 5 se muestra el resultado para los encepados estudiados.

Figura 5.

Isolíneas de cortante por unidad de longitud: a) tres pilotes: carga centrada; b) cuatro pilotes: carga centrada; c) cuatro pilotes: flexión esviada; d) cuatro pilotes: flexión recta.

4.2.3

Abertura de la fisura crítica

La cinemática del fallo por punzonamiento se describe en la figura 4c como una rotación del sólido sobre el pilote en torno a un punto situado en la cara superior del encepado en la intersección de la diagonal con el perímetro del pilar. La abertura de fisura (w) se considera proporcional a la deformación horizontal en la base (¿) por la distancia libre pilar-pilote (a_v), en vez de a la rotación del encepado entorno al pilar (ψ) por el canto útil (d), aunque son equivalentes. Se considera preferible expresarla en términos de deformación de la base para establecer una relación más sencilla con el armado dispuesto en bandas y la armadura secundaria horizontal. De esta forma, al sustituir el factor ψ·d de la ecuación 2 por ¿·a_v, resulta la propuesta para el cálculo de la contribución del hormigón a la resistencia frente a punzonamiento (V_Rd,c’, ecuación 4).

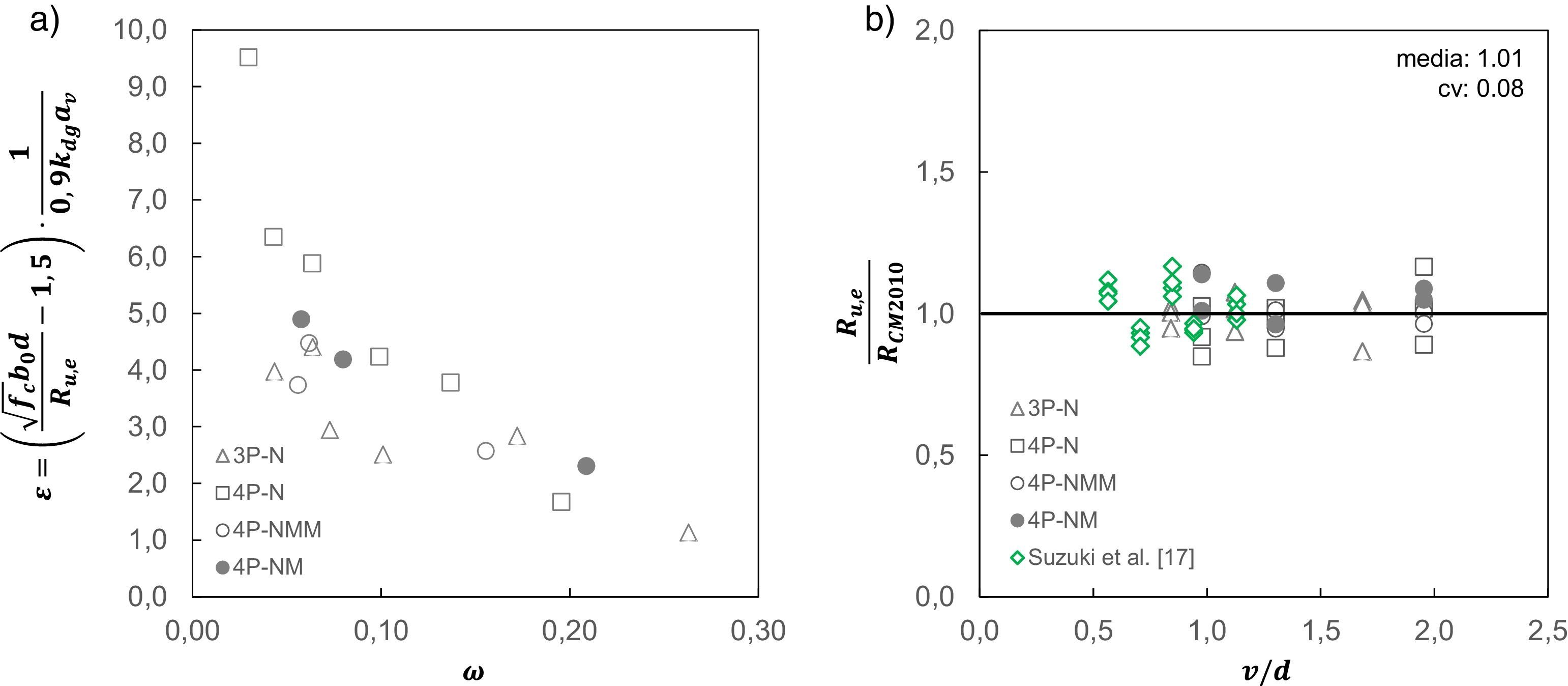
Se requiere por último definir una expresión para el cálculo aproximado de las deformaciones en la base, de forma similar a la adoptada por los dos primeros niveles de aproximación que plantea el Código Modelo 2010 [10]. Al representar gráficamente (fig. 6a) la deformación esperable en la base (¿) frente a la cuantía mecánica (ω) de cada espécimen, se observa que es decreciente con el aumento de la cuantía de armadura. Experimentalmente se comprueba que los encepados de menor canto (mayor cuantía) rompieron con deformaciones en la base menores que los de mayor canto: ¿_u,3P-N-A1 = 3,02‰ frente a ¿_u,3P-N-C1 = 8,77‰ y ¿_u,4P-N-A1 = 2,70‰ frente a ¿_u,4P-N-C1 = 17,19‰. La deformación en la base (¿) resulta en todos estos casos mayor a la de plastificación (¿_y). Por otra parte, se observa que los encepados de mayor canto (menor cuantía) resisten mayor porcentaje de carga tras la plastificación de las armaduras principales que los de menor canto, debido a la existencia de mecanismos de redistribución interna de tensiones: ΔP_u/P_y,3P-N-A1 = 12,6% frente a ΔP_u/P_y,3P-N-C1 = 32,4% y ΔP_u/P_y,4P-N-A1 = 5,8% frente a ΔP_u/P_y,4P-N-C1 = 29,4%.

Figura 6.

a) Relación entre el parámetro de deformación en la base (¿) y la cuantía mecánica (ω); b) ajuste entre la carga última y la estimada por punzonamiento basado en el CM 2010.

Ambas evidencias experimentales conducen a la definición de un factor amplificador de la deformación ¿_y, basado en la relación entre la propia resistencia a punzonamiento en torno al pilote (V_Rd,c’) y la carga de plastificación de las armaduras (R_MBT) obtenida con los MBT propuestos: MBT-1 para los encepados sin armadura secundaria vertical y MBT-1 + 2 para aquellos que sí la tienen. De forma simplificada, puede calcularse la R_MBT de los encepados con armadura vertical empleando el modelo de descarga directa, obteniendo resultados del lado de la seguridad.

Se propone la ecuación 5 para la determinación de la deformación en la base que permite obtener la resistencia a punzonamiento en encepados de pilotes, a partir de un cálculo iterativo.

Analizando las ecuaciones planteadas, en el caso de que se supere la carga de plastificación (V_Rd,c’/R_MBT) > 1, al seguir aumentando la carga resistida se incrementa a su vez la deformación en la base y se va degradando la capacidad del encepado hasta alcanzar la carga de rotura. En el caso de encepados fuertemente armados a flexión (V_Rd,c’/R_MBT) < 1 la rotura sería frágil sin plastificación de las armaduras en banda.

4.2.4

Armadura secundaria vertical

Para determinar la tensión en la armadura vertical (σ_swd) se recurre a la expresión general dada por Fernández Ruiz y Muttoni [17] para el caso de armadura sin adherencia (ecuación 6).

Según esta ecuación, la tensión dependerá tanto del ángulo de inclinación de la fisura crítica (α en la fig. 4c) como de la altura a la que la superficie de rotura cruza con el armado (z_i) y de la longitud total del cerco (l_s). La rotación de la losa (ψ) se obtiene como ¿·a_v/d para cada caso.

4.2.5

Aplicación a la base de ensayos experimental

Con el objetivo de verificar el modelo, se aplica la formulación descrita a los ensayos experimentales propios (30 especímenes) y a otros 20 ensayos de encepados de cuatro pilotes bajo carga centrada con variaciones en la configuración de armado, relación vuelo-canto y cuantías mecánicas, pertenecientes a la serie de Suzuki et al. [19]. Para analizar estos especímenes se ha considerado un coeficiente de excentricidad de 0,65, tal y como indica el Código Modelo 2010 [10] para cargas en esquina, en vez de realizar el análisis de la distribución de esfuerzos cortantes con un modelo de elementos finitos. La serie de encepados de Suzuki et al. [19] compara 10 especímenes con armadura concentrada en bandas y otros 10 con la misma armadura distribuida en la base. Para definir la carga de plastificación de las armaduras (R_MBT) en el segundo caso, se ha considerado únicamente el armado dispuesto sobre el ancho de la banda. Esta aproximación resulta más segura (media para los 10 especímenes con armado distribuido: 1,01, con γ_c = 1) que si se considera como armadura de banda la mitad del armado distribuido dispuesto en cada dirección (media 0,94, con γ_c = 1).

La gráfica de la figura 6b ilustra el buen ajuste obtenido en la predicción de cargas de rotura con la teoría de la fisura crítica adaptada a encepados (media 1,01 y coeficiente de variación 0,08).

La tabla 1 muestra las estimaciones de carga obtenidas por los MBT descritos en el apartado 3 y por la formulación de punzonamiento del Código Modelo 2010 [10] adaptada a los encepados de la campaña experimental de referencia.

5

Conclusiones

Es necesario revisar los criterios para el diseño de encepados rígidos, basados en MBT de descarga directa (MBT-1), que resultan excesivamente conservadores en algunos casos y no permiten tener en cuenta las armaduras secundarias horizontales y verticales que prescribe por ejemplo la EHE-08 [1].

El MBT-2 propuesto complementa el modelo de descarga directa, repartiendo parte de la carga sobre las bandas. Es un modelo desarrollado para los casos en los que existen estas armaduras secundarias, y la estimación de carga de rotura respecto a los encepados estudiados confirma su validez. Con el MBT-2, el diseño de las armaduras secundarias horizontales y verticales queda justificado con un criterio mecánico que otorga mayor libertad y seguridad al proyectista, al tiempo que permite optimizar la distribución de armado.

Los MBT requieren una comprobación adicional de resistencia del hormigón (bielas y nudos), que en este caso se sustituye por una verificación de la resistencia a punzonamiento. Se ha enfocado el análisis tomando como referencia la teoría de la fisura crítica, que explica la resistencia a cortante o punzonamiento en vigas y losas sin armadura vertical. De forma análoga se han encontrado posibles trayectorias de compresiones y tracciones resistidas por el hormigón que justifican el desarrollo de esta fisura crítica y el incremento de resistencia al aumentar el canto disponible.

Se presentan las claves para adaptar la formulación de punzonamiento del Código Modelo 2010 [10] al caso particular de encepados. En primer lugar, el perímetro de control básico (b₁) está condicionado por la separación en planta de pilar y pilotes. En segundo lugar, es recomendable realizar una aproximación del coeficiente de excentricidad (k_e) mediante modelos EF dada la irregularidad de la distribución de cortantes en el perímetro de control básico, aunque se considera válido el valor propuesto por el Código Modelo 2010 [10] para pilares en esquina (k_e = 0,65). Por último, se describe la abertura de fisura proporcional a la deformación horizontal (¿) en la base del encepado, cuyo valor depende de la carga de plastificación determinada a partir de los MBT propuestos. Al introducir en la formulación planteada este parámetro es posible tener en cuenta la influencia del armado dispuesto. Además, según el valor del cociente (V_Rd,c’/R_MBT) es posible determinar si la rotura se produce antes o después de la plastificación de la armadura.

También es posible considerar la contribución de la armadura secundaria vertical (V_Rd,s) acudiendo a la expresión general para el cálculo de la tensión de trabajo en función de la cinemática de la fisura crítica descrita.

Agradecimientos

Los autores agradecen la financiación recibida por el Ministerio de Economía y Competitividad a través del Subprograma de Proyectos de Investigación Fundamental no orientada al proyecto Estudio Experimental y Numérico de Regiones D Tridimensionales de Hormigón Armado: Encepados y Cálices (BIA2012-323000) y mediante las ayudas para contratos predoctorales para la formación de doctores (BES-2013-063409).