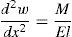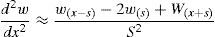Detección de daño en vigas de hormigón pretensado mediante el método de curvatura de la elástica

Resumen

En el momento de inspeccionar y garantizar la seguridad de una estructura existente es importante contar con técnicas adecuadas que permitan detectar la presencia de daño en la misma. En el presente trabajo se estudia el método de curvatura de la elástica, aplicado específicamente a la detección de fisuras por flexión en vigas de hormigón pretensado, tipología ampliamente utilizada en puentes carreteros. Los estudios se realizaron sobre un conjunto de modelos tridimensionales, mediante el método de los elementos finitos. Se realizaron distintos análisis de sensibilidad que permitieron determinar con éxito los distintos parámetros requeridos por el método de curvatura de la elástica en el momento de ser llevado a la práctica.

Abstract

At the time of inspecting and ensuring the safety of an existing structure, it is important to have proper techniques to detect the presence of damage in that structure. In this work, a study is made of the method of curvature of the elasticity, applied specifically to the detection of bending cracks in pre-stressed concrete beams, a typology widely used in highway bridges. The studies were performed on a set of three-dimensional models, using the finite element method. Different sensitivity analyses were carried out to determine, successfully, the required parameters for the implementation of the method of curvature of the elasticity in practice.

1

Introducción

Las patologías que pueden presentar las estructuras de hormigón pretensado son variadas, no obstante, al igual que en toda estructura de hormigón, la manifestación más corriente de las mismas es a través de la aparición de fisuras. Esto ha dado lugar a numerosos estudios acerca de la fisuración del hormigón pretensado en distintas edades del mismo y por diversas causas [1,2,3].

Si bien, en muchos casos, una estructura de hormigón que presenta fisuras, puede igualmente cumplir su función estructural, dependiendo del grado de avance del daño y la velocidad de extensión del mismo; la sola presencia de las mismas merece la atención, ya que pueden significar un riesgo potencial para la seguridad de la estructura. Además, en una estructura de hormigón armado o pretensado inicialmente fisurada, las mismas facilitan el ingreso de agentes corrosivos que pueden alcanzar al acero, con el agravante, en el caso del acero de pretensar, que el mismo es mucho más sensible a la corrosión que el acero de armar, al trabajar a tensiones mucho más elevadas, ya que para el mismo valor de pérdida de sección, la disminución en su resistencia resulta mucho más traumática, pudiendo llegarse a una falla progresiva de los cables de pretensado [4,5].

Dentro de las distintas patologías que pueden presentar las estructuras de hormigón pretensado, en este trabajo, se estudian aquellas que se manifiestan a través de típicas fisuras de flexión.

Las fisuras por flexión que aparecen en condiciones de servicio, en la cara inferior del elemento estructural, son fisuras verticales, normalmente de altura creciente hacia el centro de la luz. El ancho de las mismas es variable, cerrándose hacia la parte superior. Son varias las causas que pueden dar origen a la aparición de estas fisuras, encontrándose entre las más frecuentes la pérdida en la fuerza de pretensado que se da con el paso del tiempo, posibles excesos en las solicitaciones de servicio, defectos constructivos y asentamientos diferenciales en estructuras hiperestáticas, entre otras [6]. Dichas causas pueden darse en forma individual o bien combinadas entre sí, agravando la situación.

Una particularidad en las estructuras de hormigón pretensado, respecto al hormigón armado, es que en el caso de las primeras, la acción del pretensado tiende a mantener a las fisuras cerradas, una vez que la causa que las originó ha desaparecido. Esto dificulta incluso las inspecciones visuales de la estructura como primer diagnóstico general. De esta manera, surge la necesidad de desarrollar y/o validar métodos que permitan inspeccionar el estado de la estructura en cuestión con la finalidad de, primero detectar la presencia de daño, luego localizarlo y en lo posible cuantificarlo, con el objetivo de tomar posteriores medidas de intervención.

En este trabajo, se evalúa la aplicabilidad de un método de detección de daño que llamaremos método de curvatura de la elástica (MCE), sobre vigas de hormigón pretensado y las consideraciones a tener en cuenta, a fin de detectar posibles fisuras discretas presentes en las mismas. Este método presentado en el año 1991 por Pandey et al. [7] se ha aplicado con éxito en diversos tipos de estructuras. En el trabajo presente, el método es aplicado a partir de desplazamientos obtenidos en forma estática [8,9,10,11][12], aunque también puede ser aplicado a partir de desplazamientos obtenidos para excitaciones dinámicas de la estructura [7,13,14].

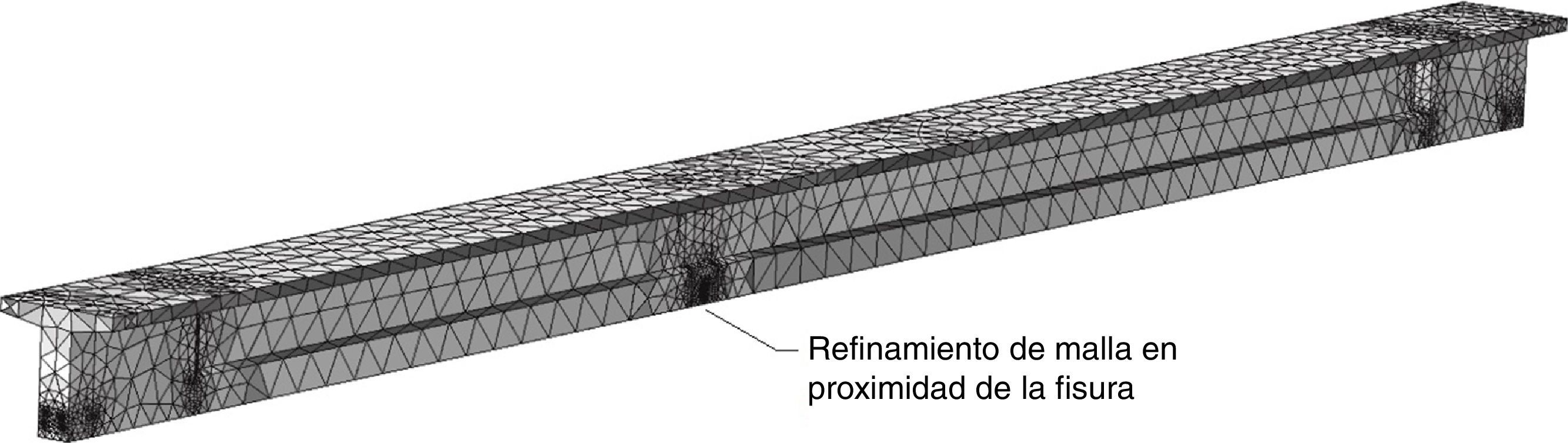
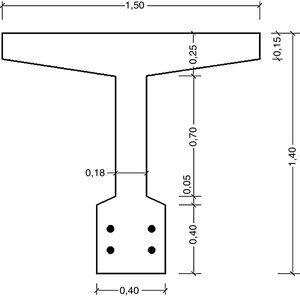
El objetivo planteado en este trabajo, fundamentalmente es profundizar en cuestiones que tienen que ver con la aplicación del método en la práctica, para lo cual se realizaron diversos análisis de sensibilidad, tales como densidad de mediciones necesarias y precisión de las mismas, entre otras que se comentan en las siguientes secciones. Para ello, se modeló mediante el método de los elementos finitos, una viga típica de un puente de hormigón pretensado, simplemente apoyada, de sección tipo T. En primer lugar, se modeló y analizó la viga no fisurada y luego se introdujo una fisura discreta, en la zona inferior de la misma, en distintas posiciones de su longitud y con profundidades variables. Un detalle de la misma puede observarse en las figuras 1 y 2. Posteriormente, se aplicó el MCE con el fin de validarlo, y de determinar su eficacia para detectar, localizar y cuantificar la presencia de daño.

Figura 1.

Vista lateral y secciones de la viga.

Figura 2.

Sección transversal de la viga en la zona central de la luz.

Cabe mencionar que el modelo analizado se proyectó de acuerdo a la norma CIRSOC 201 [15] la cual está fuertemente inspirada en la norma norteamericana ACI 318 [16].

2

Características del modelo

La modelización numérica de la estructura en estudio queda definida mediante la geometría, las propiedades mecánicas, los estados de carga y la configuración del estado de fisuración.

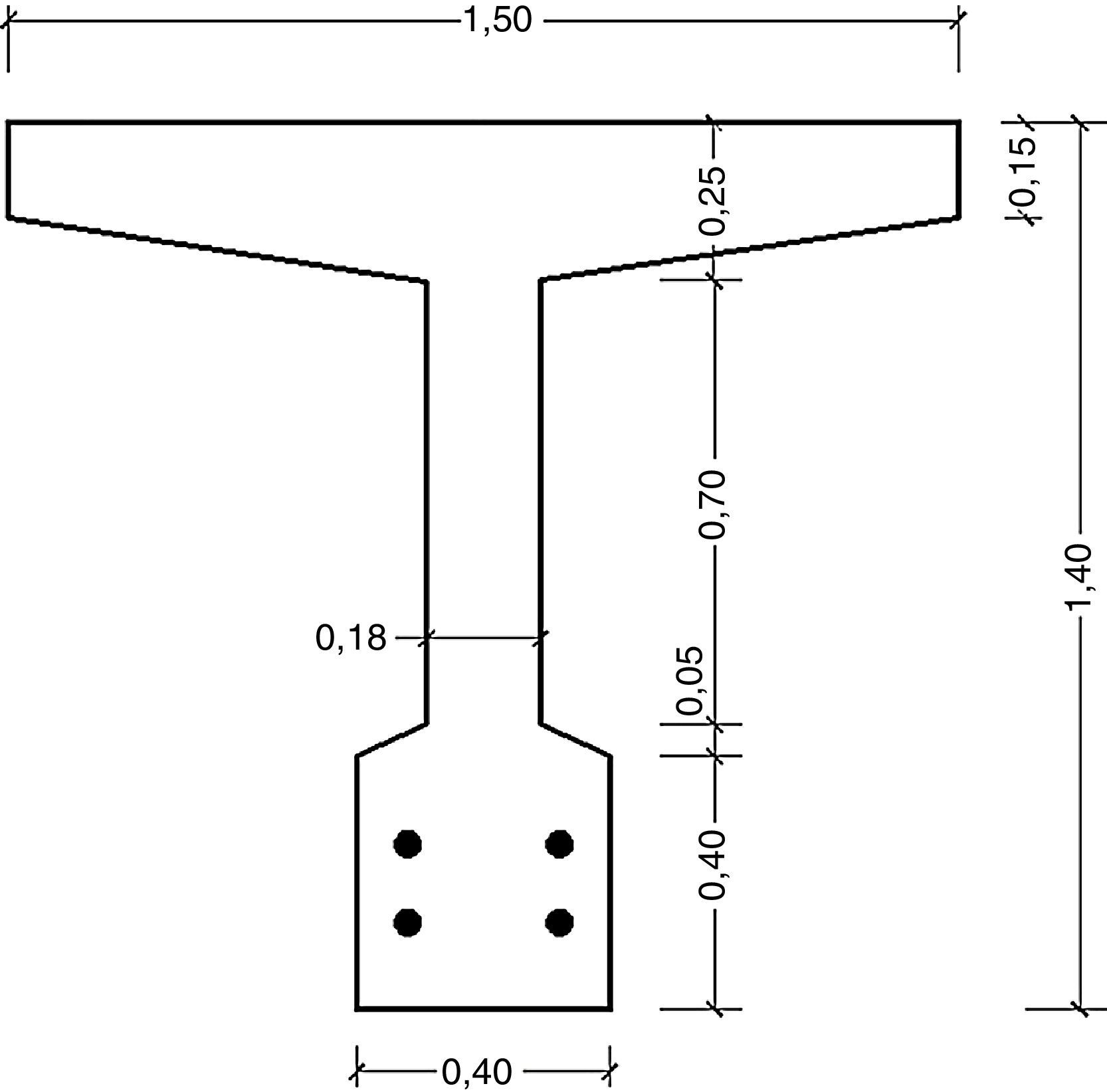
2.1

Geometría

Se trata de una viga simplemente apoyada, de sección tipo T, con cuatro cables rectos adherentes. Las características geométricas de la viga con sus dimensiones se ilustran en las figuras 1 y 2.

En cuanto a la armadura de pretensado, las características de la misma son las siguientes:

• -

  Área total del acero de pretensado: 55,42 cm².

• -

  Distancia desde la fibra superior al baricentro de la armadura de pretensado: 1,20 m.

La viga descrita corresponde al diseño del tablero de un puente, Categoría A-30 [17], formado por un total de 5 vigas tipo T dispuestas longitudinalmente. En el presente trabajo se estudia el comportamiento de una viga en forma aislada a fin de simplificar los cálculos numéricos. Las vigas fueron proyectadas para una condición de pretensado total bajo cargas de servicio, considerando las pérdidas de pretensado correspondientes, tales como acortamiento elástico del hormigón, contracción de fragüe, fluencia lenta del hormigón, acuñamiento del acero de pretensado en el momento de la transferencia y relajación de la tensión en el acero de pretensado [15].

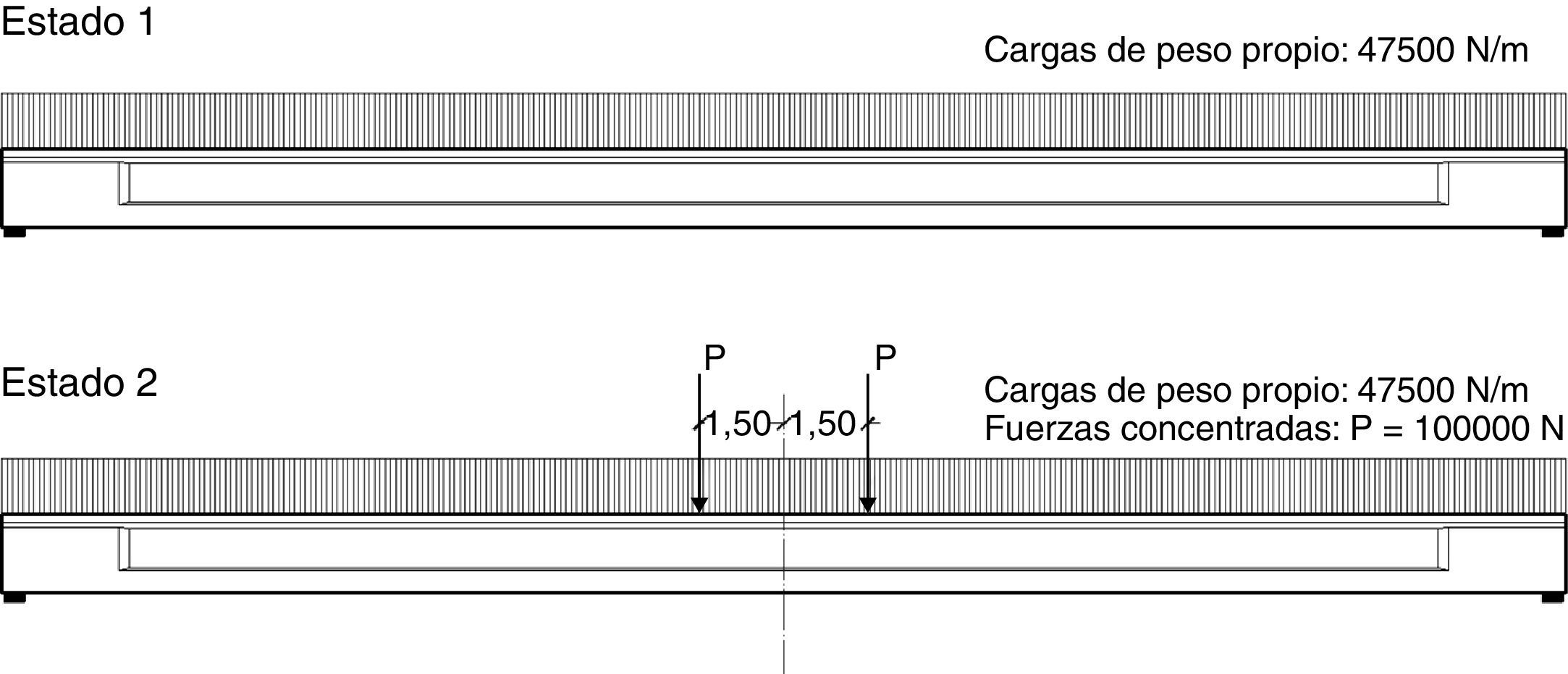
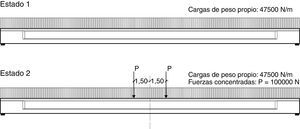
2.2

Estados de carga

La viga fue analizada bajo dos estados de carga; por un lado, sometida solo a las cargas de peso propio de la estructura y por otro, adicionando fuerzas concentradas que simularían la acción de una aplanadora que podría emplearse en un ensayo de cargas, en correspondencia a la categoría de puente [17]. Los dos estados de carga considerados pueden verse en la figura 3. Además, en ambos estados, actúa sobre la viga, una fuerza total de pretensado de 5,542 MN.

Figura 3.

Estados de carga considerados.

2.3

Hipótesis de daño

En primer término, se modeló y analizó la viga sin presencia de daño y posteriormente, agregando una fisura discreta en la zona inferior de la misma. Se consideraron para este estudio diferentes ubicaciones de la fisura y distintas profundidades de la misma.

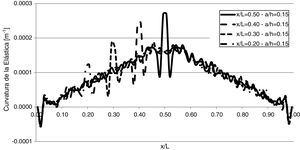
En la figura 4 se indican los parámetros que definen la configuración de la viga fisurada. El valor de los mismos se da en forma adimensional como sigue:

• -

  Ubicación: x/l.

• -

  Profundidad: a/h.

Figura 4.

Vista longitudinal de la viga, con los parámetros de definición de la fisura.

2.4

Modelo de elementos finitos

El modelo desarrollado con el método de elementos finitos se realizó mediante el software Comsol Multiphysics 4.4 [18].

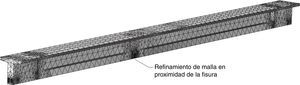
Se trabajó con un modelo en 3 D, con un mallado formado por elementos tetraédricos para ambos materiales (hormigón y acero) [19]. Fue realizado un refinamiento en la zona cercana a los cables de pretensado y en la posición de la fisura, como se muestra en la figura 5. Para simular el efecto del pretensado se aplicó una deformación inicial a dichos cables. No se contempló una modelación especial de la interface hormigón – acero, considerándose en consecuencia, una adherencia perfecta entre ambos materiales.

Figura 5.

Vista en 3 D de la viga con refinamiento de malla en la zona fisurada.

En cuanto a los materiales del modelo, se los consideró homogéneos, continuos e isótropos, con las siguientes propiedades:

Hormigón:

• •

  Módulo de elasticidad: E= 25 GPa

• •

  Coeficiente de Poisson: v= 0,20

Acero:

• •

  Módulo de elasticidad: E= 200 GPa

• •

  Coeficiente de Poisson: v= 0,30

Los análisis estructurales realizados en esta instancia fueron lineales, tanto geométricamente como constitutivamente. Cabe aclarar que esta última consideración es válida en el comportamiento del hormigón, solo hasta un determinado valor de deformaciones (zona de proporcionalidad), las cuales se deben verificar para que el modelo sea representativo de la realidad. Si las deformaciones del hormigón salen de ese rango, sería más apropiado pasar a un análisis de tipo no lineal, en el cual se introduzca la curva tensión – deformación característica. Por tratarse de hormigón pretensado, en el cual las tensiones de tracción en el hormigón quedan limitadas debido a la fuerza de pretensado, puede decirse que asumir un comportamiento lineal, si bien no representa estrictamente la realidad, se considera suficientemente aceptable.

En este caso, el pretensado aplicado es tal que, para la máxima carga aplicada en la simulación del ensayo, se tienen en la fibra inferior de la viga (zona precomprimida) tensiones de tracción limitadas en el orden de 3 MPa. Para un hormigón tipo H-30 [15] este podría considerarse un valor admisible, ya que es usual considerar una resistencia a tracción del 10% de la resistencia de compresión.

A modo ilustrativo, en la figura 6 se representan las tensiones longitudinales de uno de los modelos numéricos resueltos, pudiendo observarse la concentración de tensiones en la zona de la fisura.

Figura 6.

Tensiones longitudinales [MPa] en la viga con una fisura en x/l=0,40 y de profundidad a/h=0,25.

3

Aplicación del método de la curvatura de la elástica

La curvatura de la elástica de una estructura está dada por:

Donde w es el desplazamiento de la estructura, M es el momento flector solicitante, E es el módulo de elasticidad del material e I es el momento de inercia de la sección. Luego EI representa la rigidez flexional de la estructura y se puede apreciar que si la estructura presenta un daño localizado, dicha rigidez disminuirá en el lugar del daño y por lo tanto, la magnitud de la curvatura en ese lugar aumentará. Además, cuanto mayor sea la magnitud del daño, mayor será el aumento de la curvatura.

El cálculo de la curvatura de la elástica sobre la estructura dañada, puede llevarse a cabo a través de la medición de los desplazamientos para una cierta cantidad de puntos de la estructura y luego, a partir de los mismos, realizar una aproximación mediante diferencias finitas centrales, es decir:

Donde s es la distancia entre dos puntos adyacentes de medición.

De esta manera, el MCE consiste en medir los desplazamientos verticales para una cierta cantidad de puntos de la estructura y a partir de los mismos, obtener la curvatura de la estructura deformada, con la finalidad de detectar anomalías en la misma. Por lo dicho, puede notarse que este método, no requiere conocer los desplazamientos de la estructura sin daño, siendo esto una ventaja importante frente a otros métodos, ya que resulta frecuente no disponer de los mismos.

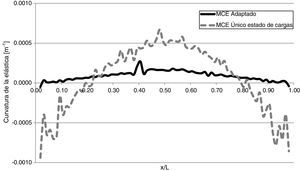
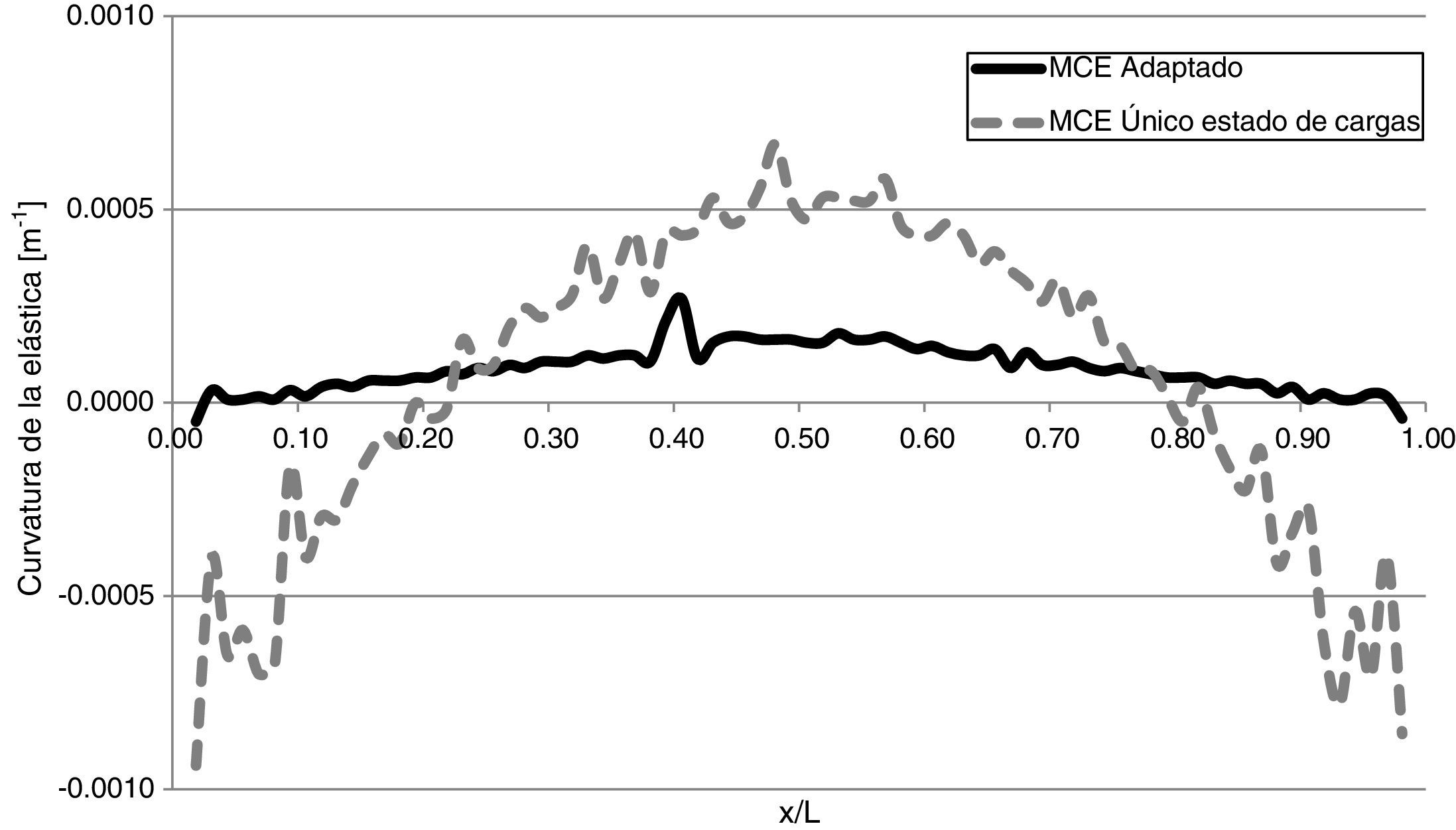
Cabe mencionar, que otros autores han aplicado este método a partir de los desplazamientos verticales de la estructura, respecto a la horizontal, para un determinado estado de cargas [8,9,11,12]. En esta investigación se ha encontrado que, para el caso de hormigón pretensado, resulta necesario aplicar el MCE a partir de los desplazamientos provocados al pasar de un estado de cargas «A» a un estado de cargas «B». La justificación se encuentra en el hecho de que la estructura pretensada sin carga alguna, ya se encuentra deformada respecto a la horizontal. Es decir, el pretensado introduce deformaciones adicionales en la estructura, cuyos efectos pueden ser simplemente neutralizados al considerarse los desplazamientos provocados por un aumento en las solicitaciones. De esta manera, el efecto del daño sobre la estructura se vuelve más notorio para su detección. Así, por ejemplo, en la figura 7 se muestra una comparación de la aplicación del MCE sobre un modelo de viga de hormigón pretensado fisurada en x/l=0,40, para un único estado de cargas y con la variante propuesta. Puede notarse que solo en este último caso es posible predecir la posición de la fisura.

Figura 7.

Método de curvatura de la elástica. x/l=0,40, a/h=0,40.

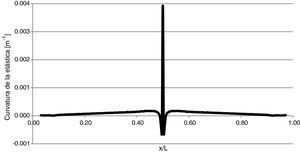
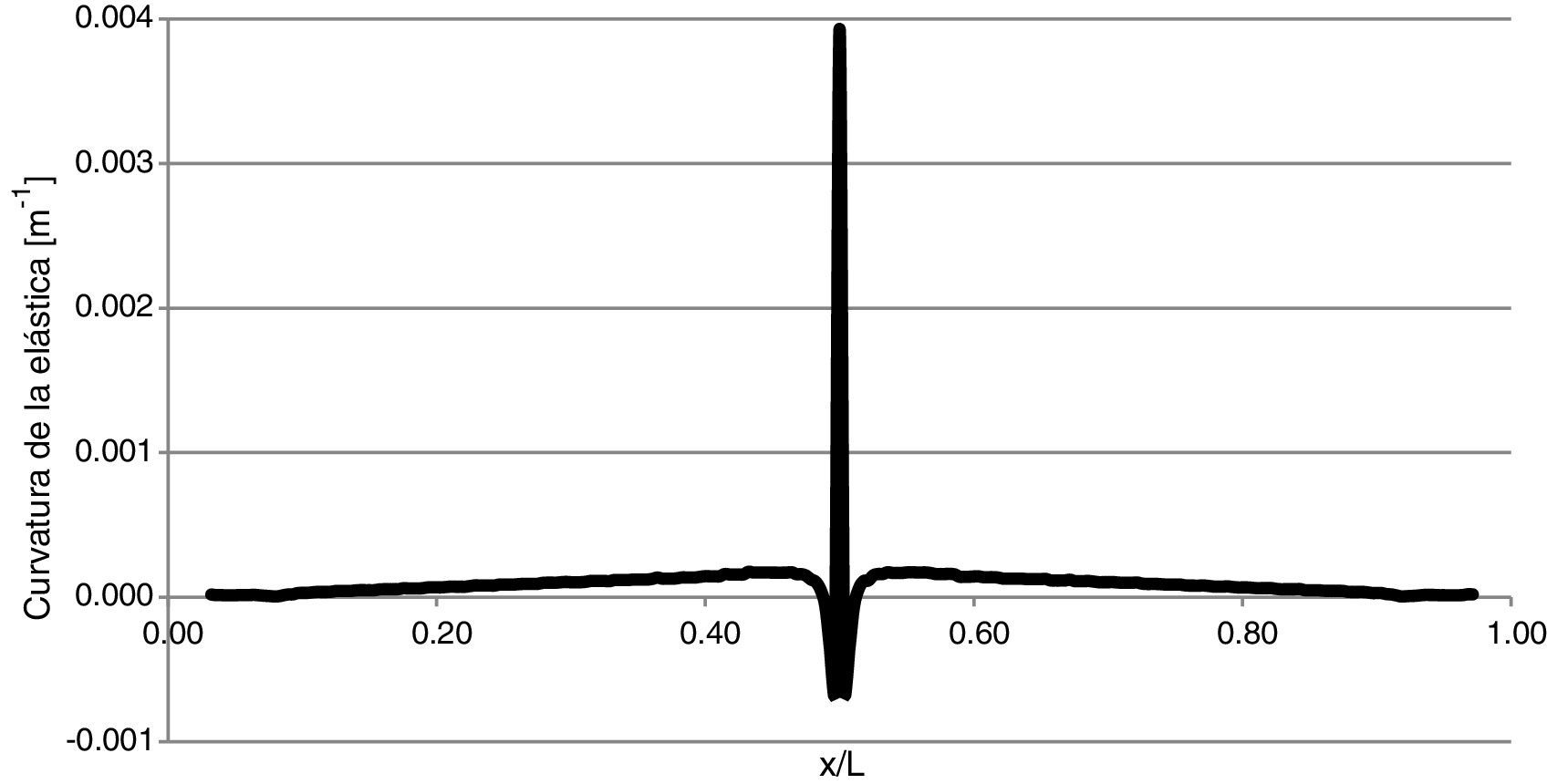
Por otro lado, en la figura 8 se muestra la aplicación del método de curvatura de la elástica adaptado, para una viga con una fisura discreta de profundidad a/h=0,15 y localizada en x/l=0,50. Puede notarse una marcada discontinuidad de la curva en coincidencia con la posición del daño. Esta curva fue obtenida trabajando con datos en forma continua a lo largo de la viga y con la precisión máxima arrojada por el software. Sin embargo, al momento de aplicarse el MCE en la práctica, esto podría resultar en un impedimento, por lo que es necesario ahondar en tales aspectos. Para ello se realizaron numerosos estudios de sensibilidad que se muestran en los puntos siguientes.

Figura 8.

MCE para datos completos arrojados por el software. x/l=0,50, a/h=0,15.

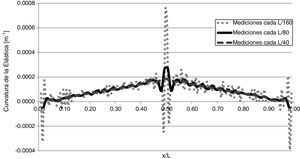
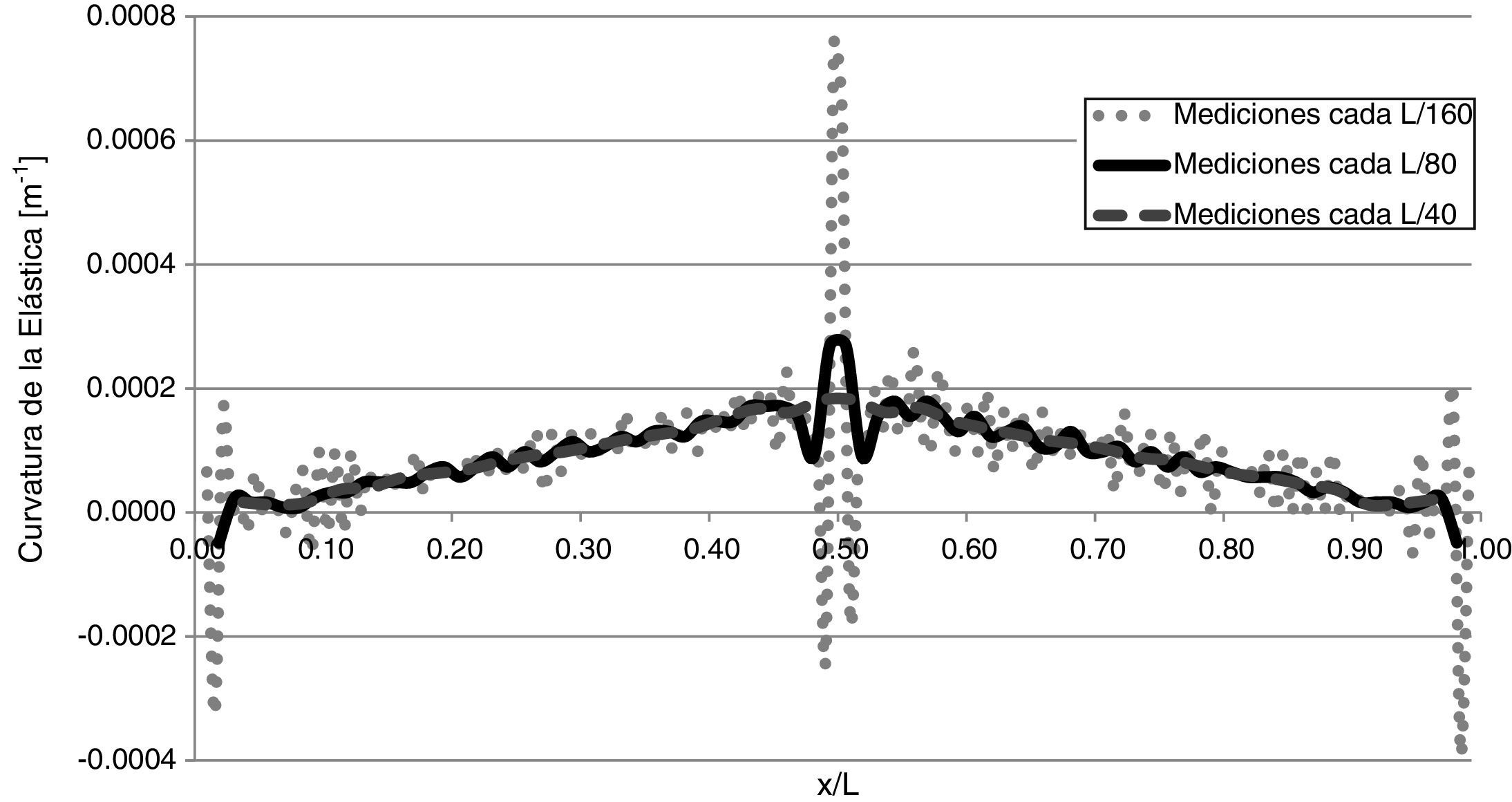
3.1

Sensibilidad a la densidad de mediciones

La separación entre los puntos de medición es uno de los factores más importantes al momento de realizar el gráfico de curvatura de la elástica y, en especial, cuando se define la cantidad de elementos de medición y/o instrumentos que se emplearán en el ensayo. Por esta razón, se analizó cómo varía dicho gráfico, en la medida que se modifica la distancia entre las mediciones, conservando todas las demás variables. Esto se muestra en la figura 9, para una viga fisurada en x/l=0,50, con una profundidad de fisura a/h=0,15.

Figura 9.

MCE para distintas densidades de medición. x/l=0,50, a/h=0,15.

Como puede verse en la figura 9, la detección de la fisura se dificulta en la medida que aumenta la distancia entre los puntos de medición, encontrándose que una separación de L/80 resulta adecuada para el caso en estudio. De la misma manera sucede cuando la fisura se encuentra en otras posiciones (x/l) de la viga.

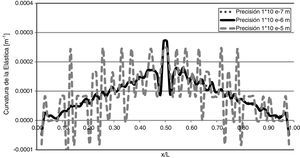
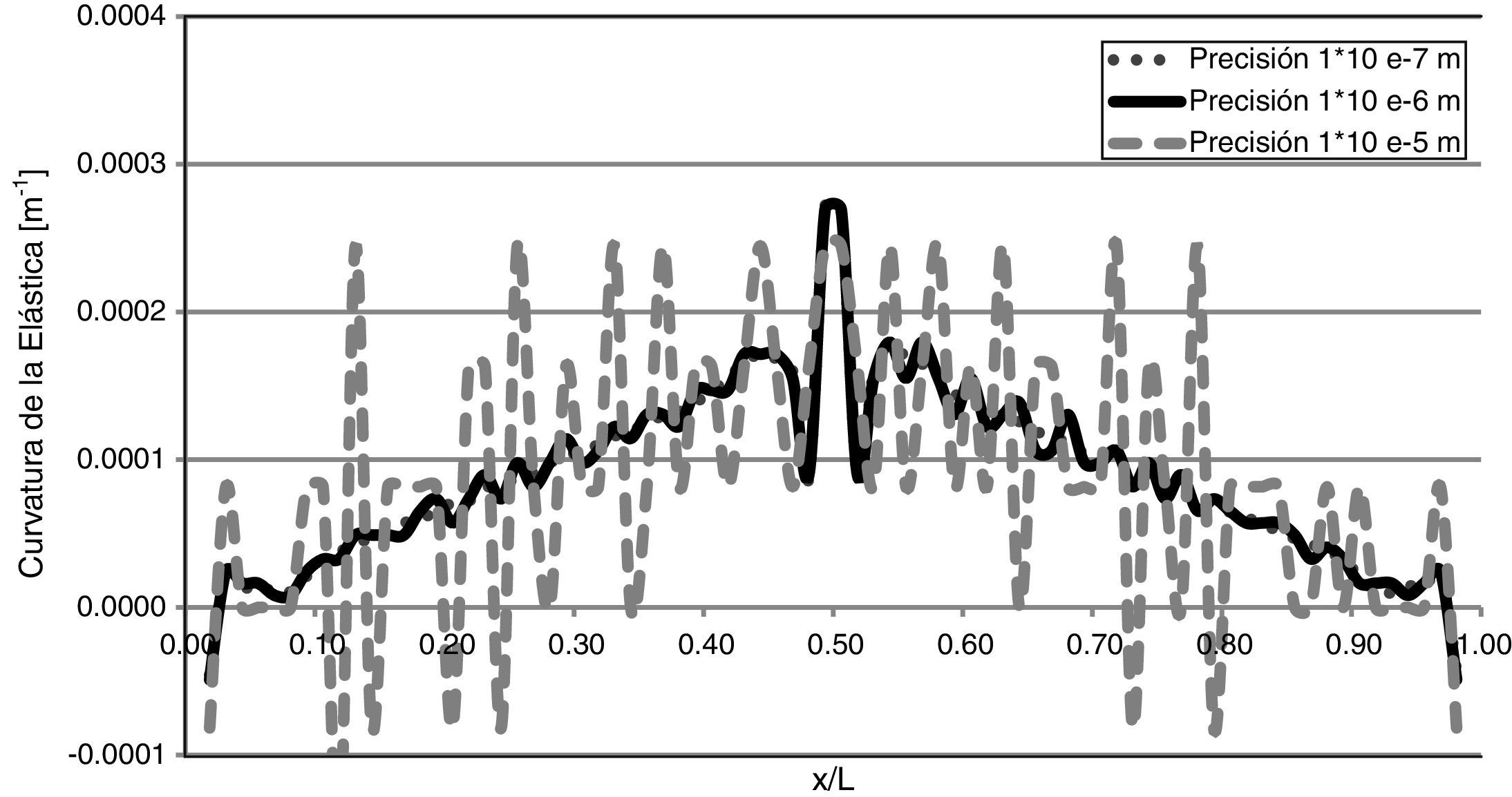
3.2

Sensibilidad a la precisión de las mediciones

De una manera similar a la descrita en 3.1, se analizó lo que sucede en la medida que se modifica la precisión en las mediciones a los fines de hallar la requerida por el MCE. En la figura 10 puede observarse la curvatura de la elástica, para mediciones tomadas con distintas precisiones, para una viga con una fisura de profundidad a/h=0,15, ubicada en x/l=0,50.

Figura 10.

MCE para distintas precisiones en la medición. x/l=0,50, a/h=0,15.

Como puede notarse en la figura 10, para el modelo en estudio, se requiere de una precisión del instrumento de medición de al menos 1x10^-6 m, a los efectos de que el daño sea detectable. Es posible obtener dicha precisión utilizando sensores como los LVDT (Linear Variable Displacement Transducers).

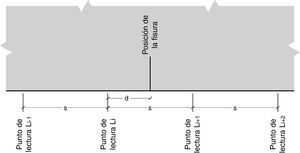
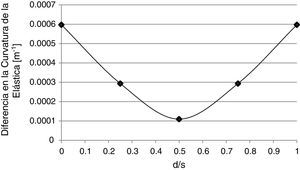
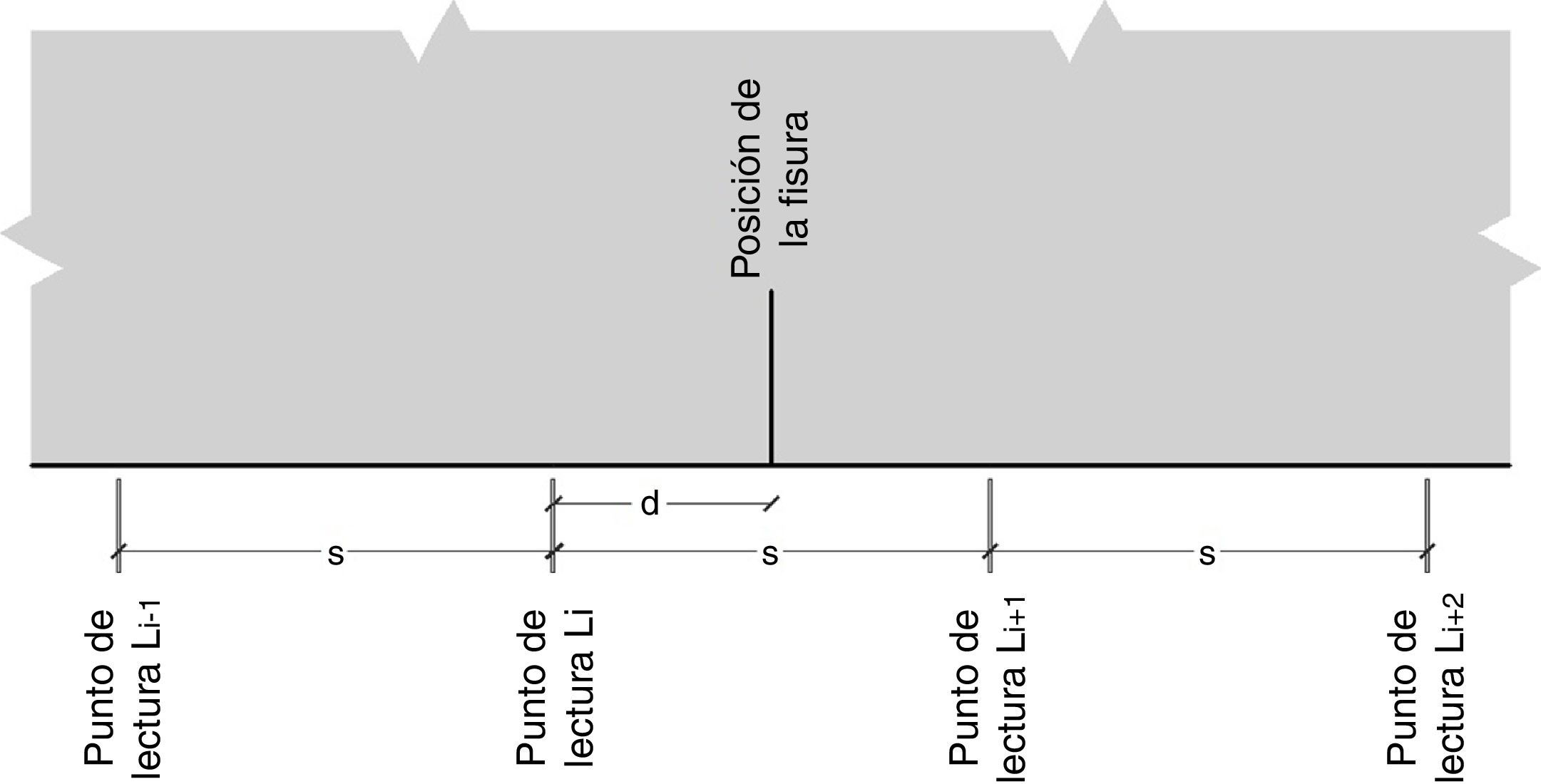
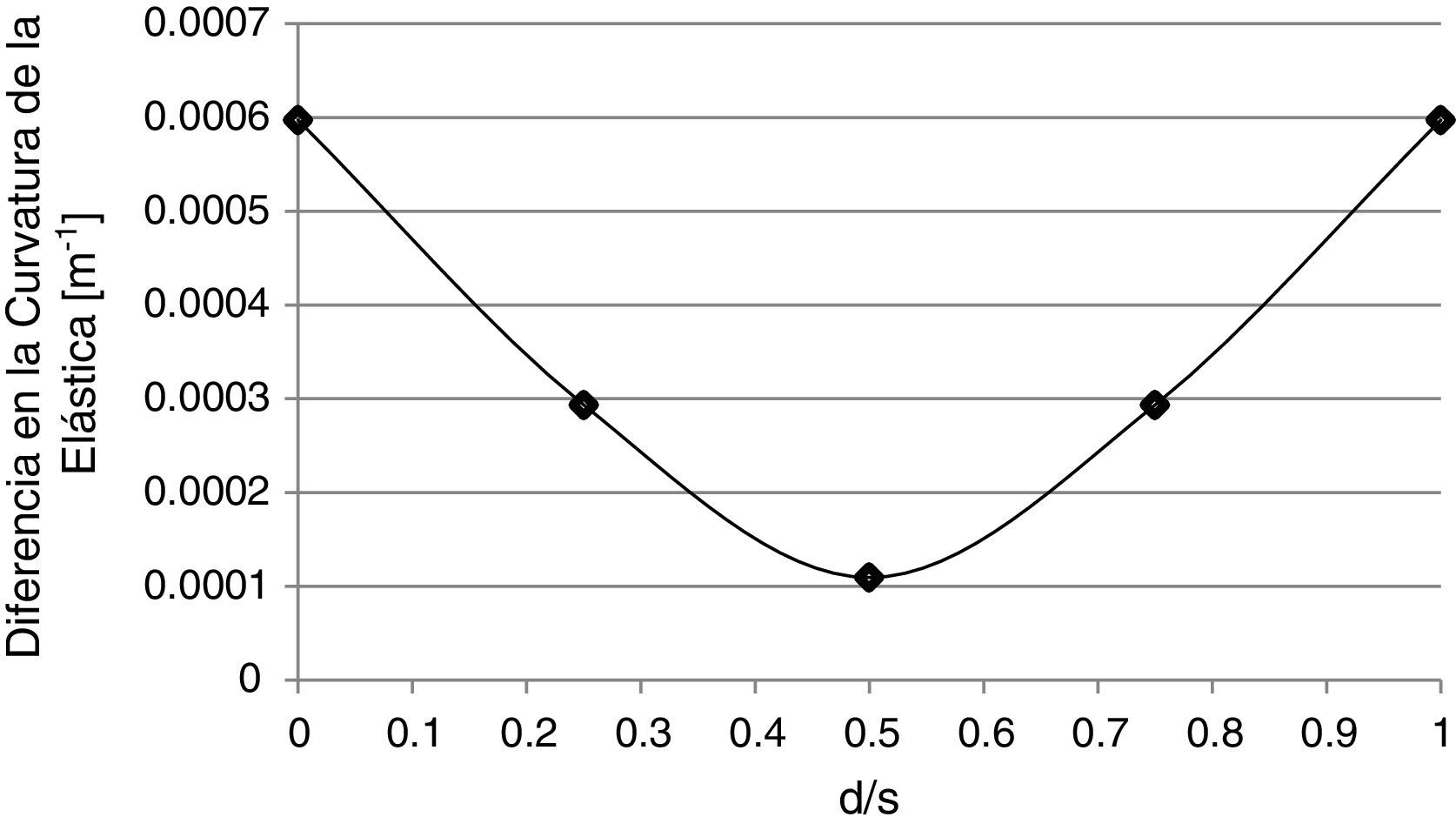
3.3

Sensibilidad a la posición de la fisura, respecto a los puntos de medición

Dado que al momento de realizar las mediciones, en general, se desconoce si existen o no fisuras y la posible ubicación de las mismas, resulta de interés analizar la sensibilidad del MCE cuando varía la distancia desde la fisura al punto de medición más cercano. Esto se esquematiza en la figura 11, siendo d la distancia desde la fisura al punto de medición más próximo y s la distancia entre dos puntos de medición sucesivos. Por otro lado, en la figura 12 se muestra la incidencia que se tiene en la aplicación del MCE, en función de la relación d/s, para una viga fisurada en x/l=0,50, con una profundidad a/h=0,15. En la misma se representó la magnitud del «salto» que se obtiene a través del MCE en la posición del daño.

Figura 11.

Esquema de ubicación de la fisura respecto al punto de medición más cercano.

Figura 12.

Diferencia en la curvatura de la elástica, en función de la distancia desde la fisura al punto de medición más próximo. x/l=0,50, a/h=0,15.

Puede observarse en la figura 12, que la sensibilidad de detección disminuye significativamente a medida que la fisura se aleja de los puntos de medición, con una pérdida máxima de sensibilidad del 81% cuando se encuentra centrada entre los mismos. Debido a ello, para todos los demás estudios se trabajó con la fisura en esta situación, de forma tal de cubrir la situación más desfavorable.

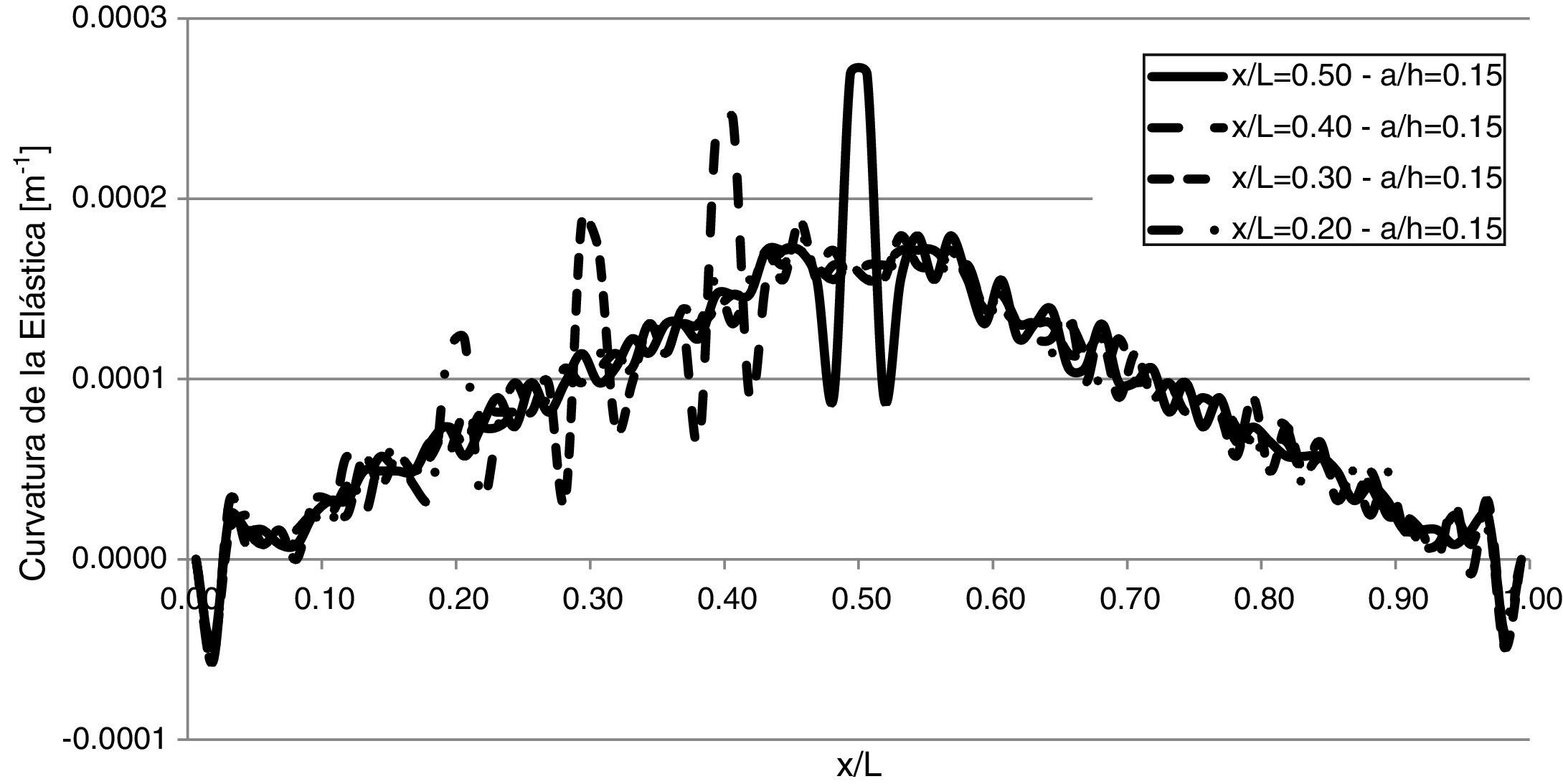
3.4

Sensibilidad a la ubicación de la fisura a lo largo de la viga

En la figura 13 se observa la aplicación del MCE sobre una viga con una fisura de profundidad a/h=0,15, ubicada en distintas posiciones a lo largo de la misma. En estos casos, se trabajó con mediciones cada L/80, con una precisión de 1x10^-6 m y la fisura centrada entre dos puntos de medición. Puede notarse que bajo dichas condiciones, el MCE fue efectivo para detectar la presencia del daño y su localización.

Figura 13.

MCE para una fisura de profundidad a/h= 0,15, ubicada en distintas posiciones a lo largo de la viga.

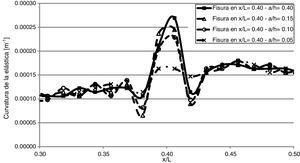
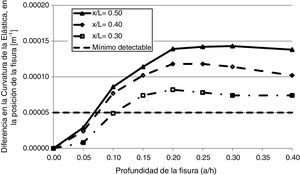
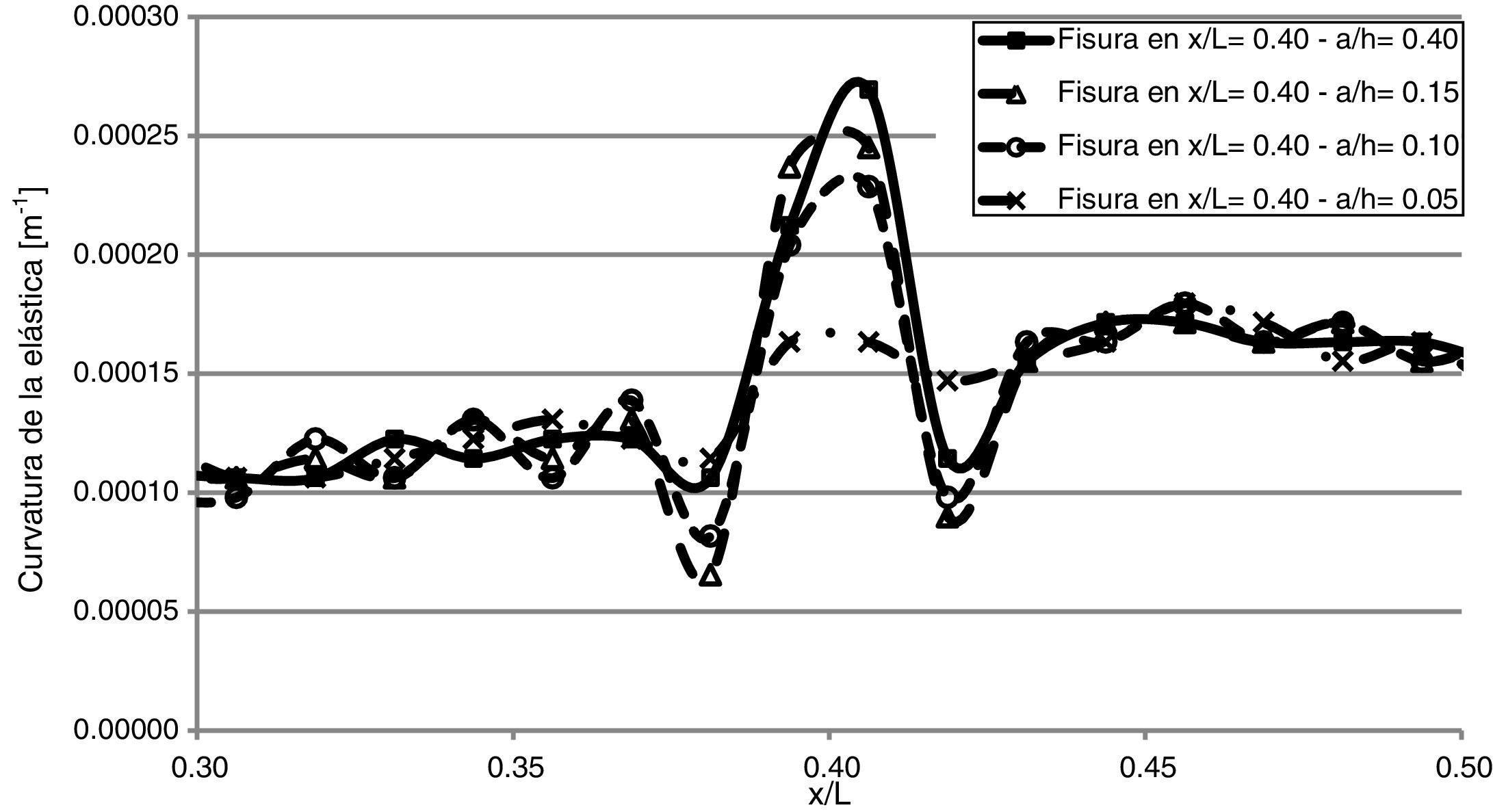
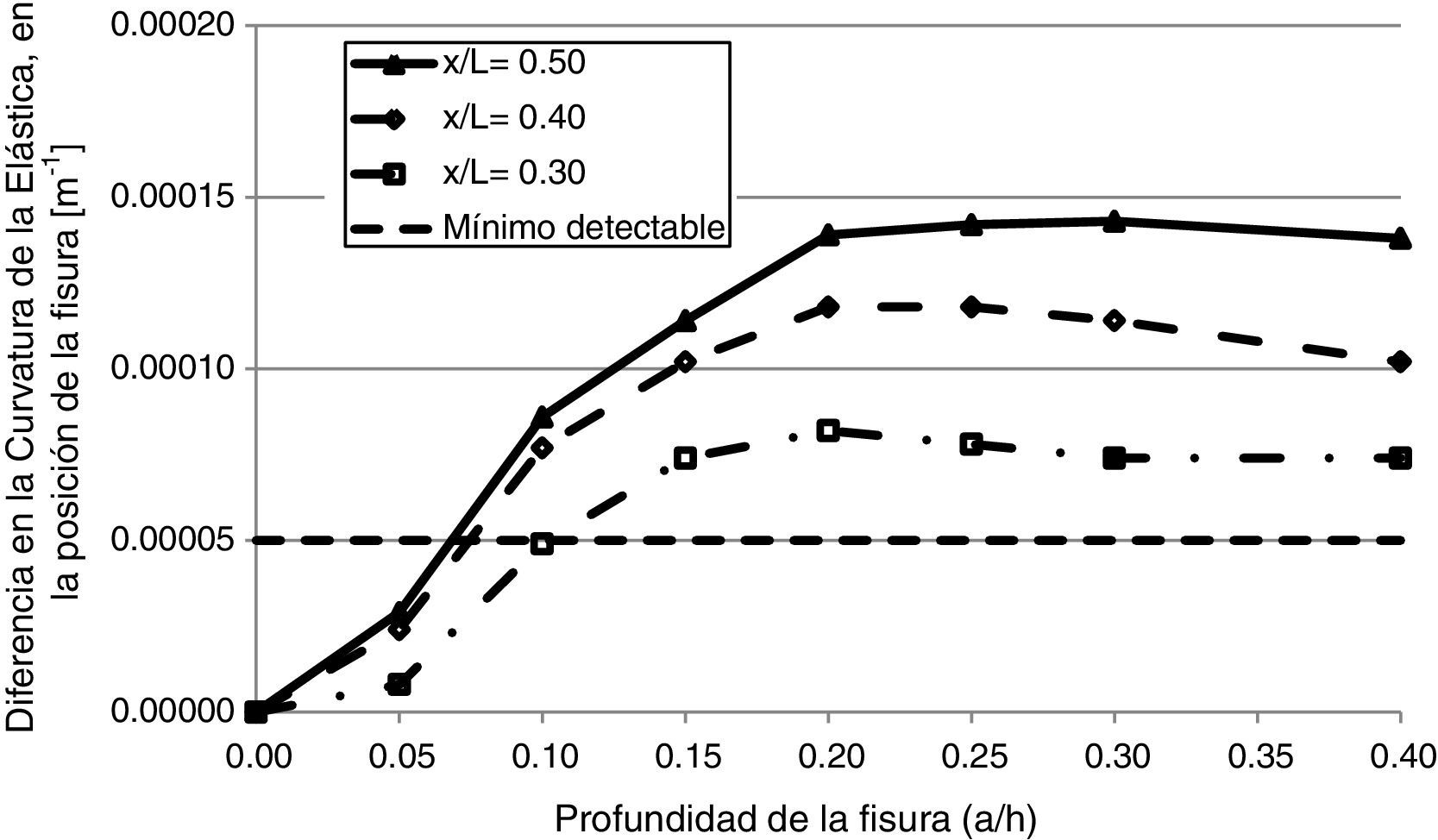
3.5

Sensibilidad a la magnitud del daño

Se realizaron modelos con distintas profundidades de fisuras y se compararon los resultados, a fin de evaluar cómo influye la magnitud del daño y de establecer la mínima profundidad de fisura que es posible detectar. En la figura 14 se muestra dicho análisis, cuando el daño se encuentra ubicado en x/l=0,40. La fisura de a/h=0,10 fue claramente detectada, pero ya no sucedió así con fisuras de a/h=0,05, ya que en este caso, la discontinuidad comenzaba a confundirse con las irregularidades del resto de la elástica.

Figura 14.

MCE para una viga con fisura ubicada en x/l=0,40 y distintas profundidades a/h.

La figura 14, también permite apreciar que se puede obtener una relación entre la discontinuidad que se aprecia en el gráfico y la magnitud del daño. En tal sentido, se realizó la figura 15, en la cual se muestran las curvas de evolución para distintas ubicaciones del daño.

Figura 15.

Diferencia en la curvatura de la elástica, para una viga con fisura ubicada en distintas posiciones, en función de la profundidad de la misma.

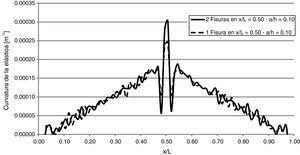
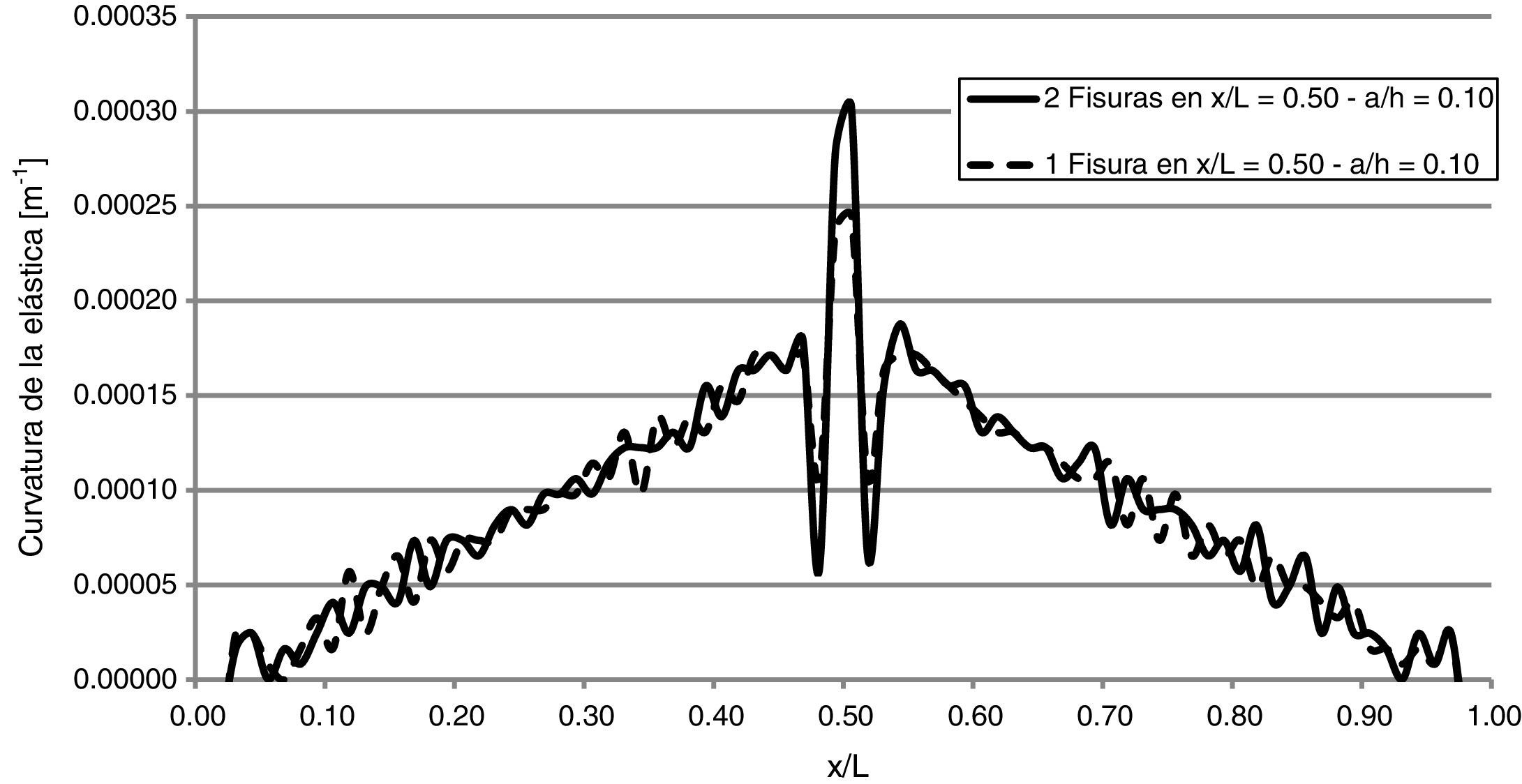
Adicionalmente, a los fines de incrementar más aún la magnitud del daño, se realizaron modelos con 2 fisuras próximas entre sí. En la figura 16 se analiza un modelo con 2 fisuras distanciadas entre sí 20 cm, ubicadas en el centro de la viga y con una relación a/h= 0,10. Los resultados obtenidos muestran que en la medida que se introducen fisuras, como es de esperar, la detección del daño se hace más efectiva.

Figura 16.

MCE, para una viga con 1 y 2 fisuras en la zona central de la misma (a/h=0,10 en ambos casos).

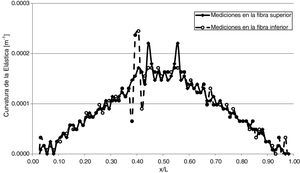
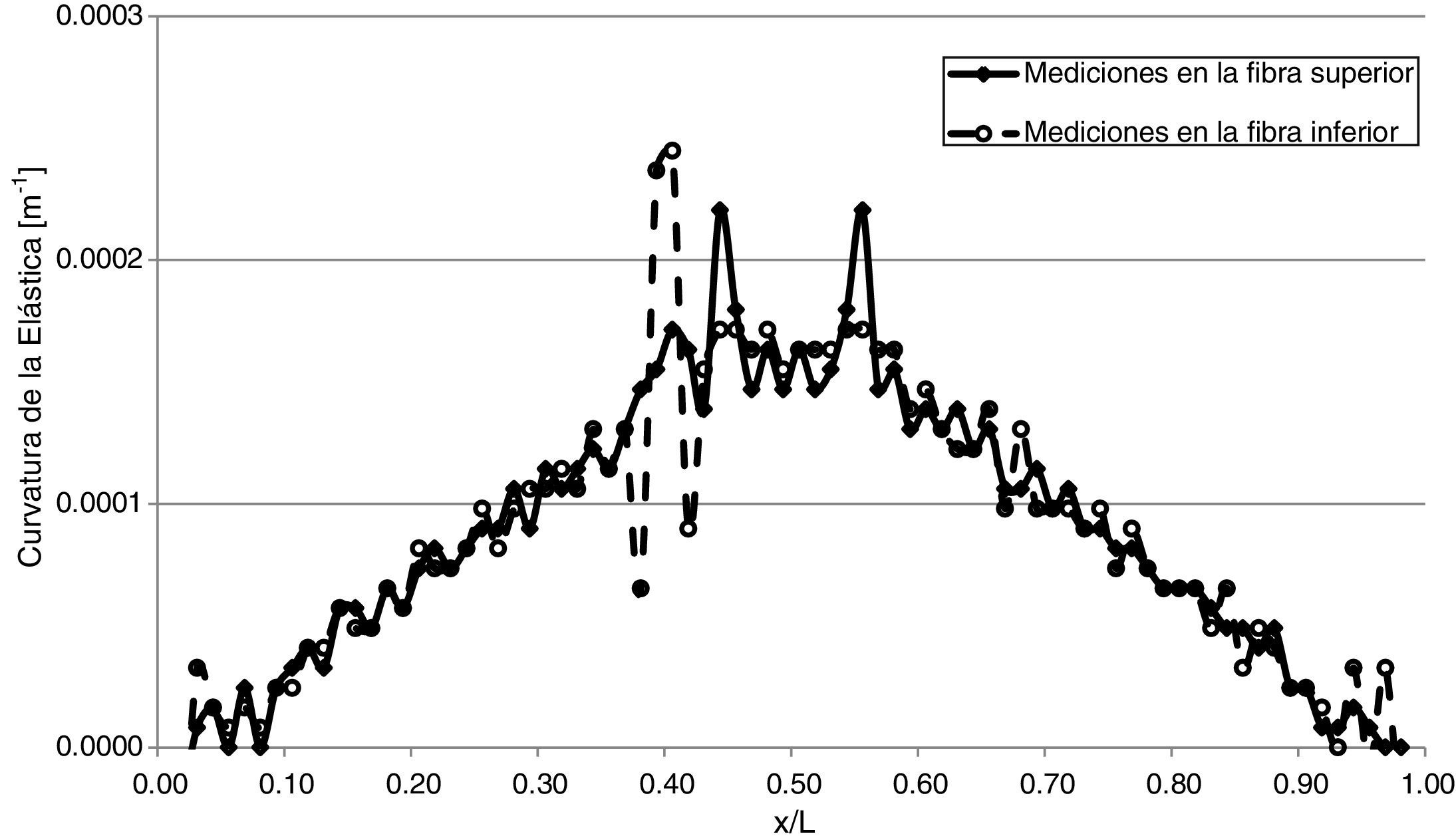
3.6

Aplicación del método con mediciones en la cara superior

Se analizó la aplicabilidad del MCE, tomando las mediciones sobre la cara superior de la viga, en lugar de la inferior (cara fisurada). Esta comparación se muestra en la figura 17, para el caso de una fisura de profundidad a/h=0,15, ubicada en x/l=0,40.

Figura 17.

MCE para lecturas en la cara superior e inferior. x/l=0,40, a/h=0,15.

Como puede observarse en la figura 17, en la aplicación del MCE, cuando se trabajó con mediciones en la cara superior de la viga, no se obtuvo una evidencia clara del daño; las discontinuidades más importantes que surgen, corresponden a las posiciones de las fuerzas concentradas, por lo cual se concluye que para una buena percepción de los posibles daños, es necesario tomar las mediciones sobre la cara inferior de la viga.

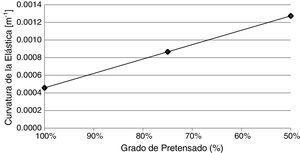
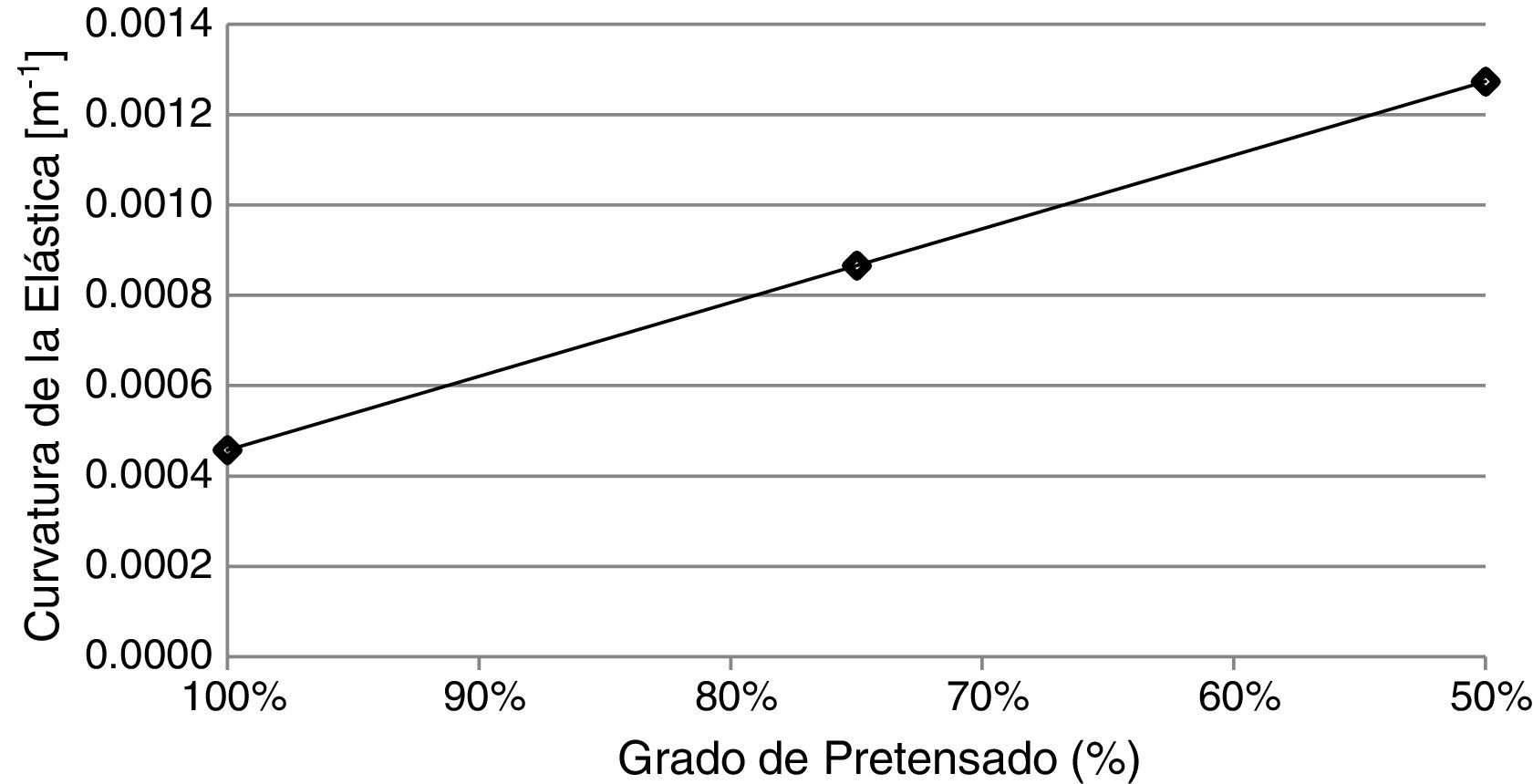
3.7

Sensibilidad al grado de pretensado

Hasta aquí se trabajó con la variación de la curvatura de la elástica que surge de pasar del estado de cargas 1 al estado de cargas 2, definidos en la Sección 2.2. Esto implica que, basados en la validez del principio de superposición de efectos, en el rango lineal de la curva tensión-deformación, al hacer la diferencia entre los estados de carga 2 y 1, el efecto del pretensado sobre la curvatura prácticamente se anula, y de esta manera, la detección del daño con este método se independiza en gran medida de la fuerza de pretensado. No obstante, las magnitudes absolutas de curvatura, desde luego se verán alteradas en caso de una disminución en la fuerza de pretensado.

Para analizar la incidencia del grado de pretensado en los valores de la curvatura de la elástica, se calculó la misma sobre un modelo de viga fisurada, para el estado 2, variando la fuerza de pretensado. Los resultados obtenidos para la curvatura de la elástica en la posición de la fisura, se muestran en la figura 18. Se aprecia cómo se incrementa la curvatura a medida que disminuye el grado de pretensado. De dicha observación surge que la metodología implementada podría poner en evidencia pérdidas de pretensado, por comparación de los resultados en distintos momentos, e independientemente de la existencia o no de daño en la viga en cuestión.

Figura 18.

Curvatura de la elástica en la posición de la fisura, en función del grado de pretensado. x/l=0,40, a/h= 0,15.

4

Conclusiones

En este trabajo, se estudiaron los parámetros a considerar para la aplicación del método de la curvatura de la elástica, con la finalidad de la detección de fisuras discretas en una viga de hormigón pretensado, a través de modelos numéricos construidos en elementos finitos. En función de lo analizado, se pueden establecer las siguientes conclusiones:

• -

  Se encontró necesaria la aplicación del MCE a partir de los desplazamientos verticales obtenidos al pasar de un estado de cargas «A» a un estado de cargas «B», en lugar de utilizar los desplazamientos verticales de un único estado de cargas respecto a la horizontal.

• -

  En cuanto a la densidad de mediciones conveniente para la aplicación del MCE en la práctica, fue necesario limitar la separación entre los puntos de medición a una distancia máxima de L/80.

• -

  La precisión de las mediciones requerida fue de 1x10^-6 m. Los avances que se han dado en cuanto a sensores e instrumentos de medición, hacen posible el trabajo con dichas precisiones, por ejemplo con el uso de LVDT.

• -

  La distancia entre la ubicación del daño y el punto de medición más cercano afectó en un 81% la sensibilidad del método. Esto no debe perderse de vista, sobre todo cuando se intenta evaluar la magnitud del daño en cuestión.

• -

  En cuanto a las mediciones de los desplazamientos en la cara inferior o superior de la viga, se requirió estrictamente de mediciones en la cara inferior de la viga (cara fisurada).

• -

  La aplicabilidad del método no se ve afectada por las pérdidas de pretensado que se dan con el paso del tiempo.

Conflicto de intereses

Los autores declaran no tener ningún conflicto de intereses.

Agradecimientos

Los autores agradecen al Departamento de Ingeniería y a la Secretaría General de Ciencia y Tecnología de la Universidad Nacional del Sur (UNS), así como al Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) y a la Comisión de Investigaciones Científicas de la Provincia de Buenos Aires (CIC), el apoyo brindado para el desarrollo de estas investigaciones.