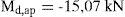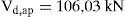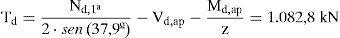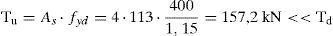La poca regulación existente para el refuerzo de estructuras hace que hasta en los casos más sencillos de edificación sea enormemente complicado tener un criterio de actuación. En la revisión de proyectos de rehabilitación hemos detectado que el denominador común en muchos refuerzos de pilares fue la ausencia de la justificación del planteamiento del refuerzo o de cómo se transmitían las cargas de la estructura existente al mismo. Sirvan como ejemplo las numerosas intervenciones llevadas a cabo tras el terremoto de Lorca de 2011, donde muchos pilares resultaron gravemente dañados. Las soluciones de refuerzo fueron diversas, aunque compartían en la mayoría de los casos la precipitación en su ejecución y la ausencia de valoración de su efectividad.
Se expone, mediante un ejemplo de un pilar dañado en una planta, la problemática del diseño del refuerzo y cómo este puede resultar de mayor alcance del esperado.
The lack of regulations with regards to strengthening reinforced structures prevents the adoption of a standardised approach to even the simplest building structures. Following the analysis of refurbishment projects, it has been concluded that the common denominator in many reinforced columns was the lack of justification of the calculation of the column reinforcement, or even the load transmission between the existing structure and this new reinforcement. Of special concern were the numerous interventions carried out following the earthquake that took place in Lorca in 2011, where many columns had been severely damaged. Although the strengthening solutions implemented in Lorca were diverse, they all followed a similar pattern presenting design solutions that were rushed and lacked a proper evaluation of their effectiveness.
This article focuses on an example of a damaged column on a random building floor and the associated challenge related to the design of a strengthening solution and how this may eventually result in a significantly larger scope than initially envisaged.
La reducción reciente de construcción de obra nueva, tanto en obra civil como de edificación, y el aumento del sector de la rehabilitación y una mayor preocupación general por el mantenimiento del patrimonio construido han supuesto que se aprecie un mayor interés por regularizar o normalizar estas prácticas, tal y como sucede con la obra nueva. A fecha de la redacción del presente artículo muchos países siguen trabajando para redactar normativas que cubran las obras existentes y el tratamiento de los refuerzos. Ejemplo de ello es el futuro Eurocódigo de estructuras existentes, que lleva varios años en fase de planteamiento y actualmente se halla en fase de redacción, si bien aún no hay fecha clara de publicación.
El problema fundamental radica en que al analizar diferentes estructuras reforzadas en las últimas décadas se observa una enorme heterogeneidad en el planteamiento y la ejecución de los refuerzos. Aunque desde hace décadas existen grupos de investigación que han tratado de analizar aspectos muy concretos del comportamiento de los refuerzos, publicando tesis doctorales y artículos de interés al respecto (véanse por ejemplo las referencias [1–20]), en muchos casos se adoptan soluciones que aparentemente son de buena praxis (muchas veces por el hecho de ver esa solución aplicada en un mayor número de obras) sin meditar si la tipología aplicada será apropiada para cada obra concreta.
La inspección reiterada de más de 350 edificios en Lorca tras el terremoto de mayo de 2011 [21] puso de manifiesto que, en aquellos cuya estructura estaba formada por pórticos de hormigón (aproximadamente la mitad), el daño estructural más habitual era el fallo del pilar (provocado lógicamente por el sismo, aunque en la totalidad de los casos debido a una configuración del mismo no adecuada: pilares enanos, cautivos, detalles de armado inadecuados, etc.). En efecto, encontramos más de 70 edificios (50 de ellos de construcción relativamente reciente, admitiendo en tal clasificación estructuras construidas en el ámbito de normativas muy parecidas a las vigentes en la actualidad) con daños muy graves en pilares (en muchos casos, incluso colapsos), que exigían una actuación de refuerzo urgente para, al menos, restituir su capacidad frente a acciones gravitatorias. Sin embargo, en ninguno de estos edificios las actuaciones de refuerzo que se llevaron a cabo atendieron a la redacción de un proyecto en el que se justificara adecuadamente su procedimiento de ejecución, dimensionamiento, entrada en carga, afectación al resto de la estructura, etc. Solo en 2 edificios se aportó un proyecto que justificaba parcialmente estos aspectos.
La urgencia de intervención se utiliza como excusa de la ausencia de dichas justificaciones o incluso del propio proyecto correspondiente. Como se expone en [22], el problema se agrava en estos casos, pues el propio apeo previo al refuerzo tiene igual o mayor complejidad que dicho refuerzo, requiriendo igualmente su adecuada concepción y justificación técnica.
Parece que se sobreentiende que en una obra nueva se exija un anejo de cálculos justificativos sobre el dimensionamiento de la estructura, pero parece haber cierta benevolencia en el sector de la rehabilitación a la hora de admitir soluciones de refuerzo estructural sin dimensionar y únicamente basadas en supuestos criterios de buena praxis, cuando en ambos casos deben exigirse soluciones técnicamente justificadas.
Como se expone en el presente artículo, hay múltiples aspectos a tener en cuenta en el dimensionamiento de refuerzos de pilares de hormigón armado, y algunos de ellos pueden suponer que el alcance del refuerzo sea mucho mayor del esperado. Todo lo que se apunta se basa en casos sencillos y habituales en edificación (pilares sometidos a compresión dominante), por lo que tampoco es de extrañar que en el caso de refuerzos necesarios por fenómenos más complejos, como es el caso de estructuras dañadas tras un terremoto, los técnicos encuentren aún más dificultad en el dimensionamiento.
Problemas de eficacia en el refuerzo de pilares de hormigón armadoA la hora de plantear el refuerzo de un pilar de hormigón armado existen diferentes tipologías y técnicas, las cuales podemos agrupar por el material empleado en el refuerzo (encamisados de hormigón, empresillados o encamisados metálicos, zunchado con materiales compuestos, etc.), o bien por su forma de trabajo [1]. En este último caso, las tipologías podrían ser las 2 siguientes, con independencia de los materiales empleados:
- Refuerzos por sustitución, en los que se desprecia la capacidad del soporte original (salvo en la zona de transferencia del refuerzo) y el refuerzo se dimensiona para recibir la totalidad de la carga.
- Refuerzos por colaboración, que tienen por finalidad aumentar la capacidad estructural, ya sea incrementando la sección del soporte existente, o simplemente mejorando su resistencia a través del confinamiento.
En el caso concreto de refuerzos ejecutados en España, las técnicas habituales de encamisado de hormigón armado o empresillado metálico estarían incluidas en el primer grupo, y las técnicas de encamisado con materiales compuestos o chapas en el segundo, si bien también se detectan casos de encamisado de hormigón con función de confinamiento.
Centrando el artículo en estos casos habituales, se exponen a continuación algunos de los condicionantes de planteamiento del refuerzo y/o de ejecución del mismo que, de no ser tenidos en cuenta, pueden limitar la efectividad del refuerzo o, incluso, hacerlo pernicioso por la falsa tranquilidad que transmite el elemento reforzado.
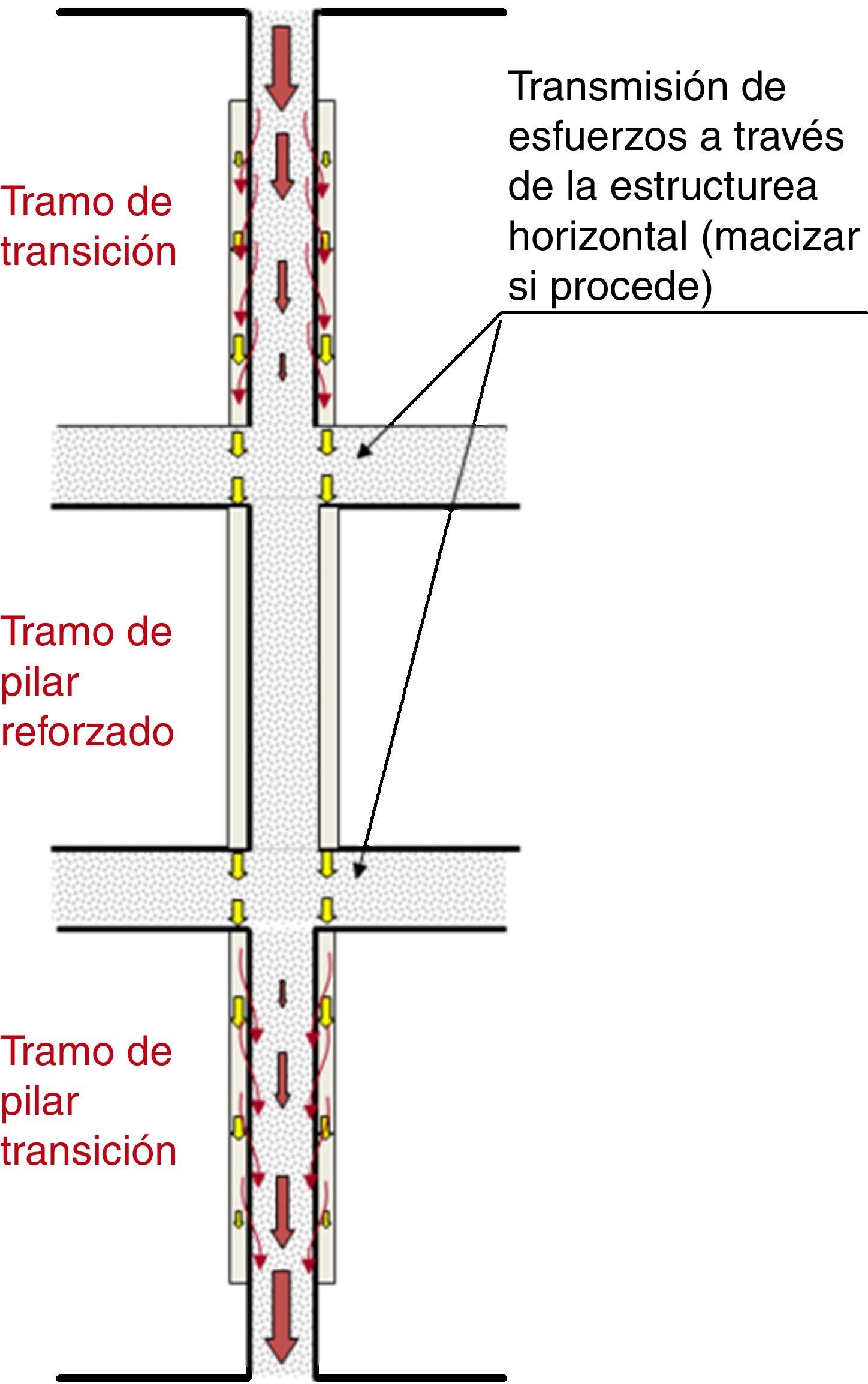
Transferencia de cargas del soporte existente al refuerzoEn los refuerzos por sustitución es fundamental analizar cómo se producirá la transferencia de esfuerzos entre el pilar existente y el refuerzo. Ello tiene una gran repercusión sobre la extensión del refuerzo. Como se expone en [1–3,11] y en la figura 1 (extractada de [1]), si existe un tramo en situación de refuerzo (por estar dañado, presentar capacidad insuficiente, etc.) se deberá realizar la transferencia de carga en el tramo superior no dañado (o que no requiere ser reforzado por condiciones de cálculo). En caso contrario, de realizar la transferencia en el tramo afectado podría producirse el agotamiento del pilar existente en los primeros centímetros donde aún no se ha transferido la carga al refuerzo.
Esquema de transferencia de cargas pilar existente-refuerzo por encamisado (croquis extractado de la referencia [1]).
Igualmente pasa en el tramo inferior, donde habría que devolver los esfuerzos al pilar existente, caso de que este, per se, no requiera ser reforzado.
Como se detalla en el siguiente apartado, se hace necesario poder determinar la longitud de transferencia de la carga entre el pilar existente y el refuerzo.
Otra opción es realizar la transferencia a través de los nudos de la estructura existente por contacto directo entre la cara inferior del forjado y el encamisado o capitel dispuesto. Este criterio exige comprobar algunos aspectos en la estructura existente, como se explica con mayor detalle en los ejemplos del siguiente apartado, y no siempre se garantiza que dicha configuración sea adecuada. Desgraciadamente, es habitual que los proyectos carezcan de las comprobaciones citadas.
Capacidad residual del soporte existenteDada la dificultad existente para valorar qué parte de las cargas seguirán conduciéndose por el soporte existente y cuáles se irán por el refuerzo, se pueden dimensionar los encamisados de hormigón armado o empresillados metálicos despreciando la capacidad del pilar existente. Además, muchas veces las dimensiones mínimas constructivas de estos refuerzos cumplen con el criterio de sustitución.
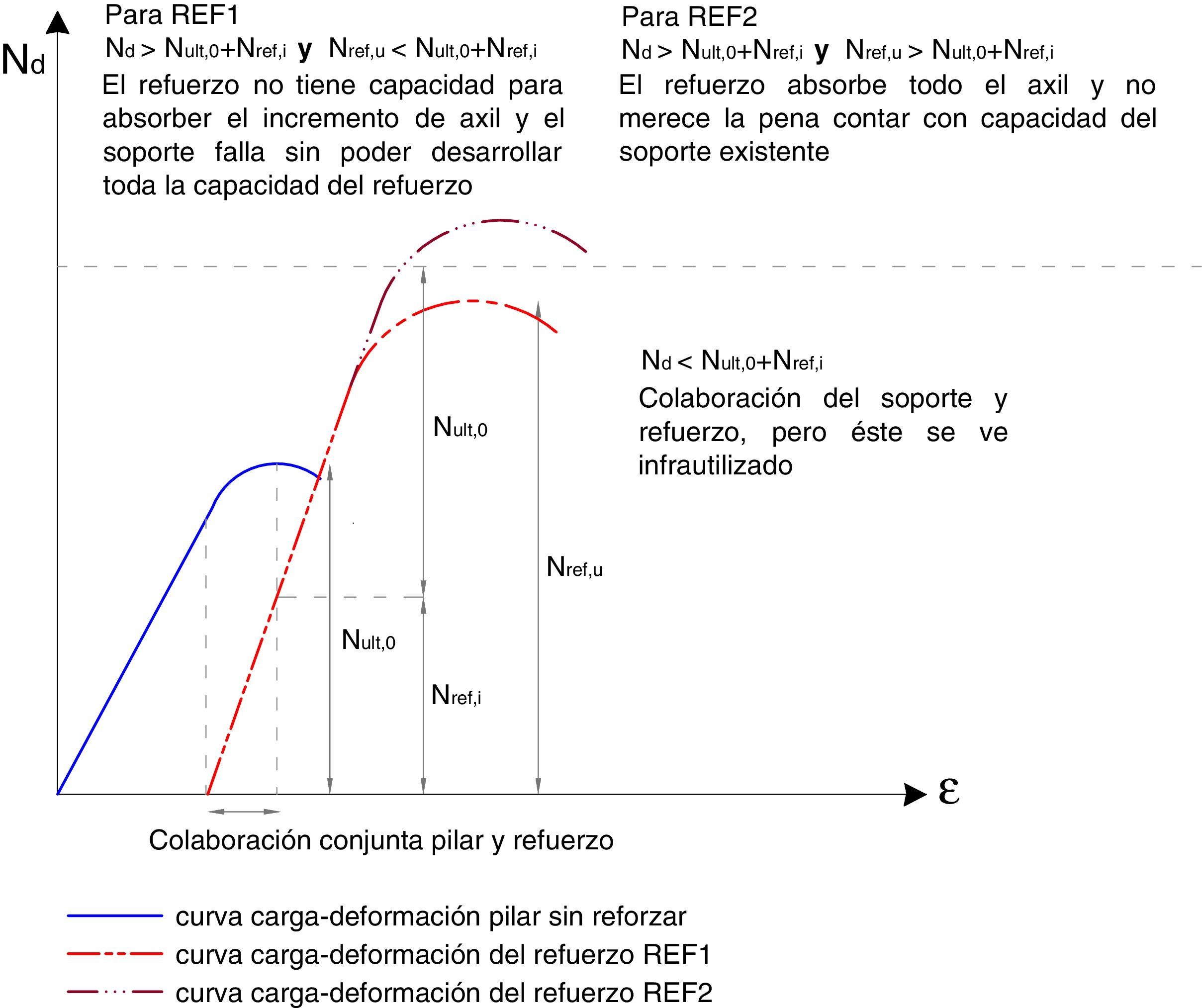
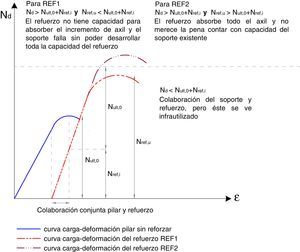
Aunque despreciar la capacidad resistente del soporte existente pueda parecer que está excesivamente del lado de la seguridad, no siempre es así. El considerar la resistencia de dicho soporte podría resultar inseguro en el caso de que un incremento de carga en el mismo tras el refuerzo agotase este y por su falta de ductilidad el refuerzo no fuera capaz de soportar la totalidad de la carga que llega al pilar (véase la figura 2). Por ello, considerar la colaboración del pilar existente exige un análisis minucioso que garantice la situación tensional del pilar previa al refuerzo. En todo caso, en soportes muy dañados o con niveles de carga axial próximos al colapso, parece razonable despreciar cualquier capacidad del pilar existente.
Contacto del soporte existente con encamisado de confinamientoPara que los refuerzos por confinamiento sean efectivos, debe garantizarse el pleno contacto entre el soporte existente y el encamisado. En los refuerzos con materiales compuestos, por condiciones de ejecución es poco probable que el aplicador deje grandes irregularidades en el pilar antes de disponer la camisa (caso distinto es el tratamiento de las esquinas, como se indica en el punto siguiente, el 2.4), pero en el caso de encamisados metálicos, muchas veces se disponen las chapas sobre superficies aparentemente regularizadas, pero sin garantizar el contacto íntimo entre ambos materiales.
Por ello, en los encamisados metálicos el mejor método para garantizar dicho contacto es dejar una pequeña holgura (entre 10 y 20mm, dependiendo del material de inyección) entre el encamisado y el soporte para permitir la correcta inyección de la interfaz encamisado-superficie de hormigón, disponiendo varios puntos de inyección y otros tantos de purga para garantizar que no quede aire ocluido.
Redondeo de esquinas del soporte existenteEn los soportes de sección rectangular que se vayan a reforzar mediante confinamiento por encamisado de materiales compuestos es necesario realizar previamente el redondeo de las esquinas para evitar la rotura prematura de las fibras y para aumentar la efectividad del confinamiento. El radio de redondeo debe de ser, al menos, de 20mm (véanse, por ejemplo, las referencias [1,4,17,18,23–26]).
Téngase en cuenta que de no llevarse a cabo dicho redondeo el coeficiente de efectividad (véanse por ejemplo las referencias [1,4]) se reduce de 1 (valor para secciones circulares) a un valor aproximado (dependiendo de la escuadría de la sección) de entre 0,25 y 0,33.
En algunas rehabilitaciones se trata de justificar la omisión del redondeo, o un valor muy reducido de este, en el hecho de que el pilar a reforzar presente recubrimientos prácticamente nulos. Para evitar esto, se podría materializar el redondeo mediante un leve recrecido de la sección, circunstancia que debería haber quedado recogida en el proyecto si durante la investigación previa se detectó el problema de los recubrimientos.
En refuerzos por sustitución mediante encamisados de hormigón es siempre recomendable el achaflanado de esquinas del pilar existente, y obligado en los tramos donde se pretenda realizar la transferencia de carga por corte fricción, pues dependiendo de la relación dimensional de la sección del pilar y el encamisado el perímetro eficaz de contacto se reduce a las partes achaflanadas [2].
Efectos indirectos del refuerzoOtro aspecto que frecuentemente no se analiza en detalle es la manera en la que el refuerzo de un soporte puede alterar la distribución de esfuerzos en la estructura. Se esbozan a continuación algunos ejemplos de estas posibles modificaciones:
Aumento de la rigidez del soporteEn el caso de optar por un refuerzo por encamisado de hormigón armado, el incremento que supone el mismo para la sección original implica un notable aumento de la rigidez del pilar. Este aumento alterará la posición del «centro de rigidez» del conjunto de pilares, lo que supondrá un cambio de comportamiento frente a cargas horizontales, sobre todo si el edificio no disponía de núcleos específicos de rigidez, habituales en edificios altos. El problema fundamental radica en no valorar este hecho, pues algunos soportes no dañados podrían ver empeorados sus esfuerzos tras el refuerzo de otros soportes próximos, mientras que en otras ocasiones la omisión de cálculos adicionales puede suponer dimensionar el refuerzo para cargas inferiores a las que le corresponde con la geometría modificada.
Por ello, además del simple análisis local de los pilares objeto de refuerzo frente a cargas gravitatorias, debe analizarse el comportamiento global de la estructura frente a todas las acciones solicitantes, con objeto de valorar si la nueva distribución de esfuerzos puede modificar el propio refuerzo planteado o exigir el refuerzo de otros pilares no contemplados inicialmente.
Sobrecarga de pilares próximos al reforzadoComo se expone con más detalle en [21], en los casos de pilares muy dañados o colapsados se debe tratar de estimar de qué manera se han sobrecargado los pilares adyacentes. De forma conservadora podría despreciarse la colaboración del pilar dañado para, mediante la modelización de la estructura, valorar cómo se incrementarían los esfuerzos en los soportes próximos. El problema en general es que dicha modelización no tendría en cuenta el efecto beneficioso de las particiones y los cerramientos, que muchas veces mitigan este efecto entrando en carga de forma no deseada tras el colapso, ni tampoco valorará adecuadamente la redistribución de esfuerzos a partes más lejanas de la estructura por el efecto de arco descarga que se produciría en los niveles superiores a los del nivel dañado, dependiendo del grado de hiperestatismo de la estructura. No obstante, al menos en el caso de la colaboración de particiones y cerramientos, se deben plantear hipótesis de cálculo no supeditadas a la resistencia de estos elementos no estructurales, por lo que habría que valorar la necesidad o no de reforzar estos soportes sobrecargados, pues difícilmente se conseguirá devolver totalmente dichos esfuerzos al pilar reforzado. En este sentido, la fluencia del hormigón colabora para que con el paso del tiempo parte de la carga que se derivó forzosamente por soportes adyacentes vuelva de nuevo al soporte dañado o colapsado, una vez reforzado. La dificultad de cuantificar este fenómeno es evidente, y empuja a valorar estos aspectos de forma conservadora.
Deformaciones en rotura de pilares confinadosCuando se plantea un refuerzo por confinamiento, las deformaciones verticales que se asumen en el soporte reforzado para que entre en funcionamiento el encamisado y, por lo tanto, se produzca la mejora por confinamiento, no son despreciables. Dichas deformaciones pueden conllevar la sobrecarga de soportes adyacentes, hecho que debería analizarse.
Casos prácticos. Ejemplos de diseñoSe plantea como base el mismo caso de siniestro de un soporte de edificación y diferentes alternativas de refuerzo. Mediante los siguientes ejemplos se trata de exponer las particularidades y dificultades del dimensionamiento del mismo.
Se trata de un edificio que consta de planta baja y 7 plantas más sobre rasante. La estructura está formada por forjados unidireccionales de 250mm de canto de viguetas semirresistentes de hormigón armado que apoyan sobre vigas de canto (300×500mm) y pilares del mismo material. Los materiales que fueron empleados para la construcción del edificio fueron un hormigón HA-20 y acero corrugado de dureza natural B400S.
El edificio presentaba locales comerciales muy diáfanos en la planta baja y viviendas en las plantas superiores, por lo que la configuración de particiones interiores favoreció el efecto desfavorable de planta débil ante el terremoto. Dicho efecto produjo que algunos soportes de la planta baja colapsaran, presentando daños irrecuperables que propiciaban que los refuerzos fueran planteados sin contar con la capacidad de las secciones residuales dañadas. Los ejemplos expuestos a continuación se centran en el refuerzo por sustitución de uno de los soportes interiores de la planta baja, con el único objeto de restituir su capacidad frente a acciones gravitatorias.
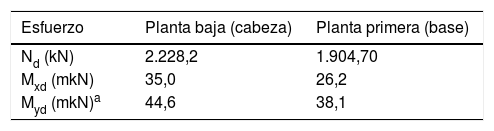
El soporte a reforzar presentaba una altura libre de 2,85m y una sección cuadrada de 450mm de lado, reduciéndose en la planta superior a 350mm. Del análisis estructural del edificio se dedujeron los esfuerzos de cálculo en dicho soporte que se muestran en la tabla 1.
Esfuerzos de cálculo del soporte a reforzar
| Esfuerzo | Planta baja (cabeza) | Planta primera (base) |
|---|---|---|
| Nd (kN) | 2.228,2 | 1.904,70 |
| Mxd (mkN) | 35,0 | 26,2 |
| Myd (mkN)a | 44,6 | 38,1 |
Para la obtención de dichos esfuerzos no se ha tenido en cuenta la acción sísmica para demostrar que, incluso para casos sencillos y habituales de edificación en el territorio nacional, existen algunas particularidades que pueden condicionar el refuerzo. Es fácil entender que la consideración de dicha acción sísmica u otras acciones horizontales relevantes pueden condicionar aún más el refuerzo, y la transferencia de carga en los nudos de la estructura.
Refuerzo mediante encamisado de hormigón armadoPor condiciones de ejecución del encamisado, para garantizar un adecuado hormigonado y un recubrimiento mínimo de 25mm, el espesor se fija en 80mm, por lo que las dimensiones exteriores de la camisa resultarán de 610×610mm (de manera que su área es de 169.600mm2). Los materiales empleados para el encamisado son un hormigón HA-25 y acero corrugado de dureza natural B500S. Dadas las dimensiones y la carga fundamentalmente de compresión centrada, se disponen 8 barras (3 por cara), si bien el diámetro de las barras de esquina se fija para que garanticen por sí solas la cuantía mecánica mínima fijada por EHE-08 [27]. De esta manera, si fuera necesario hacer continuo el refuerzo a la planta superior, solo haría falta dar continuidad a dichas armaduras, cuyos ejes no interceptan los armados de los pórticos principales. Con estos criterios se deduce un armado de 4ϕ16 (esquinas) y 4ϕ12 (caras). Como se puede comprobar, el axil último para compresión centrada de esta sección (deducida por condicionantes geométricos, de ejecución y de cuantía mínima) es netamente superior a la solicitación de la planta baja, y se garantiza la absorción de los pequeños momentos flectores solicitantes.
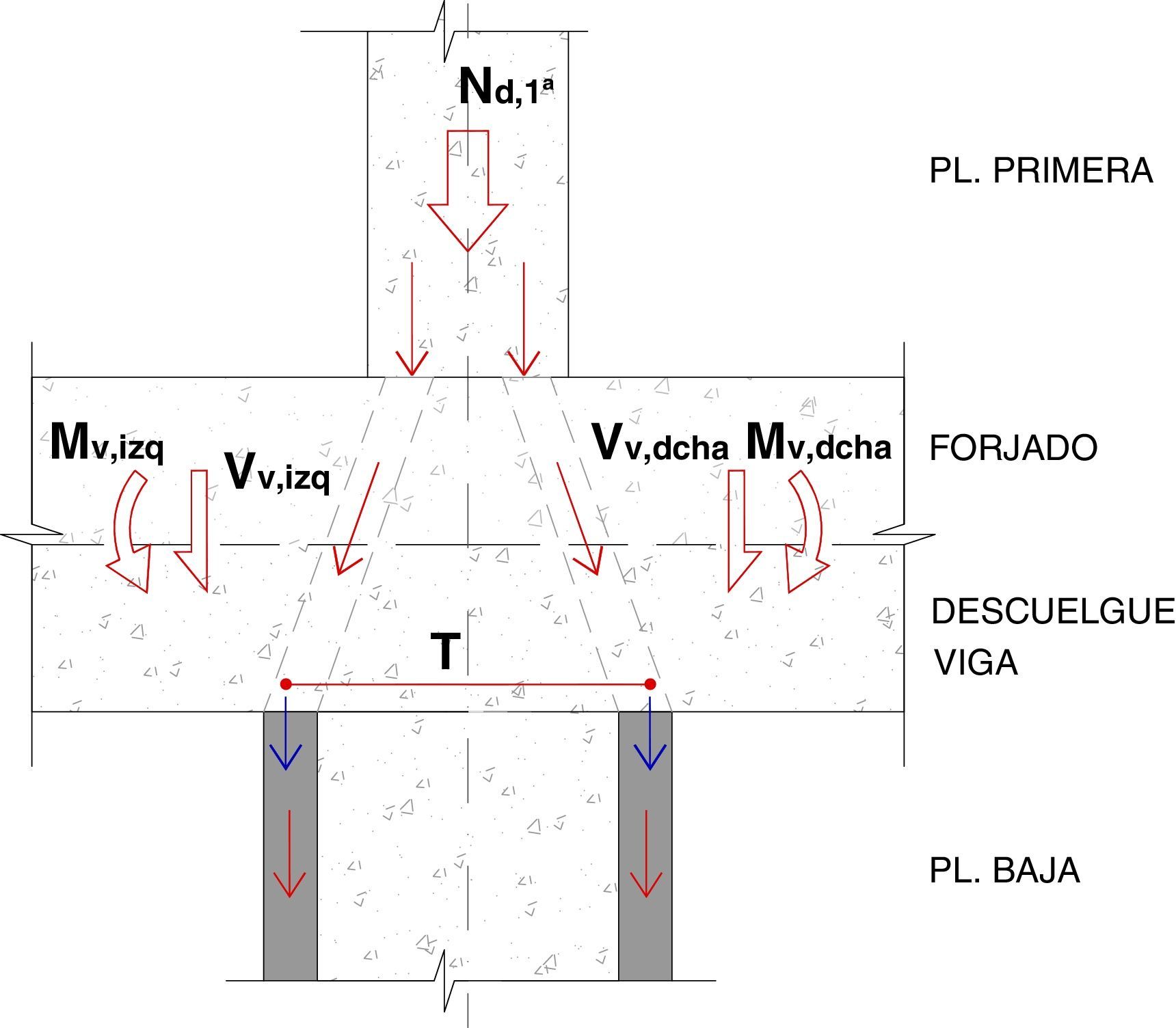
Definida la sección del refuerzo en la planta baja, se analiza la transferencia de carga entre el pilar existente y el refuerzo. Por simplicidad, primero se comprueba si es posible evitar prolongar el refuerzo al tramo superior de la planta primera, realizando la transferencia a través del nudo superior viga-pilar existente de planta baja (véase la figura 3).
Se deben realizar las siguientes comprobaciones:
a) Tracciones experimentadas en el nudo existente para desviar las cargas al encamisado.
Como se muestra en la figura 3, para lograr el desvío de cargas del pilar existente al encamisado se prevé la aparición de tracciones (T) en la parte inferior del nudo viga-pilar. En la dirección ortogonal de los forjados no se puede contar con coacción efectiva (dada la existencia de elementos de aligeramiento del entrevigado) ni con armaduras suficientemente repartidas para garantizar el desvío de cargas en el nudo.
Mediante un modelo de bielas y tirantes se puede verificar este aspecto, comprobando además si dicha tracción puede ser resistida por la armadura existente. En ese caso, tratándose de la armadura inferior de la viga, normalmente la cuantía es reducida al tratarse de un vano continuo, además de que los solapes suelen ser reducidos.
Tras el análisis del modelo de bielas y tirantes correspondiente se comprueba que, gracias a la poca inclinación de las bielas (por la existencia de vigas de canto) y a los esfuerzos que reciben las vigas en el apoyo por ser un vano continuo, no se llegan a desarrollar dichas tracciones, manteniéndose esta zona comprimida. De acuerdo con esto, no habría problemas de desvío hacia el encamisado.
b) Tensiones de compresión en el contacto con el encamisado.
Como se ha expuesto anteriormente, el desvío de las bielas comprimidas se materializa a través de las vigas de canto existentes, al no garantizarse el desvío de bielas en la dirección ortogonal de los forjados. Esta comprobación viene limitada por la resistencia del hormigón existente y la superficie de contacto entre las vigas y el encamisado (300mm de ancho de viga y 80mm de espesor de encamisado).
Las tensiones resultan excesivas en el contacto con la cara inferior de la viga, lo que haría necesario aumentar la superficie de contacto del encamisado, lo que puede resultar incompatible con la arquitectura (al menos en este caso, por las dimensiones que se requerirían para los posibles capiteles), o realizar la transferencia de carga del refuerzo en la planta superior.
Para analizar la longitud mínima de transferencia en la planta superior se puede seguir la metodología expuesta en [1]. En primera instancia se podrían considerar únicamente, con carácter conservador, los mecanismos de adhesión y de trabazón entre hormigones:
La tensión rasante de agotamiento, según el artículo 47.2.1 de EHE-08 [27], es igual a (para superficie rugosa, β=0,4):
Como se puede apreciar, la altura de encamisado necesaria en la planta primera es, como primera aproximación, superior a la altura libre de la planta (2,85m). Se justifica a continuación que dicha transferencia es posible realizarla en menor longitud, mediante el comportamiento dúctil de la unión entre el encamisado y el pilar existente. Para ello, se cuenta con las tensiones de compresión que se generan en la interfaz encamisado-pilar existente cuando se produce el «cabalgamiento» entre ambas superficies al presentar estas rugosidad (cálculo frente a tensiones rasantes según el artículo 47.2.2 de EHE-08 [27]). El valor de las tensiones de compresión generadas en la interfaz se garantiza fundamentalmente por los estribos del encamisado de refuerzo de los pilares cuando se produce el citado cabalgamiento del mismo con el mecanismo de corte fricción.
Siguiendo la metodología de Navarrete [2], para secciones rectangulares y una relación espesor de encamisado/lado = 80/350 = 0,23 <0,25, la reacción se concentra en las zonas achaflanadas de las esquinas, por lo que el perímetro eficaz se reduce a dichos chaflanes (4m, siendo m el ancho del chaflán realizado en las esquinas), resultando unas tensiones de compresión de:
Predimensionando los estribos en el tramo de transferencia como eϕ8/150mm (dicha cuantía se deduce por criterios de cuantía mecánica mínima y los criterios fijados en el artículo 42.3.1 de la EHE-08 [27]), de acuerdo con la expresión anterior, se tiene que:
Aplicando el artículo 47.2.2 de EHE-08 [27] se verifica que las tensiones de cálculo en el tramo de transferencia son elevadas y superiores al valor límite que hace que sea necesario despreciar la cohesión entre hormigones, por lo que la tensión rasante de agotamiento (para superficie tratada y rugosa, β=0,8 y μ=0,9) y la longitud de transferencia en planta primera resultarían de:
Por lo que resultaría finalmente una longitud de transferencia igual a la altura libre en la planta primera. Como se deduce de las expresiones anteriores, aumentar la cuantía transversal del encamisado no serviría para reducir la longitud de transferencia, pues las tensiones rasantes de agotamiento se ven limitadas superiormente por la resistencia del hormigón del pilar existente (mediante la condición límite indicada en la ecuación 6). Por otro lado, véanse las recomendaciones que establece Navarrete acerca de las longitudes máximas de efectividad de la transferencia, así como las propuestas para reducir dicha longitud conforme a las investigaciones experimentales realizadas y otras referencias.
En el tramo dañado de la planta baja sería necesario transferir también los esfuerzos de cálculo que solicitan al encamisado a la cimentación del edificio. De acuerdo con los ajustados resultados obtenidos para la posible transferencia directa en el contacto viga-encamisado, sería necesario realizar una comprobación análoga en el contacto inferior, de cara a establecer si es necesario realizar una pequeña zapata a modo de basamento en el encamisado para mejorar el reparto de cargas (para más detalle véase [1]).
Refuerzo mediante angulares empresillados metálicosTomando como referencia el mismo caso anterior, en primer lugar se dimensionan los angulares y las presillas de la planta baja, donde se va a realizar el refuerzo por sustitución. De acuerdo con los esfuerzos de cálculo de la tabla 1 y los criterios de la EAE [28], se plantean 4L150.150.15 con presillas 100.10 separadas 500mm a ejes.
Al igual que en el anterior ejemplo, se debe analizar cómo realizar la transferencia de esfuerzos entre la estructura existente y el refuerzo. Como primer tanteo, se plantea la transferencia directa en cabeza mediante la ejecución de un capitel metálico con angulares rigidizados. Mediante un planteamiento análogo al de la figura 3, se deduce que la comprobación crítica es la verificación de tensiones de compresión en el contacto capitel-viga existente. Teniendo en cuenta el ancho de la viga, asumiendo un reparto uniforme de tensiones se deduce que el capitel debería tener un vuelo del orden de 300mm, lo que resulta inviable arquitectónicamente en este caso. Cualquier alternativa en este sentido exigiría revisar las comprobaciones anteriores en cuanto a la posible aparición de tracciones en el nudo, pues las bielas resultarían más tendidas cuanto mayor sea el vuelo de los capiteles.
Alternativamente se plantea la transferencia de esfuerzos en la planta superior, en primera instancia mediante un encamisado continuo de acero, inyectando la interfaz con resinas. De esta manera, de acuerdo con los valores recomendados por el EC-4 [29], se obtendría una longitud de transferencia superior a la altura libre de planta primera:
Para reducir dicha longitud, se plantea la transferencia mediante la introducción de pasadores en el tramo de la planta primera, fijados al encamisado continuo exterior. Si se fija como predimensionamiento la métrica de los pasadores y su calidad (M20 8.8), de acuerdo con la EAE [28] el número de pasadores necesarios sería (n es el número de planos de corte):
Resistencia corte de los pasadores
Resistencia a aplastamiento de las chapas del encamisado
Resistencia a aplastamiento contra el hormigón, de acuerdo con las expresiones del artículo 6.6.3.1 del EC-4 [29]
Lo que se correspondería con 13 pasadores.
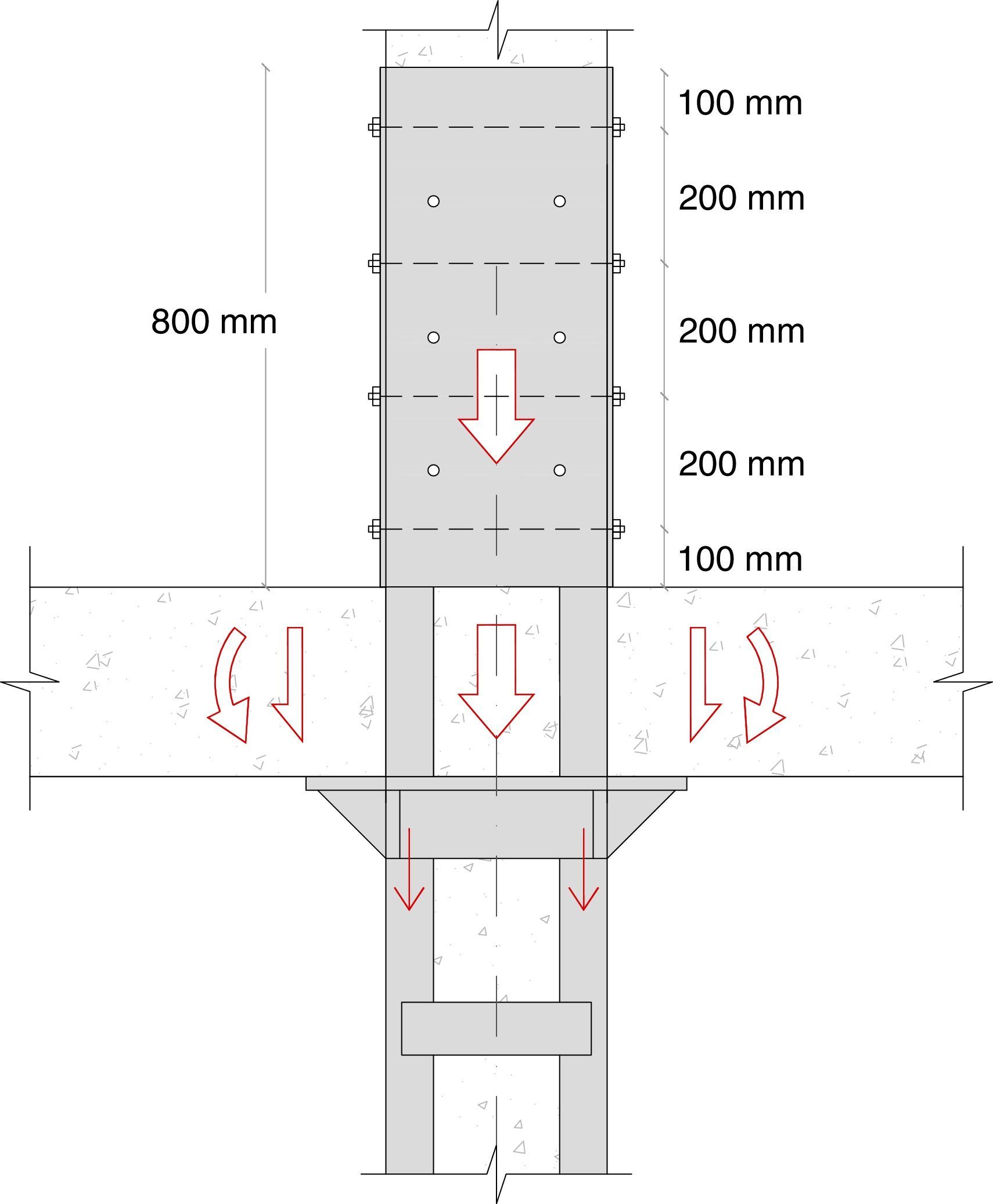
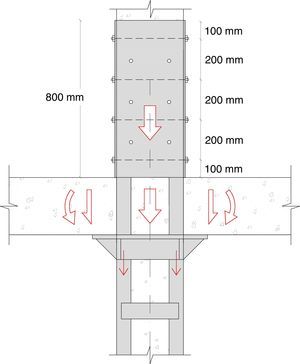
Para una disposición regular y simétrica, se dispondrían 14 pasadores distribuidos en altura por parejas y alternando las caras (véase la figura 4). Disponiendo la primera pareja a 100mm de la base y el resto cada 200mm, resultaría una altura de encamisado para la transferencia de 800mm.
Mediante el empleo de las formulaciones recogidas en el apartado 7.3.3.6 del Código Modelo [30], considerando la colaboración conjunta de la adherencia del encamisado (teniendo en cuenta que siempre se recomienda aumentar la rugosidad del hormigón y la inyección de la interfaz con resinas) y el efecto pasador, el número de pasadores podría llegar a reducirse, para este caso, a un total de 8, lo que supondría una altura del encamisado de 500mm. En todo caso, dada la falta de regulación clara al respecto, dicha propuesta quedaría supeditada al juicio del proyectista.
Por último, se debe comprobar si las tensiones transmitidas por las vigas de techo de planta baja a los angulares dispuestos en cabeza a modo de capitel resultan técnicamente admisibles. Para ello, se debe tener en cuenta que no todo el área de contacto del capitel puede resultar eficaz, dependiendo de la rigidez que tenga el mismo. Teniendo en cuenta la disposición de angulares L100.100.15 en cabeza del refuerzo de la planta baja, rigidizados con 2 cartelas de 10mm de espesor, centradas con respecto al eje de la viga y separadas 150mm entre sí, y las formulaciones indicadas en el artículo 65.2.2 de la EAE [28]:
De forma análoga se comprueban las tensiones transmitidas por los angulares dispuestos a modo de basamento sobre la cimentación existente, bastando con disponer L100.100.15 con cartelas de rigidización de 10mm de espesor (3 por cada cara) para conseguir repartir las cargas más uniformemente, limitando así las tensiones transmitidas por debajo de los valores antes indicados.
Reconstrucción del soporteEn este caso, es necesario verificar que el soporte existente presenta condiciones de seguridad correctas manteniendo la misma escuadría y esquemas de armado existentes (con independencia de que sea necesario reponer alguna armadura dañada) para los nuevos materiales empleados (de mayores capacidades que los existentes). La complejidad de esta alternativa radica en disponer una estructura de apeo bien dimensionada y concebida para garantizar el paso temporal de esfuerzos en la zona de eliminación del pilar hasta la cimentación existente.
Dicha estructura de apeo debe permitir además un espacio suficiente de trabajo para las labores de eliminación controlada y reconstrucción.
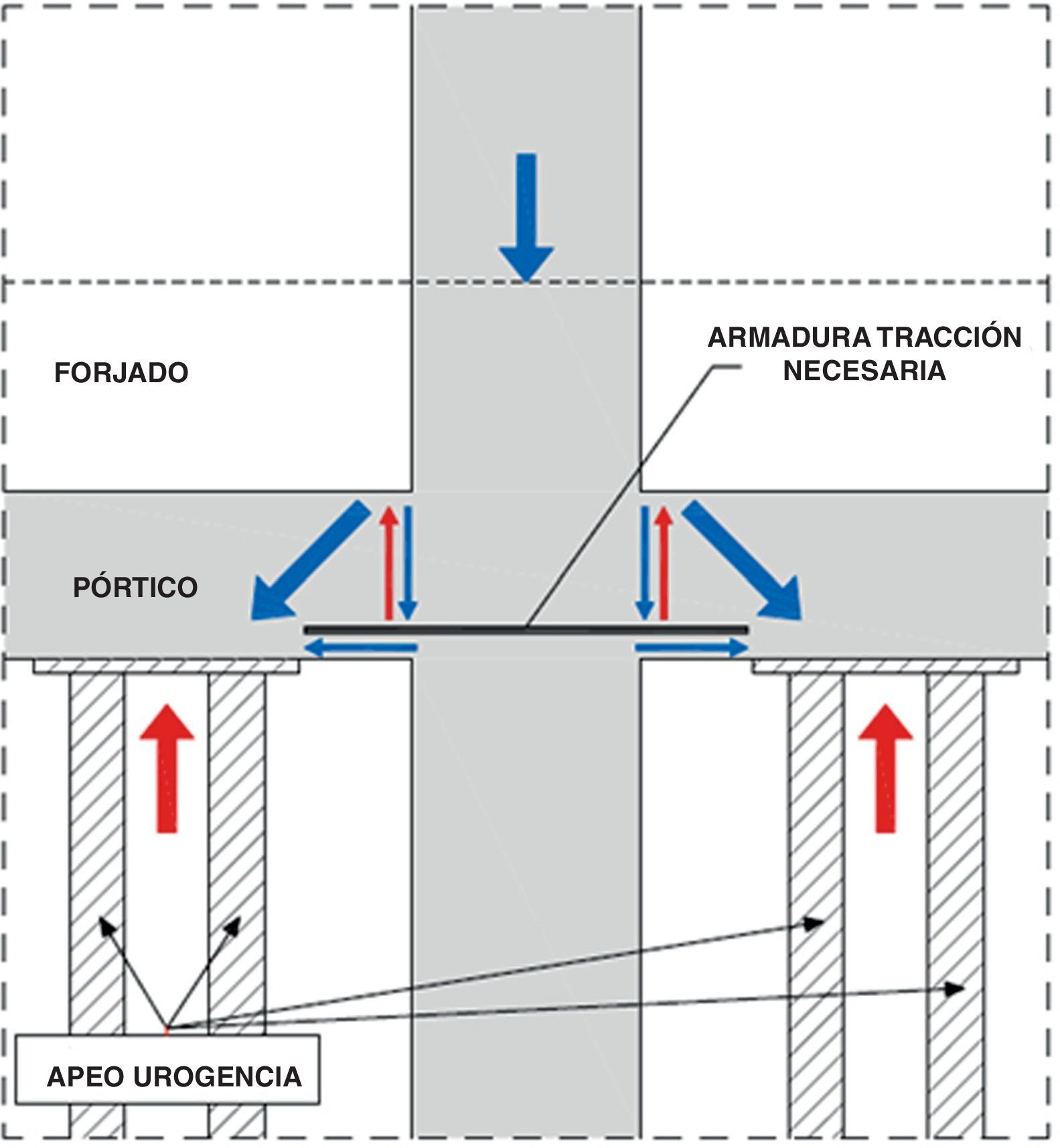
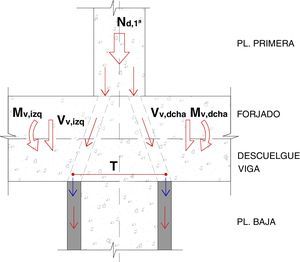
Cuando no existen problemas de intervención en las plantas superiores a la del refuerzo, la opción más sencilla puede resultar apear en toda la vertical del edificio los 2 vanos de viga adyacentes al pilar, si bien en muchos casos esto no es posible y debe verificarse que la estructura existente tenga recursos suficientes para puentear los esfuerzos hacia el apeo (véase la figura 5, extractada de la referencia [22]).
Trayectoria de las cargas de la estructura al apeo (croquis extractado de la referencia [22]).
Poniendo como ejemplo este último caso, dado el número elevado de puntales que se requerirían en la planta baja bajo cada vano de viga, resulta aconsejable disponer perfiles metálicos tipo HEB o en cajón (2UPN) lo más pegados posible al soporte a reforzar, pero lo suficientemente separados del mismo para permitir la demolición controlada y la reconstrucción. Para el ejemplo antes indicado, serían necesarios 2 soportes HEB200 (uno a cada lado del pilar), los cuales separamos al menos 300mm entre caras enfrentadas de pilar y soportes de apuntalamiento.
Además de comprobar que las tensiones localizadas entre los perfiles de apeo y la estructura existente sean técnicamente admisibles (si se realiza la comprobación para este ejemplo de forma análoga a como se hizo en la ecuación 11, se comprueba que es necesario disponer placas #300.300.20 para garantizar un mayor reparto en la cara inferior de la viga), como se ha indicado anteriormente, es necesario verificar si es necesario dar continuidad al apeo en las plantas superiores. Teniendo en cuenta el esquema mostrado en la figura 5 y un modelo de bielas y tirantes análogo al mostrado en la figura 3, las comprobaciones serían las siguientes:
Esfuerzos de cálculo en las vigas de techo de la planta baja a un canto útil de perfil de apeo:
Comprobación de la armadura necesaria en la cara inferior de la viga para garantizar la desviación de cargas en el nudo hacia los perfiles de apeo:
Al tratarse de una viga continua el armado de la cara inferior de la viga es solo el necesario para garantizar el anclaje del cortante existente en el apoyo, siendo dicho armado de 4ϕ12.
Por lo que la armadura inferior es netamente insuficiente para garantizar dicha desviación y se hace necesario subir el apeo a las plantas superiores hasta que se garantice que dicha armadura es suficiente. De acuerdo con los esfuerzos solicitantes, sería necesario subir el apeo hasta la tercera planta, si bien se podría limitar dicho apeo uno o 2 niveles si los perfiles se fueran disponiendo gradualmente cada vez más cercanos al pilar (aumentando así poco a poco el ángulo de desvío de las bielas considerado).
Por último, aunque interesa alejar los perfiles de apeo del pilar a reforzar para facilitar la ejecución, dado que en general estos deberán ser apoyados sobre la propia cimentación de dicho pilar, no conviene que se produzca una gran excentricidad de la carga transmitida por los apeos sobre la cimentación, pues ello también favorece la aparición de tracciones en el plano superior de la zapata, la cual probablemente carezca de armado superior.
ConclusionesLa falta de normativa que regule el diseño y la ejecución de refuerzos de pilares de hormigón armado ha contribuido durante décadas a la destecnificación de soluciones muy extendidas, algunas de ellas no suficientemente analizadas, hasta tal punto que por el paso del tiempo se admitían per se como de buena praxis, sin que se cuestione su eficacia real en caso de fallo del soporte reforzado.
Aunque muchos de los aspectos del dimensionamiento de refuerzos (por ejemplo, a nivel seccional o a nivel del tramo global de refuerzo) se rigen por las normativas aplicables a elementos de nueva construcción (en España, EHE o EAE en el caso de refuerzos con hormigón o acero, respectivamente), hay otros detalles fundamentales que actualmente no disponen de regulación clara y que, en caso de omisión o error, pueden determinar que la eficacia del refuerzo sea nula.
Particularmente, puede condicionar el refuerzo la transferencia de carga entre la estructura existente y el refuerzo, y viceversa. Como se expone en el presente artículo mediante 3 ejemplos sencillos, asumir que la transferencia está garantizada sin poner números a los detalles puede llevar a que la solución elegida no garantice unas adecuadas condiciones de seguridad. De hecho, en general garantizar dicha transferencia puede complicar las soluciones inicialmente planteadas.
En este mismo sentido, resulta crítica la definición de los sistemas de apeo provisionales de soportes dañados, pues deben dimensionarse según la normativa vigente, aunque se trate de estructuras provisionales (su tratamiento debe ser análogo al de estructuras permanentes), analizando la transferencia de cargas entre la estructura existente y los elementos de apeo, para que no se vean comprometidas las condiciones de seguridad de los usuarios y de los operarios que acometerán las labores de refuerzo.
Como reflexión final, tras el estudio de los refuerzos de pilares llevados a cabo en una muestra de 70 edificios de hormigón armado que resultaron dañados con el terremoto de Lorca de 2011, difícilmente se avanzará en la definición de refuerzos de estructuras solicitadas frente a sismo, si no se normaliza el análisis y la definición de refuerzos frente a cargas gravitatorias.




![Esquema de transferencia de cargas pilar existente-refuerzo por encamisado (croquis extractado de la referencia [1]). Esquema de transferencia de cargas pilar existente-refuerzo por encamisado (croquis extractado de la referencia [1]).](https://static.elsevier.es/multimedia/04395689/0000006900000284/v1_201804250433/S0439568917301006/v1_201804250433/es/main.assets/thumbnail/gr1.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
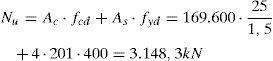
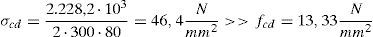
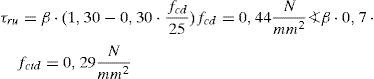
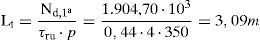
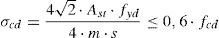
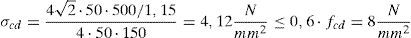
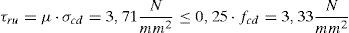
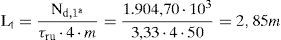
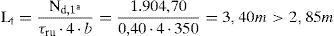
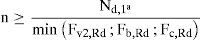
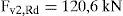
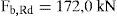
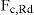
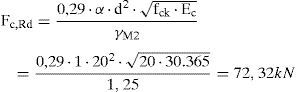
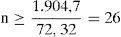

![Trayectoria de las cargas de la estructura al apeo (croquis extractado de la referencia [22]). Trayectoria de las cargas de la estructura al apeo (croquis extractado de la referencia [22]).](https://static.elsevier.es/multimedia/04395689/0000006900000284/v1_201804250433/S0439568917301006/v1_201804250433/es/main.assets/thumbnail/gr5.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)