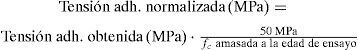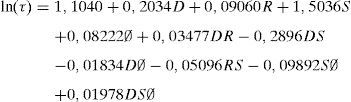Estudio de la influencia de los principales parámetros que definen un solapo de barras

Resumen

En este documento se recogen los resultados de una campaña experimental en la que se han estudiado los principales parámetros geométricos que definen un solapo de barras: diámetro de la armadura, recubrimiento, separación entre barras solapadas y distancia entre familias de barras solapadas. Para realizar esta investigación se recurrió a un ensayo de arrancamiento múltiple, recientemente desarrollado en la Universidade da Coruña, y se planteó una metodología estadística basada en el diseño de experimentos. En estas condiciones, el recubrimiento y la distancia entre familias de barras solapadas se muestran como los factores más determinantes.

Abstract

This document shows the results of an experimental work in which the main geometric factors defining lap splices were studied. The diameter of the reinforcement bar, the concrete cover, the gap between the two overlapped bars and the distance between families of overlapped bars were taken into account. The multiple pull-out test, recently developed at the University of A Coruna, was used to perform the experimental work, in combination with a statistic methodology based on the design of experiments techniques. In these conditions, the concrete cover and the distance between families of overlapped reinforcement bars resulted to be the most important factors.

1

Introducción

Durante la construcción de un elemento estructural es muy frecuente tener que empalmar dos barras según la dirección de su eje, asegurando que se comporten como una única armadura continua. Esto es así, en algunas ocasiones, por los límites existentes en la fabricación y transporte de las armaduras, y en otras por los condicionantes que impone la ejecución de ciertos elementos, que requieren armaduras de espera entre diferentes fases de hormigonado.

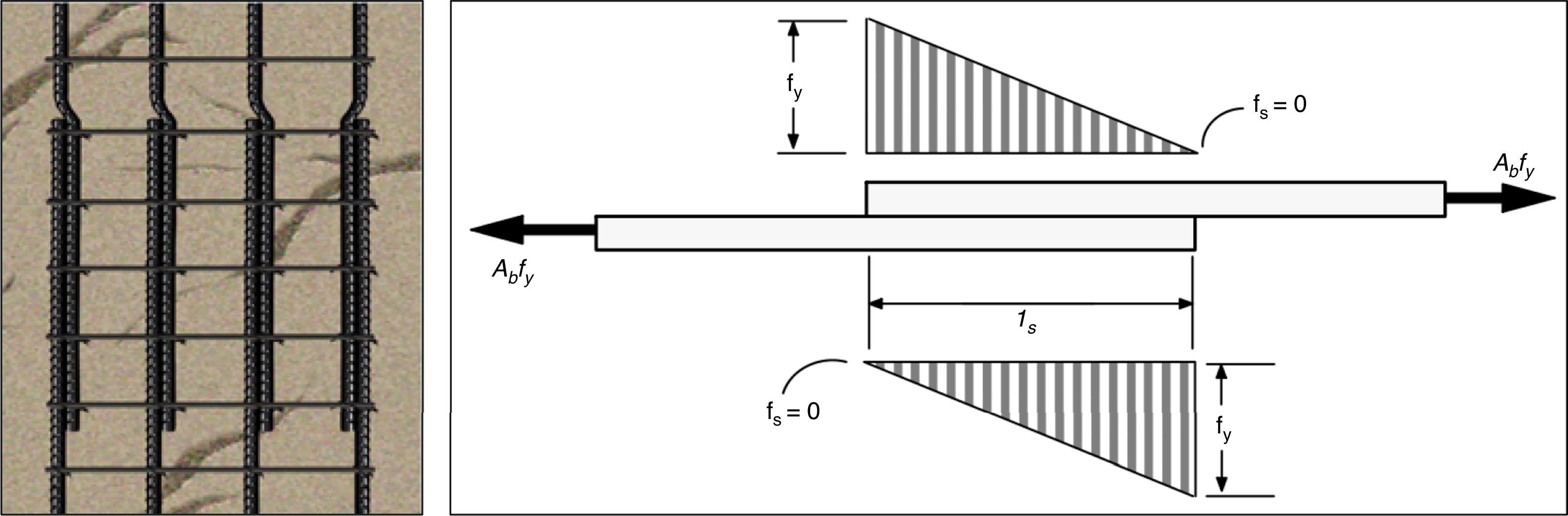
Una unión de este tipo supone un punto singular, y debe garantizarse la correcta transmisión de esfuerzos entre barras asegurando que se resiste la tensión de diseño sin que aparezcan deslizamientos ni fisuras inaceptables. En un empalme por solape, la fuerza de tracción de una de las barras se transfiere a la otra a través de los mecanismos adherentes que se producen en la zona que constituye el solapo. Correctamente dimensionado y ejecutado, un solapo crea el efecto de una armadura continua, aunque físicamente existen dos barras diferenciadas (fig. 1).

Figura 1.

A la izquierda, solape de armaduras. A la derecha, esquema conceptual propuesto por la ACI para explicar la transmisión de fuerzas entre barras solapadas [1].

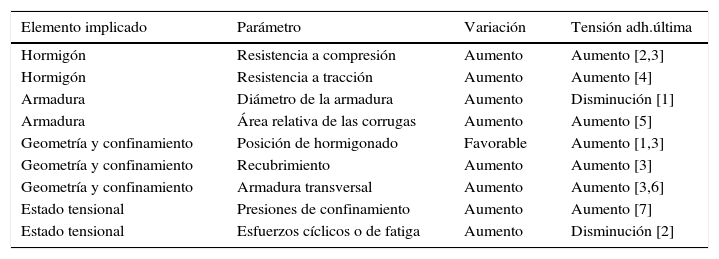
Los parámetros que determinan el funcionamiento de un solape son esencialmente los mismos que gobiernan el fenómeno de la adherencia entre las barras de acero y el hormigón, recogidos según sus efectos en la tabla 1.

Tabla 1.

Resumen de variables que influyen en el comportamiento adherente

Elemento implicado	Parámetro	Variación	Tensión adh.última
Hormigón	Resistencia a compresión	Aumento	Aumento [2,3]
Hormigón	Resistencia a tracción	Aumento	Aumento [4]
Armadura	Diámetro de la armadura	Aumento	Disminución [1]
Armadura	Área relativa de las corrugas	Aumento	Aumento [5]
Geometría y confinamiento	Posición de hormigonado	Favorable	Aumento [1,3]
Geometría y confinamiento	Recubrimiento	Aumento	Aumento [3]
Geometría y confinamiento	Armadura transversal	Aumento	Aumento [3,6]
Estado tensional	Presiones de confinamiento	Aumento	Aumento [7]
Estado tensional	Esfuerzos cíclicos o de fatiga	Aumento	Disminución [2]

A los anteriores parámetros hay que añadir ciertas variables o factores que no influyen cuando se estudia la adherencia de una barra aislada, entre ellos:

• •

  La separación entre las dos barras que constituyen un solapo. Se distinguen así los solapos con contacto (las barras se encuentran unidas en la zona de solapo) y sin contacto (están separadas hasta varias veces el diámetro de las barras).

• •

  El número de barras solapadas en una misma sección y la separación entre los solapos.

Al contrario de lo que ocurre cuando se analiza el comportamiento adherente de una única armadura, no existe un ensayo normalizado y comúnmente aceptado para caracterizar los solapos. Por ello diferentes autores y escuelas normativas atribuyen una influencia muy heterogénea a los diferentes factores que definen el fenómeno, encontrándose notables discrepancias con diferencias de más de un 50% en la longitud de solapo calculada para un mismo caso [8].

2

Objetivos

El propósito principal de este desarrollo experimental es determinar la influencia de la geometría de la sección estudiada en el comportamiento adherente de armaduras pasivas solapadas. Por ello, los objetivos particulares de esta investigación son los siguientes:

• •

  Determinar la posible influencia que tiene el diámetro de las barras solapadas. Para ello, se emplearán armaduras de diámetro nominal 12 y 16 mm.

• •

  Estudiar el papel del recubrimiento como uno de los principales factores que afecta al comportamiento de un solapo de barras.

• •

  Analizar la influencia de la separación entre las dos armaduras que constituyen un solapo. Diversas normativas permiten que se encuentren juntas o con cierta separación [1,9].

• •

  Comprobar si la distancia entre dos familias de barras solapadas presenta influencia en el comportamiento de los especímenes.

3

Programa experimental

Para realizar la investigación se planteó un exhaustivo programa en el que a cada variable estudiada se le asignaron dos valores, ensayando posteriormente todas las posibles combinaciones y comprobando estadísticamente la influencia por separado de cada factor, así como sus potenciales interacciones con otras variables. En los siguientes apartados se describen con mayor profundidad los materiales empleados, el ensayo y la metodología aplicada.

3.1

Materiales

Las barras de armadura empleadas, de acero B 500 SD y suministradas por Celsa Group Atlantic con certificado de calidad según UNE 36065:2011, contaban con diámetros nominales de 12 y 16 mm. Se realizaron controles para verificar que no existían defectos reseñables en las corrugas y que las dimensiones externas de la barra se encontraban dentro del rango tolerado.

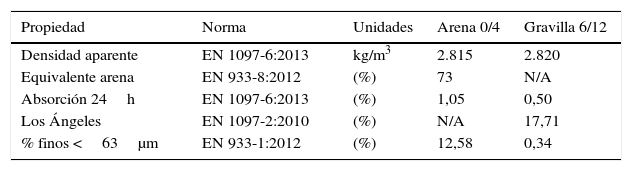
Los áridos finos y gruesos del hormigón son de origen calizo. Se utilizó una arena AF-T-0/4-C-L y una gravilla AG-T-6/12-C-L, ambas obtenidas por machaqueo de roca lavada y cuyas características se condensan en la tabla 2. Este tipo de árido, mucho menos frecuente en Galicia que el obtenido por procesamiento de granito, consigue minimizar el riesgo de desarrollar enfermedades respiratorias al no presentar apenas sílice libre [10].

Tabla 2.

Principales características de los áridos empleados

Propiedad	Norma	Unidades	Arena 0/4	Gravilla 6/12
Densidad aparente	EN 1097-6:2013	kg/m^3	2.815	2.820
Equivalente arena	EN 933-8:2012	(%)	73	N/A
Absorción 24 h	EN 1097-6:2013	(%)	1,05	0,50
Los Ángeles	EN 1097-2:2010	(%)	N/A	17,71
% finos < 63 μm	EN 933-1:2012	(%)	12,58	0,34

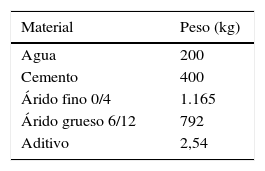
Se empleó un cemento CEM II/A-M (V-L) 42,5 R, suministrado por la fábrica de Toral de los Vados de Cementos Cosmos. Se utilizó también el superplastificante de tercera generación BASF MasterEase 3530. La tabla 3 recoge la dosificación empleada.

Tabla 3.

Peso seco de los materiales empleados para un volumen de 1 m³

Material	Peso (kg)
Agua	200
Cemento	400
Árido fino 0/4	1.165
Árido grueso 6/12	792
Aditivo	2,54

Con una cantidad de cemento de 400 kg/m³ y una relación agua/cemento de 0,5 se consiguió un hormigón de muy buenas prestaciones y de fácil colocación (consistencia líquida), lo que facilitaba mucho la elaboración de especímenes y reducía la probabilidad de que quedaran defectos en las probetas. En estas condiciones se logró un hormigón con una resistencia nominal de 50 MPa a 7 días, edad a la que se realizaron todos los ensayos.

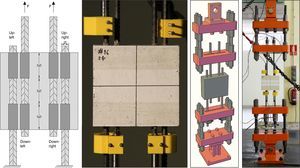
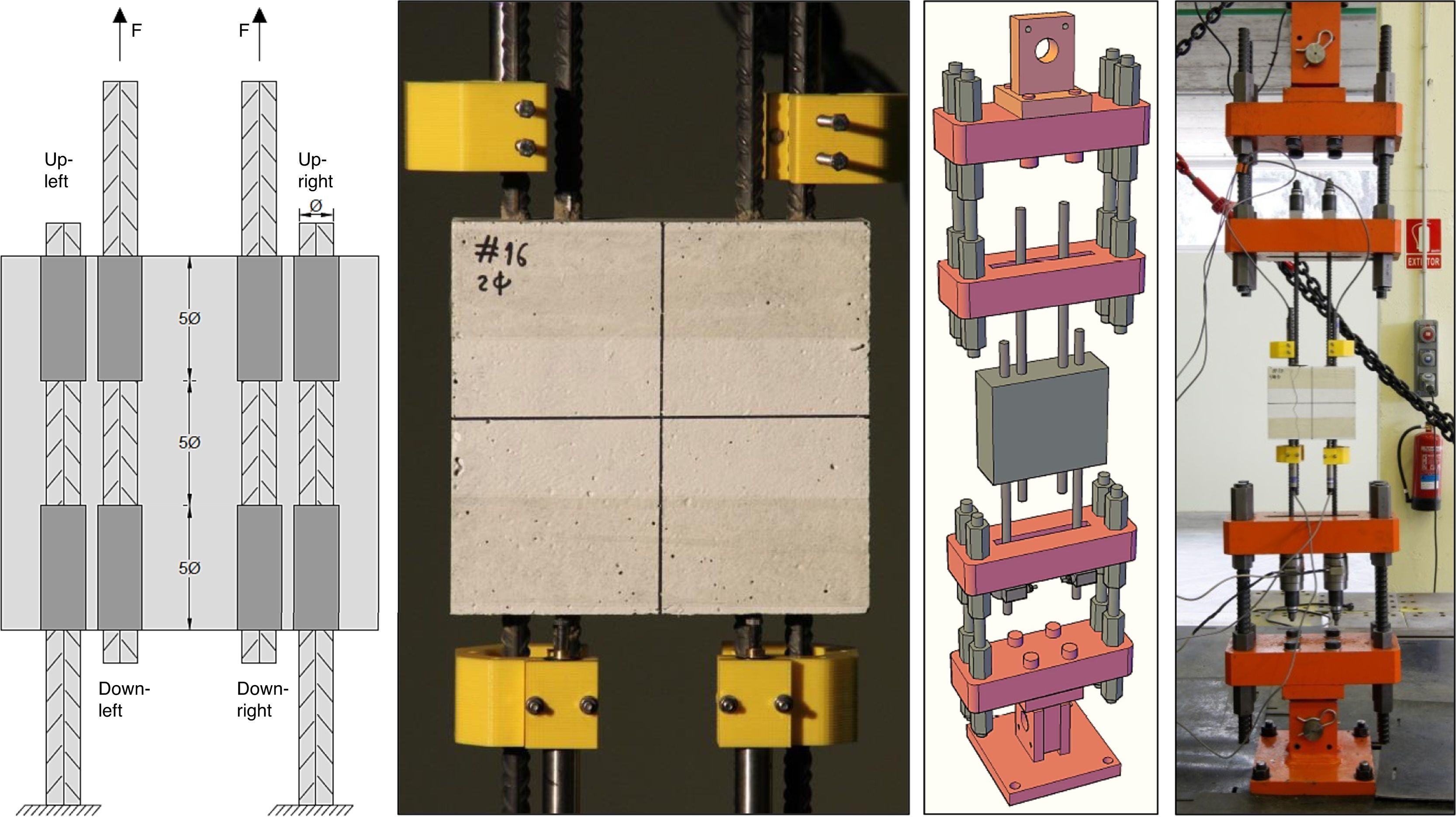
3.2

Ensayo de arrancamiento múltiple

El ensayo de arrancamiento múltiple constituye una generalización del normalizado ensayo pull-out [11]. Consiste en la aplicación de una fuerza de tracción creciente sobre una familia de barras, solapadas en el interior del espécimen de hormigón a otras cuyo extremo se ancla a un punto fijo. Durante el ensayo se registra la fuerza aplicada a cada barra y el deslizamiento producido en el extremo libre de cada armadura (en la fig. 2, los puntos en los que se mide el deslizamiento son el Up-Left, Up-Right, Down-Left y Down-Right), de forma que es posible obtener las curvas [tensión adherente] − [deslizamiento] para cada uno de los solapos.

Figura 2.

Ensayo de arrancamiento múltiple.

La zona de la probeta en la que las armaduras se solapan tiene una longitud igual a cinco veces el diámetro de la barra. Así mismo, en cada extremo de la armadura se inhibe la adherencia en una longitud también igual a cinco veces el diámetro de la armadura, de forma que la longitud total de la probeta de hormigón es de quince veces el diámetro nominal de la armadura. Todas las probetas se elaboraron con las barras en posición horizontal (fig. 3), desfavorable respecto a la adherencia por el riesgo de que queden burbujas de aire ocluido en contacto con la barra.

Figura 3.

Encofrados de contrachapado fenólico y zona de adherencia inhibida.

El ensayo se realiza bajo control por desplazamiento, imponiendo al actuador hidráulico de la máquina de ensayos una velocidad de 0,5 mm/minuto, coincidente en la rama elástica de deformación del acero con la propuesta por la RILEM para el ensayo pull-out de una armadura de 16 mm de diámetro nominal. Se constató experimentalmente que no variaban los resultados al modificarse esta velocidad, por lo que se decidió adoptarla también para ensayar las barras de 12 mm. El ensayo se mantenía hasta producirse el fallo del espécimen, y se registró la rotura con una cámara de alta velocidad (2.000 fps), lo que, unido a un extenso reportaje fotográfico, hacía posible reconstruir el patrón de fisuras y la rotura de las probetas.

En cada solapo de todos los especímenes ensayados se obtienen las curvas [tensión adherente] − [deslizamiento]. La tensión se calculó dividiendo la fuerza registrada entre la superficie adherente de cada armadura, simplificando esta como un cilindro de diámetro el nominal de la barra. El deslizamiento se registra con los transductores situados en el extremo libre de cada barra.

Aunque se tiene constatada una buena correlación entre la tensión de adherencia y la raíz cuadrada de la resistencia del hormigón [12,13], en este estudio se decidió normalizar la tensión de adherencia respecto a la resistencia media del hormigón empleado (50 MPa). Esto es así debido a la mínima diferencia observada en las resistencias obtenidas con respecto a la teórica (siempre inferiores a un 4%) y a que con esta normalización únicamente se buscaba bloquear el efecto de la resistencia sin que se produjera una merma de la precisión numérica del modelo. Para esta labor se fabricaron probetas cúbicas que se rompieron los días de ensayo.

El parámetro de respuesta que se utilizó para elaborar el modelo estadístico y comparar entre familias de probetas fue la tensión de adherencia normalizada según la ecuación (1).

3.3

Metodología estadística y variables de estudio

Para analizar la influencia que tienen las diferentes variables estudiadas se decidió recurrir a un diseño factorial completo, es decir, un diseño en el que ensayan todas las combinaciones de todos los valores que pueden adoptar todas las variables del ensayo. En argot estadístico, el valor que puede adoptar una variable se define como nivel y las variables de estudio se denominan factores. El efecto de un factor se define como el cambio en el parámetro de respuesta producido por un cambio en el nivel del factor. Aparte de los efectos principales en un experimento pueden obtenerse otros efectos, denominados interacciones, que son la combinación de dos o más factores y que tienen un efecto estadístico sobre la respuesta del experimento.

Otra posible forma de proceder es el tradicional método de bloqueo de variables, que consiste en fijar todas los factores estudiados menos uno, y este último es el que se varía para analizar cómo se modifica el parámetro de respuesta.

Las principales ventajas de los diseños factoriales frente a los diseños basados en el bloqueo de variables son las siguientes [14]:

• •

  Este tipo de diseños son más eficientes, ya que se obtiene más información con el mismo número de ensayos.

• •

  Los diseños factoriales son necesarios cuando se sospecha que puede haber interacciones entre variables, evitando llegar a conclusiones erróneas.

• •

  Los diseños factoriales permiten estimar los efectos de un factor en diversos niveles de los otros factores, aportando conclusiones que son válidas en toda la extensión de las condiciones experimentales.

Sin embargo, la principal desventaja o inconveniente que presenta este método es el número de ensayos o pruebas necesarias. Así, en el caso general de tener k factores, cada uno de ellos con n niveles, el número de experimentos necesario para realizar un diseño factorial completo es n^k, sin contar posibles repeticiones.

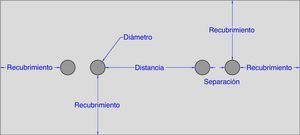
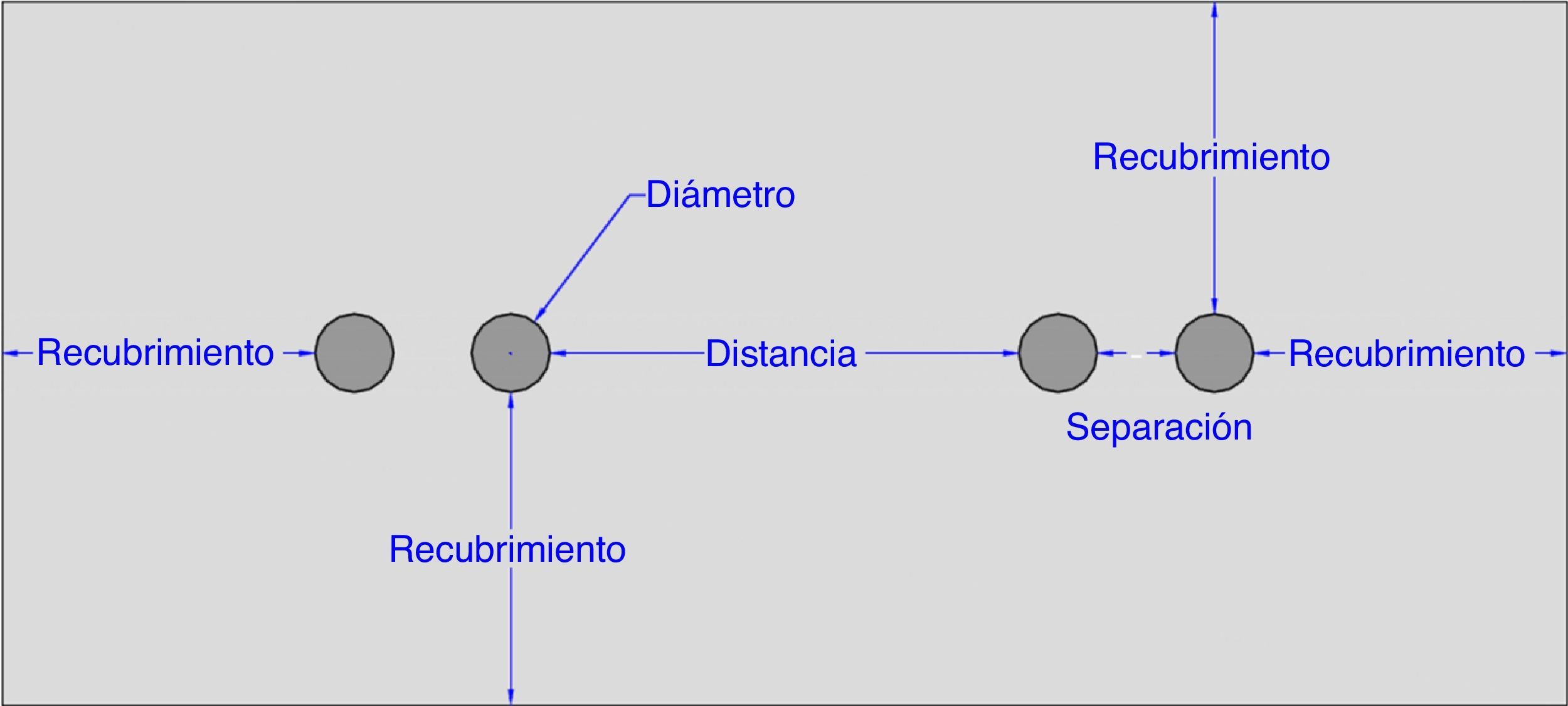
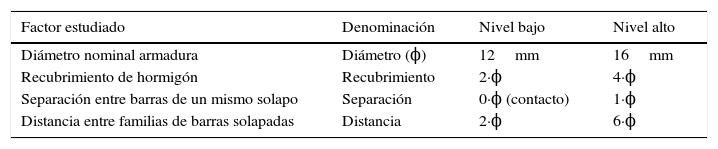
En esta investigación se recurrió a un diseño factorial completo 2⁴ donde los k = 4 diferentes factores estudiados únicamente pueden tener dos niveles, conocidos como nivel bajo y nivel alto (tabla 4 y fig. 4). De cada posible combinación de factores se realizaron tres repeticiones, quedando un total de 3·2⁴ = 48 especímenes. De cada ensayo se obtienen datos de tensión de adherencia de 4 barras, por lo que de cada posible combinación se tienen datos de 3·4 = 12 barras. Puesto que alguna probeta ha tenido que ser descartada, finalmente se utilizó el valor de 8 barras de cada posible combinación de factores, descartando los 2 valores menores y mayores. En estas condiciones, el modelo estadístico se alimenta con un total de 8·2⁴ = 128 valores, correspondientes otras tantas armaduras solapadas.

Tabla 4.

Factores estudiados y niveles analizados

Factor estudiado	Denominación	Nivel bajo	Nivel alto
Diámetro nominal armadura	Diámetro (ϕ)	12 mm	16 mm
Recubrimiento de hormigón	Recubrimiento	2·ϕ	4·ϕ
Separación entre barras de un mismo solapo	Separación	0·ϕ (contacto)	1·ϕ
Distancia entre familias de barras solapadas	Distancia	2·ϕ	6·ϕ

Figura 4.

Sección transversal de la probeta y factores del modelo.

4

Resultados obtenidos

4.1

Ajuste del modelo estadístico

Para analizar la gran cantidad de datos obtenida se ajustaron los resultados adquiridos a un modelo de regresión lineal. Puesto que la varianza de los mismos dependía en cierta medida del valor de tensión de cada familia de probetas (con mayor dispersión cuanto mayor era la tensión máxima alcanzada por los especímenes), se recurrió a una transformación Box-Cox de tipo logarítmica (λ = 0) para estabilizar las varianza y obtener un mejor ajuste [15].

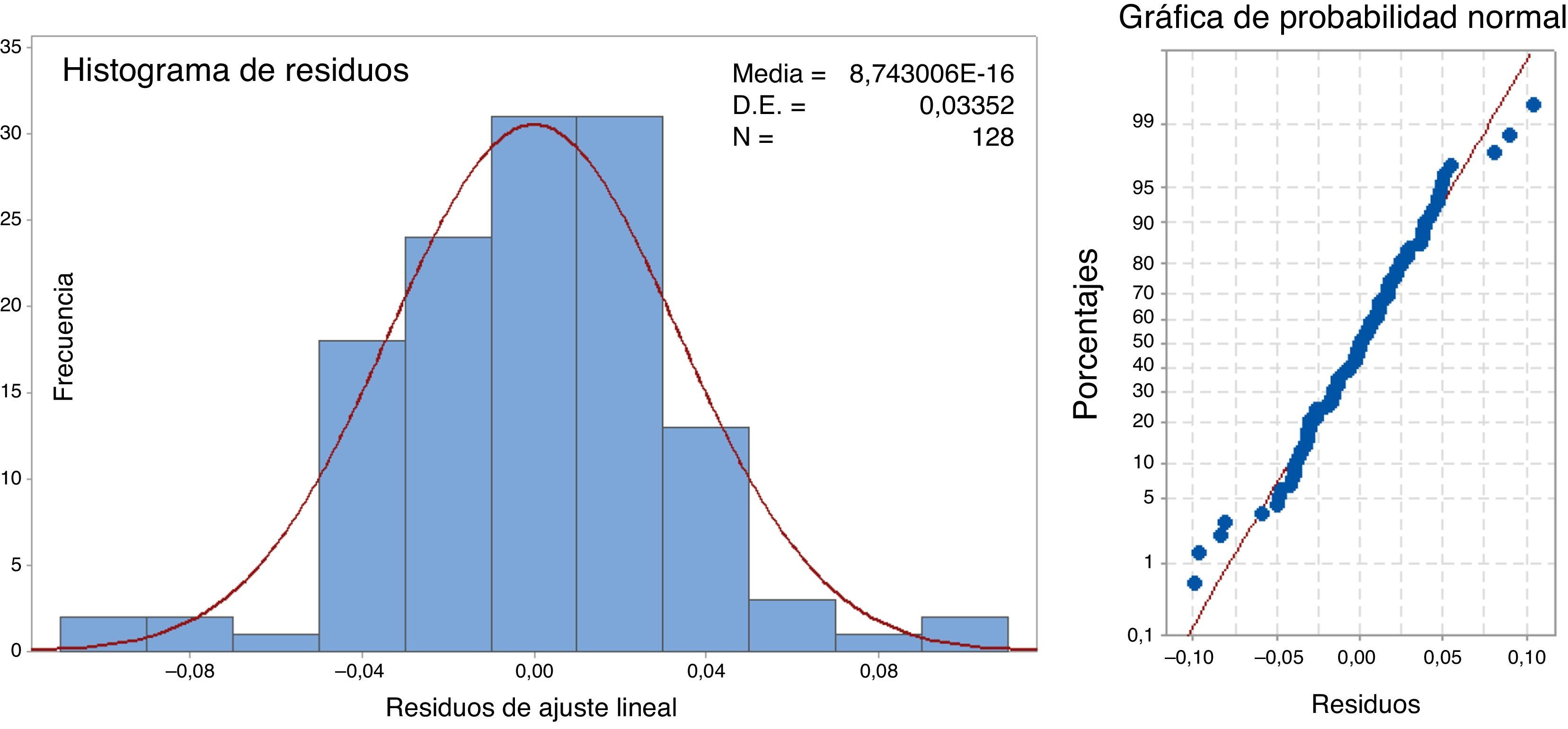
En la figura 5 se aprecia que los residuos de ajuste (diferencias existentes entre el valor observado y el valor predicho por el modelo de regresión) están agrupados alrededor del cero, ajustándose bien a una distribución normal de media 0. En la gráfica de probabilidad normal se observa que de los 128 valores únicamente 7 se alejan un poco de la recta normal, por lo que se puede concluir que el ajuste del modelo es satisfactorio.

Figura 5.

Ajuste de los datos al modelo estadístico.

En estas condiciones, el modelo ajustado queda de la siguiente forma:

En la ecuación (2) τ es la tensión adherente máxima, Ø el diámetro de la barra de armadura, R el recubrimiento de hormigón, S la separación entre barras solapadas y D la distancia entre familias de barras solapadas. El modelo mayoritariamente emplea términos de primer y segundo orden, ya que gran parte de los términos de mayor orden han podido eliminarse al tener muy poca influencia, simplificando notablemente la ecuación obtenida. El coeficiente R² del modelo que proporciona la ecuación (2) es 0,9828.

4.2

Influencia de los parámetros principales

Al ajustar los datos obtenidos a un modelo de regresión es posible analizar la influencia de cada factor y las interacciones entre los mismos (términos del modelo estadístico).

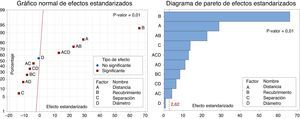
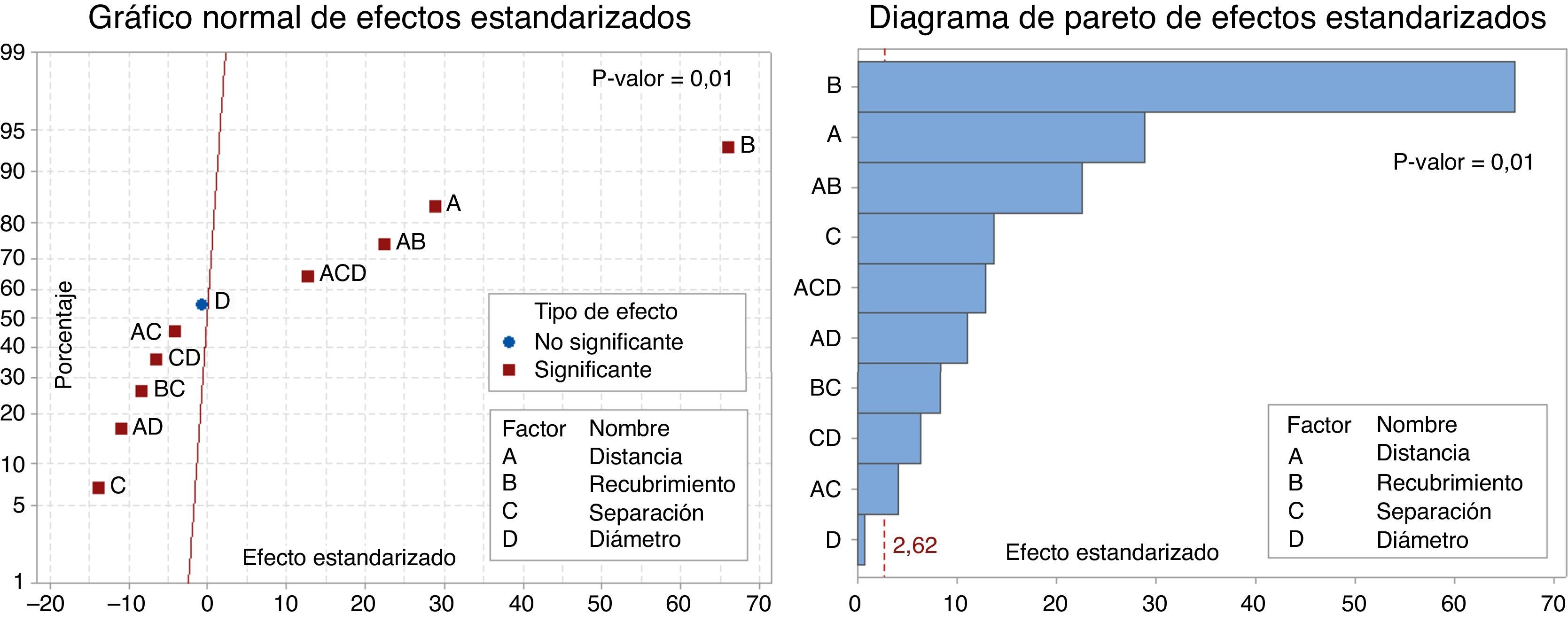
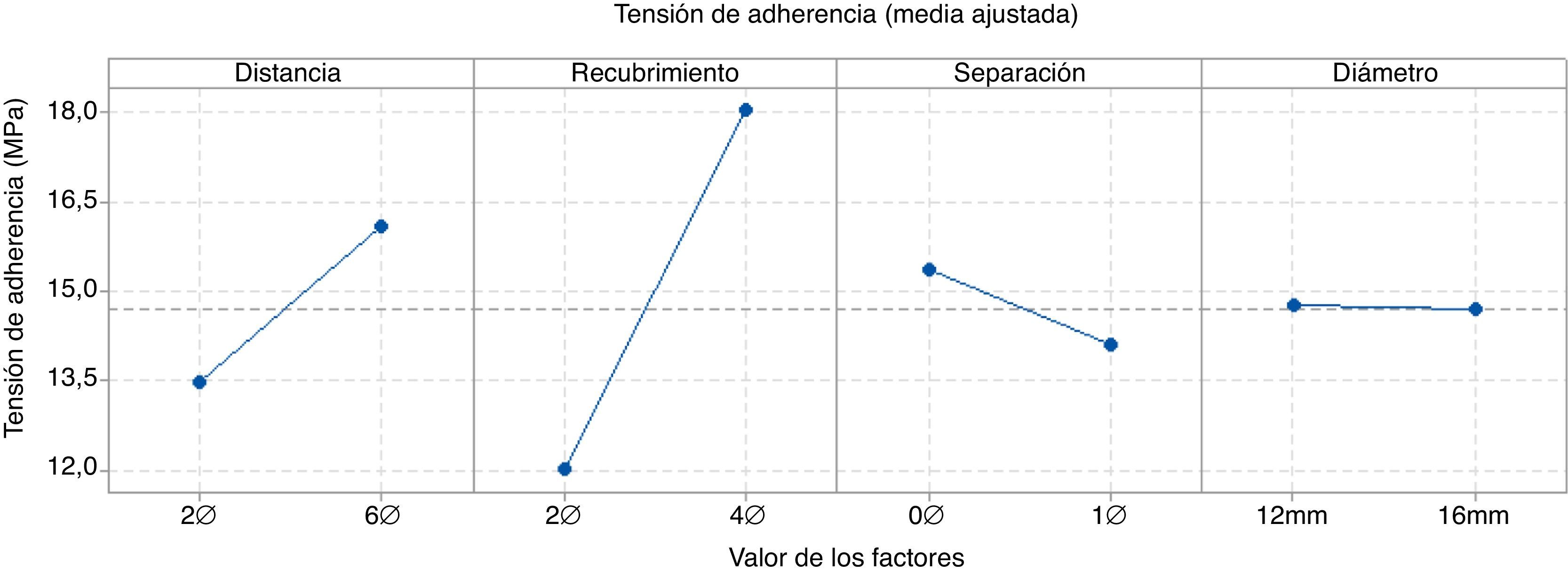
En el gráfico normal de efectos estandarizados (fig. 6, izquierda), cuanto más alejado se encuentre un término de la recta representada, mayor influencia tiene este en la respuesta (tensión adherente). Así mismo, los términos que se sitúan a la izquierda tienen efecto negativo (reducen la respuesta) y los términos que se sitúan a la derecha producen un efecto positivo (aumentan la respuesta). El recubrimiento y la distancia entre familias de barras solapadas son los términos cuyo aumento más incrementa la tensión adherente, mientras que la separación entre barras solapadas es el término cuyo aumento más la reduce. Nótese que el diámetro (término D en los gráficos) está situado sobre la recta, por lo que, por sí mismo, no tiene influencia en la tensión adherente. En el diagrama de Pareto (fig. 6, derecha) se aprecia claramente la irrelevancia que tiene el diámetro de la barra como efecto principal. No obstante, en combinación con la distancia entre familias de barras solapadas sí presenta influencia en la respuesta. Esto indica que su efecto depende del nivel en el que se encuentre otro factor (interacción).

Figura 6.

Influencia de los diferentes términos del modelo en el valor predicho de las tensiones.

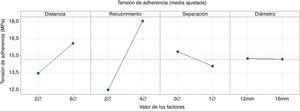
Al estudiar el valor predicho por el modelo de regresión para las tensiones de adherencia en el momento de la rotura (fig. 7), se constata de nuevo que el recubrimiento es el factor más importante. Al crecer la distancia entre familias de barras solapadas también aumenta la tensión adherente, mientras que al hacerlo la separación entre barras solapadas se produce una disminución de dicha tensión. La influencia del diámetro de la armadura es mínima.

Figura 7.

Valor medio de las tensiones adherentes máximas predicho por el modelo estadístico.

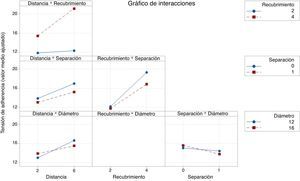
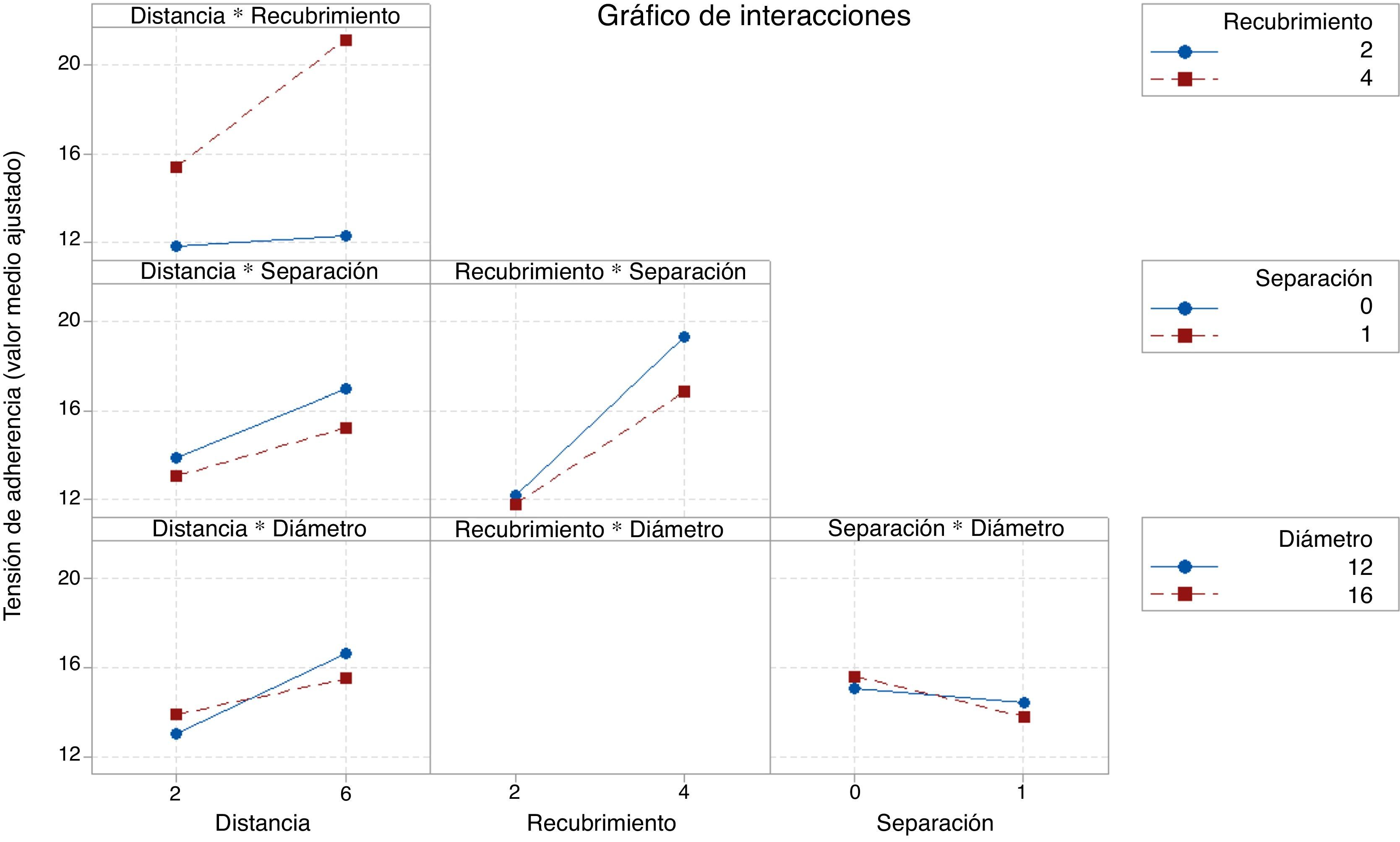
4.3

Interacciones entre parámetros

En un gráfico como el de la figura 8, dos rectas paralelas indican que no existe interacción entre factores. Por el contrario, a menor paralelismo, mayor interacción se producirá entre los factores que definen el modelo, lo que se traduce en que la influencia de un factor depende del nivel en que se encuentre otro. En el gráfico de interacciones del modelo ajustado (fig. 8) se pone de manifiesto que la mayor interacción se produce entre los factores distancia y recubrimiento, algo que se observaba en la figura 6. Así, cuando el recubrimiento es igual a dos veces el diámetro de la armadura, la distancia a la que se encuentren las familias de barras solapadas tiene muy poca influencia en la tensión de adherencia. No obstante, al aumentar el recubrimiento hasta 4 veces el diámetro de la barra, la mayor distancia entre familias de barras solapadas aumenta notablemente la tensión de adherencia (subgráfico Distancia · Recubrimiento). La explicación a este fenómeno puede radicar en la gran importancia que tiene el recubrimiento en el comportamiento de la probeta, de forma que cuando este es bajo actúa como factor limitante. Nótese que en la figura 8 falta la interacción Recubrimiento · Diámetro, ya que este término se pudo eliminar de la ecuación del modelo (2).

Figura 8.

Gráfico de interacciones del modelo.

5

Conclusiones y trabajo futuro

El ensayo y la metodología estadística empleados en esta investigación se han mostrado como herramientas muy útiles y potentes para estudiar los solapes a tracción. Se constata que el recubrimiento es un parámetro esencial, aumentando notablemente la tensión de adherencia al crecer aquel, y actuando como factor limitante cuando su valor es reducido. Aumentar la distancia entre familias de barras solapadas también incrementa la tensión de adherencia desarrollada, mientras que al crecer la separación entre las barras solapadas se produce una disminución de la adherencia. Finalmente, el diámetro nominal de las armaduras, para los valores estudiados (12 y 16 mm), tiene un efecto casi despreciable.

El trabajo futuro abre grandes posibilidades. El siguiente paso lógico es incluir en el modelo la presencia de armadura transversal y de confinamiento. Cabe señalar que el modelo estadístico desarrollado es fácilmente escalable si se añaden nuevas variables, no siendo necesario repetir los ensayos realizados y bastando con añadir los nuevos datos y reajustar el modelo.

Financiación

Esta investigación ha sido posible gracias a la ayuda del Ministerio de Educación, Cultura y Deporte a través de su programa para la Formación de Profesorado Universitario, y al Proyecto BIA2015-64672-C4-2-R, financiado por el Ministerio de Economía y Competitividad y el Fondo Europeo de Desarrollo Regional (FEDER).

Agradecimientos

Los autores muestran su agradecimiento a Cementos Cosmos, S.A. y a Basf Chemical España, S.A. por aportar el cemento y los aditivos necesarios.