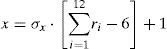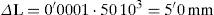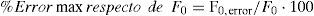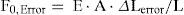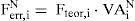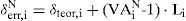Introducción de errores aleatorios en el proceso de instalación de los cables en los puentes atirantados

Resumen

Se ha detallado en este artículo un método que permite simular la introducción de errores aleatorios durante el proceso constructivo de los puentes atirantados, el cual forma parte de una investigación más amplia desarrollada por los autores en relación con este aspecto. En concreto, los errores se generan durante la instalación de los cables, bien sea en fuerzas de puesta en tensión o en la medida de los alargamientos de los cables y el replanteo de los anclajes. Una vez validado el método propuesto, se ha procedido a aplicarlo sobre una estructura real, analizando qué efecto producen respecto a los esfuerzos en los propios tirantes y en el tablero, durante las fases de construcción, en la situación final de este proceso y en la situación de servicio al aplicar las sobrecargas, en relación con la situación teórica prevista.

Abstract

In this paper, a method is proposed that allows the simulation of the introduction of random errors into the construction process of cable-stayed bridges during the installation of the cables. It particularly takes into account errors in cable tensioning, in the measurement of the shortening of cables, and in the positioning of the cable anchors. Once the proposed method was validated, it was applied to a real structure, and the effects which were generated in the different structural members have been analysed at the construction stages, at the final stage of the construction process, and on the service situation with traffic.

1

Introducción

Los puentes atirantados son una de las tipologías estructurales que más se han desarrollado en los últimos años, alcanzando luces que llegan actualmente a más de 1.000 m, como en el caso del Puente Stonecutters en Hong Kong [1], del Puente Sutong sobre el Yantgse en China [1] y del Puente de la isla Russky en Rusia [1]. De esta manera, esta tipología estructural está consiguiendo abarcar hoy en día un rango de luces que hasta hace menos de 20 años era exclusivo de los puentes colgantes.

Estos avances han venido precedidos de un importante esfuerzo, desarrollado a nivel internacional por distintos investigadores, de cara a conseguir un mejor entendimiento y aprovechamiento de su comportamiento estructural, así como orientado a mejorar tanto los métodos de cálculo, como los procesos constructivos. Este último aspecto es una de las características particulares más importantes de este tipo de estructura, ya que durante el proceso constructivo es cuando se pueden llegar a producir las situaciones que condicionan el dimensionamiento, tanto para el tablero como para el pilono.

En base a lo anteriormente indicado se ha decidido desarrollar este estudio; en concreto se ha tratado de evaluar qué influencia puede tener la introducción de unos axiles o deformaciones de montaje de los cables que no coincidan con los obtenidos en el cálculo teórico, de tal forma que simulando un proceso de construcción en el que se introduzcan errores durante la instalación de los cables, se pueda analizar qué efecto producen sobre la estructura y qué diferencias se alcanzan en relación con la situación teórica.

Es importante añadir que este estudio se ha centrado sobre el caso particular de un puente de luces medias, con tablero de hormigón y configuración simétrica. Se ha elegido el caso de un puente con tablero de hormigón, ya que es la tipología de tablero que mejor se adaptará en el rango de luces cortas y medias, quedando las grandes luces (>500 m) restringidas al uso de tableros metálicos o mixtos, por lo menos en parte del vano principal. Además, el método constructivo considerado ha sido el de construcción por dovelas mediante avance por voladizos sucesivos desde ambos lados del pilono, que se ha considerado que es el proceso que mejor se adapta a la ejecución de este tipo de estructuras, así como el que más ejemplos de aplicación real tiene.

2

Métodos de cálculo

El proceso de cálculo de cualquier estructura de este tipo se fundamenta en poder determinar los axiles o deformaciones que es necesario introducir en los tirantes en el instante de su puesta en obra, con la intención de poder llegar a una determinada situación final del proceso constructivo que se considere como situación final objetivo. De esta manera se cumplirán de forma simultánea tanto los requisitos de resistencia, como de deformación, que se consideren más adecuados a cada estructura.

En primer lugar habría que definir entonces cuál es la situación final objetivo a alcanzar, y por ello es importante puntualizar que este estudio se ha centrado en el caso de un puente con tablero de hormigón. Esta característica implica dos cuestiones fundamentales: en primer lugar la importancia de las cargas permanentes sobre el total de las cargas aplicadas, y en segundo lugar, la necesidad de considerar los efectos reológicos en todos los cálculos que se realicen.

Por los anteriores motivos, tal y como señalan diversos autores [1,2] y [3], la situación final objetivo a alcanzar que se considera más adecuada es la correspondiente a aquella en la que la configuración de esfuerzos en el tablero, al final del proceso constructivo, equivalga a la que se obtendría en una viga continua, dispuesta sobre un conjunto de apoyos que representen los puntos de anclaje de los cables en el tablero. Esta configuración se juzga la más adecuada ya que es aquella sobre la que los efectos reológicos del hormigón no producirán redistribución de esfuerzos [2]. Por ello, en este estudio, no se han contemplado configuraciones finales con niveles de esfuerzos debidos al proceso constructivo que intenten compensar los generados por las sobrecargas, ya que, en el caso de puentes con tablero de hormigón, el efecto de estas últimas será pequeño en relación con el conjunto de cargas permanentes, mientras que por otra parte los efectos de la fluencia llevarán a redistribuciones de esfuerzos, a tiempo infinito, que anularían la configuración inicial. Este último planteamiento se señala en [4] que en cambio sí podría ser adecuado para el caso de tableros metálicos o mixtos, en los que se puede intentar compensar parte del efecto de las sobrecargas de tráfico mediante el ajuste de los axiles finales en los cables.

Por otra parte, los métodos de cálculo de este tipo de estructuras pueden enmarcarse en tres categorías diferentes, tal y como señala [5]: el método del desmontaje (método backward), el método del montaje (método forward) o el método directo.

El primero de ellos es el método más extendido y permite obtener los esfuerzos de montaje de los tirantes mediante la simulación de un proceso de cálculo en orden inverso al de la construcción real, partiendo de la configuración final objetivo anteriormente definida. Con este método los axiles de montaje de los tirantes son aquellos que poseen los tirantes en la última fase del proceso de cálculo en la que están activos. En cambio, tiene como principal inconveniente que, al desarrollarse en sentido contrario al tiempo de construcción real, la implementación de los efectos de la fluencia es siempre complicada.

Para reducir el efecto de la fluencia, e implícitamente aumentar la validez de los resultados obtenidos por este método, distintos autores [1,6] o [7] proponen como objetivo, en función a su vez de la configuración geométrica del tablero en alzado, conseguir que la compresión introducida por los tirantes sobre el tablero quede alineada con el eje de este elemento, de tal manera que su excentricidad sea nula y así no se introduzcan esfuerzos de flexión por este motivo. De esta forma se consigue que la modificación en la configuración en esfuerzos y deformaciones, causada por la fluencia, se reduzca a un acortamiento de las distintas dovelas debido al axil aplicado sobre el tablero. Así, planteando ejecutar todas ellas con una longitud incrementada por la magnitud correspondiente al acortamiento por fluencia que se espera se pueda producir, se habrá incluido en el cálculo toda influencia de este efecto.

El método de cálculo del montaje (método forward) tiene la ventaja de que, al realizarse el cálculo en el mismo sentido del avance de la construcción real, los efectos reológicos son sencillos de implementar. Este método tiene el inconveniente de que, para alcanzar la situación final objetivo deseada, se debe realizar un proceso iterativo, con la consiguiente repercusión en el tiempo de cálculo necesario.

Por último, el método directo hace uso de la definición de un parámetro intrínseco a la estructura, de tal forma que el cálculo de una fase cualquiera sea independiente de lo sucedido en fases anteriores o posteriores del proceso constructivo. Este parámetro se denomina longitud en vacío del cable [8], que se define como aquella longitud que posee cualquier cable midiéndola cuando no existen cargas aplicadas sobre él, así como tampoco el efecto de la gravedad. Conocida esta longitud, es posible calcular las «predeformaciones» a aplicar a cualquier cable para alcanzar el valor del axil que le corresponde en la situación final buscada. A su vez, se puede calcular su «predeformación de montaje» para el instante de su colocación en obra, siendo entonces este valor equivalente al axil de montaje. Es decir que, usando este parámetro, teóricamente es posible evaluar cualquier fase intermedia del proceso constructivo sin necesidad de calcular las anteriores o posteriores etapas de dicho proceso. Este método en cambio no se puede utilizar en el caso de puentes con tablero de hormigón, ya que con él no es posible tener en cuenta los efectos reológicos que sufren el tablero y el pilono, quedando así reducido su ámbito de aplicación al caso de puentes con tableros metálicos o mixtos.

3

Estructura analizada

El estudio realizado lo ha sido sobre un modelo de cálculo basado en el diseño de un puente para una carretera con calzada de 2 carriles, el cual formaba parte de un proyecto constructivo asociado a las obras del Embalse de Giribaile, en la provincia de Jaén, que desarrolló el Ministerio de Fomento en los años 90.

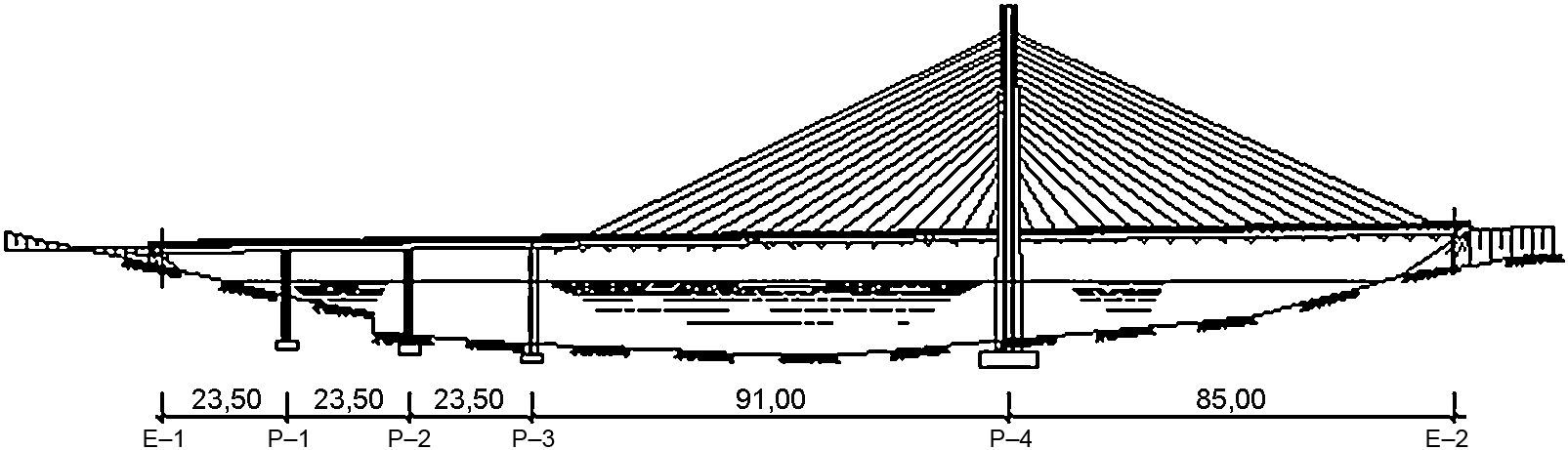
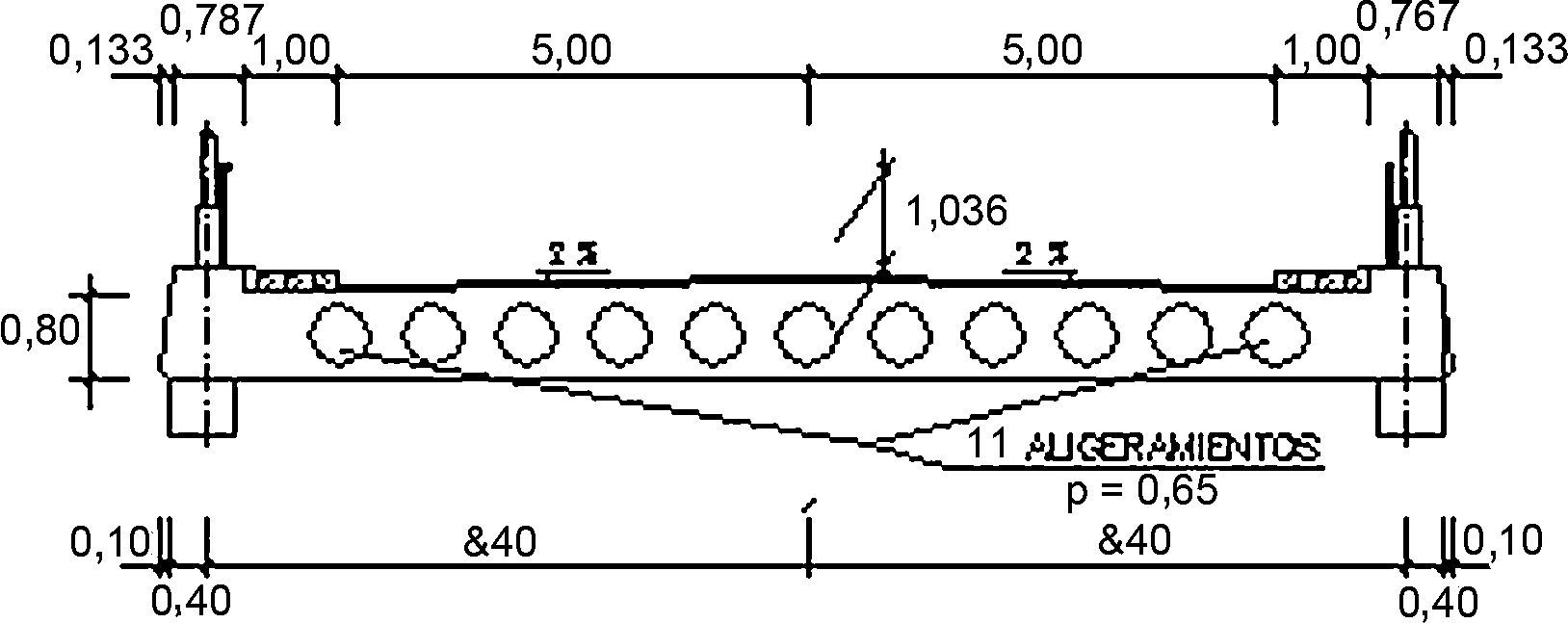
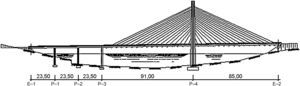
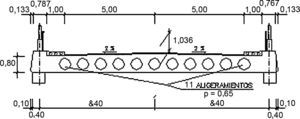
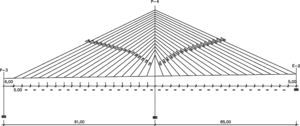
Dicha estructura consistía en un puente atirantado de 2 vanos con pilono central, con luces de 91,00 + 85,00 m (fig. 1). El tablero se constituía por una losa de hormigón de 13,80 m de ancho, planteándose dicha losa aligerada con canto mínimo 0,90 m en los bordes y 1,05 m en el centro de la sección, disponiéndose en ella 11 aligeramientos de Ø 0,65 m (fig. 2).

Figura 1.

Alzado del puente modelizado.

Figura 2.

Sección del tablero del puente modelizado.

Respecto al esquema de atirantamiento adoptado, el tablero se apoyaba sobre dos familias de cables dispuestos en ambos bordes del tablero, consistentes en 34 cables cada una, que quedaban anclados en el tablero cada 5,00 m. Los cables se conectaban en su extremo superior al pilono mediante una disposición en abanico.

El pilono a su vez se conformaba por una pila en H de 2 fustes, de 68,85 m de altura total, 44,02 m por encima de la rasante del tablero. La sección de ambos fustes era variable en altura.

Los apoyos extremos del tablero se realizaban, en el caso del estribo izquierdo, en una pila intermedia, que servía a su vez como apoyo del vano final del viaducto de acceso, y en un estribo cerrado para el caso del estribo derecho.

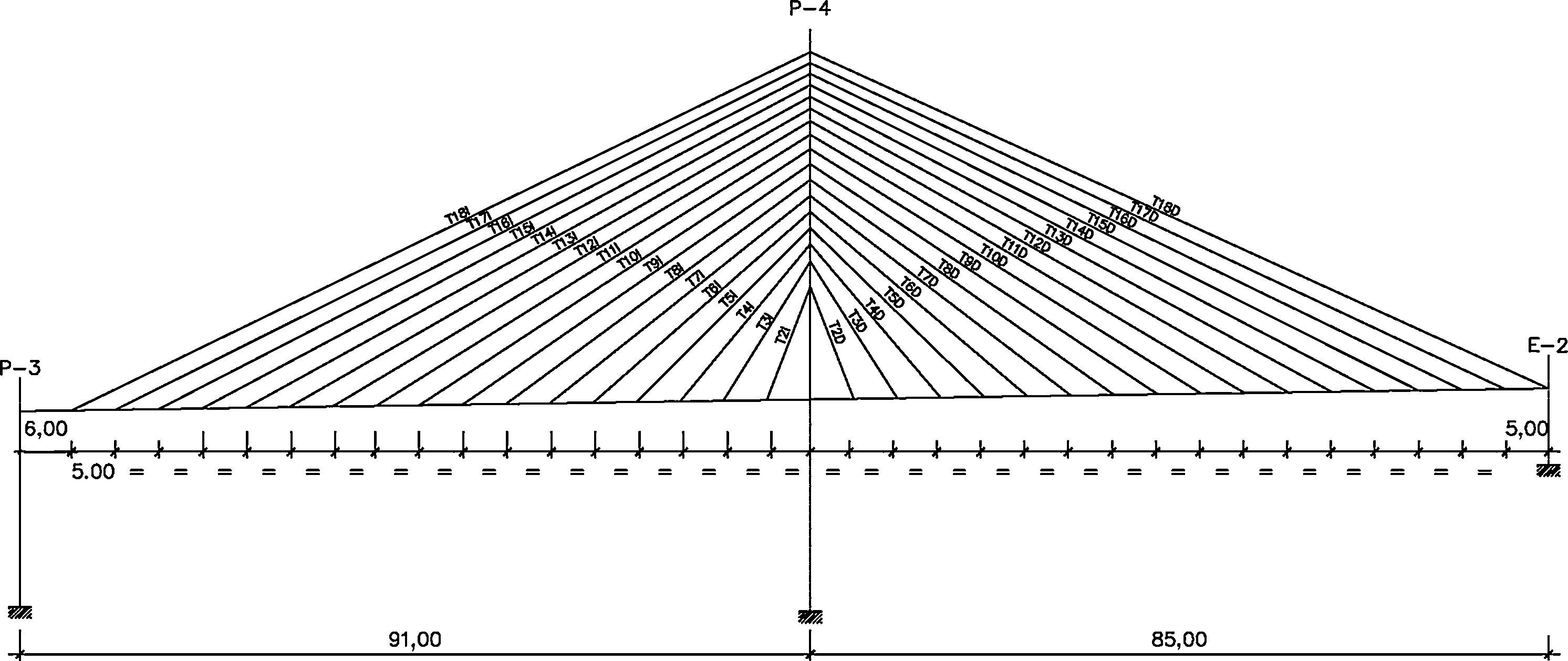
Para representar el comportamiento de la estructura se ha generado un modelo plano de elementos tipo barra (fig. 3). Se ha utilizado para ello un programa de cálculo matricial de estructuras de barras que permite además la simulación de las diferentes fases del proceso constructivo de forma secuencial.

Figura 3.

Esquema del modelo de cálculo de la estructura analizada.

Indicar que se ha considerado, para cada una de las dovelas del tablero, su discretización mediante dos barras de 2,00 y 3,00 m de longitud respectivamente cada una de ellas, de tal manera que los anclajes de los cables al tablero se materializan en su nudo intermedio, quedando estos por lo tanto a 2,00 m del frente de la dovela.

Las coacciones exteriores impuestas sobre el modelo de la estructura han consistido en empotramientos en la cimentación de ambos estribos, así como en el arranque del pilono. La vinculación entre pilono y tablero se establece coartando los desplazamientos horizontal y vertical pero permitiendo el giro del tablero en ese punto.

Por último añadir que, para simular los apoyos extremos del tablero sobre los estribos, se han creado 2 barras sin capacidad de absorción de momentos que representen los apoyos de neopreno.

El proceso constructivo previsto para la ejecución de esta estructura consiste en la siguiente secuencia de operaciones:

• •

  Ejecución de cimentaciones de pilas y estribos.

• •

  Ejecución de las dovelas 1 I y 1 D sobre cimbra y puesta en tensión de los cables 2 I y 2 D.

• •

  Avance en voladizo para la ejecución de las restantes dovelas siguiendo un esquema secuencial como el siguiente para las fase n:

  • -

    Hormigonado de las dovelas n izquierda y derecha.

  • -

    Puesta en tensión del cable n izquierda.

  • -

    Puesta en tensión del cable n derecha.

• •

  El proceso constructivo finaliza con la ejecución de la dovela 18 izquierda de apoyo sobre el estribo, dado que la estructura no es perfectamente simétrica.

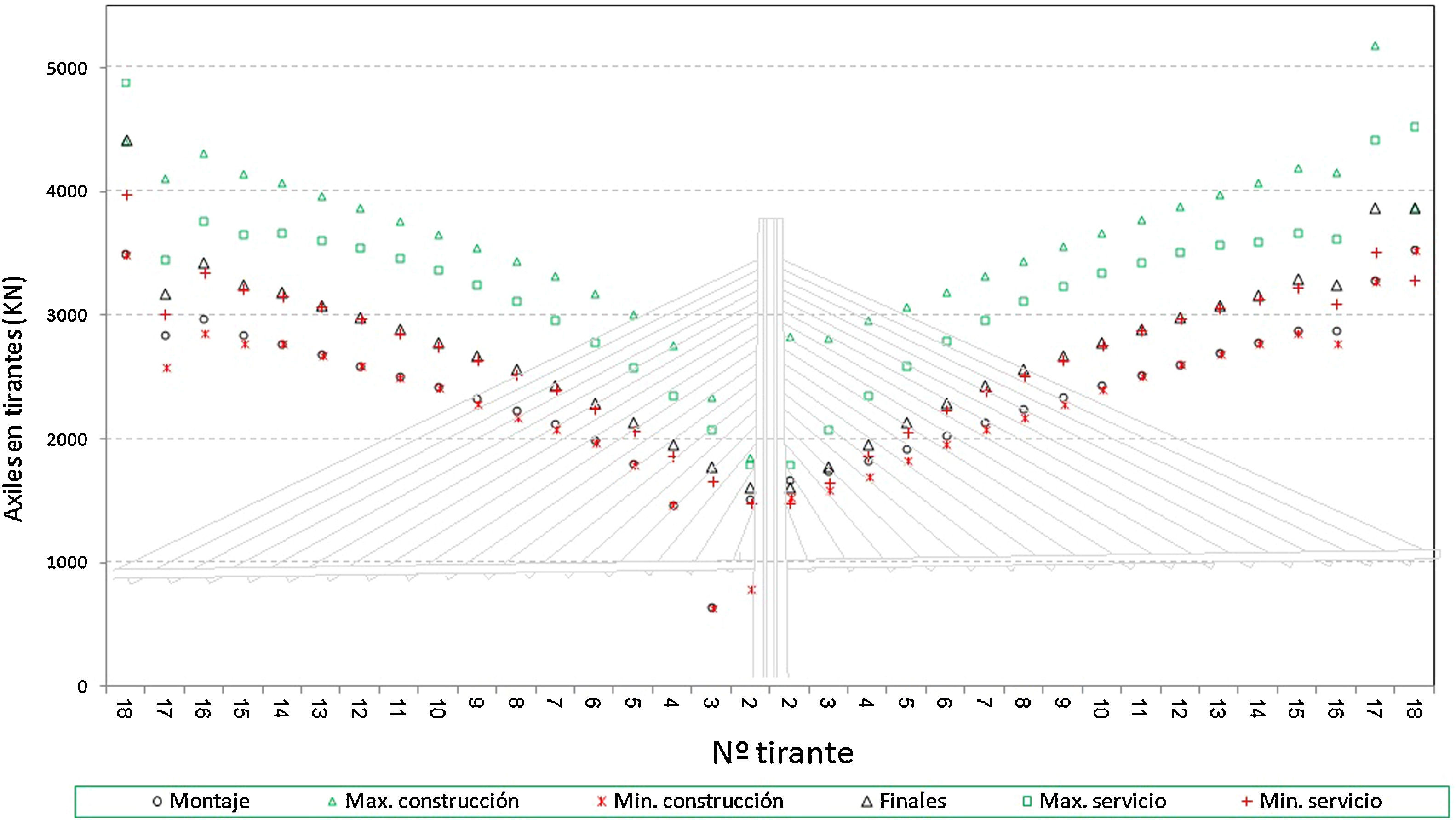
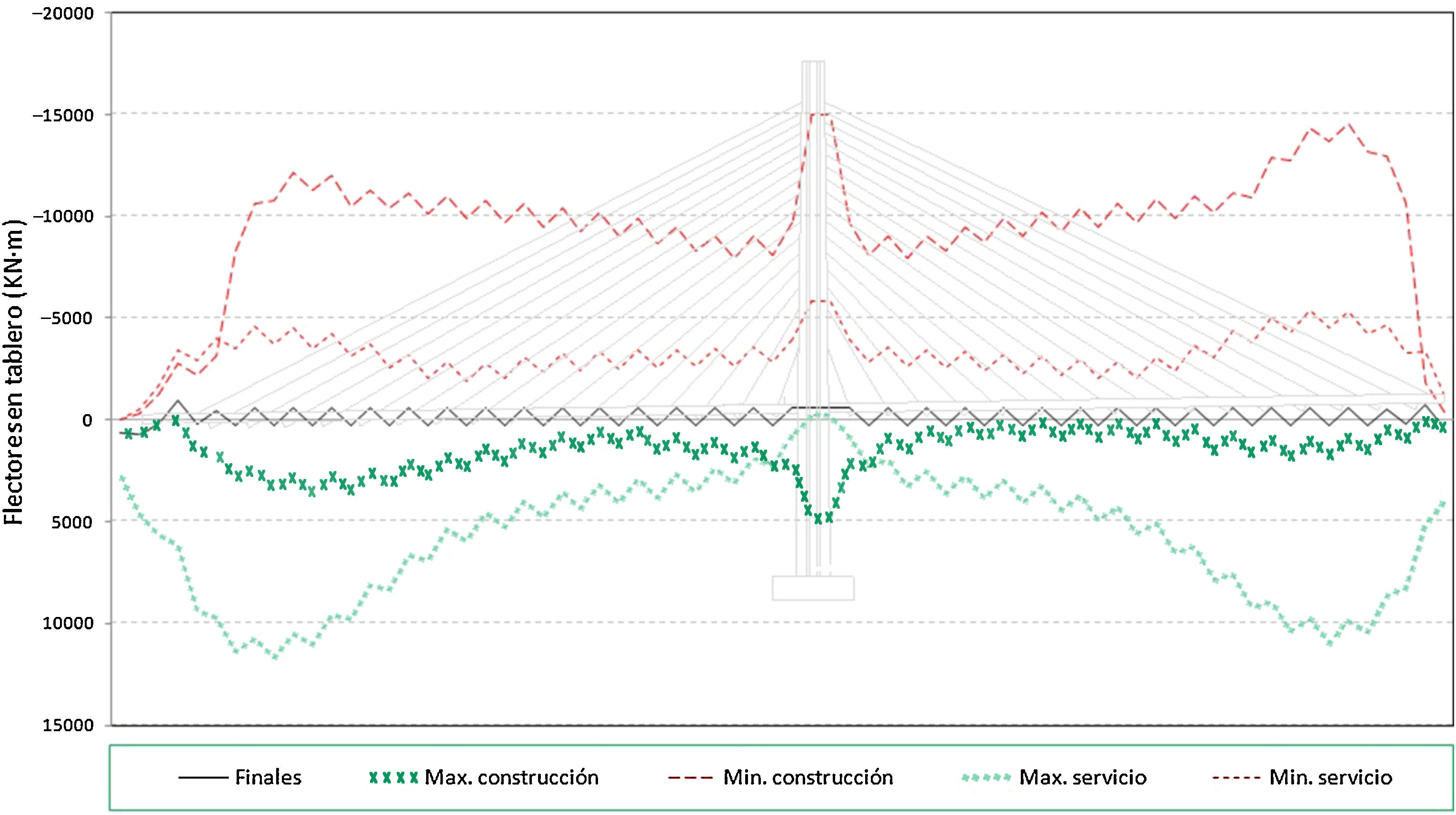
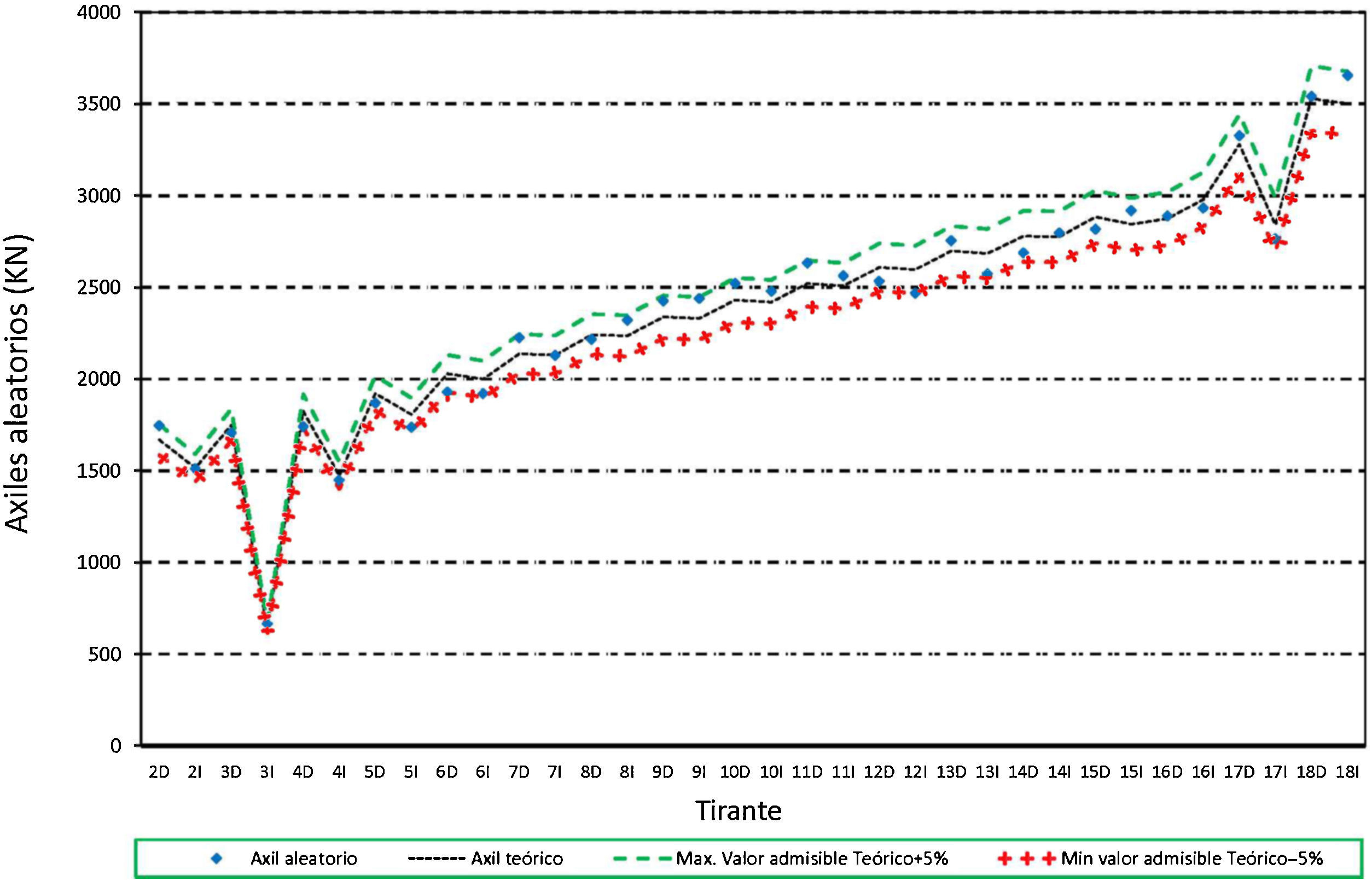
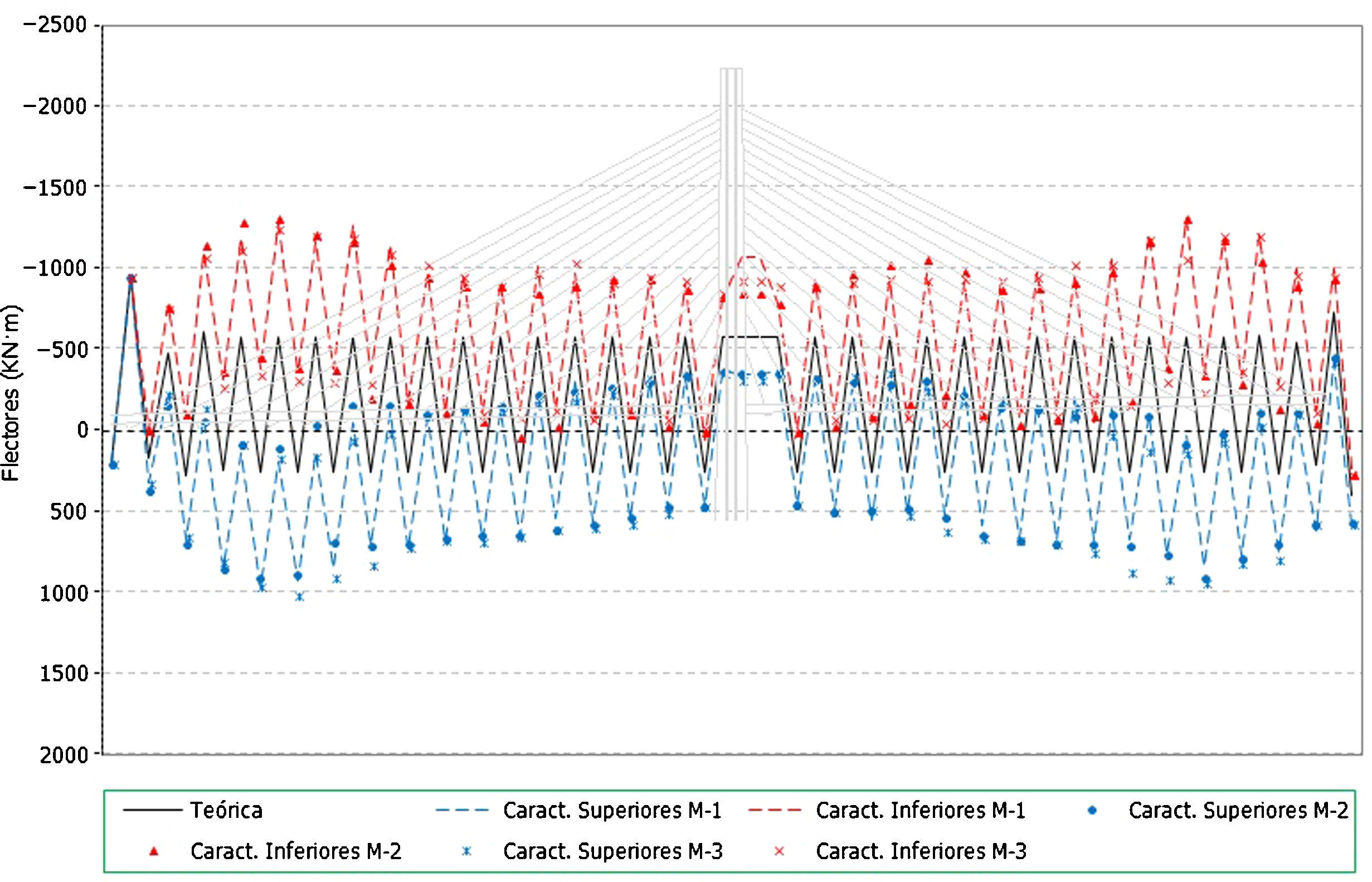
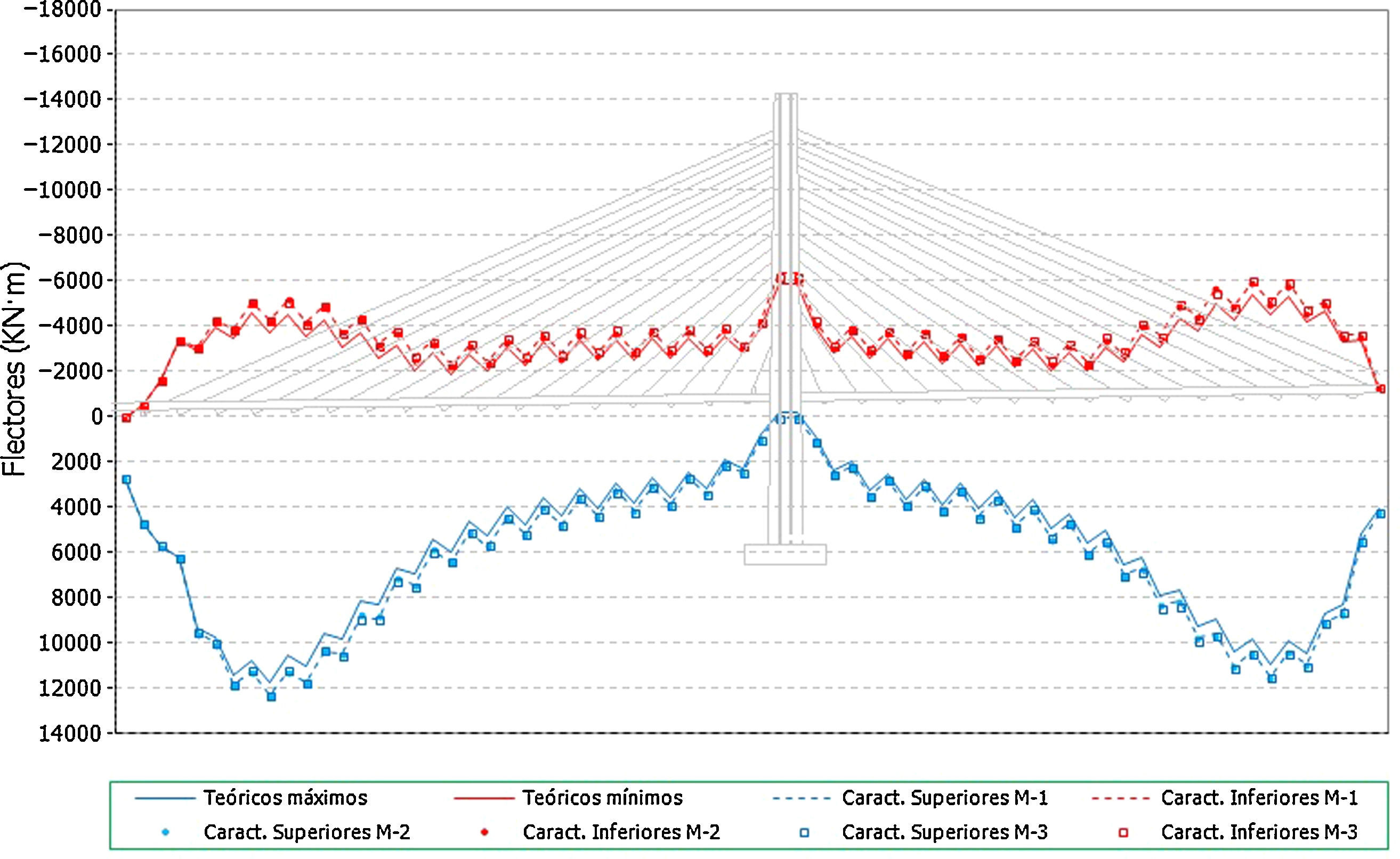
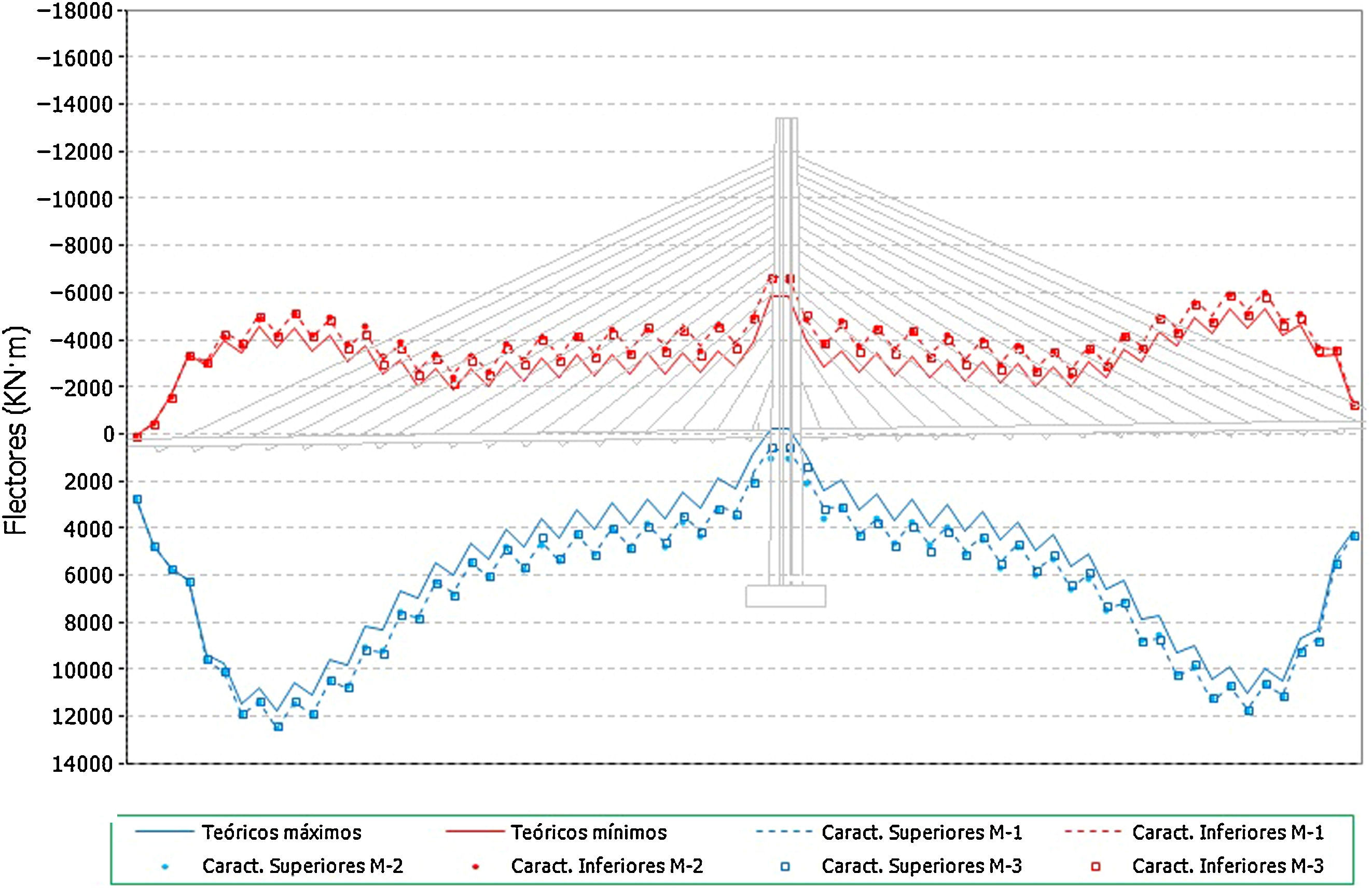
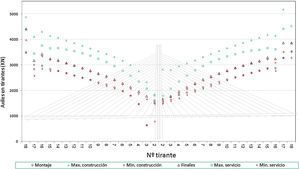
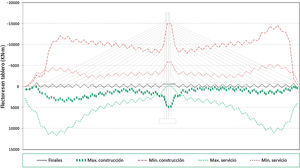
Sobre esta estructura se ha procedido a determinar las situaciones teóricas de referencia para los cálculos a realizar posteriormente, es decir se ha procedido a obtener los esfuerzos en los diferentes elementos estructurales como resultado del proceso teórico de construcción, tanto en las situaciones intermedias de dicho proceso, como en la situación final al aplicar la carga muerta sobre el tablero, así como en las situaciones de servicio, bajo la actuación de la sobrecarga de tráfico. Los resultados que se representan en las siguientes figuras son aquellos que se han considerado más representativos del comportamiento de la estructura. En concreto, en la primera de ellas (fig. 4) se representan los axiles de montaje, los máximos y mínimos de construcción, los axiles finales al terminar el proceso constructivo y los máximos y mínimos de servicio. En la segunda de ellas (fig. 5) se representan las envolventes de flectores en el tablero, tanto los máximos como los mínimos de construcción, los máximos y mínimos de servicio, al aplicar las sobrecargas de tráfico en el tablero, y la ley de flectores al final del proceso constructivo.

Figura 4.

Axiles en tirantes en fase inicial de instalación, máximos y mínimos de las fases de construcción, en la fase final del proceso constructivo y máximos y mínimos en las situaciones de servicio.

Figura 5.

Envolvente de flectores en el tablero en las fases de construcción, final y en servicio.

De los resultados aquí representados se pueden extraer varias conclusiones en relación con los axiles en tirantes y a los flectores en el tablero. En el primer caso se puede deducir que:

• •

  Los axiles de montaje de los tirantes son siempre menores que los axiles en la situación final.

• •

  Los máximos axiles en las fases de construcción y en servicio son superiores a los axiles en la situación final. En concreto las mayores diferencias entre los axiles en la situación final y en las situaciones de servicio se producen en el tramo de tablero más flexible, es decir hacia los 3/4 de la luz principal.

• •

  Los mínimos axiles en las fases de construcción y en servicio, salvo algún caso puntual, en general son superiores a los axiles en el instante del montaje. Es decir que el mínimo axil que soporta cada tirante desde su instalación es el axil de montaje.

• •

  Siendo la separación entre cables uniforme y a su vez las cargas permanentes que le corresponde soportar a cada cable del mismo orden en todos ellos, en general se observa que los axiles en los tirantes crecen conforme nos alejamos del pilono. Esto es debido a la disminución del ángulo de los cables respecto del tablero, y por lo tanto al reducirse su eficacia para soportar la misma reacción vertical, conforme más alejado del pilono se encuentre su anclaje.

Por otra parte, en el caso de los resultados en flectores, se observa que, mientras que la situación final de construcción representa unos valores iguales a los de la situación objetivo teórica planteada como viga continua, y por lo tanto sus valores absolutos resultan relativamente acotados, la envolvente total de flectores se conforma por los mínimos de la situación de construcción y por los máximos de la situación de servicio. Esta cuestión se explica por las dos siguientes razones:

• •

  En primer lugar porque el mínimo flector negativo en cada dovela, a lo largo de todo el proceso constructivo, se produce en la sección de anclaje del cable instalado sobre la última dovela terminada, cuando se ejecuta el hormigonado de la dovela adyacente y por lo tanto actúa todo su peso sobre dicha sección de anclaje. Es importante señalar que en este caso, ese valor del esfuerzo depende en gran medida del peso de la dovela y no tanto del axil en los tirantes, por lo que en los resultados sucesivos se observará que la influencia de los errores aleatorios que se introduzcan en los cálculos será pequeña en este aspecto concreto.

• •

  En segundo lugar, la envolvente de flectores positivos queda determinada por la actuación de las sobrecargas sobre la estructura terminada, momento en el cual la flexibilidad de la estructura frente a este tipo de carga descentrada, respecto del pilono, genera los valores máximos que componen la envolvente de flectores positivos. Este efecto es tanto más acusado en aquella zona donde se conjuga la cercanía al centro de vano y los ángulos de los cables son ya reducidos, es decir se produce en el entorno de los 3/4 de la luz principal.

4

Generación de errores aleatorios

Dado el objetivo de este estudio, es necesario definir y detallar qué tipo de errores se considerará que se pueden producir durante el proceso de instalación de los cables, de qué tipo pueden ser, así como cuantificar un error máximo por encima del cual los sistemas de control de la obra sean capaces de detectarlo y corregirlo.

Los métodos de instalación de los cables en los puentes atirantados según lo señalado en [9] son dos: el primero de ellos se basará en la aplicación de una tensión determinada sobre el cable, correspondiente al axil de montaje calculado, que es el método denominado en fuerzas. En este método se contralará la presión marcada en el manómetro de los gatos de puesta en tensión, y es durante este proceso en el que podrán producirse errores de medición de este valor. Hay que señalar que este método es muy sensible a las cargas aplicadas sobre la estructura en el momento de la instalación del cable, por lo que los pesos de los equipos auxiliares colocados sobre el tablero deben ser evaluados con mucha precisión. Igualmente el efecto de la temperatura deberá ser tenido en cuenta midiéndose en obra y ajustando los cálculos en función de los resultados obtenidos.

El segundo método de instalación de los cables es el método en deformaciones, en el que haciendo uso de la definición de longitud en vacío del cable, se puede proceder a calcular las deformaciones a aplicar a los cables en el instante de su puesta en obra, siendo esta longitud la medida que servirá para verificar su puesta en tensión. Este método cuenta con la ventaja de que, al ser la longitud en vacío un parámetro intrínseco de la estructura, y al establecer la colocación del cable mediante una medida que es función de ese parámetro, los efectos de las cargas aplicadas en el instante de colocación del cable y los efectos de la temperatura se pueden obviar.

Así, otro de los objetivos de este estudio va a ser analizar qué diferencias se pueden llegar a producir si aplicamos uno u otro método sobre una estructura.

Hay que reseñar que ya existen investigaciones referentes a la aplicación de parámetros aleatorios que representen una mala adecuación entre el valor real del parámetro y el teórico de cálculo como las investigaciones desarrolladas por [10] y [11], pero dichas investigaciones se centran más en la determinación de los axiles de montaje de los tirantes, incorporando las variables aleatorias en su definición, más que en el análisis de un proceso constructivo que incorpore errores no detectables en la instalación de los cables.

4.1

Tipos de errores

Por otra parte, durante el proceso de colocación y puesta en tensión de los tirantes se podría plantear la existencia de diferentes tipos de errores. En principio, para el caso de los tirantes en estudio, los errores debidos a las pérdidas se considerarán despreciables. No será así en el caso de los errores en la fuerza de aplicación en los tirantes o bien en las deformaciones a generar sobre ellos, así como los errores debidos al replanteo de los anclajes. Es decir, se va a considerar la posibilidad de la existencia de una instalación errónea de los cables, ya sea por una mala medición de la presión aplicada al gato de puesta en tensión, ya sea por un fallo al medir los alargamientos de los cables o al instalar las placas de anclaje.

Hay que distinguir entonces dos conceptos, por un lado el error de exactitud y por otro el error de precisión. Se define «precisión» como la desviación máxima que pueden presentar las diferentes medidas efectuadas con un mismo aparato de medida, mientras que se puede definir la «exactitud», que tendría ese mismo aparato de medida, como el error que pudiera tener la lectura efectuada respecto del valor real aplicado al cable.

Se deduce así que el error debido a la exactitud de la medida, al ser un valor constante en todas ellas, podría corregirse directamente realizando un control adecuado de la estructura, mientras que los errores de precisión no se eliminarían dado su carácter aleatorio, pudiéndose ejecutar la estructura incorporando dichos errores.

Por otra parte, según la «teoría de errores» (ver [12] y [13]), estos mismos podrán ser de dos tipos: errores sistemáticos y errores aleatorios. Los primeros estarían relacionados con la exactitud del sistema de medida, mientras que los segundos serían los relacionados con la precisión de dichas medidas. Es entonces sobre estos últimos sobre los que se centra el estudio realizado a continuación.

También en base a la «teoría de errores», se demuestra que, si la causa del fallo en la precisión está originada en la adición de varios errores elementales, pudiendo considerarse cada uno de ellos como una variable aleatoria independiente, el error total de precisión resultante, según el «teorema central del límite», tendrá una distribución aproximadamente normal. Es decir, que si se quiere simular la existencia de estos errores, se deberá utilizar un algoritmo que permita generar muestras aleatorias de valores erróneos que tengan una distribución normal, con media el valor teórico de la medida realizada y desviación típica a determinar.

4.2

Algoritmo para la generación de muestras de valores aleatorios

Se necesita entonces para proceder a simular un montaje erróneo de los tirantes definir una herramienta que permita la generación de variaciones aleatorias según una distribución normal. Para ello se ha utilizado un algoritmo, basado igualmente en el «teorema central del límite», que plantea la siguiente formulación:

Esta expresión indica que dados 12 números aleatorios (generados mediante la función RND de VBasic), restando a su suma 6, multiplicando este valor por la desviación típica, y sumando a este resultado uno, se verifica que los valores que se obtienen siguen una distribución normal, pudiendo definirse entonces estos valores como el coeficiente en tanto por uno de error de una cierta cantidad a la que se vaya a ponderar.

4.3

Errores máximos admisibles

Utilizando el algoritmo anterior, se pueden generar valores aleatorios de las magnitudes que se está analizando según una distribución normal estándar, lo que implica que, teóricamente, se pueden presentar todos aquellos valores que se encuentren incluidos en la curva de Gauss. Esto implicaría la posible generación de errores con valores muy altos, que en obra se detectarían con facilidad y se podrían corregir inmediatamente. Como el estudio se ha centrado en el análisis del comportamiento de los puentes atirantados bajo la introducción de errores aleatorios que no sean detectables, y por lo tanto corregibles, se necesita poder truncar las anteriores series de valores aleatorias en aquellos límites de error que se consideren inadmisibles a la hora de la puesta en obra.

Por ello se ha realizado un análisis de las diferentes tolerancias existentes en la normativa actual que serían de aplicación en nuestro caso, referentes a los errores de montaje de los cables, suponiéndose así que en obra deberán usarse elementos de control suficientes como para no permitir la aplicación de valores superiores a los máximos en ellas contemplados.

Del análisis de la normativa vigente hoy en día, se observa que se establecen una serie de limitaciones a los errores máximos admisibles que pueden producirse durante los procesos de ejecución, concretándose estos en: errores sobre los procesos de montaje utilizando la medida de la fuerza provocada por el gato de puesta en tensión, errores en la medida de las deformaciones generadas en el cable una vez que se introduce la fuerza de puesta en tensión de forma progresiva, e incluso existen también limitaciones a los errores en la geometría de un determinado elemento de hormigón.

La primera referencia analizada es [9], que señala que en la instalación de cables se podrán producir desviaciones máximas de hasta un ±5% respecto del valor teórico del axil de puesta en tensión.

Respecto a errores en la medida de los alargamientos de los cables, en [8], se establece que el error máximo en la medida de la longitud de un tirante será el 0,01% de la longitud en vacío del cable.

Por último, en relación con los errores admisibles en la posición de los anclajes, se han estudiado, dado que se analiza el caso concreto de estructuras de hormigón (tanto tablero como pilono), las tolerancias establecidas en la normativa vigente de hormigón estructural ([14,15] y [16]) en lo referente a las tolerancias en los encofrados y en las dimensiones finales de las piezas de hormigón. En general los valores obtenidos hablan todos ellos de errores admisibles del orden de 1 o 2 cm, valores que se juzgan adecuados para conseguir un buen control de ejecución de una pieza de hormigón.

Del análisis de los anteriores valores se deduce que es mucho más exigente la condición en longitud de cables que la condición en la posición de anclajes, ya que por ejemplo, si se analiza el caso de un tirante intermedio de un puente de luces medias que podría tener un longitud aproximada de 50 m, en ese caso el error en longitud admisible resultaría:

Es decir, que como más adelante se va a comprobar, y tal y como se adelantaba en [3], en el caso de los puentes con tablero de hormigón, la instalación de los cables a partir de la medición de las deformaciones de los tirantes implicará la necesidad de un control de ejecución de los encofrados y geometría final de los cajetines de anclaje de los cables, o bien del posicionado de los bastidores de anclaje metálicos, si los tirantes se llevan todos ellos contra un elemento de este tipo, que está muy por encima del control habitualmente exigido para las estructuras de hormigón.

4.4

Verificación de la normalidad de las muestras

Llegados a este punto se ha procedido a definir un algoritmo que permite obtener valores aleatorios de una variable con distribución normal, pero a su vez estas muestras van a quedar truncadas al eliminar los valores extremos obtenidos por encima de los límites marcados como admisibles por la normativa. Es decir, que debería verificarse que las muestras, que originalmente se consideraban normales, al truncarse, siguen teniendo una distribución aproximadamente normal.

Para verificar la validez de la hipótesis de normalidad de la serie de todos los valores generados, se ha utilizado el denominado test de normalidad de Anderson-Darling.

Así, siguiendo el criterio anterior, solo se dan por válidas aquellas series de datos generadas que cumplan la condición de normalidad exigida. En el caso de que la serie de datos analizada no verifique esta condición, esta se descartará y se generará una nueva, hasta obtener una serie de valores que sí cumpla este criterio.

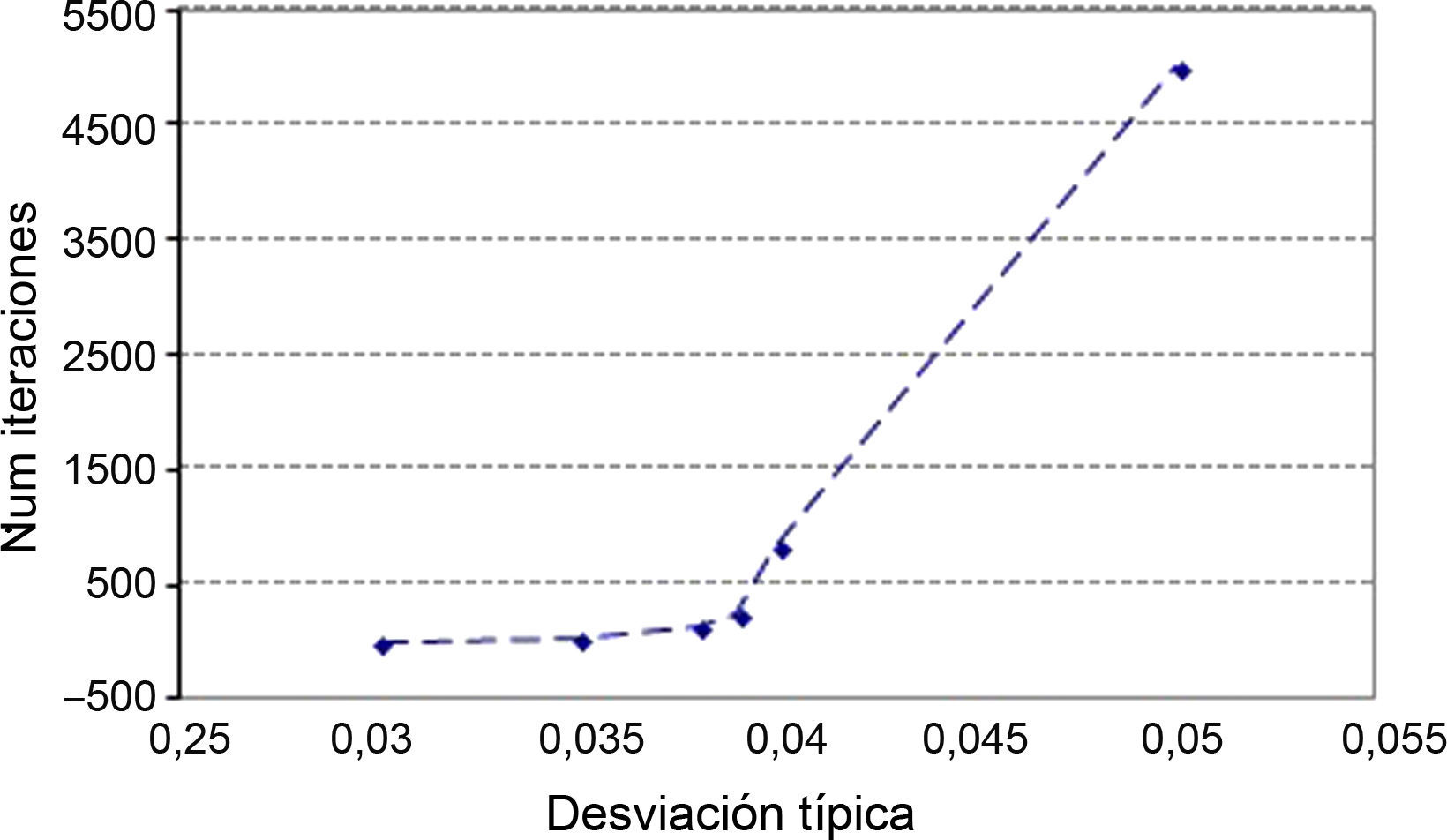
4.5

Desviación típica y tamaño de la muestra

El criterio para definir la desviación típica ha sido obtener el mayor valor de este parámetro que permite llegar a la convergencia del proceso de verificación con el test de Anderson-Darling, en un número de iteraciones razonable. Se consigue así obtener el valor de la máxima dispersión de los resultados respecto del valor medio, con la intención de poder con ellos simular un proceso lo más «erróneo» posible, pero dentro de los valores límite admisibles por la normativa.

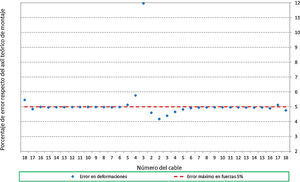
Con esta intención, en este caso se estudiaron las desviaciones típicas en función del número de iteraciones del proceso de Anderson-Darling, para el caso de la aplicación del método en fuerzas, resultando así el siguiente gráfico (fig. 6).

Figura 6.

Relación entre el número de iteraciones necesarias para la convergencia del test de Anderson-Darling y la desviación típica de las muestras.

A partir de estos valores se ha decidido adoptar una desviación típica para las muestras del 4% para el caso de instalación de los cables mediante fuerzas, mientras que haciendo un análisis similar, para el caso de la puesta en obra de los cables mediante deformaciones o de la posición de los anclajes, se ha adoptado un valor de la desviación típica del 0,008%, cuyo orden de magnitud está en relación con el error máximo en las «predeformaciones» admisibles del 0,01% de L₀.

Por otra parte, es también importante la definición del tamaño de las muestras, es decir, el número de elementos que las compondrá. Hay que pensar que, aunque cuanto mayor sea el número de elementos por muestra, más se aproximarán los resultados al valor exacto, por otra parte este aumento del número de elementos hará cada vez más laborioso y complicado de hacer converger el test de Anderson-Darling.

Por este motivo, este parámetro se ha de establecer fijando un número lo suficientemente grande de elementos por muestra como para que los resultados que se obtengan puedan ser relativamente aproximados, y lo suficientemente pequeño para minimizar el tiempo empleado en el proceso de cálculo.

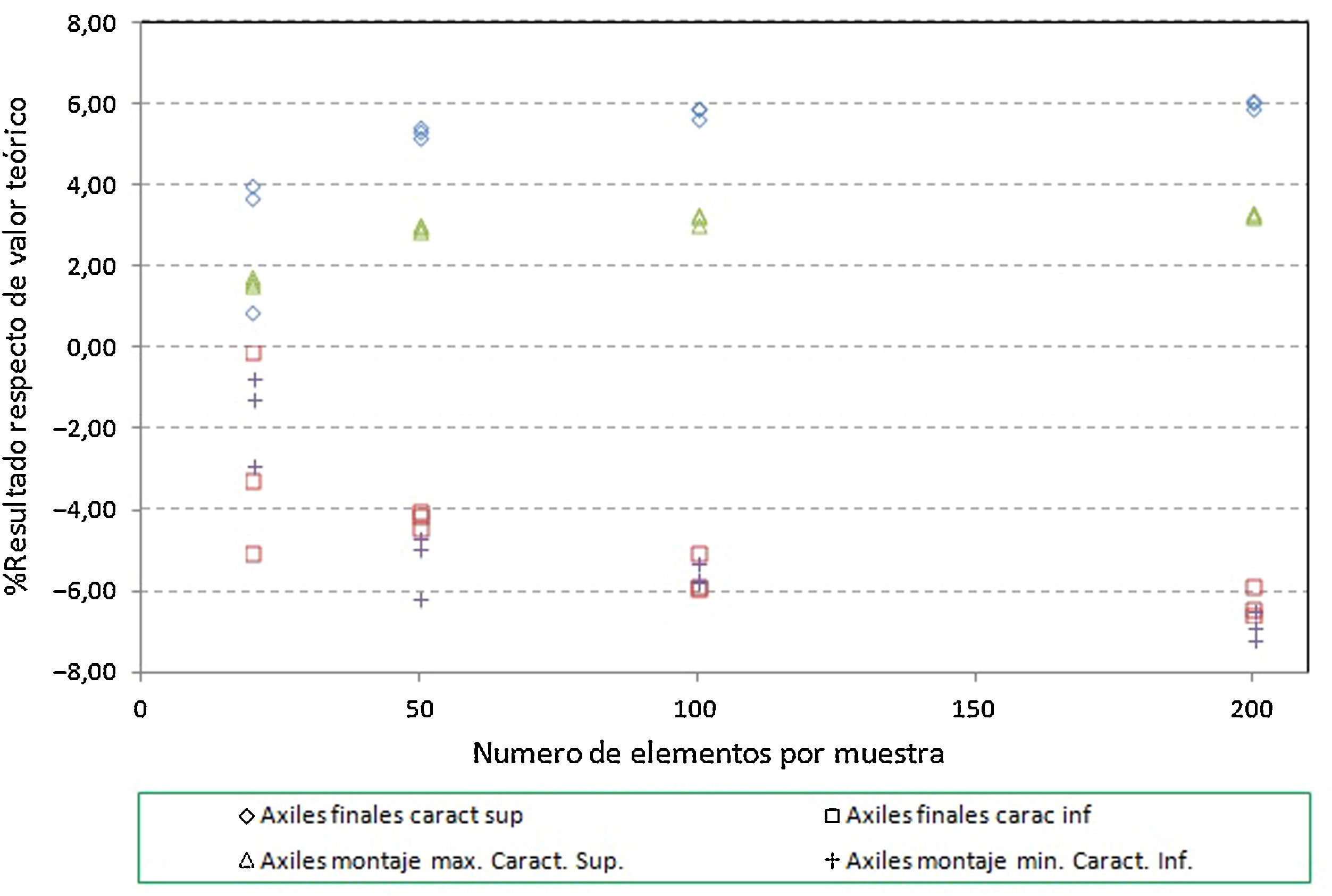
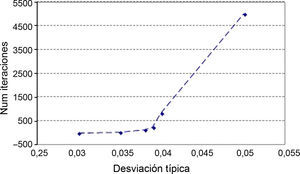
Con el objetivo de determinar este valor, se ha procedido a realizar un análisis generando muestras compuestas por un número distinto de elementos (en concreto se han generado muestras compuestas por 20, 50, 100 y 200 elementos), de tal manera que, a partir de los resultados que se obtengan, se pueda deducir con qué número de elementos la aproximación a la solución correcta se considera adecuada. Este estudio se ha realizado utilizando el método de colocación de los cables mediante fuerzas, al aplicar sobre la estructura las diferentes muestras con el número de elementos que se ha indicado anteriormente.

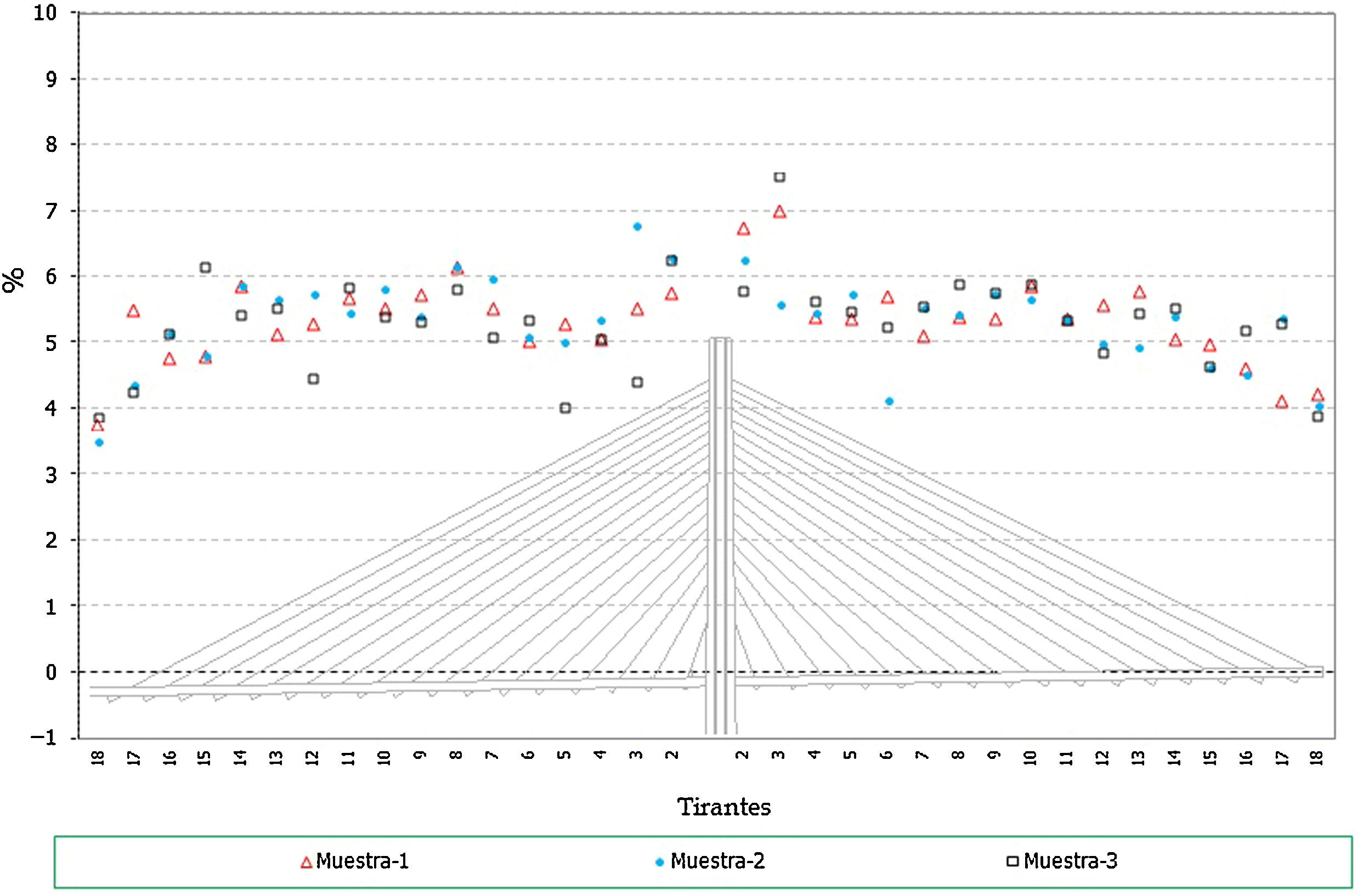
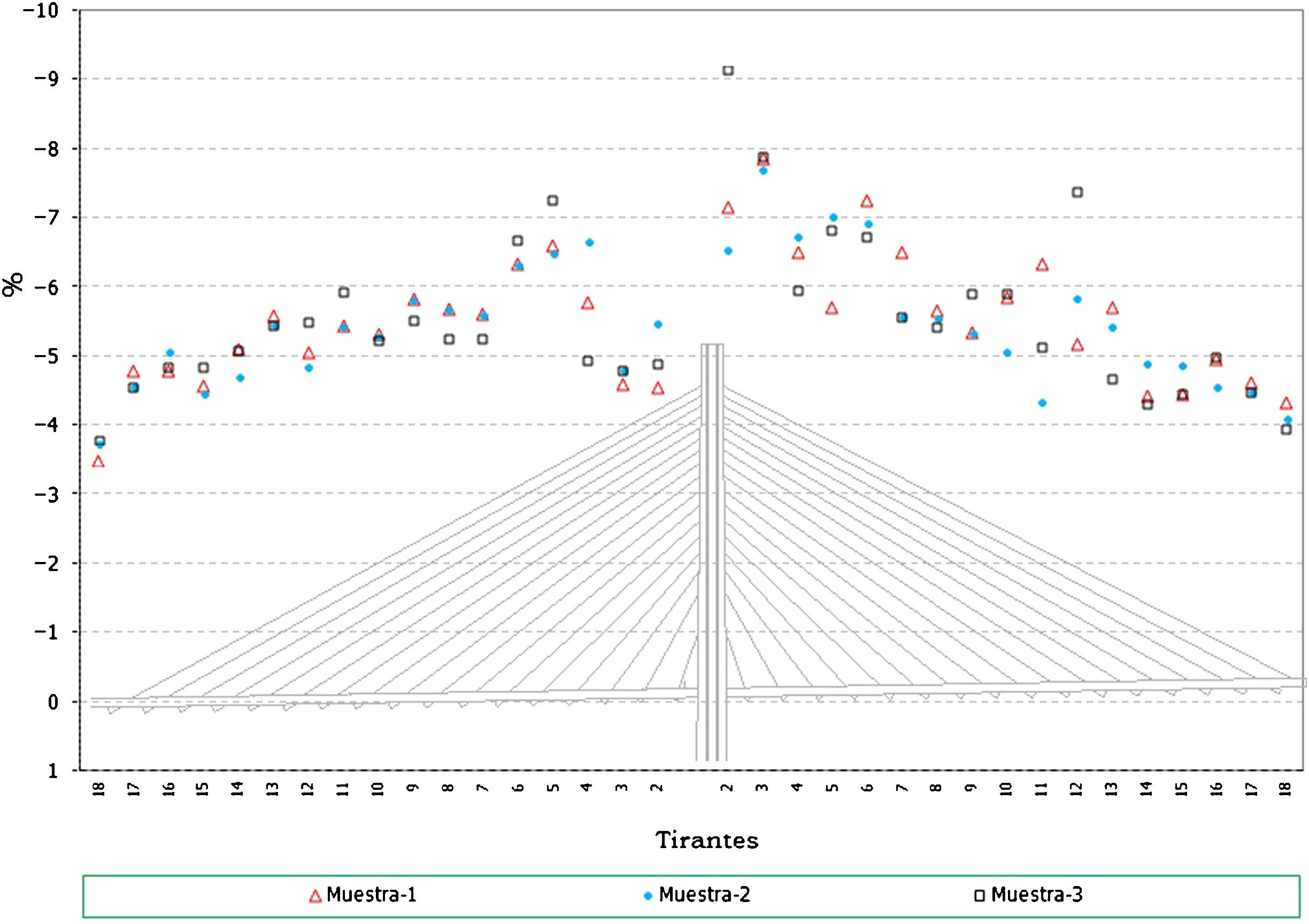
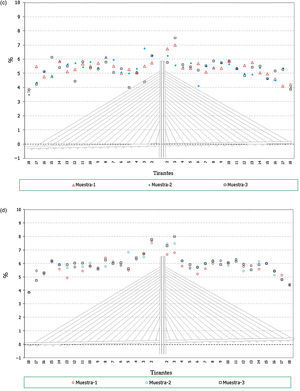
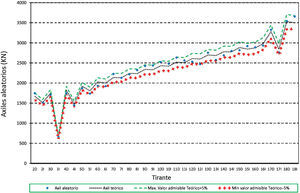
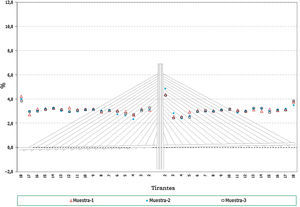
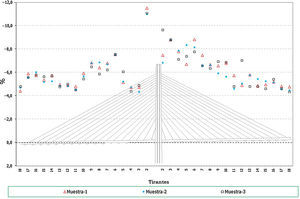
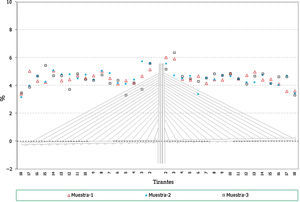
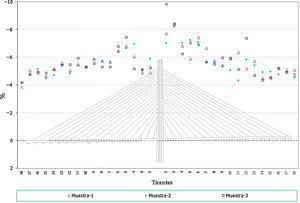
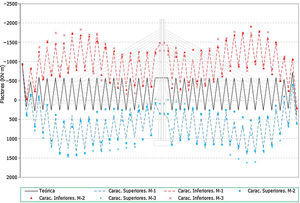
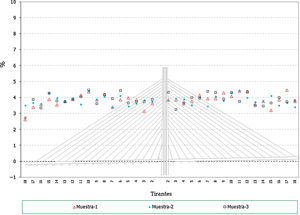
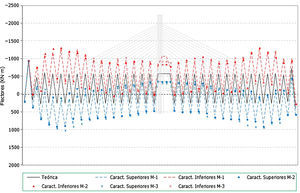
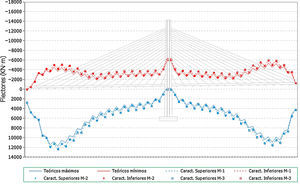
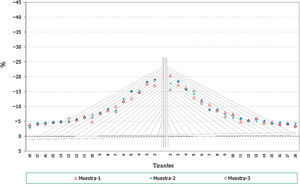
Hay que indicar además que, para cada anterior número de elementos, se han generado a su vez 3 muestras distintas, resultando entonces calculados con este análisis un total de 12 (4 × 3) muestras. Se presentan a continuación dichos resultados, en concreto los correspondientes a los valores característicos superiores e inferiores de los axiles finales de los cables, los axiles característicos superiores de los máximos de montaje y los característicos inferiores de los mínimos de montaje¹, para el cable 10D (fig. 7), y por otra parte los valores característicos de los axiles finales para el conjunto de cables de la estructura (fig. 8).

Figura 7.

Desviación máxima de los resultados (en tanto por ciento) respecto de los valores teóricos conforme se aumenta el número de elementos de la muestra. Axiles en Cable 10 D.

Figura 8.

Desviación máxima de los resultados (en tanto por ciento) respecto de los valores teóricos conforme se aumenta el número de elementos de la muestra. Axiles finales en todos los cables, valores característicos superiores. a) Muestras con 25 elementos cada una. Axiles finales en tirantes. b) Muestras con 100 elementos cada una. Axiles finales en tirantes. c) Muestras con 50 elementos cada una. Axiles finales en tirantes. d) Muestras con 200 elementos cada una.

A la vista de todos estos resultados parece claro que un número de 100 elementos por muestra aporta resultados adecuados para el objetivo buscado, no mereciendo la pena aumentar el número de elementos por encima de este valor, ya que el incremento que se conseguiría en la precisión de los resultados es pequeño en proporción al incremento del volumen de cálculos a realizar.

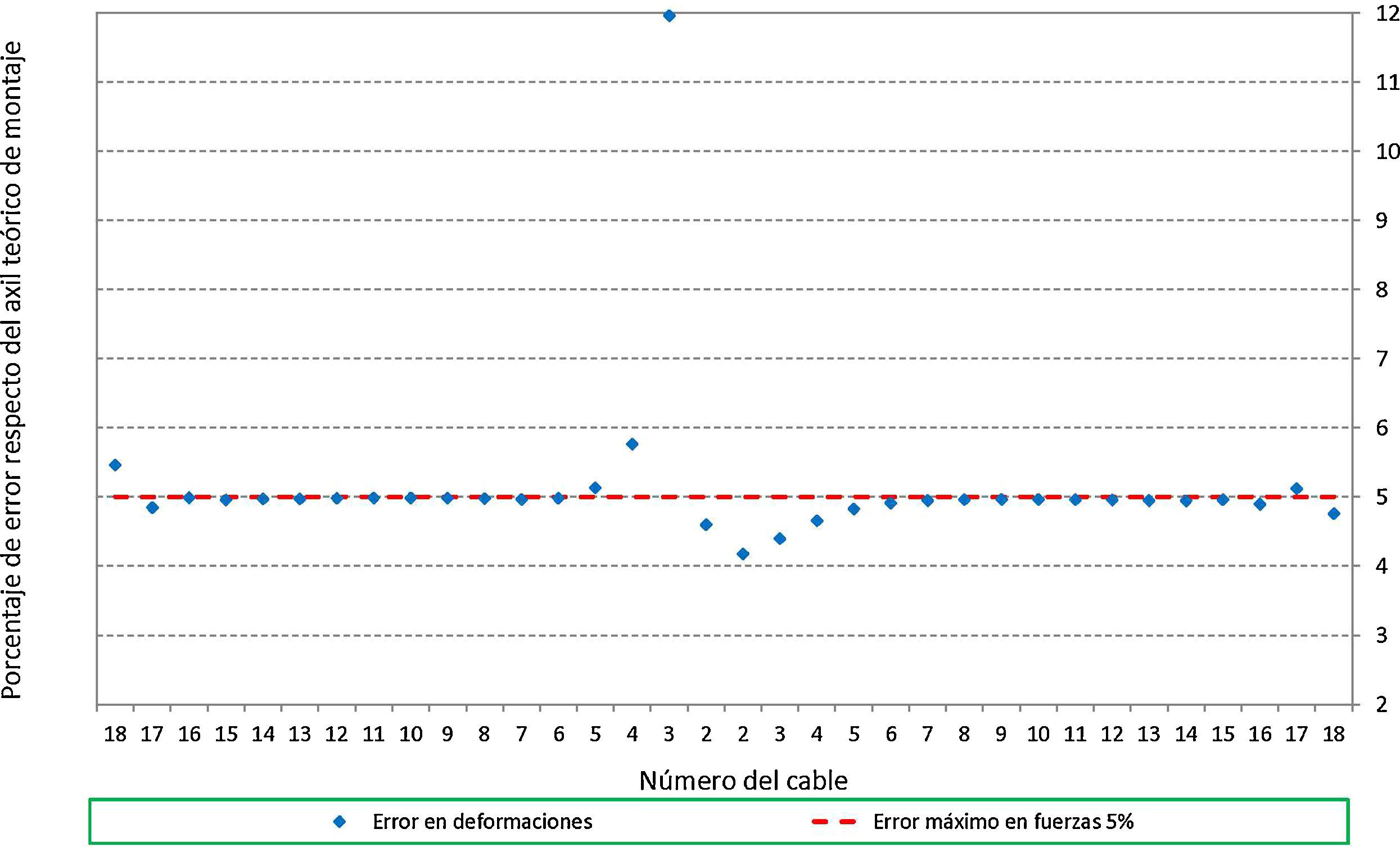
4.6

Validación del método de generación de aleatorios

Para verificar el resultado del desarrollo teórico anterior, se presentan a continuación los resultados de la aplicación de todo este procedimiento sobre el 1.^er elemento de la 1.^a muestra utilizando el método en fuerzas. En concreto, se adjunta un gráfico (fig. 9) en el que se representan los valores de los axiles de montaje de todos los cables, donde se observa que efectivamente los valores obtenidos quedan dentro del rango de error que admite la normativa, y por lo tanto sería posible que dichos valores se aplicaran en la realidad sobre la estructura.

Figura 9.

Gráfico de los axiles de montaje en todos los cables para el 1.^er elemento de la 1.^a muestra.

4.7

Comparativa de los métodos de instalación de los cables

Para evaluar si la cuantía de los errores máximos admisibles a introducir en cada método de cálculo tiene una repercusión similar en los procesos que se desarrollan a continuación, se ha llevado a cabo el siguiente análisis comparativo entre ambos.

En concreto el análisis realizado ha consistido en, a partir de las «predeformaciones» teóricas obtenidas para alcanzar en la situación final el estado de viga continua, calcular la longitud en vacío o neutra de cada cable L₀ y obtener la cuantía del error máximo que permite la normativa sobre esta medida. Esta medida del error en longitud se puede transformar en un error en fuerzas al conocer el área de cada tirante. Se puede así obtener el porcentaje que este error máximo en la medida de deformaciones significa en porcentaje respecto de los axiles teóricos de montaje de los cables.

Es decir:

siendo:

F₀ → Axil teórico de montaje de cada cable.

F_0,error → Error equivalente en fuerzas al máximo admisible en deformaciones.

E – Módulo de elasticidad del tirante: E_s = 200.000 N/mm²

A – Área de los tirantes.

L – Longitud del tirante o distancia teórica entre sus puntos de anclaje.

L₀ – Longitud en vacío o neutra del cable.

ΔL_error – Error en la medida de los alargamientos de los cables en el momento de su instalación. Se adopta el ya indicado en [8] que implica un porcentaje del error del 0,01% de L₀.

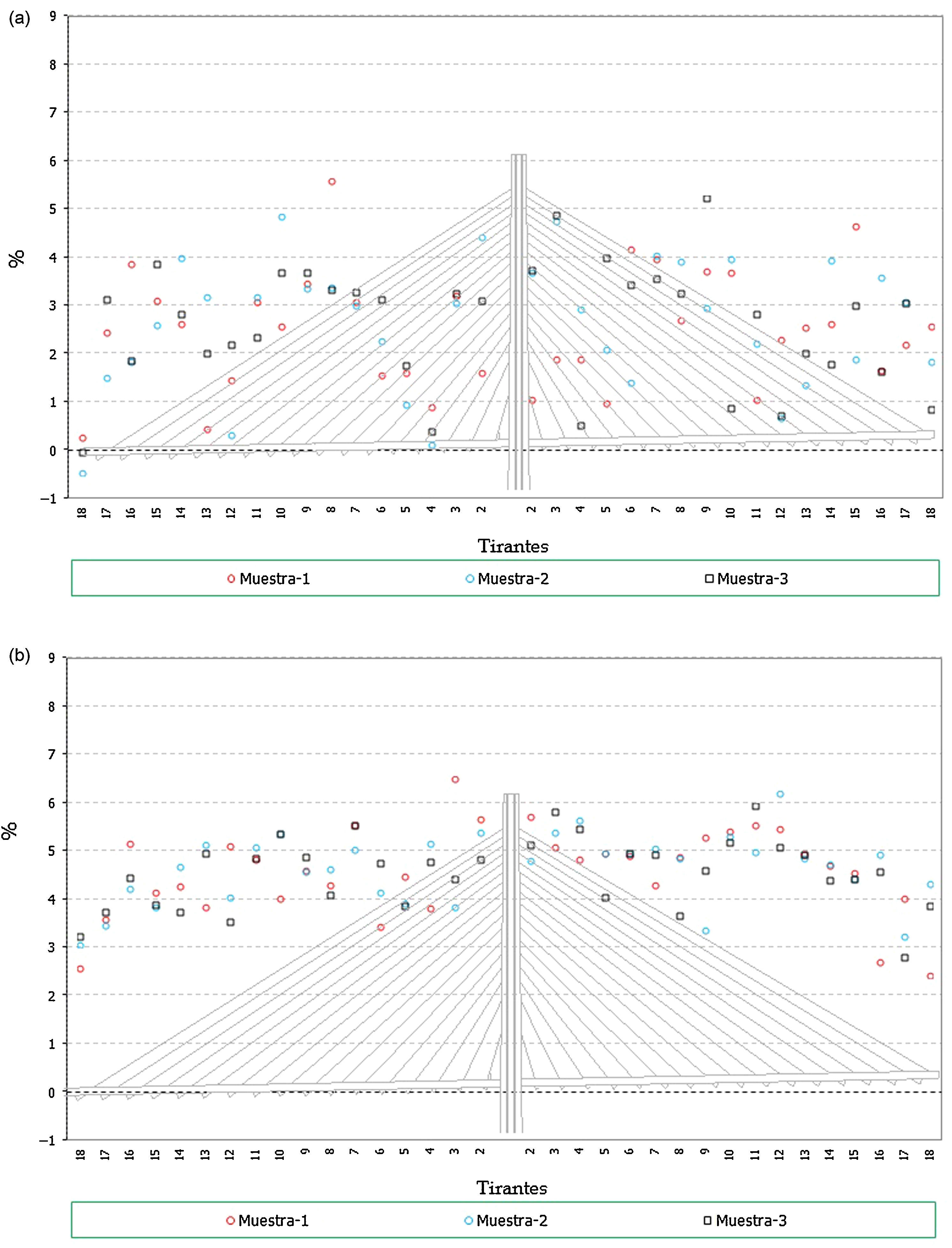
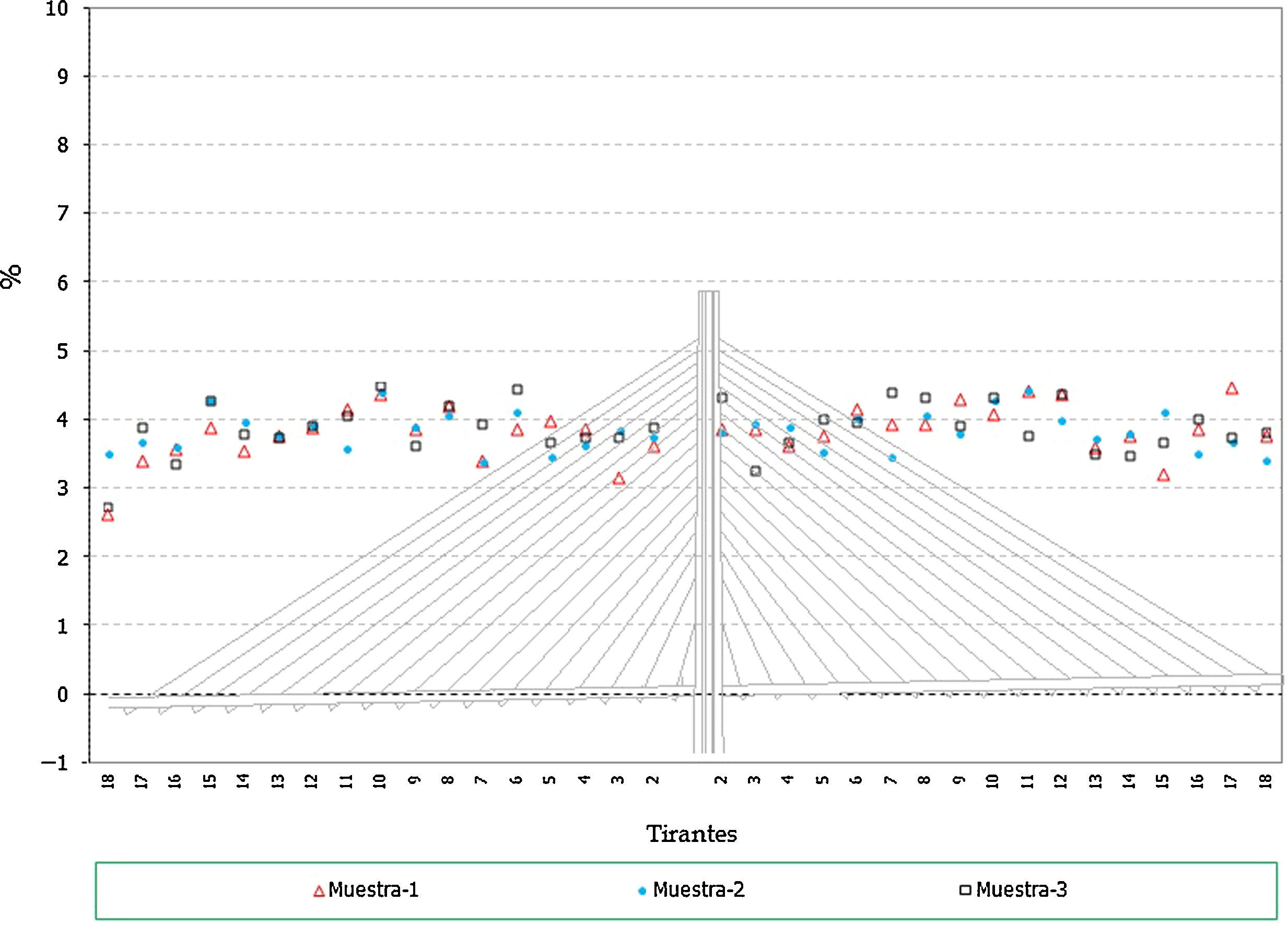
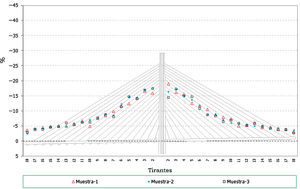
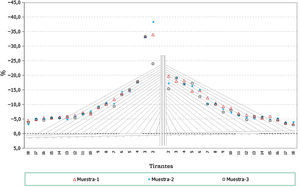
Los resultados obtenidos relativos a la implicación de los errores se representan gráficamente a continuación (fig. 10).

Figura 10.

Porcentaje de error, respecto del axil teórico de montaje (F₀), del axil de montaje equivalente al error máximo admisible en la medida de los alargamientos (F_0,error).

De los resultados anteriores se puede concluir que:

• -

  La implicación de los errores en deformaciones es similar a la planteada en el caso de la introducción de los errores en fuerzas. Resultan errores máximos del orden del 5%.

• -

  En general los valores obtenidos en cada cable son similares salvo en el entorno del cable 3-I. Esta diferencia se debe a que el análisis realizado lo es en porcentaje del axil teórico de montaje de los cables, teniendo este cable, debido al proceso constructivo proyectado, un axil muy pequeño (fig. 4), lo que a su vez conlleva que los errores planteados en deformaciones signifiquen un porcentaje muy alto respecto de las fuerzas iniciales de puesta en tensión teóricas.

5

Resultados obtenidos

Se procede en este epígrafe a desarrollar los resultados correspondientes a la aplicación de los errores aleatorios de montaje, bien por el método de las fuerzas o bien por el método de las deformaciones. En el primer caso, como ya se comentó, se introducirán errores en la fuerza de puesta en tensión, mientras que en el segundo caso se introducirán tanto errores en la medida de las deformaciones de los cables como en la posición de los anclajes. Así, los análisis realizados han sido:

• •

  Error en la medida de las fuerzas de puesta en tensión.

• •

  Error en la medida de las deformaciones de puesta en tensión.

• •

  Error en la posición de los anclajes.

Hay que indicar que, para cada uno de estos cálculos, se han generado 3 muestras de 100 elementos cada una, por lo que en total se han realizado 300 cálculos individuales de la estructura, para cada tipo de error.

Para facilitar el análisis del gran volumen de resultados obtenidos, se ha definido el valor característico de cada parámetro calculado en cada muestra, el cual corresponde a aquel valor que o bien es superado por el 95% de los elementos de la muestra, definiéndose este valor como característico inferior, o bien supera al 95% de los elementos de la muestra, definiéndose este a su vez como característico superior.

A continuación se representan los resultados que se han considerado más significativos, como son los axiles en los tirantes y los flectores en el tablero. Para cada uno de ellos se han analizado las siguientes situaciones:

• a)

  Situación final. Correspondiente al final del proceso de construcción y aplicación de la carga muerta sobre el tablero.

• b)

  Situación de construcción. Correspondiente a las diferentes fases de construcción del tablero.

• c)

  Situación de servicio. Correspondiente a la aplicación de las sobrecargas de tráfico sobre la estructura terminada.

5.1

Errores en fuerzas de puesta en tensión

El cálculo de los procesos constructivos «erróneos» parte de las series de variables aleatorias acotadas generadas con el algoritmo anteriormente indicado, y de su aplicación sobre los valores teóricos de los axiles de montaje, de tal manera que:

siendo: F^N_err,i el valor del axil erróneo N-ésimo del cable i.

F_teor,i el valor del axil teórico del cable i.

VA^N_i el coeficiente aleatorio de ponderación N-ésimo del cable i.

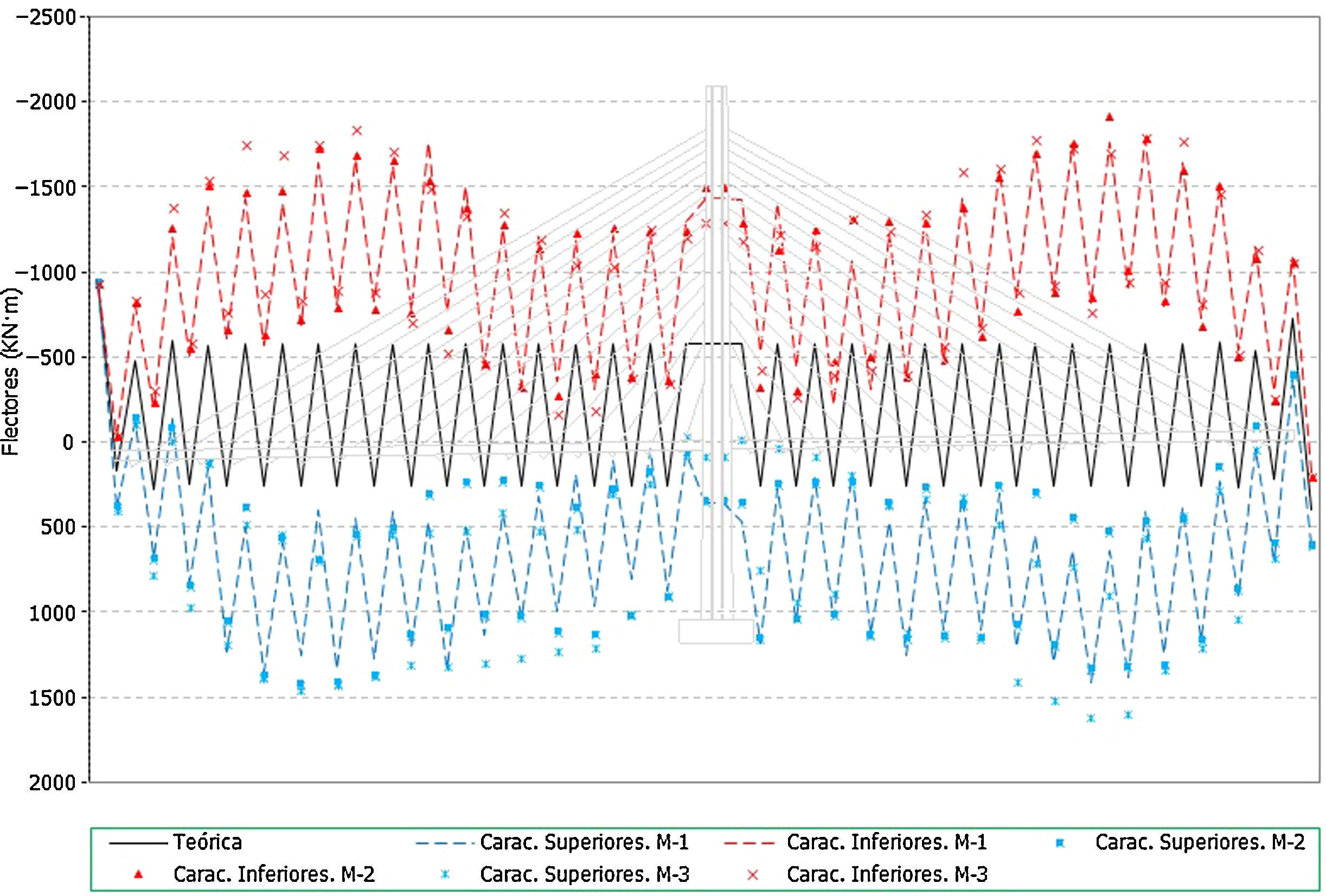
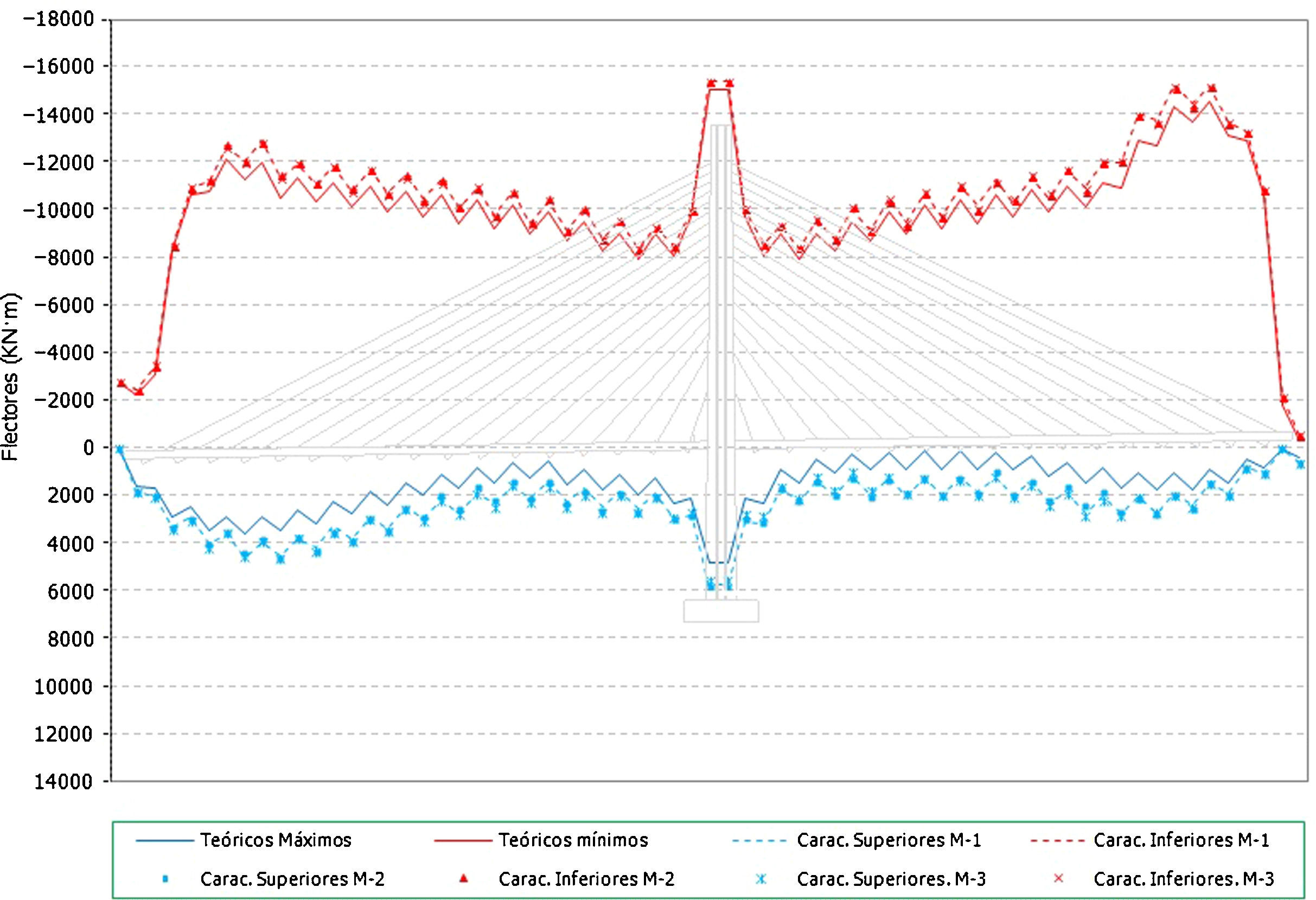
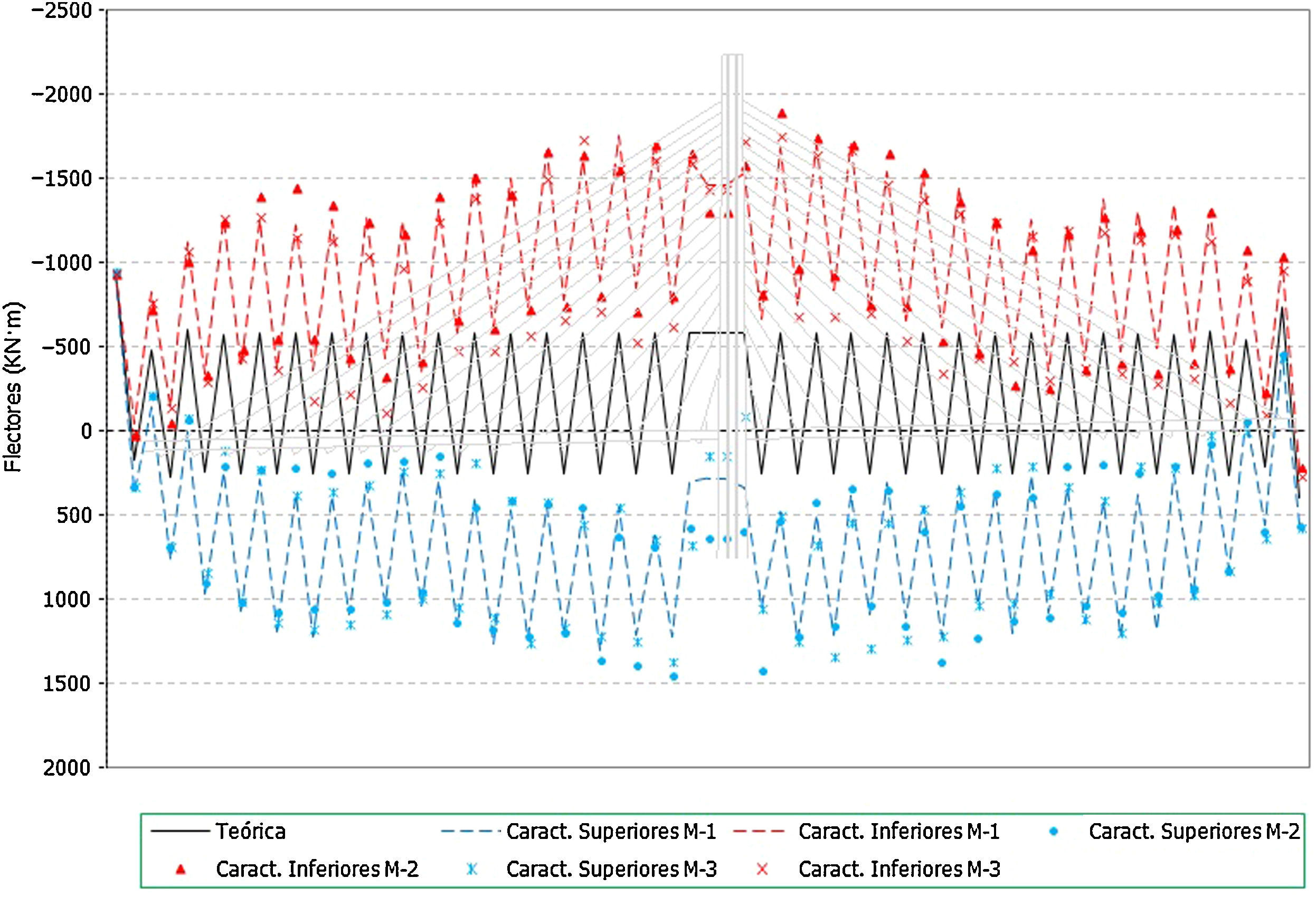
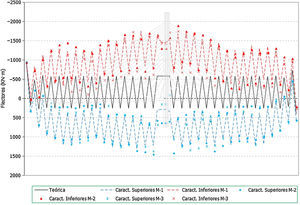
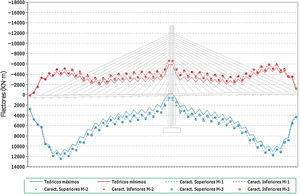
Se presentan a continuación los valores obtenidos en tirantes (figs. 11-16) y flectores en el tablero (figs. 17-19).

Figura 11.

Axiles finales en los tirantes. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 12.

Axiles finales en los tirantes. Diferencia en porcentaje de los valores característicos inferiores respecto de los teóricos.

Figura 13.

Axiles en los tirantes máximos de construcción. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 14.

Axiles en los tirantes mínimos de construcción. Diferencia en porcentaje de los valores característicos inferiores respecto de los teóricos.

Figura 15.

Axiles en los tirantes máximos de servicio. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 16.

Axiles en los tirantes mínimos de servicio. Diferencia en porcentaje de los valores característicos inferiores respecto de los teóricos.

Figura 17.

Flectores en tablero en situación final. Valores característicos superiores e inferiores.

Figura 18.

Flectores en tablero en fases de construcción. Valores característicos superiores e inferiores.

Figura 19.

Flectores en tablero en fases de servicio. Valores característicos superiores e inferiores.

5.2

Errores en alargamientos de los cables

Se adjuntan a continuación resultados de la aplicación de los errores aleatorios sobre las deformaciones teóricas de montaje de los cables. Así, el cálculo de los procesos constructivos «erróneos» tiene como base de partida en este caso la siguiente formulación:

siendo: δ^N_err,i el valor de la deformación errónea N-ésima del cable i.

δ_teor,i el valor de la deformación de montaje teórica del cable i.

VA^N_i el coeficiente aleatorio de ponderación N-ésimo del cable i.

L_i la longitud neutra o en vacío del cable i.

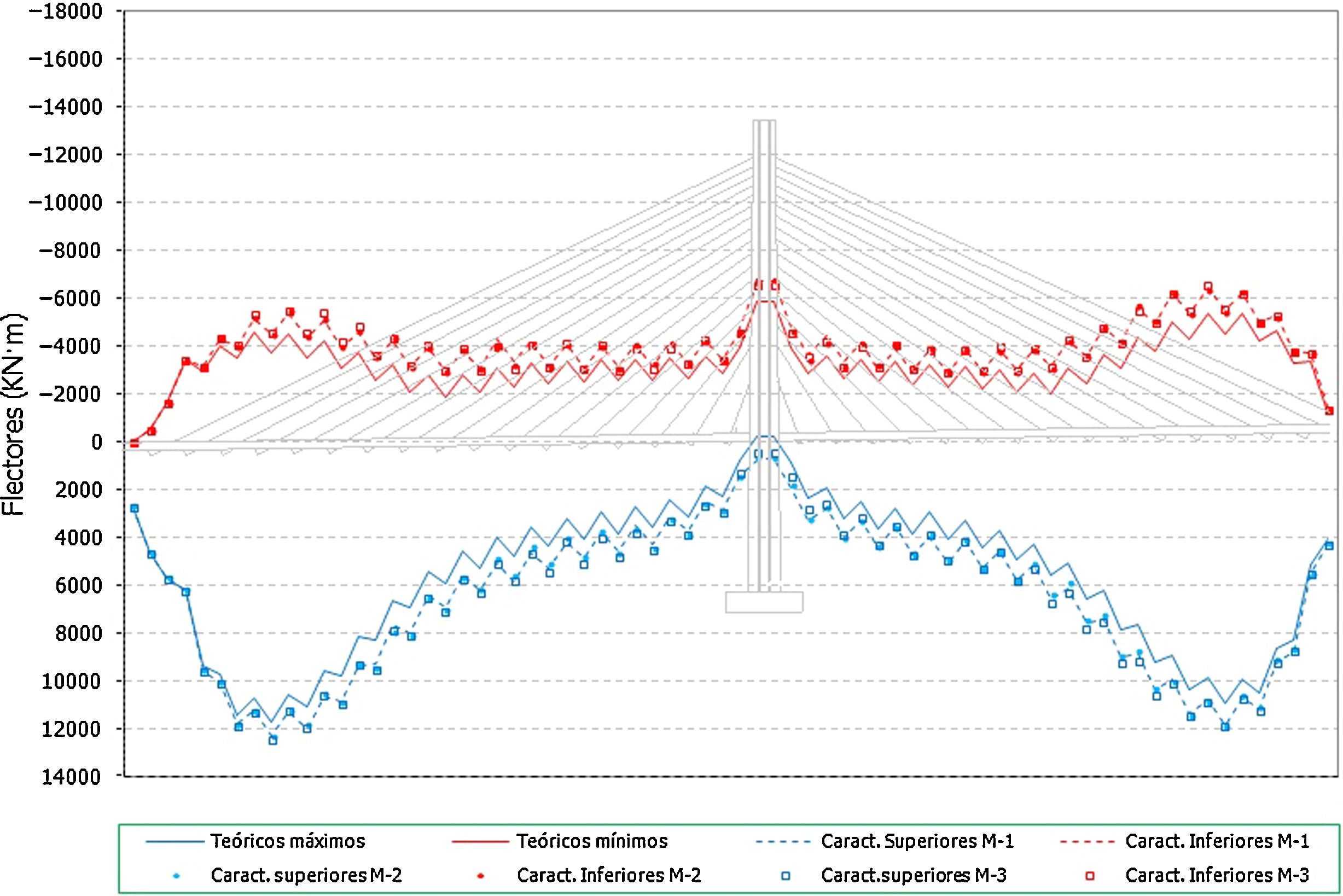
Se presentan a continuación los valores característicos superiores obtenidos en tirantes (figs. 20-23) y los flectores en situación final y de servicio (figs. 24 y 25).

Figura 20.

Axiles finales en los tirantes. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 21.

Axiles en los tirantes máximos de construcción. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 22.

Axiles en los tirantes mínimos de construcción. Diferencia en porcentaje de los valores característicos inferiores respecto de los teóricos.

Figura 23.

Axiles en los tirantes máximos de servicio. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 24.

Flectores en tablero en situación final. Valores característicos superiores e inferiores.

Figura 25.

Flectores en tablero en fases de servicio. Valores característicos superiores e inferiores.

5.3

Errores en la posición de los anclajes

El error en la posición en los anclajes se ha considerado que puede producirse con un rango de ±1 cm, habiéndose traducido dicho error en la posición del inicio y final del cable como un error en la longitud a medir de este. De esta forma el proceso seguido para la introducción de estos errores sobre el proceso constructivo es igual al planteado para el caso anterior de error en la medida de la longitud de los cables.

Se presentan a continuación los valores característicos superiores obtenidos en tirantes (figs. 26-28) y los flectores en situación final y servicio (figs. 29 y 30).

Figura 26.

Axiles finales en los tirantes. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 27.

Axiles en los tirantes máximos de construcción. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 28.

Axiles en los tirantes máximos de servicio. Diferencia en porcentaje de los valores característicos superiores respecto de los teóricos.

Figura 29.

Flectores en tablero en situación final. Valores característicos superiores e inferiores.

Figura 30.

Flectores en tablero en fases de servicio. Valores característicos superiores e inferiores.

6

Análisis de resultados

6.1

Resultados con errores en fuerzas

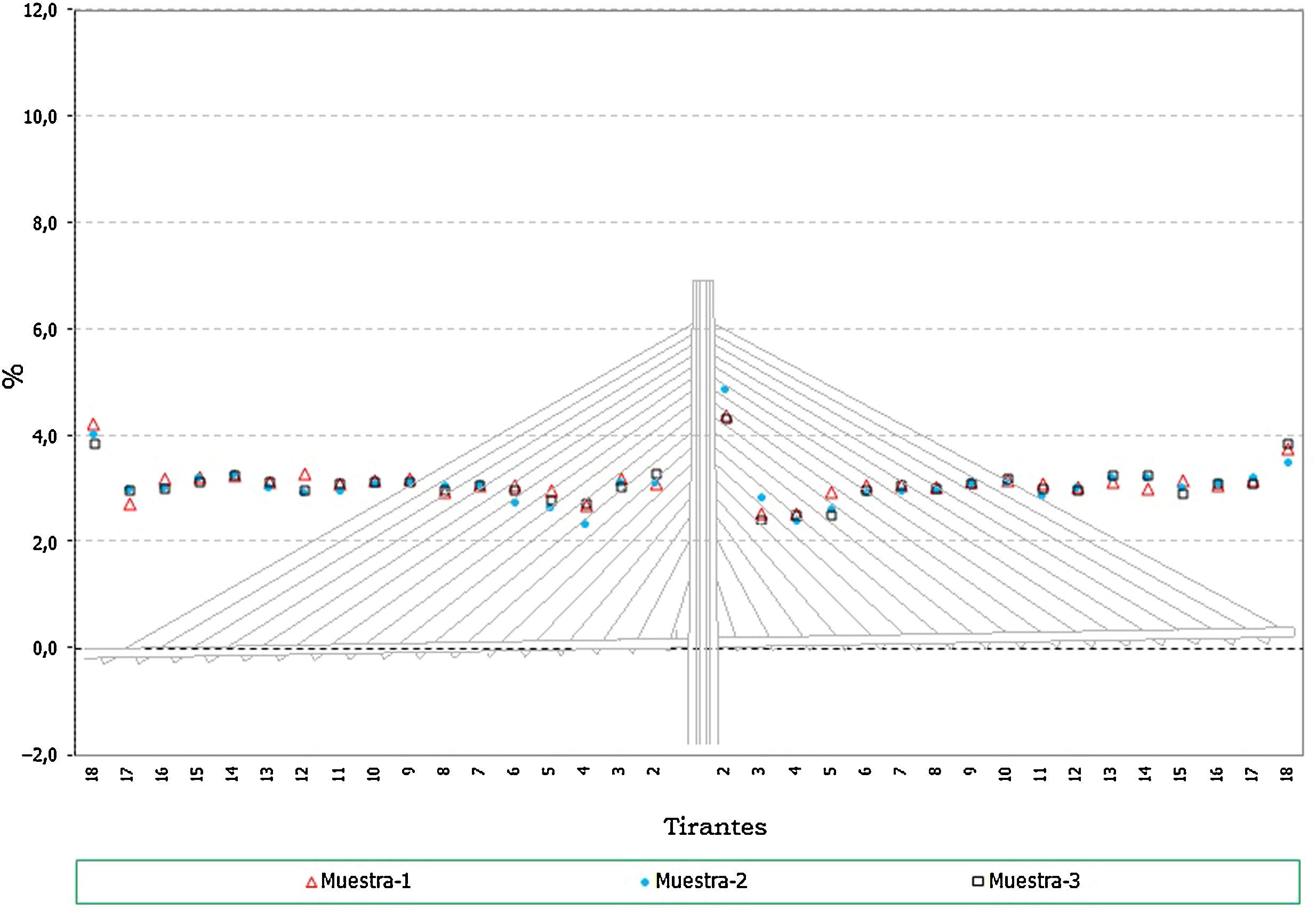
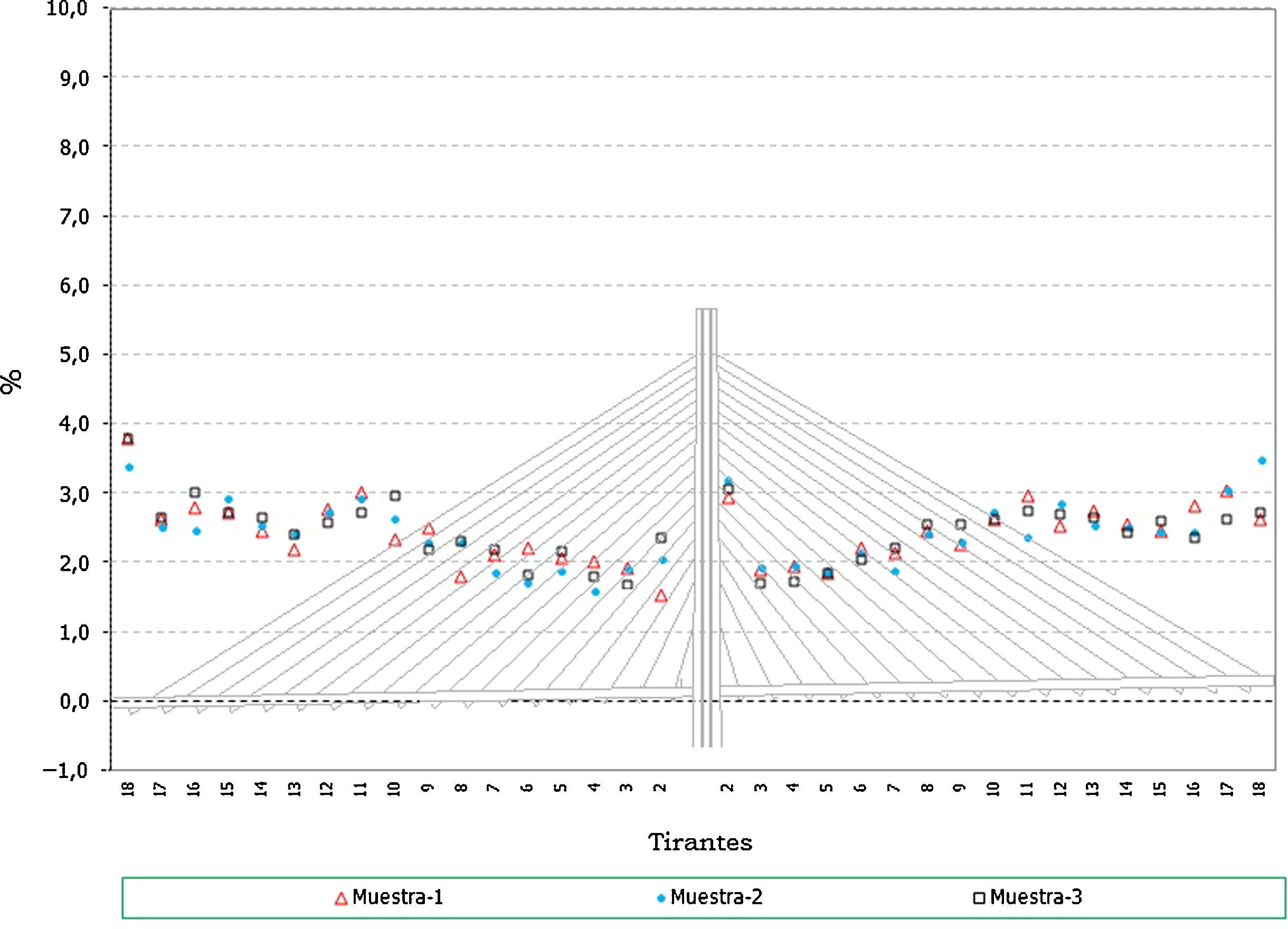
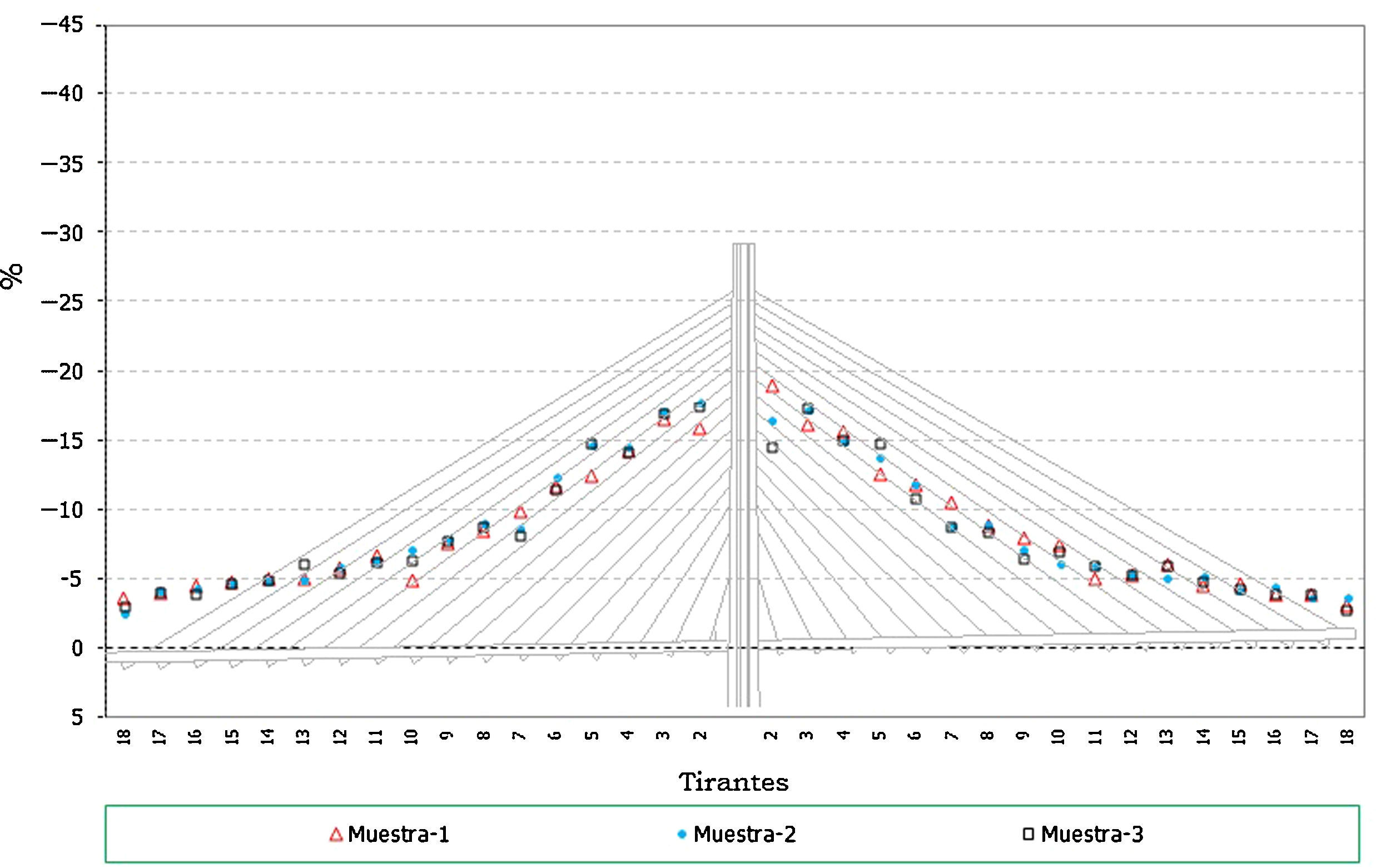
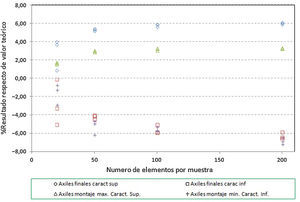
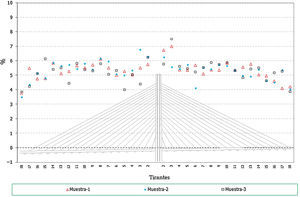
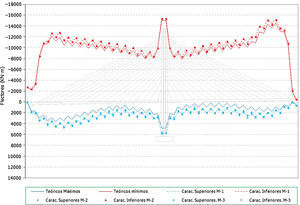
En el caso de los axiles en los tirantes se puede indicar que:

• •

  Los errores en los axiles en la fase final alcanzan valores de hasta un 8% del valor teórico, siendo mayores los errores en el caso de los valores característicos inferiores (fig. 11 y fig. 12).

• •

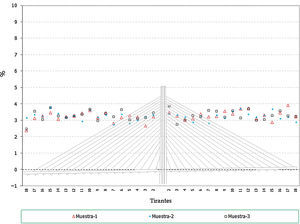
  En el caso de las envolventes de axiles en las fases de construcción se observa claramente que el axil máximo queda muy condicionado por el peso de las dovelas y por lo tanto el efecto aleatorio introducido en los cables no tiene apenas significación en este caso (fig. 13). No ocurre así en el caso de los axiles mínimos de construcción donde los errores llegan a alcanzar porcentajes de hasta un 10% (fig. 14).

• •

  En el caso de los axiles en servicio ocurre algo similar al caso de los axiles finales, siendo mayor el efecto de la aleatoriedad sobre los axiles mínimos que en los máximos (fig. 15 y fig. 16), dado que en estos últimos influye en cierta medida el valor de la sobrecarga aplicada, sobre la que se ha supuesto que no existe incertidumbre. Los errores en el caso de los axiles mínimos alcanzan hasta un 10%.

• •

  Los errores en todos los casos son mayores en los primeros cables instalados, donde el efecto de la menor longitud del cable supone una mayor repercusión de las imperfecciones en la ejecución simuladas.

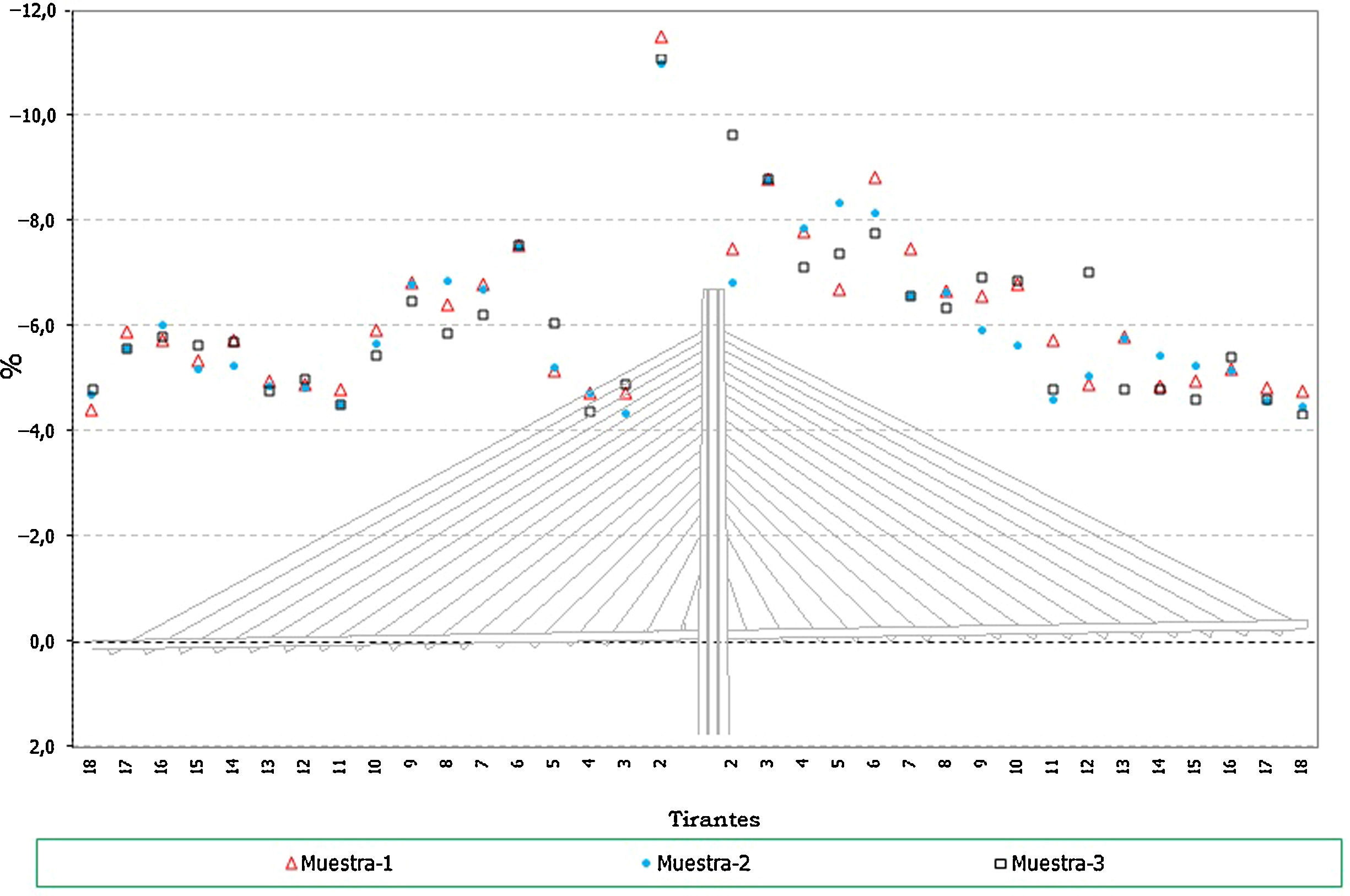
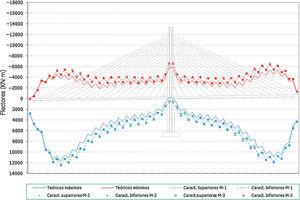
Por otra parte en el caso de los resultados en flectores del tablero:

• •

  Se observa que existe una gran influencia en la situación final del proceso constructivo, que queda relativamente alejado de la situación objetivo de la viga continua (fig. 17).

• •

  En cambio, de cara a las envolventes que verdaderamente dimensionarían el tablero, mínimos de construcción y máximos de servicio (fig. 18 y fig. 19), las diferencias obtenidas al introducir los errores de montaje resultan del orden del 5-7% para los flectores mínimos y de hasta un 20-30% en el caso de los máximos de construcción.

6.2

Resultados con errores en deformaciones

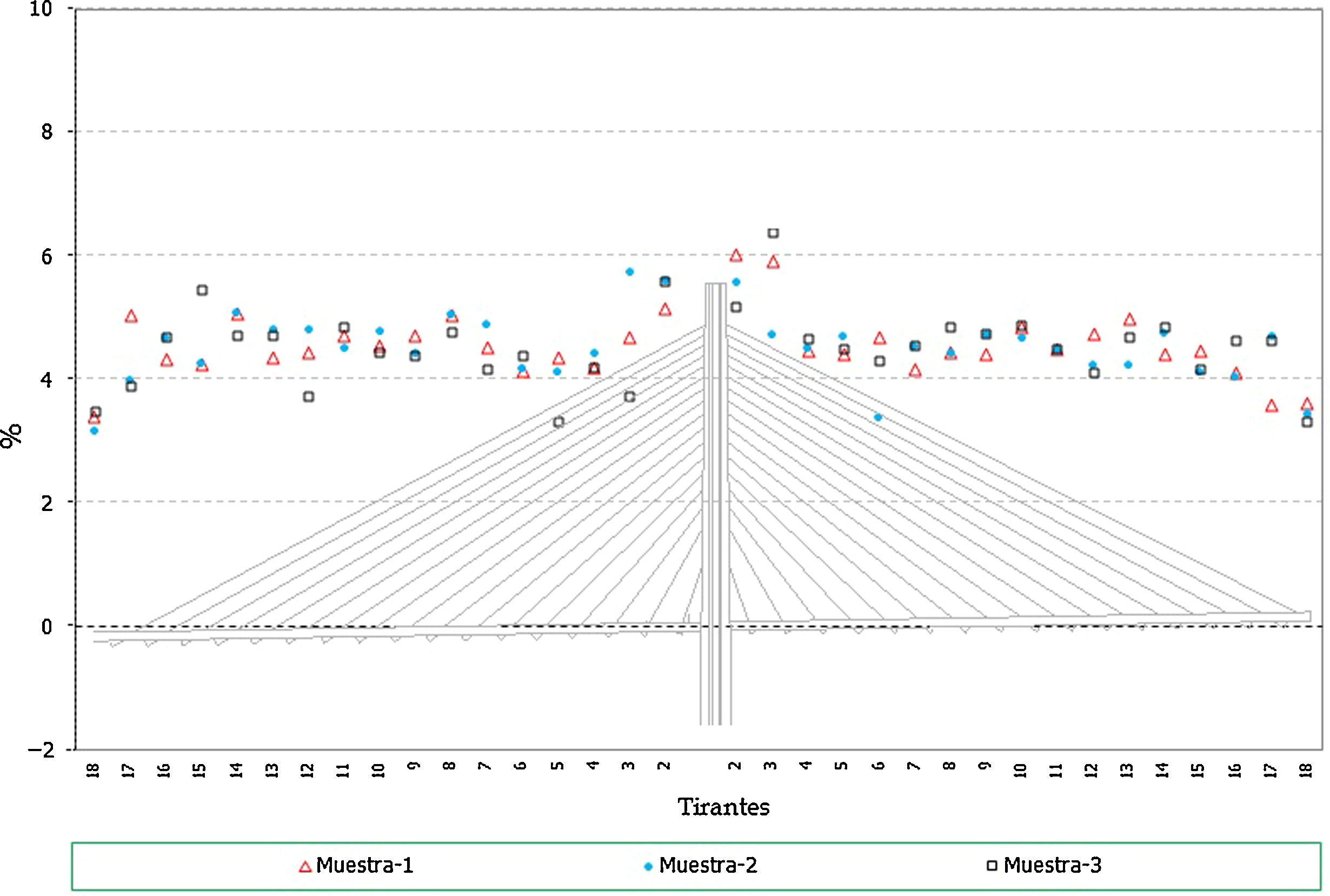
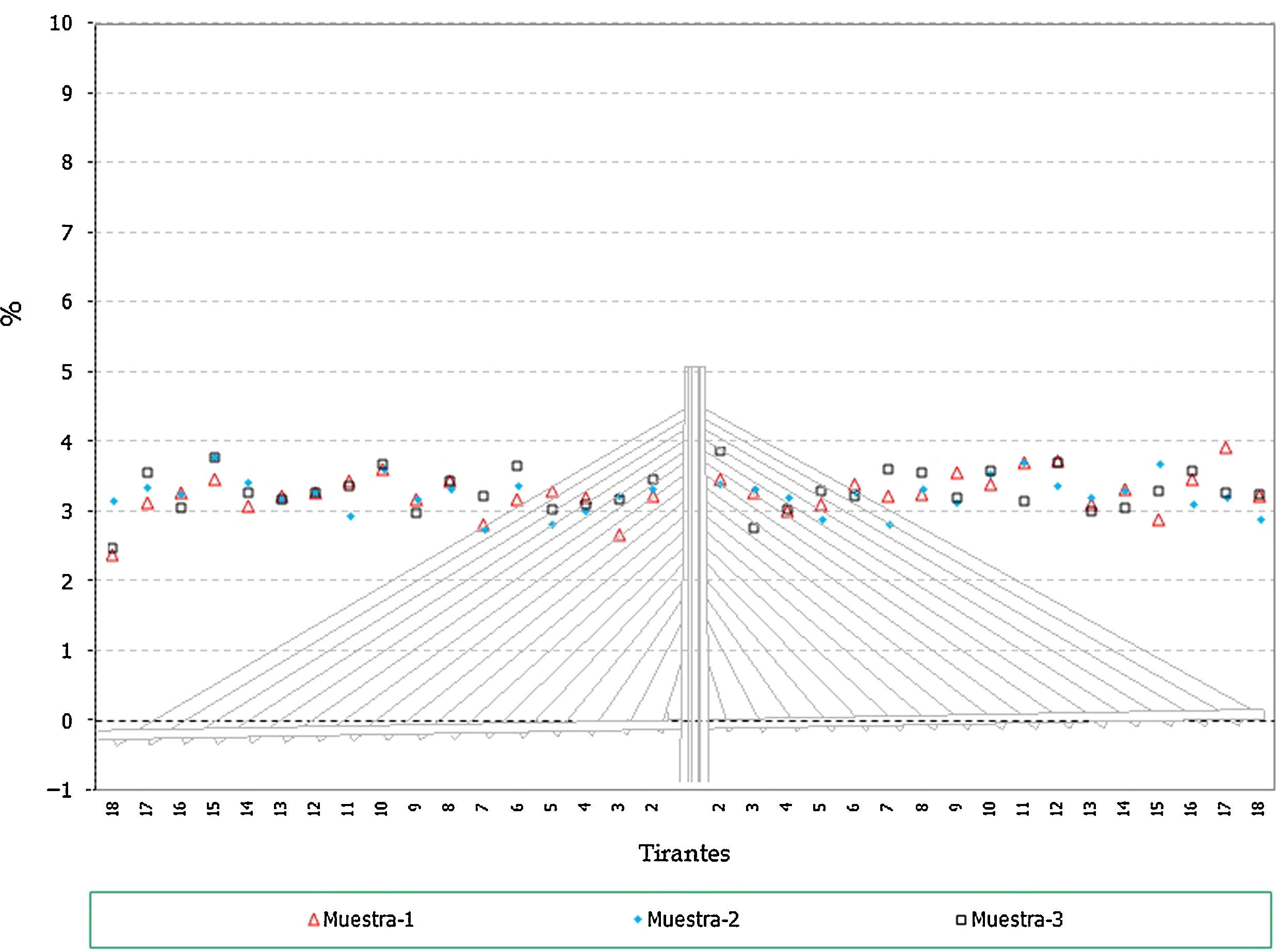
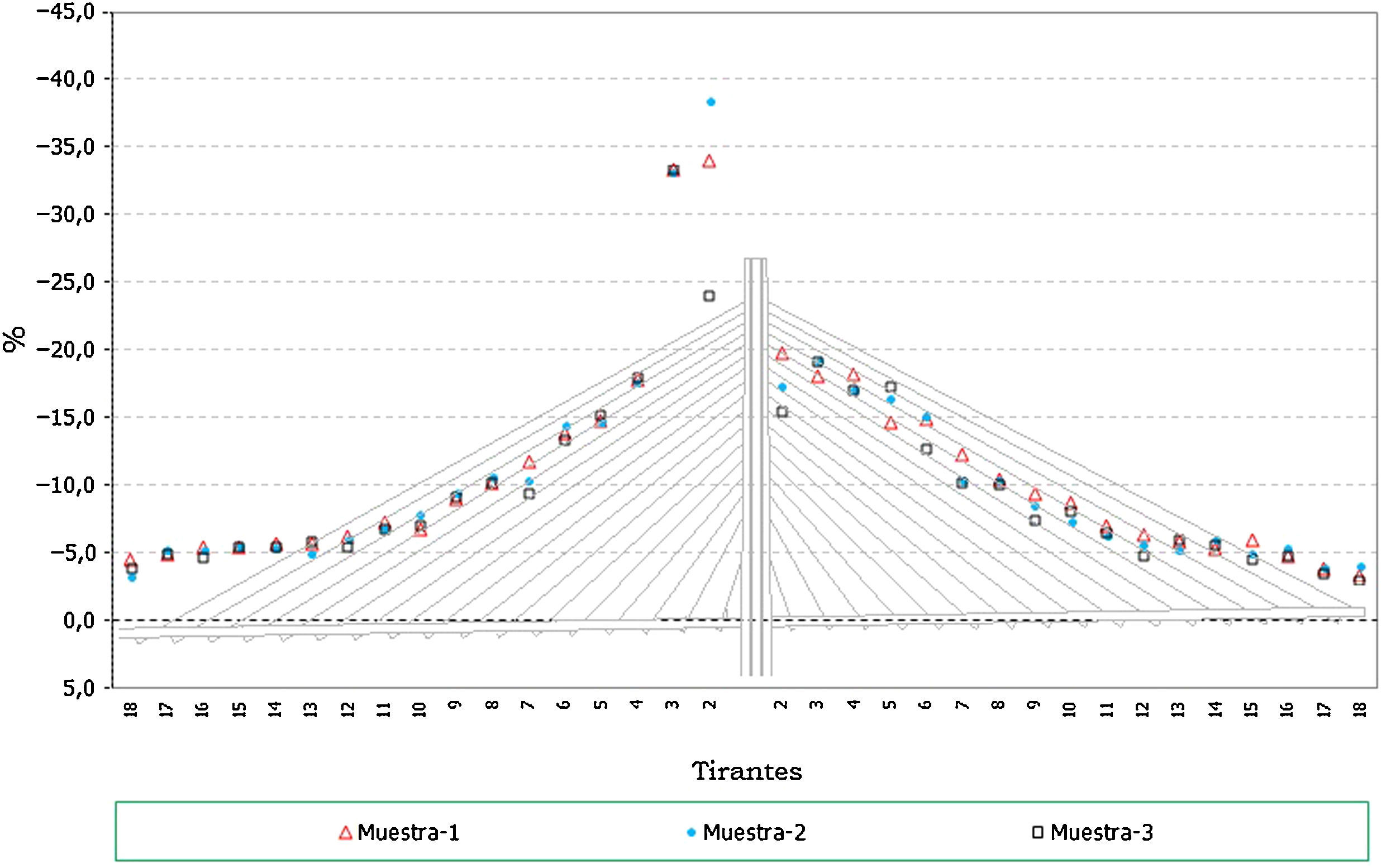
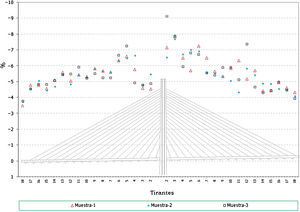
En el caso de los axiles en los tirantes:

• •

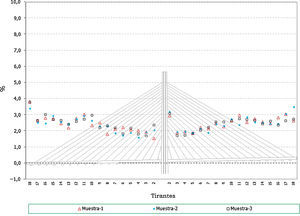
  Los errores en los axiles en la fase final alcanzan valores de hasta un 4% del valor teórico, siendo similares los niveles de error para el caso de los máximos y mínimos de la situación final (fig. 20).

• •

  Al igual que en el caso anterior, se observa que los axiles mínimos de construcción tienen porcentajes de error, de hasta un 8%, siendo en general superiores a los de los máximos (fig. 21 y fig. 22).

• •

  En el caso de los axiles en servicio los valores de los errores obtenidos quedan en el orden de entre un 3 y un 4% (fig. 23).

• •

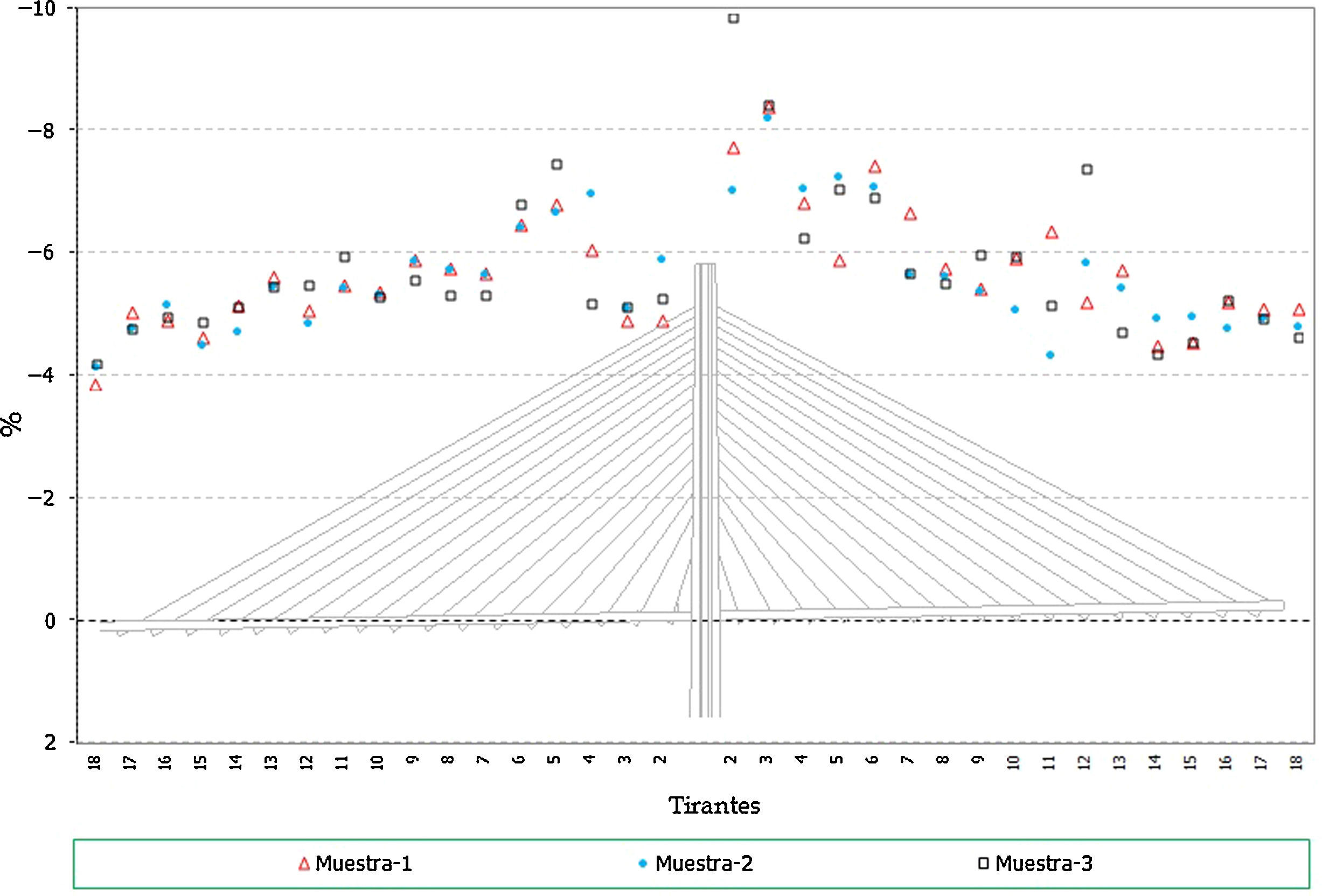
  Por otra parte en el caso de los flectores del tablero:

• •

  Se observa que existe una gran influencia de los errores aleatorios en la situación final del proceso constructivo. El efecto es más acusado en la zona situada a 3/4 de la luz, donde el esquema de atirantamiento es menos eficaz y la flexibilidad del tablero por lo tanto más alta (fig. 24).

• •

  Los efectos en las envolventes de construcción y servicio son más reducidos que en el caso anterior, aplicando errores en fuerzas de puesta en tensión, encontrándose las mayores desviaciones en la zona del tablero donde su rigidez es más reducida (fig. 25).

6.3

Resultados con errores en posición de anclajes

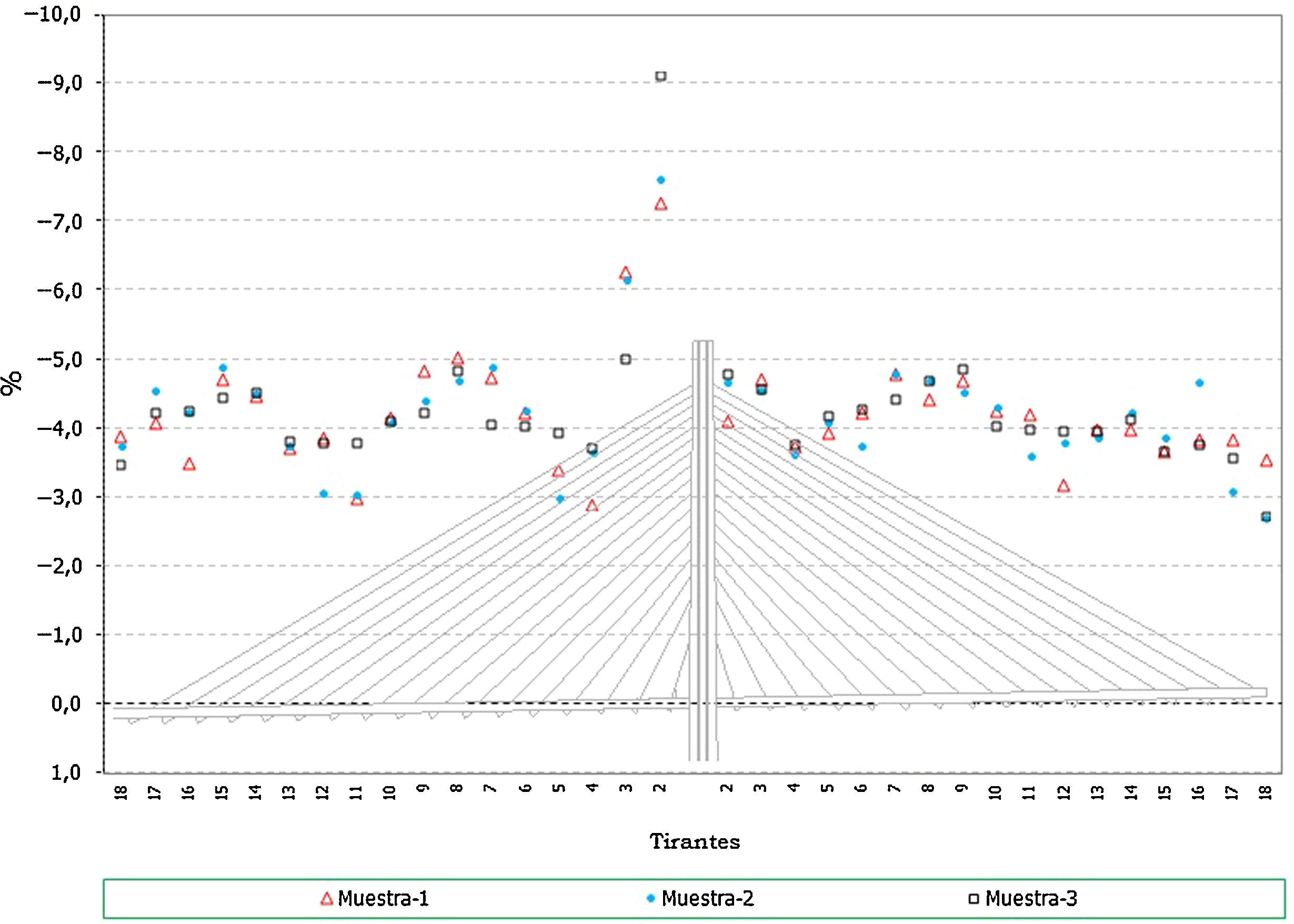
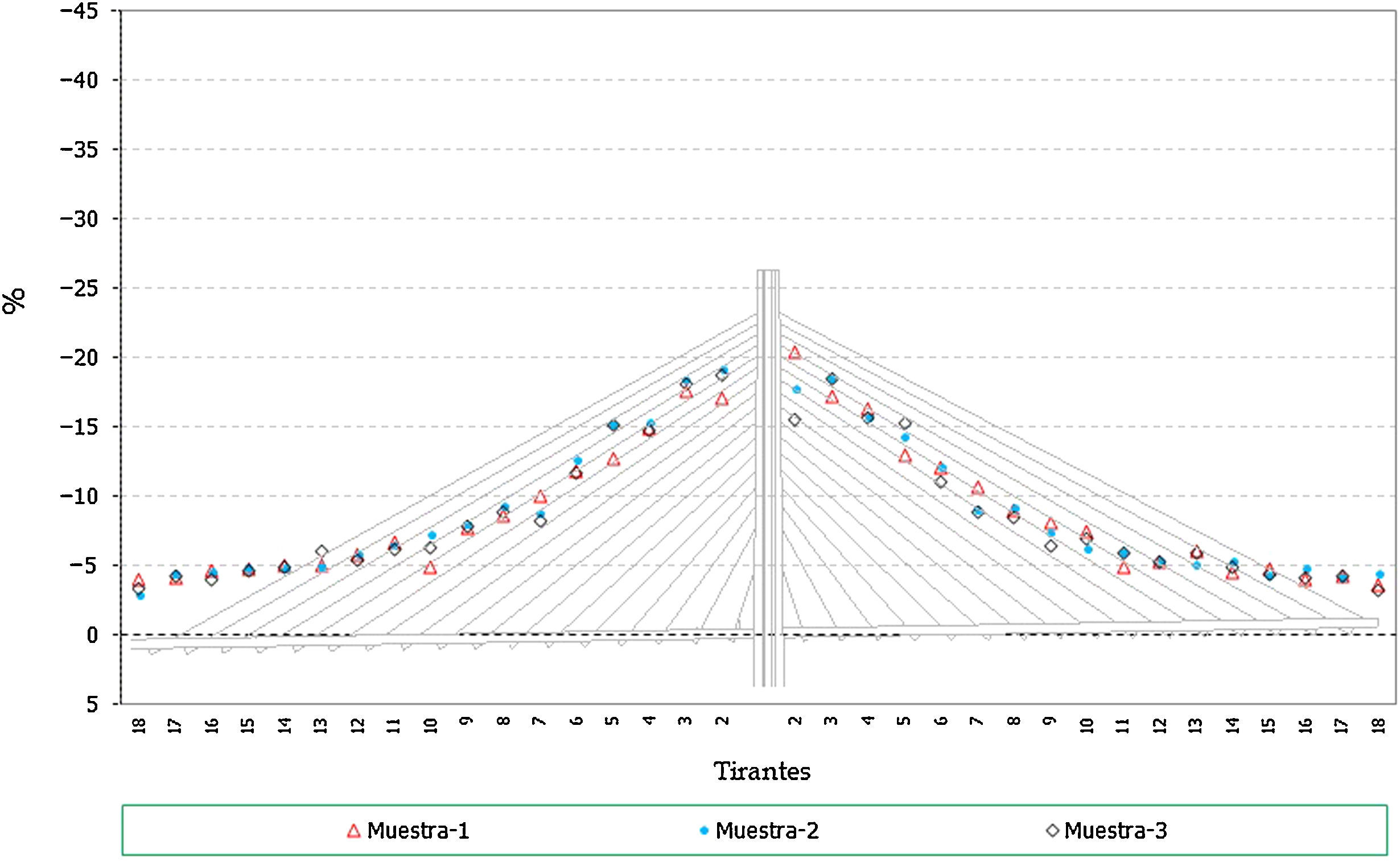
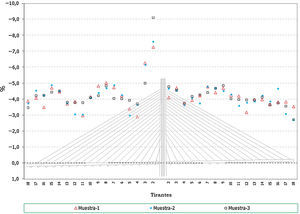
En el caso de los axiles en los tirantes:

• •

  Los errores en los axiles finales son mucho más acusados en el caso de los tirantes cortos, donde se llegan a alcanzar desviaciones de hasta un 20% (fig. 26).

• •

  En el caso de los axiles de construcción, la envolvente de máximos queda más acotada en su desviación pero en el caso de la envolvente de mínimos los errores en los tirantes más cortos quedan en el entorno de hasta un 30% (fig. 27).

• •

  Los axiles en servicio muestran un comportamiento similar al caso de los axiles finales del proceso de construcción (fig. 28).

En el caso de los flectores en el tablero:

• •

  Los flectores en la situación final resultan con una desviación importante respecto de la situación teórica. Este efecto es más acusado en las dovelas iniciales donde el error de posición en los anclajes es más acusado (fig. 29).

• •

  En las envolventes de flectores en las situaciones de construcción y servicio el efecto de la aleatoriedad queda amortiguado, siendo únicamente importante en la zona de tablero donde anclan los cables más cortos (fig. 30).

6.4

Comparación de resultados

A la vista de los resultados anteriores se puede concluir que:

• •

  El método de introducir errores en fuerzas de puesta en tensión produce en general errores mayores en los esfuerzos en tirantes y tablero que en el caso de considerar errores en deformaciones.

• •

  La introducción de errores en el replanteo de los anclajes provoca esfuerzos en los tirantes con mucha mayor desviación que las generadas en los métodos anteriores, pero no tanto en el caso de los flectores en el tablero.

7

Resumen y conclusiones

En este artículo se ha planteado un método que permite la introducción de errores aleatorios en la instalación de los cables tanto en fuerzas de puesta en tensión como en deformaciones y posición de los anclajes. En los dos primeros casos, las limitaciones establecidas por la normativa son similares, pero las tolerancias habituales en la posición de los anclajes producen efectos mucho mayores en proporción. Es por este motivo que el método de control de la puesta en tensión de los cables midiendo deformaciones debe ir acompañado de un control geométrico muy estricto, lo que hace muy difícil su aplicación al caso de puentes con tablero de hormigón.

El efecto de los errores aleatorios, sin tener en cuenta errores en el posicionado de los anclajes de los cables, es mayor en el caso del montaje de los tirantes aplicando fuerzas al caso de aplicar deformaciones, aunque en ambos casos quedan relativamente acotados. Aplicando ambos métodos, aunque sobre la situación final objetivo las desviaciones son significativas, el efecto final en las envolventes que dimensionarían el tablero (flectores mínimos de construcción y máximos de servicio) es pequeño, dada la influencia del peso de la dovela y de la sobrecarga de tráfico que las condicionan.