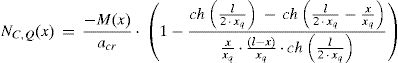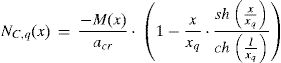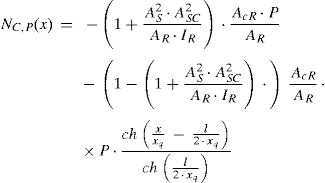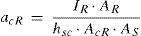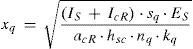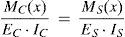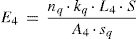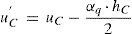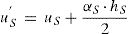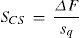En la mayoría de vigas mixtas, la conexión entre el hormigón y el acero es imperfecta y, por tanto, aparece un mayor o menor deslizamiento relativo entre ambos materiales. Este deslizamiento afecta tanto a las deformaciones como a los esfuerzos de la viga. Para simular este fenómeno, en este trabajo se propone un nuevo modelo de elementos finitos bidimensional basado en elementos tipo viga, facilitando así la interpretación y la aplicación práctica de los resultados. Para validar la precisión del modelo, se comparan los resultados obtenidos mediante el modelo con los derivados de las ecuaciones analíticas propuestas en la literatura, en dos estructuras mixtas con diferentes estados de carga.
In most composite beams, the concrete and steel connection is flexible to some extent. For this reason, a relative slip always appears at the interface. This slip is of primary importance because it affects both the deflections and the stresses in the beam. To simulate this phenomenon, a two-dimensional finite element based on frame elements model is proposed. The main advantage of this model is its easy interpretation of the results and its applicability on design practice. To validate the accuracy of the proposed model, this has been verified against those results obtained by analytical equations available in the literature for different loading cases.
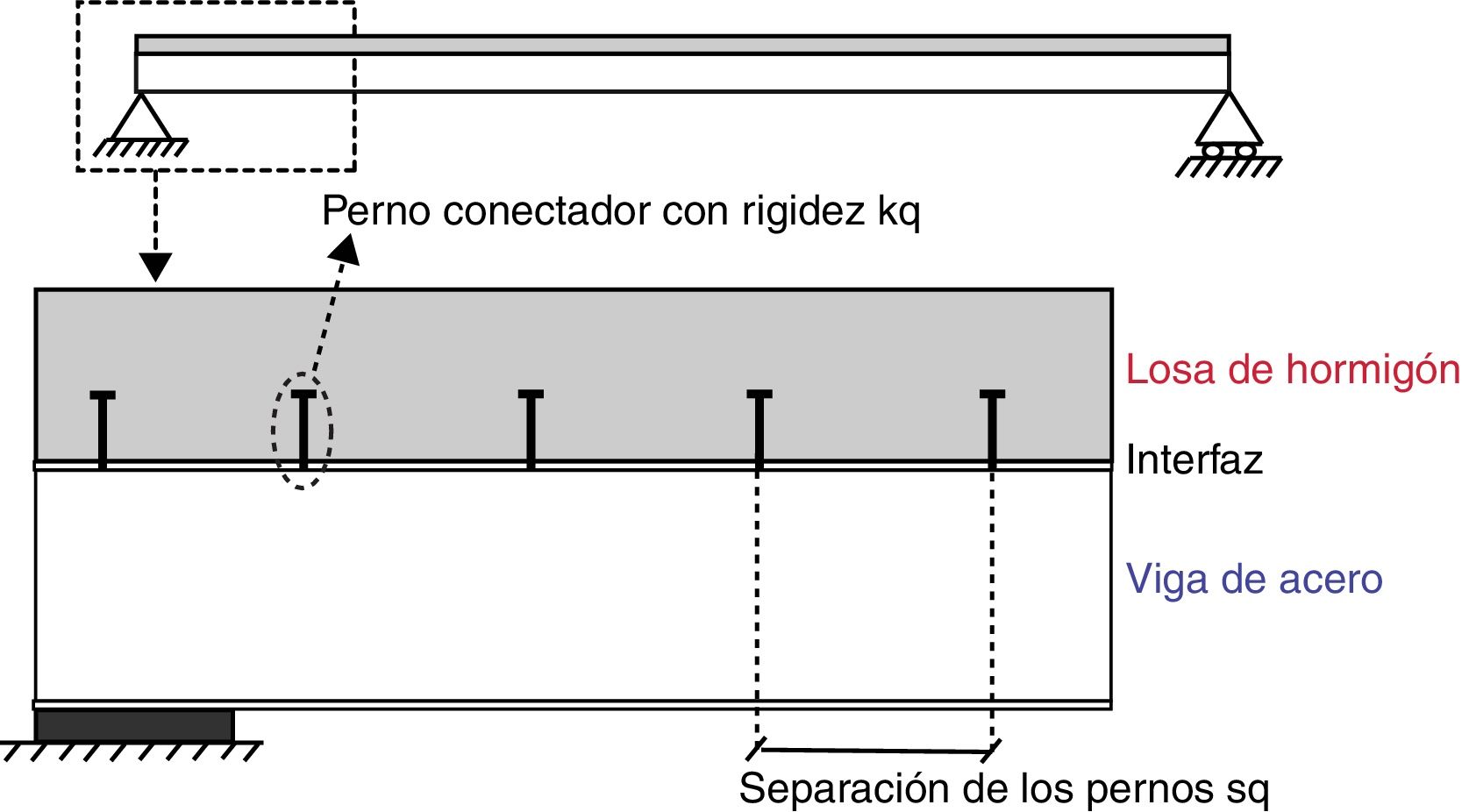
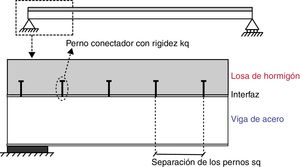
Las estructuras mixtas están formadas generalmente por un forjado o losa de hormigón y una viga de acero solidarizadas por medio de conectadores (fig. 1). El comportamiento de estas estructuras depende de la rigidez relativa de estos conectadores, kq, su número en la dirección transversal, nq y su separación longitudinal, sq. Si la conexión es muy rígida (interacción perfecta), se puede suponer que no hay deslizamiento relativo entre las superficies en contacto y que la distribución de rasantes que transmite la conexión no depende de la rigidez de la misma, que suponemos infinita, sino de las características mecánicas de las secciones de hormigón y de acero. La mayoría de normativas sobre estructuras mixtas asumen esta hipótesis [1,2]. Sin embargo, en vigas con pernos conectadores flexibles que permiten un deslizamiento relativo entre el hormigón y el acero (interacción imperfecta), el rasante que se moviliza es proporcional a este deslizamiento, siendo por tanto función no solo de las características mecánicas de las secciones transversales de la estructura, sino también de la flexibilidad de la conexión.
En la literatura se han realizado un gran número de estudios para simular el comportamiento de las vigas mixtas con interacción imperfecta. De acuerdo con Sousa et al. [3], Newmark et al. [4] presentaron el primer modelo analítico con interacción imperfecta. En este método, las ecuaciones de equilibrio y compatibilidad de cada elemento de la viga mixta se reducen a ecuaciones diferenciales de segundo orden asumiendo una conexión uniforme en la interfaz. Martínez y Ortiz [5] también utilizaron un enfoque basado en ecuaciones diferenciales para definir las ecuaciones analíticas para vigas biapoyadas sometidas a diferentes casos de carga. En este procedimiento se asume que las deformaciones en los centroides son las mismas en ambos materiales (acero y hormigón) así como una distribución uniforme de los conectadores. Los principales inconvenientes de los métodos analíticos son: 1)Esfuerzo de cálculo necesario para obtener las ecuaciones analíticas. 2)Análisis complejo limitado únicamente a vigas isostáticas de canto uniforme y a casos de carga particulares y sus combinaciones. 3)Los efectos de las distribuciones no uniformes de conectadores no se pueden analizar. Por todas estas razones, el enfoque analítico no es el más indicado para el diseño práctico de vigas mixtas.
Alternativamente, los modelos numéricos de elementos finitos (MEF) permiten un análisis más indicado para el diseño práctico [6]. Una de las primeras decisiones a la hora de abordar la simulación de estructuras mixtas mediante este procedimiento consiste en definir la dimensionalidad del modelo. Por un lado, modelos en tres dimensiones (3D) proporcionan una alta precisión indicada especialmente para estudios de regiones locales o de discontinuidades. Sin embargo, de acuerdo con Queiroz et al. [7,8], el uso de este procedimiento se desaconseja en estructuras complejas debido a los grandes costes computacionales, la necesidad de integrar esfuerzos y la dificultad de conseguir una convergencia numérica. A pesar de que el reciente desarrollo de softwares como ABAQUS/explicit [9] ha mejorado considerablemente esta convergencia, y por lo tanto la aplicabilidad de los MEF, un gran número de autores recomiendan modelos bidimensionales (2D) para el diseño práctico de vigas mixtas. Uno de los métodos basados en una simulación 2D por medio de elementos tipo viga se presenta en [8]. En este método la interfaz se simula por medio de muelles no-lineales situados a la altura del centroide de la losa de hormigón armado.
El objetivo de este artículo es proporcionar un enfoque estructurado a la simulación de vigas mixtas con interacción imperfecta utilizando software sencillo. Para ello, se propone un modelo bidimensional basado en un MEF compuesto únicamente por seis tipos diferentes de elementos tipo viga (losa de hormigón, viga de acero, conectadores verticales, muelles conectadores para el cortante, así como elementos verticales para simular el espesor del hormigón y el acero). La principal ventaja de este método es que proporciona directamente información útil para el diseño sin la necesidad de realizar una integración de esfuerzos (como en los modelos tridimensionales). Las diferencias fundamentales que presenta este modelo respecto a las ecuaciones analíticas y los modelos tridimensionales son las siguientes: 1) Intuitividad: cada elemento del modelo corresponde a un elemento de la viga mixta, lo que facilita la interpretación de los resultados. 2)Aplicabilidad: el modelo proporciona directamente información que es útil para el diseño, tal como los esfuerzos en la losa de hormigón, en la viga de acero y en los pernos conectadores, y las deformaciones en la viga mixta, sin la necesidad de realizar una integración de las tensiones en los elementos finitos. 3)Versatilidad: a diferencia de las ecuaciones analíticas, el modelo permite el análisis de estructuras hiperestáticas, de canto variable y con distribuciones no uniformes de pernos conectadores. Además, con objeto de evaluar la influencia de la deformabilidad de la conexión en el comportamiento a torsión de las vigas, el modelo permite también su generalización a tres dimensiones. 4)Fácil construcción: el modelo incluye secuencias repetitivas de elementos, por lo que la generación de la geometría de los modelos se puede programar fácilmente con algoritmos de pre-procesamiento. 5)Fácil reproducción: como el modelo está compuesto únicamente por elementos tipo viga, se puede analizar con cualquier programa sencillo de barras.
La organización del artículo es la siguiente. En la sección 2 se revisan brevemente las principales ecuaciones analíticas propuestas en la literatura para el análisis de vigas mixtas con interacción imperfecta. En la sección 3 se describen en detalle las principales características de cada uno de los elementos que componen el MEF propuesto. En la sección 4 se presenta la aplicación numérica del modelo propuesto. Para validar su precisión, esta sección incluye también la comparación con los resultados obtenidos mediante ecuaciones analíticas. En este análisis también se estudian los efectos de la rigidez de la conexión tanto en estructuras isostáticas como hiperestáticas. Tras ello, en la sección 5 se presentas las futuras líneas de investigación y finalmente en la sección 6 se resumen las conclusiones.
2Ecuaciones analíticasLas ecuaciones analíticas presentadas en la literatura están basadas en las siguientes hipótesis simplificadoras: 1)Los pernos conectadores, la losa de hormigón y la viga metálica se comportan linealmente. 2)En la posición deformada, tanto la losa de hormigón como la viga de acero tienen la misma curvatura y rotación. 3)Se desprecian los efectos de fricción y el despegue de la interfaz. 4)Los pernos conectadores se distribuyen uniformemente a lo largo de la viga mixta.
En esta sección se presentan las ecuaciones analíticas propuestas por Martínez y Ortiz [5] para el cálculo de las fuerzas de compresión en el hormigón, Nc (fig. 2A) en una sección transversal x, para tres casos de carga: 1)Nc,Q(x): una carga puntual Q en centro luz (fig. 2B); 2)Nc,q(x): una carga uniforme q en toda la viga (fig. 2C), y 3)Nc,P(x): una carga puntual P actuando en el centro de gravedad de la losa de hormigón en los extremos de la losa de hormigón armado (fig. 2D).
En estas ecuaciones, M(x) representa el momento flector en una sección transversal genérica x, Ec y Es corresponden con los módulos de elasticidad de la losa de hormigón y la viga de acero, AR e IR representan el área y la inercia de la sección mixta reducida, AcR e IcR, el área y la inercia reducida en el hormigón, As e Is, el área y la inercia de la viga de acero, hsc, la distancia entre los centroides de la losa de hormigón y la viga de acero, y acR y xq son coeficientes definidos como:
Estas ecuaciones analíticas, junto con las ecuaciones de la deformación vertical de la viga, fm, para los mismos casos de carga descritas en [5], se han utilizado en la sección 4 para validar los resultados del modelo propuesto.
3Descripción del modelo propuestoEl MEF descrito en este apartado para el análisis del comportamiento estructural de vigas mixtas con interacción imperfecta fue presentado en [10–12]. Este modelo es bidimensional, elástico y lineal y está compuesto por seis tipos de elementos tipo viga. A continuación se resumen las principales características de cada uno de estos elementos:
- -
Elementos tipo 1 (losa de hormigón). Estos elementos incluyen las propiedades mecánicas de la losa de hormigón armado en su centroide.
- -
Elementos tipo 2 (viga metálica). Estos elementos incluyen las propiedades mecánicas de la viga metálica en su centroide.
- -
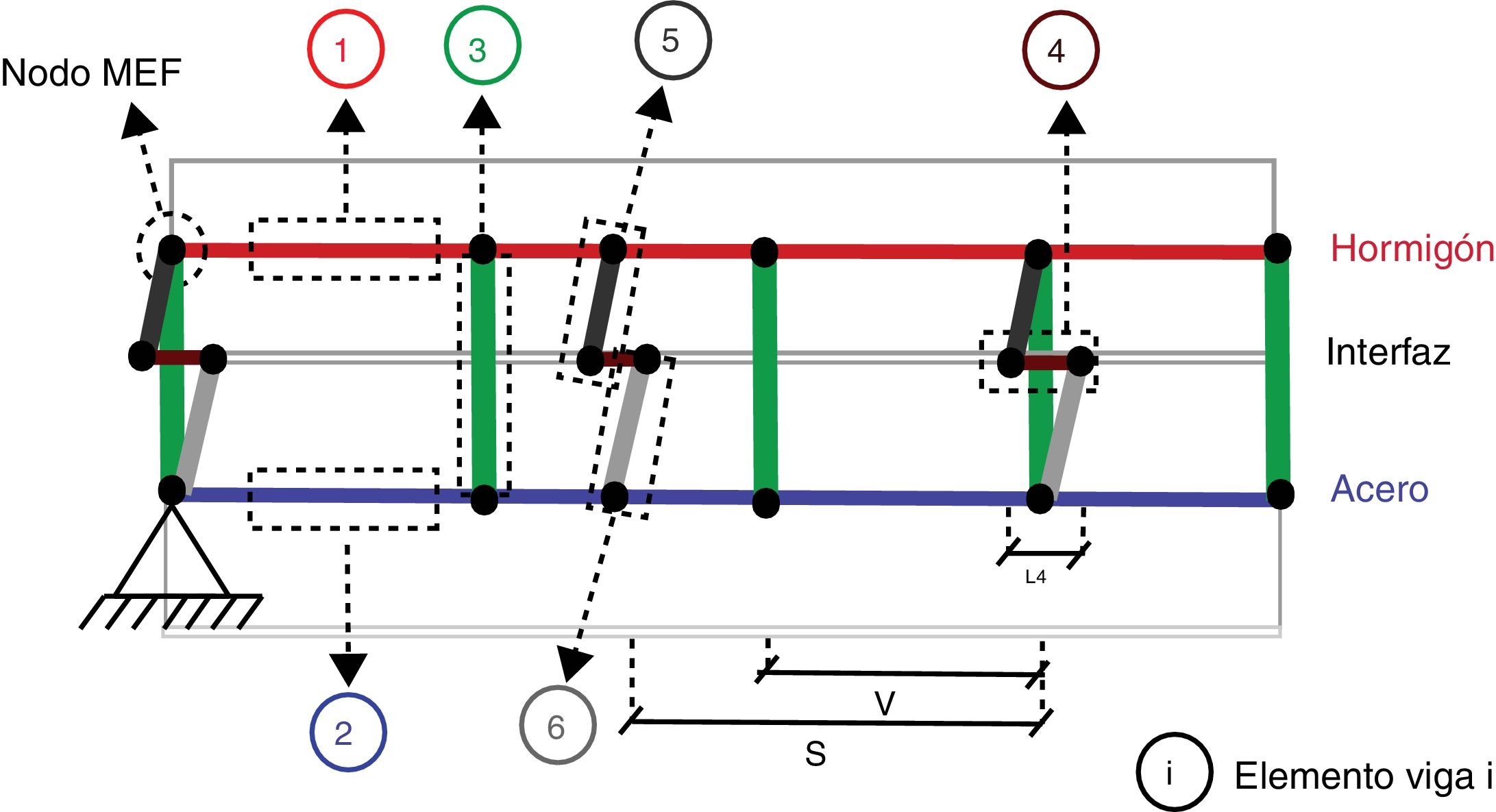
Elementos tipo 3 (conectores verticales). Estos elementos conectan verticalmente los nodos de las barras de hormigón y acero (nodos de los elementos tipo 1 y 2). Este elemento carece de rigidez a flexión y peso, cuenta con un área infinita y se puede distribuir uniformemente según una distancia V. Su principal objetivo es igualar las deformaciones verticales en los centroides de la viga metálica y la losa de hormigón a lo largo de la longitud de la viga. Siendo EcIc y EsIs las rigideces a flexión de las secciones parciales de hormigón y acero, y Mc(x) y Ms(x) los momentos flectores en dichas secciones parciales, esta condición se puede expresar matemáticamente como:
- -
Elementos tipo 4 (muelles conectadores). Estos elementos simulan el efecto de la rigidez kq de los conectadores por medio de muelles con rigidez axial (que carecen de rigidez a flexión) localizados en la interfaz. Siendo S la separación longitudinal entre los muelles, nq el número de conectadores en cada fila, sq la separación longitudinal de los conectadores, L4 una longitud arbitraria para el elemento tipo 4 y A4 un área arbitraria para el elemento tipo 4, el módulo de elasticidad de este elemento, E4, se puede determinar igualando la rigidez axial del elemento a la rigidez de los conectadores a partir de la siguiente ecuación:
- -
Elementos tipo 5 (elemento hormigón-interfaz). Estos elementos simulan la distancia entre el centroide de la losa de hormigón y la interfaz. Es por ello que conectan los nodos de las barras de hormigón con las de los muelles (esto es, los nodos de los elementos tipo 1 y 4). Estos elementos se consideran infinitamente rígidos a axil y a flexión. Para una distribución uniforme de los conectadores, estos elementos se pueden disponer con una separación S a lo largo de la viga. Siendo hc el espesor del hormigón, uc el desplazamiento horizontal en el nodo de la barra de hormigón (elemento tipo1) y αc la rotación en el mismo nodo, el elemento tipo 5 permite que se movilice el siguiente movimiento horizontal uc’ en la interfaz:
- -
Elementos tipo 6 (elemento acero-interfaz). Estos elementos simulan la distancia entre el centroide de la viga de acero y la interfaz. Es por ello que conectan los nodos de las barras de acero con las de los muelles (esto es, los nodos de los elementos tipo 2 y 4). Al igual que los elementos tipo5, cuentan con una infinita rigidez a axil y a flexión y se pueden disponer con una separación S a lo largo de la viga. Siendo hs el espesor de la viga de acero, us el desplazamiento horizontal en el nodo de la barra de acero (elemento tipo2) y αs la rotación en el mismo nodo, el elemento tipo 6 permite que se movilice el siguiente movimiento horizontal us’ en la interfaz:
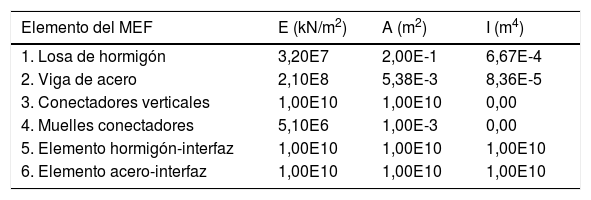
Las principales características de los diferentes tipos de elementos del MEF propuesto se resumen en la tabla 1. En esta tabla se utiliza el símbolo ∞ para indicar que el valor correspondiente es muy alto.
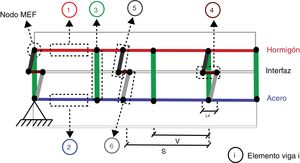
Tal y como se muestra en la figura 3, las condiciones de contorno del MEF se colocan en el centroide de la viga de acero. Esta figura incluye una propuesta de la distribución de los seis tipos de elementos que constituyen el modelo.
El análisis del MEF propuesto en cualquier programa de barras permite la obtención de resultados útiles para el diseño y análisis de vigas mixtas con interacción imperfecta. Entre estos resultados, cabe destacar: 1)Deformaciones de la viga mixta a lo largo de su eje. 2)Deslizamiento relativo en la interfaz. 3)Esfuerzos axiles y momentos flectores en los centroides del hormigón y el acero. 4)Fuerzas en los muelles que simulan la rigidez de la conexión. A partir de estos valores se puede obtener el rasante en la interfaz. 5)Reacciones en las condiciones de contorno.
4Aplicación del modelo propuestoEn esta sección se presenta la aplicación del MEF propuesto a dos vigas mixtas. La primera estructura (ejemplo1) responde a una viga biapoyada, mientras que la segunda (ejemplo2) responde a una viga continua de tres vanos.
4.1Ejemplo 1 (viga biapoyada)La estructura analizada en este ejemplo responde a una viga biapoyada de 4,5m de longitud. Esta estructura incluye una losa de hormigón armado de 1m de anchura y 0,2m de canto conectada a un perfil IPE300. Los módulos de elasticidad del hormigón, Ec, y del acero, Es, tienen un valor de 3,2E7kN/m2 y 2,1E8kN/m2, respectivamente. La conexión entre ambos materiales se realiza por medio de dos filas de pernos conectadores dispuestas cada 30cm (nq=2, sq=30cm). La rigidez de cada conectador, kq, se fija en 170.000kN/m. Para este valor se tiene una rigidez de la conexión Kq=(nq·kq)/sq de 2,26E6kN/m2. El MEF propuesto incluye una separación de 30cm para los conectadores verticales y los muelles (S=V=30cm). De esta forma se obtiene un modelo formado por 45 nodos y 90 elementos. El área y la longitud de los muelles en el modelo (A4 y L4) se han fijado con valores arbitrarios de 1E-3m2 y 0,015m, respectivamente.
El módulo de Young, E, el área, A, y la inercia, I, de cada uno de los elementos del modelo se resumen en la tabla 2. Cabe destacar que el módulo de Young de los muelles extremos es la mitad del valor presentado en la tabla 2, dado que su área tributaria es la mitad de la de los muelles interiores.
Características de los elementos del MEF propuesto en los ejemplos 1 y 2
| Elemento del MEF | E (kN/m2) | A (m2) | I (m4) |
|---|---|---|---|
| 1. Losa de hormigón | 3,20E7 | 2,00E-1 | 6,67E-4 |
| 2. Viga de acero | 2,10E8 | 5,38E-3 | 8,36E-5 |
| 3. Conectadores verticales | 1,00E10 | 1,00E10 | 0,00 |
| 4. Muelles conectadores | 5,10E6 | 1,00E-3 | 0,00 |
| 5. Elemento hormigón-interfaz | 1,00E10 | 1,00E10 | 1,00E10 |
| 6. Elemento acero-interfaz | 1,00E10 | 1,00E10 | 1,00E10 |
Para realizar la comparación con las ecuaciones analíticas se han estudiado tres casos de carga: 1)carga concentrada Q de 100kN en centro luz (fig. 2B); 2)carga uniforme q de 10kN/m (fig. 2C), y 3)dos fuerzas puntuales P de 100kN en los extremos de la losa (fig. 2D).
4.1.1Comparación con las ecuaciones analíticasEn esta sección se comparan los resultados de las ecuaciones analíticas descritas en la sección2 con los resultados del MEF presentado en el apartado anterior. Esta comparación está basada en dos parámetros: 1)la fuerza de compresión en la losa de hormigón armado en centro luz, Ncm, y 2)la deformación vertical de la viga en centro luz, fm.
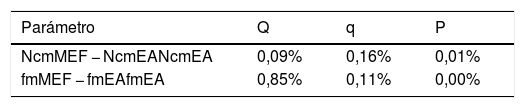
El valor absoluto de las diferencias porcentuales entre las Ecuaciones Analíticas (EA) y el MEF para los tres casos de carga analizados (Q, q y P) se resume en la tabla 3.
Los resultados de esta tabla confirman que el comportamiento de la viga biapoyada obtenido mediante el MEF propuesto está en absoluta sintonía con el derivado de las ecuaciones analíticas para los tres casos de carga estudiados.
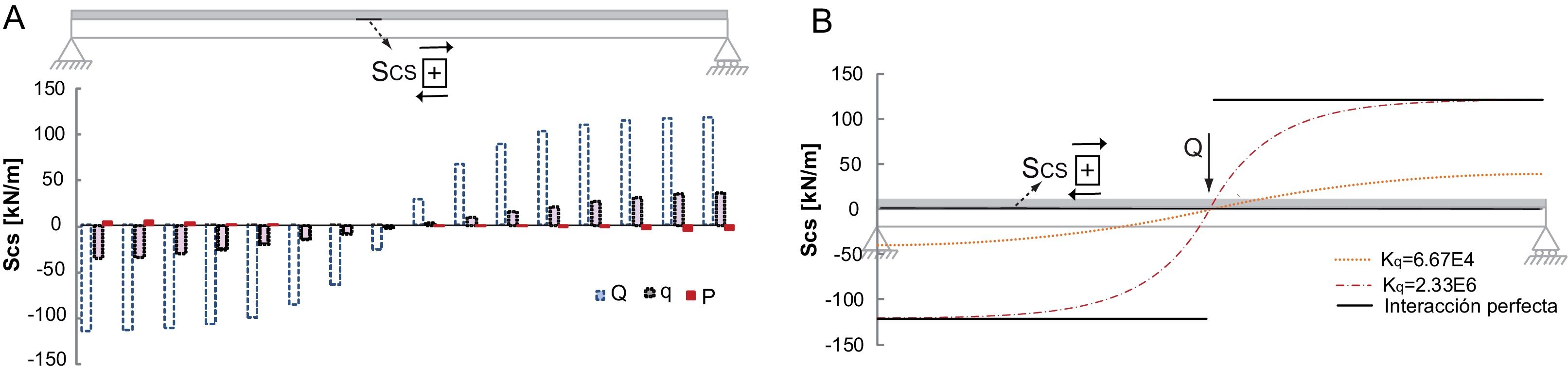
4.1.2Resultados del modelo de elementos finitosLa figura 4 muestra un resumen de los resultados del MEF. Por un lado, la figura 4A presenta los rasantes en la interfaz, SCS, para los tres casos de carga analizados. Siendo sq el espaciamiento entre los muelles, el esfuerzo rasante se puede obtener directamente a partir del incremento de fuerzas en estos elementos, ΔF (elemento tipo 4), mediante la siguiente ecuación:
Los valores máximos de los rasantes de la figura 4A (116,21kN/m) corresponden al caso de carga Q en la posición x=0m, en la zona cercana a los apoyos.
El papel de la rigidez de la conexión en el rasante se analiza en la figura 4B. Esta figura presenta una comparación de los valores obtenidos para dos rigideces de la conexión Kq (6,67E4 y 2,33E6kN/m2) con los resultados de la interacción perfecta, para el caso de una carga puntual Q. Esta comparación muestra que cuanto mayor es la rigidez de la conexión, mayor es el valor absoluto del rasante SCS y más similar es el valor máximo obtenido al de la interacción perfecta. Las mayores diferencias entre la interacción perfecta e imperfecta se encuentran en centro luz, dado que la hipótesis de interacción perfecta no puede predecir con precisión los rasantes en esta localización.
4.2Ejemplo 2 (viga continua)En esta sección se analiza una viga continua de tres vanos (3,6+4,5+3,6m). Esta viga cuenta con las mismas propiedades mecánicas que la viga descrita en el ejemplo1, esto es, una losa de hormigón armado de 1m de anchura y 0,2m de canto conectada a un IPE300. El modelo incluye un espaciamiento de 30cm para los muelles y 90cm para los conectores verticales (S=30cm y V=90cm). Estas hipótesis conducen a un MEF compuesto por 117 nodos y 208 elementos.
En la literatura no se han encontrado ecuaciones analíticas para estructuras hiperestáticas. Por esta razón se ha considerado un MEF con un reducido espaciamiento (2,5cm) tanto para los conectores verticales como para los muelles (V y S), con el objetivo de representar los resultados de las ecuaciones analíticas. Este modelo consta de 1.404 nodos y 2.808 elementos, y se ha denominado EA.
Se han analizado los mismos casos de carga (Q, q y P) descritos en el ejemplo anterior. Para cada uno de estos casos de carga se han obtenido las fuerzas de compresión en la losa de hormigón armado en centro luz, y las deformaciones verticales en la misma posición, fm.
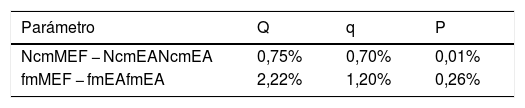
4.2.1ComparaciónEn la tabla 4 se presenta una comparación de los resultados del MEF y las EA obtenidas de forma simplificada para estructuras hiperestáticas a partir de las ecuaciones de las estructuras isostáticas presentadas en la literatura. Esta tabla incluye las diferencias porcentuales en términos de Ncm y fm para los casos de carga Q, q y P.
El análisis de la tabla 4 muestra que las diferencias son prácticamente despreciables. Las mayores diferencias se encuentran para el caso de la carga Q. Además, las diferencias en la flecha fm son mayores que en Ncm.
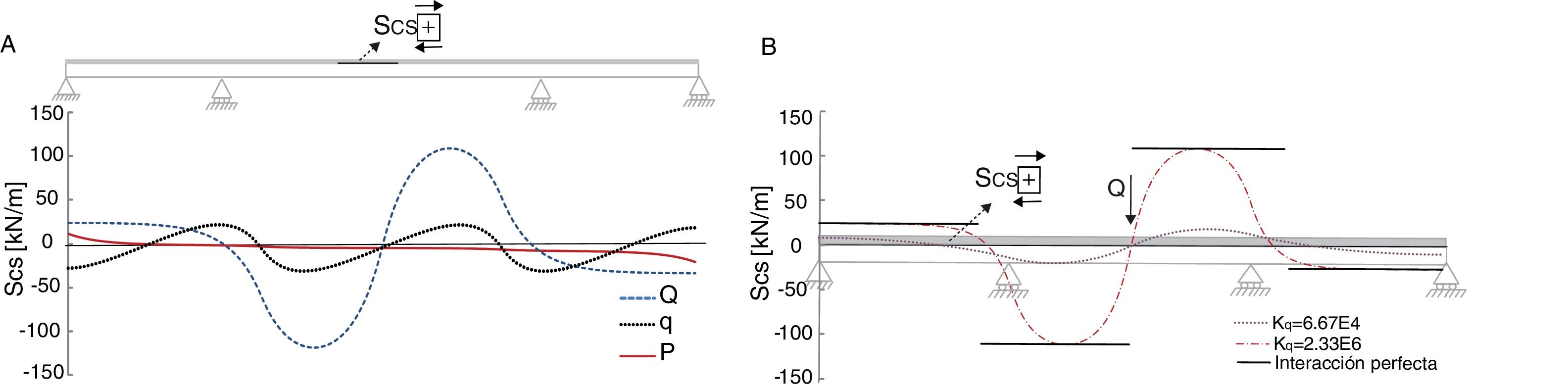
4.2.2Resultados del modelo de elementos finitosLa figura 5A presenta la distribución del rasante en la interfaz, SCS, calculado mediante la ecuación10, para cada caso de carga. Esta figura muestra que los mayores valores del rasante se localizan en las proximidades de los apoyos intermedios para Q y q.
La figura 5B presenta una comparación del rasante SCS en el caso de carga Q para dos rigideces de la conexión Kq (6,67E4 y 2,33E6kN/m2) con los resultados de la interacción perfecta. Esta figura muestra que cuanto mayor es la rigidez de la conexión, más se aproximan los resultados obtenidos a los de la interacción perfecta. Cabe destacar que las mayores diferencias entre las conexiones con conexión perfecta e imperfecta se encuentran en las proximidades de los apoyos intermedios del vano central. Debido a estas diferencias, la integral de los rasantes a lo largo de la viga obtenida en los modelos con interacción imperfecta es menor que la obtenida cuando se considera interacción perfecta.
5Futuras líneas de investigaciónHasta el momento se ha descrito el modelo reducido como respuesta a los problemas que surgen al tratar con vigas mixtas analíticamente —por ser un método poco intuitivo, complejo en su formulación y limitado a ciertos tipos de carga en estructuras isostáticas— o al modelizarlas usando MEF bidimensionales o tridimensionales —por su complejidad en la modelización y en la interpretación de resultados, que requiere una debida integración del campo de tensiones. En los párrafos anteriores se ha comparado el ajuste del modelo a la formulación analítica para los casos de carga en que la ecuación diferencial queda resuelta. Sin embargo, la formulación analítica es limitada y la universalidad del modelo ha de contrastarse con todo tipo de estructuras.
Para ello se ha previsto un programa de ensayos numéricos de vigas mixtas de hormigón y acero modelizadas con elementos finitos bidimensionales en las que la conexión sea modelizada con elementos de contacto. Con objeto de poder reproducir tanto la interacción imperfecta como la perfecta, se variará la rigidez de estos elementos. Así, se modelizarán vigas continuas y vigas de canto variable. Debido a las características inherentes a la formulación de los EF, la deformación por cortante de las estructuras estará modelizada.
Estas estructuras serán asimismo modelizadas con el modelo propuesto, verificando la capacidad de predicción de las deformaciones y de los distintos esfuerzos, tanto externos (reacciones en apoyos) como internos (axil, momento y cortante en el hormigón y en el acero). El modelo permitirá asimismo verificar no solo la capacidad para simular las deformaciones de cortante, sino también la capacidad de reproducir el comportamiento de las vigas continuas y de canto variable, tanto con interacción perfecta como imperfecta, así como la influencia de una distribución no uniforme de los conectadores a lo largo de la viga. Todos estos casos no pueden hoy en día resolverse con la formulación analítica.
Otra cuestión relevante en el comportamiento de las estructuras mixtas con interacción imperfecta es la posibilidad de que se ocasionen deslizamientos relativos importantes, lo que puede llevar a la plastificación de los conectadores y a una eventual redistribución de tensiones. En este sentido, también se modelizarán los conectadores de acuerdo con [13], y se compararán los resultados con los ensayos presentados en [14–16].
6ConclusionesEn este artículo se propone un modelo de elementos finitos (MEF) para simular el comportamiento de las vigas mixtas con interacción imperfecta. Este modelo incluye seis tipos de elementos tipo viga: 1)losa de hormigón; 2)viga de acero; 3)conector vertical; 4)muelle elástico en la interfaz; 5)elemento hormigón-interfaz, y 6)elemento acero-interfaz. Las principales ventajas que presenta este modelo respecto a las ecuaciones analíticas y los modelos de elementos finitos tridimensionales son las siguientes: 1) Intuitividad, dado que los diferentes elementos del modelo reproducen de manera ingenieril y sencilla el comportamiento de las vigas mixtas. 2)Aplicabilidad, ya que el método proporciona información útil para el trabajo de diseño. 3)Versatilidad, al permitir el análisis de cualquier distribución no uniforme de pernos conectadores, cualquier caso de carga y cualquier geometría de la viga mixta con cualquier grado de interacción, tanto para estructuras isostáticas como hiperestáticas. 4)Fácil construcción del modelo, al contar con una geometría repetitiva fácilmente programable con algoritmos de pre-procesamiento. 5)Fácil generación de resultados, al poder reproducir los mismos con cualquier programa sencillo de barras.
Para validar la simulación de la metodología propuesta se han analizado dos ejemplos (una viga biapoyada y una viga continua) sometidos a tres casos de carga diferentes. Los resultados de cada una de estas estructuras muestran una buena correlación con las ecuaciones analíticas presentadas en la literatura y los modelos equivalentes. Los resultados muestran también que los rasantes a lo largo de la viga son menores en las estructuras con interacción imperfecta que perfecta.
Los autores agradecen la financiación proporcionada por el Ministerio de Economía y Competitividad (BIA2013-47290-R) y los fondos FEDER. Parte de este trabajo se realizó mediante un acuerdo de colaboración entre Tongji University (China) y la Universitat Politècnica de Catalunya, BarcelonaTech. Este acuerdo incluía un intercambio de personal académico financiado por el Gobierno Chino. También se agradece la subvención del programa High End Foreign Experts del Gobierno Chino