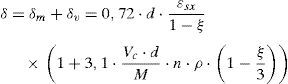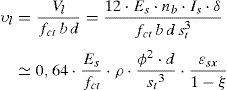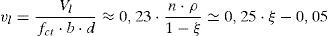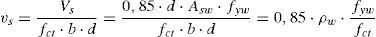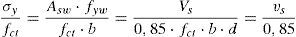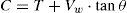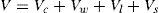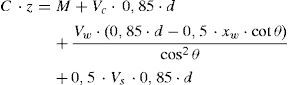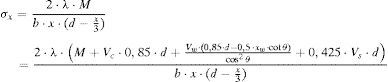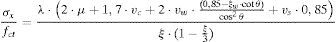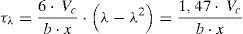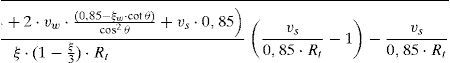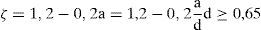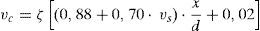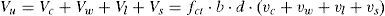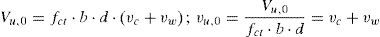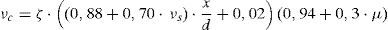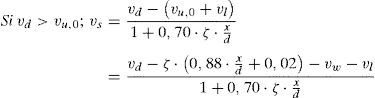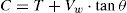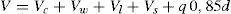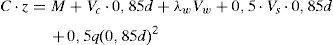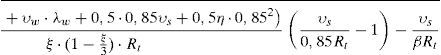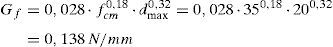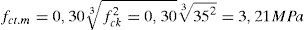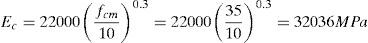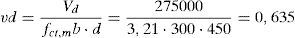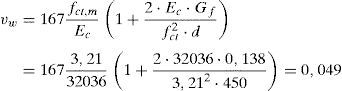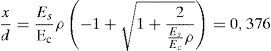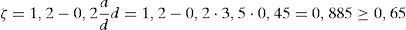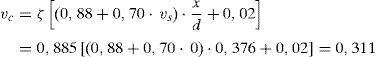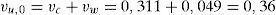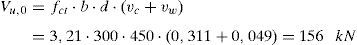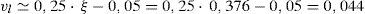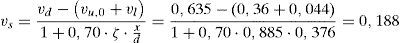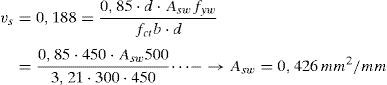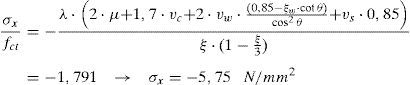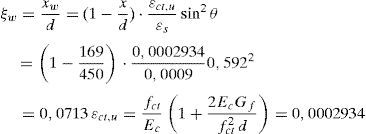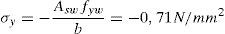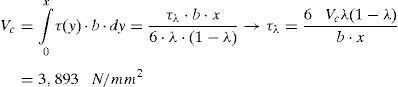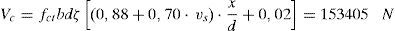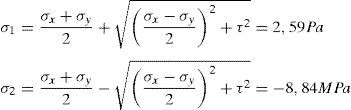Se presenta un modelo mecánico para la predicción de la resistencia a cortante-flexión de vigas esbeltas de hormigón armado sometidas a cargas puntuales y/o repartidas. El modelo incorpora las contribuciones a la resistencia a cortante de la cabeza comprimida, del alma fisurada y de las armaduras longitudinales y transversales. Se considera que la rotura tiene lugar en la cabeza comprimida no fisurada de hormigón, sometida a un estado biaxial de tensiones, cuando se alcanza la envolvente de Kupfer, habiendo plastificado las armaduras transversales. Basándose en consideraciones de equilibrio y en una distribución de tensiones en ELU para la cabeza comprimida, se proponen ecuaciones sencillas y directas para dimensionamiento y comprobación. Las predicciones del modelo se han comparado con más de 1300 ensayos a cortante de vigas, obteniéndose muy buenos resultados. El modelo proporciona una explicación física del comportamiento a cortante, lo que junto a su sencillez y precisión, le convierte en una herramienta muy útil para el proyecto basado en prestaciones.
A mechanical model is presented for shear-flexural strength of slender reinforced concrete beams under concentrated or distributed loads. The model incorporates the shear transferred by the un-cracked concrete head, by the cracked web and by the longitudinal and transverse reinforcements. Failure is assumed to occur at the un-cracked concrete zone, subjected to a biaxial stress state, when the Kupfer failure envelope is reached and the stirrups are yielded. A general procedure and simplified direct design equations are derived taking into account equilibrium and a given stress distribution at ultimate limit states (ULS). The model predictions have been compared with the results of more than 1300 tests performed on simply supported beams, having obtained very good agreement. Because of the simplicity, accuracy, and the physical insight of the problem provided by the model, it may be very useful for rational performance-based design of concrete structures in practice.
luz a cortante
anchura de la sección transversal
canto útil de la sección transversal
tamaño máximo del árido
resistencia a compresión uniaxial del hormigón
resistencia característica a compresión del hormigón ensayado en probeta cilíndrica
valor medio de la resistencia a compresión del hormigón ensayado en probeta cilíndrica
resistencia a tracción uniaxial del hormigón
valor medio de la resistencia a tracción del hormigón
límite elástico de la armadura a cortante
canto total de la sección transversal
longitud de la fisura
longitud a lo largo de la fisura en donde se extienden las tensiones de tracción
coeficiente de equivalencia (Es/Ec)
número de barras de refuerzo de la armadura longitudinal
coordenada longitudinal de la viga medida desde el eje del apoyo
coordenada de la sección donde se inicia la fisura crítica
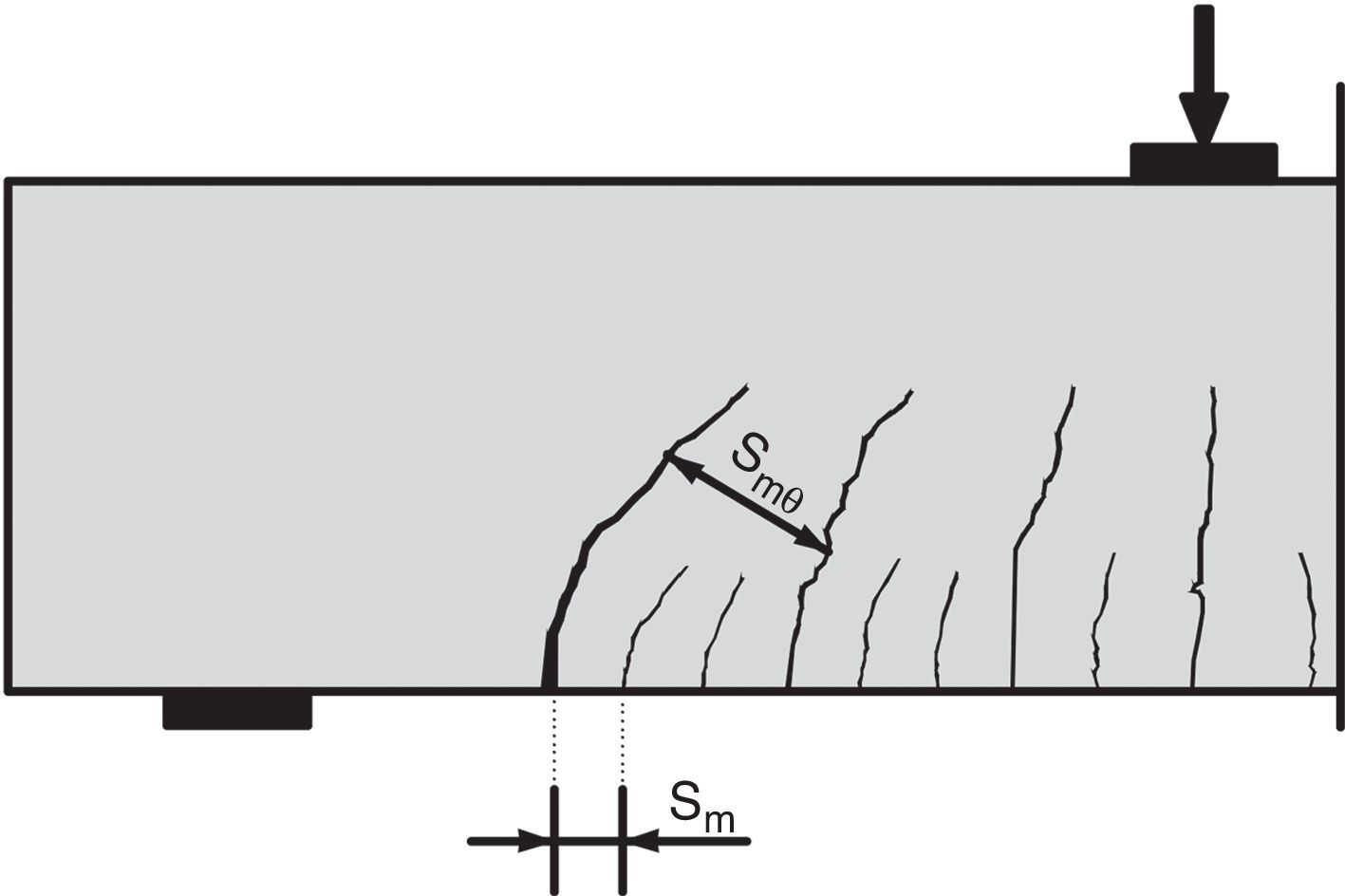
separación media de las fisuras diagonales
separación longitudinal de la armadura a cortante
coordenada longitudinal de la sección crítica a cortante
cortante adimensional resistido por la cabeza comprimida de hormigón
cortante adimensional de cálculo
cortante adimensional resistido por la armadura longitudinal
cortante adimensional resistido por la armadura transversal
esfuerzo cortante adimensional que agota una viga
esfuerzo cortante adimensional de vigas y losas unidireccionales sin armadura transversal
cortante adimensional resistido a través de la fisura
ancho de fisura
ancho máximo de fisura
profundidad del eje neutro
proyección vertical de lw
coordenada vertical medida desde la fibra superior de la sección transversal de hormigón
brazo mecánico de las fuerzas internas
área de la armadura longitudinal
área por unidad de longitud de la armadura transversal
fuerza de compresión en la cabeza comprimida de la viga
módulo de elasticidad del hormigón
módulo de elasticidad del acero
módulo de deformación a cortante de la cabeza comprimida de hormigón
energía de fractura del hormigón
módulo de inercia de una barra de refuerzo longitudinal
constante
momento flector
momento flector de fisuración
factor reductor de la resistencia a tracción por efecto de las compresiones en la dirección perpendicular
fuerza de compresión en la biela
fuerza de tracción en la armadura longitudinal
esfuerzo cortante
cortante resistido por la cabeza comprimida de hormigón
esfuerzo cortante de cálculo
valor experimental del esfuerzo cortante de rotura
cortante resistido por la armadura longitudinal
valor predicho del esfuerzo de cortante de rotura
cortante resistido por la armadura transversal
resistencia a cortante
resistencia a cortante de vigas y losas unidireccionales sin armadura transversal
cortante resistido a través de la fisura
ángulo de inclinación de la armadura transversal o de los tirantes
componente vertical de la abertura de la fisura inclinada
deslizamiento en la dirección vertical debido a la deformación de cortante de la cabeza comprimida
diámetro de la armadura de refuerzo longitudinal
deformación del hormigón al inicio de la macro-fisuración a tracción
deformación máxima a tracción correspondiente a tensión residual nula
deformación de la armadura longitudinal
deformación de la armadura longitudinal perpendicular a la fisura inclinada
deformación axial de la armadura longitudinal
factor de efecto tamaño
distorsión
distancia vertical desde el eje neutro
ángulo de inclinación de la biela
momento flector adimensional (M/(fct·b·d))
momento flector de fisuración adimensional (Mcr/(fct·b·d))
profundidad adimensional del eje neutro (x/d)
proyección vertical adimensional de lw(xw/d)
cuantía de armadura longitudinal
cuantía de armadura transversal
tensiones principales
tensión de tracción en la armadura transversal
tensión normal en la dirección longitudinal
tensión normal máxima en la dirección longitudinal
tensión normal en la dirección transversal
tensión normal a la fisura inclinada en el alma
tensión tangencial
tensión tangencial máxima
tensión tangencial para y=λ·x
La complejidad del comportamiento frente a esfuerzo cortante es enorme, debido, entre otros aspectos, a la anisotropía generada por la fisuración inclinada, a los distintos mecanismos resistentes que se generan, a la adherencia imperfecta entre hormigón y armaduras y a la fragilidad de la rotura, que conducen, entre otros, al efecto tamaño.
A fin de comprender este comportamiento tan complejo se han realizado numerosas investigaciones experimentales cuyas referencias pueden encontrase en [1,2]. Por otra parte se han desarrollado modelos numéricos sofisticados para predecir la resistencia a cortante [3–10], si bien su utilización en la ingeniería cotidiana es escasa debido al esfuerzo y coste computacional requeridos. Por ello, en su momento se desarrollaron expresiones semi-empíricas, ajustadas a resultados experimentales, algunas de las cuales fueron incluidas en códigos estructurales como el Eurocódigo 2 (EC2) [11], o el ACI-318-08 [12]. Sin embargo, estas expresiones no cubren algunos casos que se dan en la práctica o no tienen en cuenta la influencia de diversos aspectos, como la forma de la sección [13], debiendo ser adaptadas de forma artificial. Por otra parte se han desarrollado nuevos materiales (hormigones de alta resistencia, auto-compactantes, con fibras, reciclados, armaduras de materiales compuestos…), para los cuales no fueron derivadas tales expresiones. Lo cierto es que al predecir los resultados de ensayos sobre vigas biapoyadas de hormigón convencional, se obtienen dispersiones considerables y valores, en general, muy conservadores. Además, estas formulaciones no proporcionan, en general, información suficiente sobre la física del problema, que permita resolver racionalmente casos no estandarizados. A título de ejemplo se plantean aquí algunas cuestiones que no encuentran una respuesta específica mediante los planteamientos normativos considerados (EHE-08 [14], el EC2 [11] o el Código ACI-318-08 [12]):
- -
¿Es igual la contribución del cortante resistido por el hormigón en una viga con armadura transversal que sin ella? ¿Afectan a esta contribución por igual un esfuerzo axil de compresión que otro de tracción?
- -
¿Funcionan igual a cortante las zonas de apoyos extremos y las de apoyos intermedios en una viga continua?
- -
¿Resiste igual cortante una sección en T que una sección rectangular con igual canto, cuantía de armadura longitudinal y transversal e igual ancho del alma?
- -
¿Cómo influye el tipo de carga (concentrada o repartida) en la resistencia a cortante?
- -
¿Qué papel juegan la resistencia a tracción o la retracción del hormigón en la respuesta a cortante?
- -
En piezas pretensadas, ¿qué influencia tiene la excentricidad del pretensado en la resistencia a cortante? ¿Qué canto útil hay que tomar para el cálculo de Vcu o Vu2 según EHE-08 [14] y el EC2 [11]?
Estas y otras muchas cuestiones ponen de manifiesto la necesidad de disponer de modelos conceptuales que, además de predecir correctamente los resultados experimentales, tengan sentido físico y permitan adaptarse a nuevas situaciones. Ciertamente, existen modelos de este tipo, si bien las expresiones por ellos proporcionadas no son lo suficientemente prácticas de cara al proyecto cotidiano o suficientemente generales. Entre ellos cabe destacar el modelo de Reineck [15], los modelos simplificados basados en la teoría del campo modificado de compresiones [16], en la teoría de la fisura crítica [17], la analogía del ensayo de tracción indirecta [18], las teorías basadas en la resistencia de la cabeza comprimida [19–21], métodos basados en la plasticidad [22] e incluso modelos que incorporan el efecto de la fatiga [23]. Todos estos métodos predicen con razonable aproximación la carga última, a pesar de estar basados en mecanismos resistentes distintos y de utilizar expresiones distintas con parámetros no siempre iguales. Ello sugiere que en función del nivel de carga, la contribución de cada mecanismo resistente puede ser distinta, produciéndose, ante la disminución de capacidad de un mecanismo, redistribuciones súbitas de tensiones hacia el resto.
En este artículo se presenta un modelo de resistencia a cortante-flexión de elementos esbeltos de hormigón armado, basado en la mecánica de las estructuras de hormigón y en la observación experimental del comportamiento de vigas bajo carga creciente hasta rotura. El modelo es válido para vigas biapoyadas, con sección rectangular, sin y con armadura de cortante, sometidas a cargas puntuales y/o repartidas y proporciona expresiones finales muy simples para el diseño y comprobación de estructuras. En este artículo se presentan, así mismo, las posibilidades de extensión del modelo a diferentes situaciones de carga, apoyos, geometría seccional y tipos de hormigón y armaduras, como es el caso, ya estudiado por los autores, de vigas de hormigón armadas con barras de polímeros reforzados con fibras (FRP) [24], vigas con sección en T, vigas continuas, vigas pretensadas, vigas con canto constante o con hormigón reforzado con fibras.
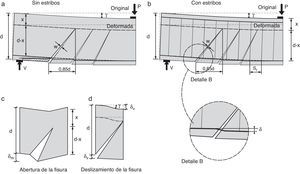
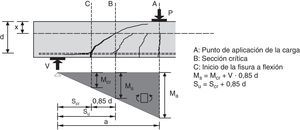
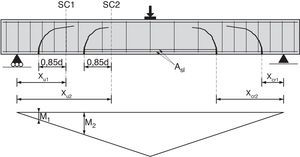
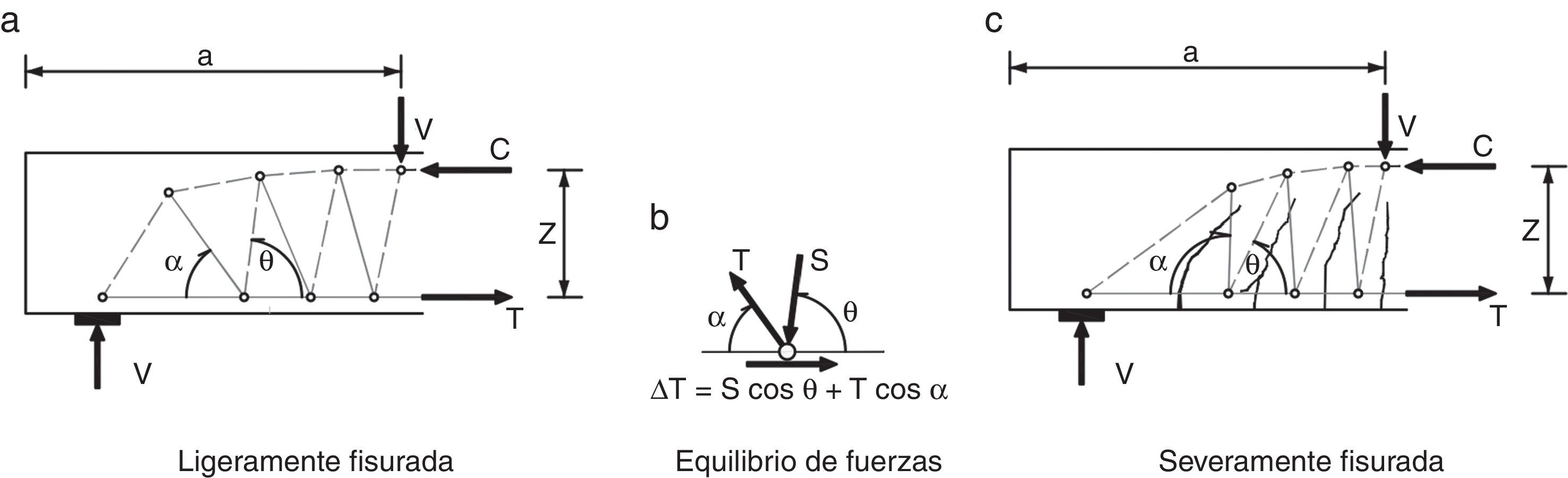
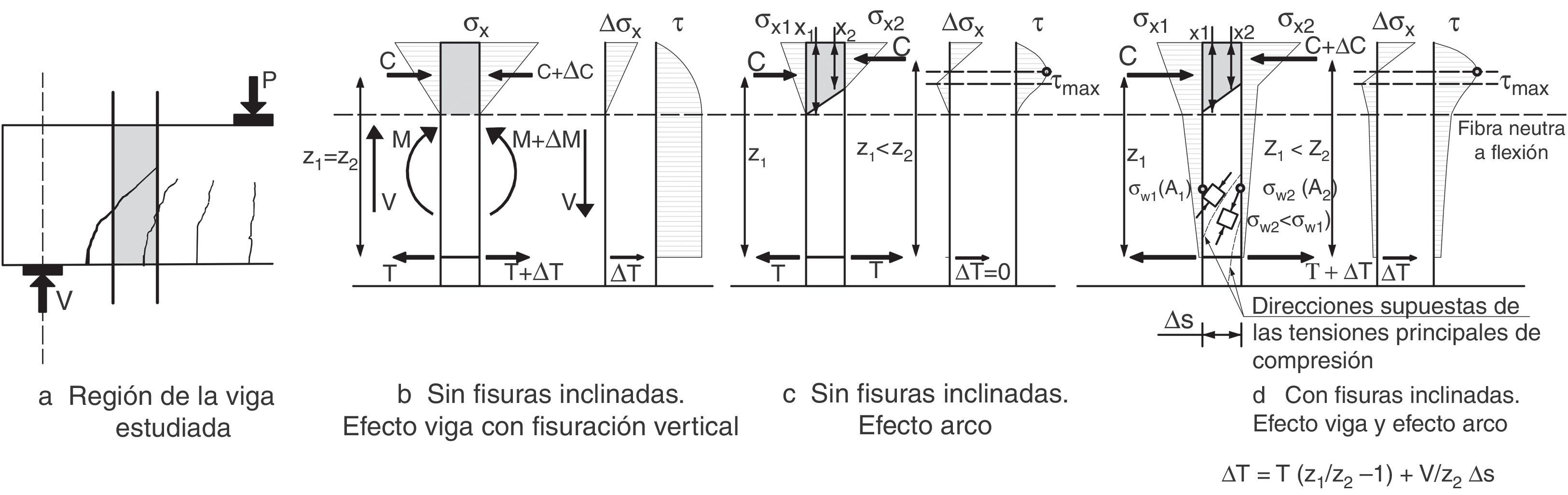
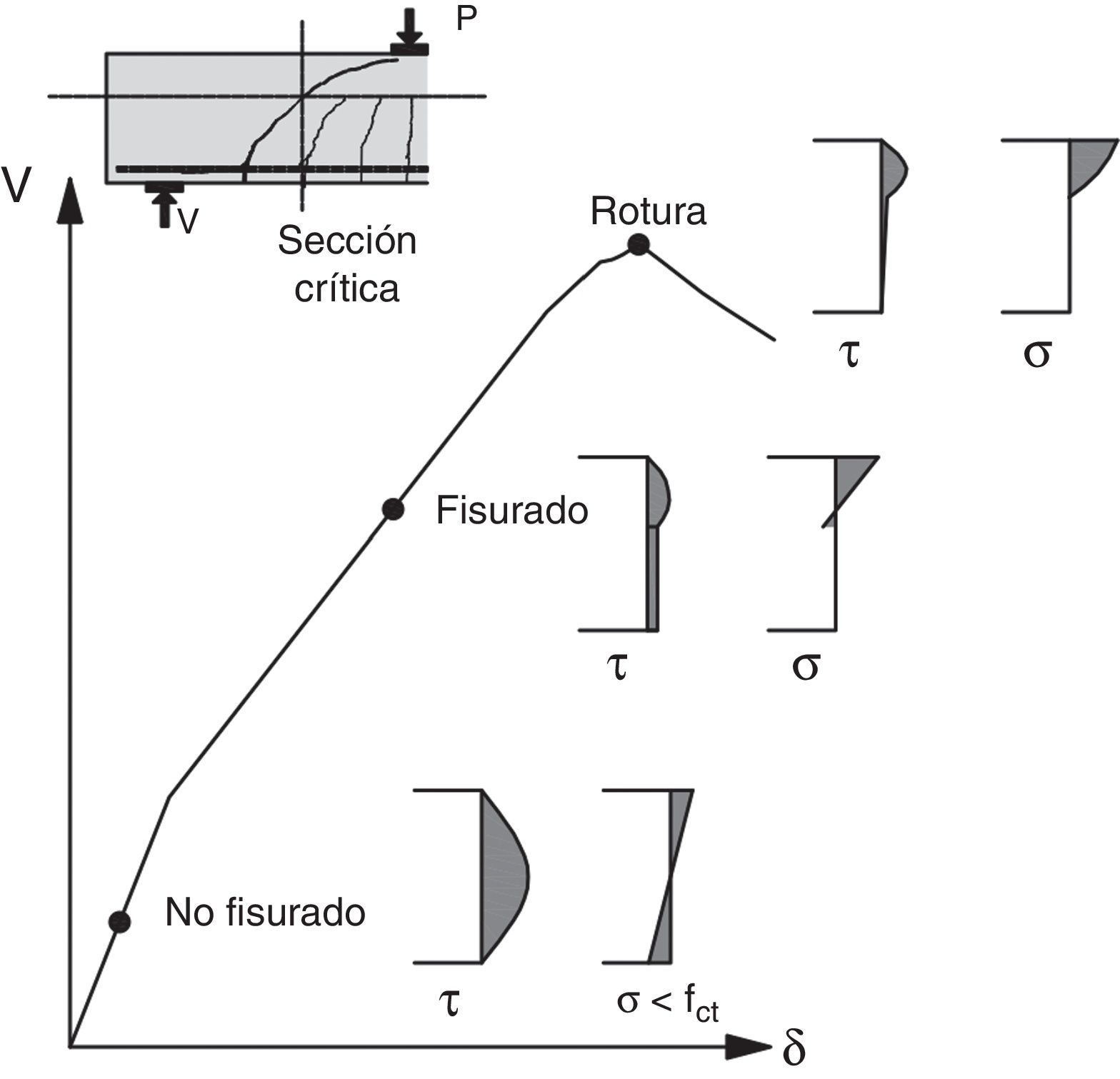
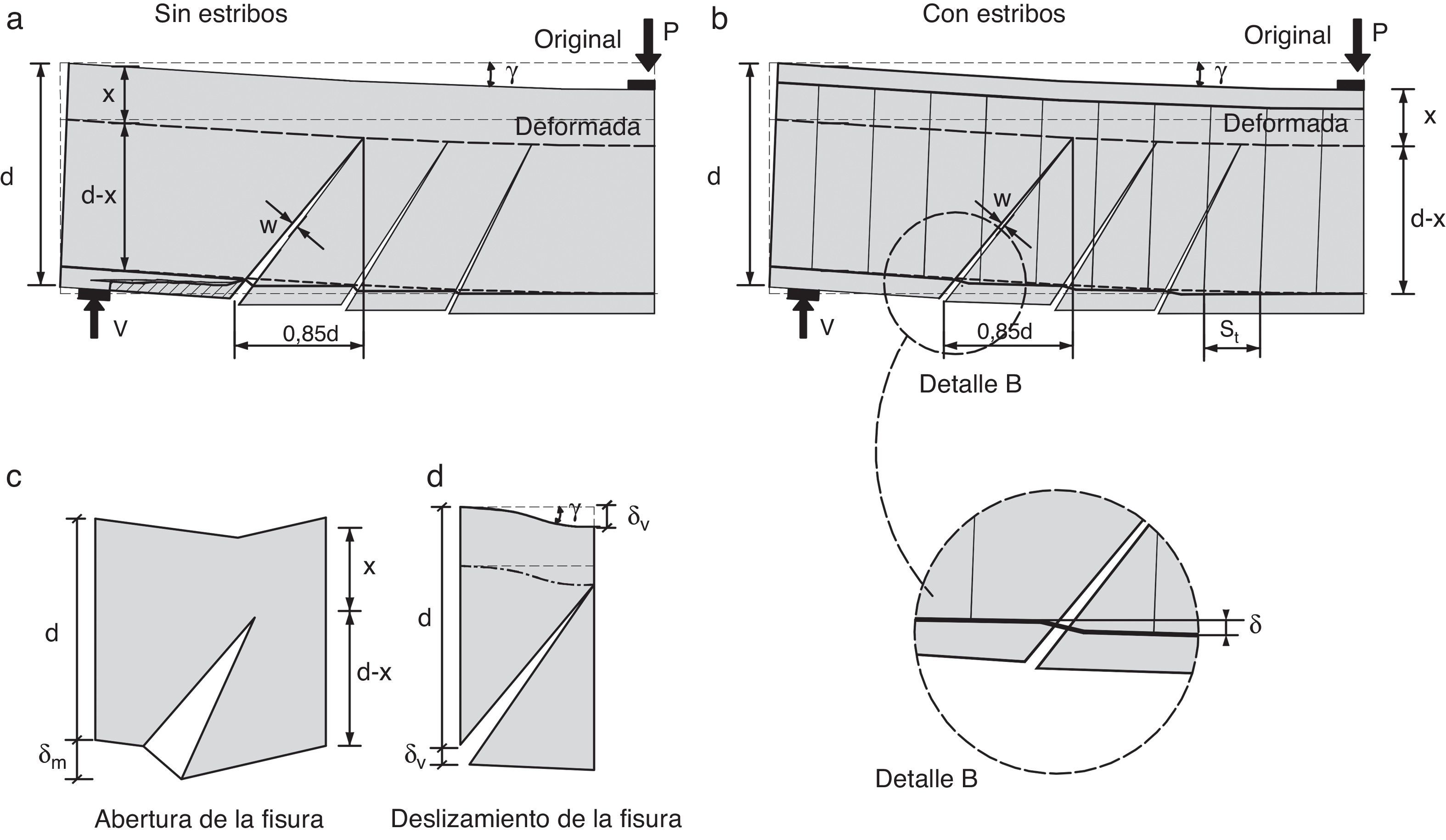
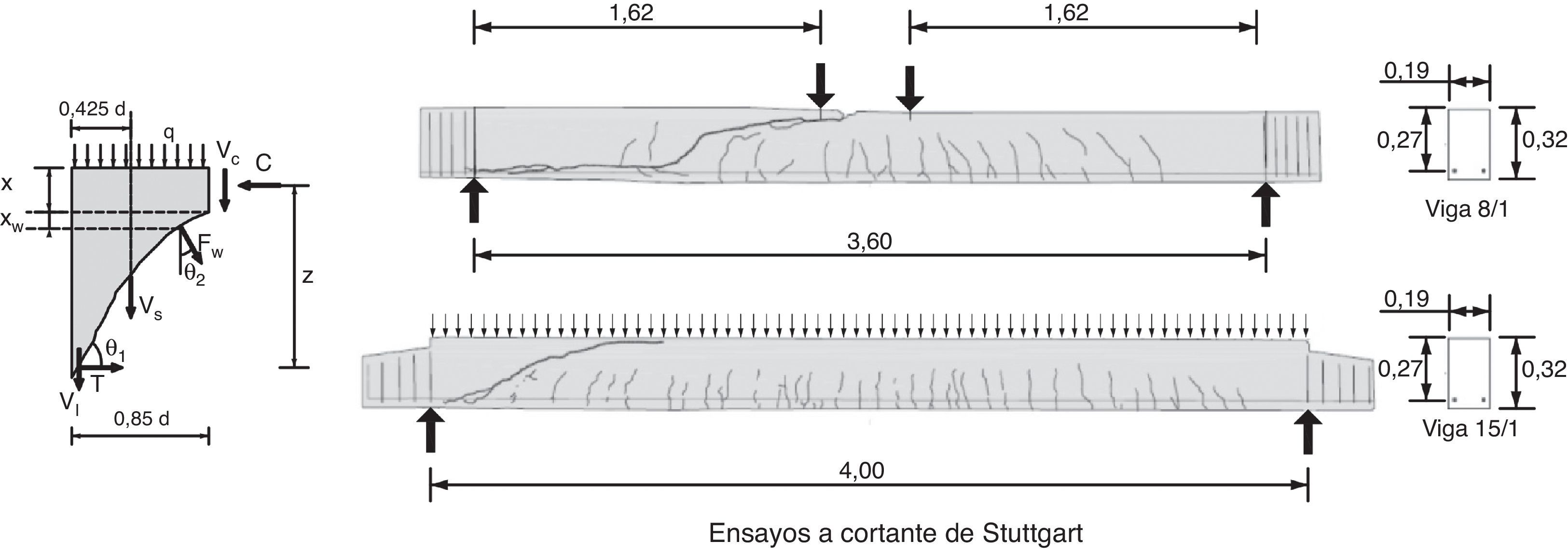
2PRINCIPIOS DEL MODELO PROPUESTO2.1Comportamiento observado y mecanismos resistentes movilizadosEn la mayoría de vigas solicitadas a cortante bajo cargas puntuales, en las que la relación a/d es mayor igual a 2,5, siendo a la luz de cortante y d el canto útil, las fisuras de cortante se originan a partir de fisuras de flexión. Estas fisuras nacen en la cara traccionada, perpendiculares al eje de la viga, y al penetrar en el alma se inclinan como consecuencia de la presencia de tensiones tangenciales. Conforme la carga aumenta, el daño se concentra en una fisura (llamada fisura crítica) la cual se desarrolla hasta alcanzar aproximadamente el eje neutro en flexión de la sección fisurada. Esta situación es estable hasta que, con el aumento de la carga, se desarrolla una segunda rama que conecta el final de la primera rama con el punto de aplicación de la carga. Además, la armadura longitudinal puede sufrir deslizamientos respecto del hormigón, fruto de las fuertes tensiones tangenciales, produciendo fisuras longitudinales cerca de su zona de anclaje (fig. 1).
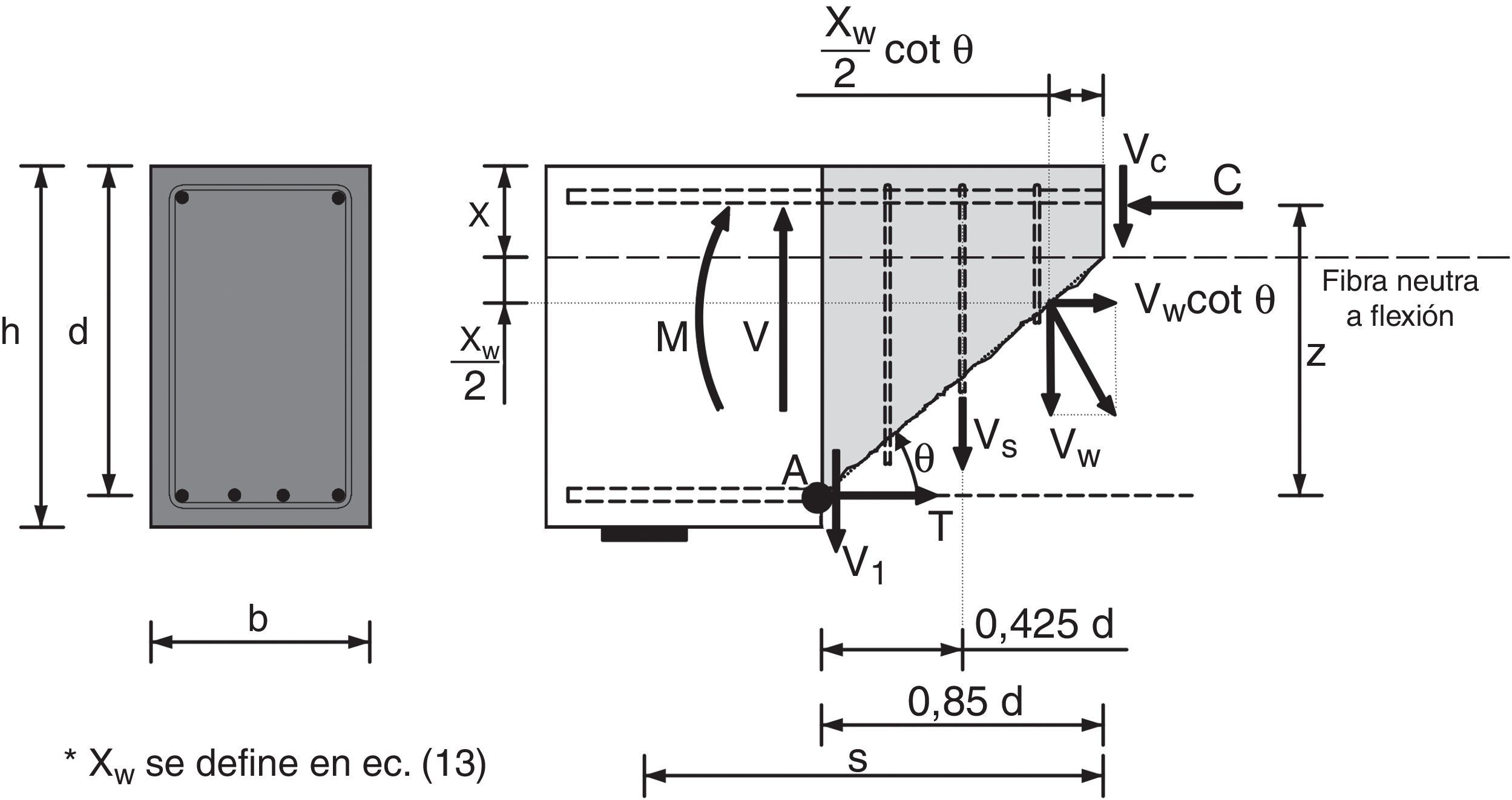
Se acepta generalmente que la resistencia a cortante de una viga consta de las siguientes contribuciones: 1) la cabeza de compresión, cuya capacidad para transferir tensiones tangenciales aumenta con el nivel de compresión axial; 2) el alma fisurada, a lo largo de cuyas fisuras se resisten tensiones tangenciales por fricción y tensiones residuales de tracción cuyas componentes verticales contribuyen a resistir cortante pero que van disminuyendo conforme la fisura crece en anchura; 3) la armadura longitudinal, capaz de resistir una cierta cizalladura (efecto pasador), pero cuya capacidad está limitada por la resistencia al empuje al vacío del recubrimiento, siendo mayor para el caso de piezas con armadura transversal; 4) la armadura transversal mediante su contribución directa al equilibrio de fuerzas verticales, pero también al confinar verticalmente la cabeza de compresión y al limitar el ancho de fisuras, aumentando así la resistencia del alma.
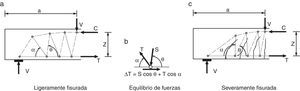
De forma simplificada, para vigas sin armadura de cortante se puede suponer que el mecanismo resistente puede asimilarse a una celosía formada por el cordón superior (cabeza de compresión de hormigón), cordón inferior (armadura de tracción), bielas inclinadas de hormigón y tirantes inclinados también de hormigón [25], que pueden cruzar las fisuras hasta cierto nivel de abertura de las mismas, tal como indica la figura 2. Este fenómeno se explica por el carácter tridimensional de la microfisuración, que permite transferencia de tracciones a través de las fisuras, cuyo valor puede aproximarse mediante la mecánica de la fractura, como se verá más adelante.
Estos tirantes, que representan la resultante de las tensiones residuales a través de la fisura y de las tensiones de fricción a lo largo de la misma, contribuyen a resistir el cortante junto con el cordón comprimido, que tiene una cierta inclinación, y se equilibran en su parte inferior con las bielas de hormigón y con la armadura longitudinal. La componente vertical del tirante es igual y opuesta a la de la biela, mientras que la suma de ambas componentes horizontales debe ser equilibrada por el incremento de fuerza en la armadura longitudinal (fig. 2).
Conforme la carga aumenta, la fisura crítica se va abriendo y va perdiendo capacidad para transferir tensiones residuales y friccionales, especialmente en la zona traccionada de la viga, donde las deformaciones longitudinales son mayores. Por ello, la inclinación de los tirantes de hormigón varía, buscando la zona más cerrada de la fisura, y su fuerza disminuye conforme la fisura se va abriendo, afectando, por equilibrio vertical del nudo inferior, también al valor de la fuerza en la biela, y por equilibrio horizontal al incremento de tracción en la armadura longitudinal ΔT. Ello conduce a la necesidad de que el par comprimido se incline para resistir el cortante que deja de resistir el tirante, produciéndose así un cierto efecto arco. En consecuencia, la distribución de tensiones tangenciales en una sección con fisuración inclinada, será como la esquematizada en la figura 3d, es decir, una combinación de la distribución correspondiente a un mecanismo de viga puro (fig. 3b) y a un mecanismo de arco puro (fig. 3c). Además, el deslizamiento de la armadura longitudinal también podría disminuir el ΔT, potenciando el efecto arco [26].
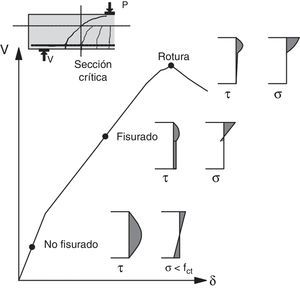
La figura 4 muestra esquemáticamente una curva carga-desplazamiento de una viga crítica a cortante y la distribución de tensiones tangenciales asociadas a la sección donde termina la primera rama de la fisura crítica. Se observa cómo las tensiones van migrando hacia la cabeza de compresión, conforme aumenta la carga. Este hecho ha sido previamente mostrado teóricamente mediante modelos numéricos [5,8] verificados experimentalmente.
2.2Hipótesis del modelo- 1)
En rotura, el cortante y el momento son resistidos por la zona de hormigón no fisurada, por los cercos que cosen la fisura diagonal, por las tensiones residuales que atraviesan fisura y por la armadura longitudinal (fig. 5).
- 2)
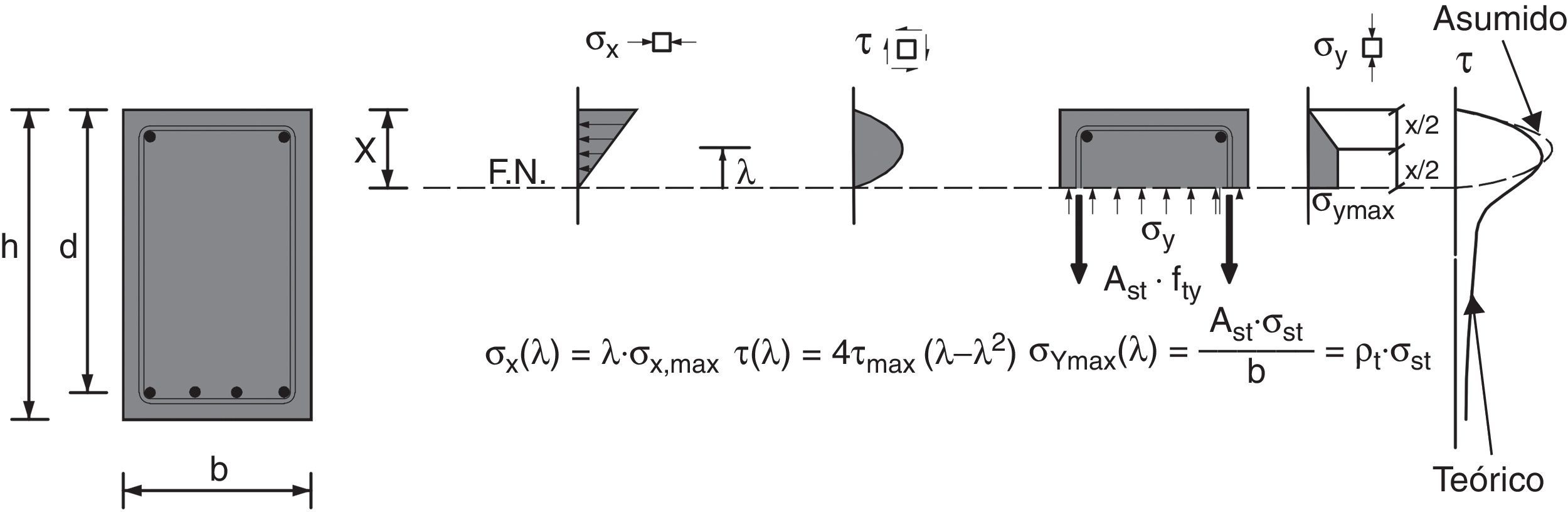
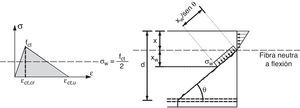
Se consideran las siguientes distribuciones de tensiones en la cabeza comprimida (fig. 6): lineal (σx), parabólica (τ) y constante (σy) a partir de una cierta profundidad para tener en cuenta el anclaje de la armadura transversal y su carácter discreto.
- 3)
Existe una fisura crítica, donde se concentra el daño, que nace a partir de una fisura de flexión y se inclina en el alma hasta llegar al eje neutro de flexión. Esta fisura tiene una primera rama, estable, cuya proyección horizontal se considera igual a βd=0,85d, valor adoptado fruto de la observación experimental.
- 4)
La profundidad de la cabeza, x, se considera igual a la profundidad de la fibra neutra en flexión pura, calculada con fct=0.
- 5)
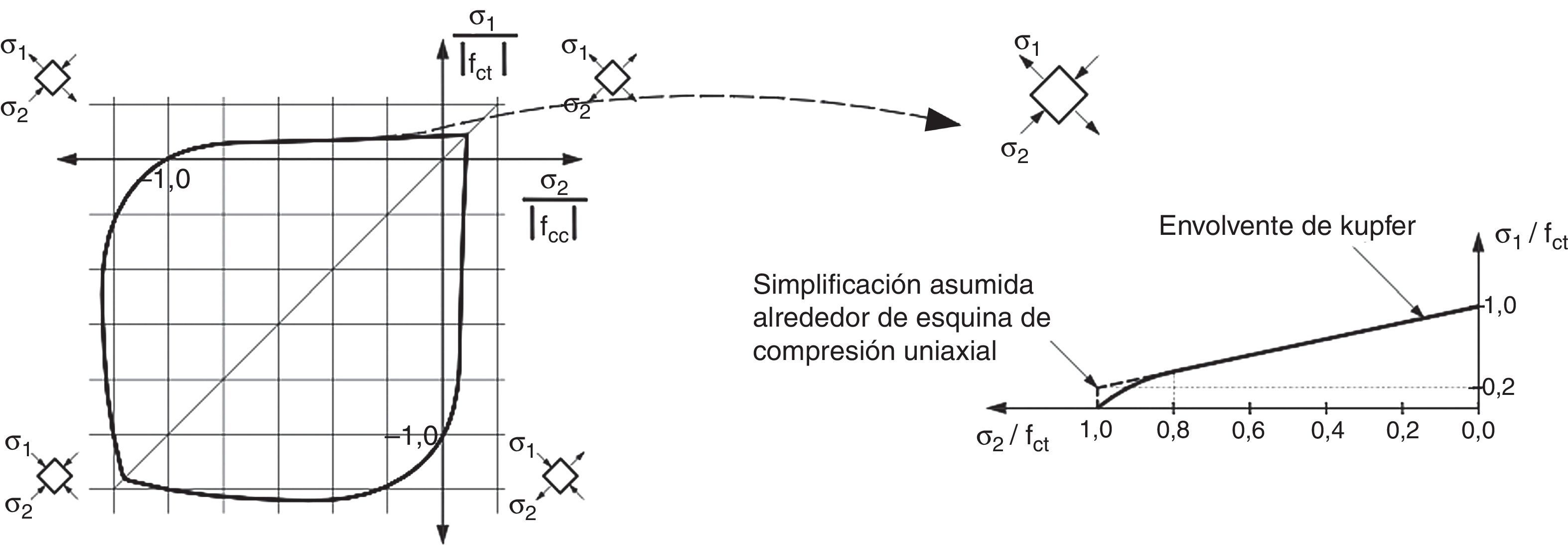
La cabeza de compresión se encuentra sometida a un estado biaxial de tensiones. El fallo se produce cuando las tensiones alcanzan la superficies de rotura de Kupfer [27] (fig. 7).
Figura 7.Envolvente de rotura de Kupfer bajo un estado biaxial de tensiones. Adaptado de [27].
(0.15MB). - 6)
Se considera que la armadura longitudinal se encuentra perfectamente anclada y que no hay deslizamiento relativo entre hormigón y acero.
- 7)
Se considera que la armadura transversal, en ELU, está plastificada.
Las tensiones principales de tracción (σ1) y de compresión (σ2) producidas en la cabeza por un estado de tensiones normales (σx, σy) y tangenciales (τ) son:
donde la tensión de tracción se considera positiva. La tensión tangencial (τ) en cualquier punto está relacionada con las tensiones normales y principales a través de la ecuación (3), obtenida resolviendo (1) y (2).
Si en un cierto punto de la cabeza situado a una distancia del eje neutro y= λ·x, se conoce el valor de la tensión tangencial τλ, la distribución de tensiones en la cabeza puede calcularse, imponiendo las condiciones τ(0)=0, τ(x)=0 y τ(λ·x) =τλ, obteniéndose:
Entonces, el cortante resultante en la cabeza se obtiene por integración de las tensiones tangenciales en la misma:
Si τλ es la tensión tangencial asociada a un estado de tensiones normales dado por la ecuación (3), ésta puede sustituirse en la ecuación (5), resultando Vc función de las tensiones normales y principales en el punto considerado (y=λ·x): indica la figura 8, donde se representa el daño para el caso de vigas sin armadura transversaldonde:
Y el eje neutro, x, se puede obtener en el caso de vigas de sección rectangular sin armadura comprimida a través de:
donde n= Es/Ec es el coeficiente de equivalencia entre acero y hormigón y ρ=As/(b·d) es la cuantía geométrica de armadura traccionada.
Si el punto considerado tiene un estado tensional que corresponde a la superficie de Kupfer, Vc será el cortante resistido por la cabeza de compresión. La ecuación de la superficie de rotura de Kupfer, en la rama compresión-tracción tiene por expresión:
Donde tanto la tensión como la resistencia a compresión se consideran negativas. El término de la izquierda de esta igualdad puede asociarse a un daño, D, que sufre el punto debido a su estado de tensión biaxial. La tensión principal de tracción puede despejarse de la ecuación (9).
Donde Rt es un factor reductor de la resistencia a tracción por efecto de las compresiones transversales. Con ello la ecuación (6) puede reescribirse como:
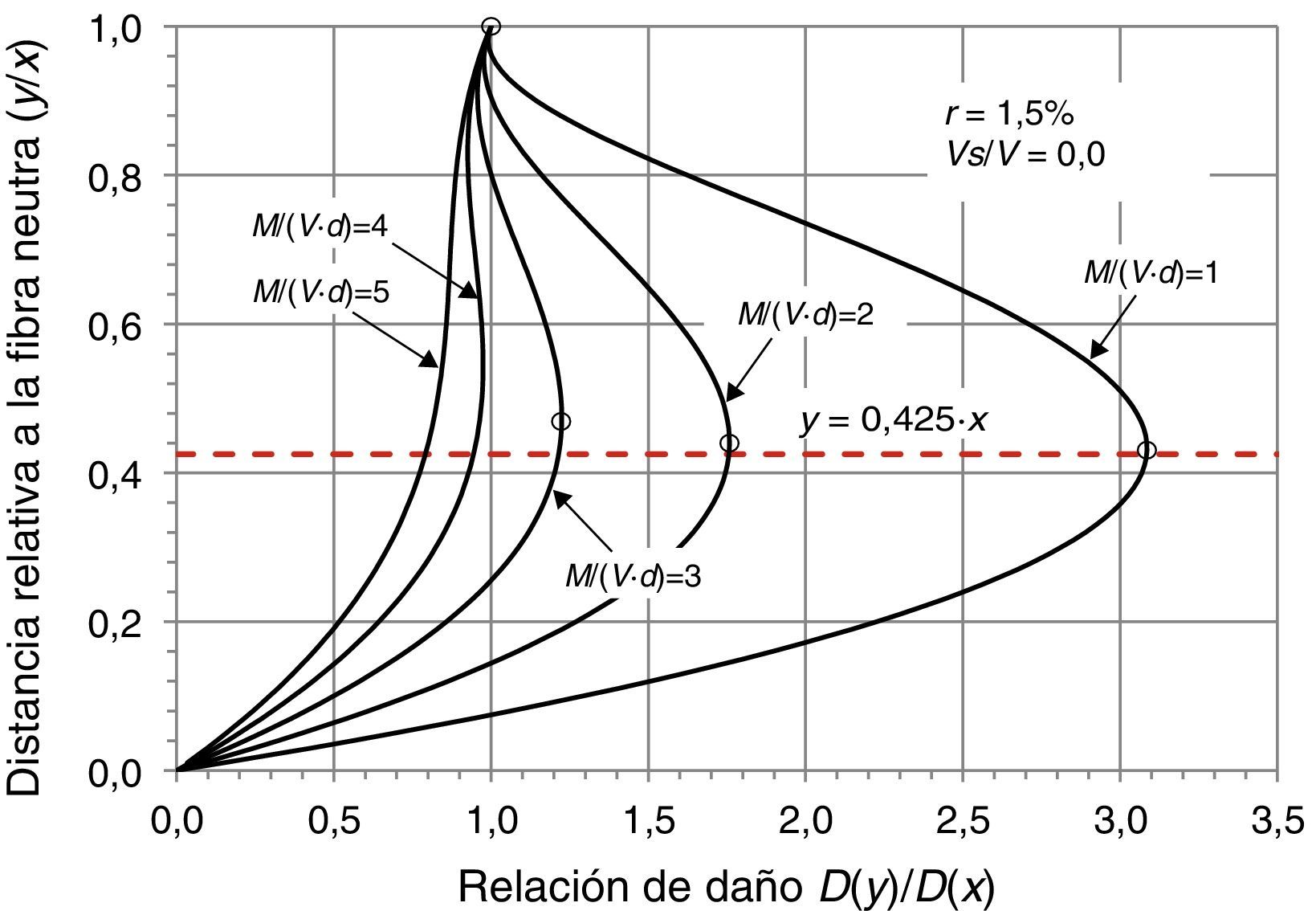
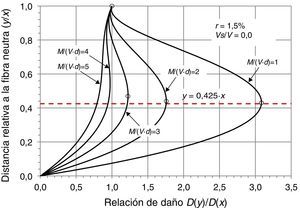
La posición del punto pésimo, donde la combinación de tensiones normales y tangenciales produce el máximo daño en la cabeza, es función de la relación entre el momento M(s) y el cortante V(s) que solicitan la sección situada a una distancia s del apoyo, así como de la cuantía de armadura transversal. Dicho punto, para valores situados entre s=d y s=3d, se encuentra entre y=0,4x e y=0,5x, como indica la figura 8, donde se representa el daño para el caso de vigas sin armadura transversal. En el caso de vigas con armadura transversal, la existencia de tensiones verticales reduce la tensión principal de tracción y aumenta algo la de compresión, incrementando ligeramente la altura del punto crítico conforme aumenta la cuantía de armadura transversal, aunque su efecto apenas es perceptible para valores de M/Vd<3. Por tanto, se adoptará en este trabajo el valor y=0,425x, es decir, λ=0,425.
Una vez λ es conocido, también lo es Kλ y por tanto en la ecuación (11) solo hará falta sustituir los valores de las tensiones normales y obtener el factor de reducción Rt para obtener el cortante resistido por la cabeza. Por tanto, es necesario determinar cuál es la sección pésima a lo largo de la viga, de cara a determinar el momento flector y las tensiones normales que éste genera en la cabeza comprimida, y para verificar que dicha sección se encuentra en el rango de valores de s/d coherentes con el valor adoptado para λ (1<s/d<3).
3.2Cortante resistido a lo largo de la fisuraConsidérese el trozo de viga situado por encima de la fisura crítica indicado en la figura 5. El cortante resistido a lo largo de la fisura procede de: 1) las tensiones de fricción en la superficie de la misma cuyo valor en cada punto depende de la abertura de la fisura y del deslizamiento entre caras de ésta; y 2) de las tensiones residuales que, por efecto de las irregularidades tridimensionales en la fisura, pueden transmitirse a través de ella, cuyo valor en cada punto disminuye a medida que aumenta el ancho de la fisura (fig. 9). En este trabajo se considerará, de forma simplificada, solo la fuerza residual, cuya dirección se considera perpendicular a la fisura, lo cual es coherente con la teoría del campo perturbado de tensiones [28,29] según la cual, la dirección principal de la tensión residual no puede desviarse más de 15° de la dirección de la fisura, a menos que se forme otra fisura.
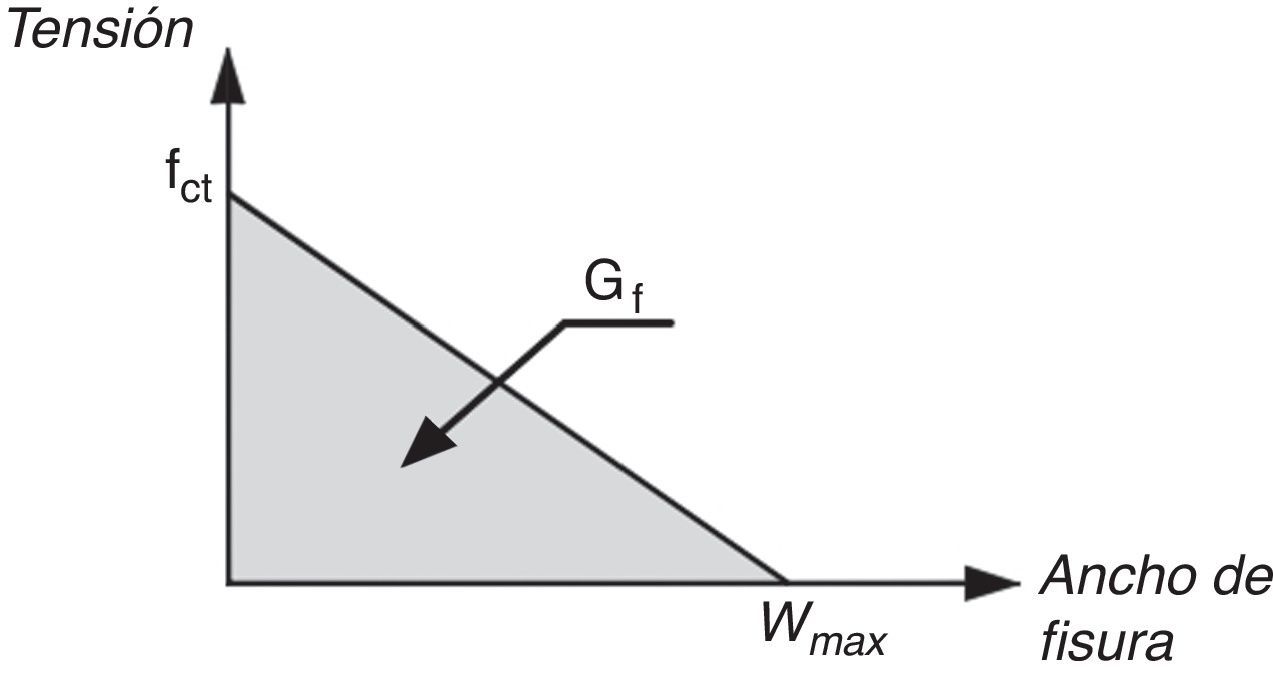
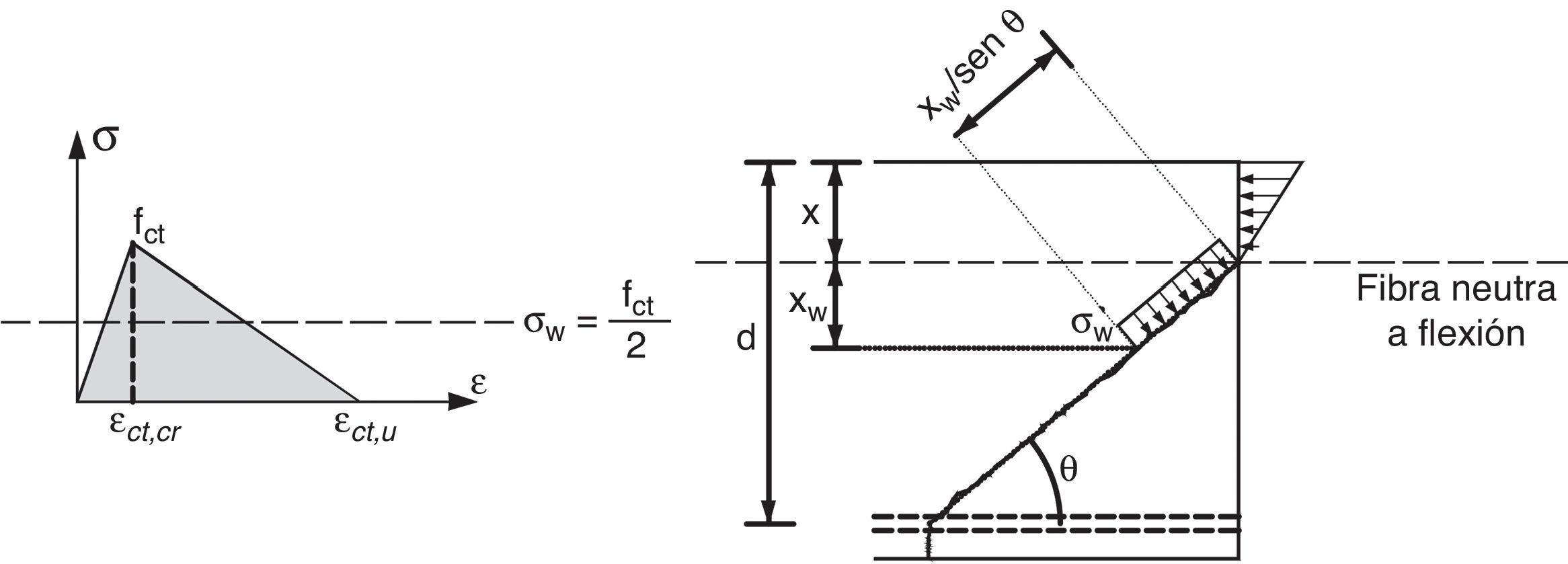
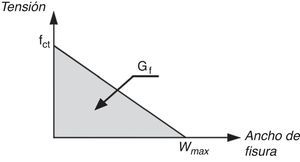
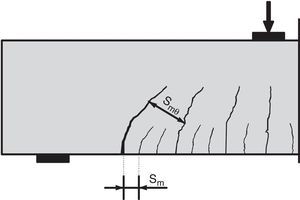
A fin de evaluar la fuerza residual se considera un diagrama tensión-deformación bilineal del hormigón con una rama descendente, una vez superada la tensión máxima fct, cuya deformación máxima, ¿ctu, corresponde a tensión residual cero, como indica la figura 10. Considerando la hipótesis de deformación plana de las secciones, se puede relacionar la deformación máxima del hormigón, ¿ctu, con la deformación de la armadura longitudinal, ¿s, y ésta última con el ancho de fisura, con lo que se puede relacionar la fuerza residual con la deformación del acero y la energía de fractura del hormigón. Aunque las tensiones residuales a lo largo de la fisura tendrían una distribución triangular, se adopta un valor constante de tensión σw=fct/2 (fig. 10) energéticamente equivalente. Por otra parte, en los cálculos de la fuerza residual se tiene en cuenta que, de acuerdo con las hipótesis del modelo, la proyección horizontal de la fisura es 0,85d, siendo d el canto útil.
Llamando lw a la longitud del tramo de fisura que transmite tracciones (fig. 11) y xw a su proyección vertical (profundidad de la zona traccionada) la fuerza residual resistida es:
xw se obtiene por compatibilidad de deformaciones en la dirección normal a la fisura (fig. 11), resultando el siguiente valor:
Donde ¿s es la deformación longitudinal de la armadura de flexión, relacionada a través del sin2θ con la deformación normal a la fisura, y ¿ctu es la deformación en la dirección normal a la fisura. Substituyendo (13) en (12), y teniendo en cuenta que el valor del ángulo θ es conocido (cotθ=0,85d/(d-x)), Vw puede expresarse como:
La energía de fractura puede expresarse como una función de las deformaciones de fisuración y última del hormigón como sigue:
Donde se supone que, en la fase de propagación de la fisura, el ancho máximo de fisura es:
siendo smθ el valor medio de la separación entre fisuras inclinadas, cuyo valor, como indica la figura 12, es mayor que la separación entre fisuras de flexión.
Con todo lo anterior, la deformación última del hormigón en tracción, se puede relacionar con la energía de fractura mediante la siguiente expresión:
Por tanto, el cortante resistido a través de la fisura, en forma adimensional puede expresarse según:
La expresión (18) indica que la contribución del alma aumenta con la energía de fractura (y por tanto con la resistencia a compresión del hormigón y el tamaño máximo del árido) y disminuye con la separación media entre fisuras diagonales y con la deformación de la armadura longitudinal ¿s. El valor de la separación media entre fisuras diagonales, smθ, varía de unos puntos a otros y de la presencia o no de armadura transversal, siendo, en la actualidad, un tema abierto de investigación. Por eso, en este trabajo se adopta el valor smθ=d que es conservador, especialmente en el caso de existencia de armaduras transversales. En cuanto a la deformación de la armadura longitudinal ¿s, dado que el momento que actúa en la sección crítica no es conocido «a priori», a fin de obtener una expresión práctica para Vw, se adopta el valor ¿s=0,0009 cuando se produce la rotura por cortante, que es un valor medio obtenido por los autores, tanto en cálculos mediante modelos teóricos [8,10,30,31] como en investigaciones experimentales [32]. Por otra parte se adopta x/d=0,38 para la profundidad de la fibra neutra, que corresponde a una cuantía geométrica ρ=1,5%, que es un valor conservador a efectos del cálculo de Vw. La expresión que proporciona el cortante resistido a través de la fisura es:
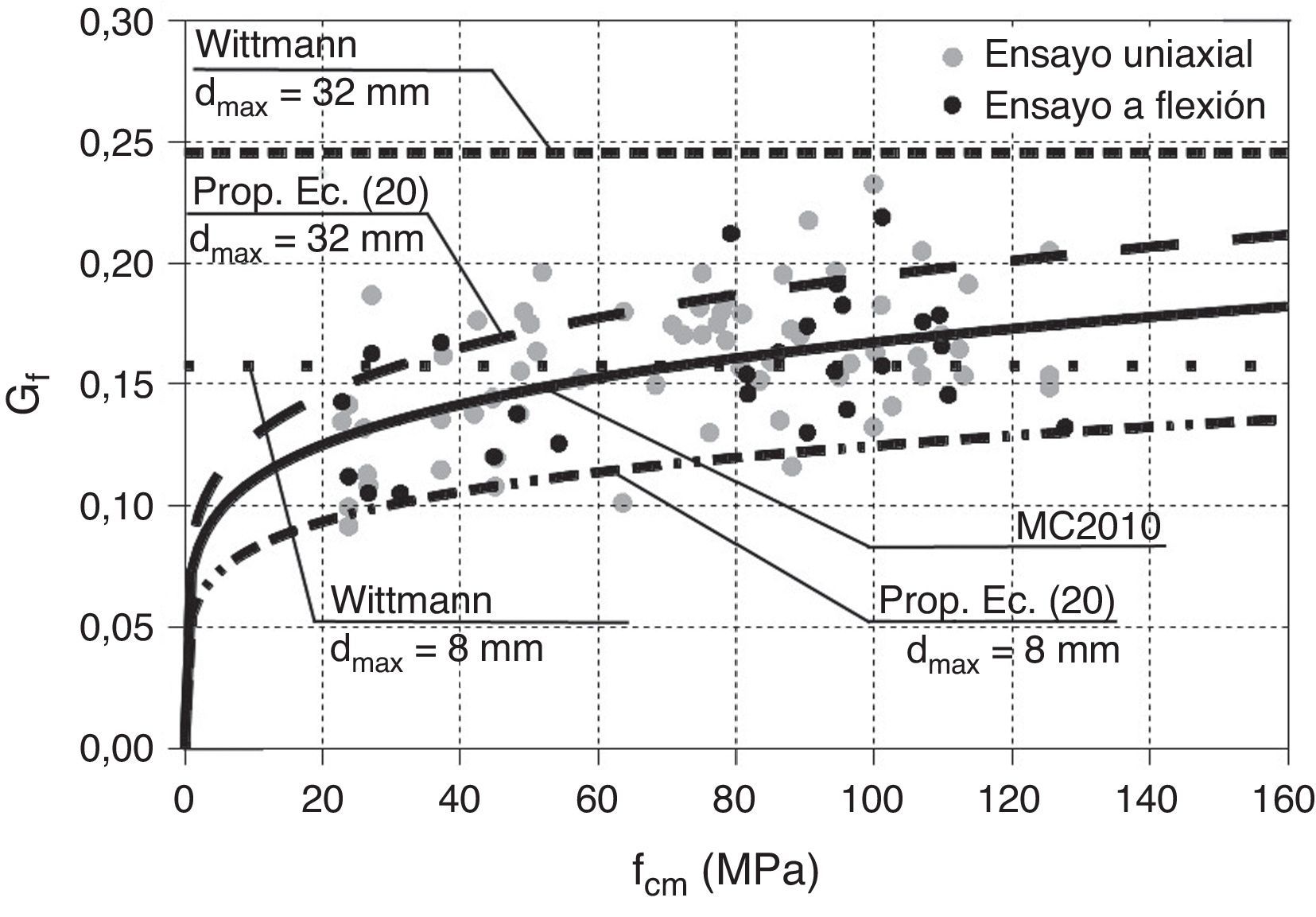
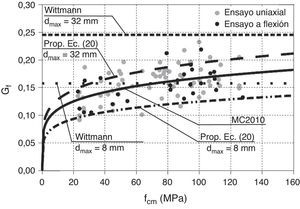
La energía de fractura depende, entre otros factores, de la relación agua/cemento, del tipo de árido, del tamaño máximo del árido y de las condiciones de curado. El Código Modelo 2010 (CM2010) [33], propone una expresión para Gf que depende solo de la resistencia media a compresión del hormigón. Sin embargo, Wittmann [34] propone una expresión que solo depende del tamaño máximo del árido, dmax, y que resulta del orden de un 50% superior a la del CM2010. En este trabajo se propone una expresión que se ajusta al CM2010 para un tamaño máximo del árido de 20mm, y además aumenta o disminuye según la resistencia del hormigón tal como indica la figura 13. Los valores experimentales de esta figura se han extraído del fib Bulletin 42 [35]. Esta expresión, en la que fcm se expresa en N/mm2, dmax en mm y Gf en N/mm, es:
Resultados experimentales de la energía de fractura en función de fcm, adaptada de [35].
Como consecuencia del deslizamiento y de la abertura de la fisura inclinada, se produce un movimiento relativo vertical entre ambas caras de la fisura, que, consecuentemente, produce una cizalladura en la armadura longitudinal. Las barras longitudinales ejercen un empuje hacia fuera del hormigón del recubrimiento que está del lado de la fisura más próximo al apoyo. En caso de que no haya estribos, ese empuje solo está equilibrado por la resistencia a tracción del hormigón del recubrimiento, que es muy reducida y, en consecuencia, dicho recubrimiento se desprende para valores del esfuerzo cortante relativamente pequeños. Por ello, en este artículo se desprecia el efecto pasador de la armadura cuando no hay estribos.
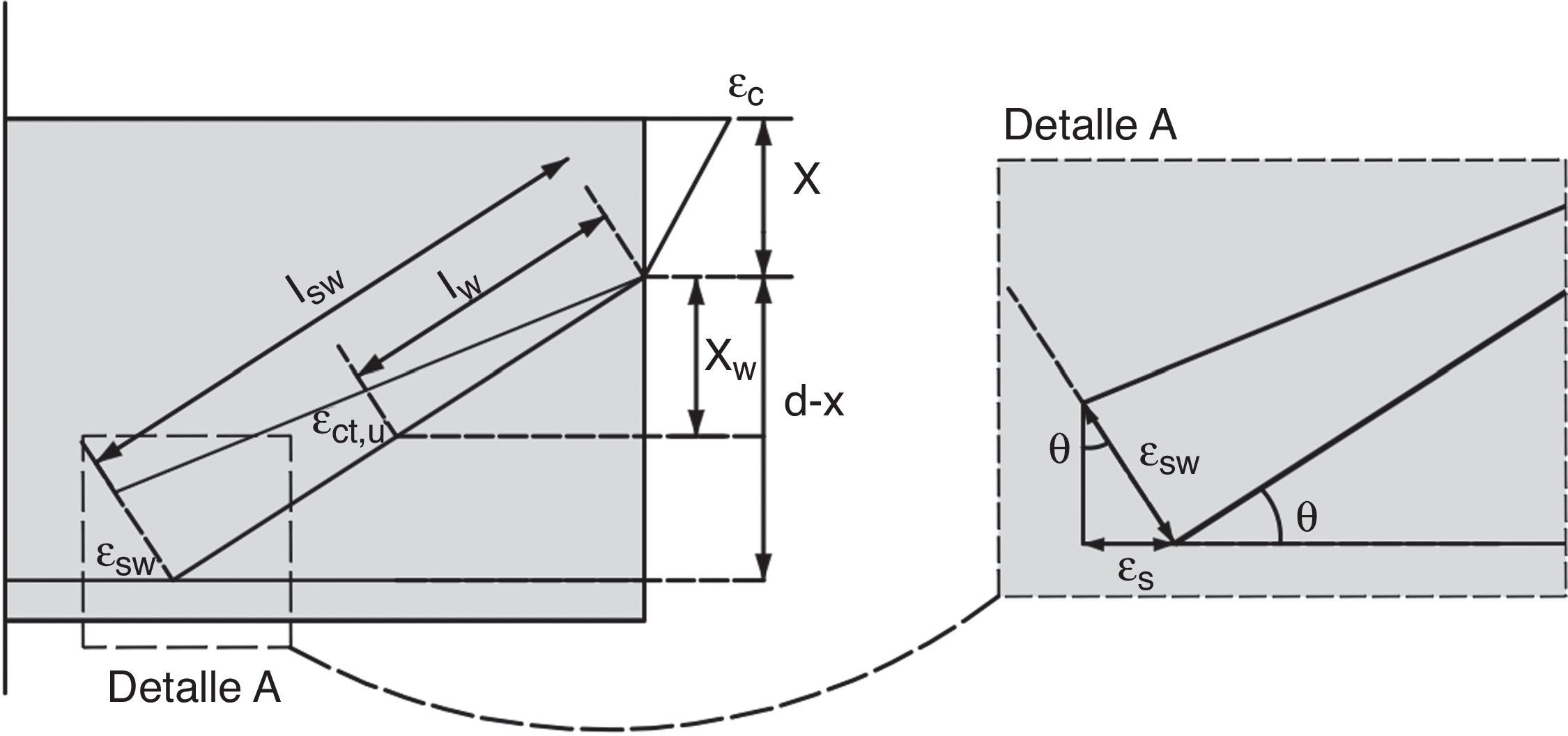
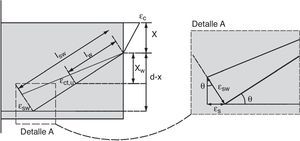
En el caso de existencia de armadura transversal, la armadura longitudinal se apoya en los cercos y es capaz de resistir el efecto de un desplazamiento vertical relativo entre los mismos. En este trabajo se considera, para simplificar los cálculos, que la armadura longitudinal está empotrada en los dos cercos adyacentes al punto donde nace la fisura crítica, cuya separación se conoce (fig. 14).
El desplazamiento vertical se considera igual a la suma de dos componentes, tal como indica la figura 14: 1) la componente vertical de la abertura de la fisura inclinada (aspecto puramente geométrico, cuyo valor es nulo en flexión pura, cuando la fisura es vertical); y 2) la deformación de cortante de la cabeza, sometida a su cortante Vc, en una longitud igual a la proyección horizontal de la fisura.
Evaluando mediante procedimientos usuales ambas deformaciones (la de flexión en sección fisurada y la de cortante en la cabeza comprimida de forma elástica) y tras algunas simplificaciones, y considerando Gc=Ec/2,2, se obtiene la siguiente expresión para la deformación total:
El valor de la fuerza cortante vendrá dado, por tanto, por el valor del desplazamiento vertical y por la rigidez de esta estructura ficticia que es la barra de armadura longitudinal biempotrada entre cercos. Con estas premisas, y tras las operaciones pertinentes, se obtiene:
Donde Es es el módulo elástico del acero, Is es el momento de inercia de la barra, cuyo diámetro es ϕ, st es la separación entre cercos y ξ=x/d. Sin embargo, esta expresión es poco operativa y, por tanto, dado que la contribución Vl es muy reducida (menor del 5% del cortante resistido en casos usuales), se adoptan una serie de valores medios que corresponden a casos usuales, como son: ¿s=0,0009, ϕ/st=0,15, d/st =2 y Ec/fct=10000, resultando la siguiente expresión simplificada:
En donde debe ser ξ=x/d>0,2, lo que ocurre para cuantías geométricas superiores a ρ=0,0036, es decir superiores a la mínima.
3.4Contribución de la armadura transversal a la resistencia a cortanteEn este modelo se considera que la armadura transversal está plastificada cuando se produce la rotura por cortante (σst=fyw). Entonces, la contribución directa de esta armadura a la resistencia a cortante es (ver fig. 5):
Donde Asw y ρw son el área por unidad de longitud y la cuantía geométrica de armadura transversal, respectivamente, y fyw es la resistencia del acero. Por otra parte, las tensiones verticales de confinamiento introducidas sobre el hormigón por la armadura transversal, obtenidas del equilibrio de fuerzas verticales en un corte horizontal en cualquier sección (fig. 6), son:
3.5Posición de la sección crítica a lo largo de la vigaEn el presente modelo, la resistencia a cortante proporcionada por la cabeza comprimida, Vc, aumenta conforme la cabeza está más comprimida ya que la tensión tangencial máxima que se puede resistir aumenta con σx, tal como se expresa en la ecuación (6). Con estas hipótesis, la sección que menos resiste a cortante será la situada donde acaba la primera rama de la fisura crítica. Ello es así porque secciones más próximas a la carga, que tienen la misma profundidad de la zona no fisurada, están sometidas a mayor compresión en la cabeza y, por tanto, resisten más cortante. Por otra parte, secciones más próximas al apoyo tienen una profundidad de la cabeza no fisurada mayor y también resisten, por tanto, más cortante.
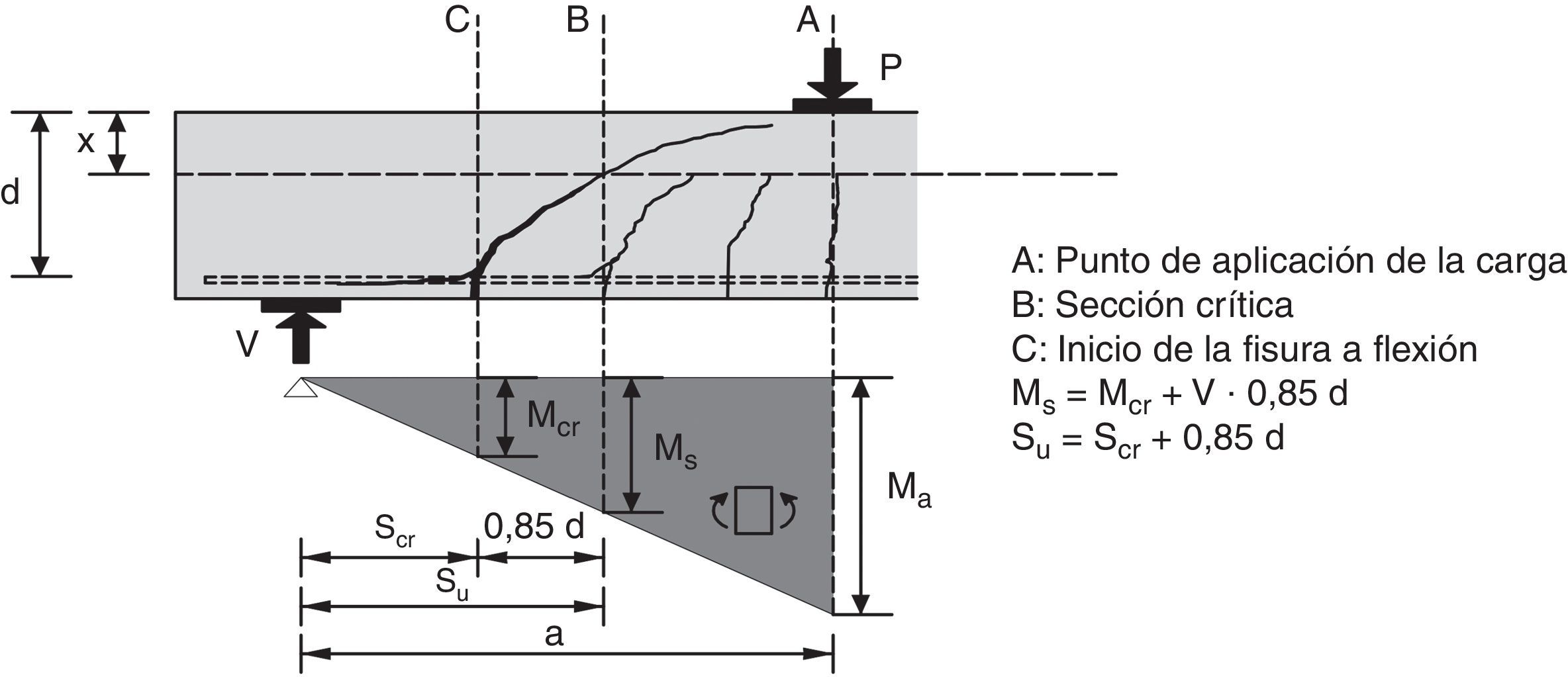
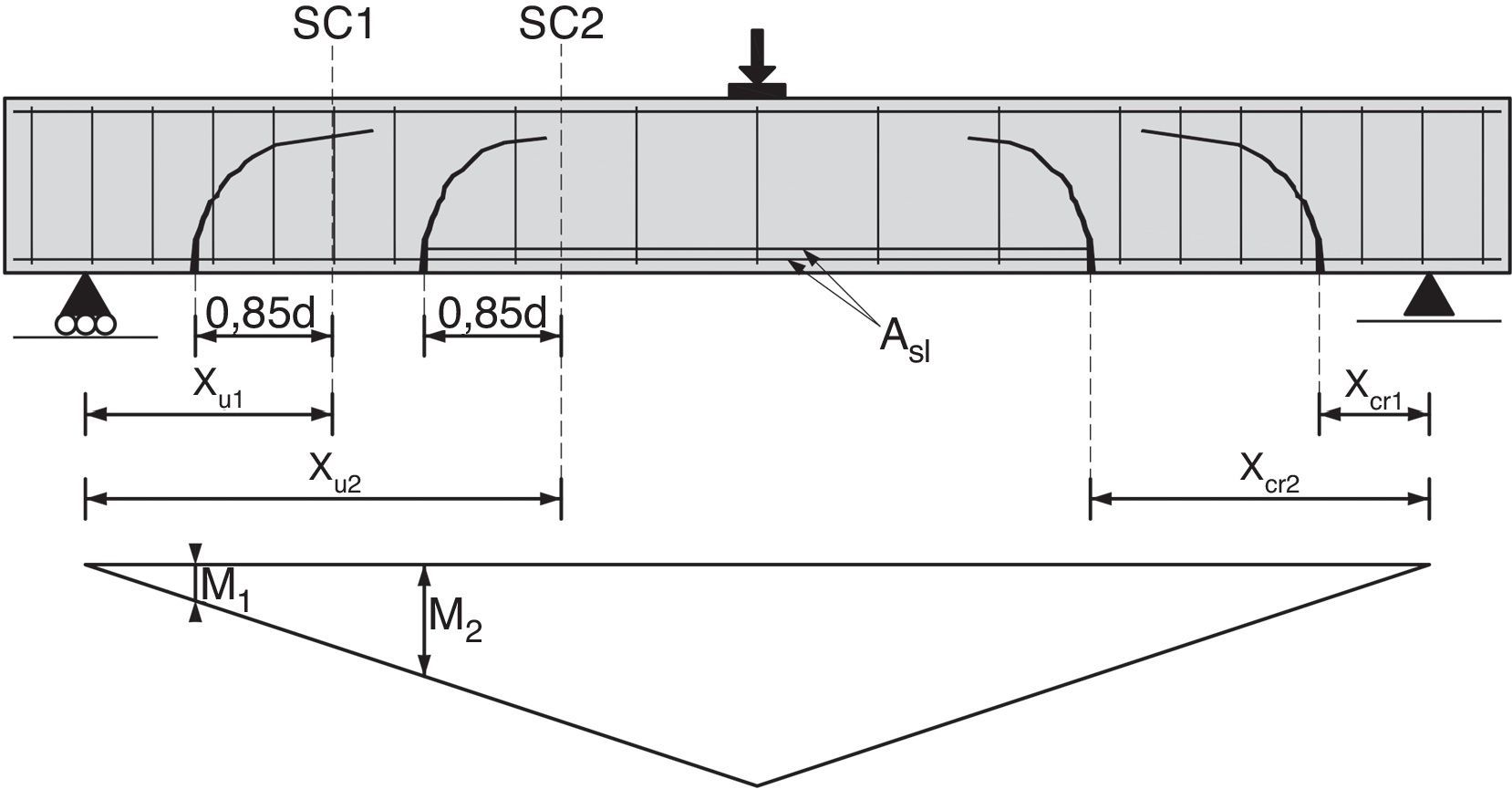
Para obtener la posición de la sección crítica es necesario determinar el punto donde nace la fisura (fig. 15). Conforme se va cargando la pieza, se van formando fisuras desde el punto de máximo momento hacia el punto de momento nulo, separadas en función de las tensiones de adherencia y la resistencia a tracción del hormigón. Por tanto, la fisura más próxima al apoyo no puede estar a una distancia menor que la separación media entre fisuras (es decir, la longitud necesaria para que se pueda formar otra fisura). Por otra parte, la fisura crítica no puede estar a una distancia del apoyo menor que scr=Mcr/Vu, donde el momento no superaría al momento de fisuración.
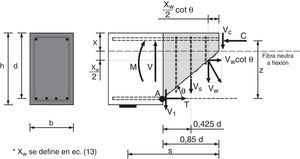
4EXPRESIÓN DE LA RESISTENCIA A CORTANTE-FLEXIÓN DE VIGAS SOMETIDAS A CARGAS PUNTUALESConsidérese la porción de viga entre las secciones donde se inicia y finaliza la primera rama de la fisura crítica por encima de ésta, como indica la figura 5. La resistencia a cortante se obtiene planteando el equilibrio entre los esfuerzos (V, M) y las resultantes de las tensiones internas en la cabeza (C, Vc), en la fisura (Vw) en la armadura longitudinal (Vl) y en las armaduras transversales (Vs).
La tensión normal σx en el punto crítico (y=λ·x) de la cabeza de compresión se puede expresar en función de los esfuerzos, como sigue:
O, en términos adimensionales:
donde ξw=xw/d, xw es la profundidad relativa de la zona donde existen tensiones residuales en la fisura, dada por la ecuación (13), vw es el cortante adimensional resistido en la fisura, dado por la ecuación (19) y μ es el momento adimensional que actúa en la sección donde nace la fisura, μ=M/(fct·b·d2). Se considera, de forma conservadora, que ese momento es el momento de fisuración, μcr=0,2, aproximadamente, para secciones rectangulares.
La tensión tangencial en el punto crítico de la cabeza de compresión (λ=0,425) vale:
Teniendo en cuenta las ecuaciones (25) y (30), y sustituyéndolas en la ecuación (6), el cortante resistido por la cabeza, puede expresarse por:
Donde Rt es el factor reductor de la resistencia a tracción por efecto de las compresiones en la dirección perpendicular, de acuerdo con el criterio de rotura adoptado, dado por la ecuación (10). Dado que Rt depende de las tensiones principales y éstas del cortante Vc, la ecuación (32) debe resolverse iterativamente. Para ello se considera un valor inicial Rt=1, obteniéndose en pocas iteraciones la convergencia.
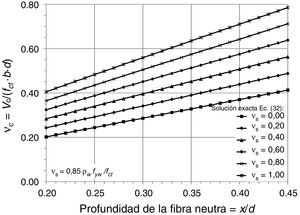
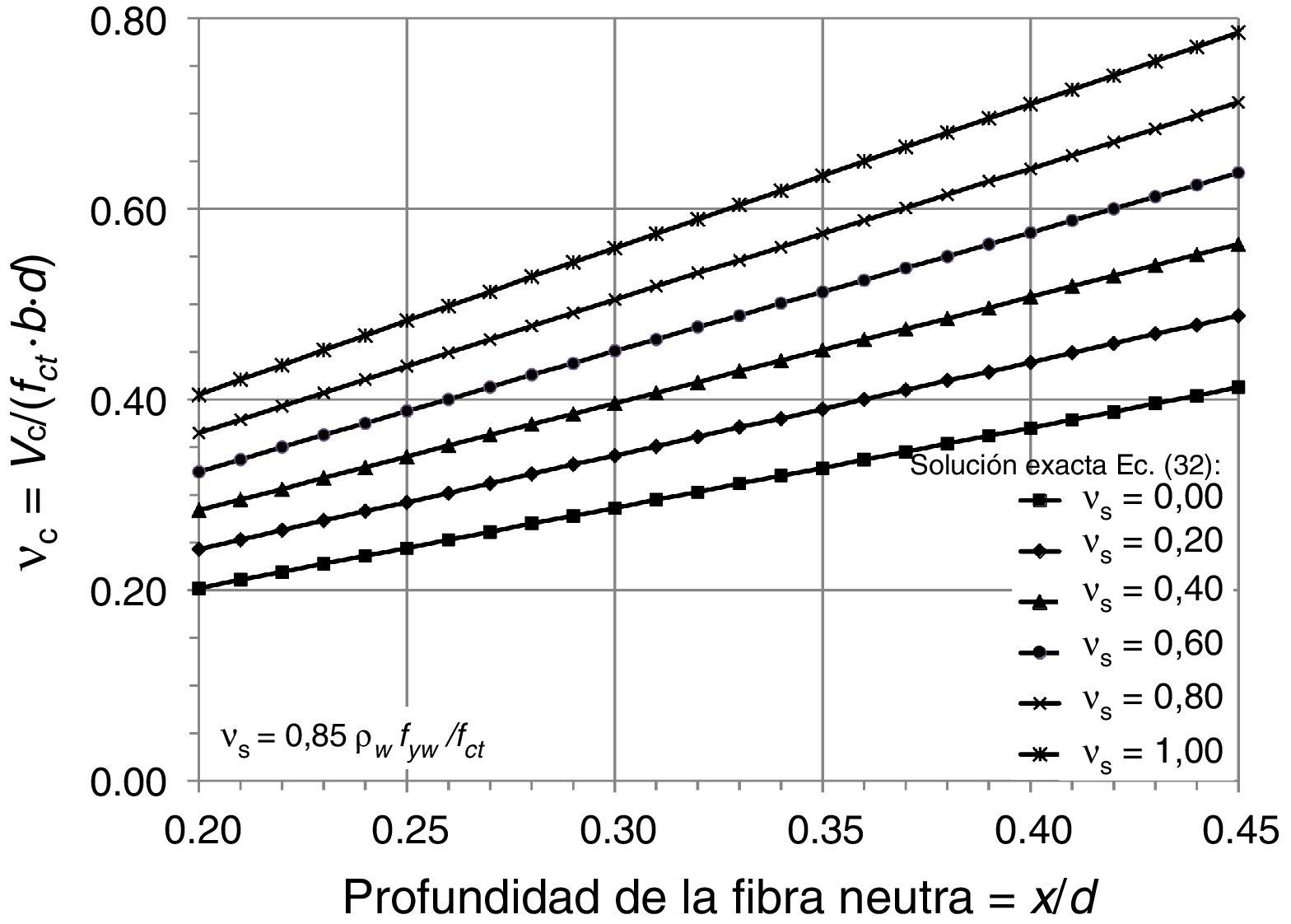
La figura 16 muestra la solución de la ecuación (32), expresando gráficamente el valor del cortante vc adimensional en función de la profundidad relativa de la fibra neutra x/d, para distintos valores de la contribución de la armadura transversal.
Se observa que existe una relación marcadamente lineal entre vc y x/d, de forma que a mayor x/d (y por tanto, mayor cuantía de armadura longitudinal), más cortante resiste la cabeza. Igualmente se observa que a mayor cuantía de armadura transversal (y por tanto mayor vs) también resiste más cortante la cabeza. Este hecho, observado ya experimentalmente por varios autores [36,37] tiene su explicación en varios fenómenos, como son: a) el confinamiento del hormigón proporcionado por la armadura transversal que genera tensiones normales verticales; b) el hecho de que al contribuir directamente la armadura transversal a resistir más cortante (Vs), también se resiste más flexión y, por tanto, hay más compresión en la cabeza, lo cual es favorable. Matemáticamente este aspecto queda reflejado en la ecuación de equilibrio de momentos, en la que participa la armadura transversal. Esta dependencia lineal entre vc y x/d también fue obtenida por Zararis y Papadakis [18] y por Tureyen y Frosch [20].
El cortante adimensional resistido por la cabeza debe ser afectado por el efecto tamaño debido al carácter frágil de la rotura de la cabeza. A tal fin, se utiliza la expresión semi-empírica propuesta por Zararis y Papadakis [18] para el factor de tamaño:
con a y d en metros. Esta expresión fue derivada [18] considerando la cabeza comprimida en la zona situada entre la carga y el final de la primera rama de la fisura crítica como un cilindro sometido a un ensayo de tracción indirecta, cuyo resultado depende del diámetro y, por tanto, en cierta forma de la luz de cortante, a.
4.1Ecuaciones simplificadas para el cálculo a cortanteLas rectas de la figura 16, incluyendo el factor de tamaño, pueden aproximarse por:
El cortante total resistido vendrá dado por:
donde vc, vw, vl y vs vienen dados, respectivamente, por las expresiones (34), (19), (23) y (24). Haciendo vs=0 y vl=0 en las expresiones (34) y (35) se obtienen las siguientes expresiones para el cortante resistido en vigas sin armadura de cortante,Vu,0:
El modelo proporciona el punto donde se incia la fisura crítica, scr=Vu/Mcr, la posición de la sección crítica su=scr+0,85·d y el momento M concomitante con el cortante último en dicha sección M=Vu·su, siendo Vu el cortante último resistido predicho por el modelo presentado, ya sea para vigas con o sin cercos (equivalente a Vu,0 en este último caso). Por tanto, también se pueden obtener las tensiones normales, tangenciales y principales en la cabeza en la sección critica en el instante de la rotura, dadas por las ecuaciones (25), (30), (32), (1) y (2), respectivamente.
Cuando la geometría de la sección o las armaduras longitudinales o transversales cambian a lo largo de la viga (fig. 17), también el momento que actúa en la sección crítica cambia.
Ello se tiene en cuenta en la ecuación (32) sustituyendo el término 0,4 por 2μ, siendo μ=M/(fct·b·d2) el momento que actúa en la base de la fisura crítica. La expresión lineal (34) que relaciona el cortante adimensional resistido por la cabeza, vc, con la profundidad relativa de la fibra neutra x/d, puede generalizarse así:
Para el caso μ=0,20 las expresiones (34) y (37) son idénticas.
4.2Dimensionamiento de las armaduras transversalesCuando el cortante de cálculo excede el cortante resistido por la viga sin armadura transversal, Vu,o, el valor de la armadura necesaria puede obtenerse de forma explícita, sin necesidad de iteraciones, despejando vs de la ecuación (35), sustituyendo vc, por la expresión (34) haciendo en la misma vs=0 e igualando el cortante resistido al cortante de cálculo para obtener la armadura estrictamente necesaria:
Donde vd es el cortante adimensional de cálculo, vd=Vd/(fctbd), que es un dato del problema.
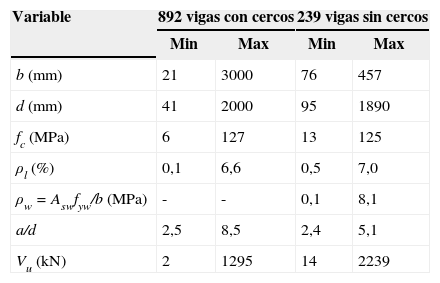
5COMPARACIÓN CON RESULTADOS EXPERIMENTALES: CARGA PUNTUALSe ha utilizado la base de datos proporcionada por Collins et al. [1] para vigas sin armadura de cortante, en la cual constan 1849 ensayos de vigas de hormgón armado simplemente apoyadas. De ellas, se han utilizado 892 en este trabajo, que corresponden a aquellos casos en los que consta que la rotura se produjo por cortante, cuya relación a/d era mayor que 2,5 y que fueron ensayadas bajo una o dos cargas puntuales. Para elementos con armadura transversal se han fundido dos bases de datos publicadas previamente [38,39] dando lugar a una nueva base de datos de 239 resultados experimentales de vigas esbeltas simplemente apoyadas con rotura a cortante. El rango de valores de los parámetros de proyecto más importantes se presenta en la tabla 1.
Rango de valores de las variables de proyecto en las bases de datos
| Variable | 892 vigas con cercos | 239 vigas sin cercos | ||
|---|---|---|---|---|
| Min | Max | Min | Max | |
| b (mm) | 21 | 3000 | 76 | 457 |
| d (mm) | 41 | 2000 | 95 | 1890 |
| fc (MPa) | 6 | 127 | 13 | 125 |
| ρl (%) | 0,1 | 6,6 | 0,5 | 7,0 |
| ρw=Aswfyw/b (MPa) | - | - | 0,1 | 8,1 |
| a/d | 2,5 | 8,5 | 2,4 | 5,1 |
| Vu (kN) | 2 | 1295 | 14 | 2239 |
Se han utilizado, además, las formulaciones de la resistencia a cortante existentes en el EC2 [11], ACI 318-08 [12] y CM2010 [33] para comparar sus resultados con los del modelo propuesto y con los experimentales. Se han eliminado de las formulaciones originales todos los coeficientes de seguridad.
Para elementos sin cercos, el EC2 [11] propone una formulación semiempírica, sin embargo, para vigas con cercos propone una fórmula basada en la analogía de la celosía, con ángulo variable, sin ninguna contribución del hormigón. En cuanto al Código ACI 318-08 [12], la contribución del hormigón, también de carácter empírico, se ha considerado a través de su ecuación 11-5 tanto para piezas con y sin armadura transversal. Por otra parte, la contribución de los cercos en este código está basada en una celosía con un ángulo de inclinación de 45°. La formulación a cortante del Código Modelo 2010 [33] está basada en tres niveles de aproximación, de menor a mayor complejidad. En este artículo se presentan los resultados de los cálculos realizados con los niveles II y III, eligiendo, en cada caso, el que proporcionaba menor dispersión con respecto a los resultados experimentales. Por esta razón, para elementos sin estribos, se ha adoptado el nivel II, mientras que para elementos con estribos se ha adoptado el nivel III. Ambos son métodos derivados directamente de la teoría del campo modificado de compresiones [3], la cual considera que la contribución del hormigón procede del rozamiento, o engranamiento de áridos, entre caras de fisuras.
La resistencia a tracción del hormigón, fundamental en el modelo propuesto, y el módulo de deformación longitudinal se han evaluado a partir del EC2 [11]. Se ha distinguido entre hormigones convencionales (fc<50MPa) y de alta resistencia, pero limitando su valor a 60MPa para hormigones sin cercos, pues parece ser que a partir de ese valor se produce la fractura de los áridos y la contribución del hormigón al cortante no aumenta más con la resistencia a compresión [36,40].
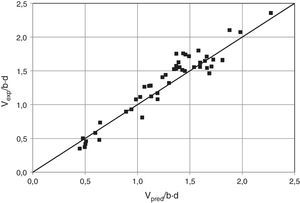
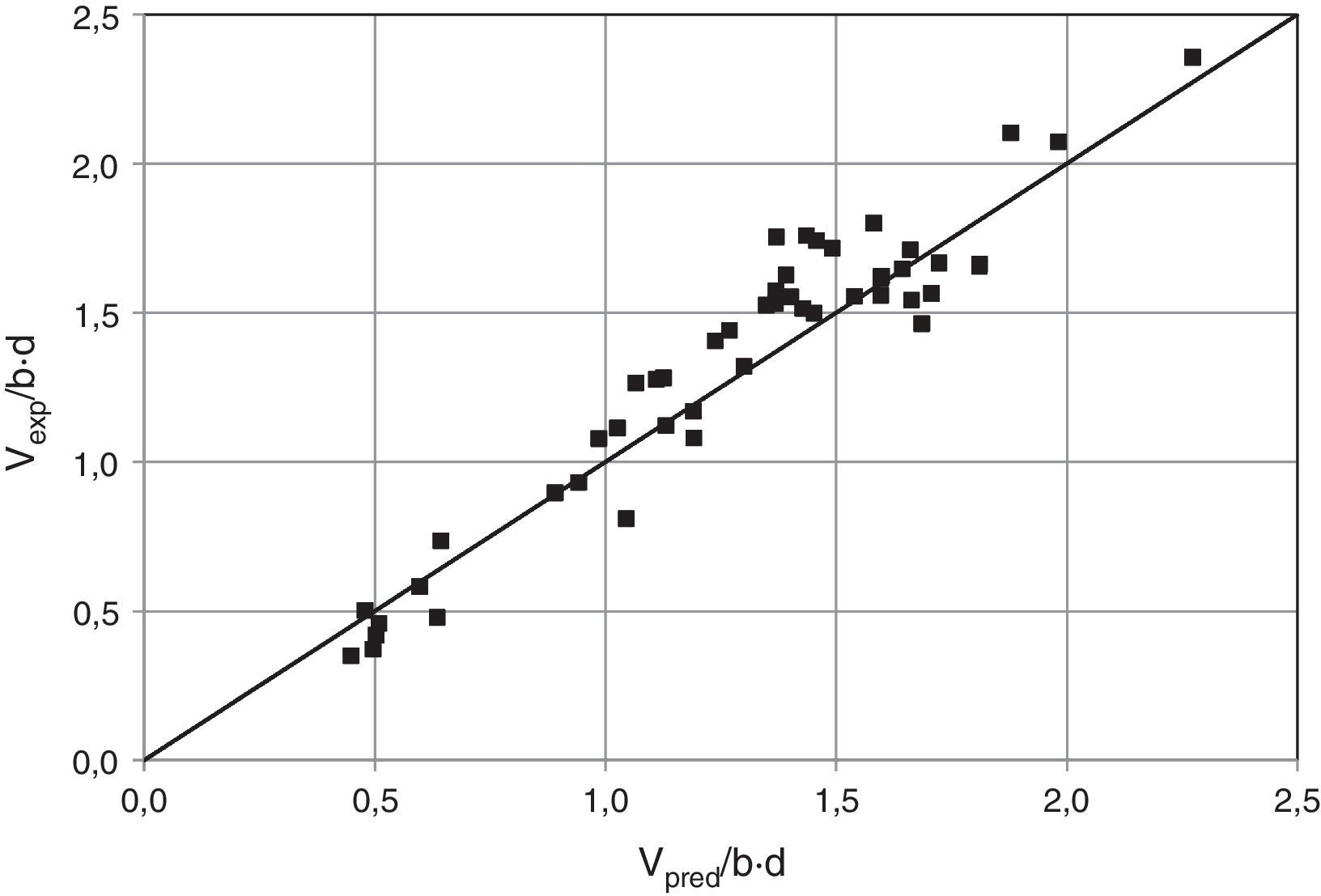
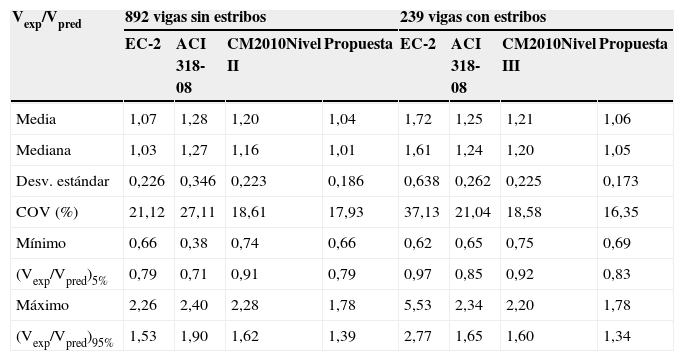
La Tabla 2 muestra la comparación entre los resultados de los ensayos y las predicciones de los distintos códigos. Puede observarse que las predicciones realizadas con el modelo propuesto se ajustan mejor, en media y dispersión, a los resultados experimentales que el resto de métodos, a pesar de la sencillez de sus expresiones finales. Es preciso señalar que se han utilizado las expresiones simplificadas para calcular según el modelo propuesto, es decir, la ecuación (35) para el cálculo de Vu, y las ecuaciones (19), (23), (24) y (34) para el cálculo de las contribuciones adimensionales vw, vl, vs y vc, respectivamente.
Verificación de diferentes formulaciones a cortante con los resultados experimentales
| Vexp/Vpred | 892 vigas sin estribos | 239 vigas con estribos | ||||||
|---|---|---|---|---|---|---|---|---|
| EC-2 | ACI 318-08 | CM2010Nivel II | Propuesta | EC-2 | ACI 318-08 | CM2010Nivel III | Propuesta | |
| Media | 1,07 | 1,28 | 1,20 | 1,04 | 1,72 | 1,25 | 1,21 | 1,06 |
| Mediana | 1,03 | 1,27 | 1,16 | 1,01 | 1,61 | 1,24 | 1,20 | 1,05 |
| Desv. estándar | 0,226 | 0,346 | 0,223 | 0,186 | 0,638 | 0,262 | 0,225 | 0,173 |
| COV (%) | 21,12 | 27,11 | 18,61 | 17,93 | 37,13 | 21,04 | 18,58 | 16,35 |
| Mínimo | 0,66 | 0,38 | 0,74 | 0,66 | 0,62 | 0,65 | 0,75 | 0,69 |
| (Vexp/Vpred)5% | 0,79 | 0,71 | 0,91 | 0,79 | 0,97 | 0,85 | 0,92 | 0,83 |
| Máximo | 2,26 | 2,40 | 2,28 | 1,78 | 5,53 | 2,34 | 2,20 | 1,78 |
| (Vexp/Vpred)95% | 1,53 | 1,90 | 1,62 | 1,39 | 2,77 | 1,65 | 1,60 | 1,34 |
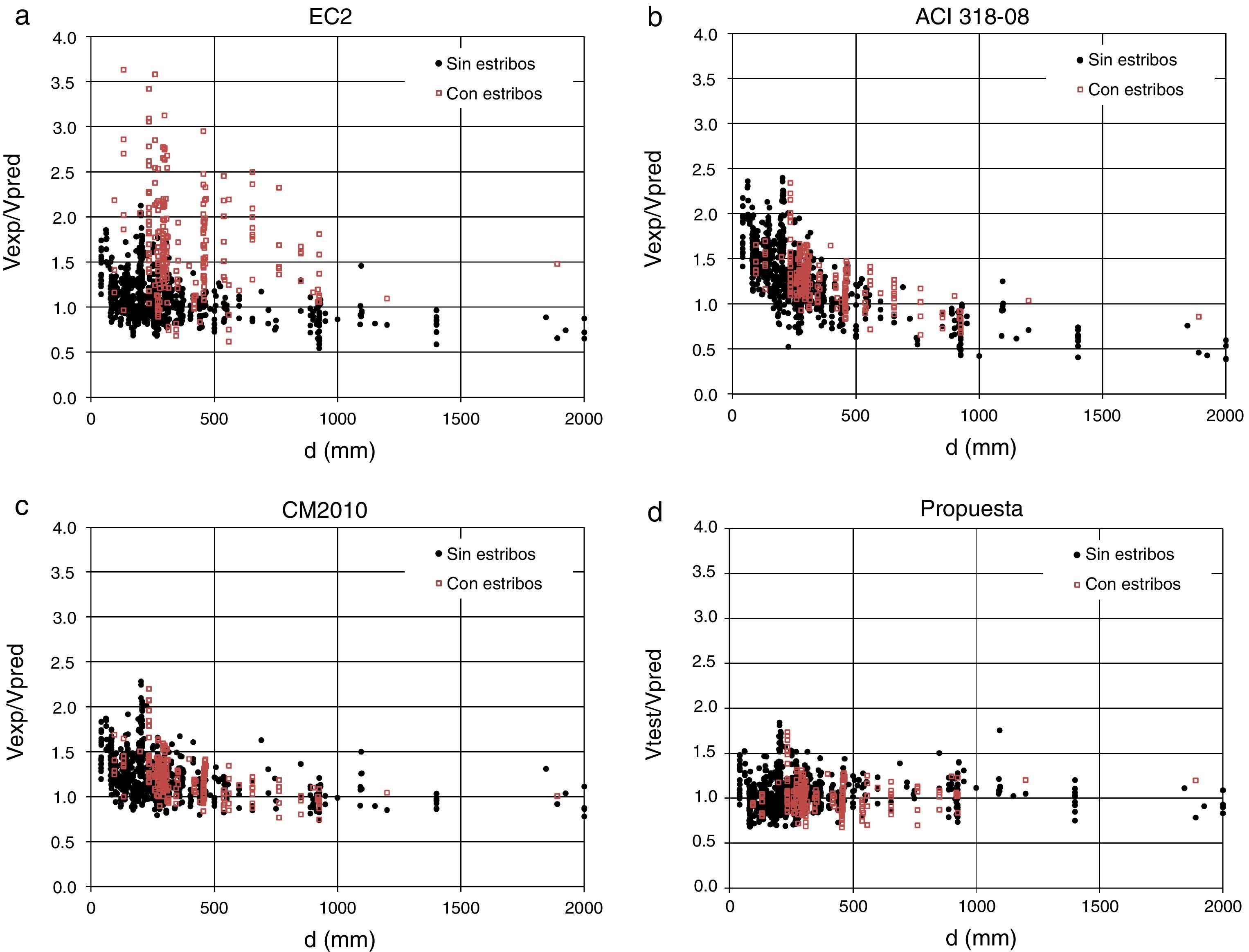
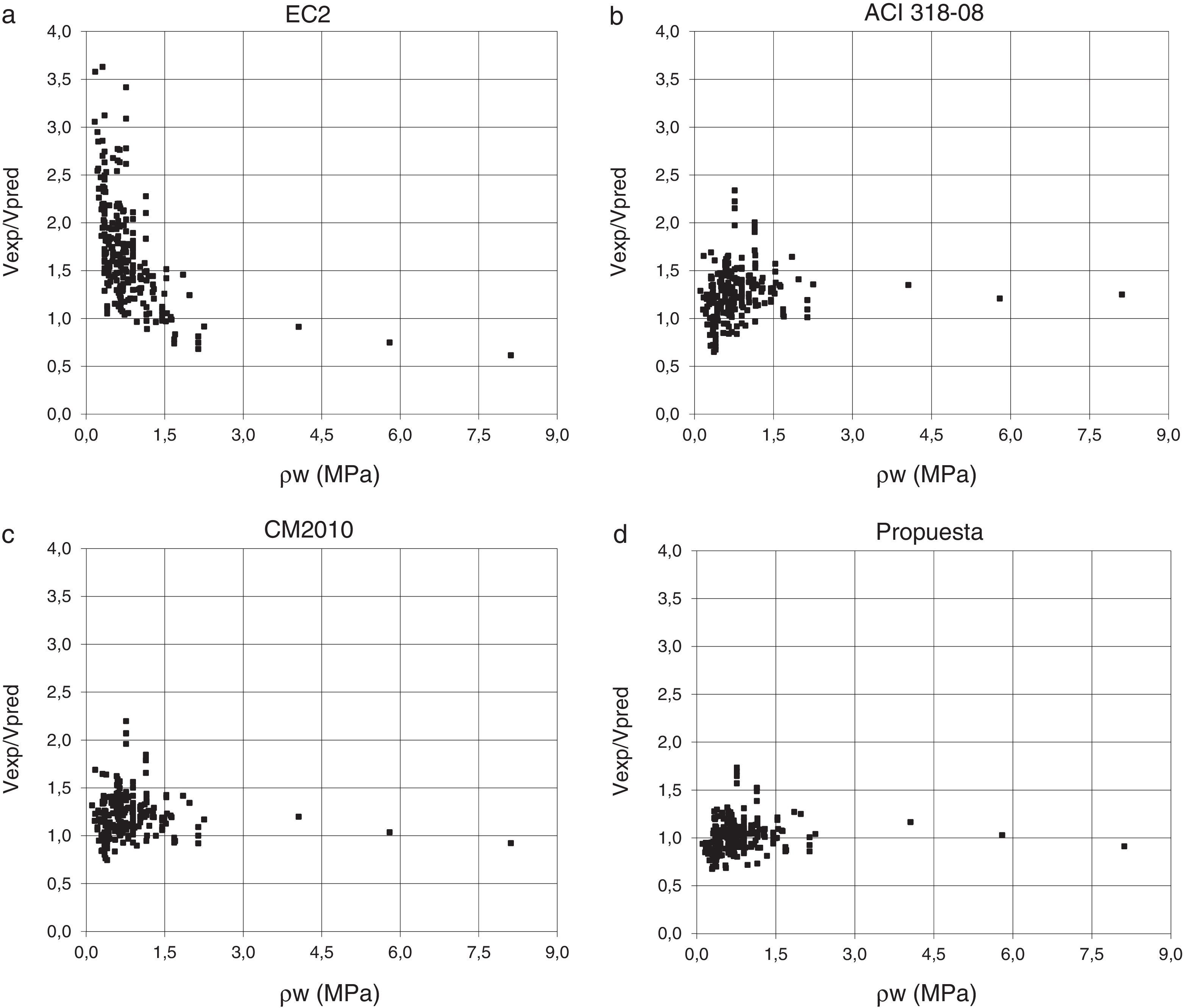
La comparación de los resultados de los diversos modelos con los experimentales se presenta también en forma gráfica, en función del canto de la pieza (fig. 18) y de la cuantía de armadura transversal (fig. 19). Se observa que conforme aumenta el canto útil del elemento, el valor medio de la razón entre los resultados experimentales y las predicciones teóricas, Vexp/Vpred, decrece para el EC2 [11] y para el CM2010 [33], mientras que permanece estable para el método propuesto. Cuando aumenta la cuantía de armadura transversal, la razón Vexp/Vpred decrece para la formulación del EC2 (de 1,95 para ρw ≤ 0,70MPa, a 0,97 para vigas fuertemente armadas, ρw≥1,50MPa), mientras que la formulación propuesta es mucho más estable.
En el caso de vigas sometidas a carga uniformemente repartida, el modelo puede aplicarse teniendo en cuenta que la ley de esfuerzos cortantes disminuye con la distancia al apoyo. Por ello, la fisura crítica estará incluso más próxima al apoyo que bajo carga puntual, como se indica en la figura 20, donde se muestran resultados de los ensayos de Stuttgart [41]. El efecto de la carga repartida se puede considerar incluyendo dicha carga en las ecuaciones de equilibrio de la porción de viga afectada por la fisura crítica:
La resistencia adimensional a cortante de la cabeza viene dada por la ecuación general, (42), en la cual el término que incluye la carga repartida es despreciable, por lo que el valor del cortante Vc puede considerarse el mismo que bajo cargas puntuales. Sin embargo, el cortante último calculado corresponde a la sección crítica, por lo que la reacción en el apoyo deberá obtenerse a partir de ese cortante, sumándole la resultante de la carga repartida entre esa sección y el apoyo.
En cuanto a la luz de cortante, a, para vigas con carga repartida, parámetro a utilizar en el cálculo del efecto tamaño, según la expresión (33), se considera a=L/4, siendo L la luz de cálculo de la viga biapoyada o la luz entre puntos de momento nulo.
Se ha verificado esta formulación con una base de datos de 49 vigas sometidas a cargas repartidas [1]. Lo que se compara son los valores de la carga última o de la reacción obtenidas, ya que el esfuerzo cortante no es constante a lo largo de la viga, por lo cual al cortante último obtenido se le ha sumado el valor ΔR=qu·d. La media del cociente entre carga experimental y teórica ha sido 1,03 y el coeficiente de variación 12,25%, que son valores muy aceptables (fig. 21).
7EXTENSIÓN DEL MODELO A OTROS CASOS DE ESTRUCTURAS USUALESEl modelo puede ser extendido a piezas con sección en T, piezas con canto variable, elementos parcialmente pretensados, vigas o columnas sometidas a axiles moderados de compresión o de tracción, a elementos armados con barras de FRP, a vigas de hormigón con fibras, a vigas continuas y a otros casos usuales en las estructuras reales. Se trata de adecuar las hipótesis de partida, las ecuaciones de equilibrio o los parámetros que intervienen en la formulación, a cada caso en concreto. Es posible incluso llegar a expresiones generales que sean válidas, como caso particular, a las expresiones obtenidas en este trabajo.
Así, en el caso de las secciones en T habrá que tener en cuenta que, caso de penetrar la fisura en la cabeza, ésta tendrá dos ramas con inclinaciones diferentes. Además, el momento de fisuración y la distancia del centro de gravedad a la fibra más traccionada aumentan respecto del de una viga rectangular del mismo canto y ancho igual al del alma, lo que podrá variar la posición de la sección crítica respecto de una viga de sección rectangular. Por otra parte, la profundidad de la fibra neutra deberá calcularse según la fisura penetre o no en la cabeza. En cualquier caso, según el presente modelo la contribución de la cabeza a la resistencia a cortante puede ser muy importante según la geometría de la sección, en contra de lo que predicen las normativas actuales. Este aspecto fue detectado por Placas y Regan [42] y ha sido recientemente predicho teóricamente por Celada et al. [30] y verificado experimentalmente en Pujol et al. [31] y Ribas y Cladera [43].
En el caso de piezas parcialmente pretensadas, será necesario incluir el esfuerzo axil, su inclinación y su excentricidad en las ecuaciones de equilibrio, lo que afectará a las tensiones de compresión de la cabeza y al valor de la profundidad del eje neutro, x/d, lo que afectará a Vc. El pretensado (o esfuerzo axil) y su excentricidad darán lugar a un cambio del momento de fisuración, y por tanto la distancia de la fisura crítica al apoyo xcr, así como a un cambio de la inclinación de la fisura, (β>0,85), que deberán ser tenidos en cuenta. Por otra parte, el ancho de fisuras será menor y ello conducirá a una mayor contribución del alma. Este aspecto deberá incluirse al calcular o estimar la deformación ¿s que consta en la expresión (18) que proporciona Vw.
En caso de un esfuerzo axil de tracción, deberá calcularse la profundidad de la fibra neutra (que será menor que en flexión simple) introduciendo el esfuerzo axil de tracción en el cálculo seccional y deberá incluirse tal esfuerzo en las ecuaciones de equilibrio.
En vigas armadas con FRP, deberá tenerse en cuenta el bajo módulo de deformación de estos materiales, que afectará a la profundidad de la fibra neutra y al ancho de fisura, reduciéndose tanto Vc como Vw. En caso de que haya armaduras transversales de FRP, deberá considerarse que los cercos no plastificarán cuando la pieza rompa a cortante, no pudiendo considerar, por tanto, la tensión de rotura máxima en todos los cercos que cruzan la fisura, debiéndose considerar una hipótesis sobre la distribución de tensiones en los cercos a lo largo de la fisura inclinada.
El modelo también puede adaptarse a vigas reforzadas externa o internamente con FRP u otros materiales, como las aleaciones con memoria de forma, con grandes aplicaciones en refuerzo estructural o para la creación de rótulas plásticas, incluyendo en la formulación las propiedades adecuadas de estos refuerzos [44,45].
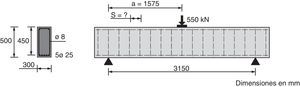
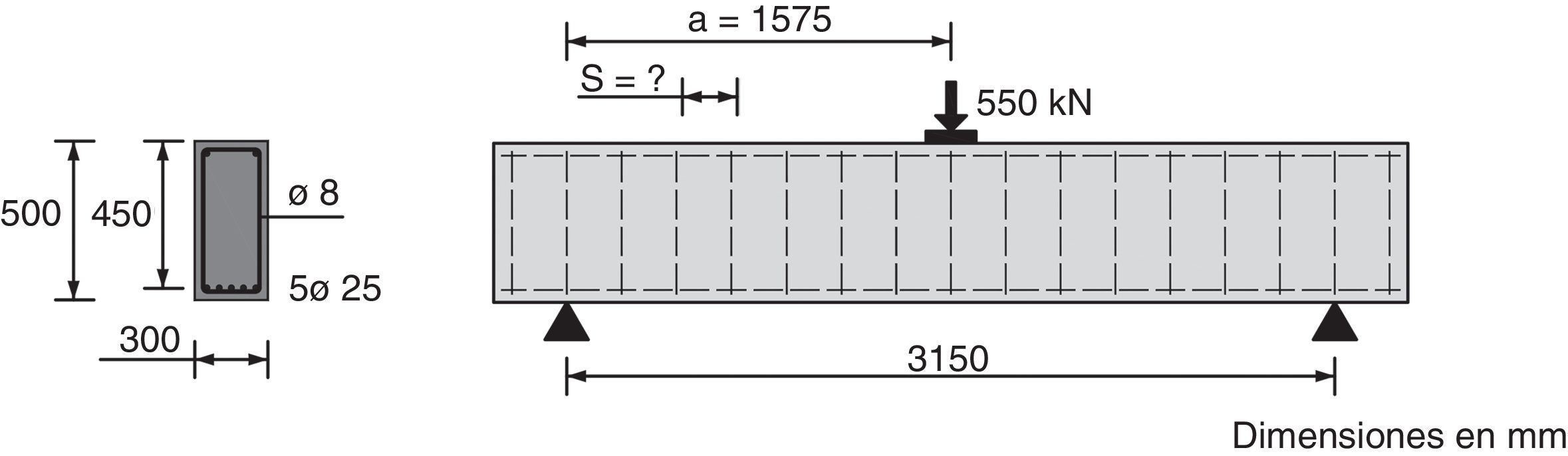
8EJEMPLO DE APLICACIÓNConsidérese una viga biapoyada cargada puntualmente en su centro de luz, cuya geometría y armado se indican en la figura 22. La resistencia a compresión del hormigón es de 35MPa, el tamaño máximo del árido es igual a 20mm y todas las armaduras son B500S. La carga máxima mayorada que tiene que resistir la viga biapoyada es de 550kN. Previamente a la resolución de este ejemplo es preciso señalar que en estos momentos se está llevando a cabo una calibración de los coeficientes de seguridad que son necesarios aplicar al modelo, por lo que el dimensionado de la armadura se llevará a cabo sin utilizar coeficientes de seguridad y mediante la utilización de los valores medios de las resistencias del hormigón.
Las propiedades mecánicas que son necesarias conocer para la aplicación del modelo son la resistencia a tracción, el módulo secante del hormigón y la energía de fractura (ec. 20). Los dos primeros valores se obtienen según la formulación del EC2:
El cortante adimensional de cálculo que debe soportar la viga es igual a:
Por medio de las ecuaciones (19), (34) y (36) se puede obtener la contribución del cortante resistido a través de la fisura, la contribución de la cabeza comprimida y el cortante total resistido por esta viga sin armadura a cortante. Resulta:
Como el cortante solicitación es mayor al cortante resistido por la viga sin cercos es preciso añadir armadura de cortante. La ecuación (38) proporciona directamente la cuantía de armado a disponer. Previamente, mediante la ecuación (23) se estima la contribución a cortante de la armadura longitudinal (efecto pasador) y también es necesario obtener el esfuerzo cortante de cálculo de forma adimensional:
A partir de la cuantía adimensional de la armadura a cortante se puede obtener qué armadura a cortante se debe disponer mediante la ecuación (24):
Por tanto, según el resultado exacto del cálculo sería necesario disponer 1 cerco ϕ8 cada 236mm. A modo de comparación, realizando los mismos cálculos según el EC2 [11], también sin utilizar coeficientes de seguridad, sería necesario disponer 1 cerco ϕ8 cada 185mm.
El momento de fisuración considerando la armadura traccionada es igual a Mcr=49,87kNm (valor adimensional μ = 0,255), Considerando un valor Vu exactamente igual a Vd, es decir, disponiendo la cuantía exacta resultante, el momento de fisuración se alcanzaría a una distancia del apoyo scr=Mcr/Vu=49,87/275=0,18m, es decir, 0,4·d. La distancia de la sección crítica al apoyo es igual a su=scr+0,85·d=0,18+0,85·0,45=0,56m (1,24 d), y el momento M concomitante con el cortante último en dicha sección M=Vu·su=275·0,56=154kNm. La primera rama de la fisura critica forma un ángulo medio con el eje longitudinal de la viga de 36,3° (cot θ =0,85/(1-0,376)=1,36).
La tensión normal en la sección crítica (su=0,56m), en el punto donde teóricamente se inicia el daño, situado a una distancia del eje neutro y=0,425x=72mm se obtiene de la expresión (30):
Donde los valores de todos los parámetros que intervienen en esta expresión se han obtenido previamente, excepto la profundidad de la zona de la fisura que transmite tracciones, cuyo valor se obtiene a continuación mediante las Ecs. (13) y (17). El valor de la deformación en la armadura, ¿s, se toma igual a 0,0009, tal y como se ha comentado en el apartado 3.2.
La tensión vertical en el hormigón en la cabeza vale, a partir de la Ec. (25):
La tensión tangencial en el punto crítico τλ se deduce de la expresión (5) que presenta el equilibrio de cortantes en la cabeza, como sigue:
Donde Vc debe ser calculado teniendo en cuenta la influencia de la armadura transversal, de acuerdo con la Ec. (34):
Entonces, las tensiones principales se pueden calcular según las Ecs. (1) y (2):
Se observa que se verifica el criterio de rotura de Kupfer (Ec. 9):
Donde tanto la tensión como la resistencia a compresión se consideran negativas.
9CONSIDERACIONES FINALES Y CONCLUSIONESSe ha presentado un modelo mecánico de cálculo a cortante que incluye la contribución de la cabeza comprimida, el cortante transmitido a través de la fisura, el resistido por las armaduras transversales, si existen y, en tal caso, el efecto pasador de las armaduras longitudinales. Las conclusiones concretas que pueden extraerse son las siguientes:
- -
En piezas sin armadura transversal, el cortante debe ser resistido por un conjunto de bielas de hormigón y tirantes también de hormigón, que atraviesan las fisuras en su parte más cerrada.
- -
El aumento de la carga, y por ello del ancho de fisura debilita el valor del tirante y cambia su inclinación, obligando a inclinarse la compresión en la cabeza para resistir el cortante que no resiste el tirante, creando un cierto efecto arco.
- -
La distribución de tensiones tangenciales en la cabeza puede considerarse, de forma simplificada, parabólica con un máximo en un punto interior de ella, fruto del comportamiento intermedio entre los mecanismos de viga y de arco.
- -
La presencia de armadura transversal incrementa la capacidad de la cabeza comprimida para resistir tensiones tangenciales, debido a las tensiones verticales de confinamiento que introduce y al hecho de que, al aumentar el cortante resistido, aumenta también el momento flector y por tanto la compresión en la cabeza.
- -
Las expresiones propuestas proporcionan información cualitativa y cuantitativa sobre los parámetros que gobiernan el comportamiento estructural, lo cual es muy útil de cara a proyecto y evaluación de estructuras existentes. Por otra parte, el método es válido para dimensionamiento y comprobación directos, sin necesidad de iteraciones.
- -
La resistencia de la cabeza resulta ser lineal con la profundidad relativa de la fibra neutra en flexión, x/d, la cual depende de la cuantía geométrica de armadura longitudinal y del coeficiente de equivalencia Es/Ec.
- -
El carácter mecánico del modelo permite adaptarlo a numerosos casos, como vigas sometidas a carga repartida, vigas continuas, secciones en T, piezas parcialmente pretensadas o solicitadas por axiles moderados, o piezas armadas con FRP para las cuales se ha explicado cuáles son los aspectos que deben modificarse para ser incluidos en el modelo.
- -
En secciones en T, la contribución de la cabeza a la resistencia a cortante puede ser muy relevante, a diferencia de lo considerado por los códigos vigentes.
- -
El modelo descrito ajusta muy bien los resultados experimentales para todos los casos estudiados y arroja mejores predicciones que las norma EC2 [11], ACI 318-08 [12] y Código Modelo 2010 [33]. Ello es muy relevante, dada la sencillez de las expresiones derivadas, evitando sobredimensionamientos injustificados. Además, en caso de utilizar la propuesta para la evaluación de estructuras existentes, se podrían evitar refuerzos estructurales innecesarios ya que la resistencia real de la estructura podría ser mayor a la reflejada por la normativa vigente.
Este trabajo se está desarrollando en el seno de los proyectos de investigación BIA2012-36848 y BIA2012-31432, ambos financiados por el Ministerio de Economía y Competitividad (MINECO) y por el Fondo Europeo de Desarrollo Regional (FEDER).








![Envolvente de rotura de Kupfer bajo un estado biaxial de tensiones. Adaptado de [27]. Envolvente de rotura de Kupfer bajo un estado biaxial de tensiones. Adaptado de [27].](https://static.elsevier.es/multimedia/04395689/0000006500000274/v1_201505200353/S0439568914000096/v1_201505200353/es/main.assets/thumbnail/gr7.jpeg?xkr=ue/ImdikoIMrsJoerZ+w96p5LBcBpyJTqfwgorxm+Ow=)
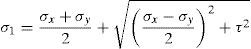
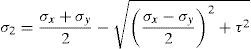
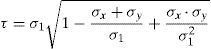
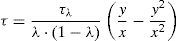
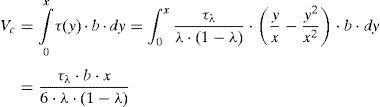
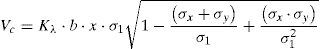
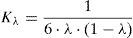
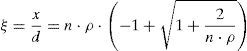
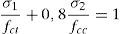
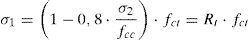
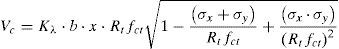
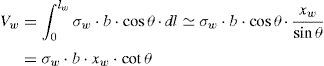
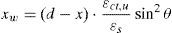
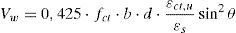
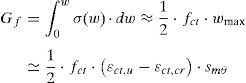
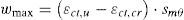
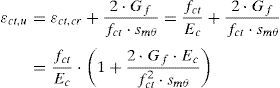
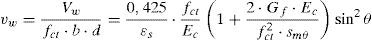
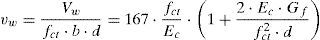
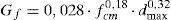
 fcm, adaptada de [35].' title='Resultados experimentales de la energía de fractura en función de
fcm, adaptada de [35].' title='Resultados experimentales de la energía de fractura en función de