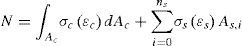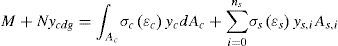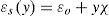Diseño óptimo de dovelas de hormigón reforzado con fibras para el revestimiento de túneles

Resumen

El uso del hormigón reforzado con fibras (HRF) para la fabricación de dovelas de túneles es una práctica en aumento. Sin embargo, aún existe cierta inercia al cambio respecto a la solución tradicional de hormigón armado con armaduras pasivas, pese a haberse demostrado desde el punto de vista técnico y económico que el uso del HRF en esta aplicación es viable y tiene ventajas. Un hecho que pone de manifiesto esta inercia al cambio es que existen numerosas aplicaciones en las que se ha empleado el HRF, en combinación con barras, si bien la contribución resistente de las fibras no se tuvo en cuenta. Esto es principalmente debido a la falta de regulaciones específicas que aborden aspectos de control, producción y diseño de estructuras de HRF. Afortunadamente, a nivel nacional, el Anejo 14 de la instrucción EHE-08 ya plantea unas guías para hacer frente a estos campos y, adicionalmente, el Código Modelo 2010 también presenta una guía para el diseño de estructuras de HRF. Este artículo tiene como objetivos, por una parte, presentar las experiencias más relevantes a nivel internacional del uso de HRF en la ejecución de anillos para el revestimiento de túneles ejecutados con tuneladora y, por otra, plantear un esquema de cálculo para abordar el diseño óptimo del refuerzo de dovelas de HRF. Asimismo, se presentan 3 ejemplos reales en los que se ha empleado el método propuesto.

Abstract

The use of fibre reinforced concrete (FRC) in precast segments for tunnel support is an increasing practice. However, although the suitability of this material seems to be proven at a technical and economic level, there is still some reluctance towards the natural implementation of this material. In fact, in those cases in which fibres were added to concrete, the structural contribution was not taken into account in the design. This is mainly due to the lack of specific regulations to deal with this, as well as other aspects related to the control, production and design of FRC structures. Fortunately, at national level, Annex 14 of the Spanish EHE-08 already proposes guidelines as regards these aspects, and the new Model Code 2010 also considers the FRC as a structural material. This paper aims, on the one hand, to analyse the most important applications of FRC in tunnel linings worldwide and, on the other hand, presents a design methodology which enables the reinforcement configuration of fibre reinforced concrete in precast segments to be optimised. Furthermore, three real examples of application in which this method has been applied are described.

1

Introducción

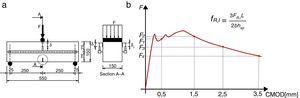
El uso de fibras estructurales en el hormigón conduce a una mejora del comportamiento resistente de la matriz cuando esta está sometida a tensiones de tracción [1–3], aumenta su tenacidad, su resistencia frente al fuego, al impacto y a tensiones concentradas debido a su acción de confinamiento. Entre las distintas mejoras, en el caso particular de dovelas de hormigón prefabricado son ya conocidas las ventajas que el uso de fibras supone cuando estas se emplean para hacer frente a las tensiones concentradas que pueden ocurrir durante las fases transitorias (desmoldeo, apilado, transporte, manipulación y empuje de los gatos; fig. 1). Adicionalmente, es sabido que la contribución estructural de las fibras puede conducir al reemplazo total o parcial de la armadura pasiva en forma de barras y, en global, aumentar la eficiencia de la producción y garantizar la competitividad del hormigón reforzado con fibras (HRF) frente a las alternativas tradicionales en este tipo de aplicación [4–9].

Figura 1.

Fases transitorias de carga de las dovelas: a) desmoldeo; b) apilado; c) transporte, y d) empuje de los gatos.

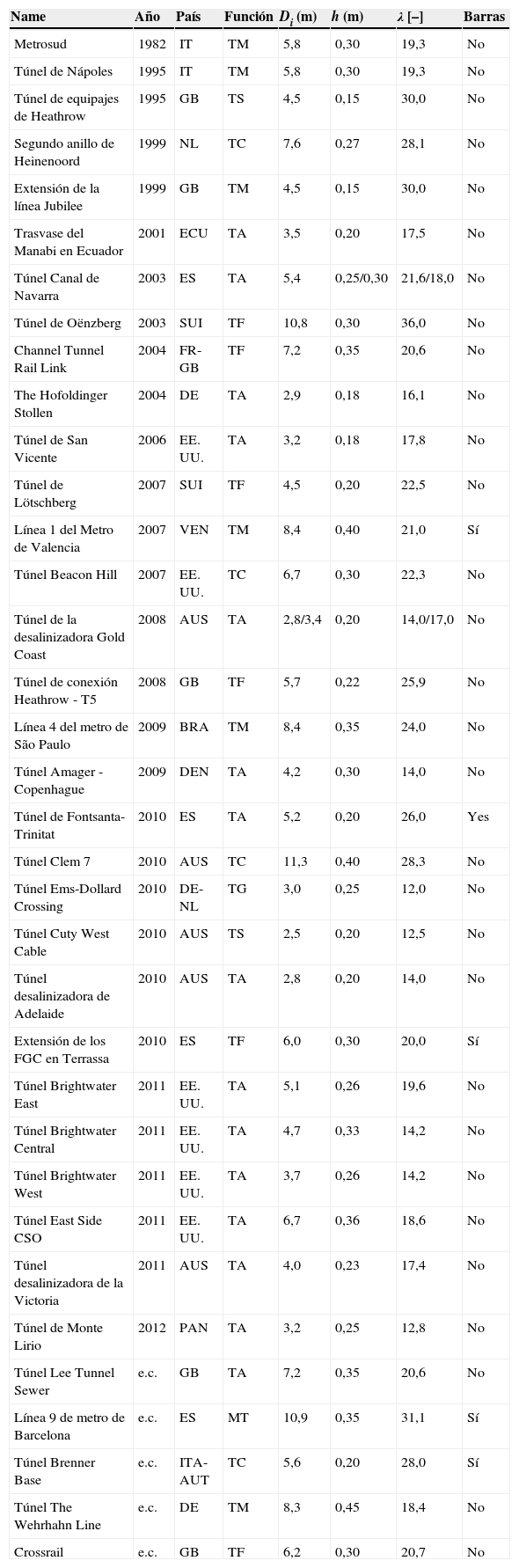
Prueba de estas ventajas son las numerosas experiencias existentes en las cuales el HRF se ha empleado para la ejecución de dovelas (tabla 1) en túneles carreteros (TC), túneles ferroviarios (TF), de metro (TM), para el transporte de agua (TA), de gas (TG) y otros servicios (TS); algunos de estos están aún en construcción (e.c.).

Tabla 1.

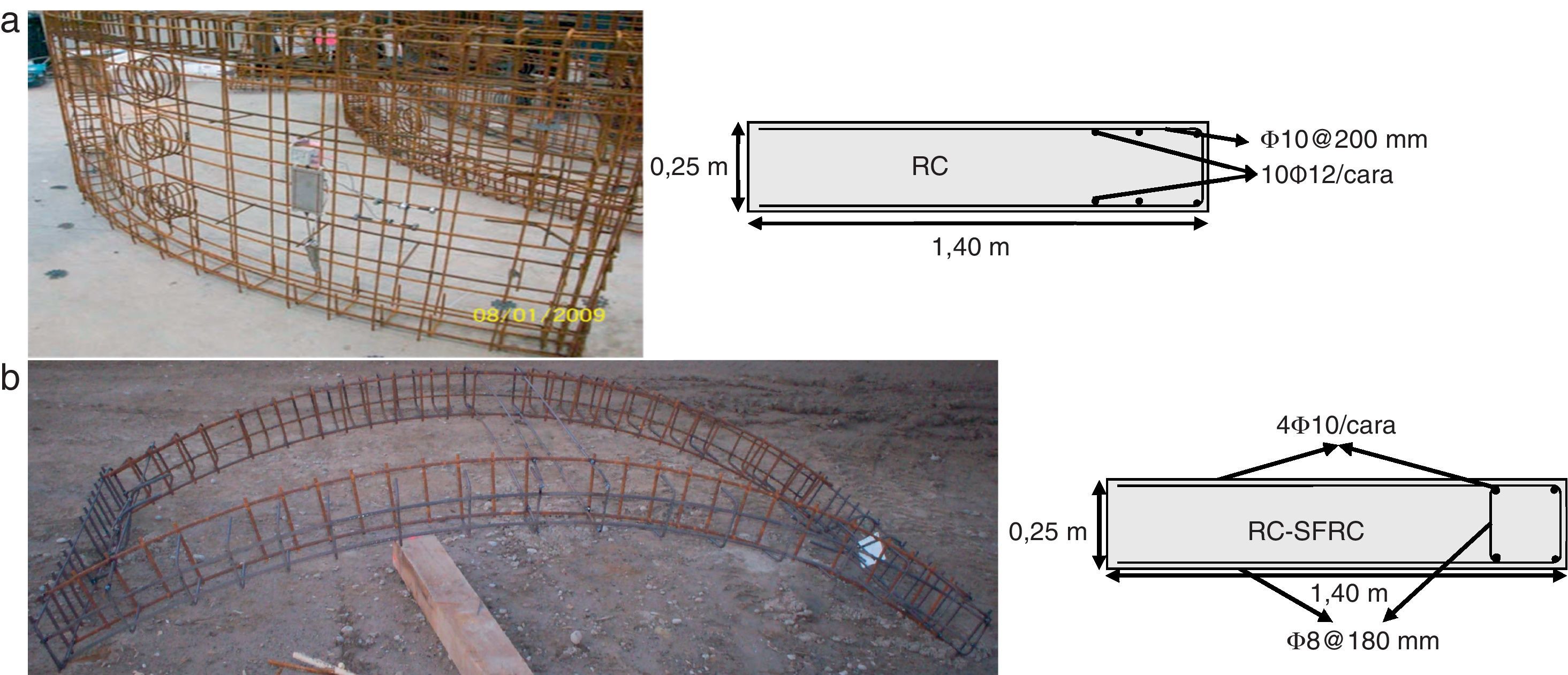
Varios ejemplos del uso de fibras para el refuerzo del hormigón prefabricado en dovelas de anillos de revestimiento

Name	Año	País	Función	Di (m)	h (m)	λ [–]	Barras
Metrosud	1982	IT	TM	5,8	0,30	19,3	No
Túnel de Nápoles	1995	IT	TM	5,8	0,30	19,3	No
Túnel de equipajes de Heathrow	1995	GB	TS	4,5	0,15	30,0	No
Segundo anillo de Heinenoord	1999	NL	TC	7,6	0,27	28,1	No
Extensión de la línea Jubilee	1999	GB	TM	4,5	0,15	30,0	No
Trasvase del Manabi en Ecuador	2001	ECU	TA	3,5	0,20	17,5	No
Túnel Canal de Navarra	2003	ES	TA	5,4	0,25/0,30	21,6/18,0	No
Túnel de Oënzberg	2003	SUI	TF	10,8	0,30	36,0	No
Channel Tunnel Rail Link	2004	FR-GB	TF	7,2	0,35	20,6	No
The Hofoldinger Stollen	2004	DE	TA	2,9	0,18	16,1	No
Túnel de San Vicente	2006	EE. UU.	TA	3,2	0,18	17,8	No
Túnel de Lötschberg	2007	SUI	TF	4,5	0,20	22,5	No
Línea 1 del Metro de Valencia	2007	VEN	TM	8,4	0,40	21,0	Sí
Túnel Beacon Hill	2007	EE. UU.	TC	6,7	0,30	22,3	No
Túnel de la desalinizadora Gold Coast	2008	AUS	TA	2,8/3,4	0,20	14,0/17,0	No
Túnel de conexión Heathrow - T5	2008	GB	TF	5,7	0,22	25,9	No
Línea 4 del metro de São Paulo	2009	BRA	TM	8,4	0,35	24,0	No
Túnel Amager - Copenhague	2009	DEN	TA	4,2	0,30	14,0	No
Túnel de Fontsanta-Trinitat	2010	ES	TA	5,2	0,20	26,0	Yes
Túnel Clem 7	2010	AUS	TC	11,3	0,40	28,3	No
Túnel Ems-Dollard Crossing	2010	DE-NL	TG	3,0	0,25	12,0	No
Túnel Cuty West Cable	2010	AUS	TS	2,5	0,20	12,5	No
Túnel desalinizadora de Adelaide	2010	AUS	TA	2,8	0,20	14,0	No
Extensión de los FGC en Terrassa	2010	ES	TF	6,0	0,30	20,0	Sí
Túnel Brightwater East	2011	EE. UU.	TA	5,1	0,26	19,6	No
Túnel Brightwater Central	2011	EE. UU.	TA	4,7	0,33	14,2	No
Túnel Brightwater West	2011	EE. UU.	TA	3,7	0,26	14,2	No
Túnel East Side CSO	2011	EE. UU.	TA	6,7	0,36	18,6	No
Túnel desalinizadora de la Victoria	2011	AUS	TA	4,0	0,23	17,4	No
Túnel de Monte Lirio	2012	PAN	TA	3,2	0,25	12,8	No
Túnel Lee Tunnel Sewer	e.c.	GB	TA	7,2	0,35	20,6	No
Línea 9 de metro de Barcelona	e.c.	ES	MT	10,9	0,35	31,1	Sí
Túnel Brenner Base	e.c.	ITA-AUT	TC	5,6	0,20	28,0	Sí
Túnel The Wehrhahn Line	e.c.	DE	TM	8,3	0,45	18,4	No
Crossrail	e.c.	GB	TF	6,2	0,30	20,7	No

En la tabla 1 puede observarse cómo la esbeltez de los anillos (λ), cociente entre el diámetro interno del túnel (D_i) y el espesor de la dovela (h), varía entre 12,0 y 36,0. En este sentido, valores bajos de λ indican mayor rigidez del mismo y menor sensibilidad de este frente a posibles flexiones derivadas de discontinuidades del terreno, y, por tanto, la sección transversal de la dovela tiende a estar comprimida en régimen de servicio. En estas situaciones, la estrategia de refuerzo responde a la necesidad de proporcionar una cuantía de armadura suficiente para garantizar un comportamiento dúctil, en caso hipotético de rotura, para las fases transitorias de carga (fig. 1). En definitiva, en estos casos, que suelen ser la mayoría, la viabilidad de sustituir la armadura tradicional por una cuantía de fibras estructurales suele ser una alternativa atractiva desde el punto de vista técnico y económico.

Por el contrario, cuanto mayor es λ, mayor es la deformabilidad del anillo y mayor es la probabilidad de producirse flexiones elevadas concomitantes con el esfuerzo axil de régimen permanente. En estas circunstancias, la condición de servicio (explotación) suele ser la más desfavorable y aquella que gobierna el diseño del refuerzo del hormigón. En consecuencia, la sustitución total de la armadura tradicional por fibras puede no ser viable por aspectos tanto técnicos como económicos. Alternativamente, configuraciones mixtas consistentes en una cuantía de barras suficiente para contribuir en ELU y una cuantía moderada de fibras para controlar el ancho de fisura en aquellos casos que en servicio se prevea la fisuración del anillo, pueden ser una solución competitiva y atractiva desde el punto de vista de la durabilidad en aquellos casos en los que se trabaje con altos valores de esbeltez (λ).

En el área metropolitana de Barcelona se han excavado —o están actualmente en proceso de excavación— varios túneles en los cuales se emplea el HRF para la ejecución de las dovelas de revestimiento [9,10]. En varios de estos, el uso de fibras, bien metálicas y/o plásticas, tiene la finalidad de mejorar la respuesta del material frente al impacto y/o la acción del fuego. Sin embargo, su contribución estructural para hacer frente a las tracciones en régimen post-fisuración no se tuvo en cuenta en el proyecto. Esto responde, por una parte, a la falta de normativa en relación al HRF en el momento de la redacción del proyecto (EHE-1998 [11] en aquel momento). Por otra parte, la falta de experiencia de los técnicos de planta y de los ingenieros en relación con aspectos de control y caracterización ha sido otro de los factores que ha frenado la tecnología del HRF en esta aplicación como material resistente principal prácticamente hasta la fecha. Si bien debe resaltarse que el interés mostrado por el sector industrial sobre esta línea es evidente y ya se han hecho pruebas experimentales de dovelas de hormigón reforzado, solo con fibras, y añadiendo además la autocompactabilidad [12,13] para mejorar aspectos de fabricación (eliminación del ruido asociado a la vibración, mejores acabados, mayores rendimientos, direccionamiento de las fibras en las direcciones de máximas tensiones en servicio).

Como resultado de esto, la misión de resistir las tensiones de tracción se ha confiado exclusivamente a las barras de acero, cuya cuantía podría haber sido reducida considerablemente si la contribución de las fibras en régimen post-fisuración se hubiese tenido en cuenta en fase de diseño.

Afortunadamente, hoy en día ya existen instrucciones y recomendaciones en las que el uso estructural del HRF está contemplado (DBV 1992 [14], CNR DT 204/2006 [15], EHE 2008 [16], Código Modelo 2010 [17]) y que proporcionan guías y herramientas para abordar el diseño de elementos de HRF.

El objetivo de este artículo es presentar un método para evaluar el diseño óptimo de dovelas de HRF utilizando las ecuaciones constitutivas presentadas en el MC-2010, como referencia internacional, para simular la respuesta resistente de este material. Para alcanzar este objetivo, primero se presentan las bases de la filosofía de diseño adoptada, y posteriormente estas se aplican para el diseño de los anillos de revestimiento de 3 túneles reales excavados con tuneladora en el área metropolitana de Barcelona. Concretamente, las dovelas de estos anillos fueron diseñadas en el proyecto inicial sin considerar la contribución resistente de las fibras, pese a que estas se incorporan en el hormigón.

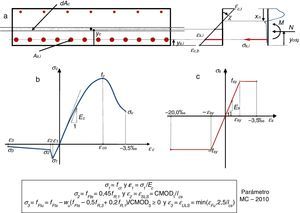
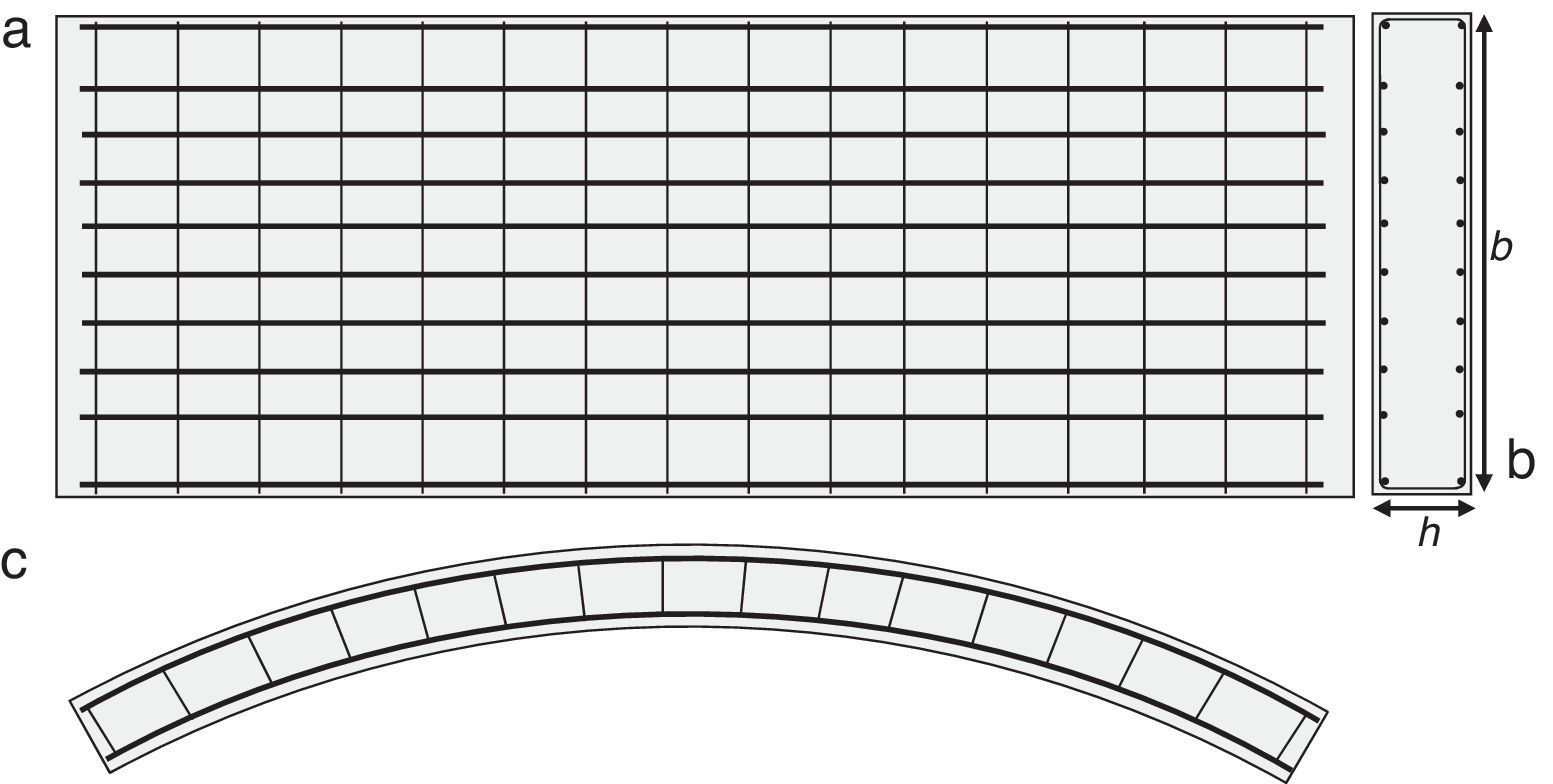
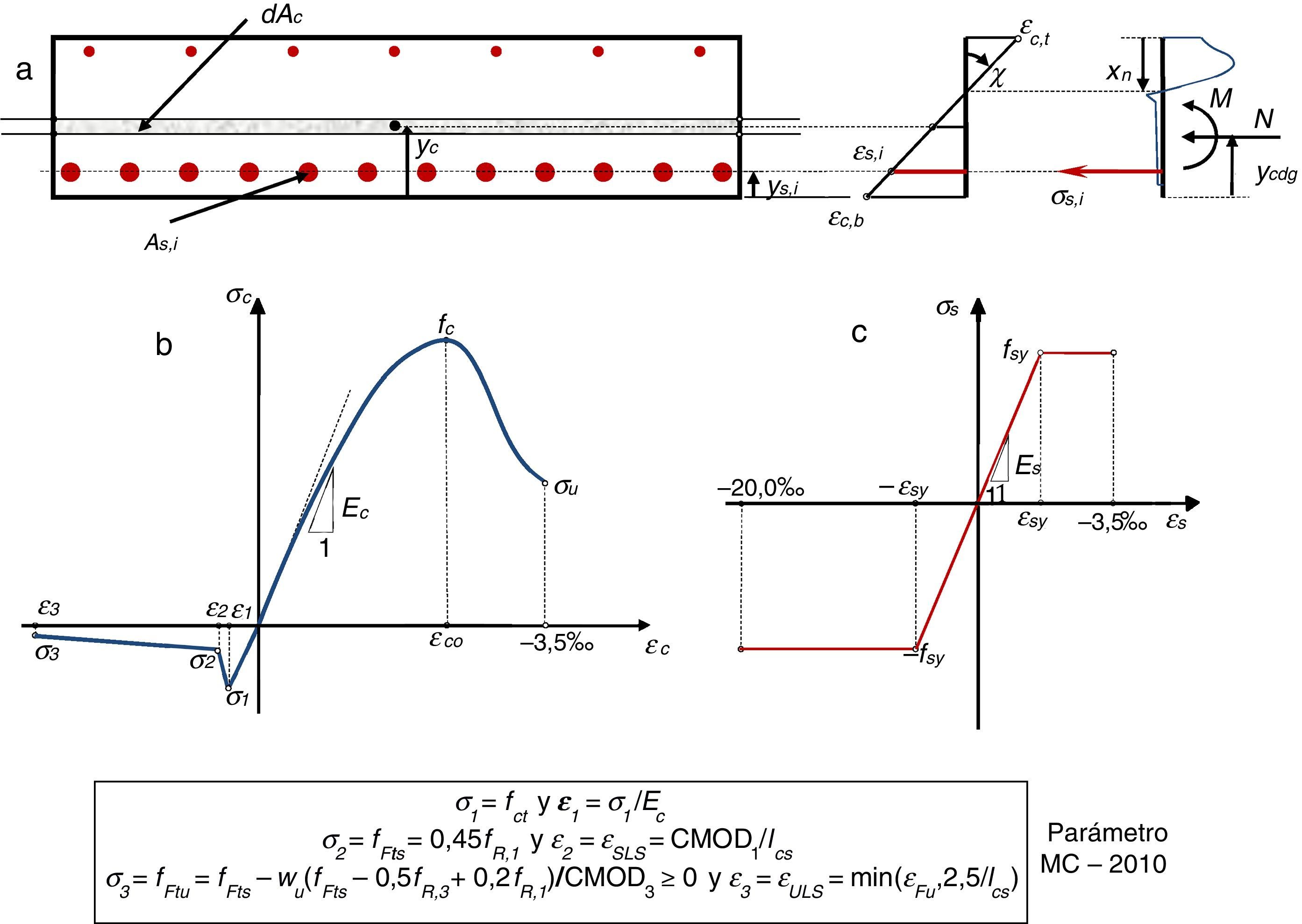
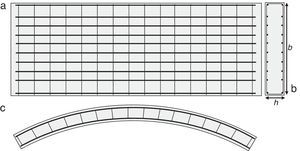
2

Filosofía de diseño propuesta para dovelas de hormigón reforzado con fibras

El refuerzo principal en ambas direcciones de la dovela (fig. 2) se dispone para hacer frente, mayoritariamente, a las tensiones de tracción que pueden aparecer durante las fases transitorias y servicio de la dovela, pudiendo tener estas origen mecánico o deformaciones impuestas de tipo térmico y/o higrométrico. Adicionalmente, se suele disponer un refuerzo complementario (no incluido en la figura 2 por no ser objeto de este estudio) en las zonas en las que se prevé concentración de tensiones con el fin de confinar localmente el hormigón y evitar así el salto del recubrimiento y/o los fenómenos de «desconchamiento» y «aplastamiento». Este tipo de refuerzo no se incluye en la figura 2, pues no es el objeto de este estudio; sin embargo, también se ha demostrado [4,5] que el efecto confinamiento que ejercen las fibras puede asimismo conducir a la reducción, e incluso a la eliminación, de estos refuerzos locales.

Figura 2.

Vistas superior (a), transversal (b) y frontal (c) del refuerzo de una dovela de hormigón armado.

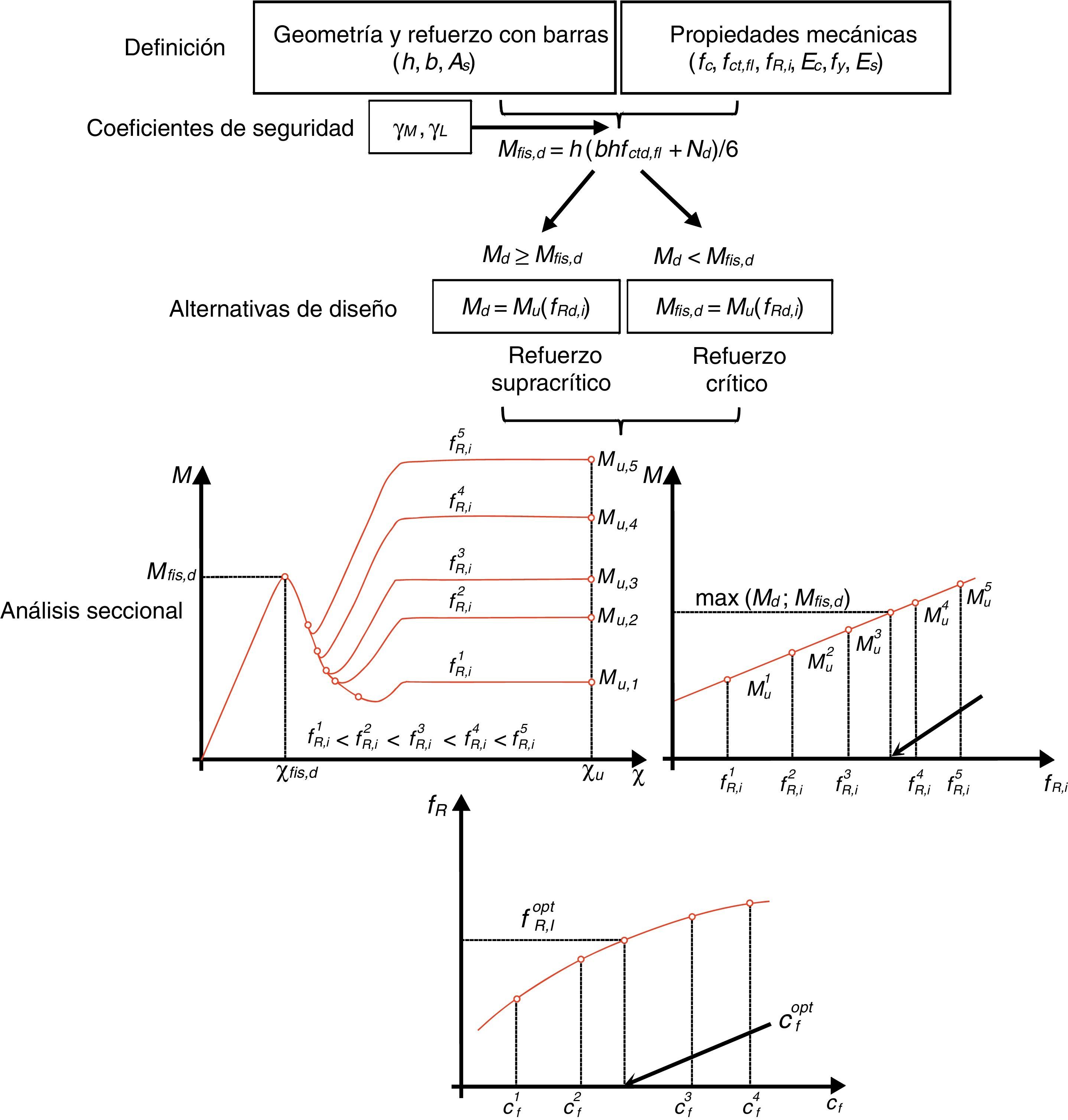
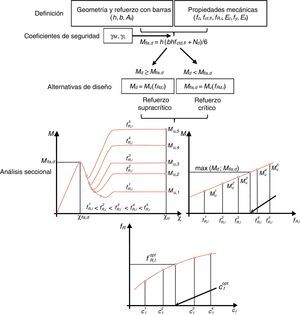
En cualquier caso, la respuesta de una dovela tiene que ser dúctil en régimen de rotura. Este tipo de respuesta se garantiza solo si se dispone una cuantía de refuerzo (A_T,min), siendo A_T la cuantía total de armadura (suma de la cuantía en forma de barras, A_s, y en forma de fibras, A_f). Dicho de otro modo, A_T,min es la mínima cuantía de refuerzo que garantiza que el momento último de la sección (M_u) coincide con el momento de fisuración de diseño (M_fis,d). Este último, función de las dimensiones de la sección transversal de la dovela (b y h; fig. 2a) y de la resistencia a flexotracción de diseño (f_ctd,fl). En este sentido, tanto M_u como M_fis,d deben evaluarse bajo el mismo axil de diseño concomitante N_d, si bien la situación más desfavorable suele darse durante las situaciones transitorias, en las que N_d es nulo o reducido (flexión simple).

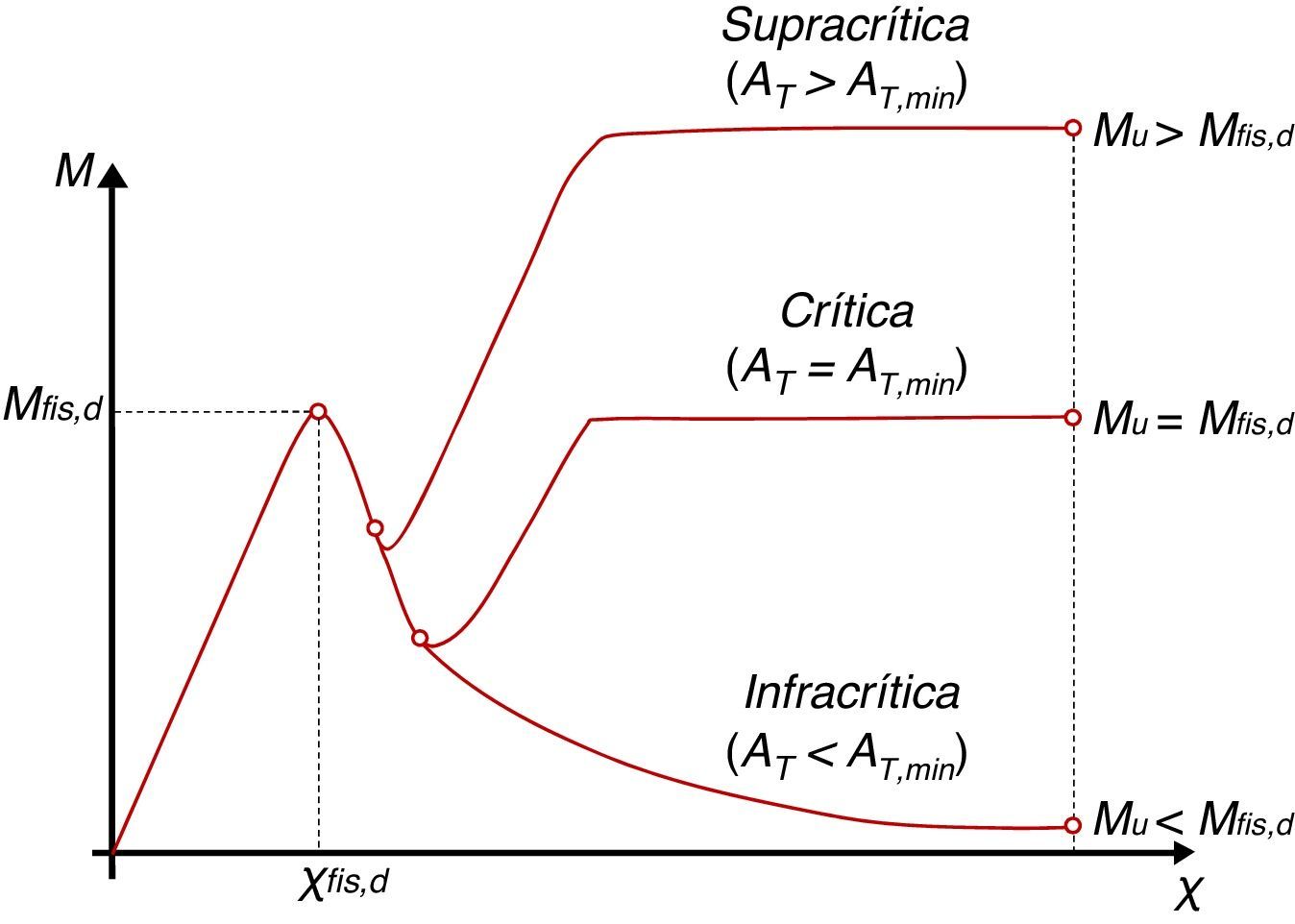
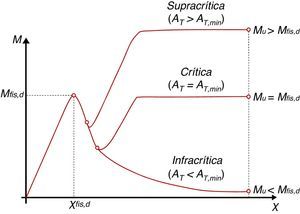
En la figura 3 se presentan los diagramas momento (M) - curvatura (χ) cualitativos para una sección de hormigón considerando distintos grados de refuerzo para visualizar los distintos tipos de rotura posibles.

Figura 3.

Modos de rotura a flexión en función de A_T.

La figura 3 pone de manifiesto que situaciones con A_T < A_T,min conducen a modos de rotura frágiles e inseguros. En la literatura técnica [18,19] estas estrategias de refuerzo se conocen como infracríticas, mientra que si A_T > A_T,min (refuerzo supracrítico) el comportamiento de la sección es dúctil. Finalmente, si A_T = A_T,min (refuerzo crítico), la respuesta de la sección es estrictamente dúctil sin ningún margen de seguridad, excepto el asociados a los coeficientes parciales de seguridad adoptados para minorar las resistencias de los materiales.

A nivel de diseño, si el momento de diseño (M_d) es menor que M_fis,d (M_d < M_fis,d), la A_T,min debe ser evaluada resolviendo la ecuación M_u = M_fis,d. Contrariamente, si M_d ≥ M_fis,d, la condición M_u = M_d es la que se debe imponer para obtener el valor de A_T (> A_T,min) que atiende a la capacidad mecánica requerida. En ambos casos, aunque la respuesta mecánica a nivel sección es distinta, la seguridad estructural que se alcanza es equivalente, pues se emplean los mismos coeficientes de seguridad parciales tanto para las resistencias como para las cargas.

En línea con lo mencionado anteriormente, en la gran mayoría de los túneles que emplean anillos de dovelas prefabricadas como sistema de revestimiento, el valor más desfavorable de M_d se alcanza en fases transitorias y suele estar asociado al peso propio de la dovela, o al conjunto de dovelas de cada anillo apiladas sobre la dovela base, y este suele ser menor que M_fis,d. Por tanto, en estas situaciones el hormigón debe reforzarse con la cuantía mínima de refuerzo A_T,min para garantizar la rotura dúctil en caso de producirse la fisuración en alguna etapa.

La experiencia indica que este tipo de roturas vienen asociadas a: 1) desmoldeos de la pieza cuando aún no se ha alcanzado la resistencia de diseño establecida en proyecto para evitar la fisuración a corto plazo; 2) excentricidades accidentales no tenidas en cuenta en el proyecto de los elementos de izado y/o de los aparatos de apoyo de las dovelas en planta o en transporte [20,21], y 3) manipulaciones indebidas durante las operaciones de colocación y montaje en el escudo; sin embargo, en estas últimas situaciones la dovela trabaja, por la configuración de apoyo, preferentemente como viga de gran canto [22].

En cualquier caso, debe añadirse que para el cálculo de M_d se acostumbran a considerar coeficientes de mayoración con los que se tienen en cuenta los posibles efectos dinámicos durante las fases transitorias y que aumentan el margen de seguridad frente a la fisuración durante estas fases.

Para la evaluación de las cuantías mínimas de armadura, las expresiones sugeridas en [14–17] tienden a arrojar valores de A_T,min y A_T muy conservadores. En esta línea y en aras de la optimización, así como para aprovechar las ventajas asociadas al uso del HRF en términos de reducción de refuerzo tradicional, queda justificado plantear el diseño de la estrategia de refuerzo acudiendo a modelos numéricos que permitan considerar la contribución resistente de las fibras, máxime cuando se trata de obras lineales con grandes volúmenes de material involucrados.

Se trata de resolver un problema de optimización con 2 variables: la cuantía de armadura tradicional A_s y la cuantía de fibras A_f. En definitiva, minimizar la función A_T = A_s + A_f de modo que se cumplan de forma simultánea las condiciones de ductilidad y alcanzar el requerimiento resistente (M_u = M_fis,d, o M_u = M_d en caso que M_d > M_fis,d).

Este problema se simplifica enormemente si de antemano se fija una de las cuantías. Así, el valor de A_s puede fijarse atendiendo a razones técnicas: 1) A_s ≠ 0 con el fin de proporcionar cierta capacidad resistente a flexión de la sección en ELU, permitiendo así trabajar con cuantías de fibras más reducidas y que conduzcan a hormigones más dóciles y trabajables. Un valor de tanteo inicial de A_s puede ser la cuantía mínima mecánica establecida en las distintas instrucciones, por ejemplo. 2) A_s = 0 en aquellos casos en que sea posible la sustitución total de las barras por una cuantía de fibras competitiva a nivel técnico y económico.

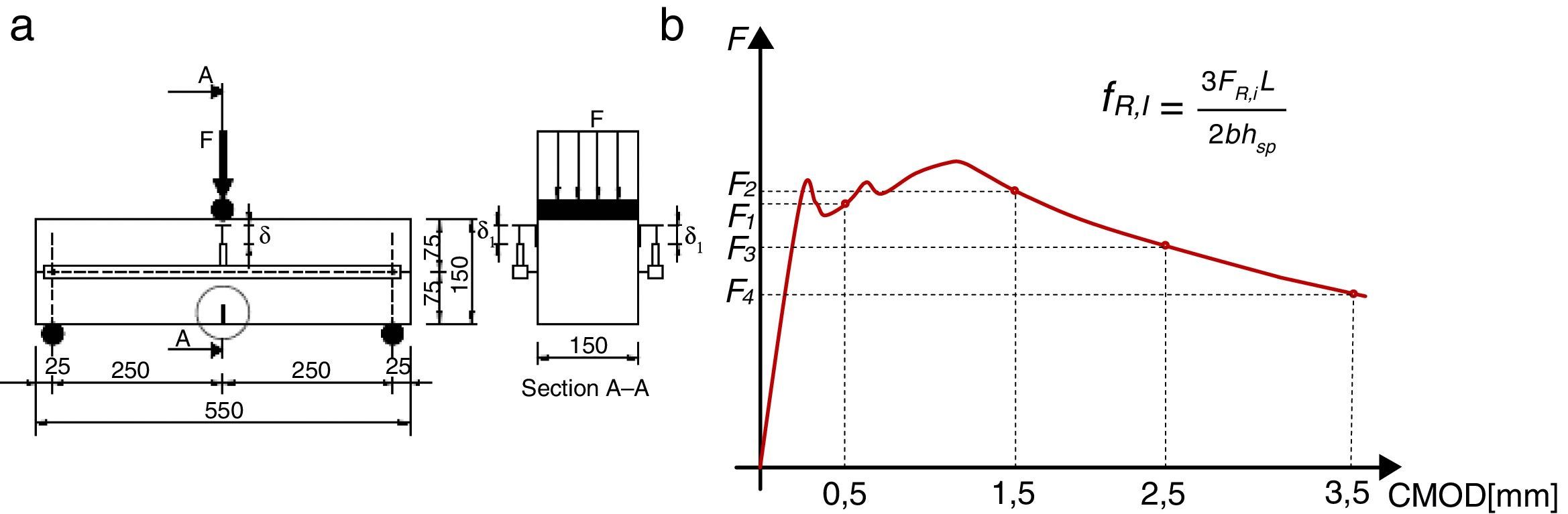
Generalmente, en fase de diseño el ingeniero no dispone de información relacionada con el comportamiento post-fisuración del HRF. Por tanto, a nivel de pre-diseño, es necesario considerar valores racionales de la resistencia residual del HRF (f_R,i), recogidos en la literatura o proporcionados por algún suministrador de HRF y/o fibras, para poder definir la ecuación constitutiva del material en régimen post-fisuración y evaluar la idoneidad del uso de fibras. En consonancia con lo establecido tanto en la EHE-08 como en el MC-2010, los valores de f_R,i deben obtenerse mediante el ensayo a 3 puntos de vigas prismáticas con entalla [23] (fig. 4).

Figura 4.

Ensayo de 3 puntos en vigas prismáticas entalladas: a) configuración del ensayo (mm), y b) curva genérica F-CMOD.

Habiendo establecido la respuesta residual del HRF para distintas dosificaciones de fibras (C_f), se pueden representar los diagramas momento-curvatura M-χ de la sección transversal de la dovela empleando algún modelo numérico. Con estos diagramas se pueden obtener los momentos últimos M_u^j asociados a cada dosificación de fibras C_f^j (que conducirán cada una de ellas a resistencias residuales f_R,i^j distintas). El diagrama de flujo de la figura 5 esquematiza el proceso a seguir para obtener el valor óptimo de C_f(C_f^opt) en dovelas de HRF.

Cfopt.'> Cfopt.' title='Procedimiento propuesto para evaluar fR,iopt y Cfopt.'/>

Figura 5.

Procedimiento propuesto para evaluar f_R,i^opt y C_f^opt.

El procedimiento de diseño presentado en la figura 5 concluye con una estimación de la resistencia residual óptima del HRF (f_R,i^opt) requerida para satisfacer los requerimientos resistentes. No obstante, en términos de producción y control del HRF, esta f_R,i^opt debe relacionarse con la dosificación de C_f^opt con el fin de formular la composición del hormigón y evaluar la idoneidad técnica y económica de la misma. Para tal fin, una vez se ha establecido el tipo de fibra a emplear, se debe llevar a cabo una campaña experimental empleando el ensayo de flexión [23] (fig. 4) e involucrando distintos valores C_f^j y así poder establecer el valor de C_f^opt real con el que deberá llevarse a cabo la producción.

En ocasiones, y tal como se ha hecho para este artículo en concreto, se pueden llevar a cabo ensayos previos del hormigón reforzados con las fibras susceptibles a ser empleadas en la fabricación de las dovelas considerando varias cuantías. Los resultados obtenidos pueden emplearse para deducir curvas tipo f_R,i-C_f y con estas plantear el diseño estableciendo las ecuaciones constitutivas del HRF que se consideren adecuadas.

Ni que decir tiene que del mismo modo general descrito anteriormente, estas resistencias residuales f_Ri deberán verificarse posteriormente en las condiciones reales de obra, con las fibras y dosificación del hormigón finalmente establecidas y, si fuere necesario, plantear los cambios pertinentes (tipo y/o cuantía de fibra) para alcanzar los requerimientos mecánicos fijados para el HRF de proyecto.

Debe recalcarse que el procedimiento planteado permite obtener la cuantía óptima de fibras C_f^opt con la que evaluar la idoneidad técnica y económica del empleo de fibras como refuerzo del hormigón en sustitución parcial o total de la armadura pasiva tradicional. Sin embargo, a nivel de proyecto suelen especificarse exclusivamente los valores característicos de las resistencias residuales f_R1 y f_R3 (o f_R4, según la normativa de referencia) que debe alcanzar el HRF, así como algún valor específico de la geometría de la fibra (longitud, diámetro y/o esbeltez); en algunos casos, también el material de la misma. Posteriormente, el suministrador del hormigón, en base a la fibra finalmente elegida, es el que sugiere la dosificación C_f necesaria para alcanzar las f_R,i establecidas en proyecto recurriendo a los ensayos característicos previos.

3

Estrategia para la simulación de la respuesta seccional

3.1

Introducción

La simulación del comportamiento mecánico de una dovela puede llevarse a cabo mediante modelos de elementos finitos. Sin embargo, las secciones críticas de una dovela de túnel en términos de solicitaciones normales es la central. Por tanto, el diseño puede llevarse a cabo simulando la respuesta σ-¿ de dicha sección.

Esta tarea puede abordarse mediante un modelo de análisis no lineal de secciones considerando la contribución resistente del HRF. Para ello, en este estudio se ha empleado el modelo de Análisis de Secciones Evolutivas (AES) [24,25] desarrollado por los mismos autores de este trabajo. Este modelo ha sido calibrado y contrastado con resultados experimentales obtenidos en diferentes campañas experimentales [26–29].

El modelo AES se emplea en este análisis para obtener el M_u asociado a cada conjunto de f_R,i considerado, habiendo establecido previamente una cuantía de refuerzo en forma de barras (A_s). En consecuencia, este procedimiento ha permitido deducir las curvas M_u-f_R,i y la determinación de f_R,i^opt que atiende a los requerimientos fijados para cada una de las dovelas diseñadas mediante el procedimiento presentado en la figura 5.

En esta sección se exponen las bases del modelo AES, centrándose en las hipótesis relacionadas con la simulación del comportamiento mecánico del HRF.

3.2

Modelo AES

3.2.1

Simulación de los materiales

La sección de hormigón se discretiza en fibras de espesor constante, y las barras de acero, en áreas de masa concentrada. Una vez se ha discretizado la sección, se asignan las ecuaciones constitutivas adecuadas a cada material para posteriormente obtener la respuesta tensodeformacional de la sección bajo una combinación de esfuerzos axil (N) y momento (M) (fig. 6a).

Figura 6.

a) Discretización de la sección; modelos constitutivos para el HRF (b) y el acero para armaduras pasivas (c).

La adición de fibras modifica la respuesta a compresión del hormigón en función del tipo y dosificación empleada [30]. Concretamente, la resistencia a compresión (f_c) tiende a reducirse con el aumento de C_f debido a un incremento del aire ocluido, mientras que, por contra, aumenta el efecto de confinamiento y la ductilidad del material. No obstante, para el tipo y las cantidades de fibras que se emplean en la fabricación de dovelas, el valor f_c no varía significativamente respecto a un hormigón convencional sin fibras con la misma dosificación; en consecuencia, se adopta la ecuación constitutiva sugerida en [31] para simular el comportamiento del HRF sometido a tensiones de compresión, siendo esta una ecuación propuesta inicialmente para hormigones convencionales.

Por otra parte, la simulación del comportamiento mecánico del HRF sometido a tracciones se puede abordar mediante ecuaciones constitutivas tipo tensión (σ_c) - ancho de fisura (w) y/o σ_c-¿_c. En el modelo AES se han implementado todas las ecuaciones constitutivas sugeridas en los códigos europeos. En estas, se ha adoptado la ecuación trilineal tipo σ_c-¿_c propuesta en el MC 2010 por tratarse de un referente internacional y que conduce a resultados suficientemente fidedignos según los estudios llevados a cabo en [28] y [32].

En la figura 6b se presenta la curva constitutiva empleada en este trabajo, así como las expresiones utilizadas para evaluar los puntos (σ_i y ¿_i) que definen la misma. Se debe remarcar que el valor de la longitud característica (l_cs) se ha considerado igual al canto de la dovela (h)[33]. CMOD₁ y CMOD₃ adoptan valores de 0,5 y 2,5 mm, respectivamente, mientras que el ancho de fisura último se evalúa como w_u = l_cs¿_Fu, siendo ¿_Fu = 20,0‰ la deformación última del HRF (asumiendo un comportamiento de reblandecimiento del material). Ni que decir tiene que para los cálculos en ELS deben considerarse los valores característicos de f_ct, f_R,1 y f_R,3 (f_ctk, f_Rk,1 y f_Rk,3) y los de diseño (f_ctd, f_Rd,1 y f_Rd,3) para los cálculos en ELU.

Por último, el acero para armaduras pasivas se ha simulado considerando un diagrama elastoplástico perfecto (fig. 6c).

3.2.2

Hipótesis básicas adicionales

Adicionalmente, se asume adherencia perfecta entre los distintos materiales. Asimismo, se considera que la distorsión angular debida al cortante es poco significativa debido a que el módulo a cortante de la sección es elevado en comparación con los esfuerzos cortantes esperados y, por tanto, no se considera el efecto del cortante en las ecuaciones.

3.2.3

Equilibrio y compatibilidad

Asignadas las ecuaciones constitutivas de cada material, se imponen las ecuaciones de equilibrio (ecuaciones 1 y 2) y compatibilidad (ecuación 3), resultando un sistema de ecuaciones no lineales. Este sistema se resuelve mediante un esquema iterativo tipo Newton-Raphson [34].

El diagrama M-χ de cualquier sección puede ser obtenido fijando un rango de curvaturas [0-χ_u] y un axil concomitante N.

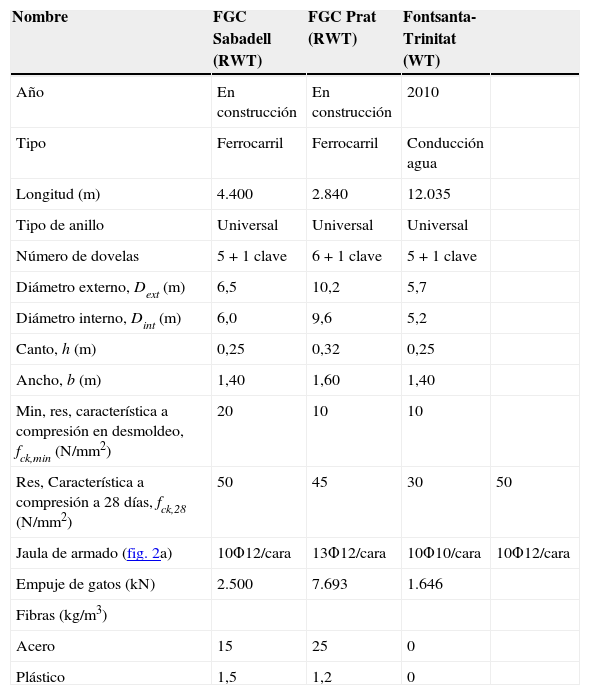
4

Implementación de la estrategia de diseño

4.1

Descripción de los túneles

Con el fin de ilustrar la metodología de diseño propuesta, se presentan a continuación 3 túneles en los que el uso de HRF es ventajoso y adecuado debido a las dimensiones de los mismos (tabla 2) y a las condiciones de carga (tabla 3). El primer túnel (túnel de FGC en Sabadell) proporcionará una nueva conexión de ferrocarril entre las localidades de Barcelona y Sabadell. El segundo túnel (túnel de FGC en el Prat) abrirá un acceso por ferrocarril a la nueva terminal (T1) del aeropuerto del Prat (Barcelona). Finalmente, el tercer túnel (túnel FontSanta-Trinitat), construido en 2010, contiene una tubería de hormigón pretensado de un diámetro de 1.800 mm que transporta agua desalinizada desde FontSanta (Sant Just Desvern, Barcelona) y el distrito de la Trinitat (Barcelona).

Tabla 2.

Información relevante de cada túnel

Nombre	FGC Sabadell (RWT)	FGC Prat (RWT)	Fontsanta-Trinitat (WT)
Año	En construcción	En construcción	2010
Tipo	Ferrocarril	Ferrocarril	Conducción agua
Longitud (m)	4.400	2.840	12.035
Tipo de anillo	Universal	Universal	Universal
Número de dovelas	5 + 1 clave	6 + 1 clave	5 + 1 clave
Diámetro externo, Dext (m)	6,5	10,2	5,7
Diámetro interno, Dint (m)	6,0	9,6	5,2
Canto, h (m)	0,25	0,32	0,25
Ancho, b (m)	1,40	1,60	1,40
Min, res, característica a compresión en desmoldeo, fck,min (N/mm^2)	20	10	10
Res, Característica a compresión a 28 días, fck,28 (N/mm^2)	50	45	30	50
Jaula de armado (fig. 2a)	10Φ12/cara	13Φ12/cara	10Φ10/cara	10Φ12/cara
Empuje de gatos (kN)	2.500	7.693	1.646
Fibras (kg/m^3)
Acero	15	25	0
Plástico	1,5	1,2	0

Tabla 3.

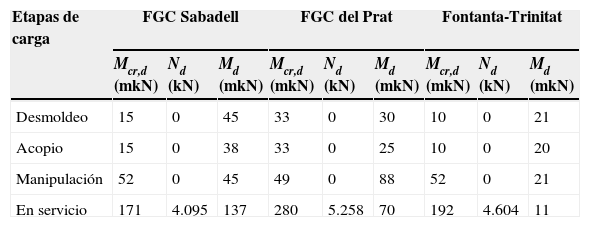
Momento de fisuración de diseño M_cr,d y esfuerzos de diseño N_d y M_d en cada etapa

Etapas de carga	FGC Sabadell			FGC del Prat			Fontanta-Trinitat
	Mcr,d (mkN)	Nd (kN)	Md (mkN)	Mcr,d (mkN)	Nd (kN)	Md (mkN)	Mcr,d (mkN)	Nd (kN)	Md (mkN)
Desmoldeo	15	0	45	33	0	30	10	0	21
Acopio	15	0	38	33	0	25	10	0	20
Manipulación	52	0	45	49	0	88	52	0	21
En servicio	171	4.095	137	280	5.258	70	192	4.604	11

A partir de los datos presentados en la tabla 2 se observa que los proyectistas de los túneles de FGC Sabadell y FGC Prat consideraron el uso de fibras de acero y fibras plásticas desde el inicio del proyecto. El motivo de su empleo corresponde a la necesidad de mejorar la respuesta mecánica de la dovela frente a hipotéticos casos de cargas por fuego y frente a las fuerzas localizadas derivadas del empuje de los gatos. Sin embargo, la contribución estructural de dichas fibras tras la fisuración no se consideró en el diseño. En consecuencia, la capacidad resistente se atribuyó al refuerzo tradicional, que corresponde a un contenido mínimo (A_s,min) en ambos casos debido al bajo nivel de carga esperado durante las etapas de carga transitoria y en servicio (tabla 2).

Por otro lado, en el túnel FontSanta-Trinitat se consideraron 2 valores diferentes de f_ck,28 y 2 configuraciones de refuerzo diferentes. Esto responde a la existencia de tramos de suelo con monteras de hasta 300 m y con altas presiones de agua que demandaban un hormigón con un valor de f_ck,28 no inferior a 50 N/mm² para poder resistir las tensiones de compresión previstas en condiciones de servicio. De aquí en adelante, el valor de f_ck,28 se tomará igual a 50 N/mm², ya que cuanto mayor sea f_ck,28, mayor será también el valor de resistencia a tracción directa característica del hormigón f_ct. Por este motivo, el valor de M_fis,d de la sección transversal es mayor, así como el contenido mínimo de refuerzo A_T,min (fig. 5).

Los esfuerzos de diseño presentados en la tabla 3 se obtuvieron recurriendo a modelos simplificados de viga asumiendo un comportamiento lineal-elástico de los materiales y las condiciones de apoyo existentes en las etapas de carga transitorias (desmoldeo, acopio y manipulación). Por otro lado, las cargas de servicio se determinaron por medio del software comercial FLAC3D^®. En este sentido, tanto el paso a paso del proceso constructivo de cada túnel como la interacción terreno-estructura fueron considerados en el análisis. Asimismo, los valores de cada M_fis,d se incluyen con el propósito de ser comparados.

En este sentido, cada valor de f_ct,d se ha definido con base en los valores de la resistencia a tracción uniaxial característica f_ct,k sugerida en el MC 2010, que depende de f_ck. Además, en aquellos casos en los que M_fis,d ≥ M_d, se tomó el valor máximo de la resistencia a tracción uniaxial característica (f_ctk,max), mientras que para M_fis,d < M_d se adoptó el valor mínimo (f_ctk,min). Finalmente, los valores de f_ct,d se determinan dividiendo f_ct,k por un factor parcial de seguridad 1,5.

De los valores presentados en la tabla 3 se concluye que se prevé que las secciones transversales se mantengan sin fisurar en condiciones de servicio, puesto que M_fis,d es mayor que M_d para los 3 casos estudiados. En consecuencia, las etapas de carga transitoria son más desfavorables en términos del diseño de la armadura. En esta línea, los túneles de FGC Sabadell y FontSanta-Trinitat presentan ambos un M_fis,d igual a 52 kNm (f_ctk,max = 5,3 N/mm²), siendo este mayor que cualquiera de los M_d con probabilidad de aparecer en las fases de carga transitoria. Contrariamente, durante la manipulación de las dovelas para el túnel FGC Prat se podría alcanzar un momento flector de diseño M_d igual a 88 kNm y superior que M_fis,d (49 kNm asumiendo f_ctk,min = 2,7 N/mm²).

Considerando lo anterior, las dovelas de los túneles de FGC Sabadell y FontSanta-Trinitat se pueden armar de forma óptima imponiendo la condición de refuerzo crítico M_u = M_fis,d (figs. 3 y 5). No obstante, las dovelas del túnel FGC Prat se deben diseñar imponiendo la condición de refuerzo supracrítico M_u = M_d (figs. 3 y 5). En cualquier caso, las cargas de flexión son bajas, y una sustitución parcial o incluso total de la armadura convencional por fibras puede ser considerada como una alternativa de refuerzo adecuada.

4.2

Parámetros de la ecuación constitutiva para el diseño de HRF

Con el fin de abordar el rediseño de la armadura que se había propuesto inicialmente en el proyecto para cada dovela (tabla 2) es necesario establecer los valores de f_R,i del HRF para definir la ecuación constitutiva y obtener los diagramas M_u-f_R,i (fig. 5) con el modelo AES. En esta etapa del pre-diseño los valores son desconocidos, y por este motivo se realizó una campaña experimental de ensayos a flexión según la norma UNE-EN 14651:2005 [23] (fig. 4) para contenidos de fibra C_f entre 20 y 50 kg/m³.

Se adoptó la dosificación de 20 kg/m³ como contenido mínimo mecánico para garantizar un confinamiento adecuado de la matriz de hormigón frente a fenómenos de «desconchamiento» y «aplastamiento» durante las fases transitorias así como en servicio, mientras que el valor de 50 kg/m³ se ha establecido como máximo por criterios económicos. En la campaña experimental se empleó una fibra estructural con extremos conformados con longitud (l_f) de 50 mm, diámetro (d_f) de 1,0 mm y una resistencia a tracción (f_f) de 1.100 N/mm². Estos ensayos corresponden al pre-diseño de las dovelas del túnel de FontSanta-Trinitat, por lo que se empleó un hormigón de f_ck igual a 50 N/mm².

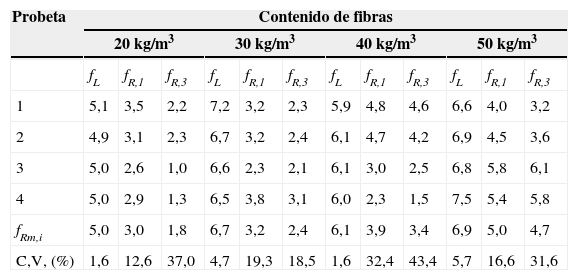
En la tabla 4 se presentan los valores de f_R,1, f_R,3 y del límite de proporcionalidad (f_L) obtenidos de 4 probetas para cada valor de C_f necesarios para definir la ecuación constitutiva del HRF (fig. 6). Asimismo, también se incluyen en la tabla los valores medios f_Lm, f_Rm,1 y f_Rm,3 y el coeficiente de variación. Los resultados muestran, tal y como se esperaba, que los valores de resistencia residual del HRF aumentan con C_f.

Tabla 4.

Valores de f_L y de f_R,i en N/mm² obtenidos en base al ensayo de viga UNE-EN 14651:2005

Probeta	Contenido de fibras
	20 kg/m^3			30 kg/m^3			40 kg/m^3			50 kg/m^3
	fL	fR,1	fR,3	fL	fR,1	fR,3	fL	fR,1	fR,3	fL	fR,1	fR,3
1	5,1	3,5	2,2	7,2	3,2	2,3	5,9	4,8	4,6	6,6	4,0	3,2
2	4,9	3,1	2,3	6,7	3,2	2,4	6,1	4,7	4,2	6,9	4,5	3,6
3	5,0	2,6	1,0	6,6	2,3	2,1	6,1	3,0	2,5	6,8	5,8	6,1
4	5,0	2,9	1,3	6,5	3,8	3,1	6,0	2,3	1,5	7,5	5,4	5,8
fRm,i	5,0	3,0	1,8	6,7	3,2	2,4	6,1	3,9	3,4	6,9	5,0	4,7
C,V, (%)	1,6	12,6	37,0	4,7	19,3	18,5	1,6	32,4	43,4	5,7	16,6	31,6

De acuerdo con lo observado por otros autores [35], la elevada dispersión de los resultados se puede atribuir a la variabilidad intrínseca del material y a la configuración del ensayo, entre otros motivos. Sin embargo, a pesar de la dispersión, el ensayo de viga con entalla [23] es universalmente aceptado por la comunidad técnica y científica para la caracterización del comportamiento residual post-fisuración del HRF. Alternativamente, existen otros métodos igualmente representativos del comportamiento del material, como el ensayo Barcelona [36,37] o su variante en probeta cúbica, también conocido como MDPT [38]. Las ventajas de este ensayo son su menor dispersión, la simplicidad en la ejecución y el menor consumo de material en cada ensayo.

Debe recalcarse que estos ensayos llevados a cabo responden a la necesidad de plantear una relación f_R,i-C_f para abordar el pre-diseño del hormigón y evaluar la viabilidad económica y técnica del empleo de fibras y, por tanto, pueden considerarse como ensayos previos. En cualquier caso, una vez elegido el tipo, la cuantía y la dosificación del hormigón, se deben llevar a cabo los ensayos característicos en planta y que, como mínimo, deberían consistir en el ensayo de 6 probetas, preferiblemente de 2 amasadas distintas.

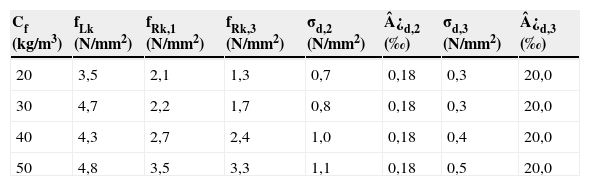
La tabla 5 incluye los valores característicos mínimos de f_L, f_R,1 y f_R,3 para cada C_f, así como los valores de tensiones de diseño (σ_d,i) y las deformaciones asociadas (¿_d,i). Los valores característicos mínimos f_Rk,i se obtuvieron multiplicando los valores medios f_Rm,i (tabla 4) por un factor de 0,7 [17].

Tabla 5.

Valores característicos de f_L y de f_R,i y valores de diseño (σ_d,i, ¿_d,i)

Cf (kg/m^3)	fLk (N/mm^2)	fRk,1 (N/mm^2)	fRk,3 (N/mm^2)	σd,2 (N/mm^2)	¿d,2 (‰)	σd,3 (N/mm^2)	¿d,3 (‰)
20	3,5	2,1	1,3	0,7	0,18	0,3	20,0
30	4,7	2,2	1,7	0,8	0,18	0,3	20,0
40	4,3	2,7	2,4	1,0	0,18	0,4	20,0
50	4,8	3,5	3,3	1,1	0,18	0,5	20,0

Los valores de σ₁ se definen como función de f_ctk,min o f_ctk,max dependiendo de cuál es más desfavorable, siendo σ_d,1 igual a 3,5 N/mm² (f_ctk,max/γ_c,R = 5,3/1,5) para los túneles de FGC Sabadell y FontSanta-Trinitat y de 1,8 N/mm² (f_ctk,min/γ_c,R = 2,7/1,5) para el túnel de FGC Prat. Por otro lado, los valores de ¿_d,1 asociados a cada σ_d,1 se determinaron dividiendo este último por el valor medio del módulo de elasticidad del hormigón (E_cm) obteniendo valores de ¿_d,1 de 0,10‰ (σ_d,1/E_cm = 3,5/36.000) para los túneles de FGC Sabadell y FontSanta-Trinitat y de 0,06‰ para el túnel de FGC Prat (σ_d,1/E_cm = 1,8/31.350).

De acuerdo con los requisitos establecidos en el MC 2010, el proyectista debe especificar:

• •

  Intervalo, que se define por 2 números consecutivos en la serie 1,0; 1,5; 2,0; 2,5; 3,0; 4,0; 5,0; 6,0; 7,0; 8,0 N/mm².

• •

  Cocientes de resistencias residuales: a) si 0,5 ≤ f_Rk,3/f_Rk,1 ≤ 0,7; b) si 0,7 ≤ f_Rk,3/f_Rk,1 ≤ 0,9; c) si 0,9 ≤ f_Rk,3/f_Rk,1 ≤ 1,1; d) si 1,1 ≤ f_Rk,3/f_Rk,1 ≤ 1,3, y f) si f_Rk,3/f_Rk,1 > 1,3.

• •

  Material de la fibra: acero en estas aplicaciones.

Considerando estas normas de clasificación, los HRF de la tabla 5 se clasifican como: 2,5a (C_f de 20 kg/m³), 2,5b (C_f de 30 y 40 kg/m³) y 3,0c para C_f igual a 50 kg/m³.

Además, los cocientes f_Rk,1/f_Lk y f_Rk,3/f_Rk deben ser superiores a 0,4 y 0,5, respectivamente, siempre que el HRF se use para remplazar el refuerzo tradicional. En este sentido, el HRF con C_f = 40 kg/m³ presenta un cociente mínimo f_Rk,1/f_Lk = 0,6. Por otro lado, el cociente de resistencia residual mínimo f_Rk,3/f_Rk,1 se alcanza con C_f = 20 kg/m³, siendo este cociente igual a 0,6. En cualquier caso, los valores mínimos de los cocientes f_Rk,1/f_Lk y f_Rk,3/f_Rk son superiores a los valores requeridos de 0,4 y 0,5, concluyendo que estos HRF pueden ser utilizados para sustituir parcial o totalmente el refuerzo tradicional de las dovelas.

Adicionalmente, debe ponerse de manifiesto que el MC-2010 sugiere el uso de un factor de orientación K para corregir los valores de las tensiones σ_i del HRF y tener de este modo en cuenta la orientación de las fibras respecto al flujo de tensiones principales a las que se espera que esté sometido el elemento estructural en fase servicio. En este sentido, en el citado código se proponen valores de K ≥ 1,0 para orientaciones favorables de las fibras y K < 1,0 en situaciones opuestas, si bien no se recogen recomendaciones o valores de referencia para establecer de forma unívoca el valor de K, dejando esta tarea a criterio del proyectista [39,40].

Para este trabajo se consideró un coeficiente K de valor unidad, del lado de la seguridad, a sabiendas de que el proceso de vertido del hormigón, la consistencia del mismo, el tipo de vibrado y los efectos de contorno generados por los moldes de la dovela, en conjunto conducen a orientaciones favorables de las fibras en referencia a los campos de tensiones de tracción principales que se producen en la dovela tanto en fases transitorias como en régimen de explotación. Este aspecto ya ha sido probado a nivel experimental en dovelas [41] y losas [42–44] y cuantificado de forma cualitativa por [43–46]; asimismo, en [47,48] se han llevado a cabo simulaciones numéricas del comportamiento mecánico en losas de HRF, empleando distintas ecuaciones constitutivas, con el fin de poder calibrar dicho coeficiente. Sin embargo, pese a los avances en esta dirección, aún no se ha podido establecer un método sistemático y fiable para poder evaluar el coeficiente K para los distintos HRF y distintas condiciones de contorno.

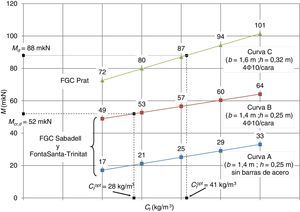
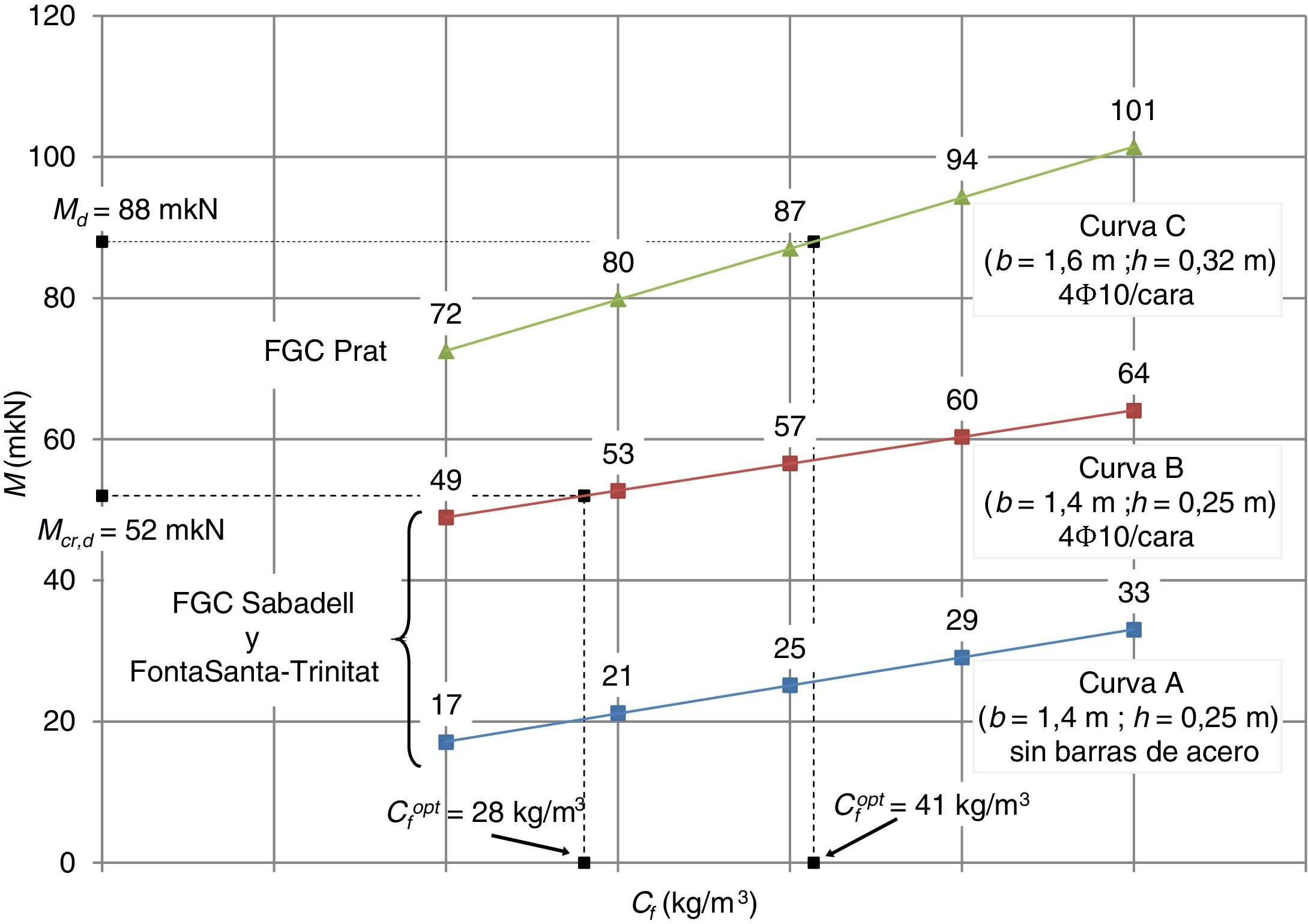
4.3

Resultados

En la figura 7 se presentan los diagramas M_u-C_f obtenidos con el modelo AES para las dovelas de los túneles de FGC de Sabadell y FontSanta-Trinitat (ambos con idénticas dimensiones b = 1,40 m y h = 0,25 m; tabla 2), considerando 2 estrategias de refuerzo: 1) la sustitución total del refuerzo tradicional (curva A), y 2) la sustitución parcial del refuerzo tradicional (reducción de un 75%) y manteniendo 4Φ10 en ambas caras de la dovela (A_s = 314 mm²/cara, curva B) a causa de las tensión de tracción por flexión que podrían aparecer en la cara superior o en la cara inferior dependiendo de la configuración de apoyo durante el acopio y el transporte, así como en la posición final en el anillo.

Figura 7.

Curvas M_u-C_f obtenidas con el modelo AES para las diferentes estrategias de refuerzo.

Asimismo, se incluye el diagrama M_u-C_f para las dovelas del túnel FGC Prat (b = 1,60 m y h = 0,32 m; tabla 2), considerando la sustitución del 80% del refuerzo tradicional (manteniendo 4Φ10/cara, A_s = 314 mm²/cara) por fibras (curva C).

Cabe destacar que, para este estudio, los autores poseían relaciones entre f_R,i y C_f para un tipo de fibra de acero establecido (tabla 4), permitiendo obtener directamente las curvas M_u-C_f. Sin embargo, tal y como se especifica en el MC 2010 para el diseño de estructuras de HRF, se deben proporcionar las características mecánicas del hormigón en términos de f_Rk,1 y el cociente f_Rk,3/f_Rk,1 para garantizar un diseño independiente del tipo de fibra.

Los resultados recogidos en la figura 7 indican que el contenido óptimo de fibras C_f^opt necesario para alcanzar los requisitos mecánicos M_u = M_fis,d = 52 kNm (refuerzo crítico) es elevado (≈ 110 kg/m³) si no se mantiene ningún armado tradicional (A_s = 0, curva A) para las dovelas de los túneles de FGC Sabadell y el Prat. En este caso, dicha estrategia de armado es inviable desde un punto de vista económico, pues sería necesario un hormigón de ultra alta resistencia (f_Rk,1 > 8,0 N/mm² y f_Rk,3/f_Rk,1 > 1,3), a no ser que se seleccione otra geometría para la dovela u otro tipo de fibra.

De forma alternativa, la curva B revela que, para el mismo requisito mecánico, la sustitución del armado tradicional (4Ф10/cara, A_s = 314 mm²/cara, en contraste con 10Ф12/cara, A_s = 1.131 mm²/cara, considerado en el proyecto inicial) es posible con valores de C_f^opt superiores a 28 kg/m³ (30 kg/m³ teniendo en cuenta su potencial producción en planta). En este contexto, esta estrategia es una alternativa atractiva posible en virtud de la sinergia de la combinación de las fibras y el armado tradicional. El mecanismo de cosido de las fibras en las fisuras permite un mejor control de su ancho y las barras de acero proporcionan una capacidad resistente significativa en ELU, ya que se encuentran colocadas de forma eficiente en el bloque traccionado.

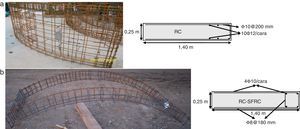
La figura 8 ilustra la configuración de armado propuesto para la dovela en el diseño inicial del túnel FontSanta-Trinitat y el proyectado tras la optimización del proceso realizado en este estudio (fig. 8a). Este último consiste en: 1) 2 estribos (Ф8/180 mm) para dotar al hormigón de confinamiento en áreas donde se esperan tensiones máximas de compresión debido a la acción del terreno, y 2) 4 barras de 10 mm de diámetro en la zona interior de las esquinas de cada estribo para resistir las tensiones de tracción previstas en las etapas de cargas transitorias. Además, se emplea un contenido de 30 kg/m³ de fibras definido en la sección 4.2 en combinación con el armado tradicional descrito. Consecuentemente, la especificación de este HRF, de acuerdo con las recomendaciones del MC 2010, es 2,5b (f_R1,k entre 2,5 y 3,0 N/mm² y 0,7 ≤ f_Rk,3/f_Rk,1 ≤ 0,9) que puede corresponder a un C_f igual a 30 kg/m³ teniendo en cuenta el comportamiento mecánico considerado en este estudio (tablas 4 y 5).

Figura 8.

Configuración de armado de las dovelas del túnel FontSanta-Trinitat; a) proyecto inicial, y b) propuesta tras el proceso de optimización.

Finalmente, la curva C de la figura 7 revela que un contenido óptimo C_f^opt igual a 41 kg/m³ (40 kg/m³ por aspectos relativos a la producción) es estrictamente necesario para cumplir con la condición mecánica M_u = M_d = 88 kNm (refuerzo supracrítico) de las dovelas del túnel FGC Prat, que por los mismos motivos técnicos del caso anterior llevan a una reducción del armado (de hasta el 80%). Finalmente, la especificación de este HRF es 3,0b (f_R1,k entre 3,0 y 4,0 N/mm² y 0,9 ≤ f_Rk,3/f_Rk,1 ≤ 1,1), que puede corresponder a un C_f igual a 40 kg/m³ teniendo en cuenta de nuevo la respuesta mecánica considerada en este estudio (tablas 4 y 5).

Cabe destacar que los requisitos mecánicos establecidos para esta dovela se pueden alcanzar con otro tipo de fibra y valores de C_f. No obstante, para hallar los nuevos valores asociados a C_f^opt sería necesario realizar una campaña experimental.

5

Conclusiones

El significativo número de túneles construidos con HRF es indicativo del creciente interés en este tipo de material desde el punto de vista económico y técnico. Los motivos principales para dicho incremento son: 1) un conocimiento más profundo del comportamiento mecánico; 2) la publicación de recomendaciones de diseño, y 3) un cambio en la inercia del sector de la construcción hacia la búsqueda de soluciones estructurales optimizadas de materiales-cementíceos que mejoran aspectos en los que el armado tradicional del hormigón pueda ser deficiente.

El método para el diseño óptimo del armado presentado en este artículo se ha aplicado a 3 casos reales, conduciendo a una reducción del armado tradicional con respecto al definido inicialmente en proyecto del 75% (en los túneles de FGC Sabadell y FontSanta-Trinitat) y del 80% (en el túnel FGC Prat). Los contenidos óptimos de fibras C_f^opt derivados del análisis son 30 y 40 kg/m³, respectivamente. Alternativamente, y siguiendo el criterio establecido en el MC 2010, las especificaciones mecánicas de dichos hormigones son 2,5b (f_R1,k entre 2,5 y 3,0 N/mm² y 0,7 ≤ f_Rk,3/f_Rk,1 ≤ 0,9) para los túneles FGC Sabadell y FontSanta-Trinitat, y 3,0b (f_R1,k entre 3,0 y 4,0 N/mm² y 0,9 ≤ f_Rk,3/f_Rk,1 ≤ 1,1) para el túnel FGC Prat.

En este estudio se ha usado únicamente un tipo de fibra y la ecuación constitutiva propuesta en el MC-2010 para simular el comportamiento post-fisuración del HRF. Sin embargo, existen otros tipos de fibras disponibles en el mercado que pueden conducir a una respuesta diferente del HRF (y en consecuencia valores diferentes de C_f^opt con respecto a los obtenidos en este análisis). Asimismo, existen ecuaciones constitutivas más sofisticadas en la literatura técnica con las que se puede alcanzar un mayor nivel de optimización.

Por último, es necesario destacar que los contenidos de fibras definidos y los requisitos mecánicos no dificultan la definición de la dosificación ni la producción de estos HRF. De ahí que su implementación puede ser incorporada y asumida sin interferir excesivamente en la producción habitual de cualquiera planta de dovelas prefabricadas.

Agradecimientos

Este artículo se ha completado bajo el marco de trabajo del proyecto «FIBHAC: self-compacting fibre reinforced concrete. Development of a new concept of precast segments for tunnels», suscrito al programa INNPACTO 2011(IPT-2011-1613-420000). En este sentido, los autores del artículo agradecen al Ministerio de Ciencia e Innovación el apoyo económico proporcionado para su ejecución. El tercer autor agradece el apoyo del Departament d’Universitats, Recerca i Societat de la Informació de la Generalitat de Catalunya.