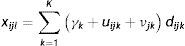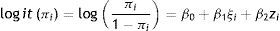Describir una estrategia que permita evaluar el efecto de la morfometría de imágenes de tomografía computarizada (TC) como factor pronóstico de la sobrevivencia de pacientes con hemorragia cerebral.
Material y métodosPara explicar y/o predecir una respuesta clínica del paciente en relación con variables morfométricas de imágenes por TC, se propone un enfoque de variables latentes que utiliza las siguientes herramientas estadísticas: regresión logística, modelación multinivel y análisis de componentes principales. Para ilustrar la metodología se utilizaron datos de las historias clínicas de 39 pacientes con hemorragia cerebral. A cada una de las 140 imágenes de TC recolectadas se le midieron cinco indicadores morfométricos.
ResultadosLa aplicación de la estrategia permitió hacer inferencias a nivel de paciente, combinando en un único modelo predictivo de variables latentes, la información morfométrica de las imágenes de TC y características de los pacientes, tales como edad y sexo. Los resultados revelan que las variables latentes representan de manera sintética las diferencias morfométricas de las imágenes entre los pacientes y que estas pueden considerarse un importante predictor de la supervivencia en determinados grupos de individuos.
ConclusionesLa estrategia propuesta proporciona una herramienta apropiada para evaluar el efecto de la morfometría de imágenes de TC sobre alguna respuesta clínica del paciente. Sobre la base de un ejemplo real se comprobó la utilidad de la estrategia en la elaboración de un modelo pronóstico de la sobrevivencia de pacientes tras un ictus.
To describe a strategy that allows to evaluate the morphometry effects of images of computed tomography (CT) as a prognostic factor for the survival of patients with cerebral hemorrhages.
Materials and methodsTo explain and/or predict a patient clinic response in relation to morphometric variables of CT images, a latent variable approach is proposed that uses the following statistical tools: logistic regression, multilevel modeling and principal component analysis. To illustrate the methodology, data from the medical records of 39 patients with cerebral hemorrhage were used. Five morphometric indicators were measured in each of the 140 collected CT images.
ResultsThe application of the strategy allowed to make inferences at patient level, combining in a single predictive model of latent variables, the morphometric information of the CT images and characteristics of the patients such as age and sex. The results reveal that the latent variables represent in a synthetic way, the morphometric differences of the images between the patients and that these can be considered an important predictor of the survival in certain groups of individuals.
ConclusionsThe proposed strategy provides an appropriate tool to evaluate the effect of morphometry of CT images on some clinical response of the patient. On the basis of a real example, the utility of the strategy in the development of a prognostic model of the survival of patients after a stroke was demonstrated.
Los estudios de neuroimágenes se han convertido en una herramienta esencial para el diagnóstico de enfermedades neurológicas, y constituyen hoy un importante campo de investigación que ha motivado el desarrollo de nuevos métodos de segmentación de imágenes y extracción de características1,2. Uno de los beneficios de la utilización de estos métodos en el área de las imágenes médicas es facilitar la detección de diferencias estructurales capaces de revelar anomalías3. En este sentido, el examen morfométrico de las imágenes médicas también es relevante para la práctica clínica.
La tomografía computarizada (TC) es una de las principales herramientas para diagnosticar múltiples patologías mediante un conjunto de imágenes de cortes o sesiones de algún objeto anatómico. En este contexto, variables independientes medidas sobre las imágenes tomográficas (unidades en el nivel micro), se supone afecten variables dependientes medidas sobre los individuos (unidades en el nivel macro). Este tipo de escenario, referido como situación micro-macro4, ha recibido poca atención en la literatura estadística. ¿Cómo abordar entonces un problema con datos en dos niveles donde se espera que una variable respuesta relacionada con la salud del paciente, medida en el nivel macro, esté influenciada por variables morfométricas de imágenes de TC, medidas en el nivel micro?
Uno de los enfoques tradicionales para analizar mediciones en múltiples niveles es usar la información del nivel más bajo de forma agregada, por ejemplo, utilizando medidas resúmenes tales como la media para relacionarla con la variable respuesta relativa al nivel más alto5. Algunas de las limitaciones de este enfoque para analizar datos morfométricos de imágenes por TC es que no se toman en cuenta los errores de medición y muestreo de la información concerniente a las mediciones morfométricas y se ignoran las diferencias entre las imágenes de cada paciente.
El análisis de observaciones de diseños micro-macro requiere una metodología que permita analizar la relación entre las imágenes y los pacientes, teniendo en cuenta las dos fuentes de variabilidad de la respuesta: la variabilidad de las imágenes intra- y entre pacientes6. Un enfoque de modelación multinivel7–12 explícitamente tiene en cuenta la existencia de los diferentes niveles e intenta formular la interacción entre estos en relación con la respuesta, pero la mayor parte de los métodos se centran solo en los denominados modelos macro-micro, donde la respuesta se mide en el nivel más bajo del modelo.
En la última década se han propuesto varios métodos para analizar datos micro-macro, motivados principalmente por investigaciones psicológicas o sociológicas que comprenden relaciones entre individuos y grupos, y donde las características de los individuos pueden afectar alguna respuesta a nivel de grupo13–16. Estos métodos se han basado fundamentalmente en enfoques de variables latentes. Desde esta perspectiva, el objetivo de este trabajo es proponer una estrategia que pueda utilizarse como punto de partida para desarrollar un enfoque de variables latentes, donde se maneje de manera apropiada la estructura multinivel de las relaciones micro-macro en el área de las neuroimágenes.
La motivación del presente trabajo parte de un problema, en el que a pesar de contarse con numerosas investigaciones, aun hoy no se tienen suficientes elementos para llegar a conclusiones consistentes. Se trata del estudio de los múltiples factores que podrían considerarse predictores de la sobrevivencia de pacientes con hemorragia intracerebral. La incorporación de nuevas estrategias de análisis, encaminadas a construir métodos apropiados para analizar datos de imágenes de TC, puede conducir al mejoramiento de la eficacia en el diagnóstico de esta u otros tipos de patologías.
En este artículo se muestra, utilizando un conjunto de datos reales, cómo el uso combinado de un modelo multinivel multivariado17,18 y un análisis de componentes principales (ACP)19,20, permite construir variables latentes capaces de sintetizar, a nivel de individuo, características morfométricas de imágenes por TC de paciente con hemorragia intracerebral espontánea (HICE). Estas variables latentes, junto a otras covariables a nivel de individuo, se consideran como variables explicativas en un modelo de regresión logística21. El modelo de variables latentes se usa para evaluar el efecto de cada una de las variables, consideradas potencialmente influyentes en la sobrevivencia de los pacientes.
Materiales y métodosProblema de estudioLa HICE es una de las formas más devastadoras de los accidentes cerebrovasculares (muchas veces nombrado como «ictus»). Un ictus ocurre cuando un vaso sanguíneo se rompe o presenta una obstrucción que impide el normal movimiento de la sangre al cerebro. Debido a la carencia de oxígeno, las células nerviosas del área afectada del cerebro dejan de realizar sus funciones básicas, produciendo una invalidez total o parcial, o causando la muerte súbita22. Un problema cardinal en Neurología es el estudio de los múltiples factores que podrían considerarse predictores de la supervivencia en pacientes con HICE.
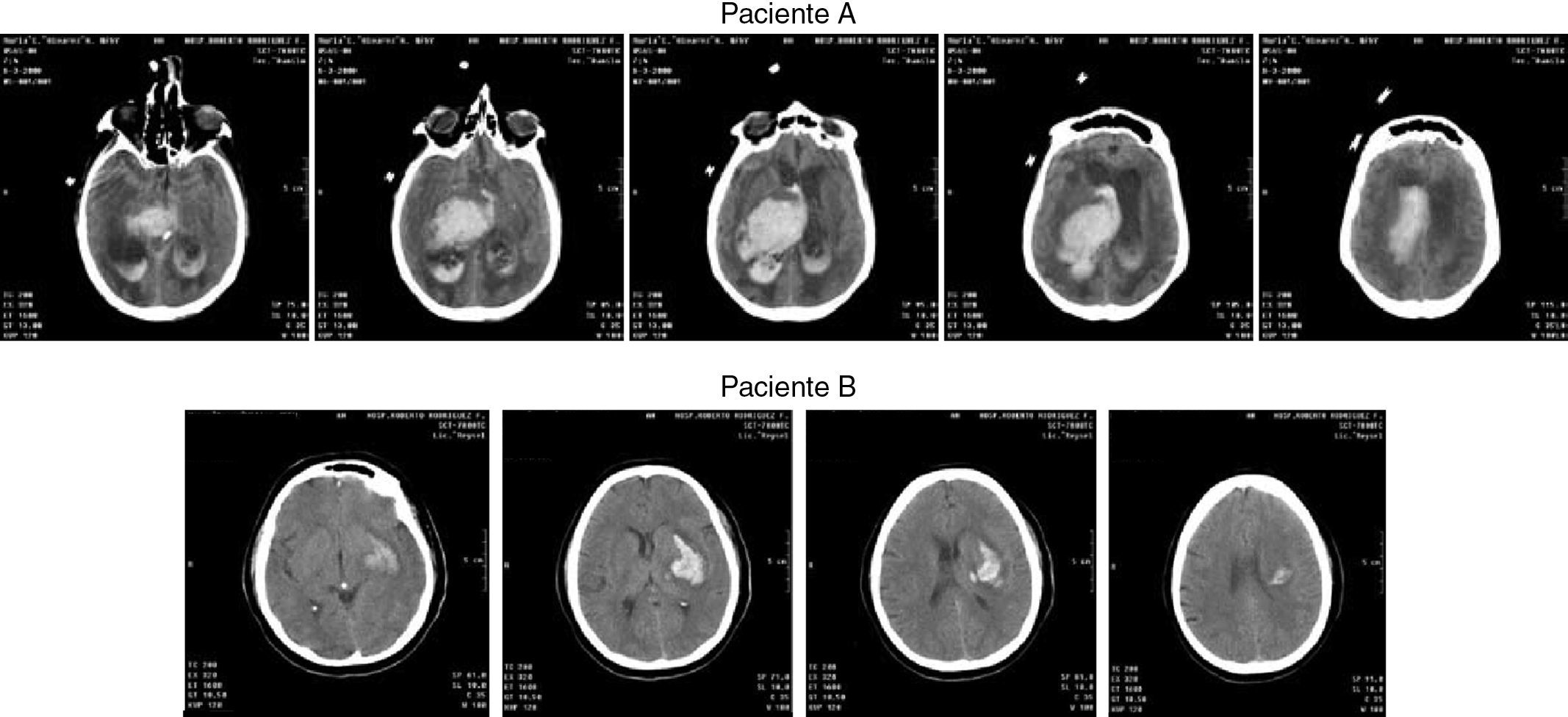
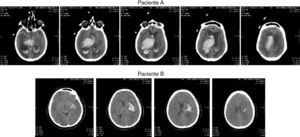
La figura 1 muestra un ejemplo de las secuencias de imágenes por TC de dos pacientes con HICE. Las zonas de hemorragia en cada corte aparecen como una región brillante (hiperdensa) en relación con su entorno. El examen de la heterogeneidad morfométrica de las imágenes entre los cortes y entre pacientes puede ser muy importante como parte de un instrumento de pronóstico que permita valorar la intensidad del daño neurológico sobre la vida del paciente. La cuestión fundamental es: ¿qué efecto tiene la morfometría de las imágenes por TC en el riesgo de no sobrevivir a la hemorragia en determinados grupos de individuos? Un problema obvio es: ¿cómo predecir o explicar variables a nivel de paciente a partir de variables morfométricas medidas a nivel de imagen? En el artículo se utilizan los datos de este ejemplo para mostrar algunas ideas para el diseño e implementación de la estrategia propuesta.
Los datosLa muestra de estudio estuvo constituida por todos los pacientes con diagnóstico de HICLE, que ingresaron en el hospital General Provincial Docente en la provincia Ciego de Ávila, durante el período comprendido entre enero de 2008 y diciembre de 2009, y a los que se le realizó una TC en las seis primeras h de iniciados los síntomas. Los datos se obtuvieron del registro de historias clínicas de 39 pacientes. De estos, 13 mujeres y 26 hombres. Las edades estuvieron comprendidas entre 48 y 87 años.
La respuesta de interés en este estudio es la supervivencia del paciente después de la hemorragia. La variable toma el valor 0 si el paciente sobrevive y el valor 1 si no sobrevive. Las variables explicativas seleccionadas para la investigación incluyen la edad y sexo de los pacientes. La edad se midió en número de años. También se consideraron como variables explicativas, las siguientes medidas morfométricas de las imágenes: área, perímetro, factor de forma elíptica, diámetro máximo y diámetro mínimo1. Estas variables se midieron utilizando el sistema de programas MADIP23 y se les aplicó una transformación para evitar la indebida importancia de rangos desproporcionados ocasionados por las diferentes unidades de medidas de algunas variables.
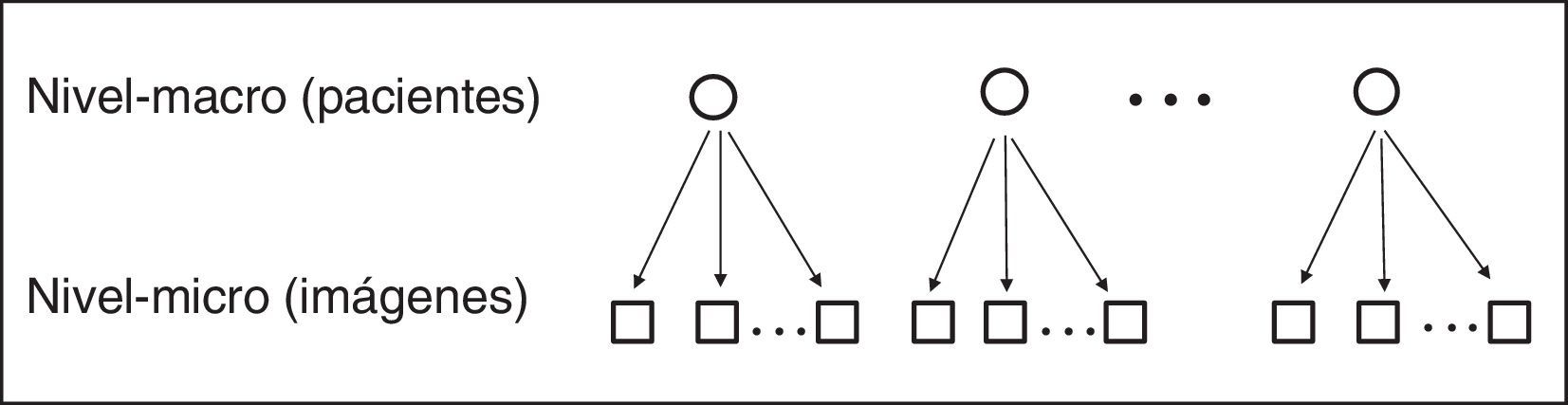
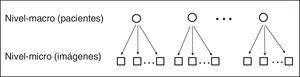
Se consideró que los datos utilizados en este estudio constituyen un sistema ordenado jerárquicamente, donde las imágenes están anidadas dentro de los individuos, estableciéndose dos niveles diferentes: las unidades de estudio en el nivel 1 (nivel micro) la constituyen las imágenes y las unidades de estudio en el nivel 2 (nivel macro) la componen los pacientes (fig. 2). Las variables en el nivel 1 se refieren a las características morfométricas de las imágenes, mientras que las variables en el nivel 2 se refieren a las características de los pacientes.
Procedimiento estadísticoEn un análisis micro-macro, los datos a nivel micro (variables morfométricas) necesitan agregarse a nivel macro, tal que los valores agregados puedan relacionarse con la variable respuesta relativa al paciente. El procedimiento propuesto en este artículo permite crear variables que capturen tanto la variabilidad entre imágenes como entre individuos, utilizando uno o más factores «latentes» o no observados en cada nivel de análisis.
La estrategia puede resumirse de la siguiente manera:
- 1.
En un primer paso, la idea es realizar un ACP a partir de la matriz de covarianza entre individuos de las variables morfométricas. Este método permitirá crear variables latentes a nivel macro (individuos), que pueden interpretarse como indicadores sintéticos que representen las diferencias morfométricas de las hemorragias entre los pacientes.
- 2.
En una segunda etapa, se ajusta un modelo de regresión logística en un único nivel, en el que variables latentes, obtenidas desde el ACP, se tratan como predictores o variables explicativas para la variable respuesta relativa al paciente.
Esta estrategia permite hacer inferencias a nivel de pacientes utilizando toda la información disponible a nivel de imagen.
Estimación de la matriz de covarianza entre individuosGoldstein9 sugirió usar un modelo multinivel multivariado para producir una estimación de la matriz de covarianza (o correlación) en cada nivel de análisis.
Para el caso de un conjunto de K variables morfométricas, sea xijl la medición de la l-ésima variable morfométrica (l=1,2,…,K) en la j-ésima imagen del i-ésimo individuo. Para cada variable morfométrica se crea una variable indicadora dijk=1 cuando l=k, 0 en otro caso. De aquí que el modelo nulo multinivel multivariado pueda describirse mediante la siguiente ecuación:
El parámetro fijo γk representa el efecto poblacional de la k-ésima variable morfométrica. Los vectores de errores no observables u′ij=uij1,uij2,⋯,uijK y ν′i=νi1, νi2,⋯,νiK se suponen independientes e idénticamente distribuidos. Más explícitamente se establecerá que uij∼NK+0,Σy vi∼NK+0,Ω para cada i y j. Cuando se hace referencia al modelo nulo multivariado, la matriz de varianza y covarianza de los errores aleatorios de nivel-1, Σ=Cov (uij), puede nombrarse matriz de covarianza intraindividuos, mientras la matriz de los errores de nivel-2, Ω=Cov (νi), puede nombrarse matriz de covarianza entre individuos. Estas matrices de covarianza pueden usarse en subsiguientes análisis como datos de entrada en un ACP en el nivel de interés.
Análisis de components principales a partir de la matriz de covarianza entre-individuosEl objetivo del ACP es reducir el número de variables de un conjunto de datos en un número más pequeño de «dimensiones». En términos matemáticos, a partir de un conjunto inicial de K variables correlacionadas, el ACP crea índices o componentes incorrelacionados, donde cada componente es una combinación lineal ponderada de las variables iniciales24.
Dentro del esquema multinivel, el procedimiento propuesto en este artículo aplica un ACP a la matriz de covarianza entre individuos9. La idea es reducir la dimensionalidad de los datos en el nivel más alto (nivel-individuo) para producir un conjunto de factores o componentes principales ξ=ξ1,ξ2,…,ξK∈ℝdxJ (d
Un modelo con variables latentes para respuesta discretaPara una respuesta dicotómica del paciente, tal como la sobrevivencia, el modelo de variable latente puede formularse como una ecuación de regresión logística.
Sea yi la realización de una variable respuesta Y medida a nivel individuo, que puede tomar los valores uno y cero con probabilidad πi y 1−πi, respectivamente, con distribución Bernoulli con parámetro πi. Considérese que la respuesta dicotómica yi puede explicarse o predecirse suponiendo que el logit de la probabilidad subyacente πi es una función lineal de una variable explicativa Z a nivel individuo, con observación zi para el individuo i, y una variable latente ξ a nivel individuo, con valor ξi para el individuo i. El modelo puede expresarse como:
El coeficiente de regresión β0 es el logit de la probabilidad de tener la respuesta con el valor uno en el nivel base de comparación. Los parámetros β1 y β2 representan, respectivamente, el cambio en el logit de la probabilidad asociada con una unidad de cambio en el correspondiente predictor, manteniendo el otro predictor constante. Es importante hacer notar que la variable latente ξ es continua, pero la variable Z puede ser de cualquier tipo y que es válido el análisis de interacciones entre la variable no observada ξ y la variable observada Z.
Hasta aquí se ha considerado un modelo con solo dos predictores: un factor y una sola covariable, pero el modelo puede extenderse a múltiples regresores.
En el caso del análisis de los datos del ejemplo para estudiar la relación entre la supervivencia después de la hemorragia y la morfometría de las imágenes por TC, se consideró una única variable latente o no observada (nombrada Factor 1), que se interpreta en términos de efectos morfométricos debidos a las diferencias entre los pacientes. Además, se adicionaron al modelo logit, las variables explicativas sexo y edad del paciente, ya que se tiene la hipótesis de que los hombres y los pacientes más jóvenes tienen menos probabilidad de sobrevivir a la hemorragia. El sexo femenino se toma como categoría de referencia. La edad se categorizó en tres grupos según los siguientes grupos etarios: menos de 60 años, entre 61 y 75 años y más de 75 años. El grupo de pacientes entre 61 y 75 años se toma como referencia. También se incluyó en el modelo, la interacción entre una única variable latente (Factor 1) y la variable edad, al considerarse que la influencia de la morfometría de las imágenes sobre la supervivencia de los pacientes puede estar mediatizada por la influencia de la edad.
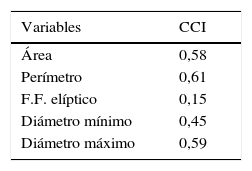
ResultadosLas variables latentesLa tabla 1 muestra los valores del coeficiente de correlación intraclase para cada variable morfométrica, que en este trabajo se refiere a la proporción de la varianza total en la variable de interés, debida a las diferencias entre los individuos. Se muestra que una proporción importante de la variabilidad de las medidas morfométricas es atribuible a las diferencias entre los individuos, más que entre las imágenes.
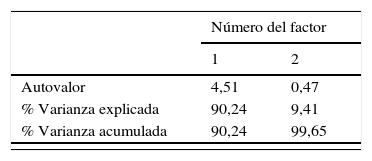
En la tabla 2 se presentan los resultados de un ACP realizado a partir de la matriz de correlación entre individuos. La primera componente o factor asociado al mayor valor propio captura más del 90% de la variabilidad de los datos entre los individuos. Este aparece correlacionado con todas las variables, aunque se distingue un contraste entre las variables, área, perímetro, diámetro mínimo y diámetro máximo (muy fuertemente correlacionadas) de un lado; y la variable factor de forma elíptica, de otro lado. Por ejemplo, valores altos del primer componente representan a pacientes con altos valores de las variables asociadas al tamaño de la hemorragia (área, perímetro, diámetro mínimo y diámetro máximo), pero con bajos valores de la variable asociada a la forma de la hemorragia (factor de forma elíptica). El segundo factor aparece relacionado con la variable factor de forma elíptica, y por tanto, parece distinguir a los pacientes que comparativamente tienen mayores puntajes en esta variable (esto es, hemorragias con estructura menos elíptica). Los dos conjuntos de variables en el primero y segundo factor son estadísticamente independientes, por lo que un paciente puede puntuar alto en solo uno de ellos, en los dos o en ninguno.
Resultados del ACP de los dos primeros factores a nivel individuo
| Número del factor | ||
|---|---|---|
| 1 | 2 | |
| Autovalor | 4,51 | 0,47 |
| % Varianza explicada | 90,24 | 9,41 |
| % Varianza acumulada | 90,24 | 99,65 |
| Variable | ||
|---|---|---|
| Factor 1 | Factor 2 | |
| Área | 0,991 | 0,100 |
| Perímetro | 0,990 | 0,121 |
| F.F. elíptico | −0,785 | 0,619 |
| Diámetro mínimo | 0,967 | 0,248 |
| Diámetro máximo | 0,999 | 0,028 |
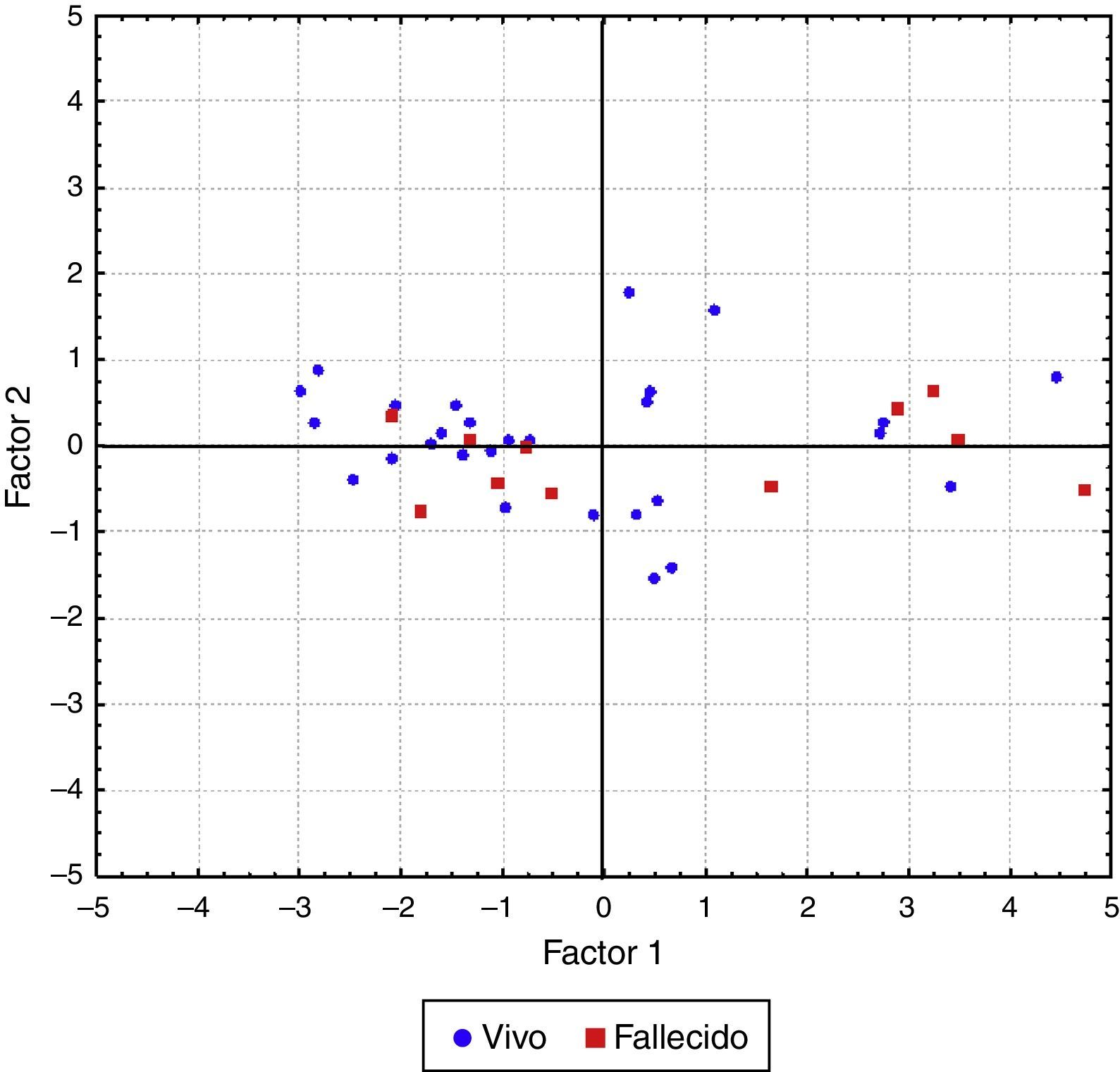
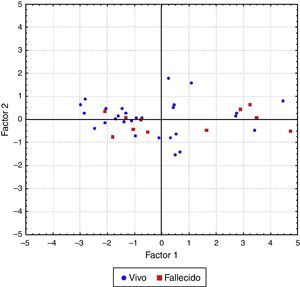
Una cuestión de particular interés es inspeccionar si los pacientes que sobrevivieron a la hemorragia muestran algunas diferencias con respecto a los que no sobrevivieron en cuanto a la morfometría de las imágenes por TC. En la figura 3 se muestran los valores de los 39 pacientes para las primeras dos componentes. El gráfico sugiere cierta evidencia de cómo pacientes con valores extremos positivos para la primera componente no pudieron sobrevivir a la hemorragia, y que los pacientes con los valores negativos más extremos de la primera componente, sobrevivieron a la hemorragia.
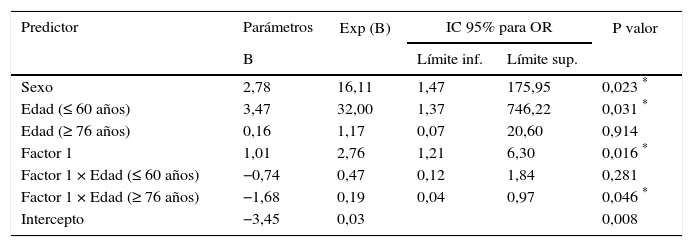
Modelo de regresión logística con variable latenteEn la tabla 3 se presentan los resultados del modelo de regresión logística propuesto. Todas las variables resultaron ser predictoras de la supervivencia. La magnitud de los efectos se evaluó a través de la exponencial de los parámetros (exp[B]) y los correspondientes intervalos de confianza del 95%. Cuando exp(B) exhibe un valor mayor que 1 y el intervalo de confianza no contiene el valor 1, el efecto puede considerarse estadísticamente significativo.
Resultados del modelo de regresión logística
| Predictor | Parámetros | Exp (B) | IC 95% para OR | P valor | |
|---|---|---|---|---|---|
| B | Límite inf. | Límite sup. | |||
| Sexo | 2,78 | 16,11 | 1,47 | 175,95 | 0,023 * |
| Edad (≤ 60 años) | 3,47 | 32,00 | 1,37 | 746,22 | 0,031 * |
| Edad (≥ 76 años) | 0,16 | 1,17 | 0,07 | 20,60 | 0,914 |
| Factor 1 | 1,01 | 2,76 | 1,21 | 6,30 | 0,016 * |
| Factor 1 × Edad (≤ 60 años) | −0,74 | 0,47 | 0,12 | 1,84 | 0,281 |
| Factor 1 × Edad (≥ 76 años) | −1,68 | 0,19 | 0,04 | 0,97 | 0,046 * |
| Intercepto | −3,45 | 0,03 | 0,008 | ||
El coeficiente de regresión (B) positivo asociado a la variable sexo, indican que los hombres tienen mayor probabilidad de fallecer después de la hemorragia en relación con las mujeres. Así mismo, la estimación positiva del parámetro asociado a la primera categoría de la variable edad (menos de 60 años), evidencian que pertenecer a este grupo etario, también aumenta el riesgo de fallecer después de la hemorragia, en comparación con el grupo de pacientes entre 61 y 75 años.
La variable latente Factor 1 mostró igualmente un coeficiente de regresión positivo. Este representa los efectos de la variable Factor 1 en el grupo de referencia de la variable moderadora (pacientes entre 61 y 75 años). Por tanto, el valor 2,756 de exp(B) es el factor multiplicativo para el cual el riesgo de fallecer cambia por cada unidad que aumente la variable latente Factor 1 en los pacientes entre 61 y 75 años de edad. El intervalo de confianza para la estimación de este parámetro proporciona un error de muestreo de [1.206, 6.301].
El efecto de la variable latente Factor 1 sobre la supervivencia es diferente a través de los estratos de la edad. La diferencia de riesgo es mayor en el estrato de los pacientes entre 61 y 75 años de edad. Por otro lado, el valor menor que 1 de exp(B) y el intervalo de confianza del término producto entre la variable latente y la variable indicadora del grupo de pacientes de mayor edad, muestra una interacción negativa sobre una escala multiplicativa. Esto significa que hay poca evidencia para la interacción entre la variable Factor 1 y el grupo de pacientes con una edad mayor a los 76 años.
DiscusiónLa metodología presentada permitió combinar características morfométricas de imágenes por TC y características de pacientes en un modelo de regresión logística en un único nivel, aplicando un enfoque de variables latentes, que explícitamente separa las asociaciones intra- e interindividuos de las variables morfométricas. Esto hace que se tengan en cuenta los errores de medición y muestreo de los valores a nivel micro (imagen) para evitar sesgos en las estimaciones de los parámetros a nivel macro (pacientes).
El procedimiento se ilustra mediante un simple análisis de datos reales, donde se muestra que el uso de conocidas herramientas estadísticas, pueden emplearse de manera combinada para construir variables latentes, capaces de modelar los efectos de la morfometría de imágenes de hemorragias cerebrales en relación con la supervivencia de los pacientes. Esto permitió hacer inferencias a nivel individuo utilizando la información disponible a nivel imagen en un modelo de regresión logística.
El modelo de regresión logística propuesto reveló que la morfometría de las imágenes (representada de manera sintética por la variable latente en el modelo), la edad y sexo de los pacientes, pueden ser predictores importantes para arribar a útiles conclusiones en el análisis de los datos. Sin embargo, la complejidad del problema y la flexibilidad de los modelos requiere que otras covariables, tales como la localización topográfica de las hemorragias, los antecedentes patológicos personales, entre otras; puedan también considerarse responsable de la mortalidad de los pacientes25–27. En este sentido, futuras investigaciones con mayores tamaños de muestra podrían contribuir a obtener conclusiones más consistentes.
En resumen, más allá de las limitaciones presentadas, la metodología propuesta en este artículo representa una primera incursión en un terreno de investigación de vastas posibilidades para el desarrollo teórico, y mayores aún para la aplicación práctica de métodos apropiados para analizar datos morfométricos de imágenes por TC como parte de un instrumento de pronóstico. Por otro lado, el estudio del efecto condicional de las variables latentes sobre determinados grupos de individuos puede incidir de manera vital en la especificación de cuáles características de los pacientes están relacionadas con bajas o elevadas tasas de respuesta en la población a estudiar.
Responsabilidades éticasProtección de personas y animalesLos autores declaran que para esta investigación no se han realizado experimentos en seres humanos ni en animales.
Confidencialidad de los datosLos autores declaran que han seguido los protocolos de su centro de trabajo sobre la publicación de datos de pacientes.
Derecho a la privacidad y consentimiento informadoLos autores declaran que en este artículo no aparecen datos de pacientes.
Conflicto de interesesLos autores declaran no tener ningún conflicto de intereses.