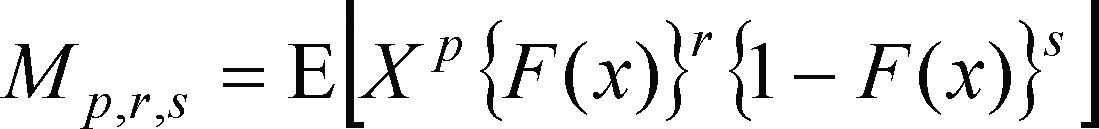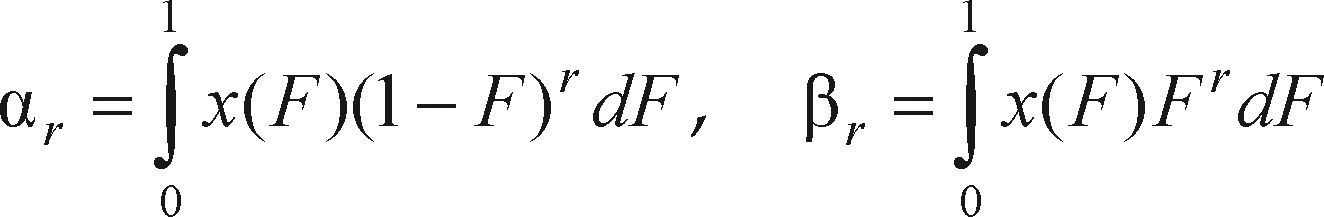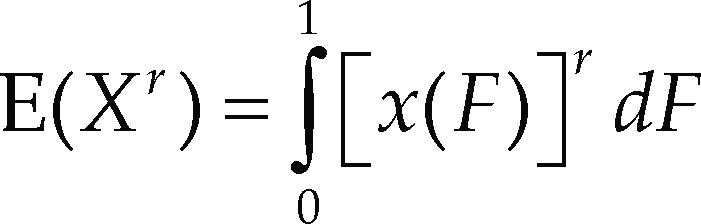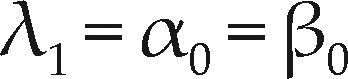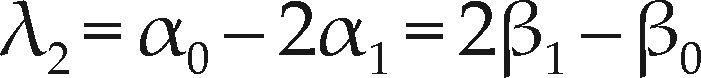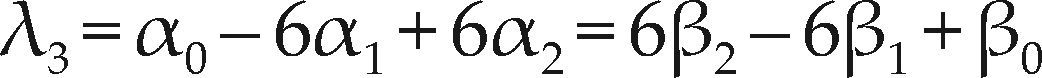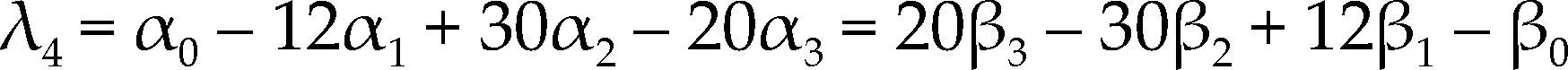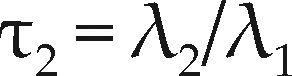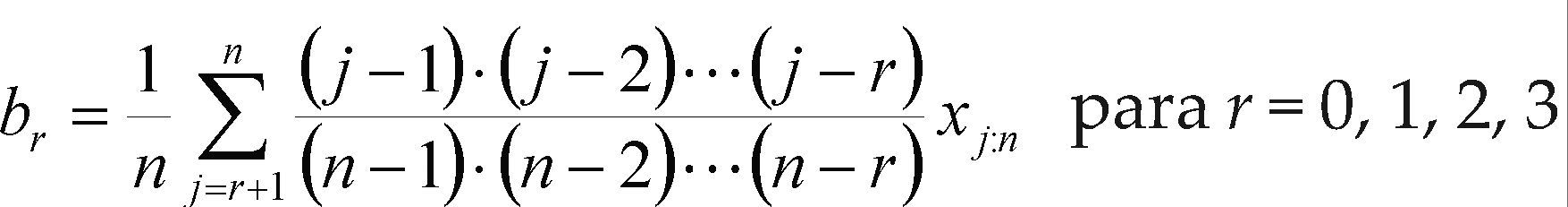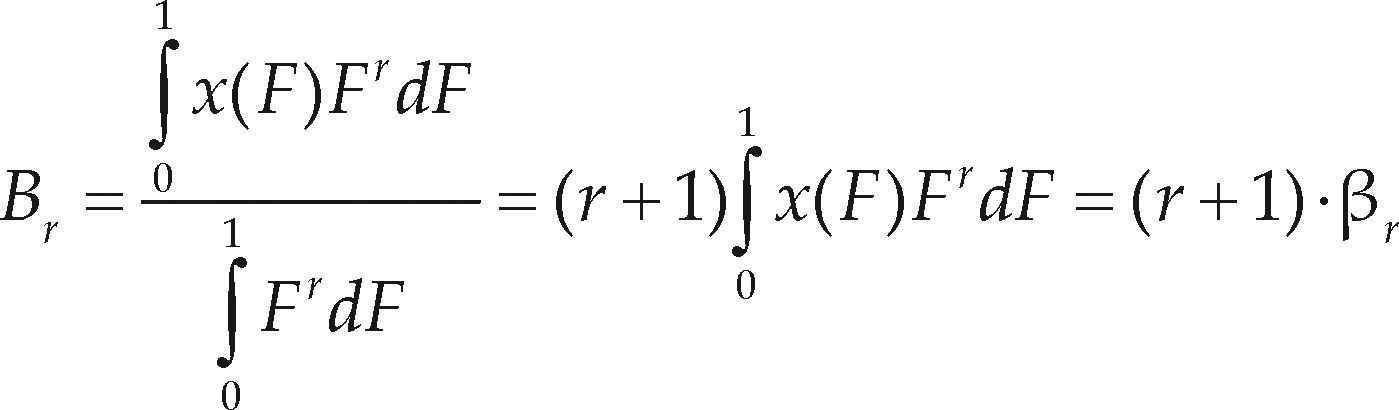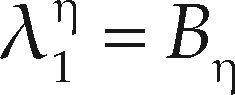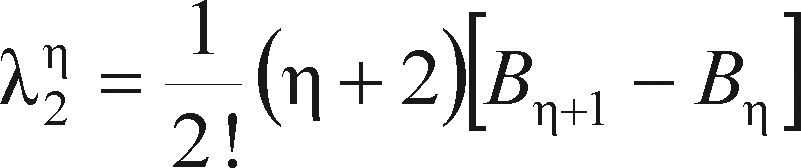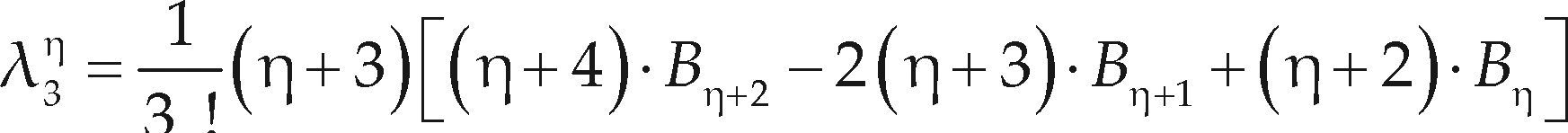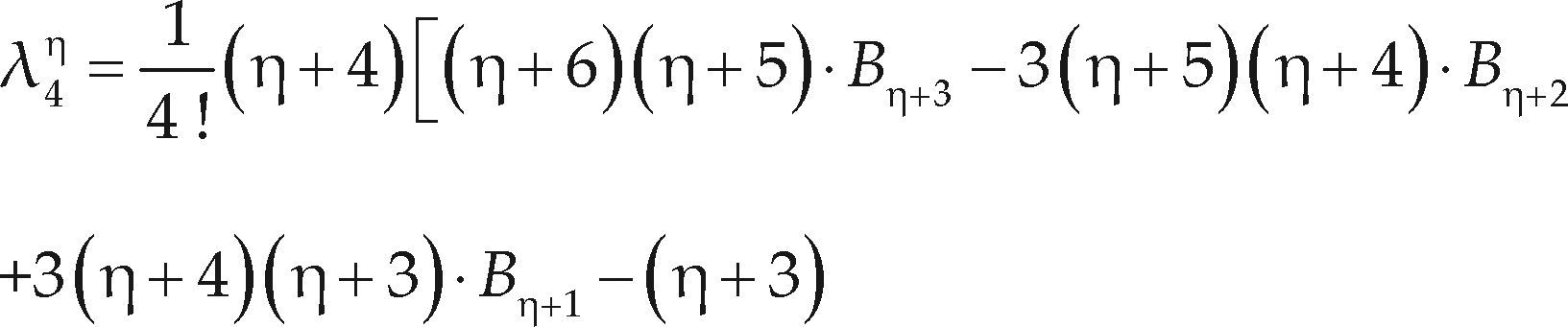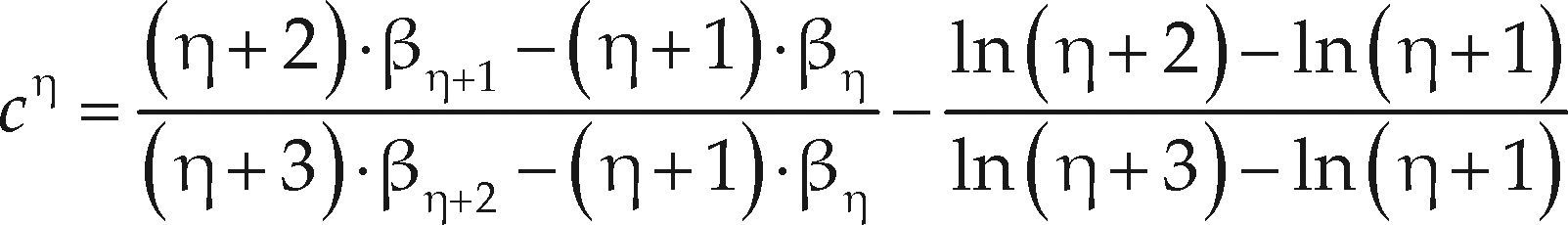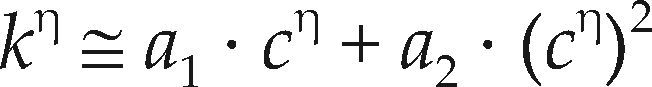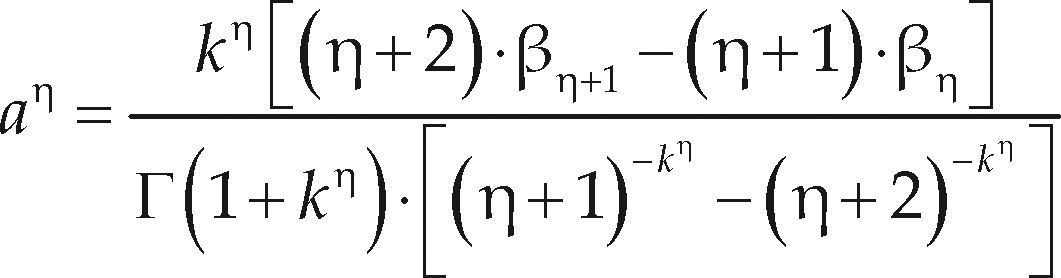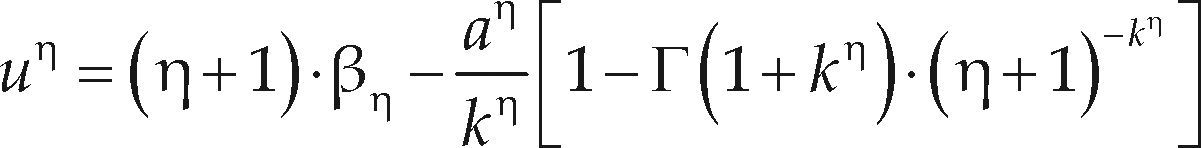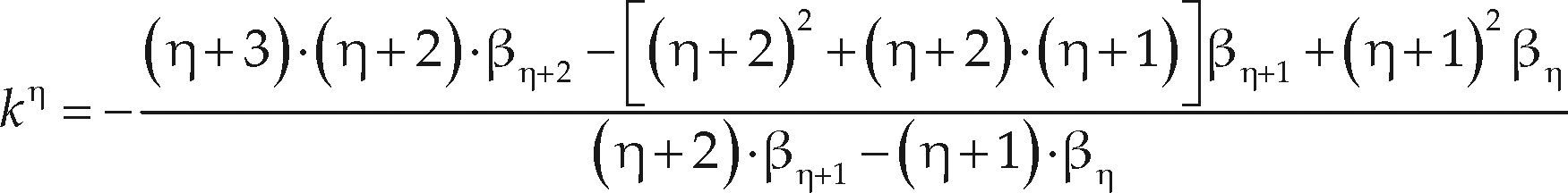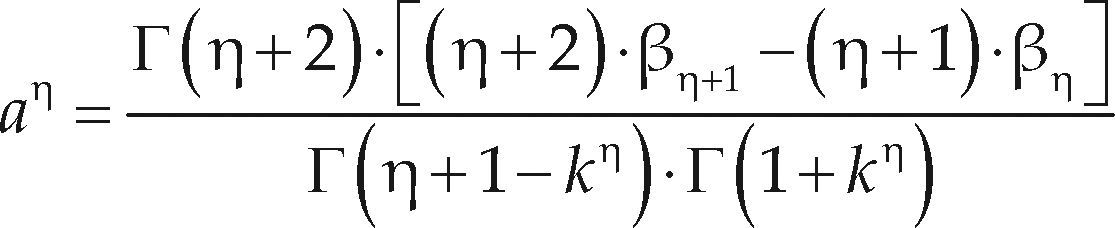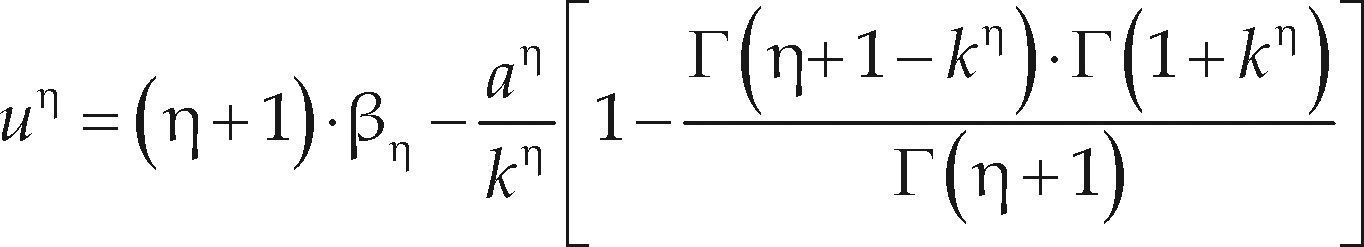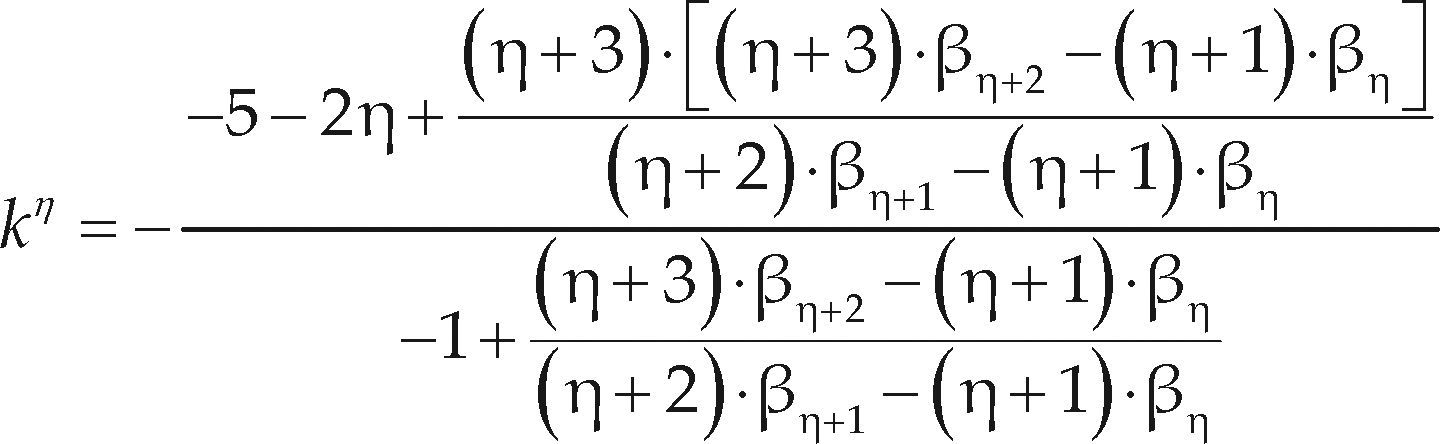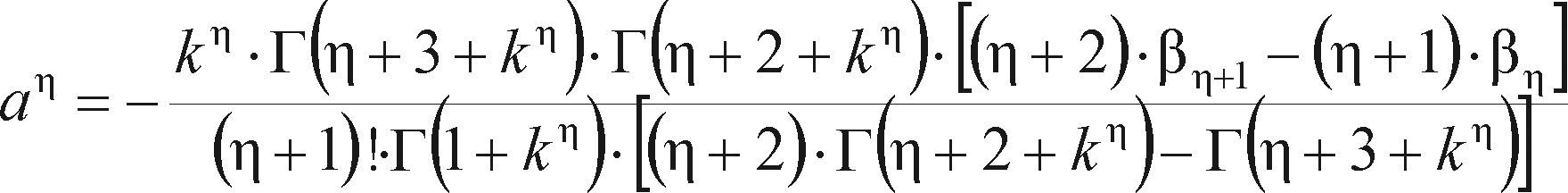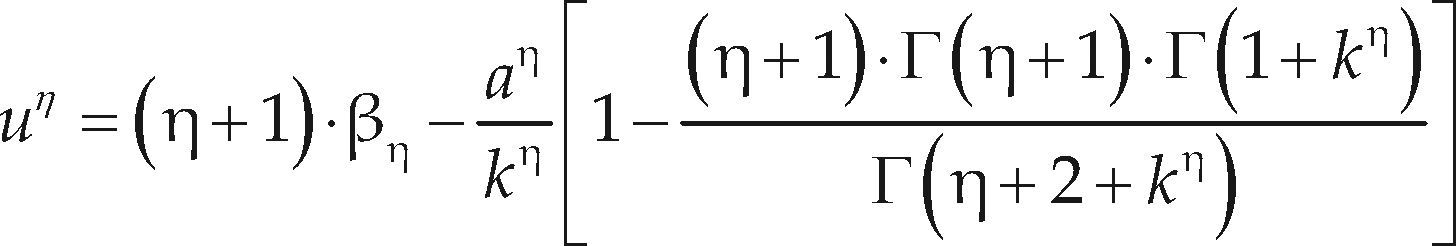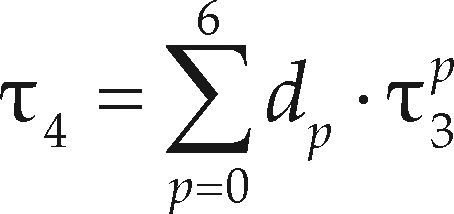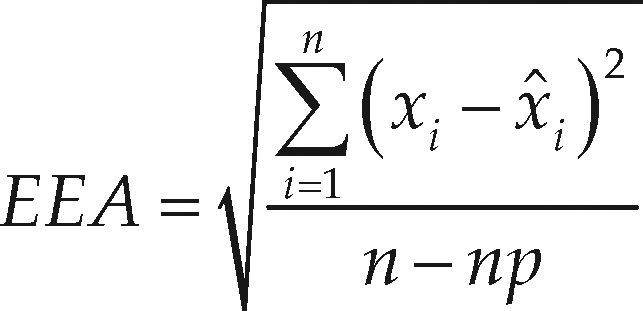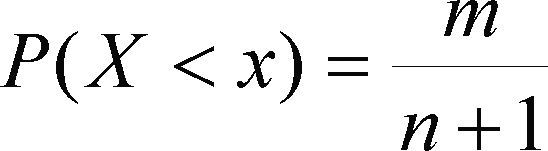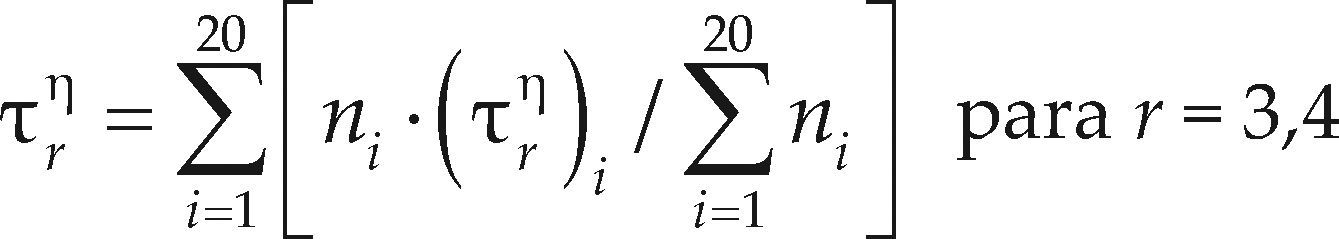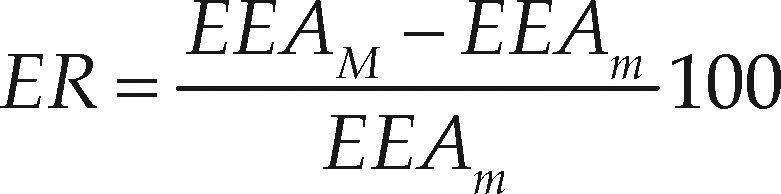Ajuste de las distribuciones GVE, LOG y PAG con momentos L de orden mayor

Resumen

El análisis probabilístico de datos hidrológicos extremos busca estimar predicciones confiables asociadas a altos periodos de retorno. Los momentos LH o de orden mayor, permiten caracterizar de una manera más eficiente la cola derecha de la función de distribución de probabilidades (FDP), al dar más importancia a los grandes valores de los datos. Usando los momentos LH se reduce la influencia indeseable que las magnitudes pequeñas de la muestra pueden tener en la estimación de las predicciones. En este trabajo se describe brevemente la teoría de los momentos L, como base para su generalización, lo cual conduce a los momentos LH, propuestos en 1997 por Wang Q.J. Se citan las ecuaciones que permiten estimar, con los métodos de momentos L y momentos LH, los tres parámetros de ajuste de las FDP: general de valores extremos (GVE), logística generalizada (LOG) y Pareto generalizada (PAG). Se realiza una aplicación numérica a los 21 registros disponibles de crecientes anuales de la Región Hidrológica Núm. 10 (Sinaloa), contrastando sus resultados con base en el error estándar de ajuste (EEA). El análisis de resultados mostró que la distribución PAG conduce a los mejores ajustes. También se observó que los momentos LH son una buena opción para abatir el EEA en las tres distribuciones utilizadas.

Abstract

The probabilistic analysis of extreme hydrological data aims to estimate reliable predictions associated with high return periods. The LH or higher-order moments can characterize in a more efficient way the right tail of the probability distribution function (PDF), by giving more importance to large data values. The undesirable influence of the sample's small quantities is reduced by using the LH moments in the estimation of predictions. This paper briefly describes the theory of L moments, as a basis for its generalization, which leads to the LH moments, proposed in 1997 by Wang Q.J. By means of the L and LH moments methods, the equations that allow the estimation of the three fitting parameters of the PDF: General Extreme Values (GEV), Generalized Logistics (GLO) and Generalized Pareto (GPA) are cited. A numerical application to the 21 available records annual floods of Hydrological Region No. 10 (Sinaloa) is performed, contrasting its results based on the standard error of fit (SEF). The analysis of results showed that the GPA distribution leads to the best fittings. It can be highlighted that LH moments are a good choice to abate the SEF in the three distributions used.

Introducción

La planeación, diseño y operación de las obras hidráulicas, se basa en las llamadas Crecientes de Diseño, cuya estimación lo más exacta posible, incrementa su seguridad hidrológica. El método más confiable para su estimación consiste en el análisis probabilístico de la información de gastos máximos anuales, a través del ajuste de una cierta función de distribución de probabilidades (FDP) y su uso posterior para realizar las predicciones buscadas. Esta técnica denominada análisis de frecuencia de crecientes (AFC) consta de cuatro etapas:

• 1)

  Recopilación de datos y verificación de su calidad estadística.

• 2)

  Selección de una FDP.

• 3)

  Elección de un método de estimación de sus parámetros de ajuste.

• 4)

  Verificación del ajuste logrado con cada FDP y técnica de estimación (Hosking y Wallis, 1997; Lee y Maeng, 2003; Gheidari, 2013).

En el AFC los periodos de retorno de diseño, comúnmente exceden varias veces la amplitud del registro disponible en años, entonces las predicciones buscadas son extrapolaciones que involucran dificultades y errores asociados. El error principal inherente a tales extrapolaciones radica en aceptar que la FDP adoptada y ajustada a los datos, es válida más allá de la magnitud máxima de los valores disponibles. Se han desarrollado dos enfoques para reducir el error citado; el primero consiste en utilizar FDP de gran flexibilidad, que están caracterizadas por más de tres parámetros de ajuste, como la distribución Kappa de cuatro parámetros y la Wakeby y las funciones mixtas de cinco parámetros. El segundo enfoque radica en seleccionar los datos de crecientes por utilizar, con la idea fundamental de dar más importancia a las observaciones grandes; se han propuesto tres técnicas:

• a.

  La más antigua consiste en emplear crecientes superiores a un valor umbral.

• b.

  Emplear muestras truncadas o censuradas.

• c.

  Las más recientes, emplear técnicas de ajuste que eliminan datos pequeños, o bien, dan mayor influencia a los valores grandes, caso de los momentos L depurados y de orden mayor (Wang, 1997b; Moisello, 2007; Meshgi y Khalili, 2009a).

El objetivo de este trabajo consiste en exponer de manera breve la teoría de los momentos LH o de orden mayor y sus ventajas en el AFC, citando las ecuaciones que permiten estimar los tres parámetros de ajuste de las distribuciones GVE, LOG y PAG, con los métodos de mo- mentos L y momentos LH. Estas FDP son de uso frecuente en los AFC. Se aplican ambas técnicas de ajuste a los 21 registros disponibles de crecientes anuales en la Región Hidrológica Núm. 10 (Sinaloa), revisando principalmente su homogeneidad hidrológica regional y después se evalúa el desempeño de las FDP mediante el error estándar de ajuste. Por último, se formulan las conclusiones del estudio.

Resumen de la teoría operativa

Momentos L poblacionales y de la muestra

Hosking y Wallis (1997) indican que los momentos L son un sistema alternativo que permite describir la forma de la FDP, cuyos antecedentes estadísticos nacieron con los momentos de probabilidad ponderada (MPP) de una variable aleatoria X con función de probabilidades acumuladas F(x), definidos por Greenwood et al. (1979) como las cantidades siguientes:

Particularmente útiles son los casos especiales: α_r =M_1,0,r y β_r = M_1,r,0 cuyas expresiones son

donde X = x(F) y F = F(x). Las ecuaciones anteriores contrastan con la definición de los momentos ordinarios, que es

Se observa que los momentos convencionales involucran potencias sucesivas de la llamada solución inversa x(F), mientras que los MPP establecen potencias sucesivas de (1 – F) o de F y ello se puede considerar como la integral de x(F) ponderada por tales polinomios. Los MPP α_r y β_r son la base de varios métodos que permiten estimar los parámetros de ajuste de una FDP. Sin embargo, de manera individual son difíciles de interpretar como medidas de escala y forma, pero tal información se obtiene con ciertas combinaciones lineales de ellos, que son precisamente los momentos L (λ). Como medidas de ubicación, escala y forma (asimetría y curtosis), estos son respectivamente (Hosking y Wallis, 1997)

Los cocientes de momentos L adimensionales se definen con similitud a los coeficientes de variación, asimetría y curtosis, como

En una muestra de tamaño n, ordenada en forma progresiva, es decir que: x_1:n ≤ x_2:n ≤ ... ≤ x_n:n , el estimador insesgado del MPP β_r es (Hosking y Wallis, 1997)

Entonces, las estimaciones con la muestra o serie de datos de los momentos L se obtienen con las ecuaciones 4 a 7 y se designan por l_r para r = 1, 2, 3, 4 y sus cocientes son t₂, t₃ y t₄.

Momentos L de orden mayor

Desde que Hosking (1990) consolidó la teoría de los momentos L, estos se han empleado para analizar valores extremos de crecientes, vientos, lluvias, etcétera. Tales análisis estadísticos se orientan a predecir eventos extremos asociados a altos periodos de retorno, es decir, a bajas probabilidades de ser excedidos. Entonces, resulta relevante en estos análisis la cola derecha de la FDP y los datos extremos superiores de la muestra; surgiendo estas dudas: ¿Son los momentos L demasiado sensitivos a los valores bajos de la muestra? O bien, ¿Dan peso insuficiente a las grandes magnitudes de los datos? Para eliminar tales dudas, Wang (1997b) propone los momentos L de orden mayor (λ^η), conocidos como “LH-moments” de higher que significa orden superior, como una generalización de los momentos L, que permiten una mejor caracterización de la cola derecha de la FDP y de los grandes eventos en los datos. Para ello, Wang (1997b) define los momentos de probabilidad ponderada normalizados, como

y entonces encuentra las expresiones siguientes para los momentos L de orden mayor

Cuando η = 0 los momentos LH son idénticos a los momentos L (ecuaciones 4 a 7). Conforme η se incrementa, los momentos LH reflejan de mejor manera las características de la parte superior de la distribución y de los grandes eventos de los datos. Los momentos L también se han definido y estudiado como estadísticos de orden, al igual que los momentos L de orden mayor; en Wang (1997b) se puede consultar tal formulación. Los cocientes de momentos L de orden superior son

Ajuste de las distribuciones GVE, LOG y PAG con momentos L

Hosking y Wallis (1997) indican en su tabla 5.1, que cuando su parámetro de forma es negativo (k < 0) en estas FDP, tienen sus colas derechas más gruesas o densas (heavy tail) que las otras que son empleadas rutinariamente en los análisis de frecuencia de datos hidrológicos extremos; además tales FDP tienen una frontera superior cuando k es positivo (k > 0) y cuando k = 0 definen funciones de dos parámetros: la Gumbel, la Logística y la Exponencial, respectivamente.

El método de obtención de los parámetros de ubicación, escala y forma (u, a y k) en las distribuciones GVE, LOG y PAG con base en los momentos L se puede consultar para cada una en: Stedinger et al. (1993), Rao y Hamed (2000) y Hosking y Wallis (1997). En la tabla 1 se enlistan para estas FDP: intervalo, fórmula matemática F(x), solución inversa x(F) y las ecuaciones del método de momentos L, para k, a y u.

Tabla 1.

Fórmulas matemáticas de las FDP indicadas y ecuaciones para estimar sus tres parámetros de ajuste (k, a, u) con el método de momentos L

Ajuste de las distribuciones GVE, LOG y PAG con momentos L de orden mayor

Wang (1997a,b) desarrolló dos procedimientos para el ajuste de la distribución GVE con el método de los momentos L de orden mayor, el segundo de ellos, estima el parámetro de forma (k) con base en el cociente y el primero se parece al de los momentos L y es el si- guiente

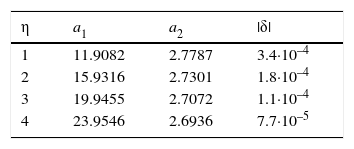
Los coeficientes a₁ y a₂ varían con el orden η de los momentos LH, tienen los valores de la tabla 2 y son aplicables en el intervalo: –0.50 ≤ k^h ≤ 0.50.

Tabla 2.

Coeficientes a₁ y a₂ de la ecuación 40 y error absoluto máximo (δ) del parámetro de forma k^h de la distribución GVE (Wang, 1997a)

η	a1	a2	|δ|
1	11.9082	2.7787	3.4·10^–4
2	15.9316	2.7301	1.8·10^–4
3	19.9455	2.7072	1.1·10^–4
4	23.9546	2.6936	7.7·10^–5

Meshgi y Khalili (2009b) obtuvieron las expresiones que permiten estimar los tres parámetros de ajuste de la distribución logística generalizada (LOG) con el método de los momentos L de orden mayor, estas son

Meshgi y Khalili (2009b) también desarrollaron las ecuaciones que permiten estimar los tres parámetros de ajuste de la distribución pareto generalizada (PAG) con el método de los momentos L de orden mayor, estas son

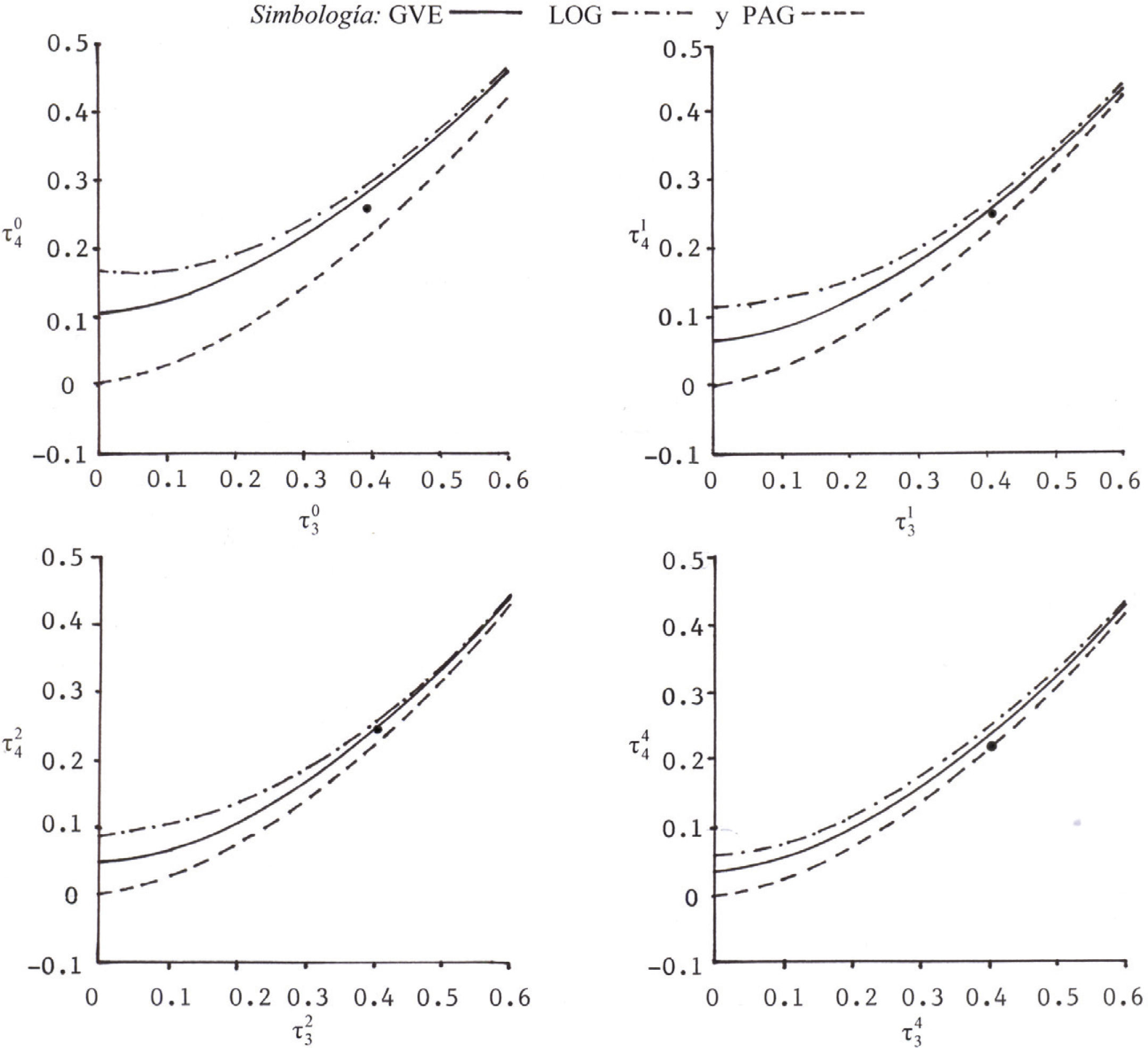
Diagramas de cocientes de momentos L de orden mayor

Hosking y Wallis (1997) presentan la relación gráfica que tiene el cociente de momentos L de asimetría (τ₃) con el de curtosis (τ₄) en cinco FDP, lo cual constituye el llamado Diagrama de cocientes de momentos L. Tal gráfica se puede utilizar para seleccionar la mejor FDP, de acuerdo con los valores t₃ y t₄ de la muestra local o a su estimación regional. Las relaciones gráficas para las distribuciones GVE, LOG y PAG son polinomios de grado (p) sexto, segundo y cuarto, cuya ecuación general es

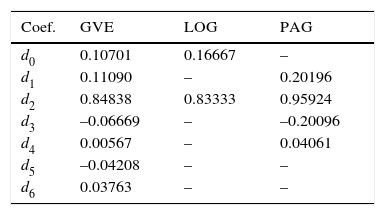
Los coeficientes d_p de la ecuación 49 se tienen en la tabla 3; tal ecuación tiene una aproximación de ± 0.0005 cuando –0.60 ≤ τ₃ ≤ 0.90.

Tabla 3.

Coeficientes de los polinomios de aproximación de τ₄ en función de τ₃ en las distribuciones GVE, LOG y PAG con momentos L, según Hoskin y Wallis (1997)

Coef.	GVE	LOG	PAG
d0	0.10701	0.16667	–
d1	0.11090	–	0.20196
d2	0.84838	0.83333	0.95924
d3	–0.06669	–	–0.20096
d4	0.00567	–	0.04061
d5	–0.04208	–	–
d6	0.03763	–	–

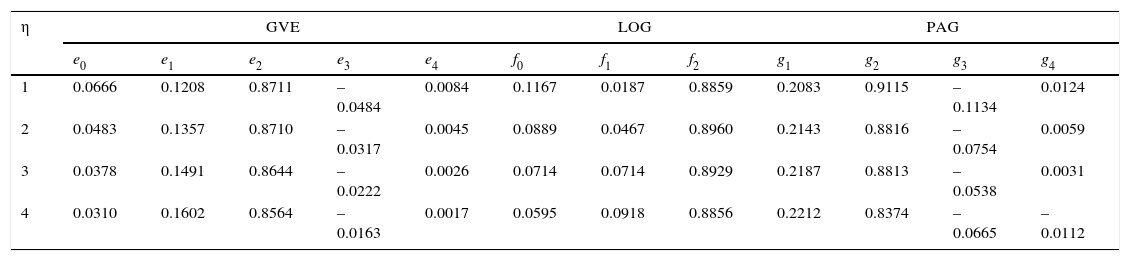
Para obtener los diagramas de momentos L de orden mayor, habrá que encontrar la relación ent re y p ara cada FDP. Wang (1997b) desarrolló tal relación para la distribución GVE, al obtener sus expresiones d e , y . Meshgi y Khalili (2009a) la exponen en forma de polinomio de grado cuarto, con sus coeficientes e_p mostrados en la tabla 4; además, desarrollan y presentan en forma similar tal relación para las distribuciones LOG y PAG, cuyos coeficientes f_p y g_p, también se citan en la tabla 4.

Tabla 4.

Coeficientes de los polinomios de a proximación de en función de (e cuación 49) en las distribuciones GVE, LOG y PAG con momentos L de orden mayor, según Meshgi y Khalili (2009a)

η	GVE					LOG			PAG
	e0	e1	e2	e3	e4	f0	f1	f2	g1	g2	g3	g4
1	0.0666	0.1208	0.8711	–0.0484	0.0084	0.1167	0.0187	0.8859	0.2083	0.9115	–0.1134	0.0124
2	0.0483	0.1357	0.8710	–0.0317	0.0045	0.0889	0.0467	0.8960	0.2143	0.8816	–0.0754	0.0059
3	0.0378	0.1491	0.8644	–0.0222	0.0026	0.0714	0.0714	0.8929	0.2187	0.8813	–0.0538	0.0031
4	0.0310	0.1602	0.8564	–0.0163	0.0017	0.0595	0.0918	0.8856	0.2212	0.8374	–0.0665	–0.0112

Medida cuantitativa del ajuste

A mediados de la década de los años setenta se estableció el error estándar de ajuste (EEA) como un indicador estadístico cuantitativo que estima la calidad del ajuste y que además permite la comparación objetiva entre las diversas FDP que se ajustan a una muestra, ya que tiene las unidades de los datos. Su expresión es la siguiente (Kite, 1977)

en donde, n y np son el número de datos de la muestra y de parámetros de ajuste, en este caso tres; x_i son los datos ordenados de menor a mayor y s on los valores estimados con la solución inversa x (F) para una probabilidad de no excedencia, estimada con la fórmula de Weibull (Benson, 1962)

donde m es el número de orden del dato, con 1 para el menor y n para el mayor.

Desarrollo del contraste numérico

Registros de crecientes anuales procesados

Fueron 21 registros de gastos máximos anuales instantáneos (m³/s) de las estaciones hidrométricas de la Región Hidrológica Núm. 10 (Sinaloa) que no tienen régimen de escurrimiento afectado por embalses o cambios drásticos en sus cuencas y que cuentan con más de 20 años de datos en el sistema BANDAS (IMTA, 2002). Los registros de las estaciones de aforos Huites y Guamuchil, llegan hasta el año en que la construcción del embalse respectivo afectó su escurrimiento. Los datos de la estación San Francisco se tomaron del Boletín Hidrológico Núm. 36 (SRH, 1975). Campos-Aranda (2014) verificó la calidad estadística de los registros citados y presenta sus momentos y cocientes L; además expone un mapa con la localización de las 21 estaciones hidrométricas y sus cuencas respectivas.

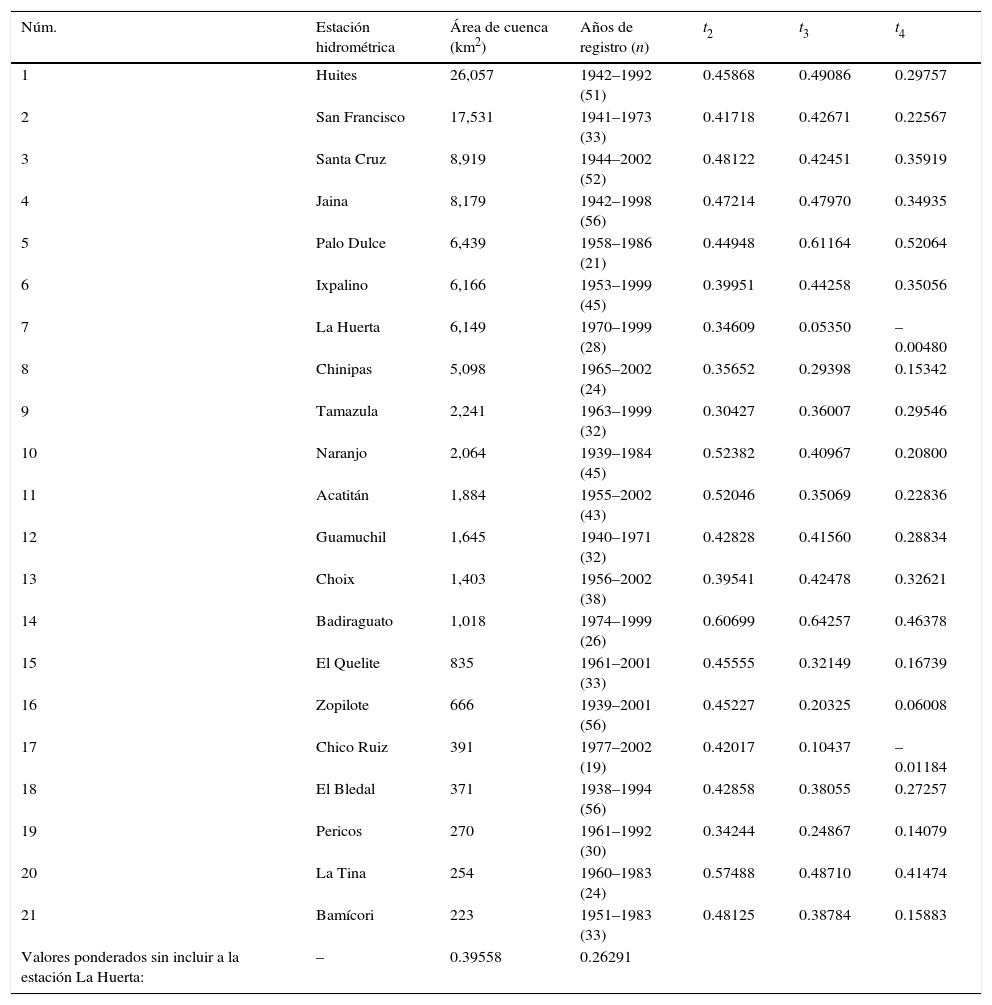
En las primeras cuatro columnas de la tabla 5 se citan las características generales de las 21 estaciones hidrométricas, expuestas en orden decreciente de tamaño de cuenca y en sus tres últimas columnas se tienen los valores de los cocientes de momentos L. Se observa que el registro más corto tiene 19 años y los más largos 56, con un valor mediano de 33 años.

Tabla 5.

Características generales de las 21 estaciones hidrométricas procesadas de la Región Hidrológica Núm. 10 (Sinaloa) y sus cocientes de momentos L de sus registros de crecientes anuales

Núm.	Estación hidrométrica	Área de cuenca (km^2)	Años de registro (n)	t2	t3	t4
1	Huites	26,057	1942–1992 (51)	0.45868	0.49086	0.29757
2	San Francisco	17,531	1941–1973 (33)	0.41718	0.42671	0.22567
3	Santa Cruz	8,919	1944–2002 (52)	0.48122	0.42451	0.35919
4	Jaina	8,179	1942–1998 (56)	0.47214	0.47970	0.34935
5	Palo Dulce	6,439	1958–1986 (21)	0.44948	0.61164	0.52064
6	Ixpalino	6,166	1953–1999 (45)	0.39951	0.44258	0.35056
7	La Huerta	6,149	1970–1999 (28)	0.34609	0.05350	–0.00480
8	Chinipas	5,098	1965–2002 (24)	0.35652	0.29398	0.15342
9	Tamazula	2,241	1963–1999 (32)	0.30427	0.36007	0.29546
10	Naranjo	2,064	1939–1984 (45)	0.52382	0.40967	0.20800
11	Acatitán	1,884	1955–2002 (43)	0.52046	0.35069	0.22836
12	Guamuchil	1,645	1940–1971 (32)	0.42828	0.41560	0.28834
13	Choix	1,403	1956–2002 (38)	0.39541	0.42478	0.32621
14	Badiraguato	1,018	1974–1999 (26)	0.60699	0.64257	0.46378
15	El Quelite	835	1961–2001 (33)	0.45555	0.32149	0.16739
16	Zopilote	666	1939–2001 (56)	0.45227	0.20325	0.06008
17	Chico Ruiz	391	1977–2002 (19)	0.42017	0.10437	–0.01184
18	El Bledal	371	1938–1994 (56)	0.42858	0.38055	0.27257
19	Pericos	270	1961–1992 (30)	0.34244	0.24867	0.14079
20	La Tina	254	1960–1983 (24)	0.57488	0.48710	0.41474
21	Bamícori	223	1951–1983 (33)	0.48125	0.38784	0.15883
Valores ponderados sin incluir a la estación La Huerta:	–	0.39558	0.26291

Verificación de la homogeneidad regional

Se realizaron dos pruebas estadísticas a los 21 registros disponibles, la primera fue el cálculo de las Discordancias (Hosking y Wallis, 1997; Campos-Aranda, 2010), basada en los cocientes t₂, t₃ y t₄ expuestos en la tabla 5, encontrado que ninguna muestra o serie de crecientes excede el valor crítico de Dc = 3.00, por lo cual no existen registros discordantes. Los dos registros con mayor discordancia fueronn La Tina (D = 2.35) y La Huerta (D = 2.13).

La segunda prueba aplicada fue el nuevo Test de Langbein (Fill y Stedinger, 1995; Campos-Aranda, 2012) donde se encuentra, que cuatro estaciones o registros quedan fuera de sus curvas de control, estas son: La Huerta, Tamazula, Chinipas y Pericos. Se eliminó la primera, ya que también fue de las más discordantes y se repitió la prueba; nuevamente aparecen las tres restantes como estaciones que se deben eliminar, pero tal número es el permitido en una región con 20 estaciones y confiabilidad de 95%. Entonces se acepta la homogeneidad regional con los 20 registros de la tabla 5, al eliminar el de la estación La Huerta (Núm. 7).

En Bhuyan et al. (2010) se puede consultar un AFC regional completo, ya que la prueba de discordancias y la verificación de la homogeneidad se realiza con cada orden (η) de los momentos L de orden mayor, así como la selección de la mejor FDP. En cambio, este trabajo se orientó al estudio de los ajustes locales, a través del EEA (ecuación 50).

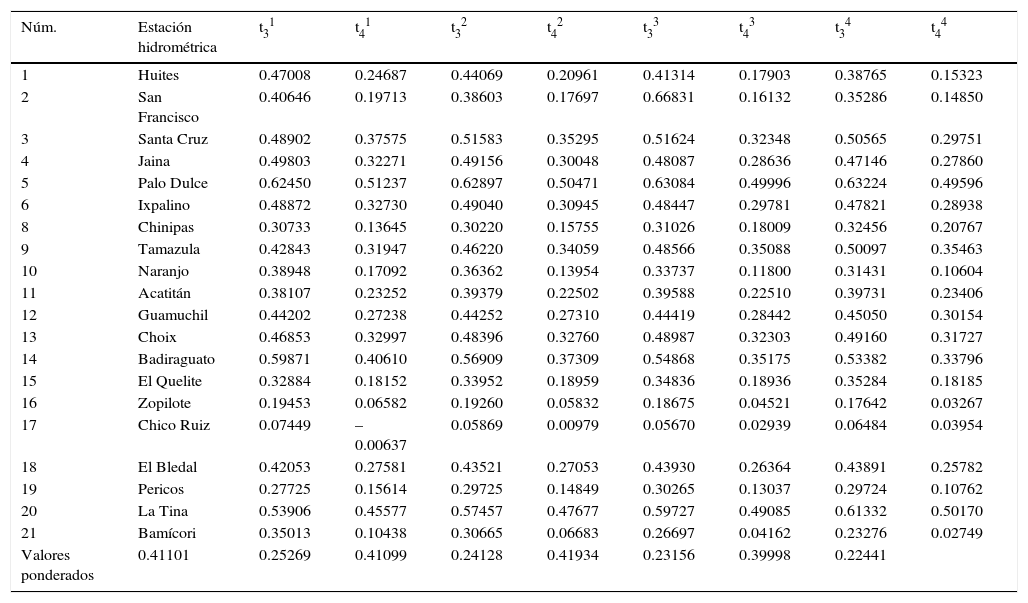
Cocientes de momentos L de orden mayor

Inicialmente, en las ecuaciones 12 a 15, se sustituyó a B_η por β_η con base en la ecuación 11 y después al aplicar la ecuación 10 se obtuvieron los valores de los momentos L de orden mayor de cada muestra y con ellos los cocientes de asimetría y curtosis según la ecuación 16. Estos valores se muestran en la tabla 6.

Tabla 6.

Cocientes de momentos L de orden mayor en los 20 registros de crecientes anuales de las estaciones hidrométricas indicadas de la Región Hidrológica Núm. 10 (Sinaloa)

Núm.	Estación hidrométrica	t3^1	t4^1	t3^2	t4^2	t3^3	t4^3	t3^4	t4^4
1	Huites	0.47008	0.24687	0.44069	0.20961	0.41314	0.17903	0.38765	0.15323
2	San Francisco	0.40646	0.19713	0.38603	0.17697	0.66831	0.16132	0.35286	0.14850
3	Santa Cruz	0.48902	0.37575	0.51583	0.35295	0.51624	0.32348	0.50565	0.29751
4	Jaina	0.49803	0.32271	0.49156	0.30048	0.48087	0.28636	0.47146	0.27860
5	Palo Dulce	0.62450	0.51237	0.62897	0.50471	0.63084	0.49996	0.63224	0.49596
6	Ixpalino	0.48872	0.32730	0.49040	0.30945	0.48447	0.29781	0.47821	0.28938
8	Chinipas	0.30733	0.13645	0.30220	0.15755	0.31026	0.18009	0.32456	0.20767
9	Tamazula	0.42843	0.31947	0.46220	0.34059	0.48566	0.35088	0.50097	0.35463
10	Naranjo	0.38948	0.17092	0.36362	0.13954	0.33737	0.11800	0.31431	0.10604
11	Acatitán	0.38107	0.23252	0.39379	0.22502	0.39588	0.22510	0.39731	0.23406
12	Guamuchil	0.44202	0.27238	0.44252	0.27310	0.44419	0.28442	0.45050	0.30154
13	Choix	0.46853	0.32997	0.48396	0.32760	0.48987	0.32303	0.49160	0.31727
14	Badiraguato	0.59871	0.40610	0.56909	0.37309	0.54868	0.35175	0.53382	0.33796
15	El Quelite	0.32884	0.18152	0.33952	0.18959	0.34836	0.18936	0.35284	0.18185
16	Zopilote	0.19453	0.06582	0.19260	0.05832	0.18675	0.04521	0.17642	0.03267
17	Chico Ruiz	0.07449	–0.00637	0.05869	0.00979	0.05670	0.02939	0.06484	0.03954
18	El Bledal	0.42053	0.27581	0.43521	0.27053	0.43930	0.26364	0.43891	0.25782
19	Pericos	0.27725	0.15614	0.29725	0.14849	0.30265	0.13037	0.29724	0.10762
20	La Tina	0.53906	0.45577	0.57457	0.47677	0.59727	0.49085	0.61332	0.50170
21	Bamícori	0.35013	0.10438	0.30665	0.06683	0.26697	0.04162	0.23276	0.02749
Valores ponderados	0.41101	0.25269	0.41099	0.24128	0.41934	0.23156	0.39998	0.22441

Selección de la FDP regional

Principalmente se obtienen las magnitudes regionales representativas de los cocientes de momentos L originales y de orden mayor, por medio de sus valores ponderados con la amplitud de cada registro en años, a través de la expresión

donde

i = contador de registros procesados y

n_i = su tamaño en años.

Los valores ponderados de los cocientes de momentos L y de los de orden mayor se tienen en los últimos renglones de las tablas 5 y 6. Con base en la ecuación 49 se han construido los diagramas de cocientes de momentos mostrados en la figura 1, donde se dibujaron los valores ponderados de ; se observa que la FDP ade- cuada es la GVE y únicamente con η = 4 es la PAG.

Figura 1.

Selección de la FDP regional en los diagramas de cocientes de momentos LH.

Errores estándar de ajuste

Con base en los momentos L y sus cocientes expuestos por Campos-Aranda (2014), se obtuvieron los tres parámetros de ajuste de las distribuciones GVE, LOG y PAG mediante las ecuaciones de la tabla 1. En seguida, haciendo uso de las soluciones inversas, ecuaciones 20, 28 y 34, se obtuvieron las estimaciones n ecesarias para aplicar la ecuación 50 del EEA. Los resultados se concentraron en la tabla 7, en las columnas indicadas con “L0”.

Tabla 7.

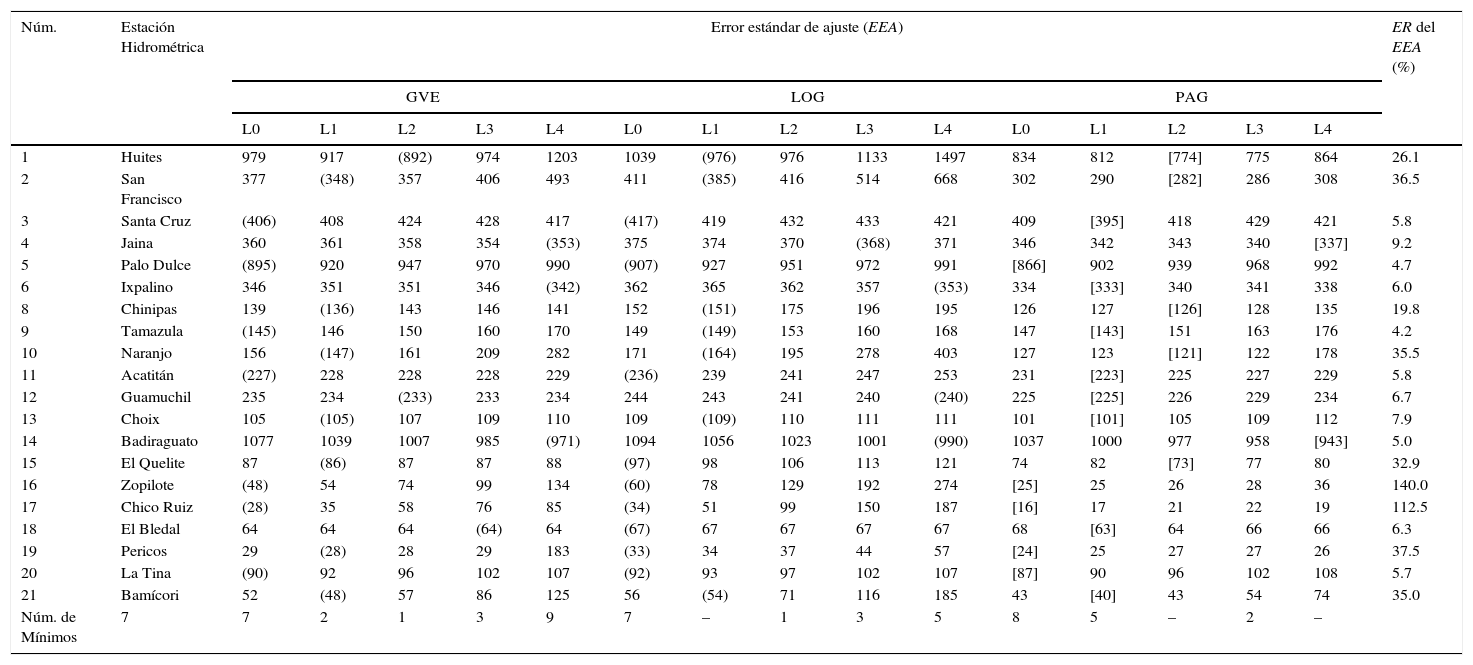
Errores estándar de ajuste (m³/s) obtenidos con los métodos de momentos L y de momentos L de orden mayor al ajustar las distribuciones GVE, LOG y PAG a los registros de crecientes anuales de las 20 estaciones hidrométricas indicadas de la Región Hidrológica Núm. 10 (Sinaloa)

Núm.	Estación Hidrométrica	Error estándar de ajuste (EEA)															ER del EEA (%)
		GVE					LOG					PAG
		L0	L1	L2	L3	L4	L0	L1	L2	L3	L4	L0	L1	L2	L3	L4
1	Huites	979	917	(892)	974	1203	1039	(976)	976	1133	1497	834	812	[774]	775	864	26.1
2	San Francisco	377	(348)	357	406	493	411	(385)	416	514	668	302	290	[282]	286	308	36.5
3	Santa Cruz	(406)	408	424	428	417	(417)	419	432	433	421	409	[395]	418	429	421	5.8
4	Jaina	360	361	358	354	(353)	375	374	370	(368)	371	346	342	343	340	[337]	9.2
5	Palo Dulce	(895)	920	947	970	990	(907)	927	951	972	991	[866]	902	939	968	992	4.7
6	Ixpalino	346	351	351	346	(342)	362	365	362	357	(353)	334	[333]	340	341	338	6.0
8	Chinipas	139	(136)	143	146	141	152	(151)	175	196	195	126	127	[126]	128	135	19.8
9	Tamazula	(145)	146	150	160	170	149	(149)	153	160	168	147	[143]	151	163	176	4.2
10	Naranjo	156	(147)	161	209	282	171	(164)	195	278	403	127	123	[121]	122	178	35.5
11	Acatitán	(227)	228	228	228	229	(236)	239	241	247	253	231	[223]	225	227	229	5.8
12	Guamuchil	235	234	(233)	233	234	244	243	241	240	(240)	225	[225]	226	229	234	6.7
13	Choix	105	(105)	107	109	110	109	(109)	110	111	111	101	[101]	105	109	112	7.9
14	Badiraguato	1077	1039	1007	985	(971)	1094	1056	1023	1001	(990)	1037	1000	977	958	[943]	5.0
15	El Quelite	87	(86)	87	87	88	(97)	98	106	113	121	74	82	[73]	77	80	32.9
16	Zopilote	(48)	54	74	99	134	(60)	78	129	192	274	[25]	25	26	28	36	140.0
17	Chico Ruiz	(28)	35	58	76	85	(34)	51	99	150	187	[16]	17	21	22	19	112.5
18	El Bledal	64	64	64	(64)	64	(67)	67	67	67	67	68	[63]	64	66	66	6.3
19	Pericos	29	(28)	28	29	183	(33)	34	37	44	57	[24]	25	27	27	26	37.5
20	La Tina	(90)	92	96	102	107	(92)	93	97	102	107	[87]	90	96	102	108	5.7
21	Bamícori	52	(48)	57	86	125	56	(54)	71	116	185	43	[40]	43	54	74	35.0
Núm. de Mínimos	7	7	2	1	3	9	7	–	1	3	5	8	5	–	2	–

De manera semejante, pero empleando los valores de β_r calculados con la ecuación 10, se estimaron los tres parámetros de ajuste de las funciones GVE, LOG y PAG, a través de las ecuaciones 39 a 48, para cada valor de η. En seguida, a partir de sus soluciones inversas, expresiones 20, 28 y 34, se obtuvieron los valores de p ara obtener los EEA, expuestos en la tabla 7 en las columnas con designación “L1, L2, L3 y L4”.

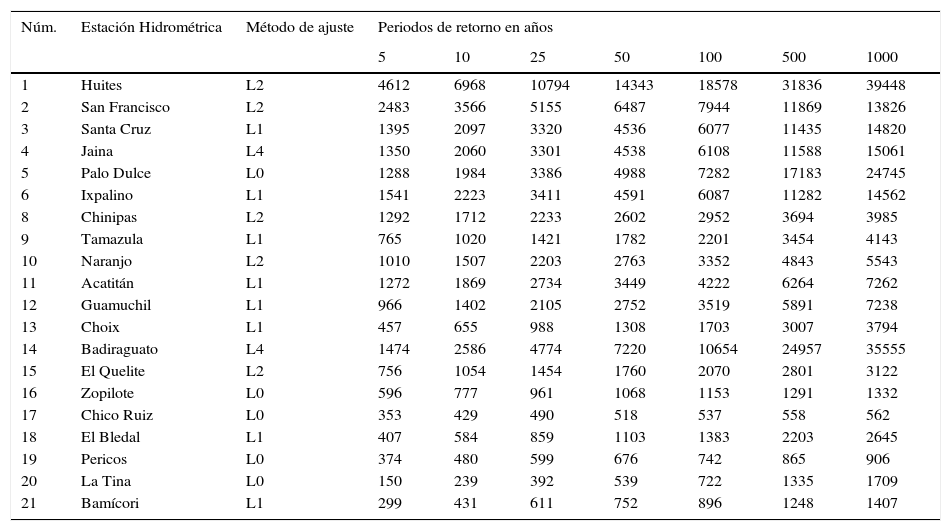
Análisis de los resultados

En la tabla 7, para cada registro procesado se tienen cinco resultados del EEA, en cada FDP; es decir, 300 resultados. Se encontraron diez casos de valores iguales, por ejemplo en Choix, Huites y Chinipas en cada FDP; se adoptó el ajuste que condujo a las predicciones más elevadas. Se indicó con paréntesis circular el valor mínimo de cada FDP y con paréntesis rectangular el menor de los tres mínimos. Se observa que todos los mínimos extremos ocurren con la distribución PAG. Por lo anterior, las predicciones mostradas en la tabla 8 corresponden a tal FDP y al orden η de momentos L que condujo al EEA mínimo extremo.

Tabla 8.

Predicciones (m³/s) obtenidas con la distribución Pareto Generalizada en los 20 registros de crecientes anuales de las estaciones hidrométricas indicadas de la Región Hidrológica Núm. 10 (Sinaloa)

Núm.	Estación Hidrométrica	Método de ajuste	Periodos de retorno en años
			5	10	25	50	100	500	1000
1	Huites	L2	4612	6968	10794	14343	18578	31836	39448
2	San Francisco	L2	2483	3566	5155	6487	7944	11869	13826
3	Santa Cruz	L1	1395	2097	3320	4536	6077	11435	14820
4	Jaina	L4	1350	2060	3301	4538	6108	11588	15061
5	Palo Dulce	L0	1288	1984	3386	4988	7282	17183	24745
6	Ixpalino	L1	1541	2223	3411	4591	6087	11282	14562
8	Chinipas	L2	1292	1712	2233	2602	2952	3694	3985
9	Tamazula	L1	765	1020	1421	1782	2201	3454	4143
10	Naranjo	L2	1010	1507	2203	2763	3352	4843	5543
11	Acatitán	L1	1272	1869	2734	3449	4222	6264	7262
12	Guamuchil	L1	966	1402	2105	2752	3519	5891	7238
13	Choix	L1	457	655	988	1308	1703	3007	3794
14	Badiraguato	L4	1474	2586	4774	7220	10654	24957	35555
15	El Quelite	L2	756	1054	1454	1760	2070	2801	3122
16	Zopilote	L0	596	777	961	1068	1153	1291	1332
17	Chico Ruiz	L0	353	429	490	518	537	558	562
18	El Bledal	L1	407	584	859	1103	1383	2203	2645
19	Pericos	L0	374	480	599	676	742	865	906
20	La Tina	L0	150	239	392	539	722	1335	1709
21	Bamícori	L1	299	431	611	752	896	1248	1407

El método de los momentos LH con la distribución GVE, condujo a menores EEA en 7, 2, 1 y 3 registros con L1, L2, L3 y L4, respectivamente (ver último renglón de la tabla 7). En cambio, con la función LOG fueron 7, 1 y 3 registros con L1, L3 y L4 y con la distribución PAG, 8, 5 y 2 registros dieron el menor EEA con los momentos L1, L2 y L4, respectivamente. Es decir que con estas dos FDP el ajuste L2 y L3 no condujo a ningún valor menor del EEA.

Un contraste individual entre las predicciones mostradas en la tabla 8 y las adoptadas por Campos-Aranda (2014), procedentes de las distribuciones GVE, LOG y Log-Pearson tipo III mostró una similitud alta en todos los resultados hasta el periodo de retorno de 100 años, pero también destacó que la distribución PAG aporta, en varios registros, predicciones menores en los periodos de retorno elevados (>100 años). Por lo anterior, se estimó el llamado error relativo del EEA, calculado con la expresión siguiente

en la cual, EEA_M es el error estándar de ajuste más grande de los tres mínimos y EEA_m es el mínimo extremo. En la última columna de la tabla 7 se observa que los ER son menores de 10% en 11 de los 20 registros procesados y en otros siete registros no excede de 40%. Entonces, los ajustes de las funciones GVE y LOG deben realizarse bajo precepto. En los dos registros en que resulta elevado el ER, Zopilote y Chico Ruiz, estos no presentan datos extremos elevados, sino lo contrario, pues definen parámetros de forma positivos (k > 0) en las tres distribuciones, entonces el ajuste con momentos LH es improcedente y ello se comprueba al encontrar EEA mínimos con los momentos L (ver columna L0 de la tabla 7).

Conclusiones

Con base en el error estándar de ajuste (EEA), los resultados de la tabla 7 indican que la distribución Pareto Generalizada condujo a las magnitudes menores de este indicador cuantitativo de la calidad estadística del ajuste, frente a las funciones GVE y LOG; debido a ello, se recomienda probarla sistemáticamente en los AFC y de otros datos hidrológicos extremos de nuestro país.

De acuerdo con los EEA mínimos que tienen errores relativos menores de 10%, en la mitad de los 20 registros procesados y en otros ocho registros no exceden 40% (ver última columna de la tabla 7), se considera conveniente seguir aplicando las distribuciones GVE y LOG bajo precepto.

Los ajustes con momentos LH en la distribución GVE aportan menores EEA en 13 registros, con la función LOG en 11 de tales series y con el modelo PAG en 15 registros; según se observa en el último renglón de la tabla 7. Por lo anterior, el ajuste con el método de momentos L de orden mayor o momentos LH, es una opción conveniente para reducir el EEA y con ello alcanzar predicciones más confiables. Entonces, se sugiere utilizar tal técnica de manera rutinaria en los análisis de frecuencia de datos hidrológicos extremos, como una técnica avanzada del método de momentos L, mismo que ya es un procedimiento de uso generalizado.

Agradecimientos

Se agradecen las observaciones y correcciones de los dos árbitros anónimos, las cuales permitieron volver más explícito el trabajo y sus conclusiones.