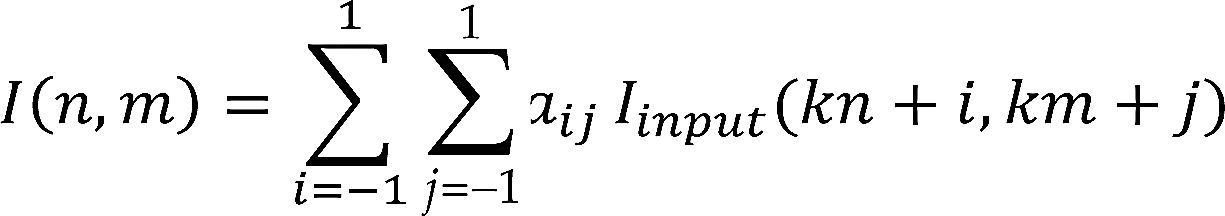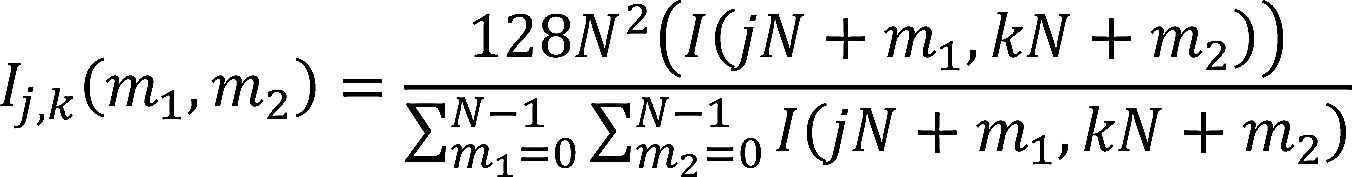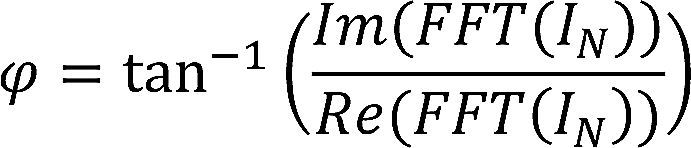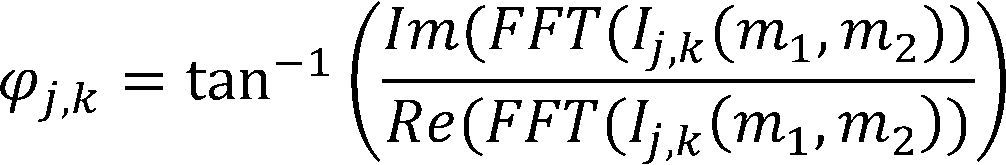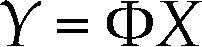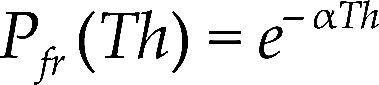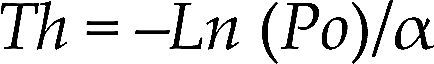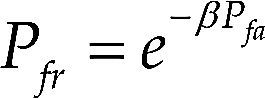Modifications to the Eigenphases Method for Face Recognition Based on SVM

Abstract

This paper presents two modifications to the eigenphases method to increase its accuracy. In the first modification, called Local Spatial Domain Eigenphases (LSDE), the face image is first segmented into blocks of N × N pixels, whose magnitudes are normalized. These blocks are then concatenated before the phase spectrum estimation, and finally Principal Component Analysis (PCA) is used for dimensionality reduction. In the second modification, called Local Frequency Domain Eigenphases (LFDE), first the face image is segmented into blocks of pixels, whose pixels are normalized. The phase spectrum of each block is estimated independently. Next, the phase spectra of all the blocks are concatenated and then are applied to the PCA stage for dimensionality reduction. The proposed approaches are evaluated using open-set and closed-set face identification, as well as identity verification, using the “AR Face Database.” The evaluation results show that the proposed modifications, using the Support Vector Machine as the classifier, perform fairly well under different illumination and partial occlusion conditions.

Resumen

Este trabajo presenta dos modificaciones del método de eigenphases para aumentar su precisión. En la primera modificación llamada Local Spatial Domain Eigenphase (LSDE), la imagen del rostro se divide en bloques de N × N píxeles, cuyas magnitudes se normalizan. Estos bloques se concatenan antes de que el espectro de fase y el PCA se estimen. En la segunda modificación llamada Local Frecuency Domain Eigenphase (LFDE), después de la segmentación de la imagen en bloques de N x N píxeles, las magnitudes de los pixeles de dichos bloques se normalizan y se calcula el espectro de fase en forma independiente. Una vez que se obtiene el espectro de fase de todos los bloques, se concatenan y se procede a la aplicación del análisis de componentes principales (PCA) para reducir la dimensionalidad del problema. Las modificaciones propuestas se evalúan en la modalidad de identificación, tanto en “open set” como en “closed-set”, así también en verificación de identidad. En ambos casos se empleó la base de datos AR Face Database. Los resultados experimentales muestran que las modificaciones propuestas presentan un funcionamiento adecuado bajo diferentes condiciones de iluminación y oclusión parcial.

Introduction

Face recognition is a widely used biometric technology because it is non-intrusive and can be performed with or without the cooperation of the person being analyzed. Thus, face recognition is one of the biometric technologies that has gained higher acceptance among users (Kung et al., 2005; Li and Jain, 2011). This technology can be used for either identity verification or person identification, depending on the way in which the system parameters are estimated during the training task. Hence, it is convenient to mention the differences between these two tasks. In the identity verification task, the system is asked to determine whether the person is who he/she claims to be, whereas during the person identification task, the system is asked to determine, among a set of persons whose facial characteristics are stored in a database, the person who most closely resembles the image under analysis. Thus, the recognition task encompasses both identification and veri- fication (Chellappa et al., 2010).

Variable illumination and occlusions are some of the relevant problems that must be solved in face recognition because these factors alter the perception of face images, which significantly decreases the accuracy of face recognition performance (Ruiz and Quinteros, 2008). In particular, improving the performance of face recognition algorithms under varying lighting conditions has attracted researchers’ attention during the last several years, because changes in lighting conditions occur during the transition between indoor and outdoor environments, as well as within both indoor and outdoor environments, due to the 3D shape of the face, which produces shadows depending on the direction of illumination (Ruiz and Quinteros, 2008). Accordingly, several approaches have been proposed for reducing the variable illumination effects (Ruiz and Quinteros, 2008), which can be divided into two groups. The first group, which employs illumination plane subtraction with histogram equalization (Ramírez et al., 2011), contrast-limited adaptive histogram equalization (CLAHE) (Benitez et al., 2011), processes the input image to reduce the illumination changes, thereby improving the face image quality. The second approach for addressing variable illumination conditions is the development of face recognition algorithms that are able to provide robust performance under varying illumination conditions. To this end, several methods have been proposed which simultaneously provide small intra-person and large interpersonal variability under varying illumination conditions. Among them, the eigenphases approach, which uses the phase spectrum (Zaeri, 2009), together with principal component analysis (PCA) and the support vector machine (SVM) (Benitez et al., 2011; Zaeri, 2009; Olivares et al., 2009; Benitez et al., 2012), appears to be a desirable approach because it provides recognition rates of over 95%. The use of other frequency transformations, such as the discrete cosine transform (Dabbaghchian et al., 2010; Ajit et al., 2014), discrete Gabor transform (Olivares et al., 2007; Thiyagarajan et al., 2010; Qin et al., 2012), discrete wavelet transform (Hu, 2011; Eleyan et al., 2008) and discrete Haar transform (Gautam et al., 2014), has also been proposed. These approaches, under controlled conditions, achieve recognition rates of over 90%. Additional methods proposed in the literature include the Eigenfaces approach (Hou et al., 2013; Belhumeur et al., 1997), which uses PCA; the Fisherfaces approach (Belhumeur et al., 1997), which uses the linear discriminant analysis (LDA) method; and Laplacianfaces (He et al., 2005), which uses locally preserving projections. Several other approaches in recent years have attempted to solve the problems due to changes in illumination conditions and partial occlusion by using image processing filters (Ramírez et al., 2011).

This paper extends the eigenphase-based face recognition algorithms (Zaeri, 2009; Olivares et al., 2009) and provides an extensive performance evaluation using the SVM (Chang, 2011). The evaluation includes closed and open set face recognition as well as rank evaluation and identity verification with several different thresholds. The performance of the proposed modifications is compared with the conventional eigenphases approach (Zaeri, 2009; Olivares et al., 2009) as well as with the Gabor- based and wavelet transform-based feature extraction methods using the SVM and the “AR Face Database” (Martínez, 1998), which includes 9360 face images from 120 persons with different variations of illumination, occlusion and facial expressions. Evaluation results show that the proposed approaches provide better convergence performance than the previously proposed algorithms under different lighting conditions.

The rest of the paper is organized as follows: Section 2 provides a description of the proposed algorithms. Section 3 provides the evaluation results for the proposed modifications and compares them with the performance provided by other well-known feature extraction algorithms, such as Gabor filter-based (GF), discrete wavelet transform-based (DWT) and standard Eigenphases feature extraction algorithms. Finally, the conclusions of this paper are provided in Section 4.

Face recognition algorithm based on eigenphases approach

A general face recognition task can be divided into two phases: face identification, in which the system output provides the identity of the most likely person, and identity verification, in which the system determines if the person is who he/she claims to be. In both cases, the face recognition algorithm consists of, among other things, training and identification or verification stages, changing only the classifier task. In a face recognition system, the face image is first captured and then fed into a preprocessing stage for noise reduction, enhancement and segmentation. Next, the processed image is analyzed by a feature extraction stage to estimate a set of near-invariant characteristics, which are then used to optimize the classifier parameters; these parameters are stored in a database for further use during the recognition task. During the face recognition task, the face image is captured and fed into the pre-processing and feature extraction stages to estimate the feature vector. Then, the feature vector is fed into the classifier to perform the recognition task using the optimal parameters stored in the database.

To improve the performance of the conventional eigenphases method under different illumination conditions, taking in account that the face texture is quite regular, first the face image is down-sampled to reduce the image size. Next, the resulting image is segmented into L×M sub-blocks of N×N pixels, which are independently processed to reduce the illumination effects before carrying out feature vector estimation. Feature vector estimation is carried out in two different forms, giving as a result to two different approaches, which are analyzed in the following sections.

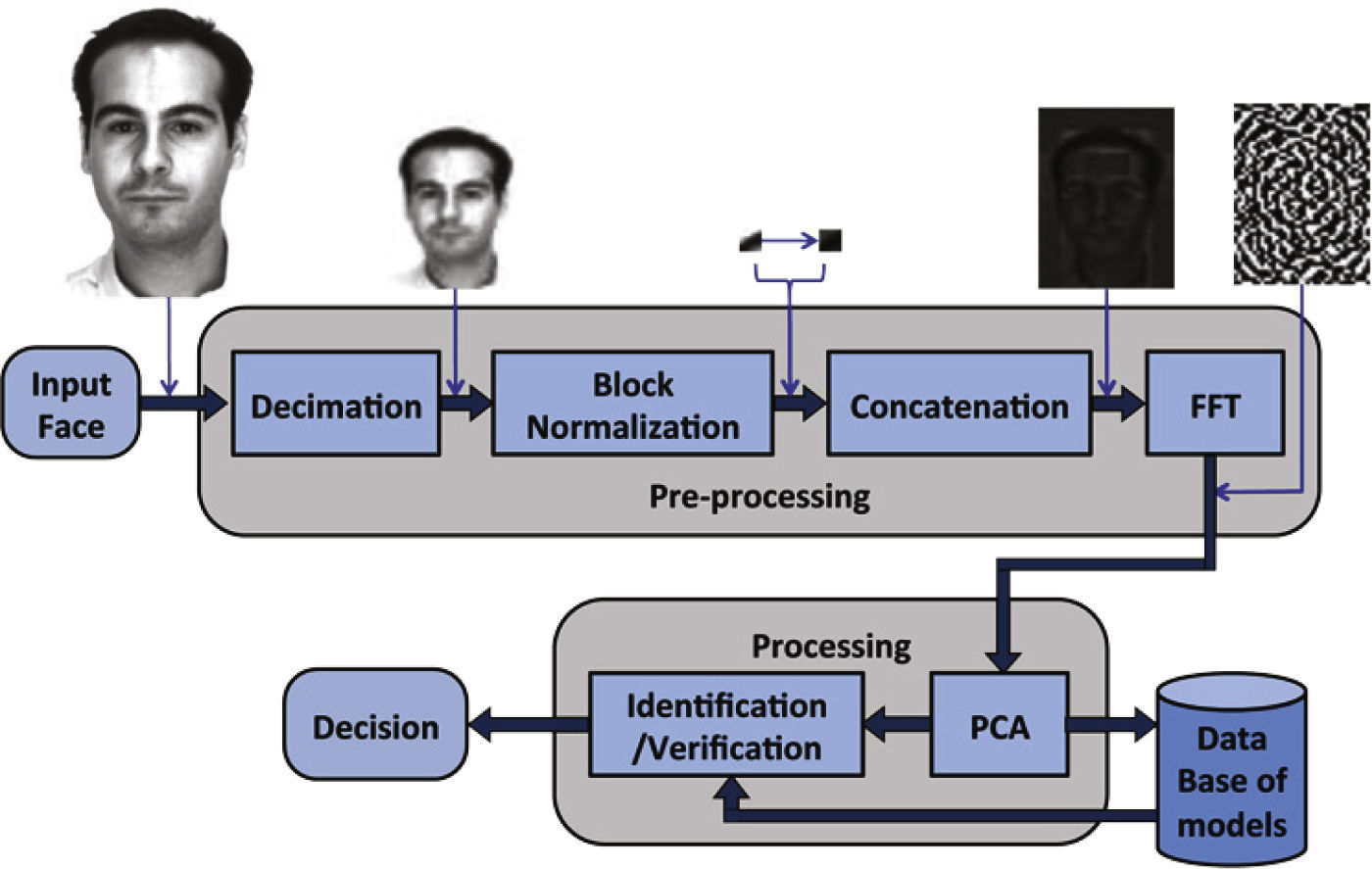
Local Spatial Domain Eigenphase Algorithm (LSDE)

In the LSDE algorithm shown in Figure 1, the input face image is first down-sampled by a factor K to reduce the image size, using the bicubic interpolation method, given as

Figure 1.

Block diagram of LSDE algorithm

where a_ij are the filter weights with i = [–1,1] and j = [–1,1], I (k, km) denotes the (kn, km) – th pixel of the input image, and I (n,m) is the (n,m) – th pixel of the output image.

I_input (nk, mk) is the face image under analysis and I (n, m) is the down-sampled image, which is divided in L × M blocks of N × N pixels, which are normalized in amplitude to reduce the illumination effect. To this end the pixel's amplitude is modified such that the (j, k) – th block, I_j,k (n) of image I (n,m) is given by

where 0 ≤ j ≤ L –1, 0 ≤ k ≤ M –1. The main idea of this process is that if we modify the input image in such way that the mean value of any image becomes equal to 128, keeping the relation between its pixels approximately unchanged, the illumination effects can be significantly reduced. This effect is illustrated is illustrated in Figure 2. If the illumination effects are significantly reduced, it can be expected that the performance of the proposed scheme will remain almost unchanged under any illumination condition. Next, after the image enhancement task, the blocks are concatenated to obtain the image I_N which is then used to estimate the phase spectrum as follows

Figure 2.

Performance of the preprocessing used to reduce the illumination effect before phase spectrum estimation. a) and b) shown the same face image with different illumination conditions, while e) and h) show the enhanced images obtained using equation (2).

Next, φ is used in the PCA (Jolliffe, 2002) module to estimate the feature vectors of the input image. The resulting feature vectors are then fed into the SVM to carry out either the identification or identity verification task.

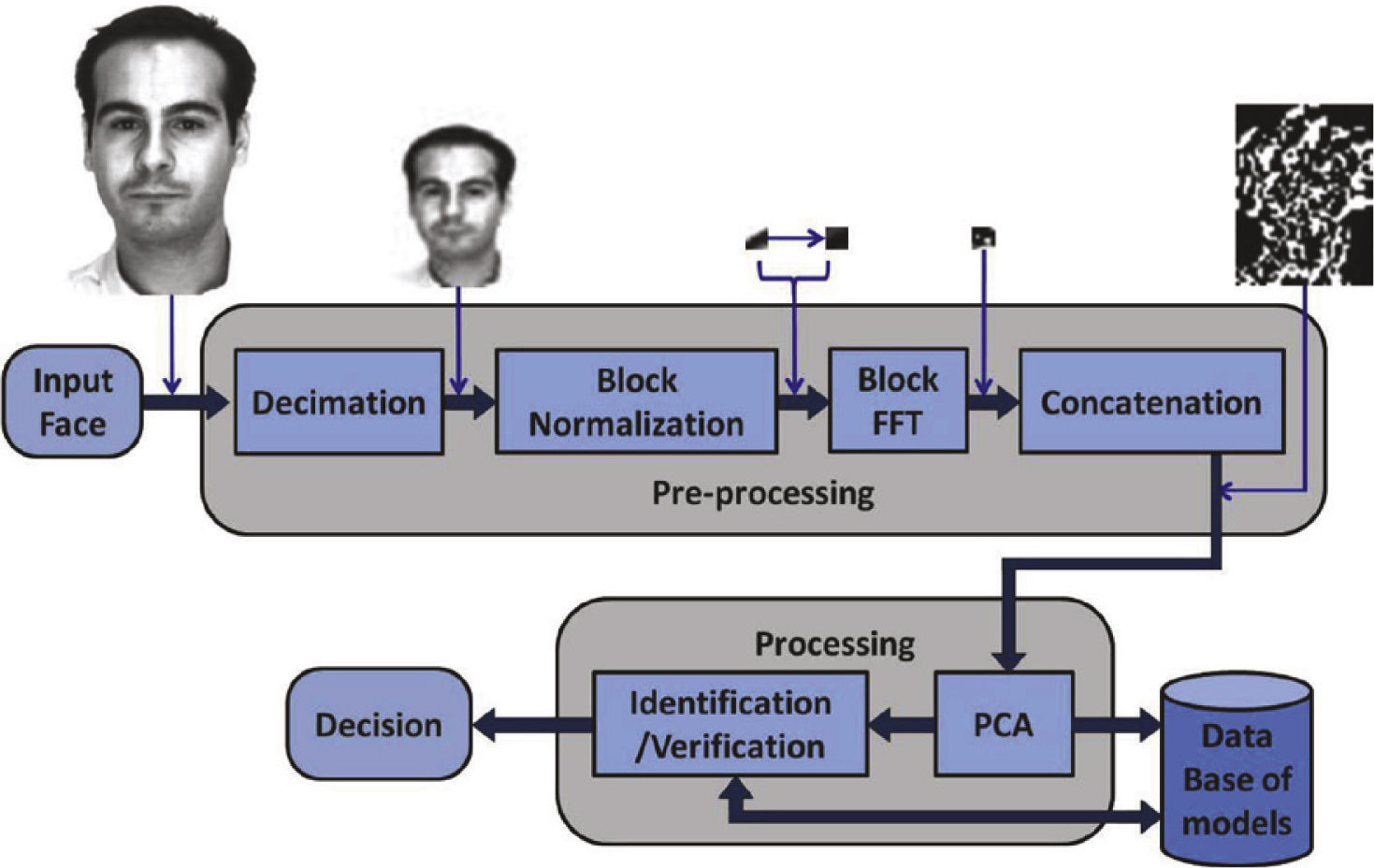
Local Frequency Domain Eigenphase Algorithm (LFDE)

In the proposed LFDE algorithm shown in Figure 3, the input image is down-sampled using the bicubic interpolation given by (1) to reduce the amount of data and segmented into L × M blocks of N × N pixels, which are enhanced using (2). Next, the phase spectrum of each normalized block image is estimated as follows

Figure 3.

Block diagram of LFDE algorithm.

where I_j,k is given by (2). Next, the phase spectrum of the image blocks φ_j,k are concatenated, yielding φ.

Finally, the PCA of φ is used to estimate the feature vectors of the face under analysis, which is fed into the SVM to carry out the identification or verification task.

Processing and decision stage

PCA is a standard tool in modern data analysis and is widely used in diverse fields ranging from neuroscience to computer graphics because it is an efficient non-parametric method that allows the extraction of relevant information from complex datasets (Jolliffe, 2002). The other main advantage of PCA is the dimensionality reduction of the extracted data without a significant loss of information. When applied to face recognition systems, this technique is used to extract the most relevant features of the face image.

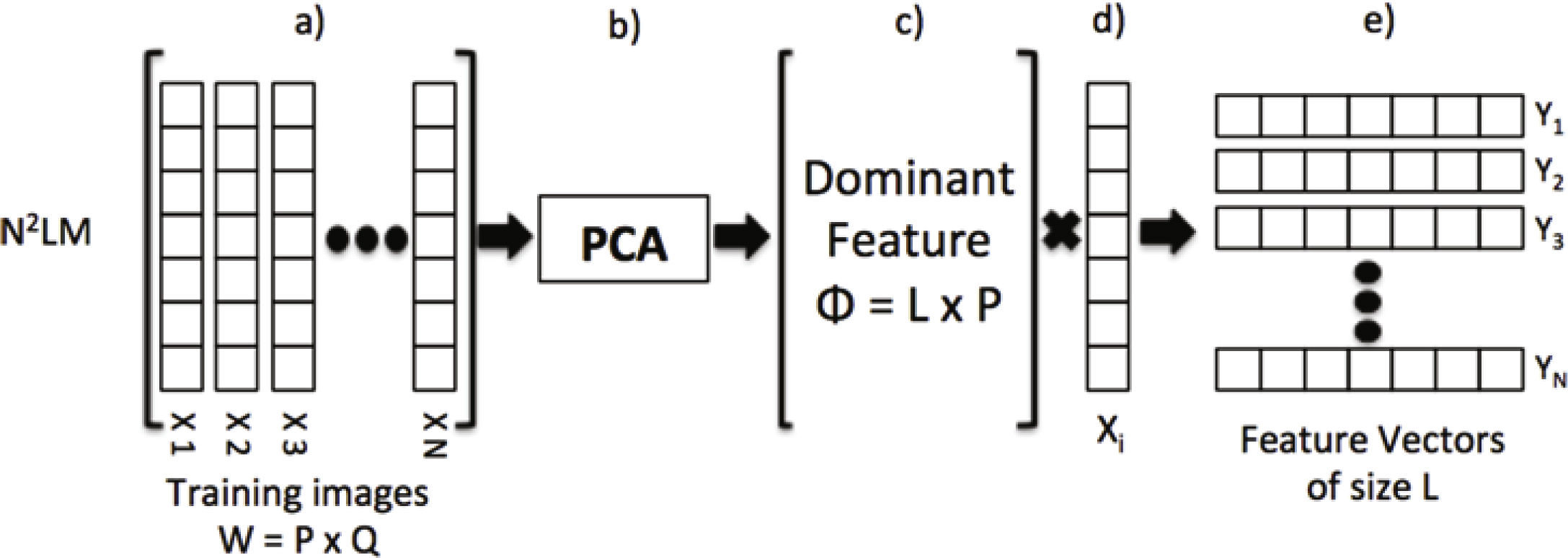
For this paper the procedure for developing PCA, which is mainly applied in the training phase, proceeds as follows. First, each image ϕ is stored in a column vector X of size (N²LM/9) x 1, which is related to the number of coefficients obtained from the down-sampled image. Next, a matrix W of size P × Q is constructed by concatenating each of the vectors Xi from the training set, where P is the dimensionality of X, and Q < P corresponds to TS, with T specified as the number of classes and S as the number of training images for each class. Next, the eigenvectors and eigenvalues of the covariance matrix given by W^TW are extracted to generate a dominant feature matrix Φ of size L × P, where L = Q corresponds to the number of the most representative eigenvectors contained in the original image. Finally, the feature vector of each image is given by

where

Y = resulting feature vector of size L × 1

Φ = dominant matrix, and

X = phase spectrum coefficient vector of the image un- der analysis.

Figure 4 presents a block diagram illustrating the complete process used to obtain the feature vectors using PCA.

Figure 4.

Process to obtain the feature vectors using PCA: a) the training images are arranged in a matrix of P×Q (P=MN), where each one of its Q columns corresponds to a training image, b) using PCA and c) the dominant features matrix of L×P, values are estimated, d) the dominant features matrix is multiplied by the feature vectors of the image under analysis, e) finally the features of size L are obtained.

Support vector machine

The Support Vector Machine (SVM) (Vapnik et al., 1996) is a universal constructive learning procedure for pattern recognition, based on statistical learning theory, whose objective is to assign a class to each pattern. In this paper, to implement the SVM, the LIBSVM library (Chih et al., 2011) is used, and the characteristics used for training and recognition tasks are: Kernel type: polynomial: (gamma × u’ × v + coef’ 0)^–degree where coef’ 0 = 1, gamma = 1, and all others parameters are used with their default values given by the LIBSVM.

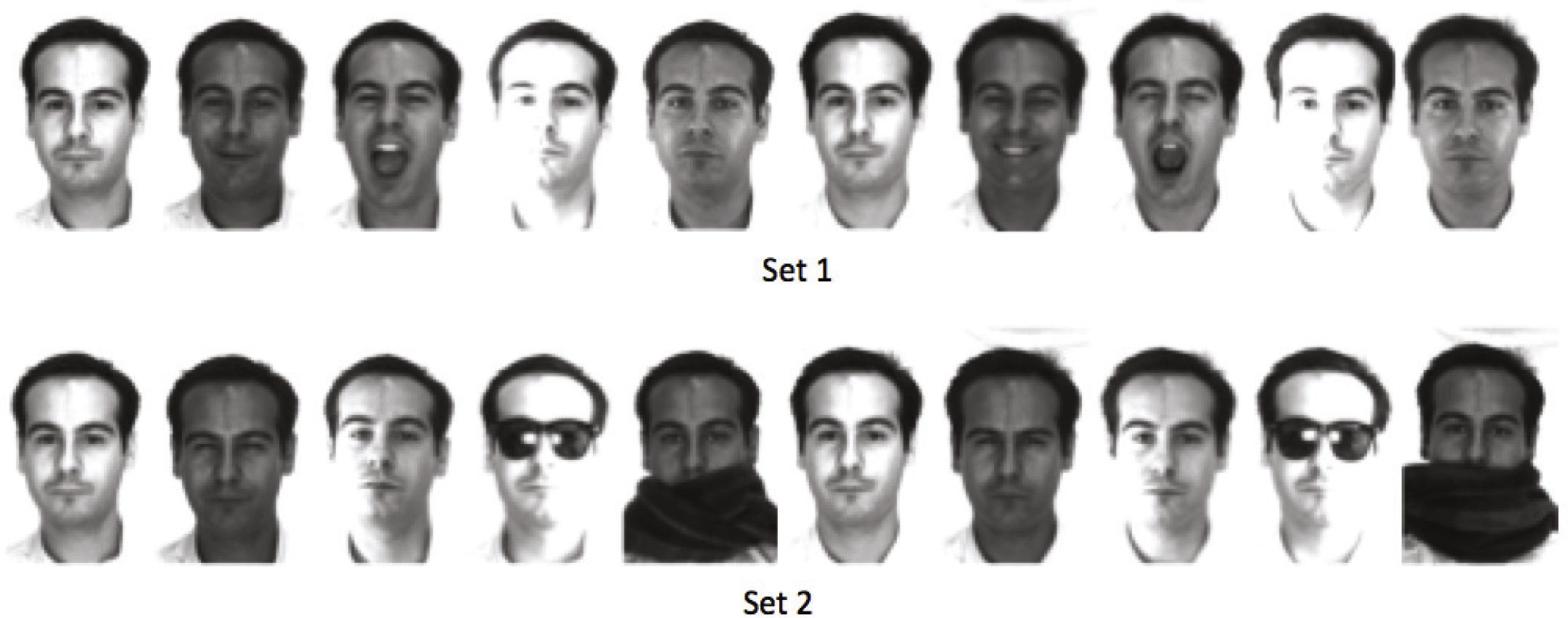
Evaluation results

The performances of the proposed face recognition methods were evaluated using the “AR Face Database,” which has a total of 9,360 face images of 120 people (65 men and 55 women). This database includes 78 face images of each person with different illuminations, facial expressions and partial occlusions of the face by sunglasses and scarves. To evaluate the performance of the proposed methods, two different training sets are used. The first one consists of 1200 face images, 10 images of each person, under different illumination and expression conditions, while the second set consists of 1200 face images, 10 per person, under different illumination conditions, expressions and occlusion. The remaining images of the AR face database are used for testing. Figure 5 shows some examples of the face images of a particular person in the “AR Face Database.”

Figure 5.

Examples of face images with different illumination, expression and partial occlusion contained in the “AR Face Database”.

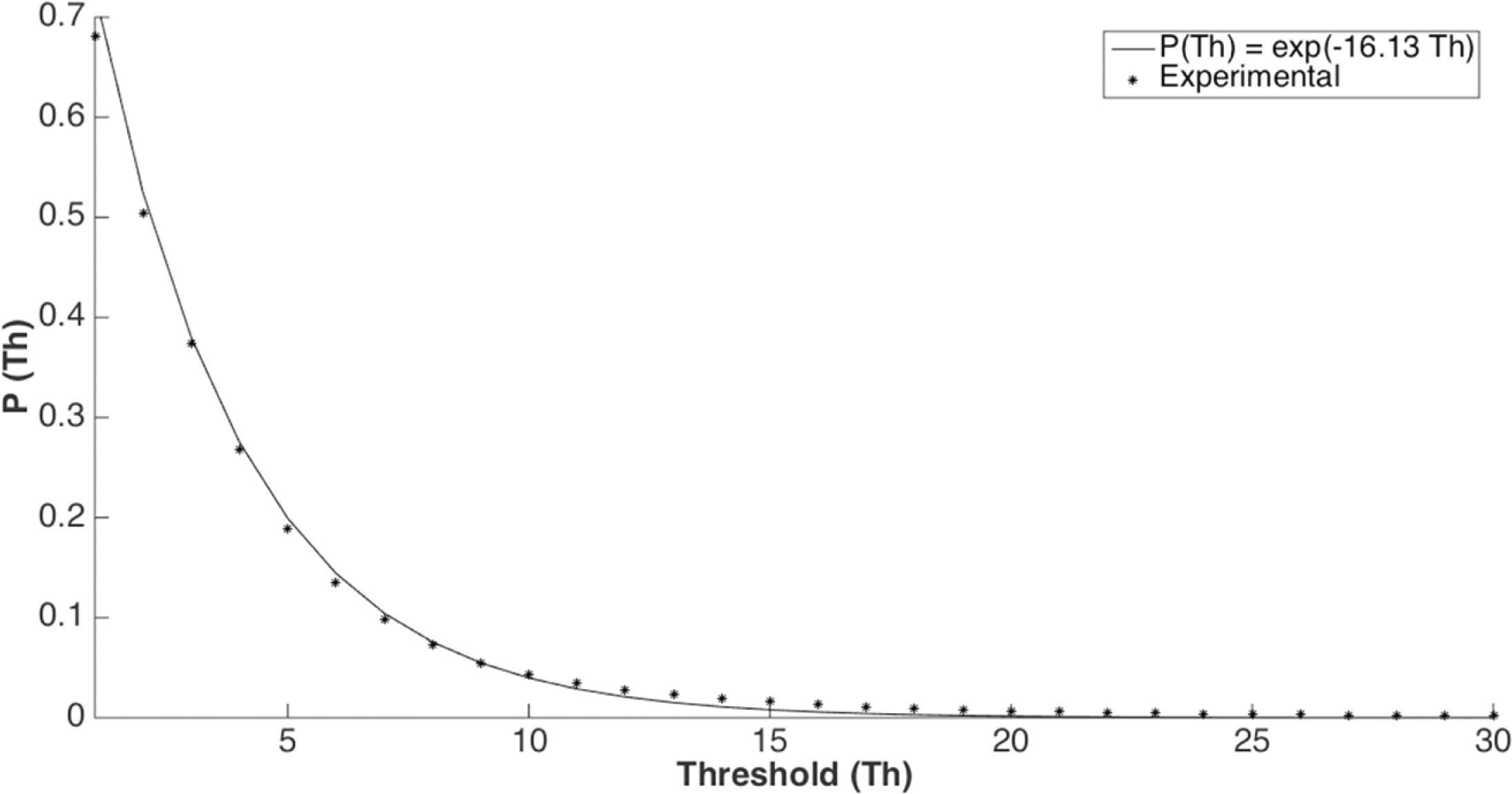
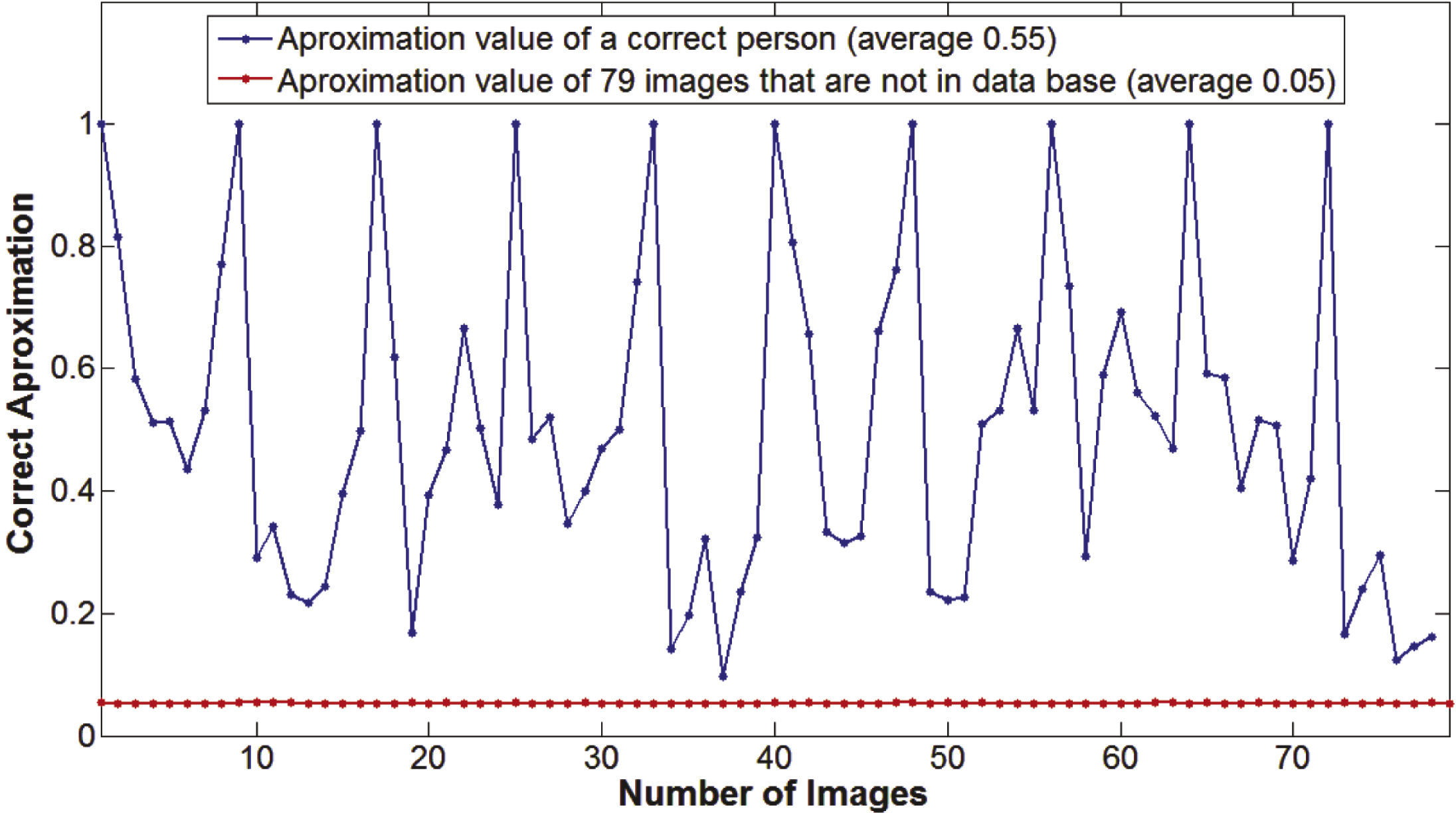
Most identity verification systems strongly depend on an appropriate selection of the threshold value to determine if the person under analysis is who she/he claims to be. To this end, a detailed evaluation of the performance of the proposed systems was carried out to find an appropriate mechanism for determining a suitable threshold value. After extensive experimental evaluation, we found that the false acceptance probability follows an exponential distribution as shown in Figure 6. Thus, assuming that the false acceptance pro- bability is given by Figure 6.

Figure 6.

Theoretical and experimental probability distribution obtained when the proposed LDFE3.

The scheme is required to perform an identity verification task

where α = –Ln (P_fa (Th_k)) / Th_k, Pf_a (Th_k) is the false acceptance rate obtained for a given threshold Th_k. In particular if P_fa (Th_k) = 0.0548 and Th_k= 0.18 it follows that α = 16.13 and P_fa(Th_k) is experimentally estimated. Hence, from (6), for a desired false acceptance probability Po the suitable value of Th is given by

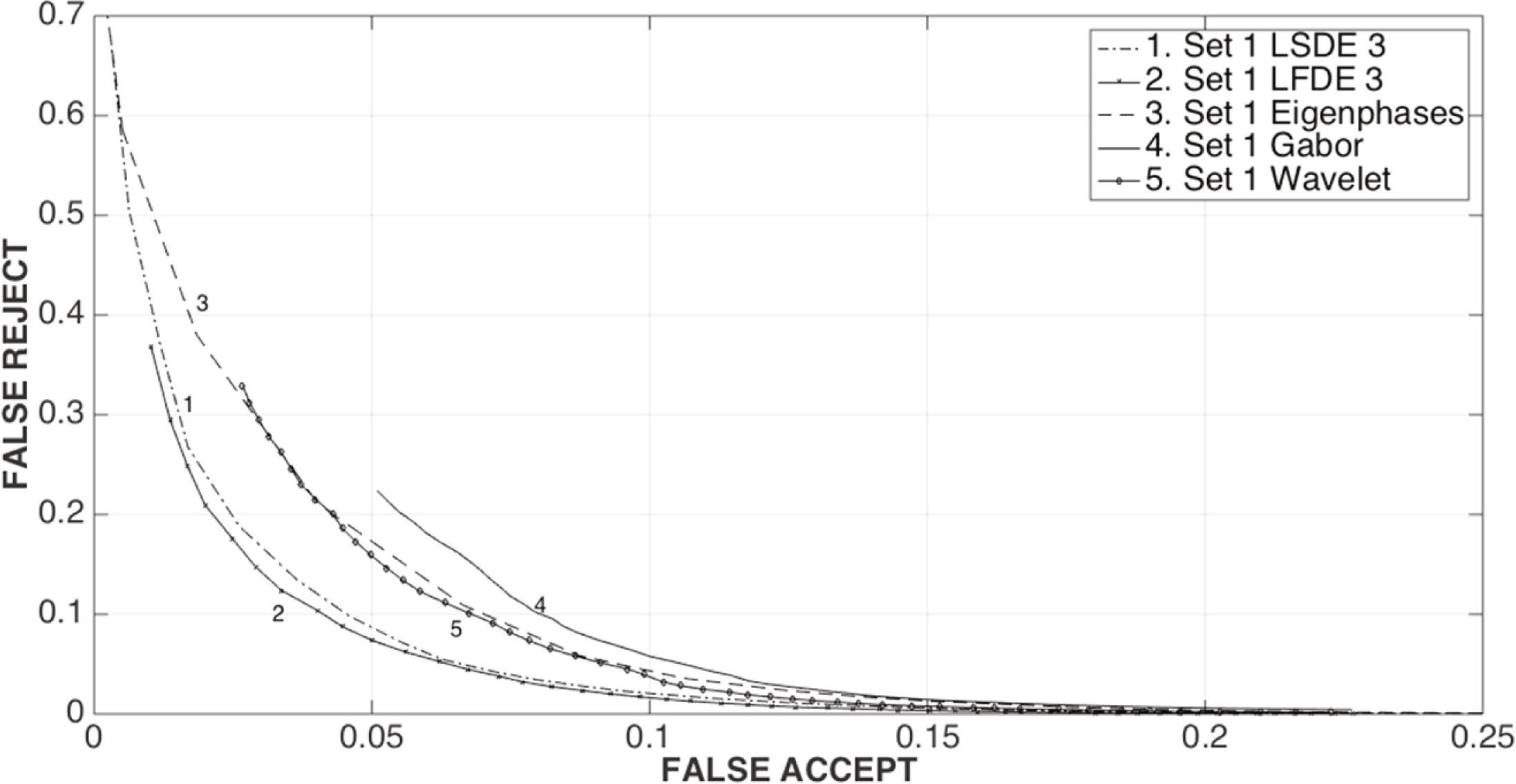
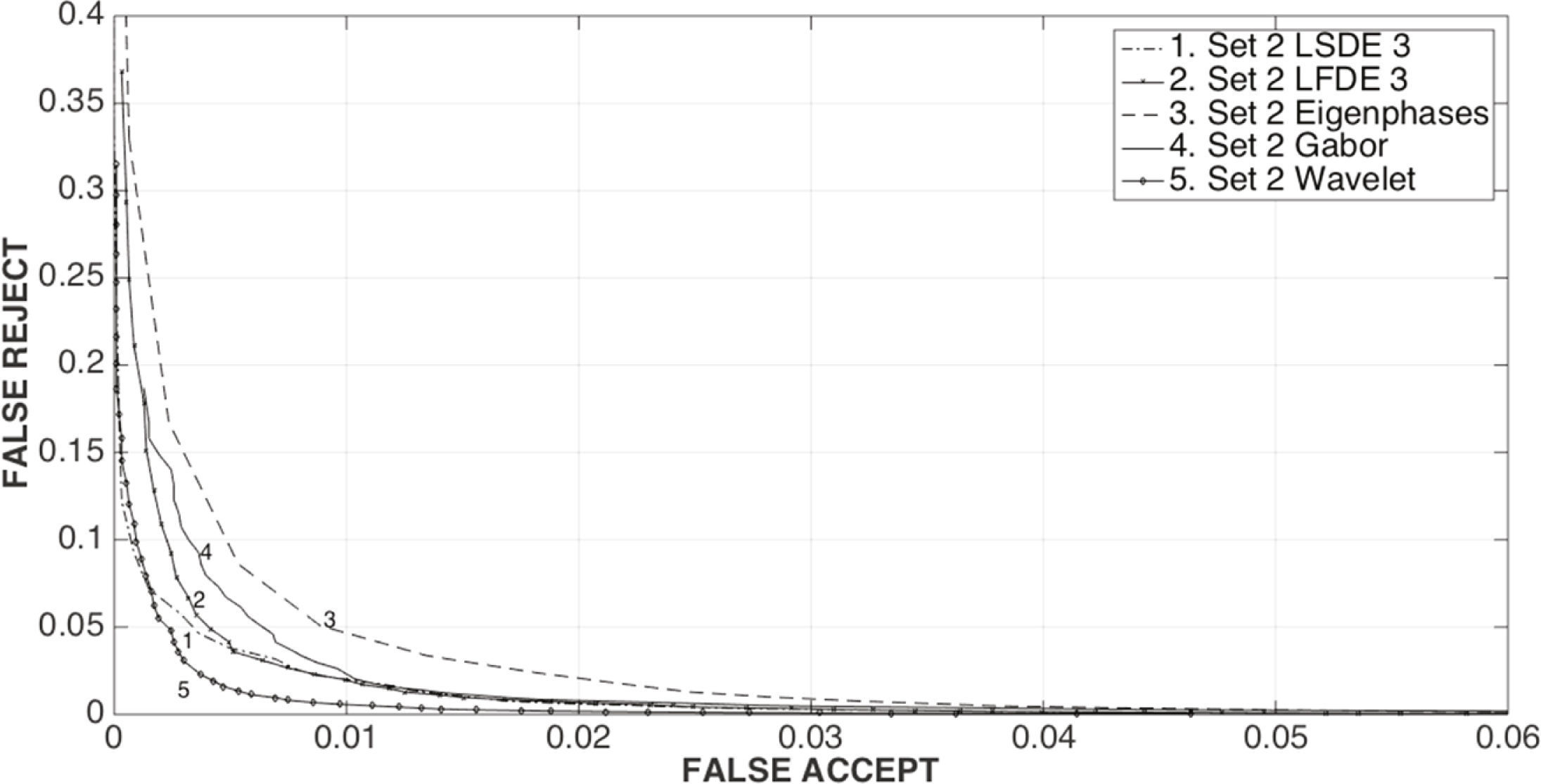
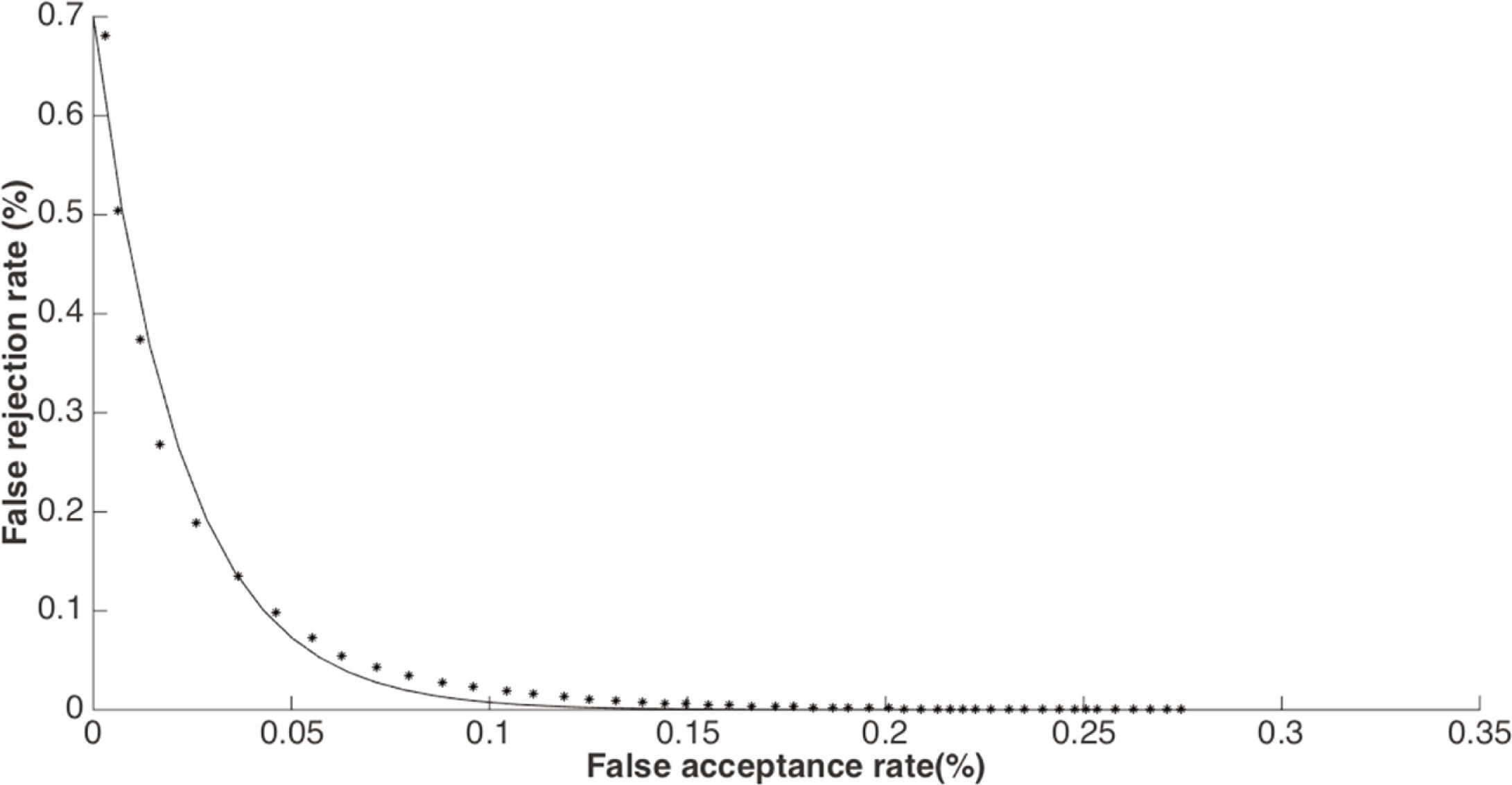
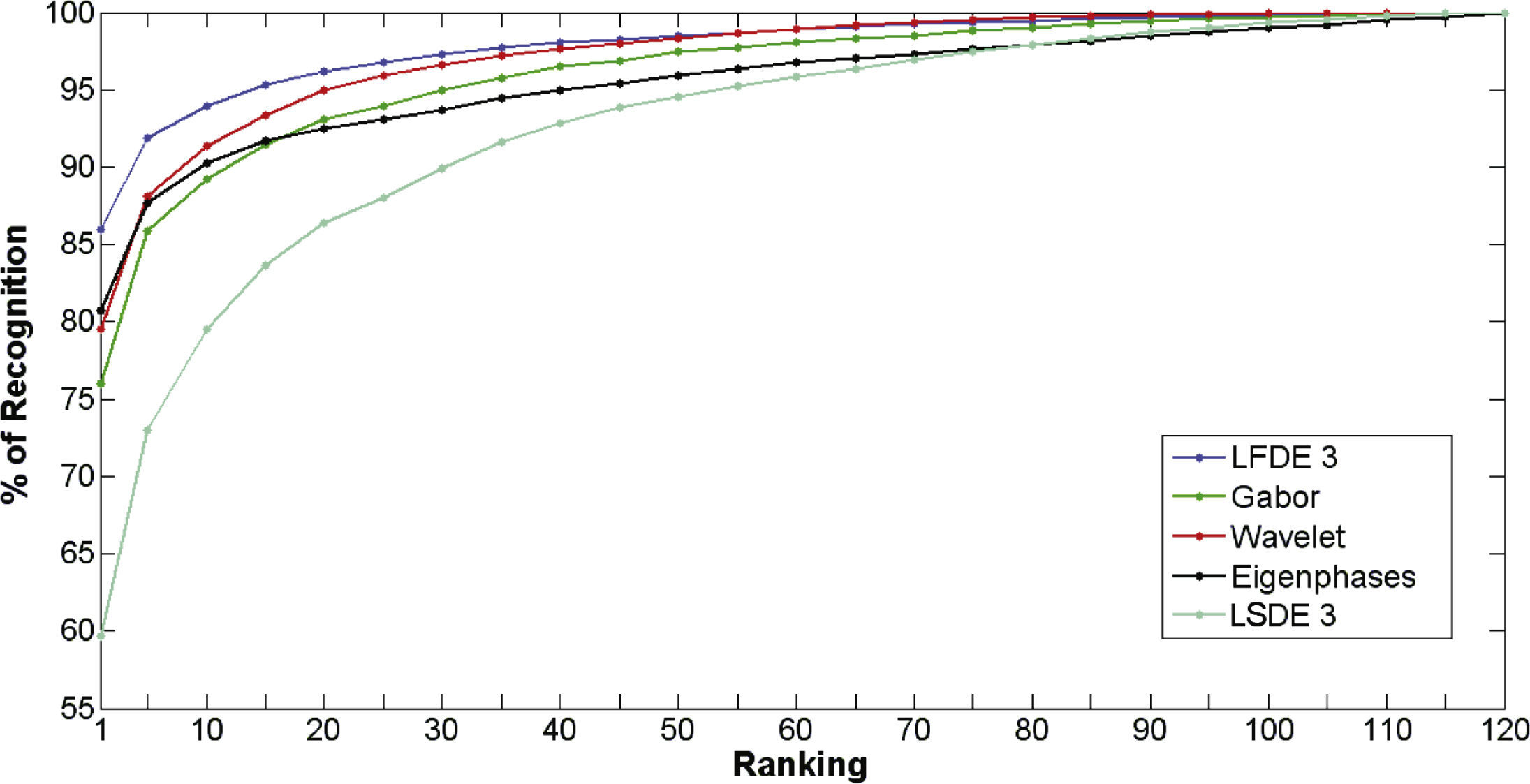
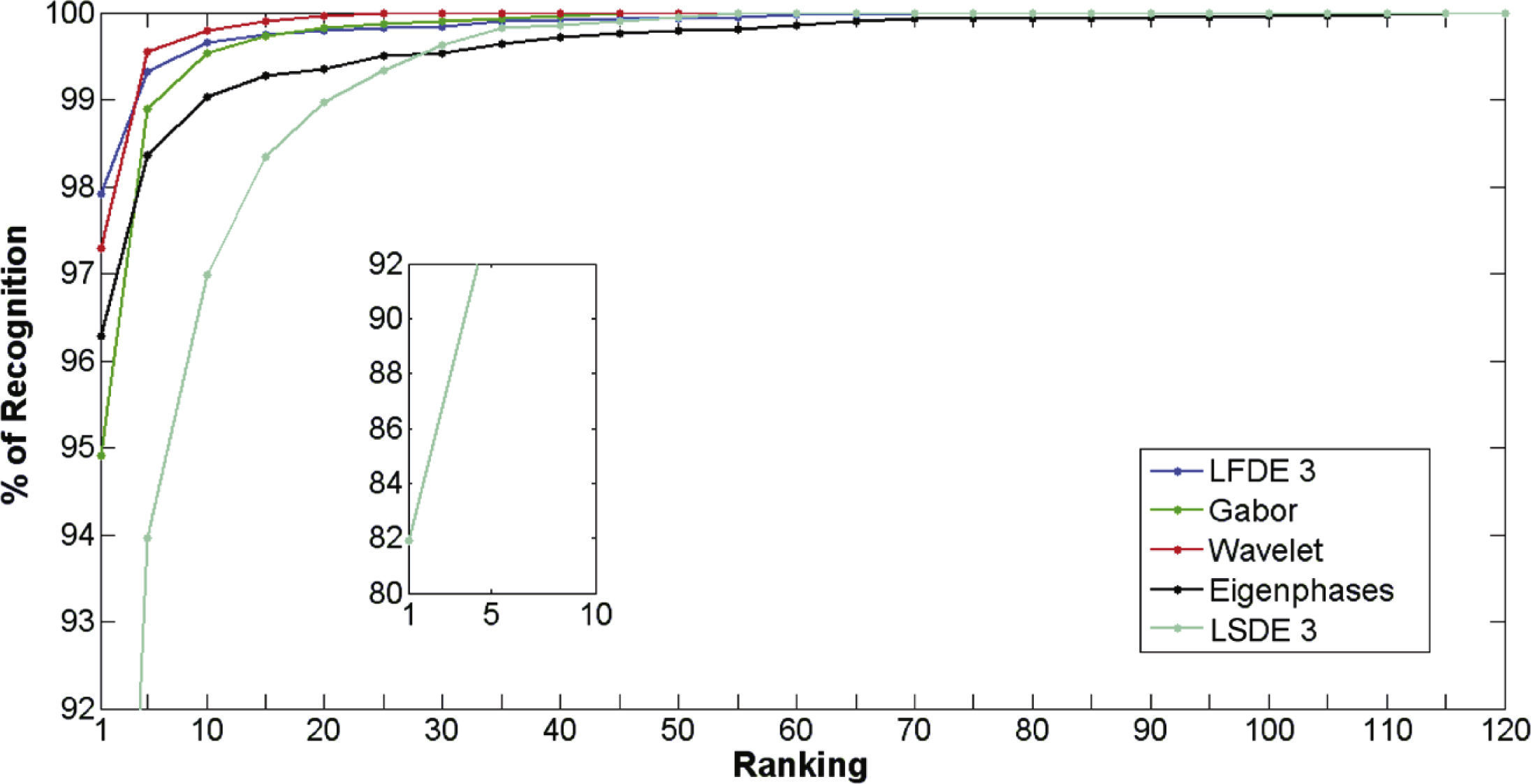
Figures 7 and 8 show the verification performance of the proposed LSDE and LFDE, with a block size of 3 × 3, when they are required to verify the identity of persons contained in the AR Face Database. From Figure 7 it can be observed that the proposed LFDE scheme provide the best performance because it is able to simultaneously provide the smallest false positive and false negative rates. Although the performance of the proposed LSDE is worse than the performance of the LFDE, it is still better than the performance provided by the other identity verification methods when the image under analysis is without occlusions. Figure 8, on the other hand, shows that LFDE provides better identification performance that the other verification methods under analysis, while the convergence performance is worse than the performance of LFDE and very close to the performance provided by the wavelet-based approach. Other important results are shown in figure 9, which shows that the relation between false acceptance rate P_fa and false rejection rate P_fr closely resembles an exponential function given by

Figure 7.

Performance of proposed LSDE and LFDE with block size of 3 × 3 performing a verification task using Set 1. The performance of standard eigenphases, Gabor and wavelet-based methods are shown for comparison.

Figure 8.

Performance of proposed LSDE and LFDE with block size of 3 × 3 performing a verification task. The performance of standard eigenphases, -Gabor- and wavelet-based methods using the Set 2 for training are shown for comparison.

Figure 9.

Theoretical and experimentally obtained relationship between the false acceptance and false rejection rates of the proposed LFDE 3 face recognition scheme.

This fact, together with (7), allows the determination of a threshold value for obtaining a desired verification performance.

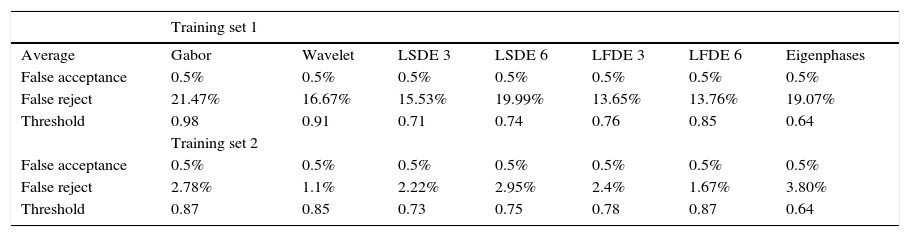
Table 1 shows the evaluation results obtained using the proposed LSDE-N, LFDE-N, Gabor filter-, Wavelet- and Eigenphases-based identity verification methods, all of them using a given threshold values providing a 0.5% false acceptance rate, which means there are only 5 errors in 1000 tests, where N denotes a window size of N×N pixels.

Table 1.

Verification using SVM.

	Training set 1
Average	Gabor	Wavelet	LSDE 3	LSDE 6	LFDE 3	LFDE 6	Eigenphases
False acceptance	0.5%	0.5%	0.5%	0.5%	0.5%	0.5%	0.5%
False reject	21.47%	16.67%	15.53%	19.99%	13.65%	13.76%	19.07%
Threshold	0.98	0.91	0.71	0.74	0.76	0.85	0.64
	Training set 2
False acceptance	0.5%	0.5%	0.5%	0.5%	0.5%	0.5%	0.5%
False reject	2.78%	1.1%	2.22%	2.95%	2.4%	1.67%	3.80%
Threshold	0.87	0.85	0.73	0.75	0.78	0.87	0.64

The evaluation results also show that, in general, the verification performance decreases when training set 1 is used, in comparison with the performance obtained using training set 2, because of the lack of information about the occlusion effects. Table 1 shows that LFDE 6 and LFDE 3 provide better verification performance than the other previously proposed systems because they provide lower false rejection rates using training set 1, even though the Wavelet-based method provides a slightly lower false rejection rate when training set 2 is used. Table 2 shows the evaluation results obtained when performing face recognition tasks. These results show that when training set 1 is used for training, the recognition performance decreases in comparison to the performance obtained using training set 2. This result occurs because training set 1 does not provide any information about occlusions and thus the system cannot identify some face images in which the people are wearing sunglasses or scarves, due to the lack of information about the occlusion effects. However, it is important to notice that the recognition results obtained with the proposed algorithm are good enough for several practical applications because the recognition rate exceeds 80%. Evaluation results show that, using both training sets, the proposed LFDE 3 performs better than the other face recognition algorithms.

Table 2.

Identification using SVM.

	Gabor	Wavelet	LSDE 3	LSDE 6	LFDE 3	LFDE 6	Eigenphases
Set 1	75.98%	79.54%	84.44%	81.05%	85.92%	85.59%	80.63%
Set 2	94.90%	97.29%	97.67%	97.29%	97.92%	97.85%	96.28%

Figures 10 and 11 show the identification performance using rank (N) evaluation of the LFDE 3 algorithm, together with the other previously proposed face recognition algorithms, when they are trained using set 1 and 2, respectively. Evaluation results show that the LFDE 3 algorithm provides better performance than the previously proposed methods when it is trained using images without occlusions, which is the most realistic situation in practical applications. Finally, Figure 12 shows the open set evaluation in which the face recognition system is required to identify face images not included in the database. Evaluation results show that the LFDE 3 algorithm is able to determine that the image under analysis does not belong to any of the possible persons in the database; this is because, in all cases, the system output is smaller than the lowest output obtained when the input image belongs to the database.

Figure 10.

Identification rank performance obtained using training set 1.

Figure 11.

Identification rank performance obtained using training set 2.

Figure 12.

Open-set performance evaluation of the modified eigenvalue approach, LFDE6.

Conclusions

This paper presented modified eigenphases algorithms that improve the eigenphases algorithms previously proposed in (Gautam et al., 2014; Hou et al.,2013). The performances of the proposed algorithms were evaluated using face images with different illumination conditions, facial expressions and partial occlusions. The proposed algorithms were compared with other methods, such as the original eigenphases method, Gabor-based and Wavelet-based feature extraction methods, using the SVM to carry out the verification and identification tasks. The evaluation results show that when the image set used for training contains images without occlusion, the performance of the proposed method becomes better than that of the other methods under analysis for both identification and verification tasks; the proposed method also provides almost the same performance as the Wavelet based method when both are trained using images with partial occlusions. Thus, in recognition tasks, the best results using images without occlusion for training are obtained by the modified eigenphases method, LFDE 3, with an accuracy of 85.92%. These results improve to 97.92% when some images with occlusion are added to the training set. In the verification task, the best results using both of the training sets are obtained using the modified eigenphases method LFDE 3. It is important to mention that, in the verification task, it is very important to keep the false acceptance rate as low as possible, without much increase in the false rejection rate. To evaluate the performance of the proposed schemes when they are required to perform an identification task, the rank (N) evaluation was also estimated. Finally, an open set evaluation of the modified eigenphase scheme was also provided. Thus we can conclude that the proposed LFDE methods provide better performance than other previously proposed algorithms because the processing into small blocks will keep more phase information for each image; i.e., the phase is calculated only in small parts, not for the full image, to avoid occlusion or lighting effects on the full image; therefore, the illumination or partial occlusion effects become almost negligible when we have a small block. Finally, we provide theoretical criteria to determine the threshold values as a function of the desired false rejection rate.

Acknowledgments

We thank the National Science and Technology Council of Mexico and the National Polytechnic Institute of Mexico for financial support during the realization of this research.