Análisis del desempeño cinetostático de un robot paralelo tipo Delta reconfigurable

Resumen

En este trabajo se presenta el análisis del desempeño cinetostático de un robot paralelo tipo Delta cuando se somete a una estrategia de reconfiguración geométrica. Se evalúan tres alternativas de reconfiguración, seleccionando la que se logra por el ajuste simétrico del tamaño de la base fija del robot. El análisis del efecto de la reconfiguración geométrica sobre el desempeño cinetostático del robot se realiza a través del número de condición de la matriz jacobiana, por lo que fue necesario desarrollar previamente el modelo cinemático del manipulador en posición y velocidad. Ambas aproximaciones son diferentes a las comúnmente encontradas en la literatura; destacándose el análisis de velocidad, el cual se realiza con teoría de tornillos. Los resultados de este trabajo apuntan a que con una estrategia de reconfiguración geométrica se puede mejorar el desempeño cinetostático del robot tipo Delta en todo su espacio de trabajo operable, además sugieren la conveniencia de la utilización del número de condición de la matriz Jacobiana como criterio para determinar la configuración geométrica óptima del manipulador dentro de ciertos parámetros.

Abstract

This paper presents the kinetostatic performance analysis of a reconfigurable Deltatype parallel robot when a geometrical reconfiguration strategy is done. Three reconfiguration alternatives were evaluated, and the chosen strategy was based on the symmetrical size adjustment of the robot's fixed base. The analysis of the geometrical reconfiguration's effect on the robot's kinetostatic performance is obtained with the condition number of the Jacobian matrix, for which it was previously needed to develop the position and velocity kinematic model of the manipulator. Both approaches are different from those commonly found in the literature; with the velocity analysis standing out by the use of screw theory. The results of this work suggest a geometric strategy of reconfiguration for the improvement of the kinetostatic performance of the Delta robot in the entirety of its operable workspace. In addition, this work shows the convenience of the use of the condition number of the Jacobian matrix as criteria for determining the optimal geometric configuration of the manipulator inside certain parameters.

Introducción

Actualmente la industria tiene la necesidad de poder ajustar sus líneas de producción para hacer frente a cambios inesperados en las exigencias del mercado. Por lo anterior, la ingeniería robótica tiene el reto de desarrollar manipuladores flexibles que puedan desempeñarse eficientemente en cualquier entorno, situación o condición de trabajo, haciendo especial énfasis en los manipuladores paralelos por sus ventajas competitivas sobre los robots tipo serie.

Una estrategia de reconfigurabilidad es quizá el enfoque más razonable para proveer de flexibilidad a un robot manipulador (El Maraghy, 2009). En el caso de manipuladores paralelos los principales avances en esta materia pueden agruparse en dos categorías; los basados en un diseño modular y los basados en un diseño con geometría variable (Zhang and Shi, 2012).

Un diseño modular consiste en un conjunto de módulos estandarizados, tales como actuadores, articulaciones, eslabones y efectores finales, los cuales pueden conectarse y desconectarse rápidamente para obtener diferentes configuraciones o grados de libertad en un robot manipulador, los trabajos presentados en Guilin et al. (2001), Brisan (2007), Gogu (2007), Haage et al. (2009) y Xi et al. (2011) constituyen ejemplos de esta estrategia aplicada a robots manipuladores paralelos.

Por otro lado, en un diseño de geometría variable las dimensiones de los parámetros geométricos del manipulador se modifican para alcanzar nuevas configuraciones. El dodecápodo (Bande et al., 2005), la plataforma Gough-Stewart reconfigurable planteada en (Ji and Song, 1998) y el robot paralelo presentado en Zhang and Shi (2012) constituyen ejemplos de este enfoque, sin embargo, se limitan únicamente al planteamiento cinemático, al desarrollo de algunas simulaciones dinámicas o bien, al análisis del efecto de la variación geométrica en la forma y volumen del espacio de trabajo del manipulador. Algunos trabajos profundizan un poco más al definir criterios como la rigidez (Simaan and Shoham, 2003) o el torque requerido por los actuadores (Du Plessis and Snyman, 2006) para determinar la configuración geométrica que optimice el desempeño del manipulador.

A pesar de los avances obtenidos, en la actualidad el desarrollo de un manipulador paralelo reconfigurable sigue siendo un desafío para la ingeniería robótica, los prototipos basados en un diseño modular se han limitado al planteamiento de arquitecturas que modifican el espacio de trabajo y los grados de libertad del manipulador y, en el caso de los basados en un diseño de geometría variable, siguen sin definir una metodología que apoyada en un criterio objetivo permita resolver el problema de determinar la configuración o geometría adecuada para optimizar el desempeño del manipulador.

En el presente trabajo se estudia el efecto generado en el desempeño cinetostático de un manipulador paralelo al aplicar una estrategia de reconfiguración con un enfoque de variación geométrica. El número de condición de la matriz jacobiana se utiliza como criterio para definir la configuración geométrica que optimiza el desempeño cinetostático del manipulador.

El manipulador objeto de estudio en este trabajo es una variante del robot Delta (Clavel, 1991; Clavel, 1990), el cual, por su simplicidad y ventajas, es quizá el robot paralelo más famoso de la historia y sobre el cual, sorpresivamente, según el conocimiento de los autores, solo existe un trabajo reportado relacionado con su reconfiguración (Maya et al., 2013).

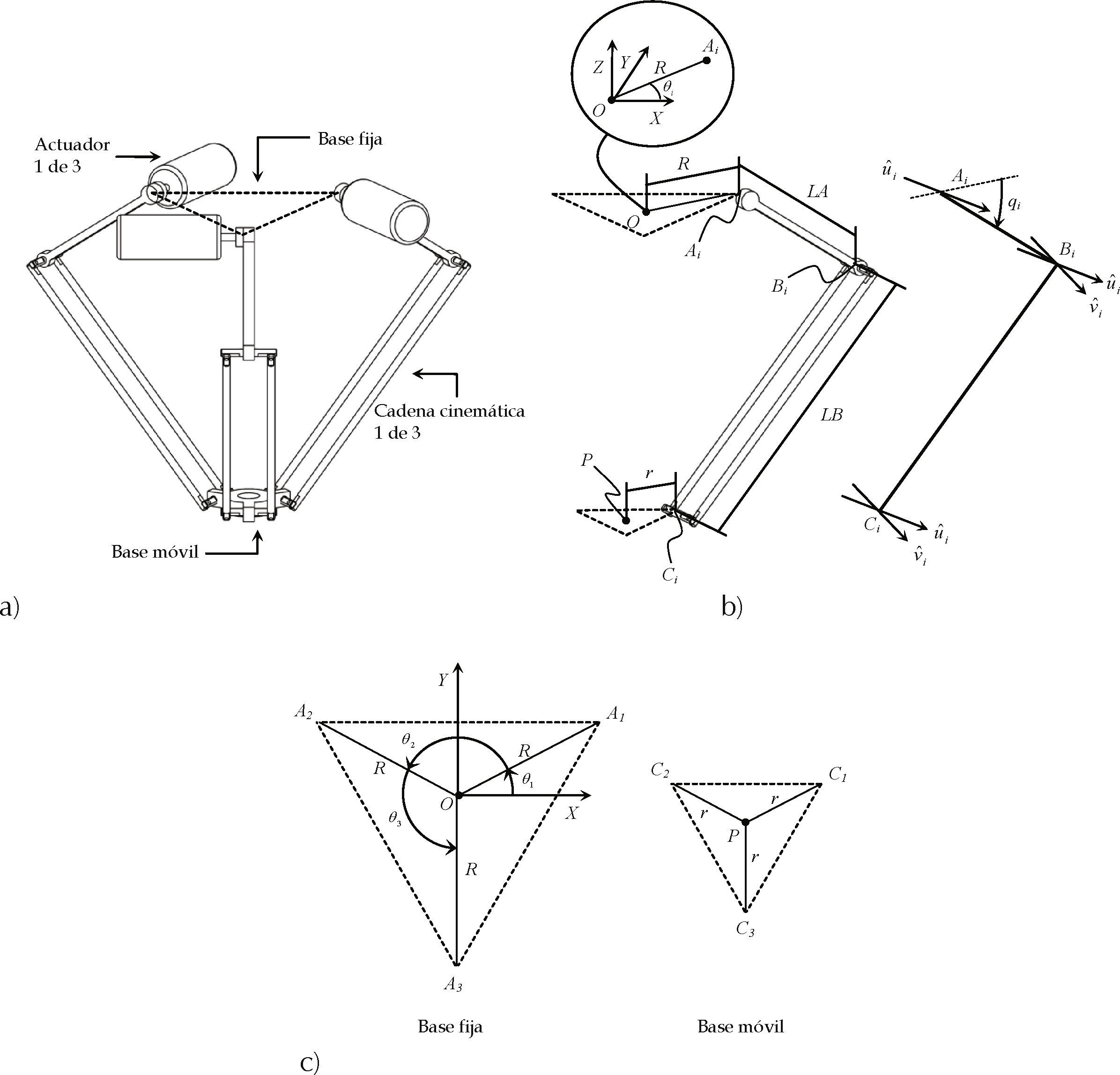
Descripción geométrica

En este trabajo se toma como modelo de estudio una versión del robot Delta integrada por una base fija y otra móvil conectadas por tres cadenas cinemáticas idénticas (figura 1a).

Figura 1.

Robot tipo Delta, a) vista general, b) estructura de la i-ésima cadena cinemática, c) configuración geométrica de la base fija y la base móvil.

Como se observa en la figura 1b, un sistema de referencia global (X, Y, Z) se define en el punto O en el centro de la base fija. Los ejes X y Y yacen en el plano de la base fija y el eje Z apunta hacia arriba verticalmente. Las articulaciones activas de revoluta, cuyas posiciones se definen por los vectores OA_i, forman un triángulo equilátero A₁A₂A₃ (figura 1c), donde A_i = (A_Xi, A_Yi, A_Zi) depende del radio R de la circunferencia donde está inscrito el triángulo y de la orientación θ_i de las i=1, 2, 3 cadenas cinemáticas. Por otro lado, B_i = (B_Xi, B_Yi, B_Zi) denota la posición, definida por el vector OB_i, de la articulación que conecta el eslabón de longitud LA con el eslabón de longitud LB (en forma de paralelogramo) en la misma cadena cinemática. De forma similar, C_i = (C_Xi, C_Yi, C_Zi) denota la posición, definida por el vector OC_i, de la articulación que conecta la base móvil con el eslabón de longitud LB. Los puntos C_i forman un triángulo equilátero C₁C₂C₃ inscrito en una circunferencia de radio r (figura 1c). Los ejes de rotación de las articulaciones de revoluta activas, definidos como, son tangentes a la circunferencia donde está inscrito el triángulo A₁A₂A₃, y debido a que los paralelogramos no permiten rotaciones entre la base fija y la móvil, existe un eje de rotación también definido como en los puntos B_i y C_i. Los puntos B_i y C_i determinan la posición de un par de articulaciones que se pueden representar como universales, por lo que es posible definir en estos puntos un eje de rotación perpendicular a y al eslabón de longitud LB. Finalmente el punto P = (P_X, P_Y, P_Z), cuya posición se define por el vector OP, es el punto de interés en la base móvil del robot (elemento efector) y está localizado por conveniencia en el centro de esta, en otras palabras, en el centro del triángulo C₁C₂C₃.

Para evaluar la reconfiguración geométrica del robot tipo Delta y el efecto en su desempeño cinetostático, es necesario definir una línea base, es decir, determinar valores de referencia para cada uno de los parámetros que definen la geometría del robot y que se presentan en la tabla 1.

Tabla 1.

Parámetros geométricos de referencia del robot tipo Delta

Parámetro	R	r	θ1	θ2	θ3	LA	LB
Valor	150 mm	50 mm	30°	150°	270°	200 mm	400 mm

Reconfiguración del mecanismo

Una reconfiguración de tipo geométrica implica la variación de uno, algunos o todos los parámetros mostrados en la tabla 1. En este trabajo se toma la opción de modificar solamente un parámetro, pues seleccionar más de uno intensifica el problema de redundancia en los grados de libertad del robot.

Selección del parámetro geométrico

Como se menciona en Maya et al. (2013), los parámetros que tienen mayor influencia sobre el volumen del espacio de trabajo son R, LA y LB, por esta razón existe una inclinación por la selección de uno de ellos como parámetro de reconfiguración.

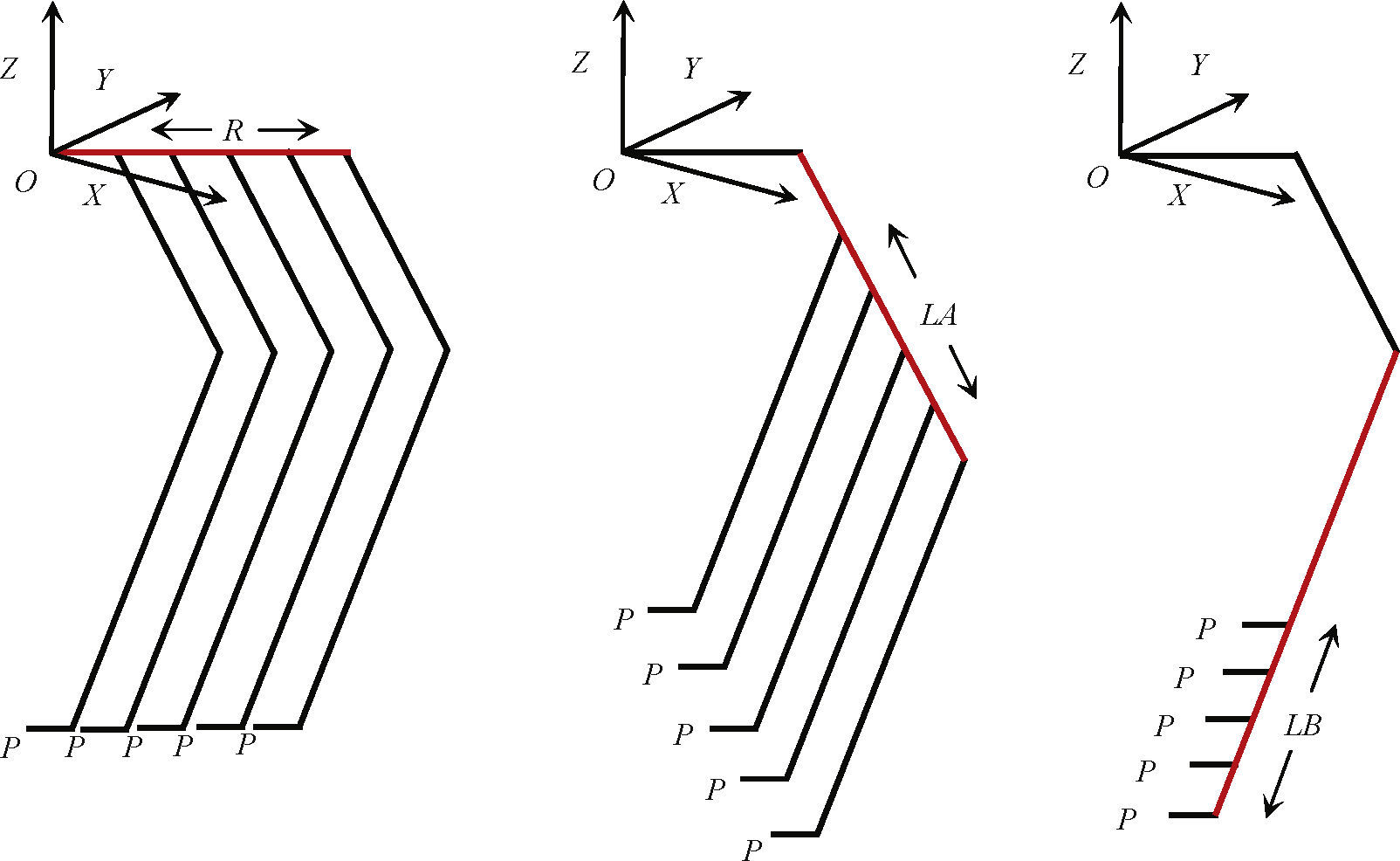
En la figura 2 se presenta un esquema para la reconfiguración geométrica de la i-ésima cadena cinemática del robot. A la izquierda se presenta una variación del parámetro geométrico R, al centro la variación del parámetro LA, y a la derecha una variación del parámetro LB.

Figura 2.

Opciones de reconfiguración, izquierda: variación del parámetro R, centro: variación del parámetro LA, derecha: variación del parámetro LB.

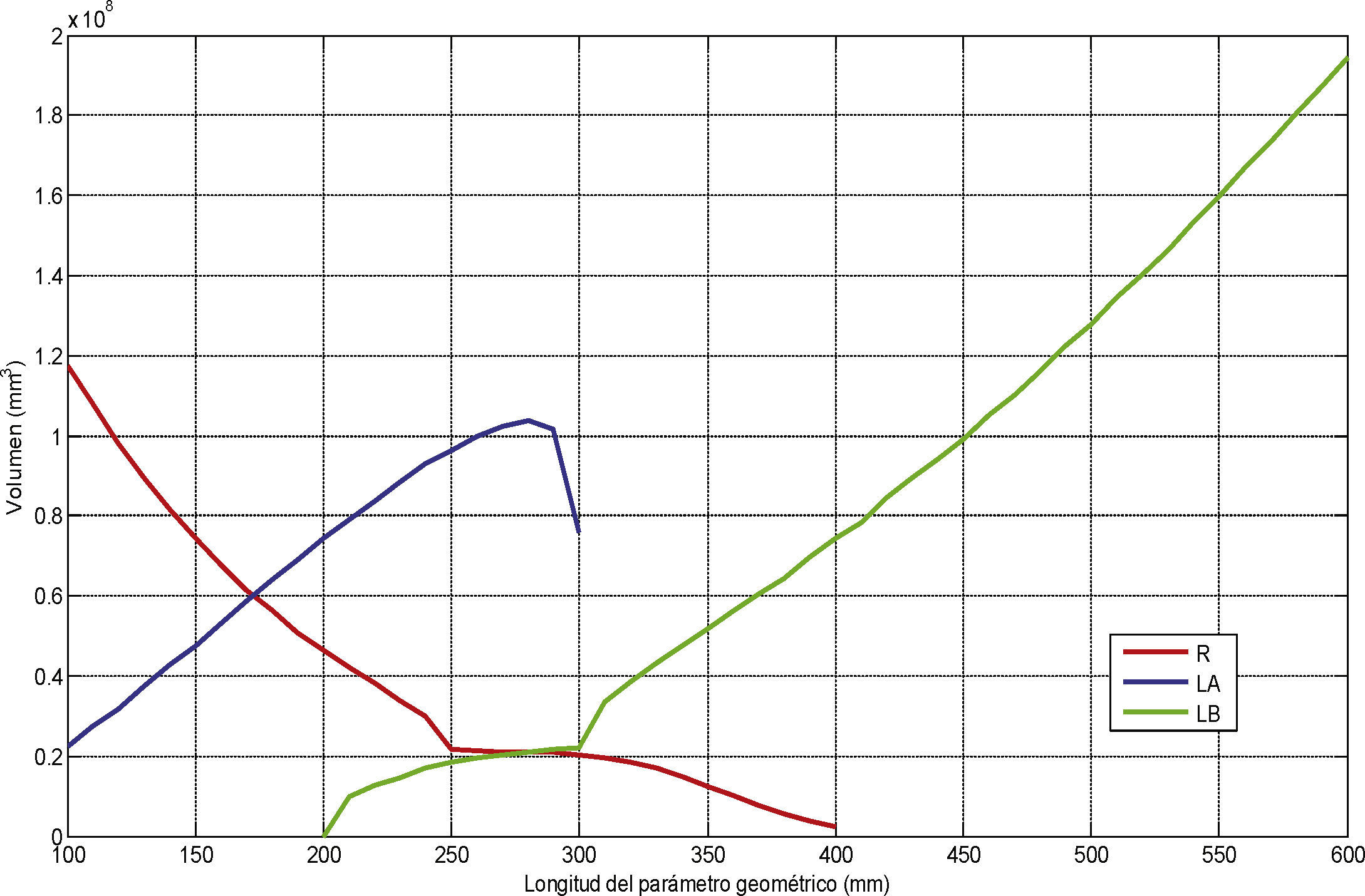
En la figura 3 se muestra el comportamiento del volumen del espacio de trabajo del robot frente a variaciones en los parámetros R, LA y LB. En el caso de los parámetros LA y LB, su relación con el volumen del espacio de trabajo es mayoritariamente directa, mientras que en el caso de R esa relación es inversa. Lo anterior significa que para obtener una configuración del robot que provea un espacio de trabajo superior al provisto por la configuración de referencia (tabla 1), si se toma LA o LB como parámetros de reconfiguración, es necesario aumentar las dimensiones de los eslabones y en consecuencia el tamaño y espacio físico del robot, mientras que si se toma R como parámetro de reconfiguración, se puede aumentar el espacio de trabajo del manipulador reduciendo el tamaño de su base fija. Por otro lado, seleccionar los parámetros LA o LB implica montar sobre cada cadena cinemática los actuadores necesarios para generar la reconfiguración, lo que afectaría negativamente la capacidad de carga del manipulador, su rigidez y por tanto la exactitud del mismo, mientras que al seleccionar el parámetro R, con un único actuador montado sobre la base fija se puede alcanzar la reconfiguración sin generar los efectos negativos mencionados. Por lo anterior se selecciona R como parámetro base para la reconfiguración del robot tipo Delta.

Figura 3.

Relación entre el volumen del espacio de trabajo del robot y los parámetros geométricos R, LA, LB.

Para estimar el volumen del espacio de trabajo del robot bajo una determinada configuración de los parámetros R, LA y LB, se realiza un barrido de coordenadas en los ejes X, Y y Z lo suficientemente amplio para contener dicho espacio de trabajo, de manera que el conjunto de posiciones que ofrezcan soluciones para el modelo inverso en posición, el cual se presenta más adelante en la sub-sección “Modelo cinemático de posición”, conforman la nube de puntos que está asociada con el espacio de trabajo del robot. Después cada uno de los puntos que conforman esta nube se considera como el centro de un cubo de arista igual al diferencial seleccionado para realizar el barrido de coordenadas en los X, Y y Z, por lo que a través de la sumatoria del volumen de cada uno de estos cubos se puede obtener una aproximación para el volumen del espacio de trabajo del robot bajo una determinada configuración de los parámetros R, LA y LB. Es importante mencionar que mientras más pequeño sea el diferencial seleccionado para el barrido de coordenadas, mejor será la aproximación al volumen del espacio de trabajo del robot, en el caso de los resultados mostrados en la figura 3 el barrido de coordenadas se realizó cada 10 mm.

El objetivo de este trabajo no es desarrollar un estrategia de reconfigurabilidad para aumentar el espacio de trabajo del robot, sino evaluar si a través de dicha estrategia de reconfiguración se puede mejorar el desempeño cinetostático del robot.

El desempeño cinetostático de un mecanismo está en función de su matriz jacobiana (Moreno et al., 2012), y a su vez esta matriz jacobiana depende de la geometría de dicho mecanismo. De lo anterior es posible plantear que a través de una estrategia de reconfiguración geométrica se puede influir positivamente sobre el desempeño cinetostático del robot tipo Delta objeto de estudio, para lo cual es necesario determinar la expresión general de la matriz jacobiana del robot.

Matriz jacobiana del robot

En esta sección se presenta la estimación de la matriz jacobiana del robot en estudio medinte la teoría de tornillos, que es un enfoque mucho más sencillo que el mostrado en planteamientos clásicos (Lung, 1999), donde es necesario derivar la ecuación de lazo de cada cadena cinemática para encontrar una expresión de la matriz Jacobiana.

Antes de determinar la matriz jacobiana es necesario resolver el modelo cinemático del robot en posición.

Modelo cinemático de posición: el análisis directo e inverso de posicionamiento del robot Delta es un tópico ya muy estudiado en la literatura, sin embargo la formulación planteada en esta sección difiere de los planteamientos clásicos, pues se basa en la idea de que las coordenadas de cualquier punto de un cuerpo rígido se pueden expresar como una combinación lineal de las coordenadas de puntos claves pertenecientes al mismo cuerpo, lo que implica una reducción importante en las ecuaciones e incógnitas a manejar.

El análisis directo consiste en encontrar las coordenadas del punto P para un conjunto dado de coordenadas generalizadas q_i. Para este fin, es necesario calcular previamente las coordenadas de los puntos A_i = (A_Xi, A_Yi, A_Zi) y B_i = (B_Xi, B_Yi, B_Zi), las cuales se pueden definir de la siguiente forma:

(1)

(2)

Para determinar las coordenadas de los puntos C_i = (C_Xi, C_Yi, C_Zi) es necesario considerar que si C₁C₂C₃ es un triángulo equilátero inscrito en una circunferencia de radio r, entonces las coordenadas de C₂ y C₃ se pueden especificar en función de las coordenadas de C₁, como se presenta a continuación

(3)

(4)

Posteriormente, para calcular C_X1, C_Y1, C_Z1 debemos considerar las tres ecuaciones generadas, para i = 1, 2, 3, por la siguiente relación

(5)

Por último, las coordenadas del punto P se pueden obtener fácilmente de la siguiente forma

(6)

Por otro lado el análisis inverso consiste en encontrar las coordenadas generalizadas q_i dadas las coordenadas del punto P. Para ello de (6) se pueden extraer las coordenadas de C_i de la siguiente forma

(7)

Sustituyendo (2) y (7) en la ecuación vectorial (5) se puede encontrar una expresión para q_i como se muestra a continuación

(8)

donde

(9)

(10)

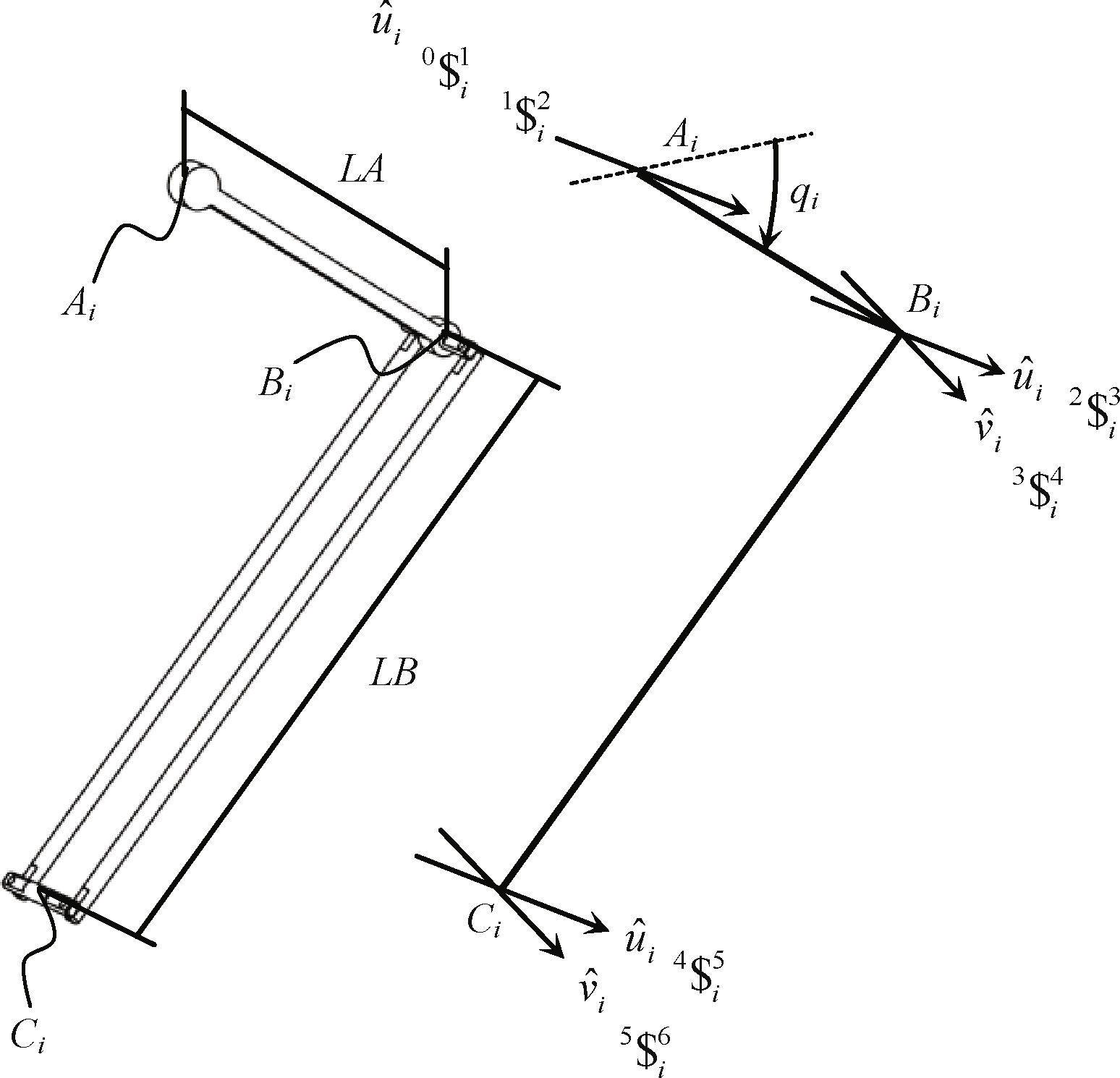
Matriz jacobiana: con el propósito de evitar una matriz jacobiana con rango deficiente, pares cinemáticos virtuales se añaden al mecanismo. Tomando en cuenta esto, los tornillos asociados con cada una de las articulaciones de la i-ésima cadena cinemática (figura 4) son: denota el tornillo asociado a una articulación de revoluta virtual, es el tornillo asociado con la articulación de revoluta activa definida en el punto y son los tornillos asociados con la articulación universal definida en el punto B_i, y finalmente y son los tornillos asociados a la articulación universal definida en el punto C_i.

Figura 4.

Definición de los tornillos asociados a las articulaciones de la i-ésima cadena cinemática.

Los tornillos, para j = (1, 2, … 6), se definen en coordenadas de Plücker de la siguiente manera

(11)

donde , llamada parte primal, es un vector unitario a lo largo del eje de rotación de la articulación asociada al tornillo , mientras que , llamada parte dual, es el par momento resultante del producto cruz entre la parte primal y el vector de posición del punto O (origen del sistema de referencia global) respecto a la posición de la articulación en cuestión.

El estado de velocidad V de un cuerpo rígido se puede expresar con tres componentes angulares (w_x, w_y, w_z) y tres lineales (v_x, v_y, v_z). En el caso del estado de velocidad de la base móvil del robot tipo Delta, las componentes angulares se consideran nulas, pues se trata de un mecanismo de tres grados de libertad puramente traslacionales, por lo que su estado de velocidad se puede representar como sigue

(12)

De lo anterior, el estado de velocidad V de la base móvil se puede expresar en forma de tornillo de la siguiente manera

(13)

donde representa la magnitud de la velocidad asociada al j-ésimo tornillo y donde, específicamente, es la magnitud de la velocidad asociada al tornillo de la articulación de revoluta virtual, mientras que es la i-ésima velocidad generalizada del robot.

Para encontrar una ecuación que relacione las velocidades generalizadas del robot con el estado de velocidad de su base móvil es necesario considerar las líneas L_i de la siguiente forma:

(14)

L_i son líneas en coordenadas de Plücker que pasan a través de los puntos B_i y C_i, donde representa la dirección de la línea, parte primal, y es la parte dual. De lo anterior L_i se puede expresar de la siguiente forma

(15)

La línea L_i es reciproca a todos los tornillos de la misma cadena cinemática, excepto al tornillo asociado a la articulación virtual y a la articulación de revoluta activa, por lo tanto, la aplicación de la forma de Klein, la cual se denota por {*;*}, de la línea L_i a ambos lados de la ecuación (13), permite, con la reducción de términos, llegar a la siguiente ecuación

(16)

La ecuación (16) relaciona las velocidades generalizadas de robot con el estado de velocidad de su base móvil , donde

(17)

(18)

Las ecuaciones (17) y (18) representan las matrices jacobianas de cinemática directa e inversa respectivamente. Con planteamientos clásicos (Lung, 1999), estas matrices están en función de sumatorias y productos de senos y cosenos de los ángulos que forman las articulaciones activas y pasivas del robot para una determinada pose, por lo que encontrar las configuraciones singulares del mecanismo resulta un poco complicado. Con el planteamiento presentado en esta sección esta tarea se vuelve muy fácil, por ejemplo, la matriz J_x es singular cuando det(J_x) = 0 y esto ocurre cuando los vectores son linealmente dependientes, es decir cuando son coplanares o paralelos. Por otro lado, la matriz J_q es singular cuando det(J_q) = 0, lo cual ocurre cuando alguno de los elementos de la diagonal de J_q se vuelve cero, es decir cuando una cadena cinemática se encuentra completamente extendida o contraída haciendo que el tornillo y la línea L_i sean recíprocos, causando que . Finalmente singularidades combinadas surgen cuando det(J_x) = det(J_q) = 0, esto sucede cuando la base fija y la móvil tienen dimensiones iguales, es decir, A₁A₂A₃ = C₁C₂C₃ y las cadenas cinemáticas están dispuestas verticalmente.

Las matrices jacobianas de las ecuaciones (17) y (18) se pueden expresar en una sola:

(19)

Para mayor información acerca de la teoría de tornillos y su aplicación para el análisis de velocidad en cadenas cinemáticas y el análisis de orden superior (aceleración, pulso e hiperpulso) consultar (Gallardo, 1999).

Análisis del efecto de la reconfiguración en el desempeño cinetostático del robot

Existen muchos índices que miden el desempeño cinetostático de un robot manipulador; el número de condición (Salisbury and Craig, 1982), la manipulabilidad (Yoshikawa, 1985), el mínimo valor singular (Klein and Blaho, 1987), entre otros. La mayoría de estos índices se encuentran íntimamente relacionados y reflejan prácticamente lo mismo, pues dependen de la matriz Jacobiana del manipulador. En este trabajo, para evaluar el efecto generado por una estrategia de reconfiguración sobre el desempeño cinetostático del robot se utiliza el número de condición, el cual es un indicador con muchas aplicaciones, entre las que destacan su utilidad para describir la exactitud de un manipulador y la cercanía de configuraciones singulares (Merlet, 2007), medir la uniformidad de la distribución de velocidades y fuerzas (Chablat and Wenger, 2003), y auxiliar el diseño de manipuladores isotrópicos (Huang et al., 2004; Moreno and Pamanes, 2011).

El número de condición k se calcula de la siguiente forma

(20)

Donde ||*|| es la norma de la matriz correspondiente, la cual, tal y como se puntualiza en Moreno et al. (2012), corresponde a la norma de Frobenius, definida en forma general a través de la siguiente expresión

(21)

donde A_ij representa el elemento de la i-ésima fila y j-ésima columna de la matriz A para la que se quiere calcular la norma de Frobenius.

El número de condición permite obtener un valor cuantitativo asociado con el desempeño cinetostático del manipulador en determinadas poses de su espacio de trabajo. El valor mínimo que puede tomar el número de condición es la unidad, en ese caso se dice que esa pose es isotrópica y evidentemente es la mejor condición esperada. Por otro lado, el número de condición puede tender a infinito y en ese caso se dice que la pose es singular.

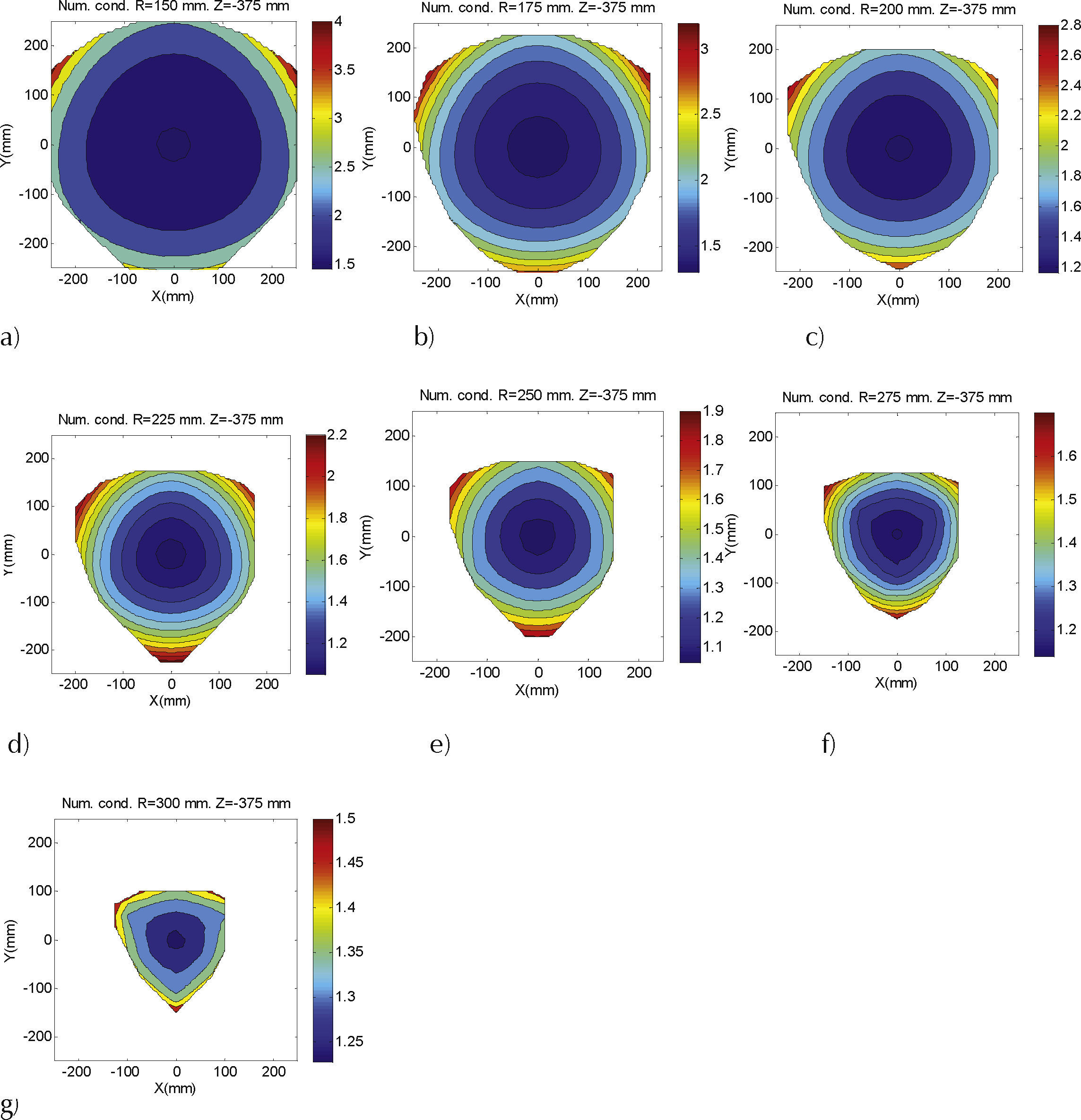
Cada variación del parámetro R implica una configuración distinta del robot y en consecuencia un determinado espacio de trabajo (ver figura 3). Se realizó el cálculo del número de condición para todos los puntos dada una determinada configuración del parámetro R, los resultados son muchos y por ello en la figura 5 se presentan únicamente resultados para un plano que pertenece al espacio de trabajo útil del robot (Z = –375 mm). Las variaciones del parámetro geométrico R van desde 150 hasta 300 mm con incrementos de 25 mm.

Figura 5.

Mapeo del número de condición, Z = –375 mm, a) R = 150 mm, b) R = 175 mm, c) R = 200 mm, d) R = 225 mm, e) R = 250 mm, f) R = 275 mm, g) R = 300 mm.

En la figura 5 se puede evidenciar un comportamiento radial y simétrico con respecto al eje Y del número de condición, donde los mejores valores se encuentran alojados al centro y van desmejorando en la medida que se acercan a las fronteras del plano de estudio.

Si se contrastan individualmente los gráficos de la figura 5 se percibe cómo, a partir de la reconfiguración inicial R = 150 mm, el número de condición tiende a mejorar en la medida que se aumenta el valor de R. Por ejemplo en la figura 5a el mejor valor registrado para el número de condición es 1.5, este mejora a aproximadamente 1.4 en la figura 5b, luego pasa a 1.2 en la figura 5c, a aproximadamente 1.1 en la figura 5d y a poco menos de 1.1 en la figura 5e. A partir de ahí con más reconfiguraciones el valor del número de condición deja de acercarse a la unidad y empieza a desmejorar, además de que la pérdida del espacio de trabajo en ese plano ya es demasiada.

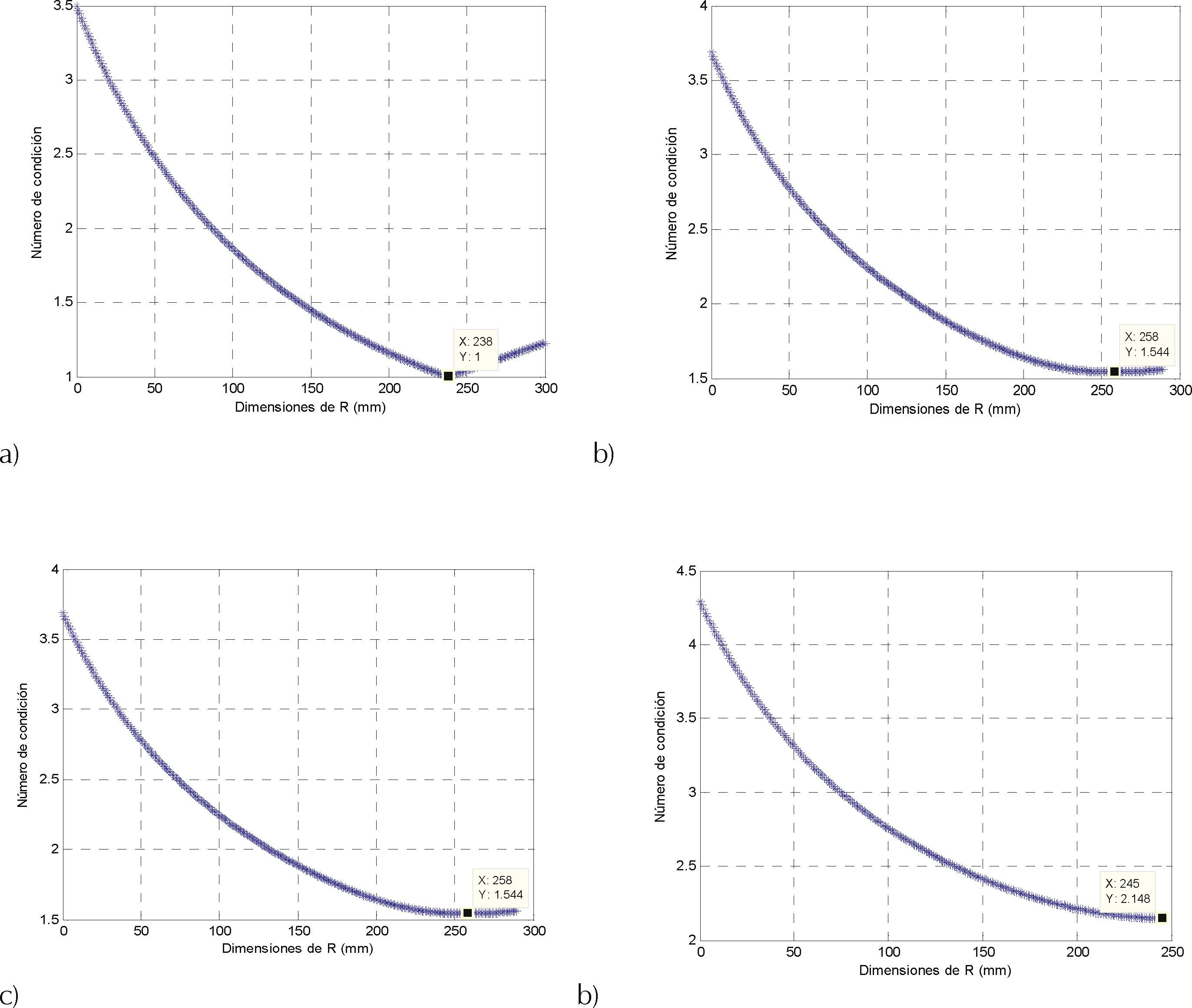
El efecto de la reconfiguración también se puede analizar puntualmente, es decir, para una determinada pose visualizar cómo se ve afectado el comportamiento cinetostático del robot. En la figura 6 se presentan algunos resultados de este análisis, tomando en cuenta el plano Z = –375 mm y los puntos P = (0, 0, –375), P = (120, 100, –375), P = (–120, 100, –375) y P = (0, –220, –375).

Figura 6.

Relación entre el número de condición y la configuración del parámetro R, a) P = (0, 0, –375), b) P = (120, 100, –375), c) P = (–120, 100, –375), d) P = (0, –220, –375).

En la figura 6 se muestra, para todas las poses presentadas, que el número de condición tiende a mejorar en la medida que se incrementa el valor de R, hasta llegar a un punto donde ya no es posible mejorar. En el caso de la figura 6a, la cual corresponde al análisis para el punto P = (0, 0, –375), la configuración que ofrece el mejor número de condición se da cuando R es de aproximadamente 238 mm y corresponde a un número de condición de 1, cuando con la configuración de referencia R = 150 mm el número de condición es de 1.45. Por otro lado, en las figura 6b y 6c, las cuales corresponden al análisis de los puntos P = (120, 100, –375) y P = (–120, 100, –375), el comportamiento del número de condición es el mismo, lo cual es lógico pues el comportamiento general del número de condición es simétrico con respecto al eje Y. En ambas figuras la configuración que ofrece el mejor número de condición se da cuando R es de aproximadamente 258 mm y corresponde a un número de condición de 1.544, cuando con la configuración de referencia R = 150 mm el número de condición es de 1.8. Finalmente, en la figura 6c, la cual corresponde al análisis del punto P = (0, –220, –375), se observa un comportamiento similar, con un valor de R = 245 mm el número de condición es de 2.148, cuando con la configuración de referencia R = 150 mm el número de condición es de 2.41. La curva de la figura 6c se vuelve discontinua a partir de R =245 mm, lo cual significa que el punto P = (0, –220, –375) no puede alcanzarlo el robot con configuraciones superiores a R =245 mm.

El comportamiento para el plano y los puntos mostrados anteriormente es similar en todo el espacio de trabajo del robot. Es decir, a medida que aumenta el valor del parámetro geométrico R el número de condición tiende a acercarse a la unidad y por consiguiente el desempeño cinetostático del robot mejora, hasta alcanzar un punto donde ya no lo hace. Esto quiere decir que la función que relaciona el parámetro R con el número de condición tiene un mínimo global que se puede identificar fácilmente a través de una estrategia de optimización.

Determinación de la configuración óptima del robot

Encontrar el valor para el parámetro R que permita obtener el mínimo número de condición k para una determinada pose del robot P bajo ciertos parámetros geométricos constantes (r, LA, LB, θ_i), se puede ver como un problema de optimización.

La estrategia a utilizar, se conoce como medida de optimización de primer orden, está basada en la condición que establece que un punto representa un mínimo en una función cuando su medida de optimización Mop, definida como el gradiente de la función en ese punto, tiende a cero, lo que para funciones sin restricciones significa que la norma infinita del gradiente de la función también tiende a cero.

En este método se debe definir previamente una tolerancia TolFun (valor muy cercano a cero) que determina la condición de paro del algoritmo, de manera que cuando la medida de optimización Mop sea menor a TolFun significa que el algoritmo ha encontrado el valor de R asociado al menor número de condición k posible. De igual manera es necesario definir un valor inicial de búsqueda R_init.

La transición entre diferentes valores de R hasta encontrar el óptimo ocurre considerando la dirección de búsqueda de máximo descenso –▿k y un escalar λ que determina la longitud de paso en la dirección –▿k, esta longitud de paso puede seleccionarse con diferentes métodos, por ejemplo, la búsqueda unidireccional en la dirección del gradiente.

Para demostrar la aplicabilidad del método se implementó un algoritmo que permite determinar las configuraciones óptimas del robot cuando su efector final describe una trayectoria en forma de espiral 3D (figura 7a), el algoritmo se presenta más adelante.

Figura 7.

Optimización para una trayectoria, a) trayectoria de espiral 3D trazada bajo la configuración de referencia R = 150 mm, b) comparativa entre el comportamiento del número de condición bajo la configuración de referencia R = 150 mm y bajo la estrategia de reconfiguración planteada.

La trayectoria de prueba seleccionada es una espiral 3D debido a que una trayectoria de este tipo representa en su totalidad los tres grados de libertad del robot. Dicha trayectoria se programó para que estuviera integrada por 1000 puntos, y para cada uno de estos puntos se calcula el valor del parámetro R que entregue el mejor número de condición. Los resultados se presentan en la figura 7b.

La figura 7b muestra, para la trayectoria en estudio, una comparación entre el comportamiento del número de condición bajo la configuración de referencia R = 150 mm (curva azul delgada) y con la estrategia de reconfiguración (curva azul gruesa). Como se observa, para cada uno de los puntos que describen la trayectoria, el número de condición obtenido con la reconfiguración es mejor que el de referencia, lo que significa que con esta estrategia se está optimizando el desempeño cinetostático del manipulador. En la figura 7b se muestra además el comportamiento del parámetro R seleccionado como óptimo (curva verde), en donde se evidencia una completa continuidad en su selección, lo que resulta conveniente durante el proceso de operación del robot, pues se evitan cambios bruscos en la configuración del mismo.

El análisis presentado en este trabajo permite determinar la configuración geométrica del robot que entrega el mejor desempeño cinetostático posible para una posición dada. Es decir, el número de condición se puede utilizar como criterio para resolver el problema de múltiples soluciones que tiene el modelo cinemático inverso de posicionamiento del robot tipo Delta cuando se somete a una reconfiguración geométrica basada en la variación del parámetro R.

Conclusiones

Se realizó el análisis del desempeño cinetostático de un robot paralelo tipo Delta cuando se somete a un estrategia de reconfiguración geométrica. Se evaluaron independientemente tres alternativas de reconfiguración, después de hacer una evaluación relacionada con la generación de espacios de trabajo y tomando en cuenta algunas consideraciones tales como el espacio físico que ocuparía el robot, la cantidad de actuadores necesarios para generar la reconfiguración y el potencial efecto sobre su capacidad de carga y rigidez, se seleccionó la estrategia que implica la modificación del tamaño de la base fija, representada por el parámetro R. Los resultados indican que a través de la reconfiguración del robot es posible mejorar su desempeño cinetostático, el cual se mide a través del número de condición.

Como se observa en la figura 3, la relación que existe entre el volumen del espacio de trabajo del robot y la longitud del parámetro R es inversa, es decir, en la medida que aumenta el parámetro R disminuye el espacio de trabajo del robot, situación que se evidencia con claridad en la figura 5, en donde desde una configuración de R = 150 mm (figura 5a) hasta una configuración de R = 300 mm (figura 5 g) se puede observar cómo para el plano presentado (Z = –375 mm) es cada vez menor el área disponible de trabajo. Pese a esta pérdida, en la figura 5 se muestra que incrementar el parámetro R dentro de ciertos rangos genera un efecto positivo en el comportamiento general del número de condición. Al analizar puntualmente ese efecto de mejoría (figura 6) es posible notar que existe un rango donde el número de condición tiende a acercarse a la unidad en la medida que se incrementa el valor de R, hasta que llega a un punto donde empieza a desmejorar, lo que significa que la función que relaciona estas dos variables tiene un mínimo global, el cual se puede identificar fácilmente a través de una estrategia de optimización.

En este trabajo se utiliza la estrategia de optimización de primer orden para la determinación del mínimo global de la función que relaciona el número de condición y la longitud del parámetro R. El resultado que se obtiene al aplicar esta estrategia representa el tamaño necesario de la base fija para alcanzar el mejor desempeño cinetostático del robot para una determinada pose. Si este proceso se aplica para cada uno de los puntos que forman una trayectoria predefinida, entonces el resultado arrojará el conjunto de configuraciones del parámetro R que entregan la trayectoria con el mejor número de condición posible, tal y como se muestra en la figura 7b.

Cuando se trabaja con robots reconfigurables por variación geométrica surge el inconveniente de redundancia en los grados de libertad, lo cual se genera debido a que el sistema está básicamente sobre actuado. Lo anterior significa que para una determinada pose del efector final existirán infinitas configuraciones para el robot que la satisfagan. La problemática anterior se soluciona fácilmente en este trabajo al seleccionar la configuración del robot que entregue el mejor número de condición, lo que trae ventajas adicionales como el hecho de permitir al robot alejarse de configuraciones singulares cuando sea necesario, y contribuir con la distribución de velocidades y fuerzas en el espacio de trabajo.

Este artículo se cita:

Citación Estilo Chicago

Sánchez-Alonso, Róger Ernesto, José Joel González Barbosa, Eduardo Castillo-Castañeda, Albert Lester Balmaceda-Santamaría. Análisis del desempeño cinetostatico de un robot paralelo tipo Delta reconfigurable. Ingeniería Investigación y Tecnología, XVI, 02 (2015): 213-224.

Citación Estilo ISO 690

Sánchez-Alonso R.E., González-Barbosa J.J., Castillo-Castañeda E., Balmaceda-Santamaría A.L. Análisis del desempeño cinetostatico de un robot paralelo tipo Delta reconfigurable. Ingeniería Investigación y Tecnología, volumen XVI (número 2), abril-mayo 2015: 213-224.

Semblanzas de los autores

Róger Ernesto Sánchez-Alonso. Obtuvo el grado de ingeniero industrial por la Universidad Nacional de Ingeniería, Nicaragua, y el grado de maestro en tecnología avanzada por el Instituto Politécnico Nacional, México, donde actualmente desarrolla estudios para obtener el grado de doctor. Es profesor titular de la Universidad Nacional de Ingeniería, Nicaragua. Trabaja en líneas de investigación vinculadas con el diseño y análisis de robots paralelos, y procesamiento de imágenes.

José-Joel González-Barbosa. Recibió el grado de maestro en ciencias de la ingeniería eléctrica en la Universidad de Guanajuato, México, y el grado de doctor en ciencias de la computación y telecomunicaciones en el Instituto Politécnico Nacional de Toulouse, Francia, en 1998 y 2004, respectivamente. Es profesor investigador en el CICATA Querétaro-IPN, México, donde imparte los cursos de visión por computadora, procesamiento de imágenes y reconocimiento de patrones. Actualmente sus líneas de investigación son: percepción y robótica móvil.

Eduardo Castillo-Castañeda. Egresado de la Universidad Nacional de México de la carrera de ingeniero mecánico electricista en 1987. Obtuvo el grado de doctor en control automático por el Instituto Politécnico Nacional de Grenoble, Francia, en 1994. En 1997 fue profesor invitado en el Laboratorio de Ingeniería Mecánica, en Tsukuba, Japón. De igual manera en 2002 fue profesor invitado en el Instituto de Tecnología de Tokyo, Japón. Actualmente es profesor investigador en el CICATA Querétaro-IPN, México, donde imparte cursos de robótica y control automático. Sus líneas de investigación son ingeniería de precisión, visión por computadora, robots manipuladores, robots de inspección y robots de rehabilitación.

Albert Lester Balmaceda-Santamaría. Obtuvo el grado de ingeniero industrial en la Universidad Nacional de Ingeniería, Nicaragua, donde se desempeña como profesor de tiempo completo. En 2011 obtuvo el grado de maestro en tecnología avanzada por el Instituto Politécnico Nacional, México, donde actualmente cursa estudios para obtener el grado de doctor. Sus líneas de investigación son: diseño y análisis de robots paralelos.