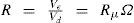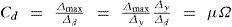Analysis of the Earthquake-Resistant Design Approach for Buildings in Mexico

Abstract

The development of new codes for earthquake-resistant structures has made possible to guarantee a better performance of buildings, when they are subjected to seismic actions. Therefore, it is convenient that current codes for design of building become conceptually transparent when defining the strength modification factors and assessing maximum lateral displacements, so that the design process can be clearly understood by structural engineers. The aim of this study is to analyze the transparency of earthquake-resistant design approach for buildings in Mexico by means of a critical review of the factors for strength modification and displacement amplification. The approach of building design codes in US is also analyzed. It is concluded that earthquake-resistant design in Mexico have evolved in refinement and complexity. It is also demonstrated that the procedure prescribed by such design codes allows the assessment of the design strengths and displacements in a more rational way, in accordance not only with the present stage of knowledge but also with the contemporary tendencies in building codes. In contrast, the procedures used in US codes may not provide a clear view for seismic response assessment of buildings.

Resumen

El desarrollo de nuevos reglamentos de diseño de estructuras sismorresistentes ha hecho posible que se garantice un mejor comportamiento de los edificios cuando éstos son sometidos a acciones sísmicas. Por tanto, es conveniente que los reglamentos actuales de diseño de edificios sean conceptualmente transparentes, en cuanto a la definición de los factores de modificación de resistencia y en la forma de evaluar los máximos desplazamientos laterales, de tal manera que los ingenieros estructurales puedan comprender claramente el proceso de diseño. El propósito de este estudio es analizar la transparencia del criterio de diseño sismorresistente para edificios en México, a partir de una revisión crítica de los factores de modificación de resistencia y de amplificación de desplazamiento. Además se analiza el enfoque de los reglamentos de diseño de edificios en Estados Unidos. Se concluye que los reglamentos de diseño sismorresistente en México han evolucionado en refinamiento y complejidad. Además se demuestra que el procedimiento especificado en dichos reglamentos permite determinar la resistencia de diseño y los desplazamientos en una forma más racional, congruente no sólo con el estado actual del conocimiento, sino con las tendencias contemporáneas de los reglamentos de edificios. Por otro lado, los procedimientos utilizados en los reglamentos de EU podrían no proporcionar una visión clara para la evaluación de la respuesta sísmica de edificios.

Introduction

Many areas of Latin America are widely known for their high seismicity. Recognizing the seismic activity in the region, earthquake-resistant design of structures is a requirement in these countries. Therefore, each country has developed their own seismic codes based on their experience and laws (Chavez, 2012). The reexamination of the fundamental precepts of seismic design has intensified in recent years, with a great number of conflicting approaches being advocated. In some cases, the differences between the approaches are fundamental, while in others the differences are conceptual (Priestley, 2000). In general, earthquake-resistant codes have become more refined and complex, including at each revision the current state-of-the-art knowledge. However, code compliance and code misinterpretation are prevalent, mainly because two reasons, users are not familiar with the concepts and technologies involved, or the parameters prescribed by codes are unclearly presented (Alcocer and Castaño, 2008).

Contemporary earthquake-resistant codes are developed with the intention of ensuring serviceability requirements, life safety and collapse prevention during frequent, moderate, and major earthquakes, respectively. In the latter case, extensive damage to the structure may be acceptable as long as collapse is prevented (Moroni et al., 1996). Design criteria admit inelastic excursions when the structure is subjected to the earthquake characterizing the life safety limit state. This situation limits the force demands in the structural elements, hence allowing the use of smaller design strengths, at the cost of certain limited levels of structural damage due to yielding of some portions of the structure (Ordaz and Meli, 2004).

In the development of seismic design provisions for building structures, the most controversial part is the development of both the strength modification and the displacement amplification factors. In the first case, while strength modification factors prescribed in seismic codes, they are intended to account for damping, energy dissipation capacity, as well as for overstrength, the level of reduction specified in seismic codes is primarily based on observation of the performance of different structural systems in previous strong earthquakes. In addition, there is a wide range of values in different codes as the appropriate level of force reduction factor, it seems that the absolute value of the strength is of relatively minor importance. In the case of displacement amplification factors, the most common assumption is the equal-displacement approximation, which states that the displacement of the inelastic system is the same as that of an equivalent system with the same elastic stiffness and unlimited strength. However, this approximation is known to be non-conservative for short period structures (FEMA-451, 2006; Priestley et al., 2007) or for structures whose period of vibration is close to the site period (Ordaz and Pérez, 1998).

The seismic design codes in Mexico are more than 70 years old. At several moments of their history, Mexican codes have contributed with new ideas and methods, some of which have later been adopted in codes elsewhere (Ordaz and Meli, 2004). Most of the efforts to develop the Mexican codes have been made in Mexico City, the capital and largest city in the country; almost 40% of the population lives in the capital and its metropolitan area. Agencies of the Federal Government have issued standards and manuals. In terms of construction practices in Mexico, observations have indicated that lack of compliance with technical standards; adequate design and construction practices are becoming problems in Mexico City. One significant reason for the lack of compliance with construction codes is that, requirements are dissociated from current construction technology and practice, and are understood and correctly applied by only a few designers and contractors. There is a vast difference between the level of expertise and quality of practice of a relatively small group of wellinformed specialist and academics, and that of most professionals and construction workers (Alcocer and Castaño, 2008). On the other hand, after some lessons learned from earthquakes that occurred in Chile and Mexico in 1985, Bertero (1986) proposed two solutions for the improvement of US earthquake-resistant design of building structures: an ideal (rational) method and a compromise solution. Bertero (1986) emphasizes that earthquake resistance cannot be significantly enhanced simply by increasing the seismic forces because the forces developed during an earthquake shake depend on the actual stiffness, strength, and hysteretic characteristic supplied to the constructed building.

The goals of this paper are: (i) to provide an overview of development and most relevant changes of earthquake-resistant design codes in Mexico, and (ii) to compare and analyze seismic-design approaches specified by US and Mexican codes. The study includes de discussion of the most important parameters for seismic design, such as strength modification factors, displacement amplification factor and drift limits. The results are presented in a common format that allows a straightforward comparison.

Strength modification factors

As an understanding developed in the 1960s and 1970s of the importance of inelastic structural response to large earthquakes, the research community became increasingly involved in attempts to quantify the inelastic deformation capacity of structural components. The seismic design philosophy of most current building codes allows most structures to undergo inelastic deformations in the event of strong earthquake ground motions. As a result, the designed lateral strength can be lower than that required to maintain the structure in the elastic range. The evolution of seismic codes and practices in US and Mexico are briefly described and critically analyzed in the following sections. In some cases, the notation has also been modified (from the original codes) in order to make comparisons among them.

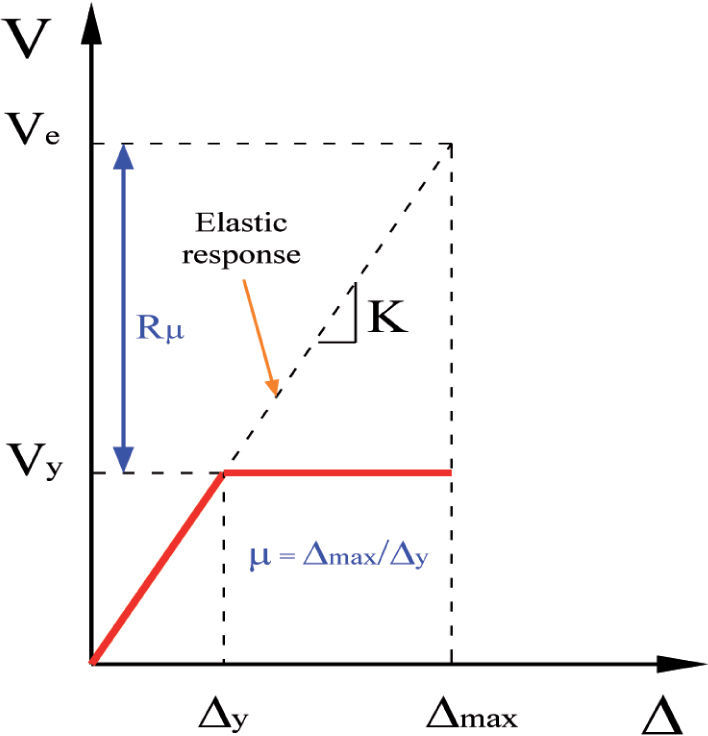
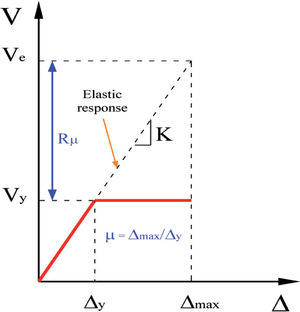
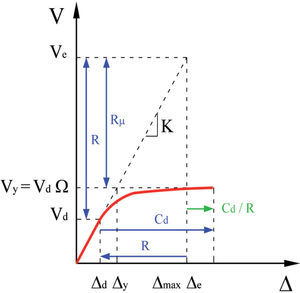
Strength reduction factor due to nonlinear hysteretic behavior

In the linearly elastic-perfectly plastic curve in Figure 1, the displacement ductility ratio μ is defined as the ratio of maximum relative displacement to its yield displacement (μ = Δ_max/Δ_y). The displacement is commonly expressed in terms of story drift. In addition, it is customary to divide the story drift by the story height and express it as a percentage of this height. An adequate design is accomplished when a structure is dimensioned and detailed in such a way that the local (story and member) ductility demands are smaller than their corresponding capacities. Thus, during the preliminary design of a structure, there is a need to estimate the lateral strength (lateral load capacity) of the structure that is required in order to limit the global (structure) displacement ductility demand to a certain pre-determined value which results in the adequate control of local ductility demands (Miranda and Bertero, 1994).

Figure 1.

Idealized structural response: equal displacement approximation

Since a properly designed structure usually can provide a certain amount of ductility, the structure has capacity to dissipate hysteretic energy. Because of this energy dissipation, the structure can be designed economically and thus, the elastic design force V_e can be reduced to a yield strength level V_y, by the factor R_μ (V_y = V_e/R_μ) (Moroni et al., 1996), and the corresponding maximum deformation demand is Δ_max (Figure 1). In a linearly elastic-perfectly plastic model (Figure 1), the yield strength level refers to the structural collapse level (D = Δ_max), not to the level of first significant yielding. For a correct evaluation of the reduction factor R_μ, it is necessary to guarantee that the structure is able to accommodate the maximum displacement demand Δ_max in Figure 1, preventing collapse.

In general, for structures responding inelastically during earthquake ground motions, inelastic deformations increase as the lateral yielding strength of the structures decreases, or as the design reduction factor increases. For design purposes, R_μ corresponds to the maximum reduction in strength that is consistent with limiting the displacement ductility ratio demand to the pre-determined target ductility μi, in a structure that will have strength equal to the designed lateral strength (Miranda and Bertero, 1994). A 5% equivalent viscous damping ratio is usually considered in the computation of the reduction factor R_μ (Uang, 1989).

Several studies (i.e., Miranda and Bertero,1994; Ordaz and Pérez, 1998; Avilés and Pérez, 2005) agree that for a given ground motion, the reduction factor R_μ is primarily influenced not only by the level of inelastic deformation, but also by the natural period of the structure T, the soil conditions at the site, and the soil-structure interaction. Since the strength reduction factor R_μ is a function of the ground motion for a given system undergoing a ductility demand μi, the reduction will be different for different ground motions. Soil conditions at site can have an important effect on R_μ, particularly for very soft soils. Other factors that may affect the reduction factor R_μ, but to a much lesser degree, are the damping and the type of hysteretic behavior of the structure (under the assumption that there is no significant strength deterioration).

Strength amplification factor due to overstrength

Real structures are usually much stronger than required by design. This extra strength, when recognized, can be used to reduce the ductility demands. For instance, if the overstrength were so large that the response was elastic, the ductility demand would be less than 1.0 (FEMA-451, 2006). The role of overstrength is even more significant for buildings with short periods, because ductility is ineffective in reducing the required elastic strength in this period range. In addition, the seismic overstrength factor will also be higher if the building is located in low seismic zones, because gravity and wind loads are more likely to govern the design (Uang, 1989). Note that overstrength did not enter into the previous discussion because the structural response was considered an idealized system.

The additional strength reduction is due to the fact that lateral strength of a structure is usually higher and, in some cases, much higher that the nominal strength capacity of the structure. We can divide this reduction to take into account the additional strength from the nominal strength to the formation of the first plastic hinge and the additional strength from this point to the formation of a mechanism (Miranda, 1997). The system's overstrength factor is defined as the product of the following independent overstrength factors (Uang, 1989):

• (i)

  development of sequential plastic hinges in redundant structures,

• (ii)

  material strengths higher than those specified in the design,

• (iii)

  strength reduction factors,

• (iv)

  specified sections and reinforcement patterns greater than those required in design,

• (v)

  nonstructural elements, and

• (vi)

  variation of lateral forces (Varela et al., 2004).

It is not uncommon for the true strength of a structure to be two or three times the design strength (FEMA-451, 2006).

One important source of overstrength in many structures is the design procedure itself. The structure must be analyzed using forces reduced with a factor that depends on the structure's global ductility capacity rather than the displacement itself. However, the global behavior of the structure is not, in general, linearly elastic- perfectly plastic; it would be so if all structural members had linearly elastic-perfectly plastic behavior and they yielded at the same time. This consideration implies that, in many cases, the real strength is higher than its nominal strength (Ordaz and Meli, 2004).

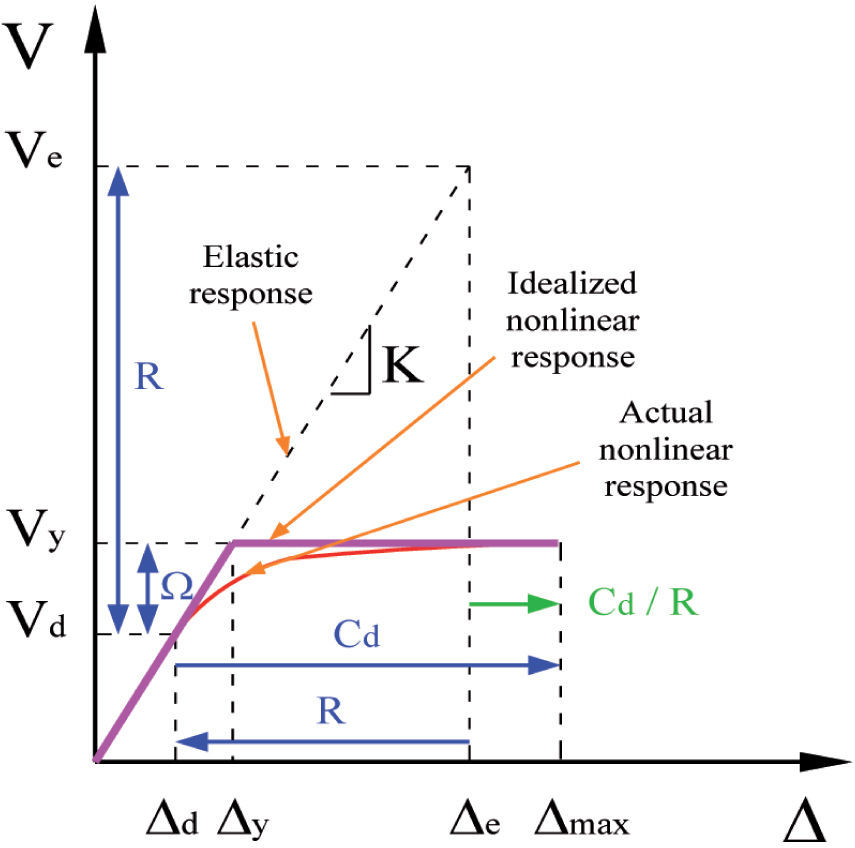
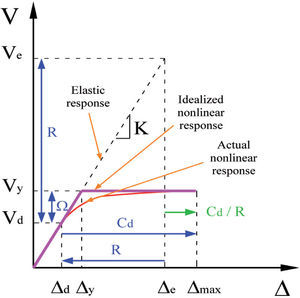
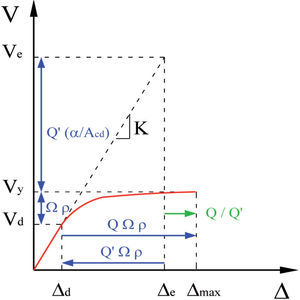
Consider, for example, the typical global structural response in Figure 2. The design strength of a structure, Vd, is equal to the resistance at “first significant yield”. If the hinging region has adequate ductility, it can sustain increased plastic rotations without loss of strength. The first hinge to form is continuing to rotate inelastically but has not reached its rotational capacity. As additional load is applied to the structure, the other potential hinging regions of the structure will attract additional moment until they begin to yield (FEMA 451, 2006). Even more load can be applied as additional hinges form. However, the first hinges to form are near their rotational capacity and may begin to loose strength. Hence, the backbone curve begins to flatten. At the ultimate stage, the structure has finally reached its strength and deformation capacity. The additional strength beyond the design strength is called the overstrength and the total strength of the system is referred to as the actual maximum strength, V_y.

Figure 2.

General structural response

Figure 2 shows that the overstrength factor Ω can be defined as the ratio between V_y and V_d (Ω = V_y/V_d), the latter being the required strength prescribed by codes that use a strength design approach (Moroni et al., 1996). Existence of structural overstrength has been explicitly recognized in some building codes in the world. Although the effect of overstrength should be accounted for when evaluating member's strength (increasing the strength), because of the limitations when using advanced non-linear analysis techniques by practicing engineers, it is necessary to continue applying the effect of overstrength as a reduction factor to the loads instead of an amplification factor to the strength (Ordaz and Meli, 2004). However, the use of force demands lower than those developed in the structure can be unsafe for designing of the foundation.

Strength modification factors in US building codes

In US building codes and provisions, such as IBC-09, NEHRP-03 and ASCE 7-10, the factor used to calculate the reduced design base shear and design seismic forces of a structural system, is called response modification factor R. This factor R is defined as the ratio between the base shear developed in the structure if it were to remain in the elastic range and the minimum required base shear to resist the seismic action and to accommodate nonlinear displacements without any risk to its stability (Moroni et al., 1996). From Figure 3, the total strength modification factor R can be considered as the product of the ductility reduction factor R_μ and the structural overstrength factor Ω (Varela et al., 2004).

Figure 3.

Procedure in US building codes

Most of investigations reviewed by Miranda and Bertero (1994) recommended the use of period-dependent strength reduction factors. In addition, Uang (1989) has established basic formulas for evaluating R factor from the global structure response characterized by the relationship between the base shear ratio and the story drift. It is noteworthy that strength reduction factor R prescribed by current US codes are independent of period of vibration, which is incorrect and thus, their use is not recommended (Miranda, 2007; Tena et al., 2009).

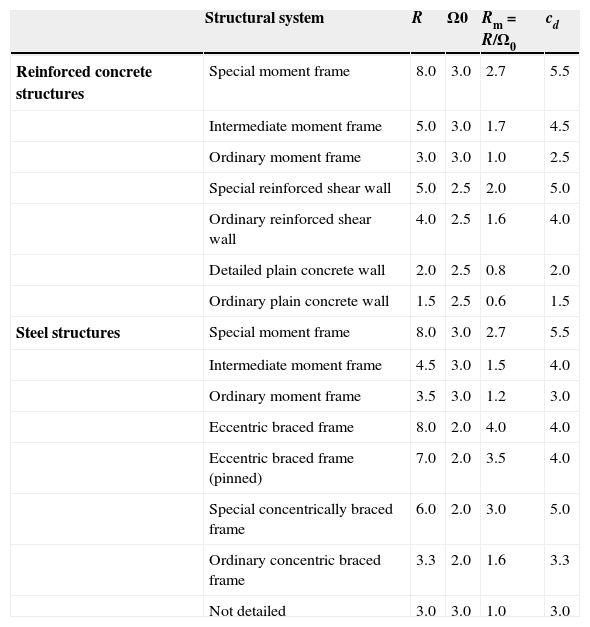
Even though the equations presented by Miranda and Bertero (1994) seem reasonable and may be incorporated in future US seismic codes, the reality is that today (2012) single values of the R factors are still proposed in those seismic codes to design different structural systems (Varela et al., 2004). For instance, current seismic design provisions in US do not require designers to quantify R and Ω factors. Table 12.2-1 of ASCE 7-10 provides R factors for a large number of structural systems. Table 1 shows the factors for a few selected concrete and steel systems.

Table 1.

Design factors specified by ASCE 7-10 for building structures

	Structural system	R	Ω0	Rm = R/Ω0	cd
Reinforced concrete structures	Special moment frame	8.0	3.0	2.7	5.5
	Intermediate moment frame	5.0	3.0	1.7	4.5
	Ordinary moment frame	3.0	3.0	1.0	2.5
	Special reinforced shear wall	5.0	2.5	2.0	5.0
	Ordinary reinforced shear wall	4.0	2.5	1.6	4.0
	Detailed plain concrete wall	2.0	2.5	0.8	2.0
	Ordinary plain concrete wall	1.5	2.5	0.6	1.5
Steel structures	Special moment frame	8.0	3.0	2.7	5.5
	Intermediate moment frame	4.5	3.0	1.5	4.0
	Ordinary moment frame	3.5	3.0	1.2	3.0
	Eccentric braced frame	8.0	2.0	4.0	4.0
	Eccentric braced frame (pinned)	7.0	2.0	3.5	4.0
	Special concentrically braced frame	6.0	2.0	3.0	5.0
	Ordinary concentric braced frame	3.3	2.0	1.6	3.3
	Not detailed	3.0	3.0	1.0	3.0

When designing the elements, the ACI 318-11 Building Code mainly relies on conventional force-based limit states (i.e. ultimate limit state) and on a serviceability limit state, but they do not include an explicit relationship between displacement demand and capacity. In an attempt to make US building codes conceptually transparent, new edition of the ACI 318-11 specifies explicitly an overstrength factor Ω₀. This factor is related to the seismic-force-resisting system used for the structure, and is used for the design of certain fragile elements that are incapable to dissipate energy in the non linear range, such as certain wall piers, anchors and collector elements, or where greater concerns about shear failure remain. For designing such elements, the design shear force need not exceed Ω₀ times the factored shear determined by analysis of the structure for earthquake effects. The amplification factor Ω₀ ranges between 1.5 and 3.0, depending on the type of seismic system. In this approach, the design shear force is computed as Ω₀ times the shear induced under design displacements.

Strength modification factors in Mexican codes

The Mexico City Building Code for seismic design of buildings NTC-S-04 has been a model code in Mexico for the drafting of most of the Mexican codes, which, by law, is of the municipal competence (Ordaz and Meli, 2004). Agencies of the Federal Government have issued standards and manuals, such as the Manual of Civil Structures MDOC-08. This manual is a very comprehensive code that specifically addresses the design of several structural systems (buildings, bridges, dams, power stations, industrial facilities, etc.) to such hazards as earthquakes and winds. This manual is another model design code in Mexico (Tena et al., 2009).

Mexico City building code (NTC-S-04) includes two procedures for seismic design of buildings: main body and appendix A. In the main body of NTC-S-04 and in the previous version of MDOC, spectra are not related to elastic seismic demands. In these codes, the elastic design spectrum is obtained by dividing the spectral ordinates by a somewhat obscure reductive seismic force factor that accounted for everything (ductility, redundancy, overstrength, etc.) (Tena et al., 2009). Hence, the overstrength parameter is implicitly included in the spectrum, so that it is an invisible parameter for the engineer. Thus, their use is not recommended. Instead, spectra specified by appendix A of NTC-S-04 or by MDOC-08 should be used (Miranda, 2007; Tena et al., 2009).

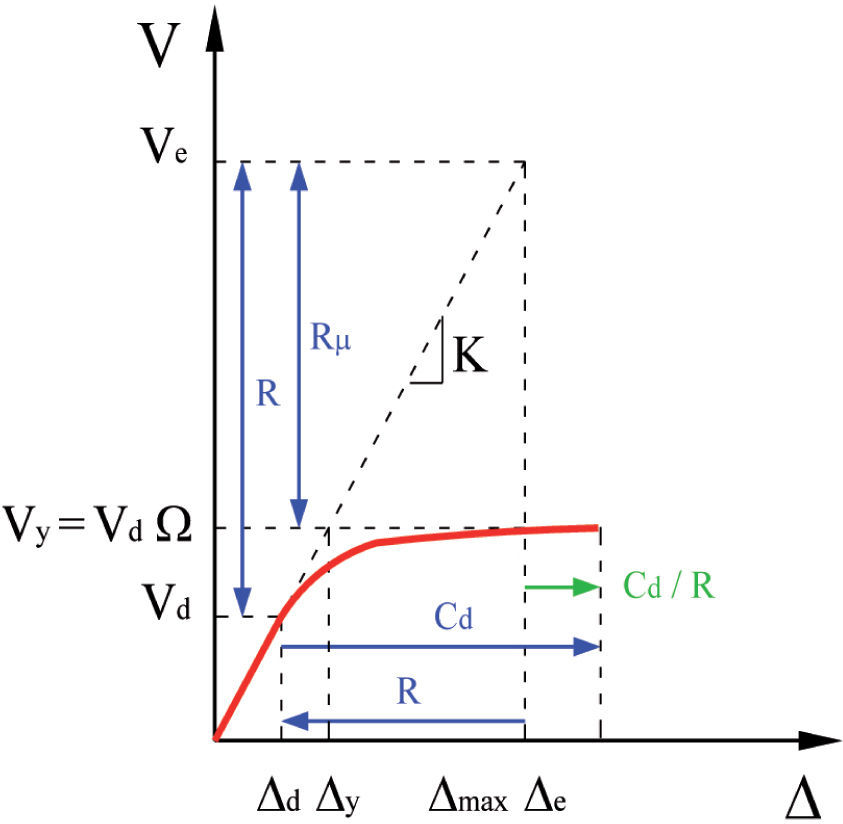
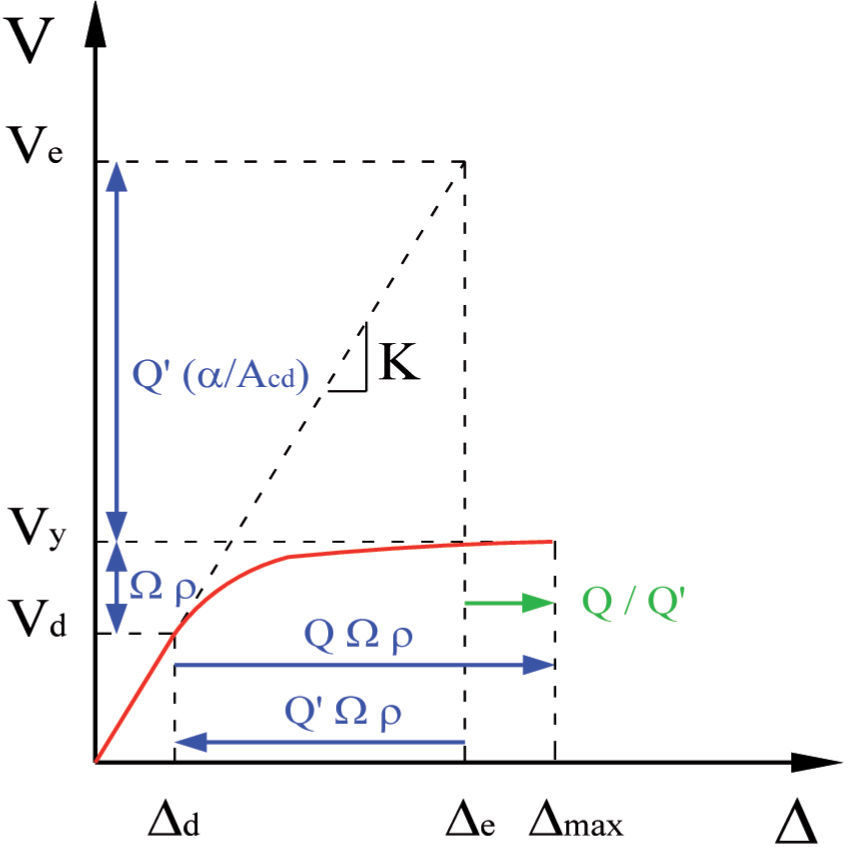
For clarity in the design process, there is an important conceptual adjustment in the reduction of elastic response parameters for design in appendix A of NTCS- 04 and in MDOC-08. In these codes, design spectra are site specific and values of overstrength parameter are explicitly specified, because the design spectra are not reduced by an overstrength parameter Ω (Alcocer and Castaño, 2008). In fact, the proposal for the Ω factor in MDOC-08 is an improved version of the one presented in appendix A of NTC-S-04. In appendix A of NTC-S-04, Ω is independent of the structural system. This conceptual shortcoming is fixed in MDOC-08, where it is also recognized that the overstrength that a structure can develop under earthquake loading strongly depends on the structural system, as it is done in other modern seismic codes, such as ASCE 7-10 and IBC-09 (Tena et al., 2009). The general procedure of seismic design prescribed by MDOC-08 and by appendix A is shown in Figure 4, where Q’ is a seismic reduction force factor that accounts primarily for ductility (deformation) capacity, Ω is an over-strength factor that depends on the structural period and/or the structural system.

Figure 4.

Procedure in modern Mexican codes

In the MDOC-08 code and in appendix A of NTCS- 04, the seismic force reduction factor Q’ stands only for the approximate ductility deformation capacity of the selected structural system, given in terms of the seismic response modification factor Q. The proposed Q’ factor is not constant and depends on the structural period T and the site period. In fact, Q’ is the ratio between the minimum strength required to limit a structural system to an elastic response and the strength required for a structural system to limit its ductility capacity to a given Q value (Tena, 2009). The seismic response modification factor Q of Mexican codes account primarily for the deformation capacity of the structural system. Therefore, it is valid to compare the Q factors used in the design of the building with respect to the global ductility demand. The values of Q established by all modern Mexican codes are 1, 1.5, 2, 3 and 4, and they depend on the selected structural system (Tena et al., 2009). Hence, parameters Q’ and Q prescribed by MDOC-08 code and by appendix A of NTC-S-04 are related to R_μ and μ, respectively.

The 1976 Mexico City Building Code was the first earthquake-resistant code to prescribe explicitly period- dependent strength reduction factors, which account for smaller reductions in the short period range (Rosenblueth, 1979). That code included a bilinear R_μ spectrum as a function of the soil condition as reflected in the micro-zonation of the city. In effect, factor R_μ was linearly interpolated between 1.0 and the displacement ductility ratio μ (termed as Q in that code) for stiff structures falling in the linear ascending branch of the design spectrum. For all other periods, the force reduction factor was μ (Alcocer and Castaño, 2008). The bilinear R_μ spectrum, similar to that used in the Mexico City Code, has also been recommended in the Argentine Building Code (Sonzogni et al., 1984). Then, bilinear expressions for R_μ,were suggested (Tso and Naumoski, 1991) to improve the period-independent reduction factors of the 1990 edition of the National Building Code of Canada. Period-dependent R_μ factors have been proposed (Uang, 1989) for new versions of the Chilean seismic code.

Parameters ρ, A_cd and α are included in MDOC-08 only. The introduction of a redundancy factor ρ in MDOC-08 is a new concept for Mexican seismic codes. Factor ρ basically corrects the previous assessment of the overstrength factor Ω, as most of the available studies where Ω has been computed using 2-D models with different degrees of redundancy. This factor recognizes directly that structural systems are able to develop more strength and increase their deformation capacity as they become more redundant. In addition, this factor takes into account unfavorable performances of weakly- redundant structures in strong earthquakes occurred worldwide in the last 35 years. This fact is well-known by the structural engineering community worldwide. However, it seems some seismic codes have come up short before, by not recognizing that a more redundant structural system under lateral loading should be allowed to be designed with higher reductions and that weakly-redundant systems should be penalized and be designed with smaller reductions. It is also worth noting that the value of ρ may vary in each main orthogonal direction (Tena-Colunga, 2009).

Factor ρ varies between 0.8 and 1.25. The value depends on number of bays and lines of defense in the direction of analysis. One-bay framed buildings are now penalized with ρ = 0.8, because they are weaklyredundant, and their observed performance during strong earthquakes have been poor. It is hoped that this approach would help structural engineers to promote the use of more redundant structural systems in zones of high earthquake hazard and to limit or avoid the use of weakly-redundant structures (Tena et al., 2009).

The introduction of a correction factor A_cd to account for stiffness and/or strength degradation under cyclic loading of reinforced concrete (RC) structural systems located in soft soils, is also a new concept for the seismic codes in Mexico. It has been shown that low-cycle fatigue is very important in the seismic behavior of stiffness and strength degrading systems such as masonry and RC structures (Carrillo and Alcocer, 2013), located in soft soils where large durations of the earthquake motions are observed, such as in the lake bed zone of Mexico City (Tena et al., 2009).

As in previous versions, MDCO-08 defines 11 conditions of regularity for elevation and plan analysis that buildings must satisfy to directly use the reductive seismic force factor Q’. If a building structure satisfies all 11 conditions of structural regularity, it is defined as a regular structure, so Q’ remains unchanged. However, if at least one conditions of structural regularity is not satisfied, the building is defined as irregular structure, and then Q’ is reduced for design purposes using the corrective reduction factor a that varies between 1.0 (regular structure) and 0.7, and depends on the degree of irregularity according to MDOC-08. For design purposes, irregular buildings must be designed for higher forces but required to comply with the lateral story drift criteria specified for regular buildings (Tena et al., 2009).

Deflection amplification factor

The requirement of a strength level is insufficient as the only parameter for seismic design. Therefore, it is necessary to combine it with an adequate criterion to estimate the maximum displacements that a structure will have to accommodate during the action of a severe earthquake. The most common assumption is the equal-displacement approximation. This approximation implies that “the displacement of an inelastic system, with stiffness K and strength V_y, subjected to a particular ground motion, is approximately equal to the displacement of the same system responding elastically” (FEMA-451, 2006). Figure 1 shows that the equal displacement approximation of seismic response implies that μ = R_μ (Priestley, 2000). The equal-displacement approximation implies that peak displacements may be related to peak accelerations assuming sinusoidal response equations, which is reasonable approximation for medium period structures (Priestley et al., 2007) of or for structures whose period of vibration is distant from the site period (Ordaz and Pérez, 1998). An apparently conservative assumption (with regard to displacements) is shown in Figure 1. The basis assumption is that the displacement demand is relatively insensitive to system yield strength V_y, because the value of Δ_max will be the same for any value of V_y (FEMA-451, 2006).

For design purposes, it may be assumed that inelastic displacements are equal to the displacement that would occur during an elastic response. The required force levels under inelastic response are much less than the force levels required for elastic response. The equal displacement concept allows structural engineers to use elastic analysis to predict inelastic displacements, that is, the displacements from the reduced-force elastic analysis must be multiplied by the ductility ratio to produce the true “inelastic” displacements.

It has been shown that the equal displacement approximation is non-conservative for short period structures and therefore, the equal energy approximation should be applied for these structures. Thus, in the first region of the spectrum, R_μ increases linearly with increasing period from R_μ = 1 to a value which is near to the value of the ductility ratio μ (FEMA-451, 2006). ASCE 7-10 effectively reduces the acceleration spectrum by a strength reduction factor at all period ranges. However, the ASCE 7-10 provisions allows no reduction to the peak ground acceleration in the very short period region (acceleration spectrum with a constant plateau that extends from T = 0 s) so this partially compensates for “error” in equal displacement assumption at short period values (FEMA-451, 2006). In the medium region of the spectrum, the reduction factor R_μ is only slightly dependent on the period of vibration T. For very long periods, the R_μ factor maintains a constant value equal to the prescribed ductility m, and thus, the equal displacement approximation can be applied (R_μ = μ) (FEMA-451, 2006). Simplified expressions to obtain analytical estimates of the strength reduction factors have been proposed. According to Newmark and Hall (1982), for structures with long, medium and short periods, R_μ = μ, R_μ = (2μ–1)0.5, and R_μ = 1, respectively. These expressions indicate that R_μ/μ is not greater than 1. Moreover, this ratio is significantly less than 1 for structures with medium and short periods.

Displacement amplification

Most codes recognize that a structure's actual deformation may be several times the elastics displacements estimated from the action on the prescribed seismic design forces (Moroni et al., 1996). In order to estimate maximum expected displacements of structure including effects of inelastic deformations Δ_max, displacements from elastic analysis, with reduced forces Δ_d, are amplified by the displacement amplification factor C_d. This factor can also be derived from Figure 2 as follows (Uang, 1989):

From these derivations, it is observed that Cd factors a function of the structural overstrength factor, the structural ductility ratio, and the damping ratio; the effect of the damping ratio is generally included in the ductility reduction factor R_μ.

Displacement amplification factor in US building codes

In US building codes, the displacement modification factor Cd is used to compute the expected maximum inelastic displacement from the elastic displacement induced by the seismic design forces. Based on the equal displacement approximation, the inelastic displacement demand is the same as the elastic displacement demand. The approach of US seismic-codes for displacements is to determine design forces generated by V_d. Then, the reduced design strength is distributed vertically and horizontally through the structure in order to determine members’ forces, and compute displacements using linear elastic analysis. The analysis domain represents the response of the linear elastic system as analyzed with the reduced forces.

Clearly in Figure 3, the displacement Δ_d predicted by this analysis would be too low. US seismic design codes compensate through the use of the C_d factor. To correct for the too-low displacement predicted by the reduced force elastic analysis, the “computed design displacement” Δ_d should be multiplied by the factor C_d to obtain estimate of true maximum inelastic response. This factor is always less than the R factor because R contains ingredients other than pure ductility (FEMA- 451, 2006). Both factors R and C_d prescribed in US seismic codes are primarily based on the observation of the performance of different structural systems in the past strong earthquakes, on consensus of engineering judgment, on technical justification, and on tradition (NEHRP- 03). Similarly to R and Ω factors, Table 1 of ASCE 7-10 provides the C_d factor (see Table 1). Table 1 of ASCE 7-10 also provides the allowable story drift to be compared with true maximum inelastic drift. Table 2 shows that allowable drift ratio depends on risk category (importance) of the building.

Table 2.

Story drift limits specified by ASCE 7-10

Structural system	Drift limit Risk category
	I or II	III	IV
Structures, other than masonry wall structures, 4 stories or less above the base with partitions that have been designed to accommodate the story drifts	2.5%	2.0%	1.5%
Masonry cantilever shear wall structures	1.0%	1.0%	1.0%
Other masonry shear wall structures	0.7%	0.7%	0.7%
All other structures	2.0%	1.5%	1.0%

Displacement amplification factor in Mexican codes

In the main body of NTC-S-04 and in the previous version of MDOC, inelastic displacement demands generally did not lead to suitable estimates because the values of the ratio Q/Q’ (Figure 4) are not adequate (Miranda, 2007; Tena et al., 2009). One more drawback of some building codes for seismic design is that lateral displacements of buildings are evaluated in a deficient way. For instance, allowable story drift ratios prescribed in the main body of the NTC-S-04 are equal to 0.6% if non-structural elements are not separated from the structure, and 1.2% if non-structural elements are isolated. Actually, these values are not related to the displacements under the design earthquake, because the expected drift values will be significantly higher. This fact results from using a design spectrum that is not adequate for calculating displacements under the ultimate level (Ordaz and Meli, 2004).

In the appendix A of NTC-S-04 and in MDOC-08, actual lateral displacements are computed multiplying those obtained under reduced loads by certain factors (Figure 4). The criterion for controlling the lateral displacements is improved, because these codes propose revision of displacements for two limit states: serviceability and collapse prevention under maximum credible earthquake. The review of drift limits for the service earthquake is a novelty in MDOC-08. It was proposed to have a clearly specified service limit state, to limit displacements for earthquakes that occur much more frequently than the collapse event. Damage to non-structural members should not be tolerated for an earthquake like this one. For the service limit state, buildings should remain elastic, so the damage control of non-structural members is achieved by comparing the calculated elastic displacements with allowable drift ratios equal to 0.2% if non-structural elements are connected to the structural system, or 0.4% if non-structural elements are properly separated from the structural system (Ordaz and Meli, 2004).

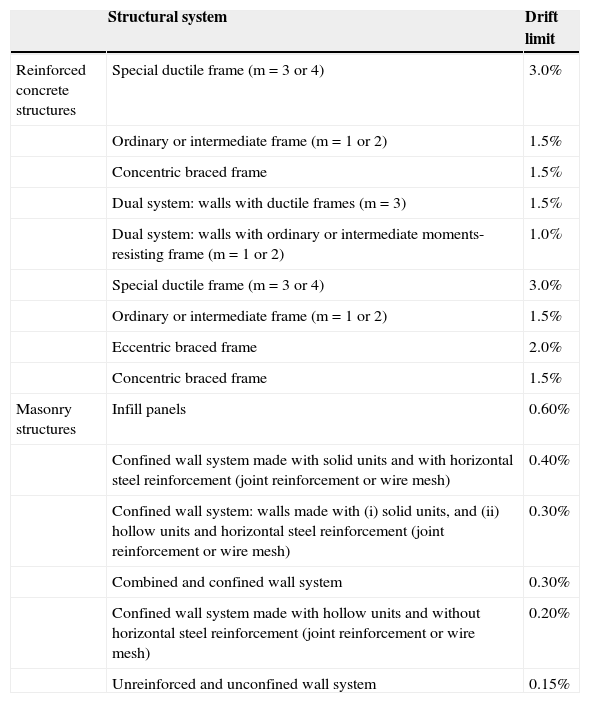
For the collapse prevention limit state, story drifts are commonly computed by multiplying the reduced displacements from linear analysis for the reduced spectrum Δ_d by QWr. In contrast with the previous versions of MDOC or in the main body of NTC-S-04, where the story drift limits are not defined in terms of the structural system, the story drift limits defined in MDOC-08 for collapse prevention are function of the structural system. The calculated displacements must be compared with allowable values (drift limits) given in Table 3 for diverse structural systems. Table 3 shows that these values are significantly higher than those specified in the main body of NTC-S-04, because the design spectrum is specified in a rational way (Ordaz and Meli, 2004). In addition, note that proposed drift limits mostly coincide with whose recommended in US codes (ASCE 7-10, IBC-09, see Table 2).

Table 3.

Story drift limits for collapse prevention specified by MDOC-08 for RC structures

	Structural system	Drift limit
Reinforced concrete structures	Special ductile frame (m = 3 or 4)	3.0%
	Ordinary or intermediate frame (m = 1 or 2)	1.5%
	Concentric braced frame	1.5%
	Dual system: walls with ductile frames (m = 3)	1.5%
	Dual system: walls with ordinary or intermediate moments-resisting frame (m = 1 or 2)	1.0%
	Special ductile frame (m = 3 or 4)	3.0%
	Ordinary or intermediate frame (m = 1 or 2)	1.5%
	Eccentric braced frame	2.0%
	Concentric braced frame	1.5%
Masonry structures	Infill panels	0.60%
	Confined wall system made with solid units and with horizontal steel reinforcement (joint reinforcement or wire mesh)	0.40%
	Confined wall system: walls made with (i) solid units, and (ii) hollow units and horizontal steel reinforcement (joint reinforcement or wire mesh)	0.30%
	Combined and confined wall system	0.30%
	Confined wall system made with hollow units and without horizontal steel reinforcement (joint reinforcement or wire mesh)	0.20%
	Unreinforced and unconfined wall system	0.15%

Final remarks

Modern design procedures give more emphasis to the deformation capacity of the system. For example, performance- based seismic design requires the explicit consideration of lateral displacement as a performance indicator, besides verifying the structural design through an essentially force-based procedure (Priestley, 2000). There is currently an intensive re-examination of the approaches for seismic design of structures. This paper has summarized and discussed the approach in the seismic design provisions for buildings in US and Mexico. The following conclusions can be drawn from this study:

• –

  In the main body of NTC-S-04 and in the previous version of MDOC, the overstrength factor is implicitly included in the spectrum, so that it is an invisible parameter for the engineer. In addition, inelastic displacement demands generally did not lead to suitable estimates because the ratio Q/Q’ (Figure 4) is not adequate. Thus, their use is not recommended. Instead, spectra specified by appendix A of NTC-S-04 or by MDOC-08 should be used (Miranda, 2007; Tena et al., 2009).

• –

  Strength modification and displacement amplification factors, which to date are empirical in nature, are based on general consensus of engineering judgment, observed structural performance in the past earthquakes, and so on (NHRP-03). The only way to rationalize these factors is to quantify the overstrength and structural ductility ratios by analytical studies and experimental testing (Uang, 1989). Rational strength modification and displacement amplification factors based on ductility, period and soil conditions, together with estimates of the overstrength of the structure and the relationship between global and local ductility demands (Varela et al., 2004), are now used to establish more rational and transparent seismic design approaches in Mexico. For instance, Mexican seismic codes are moving towards design procedures where the overstrength is directly taken on account to reduce the elastic design spectra. This is the philosophy in the procedure outlined in appendix A of NTC-S-04 and in the new guidelines MDOC- 08 (Tena et al., 2009).

• –

  It is also apparent that the design codes are often incorrectly understood or misinterpreted, and are often not complied with by lay practitioners. The lack of building code compliance shall not be regarded merely as a legal issue to be addressed only through enforcement actions. To attain a reasonable safety level, it is essential to have consistency between the regulations, the level of expertise of most design and construction professionals, and local materials and construction systems (Alcocer and Castaño, 2008).

• –

  Given that the level of expertise and quality of practice of design and construction professionals in Mexico is quite diverse, one way to reach this goal is to implements codes with procedure and requirements of different levels of complexity. The most complex and comprehensive rules should be aimed at large, important structures; simple yet conservative approaches would be followed for most common structures limited to certain size, geometry and complexity (Ordaz and Meli, 2004). This is the case of the recently released ACI 314-11 Guideto simplified design for reinforced concrete buildings of limited size and height could be also included. Finally, for non-engineered construction guidelines, other educational sources are needed in lieu of merely enforcing codes.