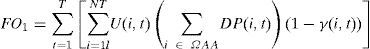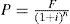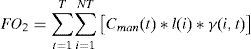Una de las principales causas de interrupción en el servicio de suministro de energía eléctrica es el contacto de la vegetación con las redes aéreas de distribución. En este artículo se presentan dos modelos matemáticos multiobjetivo que proponen minimizar el impacto negativo de la vegetación sobre la calidad de la red eléctrica, minimizando a su vez, el costo de poda de la vegetación. En el primer modelo se minimiza el nivel de energía no servida debido a fallas por vegetación, mientras que en el segundo se minimiza el porcentaje promedio de violación a la zona de seguridad entre la vegetación y las redes aéreas de distribución. En ambos modelos, la segunda función objetivo consiste en minimizar el costo de mantenimiento de la vegetación, considerando restricciones asociadas a la disponibilidad de los equipos, la confiabilidad en el servicio de energía eléctrica y el número máximo de podas en un tramo de red durante el periodo de planeación de mantenimiento de la vegetación. El resultado es la programación de las actividades de poda durante un periodo de planeación de un año. El algoritmo genético elitista de ordenamiento no dominado (NSGA-II) es la técnica de optimización multiobjetivo que se utiliza para resolver este problema en un sistema de prueba.
One of the major causes for the interruption of power service supply is the contact between vegetation and the power distribution lines. In this paper, two multiobjective mathematical models are proposed to minimize the vegetation negative impact on the electricity network quality, minimizing in turn, the cost of the vegetation pruning. In the first mathematical model, the level of energy not served due the failures from vegetation is minimized and in the second one the average percentage of violation into the safe zone between the vegetation and the overhead power distribution systems is minimized. In both models, the second objective function is to minimize the cost of maintenance of vegetation, considering restrictions associated with equipment availability, reliability in the electrical service and maximum number of prunings on a network segment for the period of vegetation maintenance planning. The scheduling result is pruning activities for a planning period of one year. The elitist non-dominated sorting genetic algorithm (NSGA-II) is the multi-objective optimization technique used to solve this problem on a test system.
Los sistemas de distribución tienen como finalidad entregar energía a los usuarios con niveles de tensión adecuados para el consumo. Generalmente estas redes se diseñan en forma aérea, debido a que presentan un menor costo de inversión y operación, en comparación con las redes subterráneas. Sin embargo, la exposición a factores climáticos y el contacto con animales y el medio ambiente hacen que los índices de confiabilidad de las redes aéreas sean menores. Uno de los aspectos ambientales que afectan la operación de los sistemas de distribución aéreos son el contacto de la vegetación con líneas energizadas, lo cual puede ocasionar cortocircuitos y en algunos casos rompimiento de los conductores, teniendo como consecuencia el accionamiento de los sistemas de protección que conllevan a interrupciones en el servicio de energía eléctrica (Goodfellow, 2005).
Adicionalmente, la vegetación urbana implica otros problemas, entre los que se encuentran: daños en las redes de distribución de energía subterránea, calles, aceras y sistemas de tubería de acueducto y alcantarillado debido a la expansión de las raíces en el subsuelo, inundación de los canales de desagüe por taponamiento ocasionado por las hojas que caen de los árboles y daños en la redes aéreas de teléfono y televisión (Fernandes y Ferreira, 2002).
A pesar de que el planeamiento de la arborización y de los sistemas de energía eléctrica tradicionalmente se han desarrollado de forma independiente, en los últimos años se ha dado mayor importancia a la preservación del medio ambiente y el incremento de la arborización urbana, por lo que las empresas de distribución tienen que enfrentar nuevas dificultades, entre las que se encuentran conservar un nivel de confiabilidad de la red eléctrica dentro de los parámetros exigidos por los usuarios y entes reguladores, así como realizar mantenimientos de la vegetación sin desmejorar la integridad física de las especies (Costa y Rodrigues, 2006).
El mantenimiento de la vegetación que crece bajo las redes aéreas de distribución generalmente es responsabilidad de la electrificadora encargada de la operación del sistema. En algunos casos, un organismo de carácter gubernamental es el que desarrolla las actividades de poda de vegetación cercana a las líneas de energía eléctrica. El procedimiento más común es realizar una inspección visual de las especies de vegetación que rodean las líneas energizadas y después llevar a cabo la intervención teniendo en consideración las técnicas de poda que evitan una pérdida total en la flora urbana (Nardez, 2010). Estas estrategias tradicionalmente han dado buenos resultados al impactar positivamente el nivel de energía no servida por el sistema. Sin embargo, como una metodología alternativa que puede proporcionar resultados complementarios a los encontrados de forma tradicional, en este artículo se propone la utilización de modelos de programación matemática, los cuales contienen diferentes características y parámetros involucrados en el problema de mantenimiento de la vegetación.
A pesar de la importancia que tiene para las administraciones locales y electrificadoras enfrentar esta problemática, son pocos los trabajos que se encuentran en revistas científicas y literatura especializada, relacionados con el desarrollo e implementación de herramientas matemáticas que permitan auxiliar el mantenimiento de la vegetación bajo redes aéreas de distribución de energía eléctrica.
Con el fin de realizar un cronograma de actividades de poda de la vegetación, Kuntz et al. (2002) proponen una metodología basada en redes neuronales artificiales que tienen como datos de entrada un conjunto de variables asociadas con el ambiente externo (cantidad de lluvia, velocidad del viento, densidad de los árboles y tiempo desde la última poda) y como datos de salida las tasas de falla por vegetación. Goodfellow (2005) plantea diferentes criterios de evaluación de riesgo que pueden aplicarse al trabajo de mantenimiento de la vegetación en sistemas de distribución. Rees (2005) presenta diversos programas de mantenimiento de la vegetación, los cuales se han dirigido a soluciones empíricas que involucran personal capacitado en áreas de electricidad y forestación con resultados que mejoran notablemente los índices de confiabilidad. Costa y Rodrigues (2006) ilustran un caso de estudio en el cual se realizan podas periódicas a la arborización de un sector, con el fin de minimizar las interferencias con la red eléctrica y preservar la continuidad del servicio. Arias et al. (2012) presentan una metodología para obtener el plan de mantenimiento de la vegetación en un periodo de un año. Para solucionar el problema se emplea un algoritmo genético de Chu-Beasley.
En este trabajo, el problema del mantenimiento óptimo de la vegetación bajo redes aéreas de distribución se aborda empleando optimización multiobjetivo, para lo cual se proponen dos nuevos modelos matemáticos. Ambos modelos consideran dos funciones objetivo: la primera función emplea criterios económicos y la segunda índices de sensibilidad. El primer modelo matemático planteado minimiza los costos del plan de mantenimiento para un periodo determinado y el nivel de energía no servida (NENS), el cual considera tasas de falla por vegetación como índices de sensibilidad. El segundo modelo minimiza los costos del plan de mantenimiento y el porcentaje promedio de violación a la zona de seguridad, la cual se define como la distancia mínima entre la vegetación y el conductor; en este caso, los índices de sensibilidad empleados son las tasas de crecimiento de la vegetación.
La importancia que tiene emplear los dos modelos matemáticos propuestos es que están enfocados a electrificadoras con características diferentes, es decir, el primero puede aplicarse para empresas que tienen datos históricos de tasas de fallas de tramos de red del sistema y el segundo está orientado a empresas que poseen un inventario de especies e índices de crecimiento de la vegetación presente en el sistema de distribución.
El conjunto de restricciones en ambos modelos corresponde a la disponibilidad de los equipos, confiabilidad en el sistema y cantidad máxima de podas per-] mitidas en un periodo determinado. Para solucionar los modelos matemáticos se emplea un algoritmo NSGA-II, donde el resultado está definido por un frente de Pareto, en el cual se establecen los cronogramas de actividades de mantenimiento de la vegetación durante el periodo de planeamiento.
El artículo está organizado de la siguiente forma. En la siguiente sección se presenta la formulación del problema, en la cual se describen los dos modelos matemáticos propuestos. En la tercera sección se describe la metodología de optimización utilizada. En la cuarta sección se ilustra la aplicación y adaptación de la metodología de optimización multiobjetivo a cada uno de los modelos matemáticos. Finalmente se presentan las conclusiones y recomendaciones derivadas de este trabajo.
Formulación del problemaEn el ámbito de los sistemas de distribución de energía eléctrica, un plan de mantenimiento óptimo de la vegetación consiste en definir los tramos en donde la vegetación será sometida a poda y el instante en el tiempo en que esta labor será ejecutada, de forma que se minimice el impacto negativo de las fallas asociadas a vegetación sobre la calidad de la red con un costo mínimo. Encontrar el mejor equilibrio entre calidad y costos constituye un problema de optimización multiobjetivo de alta complejidad.
En este trabajo se proponen dos modelos matemáticos multiobjetivo para solucionar el problema del mantenimiento de la vegetación bajo redes aéreas de distribución. El primer modelo considera como funciones objetivo las tasas de falla por vegetación y el costo de poda o mantenimiento de la misma. El segundo, considera las tasas de crecimiento de las especies de vegetación y el costo del mantenimiento. Ambos modelos están expresados de forma general de acuerdo con la ecuación (1), donde FO1 y FO2 corresponden a las dos funciones objetivo del modelo matemático.
Modelo I: basado en tasas de fallaEl primer modelo matemático describe el problema de mantenimiento de la vegetación a través de la minimización del NENS que tendrá el sistema debido a las interrupciones por vegetación durante el periodo de planeación del mantenimiento. En las ecuaciones (2) y (3) se muestran las funciones objetivo relacionadas con este modelo
donde
T = periodo de planeación para efectuar el mantenimiento de la vegetación bajo redes aéreas de distribución
NT = número de tramos de red del sistema que se toman en cuenta para realizar poda de la vegetación
U(i, t) = indisponibilidad en el tramo de red i durante el subperiodo t
DP(i, t) = demanda promedio en el tramo de red i durante el subperiodo t [kWh]
γ(i,t) = variable binaria de decisión, donde uno indica que se efectúa mantenimiento en el tramo de red i durante el subperiodo t, y cero en caso contrario
ΩAA = conjunto de tramos de red aguas abajo del tramo de red i
Cman(t) = costo del matenimiento durante el subperiodo t [$/km]
l(i) = longitud del tramo de red i [m].
La función objetivo 1 descrita en la ecuación (2) está asociada al NENS, donde los términos involucrados son la indisponibilidad y la demanda promedio del tramo de red i en el subperiodo t. Estos aspectos se evalúan bajo el criterio de contingencias NT-1, en el cual se simula una falla en cada sección con el fin de determinar la cantidad de energía no suministrada a los consumidores aguas abajo del lugar de la falla. Se supone un sistema de distribución con un esquema perfecto de protecciones, eso significa que todos los tramos de red poseen dispositivo de protección en el nodo de inicio. Para el caso en que esto no ocurra, una vez simulada una falla en la sección, se busca el dispositivo de protección más cercano aguas arriba de la falla para proceder a encontrar la cantidad de energía no suministrada. Se observa que la ecuación (2) está afectada por la expresión (1 – γ(i, t)), lo cual indica que cuando hay programada una poda en la sección i en el subperiodo t, se garantiza que el NENS no se incrementa debido a la cancelación de toda la expresión (γ(i, t) = 1). Lo contrario ocurre cuando no se programa poda de vegetación, es decir γ(i, t) = 0.
La función objetivo 2 presentada en la ecuación (3) calcula el costo de mantenimiento de la vegetación. Debido a que la poda de cada tramo de red tiene un costo establecido en un determinado subperiodo, es necesario trasladar este costo a valor presente por medio de una tasa de interés. Se puede observar que en esta ecuación el valor de mantenimiento se multiplica por la expresión γγ(i, t), indicando un aumento en el costo cuando se debe realizar una poda en el tramo de red i. Para trasladar este valor a valor presente, se utiliza la ecuación
donde
P = costo de mantenimiento de la vegetación trasladado a valor presente [$]
F = costo de mantenimiento en el periodo de planeación de la vegetación [$]
i = tasa de interés para el subperiodo [%]
n = número de subperiodos considerados
En las ecuaciones (5), (6) y (7), se describen las restricciones del problema.
donde
Lmax = máxima longitud permitida de poda de vegetación en el periodo de planeamiento T [m]
λ falla (i, t) = tasa de falla del tramo de red i en el subperiodo t debido a la vegetación [fallas/año]
NU(i) = número de usuarios del tramo de red i
NTU = número total de usuarios del sistema
FEI = índice de confiabilidad establecido para frecuencia equivalente de interrupción por usuario
NPi,t = número máximo de podas permitidas en el tramo de red i para el subperiodo t
TO(i, t) = periodo transcurrido desde la última poda en el tramo de red i para el subperido t [año].
Generalmente la disponibilidad de los equipos de mantenimiento destinados a la actividad de poda está determinada por un número de operarios. En este caso, la disponibilidad está dada por una longitud, lo que significa que existe un límite de metros lineales de red (Lmax) a los que se les puede dar mantenimiento (ecuación 5). Se observa que esta ecuación está afectada por la expresión γ(i, t), lo cual sigue la misma filosofía del costo de mantenimiento de la ecuación (3).
El índice de confiabilidad FEI definido en la ecuación (6), permite que la tasa de fallas del sistema de distribución no sobrepase un límite establecido por los organismos de regulación.
La ecuación (7) garantiza que no se sobrepase el número máximo de podas permitido para un tramo de red i en el subperiodo t.
Los índices de sensibilidad son definidos en este modelo por las tasas de falla debido a la vegetación, las cuales deben ser calculadas a partir de un estudio de confiabilidad de datos históricos con el fin de guiar a la técnica de optimización en el espacio de soluciones. A partir de las tasas de falla, se determinan los valores de indisponibilidad U(i, t), empleando la ecuación :
Donde el parámetro r es el tiempo medio de reparación para un tramo de red i expresado en horas y 8760 corresponde al número de horas de un año.
Modelo II: basado en tasas de crecimientoEste modelo representa una opción para las electrificadoras que no poseen datos históricos de fallas debido a la interferencia de la vegetación, pero conocen información correspondiente a las tasas de crecimiento de la vegetación que crece debajo de la red de distribución. De esta forma, las tasas de crecimiento son los índices de sensibilidad de este modelo, el cual se presenta en las ecuaciones (9) y (10).
donde
λcrec (i,t) = tasa de crecimiento de la vegetación para el tramo de red i en el subperiodo t [m/año]
dmin = distancia mínima permitida entre la red aérea de distribución y la vegetación [m]
ΩNP = conjunto de tramos de red i que no se les efectúa poda de vegetación o mantenimiento
To (i,t) = tiempo transcurrido desde la última poda [año].
La función objetivo 1 descrita en la ecuación (9) corresponde al porcentaje promedio de violación de la zona de seguridad o PPV (distancia mínima que debe existir entre la vegetación y las líneas aéreas) y tiene en cuenta los tramos de red en los cuales no se realizará poda durante el periodo de planeación. El producto entre la tasa de crecimiento y el tiempo transcurrido desde la última poda define la altura que la vegetación se ha introducido en la zona de seguridad (figura 1), la cual se divide entre la distancia mínima permitida para normalizarlo. Como este cálculo se realiza para los tramos que no son intervenidos, entonces se divide entre el número de tramos en los cuales no se hará mantenimiento de la vegetación, es decir, donde γ(i, t) = 0.
La ecuación (10) corresponde a la función objetivo 2, en la cual se calcula el costo de mantenimiento trasladado a valor presente. Las restricciones a las cuales está sujeto el modelo matemático están definidas por la disponibilidad de equipos (ecuación 5) y la restricción operativa del máximo número de podas (ecuación 7). No se tiene en cuenta la restricción de confiabilidad (ecuación 6) porque en este modelo no se utilizan tasas de falla por vegetación.
Metodología propuestaAlgoritmo NSGA-IIAmbos modelos matemáticos descritos en la sección anterior, se resuelven utilizando una técnica de optimización multiobjetivo llamada algoritmo genético elitista de ordenamiento no dominado NSGA-II [elitist non-dominated sorting genetic algorithm, (Deb et al., 2002)].
Se crea una población inicial Pt con m individuos y luego se aplican los operadores de selección, recombinación y mutación para generar una población Qt de igual número de individuos, como se muestra en la figura 2a. Después, las poblaciones Pt y Qt se unen para formar una población de 2m individuos, como se ilustra en la figura 2b. El objetivo de este paso es obtener una población con tamaño igual a dos veces el tamaño original, mejorada y más diversa, resultante de la aplicación de los tres operadores genéticos tradicionales. En términos generales, esta es la forma en que la metodología NSGA-II hace evolucionar el frente actual hacia un frente óptimo de Pareto.
Aplicando el concepto de dominancia (Deb et al., 2002), los individuos de la población (Pt+Qt) se ordenan por frentes, como se muestra en la figura 3, de forma que se da mayor prioridad para pasar a la siguiente generación, a los individuos ubicados en un mejor frente. En este caso, por tratarse de un problema en donde las dos funciones objetivo son de minimización, el de mayor prioridad es el frente 1. En esta etapa se hace explícito el elitismo involucrado en la metodología NSGA-II.
El siguiente paso consiste en establecer nuevamente una población del tamaño original (m individuos). Para ello, los criterios utilizados son dos: i) extraer de la población (Pt+Qt) los m mejores individuos, según el frente al que pertenecen, que conformarán la población de la siguiente generación Pt+1 y ii) si de un frente sólo pasan a la siguiente generación algunos individuos, y por consiguiente algunos deben ser descartados, entonces se utiliza el concepto de distancia de apilamiento como factor de decisión (Deb et al., 2002).
Teniendo en cuenta esta filosofía, si m = 15, entonces de la figura 3 se puede afirmar que todos los individuos del frente 1 (11 individuos) pasan a la siguiente generación y los 4 restantes deberán pasar del frente 2. Debido a que en el frente 2 hay 6 individuos, entonces se seleccionan los 4 con mayor distancia de apilamiento. De esta manera se completa la población Pt+1 y se considera, a su vez, un factor de sensibilidad que mejora la diversidad de los individuos de la población. Una descripción más detallada del algoritmo NSGA-II se puede encontrar en Deb et al. (2002).
Esquema de codificaciónEl problema se codifica por medio de un vector de variables binarias. Este vector está dividido en t secciones de igual tamaño (una por cada subperiodo). El tamaño de las secciones se debe al número total de tramos de red del sistema bajo estudio. Por lo tanto, el tamaño total del vector de codificación está dado por NT*t, como se muestra en la figura 4. La variable binaria de decisión γγ(i, t) está estrechamente conectada con la codificación, donde i es el tramo de red y t es el subperiodo de trabajo. La variable γ(i, t) es 1 cuando se realiza mantenimiento del tramo i en el periodo t y es 0 en caso contrario.
Es importante aclarar que el esquema de codificación propuesto se puede emplear en los dos modelos matemáticos descritos en la sección 2.
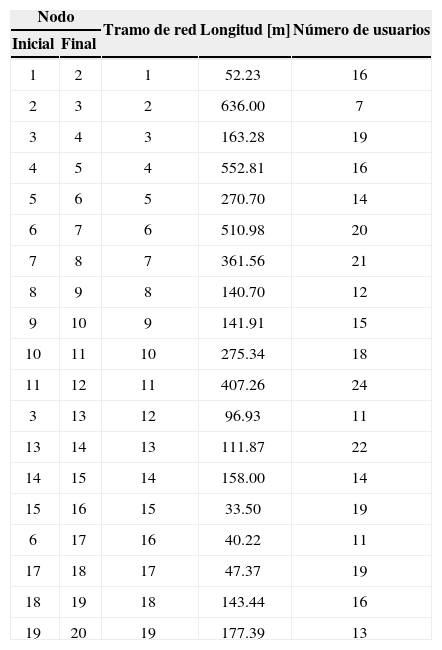
Aplicación y resultadosPara aplicar la metodología propuesta se emplea un sistema de distribución de 19 tramos de red, usando los dos modelos matemáticos presentados en la sección 2. En ambos casos de estudio se emplea un periodo de análisis de un año (8760 h) dividido en cuatro subperiodos (trimestres). Los datos de los tramos de red del sistema se ilustran en la tabla 1.
Datos de los tramos de red
| Nodo | Tramo de red | Longitud [m] | Número de usuarios | |
|---|---|---|---|---|
| Inicial | Final | |||
| 1 | 2 | 1 | 52.23 | 16 |
| 2 | 3 | 2 | 636.00 | 7 |
| 3 | 4 | 3 | 163.28 | 19 |
| 4 | 5 | 4 | 552.81 | 16 |
| 5 | 6 | 5 | 270.70 | 14 |
| 6 | 7 | 6 | 510.98 | 20 |
| 7 | 8 | 7 | 361.56 | 21 |
| 8 | 9 | 8 | 140.70 | 12 |
| 9 | 10 | 9 | 141.91 | 15 |
| 10 | 11 | 10 | 275.34 | 18 |
| 11 | 12 | 11 | 407.26 | 24 |
| 3 | 13 | 12 | 96.93 | 11 |
| 13 | 14 | 13 | 111.87 | 22 |
| 14 | 15 | 14 | 158.00 | 14 |
| 15 | 16 | 15 | 33.50 | 19 |
| 6 | 17 | 16 | 40.22 | 11 |
| 17 | 18 | 17 | 47.37 | 19 |
| 18 | 19 | 18 | 143.44 | 16 |
| 19 | 20 | 19 | 177.39 | 13 |
Los parámetros empleados por el algoritmo NSGA-II en los dos casos de estudio son:
- •
número de generaciones: 2000,
- •
tasa de mutación: 2%,
- •
número de individuos en cada generación: 20,
- •
tasa de interés: 9% trimestral.
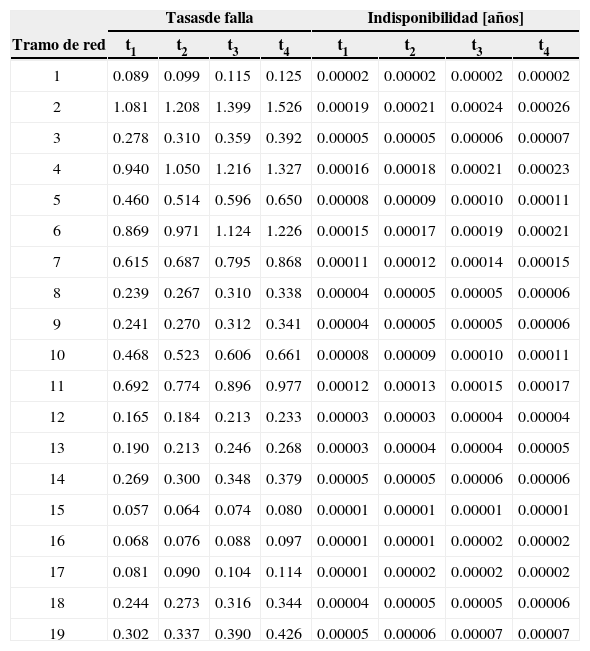
A continuación se presentan los resultados de la aplicación de la metodología de optimización NSGA-II al modelo matemático basado en tasas de falla, propuesto en el modelo I de la sección de formulación del problema. En la tabla 2 se presentan las tasas de falla y las indisponibilidades de los tramos de red del sistema, las cuales se obtienen a partir de datos históricos.
Tasas de falla e indisponibilidad de los tramos de red por trimestre
| Tramo de red | Tasasde falla | Indisponibilidad [años] | ||||||
|---|---|---|---|---|---|---|---|---|
| t1 | t2 | t3 | t4 | t1 | t2 | t3 | t4 | |
| 1 | 0.089 | 0.099 | 0.115 | 0.125 | 0.00002 | 0.00002 | 0.00002 | 0.00002 |
| 2 | 1.081 | 1.208 | 1.399 | 1.526 | 0.00019 | 0.00021 | 0.00024 | 0.00026 |
| 3 | 0.278 | 0.310 | 0.359 | 0.392 | 0.00005 | 0.00005 | 0.00006 | 0.00007 |
| 4 | 0.940 | 1.050 | 1.216 | 1.327 | 0.00016 | 0.00018 | 0.00021 | 0.00023 |
| 5 | 0.460 | 0.514 | 0.596 | 0.650 | 0.00008 | 0.00009 | 0.00010 | 0.00011 |
| 6 | 0.869 | 0.971 | 1.124 | 1.226 | 0.00015 | 0.00017 | 0.00019 | 0.00021 |
| 7 | 0.615 | 0.687 | 0.795 | 0.868 | 0.00011 | 0.00012 | 0.00014 | 0.00015 |
| 8 | 0.239 | 0.267 | 0.310 | 0.338 | 0.00004 | 0.00005 | 0.00005 | 0.00006 |
| 9 | 0.241 | 0.270 | 0.312 | 0.341 | 0.00004 | 0.00005 | 0.00005 | 0.00006 |
| 10 | 0.468 | 0.523 | 0.606 | 0.661 | 0.00008 | 0.00009 | 0.00010 | 0.00011 |
| 11 | 0.692 | 0.774 | 0.896 | 0.977 | 0.00012 | 0.00013 | 0.00015 | 0.00017 |
| 12 | 0.165 | 0.184 | 0.213 | 0.233 | 0.00003 | 0.00003 | 0.00004 | 0.00004 |
| 13 | 0.190 | 0.213 | 0.246 | 0.268 | 0.00003 | 0.00004 | 0.00004 | 0.00005 |
| 14 | 0.269 | 0.300 | 0.348 | 0.379 | 0.00005 | 0.00005 | 0.00006 | 0.00006 |
| 15 | 0.057 | 0.064 | 0.074 | 0.080 | 0.00001 | 0.00001 | 0.00001 | 0.00001 |
| 16 | 0.068 | 0.076 | 0.088 | 0.097 | 0.00001 | 0.00001 | 0.00002 | 0.00002 |
| 17 | 0.081 | 0.090 | 0.104 | 0.114 | 0.00001 | 0.00002 | 0.00002 | 0.00002 |
| 18 | 0.244 | 0.273 | 0.316 | 0.344 | 0.00004 | 0.00005 | 0.00005 | 0.00006 |
| 19 | 0.302 | 0.337 | 0.390 | 0.426 | 0.00005 | 0.00006 | 0.00007 | 0.00007 |
Como el costo de mantenimiento (CM) es directamente proporcional a la longitud de la sección, se asigna una constante dada en [$/m], la cual se multiplica por la longitud del tramo de red. Esta constante varía dependiendo del subperiodo del año. De acuerdo con esto, los valores para los cuatro trimestres son 100, 120, 110 y 140 [$/km], respectivamente. Se consideró una longitud máxima permitida de poda de vegetación de 3500 metros lineales de red. La frecuencia equivalente de interrupción por usuario del sistema y el número máximo de podas permitidas en un tramo de red son 3 fallas/año y 1 poda, respectivamente (Arias et al., 2012). En cada generación del algoritmo NSGA-II se calcula el NENS para cada propuesta de mantenimiento y de acuerdo con el programa de podas se obtiene el costo total de mantenimiento, el cual es trasladado a valor presente para todos los subperiodos del año.
A partir de una población inicial aleatoria como la mostrada en la figura 5, la cual en general no es factible por tratarse de un problema de optimización restringido, la aplicación del algoritmo NSGA-II permite obtener el frente de Pareto mostrado en la figura 6, donde cada punto de la gráfica corresponde a una propuesta de solución.
En la tabla 3 se presentan los valores de las funciones objetivo de las propuestas encontradas en el frente de Pareto. A pesar de tener una población inicial de 20 individuos, en el frente de Pareto óptimo sólo se tienen 14 propuestas no dominadas, las restantes 6 se encuentran distribuidas en otros frentes de menor calidad.
Soluciones entregadas por el algoritmo para el modelo I
| Individuo | NENS [kWh] | CM[$] |
|---|---|---|
| 1 | 54,835 | 341.421 |
| 2 | 55,584 | 298.601 |
| 3 | 56,836 | 265.915 |
| 4 | 57,400 | 239.053 |
| 5 | 59,815 | 202.604 |
| 6 | 59,954 | 196.330 |
| 7 | 60,517 | 169.469 |
| 8 | 61,288 | 166.141 |
| 9 | 61,852 | 139.280 |
| 10 | 65,857 | 116.313 |
| 11 | 66,468 | 99.520 |
| 12 | 70,902 | 84.160 |
| 13 | 74,350 | 66.231 |
| 14 | 75,621 | 36.767 |
A continuación se presentan los resultados de la aplicación de la metodología de optimización NSGA-II al modelo matemático basado en la tasa de crecimiento, propuesto en el modelo II de la sección de formulación del problema. Las tasas de crecimiento de la vegetación y el tiempo transcurrido desde la última poda para cada tramo de red del sistema se encuentran en la tabla 4. El tiempo medio de reparación (r) y la distancia mínima seguridad (dmin) para todos los tramos de red es 1,5horas y 1 m, respectivamente.
Tasas de crecimiento y tiempo transcurrido desde la última poda
| Tramode red | Tasas de crecimiento [m/año] | Tiempo transcurrido desde a última poda [años] | |||
|---|---|---|---|---|---|
| t1 | t2 | t3 | t4 | ||
| 1 | 0,8033 | 1,02 77 | 0,7532 | 0,9834 | 0,25 |
| 2 | 0,5776 | 0,9841 | 0,6104 | 1,1759 | 0,25 |
| 3 | 0,6862 | 1,0669 | 0,8905 | 0,9600 | 0,50 |
| 4 | 0,6792 | 1,1213 | 0,5870 | 1,1333 | 0,75 |
| 5 | 0,8262 | 1,0117 | 0,6550 | 0,9043 | 1,00 |
| 6 | 0,6225 | 0,9700 | 0,8891 | 1,0574 | 0,25 |
| 7 | 0,8393 | 1,0977 | 0,6639 | 0,9926 | 0,10 |
| 8 | 0,5940 | 1,0438 | 0,5103 | 1,0073 | 0,50 |
| 9 | 0,8980 | 1,2382 | 0,8142 | 0,9216 | 0,25 |
| 10 | 0,6974 | 1,0641 | 0,7199 | 0,9115 | 0,25 |
| 11 | 0,5694 | 1,0497 | 0,6094 | 1,0240 | 0,75 |
| 12 | 0,6035 | 1,1131 | 0,5410 | 1,1945 | 0,75 |
| 13 | 0,6869 | 0,9710 | 0,6336 | 1,2247 | 0,25 |
| 14 | 0,8080 | 1,1819 | 0,5774 | 1,1690 | 0,50 |
| 15 | 0,5046 | 1,2487 | 0,5941 | 1,0752 | 0,50 |
| 16 | 0,5259 | 0,9401 | 0,7830 | 1,1187 | 0,25 |
| 17 | 0,6573 | 1,1953 | 0,6493 | 0,9872 | 0,75 |
| 18 | 0,5047 | 1,1100 | 0,6126 | 1,1023 | 0,25 |
| 19 | 0,8006 | 1,2275 | 0,5219 | 1,0791 | 0,50 |
En la figura 7 se observa el frente de Pareto entregado por el NSGA-II. En la Tabla 5 se ilustran las soluciones entregadas por el algoritmo. Se utilizó una población inicial de 100 individuos.
Soluciones entregadas por el algoritmo para el modelo II
| Individuo | PPV [%] | CM[$] | Individuo | PPV [%] | CM[$] | Individuo | PPV [%] | CM[$] |
|---|---|---|---|---|---|---|---|---|
| 1 | 40,342 | 323.883 | 23 | 48,721 | 176.306 | 45 | 57,230 | 92.746 |
| 2 | 40,683 | 318.765 | 24 | 49,061 | 173.382 | 46 | 57,746 | 90.657 |
| 3 | 40,842 | 318.308 | 25 | 49,339 | 172.529 | 47 | 58,303 | 88.310 |
| 4 | 40,929 | 300.572 | 26 | 49,514 | 165.666 | 48 | 59,429 | 85.561 |
| 5 | 41,145 | 285.417 | 27 | 49,953 | 150.164 | 49 | 59,538 | 81.781 |
| 6 | 41,903 | 269.861 | 28 | 50,619 | 149.505 | 50 | 59,618 | 76.788 |
| 7 | 42,238 | 264.743 | 29 | 51,207 | 145.728 | 51 | 60,235 | 76.129 |
| 8 | 42,863 | 242.015 | 30 | 51,383 | 138.865 | 52 | 60,641 | 72.352 |
| 9 | 43,551 | 241.355 | 31 | 51,496 | 135.831 | 53 | 61,250 | 71.692 |
| 10 | 43,855 | 239.076 | 32 | 52,152 | 135.172 | 54 | 61,384 | 67.912 |
| 11 | 44,273 | 237.578 | 33 | 52,487 | 132.248 | 55 | 61,892 | 65.822 |
| 12 | 44,454 | 230.716 | 34 | 52,707 | 131.395 | 56 | 62,382 | 63.475 |
| 13 | 44,570 | 227.682 | 35 | 52,880 | 124.532 | 57 | 63,474 | 63.459 |
| 14 | 45,247 | 227.022 | 36 | 53,526 | 123.873 | 58 | 63,491 | 60.726 |
| 15 | 45,594 | 224.098 | 37 | 53,856 | 120.949 | 59 | 63,677 | 51.953 |
| 16 | 45,874 | 214.026 | 38 | 53,967 | 117.914 | 60 | 64,285 | 51.294 |
| 17 | 46,431 | 191.298 | 39 | 54,713 | 117.526 | 61 | 64,628 | 47.517 |
| 18 | 47,108 | 190.639 | 40 | 54,883 | 110.663 | 62 | 65,228 | 46.857 |
| 19 | 47,407 | 188.360 | 41 | 55,293 | 106.615 | 63 | 66,466 | 43.061 |
| 20 | 47,761 | 186.862 | 42 | 55,953 | 104.045 | 64 | 67,365 | 38.624 |
| 21 | 47,939 | 179.999 | 43 | 56,412 | 102.179 | — | — | — |
| 22 | 48,054 | 176.965 | 44 | 57,062 | 99.609 | — | — | — |
El modelado matemático del problema de mantenimiento de la vegetación bajo redes aéreas de distribución incluyó varios aspectos, entre los que se encontraron: disponibilidad de recursos por parte de la empresa de distribución, metas de cumplimiento de la confiabilidad en el sistema y restricción operativa determinada por el número de podas posibles en un tramo de red a lo largo del periodo de planeación del mantenimiento de la vegetación.
Las tasas de falla por vegetación presentadas en el primer modelo matemático, sirvieron como índices de sensibilidad adecuados para guiar el algoritmo de optimización a través del espacio de búsqueda. Debido a que las tasas de falla eran crecientes con el tiempo, el algoritmo enfocaba las actividades de poda de forma más pronunciada al final del periodo de planeación (subperiodos 3 y 4).
Una alternativa para las electrificadoras que no tienen históricos de falla por vegetación, es obtener información acerca de las especies vegetales que crecen debajo de las redes aéreas energizadas, por ejemplo, las tasas de crecimiento. Estas últimas sirven como índices de sensibilidad en el problema multiobjetivo donde se minimiza el porcentaje promedio de interrupción en la zona de seguridad.
La técnica de optimización multiobjetivo NSGA II demostró ser una alternativa favorable para el manejo del problema multiobjetivo de mantenimiento de la vegetación y permitió encontrar frentes de Pareto con alta diversidad, con un número apreciable de soluciones factibles y de buena calidad. La selección de la mejor propuesta de mantenimiento encontrada depende de los criterios definidos por cada electrificadora.
El número de operarios necesarios para realizar el mantenimiento de la vegetación, como también el tiempo de arribo al lugar de trabajo y el tiempo de ejecución de la poda, son variables que pueden considerarse para el mejoramiento de los modelos matemáticos existentes y la introducción hacia nuevas formas de codificación.
La consecución de cronogramas de mantenimiento de la vegetación a través de modelado matemático y el uso de técnicas metaheurísticas de optimización, permite a las electrificadoras llevar un control más acertado de las actividades de poda bajo las líneas aéreas de distribución. De igual manera se disminuye la cantidad de interrupciones en el suministro de energías eléctricas, provocadas por el contacto de las líneas energizadas con los árboles.
Si no se realizan planes de mantenimiento en forma conjunta entre los responsables de redes eléctricas y poda de vegetación, es posible que aumenten los cortes de energía con la consecuente falta de continuidad en el fluido eléctrico, desencadenando pérdidas económicas para los usuarios y las electrificadoras. Una solución a futuro es realizar convenios entre los responsables para diseñar e implementar estrategias para planear las rutas de redes eléctricas y siembra de vegetación, de acuerdo con las necesidades requeridas, para evitar los inconvenientes expuestos en este trabajo.
Ingeniero electricista (2010) y magister en ingeniería eléctrica (2012) por la Universidad Tecnológica de Pereira, Colombia. Actualmente se encuentra vinculado a un grupo de investigación cuyas actividades principales son la optimización y modelamiento aplicado a sistemas de energía eléctrica y procesos en general.
Citación estilo Chicago Arias-Londoño Andrés, Ricardo Alberto Hincapié-Isaza, Mauricio Granada-Echeverri. Programación óptima del mantenimiento de la vegetación bajo redes aéreas de distribución usando una técnica de optimización multiobjetivo. Ingeniería Investigación y Tecnología, XIV, 04 (2013): 139-150.
Citación estilo ISO 690 Arias-Londoño A., Hincapié-Isaza R.A., Granada-Echeverri M. Programación óptima del mantenimiento de la vegetación bajo redes aéreas de distribución usando una técnica de optimización multiobjetivo. Ingeniería Investigación y Tecnología, volumen XIV (número 4), octubre-diciembre 2013: 139-150.
Ingeniero electricista (2001) y magister en ingeniería eléctrica (2004) por la Universidad Tecnológica de Pereira, Colombia. Es estudiante de doctorado y profesor asociado del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira, Colombia. Sus intereses de investigación incluyen planeación de sistemas de distribución de energía eléctrica, protección de sistemas de potencia y optimización aplicada a sistemas de potencia.
Ingeniero electricista (2001) y magister en ingeniería eléctrica (2003) por la Universidad Tecnológica de Pereira, Colombia. Es Ph.D. en ingeniería eléctrica (2011) por la Universidade Estadual Paulista, Ilha Solteira, Brazil. Es profesor asociado del programa de ingeniería eléctrica de la Universidad Tecnológica de Pereira, Colombia. Sus áreas de interés en investigación incluyen la aplicación de metodologías matemáticas y metaheurísticas para la optimización y planeamiento de los sistemas de energía eléctrica, descomposición y modelamiento matemático aplicado a problemas de ingeniería.