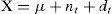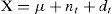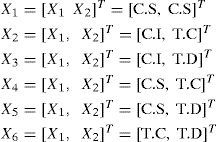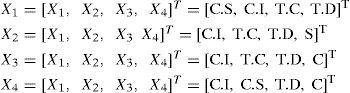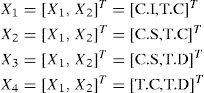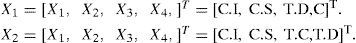Reconocimiento de variables multivariantes empleando el estadístico T2 Hotelling y MEWMA mediante las RNA’s

Resumen

En este artículo se presenta la propuesta de un método de reconocimiento de patrones multivariantes empleando redes neuronales artificiales (RNA). El método es de utilidad en la aplicación del control estadístico de procesos para el monitoreo de múltiples variables. El método emplea medidas estadísticas descriptivas y técnicas de control multivariante. Se evalúan tres diferentes RNA's con el fin de identificar la red con mejor eficiencia en el reconocimiento de patrones presentes en cada variable multivariante obtenida a partir de bases de datos. Se analizan dos bases de datos, la primera fue generada por simulación de Montecarlo y la segunda corresponde a una base de datos de dominio público. El método consta de tres etapas: generación de variables multivariantes, análisis multivariado y reconocimiento de patrones con RNA. Para llevar a cabo esta investigación se generaron distintos escenarios multivariantes combinando 2, 3 y 4 patrones en variables multivariantes en los estadísticos T² de Hotelling y MEWMA, los cuales se analizaron para conocer su comportamiento y características estadísticas. Se realizó la tarea de reconocimiento de patrones de estos estadísticos utilizando las RNA. Los resultados experimentales mostraron un mejor desempeño en el caso de la red de Perceptrón y Retropropagación comparado con la red RBF para ambos casos de estudio.

Abstract

In this article, a method for multivariate pattern recognition using artificial neural networks (ANN) is proposed. The method is useful for monitoring multiple variables during the statistical process control. It employs descriptive statistics and multivariate control techniques. Three different ANN's are evaluated to identify the network with higher efficiency during pattern recognition of multivariate variables tasks from data bases. Two data bases are analyzed; the one is generated by simulation using the Montecarlo method, and the second data base was obtained from a public data base repository. The method consists of three stages: multivariate variables generation, multivariate analysis and pattern recognition using ANN's. Several multivariate scenarios were generated using a combination of 2, 3 and 4 patterns in multivariate variables for the Hotelling's T² and MEWMA stadistics, that were analyzed to know its behavior and to determine their statistical characteristics. The pattern recognition task was evaluated using the ANN. In both study cases, experimental results showed an improved efficiency when using the Perceptron and the Backpropagation networks compared to the RBF network.

Introducción

Los gráficos del control son una herramienta del control estadístico de procesos (CEP). Resultan útiles para lograr la estabilidad y mejorar la capacidad del proceso mediante la reducción de la variabilidad. El objetivo del gráfico de control es lograr una alta calidad del producto, reduciendo costos de producción y minimizando los defectos del producto. En cualquier proceso de fabricación no siempre se producen los mismos efectos, ya que los elementos que intervienen no siempre funcionan de forma exacta, dando lugar a cierta variabilidad, cuyas causas es preciso investigar. La variabilidad de un proceso puede deberse a causas no asignables y a causas asignables. Las primeras, también llamadas aleatorias son de naturaleza probabilística y forman parte de la variación propia del proceso. Por otro lado, las causas asignables dan lugar a variaciones irregulares no predecibles, que hay que eliminar o corregir. En esta etapa es donde los gráficos de control constituyen una excelente herramienta, pues permiten decidir cuándo hay que intervenir en el proceso para modificar una evolución no deseada (Huerga et al., 2005).

Desde hace décadas se han empleado métodos “tradicionales” para monitorear procesos aleatorios tales como el control estadístico de procesos univariado, del mismo modo que en la actualidad se ha planteado el uso del control multivariado de procesos, que se encarga de analizar a múltiples variables aleatorias simultáneamente. Estos métodos revelan variaciones en las mediciones obtenidas del proceso aleatorio. Las variaciones especiales están provocadas por causas no aleatorias (causas asignables) y cuando actúan originan efectos que se pueden determinar con certeza y que persisten hasta que se elimine la causa que los produce. Por lo tanto, los dos tipos de variabilidad son variación natural y variación especial, donde estas variaciones en las series de datos presentan patrones naturales y especiales, respectivamente.

Las técnicas de control estadístico de procesos no son herramientas tan eficientes en la automatización de la industria, ya que necesitan satisfacer condiciones estadísticas tales como independencia de las variables, simetría y normalidad en su distribución para su correcta aplicación; asimismo, sólo indican la existencia de variaciones pero no indican el origen de dicha variación. Por tal motivo, en la actualidad se han propuesto alternativas a las técnicas tradicionales del control estadístico de procesos, tales como el reconocimiento de patrones con el uso de redes neuronales artificiales (RNA) con el fin de detectar patrones con más eficacia que el abordaje convencional y con el objetivo del diagnóstico automático de los patrones. Las redes neuronales artificiales no necesitan satisfacer condiciones estadísticas y manejan una gran cantidad de datos. Estas importantes características convierten a las redes neuronales artificiales en herramientas prometedoras y efectivas que se pueden implementar para mejorar el análisis de datos en aplicaciones de control de calidad. Las redes neuronales se clasifican de forma general en dos tipos: redes con aprendizaje supervisado y redes con aprendizaje no supervisado, en ambos tipos las redes neuronales con aprendizaje no supervisado y supervisado se pueden entrenar para identificar y clasificar a un grupo de series de datos muestrales en patrones típicos de variación especial y variación natural, con lo que se puede en consecuencia, diagnosticar si un proceso de manufactura opera dentro o fuera de control estadístico.

En este artículo se expone un método para el reconocimiento de patrones en variables multivariantes, mediante el uso de los estadísticos T² Hotelling y MEWMA, asimismo la implementación de diferentes redes neuronales artificiales, tales como Perceptrón, Retropropagación y función de base radial (RBF, radial based function). El reconocimiento de variables multivariantes con presencia de patrones es relevante para el control estadístico de procesos, ya que en una situación fuera de control puede localizarse la falla en una variable o un cambio en la relación existente entre las variables. El propósito de este artículo es estudiar la variable multivariante con el fin de asociar sus tipos de patrones con causas reflejadas en las variables que la conforman. Asimismo, intenta mostrar cómo la selección de una red neuronal artificial probada con técnicas multivariantes posibilita el reconocimiento de patrones multivariantes asociados a las causas especiales que le dieron origen. El trabajo está organizado de la siguiente manera: en la introducción se presenta el trabajo relacionado con la investigación, en la siguiente sección se expone el método propuesto, así como la generación de variables multivariantes, su análisis estadístico y una breve descripción sobre las RNA a utilizar. En la tercera sección se presenta la experimentación integrada por la generación de variables aleatorias multivariantes con patrones de variación usando el método de Montecarlo y una base de datos definida “Synthetic Control Chart Time Series”. En la cuarta sección se muestran los resultados obtenidos del entrenamiento y prueba de las redes neuronales y finalmente se presentan las conclusiones y trabajo futuro en la última sección.

Trabajo relacionado y contribución original

En este trabajo se consideran dos tipos de variabilidad, que son variación natural y variación especial, las cuales se observan en los gráficos de control de las mediciones de variables como patrón natural y patrones especiales. Existen varios trabajos relacionados sobre la categorización de todos los posibles patrones que comúnmente aparecen en los gráficos de control. Se definen como 30 posibles patrones gráficos de control, los cuales se clasifican como 22 patrones superpuestos y 8 patrones básicos (Guh, 2005) como se muestran en la figura 1.

Figura 1.

Patrones gráficos de control básicos

De estos patrones especiales se consideraron los patrones de tendencias, cambios, natural, sistemático y cíclico para la presente investigación. Los patrones mencionados corresponden a las siguientes causas asignables:

• 1)

  Patrones de tendencia: estos patrones pueden ser definidos como movimientos continuos de dirección positiva o negativa.

• 2)

  Patrones de cambio: un cambio se define como un cambio repentino por encima o por debajo de la media de un proceso.

• 3)

  Patrones cíclicos: en los comportamientos cíclicos se observan una serie de máximos y mínimos ocurridos en el proceso.

• 4)

  Patrones sistemáticos: la característica de los patrones sistemáticos es la presencia de una fluctuación punto a punto producida sistemáticamente. Esto significa que el punto más bajo siempre es seguido por un alto y viceversa.

Los gráficos de control (GC) estudian procesos aleatorios univariados, pero es posible que en un proceso de producción sea necesario vigilar varias mediciones, en cuyo caso se está ante un control multivariante (Huerga et al., 2005). Los GC presentan varias desventajas ante los procesos modernos, ya que para su correcta aplicación es necesario satisfacer condiciones estadísticas tales como la independencia de las variables aleatorias, simetría y normalidad en su distribución de probabilidad. Además, los GC sólo indican la existencia de una falla o anomalía en el proceso, pero no en dónde o qué sucedió; esto genera un diagnóstico apresurado y en ciertas ocasiones errado. Dada la necesidad de resolver el problema técnico planteado y contemplando las desventajas a las que conlleva la aplicación independiente de múltiples GC univariados, diferentes autores han propuesto alternativas de solución, como técnicas de control multivariante, control estadístico por reconocimiento de patrones y el uso de redes neuronales. En control estadístico de la calidad, desde un punto de vista multivariante, las herramientas más utilizadas son los gráficos de control T² Hotelling y MEWMA, estas técnicas se explicarán en la siguiente sección.

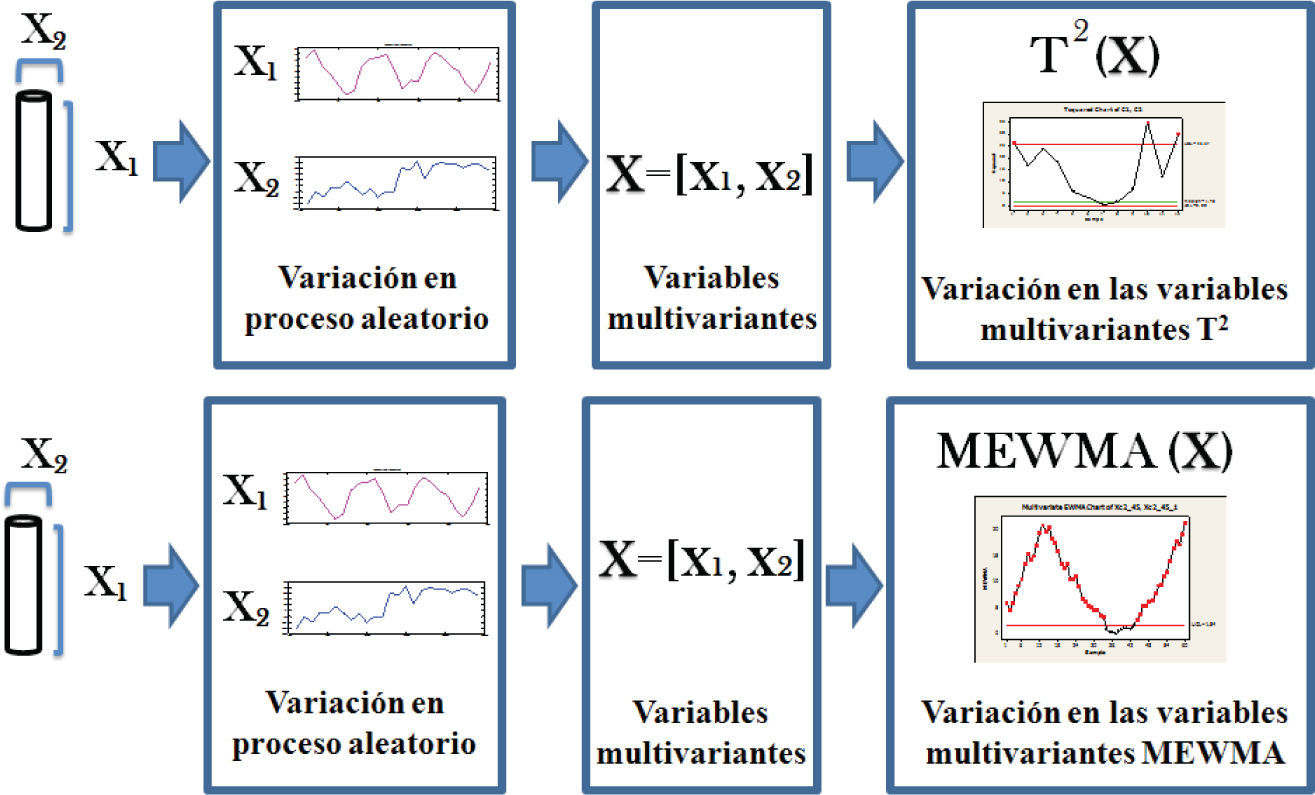
En las técnicas de gráficas de control multivariante detectar una situación fuera de control es relativamente fácil, ya que el análisis es similar al caso univariante, pero determinar las causas que provocaron ese cambio es más complicado (Marroquín y Cantú, 2010). Como se observa en la figura 2, se consideran las variables X₁ y X₂ que son las dimensiones de un producto, aunque esto se puede generalizar a X₁ y X₂, X₃,…, X_n variables. Cada una de estas variables poseerá su clase de variación (patrones especiales y patrón natural) y la combinación o composición de estas variables genera variables multivariantes sintetizadas por las variables T² Hotelling y MEWMA, la cual a su vez tendrá clases de variación como resultado de la combinación de las clases de variación presentes en X₁ y X₂, X₃,…, X_n.

Figura 2.

Variables multivariantes T² Hotelling y MEWMA con presencia de variación en sus elementos

Como se observa en la figura 2, se trata el problema del reconocimiento de patrones en dos niveles:

• 1.

  Patrones de variación o clases de variación presentes en las variables T² y MEWMA.

• 2.

  Patrones de variación o clases de variación presentes en cada una de las variables que intervienen en las variables T² y MEWMA.

De acuerdo con esto, el problema se puede analizar mediante dos enfoques:

• 1.

  Tratar de predecir las clases o patrones de variación de T² y MEWMA a partir de las clases o patrones de variación en X₁, X₂, X₃,…, X_n en el caso de ser conocidos.

• 2.

  Dado un patrón o clase reconocida en T² y MEWMA, predecir las clases o patrones de variación presentes en X₁ y X₂, X₃,…, X_n que formaron a T² y MEWMA.

Este artículo trata de resolver parte de la problemática al reconocer patrones o clases de variación en el estadístico T₂ y MEWMA, de lo cual no se tiene reporte en la literatura escrita hasta donde los autores tienen conocimiento. Entonces, la hipótesis propuesta en la investigación es que existe una asociación en las clases o patrones de variación del T² y MEWMA, y las clases o patrones de variaciones presentes en las variables que intervienen.

Una alternativa para monitorear el proceso aleatorio de un producto es el control estadístico por reconocimiento de patrones, no obstante, esto es una de las tareas complejas en la aplicación del control estadístico porque no está considerado en la metodología ofrecida por el control estadístico tradicional. Sin embargo, recientemente, se ha investigado con éxito el uso de inteligencia artificial y específicamente, el de las redes neuronales artificiales (RNA) para este propósito. Las RNA son útiles cuando un sistema numérico tiene complejidad para modelarlo debido a diversas incertidumbres o causas de variación que actúan en ese sistema. Asimismo, las RNA empleadas con el fin del reconocimiento de patrones estadísticos de los datos permiten fácilmente reconocer, en tiempo real, distribuciones no normales con rapidez y eficiencia elevadas, especialmente cuando la distribución presenta sesgos (Guh, 2005). El uso de las redes neuronales no requiere la suposición de normalidad en los datos o de la independencia de los mismos (Pacella et al., 2004).

Las RNA han tenido aplicaciones diversas en el campo de la estadística, especialmente cuando se requiere manejar una gran cantidad de datos en tiempo real que representa cierta complejidad (Pacella y Semeraro, 2005). La importancia de detectar patrones en un vector de mediciones de un proceso aleatorio, es que se relacionan directamente con las variaciones. En esta investigación se define un patrón como una secuencia numérica de dimensión n; X = [x₁, x₂, x₃,…, x_n], es decir, un patrón es el comportamiento que tiene la serie de datos producida por un proceso aleatorio.

La ecuación 1 simboliza la generación de los elementos de X:

donde el patrón de comportamiento de los datos dependerá del tipo de variabilidad presente, como variación especial d_t, variación natural n_t y la media del proceso μ. Las RNA se pueden entrenar para identificar y clasificar a un grupo de datos muestrales tomados de la línea de producción, en patrones típicos de variación especial y variación natural con lo que se puede, en consecuencia, diagnosticar si un proceso de manufactura opera dentro o fuera de control estadístico. No obstante, los antecedentes en el estudio de las RNA aplicadas como una herramienta de control de procesos, muestran que aún no es suficiente el nivel de desarrollo de dichos estudios en cuanto al perfeccionamiento de sistemas que permitan su aplicación industrial.

Los estudios están limitados al análisis de variables aleatorias univariadas, lo cual proporciona la posibilidad del análisis en un enfoque multivariado, así como la implementación de inteligencia artificial. Por tal motivo, en esta investigación se propone analizar los patrones encontrados en el proceso aleatorio de un producto por medio del uso de análisis estadístico, los estadísticos T² Hotelling y MEWMA y las redes neuronales, con la finalidad de reconocer en las variables multivariantes la presencia de patrones y, por ende, se desea monitorear el proceso aleatorio de un producto de manera multivariable y multivariante en los estados de control y fuera de control del proceso, reconociendo las variables donde se presenta dicho problema.

Método de reconocimiento propuesto

El método propuesto, como se muestra en la figura 3 consiste básicamente en el análisis multivariado de datos mediante el uso de RNA. Para validar los resultados del método en este artículo se emplearon dos bases de datos. Una de estas bases se generó por simulación empleando el método de Montecarlo (Guh, 2005) y la otra fue la base de datos “Synthetic Control Chart Time Series” obtenida de un repositorio público de datos (Frank y Asunción, 2010). El método consiste en analizar los patrones especiales que se presentan en el proceso aleatorio de un producto usando técnicas estadísticas descriptivas, estadísticos T² Hotelling y MEWMA con la finalidad de reconocer patrones de variación en el vector obtenido empleando las RNA. Se pretende que el método sea un paso para el monitoreo del proceso aleatorio de un producto de manera multivariable y multivariante en los estados de control y fuera de control del proceso, reconociendo las variables donde se presenta un problema e identificando sus causas.

Figura 3.

Método propuesto

Para mejor comprensión del método se explicará con detalle cada parte que lo integra. En las siguientes subsecciones se describen los casos de variables multivariantes (afectadas por diferentes conjuntos o combinaciones de patrones de variación), su análisis estadístico y su representación como entradas en diferentes redes usando los estadísticos T² Hotelling y MEWMA.

Generación de variables multivariantes

Simulación de Montecarlo

En esta investigación se utilizó el método de simulación de Montecarlo para generar los conjuntos de patrones gráficos de control (PGC) necesarios para el entrenamiento, prueba y evaluación del método propuesto. Hubo varias razones para esto: en primer lugar, se necesita un gran número de ejemplos de PGC en el proceso de entrenamiento y prueba; en segundo lugar, la simulación se utiliza para variar minuciosamente la dificultad de los conjuntos de datos. Los PGC se expresaron de forma general, que consiste en la media del proceso, la variación de causa común y una alteración especial por causas específicas.

Para generar las diferentes mediciones del proceso aleatorio referente a un producto se utilizó la ecuación (1).

donde

X = variable con una serie de datos que presenta un patrón en el tiempo t,

μ = efecto global o media del proceso,

n_t = efecto de la variación natural presente en el proceso,

d_t = efecto de la variación especial (diferente para cada tipo de patrón) presente en el proceso.

La simulación del proceso aleatorio de un producto se definió por medio de diferentes tipos de variables multivariantes X = [X₁, X₂,…, X_p] con p variables del proceso aleatorio, en donde cada variable se representa por un patrón de variación. Resumiendo, X se define como una variable multivariante y X como una variable univariada que presenta un patrón de variación.

En la tabla 1 se muestran tres casos de variables multivariantes utilizadas.

Tabla 1.

Casos de variables multivariantes

Casos de variables aleatoriasmultivariantes
1.- Variable con p = 2.	X = [X1, X2
2.- Variable con p = 3.	X = [X1, X2, X3]
3.- Variable con p = 4.	X = [X1, X2, X3, X4

Los tipos de patrones utilizados son de tendencia decreciente, tendencia creciente, cambio superior, cambio inferior, natural, ciclo y sistemático. Cada patrón es un vector X = {x₁, x₂, x₃,…, x_n}, donde n = 100 observaciones en el tiempo.

• 1.

  Natural: X_N = μ + n_t + d_t donde μ = 0, σ = 1, n_t = .01, d_t= 0. Los valores de μ, σ y n_t son los mismos para los demás patrones.

• 2.

  Cambio superior: X_Cs = μ + n_t + d_t, y cambio inferior: X_Ci = μ + n_t + d_t. d_t = u × d, donde u es el parámetro para determinar la posición del cambio (–1 para cambio inferior o 1 para cambio superior), d es el desplazamiento de la media en términos de σ.

• 3.

  Tendencia creciente: X_Tc = μ + n_t + d_t, y tendencia decreciente: X_Td = μ + n_t + d_t. d_t = s × t, donde s es la pendiente de la tendencia en términos de σ (un valor negativo para tendencia decreciente o un valor positivo para tendencia creciente).

• 4.

  Ciclo: X_C = μ + n_t + d_t. d_t = l × (2πt / Ω), donde l es la amplitud del ciclo en términos de σ, Ω periodo del ciclo (Ω = 8).

• 5.

  Sistemático: X_S = μ + n_t + d_t. d_t = g × (–1)_T, donde g es la magnitud de los patrones sistemáticos en términos de σ con lo cual se determinarán las fluctuaciones sobre y por debajo de la media del proceso.

Base de datos

Para validar los resultados obtenidos con el método propuesto, se utilizó una base de datos conocida para comparar los resultados. La base de datos utilizados para validación es “Synthetic Control Chart Time Series” (Frank y Asunción, 2010). Consiste en vectores correspondientes a gráficos de control generados sintéticamente. La base de datos consiste en 600 vectores correspondientes a gráficos de control generados por el proceso en Alcock y Manolopoulos (1999). En la base de datos se presentan 6 clases diferentes de patrones presentes en los gráficos de control, estos patrones son:

• 1.

  Natural (N)

• 2.

  Cambio inferior (C.I.)

• 3.

  Cambio superior (C.S.)

• 4.

  Tendencia creciente (T.C.)

• 5.

  Tendencia decreciente (T.D.)

• 6.

  Ciclo (C)

De la base de datos se tomaron 6 vectores correspondientes a los 6 tipos o clases de patrones con el fin de generar los tipos o casos de variables multivariantes con dos, tres y cuatro procesos aleatorios.

Análisis estadístico

Al generar los diferentes casos de variables multivariantes con la presencia de los patrones mencionados, se realiza un análisis estadístico para cada caso de variables como se ilustra en la figura 4, el cual consiste en calcular y examinar la covarianza y correlación. Se pretende encontrar y seleccionar las variables que presentan una covarianza y correlación significativa con la finalidad de estudiar con detalle el proceso aleatorio de dichas variables, tales como normalidad, media y varianza, con lo que se puede determinar la importancia de su aplicación en el método propuesto. Después de estudiar los procesos aleatorios en los diferentes casos de las variables multivariantes seleccionadas por su correlación significativa, se calcula el estadístico T² Hotelling y MEWMA para determinar el comportamiento de los patrones de variación desde un punto de vista multivariante.

Figura 4.

Análisis estadístico

Estadístico T² Hotelling

El estadístico T² Hotelling es una variable aleatoria, unidimensional, que se construye combinando información para la posición y dispersión de las variables del proceso aleatorio que se analizan. En este trabajo, se generaliza en forma simultánea a p variables del proceso aleatorio de un producto X = [X₁, X₂,…, X_p], las cuales presentan el comportamiento de algún patrón de variación, y se define como variable multivariante; cada elemento de X se define como una observación multivariada y el vector objetivo son los valores de μ y Σ calculados cuando el proceso está bajo control. Geométricamente, el estadístico T², es proporcional a la distancia al cuadrado entre una observación multivariada y el vector de valores objetivo, donde puntos equidistantes forman elipsoides alrededor de dicho vector.

Cuanto mayor es el valor de T², mayor es la distancia entre la observación y el valor objetivo. La variable aleatoria T² de Hotelling se expresa como:

Donde X es un vector aleatorio con vector de medias μ y matriz de covarianzas Σ > 0, (Barbiero et al., 2003). El gráfico T² controla cambios en el vector de medias suponiendo que la matriz de covarianzas del proceso es igual a la matriz de covarianzas de las mediciones cuando el proceso está bajo control (Marroquín et al., 2007). Para la investigación no es significativo el uso del gráfico sino únicamente el cálculo del estadístico T² Hotelling usando Minitab^®.

Estadístico MEWMA

Es un promedio ponderado en el tiempo, al realizar la gráfica del estadístico cada punto graficado contiene información no sólo del último periodo sino también de los anteriores. A cada periodo se le da un peso que decrece en forma exponencial a medida que se aleja del actual. El interés se centra en el control simultáneo de p características de calidad correlacionadas entre sí. En este caso X₁, X₂…X_p son vectores que representan observaciones individuales tomadas del proceso y en este trabajo son las variables generadas por simulación de Montecarlo o seleccionadas de la base de datos. Se supone que los vectores aleatorios X_i son independientes con vector de medias μ y matriz de covariancias Σ_X (Barbiero et al., 2004).

Por simplicidad se supone que se conoce Σ_X. En la práctica es necesario recolectar datos durante cierto tiempo en el que el proceso está bajo control, para estimar Σ_X. Estos datos también pueden usarse para examinar las suposiciones de normalidad e independencia.

Si estas no se cumplen, las propiedades del gráfico pueden verse afectadas y las señales de fuera de control podrían carecer de significado. Sin pérdida de generalidad se supone que el vector de medias cuando el proceso está bajo control es μ₀ = (0, 0, 0…, 0)´, (Barbiero et al., 2004). Tomando como vector de partida a Z₀ = 0, los vectores MEWMA se definen como:

donde R = diag (r₁, r₂,…, r_p) y 0 < r_j ≤ 1; j = 1, 2,…, p

Si todos los rj son iguales, los vectores MEWMA pueden reescribirse de la siguiente forma: Z_i = rX_i + (1 – r)Z_i–1. Los r_j marcan la profundidad de la memoria para cada variable. Cuanto mayor sea r_j menor será la profundidad, es decir, menor peso tendrán las observaciones anteriores. Se pueden usar valores de r_j específicos para cada variable. Aquí es donde se diferencia un análisis direccional de uno sin dirección específica. Si se usa el mismo peso r_j para todas las variables, el gráfico es de dirección invariante, debido a que una señal fuera de control no podrá atribuirse a alguna variable en especial, ya que todas tienen igual peso. Si se otorga distinto peso a las variables, el gráfico será de dirección específica y en ese caso, una señal de fuera de control se atribuye a los valores específicos de aquella variable a la que se le otorgó el mayor peso.

Cuando se utiliza un r común y éste es igual a 1, se obtiene el gráfico T² de Hotelling, (Barbiero et al., 2004). El estadístico “MEWMA” se grafica:Ti2=Zi∑z−1Zi. Para la investigación no es significativo el uso del gráfico sino únicamente el cálculo del estadístico MEWMA utilizando Minitab^®.

Redes neuronales artificiales (RNA)

Las redes neuronales artificiales son métodos diseñados para el procesado de datos y la organización del conocimiento basado en la imitación del funcionamiento de los sistemas nerviosos biológicos, son capaces de predecir con precisión diferentes clases. Una red neuronal no se basa en un modelo algebraico explícito, sino en un conjunto de “unidades” de activación, denominadas también “nodos” o “neuronas artificiales” interconectados entre sí en forma de red. Pueden ser utilizadas para resolver problemas de reconocimiento de patrones tanto supervisados como no supervisados (Soler, 2007), por tal motivo se propuso su uso en esta investigación. En la presente sección se expone una pequeña introducción de las redes neuronales utilizadas.

De acuerdo con la información obtenida de los estadísticos T² y MEWMA de las variables, se emplearán las técnicas de redes neuronales tales como Perceptrón, Retropropagación y RBF con la finalidad de dar solución a la tarea de reconocimiento de patrones multivariantes presentes en los vectores de los estadísticos T² Hotelling y MEWMA. Con la información procedente del estadístico T² Hotelling y MEWMA se generarán las bases de entrenamiento y prueba utilizadas como entrada para las redes neuronales y se obtendrá el valor de eficiencia en el reconocimiento de esas entradas, en la figura 5 se muestra el procedimiento. El valor de eficiencia indica cuál red es la más conveniente en la tarea de reconocimiento de patrones multivariantes presentes en Hotelling y MEWMA.

Figura 5.

Reconocimiento mediante redes neuronales artificiales

Perceptrón

Red neuronal artificial utilizada en problemas de clasificación. El funcionamiento de la red perceptrón es muy simple, se basa en comparar la salida del sistema con una señal deseada (que es la que debería dar el sistema). De la estructura, más concretamente de la función de activación, se deduce que éste elemento es un clasificador binario, ya que puede determinar la pertenencia por parte del vector de entrada a dos clases diferentes. El algoritmo que sigue este sistema es de tipo supervisado, ya que necesitamos un elemento exterior que plantee la clase de pertenencia del elemento de entrada.

El procedimiento de aprendizaje comienza por la inicialización de los pesos, cuyo valor inicial puede ser aleatorio, o bien, cero para tener una misma línea base y cuya selección depende de la experiencia del diseñador. Esta red puede resolver solamente problemas que sean linealmente separables en problemas cuyas salidas estén clasificadas en dos categorías diferentes y que permitan que su espacio de entrada sea dividido en estas dos regiones por medio de un hiperplano (Tanco, 2003). Para esta investigación se propusieron los pará-metros: pesos inicializados en cero a efecto de tener una misma base de comparación entre experimentos, capa de inicio con dos entradas y capa de salida. Dados los valores de los pesos, la red ajusta los pesos de manera proporcional a la diferencia entre la salida actual proporcionada por la red y la salida deseada, con el fin de minimizar el error producido por la red.

Retropropagación

Retropropagación es un tipo de red de aprendizaje supervisado que emplea un ciclo propagación-adaptación de dos fases. Una vez que se ha aplicado un patrón a la entrada de la red como estímulo, éste se propaga desde la primera capa a través de las capas superiores de la red hasta generar una salida. La señal de salida se compara con la salida deseada y se calcula una señal de error para cada una de las salidas. Las salidas de error se propagan hacia atrás, partiendo de la capa de salida, hacia todas las neuronas de la capa oculta que contribuyen directamente a la salida. Sin embargo, las neuronas de la capa oculta sólo reciben una fracción de la señal total del error, basándose aproximadamente en la contribución relativa que haya aportado cada neurona a la salida original. Este proceso se repite, capa por capa, hasta que todas las neuronas de la red hayan recibido una señal de error que describa su contribución relativa al error total. Con base en la señal de error percibida, se actualizan los pesos de conexión de cada neurona, para hacer que la red converja hacia un estado que permita clasificar correctamente todos los patrones de entrenamiento (Tanco, 2003).

La importancia de este proceso consiste en que, a medida que se entrena la red, las neuronas de las capas intermedias se organizan a sí mismas de tal modo que las distintas neuronas aprenden a reconocer distintas características del espacio total de entrada. Después del entrenamiento, cuando se les presenta un patrón arbitrario de entrada que contenga ruido o que esté incompleto, las neuronas de la capa oculta de la red responderán con una salida activa si la nueva entrada contiene un patrón que se asemeja a la característica que las neuronas individuales hayan aprendido a reconocer durante su entrenamiento (Tanco,2003). Para esta investigación se propusieron los parámetros: pesos inicializados en cero a efecto de tener una misma base de comparación entre experimentos, capa de inicio con dos entradas, dos capas ocultas y capa de salida.

Función de base radial (RBF)

Las redes RBF se caracterizan por tener un aprendizaje o entrenamiento híbrido. La arquitectura de estas redes se caracteriza por la presencia de tres capas: una entrada, una única capa oculta y una capa de salida. Sus características son:

• 1)

  El número de unidades en la capa de entrada representa la dimensionalidad del espacio de entrada.

• 2)

  La capa oculta contiene las unidades RBF. Las unidades se añaden a esta capa durante el entrenamiento. La capa está totalmente conectada a la capa oculta.

• 3)

  Cada unidad de la capa de salida representa una posible clase.

Para clasificar se escoge la unidad con mayor valor de activación. Aunque la arquitectura puede ser similar a la red Perceptrón, la diferencia fundamental está en que las neuronas de la capa oculta, en lugar de calcular una suma ponderada de las entradas y aplicar una función sigmoidal, estas neuronas calculan la distancia euclídea entre la matriz de pesos sinápticos y la entrada; sobre esta distancia se aplica una función de tipo radial con forma gaussiana (Soler, 2007). Para esta investigación se propusieron los parámetros: pesos inicializados en cero a efecto de tener una misma base de comparación entre experimentos, capa de inicio con dos entradas, dos capas ocultas y capa de salida.

En la siguiente sección se presenta la experimentación de los diferentes casos de variables multivariantes, asimismo el análisis estadístico y la aplicación de redes neuronales para cada caso.

Experimentación

Generación de variables multivariantes

Se consideró p como el número de variables de un proceso aleatorio que tienen patrones específicos, los cuales forman los diferentes casos de variables multivariantes, cada variable está conformada con X = [x₁, x₂, x₃,…, x_n] n = 100 observaciones en el caso generado por Simulación de Montecarlo y X = [x₁, x₂, x₃,…, x_n] n = 60 observaciones en el caso de la base de datos “Synthetic Control Chart Time Series”.

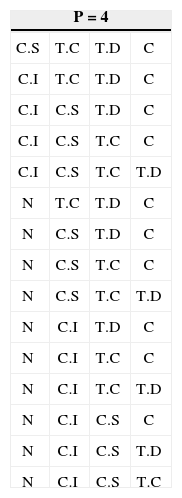
Se trabajó con p = 2, 3 y 4 variables, donde cada una sigue un patrón de variación, bajo la siguiente codificación mostrada en las tablas 2-7 : Indicados como: N: natural, C.I: cambio inferior, C.S: cambio superior, T.C: tendencia creciente, T.D: tendencia decreciente, C: ciclo, S: sistemático.

P=2
N	C.I
N	C.S
N	T.C
N	T.D
N	C
N	S
C.I	C.S
C.I	T.C
C.I	T.C
C.I	C
C.I	S
C.S	T.C
C.S	T.D
C.S	C
C.S	S
T.C	T.D
T.C	C
T.C	S
T.D	C
T.D	S
C	S

P = 3
N	C.I	C.S
N	C.I	T.C
N	C.I	T.D
N	C.I	C
N	C.I	S
N	C.S	T.C
N	C.S	T.D
N	C.S	C
N	C.S	S
N	T.C	T.D
N	T.C	C
N	T.C	S
N	T.D	C
N	T.D	S
N	C	S
C.I	C	S
C.I	T.D	S
C.I	T.D	C
C.I	T.C	S
C.I	T.C	C
C.I	T.C	T.D
C.I	C.S	S
C.I	C.S	C
C.I	C.S	T.D
C.I	C.S	T.C
C.S	C	S
C.S	T.D	S
C.S	T.D	C
C.S	T.C	S
C.S	T.C	C
C.S	T.C	T.D
T.C	T.D	C
T.C	T.D	S
T.C	C	S
T.D	C	S

P = 4
T.C	T.D	C	S
C.S	T.D	C	S
C.S	T.C	C	S
C.S	T.C	T.D	S
C.S	T.C	T.D	C
C.I	T.D	C	S
C.I	T.C	C	S
C.I	T.C	T.D	S
C.I	T.C	T.D	C
C.I	C.S	C	S
C.I	C.S	T.D	S
C.I	C.S	T.D	C
C.I	C.S	T.C	S
C.I	C.S	T.C	C
C.I	C.S	T.C	T.D
N	T.D	C	S
N	T.C	C	S
N	T.C	T.D	S
N	T.C	T.D	C
N	C.S	C	S
N	C.S	T.D	S
N	C.S	T.D	C
N	C.S	T.C	S
N	C.S	T.C	C
N	C.S	T.C	T.D
N	C.I	C	S
N	C.I	T.D	S
N	C.I	T.D	C
N	C.I	T.C	S
N	C.I	T.C	C
N	C.I	T.C	T.D
N	C.I	C.S	S
N	C.I	C.S	C
N	C.I	C.S	T.D
N	C.I	C.S	T.C

P = 2
N	C.I
N	es
N	T.C
N	T.D
N	C
C.I	C.S
C.I	T.C
C.I	T.D
C.I	C
C.S	T.C
C.S	T.D
C.S	C
T.C	T.D
T.C	C
T.D	C

P = 3
T.C	T.D	C
C.S	T.D	C
C.S	T.C	C
C.S	T.C	T.D
C.I	T.D	C
C.I	T.C	C
C.I	T.C	T.D
C.I	C.S	C
C.I	C.S	T.D
C.I	C.S	T.C
N	T.D	C
N	T.C	C
N	T.C	T.D
N	C.S	C
N	C.S	T.D
N	C.S	T.C
N	C.I	C
N	C.I	T.D
N	C.I	T.C

P = 4
C.S	T.C	T.D	C
C.I	T.C	T.D	C
C.I	C.S	T.D	C
C.I	C.S	T.C	C
C.I	C.S	T.C	T.D
N	T.C	T.D	C
N	C.S	T.D	C
N	C.S	T.C	C
N	C.S	T.C	T.D
N	C.I	T.D	C
N	C.I	T.C	C
N	C.I	T.C	T.D
N	C.I	C.S	C
N	C.I	C.S	T.D
N	C.I	C.S	T.C

De acuerdo con las combinaciones mostradas en las tablas 2 a 7, se utilizaron esas combinaciones para generar los tipos de variables aleatorias multivariantes propuestas, utilizando las bases de datos generadas por simulación de Montecarlo y la base de datos “Synthetic Control Chart Time Series”. En los diferentes tipos de variables aleatorias cada proceso o elemento presenta un tipo de patrón; con Matlab® se determinó el número y composición de las variables aleatorias con dos, tres y cuatro procesos aleatorios.

La composición se refiere a las diferentes combinaciones de los patrones presentes en cada proceso, mostrados en las tablas 2 a la 7.

• 1.

  Variables aleatorias multivariantes con dos procesos aleatorios. Se considera p = 2 variables procesos aleatorios X = [X₁, X₂]_T. Se generaron 21 variables multivariantes por simulación de Montecarlo y 15 variables multivariantes de la base de datos.

• 2.

  Variables aleatorias multivariantes con tres procesos aleatorios. Se considera p = 3 procesos aleatorios X = [X₁, X₂, X₃]_T. Se generaron 35 variables multivariantes por simulación de Montecarlo y 20 variables multivariantes de la base de datos.

• 3.

  Variables aleatorias multivariantes con cuatro procesos aleatorios. Se considera p = 4 procesos aleatorios X = [X₁, X₂, X₃, X₄]T. Se generaron 35 variables multivariantes por simulación de Montecarlo y 15 variables multivariantes de la base de datos.

Codificación para la Simulación de Montecarlo

En las tablas 2, 3 y 4 se presentan las posibles combinaciones de patrones en variables multivariantes de dos, tres y cuatro elementos respectivamente.

Codificación para la base de datos

En las tablas 5, 6 y 7 se presentan las posibles combinaciones de patrones (base de datos) en variables multivariantes de dos, tres y cuatro elementos respectivamente.

Análisis estadístico

Para cada variable multivariante se realizó un análisis estadístico calculando la matriz de covarianza y correlación mediante Matlab^® con el propósito de observar su comportamiento y características estadísticas, asimismo de encontrar las variables con valores de covarianza y correlación significativa. Se propuso como índice de correlación significativa los valores de ρ > 0.75 y ρ < –0.75. Se analizaron mediante el índice de correlación las 141 variables tomando en cuenta las variables generadas por simulación de Montecarlo y de la base de datos “Synthetic Control Chart Time Series”.

Con base en los resultados, se obtuvieron 24 variables con correlación significativa, las cuales se seleccionan como entradas de las redes neuronales. Las variables multivariantes que presentaron una relación y correlación significativa en todos sus componentes se presentan más adelante como X_k para indicar los diferentes patrones que lo conforman como N: natural, C.I: cambio inferior, C.S: cambio superior, T.C: tendencia creciente, T.D: tendencia decreciente, C: ciclo, S: sistemático.

Simulación de Montecarlo

1. Variables multivariantes con dos procesos aleatorios:

2. Variables multivariantes con tres procesos aleatorios:

3. Variables multivariantes con cuatro procesos aleatorios:

Base de datos: Synthetic Control Chart Time Series

1. Variables multivariantes con dos procesos aleatorios:

2. Variables multivariantes con tres procesos aleatorios:

3. Variables multivariantes con cuatro procesos aleatorios:

De acuerdo con los resultados obtenidos, se puede concluir que a medida que aumenta el número de procesos aleatorios involucrados en los diferentes casos de variables aleatorias multivariantes se observa que el número de variables con correlaciones significativas disminuye. Con los resultados del índice de correlación, se eligieron las variables multivariantes con correlación significativa, ya que es una característica importante debido a que no es analizada mediante técnicas tradicionales de control, lo cual representa una pérdida de información del proceso, por tal motivo se desean analizar datos que presentan correlación en su información para observar su comportamiento. Después de analizar las diferentes variables multivariantes generadas, se utilizó el programa Minitab^® para el cálculo de los estadísticos T² Hotelling y MEWMA de cada variable multivariante con correlación significativa y valores homogéneos de covarianza, media y varianza con el fin de determinar si las series de datos son caracterizables estadísticamente. Se realizó el cálculo de medidas estadísticas descriptivas como la media, desviación estándar, varianza, curtosis, sesgo, intervalos de confianza y normalidad.

De acuerdo con este análisis se concluyó que son series de datos caracterizables debido a que sus características pueden ser obtenidas y la combinación de diferentes patrones en las variables multivariantes muestra visualmente la formación de ciertos patrones multivariantes. Asimismo, se observó que gran parte de las variables multivariantes presentan un comportamiento no normal, esto no es un impedimento para la investigación, ya que el uso de las redes neuronales no requiere la suposición estadística en la normalidad de los datos.

Reconocimiento de patrones

Para formar las bases de “Entrenamiento y Prueba” se calcularon seis vectores T² y MEWMA de cada variable multivariante seleccionada, formando grupos conformados por dos T² y MEWMA respectivamente (por ej. T² (X₁) y T² (X₂) y ME(X₁) y ME (X₂) y se generan dos matrices 3 × n, una para entrenamiento y otra para prueba como entradas de la red. En la figura 6 se presenta el ejemplo de la clasificación de las bases de datos, asimismo, se muestran las salidas predefinidas y deseadas para las etapas de entrenamiento y pruebas de la red.

Figura 6.

Reconocimiento y clasificación mediante RNA

Las tareas de reconocimiento de los vectores T² y MEWMA correspondientes a las diferentes variables se realizaron en el Toolbox nntool de MATLAB^® con las diferentes topologías de RNA, tal como Perceptrón, Retropropagación y RBF. Se evaluaron las bases de datos de entrenamiento y pruebas correspondientes a los resultados de T² y MEWMA de las diferentes variables, las cuales son las entradas de las diferentes topologías de redes neuronales utilizadas en la presente investigación.

En la siguiente sección se presentan los resultados obtenidos en la tarea de reconocimiento de los vectores T² y MEWMA correspondientes a las diferentes variables multivariantes que presentaron covarianza y correlación significativa, generados por simulación de Montecarlo y utilizando la base de datos “Synthetic Control Chart Time Series”.

Resultados

Reconocimiento de T² y MEWMA de variables multivariantes por simulación de Montecarlo

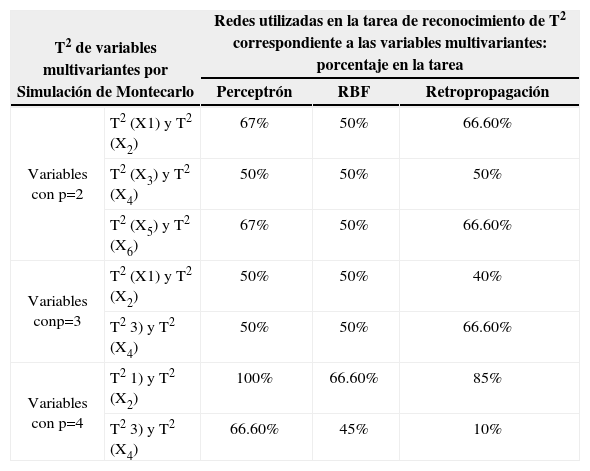
Con base en la experimentación, los resultados obtenidos con el estadístico T² y MEWMA se muestran en las tablas 8 y 9, respectivamente.

Tabla 8.

Porcentajes de reconocimiento de T² basados en simulación de Montecarlo

T^2 de variables multivariantes por Simulación de Montecarlo		Redes utilizadas en la tarea de reconocimiento de T^2 correspondiente a las variables multivariantes: porcentaje en la tarea
		Perceptrón	RBF	Retropropagación
Variables con p=2	T^2 (X1) y T^2 (X2)	67%	50%	66.60%
	T^2 (X3) y T^2 (X4)	50%	50%	50%
	T^2 (X5) y T^2 (X6)	67%	50%	66.60%
Variables conp=3	T^2 (X1) y T^2 (X2)	50%	50%	40%
	T^2 3) y T^2 (X4)	50%	50%	66.60%
Variables con p=4	T^2 1) y T^2 (X2)	100%	66.60%	85%
	T^2 3) y T^2 (X4)	66.60%	45%	10%

Tabla 9.

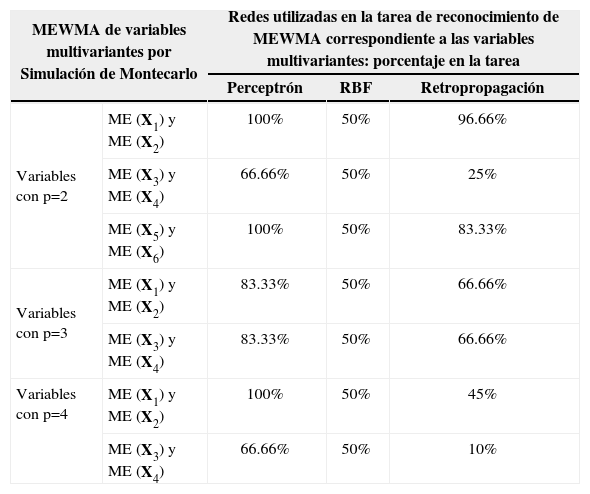
Porcentajes de reconocimiento de MEWMA basados en simulación de Montecarlo

MEWMA de variables multivariantes por Simulación de Montecarlo		Redes utilizadas en la tarea de reconocimiento de MEWMA correspondiente a las variables multivariantes: porcentaje en la tarea
		Perceptrón	RBF	Retropropagación
Variables con p=2	ME (X1) y ME (X2)	100%	50%	96.66%
	ME (X3) y ME (X4)	66.66%	50%	25%
	ME (X5) y ME (X6)	100%	50%	83.33%
Variables con p=3	ME (X1) y ME (X2)	83.33%	50%	66.66%
	ME (X3) y ME (X4)	83.33%	50%	66.66%
Variables con p=4	ME (X1) y ME (X2)	100%	50%	45%
	ME (X3) y ME (X4)	66.66%	50%	10%

Los resultados se describen como el porcentaje de eficiencia de las topologías utilizadas para las tareas de reconocimiento de las variables multivariantes con procesos aleatorios, los cuales presentan patrones de variación (especial y natural). Los porcentajes más elevados fueron obtenidos con las redes Perceptrón y Retropropagación en los diferentes tipos de variables multivariantes y con los diferentes estadísticos multivariantes (Hotelling y MEWMA). Asimismo, se puede observar que los valores de reconocimiento de los vectores MEWMA son mayores en comparación con los obtenidos con T² Hotelling.

Reconocimiento de T² Y MEWMA de variables multivariantes de la base de datos “Synthetic Control Chart Time Series”

Los resultados obtenidos del reconocimiento de T² y MEWMA de variables multivariantes de la base de datos “Synthetic Control Chart Time Series” se presentan en las tablas 10 y 11, respectivamente.

Tabla 10.

Porcentajes de reconocimiento de T² de la base de datos “Synthetic Control Chart Time Series”

T^2 de variables multivariantesde base de datos “SyntheticControl Chart Time Series”		Redes utilizadas en la tarea de reconocimiento de T^2 correspondiente a las variables multivariantes: porcentaje en la tarea
		Perceptrón	RBF	Retropropagación
Variables con p=2	T^2 (X1) y T^2 (X2)	33.33%	50%	50%
	T^2 (X3) y T^2 (X4)	67%	50%	61.67%
Variables con p=3	T^2 (X1) y T^2 (X3)	33.33%	50%	28%
	T^2 (X2) y T^2 (X4)	67%	50%	55.16%
Variablescon p=4	T^2 (X1) y T^2 (X2)	83%	50%	50%

Tabla 11.

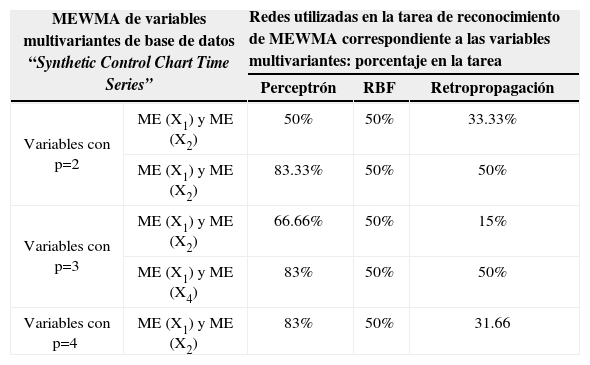
Porcentajes de reconocimiento de MEWMA de la base de datos “Synthetic Control Chart Time Series”

MEWMA de variables multivariantes de base de datos “Synthetic Control Chart Time Series”		Redes utilizadas en la tarea de reconocimiento de MEWMA correspondiente a las variables multivariantes: porcentaje en la tarea
		Perceptrón	RBF	Retropropagación
Variables con p=2	ME (X1) y ME (X2)	50%	50%	33.33%
	ME (X1) y ME (X2)	83.33%	50%	50%
Variables con p=3	ME (X1) y ME (X2)	66.66%	50%	15%
	ME (X1) y ME (X4)	83%	50%	50%
Variables con p=4	ME (X1) y ME (X2)	83%	50%	31.66

Con base en los resultados experimentales, se observó un número mayor de variables multivariantes con correlación significativa generadas por simulación de Montecarlo al compararlas con las variables con correlación significativa encontradas en la base de datos “Synthetic Control Chart Time Series”. Se puede observar además que los resultados en la tarea de reconocimiento son mejores utilizando las técnicas Perceptrón y RBF para el caso de MEWMA, para el caso de Hotelling, se obtuvieron de forma general mejores resultados con Perceptrón seguido de Retropropagación y RBF.

Conclusiones

De acuerdo al análisis de los vectores T² y MEWMA se puede concluir que son series de datos caracterizables debido a que se pueden obtener sus características estadísticas. Se observó que al aumentar el número de patrones o el número de procesos aleatorios con presencia de patrones de variación en la generación de los diferentes tipos de variables multivariantes, disminuyó el número de combinaciones que presentan covarianza y correlación significativa en todos sus componentes y se encontraron un número mayor de variables multivariantes con correlación significativa, generadas por simulación de Montecarlo al compararlas con las variables con correlación significativa encontradas en la base de datos “Synthetic Control Chart Time Series”.

Se observó en los resultados que la tarea de reconocimiento de patrones resulta ser más eficiente de forma global utilizando las técnicas de Retropropagación y Perceptrón.

Las redes Perceptrón y Retropropagación fueron capaces de distinguir ciertos valores entre las diferentes clases o tipos de variables conformadas por los 7 patrones utilizados y del mismo modo se observó que al tener las clases datos cercanos entre sí, las redes no son capaces de clasificarlos de manera eficiente. Esto quizás se debe a que la red Perceptrón clasifica de manera lineal y Retropropagación, aunque clasifica patrones con naturaleza no-lineal de forma eficiente, es susceptible a fallar en el entrenamiento y nunca converger debido al uso de la técnica por gradiente descendiente durante la optimización, lo que significa que sigue la “superficie del error” siempre hacia abajo, hasta alcanzar un mínimo local, lo que no garantiza que se alcance siempre una solución globalmente óptima para la clasificación de datos.

El trabajo que se desarrolla actualmente contempla la comparación con otras RNA, con el objetivo de seleccionar la mejor red y probar su eficiencia en el reconocimiento de patrones multivariantes en casos reales de producción industrial. Por tal motivo, se propone utilizar otras técnicas como Support Vector Machines (SVM) y Fuzzy ARTMAP que muestran mayor flexibilidad para clasificar los valores de los vectores de Hotelling y MEWMA pertenecientes a las diferentes variables, dado que las redes SVM poseen la capacidad para clasificar los datos lineales o no lineales gracias a los diferentes Kernels que se emplean para la formación de hiperplanos que clasifican los datos. Por otro lado, la red Fuzzy ARTMAP tiene una estructura con entrenamiento más rápido y eficiente.

Agradecimientos

Los autores agradecen al Consejo Nacional de Ciencia y Tecnología (CONACyT) el apoyo otorgado a la M en C Pamela Chiñas durante sus estudios doctorales para desarrollar la presente investigación.