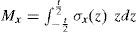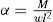Coeficientes de diseño y trayectorias de agrietamiento de losas aisladas circulares, elípticas y triangulares

Resumen

Se determinan, mediante la mecánica del daño continuo, coeficientes de diseño y trayectorias de agrietamiento en losas circulares, elípticas y triangulares. El comportamiento no lineal del concreto reforzado se simuló con un modelo de daño, el cual considera ablandamiento, mientras que el comportamiento del acero de refuerzo con un modelo de plasticidad bilineal con superficie de fluencia de Von Misses. Los modelos constitutivos y el método de los elementos finitos se validan comparando los resultados numéricos con los experimentales de una losa rectangular reportada en la literatura. La distribución del acero de refuerzo se propone con base en análisis elásticos lineales con elementos placa. Los coeficientes se calcularon con análisis elásticos y no lineales, observándose que en estos últimos existe una variación debido a la redistribución de esfuerzos. Se muestran las trayectorias del agrietamiento, las cuales son dependientes de las condiciones de apoyo. Los coeficientes y la distribución del acero de refuerzo para losas con estas geometrías son una base en la reglamentación para el análisis y diseño de losas con este tipo de geometrías.

Abstract

Design coefficients and cracking paths for circular, elliptical and triangular labsare obtained by damage mechanics were determined. The nonlinear behavior of the reinforced concrete was simulated with a damage model which considers softening, whereas the behavior of the reinforcing steel was modeling with a bilinear plasticity model which has a Von Mises yield surface. The constitutive models and the finite element method were validated by comparing the computed numerical results with the experimental results of a rectangular slab reported in the scientific literature. The distribution of the reinforcing steel was proposed based on linear elastic analysis with plate elements. The coefficients were computed with elastic and nonlinear analyses, noticing that the last has a variation because of the stress redistribution. The crack paths are shown, which are dependent on the boundary conditions. The coefficients and the distribution of the reinforcing steel are a base on the regulation for the analysis and design of slabs with this kind of geometry.

Introducción

Los sistemas de piso son subsistemas estructurales de los más antiguos y utilizados por la humanidad, pues se les han dado diversos usos en la mayoría de las construcciones. La gran aceptación que tienen estos elementos como parte de un sistema estructural, se debe a las ventajas que presentan en cuanto a la transferencia de cargas verticales y horizontales.

Los sistemas de piso en estructuras de concreto y mampostería generalmente contemplan las geometrías rectangulares; sin embargo, algunos diseños arquitectónicos requieren de geometrías irregulares en planta. Para el diseño de losas de geometría rectangular existen métodos de análisis elásticos, o bien, se utilizan coeficientes tabulados en normas de diseño, mientras que las losas no rectangulares, como las mostradas en la figura 1, se caracterizan por no presentar formas comunes de estructuración y por carecer de metodologías de análisis.

Figura 1.

Losas con geometrías no rectangulares

Para el análisis de losas rectangulares, Westergaard y Slater (1921) propusieron una metodología con base en la teoría de la elasticidad, particularmente de losas apoyadas en dos direcciones y losas planas apoyadas en capiteles circulares mediante una redistribución de esfuerzos dependientes de la redistribución de rigideces, estos autores consideraron dos variables elementales: las condiciones de apoyo y el tipo de carga; algunos de estos resultados se compararon con pruebas experimentales reportadas en la literatura. Tiempo después, Marcus (1929) desarrolló un procedimiento aproximado, mediante el cual los momentos máximos elásticos en una placa apoyada sobre vigas rígidas se pueden determinar tomando como base el análisis de una franja de losa y obteniendo factores de reducción para corregir los momentos obtenidos. Además, realizó cuatro tablas de coeficientes de momentos, los cuales proporcionan valores para la distribución del panel de carga en dos direcciones, la evaluación de momentos negativos en bordes continuos y positivos para la mitad del centro del claro.

Fue hasta 1940 que el Comité del American Concrete Institute, ACI, realizó modificaciones a las propuestas realizadas por Westergaard y Slater (1921), extendiendo el método de análisis para cubrir todas las posibles combinaciones de paneles en un sistema de piso. Esto llevó a una tabla de coeficientes para momento positivo en el centro del claro y momento negativo en los bordes, ya sean continuos o discontinuos, considerando las condiciones de forma y de apoyo adyacentes al panel. Posteriormente, Newmark y Siess (1950)Newmark and Siess, 1950 propusieron un método de diseño para losas en dos direcciones, resultado de estudios analíticos mediante un proceso de distribución de momentos; estos autores estudiaron diferentes condiciones de placas continuas con el fin de verificar los efectos relativos de las variables que influyen en el desarrollo de momentos en losas soportadas por vigas rígidas. El desarrollo en detalle del procedimiento aproximado de distribución de momentos fue reportado por estos mismos autores en Siess y Newmark (1950).

Para determinar los coeficientes de momentos en losas rectangulares, como los que se tienen tabulados en los reglamentos actuales de diseño, se realizaron calibraciones con pruebas de laboratorio como las reportadas por Bach y Graf (1915), Mayes et al. (1959), Hatcher et al. (1960), Hatcher et al. (1961),emsp Vanderbilt et al. (1961), Gamble et al. (1961), Jirsa et al. (1962), Girolami et al. (1970), Foster et al. (2004), Casadei et al. (2005) y Galati et al. (2008), entre otros. Es de interés señalar que las referencias mencionadas son la base de las investigaciones y aplicaciones que se realizan en el análisis y diseño de losas rectangulares actualmente. Sin embargo, al revisar normatividades vigentes de diseño de losas como el ACI 318-11, Eurocódigo 2 (EC2), y el Reglamento de Construcciones para el Distrito Federal (RCDF-04) y sus Normas Técnicas Complementarias para Diseño y Construcción de Estructuras de Concreto (NTCC-04), no se encontraron recomendaciones para el análisis y diseño de losas con geometría diferente a la rectangular.

Para determinar los momentos de diseño en losas rectangulares, el ACI 318-11 sugiere los métodos directo y el equivalente, las NTCC-04 proporcionan una tabla de coeficientes y el EC2, aunque sólo recomienda utilizar algún método válido, también proporciona como opción el uso de una tabla de coeficientes reportada en IStructE, (2006). Es de interés mencionar que la tabla de coeficientes que proporcionan las NTCC-04 fue tomada del ACI 318-63, los cuales, como lo demuestran Gutiérrez-Morgado y Juárez-Luna (2012), en algunos casos subestiman los momentos de diseño.

Por lo anterior, este artículo tiene por objetivo determinar coeficientes de diseño y recomendaciones de la ubicación del acero de refuerzo, utilizando la mecánica computacional para losas con geometría circular, triangular y elíptica. Se realizaron análisis elásticos para establecer las recomendaciones de la ubicación del acero de refuerzo. Posteriormente se realizaron análisis no lineales de estas losas para determinar la variación de los coeficientes de diseño, así como el inicio y las trayectorias de agrietamiento. El modelo de daño utilizado para el concreto considera umbrales diferentes para la tensión y la compresión, el cual presenta ablandamiento por deformación; mientras que el modelo constitutivo para el acero fue el de plasticidad de Von Mises con endurecimiento por deformación. Estos modelos constitutivos se validan mediante la simulación numérica del experimento de una losa cuadrada reportada en la literatura, garantizando la representación adecuada con las curvas carga contra desplazamiento al centro de la losa y las trayectorias de agrietamiento.

El resto del artículo se describe a continuación. En la siguiente sección se presentan los modelos constitutivos del concreto y el acero utilizados en los análisis no lineales. La tercera sección presenta la validación del método de los elementos finitos y de los modelos constitutivos con el modelado numérico de un experimento de laboratorio reportado en la literatura. Después se presentan los modelos numéricos de las losas en estudio, determinándose la distribución del acero con análisis elásticos y las curvas carga contra desplazamiento al centro, resultado de los análisis no lineales del material. En la quinta sección se determinan los coeficientes de diseño para las losas con las geometrías estudiadas. La sexta sección muestra el inicio y la evolución de las trayectorias del agrietamiento de losas empotradas y simplemente apoyadas. En la última sección se presentan las conclusiones derivadas de esta investigación.

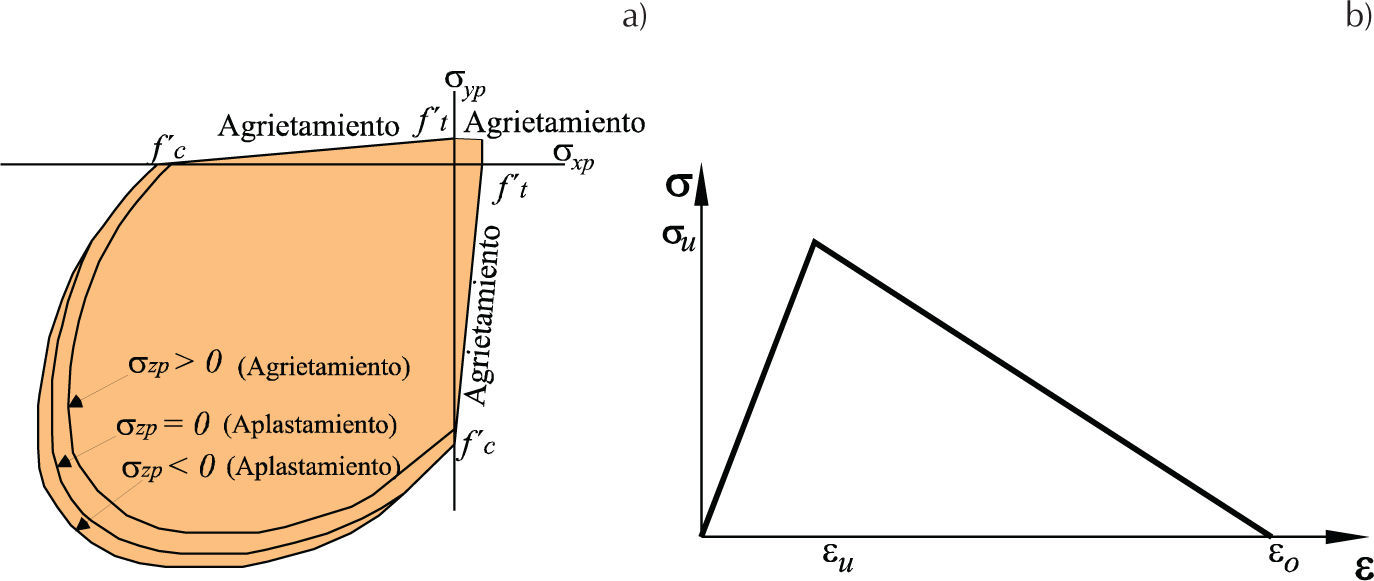
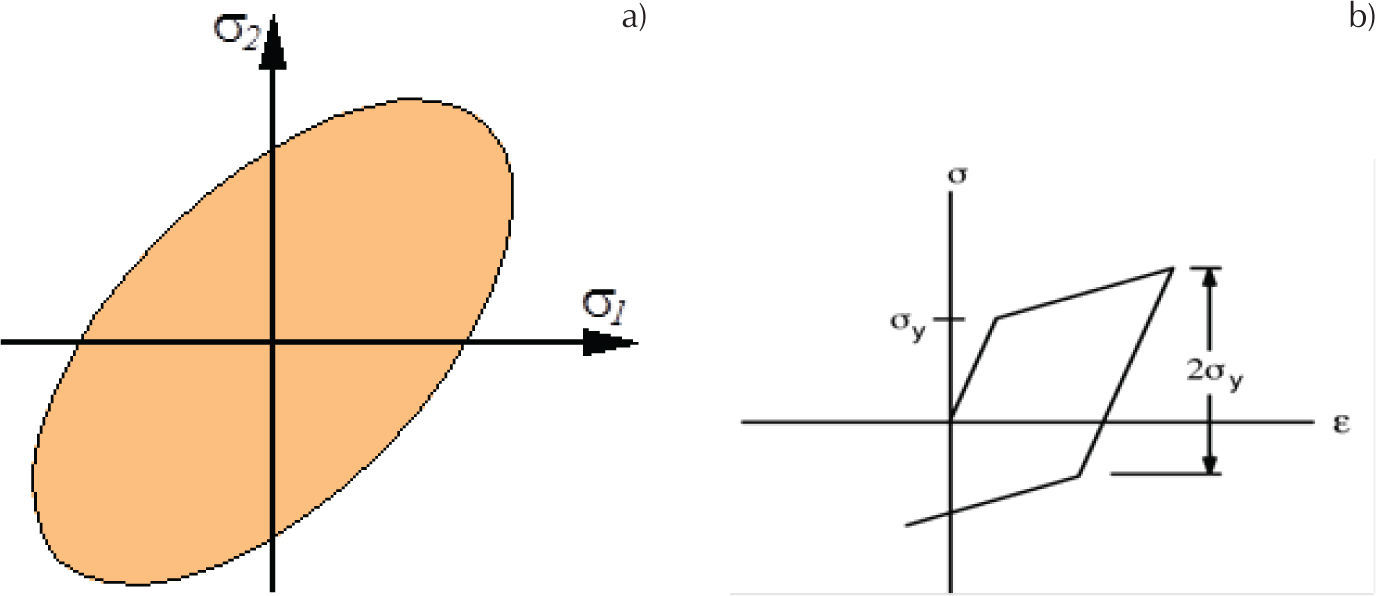
Modelos constitutivos

Para modelar el comportamiento del concreto se utilizó un modelo de daño con diferente umbral en tensión y en compresión, el cual fue propuesto por William y Warnke (1975), consistente con el comportamiento constitutivo experimental reportado en la literatura, como se muestra en la figura 2a. El concreto considera el ablandamiento por deformación después de alcanzar el esfuerzo último; aunque existen otras funciones de ablandamiento como la exponencial, bilineal, trilineal, etcétera, en los análisis no lineales, este ablandamiento se idealizó con una función lineal (figura 2b). Para modelar el acero de refuerzo se utilizó un modelo de plasticidad con superficie de fluencia de Von Mises, en el cual se supone el mismo umbral en tensión y compresión, como se muestra en la figura 3a; el endurecimiento se idealizó como una función bilineal mostrada en la figura 3b.

Figura 2.

Modelo constitutivo del concreto: a) superficie de falla y b) ablandamiento por deformación

Figura 3.

Modelo constitutivo del acero: a) superficie de falla y b) endurecimiento

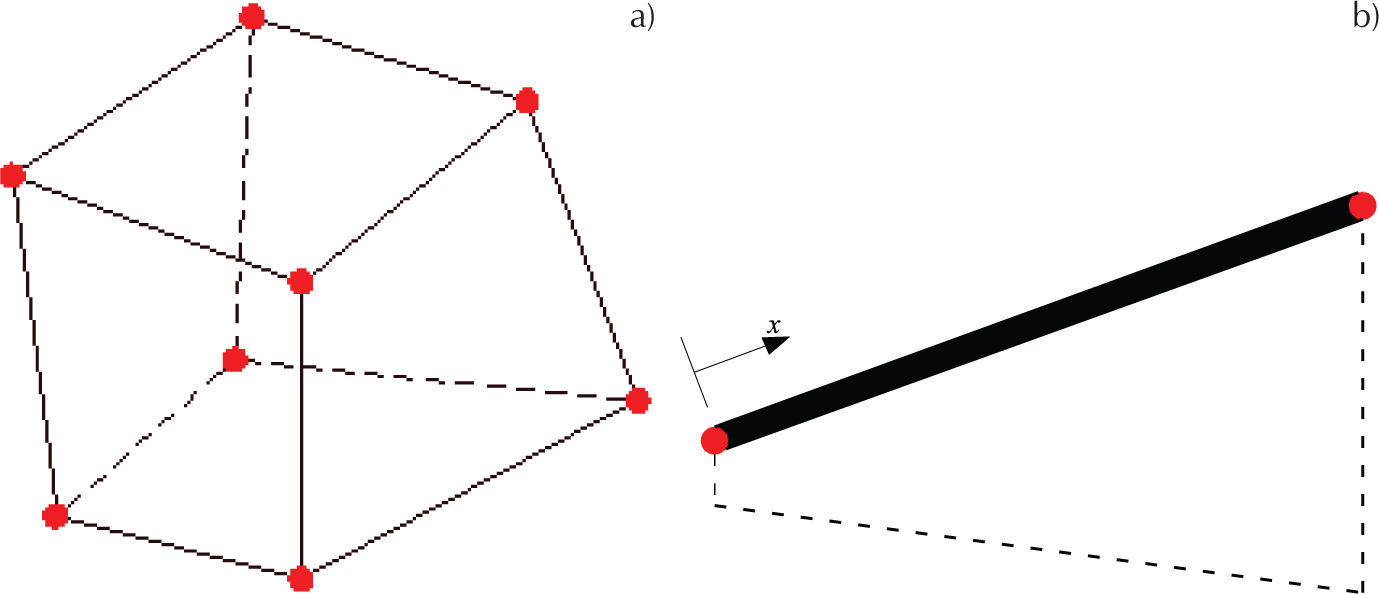
Los modelos no lineales se realizaron en el programa de elementos finitos Ansys 13.0. El concreto se discretizó con el elemento finito sólido hexaedro de ocho nodos del tipo solid 65 mostrado en la figura 4a, el cual tiene la capacidad de simular de manera distribuida el agrietamiento en tensión y aplastamiento en compresión, en tanto que el acero se discretizó con el elemento finito unidimensional lineal link 180 mostrado en la figura 4b, al que se le asignó el modelo de plasticidad de Von Mises. Ambos elementos finitos tienen tres grados de libertad traslacional por nodo, así como la capacidad de representar deformaciones grandes.

Figura 4.

Elementos finitos: a) hexaedro y b) unidimensional

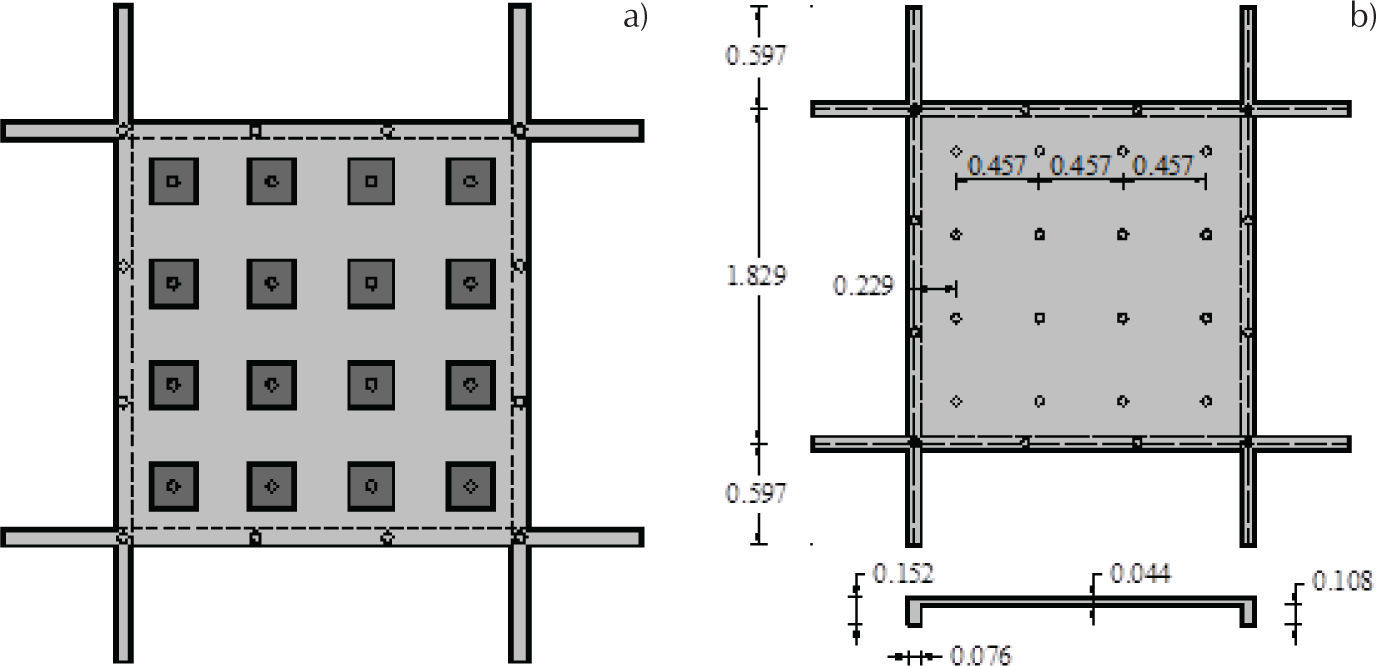
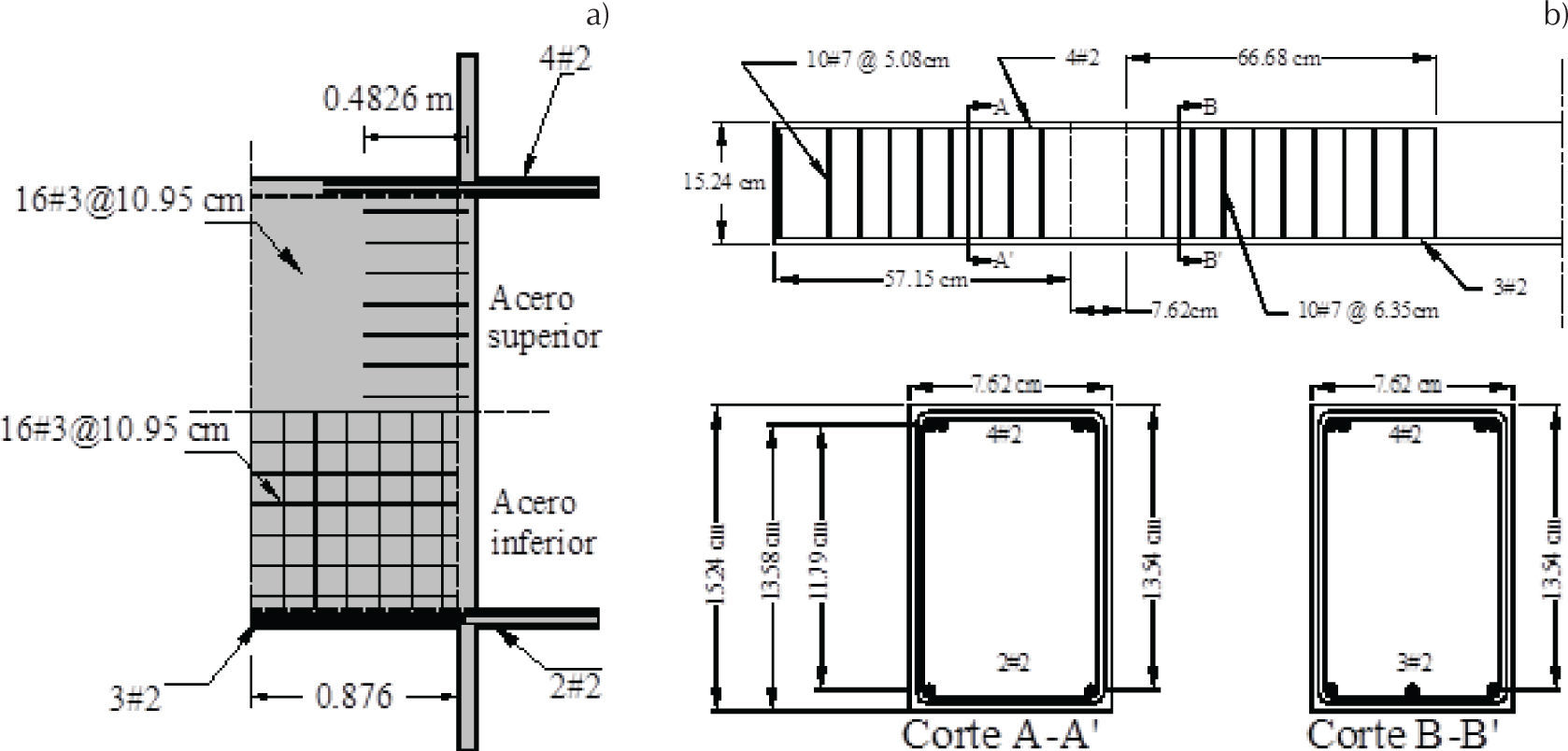
Validación

En este artículo no se realizaron modelos experimentales de laboratorio debido a que está fuera del objetivo del trabajo, por lo que, para validar los modelos constitutivos del concreto y el acero, se modeló uno de los seis especímenes probados por Girolami et al. (1970). El espécimen consistió de una losa de 1.829 × 1.829 m y 0.044 m de espesor, en la que se aplicaron únicamente cargas verticales (figura 5a). Cada carga vertical se aplicó sobre cuatro gatos, distribuida sobre 16 placas, mediante cuatro árboles de carga como se muestra en la figura 5b. Cada placa de distribución se centró sobre los huecos del espécimen de la losa. Las placas de distribución de cargas eran cuadradas de 0.2038 m por lado y de 0.0254 m de ancho; cada placa tenía un asiento esférico cóncavo para una junta esférica cóncava. El concreto tenía un módulo elástico E_c =19.90 GPa y su resistencia a compresión era de σ_uc =31.026 MPa, el acero de refuerzo tenía un módulo elástico E_a = 206 GPa y un esfuerzo de fluencia σ_y = 330.95 MPa.

Figura 5.

a) Modelo geométrico del experimento y b) cargas en el experimento

El sistema de losa y vigas perimetrales tenía acero en la parte superior e inferior, diseñado para soportar una carga uniformemente distribuida de 7.182 kPa. La distribución del acero de refuerzo de la losa se muestra en la figura 6a y el de las vigas en la figura 6b. El hecho que las vigas perimetrales tengan bastante acero por cortante, estribos del #7, se debe a que a cinco de los seis especímenes probados por Girolami et al. (1970) se les aplicó cargas en su plano, además de las cargas perpendiculares a su superficie; con este acero por cortante se buscó evitar el daño en las vigas y transmitirlo al plano de las losas.

Figura 6.

Distribución de acero de refuerzo del espécimen de prueba en estudio donde: a) losa y b) vigas perimetrales

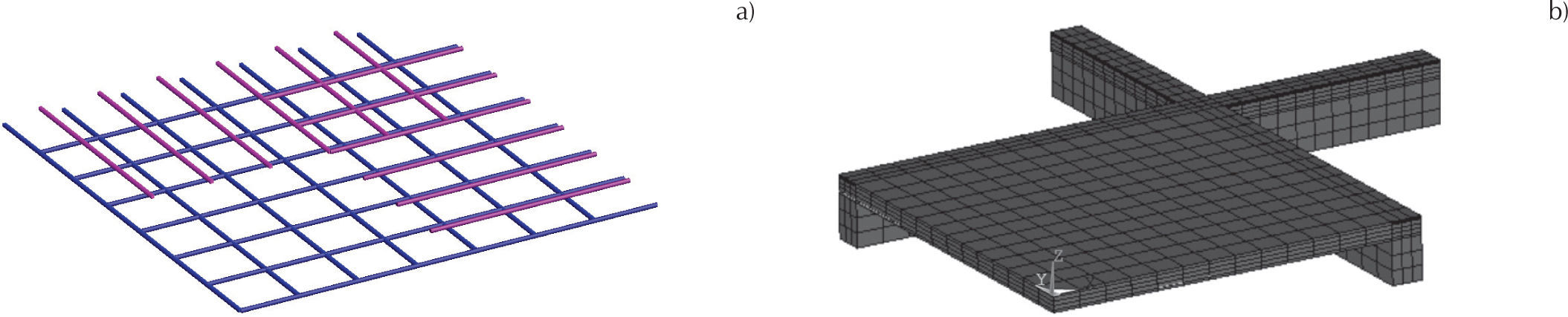
El análisis no lineal de esta losa se realizó considerando los dos ejes de simetría del espécimen, por lo que sólo se modeló un cuarto del espécimen, restringiendo respectivamente los grados de libertad perpendiculares a cada eje de simetría. La malla de acero de refuerzo de la losa se muestra en la figura 7a, la cual se estructuró de tal forma que los elementos lineales coincidan con los bordes de los elementos sólidos, mientras que la malla del concreto de la losa y las vigas con la malla del acero de refuerzo embebido se muestra en la figura 7b, los nodos del acero de refuerzo coinciden con los nodos de los elementos sólidos. En éste y en el resto de los ejemplos numéricos del artículo se consideró el acoplamiento perfecto entre los grados de libertad del acero y del concreto.

Figura 7.

Malla de elementos finitos: a) acero de refuerzo de la losa y b) concreto reforzado

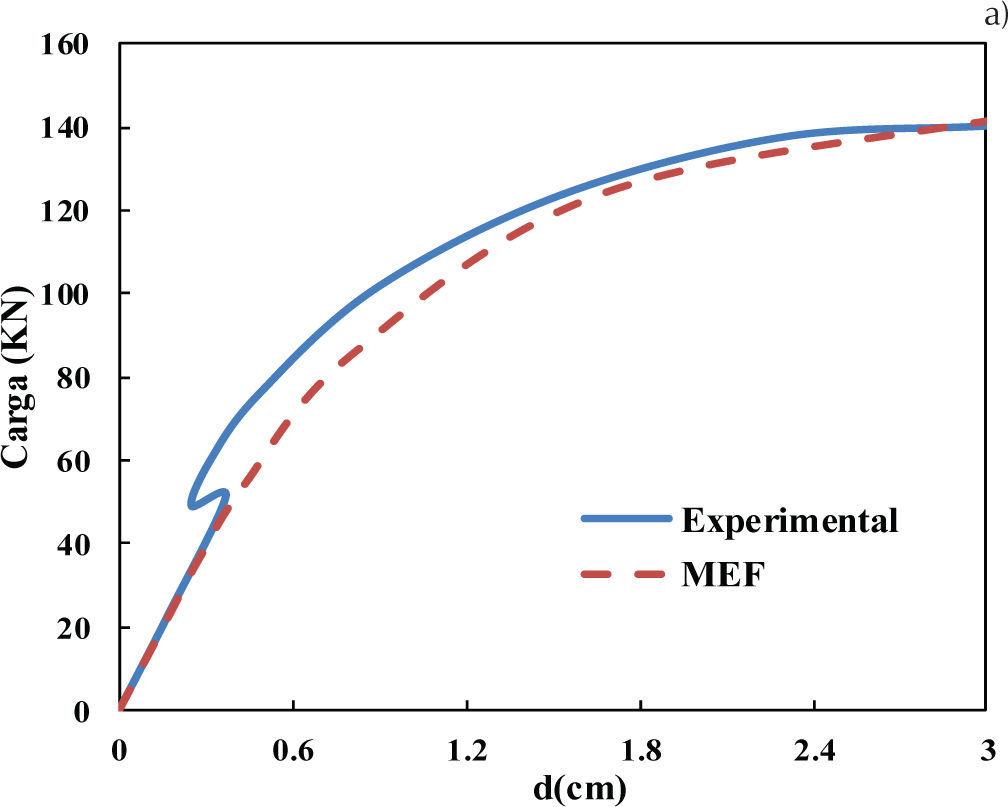
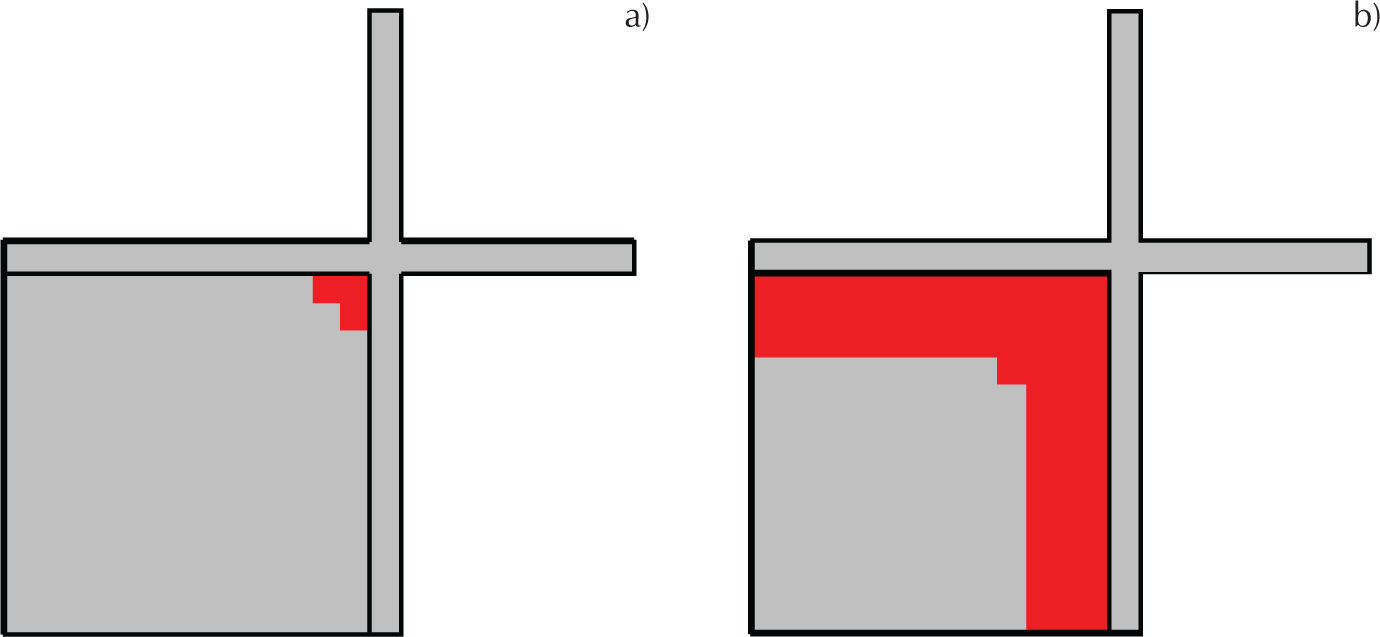
En la figura 8 se muestra la comparación de las curvas del desplazamiento en el centro de la losa contra la carga entre la prueba experimental y la obtenida con el método de los elementos finitos (MEF), se puede observar que en la trayectoria ab coinciden ambos resultados; sin embargo, en la trayectoria bc de los resultados experimentales se observa una recuperación del desplazamiento, el cual se puede atribuir a un corrimiento de los dispositivos de medición, pues al incrementarse la carga sobre la losa difícilmente se recuperaría el desplazamiento al centro, es en el punto d donde se presenta una intersección de ambas curvas, las cuales siguen una misma trayectoria hasta e. Respecto a la evolución del agrietamiento, en la figura 9 se muestra su inicio en la esquina de la parte superior de la losa; posteriormente, el agrietamiento se propaga sobre los bordes y hacia el centro, lo cual es consistente con los resultados experimentales reportados por Girolami et al. (1970).

Figura 8.

Comparación entre curva experimental y analítica

Figura 9.

Evolución del agrietamiento: a) inicio y b) final

Ejemplos numéricos

Para el estudio de losas, inicialmente se realizaron análisis elásticos con elementos finitos placa, los cuales tienen un grado de libertad traslacional y dos angulares en cada nodo; posteriormente se realizaron análisis no lineales con elementos sólidos con ocho nodos y barras con dos nodos, ambos elementos con tres grados de libertad traslacionales por nodo. Con los análisis elásticos se determinan las distribuciones de momento, las cuales son de utilidad para proponer el acero de refuerzo superior e inferior; mientras que con los análisis no lineales se determinaron las trayectorias de agrietamiento, así como la evolución de los coeficientes de diseño al existir una redistribución de esfuerzos debido al agrietamiento.

En los ejemplos elásticos se utilizó un mallado con elementos finitos placa para obtener la distribución de momentos de las losas circular, elíptica y triangular mostradas respectivamente en las figuras 10,12 y 14. En estos modelos se utilizó un módulo elástico equivalente al concreto reforzado de E = 21.673 GPa y relación de Poisson de ν = 0.25 bajo condiciones de apoyo empotrado, pues las condiciones de apoyo simple proporcionan distribuciones de momentos que sólo requieren acero en la parte inferior de la losa.

Figura 10.

Distribución de momentos en losa circular

Figura 11.

Configuración del acero de refuerzo: a) positivo, b) negativo y c) ambos

Figura 12.

Distribución de momentos losa elíptica: a) horizontal y b) vertical momento negativo en la losa elíptica, teniendo que la longitud

Figura 13.

Configuración del acero de refuerzo en losas elípticas de concreto reforzado: a) refuerzo positivo, b) refuerzo negativo y c) ambos

Figura 14.

Distribución de momentos en losa triangular: a) horizontal y b) vertical

En los modelos no lineales se utilizaron elementos sólidos en 3D para el concreto simple con un módulo elástico E_c = 17GPa, relación de Poisson ν = 0.20, esfuerzo último a tensión σ_ut = 5MPa y a compresión σ_uc = 25 MPa. Para el acero de refuerzo se utilizó un módulo elástico E_a = 2.05 × 105 MPa, relación de Poisson ν = 0.30 y esfuerzo de fluencia σ_y = 410 MPa. En estos modelos el espesor de la losa es 0.10 m con un recubrimiento de 0.025 m para ambos lechos de acero. Los modelos se analizaron en condiciones de apoyo simple y empotrado, en los cuales se aplicaron incrementos de carga distribuida sobre la superficie. En la generación del mallado se consideraron los dos ejes de simetría de las losas, modelando sólo una cuarta parte de su geometría para reducir el costo computacional.

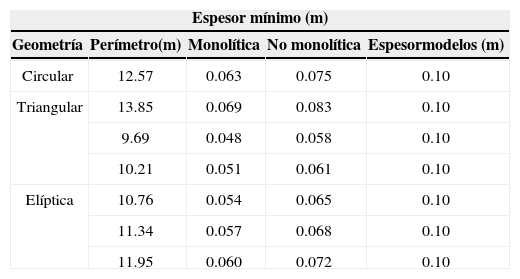
Se utilizó un espesor de 10 cm para todas las geometrías estudiadas, el cual se revisó con el peralte mínimo sugerido por las NTCC-04, encontrándose que este peralte es satisfactorio cuando la losa se cuela monolíticamente y no monolíticamente con sus vigas, como se muestra en la tabla 1. No se incluyeron en el artículo recomendaciones sobre el espesor, ya que era necesario un estudio fundamentado en la vibración de la losa, que está fuera del alcance de este estudio.

Tabla 1.

Revisión de espesores utilizados en modelos numéricos

Espesor mínimo (m)
Geometría	Perímetro(m)	Monolítica	No monolítica	Espesormodelos (m)
Circular	12.57	0.063	0.075	0.10
Triangular	13.85	0.069	0.083	0.10
	9.69	0.048	0.058	0.10
	10.21	0.051	0.061	0.10
Elíptica	10.76	0.054	0.065	0.10
	11.34	0.057	0.068	0.10
	11.95	0.060	0.072	0.10

Distribución del acero de refuerzo

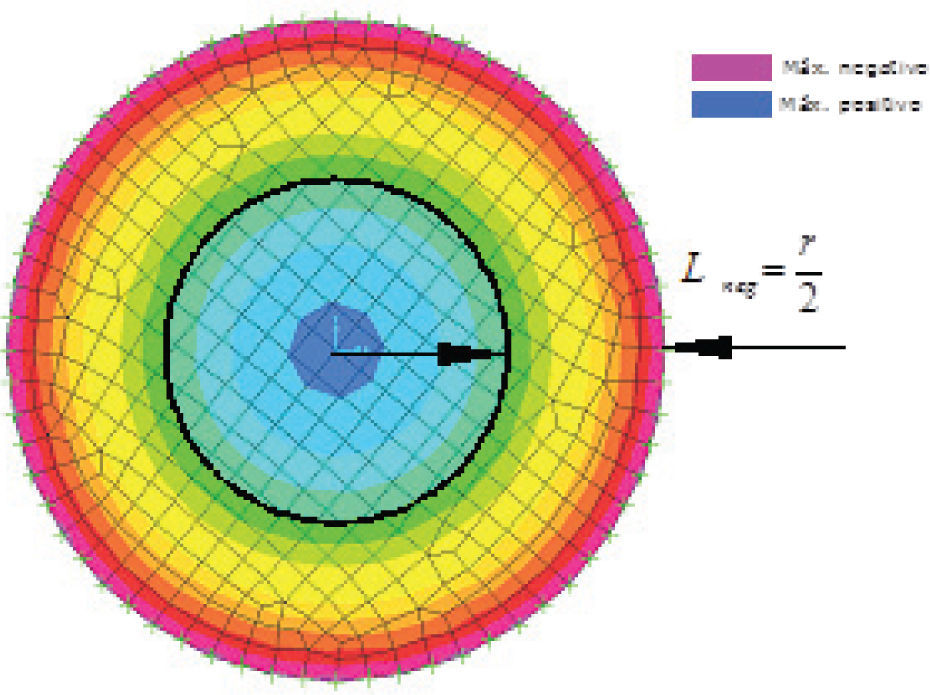
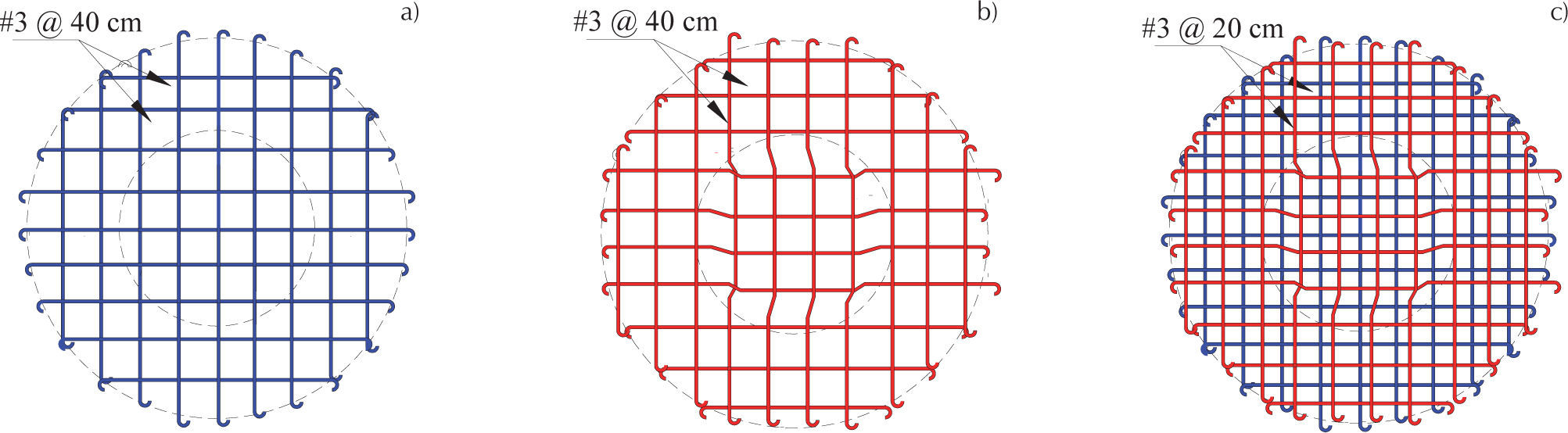
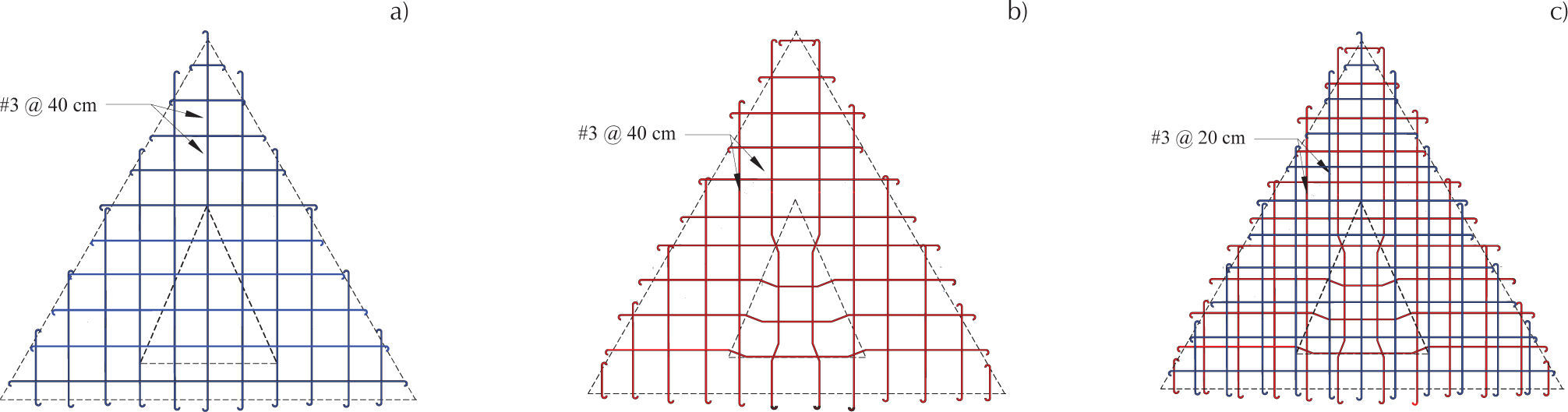
La obtención de momentos elásticos en losas circulares se realizó mediante un modelo numérico con radio r = 2 m, en el que el mallado se estructuró con elementos cuadriláteros placa, evitando tener elementos triangulares en el centro con relaciones de aspecto relativamente grandes que pudieran producir inestabilidades numéricas. A partir de la distribución de momentos mostrada en la figura 10, se identificaron las zonas de momento negativo en la losa circular, la cual está delimitada por la línea punteada y los bordes, obteniéndose una longitud del acero superior en el borde de L_neg = r/2; es de interés mencionar que esta longitud es análoga a una losa cuadrada en la que se recomienda una longitud de acero negativo de un cuarto del claro, que para el caso de losa circular es un cuarto del diámetro. Se propuso una distribución típica del acero de refuerzo como se muestra en la figura 11, en la que el acero positivo se coloca en la parte inferior de la losa y el acero negativo ubicado en la parte superior en los bordes, el cual baja al emparrillado inferior en la zona central mediante un columpio o bayoneta realizado en la línea punteada.

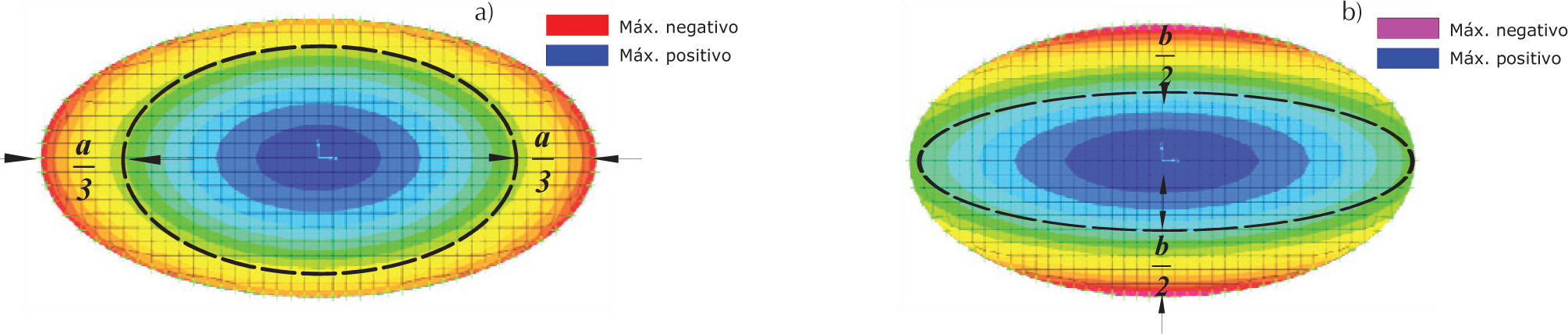
La distribución de momentos en la sección elíptica se determinó mediante modelos en los que se varió la relación del eje menor b respecto al eje mayor a, i.e., b/a=0.5,0.6,0.7,0.8 y 0.9, respectivamente, considerando constante el valor del eje mayor a = 4 m; al igual que en las losas circulares. En el mallado de las losas elípticas se utilizaron elementos cuadriláteros placa, de tal forma que los nodos de los elementos coincidan con los nodos del acero de refuerzo. A partir de la distribución de momentos mostrada en la figura 12 se identificaron las zonas de momento negativo en la losa elíptica, teniendo que la longitud del acero superior es en el eje mayor l_neg = a/3 y en el eje menor l_neg= b/3. Con base en esta distribución de momentos, se propuso el armado típico mostrado en la figura 13, en el que en la zona central se tiene sólo acero en el lecho inferior, y en el borde, delimitado por la línea punteada, se tiene acero en las partes superior e inferior.

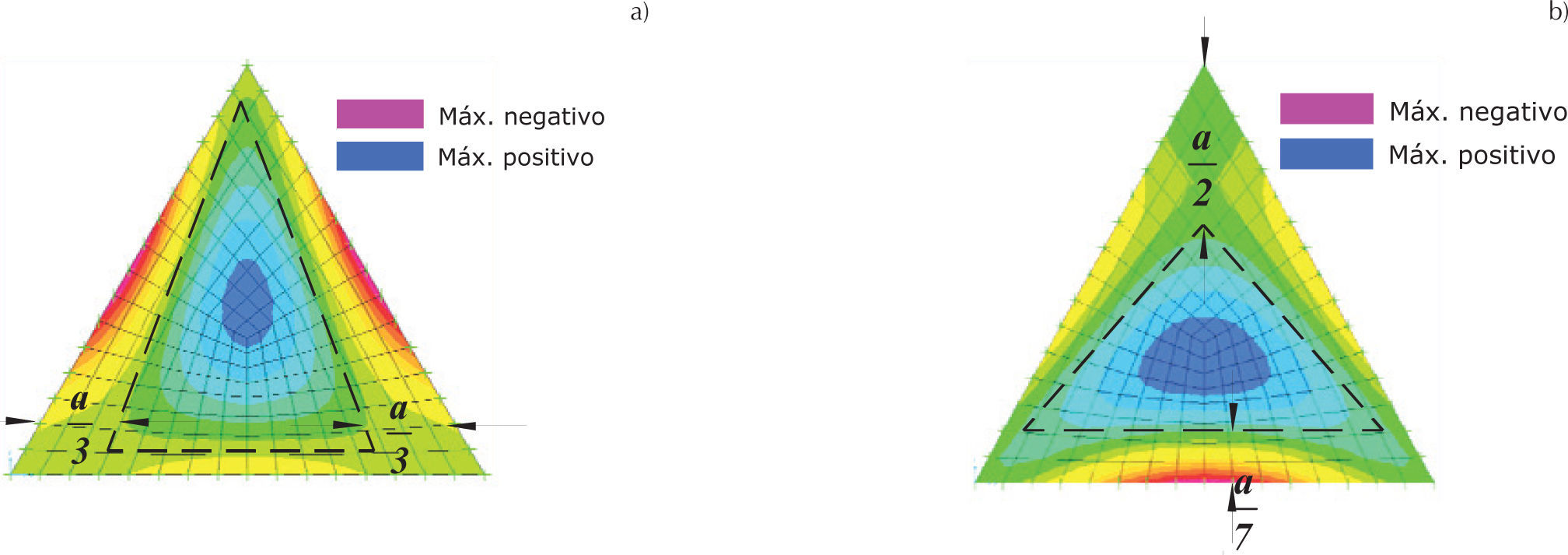
La distribución de momentos de la sección triangular se determinó mediante un modelo numérico, el cual tiene una altura a = 4 m y de base 2a/√3 y un mallado estructurado con elementos cuadriláteros placa, que evita singularidades numéricas. En la figura 14 se muestran las longitudes correspondientes al momento negativo en ambas direcciones: en dirección horizontal se tiene una longitud de a/3, mientras que en dirección vertical se tiene una longitud de a/7 en la base y a/2 en parte superior. Con base en estas longitudes, en la figura 15 se muestra el armado propuesto con acero sólo en la parte inferior de la zona central, delimitada por la línea punteada y con acero en el lecho superior e inferior en los bordes.

Figura 15.

Configuración del acero de refuerzo en una losa triangular: a) refuerzo positivo, b) refuerzo negativo y c) ambos

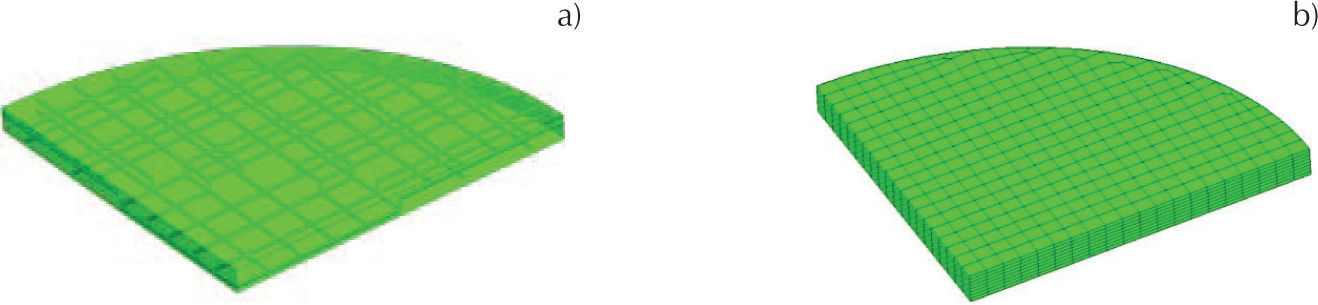
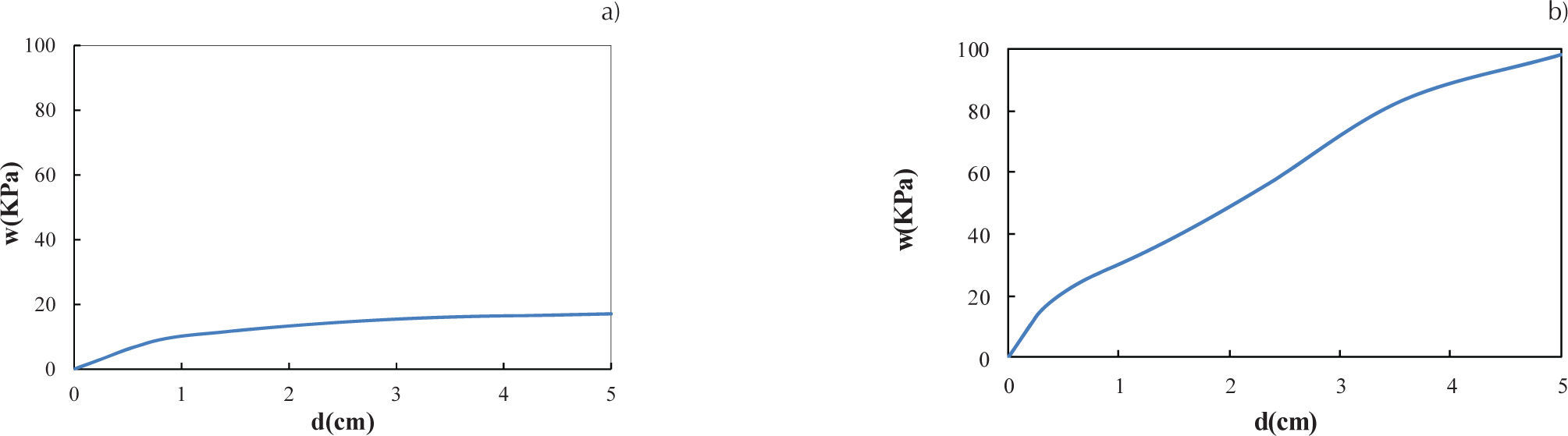
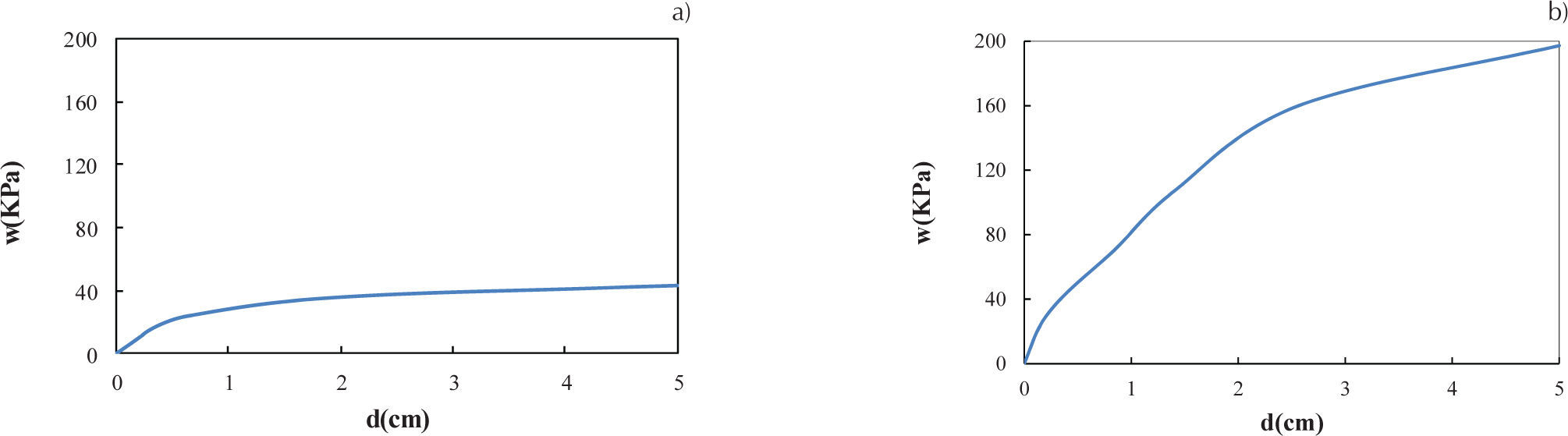
Análisis no lineal

En el análisis no lineal de la losa circular se utilizó un modelo con radio r = 2 m, la malla del acero de refuerzo, del lecho inferior y superior, así como los bastones, se muestra en la figura 16a, la cual está formada por barras de acero del número 3 separadas a cada 0.20 m; mientras que la malla del concreto con el acero embebido se muestra en la figura 16b, los nodos del acero de refuerzo coinciden con los nodos de los elementos sólidos. Las curvas de la variación de la carga distribuida con respecto al desplazamiento en el centro de la losa se muestran en la figura 17, donde se observa que las condiciones de apoyo en el perímetro de la losa influyen en el desplazamiento vertical en el centro, ya que para desarrollar un desplazamiento al centro de 5 cm se necesitó una carga distribuida de 17 KPa en la losa simplemente apoyada y una carga de 98 KPa para la losa empotrada.

Figura 16.

Malla de elementos finitos en losa circular: a) acero de refuerzo y b) concreto reforzado

Figura 17.

Curva carga contra desplazamiento en el centro de losa circular en condición de apoyo: a) simple y b) empotrado

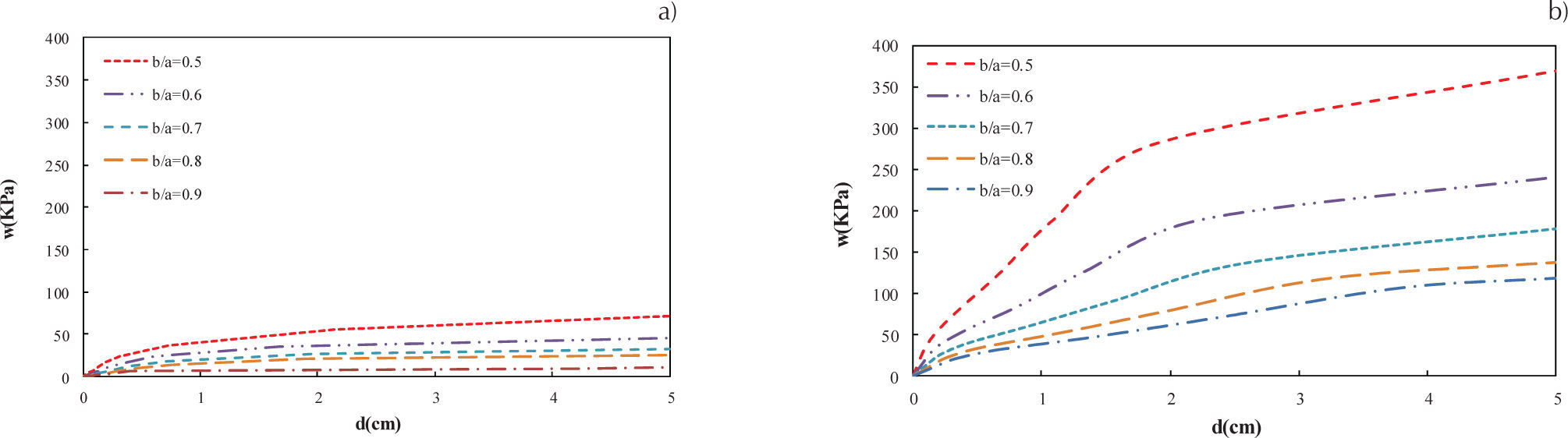
El análisis no lineal de las losas elípticas se realizó considerando relaciones eje menor entre eje mayor b/a = 0.5, 0.6, 0.7, 0.8 y 0.9. El acero de refuerzo está formado por barras de acero del número 3 separadas a cada 0.20 m, que incluye el acero superior, inferior y bastones, la malla del refuerzo discretizada con elementos lineales se muestra en la figura 18a. La malla del concreto de la losa con el acero embebido se muestra en la figura 18b, observe que la malla de concreto se estructuró para que los nodos de los elementos sólidos coincidan con los del acero de refuerzo y para tener sólo elementos hexaedros. Las curvas de la variación de la carga distribuida con respecto al desplazamiento en el centro de la losa se muestran en la figura 19, donde se observa que la carga necesaria para desarrollar un desplazamiento al centro de la losa es inversamente proporcional a la relación b/a en ambas condiciones de apoyo; además se observa que esta carga en las losas simplemente apoyadas es aproximadamente 20% de la carga de las losas empotradas para desarrollar el mismo desplazamiento en el centro.

Figura 18.

Malla de elementos finitos en losa elíptica: a) acero de refuerzo y b) concreto reforzado

Figura 19.

Curva desplazamiento al centro contra carga distribuida de losas elípticas en condición de apoyo: a) simple y b) empotrado

Respecto al análisis de la losa triangular, el acero de refuerzo consiste de barras de acero del número 3 a cada 0.20 m, su mallado se realizó con elementos finitos lineales como se muestra en la figura 20a, la malla del concreto de la losa con el acero embebido se muestra en figura 20b, se realizó el mallado de la mitad del modelo por sólo tener un eje de simetría en esta losa triangular. Las curvas de la variación de la carga distribuida con respecto al desplazamiento en el centro de la losa se muestran en la figura 21, donde nuevamente se observa que las condiciones de apoyo influyen en el comportamiento global, de tal forma que la losa triangular simplemente apoyada requiere de una carga aproximada 20% en comparación con la losa empotrada para desarrollar el mismo desplazamiento en el centro.

Figura 20.

Malla de elementos finitos en losa triangular con a = 4m: a) acero de refuerzo y b) concreto

Figura 21.

Curva desplazamiento al centro contra carga distribuida de losa triangular con a=4m en condición de apoyo: a) simple y b) empotrado

Determinación de coeficientes de diseño

Puesto que se utilizan elementos sólidos para modelar el concreto y elementos lineales para modelar el acero, en los análisis no lineales se obtienen estados de esfuerzos,σ, en los puntos de integración, los cuales mediante un proceso de suavizado, se calculan en los nodos; sin embargo, para obtener los coeficientes de diseño se necesitan los valores de momentos por unidad de longitud, los cuales se determinaron con la siguiente ecuación:

donde σ_x es la función que describe el esfuerzo en la dirección x, z es el eje de referencia y t es el peralte de la losa. En los análisis elásticos presentados en la sección de distribución del acero de refuerzo no fue necesario utilizar la ecuación (1) para determinar los momentos, puesto que el elemento placa los proporcionó directamente. es la función que describe el esfuerzo en la dirección x, z es los análisis elásticos presentados en la sección de distribución ecuación (1) para determinar los momentos, puesto que el elemento

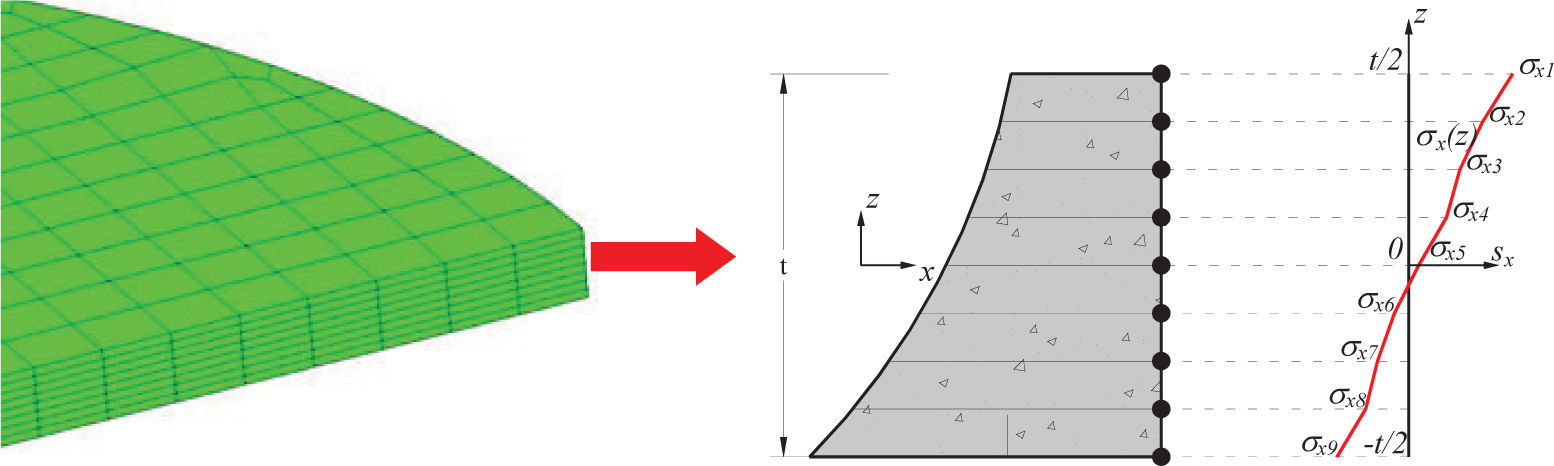
En los análisis no lineales, el cálculo de los momentos flexionantes con la ecuación (1) se realizó integrando en ocho tramos la función de esfuerzos, la cual se describe por funciones de interpolación lineales, como se muestra en la figura 22 en el ancho de la losa; el orden de las funciones de interpolación de esfuerzos es consistente con el de la derivada de las funciones de interpolación de los desplazamientos nodales.

Figura 22.

Distribución de esfuerzos en borde de losa

Una vez obtenido el momento, los coeficientes se calcularon con la siguiente ecuación:

donde α es el coeficiente de diseño, w carga por unidad de área, l longitud de referencia (r para la losa circular, b para la elíptica y a para la triangular) y M el momento calculado con la ecuación (1).

Los coeficientes calculados con análisis no lineales presentan una variación, decremento o incremento, con respecto a los coeficientes elásticos, tomándose los valores máximos de la variación respecto al incremento de carga; esto se debe a la influencia del agrietamiento en el concreto y el endurecimiento del acero de refuerzo en las zonas más esforzadas de la losa. Por lo tanto, se propone utilizar aquellos coeficientes con valores máximos con el fin de garantizar la seguridad estructural de las losas, para que tanto el concreto como el acero de refuerzo brinden una resistencia adecuada en el intervalo elástico.

Los valores de los coeficientes calculados en esta sección deben multiplicarse por 10^-4wl² para obtener momentos de diseño por unidad de ancho. El índice I indica la condición de colado monolíticamente, mientras que el índice II indica la condición de colado no monolíticamente. Es en esta última condición que los coeficientes negativos en los bordes tienen un valor de cero, pues sólo existe momento positivo en toda la losa debido a la condición de apoyo.

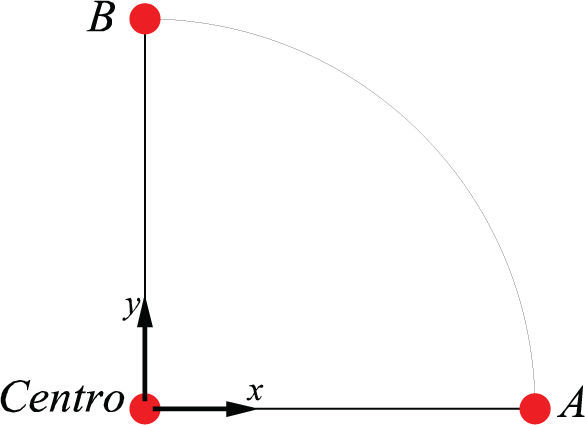
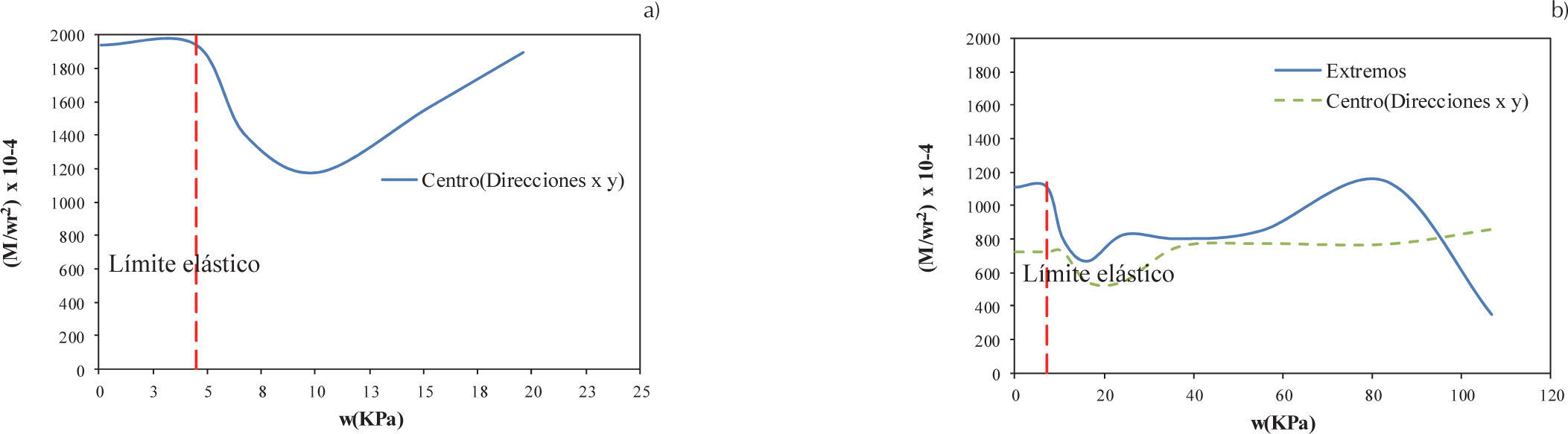
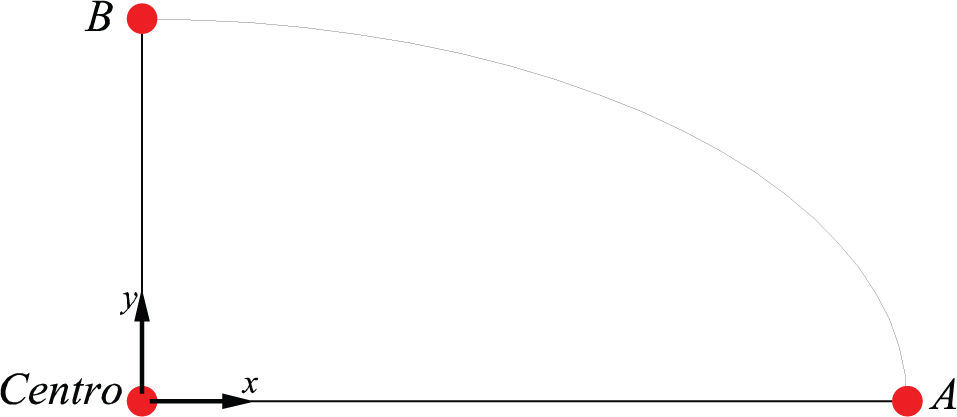
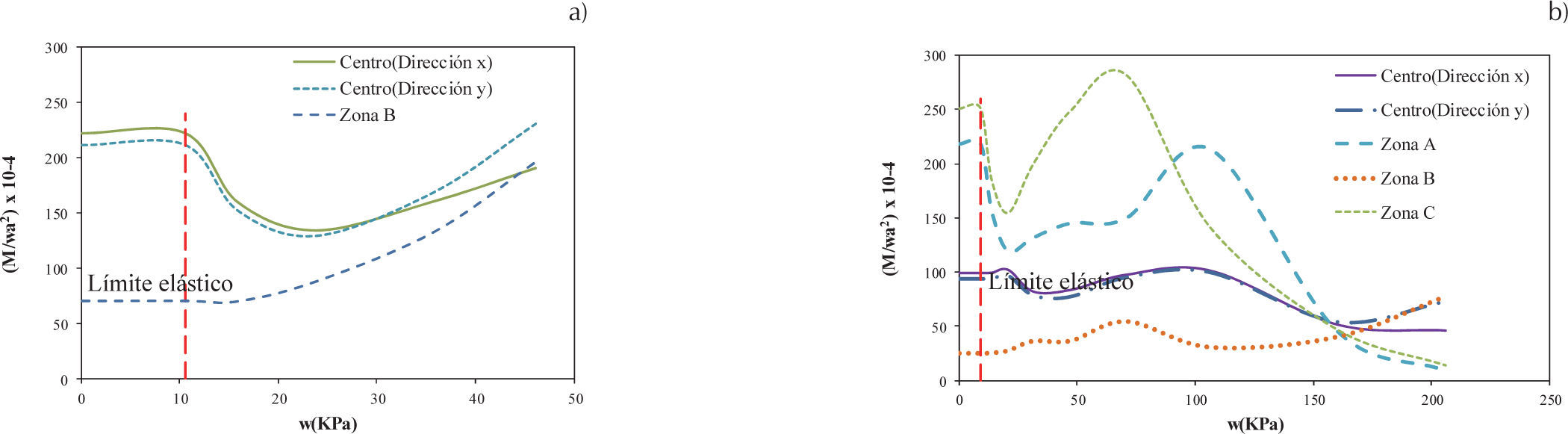
Losas circulares

La obtención de los coeficientes en losas circulares se realizó en el centro, donde se presentan los momentos máximos positivos, y en los extremos A y B, donde se presentan los momentos máximos negativos, los cuales se muestran en la figura 23. Los valores de los coeficientes son idénticos en A, B y en cualquier punto sobre el borde, por tratarse de una estructura que se puede considerar como axisimétrica.

Figura 23.

Zonas de análisis de momentos en losa circular

La variación de los coeficientes de diseño calculados para la losa circular en la condición de apoyo simple se muestran en la figura 24a, la cual es idéntica en cualquier dirección por ser una estructura axisimétrica; mientras que en el caso de la losa empotrada se presenta el momento máximo negativo en los extremos y positivo en el centro como se muestra en la figura 24b. En ambas condiciones de apoyo se observa que al iniciar el agrietamiento los coeficientes decrecen en el centro y en los bordes debido al agrietamiento en el concreto, posteriormente los coeficientes se incrementan debido a la redistribución de esfuerzo y plastificación del acero, sólo los coeficientes en los extremos superan su valor en el intervalo elástico y los del centro quedan debajo de este valor. De los coeficientes mostrados en la figura 24 se tomaron los valores de los coeficientes de diseño elásticos, los cuales se muestran en la tabla 2, para el caso de los coeficientes en el intervalo inelástico se tomaron los correspondientes a los valores máximos, que para el centro corresponden a los mismos valores elásticos y para los bordes se tiene un valor mayor a este intervalo como se muestra en la tabla 3.

Figura 24.

Variación del coeficiente contra carga distribuida en losa circular en apoyo: a) simple y b) empotrado

Tabla 2.

Coeficientes de diseño elásticos de losas circulares

Momento	I	II
Neg. en los bordes	677	0
Positivo	1095	1026

Tabla 3.

Coeficientes de diseño inelásticos de losas circulares

Momento	I	II
Neg. en los bordes	1147	0
Positivo	1095	1939

Losa elíptica

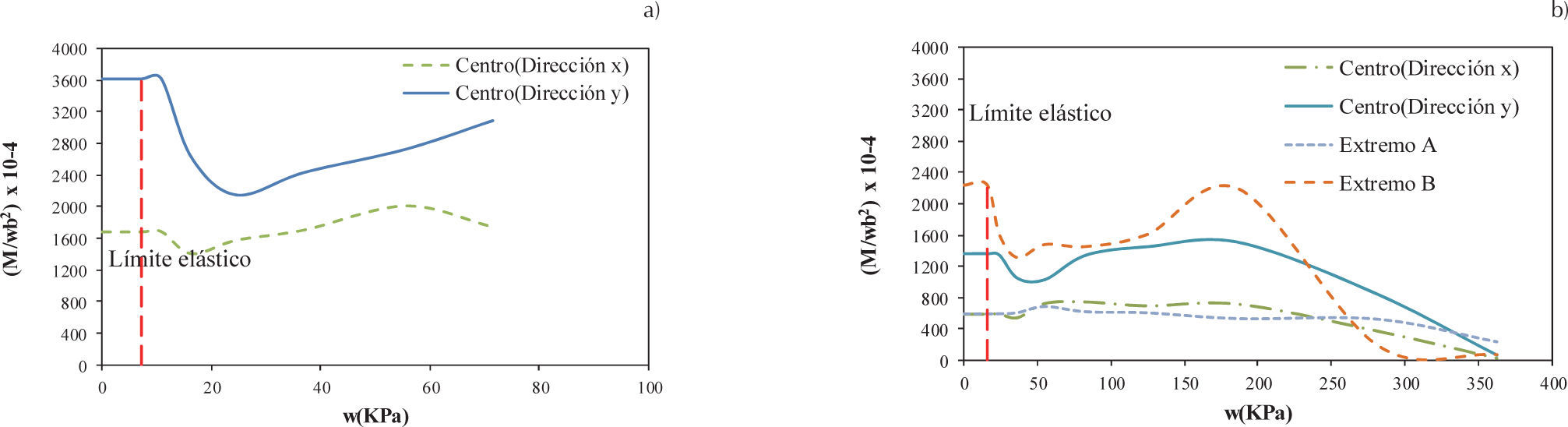
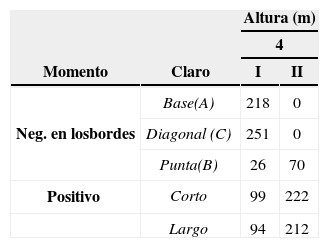
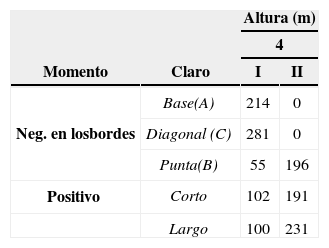
La obtención de los coeficientes en las losas elípticas se realizó en los puntos donde se obtienen los valores de momento máximo negativo, puntos A y B, y momento máximo positivo, centro (figura 25). En losas con esta geometría se tienen diferentes magnitudes de los coeficientes en las dos direcciones en el centro; en el punto A, los coeficientes tienen valores para determinar el momento en la dirección horizontal y para el punto B, el momento en la dirección vertical.

Figura 25.

Zonas de análisis de momentos en losas elípticas

Las figuras 26 a 30 muestran la variación del coeficiente para las relaciones 0.5, 0.6, 0.7, 0.8 y 0.9, respectivamente. La variación de los coeficientes en el centro de las losas mayor en la dirección y para la condición de apoyo simple, este mismo comportamiento se observa en el intervalo elástico y en el no lineal, aunque en el segundo intervalo, la magnitud de los coeficientes decrece y posteriormente vuelven incrementarse sin alcanzar magnitud del intervalo elástico. Para el caso de losas con empotramiento, la magnitud máxima de los coeficientes se presentan en el extremo B en el intervalo elástico, posteriormente, en el intervalo no lineal, la magnitud de estos coeficientes decrece y después muestran un incremento, particularmente para las relaciones 0.5 a 0.7; en el resto de las relaciones el momento máximo se presentó en el centro en la dirección x en el intervalo no lineal, esto se debe a la influencia de la redistribución de esfuerzos por el agrietamiento del concreto y la plastificación del acero de refuerzo. Como resultado de este análisis, los coeficientes elásticos e inelásticos se muestran respectivamente en las tablas 4 y 5.

Figura 26.

Variación del coeficiente contracarga distribuida en elipse con relación b/a = 0.5 en apoyo: a) simple y b) empotrado

Figura 27.

Variación del coeficiente contra carga distribuida en elipse con relación b/a=0.6 en apoyo: a) simple y b) empotrado

Figura 28.

Variación del coeficiente contra carga distribuida en elipse con relación b/a=0.7 en apoyo: a) simple y b) empotrado

Figura 29.

Variación del coeficiente contra carga distribuida en elipse con relación b/a=0.8 en apoyo: a) simple y b) empotrado

Figura 30.

Variación del coeficiente contra carga distribuida en elipse con relación b/a=0.9 en apoyo: a) simple y b) empotrado

Tabla 4.

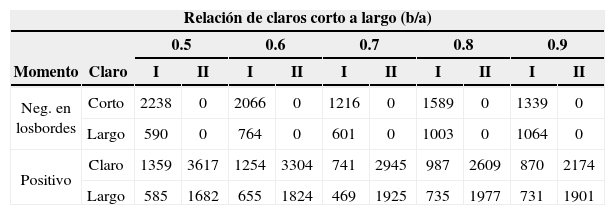
Coeficientes de diseño elásticos de losas elípticas

Relación de claros corto a largo (b/a)
Momento	Claro	0.5		0.6		0.7		0.8		0.9
		I	II	I	II	I	II	I	II	I	II
Neg. en losbordes	Corto	2238	0	2066	0	1216	0	1589	0	1339	0
	Largo	590	0	764	0	601	0	1003	0	1064	0
Positivo	Claro	1359	3617	1254	3304	741	2945	987	2609	870	2174
	Largo	585	1682	655	1824	469	1925	735	1977	731	1901

Tabla 5.

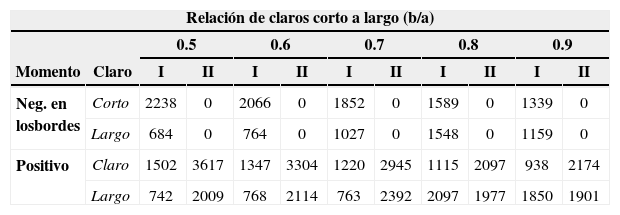
Coeficientes de diseño inelásticos de losas elípticas

Relación de claros corto a largo (b/a)
Momento	Claro	0.5		0.6		0.7		0.8		0.9
		I	II	I	II	I	II	I	II	I	II
Neg. en losbordes	Corto	2238	0	2066	0	1852	0	1589	0	1339	0
	Largo	684	0	764	0	1027	0	1548	0	1159	0
Positivo	Claro	1502	3617	1347	3304	1220	2945	1115	2097	938	2174
	Largo	742	2009	768	2114	763	2392	2097	1977	1850	1901

Losas triangulares

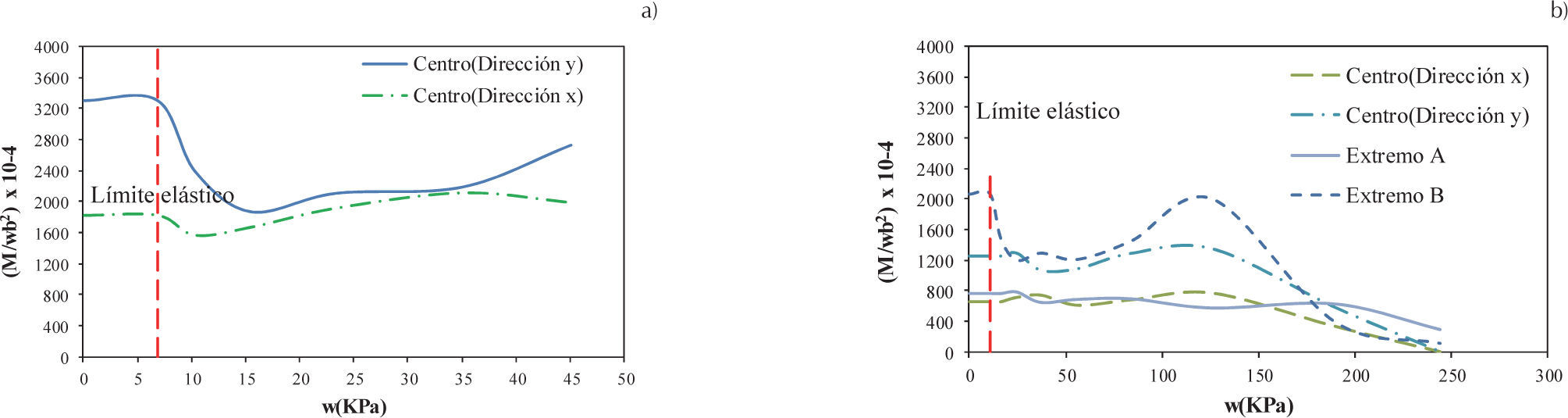
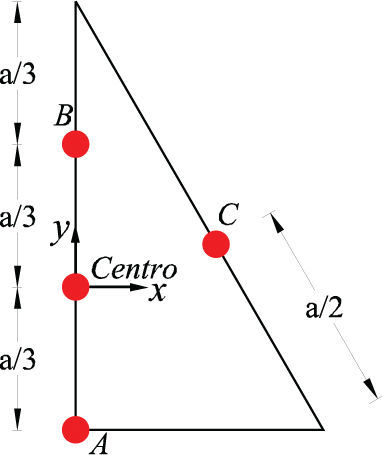
En losas triangulares, las zonas A, B y C presentan momento negativo, por el contrario, en el centro presentan momento positivo, como se muestran en la figura 31. Los momentos en C se calcularon en la dirección θ = 30° respecto al eje horizontal, puesto que los esfuerzos principales en C se presentaron en esta dirección. Las zonas de interés para la condición simplemente apoyada son en el centro, porque sólo se presenta momento positivo, mientras que para la condición empotrada son de interés todos los puntos mostrados en la figura 31 por presentarse momentos con ambos signos.

Figura 31.

Zonas de análisis de momentos en losas triangulares

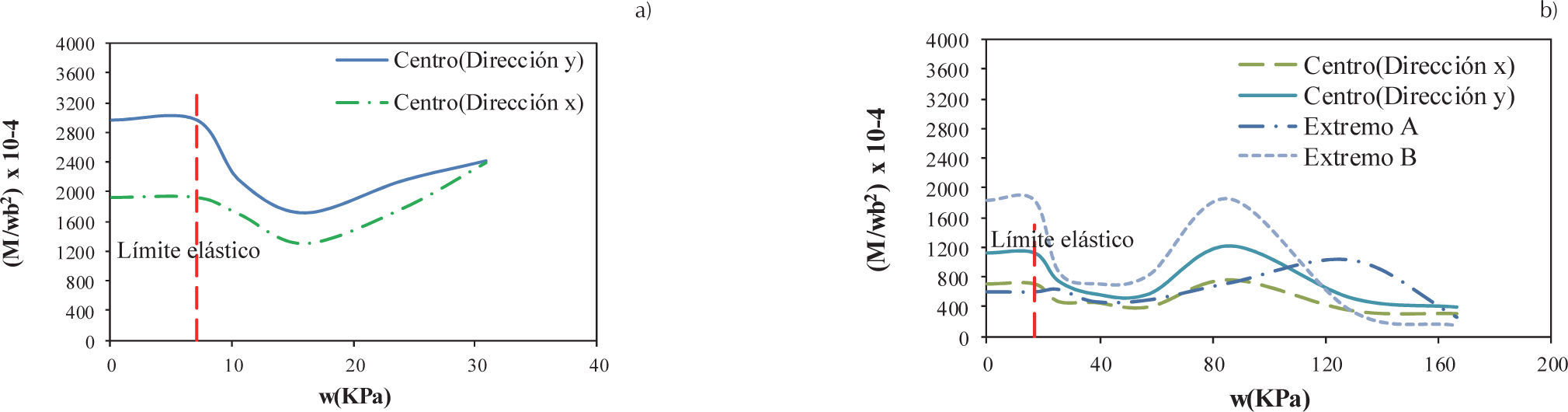
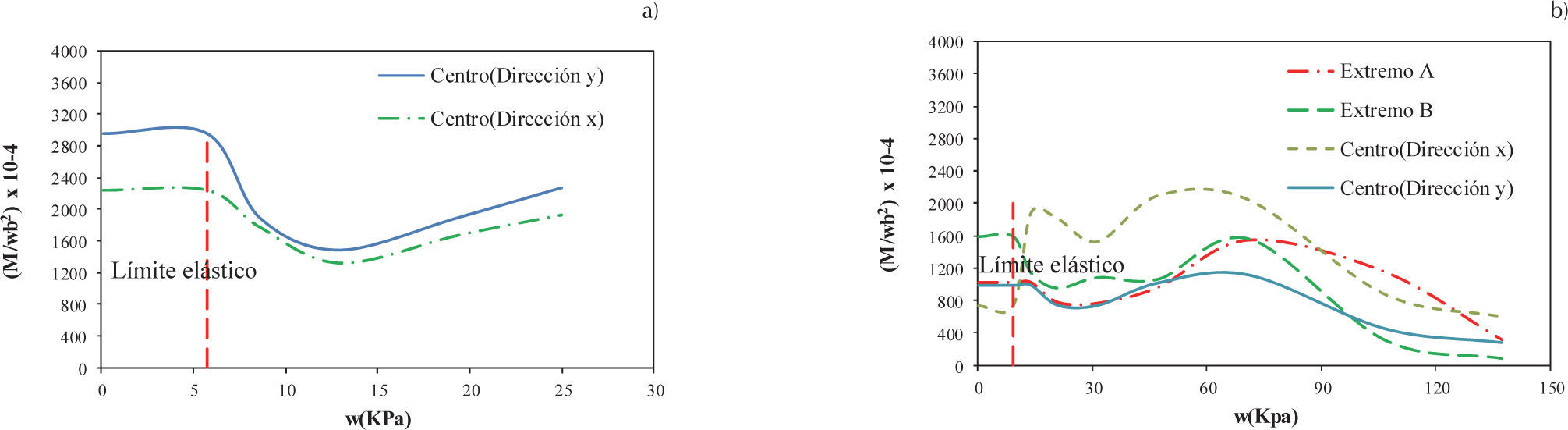
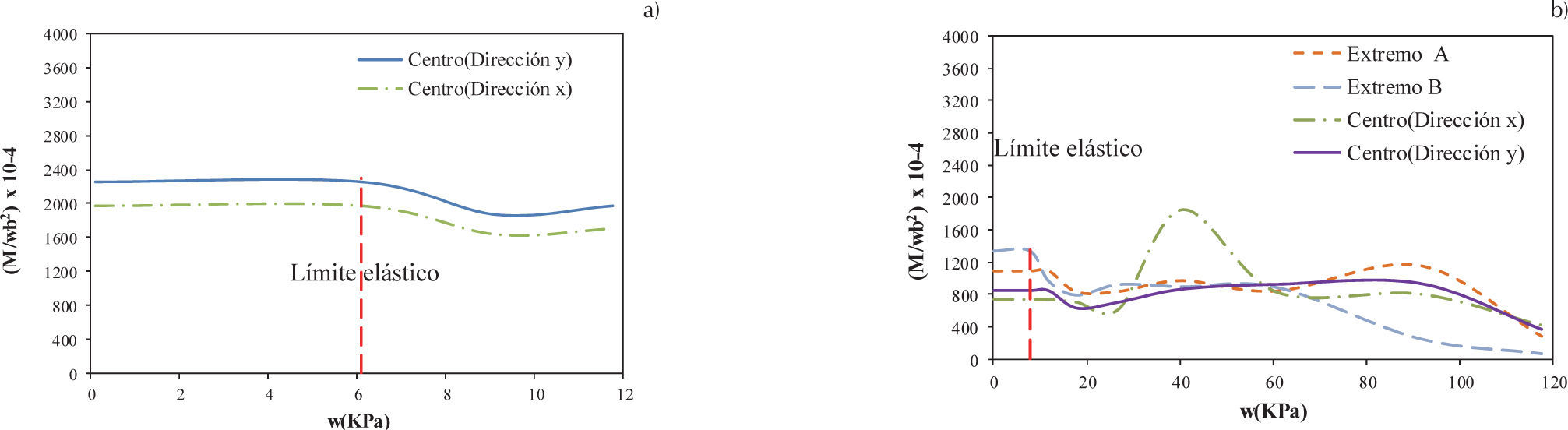
En la losa triangular simplemente apoyada, la magnitud de los coeficientes son mayores en el centro en la dirección horizontal en el intervalo elástico, condición que cambia cuando se está en el intervalo no lineal, puesto que los momentos máximos se presentan en el centro en dirección y, como se muestra en la figura 32a. Por otra parte, en la condición de empotramiento, el momento máximo se presenta en la zona C en ambos intervalos, aunque en principio existe una reducción del coeficiente, posteriormente éste se incrementa superando su magnitud respecto al intervalo elástico (figura 32b). Con base en lo anterior, los coeficientes para los intervalos elásticos e inelásticos obtenidos para losa triangular se muestran, respectivamente, en las tablas 6 y 7.

Figura 32.

Variación del coeficiente contra carga distribuida con apoyo: a) simple y b) empotrado

Tabla 6.

Coeficientes de diseño elásticos de losas triangulares

Momento	Claro	Altura (m)
		4
		I	II
Neg. en losbordes	Base(A)	218	0
	Diagonal (C)	251	0
	Punta(B)	26	70
Positivo	Corto	99	222
	Largo	94	212

Tabla 7.

Coeficientes de diseño inelásticos de losas triangulares

Momento	Claro	Altura (m)
		4
		I	II
Neg. en losbordes	Base(A)	214	0
	Diagonal (C)	281	0
	Punta(B)	55	196
Positivo	Corto	102	191
	Largo	100	231

Trayectorias de agrietamiento

Las trayectorias de agrietamiento son de utilidad para identificar zonas de mayor concentración de esfuerzos, con las que se determinan cualitativamente la ubicación del acero de refuerzo. Dentro de la mecánica computacional existen principalmente tres modelos para representar el agrietamiento:

• 1.

  La mecánica de fractura, que localiza en una línea o superficie las grietas, pero tiene la desventaja de necesitar grietas iniciales, proceso de remallado costoso y se aplica sólo a materiales frágiles;

• 2.

  El agrietamiento distribuido, que las grietas aparecen en cualquier parte del modelo, por lo que no necesita grietas iniciales. Una de sus ventajas principales en que no necesita remallado, pero presenta problemas de atoramiento de esfuerzos; y

• 3.

  El modelo de discontinuidades interiores, que toma las ventajas de los dos anteriores, al no necesitar el remallado e introducir las discontinuidades (grietas) en cualquier lugar y dirección dentro de los elementos finitos. En estos dos últimos no se observa como tal una discontinuidad física (grieta), sino que se presentan zonas con desplazamientos mayores y, en consecuencia, deformaciones con gradientes grandes.

Es de interés mencionar que en este artículo el agrietamiento se modeló como un agrietamiento distribuido, asociado al estado de esfuerzos en los puntos de integración Gaussiana del elemento, donde el material alcanza la superficie de falla, por lo que no se muestran discontinuidades físicas (grietas), sino que se presentan zonas con grandes desplazamientos y, en consecuencia, concentración de gradientes grandes de deformaciones donde se degrada el material. El software ANSYS, donde se realizaron estos análisis, despliega círculos en los puntos de integración que se agrietan o aplastan; el agrietamiento se muestra con un círculo en dirección del plano de agrietamiento, mientras que el aplastamiento se muestra con un octaedro. Si la grieta se abre y posteriormente se cierra, se despliega una X dentro del círculo. En las figuras mostradas en esta sección se delimitaron las zonas que contienen los puntos de integración dañados, las cuales se muestran en color rojo donde los estados de esfuerzo están dominados por la tensión y en azul los que están en compresión.

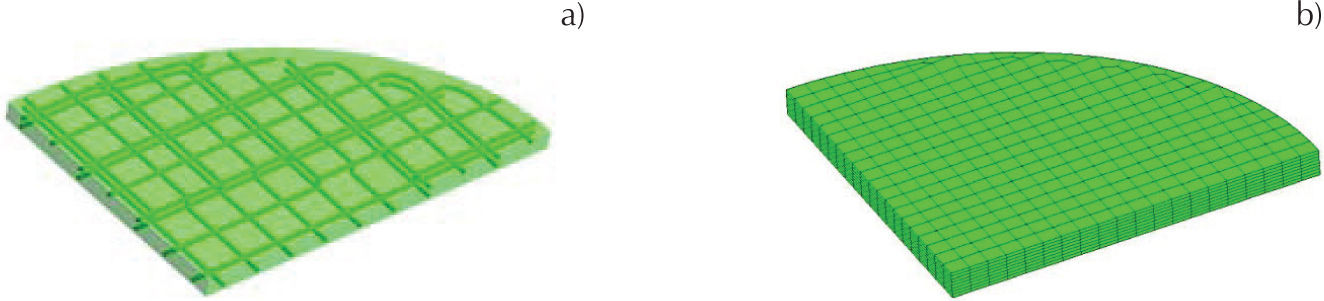
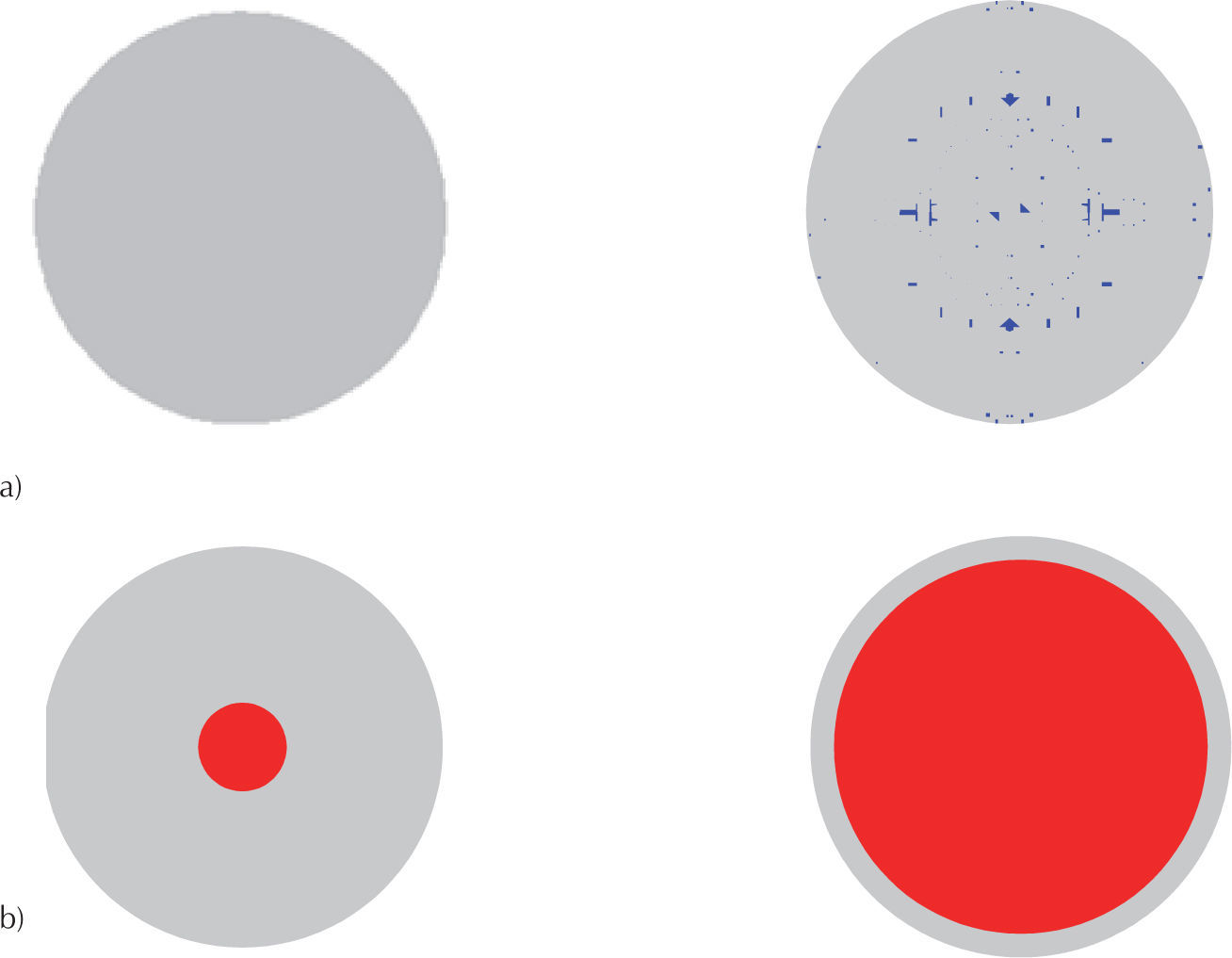
Losas circulares

En losas circulares empotradas en sus bordes, el agrietamiento inicia en todo el borde por la parte superior de la losa debido a que es axisimétrica, como se muestra en la figura 33a, posteriormente, el agrietamiento se presenta al centro del claro en la parte inferior (figura 33b). Se observó que el agrietamiento evoluciona, de manera que en la parte superior éste se propaga de los bordes hacia la parte central, no obstante, en el centro se presenta un aplastamiento y en la parte inferior, el agrietamiento se propaga del centro hacia los bordes.

Figura 33.

Evolución del agrietamiento en losa circular empotrada: a) parte superior y b) parte inferior

Cuando las losas circulares están simplemente apoyadas en sus bordes, el agrietamiento inicia en el centro de la parte inferior, el cual, posteriormente, se propaga hacia los bordes, como se muestra en la figura 34b, y en la parte superior se presenta un aplastamiento incipiente como se muestra en la figura 34a. El que nada más exista momento positivo en la losa demuestra que sólo existen esfuerzos a compresión en la parte superior de la losa, por lo que aparecen aplastamientos, y esfuerzos de tensión en la parte inferior, con lo que aparecen agrietamientos.

Figura 34.

Evolución del agrietamiento en losa circular simplemente apoyada: a) parte superior y b) parte inferior

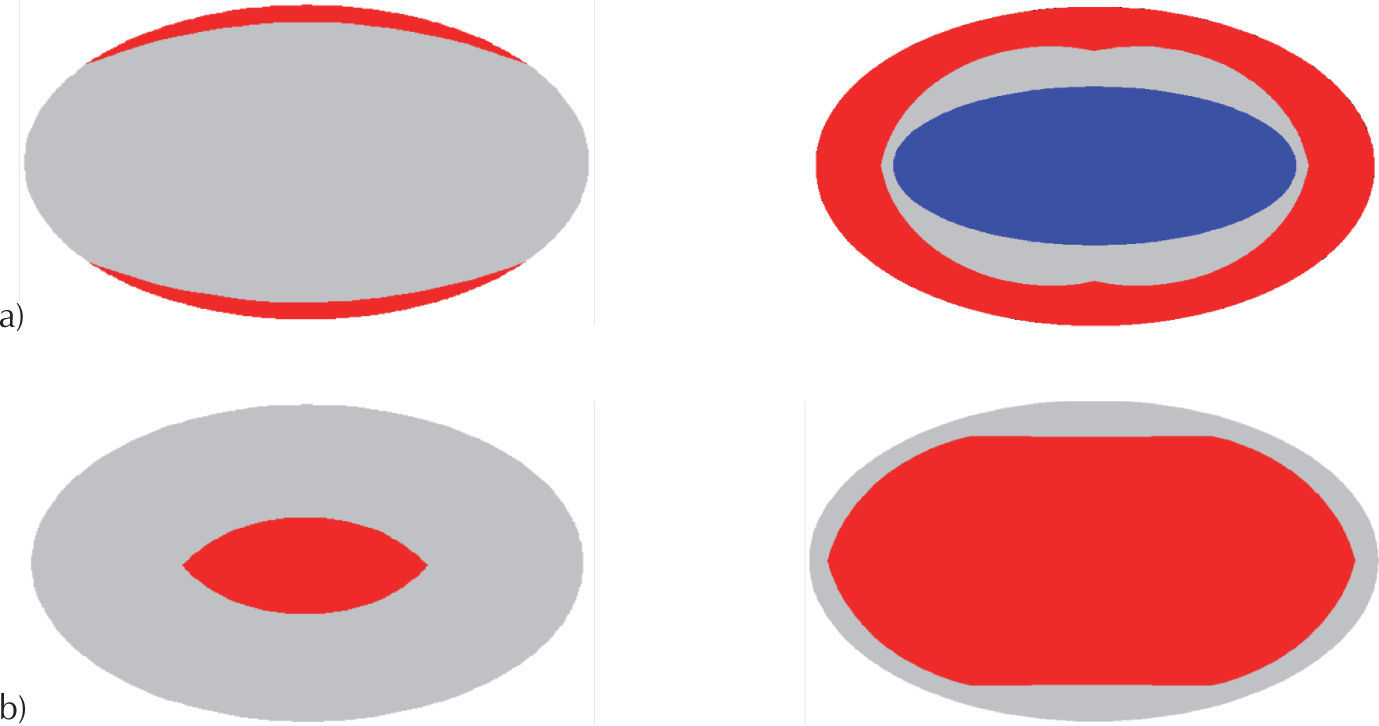
Losas elípticas

En las losas elípticas empotradas, el agrietamiento inicia en la parte superior de los bordes aproximadamente perpendiculares al eje mayor, como se muestra en la figura 35a, posteriormente, el agrietamiento aparece en el centro de la parte inferior de la losa, como se muestra en la figura 35b. Al incrementar la carga distribuida, el agrietamiento se propaga análogamente a la losa circular, pues en la parte superior de la losa, el agrietamiento se propaga de los bordes hacia la parte central generándose aplastamiento en el centro; mientras que en la parte inferior de la losa el agrietamiento se propaga del centro hacia el borde.

Figura 35.

Evolución del agrietamiento en losa elíptica empotrada: a) parte superior y b) parte inferior

Es en la condición de apoyo simple, que las losas elípticas comienzan a agrietarse en su parte inferior, como se observa en la figura 36b, posteriormente, éste se propaga del centro hacia los bordes. Al incrementar la carga distribuida, un incipiente aplastamiento aparece en la parte superior de la losa como se observa en la figura 36a.

Figura 36.

Evolución del agrietamiento en losa elíptica simplemente apoyada: a) parte superior y b) parte inferior

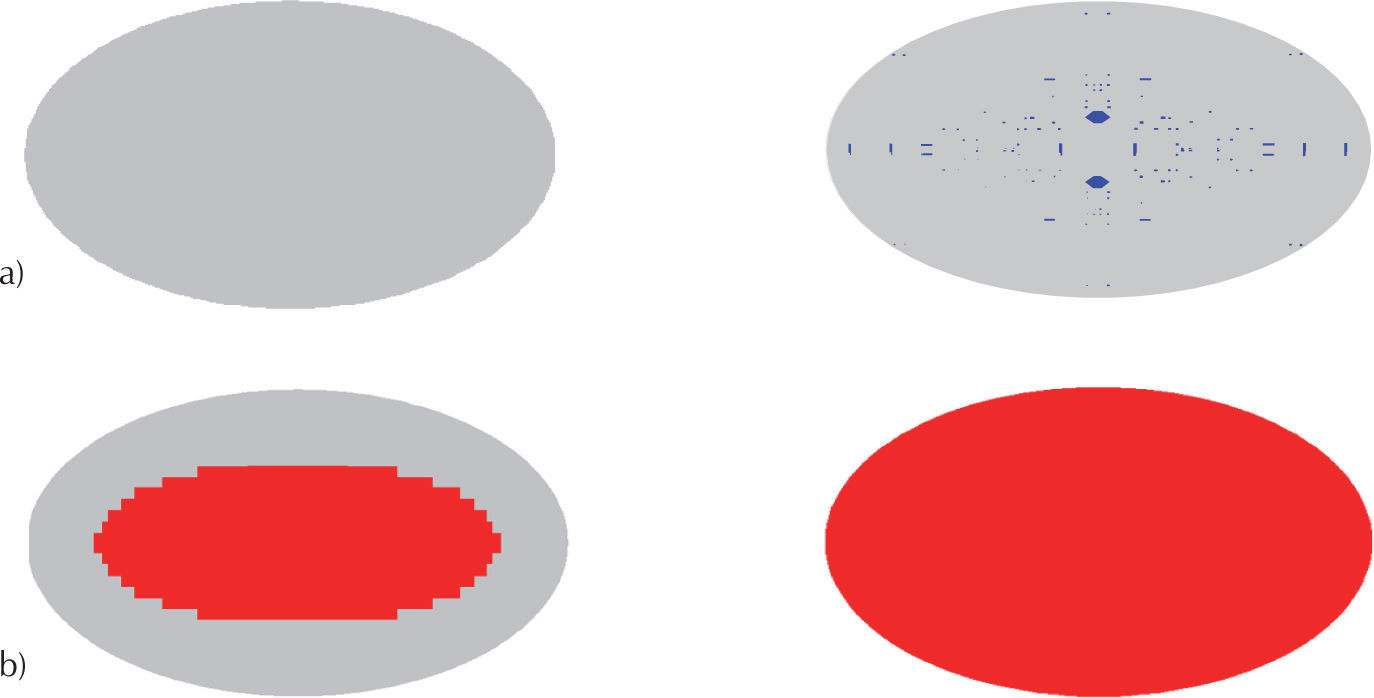
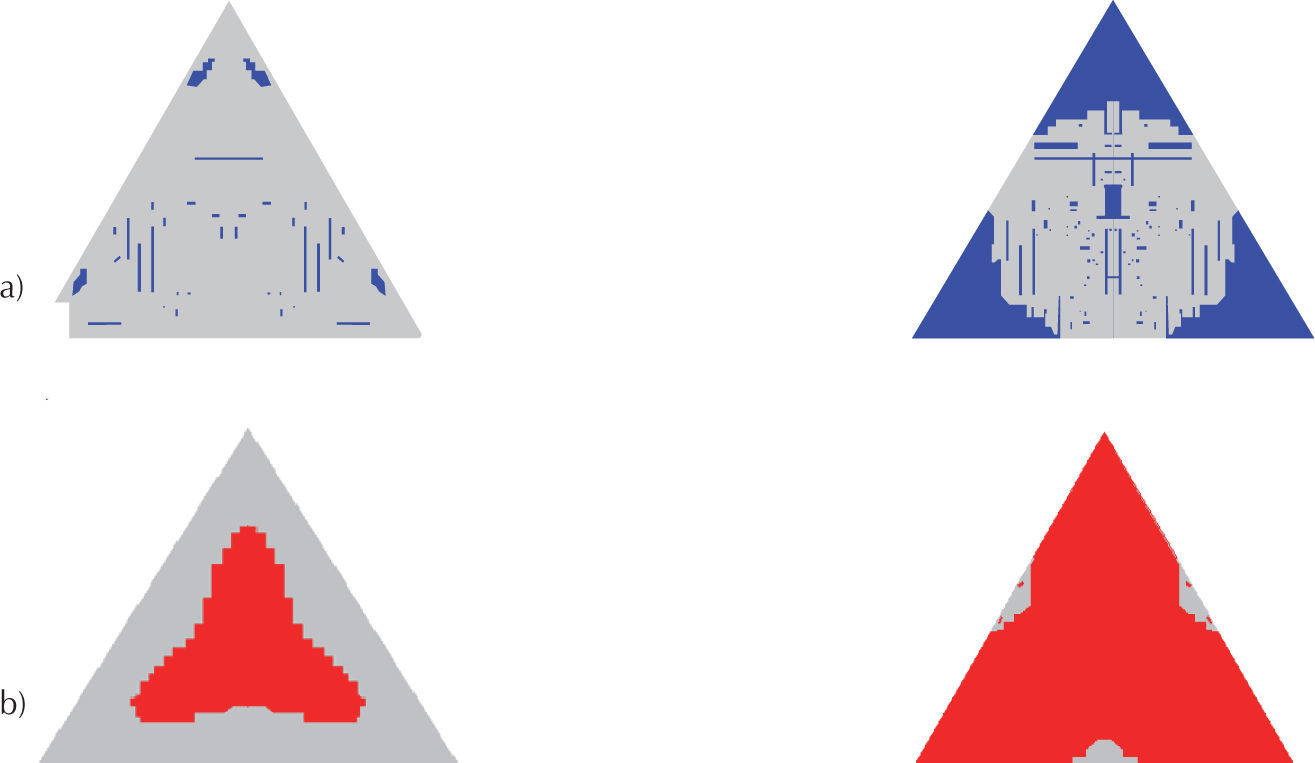
Losas triangulares

El agrietamiento en la losa triangular empotrada inicia en los tres bordes de la parte superior de la losa, como se muestra en la figura 37a, donde se tienen estados de esfuerzos negativos; posteriormente, el agrietamiento aparece en la zona central de la parte inferior de la losa, como se muestra en la figura 37b. Al incrementar la carga distribuida, el agrietamiento se propaga del centro de los bordes hacia los vértices en la parte superior, en cuanto que éste se propaga del centro a los vértices en la cara inferior.

Figura 37.

Evolución del agrietamiento en losa triangular empotrada: a) parte superior y b) parte inferior

Cuando la losa triangular está simplemente apoyada en sus bordes, el agrietamiento inicia en el centro de la parte inferior de la losa, propagándose hacia los vértices conforme se incrementa la carga distribuida, como se muestra en la figura 38b. Por otra parte, debido a los estados de esfuerzos a compresión en la parte superior se presenta aplastamiento, como se muestra en la figura 38a.

Figura 38.

Evolución del agrietamiento en losa triangular simplemente apoyada: a) parte superior y b) parte inferior

En general, cuando las losas se encuentran empotradas, el agrietamiento inicia en los bordes de la parte superior, posteriormente en el centro de la parte inferior. En las losas simplemente apoyadas, el agrietamiento inicia en la cara inferior de la losa, al centro, propagándose en todo el sistema; posteriormente se presenta un aplastamiento incipiente al centro de la parte superior. El que el agrietamiento sea mayor en la cara inferior de las losas respecto al aplastamiento que aparece en la cara su se debe directamente a la redistribución de esfuerzos y a la diferencia de resistencia que tiene el concreto al someterse a tensión que es de 5% a 20% de la resistencia a compresión.

Conclusiones

El comparar la curva carga contra desplazamiento de los resultados numéricos con los experimentales reportados en la literatura se válida el MEF y los modelos constitutivos utilizados para el estudio de losas con geometría triangular, circular y elíptica, pues a pesar de que la curva experimental muestra una recuperación de desplazamiento, se considera que éste posiblemente se debió a un deslizamiento de los instrumentos de medición, pues ante una carga vertical incremental como la del experimento no puede presentarse una recuperación de desplazamientos al centro.

Se descarta el método de líneas de fluencia para determinar las trayectorias de agrietamiento y los coeficientes de diseño o la carga de colapso, pues a pesar de que este método proporciona trayectorias de agrietamiento, no lo proporciona en la parte superior o inferior de la losa; además, estos métodos sólo proporcionan un valor de la carga de colapso, que puede ser mayor o menor a la carga real de colapso. Por lo anterior, se utilizó la mecánica numérica que proporciona el inicio y evolución del agrietamiento, así como la variación de los momentos en el intervalo no lineal.

El armado propuesto para cada geometría de losa, con base en análisis elásticos de placas homogéneas de concreto reforzado resulta adecuado, pues se obtiene una buena aproximación de la distribución de momentos y de la localización e inicio del agrietamiento en el sistema. Estas longitudes de acero negativo y positivo se recomiendan para el diseño y construcción de losas con estas geometrías. De las gráficas carga distribuida contra desplazamiento al centro de la losa con las tres geometrías estudiadas, se observó que la carga distribuida sobre las losas con apoyo simple es aproximadamente 20% de la magnitud de la carga sobre las losas empotradas en sus apoyos para desarrollar un mismo desplazamiento en el centro de la losa.

Los coeficientes elásticos obtenidos con los modelos de elementos finitos sólidos y barra son consistentes en el intervalo elástico con aquellos obtenidos con elementos finitos placa. Después, cuando se agrieta el concreto y/o fluye el acero de refuerzo, el valor de estos coeficientes cambia debido a la redistribución de esfuerzos.

En las tablas de coeficientes, resultado de los análisis no lineales, se proporcionan los valores máximos como los de diseño, con la finalidad de garantizar un comportamiento estructural adecuado. Sin embargo, se recomienda utilizar los coeficientes del análisis elástico, pues se puede observar que en la mayoría de los casos los coeficientes decrecen debido al agrietamiento y luego se incrementan por la plastificación del acero, teniendo en la mayoría de los casos el valor de los coeficientes elásticos como máximo.

En general, el agrietamiento en las losas empotradas inicia en los bordes de la cara superior, posteriormente en el centro de la parte inferior, propagándose al incrementar la carga; mientras que en las losas simplemente apoyadas inicia en el centro del claro en la cara inferior, propagándose hacia los bordes.

Agradecimientos

A la Universidad Autónoma Metropolitana por las facilidades proporcionadas en la realización de este trabajo y al patrocinio proporcionado por el Programa de Mejoramiento del Profesorado. El primer autor agradece al proyecto “182736 Análisis y diseño de losas de concreto” auspiciado por la Secretaría de Educación Pública (SEP) y al Consejo Nacional de Ciencia y Tecnología (CONACyT). El segundo autor agradece la beca al CONACyT por la beca para la realización de estudios de maestría.