Use of Artificial Neural Networks for Prediction of Convective Heat Transfer in Evaporative Units

Abstract

Convective heat transfer prediction of evaporative processes is more complicated than the heat transfer prediction of single-phase convective processes. This is due to the fact that physical phenomena involved in evaporative processes are very complex and vary with the vapor quality that increases gradually as more fluid is evaporated. Power-law correlations used for prediction of evaporative convection have proved little accuracy when used in practical cases. In this investigation, neural-network-based models have been used as a tool for prediction of the thermal performance of evaporative units. For this purpose, experimental data were obtained in a facility that includes a counter-flow concentric pipes heat exchanger with R134a refrigerant flowing inside the circular section and temperature controlled warm water moving through the annular section. This work also included the construction of an inverse Rankine refrigeration cycle that was equipped with measurement devices, sensors and a data acquisition system to collect the experimental measurements under different operating conditions. Part of the data were used to train several neural-network configurations. The best neural-network model was then used for prediction purposes and the results obtained were compared with experimental data not used for training purposes. The results obtained in this investigation reveal the convenience of using artificial neural networks as accurate predictive tools for determining convective heat transfer rates of evaporative processes.

Resumen

La predicción de la transferencia de calor en procesos de evaporación es una tarea complicada comparada con la de un proceso sin cambio de fase, ya que la física del fenómeno de evaporación es mucho más diversa y se modifica continuamente conforme la calidad del vapor aumenta. Las correlaciones tradicionales basadas en leyes de potencia que se utilizan para la determinación de la transferencia de calor en evaporadores han probado su falta de efectividad cuando se requie re la predicción correcta de absorción de calor del proceso de evaporación. En este trabajo se utilizaron modelos basados en redes neuronales artificiales para predecir el desempeño térmico de unidades evaporadoras y, para ello, se obtuvieron datos experimentales en un módulo de pruebas consistente en un evaporador tipo intercambiador de calor de doble tubo a contraflujo, por cuya sección circular fluye refrigerante R134a y por cuya sección anular fluye agua a una temperatura mayor controlada. Para determinar los datos experimentales se construyó un banco de pruebas basado en el ciclo Rankine inverso, el cual se equipó con instrumentos de medición, sensores y una tarjeta de adquisición de datos para el monitoreo de señales. Una parte de los datos obtenidos en los experimentos se usaron para entrenar a distintas configuraciones de redes neuronales a fin de obtener el mejor modelo. Este modelo se usó para efectos predictivos y los resultados obtenidos se compararon con datos experimentales que no fueron usados durante el entrenamiento de la red neuronal artificial. Los resultados obtenidos en esta investigación demuestran la conveniencia de usar redes neuronales artificiales para la determinación correcta de la transferencia de calor en procesos de evaporación de refrigerantes.

Introduction

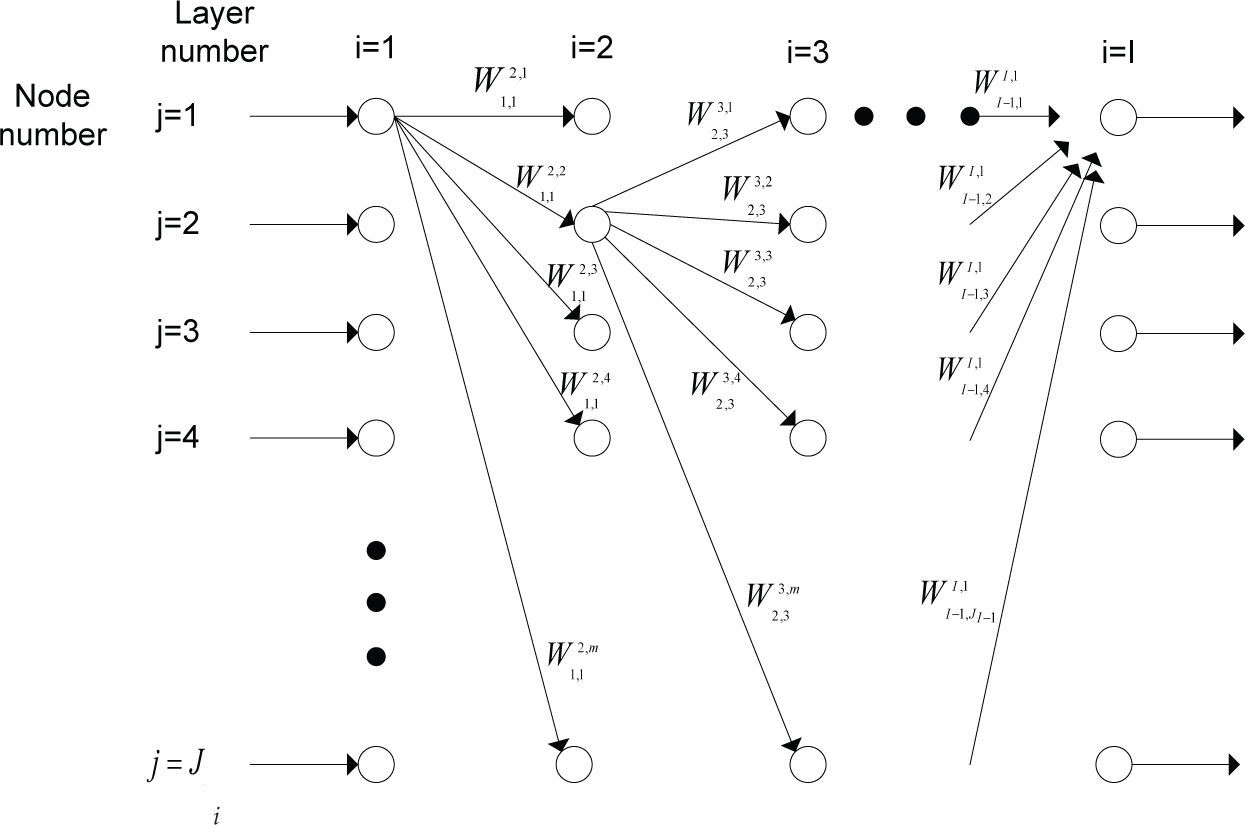
Thermal systems are engineering systems that involve temperature differences. Heat transfer is devoted to the analysis, design and control of these systems, and has a long history of development in response to the needs of a great variety of applications. One of the modern technologies that has been successful as an analysis tool is the technique of artificial neural networks. This technique has been applied for pattern recognition, decision making, control systems, information processing, symbolic mathematics, computer vision and robotics. The use of artificial neural networks can be extended to a wide variety of disciplines, among which are the thermal sciences, because it allows to study complex thermal systems that otherwise would be impossible to characterize with conventional analytical techniques. Heat transfer is part of daily life of human beings; there is a need for buildings and homes that provide comfort minimizing energy losses. Artificial neural networks have been studied over the last decades and are an excellent option for modeling complex systems. Some of the thermal systems that have been studied with this technique are the prediction of heat transfer coefficients (Jambunathan et al., 1996), determination of Nusselt number (Thibault and Grandjean, 1991), prediction of heat transfer in heat exchangers (Díaz et al., 1996; Pacheco- Vega et al., 2002, 2001a, 2001b), estimation of heat transfer in the transition region of a circular tube (Ghajar et al., 2004), the thermal performance of cooling towers (Islamoglu, 2005), analysis of shell and tube heat exchangers (Wang et al., 2006), phase change in finned tubes (Ermis et al., 2007), friction and heat transfer in helically finned tubes (Zdaniuk et al., 2007), the modeling of evaporative air coolers (Hosoz et al., 2008), the characterization of compact heat exchangers (Ermis, 2008), the estimation of thermal performance of plate and tube heat exchangers (Peng and Ling, 2009), evaluation of finned tube condensers (Zhao and Zhang, 2010), performance of finned tube evaporators (Zhao et al., 2010) and indirect evaporative cooling (Kiran and Rajput, 2011). The artificial neural network (ANN) is a procedure that permits the modeling of complex systems that cannot be described with simple mathematical models. One of the main advantages is that it does not require a detailed knowledge of the physical phenomena describing the system under analysis. The principle of the ANN is based on the structure and functioning of neural systems, where the neuron is the fundamental element. There are neurons of different shapes, sizes and lengths. The biological neuron, as shown in Figure 1, is formed by the body of the cell, anaxon and dendrites. The axon is a protuberance that transports the signal coming from a neuron to other neurons at subsequent layers, and the dendrites provide enough surface area to facilitate connection with neurons of previous layers. The dendrites divide in such a way that they form dense dendritic trees, and the axons also divide to some extent, but not so much as the dendrites. Artificial neural networks have nodes (or neurons), as shown in Figure 2, whose function is to make mapping operations between inputs and outputs. The artificial neuron is treated as a node connected to others through linkages corresponding to connections axon-synapsis-dendrite. Each link is associated with a weight; as in the case of a synapsis, this weight determines the nature and intensity of influence of one node on another. Specifically, the influence of a node on another is the product of the output of a neuron and the weight that connects them. Therefore a positive (or negative) weight of large value corresponds to a large excitation, while a small weight corresponds to a negligible excitation. There are different configurations of artificial neural networks; the fully connected is the most commonly employed in engineering problems. This kind of neural network is called multilayered perceptron or feed forward network. This configuration is shown in Figure 3, and has a series of layers, each formed by a set of nodes (or neurons). The first layer is called input layer; the last one is called output layer, while the inner layers are the hidden layers. A neural network is fully connected when each node of a layer is connected to all the nodes of the adjacent layers. The objective of this investigation was to make use of artificial neural networks for the characterization of a refrigeration system. For this purpose an experimental setup was built and a significant amount of heat transfer data was obtained. With that information several configurations of neural networks were trained and the results obtained were reported in terms of the accuracy of the prediction.

Figure 1.

Biological neuron

Figure 2.

Artificial neuron

Figure 3.

Artificial neural network

Experimental setup and procedure

An experimental apparatus based on the inverse Rankine cycle, which includes an expansion thermoelectric valve, was built in the thermo-fluids lab of the Faculty of Engineering of the Universidad Autónoma de San Luis Potosí. The experimental setup is photographed in Figure 4 and shown schematically in Figure 5. The main part of it is the test section, in which a refrigerant is evaporated by circulation through a concentric pipes heat exchanger and hot water flows through the annular section. This apparatus has the following subsystems: condensing unit, experimental evaporator test zone, evaporator heating, power supply, measurements and control devices. These subsystems are described as follows:

• •

  Condensing unit, it has an alternative piston compressor with a 3500 Watts capacity, for R-134a refrigerant, a forced air condenser, a receiving tank and service valves for refrigerant loading (Figure 6).

  
  

  Figure 6.

  Condensing unit
• •

  Experimental evaporator test zone, which has a concentric pipes heat exchanger, as shown in Figure 7, in which the refrigerant R134a flows inside the inner tube while hot water circulates at counter-flow inside the annular section. The heat exchanger is 112 mm long; the inner tube has an outer diameter of 12.7 mm and is 0.89 mm thick, the outer tube has an inner diameter of 19.05 mm, both tubes are made of copper. In order to minimize heat losses to the exterior, the outer surface of the outer tube is covered with an insulating material.

  
  

  Figure 7.

  Test section
• •

  Evaporator heating system, formed by a reservoir for storage of water, a section for water heating with three heating resistances of 15 Amperes, 127 Volts each, a 0.5 HP pump and a flow regulation valve.

• •

  Power supply with three phases, 220 Volts C.A. each, and formed by 12 derived circuits.

• •

  Measurements and control devices, with 12 measurements among which are temperatures, pressures and mass flow rates, it also includes controls for the evaporator heating water temperature and the refrigerant flow rate.

Figure 4.

Photograph of the experimental equipment

Figure 5.

Schematic diagram of the experimental equipment

The measurements performed during the experiments are the following: Refrigerant temperature at the inlet and outlet of the test section, refrigerant temperature before the expansion valve, water temperature at the inlet and outlet of the test section, liquid R134a refrigerant mass flow rate, water volumetric flow rate, refrigerant pressure at the inlet and outlet of the compressor, subcooled refrigerant pressure before the expansion valve, and refrigerant pressure after the test section. The temperature sensors are all RTD-100PT type with a third wire for load compensation and are mounted on the outer surface of the pipes. The temperature sensors have capabilities such as controllers, allowing outputs to relay, retransmission of the process output variable or communication to a serial port RS-485. With this capability, the temperature sensor that measures the water temperature at the inlet of the test section is treated as an on/off controller with output to relay with the objective of maintaining a constant water temperature at the input of the test section. This relay controls the heating electric resistances power with the purpose of maintaining the water temperature at the desired value. The refrigerant volumetric flow rate is determined when this is liquid at the exit of the condenser. This measurement is made with a rotameter type flow transmitter that registers a signal ranging from 4 to 20 mA with a precision of 0.5%. The refrigerant volumetric flow rate ranges from 0 to 4.1635 l/min. The water volumetric flow rate is measured at the output of the evaporator with a tangential turbine type flow transmitter that registers a signal ranging from 4 to 20 mA with a precision of 0.5% throughout the range of measurements. The water volumetric flow rate ranges from 0 to 60 l/min. The refrigerant pressure at the inlet and outlet of the compressor are measured with Bourdon type manometers, which have reading precision of 1%. The refrigerant pressure at the inlet to the condenser is read with a pressure transductor that has a precision of 0.25% in the range of measurements that goes from 0 to 3448 kPa, which is registered with an output from 4 to 20 mA.

The thermoelectric expansion valve produces the low pressure needed for evaporation of the refrigerant. The valve used in this investigation is electronically controlled by means of a step motor, a control card, a temperature sensor, a pressure transductor and a manual parameter programmer. With the use of this thermoelectric expansion valve it is possible to guarantee repeatability in the experiments, setting the refrigerant degree of superheating at the outlet of the test section, and automatically adjusting the refrigerant mass flow rate.

The objective of the experiments was to obtain 200 data points in a wide range of variation of the parameters of the refrigerant evaporation process, that when used to train the neural network was representative of the phenomenon being analyzed. The water temperature was varied from 5.5°C to 8.8°C and the volumetric flow rate of water was varied from 3.56 l/min to 31.68 l/min, while the other parameters adjusted according to the conditions of thermal balance through the change of position of the thermoelectric expansion valve, in a process that may take from 20 minutes to 2 hours to stabilize. The parameters that adjust to the position of the valve took values within the following ranges: refrigerant mass flow rate from 0.257 kg/min to 4.219 kg/min, vapor quality lower than 50% and refrigerant evaporation pressure from 151.74 kPa (abs) to 448.11kPa (abs). With these data, and applying an energy balance, the heat absorbed by the refrigerant was calculated and compared with the heat released by the water. An uncertainty analysis of both calculations determined that the inaccuracy of the calculation of heat transferred due to errors in the measurements was 1.4% if calculated from the refrigerant side information, and larger if calculated from the water side information.

Results and discussion

From the data obtained in the experiments, five parameters were chosen as relevant input data for characterization of the thermal phenomena of evaporation of refrigerant in the concentric pipes heat exchanger described before. These parameters are: saturation pressure during the evaporation process (P_sat), mass flow rate of the refrigerant (mr•), mass flow rate of water (ma•), temperature of water at the inlet of the heat exchanger (T_ea) and vapor quality at the inlet of the heat exchanger (X). The output obtained from this input information is the heat transfer to the refrigerant (Qre•). The Fortran 77 code used for training and prediction through artificial neural networks was developed by Díaz (2000) and Pacheco-Vega (2002) in the Hydronics Lab of the University of Notre Dame. The training process was made by adjusting the synaptic weights and biases for the different values of input and output variables. The neural network was trained using the technique of back propagation, as described by Rumelhart et al. (1986). Once the configuration of the neural network was chosen, the first step of the algorithm was the assignment of initial synaptic weights and biases. The second step was to feed forward, that starts by feeding data for the first layer (input layer). That information is transferred forward to reach the nodes of the last layer (output layer), and compared with the known output data to generate an error. The third step was back propagation, in which an error is quantified in each layer and node by means of a sigmoid function, which is used later to change the synaptic weights and biases. The training process ended when the error in the last cycle decreased below an established threshold value.

Nineteen different artificial neural network configurations were analyzed and compared to determine which was better for prediction of thermal behavior of the evaporation process. Table 1 shows all the network configurations tested. The number of layers used was 1, 2 or 3, with a different number of nodes per layer. For each one of the 19 configurations, the mean error value R, the maximum error and the standard deviation σ were calculated while the number of training cycles was increased. The calculations were made with the following equations:

Table 1.

Artificial neural network configurations.

Internal layers	Configuration	R	σ	Maximum error (%)
1	5-1-1	0.9976	0.0156	7.13
1	5-3-1	0.9981	0.0074	5.44
1	5-5-1	0.9999	0.0052	2.49
1	5-7-1	1.0000	0.0052	2.56
1	5-9-1	1.0003	0.0052	2.50
1	5-11-1	0.9998	0.0051	2.46
1	5-13-1	0.9999	0.0053	2.48
2	5-1-1-1	0.9969	0.0182	7.18
2	5-3-1-1	0.9953	0.0093	2.92
2	5-5-1-1	0.9995	0.0055	2.62
2	5-5-3-1	1.0008	0.0052	2.53
2	5-5-5-1	0.9988	0.0057	2.70
2	5-6-4-1	0.9996	0.0054	2.48
3	5-1-1-1-1	0.9960	0.0206	7.31
3	5-3-1-1-1	1.0076	0.0217	6.69
3	5-5-1-1-1	0.9990	0.0053	2.84
3	5-5-3-1-1	0.9994	0.0053	2.63
3	5-5-5-1-1	0.9996	0.0059	2.58
3	5-5-5-3-1	0.9996	0.0056	2.55

Where Qre• is the heat transfer determined from the experimental data and Qrp• is the heat transfer predicted by the artificial neural network. About 75% of the 200 experimental data were used to train every one of the neural network configurations, reserving the other 25% for comparison of the experimental results with the prediction obtained from the neural network (for calculating R and σ of each configuration). As in Pacheco-Vega et al. (2001a, 2001b), the final model of the artificial neural network was built with 100% of the available experimental data, because this allows for an optimum model in the range of the parameters.

The number of training cycles was defined in terms of the minimum value of the maximum error and standard deviation. An example of the behavior observed is shown in Figure 8 for the case of the neural network 5-11-1. From the observations of this and other cases not shown in the paper, it was concluded that after 120,000 cycles the reduction of the error was negligible, and this number of training cycles was taken as the standard throughout this investigation.

Figure 8.

Plots of a) standard deviation and b) maximum error as a function of training cycles for the neural network configuration 5-11-1

While analyzing these 19 configurations it was possible to observe that the configuration proposed by Hecht (1987), a single intermediate layer with 2n + 1 nodes, with n = 5 (configuration 5-11-1) was the best choice in terms of the standard deviation, R = 0.9998 and σ = 0.0051. However, when searching for a more robust model, there are other configurations, as configurations 5-5-3-1, 5-6-4-1, 5-5-5-1-1 y 5-5-5-3-1, that are also very competitive. Configuration 5-5-3-1, R = 1.0008 and σ = 0.0051 would be a good second option. Figure 9 shows the heat transfer obtained experimentally, Qre• versus the prediction of the neural network 5-11-1, Qrp• for each one of the 200 experimental data. It can be seen from the figure that the experimental and predicted values are very close to the ideal straight line that describes the perfect prediction. It is important to mention that the error in the prediction is less than the 10% established as a limit in the figure, and much less than the errors encountered in predictions obtained with correlations that use conventional prediction techniques. It is evident that neural networks are an excellent tool for prediction of the thermal performance of the evaporation of a refrigerant inside a concentric pipes heat exchanger. Liu and Winterton (1991) presented a correlation which is one of the most accepted for prediction of heat transfer during evaporation of a refrigerant inside flat tubes, and the mean error reported in the correlation is 30% when compared with their own data. In contrast, the maximum error obtained in the prediction of heat transfer in the evaporator with the optimal neural network configuration was 2.6%, and the mean quadratic error was 0.52%. Artificial neural networks are a good option for prediction of heat transfer in evaporators with errors of the same order of magnitude as the experimental uncertainty.

Figure 9.

Qre• vs. Qrp• for two configurations: a) 5-11-1 y b) 5-5-3-1

Conclusions

The physics involved in convective evaporation has increased its complexity since the emergence of enhanced surfaces for evaporators and the change of refrigerants for others more environmentally friendly. For those reasons now it is even harder to have good correlations for prediction of the thermal performance of evaporators, based on models that consider forced convection and flooded evaporation as separate phenomena.

The results obtained by using the technique of artificial neural networks, as developed in this investigation, are encouraging. The prediction of heat transfer obtained in this work has a maximum error of 2.46% and a mean quadratic error of 0.51%, which is by far lower than the 30% obtained by other authors, as Liu and Winterton (1991) that use conventional correlation techniques. The technique of artificial neural networks is an excellent option for reliable and precise characterization of thermal systems where evaporation processes occur, such as in refrigeration and air conditioning units.