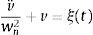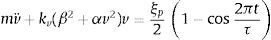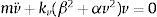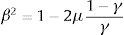El desarrollo de estrategias de control y aislamiento de vibraciones mecánicas inducidas por impacto ha experimentado un reciente interés, debido al incremento en la demanda de aislamientos vibratorios más eficaces en ambientes extremos. Es en este tipo de ambientes donde los impactos son comunes, por ejemplo, aplicaciones militares, navales, en donde fenómenos como explosiones y choques son usuales. Este trabajo presenta los avances más importantes en el área, considerando enfoques de control de vibracio-nes basados en elementos no lineales. Se presentan las tendencias más nove-dosas que pueden dar al investigador en el área ideas sobre trabajo a futuro en el campo del aislamiento de vibraciones por impacto y se propone un modelo de aislamiento con base en la rigidez no lineal, demostrando teórica y experimentalmente su factibilidad en la reducción de aceleración máxima de sistemas sometidos a impacto.
The development of control and isolation strategies for shock induced vibration has experienced a recent interest due to the increasing demand in improved isolation requirements for sensitive equipment subjected to harsh environments. Shock vibration is a common problem that is present in many situations, such as ground motions, blast, explosions, crash, impact, etc. This paper reviews the fundamentals of shock isolation theory, and presents a literature survey of the most important works developed in the field, focusing on non linear shock isolation systems exploring theoretical and experimental results, focusing on recent advances. A model for a shock isolation system based on nonlinear stiffness is proposed, showing theoretically and experimentally its feasibility in the reduction of maximum transmitted acceleration in impact subjected systems.
El término “vibración transitoria” se refiere a una excitación temporal en un sistema mecánico. Los impactos y choques son casos típicos de excitaciones que pueden inducir vibración transitoria no periódica y que normalmente se caracterizan por su aplicación repentina, tener una alta severidad y ser de corta duración. Impactos causados por diferentes fuentes se encuentran normalmente en la vida cotidiana, por ejemplo aquellos causados por prensas, troqueladoras, caída libre de objetos, automóviles pasando por topes, etcétera.
Este tipo de vibraciones suelen ser bastante dañinas en muchos aspectos, principalmente por su naturaleza no periódica y porque suelen estar involucrados altos niveles de aceleración y grandes deformaciones, que hacen que su control y aislamiento efectivo se vuelvan complicados. Esto puede causar daños a equipos sensibles al exceder niveles permisibles de esfuerzos y deformaciones.
De manera general, el objetivo del aislante vibratorio es reducir las fuerzas y desplazamientos transmitidos de una fuente al receptor, normalmente con un aislante elástico que se idealiza como la combinación de un elemento elástico lineal y un elemento amortiguante viscoso. Cuando las propiedades físicas del aislante permanecen constantes, se dice que el aislante es pasivo (Mead, 1999). Este tipo de aislante casi siempre es económico y eficiente para ciertos escenarios, pero puede no ser óptimo en ciertos casos, como en excitaciones vibratorias altamente impredecibles o cambiantes. Cuando las propiedades del aislante pueden ser alteradas en tiempo real, o según el tipo de excitación, se le llama control activo de vibraciones (Harris y Crede, 1996). Estos medios de control pueden ser más eficaces, pero normalmente son más caros, al requerir sistemas de control, sensores y actuadores.
Fundamentos de aislamiento de impactosEl enfoque más común es considerar un sistema MKC (masa-rigidez-amortiguador) de un grado de libertad. En dicho sistema, la masa puede representar una fuente de vibraciones, o bien, el elemento a proteger de vibraciones externas y se analiza con base en su dinámica e interacción con el conjunto rigidez-amortiguador que, a su vez, representa el medio aislante. Este sistema aislante tiene como objetivo absorber la energía proveniente del impacto en forma de deformación y disiparla posteriormente. Para modelar matemáticamente la respuesta de impacto, se considera que el sistema tiene una entrada o excitación de tipo impulsiva, representada por una función de duración finita, por ejemplo, un pulso rectangular, medio ciclo de la función seno, etcétera. Con esto se puede aplicar un método de solución del modelo matemático del sistema y encontrar la respuesta de impacto. Debido a que existen diferentes posibilidades en cuanto a las relaciones entrada-salida del sistema, por ejemplo, la entrada puede ser una fuerza, un desplazamiento o aceleración impulsivos y la salida puede ser un desplazamiento absoluto o relativo, o bien, una aceleración. El modelo matemático del sistema se define por la ecuación 1 como
Así, la ecuación se representa de manera genérica donde la respuesta del sistema está dada por v, y ξrepresenta la entrada o excitación, donde ambas son funciones del tiempo. La respuesta de impacto del sistema depende principalmente de la duración de la excitación impulsiva τ, concretamente de su relación con el periodo natural del sistema T, es decir, τ/T, y de la forma del pulso aplicado. Para el caso de un sistema sujeto a impacto, la respuesta se divide en dos etapas, vibración forzada durante el pulso y vibración residual a la frecuencia natural del sistema una vez que el impacto ha terminado. Se define la respuesta máxima x como la máxima respuesta que ocurre en cualquier instante (puede ocurrir durante o después del impacto), la respuesta residual que ocurre después del impacto y la respuesta relativa, que es la diferencia entre la amplitud de entrada y salida. Esta última respuesta es de gran importancia, ya que representa la deformación en el elemento elástico y se relaciona con el espacio disponible para el aislante. Los parámetros que se usan para evaluar la severidad del impacto suelen ser la máxima aceleración transmitida y el máximo desplazamiento relativo, relacionados con las fuerzas y deformaciones, respectivamente (Snowdon, 1968; Lalanne, 2002).
La gráfica de respuesta al impacto en función de la razón de periodos τ/T se conoce como espectro de respuesta de impacto (SRS, shock response spectra). Según la razón de los periodos, es decir, la duración relativa del impacto, se definen diferentes zonas en el SRS. Cuando la excitación es de muy corta duración con respecto al periodo natural, es decir τ/T > 0.25, se dice que el impacto es impulsivo y la respuesta del sistema es menor que la amplitud de entrada, esto es, el sistema aislante efectivamente disminuye la transmisión de vibración.
Para impulsos de duración similar al periodo natural, τ/T ≈ 1, la respuesta es mayor que la amplitud de entrada, por lo tanto, la respuesta se amplifica. Cuando el impulso es de muy larga duración, este se aplica muy lentamente y se considera cuasi estático. Se dice que la excitación es impulsiva mientras la duración no sea mayor a dos veces el periodo natural. Desde un punto de vista práctico es deseable tener un sistema aislante de baja frecuencia natural para conseguir aislamiento, de esta manera se tiene un soporte flexible capaz de almacenar la energía del impacto. Cuando se considera amortiguamiento en el sistema, el efecto principal es reducir rápidamente las vibraciones residuales. La respuesta durante el impacto también se reduce, pero en menor proporción si se compara con otros tipos de excitaciones armónicas.
Avances en aislamiento de impacto con métodos no linealesA pesar de que el uso de aislantes lineales es muy extenso, el uso de aislantes no lineales no está del todo generalizado, aunque recientemente el interés por este tipo de aislantes ha crecido. Esto se debe principalmente a dos causas, una es que la excitación de impacto es un fenómeno inherentemente no lineal debido a los altos niveles de energía y deformación involucrados, y la otra que el uso de aislantes no lineales puede ser benéfico al conseguir sistemas con una baja rigidez dinámica y alta rigidez estática, lo cual puede ser particularmente útil en el caso de impactos.
Ibrahim (2008) publicó una revisión de literatura sobre aislamiento no lineal, enfocándose al aislamiento de vibración en general, no solo al tema de impacto. Para obtener mas información sobre el tema, el lector puede referirse al trabajo de este autor, donde documenta algunos de los avances más importantes en el uso de aislantes no lineales enfocados a impactos.
Snowdon (1961), Snowdon (1963a) y Snowdon (1963b) fue uno de los primeros investigadores en incorporar elementos no lineales en la teoría de aislamiento de impactos, al considerar rigidez tangencial (cúbica) encontrando que este tipo de sistemas puede proveer aislamiento mejorado. Kemper y Ayre (1971) estudiaron la respuesta de un modelo de cuatro grados de libertad sujeto a un reductor de velocidad (speed bump) modelado como un pulso de desplazamiento tipo verseno, considerando rigidez y amortiguamiento no lineal de tipo exponencial, y encontrando respuestas óptimas de acuerdo a combinaciones de los parámetros involucrados. El efecto del amortiguamiento no lineal cuadrático fue estudiado por Hundal, quien consideró la minimización de la fuerza transmitida como criterio de diseño para un aislante óptimo, logrando un rendimiento mejorado en términos de aceleración transmitida comparado con sistemas lineales y encontró que el valor óptimo de aislamiento cambia según el tipo y duración del pulso (Hundal, 1981). Guntur y Sankar (1982) estudiaron seis tipos de amortiguamiento dual y encontraron que cuando la razón de amortiguamiento es función de la velocidad relativa, el rendimiento es mayor, comparado con sistemas lineales equivalentes, es decir, la razón de amortiguamiento es baja para valores altos de la velocidad relativa y viceversa. Shekhar y Hatwal (1998), analizaron la respuesta teórica de un sistema no lineal de un grado de libertad sujeto a diferentes entradas transitorias tipo pulso y escalón, comparando respuestas exactas y numéricas.
Este trabajo tiene aplicación directa en el modelaje de aislantes elastoméricos y viscosos, ya que los amortiguadores de fluido se pueden considerar como un término positivo cuadrático de amortiguamiento y los elastómeros se pueden representar con una combinación de un término lineal o un término negativo cuadrático. Shekhar concluye que el rendimiento de un aislante con un coeficiente de amortiguamiento no lineal positivo es peor, comparado con el sistema lineal. Por el contrario, un coeficiente negativo pequeño se refleja en disminuciones considerables en la respuesta. En otro trabajo, Shekhar y Hatwal (1999) estudiaron 4 modelos no lineales, a saber, un modelo de fricción seca, un modelo de 3 elementos, un absorsor dinámico no lineal y un modelo de dos etapas. Se encontró que el modelo de fricción seca provee un mejor aislamiento para impactos de alta severidad y que, de manera general, la inclusión de un elemento amortiguante no lineal conectado elásticamente se recomienda para limitar el incremento en la respuesta causado por la no linealidad en el amortiguamiento. Sin embargo el aislante de dos etapas, que es realmente un sistema de dos grados de libertad es el que proporciona mejor aislamiento de impacto para todos los criterios considerados, es decir, desplazamiento y aceleración máximos, y desplazamiento relativo. Los resortes neumá-ticos son inherentemente no lineales y se usan ampliamente como aislantes de vibración e impacto. Diferentes estudios analizan estos sistemas (Hundal, 1982a, 1982b, 1983; Hundal y Fitzmorris, 1985), que han presentado guías de diseño y selección para parámetros óptimos.
El concepto de rigidez variable fue investigado recientemente por Ledezma et al. (2011a), Ledezma et al. (2011b) como un medio de reducción de la respuesta de impacto y la posterior disipación de la energía en sistemas con bajo amortiguamiento, cuando es difícil implementar algún otro medio de amortiguamiento. Los autores consideraron una estrategia semiactiva basada en un modelo de un grado de libertad soportado por dos elementos elásticos en paralelo, uno de los cuales puede conectarse y desconectarse de la masa principal a voluntad. El control de este elemento elástico se da en dos etapas, la reducción de la rigidez durante un impacto y el control en tiempo real durante cada ciclo en la parte de la vibración residual, es decir, una vez que el impacto termina y el sistema está en oscilación libre. Se presentaron simulaciones teóricas que demostraron la factibilidad del concepto al conseguir niveles de reducción de impacto considerables y una rápida disminución de las vibraciones residuales en sistemas con bajo amortiguamiento. Más tarde se desarrolló un sistema de rigidez variable experimental para probar estos conceptos (Ledezma et al., 2012). El sistema es de un grado de libertad y consta de una masa compuesta por imanes permanentes, la cual está suspendida por medio de cables de nylon entre dos electroimanes. De esta manera, al controlar el voltaje suministrado a los electroimanes y la polaridad, se puede controlar la rigidez del sistema a voluntad. Con este sistema se consiguieron cambios en la rigidez de hasta 50%. Se desarrolló un circuito de control análogo para implementar el control en dos etapas, durante y después del impacto. En el sistema experimental, se obtuvieron reducciones de la respuesta máxima de aceleración de 53% y el amortiguamiento se incrementó de 5% a 13%.
De manera similar al concepto de rigidez variable, el uso de rigidez no lineal se ha investigado recientemente como alternativa al aislamiento de impacto. Particularmente la idea de baja rigidez dinámica y alta rigidez estática, también conocida como rigidez cuasi cero, pues puede proporcionar aislamiento vibratorio mejorado seleccionando el punto de equilibrio adecuado alrededor del cual la pendiente de la curva fuerza deformación es muy baja. Se han desarrollado diferentes estudios relativos a este tipo de aislantes, en cuanto al comportamiento estático y dinámico (Waters 2007, Carrella, 2008, Kovacic, 2008). También se ha extendido el uso de estas estrategias en el desarrollo de absorsores dinámicos ajustables (Zhou y Liu, 2010). Sin embargo, en estos estudios no se ha considerado la respuesta de impacto, aunque esta idea presenta gran potencial para aislamiento de impactos, ya que lo ideal para esta situación es un aislante de baja frecuencia natural capaz de almacenar grandes cantidades de energía, lo cual es muchas veces impráctico dadas las restricciones de espacio y rigidez requerida para soportar el peso del sistema que se quiere aislar. Un estudio reciente de Xingtian (2013) demostró teóricamente que el uso de rigidez cuasi cero beneficia el aislamiento de impactos, reduciendo los valores de aceleración máximos. Sin embargo, el desplazamiento relativo puede verse afectado. Queda la tarea de validar experimentalmente estas estrategias e investigar aspectos prácticos en la implementación de esta estrategia. Actualmente, el autor de este estudio se encuentra trabajando en las demostraciones prácticas pertinentes y diversas simulaciones teóricas de respaldo.
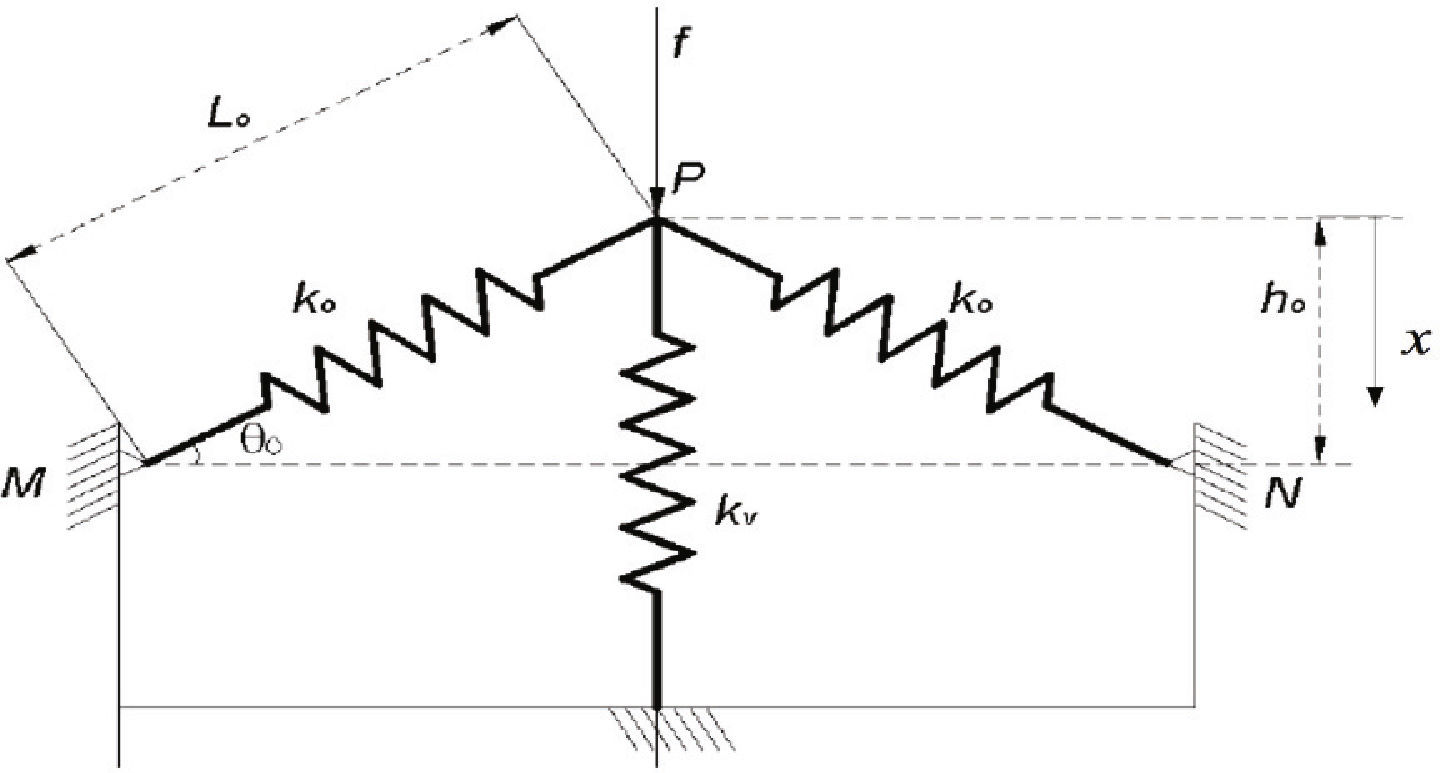
Modelo de baja rigidez dinámica para aislamiento de impactosModelo matemáticoUn método para conseguir baja rigidez dinámica es la combinación de un elemento elástico lineal positivo, con un elemento elástico negativo. La rigidez negativa puede visualizarse como un elemento que provee una fuerza que ayuda al sistema a salir del equilibrio, en lugar de restaurar el equilibrio, como lo hace un resorte positivo. Esta combinación se puede lograr con dos resortes inclinados (rigidez negativa) y un resorte vertical de soporte (positiva). Este arreglo se muestra en la figura 1.
Cuando se coloca una masa en el sistema de resortes inclinados y el sistema parte de la posición de equilibrio estático, la ecuación de movimiento para una excitación de tipo pulso verseno se expresa en dos partes, durante el pulso y la vibración libre una vez que termina el pulso, como se representa en las siguientes ecuaciones
donde
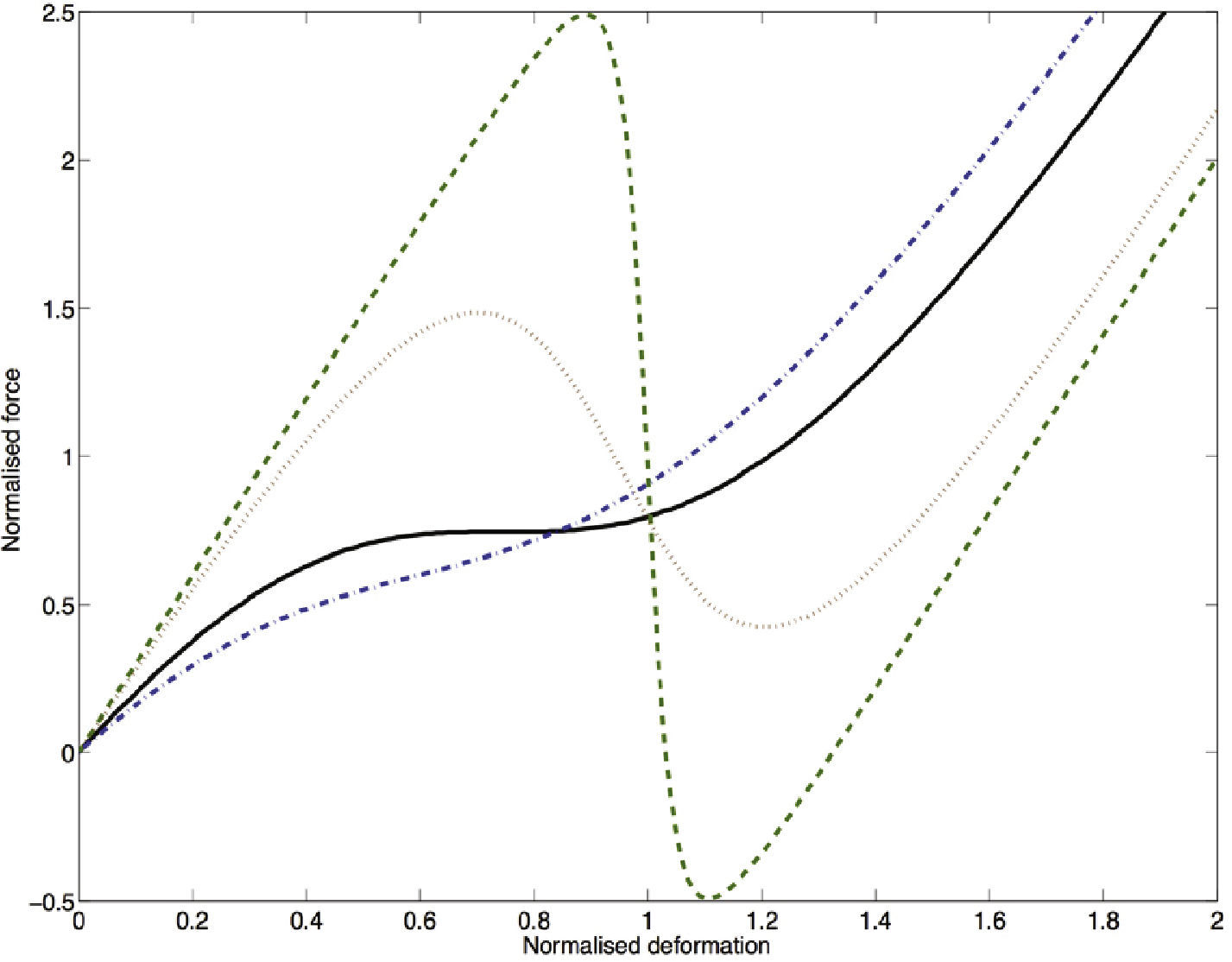
El término μ = ko/kv representa la razón de rigidez entre el resorte vertical y los resortes inclinados, y γ es un parámetro geométrico que depende de la condición del modelo, como el ángulo y longitud inicial, de manera que este parámetro geométrico es 0 cuando los resortes ko están inicialmente verticales, y 1 cuando están inicialmente horizontales. Esta ecuación representa un sistema de un grado de libertad con rigidez cúbica. Las relaciones de fuerza-deformación típicas para este modelo de rigidez cúbica se presentan en la figura 2, para diferentes valores del parámetro geométrico. Existe un valor óptimo del parámetro geométrico que equivale a 2/3 y representa la curva para la cual la pendiente en el punto de equilibrio estático es cero, lo que implica una rigidez cero. Si el parámetro geométrico es menor que 2/3 el sistema se vuelve inestable por ser de rigidez negativa. Para efectos prácticos se busca un valor ligeramente mayor al óptimo para evitar posibles inestabilidades.
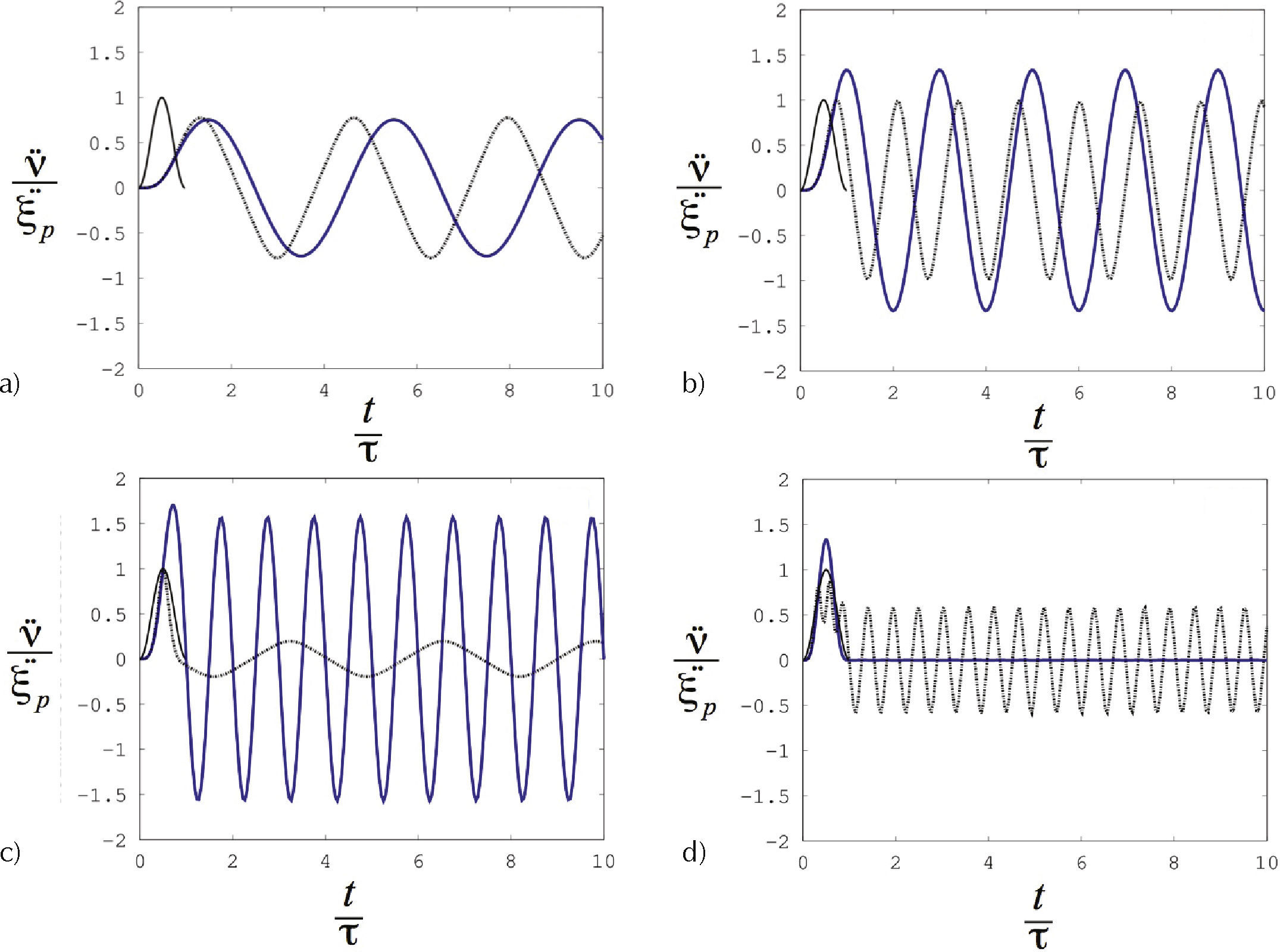
Respuesta al impactoPara resolver la ecuación de movimiento del sistema se aplicó el método numérico de Runge-Kutta con ayuda de MATLAB. Se presenta a continuación la respuesta de aceleración máxima por ser el parámetro más importante para cuantificar la severidad del impacto. Estos resultados se presentan para cuatro valores característicos de la duración relativa del impacto τ/T en la figura 3, y se comparan con la respuesta del sistema lineal sometido al mismo pulso de entrada. Para el sistema no lineal, se considera el parámetro geométrico en su valor óptimo de 2/3. La respuesta se presenta normalizada tomando como referencia la máxima amplitud del pulso, ξ¨p, y el tiempo se normaliza con respecto a la duración del pulso τ.
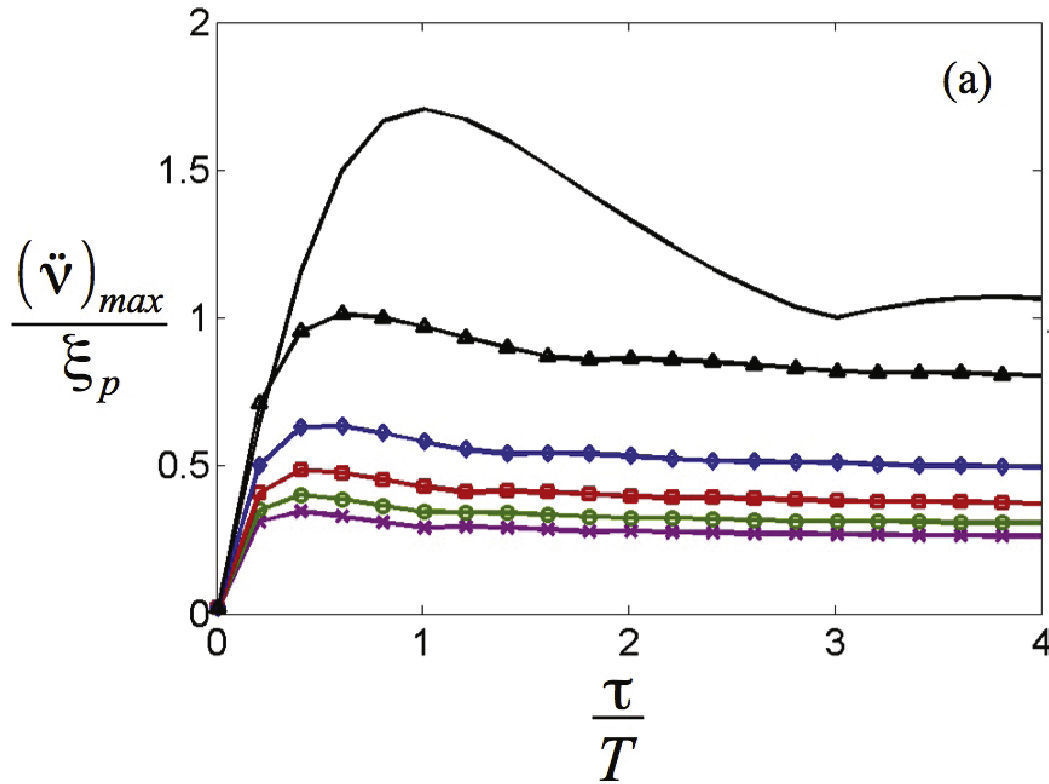
Se puede observar que la duración relativa del impacto juega un papel muy importante en la respuesta del sistema no lineal comparado con el sistema lineal. Para duraciones cortas, ambas respuestas son muy similares, dado que en esta zona la respuesta típica al impacto es de baja amplitud, por ende, el comportamiento no lineal se minimiza y se asemeja al del sistema lineal. Sin embargo, para duraciones medias, especialmente cuando la duración del pulso es igual al periodo natural, la respuesta del sistema no lineal es considerablemente menor y la respuesta residual, además de disminuir, presenta una oscilación de menor frecuencia, ya que el sistema tiene una rigidez dinámica menor. Para pulsos de mayor duración, la respuesta sigue de manera cercana la forma del pulso de entrada y de nuevo se observa que las respuestas de los sistemas lineal y no lineal son semejantes. Estos datos se pueden ver de manera más completa en la gráfica de espectro de impacto SRS presentada en la figura 4, donde se estudiaron diferentes niveles de amplitud del pulso de entrada. Se observa claramente la relación no lineal entre la entrada y la salida del sistema, dado que al aumentar la amplitud de entrada, la respuesta no aumenta en la misma proporción. De manera general, se puede decir que al incluir rigidez no lineal en el sistema de forma que dinámicamente se tenga una baja frecuencia natural, se puede reducir la respuesta de impacto en la zona crítica del SRS.
Validación experimentalModelo experimentalEl dispositivo experimental presentado en la figura 5 se basa en un diseño previo presentado por los autores (Ledezma et al., 2012). En la figura 6 se muestra un diagrama y la figura 7 muestra una fotografía del sistema montado en un excitador electrodinámico. El sistema consta de una masa suspendida formada por un disco de aluminio y dos imanes permanentes de neodimio, sujetada por cuatro hilos de nylon a un soporte de aluminio. Alineado a los imanes permanentes se tienen dos electroimanes, uno en la parte superior y otro en la parte inferior. Se puede controlar la distancia entre imanes permanentes y electroimanes, así como el voltaje suministrado a estos últimos. La intención de este modelo es suspender la masa con resortes lineales y positivos (cables de nylon) y aprovechar la fuerza magnética de repulsión o atracción entre imanes permanentes y electroimanes como una fuerza de rigidez controlable. La masa total suspendida es de 0.075kg, y el voltaje máximo suministrado a los electroimanes fue de 20 VDC. Se limitó la distancia entre imanes a 10 mm para evitar impactos durante las pruebas.
Respuesta del modelo experimental a pulsos tipo verseno de diferente duración y diferentes configuraciones del voltaje suministrado a los electroimanes, a) duración 5 ms, b) duración 10 ms, c) duración 15 ms, d) duración 20ms. (- Electroimanes encendidos en atracción, - - Electroimanes encendidos en repulsión, ××× Electroimanes apagados, -×- Sin electroimanes).
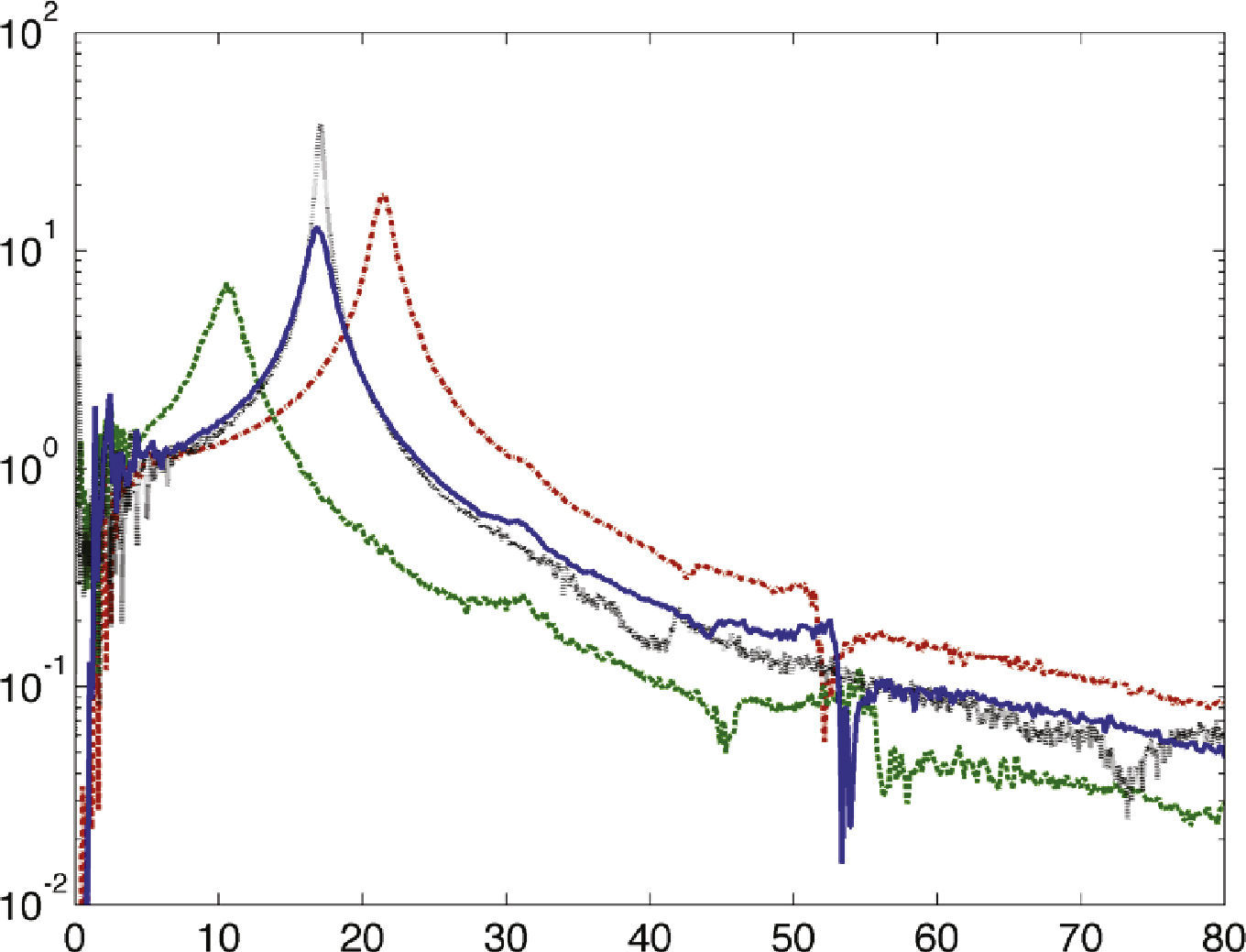
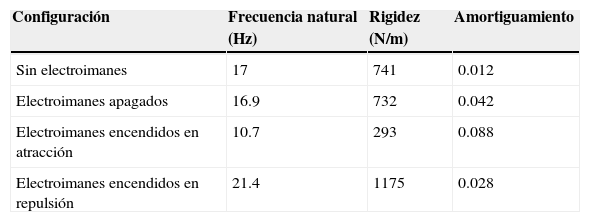
Para encontrar las propiedades de rigidez y frecuencia natural, el modelo se sometió a una prueba de vibración aleatoria por la base, con la intención de medir la función de respuesta en frecuencia (FRF). El modelo se sujetó a un excitador de vibraciones LDS modelo V408 y se midió simultáneamente la aceleración en la base y en la masa suspendida con dos acelerómetros KISTLER miniatura. Las señales se registraron y analizaron en un módulo de adquisición DataPhysics Quattro, en el cual se realizó el análisis FFT en un rango de 1000 Hz para obtener la Respuesta en Frecuencia. Se probaron diferentes configuraciones para estimar la frecuencia natural y rigidez dinámica, a saber: modelo sin electroimanes, electroimanes apagados, electroimanes encendidos en repulsión, y electroimanes encendidos en atracción. Las dos últimas situaciones son con respecto a los imanes permanentes y se alimentaron 20 VDC a los electroimanes. La gráfica de magnitud de la respuesta en frecuencia se presenta en la figura 6, de acuerdo a las configuraciones descritas. La línea continua (azul) representa el sistema sin electroimanes, la línea discontinua (verde) es para los electroimanes encendidos en atracción, la línea discontinua/punto (roja) representa los electroimanes encendidos en repulsión, y por último el sistema con electroimanes apagados está dado por la línea punteada (negro). La tabla 1 resume los resultados según las condiciones descritas. Se observa claramente como la frecuencia natural es significativamente menor cuando los electroimanes están encendidos en configuración de atracción. Esto se debe a que la fuerza electromagnética se reduce a una rigidez negativa, que en combinación con la rigidez provista por los cables resulta en una baja rigidez dinámica. Se incluye también como referencia la razón de amortiguamiento viscosa calculada con base en los picos de resonancia de la figura 6 con el método de ancho de banda.
Resumen de propiedades de frecuencia natural, rigidez y amortiguamiento viscoso equivalente para diferentes condiciones de voltaje aplicado a los electroimanes, medidos a partir de la respuesta en frecuencia
| Configuración | Frecuencia natural (Hz) | Rigidez (N/m) | Amortiguamiento |
|---|---|---|---|
| Sin electroimanes | 17 | 741 | 0.012 |
| Electroimanes apagados | 16.9 | 732 | 0.042 |
| Electroimanes encendidos en atracción | 10.7 | 293 | 0.088 |
| Electroimanes encendidos en repulsión | 21.4 | 1175 | 0.028 |
Para la medición de la respuesta al impacto, el modelo se montó en un shaker electrodinámico LDS modelo V721. Se generaron impactos de tipo pulso verseno, en amplitudes de 3, 4, y 5 g's de aceleración, en duraciones de 5, 10, 15, 20, y 25 milisegundos. Se registró la aceleración en la base y en la masa suspendida simultáneamente con acelerómetros KISTLER miniatura, y el registro de datos se hizo con ayuda del controlador del shaker, LDS Laser USB.
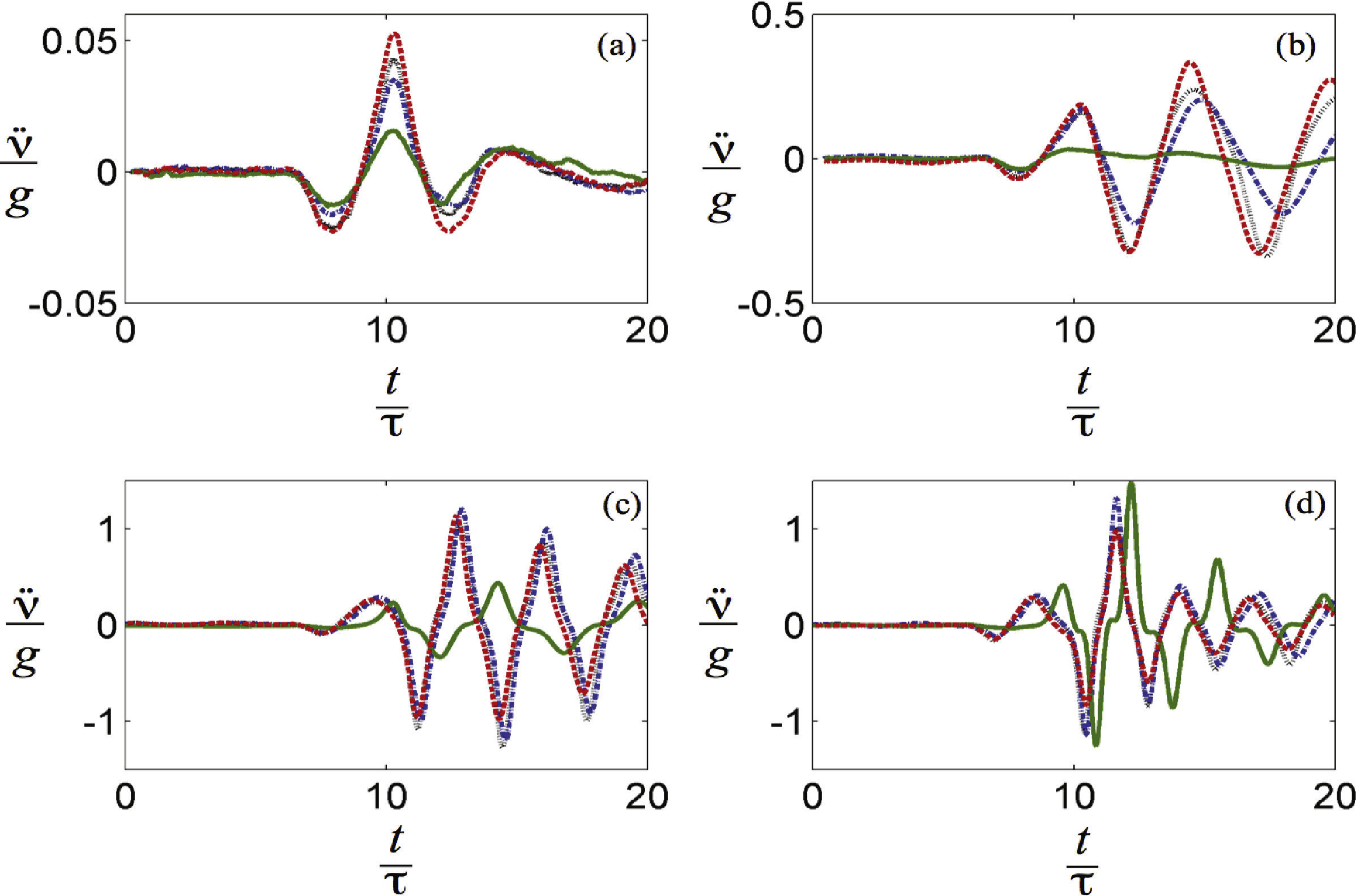
La figura 7 muestra la respuesta en tiempo para el pulso de 5 g de amplitud, en duraciones de 5, 10, 15 y 20 milisegundos para cada gráfica. La línea continua (verde)* representa el sistema con electroimanes encendidos en atracción, la línea discontinua (rojo) es para los electroimanes encendidos en repulsión, la línea discontinua/punto (azul) representa los electroimanes apagados, y por último el sistema sin electroimanes está dado por la línea punteada (negro).
De manera general se observa como la aceleración máxima se reduce cuando el sistema trabaja con electroimanes en atracción. Como se mencionó anteriormente, este caso representa una baja rigidez dinámica, y coincide con las predicciones teóricas establecidas. La reducción en la respuesta es más importante para pulsos menores a 15 milisegundos, sin embargo, para pulsos de duraciones superiores la respuesta del sistema aumenta. Un detalle importante es que para los pulsos de larga duración, la respuesta oscilatoria del sistema no es una sinusoide, sino una respuesta compleja típica de un sistema no lineal, lo cual ocurre por la alta no linealidad de las fuerzas magnéticas cuando la amplitud de la masa suspendida es elevada. Para las otras configuraciones de voltaje consideradas, la respuesta es muy similar entre ellas, observándose mayores amplitudes de aceleración.
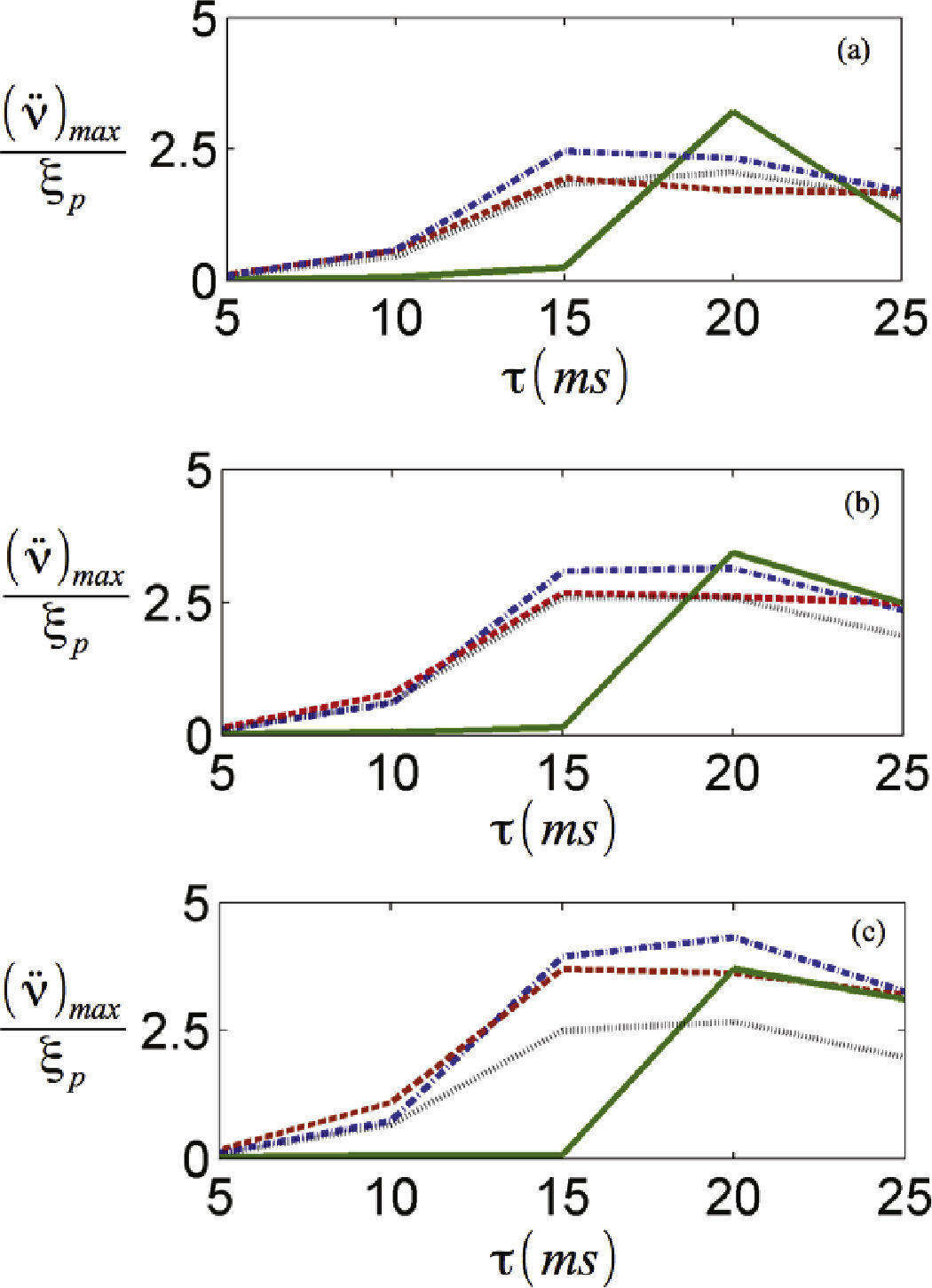
Un panorama más completo de la respuesta a diferentes amplitudes de entrada y duraciones del pulso se puede observar en la figura 8, que representa el SRS para los pulsos considerados. Las diferentes líneas representan las configuraciones de voltaje mencionadas anteriormente, y los incisos a), b) y c) representan amplitudes de 3, 4 y 5 g, respectivamente. Se puede corroborar como la respuesta se reduce considerablemente al usar una configuración de baja rigidez dinámica, especialmente para pulsos menores a 15 milisegundos. Se observa una tendencia similar para las diferentes amplitudes de entrada consideradas.
Espectro de respuesta de impacto medido en base a pulsos tipo verseno de diferente duración y amplitud, a) amplitud 3g, b) amplitud 4g, c) amplitud 5g. (- Electroimanes encendidos en atracción, - - Electroimanes encendidos en repulsión, ××× Electroimanes encendidos apagados, -×- Sin electroimanes).
Sin embargo, cuando se demuestran mejoras considerables en la aceleración máxima transmitida, y este parámetro es muy importante ya que representa la fuerza resultante del impacto, existe la posibilidad de que el comportamiento de otros parámetros de respuesta no sea tan benéfico. En particular, el desplazamiento relativo representa la deformación del sistema aislante, y por ende, el espacio requerido. Este parámetro puede verse incrementado por el uso de esta estrategia, ya que un sistema con baja rigidez presenta mayores deformaciones. Esta deformación es la que efectivamente permite el almacenamiento de la energía del impacto, y es la base elemental de un buen aislamiento. Sin embargo, es necesario estudiar este parámetro de respuesta para definir si existen desventajas comparado con los sistemas clásicos de aislamiento pasivo, o bien, investigar estrategias para restringir o controlar los desplazamientos relativos sin sacrificar el rendimiento aislante. Queda como posibilidad de trabajo a futuro el contemplar este fenómeno.
ConclusionesEn este trabajo se discutieron los fundamentos de teoría de aislamiento de vibraciones de impacto, basado en un sistema de un grado de libertad. La respuesta de impacto es dependiente del tipo de función de entrada, pulso o escalón, de la duración de este, y de las propiedades del sistema sujeto a impactos, es decir, masa rigidez y amortiguamiento. Usualmente el sistema aislante se diseña para obtener una baja frecuencia natural, lo que conlleva a un aislamiento vibratorio aceptable. Este sistema aislante es pasivo, es decir, que sus propiedades permanecen constantes y en la práctica se obtiene con soportes elásticos de diferentes tipos, por ejemplo, resortes helicoidales, resortes de cable, elastómeros, reportes neumáticos, etcétera.
Dada la naturaleza de los impactos al implicar grandes cantidades de energía y deformaciones, el uso de sistemas aislantes no lineales es relativamente común, y se ha desarrollado una cantidad notable de trabajo en esta área, especialmente considerando amortiguamiento cuadrático, rigidez tangencial, y fricción seca. En este trabajo se presentaron resultados teóricos y experimentales considerando un modelo basado en rigidez no lineal, demostrando que se puede conseguir una disminución considerable en la respuesta máxima de aceleración de un sistema sometido a impactos, cuando se usa una estrategia de rigidez dinámica baja. Se desarrolló un modelo experimental que validó las predicciones teóricas.
De esta manera se contempla como posibilidad de estudio a futuro el uso de rigidez no lineal, particularmente los sistemas con baja rigidez dinámica y alta rigidez estática, que han despertado reciente interés, pero el estudio de su respuesta de impacto no está del todo desarrollado. Los resultados presentados en el prototipo desarrollado se muestran prometedores en la reducción de la aceleración máxima, sin embargo queda por estudiar el efecto de dichas estrategias no lineales en otros parámetros de respuesta, tal como el desplazamiento relativo, el cual es de gran importancia por representar la deformación efectiva del sistema aislante y por ende el espacio requerido para este. También será necesario considerar la implementación práctica del concepto, el cual se demuestra en los avances presentados, pero que es necesario aterrizar en un dispositivo para aplicaciones reales.
Por otra parte, dadas las tendencias y avances en materia de aislamiento no lineal, el uso de otros métodos de disipación de energía puede ser provechoso, por ejemplo, el caso del amortiguamiento por fricción seca que se encuentra en ciertos resortes de cable usados para el aislamiento de vibraciones extremas, los cuales por su configuración presentan también curvas de rigidez no lineal. Estos dispositivos no se han estudiado adecuadamente, por lo que es necesario establecer modelos matemáticos y validarlos con ayuda de caracterizaciones experimentales, en particular en lo que concierne a la respuesta de impacto.
AgradecimientosEste trabajo fue financiado parcialmente por CONACyT [CB 2010 152241], y PROMEP [PROMEP 103.5/10/7303], así como la Universidad Autónoma de Nuevo León [PAICyT 2010].
Este artículo se cita:
Citación estilo Chicago
Ledezma-Ramirez, Diego Francisco. Avances en aislamiento de vibración por impacto usando rigidez no lineal. Ingeniería Investigación y Tecnología, XVI, 02 (2015): 307-316.
Citación estilo ISO 690
Ledezma-Ramirez D.F. Avances en aislamiento de vibración por impacto usando rigidez no lineal. Ingeniería Investigación y Tecnología, volumen XVI (número 2), abril-junio 2015: 307-316.
Semblanza del autor
Diego Francisco Ledezma-Ramirez. Ingeniero mecánico electricista por la Universidad Autónoma de Nuevo León, egresado en 2003. Cursó estudios de doctorado en el Institute of Sound and Vibration, University of Southampton de 2004 a 2008, obteniendo el grado en enero del 2009. Actualmente se desempeña como profesor investigador de tiempo completo en la FIME-UANL en el área de dinámica estructural, control y aislamiento de ruido y vibraciones y es miembro del núcleo básico de la carrera de ingeniería aeronáutica. Ha publicado artículos en revistas indexadas y arbitradas, así como presentaciones en congresos a nivel nacional e internacional.