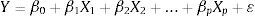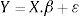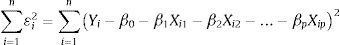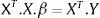Estimación simultánea de datos hidrológicos anuales faltantes en múltiples sitios

Resumen

La deducción de los datos anuales faltantes en los registros hidrológicos, es necesaria para integrar series con un periodo común, las cuales son requeridas en los estudios de simulación de los sistemas hidráulicos y en varios métodos regionales de estimación de crecientes. Además, las estimaciones estadísticas se vuelven más confiables y exactas conforme proceden de series completas más amplias. La regresión lineal múltiple (RLM) permite estimar datos anuales faltantes con base en los registros cercanos que tienen dependencia o correlación con la serie incompleta. El algoritmo de Beale–Little se basa en la RLM y considera cada registro como variable dependiente y el resto como regresores; emplea toda la información disponible, no únicamente el periodo común de datos y conduce a una estimación simultánea de los valores anuales faltantes en los registros procesados. Se describen tres aplicaciones numéricas del algoritmo de Beale-Little para estimar datos anuales faltantes de volumen escurrido y de gasto máximo, en el sistema del río Tempoal y en el Alto río Grijalva de las Regiones Hidrológicas Núm. 26 (Pánuco) y Núm. 30 (Grijalva–Usumacinta), que tienen cinco estaciones hidrométricas, cuatro de ellas completas. Las conclusiones destacan las ventajas del procedimiento descrito e ilustrado numéricamente y recomiendan su aplicación sistemática debido a que su implementación es sencilla.

Abstract

The deduction of annual missing data in hydrological records is necessary to integrate series with a common period, which are required in simulation studies of hydraulic systems and several regional flood estimation methods. Besides, the statistical estimates become more reliable and accurate when full and extensive series are utilized. Multiple linear regression (MLR) allows estimating annual missing data based on close records that have dependence or correlation with the incomplete sequence. The Beale–Little algorithm is based in MLR where each record considered as a dependent variable and the rest as regressors; uses all available information, not only the common data period and leads to a simultaneous estimation of annual missing values in the records processed. Three numerical applications of the Beale–Little algorithm are described to estimate annual missing data of runoff volume and maximum flow in the system Tempoal River and Upper Grijalva River of the Hydrological Regions No. 26 (Panuco) and No. 30 (Grijalva–Usumacinta), which has five hydrometric stations, four of which are complete. The conclusions pointed out the advantages of the procedure described and illustrated numerically and recommend its systematic application given its ease of implementation.

Introducción

En hidrología superficial las aplicaciones de la regresión lineal múltiple (RLM) más comunes, emplean diversas variables explicativas y una variable de respuesta. Con frecuencia, las variables explicativas o regresores son causales, como en el caso de la lluvia que origina el escurrimiento. En ocasiones, los regresores no son directamente causales, sino que establecen el escalamiento, como el tamaño de cuenca y la longitud o la pendiente del colector principal, en relación con las crecientes o gastos máximos. Cuando la RLM se emplea con varias variables de respuesta de manera simultánea, se trabaja en el campo del análisis multivariado (AM).

Una aplicación práctica del AM consiste en estimar datos hidrológicos anuales faltantes, tanto de escurrimiento como de lluvia o de gasto máximo; los cuales no existen debido a fallas o pérdida del equipo de muestreo, enfermedad o abandono de los operadores o simplemente por un inicio retrasado de la operación de la estación hidrométrica o pluviométrica. Los dos objetivos básicos de la estimación de datos faltantes son: 1) completar las series disponibles para poder realizar análisis hidrológicos del tipo de periodo común y 2) mejorar la calidad estadística de los parámetros que se estiman, al emplear series completas y más largas (Gyau y Schultz, 1994; Simonovic, 1995; Salas et al., 2008).

Diversos enfoques han sido aplicados en la estimación de datos hidrológicos faltantes, por ejemplo, Bennis et al. (1997) usan la regresión lineal para deducir los valores perdidos, corrigiendo estos con factores deducidos de la aplicación de dos procesos autorregresivos que operan hacia atrás y hacia adelante del periodo de datos faltantes. Khalil et al. (2001) toman en cuenta el efecto de las estaciones o épocas al usar grupos de registros hidrométricos y redes neuronales artificiales basadas en tal grupo, para estimar los datos faltantes. Ulke et al. (2009) calculan valores faltantes de carga de sedimentos en suspensión con base en datos de precipitación y gasto, usando diversos métodos como regresión lineal y no lineal múltiple, redes neuronales artificiales y sistemas de inferencia neurodifusa.

El algoritmo de Beale-Little, es una técnica del AM que permite estimar de manera simultánea los datos anuales faltantes en registros de estaciones hidrométricas o pluviométricas de una zona geográfica, los cuales muestran una correlación significativa, pero no tienen persistencia. Es únicamente apropiado para estimar datos faltantes que fueron perdidos de una manera aleatoria; consideración que es válida cuando hubo ausencia del operador, o una suspensión temporal por pérdida o mantenimiento del equipo, o bien, por mejoras en la instalación; sin embargo, no han cambiado las condiciones ambientales regionales. Por el contrario, cuando la parte baja de una cuenca grande es colonizada y se establecen estaciones de aforos en sus cercanías, estos datos no se pueden utilizar para ampliar los registros cortos de las estaciones hidrométricas que se ubicaron posteriormente en la zona alta con dificultades de acceso, pues tales registros seguramente estarán afectados por la deforestación, los desarrollos agrícolas, los aprovechamientos hidráulicos, o bien, la urbanización (Beale y Little, 1975; Clarke, 1994).

La ausencia de persistencia implica que los datos de cada serie no muestran correlación o dependencia serial, lo cual es una consideración aceptable cuando se procesan registros de valores anuales de gasto máximo de cuencas de cualquier tamaño; así como registros de escurrimiento anual procedentes de cuencas que no presentan un efecto de almacenamiento considerable, como son cuencas pequeñas montañosas con suelos someros, o cuencas medianas con áreas impermeables importantes que generan mucho escurrimiento directo. La condición de independencia serial deberá ser cuestionada en registros de volumen escurrido anual de cuencas grandes o medianas y pequeñas, pero con grandes áreas permeables o con almacenamiento importante en acuíferos de respuesta lenta (Clarke, 1994).

El objetivo de este trabajo consiste en exponer con detalle el procedimiento operativo del algoritmo de Beale–Little, describiendo dos aplicaciones numéricas en el sistema del Río Tempoal, de la Región Hidrológica Núm. 26 (Pánuco); la primera permite deducir los datos faltantes de volumen escurrido anual y la segunda los de gasto máximo anual (crecientes), en las cinco estaciones hidrométricas que se procesan simultáneamente, que son: Tempoal, El Cardón, Platón Sánchez, Los Hules y Terrerillos. Los resultados del algoritmo de Beale-Little se comparan con los obtenidos previamente empleando la RLM aplicada durante el periodo común de datos. La tercera aplicación numérica se desarrolla en cinco cuencas del Alto río Grijalva de la Región Hidrológica Núm. 30 (Grijalva–Usumacinta), tres de ellas incompletas en su registro de volumen escurrido anual.

Procedimientos aplicados

Descripción operativa del algoritmo de Beale-Little

En Beale y Little (1975) se pueden consultar los aspectos teóricos del algoritmo y en Clarke (1994) los relativos a su aplicación práctica. Su proceso operativo consta de los cinco pasos siguientes:

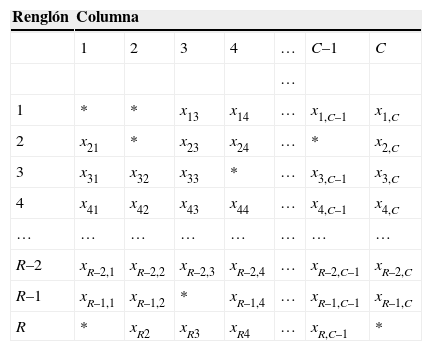
Paso 1: Recopilación de información disponible. El arreglo para la disponibilidad de información hidrológica, que concuerda con las matrices que resuelven la RLM, establece una matriz de R renglones y C columnas, donde los primeros pertenecen a los años de registro y las segundas a las estaciones hidrométricas o pluviométricas, indicando con un asterisco los datos faltantes. Lo anterior se ilustra en la tabla 1 siguiente.

Tabla 1.

Arreglo matricial para la disponibilidad de información hidrológica

Renglón	Columna
	1	2	3	4	…	C–1	C
					…
1	*	*	x13	x14	…	x1,C–1	x1,C
2	x21	*	x23	x24	…	*	x2,C
3	x31	x32	x33	*	…	x3,C–1	x3,C
4	x41	x42	x43	x44	…	x4,C–1	x4,C
…	…	…	…	…	…	…	…
R–2	xR–2,1	xR–2,2	xR–2,3	xR–2,4	…	xR–2,C–1	xR–2,C
R–1	xR–1,1	xR–1,2	*	xR–1,4	…	xR–1,C–1	xR–1,C
R	*	xR2	xR3	xR4	…	xR,C–1	*

Paso 2: Sustitución inicial de datos faltantes. Partiendo del arreglo matricial de disponibilidad de información, se comienza por identificar y anotar cada uno de los datos o secuencia de valores faltantes en los registros. Después se obtienen las medias aritméticas de cada columna y tales magnitudes se sustituyen en cada dato faltante del registro.

Paso 3: Se calcula la RLM de cada registro y se obtienen nuevas estimaciones de datos faltantes. Se obtiene la RLM de cada registro X_ij, considerado como variable dependiente (Y) y el resto de los registros tomados regresores X_ij. Con base en tal RLM se define una nueva estimación de cada dato faltante del registro procesado.

Paso 4: Se calculan las diferencias entre el dato anterior y el nuevo. En el primer ciclo del algoritmo de Beale-Little corresponden a las diferencias entre las medias del registro y la nueva estimación de cada dato faltante. Estas diferencias ayudarán a definir cuando terminan los ciclos del algoritmo; lo anterior cuando estas son muy reducidas o tienden a ser despreciables; por ejemplo, menores de una unidad.

Paso 5: Se remplazan las estimaciones anteriores por las nuevas y se realiza otro ciclo. Cada nuevo ciclo inicia sustituyendo las nuevas estimaciones por las anteriores y se repiten los pasos 3 y 4.

Antes de aplicar el algoritmo de Beale-Little se debe verificar que los registros involucrados tienen las características estadísticas siguientes:

• 1)

  Se puede aceptar que proceden de distribuciones normales, lo que implica que los datos X_ij tienen una distribución multivariada normal. Lo anterior se puede verificar con alguna prueba estadística, por ejemplo el Test W de Shapiro y Wilk (1965), o el cociente de Geary (Machiwal y Jha, 2012). Cuando los datos no son normales se usa una transformación, la más simple consiste en emplear los logaritmos de los datos.

• 2)

  Una estrategia apropiada cuando se estiman valores hidrológicos anuales faltantes, recomienda emplear el mayor número de registros posibles o columnas en la matriz definida en la tabla 1, siempre y cuando tales registros estén correlacionados. Por lo anterior, es aconsejable antes de aplicar el algoritmo de Beale–Little, verificar que las correlaciones entre los registros (r_xy) son importantes; por ejemplo superiores a 0.80.

• 3)

  El algoritmo de Beale-Little requiere que no exista correlación entre los datos de cada renglón de la matriz de la tabla 1, lo cual significa que no exista persistencia en los registros procesados. Entonces el algoritmo de Beale-Little no es adecuado para estimar valores anuales faltantes de gasto mínimo o de cualquier otro indicador de sequías hidrológicas, pues tales parámetros por lo general reproducen el comportamiento de las secuencias de años secos.

Formulación matemática de la RLM

Considerando que existen p variables independientes o regresores la RLM establece el modelo siguiente (Ryan, 1998):

Aceptado que se tienen n observaciones de Y, X₁, X₂, . . . . . , X_p, la expresión anterior en notación matricial será cuyas matrices son

En la matriz X, X_ij representa a la i–ésima observación o dato en la j–ésima variable independiente. El método de mínimos cuadrados de los residuos establece que la suma de los errores (¿_i) elevados al cuadrado debe ser minimizada, esto es

La diferenciación del lado derecho de la ecuación anterior con respecto a β₀, β₁, β₂, . . . , β_p, por separado e igualada a cero, produce p ecuaciones con p parámetros desconocidos, las cuales se conocen como ecuaciones normales, su notación matricial es

y cuya solución es

En la ecuación anterior, X^T es la matriz transpuesta de X y (X^T·X)–1 es la matriz inversa de X^T·X.

Programa de cómputo desarrollado

A continuación se describen los aspectos relevantes del programa de cómputo generalizado desarrollado para este trabajo, el cual se modifica según cada aplicación numérica.

Aspectos relevantes:

• 1)

  Los datos disponibles en cada registro completados con sus medias, se guardan en vectores renglón, que después se acomodan como vectores columna al formar las matrices Y y X correspondientes a cada RLM. En estos vectores renglón es donde se sustituyen las nuevas estimaciones de cada dato faltante.

• 2)

  Las matrices Y y X se forman en arreglos bidimensionales: Y(n,1) y X(n,p), donde n es el número de años de los registros y p el número de regresores. La matriz X en su primera columna tiene a la unidad.

• 3)

  Una subrutina llamada CALBETA aplica la ecuación 5, después que se han formado las matrices Y y X relativas a cada RLM. En esta subrutina se comienza por obtener la transpuesta de X, para multiplicarla por la matriz Y y así definir la matriz X^T·Y. Después se multiplican las matrices X^T por X y se obtiene su inversa. Por último, se multiplican las matrices, inversa de X^T·X por X^T·Y, para obtener el vector columna de coeficientes β_i. Calculada cada RLM se obtienen las nuevas estimaciones de datos faltantes. Al término de cada ciclo del algoritmo de Beale-Little el programa pregunta si se imprimen sus resultados parciales.

Modificaciones particulares: En cada aplicación numérica se ubican o definen los datos faltantes de cada registro, los cuales se estiman con cada RLM, que se calcula considerando tal registro como variable dependiente y el resto como regresores. Calculados los datos faltantes de todos los registros incompletos, se muestran sus valores anteriores y los del ciclo que se está realizando, así como sus diferencias, para definir si se efectúa otro ciclo o si ya estas son muy reducidas o despreciables; por ejemplo, menores de la unidad.

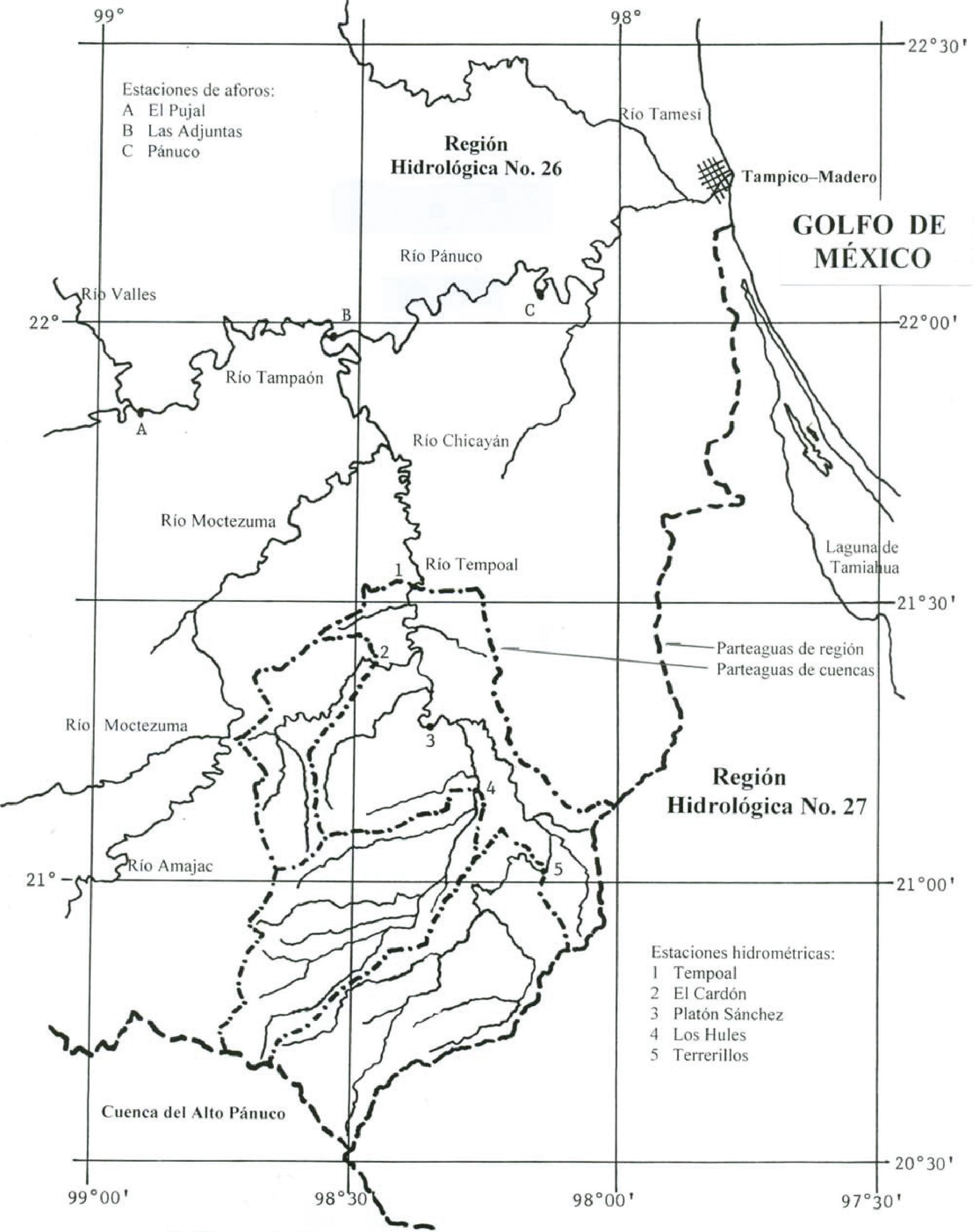
Resultados y su análisis

Primera aplicación numérica

El río Tempoal pertenece a la Región Hidrológica Núm. 26 (Pánuco), es el último afluente importante del río Moctezuma que junto con el Tampaón forman el río Pánuco. En la figura 1 se muestra la morfología y localización geográfica del sistema del río Tempoal. En este río existen cinco estaciones hidrométricas, cuyos datos disponibles en el sistema BANDAS (IMTA, 2002), de volumen escurrido anual en millones de metros cúbicos (Mm³) se muestran en la tabla 2.

Figura 1.

Localización y morfología del sistema del río Tempoal.

Tabla 2.

Volúmenes escurridos anuales (Mm³) en las estaciones hidrométricas del Río Tempoal en el periodo común de 1961 a 2002

Núm.	Año	Tempoal	El Cardón	P.Sánchez	Los Hules	Terrerillos
1	1961	3150.302	386.787	–	1021.195	1211.240
2	1962	1796.844	272.019	–	677.758	628.203
3	1963	1655.044	197.102	–	661.475	668.833
4	1964	1076.755	145.934	–	378.162	324.150
5	1965	2293.958	244.780	–	749.130	865.133
6	1966	2786.573	235.217	–	1011.194	1020.039
7	1967	3263.920	548.409	–	1080.269	1067.163
8	1968	2837.862	511.579	–	945.499	985.655
9	1969	3323.340	488.246	–	1127.562	1336.178
10	1970	2863.385	412.411	–	941.203	944.250
11	1971	2441.337	336.091	–	808.878	1072.324
12	1972	2566.835	373.829	–	950.725	915.385
13	1973	3599.619	522.902	–	1160.392	1243.497
14	1974	4296.827	642.511	–	1312.057	1428.909
15	1975	4298.112	570.883	–	1656.828	1446.878
16	1976	4241.779	673.933	–	1564.284	1868.405
17	1977	1332.365	134.540	–	466.286	521.217
18	1978	3688.256	547.106	–	1376.984	1406.349
19	1979	2103.745	284.234	2995.751	796.465	829.710
20	1980	1586.278	227.079	1325.674	586.212	702.483
21	1981	4491.975	728.237	3666.737	1665.041	–
22	1982	880.923	148.206	776.575	359.815	394.620
23	1983	2187.518	271.316	2116.887	967.822	1190.780
24	1984	5057.565	636.325	4065.671	1832.083	2444.332
25	1985	2607.572	361.991	2257.756	936.464	1390.327
26	1986	1807.878	264.761	1654.262	688.127	891.569
27	1987	2213.954	322.006	2018.218	815.745	1418.647
28	1988	2325.627	274.661	1955.431	729.049	1312.224
29	1989	1749.932	288.773	1457.954	1032.017	958.891
30	1990	2680.279	359.339	2413.499	–	1209.258
31	1991	4016.997	713.490	2682.264	–	1712.530
32	1992	4134.539	607.888	3144.544	1545.657	1929.711
33	1993	5629.170	749.586	4291.278	2230.109	2370.400
34	1994	1634.689	305.695	1228.833	809.173	703.788
35	1995	1861.508	343.729	1542.547	1081.871	843.071
36	1996	1250.085	185.781	1034.440	778.378	594.657
37	1997	1180.939	152.708	1046.949	651.170	520.502
38	1998	3314.234	–	2475.934	950.051	1523.011
39	1999	3206.621	–	2456.724	1294.764	1481.634
40	2000	1710.830	–	1426.170	425.543	839.818
41	2001	1929.465	277.771	1281.262	535.401	805.264
42	2002	1411.568	172.370	1058.208	644.391	683.526
Valor Medio		2678.262	382.570	2098.899	943.131	1114.745

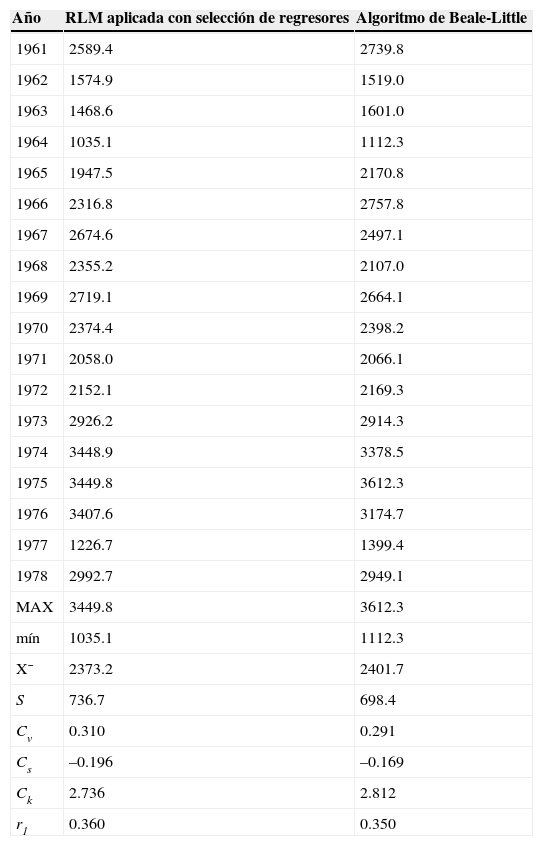
Campos (2011b) procesó esta información, verificando primeramente que tales muestras pueden ser consideradas procedentes de poblaciones normales, además encontró que tales registros tienen fuerte dependencia, con valores del coeficiente de correlación lineal (r_xy) que varían de 0.858 a 0.949. Después, aplicó la RLM en el periodo común de datos de 1979 a 2002 con 18 datos en cada registro y el método de selección óptima de regresores, para obtener la secuencia inicial faltante en Platón Sánchez, los resultados adoptados se exponen en la segunda columna de la tabla 3.

Tabla 3.

Volúmenes escurridos anuales (Mm³) estimados en la estación Platón Sánchez con los métodos indicados

Año	RLM aplicada con selección de regresores	Algoritmo de Beale-Little
1961	2589.4	2739.8
1962	1574.9	1519.0
1963	1468.6	1601.0
1964	1035.1	1112.3
1965	1947.5	2170.8
1966	2316.8	2757.8
1967	2674.6	2497.1
1968	2355.2	2107.0
1969	2719.1	2664.1
1970	2374.4	2398.2
1971	2058.0	2066.1
1972	2152.1	2169.3
1973	2926.2	2914.3
1974	3448.9	3378.5
1975	3449.8	3612.3
1976	3407.6	3174.7
1977	1226.7	1399.4
1978	2992.7	2949.1
MAX	3449.8	3612.3
mín	1035.1	1112.3
X¯	2373.2	2401.7
S	736.7	698.4
Cv	0.310	0.291
Cs	–0.196	–0.169
Ck	2.736	2.812
r1	0.360	0.350

Para el arreglo mostrado en la tabla 2, se tiene n = 42 y p = 4. En la estación El Cardón están faltantes los renglones (años) 38, 39 y 40; en Los Hules los renglones 30 y 31; en Terrerillos el renglón 21 y por último, en Platón Sánchez falta el lapso inicial de 18 renglones (años). Se utilizaron en los registros de las cuatro estaciones incompletas los siguientes valores medios: 383, 943, 1115 y 2099 Mm³, respectivamente y después de 80 ciclos se obtuvieron las estimaciones siguientes: en El Cardón 473.1, 478.1 y 231.0 Mm³; en Los Hules 1007.6 y 1510.8 Mm³; en Terrerillos 1773.2 Mm³ y en Platón Sánchez la secuencia mostrada en la columna tres de la tabla 3.

Segunda aplicación numérica

También se realiza en el sistema del río Tempoal, pero ahora se completan los datos disponibles de gasto máximo anual (m³/s), procedentes del sistema BANDAS (IMTA, 2002), los cuales se exponen en la tabla 4.

Tabla 4.

Gastos máximos anuales (m³/s) en las estaciones hidrométricas del Río Tempoal en el periodo común de 1960 a 2002

Núm.	Año	Tempoal	El Cardón	P.Sánchez	Los Hules	Terrerillos
1	1960	1277.0	1080.0	–	452.6	314.0
2	1961	852.9	303.5	–	434.5	525.0
3	1962	739.2	262.0	–	457.5	565.9
4	1963	1800.0	481.0	–	947.4	895.9
5	1964	748.0	188.6	–	258.0	397.1
6	1965	792.7	338.0	–	414.9	659.4
7	1966	1778.0	287.0	–	742.2	1121.7
8	1967	2245.0	854.2	–	1009.4	1153.0
9	1968	1145.0	476.0	–	1096.0	611.2
10	1969	1948.0	555.8	–	825.0	2224.2
11	1970	1418.0	560.0	–	800.0	1420.0
12	1971	1630.0	720.4	–	1064.0	1488.5
13	1972	989.0	320.0	–	1110.0	529.0
14	1973	1668.0	392.0	–	749.0	1740.0
15	1974	4950.0	1198.3	–	1950.0	3187.8
16	1975	4040.0	1204.2	–	2470.0	2085.0
17	1976	1275.0	419.7	–	937.7	1000.5
18	1977	514.0	179.1	–	559.0	291.2
19	1978	3725.0	1390.0	2898.0	2874.0	2152.3
20	1979	1655.9	667.0	1040.0	1082.0	659.1
21	1980	1162.0	357.0	976.0	583.2	994.1
22	1981	2020.0	765.2	1940.0	1650.3	–
23	1982	539.6	182.3	589.8	340.0	491.4
24	1983	868.0	269.8	827.3	544.0	768.4
25	1984	4030.0	572.0	4530.0	2834.9	2981.0
26	1985	1882.0	457.0	1608.0	938.4	1487.7
27	1986	476.0	192.0	462.0	308.0	434.0
28	1987	1765.0	346.8	1773.0	1440.0	2635.0
29	1988	3265.0	356.0	3653.0	4350.0	3710.0
30	1989	649.0	306.0	653.0	644.0	2100.0
31	1990	1611.0	306.0	4115.0	–	702.0
32	1991	3532.0	1248.0	1916.0	–	2860.0
33	1992	2291.0	790.0	1494.9	762.8	1607.5
34	1993	6120.0	865.5	4380.0	1684.1	3422.5
35	1994	1133.0	412.0	1153.8	723.8	1237.9
36	1995	741.9	412.2	537.0	568.0	531.0
37	1996	683.0	218.0	758.0	804.0	507.6
38	1997	905.0	348.2	1217.5	428.4	362.5
39	1998	1266.9	–	1259.3	260.9	1605.9
40	1999	2693.7	602.9	2776.6	630.9	3328.3
41	2000	641.2	–	580.4	84.9	753.4
42	2001	1847.9	498.3	1201.3	278.5	1512.2
43	2002	926.4	134.0	774.8	496.7	822.2
Valor Medio		1773.0	524.8	1724.6	990.0	1378.0

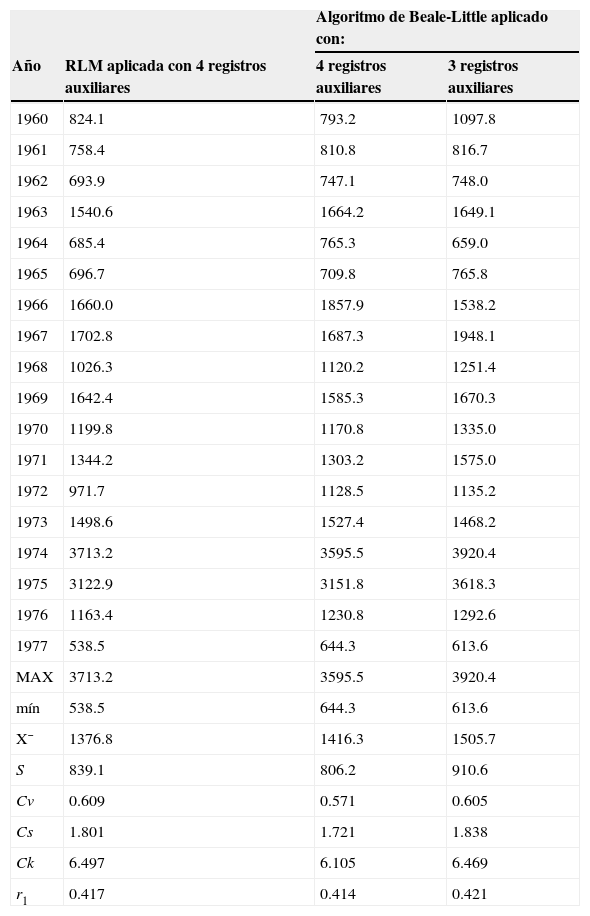
Se observa que los lapsos disponibles y los datos faltantes son escasamente diferentes a los de la aplicación anterior. Campos (2011a) utilizó la RLM para estimar la secuencia inicial de datos en la estación hidrométrica Platón Sánchez; la aplicó en el periodo común de 1978 a 2002, empleando 20 datos en los registros auxiliares. Como en los registros de gasto máximo anual no se puede aceptar que provengan de una distribución Normal, trabajó con los logaritmos naturales de los datos. Los resultados obtenidos se muestran en la segunda columna de la tabla 5.

Tabla 5.

Gastos máximos anuales (m3/s) estimados en la estación Platón Sánchez con los métodos indicados

		Algoritmo de Beale-Little aplicado con:
Año	RLM aplicada con 4 registros auxiliares	4 registros auxiliares	3 registros auxiliares
1960	824.1	793.2	1097.8
1961	758.4	810.8	816.7
1962	693.9	747.1	748.0
1963	1540.6	1664.2	1649.1
1964	685.4	765.3	659.0
1965	696.7	709.8	765.8
1966	1660.0	1857.9	1538.2
1967	1702.8	1687.3	1948.1
1968	1026.3	1120.2	1251.4
1969	1642.4	1585.3	1670.3
1970	1199.8	1170.8	1335.0
1971	1344.2	1303.2	1575.0
1972	971.7	1128.5	1135.2
1973	1498.6	1527.4	1468.2
1974	3713.2	3595.5	3920.4
1975	3122.9	3151.8	3618.3
1976	1163.4	1230.8	1292.6
1977	538.5	644.3	613.6
MAX	3713.2	3595.5	3920.4
mín	538.5	644.3	613.6
X¯	1376.8	1416.3	1505.7
S	839.1	806.2	910.6
Cv	0.609	0.571	0.605
Cs	1.801	1.721	1.838
Ck	6.497	6.105	6.469
r1	0.417	0.414	0.421

La aplicación del algoritmo de Beale-Little con n = 43, p = 4 y datos transformados (Z_ij= ln X_ij), después de 35 ciclos aporta las estimaciones mostradas en la tercera columna de la tabla 5, para la secuencia inicial de datos faltantes en la estación Platón Sánchez y los valores siguientes en El Cardón 271.9 y 185.5 m³/s. En la estación Los Hules se estimaron 3463.7 y 1072.2 m³/s y por último, en Terrerillos 1151.3 m³/s, como datos faltantes.

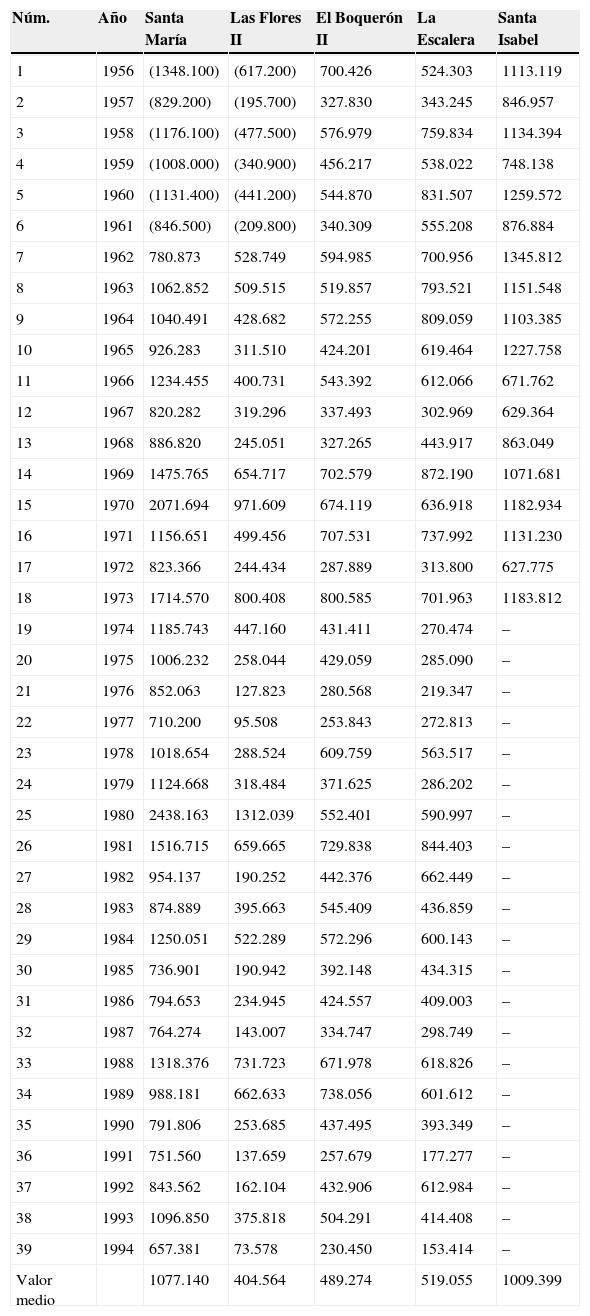
Tercera aplicación numérica

Se ubica dentro de la Región Hidrológica Núm. 30 (Grijalva-Usumacinta) y corresponde a cinco cuencas de la vertiente de margen izquierda del Alto Río Grijalva, pues estas se localizan antes de la Presa Netzahualcóyotl (Malpaso). En la figura 2 se muestra su ubicación geográfica y en la tabla 6 sus registros disponibles de volumen escurrido anual en millones de metros cúbicos (Mm³).

Figura 2.

Localización de las cinco estaciones hidrométricas procesadas del Alto Río Grijalva.

Tabla 6.

Volúmenes escurridos anuales (Mm³) en las estaciones hidrométricas del Alto Río Grijalva en el periodo común de 1956 a 1994

Núm.	Año	Santa María	Las Flores II	El Boquerón II	La Escalera	Santa Isabel
1	1956	(1348.100)	(617.200)	700.426	524.303	1113.119
2	1957	(829.200)	(195.700)	327.830	343.245	846.957
3	1958	(1176.100)	(477.500)	576.979	759.834	1134.394
4	1959	(1008.000)	(340.900)	456.217	538.022	748.138
5	1960	(1131.400)	(441.200)	544.870	831.507	1259.572
6	1961	(846.500)	(209.800)	340.309	555.208	876.884
7	1962	780.873	528.749	594.985	700.956	1345.812
8	1963	1062.852	509.515	519.857	793.521	1151.548
9	1964	1040.491	428.682	572.255	809.059	1103.385
10	1965	926.283	311.510	424.201	619.464	1227.758
11	1966	1234.455	400.731	543.392	612.066	671.762
12	1967	820.282	319.296	337.493	302.969	629.364
13	1968	886.820	245.051	327.265	443.917	863.049
14	1969	1475.765	654.717	702.579	872.190	1071.681
15	1970	2071.694	971.609	674.119	636.918	1182.934
16	1971	1156.651	499.456	707.531	737.992	1131.230
17	1972	823.366	244.434	287.889	313.800	627.775
18	1973	1714.570	800.408	800.585	701.963	1183.812
19	1974	1185.743	447.160	431.411	270.474	–
20	1975	1006.232	258.044	429.059	285.090	–
21	1976	852.063	127.823	280.568	219.347	–
22	1977	710.200	95.508	253.843	272.813	–
23	1978	1018.654	288.524	609.759	563.517	–
24	1979	1124.668	318.484	371.625	286.202	–
25	1980	2438.163	1312.039	552.401	590.997	–
26	1981	1516.715	659.665	729.838	844.403	–
27	1982	954.137	190.252	442.376	662.449	–
28	1983	874.889	395.663	545.409	436.859	–
29	1984	1250.051	522.289	572.296	600.143	–
30	1985	736.901	190.942	392.148	434.315	–
31	1986	794.653	234.945	424.557	409.003	–
32	1987	764.274	143.007	334.747	298.749	–
33	1988	1318.376	731.723	671.978	618.826	–
34	1989	988.181	662.633	738.056	601.612	–
35	1990	791.806	253.685	437.495	393.349	–
36	1991	751.560	137.659	257.679	177.277	–
37	1992	843.562	162.104	432.906	612.984	–
38	1993	1096.850	375.818	504.291	414.408	–
39	1994	657.381	73.578	230.450	153.414	–
Valor medio		1077.140	404.564	489.274	519.055	1009.399

Campos (2014) primeramente verificó que las muestras de la tabla 6 pudieran ser consideradas procedentes de distribuciones normales. Por otra parte, como las estaciones hidrométricas Santa María y Las Flores II comenzaron a operar en 1962, para completar el periodo común de datos de 18 años de 1956 a 1973 que define la estación incompleta Santa Isabel; Campos (2014) estimó sus primeros seis valores faltantes por regresión lineal con la estación El Boquerón II, tales magnitudes se muestran en la tabla 6 entre paréntesis.

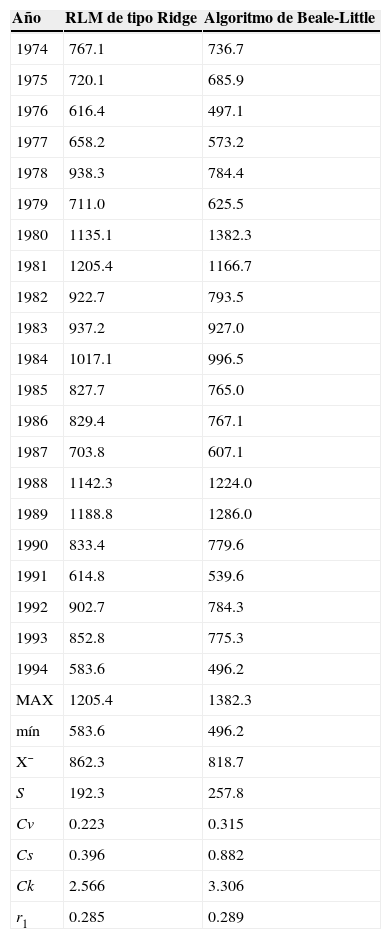
Campos (2014) procesó la información de la tabla 6 a través de la RLM de tipo Ridge y estimó la secuencia faltante de 21 años en la estación Santa Isabel con un parámetro de sesgo (k) de 0.350, la cual se muestra en la segunda columna de la tabla 7.

Tabla 7.

Volúmenes escurridos anuales (Mm³) estimados en la estación Platón Sánchez con los métodos indicados

Año	RLM de tipo Ridge	Algoritmo de Beale-Little
1974	767.1	736.7
1975	720.1	685.9
1976	616.4	497.1
1977	658.2	573.2
1978	938.3	784.4
1979	711.0	625.5
1980	1135.1	1382.3
1981	1205.4	1166.7
1982	922.7	793.5
1983	937.2	927.0
1984	1017.1	996.5
1985	827.7	765.0
1986	829.4	767.1
1987	703.8	607.1
1988	1142.3	1224.0
1989	1188.8	1286.0
1990	833.4	779.6
1991	614.8	539.6
1992	902.7	784.3
1993	852.8	775.3
1994	583.6	496.2
MAX	1205.4	1382.3
mín	583.6	496.2
X¯	862.3	818.7
S	192.3	257.8
Cv	0.223	0.315
Cs	0.396	0.882
Ck	2.566	3.306
r1	0.285	0.289

La aplicación del algoritmo de Beale–Little con n = 39 y p = 4, se realizó considerando faltantes los seis valores iniciales de las estaciones Santa María y Las Flores II; después de 95 ciclos estima los siguientes seis valores en la primera: 1467.4, 929.4, 1208.4, 943.1, 1203.7 y 859.9 Mm³ y estos seis en la segunda: 748.1, 335.5, 524.8, 251.9, 554.0 y 245.8 Mm³. La secuencia obtenida de 21 años en Santa Isabel se tiene en la tabla 7. Se observa que ambas series estimadas en Santa Isabel tienen el mismo comportamiento serial, pero la procedente del algoritmo de Beale-Little tiene mayor dispersión y sesgo, así como menor valor promedio.

Análisis de los resultados

Los resultados mostrados en las tablas 3 y 5, tienen el mismo comportamiento secuencial de valores y ello genera confianza en tales estimaciones, ya que proceden de periodos comunes bastante diferentes. La similitud serial observada también se detecta en la semejanza que muestran los parámetros estadísticos, sobre todo los de la tabla 3; un poco menos en la tabla 5. Tal similitud se debe a la correlación general que guardan los registros procesados de volumen escurrido anual, la cual se muestra en la parte superior de la tabla 8 para los registros incompletos y en su parte inferior, para tales series completadas con los datos estimados con el algoritmo de Beale-Little.

Tabla 8.

. Coeficientes de correlación lineal (r_xy) entre los registros de volumen escurrido anual (Mm³) del sistema del río Tempoal, durante el periodo 1961 a 2002

Datos disponibles (número de años del periodo común)
Estación	Tempoal	El Cardón	Platón S.	Los Hules	Terrerillos
Tempoal	1.000	0.949	0.948	0.934	0.921
El Cardón	(39)	1.000	0.881	0.912	0.858
Platón Sánchez	(24)	(21)	1.000	0.887	0.921
Los Hules	(40)	(37)	(22)	1.000	0.889
Terrerillos	(41)	(38)	(23)	(39)	1.000
Datos completados (42 años)
Estación	Tempoal	El Cardón	Platón S.	Los Hules	Terrerillos
Tempoal	1.000	0.950	0.955	0.936	0.924
El Cardón		1.000	0.860	0.907	0.866
Platón Sánchez			1.000	0.890	0.873
Los Hules				1.000	0.898
Terrerillos					1.000

Se observa en la tabla 8 que la mayoría de los coeficientes r_xy aumentan ligeramente con los registros completos, lo cual indica que la aplicación del algoritmo de Beale-Little es conveniente desde un punto de vista estadístico. Esta correlación elevada entre todos los registros genera un problema de multicolinealidad al aplicar la RLM (Montgomery et al., 1998); problema que se detecta y evalúa con los factores de inflación de la varianza y el análisis de residuos (Campos, 2011b).

Respecto a la segunda aplicación numérica, en la tabla 9 se observa que la estimación de datos faltantes con el algoritmo de Beale-Little en la estación hidrométrica Platón Sánchez, mejora todas sus correlaciones con las otras estaciones, lo cual destaca la conveniencia de tal deducción. Lo contario ocurre en la estación Los Hules, cuyos valores estimados para los años 1990 y 1991 con el algoritmo de Beale-Little resultan con magnitud inversa a la que presentan las estaciones El Cardón, Terrerillos y Tempoal (tabla 4), y debido a ello su correlación disminuye al procesar los registros completos.

Tabla 9.

. Coeficientes de correlación lineal (r_xy) entre los registros de gasto máximo anual (m³/s) del sistema del río Tempoal, durante el periodo 1960 a 2002

Datos disponibles (número de años del periodo común)
Estación	Tempoal	El Cardón	Platón S.	Los Hules	Terrerillos
Tempoal	1.000	0.729	0.833	0.711	0.818
El Cardón	(41)	1.000	0.401	0.476	0.490
Platón Sánchez	(25)	(23)	1.000	0.784	0.700
Los Hules	(41)	(39)	(23)	1.000	0.686
Terrerillos	(42)	(40)	(24)	(40)	1.000
Datos completados (43 años)
Estación	Tempoal	El Cardón	Platón S.	Los Hules	Terrerillos
Tempoal	1.000	0.736	0.867	0.627	0.816
El Cardón		1.000	0.487	0.387	0.481
Platón Sánchez			1.000	0.832	0.740
Los Hules				1.000	0.552
Terrerillos					1.000

En la porción superior de la tabla 9 se observa que el registro de la estación El Cardón no presenta correlación con el resto y que únicamente tiene una dependencia baja (r_xy = 0.729) con la estación Tempoal; además con la estación Platón Sánchez es la que presenta menor correlación (r_xy = 0.401). Debido a lo anterior, se considera conveniente aplicar el algoritmo de Beale-Little sin tal registro, entonces ahora se tienen n = 43 y p = 3. Empleando datos transformados y después de 20 ciclos se obtuvieron las siguientes estimaciones: en Los Hules 3819.5 y 872.2 m³/s, en Terrerillos 1421.1 m³/s y en Platón Sánchez la secuencia mostrada en la cuarta columna de la tabla 5.

Se observa que estas últimas estimaciones en la estación Platón Sánchez tienen semejanza serial con las anteriores y que sus parámetros estadísticos son similares. Como esta última secuencia es ligeramente más extrema que las dos anteriores, en sus valores: máximo, media y variabilidad, según su coeficiente de variación (Cv), es la que se recomienda adoptar por seguridad hidrológica, ya que las predicciones (crecientes) que se obtengan con tales datos seguramente serán mayores.

Por el contrario, cuando se trate de seleccionar una secuencia de estimaciones de volumen escurrido anual, se recomienda adoptar por seguridad hidrológica de la disponibilidad, la de menor valor medio (volumen escurrido medio anual, VEMA) y Cv mayor, pues tal dispersión se reflejará en una mayor capacidad de regulación necesaria en el embalse que se dimensiona hidrológicamente para aprovechar un cierto porcentaje del VEMA.

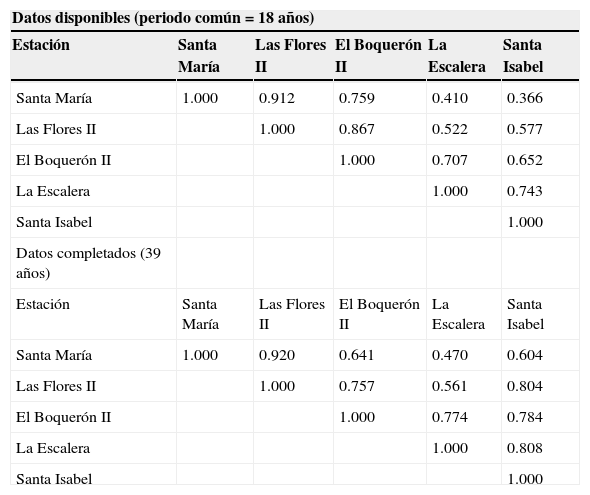
Por último, en la parte superior de la tabla 10 se muestran las correlaciones que tienen los registros de la tercera aplicación numérica, en el periodo común de 18 años de 1956 a 1973, definido este por los datos disponibles en la estación incompleta Santa Isabel. En la porción inferior de la tabla 10 se muestran las dependencias de los registros completados con base en las estimaciones del algoritmo de Beale-Little, se observa que todas las correlaciones de la estación Santa Isabel aumentan de manera importante, sobre todo con las estaciones más alejadas que son Santa María y Las Flores II.

Tabla 10.

Coeficientes de correlación lineal (r_xy) entre los registros de volumen escurrido anual (Mm³) de la cuenca Alta del Río Grijalva, durante el periodo 1956 a 1994

Datos disponibles (periodo común = 18 años)
Estación	Santa María	Las Flores II	El Boquerón II	La Escalera	Santa Isabel
Santa María	1.000	0.912	0.759	0.410	0.366
Las Flores II		1.000	0.867	0.522	0.577
El Boquerón II			1.000	0.707	0.652
La Escalera				1.000	0.743
Santa Isabel					1.000
Datos completados (39 años)
Estación	Santa María	Las Flores II	El Boquerón II	La Escalera	Santa Isabel
Santa María	1.000	0.920	0.641	0.470	0.604
Las Flores II		1.000	0.757	0.561	0.804
El Boquerón II			1.000	0.774	0.784
La Escalera				1.000	0.808
Santa Isabel					1.000

También se observa que las correlaciones del registro completo de la estación El Boquerón II disminuyen con las de las estaciones Santa María y Las Flores II, pues ahora los valores faltantes en estas dos estaciones proceden de la RLM con cuatro regresores no únicamente de la regresión lineal con los datos de El Boquerón II, como se estimaron los indicados entre paréntesis en la tabla 6.

Conclusiones

Verificando previamente que los datos faltantes se perdieron de una manera aleatoria, o que no existen debido a un inicio posterior de la operación de la estación hidrométrica o climatológica, el algoritmo de Beale-Little es aplicable. Lo que se debe evitar es estimar datos faltantes que están asociados a condiciones severas del clima y que por ello, no se registraron. Caso común de las crecientes extremas que dañan las instalaciones de aforos, o de los periodos de sequía extrema en los cuales no se mide ni la lluvia ni el escurrimiento porque toda la población ya emigró.

El algoritmo de Beale-Little, permite utilizar toda la información hidrológica disponible, de una manera conjunta, no exclusivamente en el periodo común, como opera la regresión lineal múltiple (RLM). Lo anterior seguramente conduce a estimaciones más exactas para los datos faltantes.

Otra ventaja del procedimiento descrito, consiste en obtener de forma simultánea todos los datos anuales faltantes en los registros procesados, con lo cual queda integrado un grupo de series de datos hidrológicos en un periodo común. Esto permite aplicar técnicas hidrológicas de simulación de aprovechamientos hidráulicos o de estimación regional de crecientes, que requieren muestras que tienen un lapso común de registro.

Siendo el algoritmo de Beale-Little descrito, un procedimiento bastante simple de implementar, se recomienda su aplicación sistemática para procesar información regional que está correlacionada y obtener resultados que permitan verificar y complementar las estimaciones de la RLM, aplicada según los enfoques de selección óptima de regresores o de tipo Ridge, para el caso del volumen escurrido anual, o de su conveniencia estadística en la transferencia de información de gasto máximo anual (crecientes).

Este artículo se cita:

Citación estilo Chicago

Campos-Aranda, Daniel Francisco. Estimación simultánea de datos hidrológicos anuales faltantes en múltiples sitios. Ingeniería Investigación y Tecnología, XVI, 02 (2015): 295-306.

Citación estilo ISO 690

Campos-Aranda D.F. Estimación simultánea de datos hidrológicos anuales faltantes en múltiples sitios. Ingeniería Investigación y Tecnología, volumen XVI (número 2), abril-junio 2015: 295-306.

Semblanza del autor

Daniel Francisco Campos-Aranda. Obtuvo el título de ingeniero Civil en diciembre de 1972, en la entonces Escuela de Ingeniería de la UASLP. Durante el primer semestre de 1977, realizó en Madrid, España un diplomado en hidrología general y aplicada. Posteriormente, durante 1980-1981 llevó a cabo estudios de maestría en ingeniería en la especialidad de Hidráulica, en la División de Estudios de Posgrado de la Facultad de Ingeniería de la UNAM. En esta misma institución, inició (1984) y concluyó (1987) el doctorado en ingeniería con especialidad en aprovechamientos hidráulicos. Ha publicado artículos principalmente en revistas mexicanas de excelencia: 46 en Tecnología y Ciencias del Agua (antes Ingeniería Hidráulica en México), 18 en Agrociencia y 15 en Ingeniería. Investigación y Tecnología. Es profesor jubilado de la UASLP, desde el 1¿ de febrero de 2003. En noviembre de 1989 obtuvo la medalla Gabino Barreda de la UNAM y en 2008 le fue otorgado el Premio Nacional “Francisco Torres H.” de la AMH. A partir de septiembre de 2013 vuelve a ser investigador nacional nivel I.