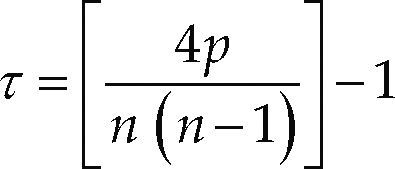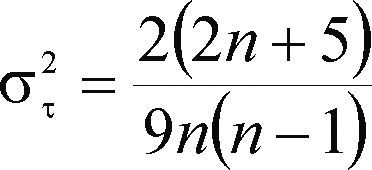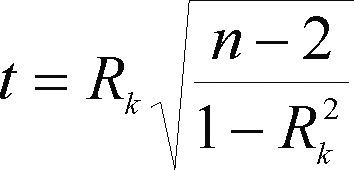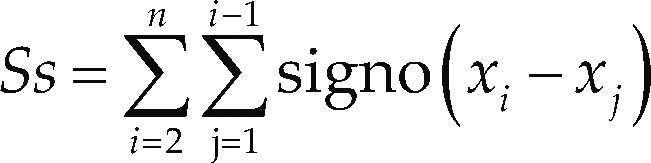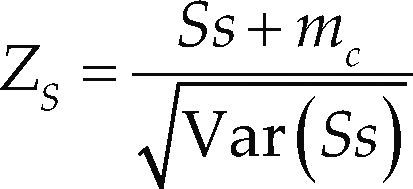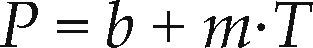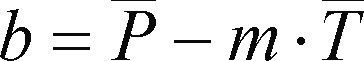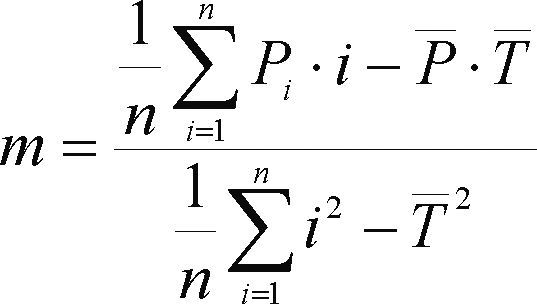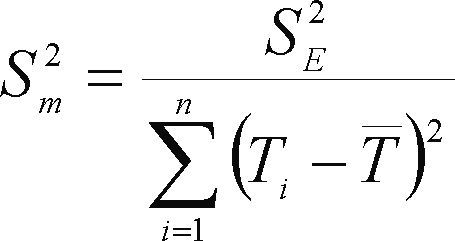Las primeras predicciones del cambio climático para México han establecido que en general la precipitación disminuirá y la temperatura ambiente aumentará. Por ello, en este trabajo se aborda el estudio de la precipitación anual del estado de Zacatecas, México, para buscar tendencias climáticas, a través de dos enfoques: el primero de carácter estadístico para detectar tendencia o cambios en la media, lo que significa pérdida de homogeneidad en los registros analizados; el segundo de tipo cuantitativo consistente en evaluar el cociente entre la precipitación media reciente y la de largo plazo para observar si se aparta de la unidad. Para estimar una precipitación media estable, únicamente se procesaron 30 estaciones pluviométricas con registros de más de 50 años. Se encontró que no existe evidencia estadística general de tendencia, pues únicamente dos registros mostraron un comportamiento decreciente; sin embargo, la lluvia anual se está reduciendo como lo detecta el cociente (CO15) entre la lluvia media de los últimos 15 años y la de largo plazo, cuya moda de 27 valores es 0.975.
For Mexico, it has been predicted that climatic change will generally decrease precipitation and increase the mean temperature. In this paper the annual rainfall of the state of Zacatecas, Mexico was studied. Two approaches were used to look for climatic trends: the first one, a statistical approach to detect trends and/or changes in the mean, which means a loss of homogeneity in the records analyzed; the second one, a quantitative approach which consists in evaluating the ratio of the recent average precipitation to the long run, to observe if it deviates from the unit. To estimate a stable average precipitation only 30 rain gauge stations with records of more than 50 years were processed. It was found that there is no general statistical evidence of trend, because only two records showed a decreasing behavior; however, through the ratio (CO15) between the average rainfall of the last 15 years and the long run (whose mode of 27 values is 0.975) shows a decrease in the annual rainfall.
Durante las dos últimas décadas se han planteado dos preguntas fundamentales en relación con el cambio climático (CC), la primera es si realmente existe a nivel global y a corto plazo; la segunda es si son las actividades humanas las que lo han originado. En 2007, con el 4° reporte del Panel Intergubernamental sobre Cambio Climático (IPCC), estas preguntas fueron contestadas afirmativa y categóricamente. La consecuencia fundamental del CC es una elevación significativa de la temperatura ambiente del planeta, la cual pone en marcha una serie de efectos como el derretimiento de los glaciares y polos, con la consecuente elevación del nivel del mar, el incremento en la evaporación en suelos y superficies de agua, lo cual origina un cambio en los patrones de lluvia, generándose una alteración de los ecosistemas, etcétera (Raynal, 2011).
Los últimos escenarios del IPCC establecen, en términos generales, que en México, por su ubicación geográfica, las precipitaciones disminuirán y las temperaturas aumentarán (Martínez y Aguilar, 2008). Además, debido a sus condiciones socioeconómicas, México presentará una elevada vulnerabilidad al CC. Las afectaciones al ciclo hidrológico de las cuencas, establecen la necesidad de revisar con detalle los planes actuales y futuros sobre el aprovechamiento de los recursos hídricos (Martínez y Patino, 2010). Entonces, para formular las medidas de adaptación que permitan mitigar los efectos del CC, con el propósito de alcanzar niveles razonables de sustentabilidad en el uso del agua, primero se deben identificar los cambios en tales variables meteorológicas, tanto en forma cualitativa como cuantitativa (Kundzewicz y Robson, 2004; Madsen et al., 2013).
El objetivo de este trabajo consiste en buscar cambios significativos en la precipitación anual del estado de Zacatecas, México. Lo anterior se hizo mediante dos enfoques, el primero de tipo estadístico intenta detectar componentes determinísticas como tendencia y cambios en la media en los registros de lluvia y el segundo de carácter cuantitativo, evalúa un cociente entre la precipitación media reciente y la de largo plazo del registro analizado. Para ello, se procesaron 30 registros de precipitación anual con más de 50 años y se utilizaron tres pruebas estadísticas generales y 13 específicas, citando sus referencias básicas y describiendo con detalle el procedimiento operativo de las relativas a la tendencia en los apéndices. Los resultados indican que en el estado de Zacatecas no existe evidencia estadística general del CC, pues los registros no muestran tendencia, sin embargo, la lluvia anual se está reduciendo como lo detecta el cociente (CO15) entre la lluvia media de los últimos 15 años y la de largo plazo, cuya media y moda son 0.978 y 0.975, respectivamente.
MetodologíaEstaciones pluviométricas procesadasDe inicio se estableció emplear solo estaciones pluvio-métricas con un periodo amplio de registro; se encontró conveniente, por disponibilidad, usar las de más de 50 años de registro. El archivo en Excel de la precipitación mensual de la Dirección Local Zacatecas de la Comisión Nacional del Agua (CONAGUA), cuenta con 133 estaciones pluviométricas. De ellas únicamente 22 tienen un registro mayor de 50 años, pero las estaciones Trancoso, Jeréz y Teúl de González Ortega, fueron eliminadas por tener muchos años incompletos; entonces se utilizaron las 19 mostradas en la tabla 1, que no contienen datos en la columna 7 de dicha tabla.
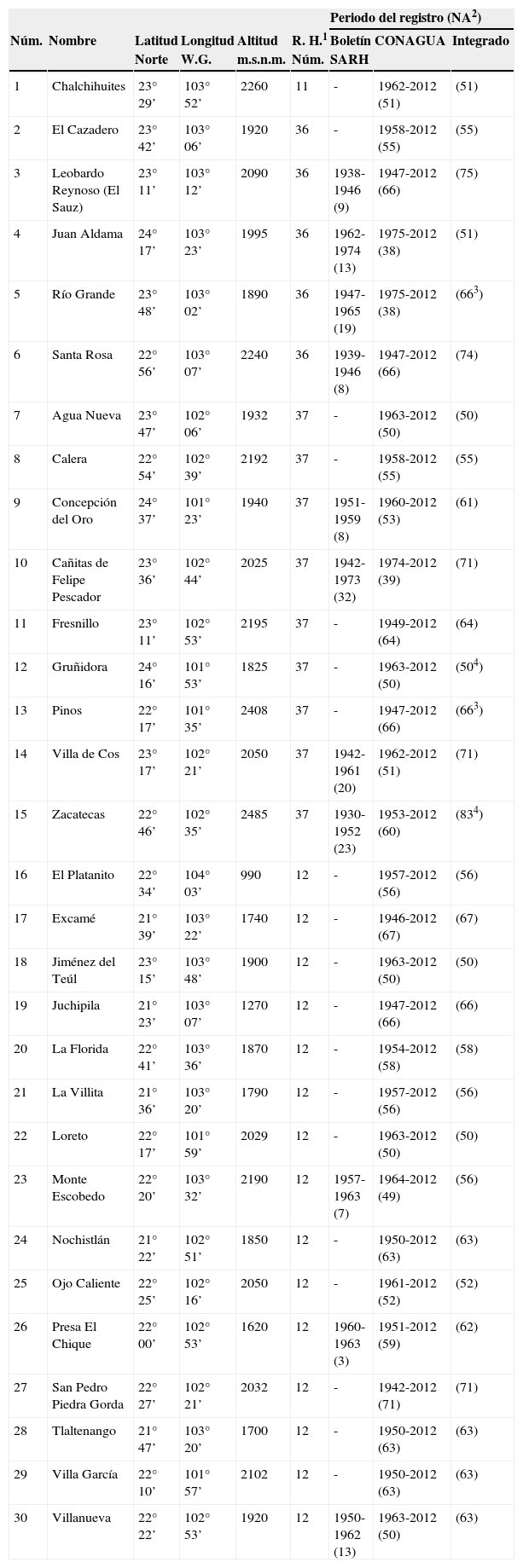
Características generales de las 30 estaciones pluviométricas procesadas del estado de Zacatecas, México
| Periodo del registro (NA2) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Núm. | Nombre | Latitud Norte | Longitud W.G. | Altitud m.s.n.m. | R. H.1 Núm. | Boletín SARH | CONAGUA | Integrado |
| 1 | Chalchihuites | 23° 29’ | 103° 52’ | 2260 | 11 | - | 1962-2012 (51) | (51) |
| 2 | El Cazadero | 23° 42’ | 103° 06’ | 1920 | 36 | - | 1958-2012 (55) | (55) |
| 3 | Leobardo Reynoso (El Sauz) | 23° 11’ | 103° 12’ | 2090 | 36 | 1938-1946 (9) | 1947-2012 (66) | (75) |
| 4 | Juan Aldama | 24° 17’ | 103° 23’ | 1995 | 36 | 1962-1974 (13) | 1975-2012 (38) | (51) |
| 5 | Río Grande | 23° 48’ | 103° 02’ | 1890 | 36 | 1947-1965 (19) | 1975-2012 (38) | (663) |
| 6 | Santa Rosa | 22° 56’ | 103° 07’ | 2240 | 36 | 1939-1946 (8) | 1947-2012 (66) | (74) |
| 7 | Agua Nueva | 23° 47’ | 102° 06’ | 1932 | 37 | - | 1963-2012 (50) | (50) |
| 8 | Calera | 22° 54’ | 102° 39’ | 2192 | 37 | - | 1958-2012 (55) | (55) |
| 9 | Concepción del Oro | 24° 37’ | 101° 23’ | 1940 | 37 | 1951-1959 (8) | 1960-2012 (53) | (61) |
| 10 | Cañitas de Felipe Pescador | 23° 36’ | 102° 44’ | 2025 | 37 | 1942-1973 (32) | 1974-2012 (39) | (71) |
| 11 | Fresnillo | 23° 11’ | 102° 53’ | 2195 | 37 | - | 1949-2012 (64) | (64) |
| 12 | Gruñidora | 24° 16’ | 101° 53’ | 1825 | 37 | - | 1963-2012 (50) | (504) |
| 13 | Pinos | 22° 17’ | 101° 35’ | 2408 | 37 | - | 1947-2012 (66) | (663) |
| 14 | Villa de Cos | 23° 17’ | 102° 21’ | 2050 | 37 | 1942-1961 (20) | 1962-2012 (51) | (71) |
| 15 | Zacatecas | 22° 46’ | 102° 35’ | 2485 | 37 | 1930-1952 (23) | 1953-2012 (60) | (834) |
| 16 | El Platanito | 22° 34’ | 104° 03’ | 990 | 12 | - | 1957-2012 (56) | (56) |
| 17 | Excamé | 21° 39’ | 103° 22’ | 1740 | 12 | - | 1946-2012 (67) | (67) |
| 18 | Jiménez del Teúl | 23° 15’ | 103° 48’ | 1900 | 12 | - | 1963-2012 (50) | (50) |
| 19 | Juchipila | 21° 23’ | 103° 07’ | 1270 | 12 | - | 1947-2012 (66) | (66) |
| 20 | La Florida | 22° 41’ | 103° 36’ | 1870 | 12 | - | 1954-2012 (58) | (58) |
| 21 | La Villita | 21° 36’ | 103° 20’ | 1790 | 12 | - | 1957-2012 (56) | (56) |
| 22 | Loreto | 22° 17’ | 101° 59’ | 2029 | 12 | - | 1963-2012 (50) | (50) |
| 23 | Monte Escobedo | 22° 20’ | 103° 32’ | 2190 | 12 | 1957-1963 (7) | 1964-2012 (49) | (56) |
| 24 | Nochistlán | 21° 22’ | 102° 51’ | 1850 | 12 | - | 1950-2012 (63) | (63) |
| 25 | Ojo Caliente | 22° 25’ | 102° 16’ | 2050 | 12 | - | 1961-2012 (52) | (52) |
| 26 | Presa El Chique | 22° 00’ | 102° 53’ | 1620 | 12 | 1960-1963 (3) | 1951-2012 (59) | (62) |
| 27 | San Pedro Piedra Gorda | 22° 27’ | 102° 21’ | 2032 | 12 | - | 1942-2012 (71) | (71) |
| 28 | Tlaltenango | 21° 47’ | 103° 20’ | 1700 | 12 | - | 1950-2012 (63) | (63) |
| 29 | Villa García | 22° 10’ | 101° 57’ | 2102 | 12 | - | 1950-2012 (63) | (63) |
| 30 | Villanueva | 22° 22’ | 102° 53’ | 1920 | 12 | 1950-1962 (13) | 1963-2012 (50) | (63) |
1región hidrológica 2 número de años 3 se estimaron varios años por regresión 4 se transportó información de estación cercana
Utilizando la información histórica contenida en los Boletines Climatológicos (SARH, 1977; 1980a; 1980b) para 11 estaciones más se logró completar sus registros, según se indica en la columna 7 de la tabla 1, integrando un total de 30 registros por procesar de precipitación anual en milímetros. En la figura 1 se muestra la ubicación geográfica de las 30 estaciones pluviométricas procesadas.
En la figura 1 se indican los parteaguas de las cuatro regiones hidrológicas que comprende el estado de Zacatecas. La región hidrológica núm. 11 de los Ríos Presidio y San Pedro que drenan al Océano Pacífico, abarca la porción menor en el oeste del estado, en esa zona únicamente se ubicó la estación Chalchihuites. En la región hidrológica núm. 12 Parcial del Río Santiago, que también fluye al Océano Pacífico, se ubican las zonas sur del estado y centro poniente; en esta región se procesaron 15 estaciones pluviométricas.
La región hidrológica núm. 36 de los ríos Nazas y Aguanaval es endorreica y estos confluyen a lo que era la Laguna de Mayrán, cerca de la Comarca Lagunera. Esta región comienza en la zona centro del estado y avanza hacia el norte con la cuenca del río Aguanaval y en ella se ubican las cinco estaciones pluviométricas analizadas. Otra porción de esta región se ubica en el norte del estado. Finalmente, la región hidrológica núm. 37 denominada El Salado que también es endo-rreica y está integrada por ríos y corrientes de poca importancia, comprende la porción norte y oriente del estado. En esta zona se procesaron nueve estaciones pluviométricas.
Deducción de datos faltantesCon excepción de las estaciones pluviométricas Fresni-llo y Leobardo Reynoso (El Sauz), el resto tienen registros de precipitación mensual incompletos, por ello se adoptó el proceso siguiente para su estimación. Cuando en un año incompleto faltaba un máximo de tres meses, estos se consideraron iguales a la media mensual. Si los tres meses faltantes se ubicaban en la época de lluvias (junio a septiembre) o bien eran más, se estimó el valor anual de la precipitación mediante regresión lineal con el registro más cercano.
Con este procedimiento se estimó el lapso faltante de 1966 a 1975 en la estación pluviométrica Río Grande, con base en los datos de El Cazadero, usando como periodo común 1975 a 2012 (n = 38) y suprimiendo seis valores dispersos para mejorar el coeficiente de correlación lineal (r) de 0.7536 a 0.8912. Para estimar el lapso de 1987 a 1992 en la estación pluviométrica Pinos, no se pudieron utilizar los registros cercanos, pues también carecen de información, por ello se empleó la estación El Nigromante, con un periodo común de 22 datos en el lapso de 1984 a 2012; al suprimir dos valores dispersos el r resultó de 0.7083.
Para completar el registro incompleto de la estación pluviométrica Zacatecas en los años 2010 a 2012, los datos mensuales faltantes se consideraron iguales a los registrados en la estación Guadalupe, que es bastante cercana, pues dista menos de 8km en línea recta y se ubica en la misma zona geográfica. Por último, en la estación pluviométrica Gruñidora los años faltantes 2008, 2011 y 2012 se dedujeron con proporcionalidad de medias anuales en el lapso 1995 a 2012, con base en los datos de la estación Nuevo Mercurio que es la más cercana.
Pruebas estadísticasRequerimientos estadísticos de los registrosTodos los análisis estadísticos y probabilísticos realizados con los registros hidrológicos o climatológicos de datos anuales, se basan en una serie de requerimientos estadísticos básicos, como son que la serie o registro sea consistente, libre de tendencia, no periódica y que constituya un proceso estocástico, cuya componente aleatoria siga una determinada función de distribución de probabilidades. La consistencia implica que todos los datos medidos pertenecen a la misma población estadística y tienen por lo tanto una media invariante en el tiempo; esta propiedad también se conoce como homogeneidad y sus pruebas estadísticas buscan cambios significativos en la media.
La tendencia ocurre en los datos si existe una correlación significativa (positiva o negativa) entre los datos y el tiempo. La tendencia vuelve a la serie no estacionaria, es comúnmente introducida por los cambios en el uso del suelo o por el cambio climático. Finalmente, la alea-toriedad en un registro hidrológico o climatológico significa que los datos fluctúan exclusivamente por el fenómeno natural (lluvia o escurrimiento); cuando no hay aleatoriedad el registro es persistente. La persistencia se define como la propensión de los datos de una serie a recordar la magnitud de sus valores antecedentes o a ser influenciados por ellos. Debido a lo anterior, se cuantifica con base en el coeficiente de correlación serial que define la dependencia entre cada elemento i y el i-k; por ello k se llama “tiempo de retraso” (Adeloye y Montaseri, 2002; Machiwal y Jha, 2008; 2012).
Pruebas y tests aplicadosLas pruebas estadísticas pueden ser paramétricas y no paramétricas; las segundas no están basadas en la consideración de que la población de los datos es normal, por ello se utilizan ampliamente, pero son pruebas que tienen menor potencia que los tests paramétricos. Se ha llegado a establecer que para obtener la misma conclusión con igual nivel de confianza, las pruebas no para-métricas requieren de 5 a 35% más datos que los tests paramétricos (Machiwal y Jha, 2012).
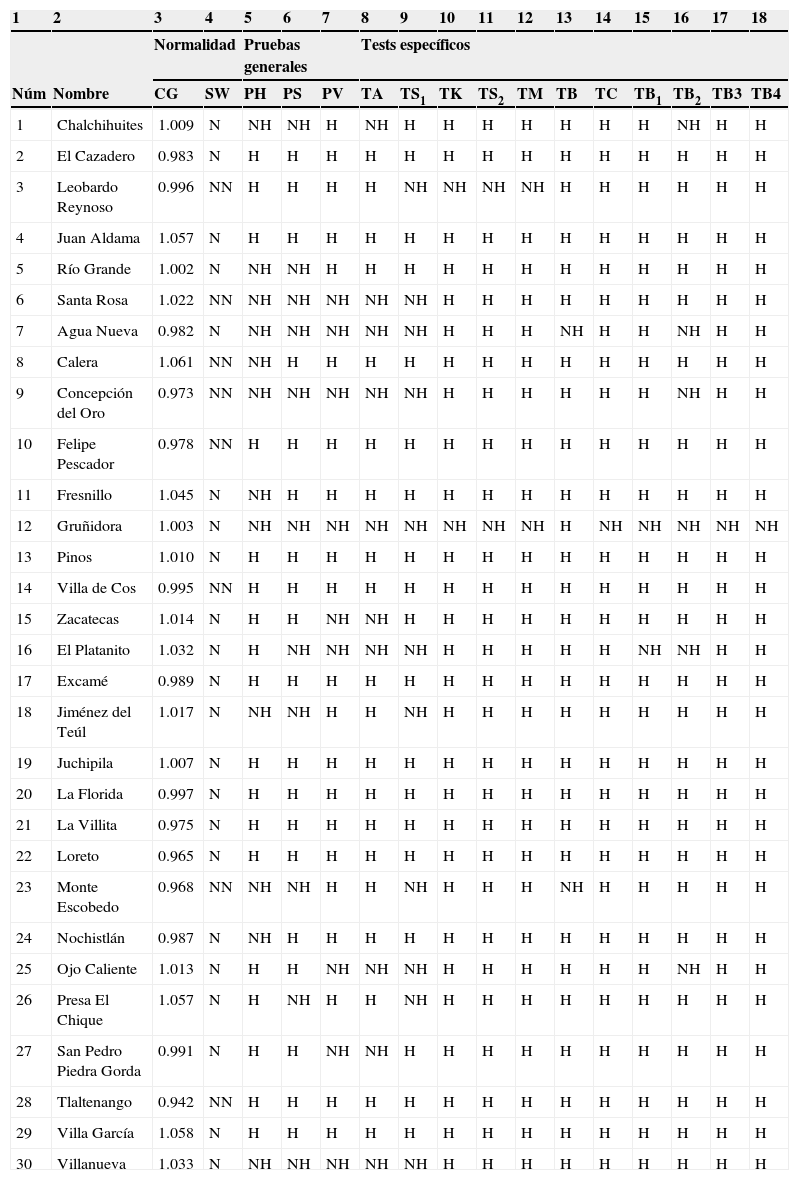
La aplicación de las pruebas paramétricas requiere que los datos sigan una distribución normal, entonces primero se determinó con los tests del cociente de Geary (CG) y de Shapiro-Wilk (SW) que si para los registros procesados de precipitación anual se puede aceptar que provengan de una distribución normal. Los resultados de ambos tests se tienen en la tabla 2, las columnas 3 y 4 indican la normalidad con N y la no procedencia de una distribución normal con NN.
Resultados de las pruebas estadísticas en las 30 estaciones pluviométricas procesadas, del estado de Zacatecas, México
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Normalidad | Pruebas generales | Tests específicos | |||||||||||||||
| Núm | Nombre | CG | SW | PH | PS | PV | TA | TS1 | TK | TS2 | TM | TB | TC | TB1 | TB2 | TB3 | TB4 |
| 1 | Chalchihuites | 1.009 | N | NH | NH | H | NH | H | H | H | H | H | H | H | NH | H | H |
| 2 | El Cazadero | 0.983 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 3 | Leobardo Reynoso | 0.996 | NN | H | H | H | H | NH | NH | NH | NH | H | H | H | H | H | H |
| 4 | Juan Aldama | 1.057 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 5 | Río Grande | 1.002 | N | NH | NH | H | H | H | H | H | H | H | H | H | H | H | H |
| 6 | Santa Rosa | 1.022 | NN | NH | NH | NH | NH | NH | H | H | H | H | H | H | H | H | H |
| 7 | Agua Nueva | 0.982 | N | NH | NH | NH | NH | NH | H | H | H | NH | H | H | NH | H | H |
| 8 | Calera | 1.061 | NN | NH | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 9 | Concepción del Oro | 0.973 | NN | NH | NH | NH | NH | NH | H | H | H | H | H | H | NH | H | H |
| 10 | Felipe Pescador | 0.978 | NN | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 11 | Fresnillo | 1.045 | N | NH | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 12 | Gruñidora | 1.003 | N | NH | NH | NH | NH | NH | NH | NH | NH | H | NH | NH | NH | NH | NH |
| 13 | Pinos | 1.010 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 14 | Villa de Cos | 0.995 | NN | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 15 | Zacatecas | 1.014 | N | H | H | NH | NH | H | H | H | H | H | H | H | H | H | H |
| 16 | El Platanito | 1.032 | N | H | NH | NH | NH | NH | H | H | H | H | H | NH | NH | H | H |
| 17 | Excamé | 0.989 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 18 | Jiménez del Teúl | 1.017 | N | NH | NH | H | H | NH | H | H | H | H | H | H | H | H | H |
| 19 | Juchipila | 1.007 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 20 | La Florida | 0.997 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 21 | La Villita | 0.975 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 22 | Loreto | 0.965 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 23 | Monte Escobedo | 0.968 | NN | NH | NH | H | H | NH | H | H | H | NH | H | H | H | H | H |
| 24 | Nochistlán | 0.987 | N | NH | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 25 | Ojo Caliente | 1.013 | N | H | H | NH | NH | NH | H | H | H | H | H | H | NH | H | H |
| 26 | Presa El Chique | 1.057 | N | H | NH | H | H | NH | H | H | H | H | H | H | H | H | H |
| 27 | San Pedro Piedra Gorda | 0.991 | N | H | H | NH | NH | H | H | H | H | H | H | H | H | H | H |
| 28 | Tlaltenango | 0.942 | NN | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 29 | Villa García | 1.058 | N | H | H | H | H | H | H | H | H | H | H | H | H | H | H |
| 30 | Villanueva | 1.033 | N | NH | NH | NH | NH | NH | H | H | H | H | H | H | H | H | H |
Las pruebas de Helmert (PH) y de las secuencias (PS) detectan si la serie o registro es homogéneo, debido a que no tiene persistencia o tendencia, cambio en la media, o bien, no oscila demasiado. En cambio, la prueba de Von Neumann (PV) es de aleatoriedad contra componentes determinísticas no especificadas. Los resultados de estas pruebas se exponen en las columnas 5 a 7 de la tabla 2, con H para registros homogéneos y con NH para los no homogéneos.
Respecto a los tests específicos, se aplicaron los 11 siguientes:
- 1.
Dos de persistencia, el de Anderson (TA) y el de Sne-yers (TS1).
- 2.
Tres de tendencia, el de Kendall (TK), el de Spearman (TS2) y el de Mann-Kendall (TM).
- 3.
Uno de variabilidad, el de Bartlett (TB).
- 4.
Uno de cambio en la media, el de Cramer (TC) y
- 5.
Cuatro que buscan cambios en la media o pérdida de homogeneidad con estadísticos basados en la curva de masa residual (TB1 a TB4).
Todas las pruebas se aplicaron con un nivel de significancia (a) de 5%. En el apéndice 1 se citan las referencias donde se pueden consultar 13 de los tests anteriores, pues los tres relativos a la tendencia se exponen en el apéndice 2. Los resultados de estos 11 tests específicos se muestran en las columnas 8 a 18 de la tabla 2, usando H cuando no detectan la componente que buscan y NH cuando la encuentran.
Discusión de resultadosPruebas estadísticasRelación de estaciones pluviométricas que mostraron componentes determinísticas y su descripción
| Núm. | Nombre de la estación | Componentes determinísticas detectadas |
|---|---|---|
| 1 | Chalchihuites | Oscila poco, persistencia ligera |
| 2 | Leobardo Reynoso | Persistencia ligera y tendencia |
| 3 | Río Grande | Oscila poco |
| 4 | Santa Rosa | Oscila poco y persistencia |
| 5 | Agua Nueva | Oscila poco, persistencia y exceso de variabilidad (TB y TB2) por valor muy bajo de precipitación (38.0mm en 1987) |
| 6 | Calera | Oscila pocoOscila poco, no aleatorio, persistencia y cambio en la |
| 7 | Concepción del Oro | media (TB2) por valor muy bajo de lluvia (95.7mm en 1960) |
| 8 | Fresnillo | Oscila poco |
| 9 | Gruñidora | Persistencia, tendencia y cambio en la media |
| 10 | Zacatecas | No aleatorio y persistencia ligera |
| 11 | El Platanito | Oscila poco, no aleatorio, persistencia y cambio en la media (TB1 y TB2) por valor muy bajo de lluvia (261.8mm en 2011) |
| 12 | Jiménez del Teúl | Oscila poco, persistencia ligera |
| 13 | Monte Escobedo | Oscila poco, persistencia ligera y exceso de variabilidad (TB) por valores altos de lluvia (1197.5mm en 1958 y 1242.7 en 1963) |
| 14 | Nochistlán | Oscila poco |
| 15 | Ojo Caliente | No aleatorio y persistencia |
| 16 | Presa El Chique | Oscila poco, persistencia ligera |
| 17 | San Pedro Piedra Gorda | Oscila poco, persistencia ligera |
| 18 | Villanueva | Oscila poco, no aleatorio y persistencia |
El test de Shapiro-Wilk detecta ocho registros que no proceden de una distribución normal. La correspondencia entre estos resultados y los valores del cociente de Geary (CG), permite establecer que cuando excede a 1.060 o es menor que 0.940, la serie no presenta normalidad. Las diferencias encontradas en los resultados de ambos tests (tabla 2), ratifican que el CG es menos consistente, según señalan Machiwal y Jha (2012). Según valores de la tabla 4, cuando el coeficiente de asimetría (Cs) es mayor de 0.600, el registro no procede de una distribución normal.
Parámetros estadísticos y cocientes de medias de la precipitación anual en las 2 7 estaciones pluviométricas de amplio registro del estado de Zacatecas, México
| Parámetros estadísticos | Medias | Cocientes x¯/X¯ | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Núm. | Nombre | XX¯ | S | Cv | Cs | Ck | r1 x¯5 | x¯10 | x¯15 | CO5 | CO10 | CO15 | |
| 1 | Chalchihuites | 529.8 | 166.4 | 0.314 | -0.315 | 2.694 | 0.220 | 528.5 | 596.4 | 564.6 | 0.998 | 1.126 | 1.066 |
| 2 | El Cazadero | 403.5 | 125.0 | 0.310 | 0.491 | 3.459 | 0.105 | 355.6 | 443.4 | 408.6 | 0.881 | 1.099 | 1.013 |
| 3 | Juan Aldama | 427.8 | 121.1 | 0.283 | 0.362 | 2.204 | -0.041 | 427.5 | 475.6 | 436.9 | 0.999 | 1.112 | 1.021 |
| 4 | Río Grande | 382.9 | 126.3 | 0.330 | 0.461 | 3.303 | -0.034 | 354.2 | 393.7 | 379.2 | 0.925 | 1.028 | 0.991 |
| 5 | Santa Rosa | 452.3 | 143.4 | 0.317 | 0.668 | 3.682 | 0.194 | 398.0 | 474.5 | 474.2 | 0.880 | 1.049 | 1.048 |
| 6 | Agua Nueva | 330.1 | 140.6 | 0.426 | 0.682 | 3.571 | 0.250 | 410.1 | 390.0 | 354.7 | 1.242 | 1.182 | 1.075 |
| 7 | Calera | 429.0 | 137.2 | 0.320 | 0.557 | 2.717 | 0.122 | 350.2 | 444.1 | 421.8 | 0.816 | 1.035 | 0.983 |
| 8 | Concepción del Oro | 418.5 | 163.9 | 0.392 | 0.832 | 5.164 | 0.243 | 327.7 | 402.5 | 368.5 | 0.783 | 0.962 | 0.880 |
| 9 | Felipe Pescador | 375.3 | 125.4 | 0.334 | 0.954 | 5.176 | -0.134 | 311.1 | 364.5 | 359.2 | 0.829 | 0.971 | 0.957 |
| 10 | Fresnillo | 411.3 | 120.1 | 0.292 | 0.222 | 2.448 | 0.100 | 357.9 | 432.0 | 406.3 | 0.870 | 1.050 | 0.988 |
| 11 | Pinos | 447.4 | 149.0 | 0.333 | 0.306 | 2.734 | 0.103 | 454.1 | 470.8 | 427.3 | 1.015 | 1.052 | 0.955 |
| 12 | Villa de Cos | 422.2 | 159.6 | 0.378 | 0.780 | 3.866 | 0.055 | 362.2 | 421.4 | 385.0 | 0.858 | 0.998 | 0.912 |
| 13 | Zacatecas | 472.9 | 139.8 | 0.296 | 0.374 | 3.205 | 0.181 | 404.3 | 458.8 | 461.2 | 0.855 | 0.970 | 0.975 |
| 14 | Excamé | 733.1 | 153.1 | 0.209 | -0.177 | 2.988 | 0.089 | 632.5 | 720.0 | 683.0 | 0.863 | 0.982 | 0.932 |
| 15 | Jiménez del Teúl | 473.8 | 127.2 | 0.269 | 0.064 | 3.535 | 0.171 | 435.3 | 454.5 | 448.8 | 0.919 | 0.959 | 0.947 |
| 16 | Juchipila | 694.8 | 142.5 | 0.205 | 0.038 | 3.301 | 0.077 | 583.5 | 663.1 | 666.2 | 0.840 | 0.954 | 0.959 |
| 17 | La Florida | 582.9 | 142.6 | 0.245 | 0.235 | 2.808 | 0.119 | 554.3 | 611.4 | 572.0 | 0.951 | 1.049 | 0.981 |
| 18 | La Villita | 771.7 | 178.7 | 0.232 | 0.570 | 3.657 | 0.139 | 625.8 | 730.3 | 726.7 | 0.811 | 0.946 | 0.942 |
| 19 | Loreto | 442.1 | 124.6 | 0.282 | -0.505 | 3.691 | 0.011 | 397.6 | 435.2 | 415.2 | 0.899 | 0.984 | 0.939 |
| 20 | Monte Escobedo | 717.4 | 169.1 | 0.236 | 0.831 | 4.391 | 0.059 | 681.0 | 738.0 | 693.3 | 0.949 | 1.029 | 0.966 |
| 21 | Nochistlán | 699.9 | 164.6 | 0.235 | 0.006 | 3.061 | 0.065 | 594.7 | 644.1 | 610.8 | 0.850 | 0.920 | 0.873 |
| 22 | Ojo Caliente | 390.8 | 141.7 | 0.363 | -0.057 | 2.788 | 0.337 | 436.4 | 442.7 | 407.7 | 1.117 | 1.133 | 1.043 |
| 23 | Presa El Chique | 541.5 | 118.2 | 0.218 | -0.021 | 2.459 | 0.160 | 487.5 | 552.1 | 532.5 | 0.900 | 1.020 | 0.983 |
| 24 | San Pedro Piedra Gorda | 415.4 | 136.6 | 0.329 | 0.207 | 2.755 | 0.186 | 364.6 | 418.6 | 401.5 | 0.878 | 1.008 | 0.967 |
| 25 | Tlaltenango | 699.4 | 158.3 | 0.226 | 0.606 | 3.917 | 0.020 | 651.9 | 676.7 | 644.7 | 0.932 | 0.968 | 0.922 |
| 26 | Villa García | 441.2 | 126.4 | 0.286 | 0.046 | 2.227 | -0.037 | 474.6 | 507.8 | 488.0 | 1.076 | 1.151 | 1.106 |
| 27 | Villanueva | 466.5 | 145.9 | 0.313 | 0.213 | 2.254 | 0.399 | 423.8 | 498.1 | 459.9 | 0.908 | 1.068 | 0.986 |
| Valores mínimos | – | – | – | – | – | – | – | – | 0.783 | 0.920 | 0.873 | ||
| Valores máximos | – | – | – | – | – | – | – | – | 1.242 | 1.182 | 1.106 | ||
| Valores promedio | – | – | – | – | – | – | – | – | 0.920 | 1.030 | 0.978 | ||
| Valor de la moda | – | – | – | – | – | – | – | – | 0.910 | 1.025 | 0.975 | ||
En la tabla 3 se citan las componentes determinísti-cas detectadas en 18 estaciones pluviométricas que mostraron anomalías según las 14 pruebas estadísticas aplicadas. En general, cuando la prueba de Helmert o la de las Secuencias muestran falta de homogeneidad, se debe a exceso de secuencias y se señala como “oscila poco”. Cuando con la prueba de Von Neumann se encontró pérdida de homogeneidad, el registro se indicó como “no aleatorio”. Por último, cuando la persistencia se detectó únicamente con alguna de las dos pruebas, se señaló como “persistencia ligera”.
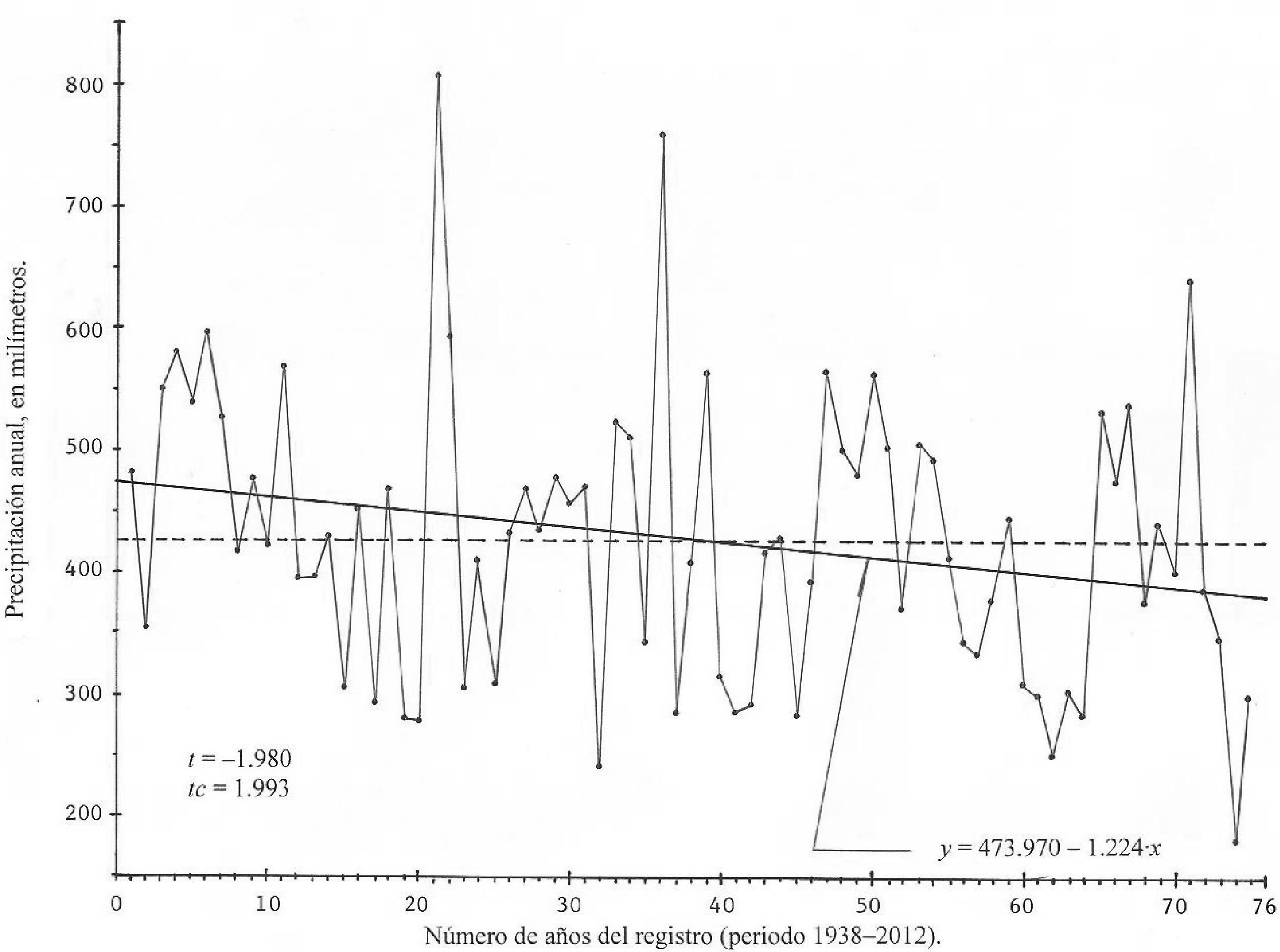
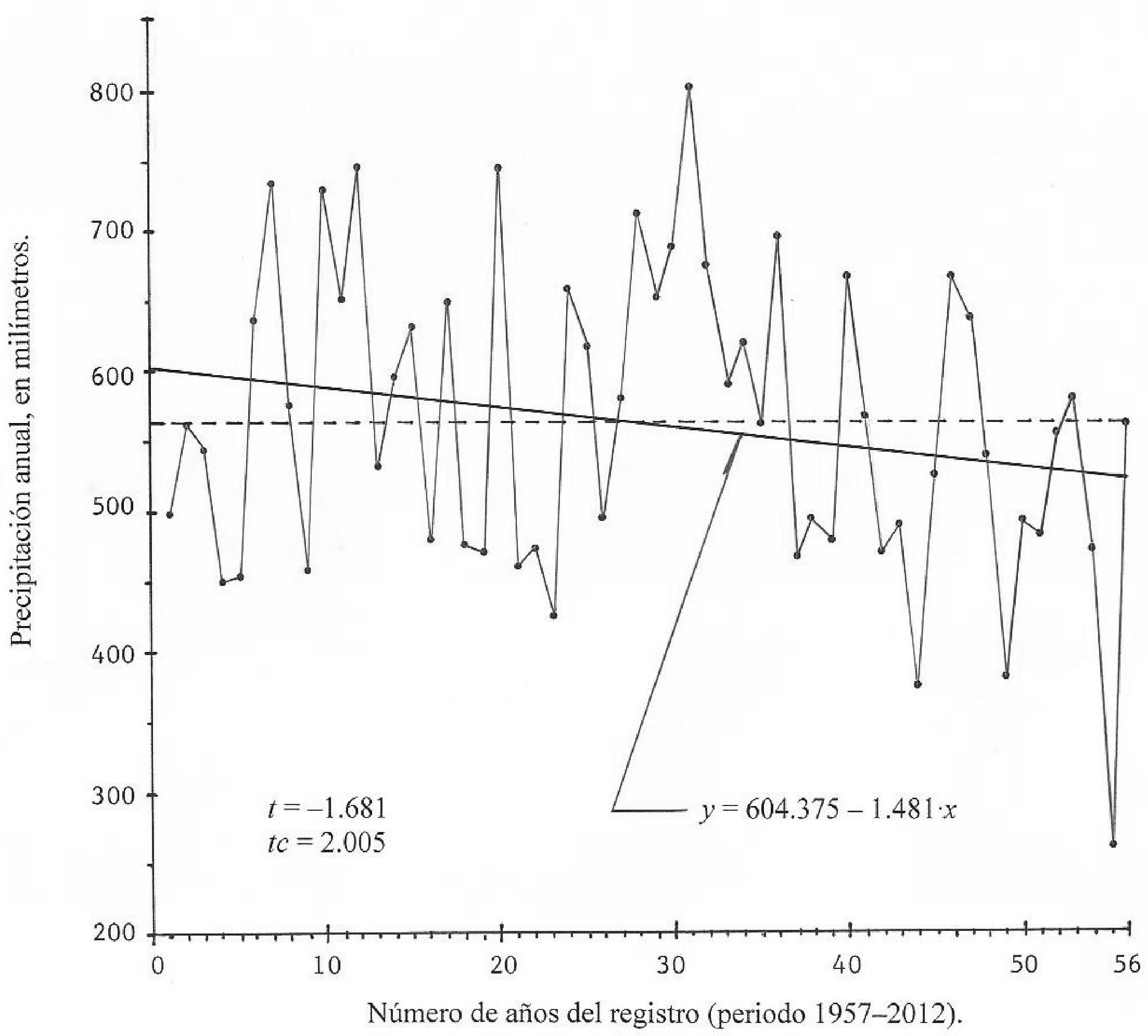
La persistencia puede considerarse una característica estadística del registro que se procesa, la cual se debe tomar en cuenta al realizar el análisis estocástico de la serie, a través de los modelos ARMA (Adeloye y Mon-taseri, 2002; Machiwal y Jha, 2008). Por lo anterior, todas las estaciones pluviométricas que mostraron esta característica no se eliminan. En las figuras 2, 3 y 4 se muestra el comportamiento de los registros de las estaciones Leobardo Reynoso, Gruñidora y El Platanito, las dos primeras presentaron tendencia y la tercera, cambio en la media, según las pruebas TBj y TB2. La estación Gruñidora solo resultó homogénea en el test de Bartlett. Es importante destacar que cada una de estas tres estaciones pluviométricas que resultaron no homogéneas, pertenecen a las regiones hidrológicas números 36, 37 y 12, respectivamente; indicando con ello que todos los ambientes geográficos del estado de Zacatecas son susceptibles de esas anomalías.
En estos registros se ajustó un modelo lineal para la tendencia y se buscó si su pendiente resultaba estadísticamente diferente de cero con una prueba basada en la distribución t de Student, únicamente en la estación Gruñidora resultó significativa, pero en Leobardo Reynoso quedó en el límite, pues su estadístico alcanzó un valor de 1.980 y el crítico es 1.993, con a = 5%. La descripción de esta prueba se presenta en el apéndice 3. Tomando en cuenta estos resultados y los de la tabla 3, se consideró necesario eliminar las estaciones Leobardo Reynoso, Gruñidora y El Platanito.
Cociente de precipitaciones mediasHu y Liu (2010) analizaron 31 registros de precipitación anual de periodo amplio (más de 50 años) a través de China, cuyo valor medio oscila de menos de 50mm a más de 2000mm, es decir, abarcan desde los climas áridos hasta los húmedos; encontrando que el cociente de la lluvia reciente (últimos 10 años) a la de largo plazo fluctuó de 0.89 a 1.11, con un valor medio igual a la uni dad. Por ello, concluyen que la lluvia en tal país no muestra efectos del cambio climático.
La tabla 4 se forma por tres partes, en la primera se exponen los parámetros estadísticos de la precipitación anual: media (X), desviación estándar (S) y coeficientes de variación (Cv), asimetría (Cs), curtosis (Ck) y correlación serial de orden uno (r1). En la segunda parte, se tienen las medias (x¡) de los últimos 5, 10 y 15 años del registro y en la tercera los cocientes de x, entre X .
Los últimos dos renglones de la tabla 4 muestran que los valores de la media y de la moda de los tres cocientes son casi iguales, con una moda ligeramente menor. Lo anterior implica que los 27 valores calculados de cada cociente no están sesgados, indicando que varían poco, como lo demuestran sus magnitudes mínima y máxima. El cociente CO5 es el más bajo, debido a la presencia de la sequía de los años 2010 a 2012. El cociente CO10 es cercano a la unidad y además en 16 de los 27 valores calculados, excede la unidad. Desafortunadamente, el cociente CO15 tiene una media y moda menores que la unidad (0.978 y 0.975) y solo ocurren siete con magnitud mayor que uno y seis de ellos no exceden 1.10. La moda se estimó con base en la distribución gamma mixta.
ConclusionesEl resultado relevante de este estudio, es que la precipitación anual del estado de Zacatecas, México, está disminuyendo, pues el cociente CO15 fue menor que la unidad en 20 de los 27 registros procesados y donde excedió a uno, la mayoría no llegó a 1.10; además la media y la moda fueron semejantes con los valores siguientes: 0.978 y 0.975, respectivamente.
Por otra parte, la comparación entre los tres cocientes (CO5, CO10 y CO15), conduce a detectar la presencia de una sequía importante en los últimos 5 años, ya que el CO5 es el más bajo con un valor medio de 0.92. Como el CO10 se recupera a un valor medio de 1.030, se intuye que la sequía citada tuvo una duración breve.
Aunque estadísticamente no existe evidencia general del cambio climático, pues únicamente dos registros de los 30 procesados, mostraron tendencia (estaciones pluviométricas Leobardo Reynoso y Gruñidora), esta fue decreciente en ambos y significativa en la estación Gruñidora y casi diferente de cero en la segunda (figuras 2 y 3). Los cocientes CO15 de las tres estaciones eliminadas (las dos anteriores y El Platanito), son respectivamente los siguientes: 0.901, 0.858 y 0.888.
En la estación pluviométrica El Platanito se han medido en los últimos 15 años, los tres valores más bajos de precipitación de todo su registro de 56 años (figura 4). Esto influye, para ser detectado por dos pruebas basadas en la curva masa residual (TB1 y TB2) y encontrar cambio en la media o pérdida de homogeneidad en tal registro.
Es importante señalar que las estaciones pluviomé-tricas que resultaron no homogéneas, pertenecen a las regiones hidrológicas 36, 37 y 12, por esto se intuye que todos los ambientes geográficos del estado de Zacatecas son susceptibles de tales anomalías.
Se sugiere realizar este análisis en otros estados de la República Mexicana, o bien, en otras regiones o su-bregiones hidrológicas, para establecer si esta disminución de la precipitación es generalizada y donde se encuentre, como en el estado de Zacatecas, México, formular medidas orientadas a considerar esa reducción de lluvia y redimensionar los aprovechamientos hidráulicos de todo tipo.
Este artículo se cita
Citación estilo Chicago
Campos-Aranda, Daniel Francisco. Búsqueda de tendencias en la precipitación anual del estado de Zacatecas, México; en 30 registros con más de 50 años. Ingeniería Investigación y Tecnología, XVI, 03 (2015): 355-368.
Citación estilo ISO 690
Campos-Aranda D.F. Búsqueda de tendencias en la precipitación anual del estado de Zacatecas, México; en 30 registros con más de 50 años. Ingeniería Investigación y Tecnología, volumen XVI (número 3), julio-septiembre 2015: 355-368.
Se agradecen las observaciones y correcciones sugeridas por el árbitro anónimo A, las cuales permitieron mejorar el enfoque general del trabajo y ayudaron a destacar sus resultados prácticos.
Referencias de consulta de las pruebas estadísticas aplicadas
| Prueba o Test | Símbolo | Referencias |
|---|---|---|
| Cociente de Geary | CG | Machiwal y Jha (2012) |
| Shapiro-Wilk | SW | Shapiro y Wilk (1965), Ruiz (1977) y Shapiro (1998) |
| Helmert | PH | Mather (1977) y Campos (1998) |
| Secuencias | PS | Thom (1971) y Campos (1998) |
| Von Neumann | PV | WMO (1971), Buishand (1982) y Machiwal y Jha (2012) |
| Anderson | TA | WMO (1971), Linsley et al. (1988) y Campos (1998) |
| Sneyers | TS, | WMO (1971) |
| Bartlett | TB | WMO (1971) y Ruiz (1977) |
| Cramer | TC | WMO (1971) y Campos (1998) |
| Buishand | TBj a TB2 | Buishand (1982), Gutiérrez et al (2007) y Campos (2008) |
Machiwal y Jha (2008) aplicaron 12 pruebas para detección de tendencia, la mayoría paramétricas y encontraron que los tres tests que serán expuestos, fueron los de mayor potencia o más confiables.
Esta prueba paramétrica también se conoce como de correlación de rangos (Machiwal y Jha, 2012), es muy efectiva si la tendencia fundamental es de tipo lineal o se aproxima a esta. Su procedimiento consiste en evaluar el número p, en todos los pares de observaciones (xi, x; con i = 1 a n-1; j = i + 1 a n) en que Xj es mayor que x, después se calculan las estadísticas siguientes (Kottegoda, 1980):
Si el cociente x/aT es menor que ±1.960, el registro no presenta tendencia en una prueba de dos colas con un nivel de significancia a de 5%.
En esta prueba no paramétrica que se conoce como correlación del orden de rangos (Machiwal y Jha, 2012), primero se ordenan los datos de menor a mayor y se sustituye cada elemento del registro por su rango después para cada dato de la serie original se calculan las diferencias: di = ki - i, con i = 1 a n y se evalúan las estadísticas siguientes (WMO, 1971; Adeloye y Montaseri, 2002):
El valor de la ecuación anterior se compara con el intervalo que define ±tc tomado de la distribución t de Student con n - 2 grados de libertad y nivel de significancia a, para una prueba de dos colas; si lo excede (t > tc) existe tendencia.
Es una prueba no paramétrica que busca tendencia en la serie sin importar si es lineal o no lineal; pero el registro no debe mostrar persistencia. Su estadístico operativo Ss es la suma de los signos de las diferencias (z) de todas las parejas factibles de formar, por ello su expresión es (Manly, 2001):
en la cual, el signo(z) es -1 para z < 0, 0 para z = 0 y +1 para z > 0. Para una serie con valores aleatorios se espera que Ss = 0, cuya varianza es (Hirsch et al., 1993; Ma-chiwal y Jha, 2012):
El estadístico de la prueba es
En la expresión anterior, mc = 1 cuando Ss < 0 y mc = -1 para Ss > 0. Si el valor absoluto de ZS es mayor que el valor crítico de la distribución normal estándar, la serie presenta tendencia creciente o decreciente con un nivel de significancia a. Para a = 5% el valor crítico es 1.960. La varianza (ecuación 6) se debe corregir cuando existen datos iguales o la muestra es censurada (Hirsch et al., 1993).
Recta de regresión para una tendencia lineal
Se considera que la variable dependiente (y) representa las precipitaciones anuales Pi en milímetros y los tiempos o años Ti son las abscisas (x), en este caso iguales al i-ésimo valor i. Para probar si la pendiente (m) de la recta de regresión ajustada por mínimos cuadrados de los residuos, es estadísticamente diferente de cero, se usa una prueba basada en la t de Student definida por las ecuaciones siguientes (Ostele y Mensing, 1975):
P¯ y T¯ son las medias; en la ecuación anterior, Pˆi es el valor estimado con la recta de regresión (ecuación 8). SE2 y Sm2 son las varianzas de los errores y de la pendiente. Si el valor calculado t es mayor que el crítico (tc), obtenido para la distribución t de Student con n - 2 grados de libertad y a = 5%, en una prueba de dos colas, la pendiente m es significativa, es decir, existe tendencia lineal. El problema de esta prueba es que no distingue entre persistencia y tendencia (Adeloye y Montaseri, 2002).
Daniel Francisco Campos-Aranda. Obtuvo el título de ingeniero Civil en diciembre de 1972, en la entonces Escuela de Ingeniería de la UASLP. Durante el primer semestre de 1977, realizó en Madrid, España un diplomado en hidrología general y aplicada. Posteriormente, durante 1980-1981 llevó a cabo estudios de maestría en ingeniería en la especialidad de Hidráulica, en la División de Estudios de Posgrado de la Facultad de Ingeniería de la UNAM. En esta misma institución, inició (1984) y concluyó (1987) el doctorado en ingeniería con especialidad en aprovechamientos hidráulicos. Ha publicado artículos principalmente en revistas mexicanas de excelencia: 46 en Tecnología y Ciencias del Agua (antes Ingeniería Hidráulica en México), 18 en Agrociencia y 16 en Ingeniería. Investigación y Tecnología. Es profesor jubilado de la UASLP, desde el 1° de febrero de 2003. En noviembre de 1989 obtuvo la medalla Gabino Barreda de la UNAM y en 2008 le fue otorgado el Premio Nacional “Francisco Torres H.” de la AMH. A partir de septiembre de 2013 vuelve a ser investigador nacional nivel I.