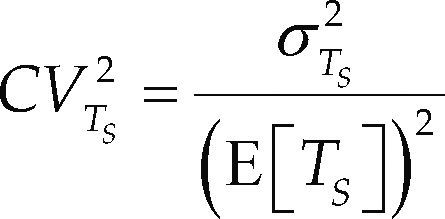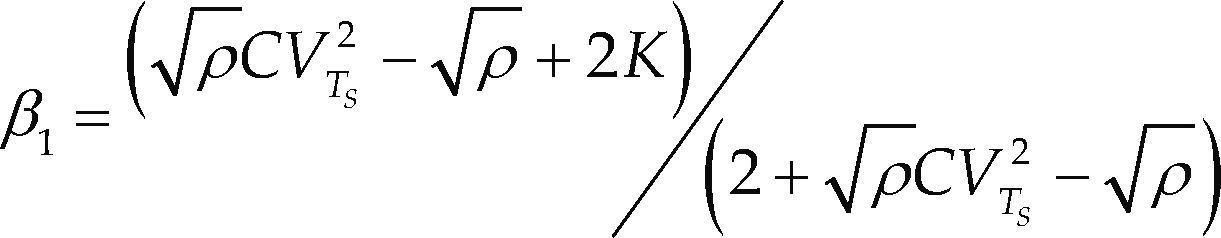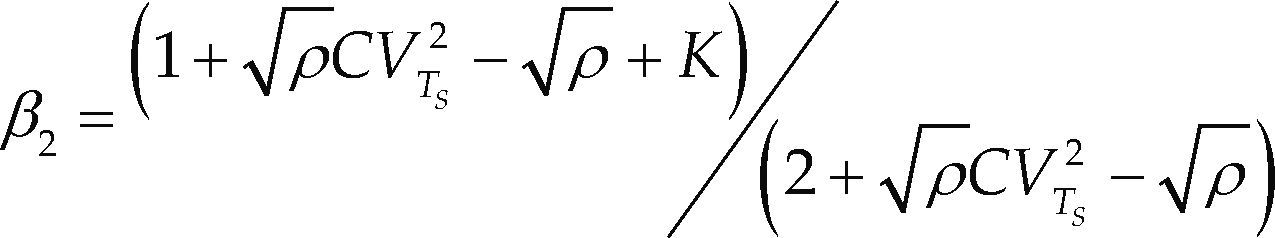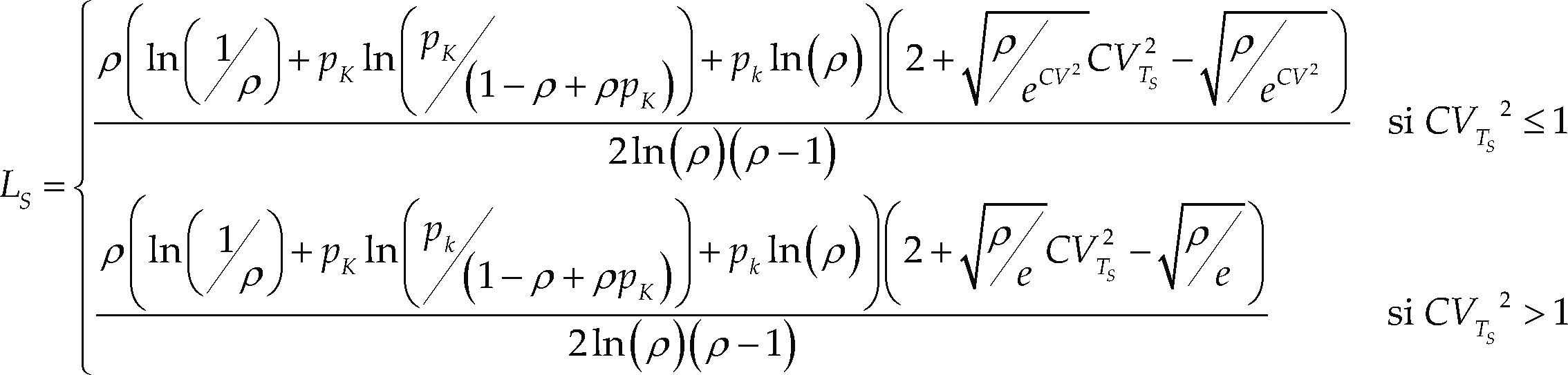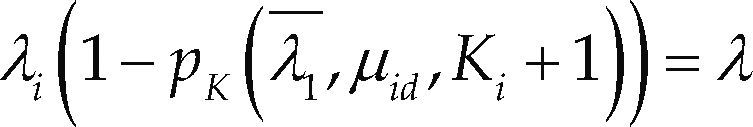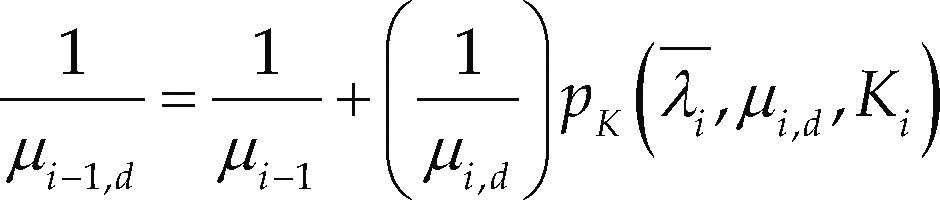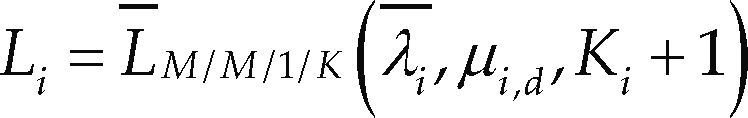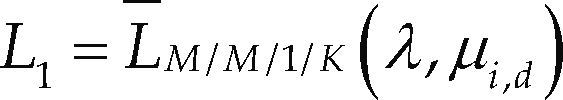Propiedades de sistemas tipo M/G/1/K con estaciones en serie

Resumen

En este trabajo se presenta una adecuación al método de Buzacott y Shanthikumar (1993) para calcular analíticamente las propiedades de sistemas de líneas de espera tipo M/G/1/K y arreglo en serie. Se realizaron pruebas de validación empleando simulación y se observó que, con la modificación propuesta, el método tiene un grado de exactitud aceptable para obtener las propiedades de sistemas M/G/1/K en serie, con lo que se puede considerar como una alternativa a otro método propuesto en la literatura para dicha clase de sistemas. Al ser un procedimiento que requiere menos cálculos, es de gran utilidad para responsables en la toma de decisiones, que requieren implementar herramientas para analizar el desempeño de sistemas de líneas de espera en ambientes de producción y servicios.

Abstract

We propose a modification to the Buzacott & Shantikumar (1993) method to evaluate the properties of M/G/1/K queues with series arrangement. We made several tests and compared with simulation to validate the results. We observed that, with the proposed modification, the method has an acceptable level of exactitude. It can be considered an alternative calculation to other methods in the literature. The fact that this method requires less computational effort, can be useful to practitioners and managers that require tools to analyze the performance of systems in production and services areas.

Introducción

Aunque no siempre evidente, las filas o líneas de espera que se forman ante una estación o servidor son parte de las propiedades de cualquier sistema, sea de producción, manufactura o de servicios. En la administración de un sistema, es frecuente tomar decisiones tomando como base la perspectiva de reducir en lo posible los costos asociados con la espera por parte de los clientes.

El estudio de las líneas de espera se relaciona con la cuantificación del fenómeno de esperar a ser atendido, por medidas de desempeño representativas, tales como el número promedio de clientes esperando ser atendidos, tiempo promedio de espera en la fila o el uso promedio de la instalación.

Problema

El estudio y análisis de los sistemas de líneas de espera requiere métodos y modelos para calcular sus propiedades con un alto grado de exactitud; de especial interés son los sistemas con estaciones en serie y capacidad limitada en la línea de espera (comúnmente llamado buffer). Esta clase de sistemas son comunes en prácticamente cualquier ámbito, por ejemplo, en los sistemas de manufactura y producción existe por lo general un espacio destinado al almacenamiento de piezas o lotes que serán procesados en los equipos, este inventario se mantiene para que en caso de que una estación detenga su producción, la siguiente estación en la línea no deba parar por falta de suministro. Si el buffer de una máquina se encuentra lleno, entonces la estación anterior detiene su producción hasta que exista espacio suficiente para recibir al menos una unidad de producción (Buzacott y Shanthikumar, 1993).

Si se suponen tiempos exponenciales, o bien tipo Erlang, entonces se pueden utilizar cadenas de Markov para obtener los valores exactos de las propiedades de estos sistemas, sin embargo el número de estados crece de manera explosiva y por lo tanto las cadenas son poco prácticas. Otro medio son las aproximaciones por ecuaciones y modelos analíticos.

Para el caso en donde el tiempo de servicio en la estación es de tipo Markoviano existen modelos analíticos conocidos, sin embargo, cuando el tiempo de servicio de las estaciones es no-Markoviano (M/G/1/K según la notación Kendall), el cálculo de las propiedades se dificulta por la carencia (al menos hasta hace algunos años) de modelos analíticos y expresiones para realizar el análisis de dicha clase de sistemas. Para su estudio, lo común era recurrir a modelos de simulación para caracterizar y analizar dicha clase de sistemas, dada la carencia de modelos analíticos para aproximar sus propiedades. Con esta perspectiva, este trabajo tiene como objetivos:

• 1.

  Presentar una adecuación a un método conocido, que permite calcular analíticamente las propiedades de sistemas M/G/1/K en serie.

• 2.

  Validar y cuantificar el grado de exactitud del método con las adecuaciones propuestas.

Antecedentes

Los métodos desarrollados para el cálculo de las propiedades de sistemas de líneas de espera M/G/1/K con varias etapas o estaciones dispuestas en serie, se pueden encontrar en: Hillier y Boling (1967); Takahashi, Miyahara y Hasegawa (1980) en donde se utiliza el enfoque de Jackson de redes de líneas de espera; en Perros y Altiok (1986) y Gershwin (1987), donde se utilizan cadenas de Markov, en Kerbache y MacGregor (1987); en MacGregor y Daskalaki (1988) en donde proponen el método de expansión generalizada (GEM); en Tan y Yeralan (1997) que emplean programación lineal, y Van-Vuuren, Adan y Resing-Sassen (2005) donde emplean descomposición. Finalmente, en los libros de Buzacott y Shanthikumar (1993); Altiok (1996); Curry y Feldman (2011) se pueden encontrar los respectivos procedimientos.

En los trabajos mencionados los supuestos son: un solo servidor, llegadas de clientes tipo Poisson, y tiempos de servicio exponenciales para realizar el análisis. Para el caso de los tiempos de servicio generales (G) solo se reportaron casos resueltos muy pequeños como por ejemplo en Pollock, Birge y Alden (1985), esto se debe a que aún no se obtenían ecuaciones que fueran fáciles de manipular y que permitieran aproximar el número de clientes en el sistema, probabilidad de bloqueo y tiempo ciclo de esta clase de sistemas; en consecuencia se debía recurrir a modelos de simulación para determinar estas propiedades (tabla 1 para la notación y la relación de símbolos empleados).

Tabla 1.

Notación y símbolos utilizados

K	Espacio de almacenamiento disponible fuente a la estación (Buffer)
k	Parámetro de forma de la función de distribución gamma
E [TS]	Valor esperado del tiempo de servicio de la estación
Lq	Número de clientes promedio formados frente a la estación
LS	Número de clientes promedio en el sistema índice de estación
i	Índice de estación
m	Número total de estaciones o máquinas
pK	Probabilidad de bloqueo de la estación (Búffer lleno)
p0	Probabilidad de que la estación se encuentre vacía
M	Sistema markoviano
G	Sistema no Markoviano o general
e	Número natural=2.7182
c	Número de servidores
λ	Tasa de llegadas
μ	tasa de servicio
ρ	Congestión del sistema, λ/μ
CVTS2	Varianza del tiempo de servicio
μid	Tasa efectiva de salida dela estación i
θ	Parámetro de escala de la función de distribución gamma
λ¯i	Tasa efectiva de llegadas a la estación i
CVTS2=σTS2(E[TS])2	Coeficiente de la variiación cuadrático del tiempo de -servicio

En el trabajo de Gelenbe (1975) se reporta una ecuación para aproximar el tamaño de una línea de espera con buffer frente a una estación y tiempos de servicio no-Markovianos, sin embargo es poco práctica como medio analítico; en realidad es con el trabajo de Kimura (1996) donde hay un gran avance, ya que se desarrolla una ecuación para calcular el tamaño del buffer en un sistema con servicio general, la cual es muy práctica. El siguiente paso lo da MacGregor en 2004; retoma la propuesta de Kimura y desarrolla las ecuaciones respectivas para aproximar el número de clientes en el sistema, la probabilidad de bloqueo y la probabilidad de que la estación se encuentre desocupada, para el caso en donde los tiempos de servicio son no Markovianos.

Es importante resaltar que las ecuaciones referidas en el párrafo anterior requieren como parámetros la congestión del sistema (ρ), el tamaño del buffer (K) y el coeficiente de variación cuadrático del servicio de la estación (CVTS2) (tabla 1), en donde este último es una medida de la variación del servicio que proporciona una estación; se calcula como sigue:

El coeficiente de variación cuadrático del servicio es la relación de la varianza del tiempo de servicio (σT2) y el cuadrado del valor esperado del tiempo de servicio (E[T_S])².

Con los resultados de MacGregor fue posible extender el GEM a los sistemas M/G/1/K y M/G/c/K con estaciones en serie y realizar el cálculo y caracterización de sus propiedades. En la serie de trabajos de Cruz y MacGregor (2007); Cruz, Duarte y Van-Woensel (2008) y Van-Woensel, Andriansyah, Cruz, MacGregor y Kerbache (2010) se han reportado de manera muy completa las características de sistemas M/G/1/K y M/G/c/K; cabe resaltar que esto ha permitido desarrollar métodos heurísticos para la solución analítica de otro problema conocido como problema de localización del buffer (BAP).

El método de expansión generalizada (GEM) es un procedimiento de descomposición que consta de tres fases:

• 1.

  Reconfiguración de la red de estaciones.

• 2.

  Estimación de parámetros.

• 3.

  Eliminación y actualización hacia atrás.

Se trata de un método en donde el paso más importante es la reconfiguración, ya que el sistema original se modifica agregando una estación o nodo ficticio antes de cada estación, el cual sirve para modelar el bloqueo de dicha estación. Una vez realizada la expansión, el siguiente paso es calcular las propiedades de cada estación o nodo (incluyendo los ficticios).

Un inconveniente del método GEM es la adición de nodos nuevos, lo que aumenta la cantidad de cálculos. Se recomienda consultar Kerbache y MacGregor (1987); MacGregor y Daskalaki (1988) para una descripción completa de dicho método.

La aportación de este trabajo es mostrar el cálculo analítico de las propiedades de sistemas M/G/1/K en serie, empleando el método de Buzacott y Shanthikumar (1993) y las ecuaciones reportadas en MacGregor; usando simulación se verificó el grado de exactitud, el cual resultó ser aceptable; el método de Buzacott y Shanthikumar tiene la ventaja de que requiere menos cálculos (no es necesario agregar nodos nuevos para modelar el bloqueo) y es viable su implementación como plantilla de hoja de cálculo, lo cual en términos prácticos es muy importante en ambientes sumamente dinámicos que es lo común en la vida real.

Fórmulas para el cálculo de p₀, p_K y L_S en sistemas M/G/1/K

Como se comentó, Kimura propuso en 1996 una ecuación para calcular el tamaño del buffer para sistemas con tiempos de servicio generales, MacGregor (2004) retoma y modifica esta fórmula de manera empírica; además ahí se proponen las ecuaciones para aproximar los valores de la probabilidad de bloqueo de la estación y el número promedio de clientes en el sistema. Para el caso de la probabilidad de bloqueo p_K la ecuación es la siguiente:

donde los términos β₁ y β₂ tienen las siguientes expresiones

La probabilidad de que el sistema se encuentre vacío p₀ se calcula con la siguiente expresión

donde (2c) corresponde al término β₂. Se debe señalar que, como información, se requieren el cuadrado del coeficiente de variación del servicio y la congestión del sistema (tabla 1). Para el caso del número de clientes en el sistema (L_S), ver la ecuación 4.

En este caso, es necesario contar con el parámetro de congestión del sistema (ρ), la probabilidad de bloqueo (p_K) y el coeficiente de variación cuadrático del servicio de la estación (CVTS2).

Método de descomposición para sistemas en serie

A continuación se muestra el método de descomposición propuesto por Buzacott y Shanthikumar (1993) para calcular las propiedades de sistemas de M/M/1/K en serie. El método calcula de manera recursiva las propiedades de un sistema formado por las estaciones m, m–1, …, 2, 1. La máquina m nunca está bloqueada y la máquina 1 nunca sufre de escasez de material (no requiere buffer). El procedimiento es el siguiente

Paso 1. Fijar μ_md = μ_m

Paso 2. Para i = m,…,2, hacer

Si, μ_id < λ entonces el sistema es inestable, ter-minar

En otro caso, encontrar λ¯i resolviendo

Establecer

Paso 3. Calcular

Paso 4. Terminar

En el primer paso, la tasa efectiva de salida de la última estación es igual a su tasa nominal de servicio. En el paso 2 se verifica que la estación i tenga capacidad para atender la demanda, si esta condición se cumple entonces se calcula la probabilidad de que la estación se encuentre bloqueada (p_K) y a continuación se resuelve la ecuación no lineal (5) para obtener la tasa efectiva de llegadas a la estación (λ_i); para tal efecto puede utilizarse algún método de búsqueda como Regula-falsi. En el mismo paso 2, se debe calcular el tiempo de salida efectivo (6) y a continuación el número de clientes en el sistema (7). Estos cálculos se inician en la máquina m y se repiten hasta la máquina 2. En el paso 3 se determina el número de clientes en el sistema de la máquina 1 con (8), deteniendo el método en el paso 4.

Como se mencionó, el método se desarrolló para sistemas donde la tasa de servicio es de tipo exponencial y en esencia se resuelven de manera recursiva los balances de flujo de entrada-salida hacia cada estación o nodo.

Para el caso de sistemas M/G/1/K en serie, se pueden sustituir las ecuaciones propuestas por MacGregor: para calcular la probabilidad de bloqueo del sistema se debe utilizar (2a, b y c), la probabilidad de que el sistema esté vacío se calcula con (3) y para el cálculo del número de clientes en el sistema se debe emplear (4), el resto del método no requiere modificaciones, a continuación se muestran las pruebas y la validación correspondiente.

Experimentos y resultados

Se realizó un conjunto de pruebas para verificar el desempeño del método en el cálculo de las propiedades de sistemas tipo M/G/1 en serie, con distintos escenarios del coeficiente de variación cuadrático que es el parámetro que incorpora la variación del sistema y permite aproximar aquellos sistemas con servicios que no son de tipo exponencial; para tal efecto se utilizaron las ecuaciones de MacGregor. Se resalta el hecho de que dicho método de Buzacott en su forma original supone que CVTS2=1.

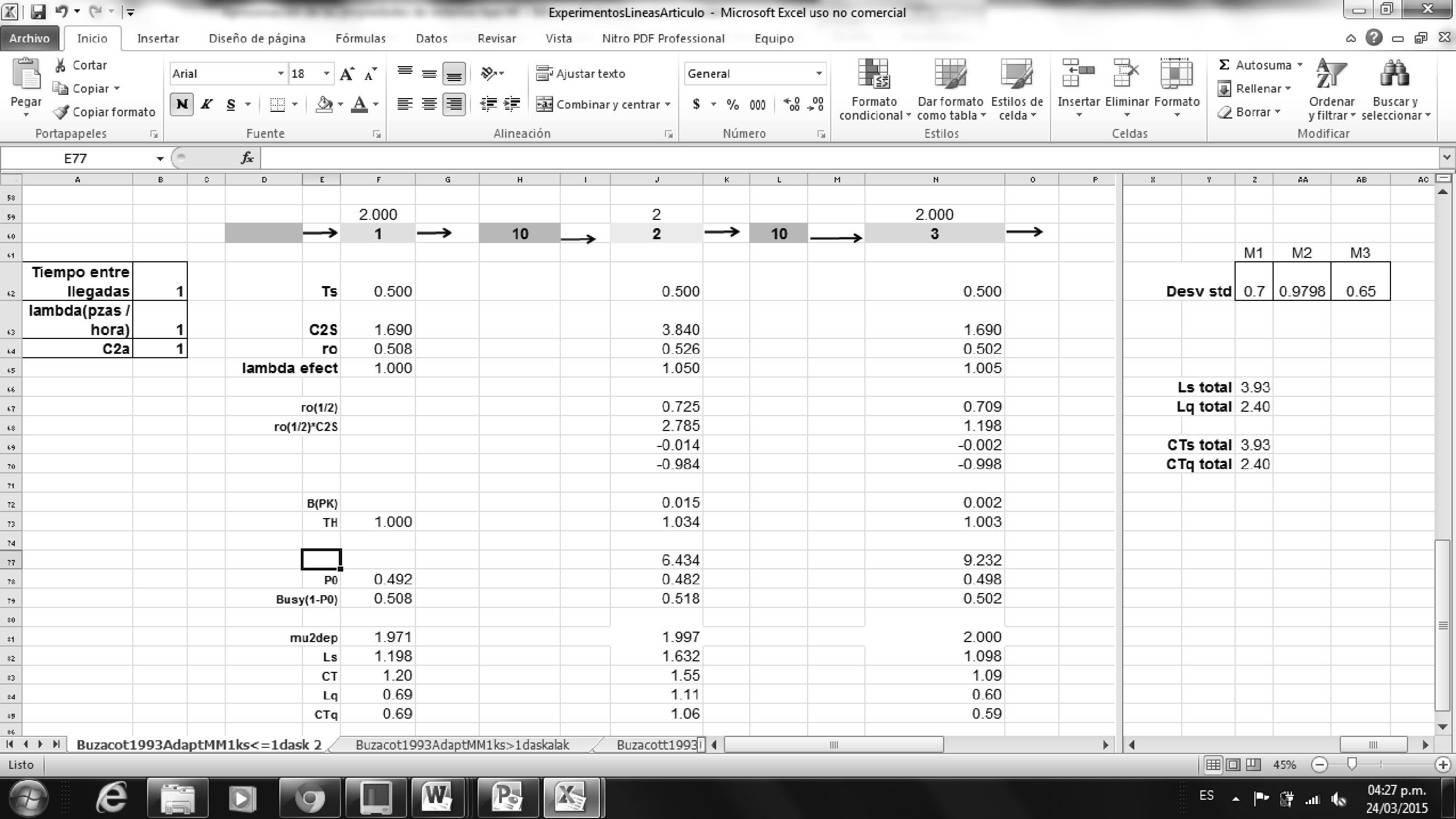
Las ecuaciones se programaron en una plantilla de hoja de cálculo; por el momento solo se muestra la imagen del arreglo de dicha plantilla para efectos ilustrativos, dado que el objetivo principal de este reporte es estudiar la efectividad de las ecuaciones para predecir las propiedades, así como realizar algunas conjeturas sobre el efecto de la variación (medida a través de) sobre las propiedades del sistema (figura 1).

Figura 1.

Plantilla para análisis de sistemas M/G/1/K con estaciones en serie.

Las pruebas se dividieron en dos partes. En la primera serie se considera que todas las estaciones tienen el mismo tiempo de servicio, en la segunda serie de pruebas, se consideró que la estación central es el cuello de botella del sistema; los resultados obtenidos de manera analítica se validaron mediante simulación.

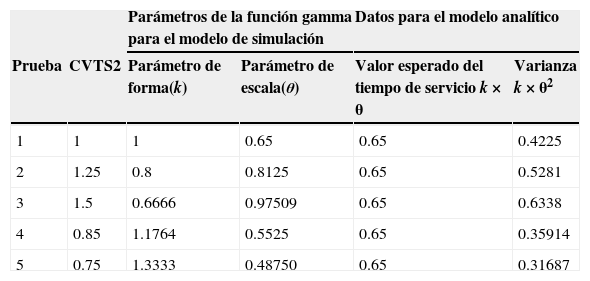
Servicio uniforme

En la tabla 2 se muestran los datos empleados para las pruebas en donde la tasa de servicio y el son iguales en todas las estaciones. En la columna 2 se muestra el coeficiente de variación, en las columnas 3 y 4 se dan los datos del parámetro de escala y parámetro de forma de la función de distribución gamma, con estos datos se obtienen el valor esperado y la varianza del tiempo de servicio, los cuales se muestran en las columnas 5 y 6.

Tabla 2.

Parámetros de la función gamma, valor esperado y varianza de las 3 estaciones

		Parámetros de la función gamma para el modelo de simulación		Datos para el modelo analítico
Prueba	CVTS2	Parámetro de forma(k)	Parámetro de escala(θ)	Valor esperado del tiempo de servicio k × θ	Varianza k × θ^2
1	1	1	0.65	0.65	0.4225
2	1.25	0.8	0.8125	0.65	0.5281
3	1.5	0.6666	0.97509	0.65	0.6338
4	0.85	1.1764	0.5525	0.65	0.35914
5	0.75	1.3333	0.48750	0.65	0.31687

A modo de ejemplo se describe la prueba 1: a la función gamma con k = 1 y θ = 0.65, le corresponde un tiempo de servicio con valor esperado de 0.65 h y varianza de 0.4225 h² y se puede verificar que corresponde al caso donde el tiempo de servicio es de tipo exponencial; los parámetros del valor esperado y coeficiente de variación son los requeridos para realizar el cálculo analítico.

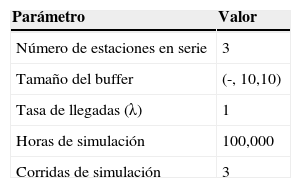
Para validar los resultados obtenidos con el método analítico se construyó el modelo respectivo de simulación en el paquete Arena (Altiok y Melamed, 2007), se utilizó una tasa de llegadas λ = 1 de tipo exponencial; en el mismo modelo de simulación se utilizó la función de distribución gamma para los tiempos de servicio utilizando los datos de la columna 3 para el parámetro de forma y de la columna 4 para el parámetro de escala (tabla 2). Los parámetros de tamaño de buffer de cada estación, el número de horas de simulación y el número de corridas de simulación realizadas se muestran en la tabla 3.

Tabla 3.

Datos adicionales de las pruebas

Parámetro	Valor
Número de estaciones en serie	3
Tamaño del buffer	(-, 10,10)
Tasa de llegadas (λ)	1
Horas de simulación	100,000
Corridas de simulación	3

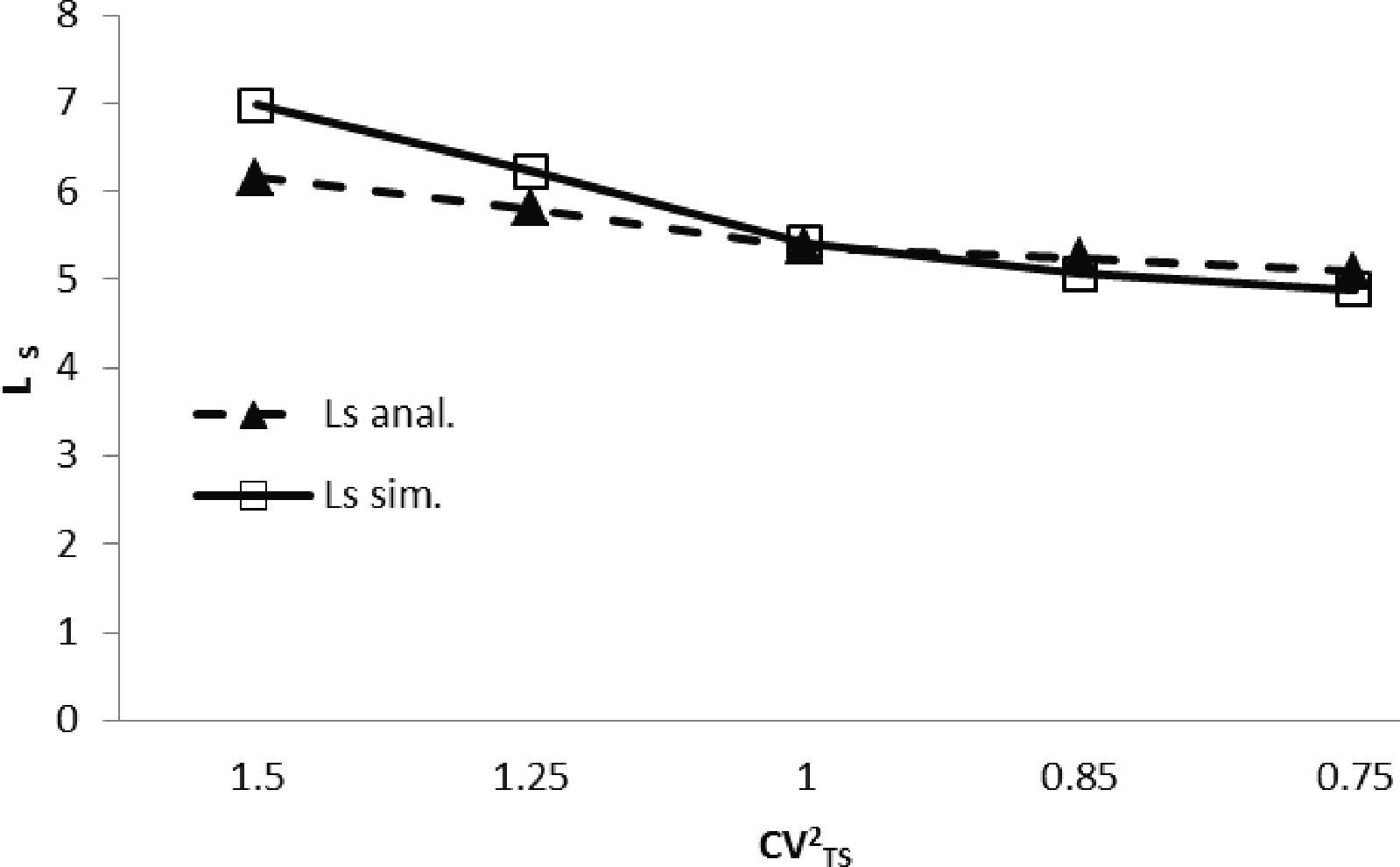
En la figura 2 se muestran de manera simultánea el número de clientes (L_S) obtenido de manera analítica y con el modelo de simulación; se observa que a medida que existe mayor variación en el servicio (CVTS2>1), el número de clientes promedio en el sistema se incrementa. Lo anterior es acorde con lo que sucedería en la realidad: una mayor variación en todas las estaciones puede implicar en una operación real que, de cliente a cliente, existen diferencias considerables en el servicio; aquí las causas son diversas y el parámetro que proporciona la información de esas variaciones es el coeficiente de variación cuadrático.

Figura 2.

Número de clientes en el sistema vsCVTS2.

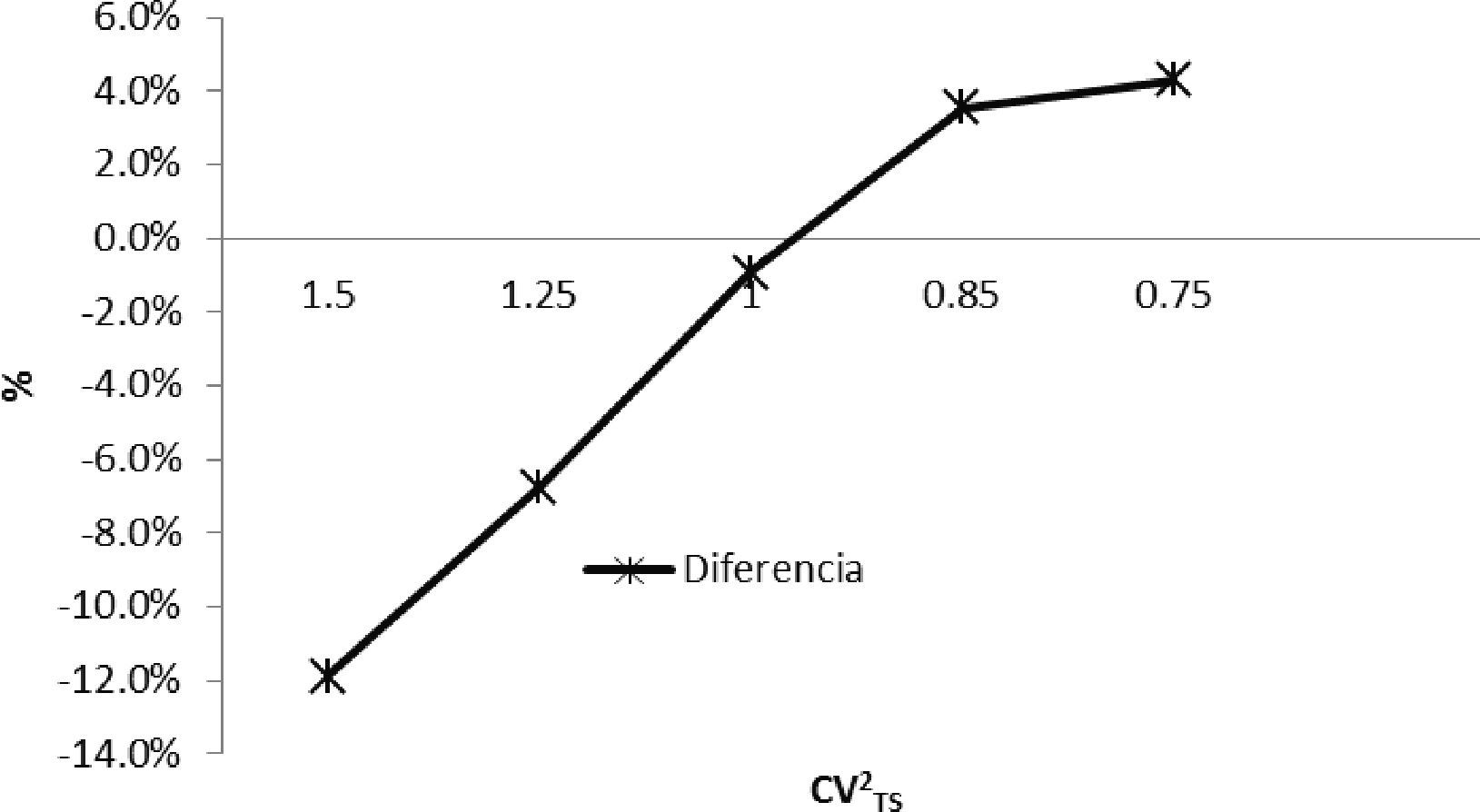
En cuanto a la exactitud de las ecuaciones se puede observar en la tabla 4 que cuando CVTS2=1.25 y 1.5 la diferencia del resultado analítico con respecto al simulado es –6.7 y –11.9% respectivamente, en las pruebas CVTS2=1, 0.85 y 0.75, las diferencias son –0.9, 3.6 y 4.3% respecto al resultado que se obtiene mediante simulación (figura 3, tabla 4).

Tabla 4.

Número de clientes en el sistema

LS
CVTS2	Analítico	Simulado	Diferencia
1.5	6.15	6.98	-11.9%
1.25	5.81	6.23	-6.7%
1	5.37	5.42	-0.9%
0.85	5.25	5.07	3.6%
0.75	5.09	4.88	4.3%

Figura 3.

Diferencia vsCVTS2.

En cuanto a la probabilidad de bloqueo (p_K) se aprecia que a medida que CVTS2 aumenta, entonces la probabilidad de que una estación se encuentre bloqueada se incrementa también (tabla 5).

Tabla 5.

Resultados de p_K y p₀

	pK		p0			pK		p0
Estaciones	analítico	simulado	analítico	simulado	Estaciones	analítico	simulado	analítico	simulado
		CVTS2=0.75						CVTS2=0.85
1	N/A	0.348	0.355	1	N/A	0.347	0.35
2	0.003	0.0008	0.348	0.353	2	0.0039	0.0014	0.347	0.34
3	0.003	0.00101	0.35	0.35	3	0.0038	0.0012	0.35	0.35

	pK		p0				pK		p0
Estaciones	analítico	simulado	analítico	simulado	Estaciones	analítico	simulado	analítico	simulado
			CVTS2=1				CVTS2=1.25
1	N/A	0.346	0.352	1	N/A	0.34	0.343
2	0.005	0.00263	0.346	0.354	2	0.007	0.0062	0.34	0.345
3	0.00499	0.00248	0.35	0.355	3	0.007	0.0059	0.35	0.351

	pK		p0
	analítico	simulado	analítico	simulado
Estaciones			CVTS2=1.5
1	N/A		0.34	0.34
2	0.01	0.0115	0.34	0.336
3	0.009	0.0112	0.35	0.33

Se observa también que para valores de CVTS2=1.25 y 1.5 el modelo analítico aproxima bien el valor de p_K, en cambio, cuando CVTS2=1, 0.85 y 0.75, el resultado obtenido de manera analítica es mayor que el resultado obtenido con simulación.

Por último, en cuanto a la probabilidad de que la estación se encuentre vacía (p₀), en todos los casos el modelo analítico obtiene el mismo valor que se obtiene mediante simulación.

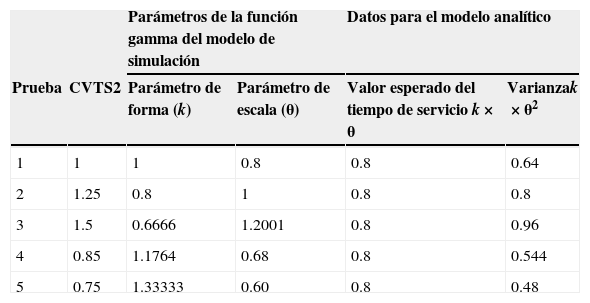
Cuello de botella

En la segunda serie de experimentos se estudió la capacidad del método analítico para predecir las propiedades de sistemas que tienen cuello de botella. El cuello de botella se define como la máquina o estación más lenta (Lawrence y Buss, 1996) y en esta serie de pruebas se colocó en la máquina del centro. Para las máquinas 1 y 3 se mantuvo en todas las pruebas un tiempo de servicio de 0.65 h de tipo exponencial (CVTS2=1). En el caso del cuello de botella, se experimentó incrementando a 0.8 h el tiempo de servicio y las pruebas se llevaron a cabo con los parámetros de la tabla 6.

Tabla 6.

Parámetros de la función gamma, valor esperado y varianza del cuello de botella

		Parámetros de la función gamma del modelo de simulación		Datos para el modelo analítico
Prueba	CVTS2	Parámetro de forma (k)	Parámetro de escala (θ)	Valor esperado del tiempo de servicio k × θ	Varianzak × θ^2
1	1	1	0.8	0.8	0.64
2	1.25	0.8	1	0.8	0.8
3	1.5	0.6666	1.2001	0.8	0.96
4	0.85	1.1764	0.68	0.8	0.544
5	0.75	1.33333	0.60	0.8	0.48

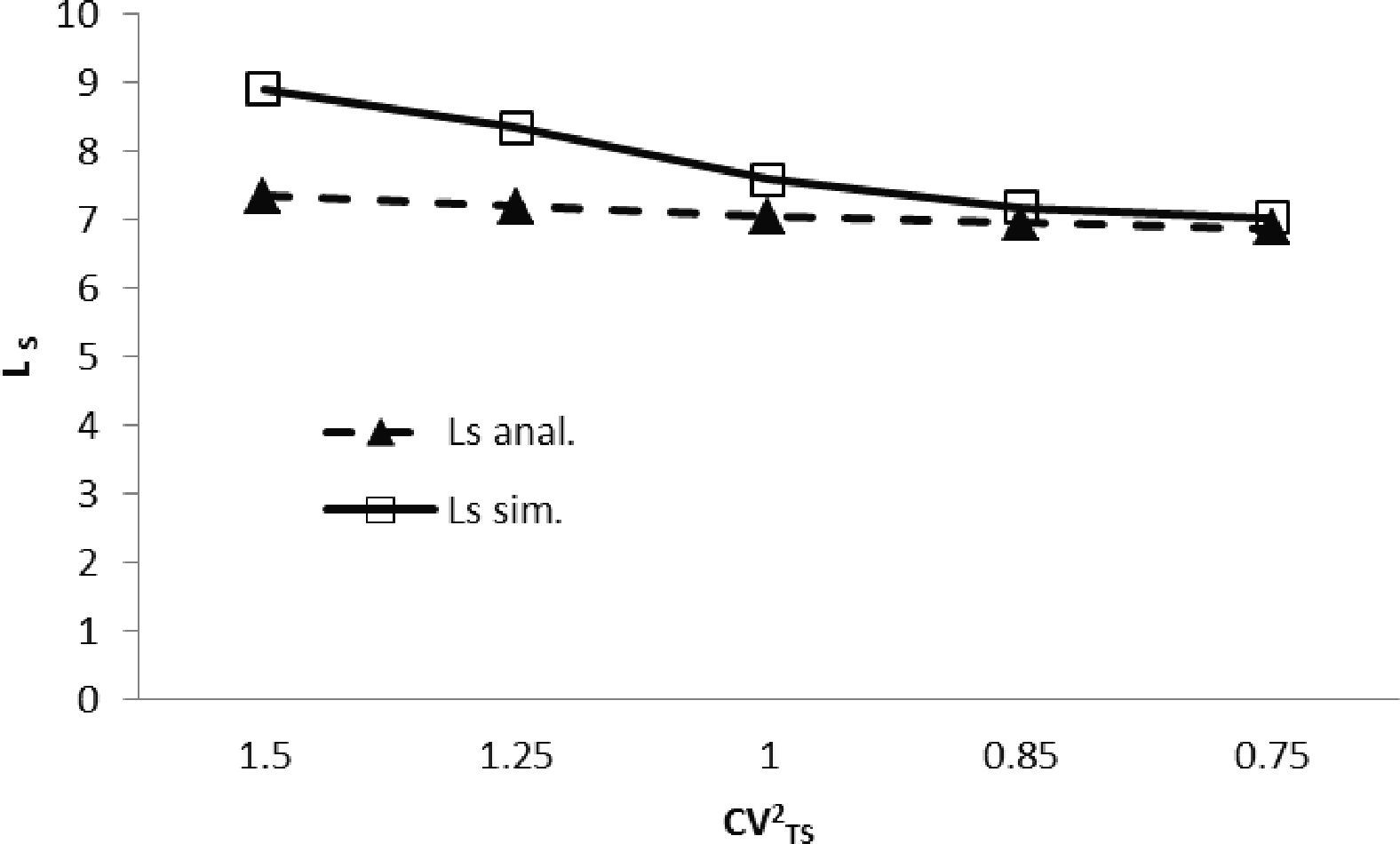
En la figura 4 se muestra L_S para cada prueba de CVTS2, como es de esperarse, al aparecer un cuello de botella el valor crece de manera considerable en comparación con las pruebas con servicio uniforme y, más aún, si en dicho cuello de botella aumenta la variación, también aumenta L_S.

Figura 4.

Número de clientes en el sistema vsCVTS2. Cuello de botella en la estación 2.

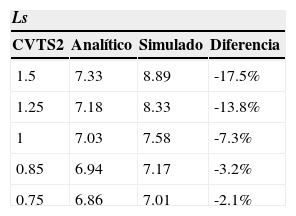
A modo de ejemplo, si por alguna circunstancia apa- rece un cuello de botella y suponiendo que el tiempo de servicio sigue siendo de tipo exponencial (CVTS2=1), entonces el valor de L_S cambia de 5.37 a 7.03 de acuerdo con el modelo analítico, en otras palabras, hay un incremento de 30% (tabla 7); más aún, si dicho cuello de botella además presenta una variación muy alta, por ejemplo CVTS2=1.5, entonces L_S aumenta a 7.33, o bien, 36.49%.

Tabla 7.

Número de clientes en el sistema con cuello de botella

Ls
CVTS2	Analítico	Simulado	Diferencia
1.5	7.33	8.89	-17.5%
1.25	7.18	8.33	-13.8%
1	7.03	7.58	-7.3%
0.85	6.94	7.17	-3.2%
0.75	6.86	7.01	-2.1%

También en la figura 4 se observa que L_S obtenido de manera analítica se ve afectado a medida que se incrementa la variación del sistema (figura 4 y tabla 7).

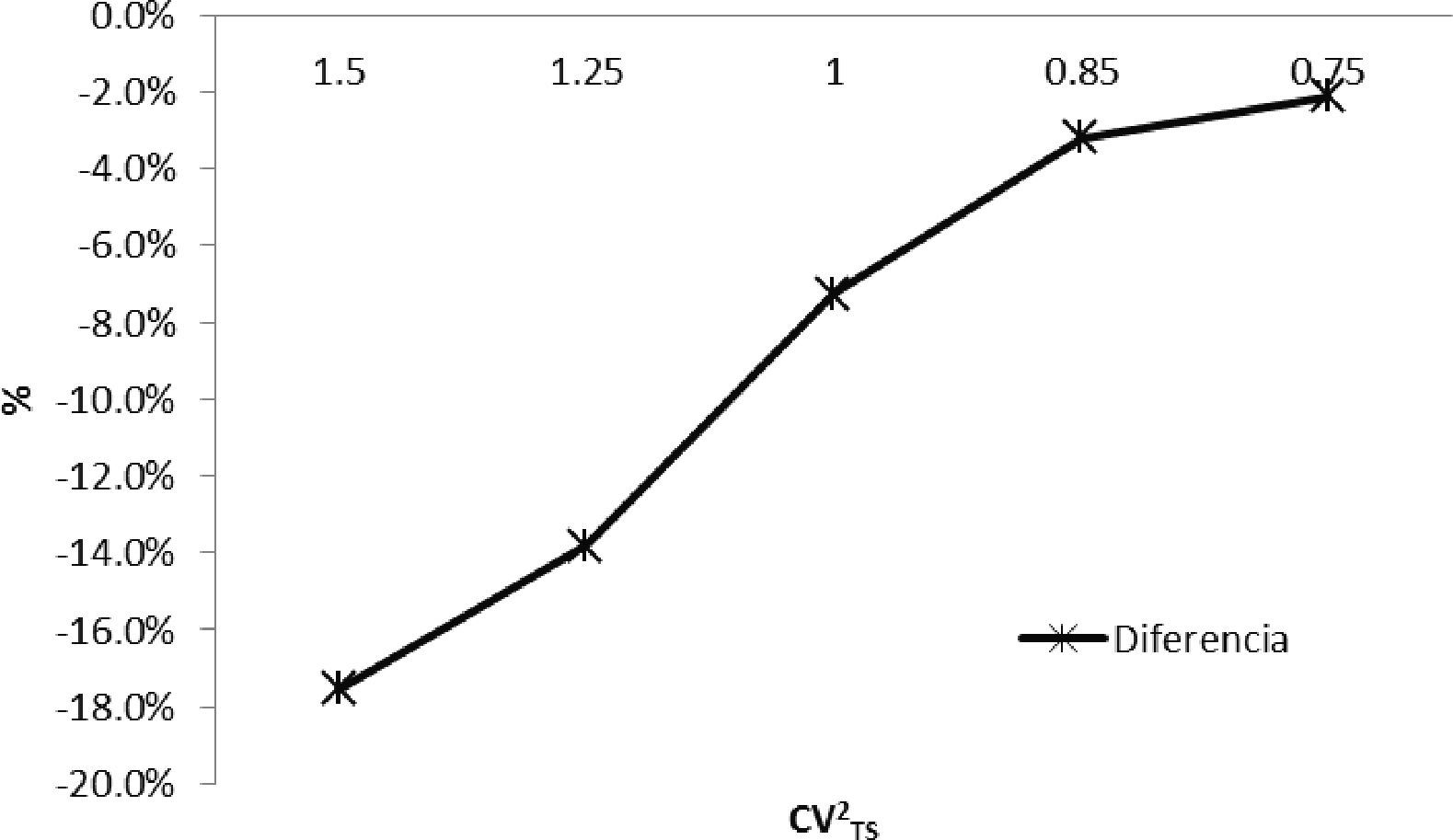
En la figura 5 se observa graficada la diferencia de L_S obtenida con el modelo analítico, y la obtenida mediante simulación, el comportamiento es el mismo que se obtuvo en la serie de pruebas anterior: si CVTS2 disminuye, mejora la exactitud del modelo analítico.

Figura 5.

Diferencia vsCVTS2 con cuello de botella.

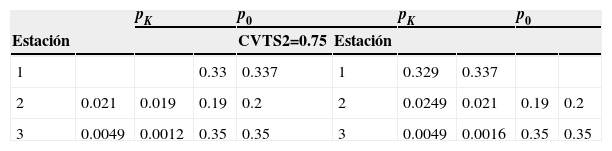
En la figura 6 se muestra el número de clientes formados frente al cuello de botella (estación 2) y se observa que este disminuye a medida que el CVTS2 disminuye también. En la operación, una disminución de la variación puede implicar, por ejemplo, que el servicio se realiza con mayor uniformidad entre cliente y cliente. También se aprecia que a medida que disminuye el valor de, CVTS2, el valor aproximado por el modelo analítico mejora.

Figura 6.

Número de clientes en la estación 2 (cuello de botella) v sCVTS2.

El modelo analítico predice con bastante exactitud la probabilidad de bloqueo (p_K) de la estación 2 (cuello de botella) para todas las pruebas de CVTS2 (tabla 8). Para el caso de la estación 3, se presenta la misma situación que en las pruebas con servicio uniforme: cuando CVTS2>1 la diferencia con respecto al valor obtenido vía simulación disminuye.

Tabla 8.

Resultados de p_K y p₀ con cuello de botella

		pK		p0		pK		p0
Estación				CVTS2=0.75	Estación
1			0.33	0.337	1	0.329	0.337
2	0.021	0.019	0.19	0.2	2	0.0249	0.021	0.19	0.2
3	0.0049	0.0012	0.35	0.35	3	0.0049	0.0016	0.35	0.35

	pK		p0			pK		p0
Estación	CVTS2=1				Estación			CVTS2=1.25
1			0.32	0.32	1			0.31	0.31
2	0.029	0.028	0.19	0.2	2	0.04	0.038	0.19	0.196
3	0.0049	0.002	0.35	0.35	3	0.003	0.0049	0.35	0.35

	pK		p0
Estación			CVTS2=1.5
1	N/A	0.31	0.3
2	0.047	0.049	0.19	0.19
3	0.0049	0.0044	0.35	0.35

Conclusiones

En este trabajo se presenta una adecuación al método de Buzacott que permite calcular de manera analítica las propiedades de sistemas de líneas de espera M/G/1/K con arreglo en serie y los resultado se validaron mediante simulación.

El método tiene un grado de exactitud aceptable cuando se desea aproximar las propiedades de sistemas M/G/1/K con arreglo en serie, congestión uniforme en las estaciones y valores del coeficiente de variación moderado. El valor de p₀ calculado es similar al obtenido mediante simulación, en el caso de p_K la exactitud mejora a medida que el valor de aumenta.

Para el caso donde existe cuello de botella, los resultados indican que el método es efectivo para calcular L_S cuando la variación del cuello de botella es moderada (≤ 1.25); a medida que la variación en el cuello de botella se incrementa más allá de este valor, la aproximación de L_S se deteriora y por lo tanto los resultados deberán tomarse con reserva, en cambio, el valor de p_K del cuello de botella se obtiene con un alto grado de exactitud.

La adecuación propuesta en este trabajo permite calcular las propiedades de sistemas M/G/1/K con estaciones en serie. El grado de exactitud se ve afectado por, CVTS2 para valores bajos la exactitud de las ecuaciones mejora; por otro lado, el método tiene la ventaja de que su implementación en hoja de cálculo es rápida y sencilla.

El trabajo futuro puede encaminarse a estudiar la exactitud en sistemas con servidores múltiples, o bien, mejorar la plantilla en hoja de cálculo, por ejemplo para realizar cálculos dirigidos a optimización, sacando provecho de los complementos y macros disponibles o resolver instancias del problema de la localización del buffer (BAP), el cual hasta ahora se resuelve empleando técnicas heurísticas y metaheurísticas.

Este artículo se cita:

Citación estilo Chicago

Hernández-González, Salvador, Manuel Darío Hernández-Ripalda, Idalia Flores-De la Mota, José Antonio Vázquez-López. Propiedades de sistemas tipo M/G/1/K con estaciones en serie. Ingeniería Investigación y Tecnología, XVI, 03 (2015): 345-354.

Citación estilo ISO 690

Hernández-González S., Hernández-Ripalda M.D., Flores-De la Mota I., Vazquez-Lopez J.A. Propiedades de sistemas tipo M/G/1/K con estaciones en serie. Ingeniería Investigación y Tecnología, volumen XVI (número 3), julio-septiembre 2015: 345-354.