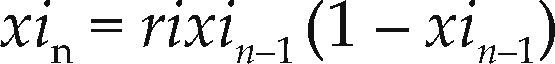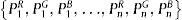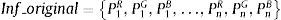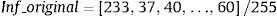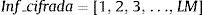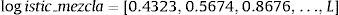En este artículo se propone un algoritmo de cifrado simétrico que toma como entrada la información original de longitud L y al codificarla genera el texto cifrado de longitud mayor LM. Se implementa el sistema discreto caótico mapa logístico para generar 3 órbitas diferentes: la primera se utiliza para aplicar una técnica de difusión con la finalidad de mezclar la información original, la segunda órbita se combina con la información mezclada y se incrementa la longitud de L hasta LM y con la tercer órbita se implementa la técnica de confusión. El algoritmo de cifrado se aplicó para codificar una imagen que después se recupera totalmente mediante las llaves que se utilizaron para cifrar y su respectivo algoritmo para descifrar. El algoritmo puede codificar cualquier información con solo dividirla en bloques de 8 bits, puede cumplir con los requerimientos de alto nivel de seguridad, utiliza 7 claves para cifrar y además proporciona buena velocidad de cifrado.
This article proposes a symmetric encryption algorithm that takes, as input value, the original information of length L, that when encoded, generates the ciphertext of greater length LM. A chaotic discrete system (logistic map) is implemented to generate 3 different orbits: the first is used for applying a diffusion technique in order to mix the original data, the second orbit is combined with the mixed information and increases the length of L to LM, and with the third orbit, the confusion technique is implemented. The encryption algorithm was applied to encode an image which is then totally recovered by the keys used to encrypt and his respective, decrypt algorithm. The algorithm can encode any information, just dividing into 8 bits, it can cover the requirements for high level security, it uses 7 keys to encrypt and provides good encryption speed.
Cada día se generan y avanzan constantemente las nuevas tecnologías y, con estas, también se incrementa la necesidad de utilizarlas para mantenerse en comunicación constante con diferentes personas ubicadas en cualquier lugar del mundo. Pero este crecimiento exponencial también genera un problema de seguridad muy importante, ya que cualquier información que se encuentre en un dispositivo conectado a la red de comunicaciones o que viaje a través de ella, puede ser susceptible a ser detectada o interceptada por alguna persona no autorizada que puede utilizarla indebidamente, ocasionando grandes pérdidas económicas a las empresas o problemas personales. Por tal razón, es indispensable utilizar algún mecanismo que ayude a resguardar la información de algún ataque malicioso, uno de los más utilizados es la criptografía que se encarga de escribir en secreto, proporcionando confidencialidad a la información mediante un método de cifrado (Oppliger, 2005). El caos es el comportamiento de un sistema dinámico que cambia de manera irregular en el tiempo (Hilborn, 1999). Muchos métodos o esquemas de comunicación segura se han desarrollado para cifrar información basándose en sistemas discretos caóticos (Hossam, Hamdy, & Osama, 2007; Pisarchik y Zanin, 2008; Pareek, Patidar, & Sud, 2005; Pisarchik y Flores, 2006; Ranjan y Saumitr, 2006). Esto se debe a la relación cercana que existe entre el caos y la criptografía; porque los sistemas caóticos tienen características como: ergodicidad, propiedades de mezcla, sensibilidad a los parámetros y las condiciones iniciales, que pueden considerarse análogos a las técnicas de difusión y confusión integrados en muchos sistemas criptográficos (Chong et al., 2011). Se desarrolló un sistema en el que se implementó una técnica que combina el comportamiento impredecible de la función logística con un código aritmético adaptativo, en el cual se usan la condición inicial y el parámetro del mapa caótico logístico como llave para cifrar y comprimir un archivo de texto, después se utiliza un canal inseguro para transmitir los datos codificados y un canal seguro para transmitir la llave (Ranjan y Saumitr, 2006). También se elaboró un algoritmo de llave simétrica para cifrar, mediante múltiples mapas caóticos unidimen- sionales y una llave externa de 128 bits, el texto plano se divide en 8 bits y se hacen grupos de bloques variables; después se cifra de forma secuencial usando los mapas caóticos de manera aleatoria (Pareek et al., 2005). También realizan un algoritmo basado en redes de mapas caóticos para cifrar imágenes de color mediante el mapa logístico; como llaves de cifrado se usan los parámetros, el tamaño de la imagen, un número de iteraciones y de ciclos (Pisarchik y Flores, 2006). Se desarrolló otro criptosistema para cifrar imágenes o videos, en él se normaliza el texto plano para utilizarlo como condición inicial de un mapa caótico (Pisarchik y Zanin, 2008). En otro estudio se creó un sistema para cifrar imágenes mediante un cifrado por bloques de 8 bits y una llave secreta externa alfanumérica o ASCII, de 256 bits de longitud. El cifrado de cada pixel de la imagen depende de la llave secreta, de la salida del mapa logístico y del pixel cifrado antes, lo que significa que al cifrar dos imágenes casi idénticas, una pequeña diferencia en la imagen puede ocasionar que el sistema genere imágenes cifradas muy diferentes (Hossam et al., 2007).
Pecora y Carroll, en 1990, demostraron que dos sistemas caóticos idénticos se pueden sincronizar mediante el acoplamiento de una señal común, es decir, cuando un sistema caótico maestro (emisor) se acopla a un sistema esclavo (receptor), los dos se sincronizan evolucionando en un atractor caótico donde el esclavo comienza a oscilar de igual forma que el maestro. Existen varias investigaciones que se basan en la sincronización caótica para codificar información, donde el emisor cifra un mensaje que luego transmite al receptor, que se encarga de recuperarlo regenerando la misma señal (Cuomo et al., 1993; Annovazzi, Donati, & Scire, 1996). También se desarrolló un esquema de cifrado donde se implementaron dos sistemas caóticos, uno discreto para aplicar la técnica de difusión y la sincronización caótica de dos osciladores acoplados Rössler para la confusión (Jiménez et al., 2012). Se han desarrollado otras aplicaciones de codificación para demostrar de forma experimental el proceso de sincronización de varios circuitos receptores, sin necesidad de acoplamiento alguno entre ellos (Núñez, 2012). En esta investigación se presenta un algoritmo de cifrado que utiliza las propiedades de los sistemas caóticos para codificar información, se toman en cuenta las recomendaciones de otras investigaciones de utilizar varias órbitas caóticas mezcladas o truncadas con la finalidad de que sea más difícil para un atacante detectarlas (Ranjan y Saumitr, 2006; Arroyo et al., 2008). A diferencia del algoritmo realizado por Pareek et al. (2005) el sistema que se propone no se basa en el cifrado utilizando solo las propiedades de confusión y difusión que proporcionan los sistemas caóticos. Es decir, para dar más seguridad se implementa la técnica de difusión sin depender solamente de la probabilidad de la función de distribución de la órbita derivada del sistema caótico, además, para evitar que la órbita pueda ser reconstruida se mezcla con la información y luego se aplica la técnica de confusión utilizando una órbita diferente. El algoritmo se puede utilizar para cifrar cualquier tipo de información a diferencia del desarrollado por Pareek et al. (2005) que solo codifica texto; otros cifran imágenes o video (Pisarchik y Zanin, 2008; Pisarchik y Flores, 2006). En el algoritmo se implementa el sistema discreto mapa logístico debido a que es uno de los más sencillos y al momento de ejecutar el programa proporciona mayor velocidad.
El resto de este documento se organiza de la siguiente manera: en la experimentación se explica el sistema caótico que se implementó y los algoritmos de cifrado y descifrado utilizados. En la sección de discusión y análisis se presentan los resultados obtenidos con el algoritmo al aplicarlo para codificar una imagen y finalmente, se muestran las conclusiones obtenidas en esta investigación.
ExperimentaciónDentro de los sistemas discretos caóticos uno de los más utilizados para codificar información es el mapa logístico, esto se debe a que es muy sencillo, rápido y sensible a las condiciones iniciales y a los parámetros. El mapa logístico se define en la ecuación 1.
donde la variable xin ∈ (0,1), i = 1, 2 y 3; n es el número de iteraciones y el parámetro ri ∈ [3.57, 4] para que la órbita sea caótica (Pisarchik y Flores, 2006).
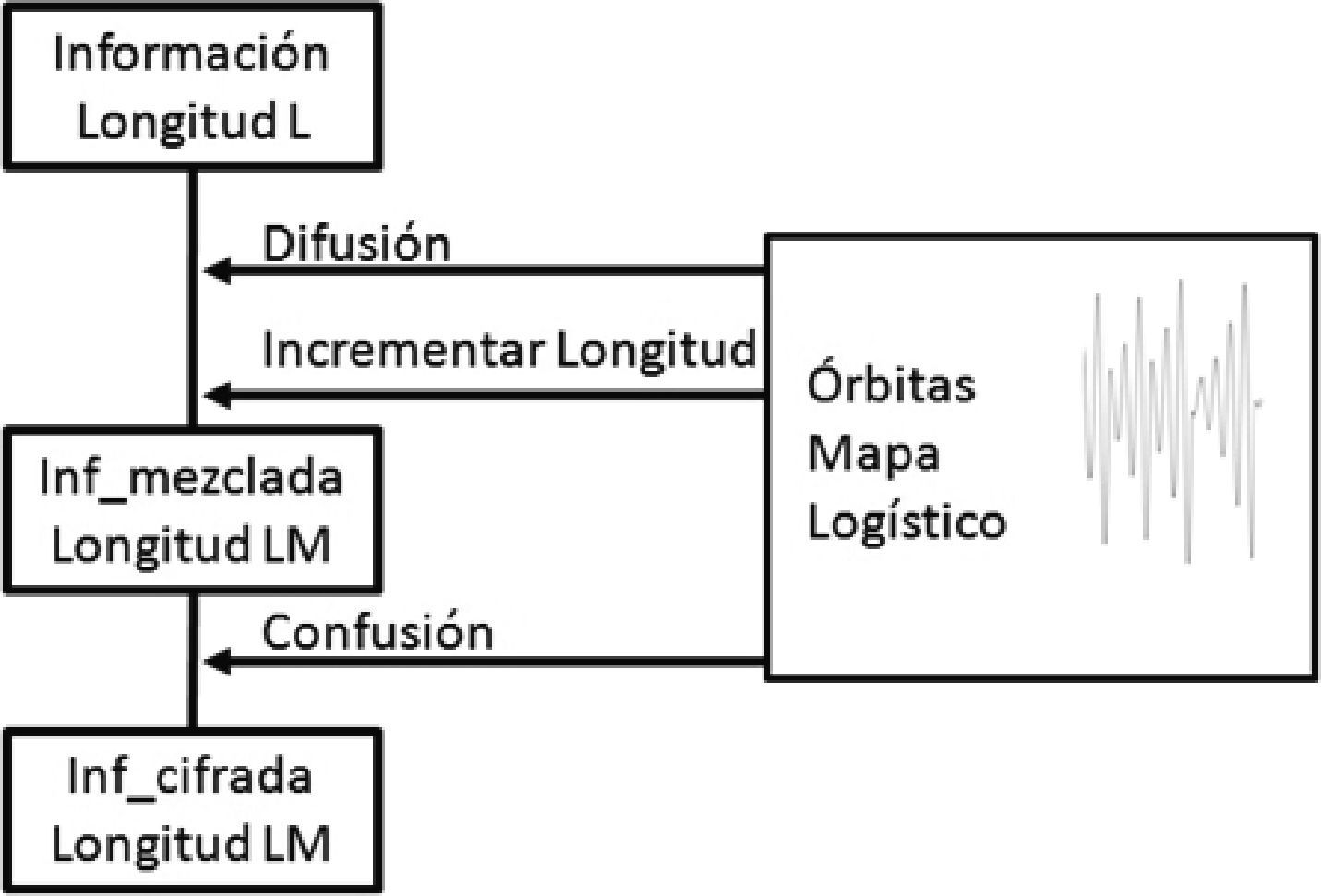
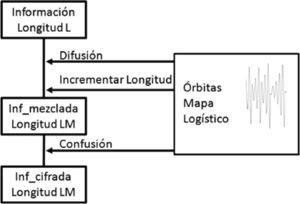
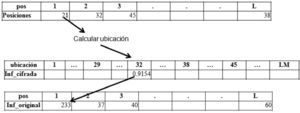
El mapa logístico se utiliza en este trabajo para codificar, implementando un algoritmo que toma inicialmente la información original de longitud L y obtiene como resultado la información cifrada de longitud LM. En el algoritmo se generan 3 órbitas caóticas, las cuales se obtienen con diferentes condiciones iniciales y parámetros que se utilizan como llaves de cifrado. La primer órbita se emplea para aplicar la técnica de difusión, es decir, se cambian de sitio elementos individuales de la información original, la segunda se usa para mezclarla con la información e incrementar la longitud de L a LM y la tercera se utiliza para aplicar la técnica de confusión que consiste en ocultar la relación entre la información original, la cifrada y la clave. En la figura 1 se muestra el proceso que se sigue para codificar la información.
AlgoritmosEnseguida se explica cómo funcionan los algoritmos en un caso práctico para cifrar imágenes, pero se puede codificar cualquier tipo de información.
Una imagen es una matriz de números que representa la intensidad del color de los píxeles y se compone de 3 bytes o subpixeles representados con un valor decimal entre 0 y 255, que corresponden a los colores R (rojo), G (verde) y B (azul), estos se presentan en un vector de la siguiente forma:
Nomenclatura utilizada en el algoritmo:
L = longitud del vector con la información original.
LM = longitud del vector con la información cifrada.
Llaves de cifrado:
r1 y x10 = parámetro y condición inicial usados para generar la órbita empleada en la técnica de difusión.
r2 y x20 = parámetro y condición inicial para generar la órbita de tamaño LM – L, la cual se emplea para incrementar la longitud de L a LM.
r3 y x30 = parámetro y condición inicial utilizados para generar la órbita que se implementa en la técnica de confusión.
ubicación inicial = posición inicial del vector información cifrada, entre 1 y LM.
Algoritmo para cifrar
Paso 1. Digitalizar la imagen para guardar cada uno de los subpixeles en el vector Inf_original, el cual es de longitud L=PnR+PnG+PnB.
Paso 2. Dividir cada subpixel que contiene el vector Inf_original entre 255, para obtener valores entre 0 y 1.
Paso 3. Generar el vector Inf_cifrada de longitud LM, (L debe ser menor que LM); donde se almacenará la información codificada.
Paso 4. Utilizar las llaves de cifrado r1 y x10 para resolver la ecuación 1 L veces y generar una órbita caótica de longitud L con valores entre 0 y 1 que se almacenarán en el vector logistic_mezcla.
Paso 5. Multiplicar cada valor del vector logistic_mezcla por LM, después redondear para obtener L valores entre 1 y LM, que servirán como posiciones para aplicar la técnica de difusión.
posiciones[i] = redondear(LM*logistic_mezcla[i])
posiciones= [pos1, pos2, pos3, pos4,…, L]
Aplicación de la técnica de difusión
Consiste en mezclar los valores del vector Inf_original en Inf_cifrada.
Paso 6. Asignar a ubicación el valor de la llave de cifrado ubicación_inicial.
ubicación = ubicación inicial
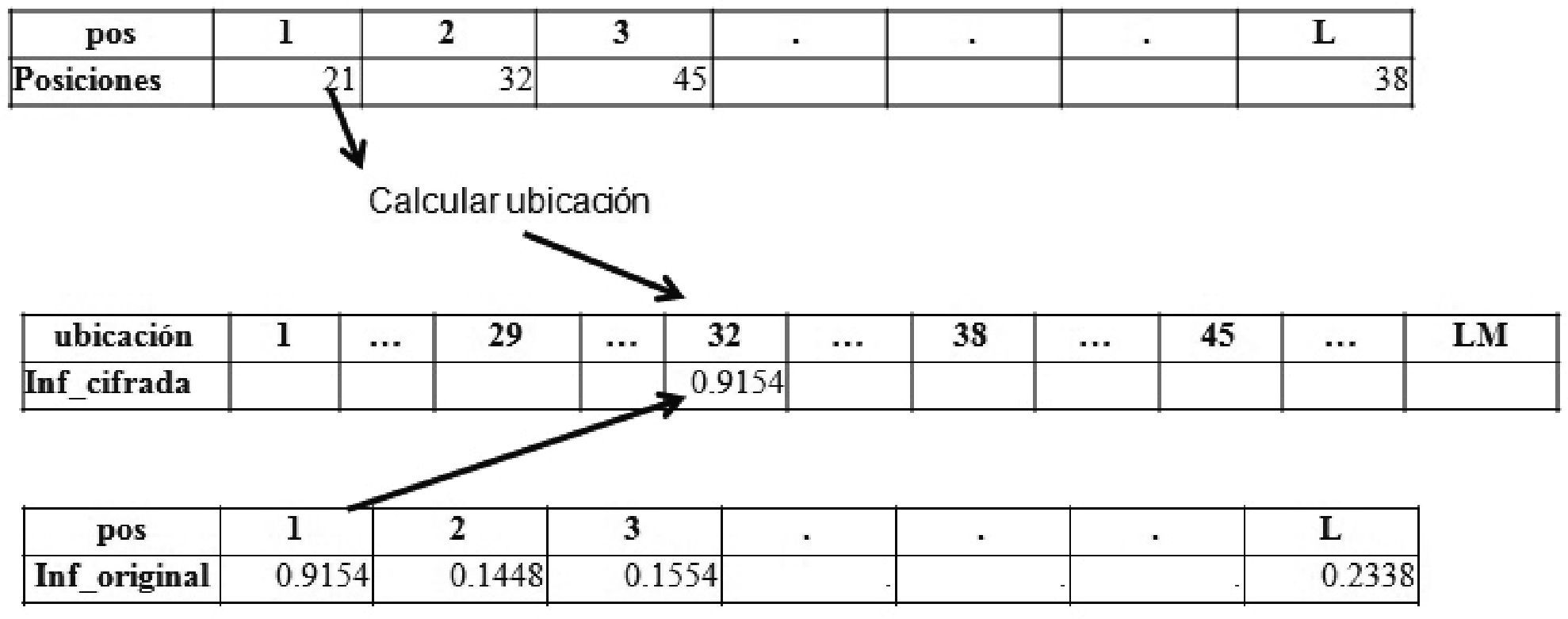
Paso 7. Calcular la ubicación donde se posicionará el valor de Inf_original en Inf_cifrada, también se utiliza el siguiente valor del vector posiciones.
ubicación = ubicación + (L MOD posiciones [pos])
Paso 8. Si ubicación ≤ LM, colocar en la ubicación del vector Inf_cifrada el valor de Inf_original, en caso de que la ubicación ya tenga algún valor, entonces se coloca en la siguiente posición vacía.
Paso 9. Si ubicación > LM excede la longitud del vector Inf_cifrada, por lo tanto, se le asigna ubicación = L MOD posiciones [pos], con la finalidad de volver a recorrer el vector Inf_cifrada; en la nueva ubicación se almacena el valor de Inf_original. En caso de ya haber acomodado un valor, entonces se coloca en la siguiente posición que este vacía.
Paso 10. Realizar los pasos 7 y (8 o 9) hasta acomodar cada valor del vector Inf_original en alguna ubicación de Inf_cifrada como se muestra en la figura 2.
Paso 11. En los pasos 7 a 10 se acomodan los L términos entre [0,1] del vector Inf_original en Inf_cifrada, pero como Inf_cifrada es de longitud LM, quedan LM – L ubicaciones vacías, para llenar, se resuelve la ecuación 1 con las llaves de cifrado r2 y x20, para generar otra órbita caótica con valores también entre 0 y 1, la cual se guarda en el vector denominado Relleno.
Paso 12. Tomar un valor del vector Relleno y colocarlo en la siguiente ubicación vacía de Inf_cifrada. Repetir este paso LM – L veces; como se observa en la figura 3.
Al finalizar este paso el vector Inf_cifrada contiene LM valores entre 0 y 1, que corresponden a la información original mezclada con una órbita caótica.
Aplicación de la técnica de confusión
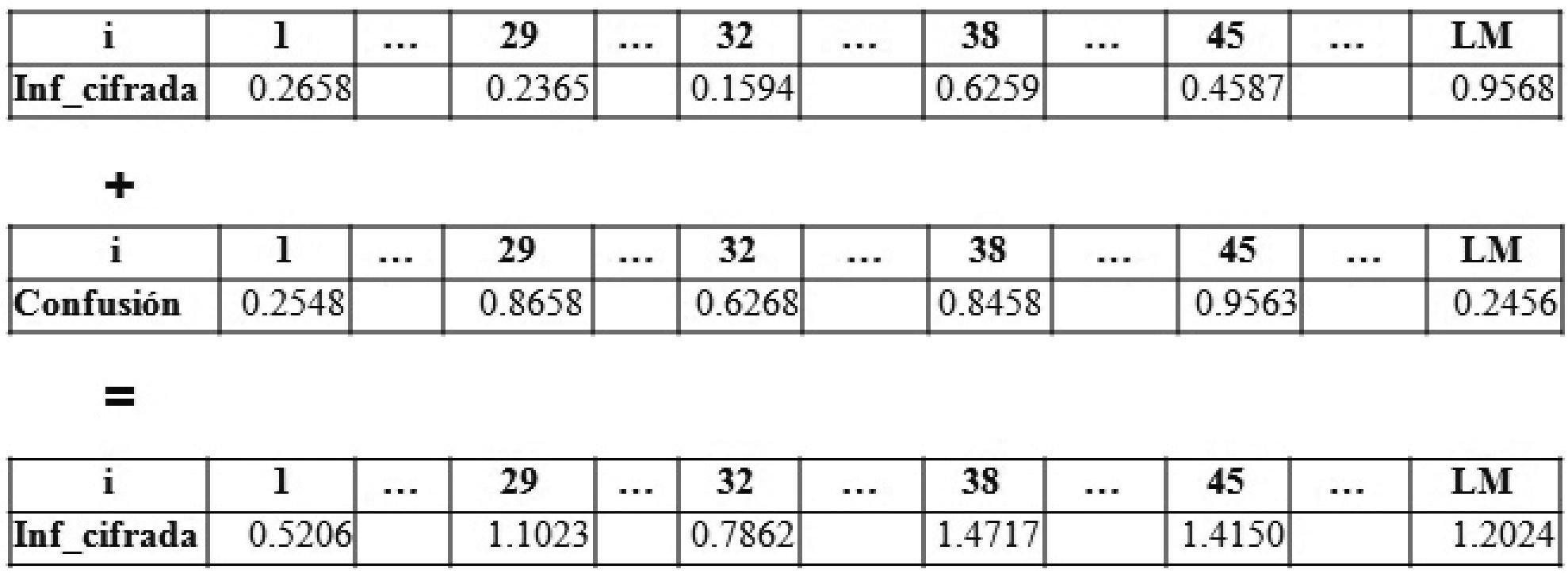
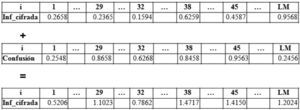
Paso 13. Utilizar las llaves r3 y x30 para resolver la ecuación 1 y obtener valores caóticos que se almacenen en el vector denominado Confusión. Repetir este paso LM veces.
Paso 14. Aplicar la técnica de confusión: sumando a cada valor del vector Inf_cifrada uno de Confusión, en forma ordenada, como se presenta en la figura 4.
Algoritmo para descifrarPara descifrar la información se necesitan el vector Inf_cifrada, el valor de LM y las llaves de cifrado.
Eliminar confusión
Paso 1. Utilizar las llaves r3 y x30 para generar el vector Confusión como se indica en el paso 13 del algoritmo para cifrar.
Paso 2. Restar a cada valor del vector Inf_cifrada el respectivo elemento del vector Confusión de manera ordenada.
Inf _cifrada[i] = Inf _cifrada[i] - Confusión[i]
Eliminar difusión
Paso 3. Utilizar las llaves r1 y x10 para generar el vector posiciones, realizando los pasos 4 y 5 del algoritmo para cifrar.
Paso 4. Asignar ubicación_inicial como en el paso 6 del algoritmo para cifrar.
Paso 5. Calcular ubicación como en el paso 7 del algoritmo para cifrar.
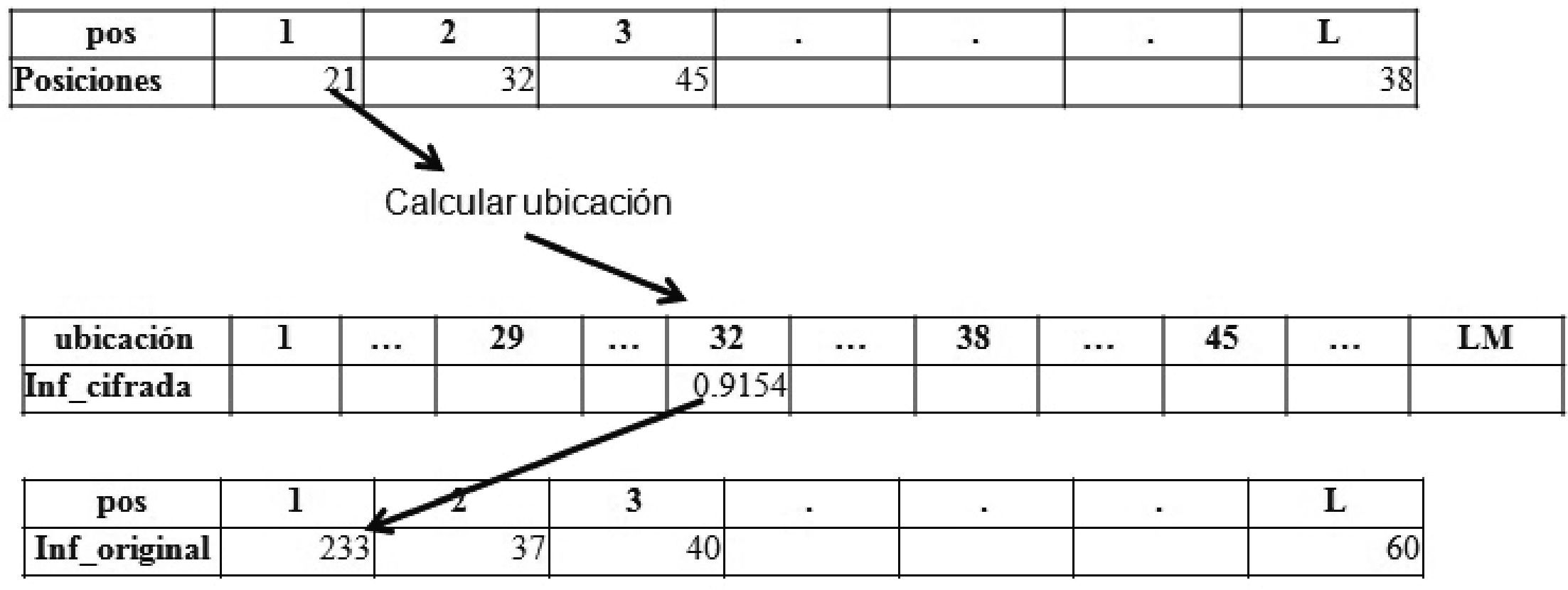
Paso 6. Si ubicación ≤ LM, se toma el valor almacenado en esta ubicación dentro del vector Inf_cifrada, en caso de no encontrarse, se toma el de la siguiente posición que sí contenga valor.
Paso 7. Si ubicación > LM, se asigna ubicación = L MOD posiciones [pos], para recorrer de nuevo el vector Inf_cifrada, enseguida se toma el valor de la ubicación en Inf_cifrada, en caso de no encontrarse, se toma el de la siguiente posición que sí contenga valor.
Paso 8. El valor que se obtuvo en el paso 6 ó 7, se multiplica por 255 y se redondea. Posteriormente se almacena el resultado en la siguiente posición vacía de Inf_original y se elimina el valor de la ubicación que se tomó en Inf_cifrada.
Inf_original[pos] = redondear (Inf_cifrada[ubicación]*255)
Paso 9. Repetir los pasos 5 a 8 L veces para eliminar la técnica de difusión y reacomodar todos los datos del vector Inf_original con los valores de los subpixeles entre 0 y 255, como se puede observar en la figura 5.
Discusión y análisis de los resultadosEn la figura 6 se exhibe la imagen original de longitud L y en la figura 7, la imagen cifrada usando el algoritmo propuesto en la sección de algoritmos para cifrar, la cual es de longitud LM = 2L.
En el sistema para cifrar desarrollado por Pisarchik y Zanin (2008), la longitud de la información codificada es igual que la original, lo cual ofrece una pista al atacante para descifrarla, por lo tanto, el algoritmo que proponemos da mayor seguridad porque la información cifrada que genera es más grande y ocasiona que sea más difícil para el atacante determinar el tamaño de la información original para poder descifrarla.
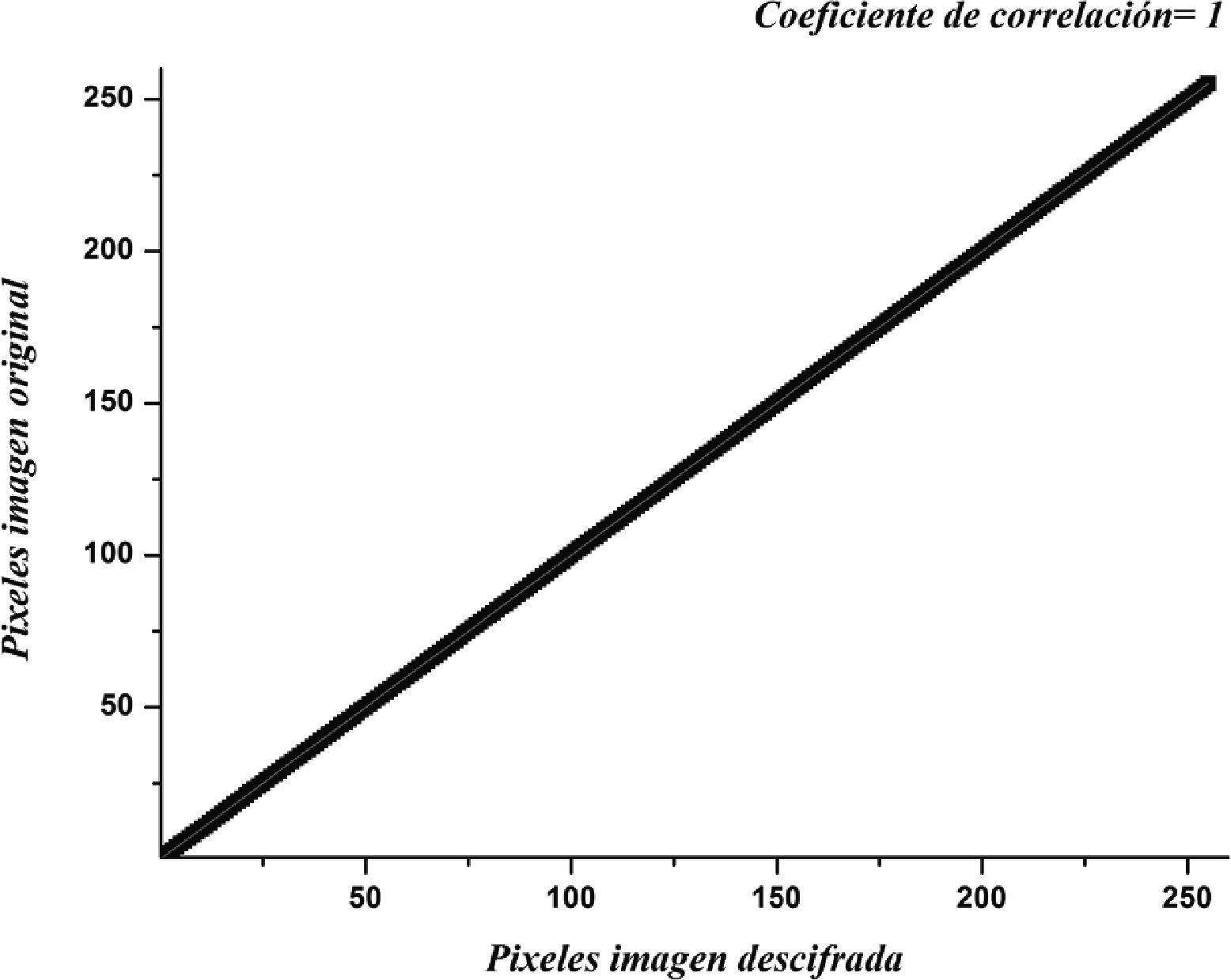
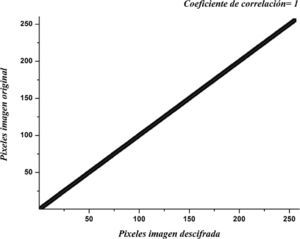
Análisis de correlaciónSe realizó un análisis de correlación donde se midió la asociación lineal entre la imagen original y la descifrada, con la finalidad de determinar si existe alguna pérdida de información al utilizar los algoritmos pro- puestos. El diagrama de correlación de la figura 8, arrojó un coeficiente de correlación de 1, esto demuestra que existe una fuerte asociación lineal entre las dos imágenes, por lo tanto, la imagen descifrada es idéntica a la imagen original.
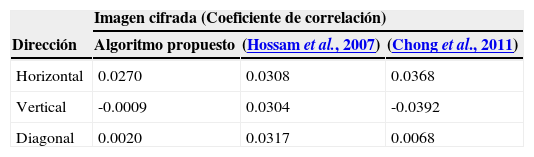
A fin de determinar el nivel de entropía o desorden de la imagen cifrada, se realizó un análisis sobre la correlación de 1000 puntos tomados de forma aleatoria en la imagen cifrada. En la tabla 1, se muestra el resultado de la correlación horizontal, vertical y diagonal de dos pixeles adyacentes.
Comparación del coeficiente de correlación del algoritmo propuesto vs otras referencias
| Imagen cifrada (Coeficiente de correlación) | |||
|---|---|---|---|
| Dirección | Algoritmo propuesto | (Hossam et al., 2007) | (Chong et al., 2011) |
| Horizontal | 0.0270 | 0.0308 | 0.0368 |
| Vertical | -0.0009 | 0.0304 | -0.0392 |
| Diagonal | 0.0020 | 0.0317 | 0.0068 |
En la tabla 1, se puede observar que el algoritmo propuesto genera un coeficiente de correlación más cercano a 0 respecto a las otras dos referencias; lo cual indica que es más difícil para un atacante determinar algún orden en la imagen cifrada.
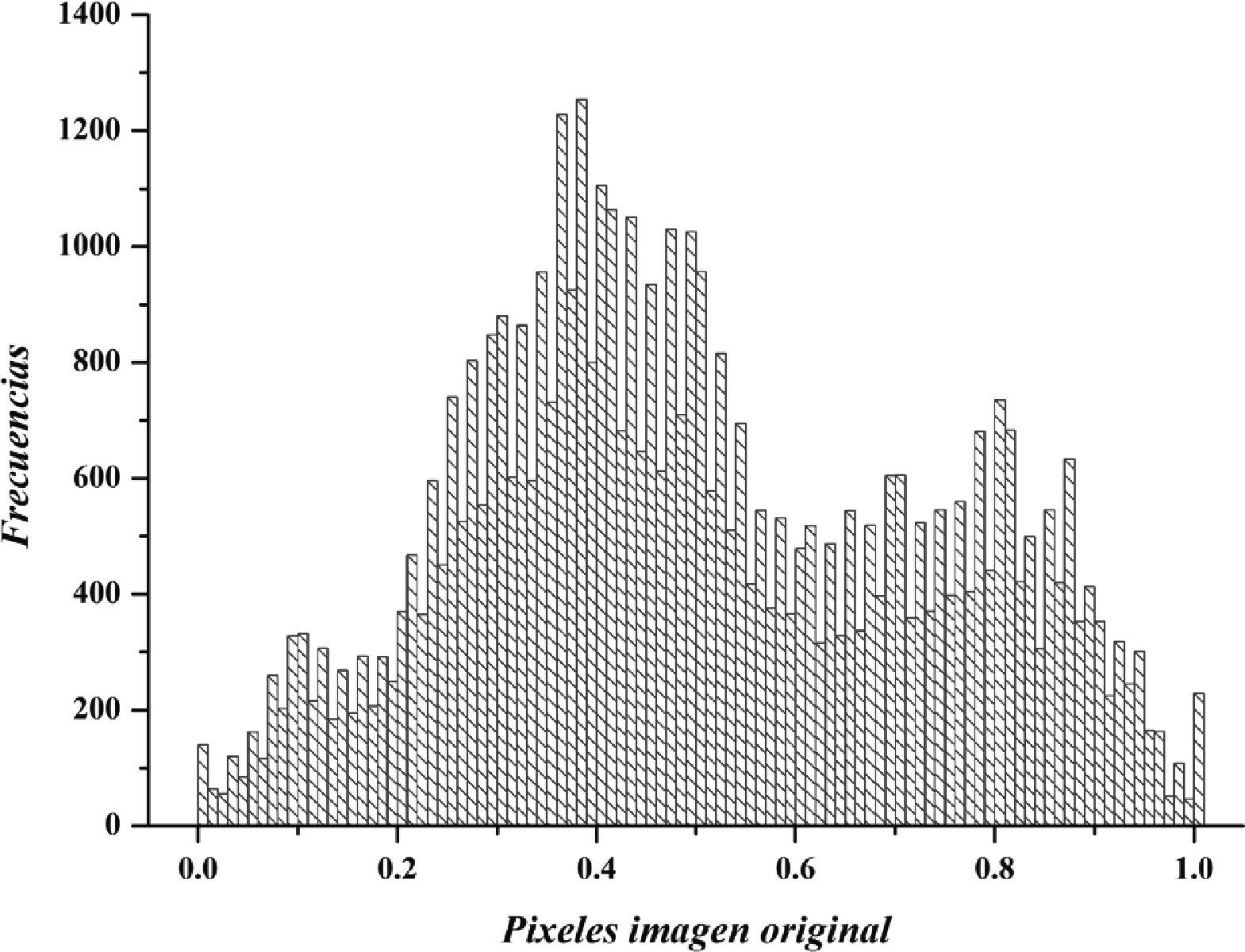
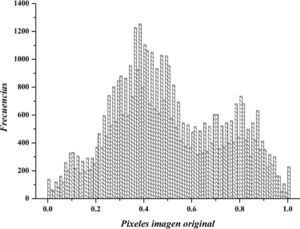
HistogramasLos histogramas permiten representar de forma gráfica cómo se distribuyen los pixeles en una imagen de acuerdo con la intensidad de sus colores. En la figura 9 se muestra el histograma de la imagen original, que exhibe en el eje horizontal los valores de los pixeles de la imagen en el rango de 0 a 1, las barras más altas indican los colores que se repiten con mayor frecuencia.
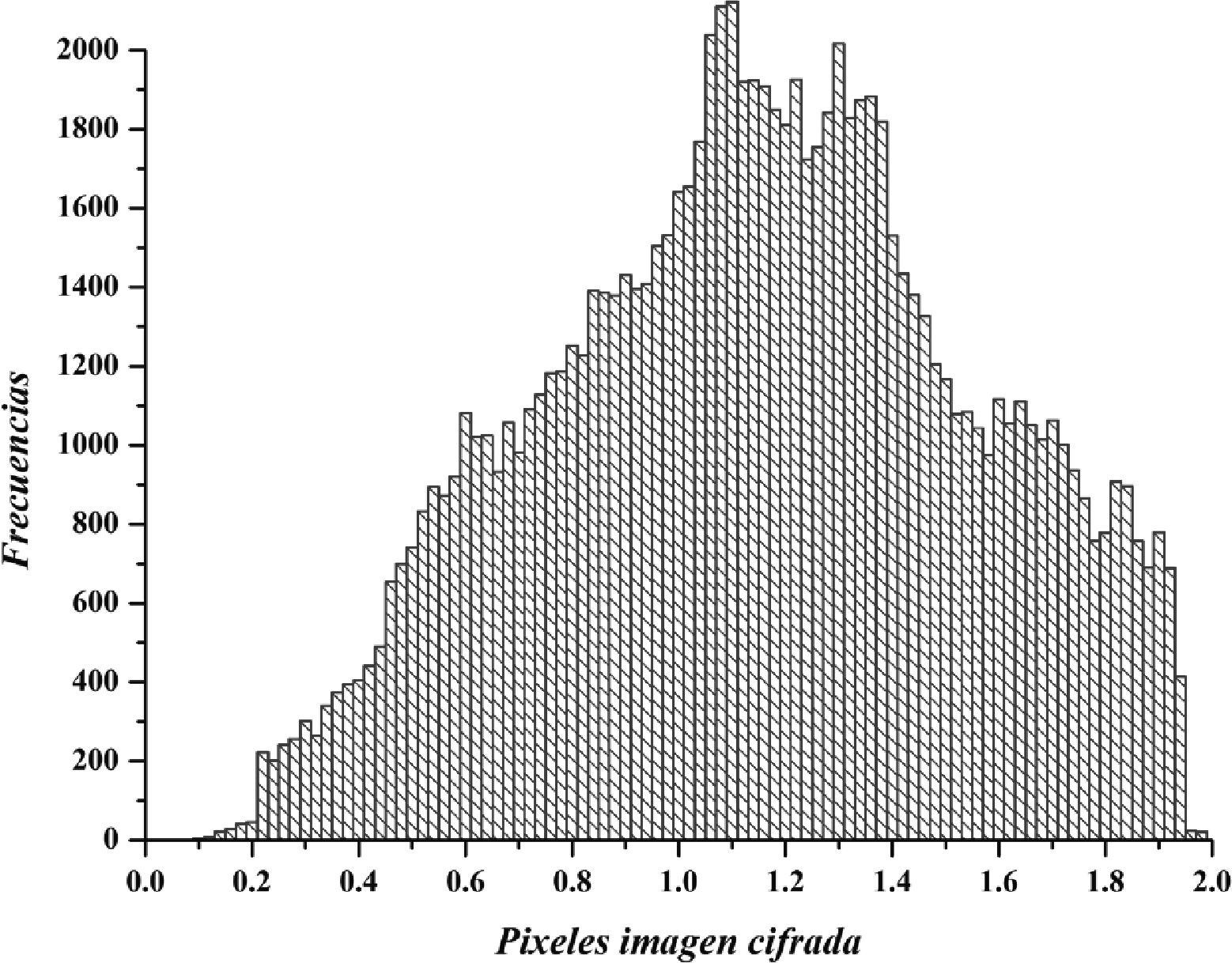
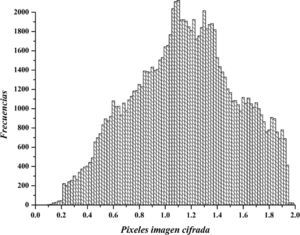
La figura 10 exhibe el histograma de la imagen cifrada, con el algoritmo propuesto en la parte de algoritmo para cifrar. En el eje horizontal muestra los valores de los pixeles ya cifrados entre el rango de 0 a 2, a diferencia del histograma de la imagen plana figura 9 que son entre 0 y 1.
Al observar los histogramas de las figuras 9 y 10, se puede determinar que tienen diferente distribución de las frecuencias de la imagen original respecto a la imagen cifrada. Además en el eje horizontal los rangos son diferentes. Lo cual ocasiona mayor dificultad para un atacante al momento de analizar las frecuencias, y por lo tanto descifrar.
ConclusionesEl algoritmo propuesto emplea el mapa logístico para generar 3 diferentes órbitas caóticas, lo cual aumenta la seguridad porque se usan 7 claves, una condición inicial y un parámetro por cada órbita y además se asigna una ubicación_inicial, con la finalidad de que exista menor probabilidad de que un atacante pueda descifrar la información; el sistema es más robusto porque mezcla y trunca las órbitas. Es recomendable que la longitud LM ≥ 2L para que se pueda ocultar fácilmente la información original con la órbita caótica. Los algoritmos utilizan su propia técnica para ocultar las redundancias entre el texto plano y disimularlas por todo el texto cifrado. Además los elementos de la información original se sustituyen por otros diferentes y de esta forma no depende directamente de la probabilidad de confusión y difusión de la órbita derivada del sistema caótico.
El sistema propuesto no depende del bloque de información cifrado previamente (Pareek et al., 2005; Hossam et al., 2007); lo cual significa que si existe un error al cifrar inicialmente la información, ocasionará que al descifrar no se recupere totalmente. Otra ventaja del algoritmo es que para cifrar/descifrar solo se necesitan las claves a diferencia del sistema Pareek et al. (2005) que está gobernado por la información de tablas dinámicas, las cuales deben actualizarse durante el proceso de cifrado y descifrado. El algoritmo propuesto puede cifrar cualquier tipo de información, no solo texto como el desarrollado por Pareek et al. (2005) o el que propusieron Pisarchik y Zanin (2008) y Pisarchik y Flores (2006) que codifica imágenes o video.
El algoritmo desarrollado en esta investigación ofrece confidencialidad porque solo se puede recuperar la información con las respectivas claves de cifrado que se utilizaron para generar las diferentes órbitas caóticas implementadas en el sistema. El mapa logístico es muy sencillo y por lo tanto ofrece buena velocidad; además se pueden implementar diferentes sistemas discretos para cada órbita.
El trabajo descrito en este artículo fue apoyado por el Programa de mejoramiento del profesorado, mediante el proyecto (PROMEP/103.5/12/8149).
Este artículo se cita:
Citación estilo Chicago
Jiménez-Rodríguez, Maricela, Octavio Flores-Siordia, María Guadalupe González-Novoa. Sistema para codificar información implementando varias órbitas caóticas. Ingeniería Investigación y Tecnología, XVI, 03 (2015): 335-343.
Citación estilo ISO 690
Jiménez-Rodríguez M., Flores-Siordia O., González-Novoa M.G. Sistema para codificar información implementando varias órbitas caoticas. Ingeniería Investigación y Tecnología, volumen XVI (número 3), julio-septiembre 2015: 335-343.
Maricela Jiménez-Rodríguez. Graduada por la Universidad de Guadalajara como ingeniera en computación, obtuvo el título de maestría en computación aplicada en 2003 por la Universidad Central ‘Martha Abreu’ de Las Villas Cuba. En 2005 obtuvo la certificación en (Cisco Certified Network Associate CCNA). Adquirió el grado de doctora en ciencia y tecnología por el Centro Universitario de los Lagos, de la UdeG en 2012. Actualmente es profesora del Departamento de Ciencias Tecnológicas en el Centro Universitario de la Ciénega y realiza investigación en las áreas de matemáticas aplicadas en el desarrollo de sistemas y en desarrollo de sistemas de seguridad y comunicaciones.
Octavio Flores-Siordia. Es ingeniero químico por la Facultad de Ciencias Químicas de la Universidad de Guadalajara, obtuvo el grado de maestro en ciencias de la ingeniería química, realizó el diplomado en enseñanza de las matemáticas, estudió el doctorado en el Instituto Mexicano de Estudios Pedagógicos obteniendo el grado en metodología de la enseñanza. Ha sido profesor del Departamento de Ciencias Básicas del Centro Universitario de la Ciénega impartiendo cursos del área de matemáticas, actualmente se encuentra realizando investigación en el área de matemáticas aplicadas en el desarrollo de sistemas.
María Guadalupe González-Novoa. Obtuvo el título de ingeniero en computación en 2001, realizó la maestría en computación aplicada con especialidad en bases de datos en junio de 2005 por la Universidad de Guadalajara. Actualmente es profesora en el departamento de Ciencias Básicas del Centro Universitario de la Ciénega y realiza investigación en el área de desarrollo de sistemas de seguridad y comunicaciones.