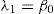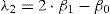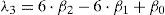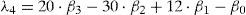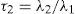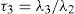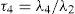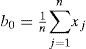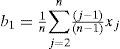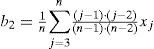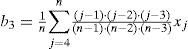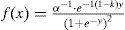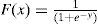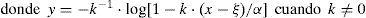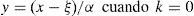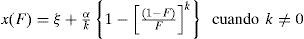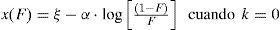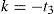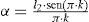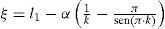Contraste de la distribución Logística Generalizada en 31 registros históricos de eventos máximos anuales

Resumen

La distribución Logística Generalizada es la más reciente cuya aplicación ha sido establecida bajo precepto, por ello es importante su contraste con las otras dos que le precedieron, la Log-Pearson tipo III en USA y la General de Valores Extremos en Inglaterra. Se comenzó por destacar la importancia en la estimación de las crecientes de diseño, de los análisis probabilísticos y de las distribuciones citadas. Para la más reciente se describe con detalle la estimación de sus tres parámetros de ajuste por el método de momentos L. Además se propone su ajuste por minimización del error cuadrático medio a través optimización numérica. Los resultados de la aplicación de esta distribución en 31 registros de eventos máximos anuales, con base en los dos métodos citados, se contrastan con los óptimos obtenidos previamente con los modelos General de Valores Extremos y Log-Pearson tipo III. Se concluye que la distribución Logística Generalizada (LOG) es una opción conveniente para registros que muestran grandes cocientes L de curtosis y que en general sus resultados conducen a las predicciones más severas en los periodos de retorno extremos, en registros con valores dispersos.

Abstract

The Generalized Logistic distribution is the most recent whose application has been established as precept. Thus, comparing it with the other two that preceded it: the Log-Pearson type III in USA and the General Extreme Values in England, is of high importance. In this work, the relevance of probabilistic analysis and the above mentioned distributions in design flood estimation is pointed out. For the most recent, a fitting method of L-moments is described in detail for the estimation of its three parameters, also a fitting by minimizing the quadratic mean error through numerical optimization is proposed. The results of the application of this distribution to 31 records, using both cited methods, are compared with the optimal ones obtained using the General Extreme Values and Log-Pearson type III models. It is concluded that the Generalized Logistic distribution is a good choice for records with high L-kurtosis quotients and its predictions in general are more extreme in high return periods when applied to records with outliers.

Introducción

Las estimaciones fundamentales de los hidrólogos están relacionadas con el escurrimiento en dos escalas de tiempo, la mensual y la instantánea. En el primer caso, se buscan los volúmenes escurridos disponibles para el diseño hidrológico de embalses de aprovechamiento. En el segundo caso, se intenta obtener las crecientes que generan la cuenca estudiada, asociadas éstas a diversas probabilidades de excedencia, cuyo recíproco es el periodo de retorno o intervalo promedio de recurrencia en años. Las crecientes son básicas en el diseño y la revisión hidrológica de todo tipo de obras hidráulicas de protección como son: presas, diques, rectificaciones y encauzamientos; además permiten el dimensionamiento de las obras de cruce (alcantarillas y puentes).

La estimación de crecientes de diseño más confiable es la que está basada en los registros de gastos máximos anuales, existiendo actualmente dos enfoques de procesamiento, el local y el regional. El tratamiento local de los datos disponibles se aplica donde el registro es amplio (> 50 años), si es menor, pero cuenta con más de 25 años, los resultados de procesamiento local se deben ratificar mediante comparación con cuencas vecinas (WRC, 1977). Cuando el registro tiene menos de 25 años las estimaciones de crecientes deben estar basadas en el enfoque regional.

La estimación probabilística de crecientes ha evolucionado desde sus inicios en 1930 y 1941 con los estudios de Hazen y Gumbel (Maidment, 1993), hasta el uso de modelos probabilísticos físicamente basados. Una etapa importante aconteció a mediados de los años sesenta, cuando el Subcomité de Hidrología del US Water Resources Council, contrastó seis distribuciones comúnmente empleadas en esa época y concluyó que el modelo Log-Pearson tipo III (LP3) era el más conveniente y lo recomendó para uso general en las agencias de gobierno (Ponce, 1989). En un estudio similar en Inglaterra se determinó que las distribuciones de tres parámetros de ajuste (General de Valores Extremos, Pearson tipo III y LP3) conducían a mejores ajustes que los modelos de dos parámetros (NERC, 1975).

La propuesta de uso generalizado de la distribución general de valores extremos (GVE) incluye como caso especial a la distribución Gumbel, la cual ya era conocida y utilizada; además define a los modelos Log-Gumbel y Weibull, que son curvas en el papel de probabilidad Gumbel-Powell, el primero con concavidad hacia arriba y el segundo hacia abajo. La nueva versión del Flood Studies Report (NERC, 1975) se llama Flood Estimation Handbook y recomienda para los análisis de frecuencia de crecientes a la distribución Logística Generalizada, ajustada mediante el método de los momentos L, que es más confiable y consistente en registros sesgados (Mansell, 2003; Shaw et al., 2011).

Ya se han realizado contrastes de las distribuciones GVE y LP3 (Campos, 2001 y 2002a, b) en 31 registros históricos de eventos máximos anuales con amplitudes variando de 16 a 113 años. Por tanto, el objetivo de este estudio fue aplicar la distribución Logística Generalizada (LOG) a tales registros históricos mediante dos métodos de ajuste, el de momentos L y el de optimización numérica y confrontar sus resultados con los óptimos obtenidos para los modelos citados, finalmente formular conclusiones relativas a esta última distribución.

Desarrollo

Momentos y cocientes L muestrales

Son un sistema alternativo para describir las formas de las funciones de distribución de probabilidades (FDP). Históricamente aparecen como modificaciones de los momentos de probabilidad pesada (MPP) desarrollados por Greenwood et al. (1979). Los momentos L son combinaciones lineales de los MPP, de manera que (Hosking y Wallis, 1997):

Además se definen los cocientes (τ) de momentos L, comenzando con L-Cv que es análogo al coeficiente de variación y después los de similitud con los coeficientes de asimetría (Cs) y de curtosis (Ck):

En una muestra de tamaño n, con sus elementos arreglados en orden ascendente (x₁ ≤ x₂ ≤ … ≤ x_n) los estimadores insesgados de β_r son:

Los estimadores muestrales de λ_r, serán l_r estando definidos por las ecuaciones 1 a 4 y los de los cocientes serán t₂, t₃ y t₄, según las ecuaciones 5 a 7.

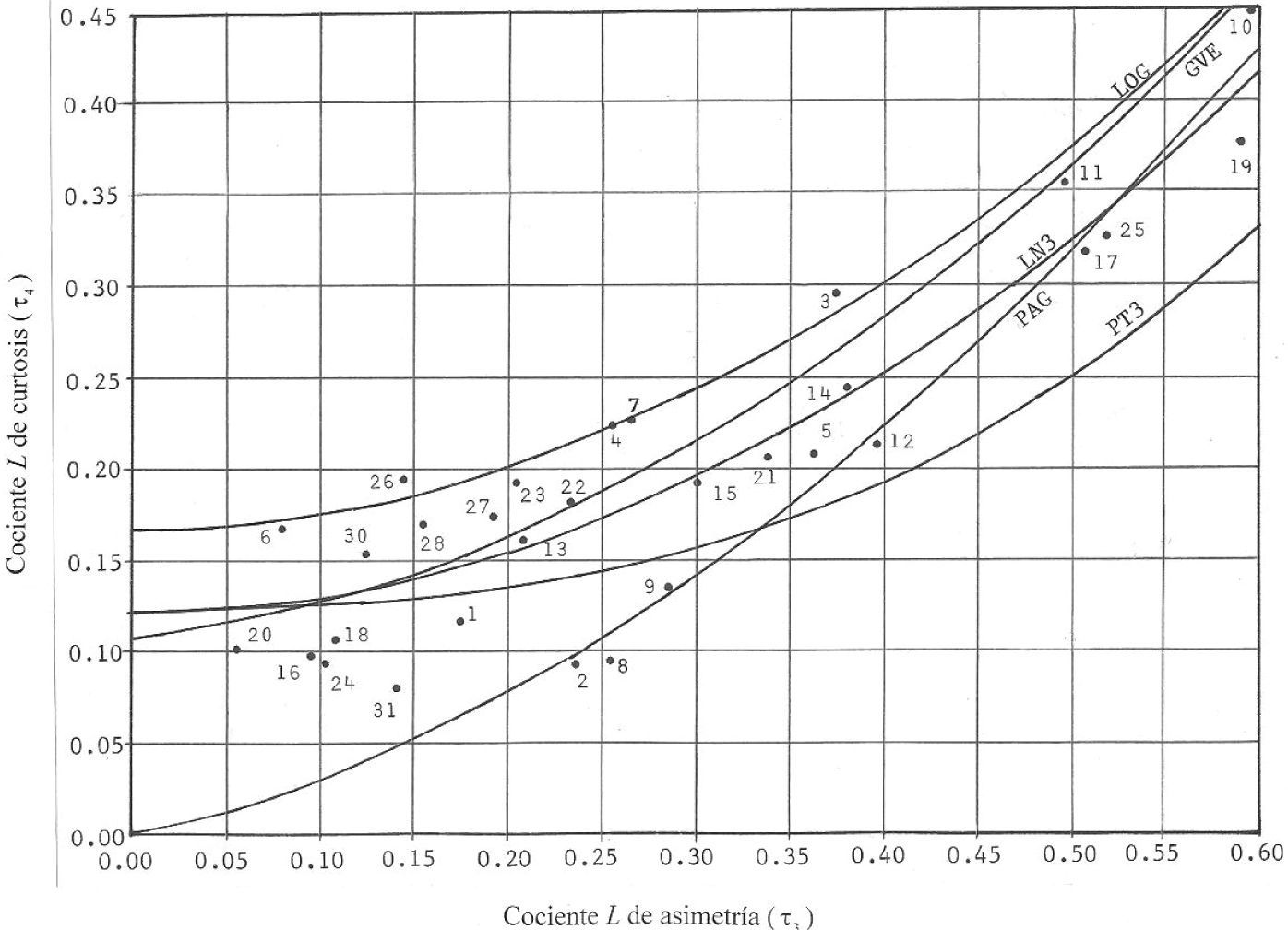
Diagrama de momentos L

Hosking y Wallis (1997) establecieron la relación que guardan los cocientes de momentos L de asimetría y curtosis en cinco distribuciones de probabilidad (figura 1): logística generalizada (LOG), general de valores extremos (GVE), Log-Normal de 3 parámetros (LN3), Pearson tipo III (PT3) y pareto generalizada (PAG).

Figura 1.

Ubicación de los 31 registros históricos procesados en el diagrama de cocientes de momentos L

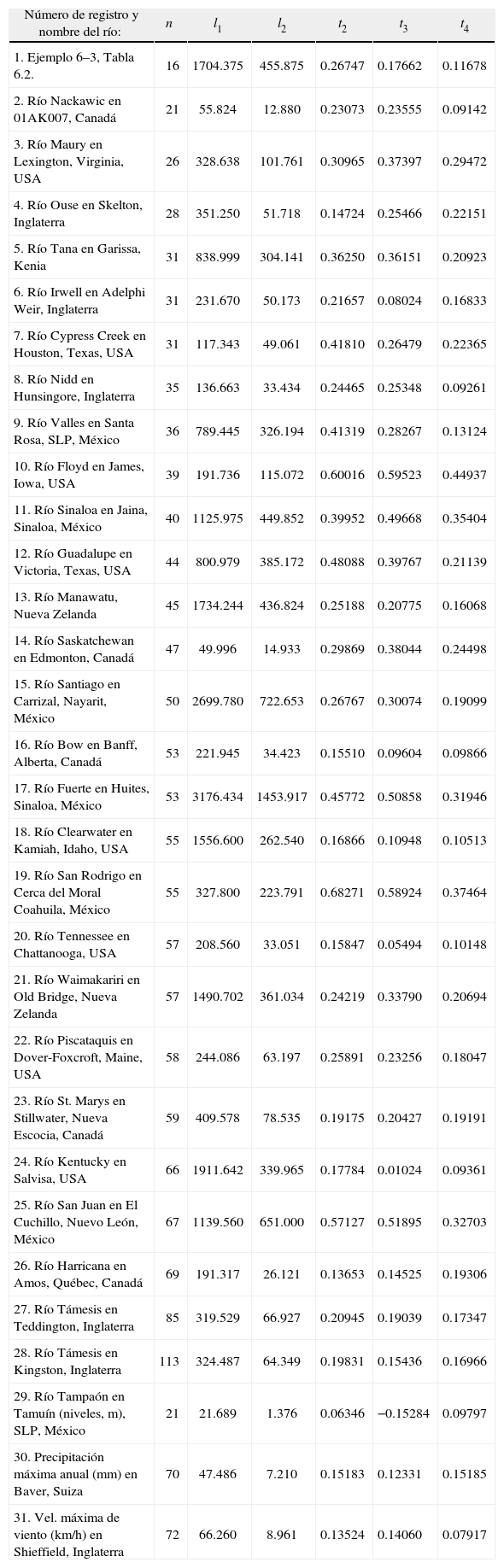
Registros procesados

Las referencias de procedencia de los 31 registros históricos que se usarán se pueden consultar en Campos (2001, 2002a, b), así como sus parámetros estadísticos insesgados. En cambio, en el cuadro 1 se presentan los valores de sus momentos y cocientes L, según las ecuaciones 1 a 7. Los valores de los cocientes τ₃ y τ₄ de cada registro se llevaron al diagrama de momentos L para dibujar puntos que por su cercanía a una cierta curva, definen la distribución de probabilidades más conveniente (figura 1).

Cuadro 1.

Momentos y cocientes de momentos L de los 31 registros históricos procesados

Número de registro y nombre del río:	n	l1	l2	t2	t3	t4
1. Ejemplo 6–3, Tabla 6.2.	16	1704.375	455.875	0.26747	0.17662	0.11678
2. Río Nackawic en 01AK007, Canadá	21	55.824	12.880	0.23073	0.23555	0.09142
3. Río Maury en Lexington, Virginia, USA	26	328.638	101.761	0.30965	0.37397	0.29472
4. Río Ouse en Skelton, Inglaterra	28	351.250	51.718	0.14724	0.25466	0.22151
5. Río Tana en Garissa, Kenia	31	838.999	304.141	0.36250	0.36151	0.20923
6. Río Irwell en Adelphi Weir, Inglaterra	31	231.670	50.173	0.21657	0.08024	0.16833
7. Río Cypress Creek en Houston, Texas, USA	31	117.343	49.061	0.41810	0.26479	0.22365
8. Río Nidd en Hunsingore, Inglaterra	35	136.663	33.434	0.24465	0.25348	0.09261
9. Río Valles en Santa Rosa, SLP, México	36	789.445	326.194	0.41319	0.28267	0.13124
10. Río Floyd en James, Iowa, USA	39	191.736	115.072	0.60016	0.59523	0.44937
11. Río Sinaloa en Jaina, Sinaloa, México	40	1125.975	449.852	0.39952	0.49668	0.35404
12. Río Guadalupe en Victoria, Texas, USA	44	800.979	385.172	0.48088	0.39767	0.21139
13. Río Manawatu, Nueva Zelanda	45	1734.244	436.824	0.25188	0.20775	0.16068
14. Río Saskatchewan en Edmonton, Canadá	47	49.996	14.933	0.29869	0.38044	0.24498
15. Río Santiago en Carrizal, Nayarit, México	50	2699.780	722.653	0.26767	0.30074	0.19099
16. Río Bow en Banff, Alberta, Canadá	53	221.945	34.423	0.15510	0.09604	0.09866
17. Río Fuerte en Huites, Sinaloa, México	53	3176.434	1453.917	0.45772	0.50858	0.31946
18. Río Clearwater en Kamiah, Idaho, USA	55	1556.600	262.540	0.16866	0.10948	0.10513
19. Río San Rodrigo en Cerca del Moral Coahuila, México	55	327.800	223.791	0.68271	0.58924	0.37464
20. Río Tennessee en Chattanooga, USA	57	208.560	33.051	0.15847	0.05494	0.10148
21. Río Waimakariri en Old Bridge, Nueva Zelanda	57	1490.702	361.034	0.24219	0.33790	0.20694
22. Río Piscataquis en Dover-Foxcroft, Maine, USA	58	244.086	63.197	0.25891	0.23256	0.18047
23. Río St. Marys en Stillwater, Nueva Escocia, Canadá	59	409.578	78.535	0.19175	0.20427	0.19191
24. Río Kentucky en Salvisa, USA	66	1911.642	339.965	0.17784	0.01024	0.09361
25. Río San Juan en El Cuchillo, Nuevo León, México	67	1139.560	651.000	0.57127	0.51895	0.32703
26. Río Harricana en Amos, Québec, Canadá	69	191.317	26.121	0.13653	0.14525	0.19306
27. Río Támesis en Teddington, Inglaterra	85	319.529	66.927	0.20945	0.19039	0.17347
28. Río Támesis en Kingston, Inglaterra	113	324.487	64.349	0.19831	0.15436	0.16966
29. Río Tampaón en Tamuín (niveles, m), SLP, México	21	21.689	1.376	0.06346	−0.15284	0.09797
30. Precipitación máxima anual (mm) en Baver, Suiza	70	47.486	7.210	0.15183	0.12331	0.15185
31. Vel. máxima de viento (km/h) en Shieffield, Inglaterra	72	66.260	8.961	0.13524	0.14060	0.07917

Estos resultados están en la columna 2 del cuadro 2 y lógicamente sólo pueden ser los modelos: LOG, GVE, LN3, PT3 y PAG. Además se observa que únicamente los registros números 3, 4, 6, 7, 10, 23, 26 y 28 se aproximan a la curva de la distribución LOG y que los registros números 2, 8, 9 y 31 son los más alejados de ella.

Cuadro 2.

Resultados del mejor método de ajuste (<EEA) y de la optimización numérica para las distribuciones GVE, Log-Pearson tipo III y Logística Generalizada en los 31 registros históricos procesados

			Parámetros o variables de ajuste						Periodos de retorno en años
NR	DA	MA	u ó Ym	α ó Sy	k ó gc	EEA (m^3/s)	(etapas) No.eval.	10	25	50	100	500	1 000	10 000
1		MOL	1354.333	651.656	−0.01045	152.8	−	2838	3474	3950	4425	5538	6022	7654
1		OPN	1314.343	710.061	−0.04934	118.7	(6) 77	3004	3775	4370	4981	6477	7158	9593
1		MML	7.33750	0.47700	−0.16191	164.1	−	2805	3448	3927	4406	5532	6026	7715
1		OPN	7.33095	0.54632	−0.05204	115.8	(5) 59	3063	3934	4620	5333	7116	7943	10979
1	PT3	MOL	1573.953	432.840	−0.17662	187.1	−	2736	3419	3996	4641	6466	7423	11590
1		OPN	1585.836	495.145	−0.22334	127.0	(9) 96	2990	3877	4656	5556	8248	9737	16711
2		MOL	44.431	16.805	−0.10008	5.0	−	87	108	125	143	189	212	299
2		OPN	44.284	18.678	−0.11427	4.0	(5) 64	92	116	136	157	213	241	349
2		MML	3.94563	0.39843	0.25293	5.0	−	87	107	124	141	184	205	285
2		OPN	3.95179	0.44325	0.03372	4.0	(2) 32	92	114	130	148	190	209	280
2	PAG	MOL	50.968	11.736	−0.23555	5.8	−	85	107	126	148	216	255	437
2		OPN	51.399	13.045	−0.29079	4.3	(3) 29	92	120	146	177	280	341	660
3		MOL	228.506	102.689	−0.29557	73.8	−	557	775	982	1234	2061	2557	5166
3		OPN	222.626	103.217	−0.48721	34.4	(5) 35	645	1017	1429	2003	4384	6142	18836
3		MMM	5.64795	0.53160	0.60848	69.3	−	563	733	870	1017	1401	1587	2306
3		OPN	5.68859	0.58065	0.28644	34.1	(12) 123	631	863	1063	1289	1931	2267	3707
3	LOG	MOL	270.220	79.914	−0.37397	77.9	−	543	758	973	1248	2238	2885	6750
3		OPN	256.736	73.615	−0.65487	31.4	(14) 130	618	1045	1582	2423	6717	10499	46943
4		MOL	304.603	65.360	−0.12830	21.2	−	475	563	636	714	926	1031	1456
4		OPN	302.703	70.727	−0.18816	15.1	(3) 36	501	613	710	820	1137	1306	2053
4		MMM	5.82925	0.25088	0.98022	21.1	−	471	535	582	628	737	784	946
4		OPN	5.83748	0.28246	0.16921	15.1	(3) 38	495	571	628	685	820	880	1089
4	LOG	MOL	330.268	46.375	−0.25466	23.1	−	467	557	639	735	1034	1205	2049
4		OPN	329.236	51.012	−0.33106	14.7	(2) 25	494	616	734	881	1380	1692	3426
5		MMV	524.470	277.582	−0.43927	104.4	−	1591	2468	3400	4660	9576	13026	36002
5		OPN	530.981	307.901	−0.42979	83.1	(7) 85	1699	2647	3647	4988	10165	13760	37329
5		MML	6.53361	0.62233	0.48521	140.6	–	1564	2252	2888	3646	6003	7343	13795
5		OPN	6.55752	0.66673	0.12861	85.4	(12) 128	1668	2330	2901	3542	5339	6266	10153
5	PAG	MOL	669.452	242.847	−0.36151	173.0	–	1484	2117	2741	3535	6345	8156	18757
5		OPN	661.434	250.600	−0.50781	82.3	(7) 95	1674	2646	3729	5258	11740	16630	53191
6		MMV	193.794	77.343	0.09530	19.9	–	350	407	446	482	556	585	668
6		OPN	194.915	80.472	0.05088	18.2	(6) 82	366	432	480	525	623	663	786
6		MME	5.36830	0.40380	0.03810	18.6	–	360	435	492	550	689	751	969
6		OPN	5.37352	0.41913	−0.03141	18.0	(7) 97	368	447	507	567	710	774	998
6	LOG	MOL	225.069	49.643	−0.08024	19.7	–	344	405	452	501	625	683	902
6		OPN	222.698	53.671	−0.15198	16.0	(4) 60	363	442	508	580	777	878	1301
7		MOL	72.670	60.935	−0.14309	20.9	–	234	320	391	469	683	791	1238
7		OPN	69.492	61.054	−0.27199	11.6	(17) 142	259	381	494	629	1062	1314	2593
7		MPD	4.40899	0.93576	−0.75429	21.2	–	269	406	527	665	1056	1257	2088
7		OPN	4.51265	0.80294	0.01951	12.9	(15) 157	255	374	479	598	939	1117	1872
7	LOG	MOL	96.701	43.595	−0.26479	22.3	–	227	314	394	488	785	957	1819
7		OPN	93.038	45.880	−0.39338	10.1	(29) 254	253	384	516	687	1320	1742	4345
8		MOL	106.538	42.321	−0.12686	9.7	–	217	273	320	371	507	574	846
8		OPN	105.907	38.949	−0.23170	9.6	(1) 9	221	291	353	426	647	771	1358
8		MML	4.82973	0.41880	0.40433	9.7	–	217	275	323	375	516	586	870
8		OPN	4.83029	0.46171	0.02776	7.4	(3) 59	227	282	326	370	481	532	718
8	PAG	MOL	123.158	30.011	−0.25348	11.8	–	211	270	322	384	577	687	1227
8		OPN	124.751	32.826	−0.27250	9.1	(3) 40	224	291	352	426	659	795	1486
9		MMV	472.973	355.577	−0.27754	89.5	–	1584	2305	2976	3785	6379	7905	15700
9		OPN	488.439	431.984	−0.17485	61.4	(8) 83	1680	2340	2906	3540	5340	6284	10382
9		MPD	6.36414	0.84715	−0.60666	84.5	–	1701	2483	3160	3916	6007	7064	11339
9		OPN	6.36414	0.94710	−0.12772	55.0	(1) 9	1925	2921	3807	4815	7677	9156	15279
9	PAG	MOL	643.642	284.979	−0.28267	112.0	−	1512	2111	2664	3031	5473	6738	13256
9		OPN	643.642	313.477	−0.28267	82.3	(1) 9	1598	2258	2867	3599	5956	7348	14517
10		MMV	68.104	61.520	−0.69011	155.1	−	400	789	1296	2111	6471	10457	51308
10		OPN	64.609	28.076	−1.19579	62.7	(10) 94	387	1117	2536	5791	39629	90785	1.4106
10		MML	4.62216	1.06880	0.41776	170.0	−	415	763	1153	1694	3837	5329	14799
10		OPN	4.56416	1.17500	0.29390	71.3	(5) 36	446	841	1287	1904	4332	6004	16361
10	LOG	MOL	97.204	58.803	−0.59523	193.8	−	364	653	1000	1521	3986	6026	23743
10		OPN	80.8544	29.823	−1.17626	63.3	(18) 170	392	1121	2522	5697	37875	85625	1.3106
11		MMV	653.307	326.064	−0.53163	435.4	−	2069	3399	4922	7116	16724	24165	82090
11		OPN	647.115	217.322	−0.86285	239.4	(24) 197	2151	4374	7696	13730	54049	98018	712207
11		MML	6.77948	0.64206	1.12598	464.7	−	2069	3315	4662	6498	13755	18888	53440
11		OPN	6.83418	0.69789	0.42785	245.6	(17) 176	2328	3471	4551	5859	10031	12452	24405
11	GVE	MOL	800.681	288.286	−0.49667	527.8	−	1949	3034	4231	5908	12921	18150	56505
11		OPN	770.339	204.980	−0.88059	241.6	(15)155	2149	4360	7704	13851	55856	102475	775362
12		MMV	389.809	317.042	−0.50729	254.6	−	1722	2931	4289	6211	14380	20544	66581
12		OPN	443.176	288.938	−0.58068	245.1	(16)164	1784	3133	4742	7140	18305	27412	104528
12		MMV	6.27776	0.92300	0.13929	286.3	−	1740	2700	3589	4638	7804	9537	17309
12		OPN	6.39346	0.81139	0.17226	248.8	(13)162	1713	2594	3410	4379	7345	8996	16629
12	PAG	MOL	567.972	292.512	−0.39767	336.2	−	1595	2436	3290	4406	8534	11300	28491
12		OPN	605.449	328.265	−0.48604	255.8	(3) 30	1895	3095	4408	6233	13764	19315	59312
13		MOL	1360.919	595.786	−0.05831	104.6	–	2794	3456	3971	4504	5822	6428	8625
13		OPN	1336.472	604.967	−0.12056	70.6	(10) 125	2900	3698	4351	5056	6932	7858	11550
13		MMV	7.35932	0.45244	0.16003	89.2	–	2807	3483	4005	4543	5868	6476	8683
13		OPN	7.36468	0.47102	0.02658	74.0	(17) 171	2890	3618	4184	4771	6227	6900	9364
13	LN3	MOL	1588.111	406.465	−0.20775	114.3	–	2720	3418	4023	4714	6744	7847	12889
13		OPN	1584.220	434.086	−0.25198	66.2	(7) 108	2858	3699	4455	5345	8104	9680	17404
14		MMV	34716	13.742	−0.40480	4.6	–	85	125	166	219	421	557	1413
14		OPN	34.777	13.907	−0.45370	3.0	(7) 74	89	135	184	251	518	708	2005
14		MML	3.77705	0.49605	0.85605	6.6	–	85	118	150	188	309	381	745
14		OPN	3.79532	0.53169	0.20937	3.1	(7) 78	89	117	141	166	236	271	411
14	LN3	MOL	41.296	11.623	−0.38044	7.8	–	81	113	145	186	336	434	1026
14		OPN	41.308	12.602	−0.47430	2.9	(12) 126	90	135	183	250	521	718	2111
15		SEX	2003.078	831.726	−0.21273	267.4	–	4404	5814	7060	8496	12756	15087	25828
15		OPN	2026.598	935.595	−0.17413	232.5	(6) 68	4604	6031	7253	8624	12507	14542	23365
15		MML	7.79066	0.46651	0.30729	254.4	–	4451	5736	6798	7953	11059	12607	18866
15		OPN	7.79009	0.50601	0.03126	223.4	(7) 126	4626	5892	6892	7939	10581	11820	16438
15	LN3	MOL	2357.902	619.836	−0.30074	303.7	−	4288	5657	6940	8505	13648	16748	33184
15		OPN	2433.709	702.022	−0.27764	258.1	(5) 68	4559	6016	7355	8961	14095	17110	32518
16		MOL	195.995	54.827	0.11901	4.7	−	304	342	367	390	437	454	503
16		OPN	196.590	56.643	0.12102	4.2	(4) 86	308	347	373	396	444	462	511
16		MML	5.36596	0.27474	−0.14776	5.3	–	303	341	368	394	450	473	546
16		OPN	5.36446	0.29216	−0.04168	4.1	(3) 52	310	355	387	418	488	518	618
16	PT3	MOL	216.532	33.904	−0.09604	6.9	−	300	343	377	412	505	549	719
16		OPN	216.972	35.451	−0.10079	6.3	(4) 61	304	350	386	424	523	571	755
17		MMV	1628.807	996.848	−0.57129	836.9	−	6195	10732	16097	24045	60616	90152	336240
17		OPN	1616.945	1421.410	−0.44506	675.4	(20) 276	7118	11683	16557	23166	49158	67510	190924
17		MML	7.73260	0.76133	0.85203	815.7	−	6290	10492	15061	21301	45851	63053	175998
17		OPN	7.68163	0.95060	0.02212	611.7	(10) 150	7337	11533	15458	20126	34382	42580	78020
17	PAG	MOL	2106.257	909.645	−0.50858	1085.8	−	5786	9322	13263	18830	42460	60302	193860
17		OPN	2195.905	1188.785	−0.50726	706.0	(15) 153	6996	11601	16727	23962	54619	77735	250383
18		MOL	1354.106	411.226	0.09683	61.4	−	2186	2485	2690	2881	3274	3425	3860
18		OPN	1346.534	417.847	0.05730	55.3	(11) 98	2229	2568	2808	3036	3531	3730	4337
18		MML	7.30675	0.29893	−0.05445	60.5	−	2181	2501	2730	2953	3457	3671	4380
18		OPN	7.30704	0.31356	−0.01055	54.8	(4) 39	2226	2578	2834	3086	3664	3913	4755
18	PT3	MOL	1509.599	257.393	−0.10948	64.9	−	2149	2488	2759	3047	3800	4167	5603
18		OPN	1504.580	268.004	−0.13962	56.7	(6) 86	2194	2577	2890	3231	4155	4620	6530
19		SEX	85.404	126.713	−0.59493	218.2	−	685	1301	2043	3160	8458	12845	50915
19		OPN	78.052	197.718	−0.52828	152.5	(30) 257	933	1732	2644	3956	9676	14089	48253
19		MML	4.78295	1.48007	0.10623	160.8	−	807	1681	2718	4203	10282	14564	41466
19		OPN	4.92462	1.59587	−0.06368	132.6	(5) 46	1050	2171	3458	5242	12065	16576	42118
19	LN3	MOL	145.161	116.174	−0.58924	235.1	–	668	1231	1901	2904	7615	11490	44792
19		OPN	159.423	126.657	−0.70133	169.5	(3) 21	822	1656	2746	4511	14071	22909	115314
20		MOL	185.436	55.216	0.18829	7.8	–	287	318	338	355	388	388	399
20		OPN	184.502	56.305	0.16552	7.4	(7) 89	290	324	346	366	403	416	451
20		MMM	5.30009	0.29080	−0.43105	7.8	–	290	331	360	388	451	478	566
20		OPN	5.29866	0.30391	−0.07483	7.4	(5) 74	295	338	369	399	467	496	591
20	GVE	MOL	205.577	32.887	−0.05494	8.0	–	282	320	348	378	449	482	600
20		OPN	205.398	34.361	−0.06724	7.5	(3) 49	287	327	358	390	470	507	644
21		MMV	1136.232	375.284	−0.29940	102.7	–	2342	3149	3914	4852	7937	9797	19636
21		OPN	1138.408	425.841	−0.25562	83.6	(1) 9	2434	3246	3989	4872	7628	9210	17014
21		MML	7.21845	0.40700	0.77811	111.8	–	2345	3061	3691	4413	6534	7686	12929
21		OPN	7.22440	0.43891	0.13107	79.6	(8) 96	2421	3018	3487	3977	5213	5794	7968
21	LN3	MOL	1301.039	296.947	−0.33790	134.3	–	2269	2994	3696	4574	7593	9489	20167
21		OPN	1318.203	332.770	−0.34981	93.0	(10) 118	2419	3258	4079	5114	8726	11023	24219
22		MOL	188.371	82.858	−0.09563	13.9	–	396	498	580	667	891	999	1412
22		OPN	186.696	90.853	−0.09092	11.5	(5) 30	414	524	612	706	946	1060	1496
22		MMV	5.39146	0.46596	0.11666	12.7	–	399	498	575	654	850	940	1268
22		OPN	5.39286	0.48836	0.00813	11.0	(9) 97	411	518	601	687	902	1001	1365
22	GVE	MOL	220.547	57.723	−0.23256	16.7	–	386	492	586	695	1025	1209	2086
22		OPN	220.547	63.495	−0.23256	13.5	(1) 9	403	519	623	742	1105	1308	2273
23		MOL	342.811	107.694	−0.05301	25.0	–	600	718	810	904	1135	1241	1621
23		OPN	329.147	117.360	−0.10033	21.6	(6) 91	625	772	890	1015	1341	1498	2106
23		MMM	5.95790	0.33555	0.34764	23.8	–	596	701	779	857	1041	1123	1406
23		OPN	5.96422	0.34782	0.10830	18.4	(9) 113	610	725	812	899	1110	1205	1542
23	LOG	MOL	383.728	73.255	−0.20427	23.7	–	587	712	819	942	1301	1495	2378
23		OPN	381.324	76.095	−0.27097	14.5	(6) 75	610	765	907	1076	1613	1925	3507
24		MOL	1695.071	594.815	0.26634	51.2		2702	2976	3138	3272	3502	3574	3736
24		OPN	1687.454	607.700	0.25752	48.7	(5) 56	2725	3012	3183	3326	3571	3649	3827
24		MPD	7.50196	0.34210	−0.78476	54.6	–	2793	3246	3571	3887	4598	4899	5890
24		OPN	7.49805	0.35951	−0.14677	50.0	(6) 93	2842	3324	3670	4008	4769	5082	6156
24	PT3	MOL	1905.918	339.906	−0.01024	65.6	–	2661	3004	3256	3505	4086	4339	5189
24		OPN	1904.117	351.197	−0.01525	62.6	(4) 65	2689	3048	3312	3576	4193	4462	5377
25		MMV	425.699	403.393	−0.67640	286.2	–	2562	5019	8180	13221	39714	63594	302482
25		OPN	501.829	501.411	−0.55541	206.3	(7) 92	2749	4934	7484	11219	28068	41450	149948
25		MMV	6.43847	1.10027	0.08350	304.9	–	2562	4315	6046	8191	15158	19208	38805
25		OPN	6.38270	1.22503	0.00709	165.5	(5) 45	2841	5066	7362	10307	20369	26467	57562
25	PAG	MOL	653.192	398.602	−0.51895	453.1	–	2287	3882	5673	8223	19187	27557	91326
25		OPN	720.342	460.704	−0.57561	212.5	(10) 84	2755	4906	7439	11192	28519	42565	160487
26		MOL	169.825	39.034	0.03898	7.9	–	254	287	311	334	385	406	472
26		OPN	172.115	40.304	0.02645	7.7	(12) 131	260	296	322	347	403	427	502
26		MMV	5.22410	0.24629	0.13407	7.6	–	255	286	309	331	380	401	470
26		OPN	5.22655	0.25159	0.05087	7.2	(11) 114	257	290	314	338	390	413	488
26	LOG	MOL	185.141	25.224	−0.14524	7.2	–	250	287	317	350	440	485	673
26		OPN	185.141	27.746	−0.14524	6.5	(1) 9	257	297	330	367	465	515	722
27		MOL	264.123	93.736	−0.03176	16.3	–	483	580	654	728	908	988	1267
27		OPN	260.254	92.497	−0.09044	13.5	(20) 184	491	603	693	788	1032	1148	1590
27		MMV	5.69544	0.38280	0.04381	15.8	–	486	582	654	727	899	976	1244
27		OPN	5.70070	0.38211	0.04334	14.0	(11) 108	489	587	662	737	917	998	1285
27	GVE	MOL	298.941	63.007	−0.19039	15.1	–	471	574	662	762	1048	1201	1879
27		OPN	298.941	69.308	−0.19039	12.9	(1) 9	488	602	699	808	1123	1291	2037
28		SEX	271.602	93.018	0.00843	14.1	–	479	565	629	691	835	896	1096
28		OPN	268.694	94.484	−0.03379	11.8	(7) 71	490	588	663	739	922	1004	1290
28		MMV	5.71768	0.36916	0.11273	12.4	–	488	582	652	722	888	962	1220
28		OPN	5.72233	0.36126	0.02357	12.3	(4) 61	486	577	645	713	874	946	1194
28	LOG	MOL	308.338	61.857	−0.15437	11.3	–	470	562	638	722	953	1071	1568
28		OPN	308.338	68.042	−0.15437	10.9	(1) 9	486	588	671	764	1018	1148	1694
29		MOL	21.178	2.704	0.57722	0.333	–	24.6	25.1	25.4	25.5	25.7	25.8	25.8
29		OPN	21.157	2.935	0.66494	0.252	(4) 46	24.6	25.0	25.2	25.4	25.5	25.5	25.6
29		MML	3.07058	0.11604	−1.20543	0.420	–	24.4	25.0	25.3	25.5	25.9	25.9	26.1
29		OPN	3.06430	0.13545	−0.23489	0.260	(3) 38	25.4	26.9	27.8	28.7	30.5	31.1	33.2
29	GVE	MOL	22.031	1.324	0.15284	0.444	–	24.5	25.4	25.9	26.4	27.3	27.7	28.6
29		OPN	22.026	1.467	0.19819	0.293	(3) 40	24.6	25.5	26.0	26.5	27.3	27.5	28.2
30		MOL	41.793	11.095	0.07426	1.5	–	65	73	79	85	97	102	116
30		OPN	41.445	11.363	0.03287	1.3	(10) 98	66	76	83	90	105	112	132
30		MMV	3.82453	0.27009	0.14311	1.4	–	65	74	80	86	101	107	127
30		OPN	3.82584	0.27985	0.02164	1.3	(5) 67	66	75	82	88	104	110	132
30	GVE	MOL	46.034	7.031	−0.12331	1.4	–	64	73	81	89	112	123	167
30		OPN	45.908	7.343	−0.15104	1.0	(6) 62	65	76	85	95	122	135	193
31		MOL	58.959	13.476	0.04642	1.6	–	88	99	107	115	132	139	160
31		OPN	59.519	12.980	0.02113	1.7	(3) 29	88	100	108	116	135	143	168
31		MML	4.16632	0.23395	0.19732	1.7	–	87	99	107	115	134	142	170
31		OPN	4.16678	0.24590	0.01540	1.5	(3) 61	88	99	107	115	132	139	162
31	PAG	MOL	64.207	8.672	−0.14059	2.3	–	87	99	109	120	150	165	228
31		OPN	64.609	8.889	−0.14059	2.2	(2) 14	88	100	111	122	153	168	232

La distribución LOG se aplicará a los 31 registros procesados, pero en el análisis de resultados se revisará con mayor acuciosidad estos dos grupos de registros.

Ajuste de la distribución Logística Generalizada mediante momentos L

Este modelo probabilístico tiene tres parámetros: ξ(ubicación), α (escala) y k (forma). La variable x fluctúa así: − ∞ < x ≤ ξ + α/k si k > 0, de − ∞ < x < ∞ si k = 0 y de ξ + α/k ≤ x < ∞ si k < 0. Incluye como caso especial a la distribución Logística cuando k = 0, sus funciones de densidad y de distribución de probabilidades son (Hosking y Wallis, 1997):

Las soluciones inversas son:

donde F es probabilidad de no excedencia. Las expresiones de los parámetros de ajuste son:

Ajuste de la distribución Logística Generalizada mediante optimización numérica

Las distribuciones general de valores extremos (GVE) y Log-Pearson tipo III (LP3) se ajustaron mediante optimización numérica para minimizar el error cuadrático medio y el error absoluto medio. Los resultados muestran (Campos, 2001; 2002b) similitud en las predicciones alcanzadas con cada enfoque, además de que se observa una correspondencia numérica entre los valores mínimos de tales errores que son alcanzados en cada registro. Debido a lo anterior, se consideró suficiente contrastar la distribución logística generalizada (LOG) minimizando únicamente el error cuadrático medio, usualmente conocido como error estándar de ajuste (EEA). Nuevamente, este proceso se realizó con base en el algoritmo de múltiples variables no restringidas de Rosenbrock (Kuester y Mize, 1973; Campos 2003), considera como variables a optimizar sus tres parámetros de ajuste, al igual que en el modelo GVE, cuyos valores iniciales fueron los del método de momentos L. En cambio, en la distribución LP3 tales variables de ajuste corresponden a los estadísticos logarítmicos, media, desviación estándar y coeficiente de asimetría corregido, es decir: Ym, Sy y g_c (Campos, 2002b).

Resultados y discusión

Resumen de resultados

En el cuadro 2 para cada registro procesado hay seis renglones de resultados, los dos primeros proceden de Campos (2001) y corresponden a los parámetros de ajuste (u, α, k), EEA y predicciones con periodos de retorno 10, 25, 50, 100, 500, 1 000 y 10 000 años obtenidas con la distribución GVE, con uno de los cuatro métodos de ajuste, el que condujo al EEA mínimo y con el ajuste mediante optimización numérica (OPN), indicando, en la columna 8 del cuadro 2, los números de etapas y evaluaciones de la función objetivo (EEA) realizadas; en la columna 3 se indica el método de ajuste (MA): momentos L (MOL), optimización numérica (OPN), máxima verosimilitud (MMV), sextiles (SEX), momentos en el dominio logarítmico (MML), mezcla de momentos (MMM), máxima entropía (MME) y promedios diversos (MPD). Los siete periodos de retorno citados, cubren los diversos dimensionamientos y/o revisiones hidrológicas de las obras hidráulicas.

De manera similar, en los renglones 3 y 4 de cada registro se presentan idénticos resultados para la distribución LP3, pero utilizando alguno de sus seis métodos de ajuste y el de OPN. Finalmente en los renglones 5 y 6 de cada registro están los resultados de la distribución LOG, en este caso, ajustada mediante el método de momentos L (ecuaciones 16 a 20) y de OPN.

El algoritmo de OPN únicamente falló en los registros 19, 25 y 31 al ajustar la distribución LOG, lo cual se corrigió limitando el número de etapas permitido a la última en que se tenían resultados consistentes.

Análisis global de resultados

En el cuadro 2 se presenta un contraste global de los resultados obtenidos para los tres modelos probabilísticos probados (GVE, LP3 y LOG), concluyéndose:

• 1)

  En todos los casos, con el método de optimización numérica (OPN), el EEA es reducido más allá del mínimo obtenido con los procedimientos estadísticos;

• 2)

  Las tres distribuciones conducen a valores del EEA del mismo orden de magnitud, ya sea a través de los métodos estadísticos o con el de OPN;

• 3)

  Lo mismo se puede decir para sus parámetros de ajuste, los cuales no cambian radicalmente con el método de ajuste;

• 4)

  Respecto a las predicciones, en general, sus magnitudes son bastante coincidentes en periodos de retorno bajos (< 50 años), incluso en ciertos registros hasta los periodos de retorno elevados (>1,000 años), tal es el caso de los registros 2, 6, 9, 16, 18, 20, 22, 26, 27, 28 y 31;

• 5)

  En registros que presentan valores extremos dispersos (outliers), sus predicciones en los periodos de retorno altos (> 1,000 años) varían notablemente, como en los registros 10, 11, 12, 17 y 25.

Las observaciones globales del cuadro 2 destacan que la distribución LP3 es mucho menos flexible en la búsqueda del EEA mínimo a través del método de OPN, como se muestra por la similitud entre sus predicciones en los periodos de retorno de 1,000 y 10,000 años, las cuales casi siempre resultaron similares con el método estadístico y el de OPN. Lo contrario ocurre con las distribuciones GVE y LOG, las cuales casi siempre conducen a predicciones bastante dispersas en los periodos de retorno citados, con el método estadístico de ajuste y con la OPN.

Análisis específico de resultados

Para los ocho registros donde es recomendable la distribución LOG se observa (cuadro 2) que sus EEA mínimos son plenamente coincidentes con los de los modelos GVE y LP3. También son similares las predicciones de los tres modelos en los periodos de retorno reducidos, pero en general resultan superiores las de la distribución LOG en relación con las otras dos, en los periodos de retorno de 1 000 y 10 000 años. Cuando el modelo LOG no es el más conveniente, por ejemplo en los registros 2, 8, 9 y 31, sus EEA mínimos son mayores que los obtenidos con las distribuciones GVE y LP3 y también sus predicciones resultan superiores en los periodos de retorno elevados.

Conclusiones

La aplicación de las tres distribuciones de probabilidad contrastadas (general de valores extremos, Log-Pearson tipo III y logística generalizada) es recomendable en los análisis probabilísticos de crecientes y de otros datos hidrológicos extremos, debido a la consistencia o similitud numérica que presentan todas sus predicciones en los periodos de retorno reducidos (< 50 años), sin importar el método de ajuste. La distribución logística generalizada ofrece una opción probabilística adecuada o conveniente a los registros con valores grandes del cociente L de curtosis (τ₄), tanto en los análisis probabilísticos locales como regionales. En registros que presenten valores extremos dispersos (outliers), la distribución logística generalizada, permitirá un ajuste muy bueno a los datos, por medio del método de optimización numérica, pero debido a ello sus predicciones en los periodos de retorno elevados serán muy grandes.