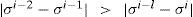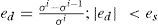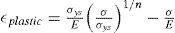Aproximación de perfiles discretos en elementos de contacto de ensambles mecánicos

Resumen

En el artículo se analizan tres tipos de aproximaciones usadas en la discretización de perfiles de superficies de contacto. El ensamble que se estudia corresponde a la unión flecha-cubo de rueda, la cual se usa comúnmente en la transmisión de movimiento rotatorio. Los perfiles que se analizan son 2D axisimétricos, los cuales representan las superficies de elementos mecánicos de revolución. El proceso de análisis consiste en: a) simular la geometría nominal ideal sin claros en la región de contacto, b) obtener la convergencia de esfuerzos de contacto para la geometría nominal en la interfaz flecha-aro y c) adicionar claros a la geometría y variaciones en el perfil de contacto a nivel de ondulación. Las variaciones del perfil se obtienen de mediciones de diámetro de los elementos de unión en sus regiones de interés. El estudio se centra en el análisis de variaciones de esfuerzos de contacto, generados por diferentes representaciones de las superficies discretas. Para este análisis se consideran mediciones que indican variaciones de diámetro en dirección axial, esa variación del diámetro se ajusta mediante curvas Bezier y spline. Se indica la influencia de las aproximaciones en la discretización de zonas de contacto de los modelos simulados, mediante el método de elementos finitos.

Abstract

The article examines three types of approximation used for the discretization of contact surface profiles. The assembly under study corresponds to a hub-shaft connection, which is commonly used for the transmission of rotational motion. The profiles that are analyzed are 2D axisymmetric and represent the surfaces of the mechanical elements. The analysis process consists of: a) simulating the ideal nominal geometry without clearances in the contact region, b) obtaining a convergence of contact stresses for the nominal geometry ring-shaft interface, and c) adding clearances to the geometry and changes in the profile contact, at the surface waviness level. The variations of the profile are obtained from measurements of the diameter of the connecting elements within the regions of interest. The study focuses on the analysis of variations of contact stresses generated by different representations of the discrete surfaces. For this analysis, variations in diameter measurements are considered, as are Bezier and spline curve fitted to these variations. The influence of the approximations on the discretization of the contact zones of the finite element models is indicated.

Introducción

Para el análisis del problema de contacto mecánico existen diversas representaciones de las superficies. Como ejemplo característico se tienen las curvas usadas en el diseño geométrico asistido por computadora (CAGD por sus siglas en inglés), que se usan en conjunto con el método de elemento finito (FEM) para analizar contacto (Jacobi, 2009; Gout et al., 2008). Entre las curvas comúnmente usadas en la representación de superficies se encuentran las Bezier y spline, por su conveniencia y simplicidad de aplicación. En la práctica es complicado especificar una curva inicial a priori con un número adecuado de puntos de control, de forma que se pueda obtener una aproximación satisfactoria a un perfil de superficie dado (Yang et al., 2004). Un tópico de interés para reducir el gasto computacional es reducir la cantidad de información representada por el número de datos de los puntos medidos (Flöry, 2009; Flöry y Hofer, 2010), y sustituirla por una aproximación de las superficies. Para representar superficies de contacto en FEM se usan elementos discretos, cuyo proceso en sí mismo tiene problemas inherentes a la discretización, que se manifiestan en desviaciones de los ajustes de perfiles continuos mediante elementos discretos. En adición, se presenta el problema de establecer un tamaño adecuado de los elementos discretos en contacto que representen adecuadamente la superficie.

La geometría nominal supuesta en las superficies de contacto de elementos de ensamble, en principio fácil de representar en sistemas CAD, difiere del perfil de contacto de elementos mecánicos (Chen et al, 2008). La variación en el perfil tiene componentes de distintas magnitudes, las cuales tienen que estar contenidas en la zona de tolerancia del elemento. Las variaciones del perfil de las superficies comúnmente se caracterizan en órdenes de ondulación y rugosidad, las cuales, en función de las dimensiones nominales de las piezas, se encuentran en magnitudes de micrómetros.

Los datos obtenidos de mediciones de rugosidad y ondulación pueden usarse como base en la representación de perfiles de contacto. Sin embargo, dado que en simulaciones numéricas de contacto se requieren relacionar características dimensionales de las superficies de contacto con el tamaño del elemento finito, surge la necesidad de aproximar la superficie medida o su perfil, mediante elementos discretos. Generalmente la representación discreta se hace con aproximación o interpolación de los puntos medidos y se relaciona con los nodos que forman las mallas discretas (Wang et al., 2006). Este proceso implica modificaciones del perfil de la superficie, una causa común de esto es que la ubicación de los puntos medidos no coincide con la posición de los nodos de la superficie discreta (Dan y Lancheng, 2006). En consecuencia, se presentan modificaciones del perfil, porque por un lado las mediciones son función del sistema de medición y por otro, el espacio entre nodos se obtiene en un proceso independiente iterativo de refinamiento de malla.

La representación discreta de superficies tiene como inconveniente que en problemas de análisis de contacto no basta con la geometría nominal. Por otro lado, las mediciones de piezas mecánicas presentan un carácter casi aleatorio, lo cual complica su representación mediante curvas. Como alternativa, es práctica común usar interpolaciones entre puntos predefinidos y pueden realizarse mediante curvas Bezier o splines (Cheng et al, 2007; Chen et al, 2008; Zhao et al, 2009). La primera da como resultado un polinomio de grado n–1 (n es el número de puntos en la interpolación). La característica principal que la hace aplicable es que guardan relación física con los puntos medidos. Su punto inicial y final coinciden con los medidos y el resto presenta un doblez dentro del rango de las mediciones (szwedowicz et al, 2006) que limitan el ajuste. En la interpolación mediante splines, los resultados son similares a los obtenidos con grandes matrices de datos, pero requiere solamente el uso de polinomios de bajo grado. Esto evita características indeseables en polinomios de grados elevados, como oscilaciones. Las curvas Bezier y spline se usan para aproximar geometrías complejas, como es el caso de perfiles aleatorios de contacto que se obtienen de superficies de elementos mecánicos.

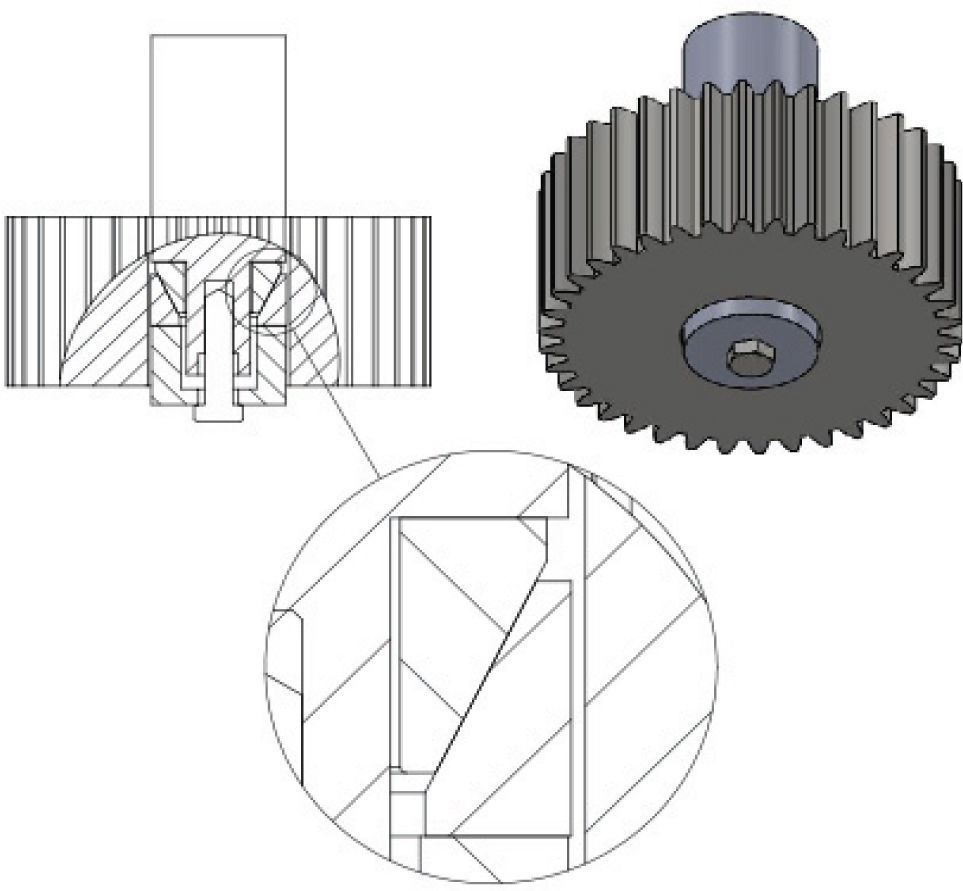
El presente artículo se enfoca al análisis de la representación de superficies discretas en problemas de contacto por el método de elemento finito, y su influencia en la distribución de esfuerzos. Para esto, se simula una unión representativa flecha cubo, con elementos deformables como interfaz de unión. La unión considerada corresponde a un engrane, una flecha y con un par de aros cónicos deformables. La unión flecha cubo se usa ampliamente en la industria, ya que en general la principal fuente de movimiento y potencia corresponde a un sistema rotatorio y motores eléctricos, en la mayoría de los casos. El tipo particular de unión usada en el estudio, que se describe en la sección de unión mecánica, se seleccionó tomando en cuenta su configuración axisimétrica, lo cual elimina en principio la concentración de esfuerzos a causa de cambios bruscos de sección o de su geometría. Por lo tanto, las concentraciones de esfuerzo se relacionarán con las características de contacto y con la discretización de la superficie.

El análisis inicial considera la geometría nominal de la unión, sin claros. Dicha configuración se usa para obtener la convergencia de la presión de contacto entre flecha y aro interno, región de interés para el estudio, porque es donde se presenta el menor radio de deslizamiento de las superficies. Posteriormente, se modifica la geometría del modelo discreto para incluir la zona de tolerancia que corresponde a un ajuste E7/h6 (sección 2). Con el ajuste de las piezas, se establece el claro máximo del ensamble. Adicional al claro se incluye la modificación del perfil, para lo cual se consideran tres condiciones: a) se usan puntos obtenidos de mediciones, para ajustarlos al perfil de contacto se usa interpolación lineal; b) se emplean los puntos de medición para interpolaciones utilizando curvas Bezier; y c) se repite el proceso con spline de tercer orden (spline comúnmente usada en interpolación). El resultado de cada curva se aplica por separado al perfil nominal con claro de la unión mecánica, para analizar su influencia en deformaciones y esfuerzos. Como parte de los resultados se presenta el refinamiento de malla y las distribuciones de esfuerzos de contacto para las diferentes aproximaciones del perfil.

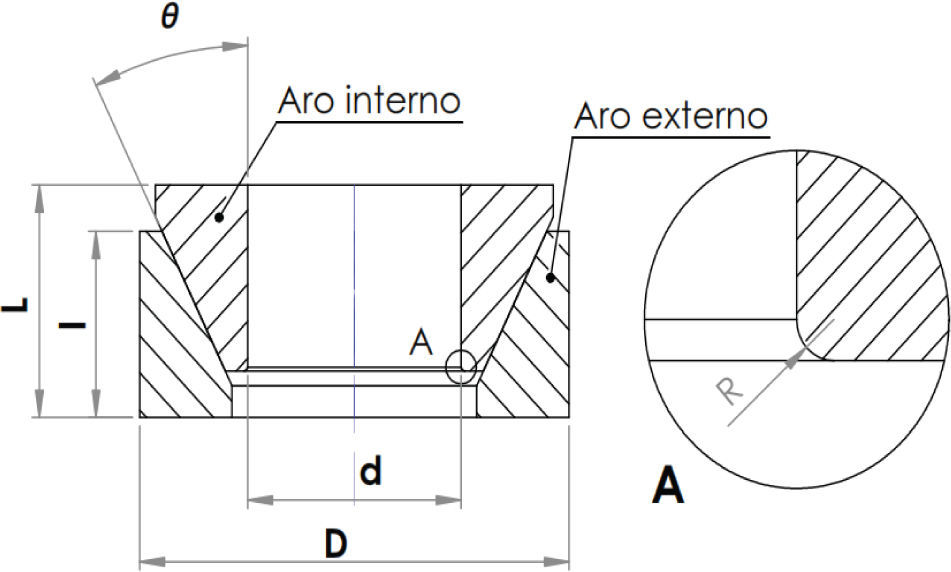
Unión mecánica

La unión mecánica considerada es una flecha-cubo de rueda con un par de aros cónicos en la interfaz de unión. La figura 1 muestra un esquema del par de aros, su geometría corresponde a Ringfeder RfN S8006 20 × 25 mm, los cuales tienen longitud axial (L) de 6.3 mm, longitud axial de aro (1) de 5.3 mm, ángulo de conicidad (θ) de 16.7°, diámetro externo (D) de 25 mm, diámetro interno (d) de 20 mm, y ajuste E7/f7. En el modelo discreto la geometría del cubo de rueda corresponde a un engrane ondrives G3-25, con diámetro interno de 25 mm, diámetro externo de 50 mm, longitud axial de 50 mm y ajuste H8 en el agujero. La flecha del modelo discreto se considera maciza de longitud axial igual a la del cubo, diámetro externo de 20 mm y ajuste h6.

Figura 1.

Esquema de un par de aros cónicos elásticos deformables, donde A es la región del radio R = 0.2 mm

La figura 2 representa una sección de la unión mecánica con aros deformables. Para el análisis se considera de interés la región de contacto entre el aro interno y la flecha. Dado que las concentraciones de esfuerzo de contacto adquieren su valor máximo en las discontinuidades del contacto, se usa un radio R de 0.2 mm en el aro interno en su sección más delgada (figura 1), lo cual permite suavizar la discontinuidad del contacto y evitar singularidades. En la sección transversal más gruesa del aro no se considera esa modificación, ya que como se confirma más adelante el esfuerzo de contacto en esa región no es comparable al de la sección de menor espesor.

Figura 2.

Representación esquemática de la unión con aros cónicos deformables

Para simular el proceso de ensamble de la unión mecánica se restringe el movimiento axial a un aro, y al otro, se le aplica fuerza de compresión en dirección axial, que incrusta un aro en el otro. Esto genera deformación radial en ambos aros y se logra el contacto entre las piezas. La resistencia portante del ensamble es función de la fuerza de apriete axial aplicada a los aros, ya que la deformación radial de los aros se relaciona con la presión que ejercen sobre el cubo de rueda y la flecha. En la práctica, la restricción de movimiento generalmente se logra con una modificación del diámetro del cubo o de la flecha (figura 2), generando un asiento para un aro.

La geometría de revolución de la unión mecánica en el modelo discreto, permite usar elementos finitos axisimétricos. El eje del sistema axisimétrico coincide con el eje geométrico de la flecha. Se restringen los desplazamientos axiales del aro externo, flecha y cubo de rueda. La presión se aplica al aro interno, lo cual provoca deformación radial y esfuerzo de contacto entre las superficies.

Refinamiento de malla

Para el análisis de refinamiento de malla se considera el pico de esfuerzo en la región de contacto entre aro interno y flecha, que se ubica donde el aro interno tiene menor espesor radial. Los elementos simulados tienen el espesor radial de una pieza mecánica real, solamente se restringe el movimiento axial, y no se restringe movimiento en dirección radial. El comportamiento del material se considera isotrópico con endurecimiento por deformación. Todas las superficies en contacto cumplen las siguientes condiciones: los pares en contacto tienen los mismos esfuerzos y deformaciones para la misma posición. La fuerza de fricción se limita a una porción μ de la fuerza normal en presencia de deslizamiento, y disminuye en ausencia de deslizamiento. Las restricciones de contacto garantizan que en todos los pares de contacto las presiones son positivas, esto se revisa en cada simulación para prevenir penetración inicial de las superficies de contacto.

En la discretización de la unión, para el proceso de refinamiento de malla y simulación de esfuerzos de contacto con la interpolación de las curvas medidas, Bezier y spline, se usan elementos axisimétricos CAX4 (Abaqus, 2010). La malla en las regiones de contacto se refina sistemáticamente dividiendo en 4 nuevos elementos a cada elemento del refinamiento previo. Fuera de la región de contacto de la flecha y aro interno, se conservan los elementos usados en la discretización inicial.

Para monitorear las condiciones de contacto se usa la definición superficie-nodo. Se adicionan mediante Abaqus^® los elementos de contacto para establecer la interacción de contacto y la identificación de las potenciales zonas de contacto. Para todas las modificaciones de perfil se revisa que no existan concentraciones de esfuerzo al inicio de la simulación; esto se logra con la eliminación de interferencia entre superficies al inicio del proceso de simulación.

La malla que se toma como “inicial” en la primera aproximación para el proceso de refinamiento se muestra en la figura 3, representa los pares de aros, la flecha y el cubo de rueda. Por simplificación del contacto, se elimina el cambio de diámetro de la flecha y se restringe el movimiento axial de la base del aro externo mediante condiciones de frontera de sus nodos. La fuerza de apriete, aplicada al aro interno para lograr la unión entre cubo y flecha, tiene el mismo valor para los diferentes refinamientos de malla usados en el proceso de convergencia de esfuerzos de contacto. La fuerza axial de presión usada en la configuración nominal ideal, es decir sin claros, es 18 kN. De acuerdo con Ringfeder (2007) esa presión garantiza una adecuada carga portante de la unión cuando no se presentan claros en la interfaz de contacto.

Figura 3.

Discretización con malla inicial de la unión flecha-cubo de rueda, donde: a) geometría discreta completa y b) ampliación de la región de los aros cónicos, A indica la región del pico de esfuerzos

El número de refinamientos requeridos para la convergencia de esfuerzos de contacto se consideró en relación al pico de esfuerzo máximo de contacto en la interfaz flecha –aro interno, en la región indicada como A en la figura 3.

Los datos obtenidos del pico de esfuerzo de contacto en los respectivos refinamientos se sustituyen en la ecuación (1), usada para obtener la convergencia (Beisheim y Sinclair, 2008):

donde el i se refiere al refinamiento actual, i − 1 al refinamiento previo y así sucesivamente. Este procedimiento de verificación de convergencia ha mostrado ser efectivo para problemas de contacto (Sinclair et al., 2002). Se considera que el criterio descrito por la ecuación (1) es preferido sobre otros donde solamente se comparan resultados de 2 refinamientos sucesivos. En conjunto con la equación (1), se considera cubierto el criterio de convergnecia si se cumple que la diferencia de discretización (e_d) es menor que el error predefinido (e_s). En análisis de esfuerzos se considera el nivel de exactitud como: e_s = 1% es excelente, e_s = 5% es bueno, y e_s = 10% es satisfactorio (Beisheim y Sinclair, 2008). El error estimado de la discretización en refinamientos sucesivos se calcula con la ecuación (2).

La longitud característica de los elementos finitos en el modelo discreto en la configuración base fue de 0.05 mm. En cada refinamiento sucesivo se conservan al menos 2 hileras secuenciales de elementos finitos de las mismas dimensiones en la región de contacto. Esto se logra ya que cada elemento en la región de contacto se divide en 4 nuevos elementos en el refinamiento posterior, formando dos hileras idénticas de elementos en la región de contacto. En el subsecuente refinamiento solamente la hilera en contacto se divide, logrando dos nuevas hileras con la longitud del elemento finito igual a la mitad del refinamiento previo. Los elementos finitos se orientan para que dos de sus lados sean paralelos a la interfaz inicial de contacto. Al inicio del proceso de cálculos de cada refinamiento se verifica que no exista penetración ni presión de contacto, esto previene posibles penetraciones generadas por el aumento de nodos en la región de contacto en cada refinamiento.

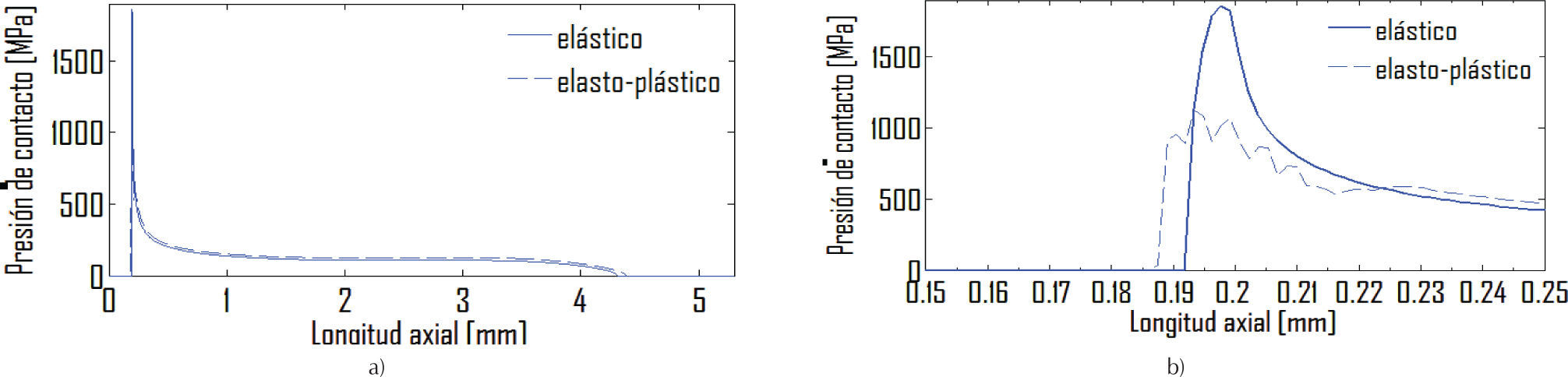
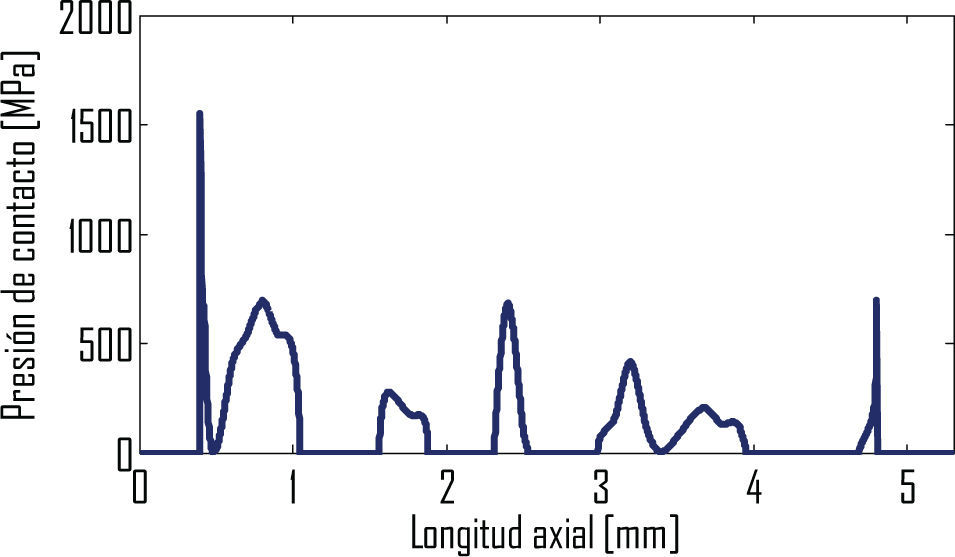
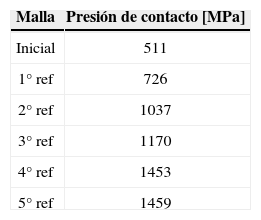
Las ecuaciones 1 y 2 permiten establecer el número mínimo requerido de refinamientos. Los valores picos de esfuerzo obtnenidos en refinamientos secuenciales de la unión mecánica se presentan en la tabla 1. Con el 5o refinamiento realizado se obtuvo e_d = 0.4% (ec. 2 y tabla 1). La figura 4 muestra la curva y el pico de esfuerzo de contacto entre el aro interno y la flecha para los refinamientos 4o y 5o. El eje horizontal de la figura 4 considera la longitud axial total del aro interno (l = 5.3 mm, ver figura 1).

Tabla 1.

Pico de esfuerzo de contacto entre la flecha y el aro interno para diferentes refinamientos [MPa]

Malla	Presión de contacto [MPa]
Inicial	511
1° ref	726
2° ref	1037
3° ref	1170
4° ref	1453
5° ref	1459

Figura 4.

Presión de contacto entre flecha y aro interno para los refinamientos 4 y 5 (tabla 1), donde: a) representa la curva total de contacto del aro y b) es una ampliación de la región del pico de presión de contacto, “i” corresponde al 5o refinamiento

La ubicación del radio R de 0.2 mm en el aro, región A de la figura 1, corresponde a la ausencia de contacto cercano al origen (figura 4). En la región del primer contacto (cerca del origen) se presenta el pico de esfuerzo de contacto, como consecuencia de la discontinuidad que se aprecia de la geometría del aro interno (figura 1) y la ampliación del pico de esfuerzo en la figura 4. En el extremo grueso del aro interno, dada la magnitud de la fuerza axial de pariete (18 kN), no se logra contacto en toda su longitud axial (Szwedowicz y Bedolla, 2007). El contacto del aro se termina aproximadamente a 5 mm del origen, que corresponde a la proximidad del extremo grueso del aro interno.

Una vez que el refinamiento de malla permitió la convergencia de los picos de esfuerzo de contacto, se utiliza ese tamaño de elemento para modificar los perfiles de contacto.

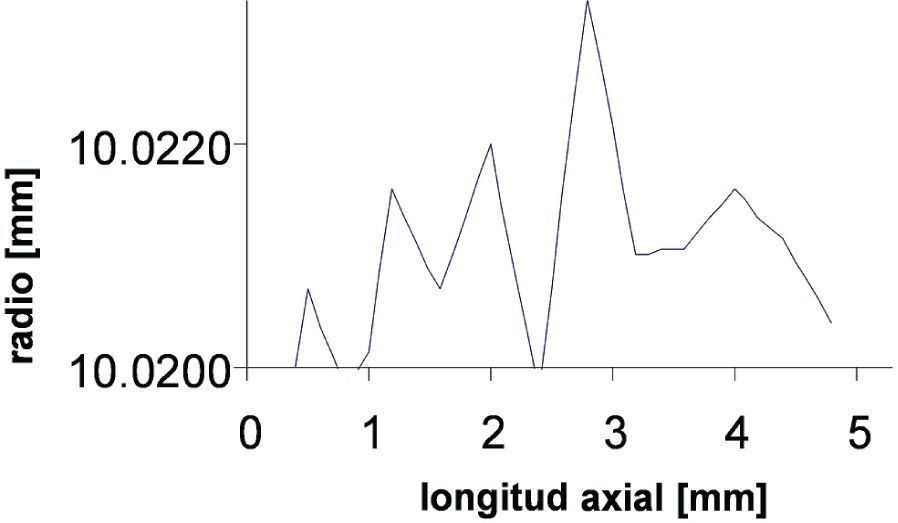
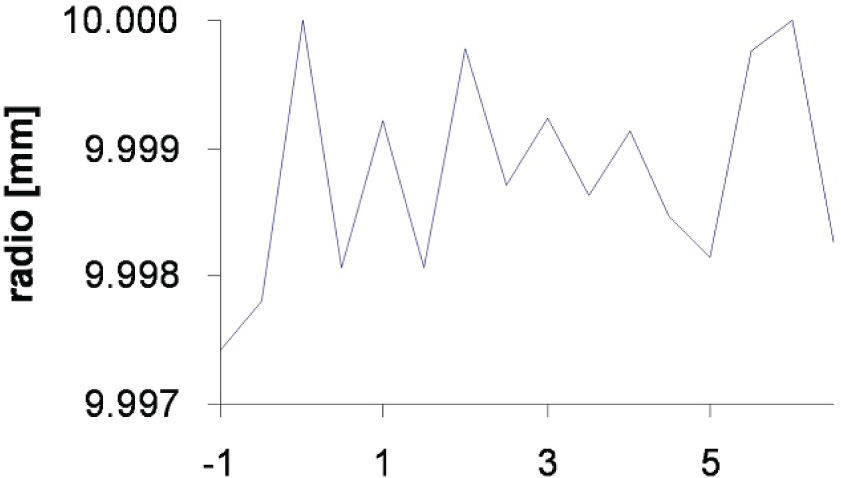
Modificación de perfiles de contacto

Para analizar las variaciones de contacto en el modelo discreto, a causa de representación de irregularidades de superficies de la unión, se consideran diferentes tipos de interpolación. Como paso inicial se adiciona al modelo discreto el claro entre las superficies de flecha-aro interno y entre aro externo-cubo, lo cual modifica el contacto nominal de la unión, pero la característica nominal de cada superficie se mantiene. Posteriormente, se consideran las variaciones de diámetro a lo largo del eje axial en la región de contacto entre el aro interno y la flecha. Las variaciones que se consideran para la simulación se obtuvieron a partir de mediciones con una máquina de medición por coordenadas en 3D Mitutoyo Apex 710. Por la magnitud de las variaciones obtenidas de las mediciones, se considera que éstas se encuentran en el orden de ondulaciones de las superficies, la máquina no cuantifica rugosidad. En función de lo anterior, la magnitud que se considera para el análisis está en el orden de las ondulaciones superficiales. Las variaciones de diámetros se incluyen en el modelo discreto como parte de la región de tolerancia de las piezas.

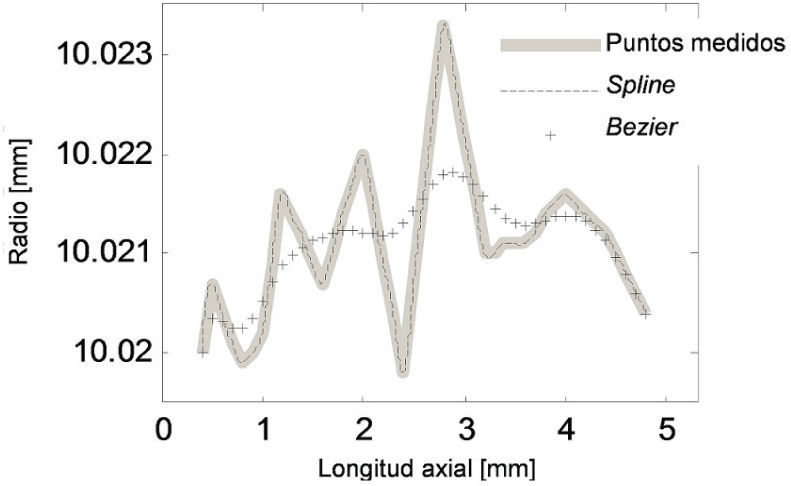
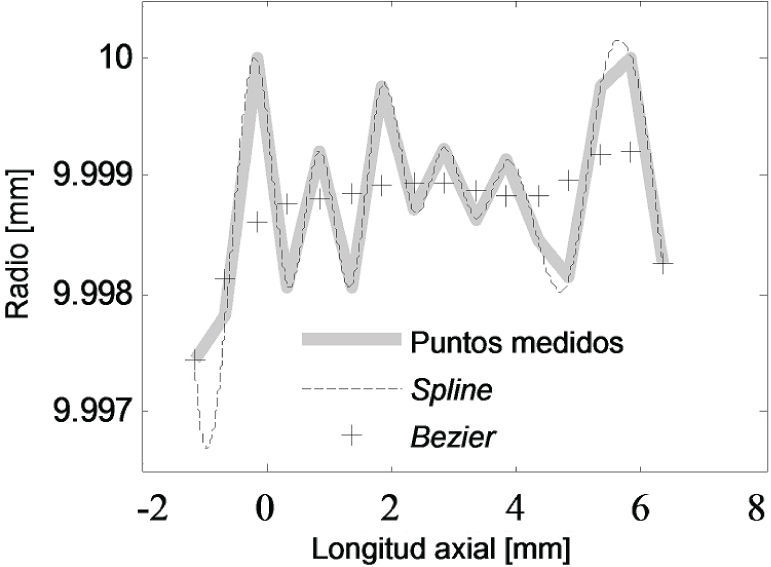
La región de claro para la unión mecánica está dada por sus ajustes, que son: 20 E7/h6 mm entre flecha y aro interno y 25 H8/f7 mm entre aro externo y cubo. Si se consideran características axisimétricas de los elementos de la unión, así como el concepto de máxima condición de material (MMC) los claros radiales entre las superficies de contacto se determinan de los diámetros máximos y mínimos. Si bien, el claro resultante del ajuste se obtiene en función del diámetro, para efectos prácticos del modelo axisimétrico se usan variaciones radiales. Para este caso, los radios considerados se indican a continuación: Radio máximo del eje: 10 mm, radio mínimo del aro interno: 10.02 mm, radio máximo del aro externo: 12.49 mm, radio mínimo del cubo: 12.5 mm. Las variaciones que modifican el perfil de contacto en la región de interfaz de la flecha y aro interno, así como los claros se esquematizan en la figura 5. Para efectos de análisis y de representación de la modificación en las superficies, se considera un sistema coordenado local, cuyo eje horizontal (axial) es paralelo al eje axial del modelo y el eje vertical (radio) coincide con el borde del aro interno (figura 5). Tomando como referencia el sistema local de la figura 5, las modificaciones que se usan para cambiar el perfil de contacto en la configuración sin deformar se presentan en las figuras 6 y 7, para el aro interno y para la flecha. Con el objeto de analizar la interacción de contacto entre flecha y aro interno, se considera en el sistema local que el eje radial se desplaza con el borde del aro interno.

Figura 5.

Esquema de modificación de geometría donde:

• a)

  representación de claro (0.02 mm entre aro y flecha) y

• b)

  ampliación de los aros y modificación del perfil de contacto entre aro interno y flecha

Figura 6.

Perfil del aro cónico interno a partir de puntos medidos

Figura 7.

Perfil de la flecha a partir de puntos medidos

La modificación en el modelo discreto en función de los puntos medidos se realiza para tres condiciones de aproximación, mediante interpolación lineal de nodos de la malla y puntos medidos, posteriormente se incluyen dos consideraciones comúnmente usadas en representaciones gráficas, mediante curvas Bezier y mediante curvas spline. Las modificaciones del perfil de contacto, tanto para el aro como para la flecha, se presentan en las figuras 8 y 9. Estos perfiles se incluyen por separado, uno a la vez en la malla con claros del modelo discreto de la unión.

Figura 8.

Perfiles modificados para la superficie de contacto del aro interno

Figura 9.

Perfiles modificados para la superficie de contacto de la flecha

Comportamiento del material

Los resultados obtenidos en las pruebas de convergencia de malla, indican que los picos de esfuerzos de contacto para la geometría nominal superan el límite elástico (figura 4) para materiales estructurales. Tomando en cuenta esa característica, para las simulaciones con los modelos discretos que incluyen claros y modificación del perfil de la superficie de contacto, se incluye comportamiento elástico y plástico con endurecimiento del material. Para aproximar el comportamiento plástico se usa la ecuación (3) y las propiedades del acero AISI 1045, que son: módulos elástico (E) 205 GPa (Matweb, 2010), límite elástico (σ_ys) 310 MPa y coeficiente de endurecimiento de 0.1736 (Özel y Zeren, 2006). Los resultados de la ecuación 3 se presentan en la figura 10.

donde

• ε_plastic es la deformación en la región plástica,

• E el módulo elástico,

• σ_ys el esfuerzo de fluencia,

• σ es el esfuerzo y

• n es el índice de endurecimiento del material.

Figura 10.

Comportamiento plástico para el material de la simulación

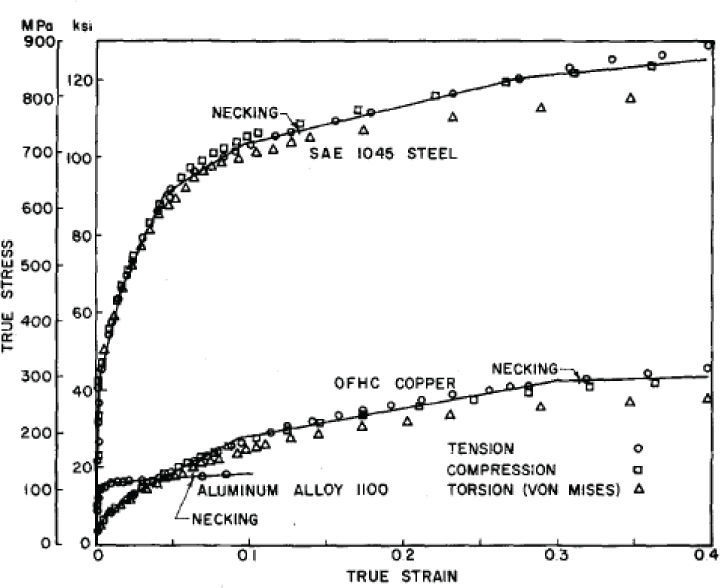
Los resultados obtenidos de la ecuación 3 presentan muy buena correspondencia con pruebas experimentales (Sidebottom y Chu, 1975), como se puede observar de la figura 11.

Figura 11.

Comportamiento plástico del material (Sidebottom y Chu, 1975)

Resultados

Los resultados corresponden a las 3 aproximaciones del perfil de contacto del aro interno y la flecha usados en el análisis. Para simular los cambios del perfil de la unión mecánica se usa el tamaño característico del elemento de contacto que se obtuvo del 5o refinamiento (tabla 1). Ese refinamiento proporciona e_d = 0.4%, lo cual se considera como un excelente nivel de exactitud. Para el análisis del esfuerzo de contacto en la unión se incluyen claros radiales para la geometría nominal en el modelo discreto axisimétrico. Posteriormente y en forma separada se incluyen las modificaciones del perfil de contacto con modificación directa con puntos medidos, interpolación mediante curva spline, e interpolación mediante curva Bezier. En las figuras 8 y 9 se observa que los puntos iniciales y finales son coincidentes para las diferentes representaciones del perfil de contacto; sin embargo, el resto de los puntos difieren, lo que produce variaciones en los resultados de esfuerzos de contacto. Para garantizar que las variaciones de los diámetros correspondan a efectos de las tolerancias de manufactura (considerada como ondulación), la región de interés se limita al rango de variaciones radiales presentado en las figuras 8 y 9. De igual manera, por esta razón no se consideran variaciones cercanas a los bordes del aro cónico donde el rebaje en las esquinas no corresponde a ondulación, sino a la característica de acabado.

Las dimensiones y geometría de la unión simulada corresponden a una flecha sólida, un par de aros Rin- gfeder RfN S8006 20 × 25 mm, y el cubo de un engrane ondrives. La fuerza de apriete aplicada en el modelo discreto con claros, al aro interno en dirección axial es 30.5 kN. El coeficiente de fricción en las superficies de contacto se considera de 0.12 (Ringfeder, 2007).

Previamente se estableció el radio mínimo del aro interno en 10.020 mm. Con el objeto de tomar en cuenta las incorporaciones de las modificaciones del perfil (figuras 8 y 9), se modifica el radio nominal del aro interno a 10.021 mm (aún dentro de su región de tolerancia), para evitar que al adicionar las modificaciones al perfil se rebase la región de tolerancia. De forma análoga para la flecha, su radio máximo es de 10 mm y se modifica a 9.999 mm. Con esa consideración se logra que las modificaciones en el perfil de la superficie de contacto sean mayor al radio mínimo del aro interno y menores para el diámetro de la flecha, correspondientes al ajuste E7/h6 (figuras 8 y 12).

Figura 12.

Representación esquemática de las modificaciones en el perfil de contacto

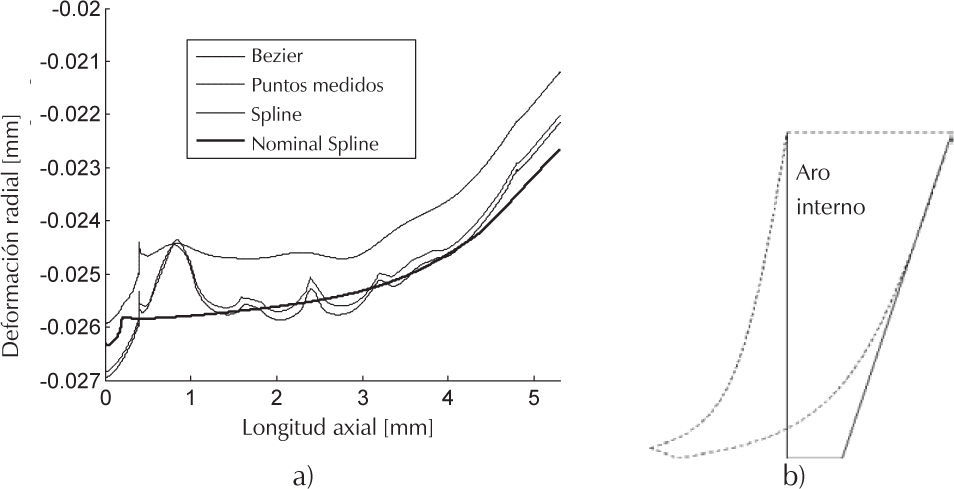
En condiciones ideales del proceso de unión, la deformación radial del aro interno se supone igual en toda su longitud axial. Sin embargo, por la geometría cónica de los aros, la porción del aro de menor espesor presenta la mayor deformación radial. La figura 13 muestra la deformación del aro interno para la configuración con claro y geometría nominal para dos condiciones: a) deformación radial del aro antes de alcanzar el contacto con la flecha y b) deformación radial con la carga total aplicada para lograr la capacidad portante en la unión. En ambos casos la deformación radial es mayor en la región de menor espesor del aro. Se aprecia que para la curva sin contacto la deformación es proporcional al espesor del aro. Para la condición con contacto la restricción cinemática que impone el contacto modifica la curva de deformación. La región con menor espesor del aro alcanza el primer contacto, en consecuencia en esta región se presenta el pico de esfuerzos de contacto para la geometría nominal, como se presenta en la figura 14. La condición anterior se presenta independientemente del tipo de comportamiento del material. Se observa que el material con deformación elasto-plástica presenta un pico de esfuerzo menor y una mayor longitud axial de contacto, en comparación con el material elástico. Adicionalmente para el material elasto-plástico, en la región del pico de esfuerzo, se presenta un conjunto de oscilaciones del valor del esfuerzo de contacto generado por la fluencia que progresivamente se alcanza en nodos consecutivos de los elementos finitos. Fuera de la región del pico de esfuerzo, el comportamiento de ambos tipos de materiales es simular. Los resultados de la simulación para el material con comportamiento elasto-plástico y claro nominal modificado son los que se usan como referencia para analizar la influencia de las aproximaciones de superficies, con variaciones en las superficies de contacto. Las figuras 15 a 17 presentan los resultados de los esfuerzos de contacto para:

• a)

  interpolación directa con puntos medidos,

• b)

  interpolación con curva spline de tercer orden,

• c)

  interpolación con curva Bezier, respectivamente.

Figura 13.

Deformación radial del aro interno en su radio interno, donde: a) curvas de deformación y b) correspondencia de los ejes en el aro interno

Figura 14.

Presión de contacto usando material con comportamiento elasto-plástico para la geometría nominal con claro, donde: a) toda la longitud del aro y b) ampliación alrededor del radio R = 0.2 mm

Figura 15.

Comportamiento plástico del material con aproximación de superficie por puntos medidos

Figura 16.

Comportamiento plástico del material con interpolación de curva spline de tercer orden

Figura 17.

Comportamiento plástico del material con interpolación de curva Bezier

Esas curvas se comparan contra la curva de la figura 14 para identificar las variaciones en las presiones de contacto a causa de la aproximación del perfil mediante las diferentes técnicas usadas.

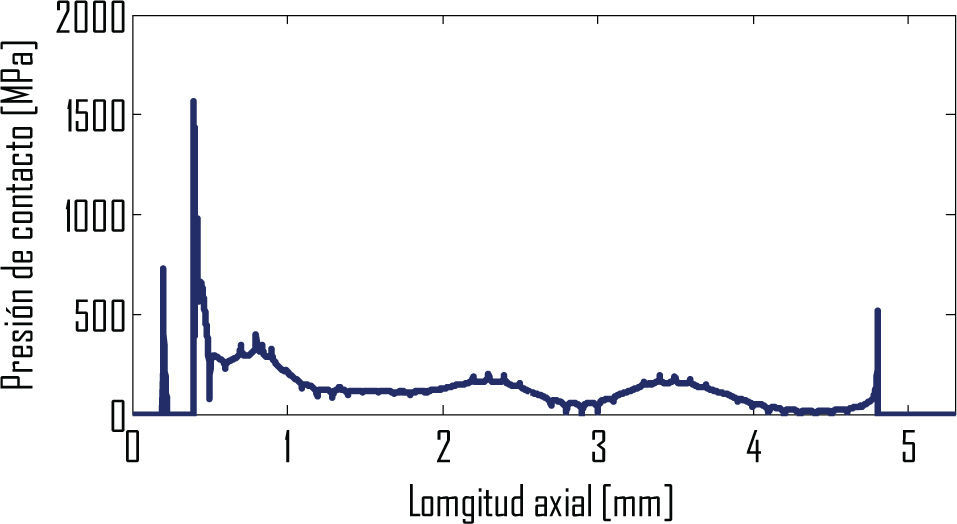
Retomando la figura 8, para los puntos medidos y la aproximación de estos con spline, las curvas son prácticamente las mismas, esto se aprecia también en los esfuerzos de contacto en las figuras 15 y 16. Sin embargo, el carácter de la figura 17 para la interpolación Bezier,muestra diferencia en las amplitudes de esfuerzos con relación a las otras dos aproximaciones. La curva de esfuerzos de contacto usando puntos medidos en la representación del perfil, muestra picos más altos que las otras dos aproximaciones. Esto se explica porque para esa aproximación del perfil de contacto no se suavizan los picos obtenidos de las mediciones, a diferencia del resultado de las aproximaciones Bezier y spline. En consecuencia, se generan valores altos de esfuerzo en ubicaciones coincidentes con esos cambios de pendiente del perfil de contacto.

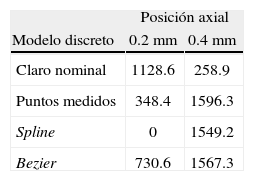
Para analizar las variaciones de las curvas de esfuerzo de contacto, se seleccionan dos ubicaciones a lo largo de la longitud axial de contacto del aro interno (figuras 14 y 17), esto es a 0.2 mm y 0.4 mm del origen. La ubicación 0.2 mm corresponde a la ubicación donde se presenta el primer contacto como función del radio R en el extremo del aro interno y su deformación radial (figura 3b, región A y figura 13). La ubicación 0.4 mm a partir del origen, corresponde al inicio de la modificación geométrica del perfil de contacto para las aproximaciones usadas (figuras 6 y 8). La tabla 2 presenta los valores de picos de esfuerzo para esas posiciones axiales, donde se obtiene que en la posición 0.2 mm el pico de esfuerzo de contacto con aproximación Bezier es 35% menor que el perfil con claros y geometría nominal, esta diferencia se explica porque en el perfil modificado la ubicación axial de 0.2 no es el inicio del contacto y en consecuencia, los esfuerzos en esa región serán menores. Para 0.4 mm la aproximación mediante curva Bezier es solamente 1.8 % menor a la obtenida con los puntos medidos. Esto sin importar que el perfil de contacto modificado se aprecie diferente en ambas aproximaciones (figura 8). Esto es un indicativo de que la aproximación con curvas Bezier es comparable con relación a los esfuerzos en las otras aproximaciones, y además mantiene correspondencia con la característica de la superficie medida de la pieza en contacto.

Tabla 2.

Pico de esfuerzo de las diferentes configuraciones [MPa]

	Posición axial
Modelo discreto	0.2 mm	0.4 mm
Claro nominal	1128.6	258.9
Puntos medidos	348.4	1596.3
Spline	0	1549.2
Bezier	730.6	1567.3

Para la aproximación con spline, el carácter de picos de esfuerzo es de menor amplitud que la interpolación con puntos medidos, pero similar en cuanto a su forma (figuras 15 y 16). Mientras que el carácter de la aproximación Bezier se aproxima a la forma del esfuerzo nominal (figuras 14 y 17), pero adiciona las concentraciones de esfuerzo atribuidas a las variaciones de diámetros (figura 8). Lo cual nuevamente presenta correspondencia con el contacto esperado (en el nominal), pero con la adición de las características particulares de la variación de superficie.

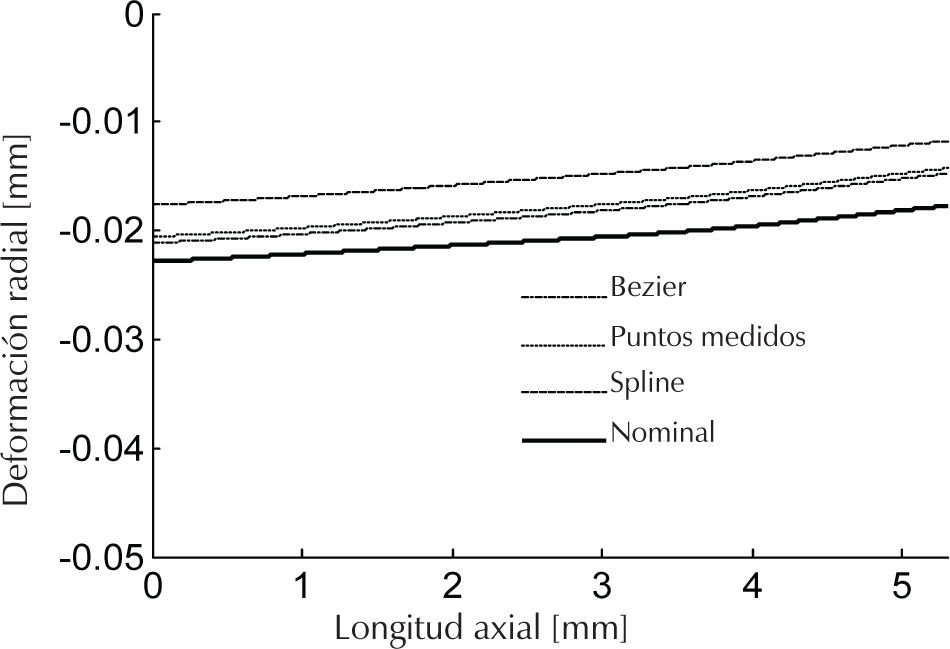
Si se considera nuevamente la esquematización de la figura 12, es claro identificar la diferencia de radios para los perfiles con interpolación de los puntos y el perfil considerado como nominal modificado. Los cambios adicionados con esa variación de radios de contacto generan que la deformación para iniciar el contacto y la deformación al final de la carga total aplicada se modifique. En la figura 18 se muestran las curvas de deformación radial del aro interno para una diferencia de carga antes de iniciar presión de contacto en la flecha. Como se esperaba, la curva que presenta la mayor deformación radial es la correspondiente a la geometría nominal, ya que ésta presenta un radio inicial constante en todo el aro interno. Como se representa en la figura 12, el claro en esa configuración es mayor que en las aproximaciones donde existe variación de radio de la región de contacto. En la figura 12 se indicia que el calor nominal de 0.02 mm se incrementa para permitir modificar las superficies de contacto, y que éstas se mantengan dentro de la zona de tolerancia. Como se observa de la figura 18, para todas las aproximaciones de superficies el primer contacto ocurre alrededor de 0.02 mm y se modifica por la aproximación que se hace en cada caso (figuras 8 y 9).

Figura 18.

Deformación radial del aro para antes de iniciar el contacto con la flecha. El signo menos obedece a qué radio interno del aro interno disminuye

La deformación radial final del aro con el total de carga de apriete aplicada a la unión (figura 19), presenta prácticamente el mismo carácter entre la curva nominal y la curva Bezier, salvo por el desfasamiento en magnitudes que corresponde a la diferencia de claro inicial de ambos perfiles de contacto. Mientras que las curvas con puntos medidos e interpolación spline presentan oscilaciones (más pronunciadas que la aproximación con Bezier) de la curva de deformación a causa de los picos en la geometría de contacto. La deformación que se presenta para la aproximación con curvas Bezier es la menor de todos los casos analizados, pero sin que esto represente cambios significativos de esfuerzo (figuras 14 y 17), para la región donde se ubica el contacto inicial del aro, en comparación con las otras aproximaciones. En la figura 19 se observa que las deformaciones están por arriba del valor del claro nominal de 0.02 mm, lo cual se esperaba por la deformación que presenta la flecha en contacto y que permite que los nodos del aro interno tengan una deformación mayor a la del claro inicial, con las restricciones que impone el contacto entre las piezas.

Figura 19.

Deformación radial final del aro interno para la carga total aplicada (30.5 kN), donde: a) deformación del aro para las diferentes aproximaciones y b) representación esquemática deformada del aro

Conclusiones

Se presentó el análisis de tres métodos diferentes de discretización de superficies de contacto para representar una unión mecánica eje cubo, la cual se realiza mediante presión y contacto. Se analizó su geometría nominal para lograr la convergencia del pico de esfuerzos, obteniéndose una exactitud en ese proceso de 0.4 %, en el 5o refinamiento de malla del modelo propuesto.

Se concluye que la aproximación de perfiles de contacto mediante curvas Bezier presenta las mejores característica, ya que en la región del pico de esfuerzo de contacto la diferencia obtenida en relación al perfil con puntos medidos es solamente 1.8 %. Mientras que para el resto de la longitud axial el perfil de la curva de esfuerzo de contacto es aproximadamente el mismo que para el caso de la geometría nominal, a diferencia de los otros dos métodos analizados. Se concluye que la representación con curvas Bezier proporciona las características relevantes de la curva de esfuerzo de contacto en la región del pico máximo de éste, y de igual manera se aproxima acorde a la curva esperada teóricamente (geometría nominal) para la zona fuera de la región del pico de máximo esfuerzo. Para esta última región, las otras aproximaciones con puntos medidos y spline modifican el perfil de la curva de esfuerzo de contacto, por los picos presentados en los perfiles de esas geometrías. La aproximación con Bezier suaviza esa región, sin eliminar las fluctuaciones de esfuerzo por la variación de diámetros, y su distribución de esfuerzo concuerda con las características correspondientes a la geometría nominal simplificada, la cual se usa comúnmente en cálculos de contacto. Las curvas Bezier mantienen relación física con la modificación de la superficie y a la vez con el carácter esperado de la región de contacto. Esta característica las hace útiles en la representación de superficies y además no se limitan a aplicaciones en 2D (o axisimétricas), sino también pueden ser extendidas a superficies o curvas 3D.

Agradecimientos

Los autores agradecen el apoyo otorgado al Fondo de Ciencia Básica Conacyt para la realización del presente trabajo dentro del proyecto Conacyt CB 102025.